Arrhenius kinetics driven nonlinear mixed convection flow of Casson liquid over a stretching surface in a Darcian porous medium

Abstract

The non-linear mixed convective heat and mass transfer features of a non-Newtonian Casson liquid flow over a stretching surface are investigated numerically. The stretching surface is embedded in a Darcian porous medium with heat generation/absorption impacts. The fluid flow is assumed to be driven by both buoyancy and Arrhenius kinetics. The governing equations are modelled with the help of Boussinesq and Rosseland approximations. The similarity solutions of the non-dimensional equations are obtained using two numerical approaches, namely fourth fifth Runge - Kutta Fehlberg method and the shooting approach. The velocity, temperature and concentration profiles are discussed for important physical parameters through various graphical illustrations. The skin friction, the non-dimensional wall temperature, and the concentration expressions were derived and analysed. The results indicate that the increasing values of linear and nonlinear convection due to temperature, nonlinear convection due to concentration, and heat of reaction increase the dimensionless wall temperature. The dimensionless wall concentration rises with the increasing values of heat of reaction, linear and nonlinear convection due to temperature, and nonlinear convection due to concentration parameters.

1. Introduction

The fluid flow along with heat and mass transport in a porous medium has gained major attention of researchers in the previous few decennaries. The thermo-physical properties of the fluid and the features of the permeability of the porous medium possess a primary role in controlling the performance of heat and mass transfer in fluids. The number of research studies in this topic has increased because of its various engineering applications, such as geophysical, crystal growth in fluids, pollutant dispersion in aquifers, petroleum reservoirs, nuclear waste repositories, chemical catalytic reactors, ground hydrology, solidification of casting, thermal and insulating engineering, etc. To predict the fluid flow in a porous space, the law of Darcy has been widely used by researchers [1]. The law of Darcy is a proportional relationship between the viscosity of fluid, the immediate expulsion rate through porous space, and the pressure drop over a certain distance. It is valid only for laminar, viscous, and slow fluid flow where the inertial effects are neglected. The advancement in porous medium studies has been summarised in the following books [[2], [3], [4], [5], [6]].

Non-Newtonian liquids are liquids that exhibit a nonlinear relationship among the shear rate and shear stress. The rheological behaviour of these liquids plays a dynamic role in many cosmetic, pharmaceutical, and chemical industries. It is very difficult to derive a single model to predict non-Newtonian liquids due to the nonlinear relationship between stress and strain movement. Several researchers have developed various mathematical models of non-Newtonian liquids, such as Walter-B [7,8], Maxwell [9], viscoelastic type [10], Casson [11], Brinkman type [12], Jeffrey [13], power law [14], second-grade [15] model, Bingham plastic [16], and Oldroyd-B [17]. Casson liquid is a subset of a non-Newtonian model that acts like an elastic solid. These liquids have infinite viscosity at zero shear rate as well as infinite shear rate at zero viscosity. Human blood, concentrated juices, honey, and lubricants are some of the Casson liquid examples [18]. The Casson property of the fluids is also important in industrial processes such as coating, manufacturing, metal spinning, biomimetics, etc. In addition to this, the theoretical investigations on mixed convection flow of non-Newtonian fluids over a stretching material problem might have enormous economic and energy saving implications for the industries that involve extrusion of molten polymers, hot rolling, food stuffs processing, paper production, and glass fibre production. The Newtonian/non-Newtonian fluid flow problems over a stretching surface in a porous medium have attracted many researchers in recent years [[19], [20], [21], [22], [23], [24]].

Bhattacharyya [25] examined the two-dimensional stagnation point flow of Casson liquid towards a stretching surface with magnetic field effects and found that Casson fluid has a thicker velocity boundary layer than Newtonian fluid. Shehzad et al. [26] investigated the 3D (three-dimensional) flow of Casson liquid in a Darcian porous medium with a uniform heat source/sink and magnetic field effects. Their investigation showed that a greater Casson value increased the skin friction coefficient. Mabood et al. [27] inspected the Casson liquid flow under MHD effects in a Darcian porous medium, taking into account of melting heat transfer and radiation, and reported that the Casson parameter enhances the heat transfer rate. The impacts of cross diffusion and a heat source on the boundary layer flow of Casson liquid in the porous medium in the presence of non-linear thermal radiation were analysed by Patel [28]. The same author [29] studied the Casson liquid flow over an oscillating plate embedded in a porous space under the effects of heat generation, hall current, and radiation. The heat and mass transport characteristics of Casson liquid over a shrinking sheet in a porous medium in the presence of a heat source/sink were examined by Awais et al. [30]. Nandkeolyar and Chamkha [31] analysed the unsteady Casson liquid flow in three-dimensional stretching material in a porous medium with Hall and MHD effects. Eldabe et al. [32] discussed the impacts of the electromagnetic field on the heat and mass transfer of Casson liquid in a porous medium.

The present study mainly focused on the mixed convection flow of Casson liquid, which is purely driven by the heat provided to the fluid due to exothermic surface reactions and non-uniform internal heat generation/absorption over a stretching surface in a Darcian porous medium. The exothermic reactions were derived and utilised by the following researchers [[33], [34], [35], [36], [37], [38]]. The derived model was dependent on the Arrhenius temperature and a first order kinetics. The forth mentioned model was successfully applied to the boundary layer flow problems over a stretching sheet [[39], [40], [41], [42], [43], [44], [45]]. Very recently, the second grade nanofluid boundary layer flow was investigated over a stretching surface that was driven by Arrhenius kinetics [46].

To the best of the author's knowledge, the problem of nonlinear mixed convection flow of Casson liquid over a stretching surface in a porous medium driven by Arrhenius kinetics, which has applications in many engineering processes as mentioned earlier, has not been considered yet. Hence in the present work, Arrhenius kinetically driven boundary layer flow of non-Newtonian Casson liquid over a stretching surface in a Darcian porous medium with the impacts of thermal radiation, non-uniform heat generation, and heat absorption. The numerical results are obtained for the governing equations through the fourth fifth Runge-Kutta Fehlberg method along with shooting technique. The results are discussed through graphical illustrations.

2. Problem formulation

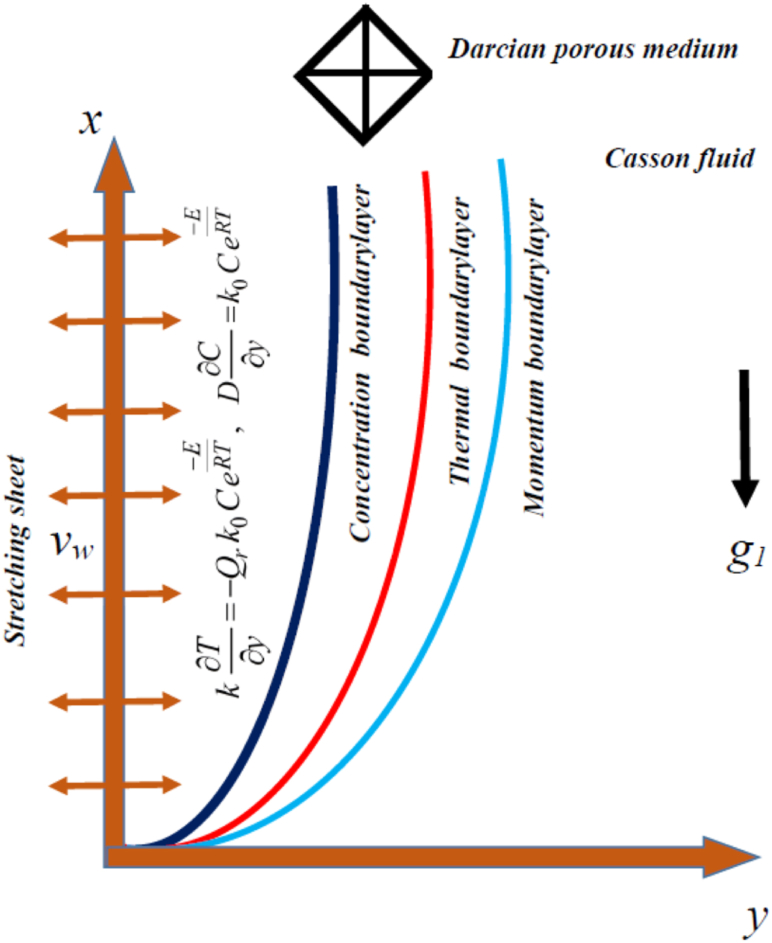
We consider the steady, incompressible, two-dimensional, nonlinear mixed convection flow of a non-Newtonian Casson liquid over a stretching surface that is embedded in a porous medium. The porous medium is considered as a Darcian porous medium. The impacts of space and temperature dependent heat generation/absorption, and Rosseland thermal radiation impacts are taken into account with negligible viscous dissipation impacts. Flow is assumed to be happening in a cartesian framework in which the x axis is taken along the surface and the y axis vertical to it (Fig. 1). The stretching surface is assumed to be at temperature T_w (ambient temperature $T_{\infty }$) and concentration C_w (ambient concentration $C_{\infty }$) with stretching velocity $u_w=a/x^{-1}$. The exothermic reaction is presumed to take place at the surface.

Fig. 1.

Physical configuration of the present problem.

The governing equations can be written under the above and Boussinesq assumptions as [[27], [28], [29], [30]].

$$\left(\frac{\partial u}{\partial x}\right)+\left(\frac{\partial v}{\partial y}\right)=0\text{,}$$ (1)

$$\frac{\partial u}{\partial x}u+v\frac{\partial u}{\partial y}=\frac{\vartheta }{{\beta }_1}\frac{{\partial }^{2}u}{\partial y^2}\left({\beta }_1+1\right)+g_1\left[{\beta }_{t2}{\left(T-T_{\infty }\right)}^2+{\beta }_{t1}\left(T-T_{\infty }\right)\right]+g_1\left[{\beta }_{c2}{\left(C-C_{\infty }\right)}^2+{\beta }_{c1}\left(C-C_{\infty }\right)\right]-\vartheta \left(1+\frac{1}{{\beta }_1}\right){\left(\frac{k_p}{u}\right)}^{-1}\text{,}$$ (2)

$$\rho c_p\left(\frac{\partial T}{\partial x}u+v\frac{\partial T}{\partial y}\right)=\frac{{\partial }^{2}T}{\partial y^2}k+Q_{ST}-\frac{\partial q_r}{\partial y}\text{,}$$ (3)

$$\frac{\partial C}{\partial x}u+v\frac{\partial C}{\partial y}=\frac{{\partial }^{2}C}{\partial y^2}D\text{.}$$ (4)

Where u and v are the velocity components along x and y axes respectively, β₁ is the Casson parameter, $\vartheta$ is the kinematic viscosity, $g_1$ is acceleration due to gravity, β_t1 is first order thermal expansion coefficient, β_t2 is second order thermal expansion coefficient, β_c1 is the first order solutal coefficient, β_c2 is the second order solutal coefficient, T is the temperature of the fluid, k_p is the permeability of the porous medium, ρ is the density of the Casson liquid, k is the thermal conductivity, C_p is the specific heat capacitance, C is the concentration of fluid, and D is the molecular diffusion coefficient.

The non-uniform heat generation/absorption can be chosen as [47].

$$Q_{ST}=u_w\left[\left(T_w-T_{\infty }\right)Q{}_1+Q{}_2\left(T-T_{\infty }\right)\right]{\left(\frac{\vartheta x}{k}\right)}^{-1}\text{,}$$ (5)

where Q₁ is the parameter for space dependent heat generation/absorption and Q₂ is the parameter for temperature dependent heat generation/absorption. It should be mentioned here that Q₁ < 0 and Q₂ < 0 represent the heat absorption case, while Q₁ > 0 and Q₂ > 0 represent the heat generation case.

Utilising the linear Rosseland formulation for radiative heat flux q_r, which can be defined as [27].

$$q_r=-\frac{4}{3}\left(\frac{\partial T^4}{\partial y}\right){\left(\frac{k_{ab}}{{\sigma }_{sb}}\right)}^{-1}\text{,}$$ (6)

where σ_sb is the constant of Stefan-Boltzmann and k_ab is the coefficient of mean absorption. The 4th power of temperature can be expressed as a linear function of temperature as follows:

$$T^4=-3T_{\infty }^4+4T_{\infty }^{3}T\text{.}$$ (7)

Invoking eqs (5), (6), (7) in (3), we get

$$\rho c_p\left(\frac{\partial T}{\partial x}u+v\frac{\partial T}{\partial y}\right)=\frac{{\partial }^{2}T}{\partial y^2}k+u_w\left[\left(T_w-T_{\infty }\right)Q{}_1+Q{}_2\left(T-T_{\infty }\right)\right]{\left(\frac{\vartheta x}{k}\right)}^{-1}+\frac{16}{3}{T}_{\infty }^3\left(\frac{{\partial }^{2}T}{\partial y^2}\right){\left(\frac{k_{ab}}{{\sigma }_{sb}}\right)}^{-1}$$ (8)

The boundary conditions for the catalytic surface are [[40], [41], [42], [43], [44], [45], [46]].

$$u-u_w=0,v-v_w=0,k\frac{\partial T}{\partial y}=-Q_r{e}^{\frac{-E}{RT}}\left(k_{0}C\right)and\frac{\partial C}{\partial y}=k_0{e}^{\frac{-E}{RT}}\left(\frac{C}{D}\right),aty=0\text{,}$$

$$u\to 0,T\to T_{\infty },C\to C_{\infty },asy\to \infty \text{.}$$ (9)

Where E is the activation energy Q_r is the exothermicity of reaction and R is gas constant.

By introducing the following dimensionless transformations [46]

$$\begin{array}{l}u=g{}^{\prime }\left(\zeta \right)ax,v=-g\left(\zeta \right){\left(a\vartheta \right)}^{1/2},\zeta =y{\left(\frac{\vartheta }{a}\right)}^{-1/2}\text{,}\\ \theta \left(\zeta \right)=\left(\frac{E}{R}\right)\left(\frac{1}{T_{\infty }^2}\right)\left(T-T_{\infty }\right)\text{and}\phi \left(\zeta \right)=\left(\frac{1}{C_{\infty }}\right)\left(C-C_{\infty }\right)\text{,}\end{array}$$ (10)

the governing equations in (2), (3), (4), (8) are transformed into the following dimensionless form and also the transformations in (10) satisfies the continuity eq. (1),

$$\left({{\beta }_1}^{-1}+1\right)g^{‴}+g{g}^{″}+\left(1+{\lambda }_{t2}\theta \right)\theta {\lambda }_{t1}+{\lambda }_{c1}\phi \left(1+{\lambda }_{c2}\phi \right)=g{\prime }^2+g\prime k_1\left({{\beta }_1}^{-1}+1\right)\text{,}$$ (11)

$$\left(1+\frac{4}{3N^{-1}}\right){\theta }^{″}+\mathrm{Pr}\theta \text{'}g+g\text{'}{Q}_1+Q_2\theta =0\text{,}$$ (12)

$$\phi {}^{″}+\phi \prime gSc=0\text{,}$$ (13)

Consequently, the corresponding boundary conditions in (9) become

$$g\left(0\right)=s,g{}^{\text{'}}\left(0\right)=1,g^{\text{'}}\left(\infty \right)=0,\frac{\theta {}^{\text{'}}\left(0\right)}{\left(1+\phi \left(0\right)\right)}=-e^{\left(\raisebox{1ex}{$\theta \left(0\right)$}\!\left/ \!\raisebox{-1ex}{$1+\epsilon \theta \left(0\right)$}\right.\right)}\alpha and\theta \left(\infty \right)=0.\frac{{\phi }^{\text{'}}\left(0\right)}{\left(1+\phi \left(0\right)\right)}=e^{\left(\raisebox{1ex}{$\theta \left(0\right)$}\!\left/ \!\raisebox{-1ex}{$1+\epsilon \theta \left(0\right)$}\right.\right)}\beta and\phi \left(\infty \right)=0\text{.}$$ (14)

Where ${\lambda }_{t1}=\left(\frac{R}{E}\right)\left(\frac{T_{\infty }^2{\beta }_{t1}}{u_w}\right)\left(\frac{g_1}{a}\right)$ is the mixed convection parameter due to temperature, ${\lambda }_{t2}=\left(\frac{R}{E}\right)\left(\frac{{\beta }_{t2}}{{\beta }_{t1}}\right)T_{\infty }^2$ is the nonlinear convection parameter due to temperature, ${\lambda }_{c1}=C_{\infty }\left(\frac{{\beta }_{c1}}{u_w}\right)T_{\infty }^2$ is the mixed convection parameter due to concentration, ${\lambda }_{c2}=\left(\frac{{\beta }_{c2}}{{\beta }_{c1}}\right)C_{\infty }$ is the nonlinear convection parameter due to concentration, $k_1=\frac{1}{k_{p}a}\left(\frac{\mu }{\rho }\right)$ is the porous medium parameter, $N=4\left(\frac{{\sigma }_{sb}}{k_{ab}}\right)\left(\frac{1}{k}\right)T_{\infty }^3$ is the radiation parameter, $\mathrm{Pr}=\left(\frac{\vartheta }{\alpha }\right)$ is the Prandtl number, $Sc=\left(\frac{D}{\vartheta }\right)$ is the Schmidt number, $\alpha =\frac{Q{k}_0}{k_c}\left(\frac{E}{R}\right)e^{\frac{-E}{R{T}_{\infty }}}\sqrt{\frac{\vartheta }{a}}\left(\frac{C_{\infty }}{T_{\infty }^2}\right)$ is the heat of reaction parameter, $\beta =\left(\frac{1}{D}\right)k_0^{}{e}^{\frac{-E}{R{T}_{\infty }}}\sqrt{\frac{\vartheta }{a}}$ is the reaction rate and $\epsilon =\left(\frac{R}{E}\right)T_{\infty }$ is the activation energy parameter.

3. Physical quantities of attention

The physical quantities on which present research focuses are the skin friction coefficient, non-dimensional wall temperature and non-dimensional wall concentration.

The shear stress at the surface of the wall is given by

$${\tau }_w=\mu \left({{\beta }_1}^{-1}+1\right){\left(\frac{\partial u}{\partial y}\right)}_{y=0}$$

The skin friction coefficient C_f can be defined as

$$\begin{array}{l}{C}_f=\frac{{\tau }_w}{\rho u_w^2}=\frac{\mu \left({{\beta }_1}^{-1}+1\right){\left(\frac{\partial u}{\partial y}\right)}_{y=0}}{\rho u_w^2}\\ \end{array}\text{.}$$

$$\begin{array}{l}{\mathrm{R}\mathrm{e}}_x^{1/2}{C}_f=g\text{'}\text{'}\left(0\right)\left({\beta }_1^{-1}+1\right)\text{.}\\ \end{array}$$

The non-dimensional wall temperature and wall concentration can be obtained from the following equations.

$$T_w=T_{\infty }+\left(\frac{R}{E}\right)T_{\infty }^2\theta \left(0\right)\text{and}{C}_w=C_{\infty }+C_{\infty }\phi \left(0\right)\text{.}$$

4. Method of solution

The governing eqs (11), (12), (13) along with the boundary conditions in (14) are numerically solved using fourth fifth Runge-Kutta Fehlberg integration scheme along with the shooting iteration approach. Runge-Kutta Fehlberg method is a numerical scheme of order two with an error estimator of order 5 that is used to solve ordinary differential equations. The steps involved in the numerical procedure are as follows:

First the boundary value problem is transformed into the following first order initial value problem:

$$y_1^{\prime }=y_2,y_2^{\prime }=y_3,y_3^{\prime }=\frac{\left[y_2^2-y_1{y}_3-{\lambda }_{t1}{y}_4\left(1+{\lambda }_{t2}{y}_4\right)-{\lambda }_{c1}{y}_6\left(1+{\lambda }_{c2}{y}_6\right)+k_1\left({{\beta }_1}^{-1}+1\right)y_2\right]}{\left({{\beta }_1}^{-1}+1\right)}$$

$$y_4^{\prime }=y_5,y_5^{\prime }=\frac{\left[-\mathrm{Pr}{y}_1{y}_5-Q_1{y}_2-Q_2{y}_4\right]}{\left(1+\frac{4}{3N^{-1}}\right)},y_6^{\prime }=y_7,y_7^{\prime }=-Sc{y}_1{y}_7\text{.}$$ (18)

with the boundary conditions

$$y_1\left(0\right)=s,y_2\left(0\right)=1,y_3\left(0\right)={\text{guess}}_1,y_4\left(0\right)={\text{guess}}_2,y_5\left(0\right)=-\alpha \left(1+y_6\left(0\right)\right)e^{\left(\raisebox{1ex}{$y_4\left(0\right)$}\!\left/ \!\raisebox{-1ex}{$1+\epsilon y_4\left(0\right)$}\right.\right)}\text{.}$$

$$y_6\left(0\right)={\text{guess}}_3,y_7\left(0\right)=\beta \left(1+y_6\left(0\right)\right)e^{\left(\raisebox{1ex}{$y_4\left(0\right)$}\!\left/ \!\raisebox{-1ex}{$1+\epsilon y_4\left(0\right)$}\right.\right)}\text{.}$$ (19)

The initial guesses (${\text{guess}}_1$, ${\text{guess}}_2$ and ${\text{guess}}_3$) are chosen, and the Runge Kutta Fehlberg method is used to integrate the first order systems. Then the computed values are compared with the boundary conditions. The shooting method is used to update the initial guesses to satisfy the boundary conditions, and the process is repeated until the results reach the preferred accuracy of 10⁻⁶.

5. Results and discussion

The set of first order ordinary differential eq. (18) and the corresponding initial conditions (19) with guess values are numerically solved using the Runge - Kutta Fehlberg method along with the shooting approach. The present numerical code is validated with those of Khan and Pop [48] and Ullah et al. [49]. The comparison results are tabulated in Table .1. An excellent agreement is observed in the $-\theta {}^{\prime }$ (0) values for various Prandtl numbers in the absence of β₁ and α = 0, β = 0, N = 0, k₁ = 0, Q₁ = 0, Q₂ = 0, Ɛ = 0, λ_t1 = 0, λ_t2 = 0, λ_c1 = 0, λ_c2 = 0 and Sc = 0. The impacts of the radiation parameter (N), porous medium parameter (k₁), space dependent heat generation/absorption parameter (Q₁), temperature dependent heat generation/absorption parameter (Q₂), heat of reaction parameter (α), reaction rate parameter (β), Casson parameter (β₁) and activation energy parameter (Ɛ) on Casson liquid velocity, temperature, and concentration profiles are plotted in Fig. 2- 13. The variation of skin friction, non-dimensional wall temperature, and concentration are illustrated in Fig. 14, Fig. 15, Fig. 16. We fixed Pr = 3, β₁ = 1, α = 0.5, β = 0.5, N = 1, k₁ = 1, Q₁ = 0.5, Q₂ = 0.5, Ɛ = 0.5, λ_t1 = 0.5, λ_t2 = 0.3, λ_c1 = 0.4, λ_c2 = 0.5 and Sc = 1 throughout the investigation when studying a particular parameter. It is worth mentioning that when ${\beta }_1\to \infty$, the present Casson liquid model is reduced to a Newtonian liquid case, the present problem is also be reduced to a problem of Casson liquid flow over a flat catalytic surface when λ_t1 = 0 and λ_c1 = 0.

Table 1.

Comparison of $-\theta {}^{\prime }$ (0) in the absence of β₁ and α=0, β=0, N=0, k₁=0, Q₁=0, Q₂=0, Ɛ=0, λ_t1=0, λ_t2=0, λ_c1=0, λ_c2=0 and Sc = 0 with boundary condition $\theta \left(0\right)=1$ and $\theta \left(\infty \right)=0$.

Pr	Khan and Pop [48]	Ullah et al. [49]	Present results
0.7	0.4539	0.4544	0.45391620
2.0	0.91130	0.9113	0.91135764
7.0	1.8954	1.8953	1.89540326
20.0	3.3539	3.3538	3.35390651

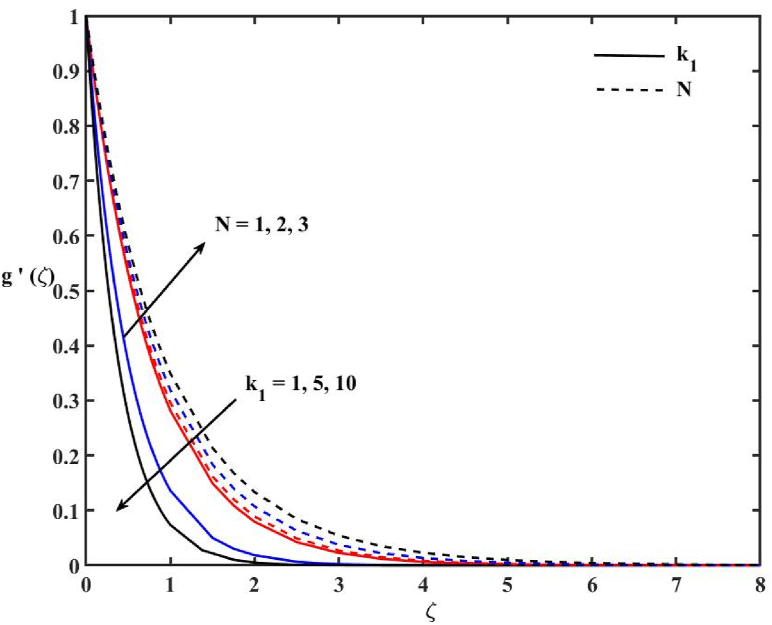
Fig. 2.

Effects of N and k₁ on velocity profile.

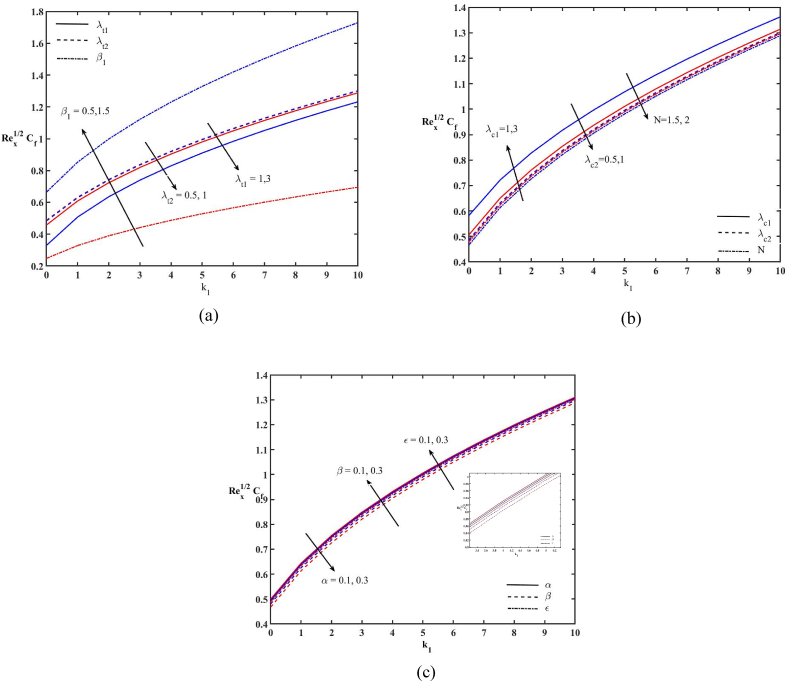
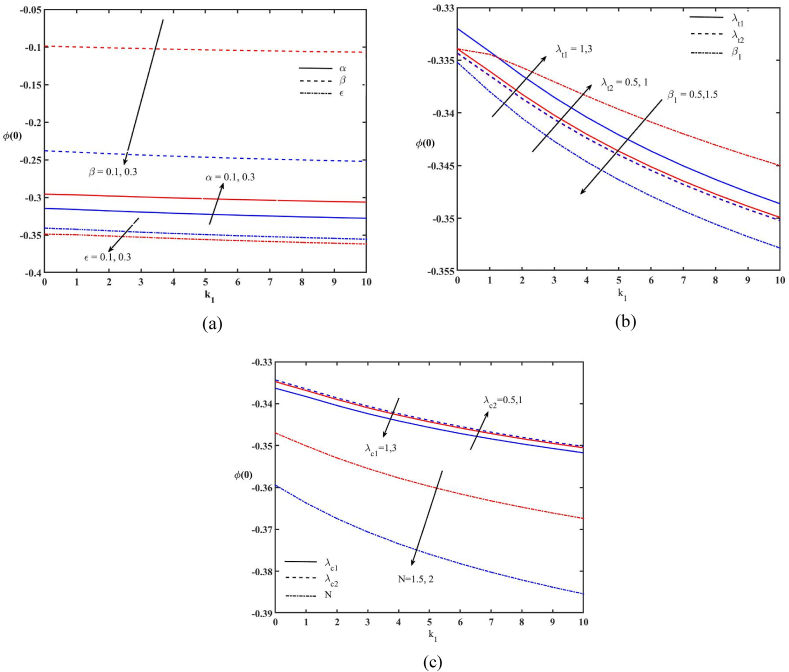
Fig. 14.

Variations of skin friction coefficient (a) Effects of λ_t1, λ_t2 and β (b) Effects of λ_c1, λ_c2 and N (c) Effects of α, β and Ɛ.

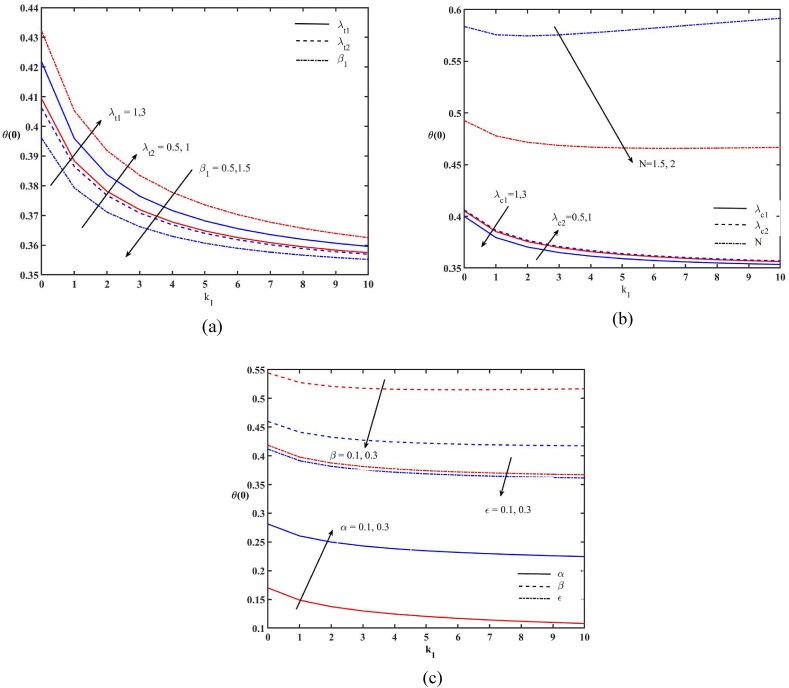
Fig. 15.

Variations of non-dimensional wall temperature (a) Effects of λ_t1, λ_t2 and β (b) Effects of λ_c1, λ_c2 and N (c) Effects of α, β and Ɛ.

Fig. 16.

Variations of non-dimensional wall concentration (a) Effects of λ_t1, λ_t2 and β (b) Effects of λ_c1, λ_c2 and N (c) Effects of α, β and Ɛ.

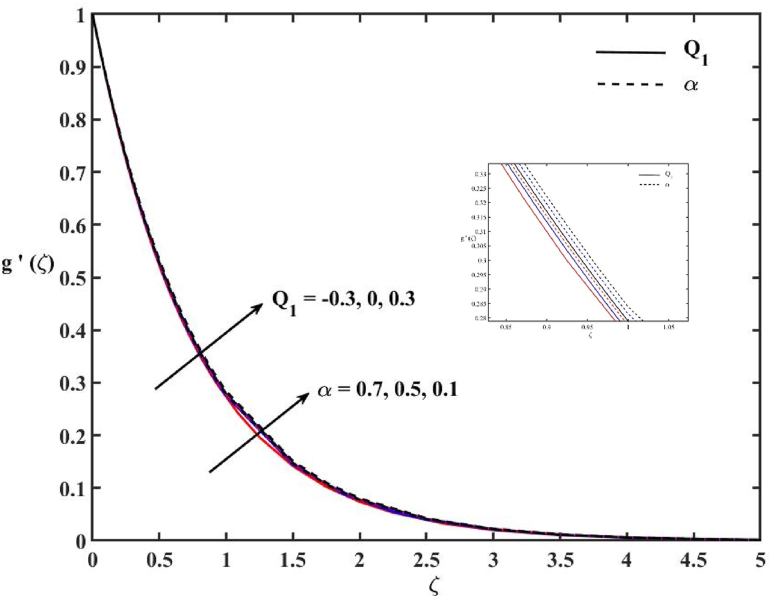
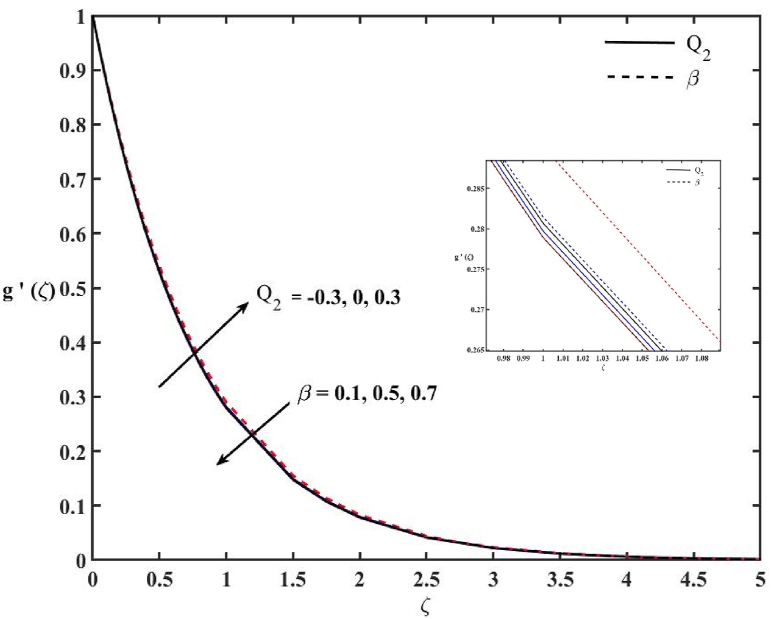
Due to the presence of concentration and thermal buoyancies in the momentum Eq. (11), the parameters N, Q₁, Q₂, α, β, and Ɛ have influence on the velocity profile of the Casson liquid. The combined impacts of N and k₁ on the Casson liquid velocity profile are represented in Fig. 2. Both N and k₁ show significant impacts on velocity profile (g '(ζ)). It is observed that the increase in N accelerates the velocity profile while the enhancement in k₁ decelerates the velocity profile of the Casson liquid. This is because the increase in N enhances the velocity boundary layer thickness. The parameter k₁ is related to the sizes of pores. From the definition of parameter k₁, one may see that the increase of k₁ leads to a decrease in the size of pores, which causes higher resistance to the Casson liquid flow inside the porous medium. Consequently, the velocity profile decreases with k₁. Fig. 3 reveals the impacts α and Q₁ on g ՛ (ζ). The positive value of Q₁ denotes the presence of space dependent heat generation while the negative value denotes space dependent heat absorption. Both Q₁ and α do not show a significant impact on g ՛ (ζ). A slight growth in the g ՛ (ζ) is traced when Q₁ > 0, and a reverse trend is observed and felt when Q₁ < 0. The reason for this is that the velocity boundary layer thickness reduces in the heat absorption case and enhances in the heat generation case. A slight enhancement is observed with the increase of the heat of reaction parameter α. The impacts of Q₂ and β on g ՛ (ζ) are demonstrated in Fig. 4. It is observed that the impacts of Q₂ are similar to those of Q₁ on the g ՛ (ζ) as explained in the earlier figure. The increase in the reaction rate β gives a diminution in g ՛ (ζ), consequently shrinking the momentum boundary layer of the Casson liquid.

Fig. 3.

Effects of Q₁ and α on velocity profile.

Fig. 4.

Effects of Q₂ and β on velocity profile.

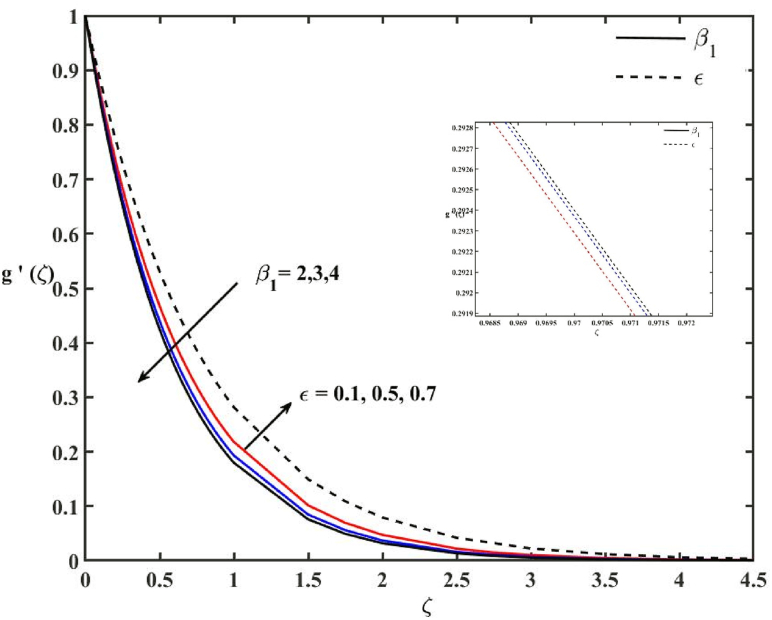
Fig. 5 shows the impacts of β₁ and Ɛ on g ՛ (ζ). The results shown in this figure came in response to a suppression in fluid velocity due to increase in β₁. An enhancement in β₁ increases the viscosity of fluid, consequently momentum boundary layer thickness and velocity decreases. An insignificant enhancement is observed in the momentum boundary layer with the activation energy parameter (Ɛ).

Fig. 5.

Effects of Ɛ and β₁ on velocity profile.

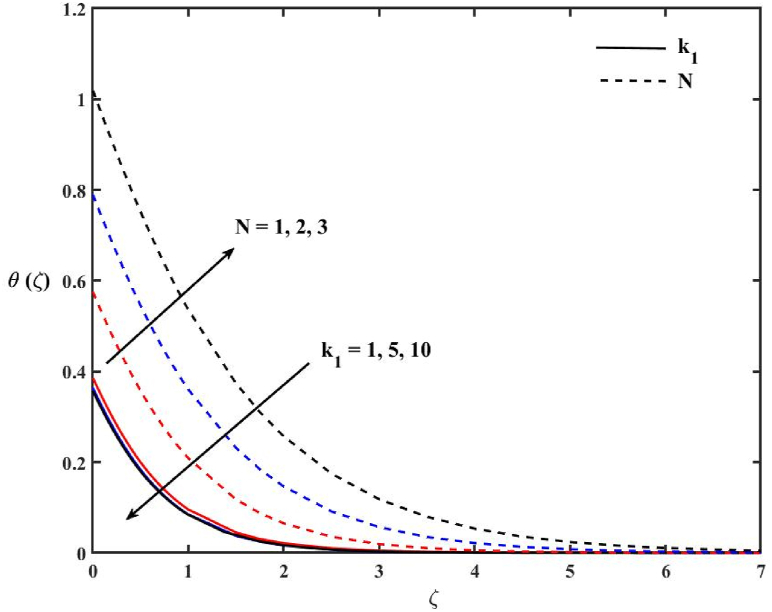
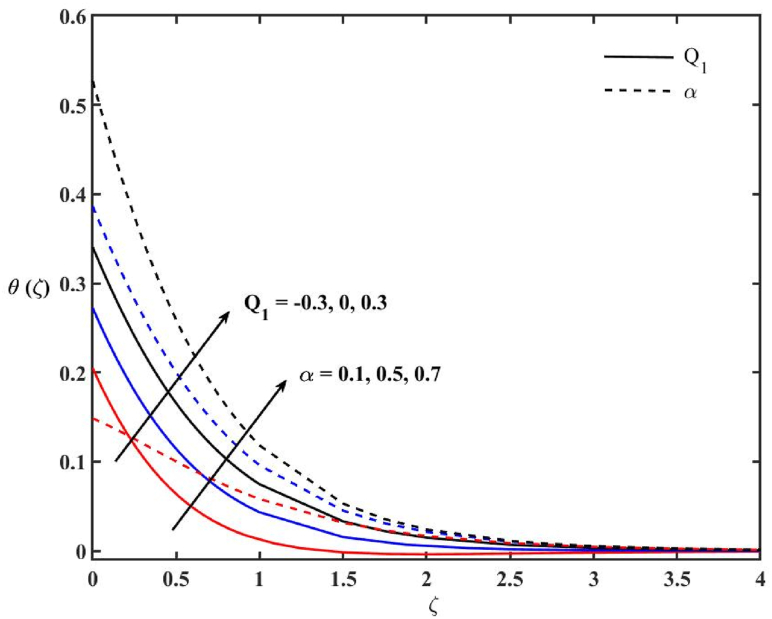
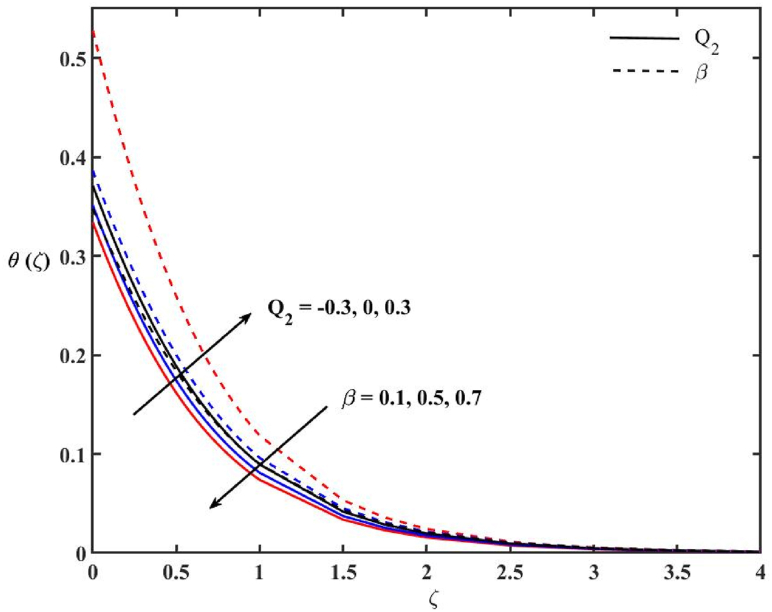
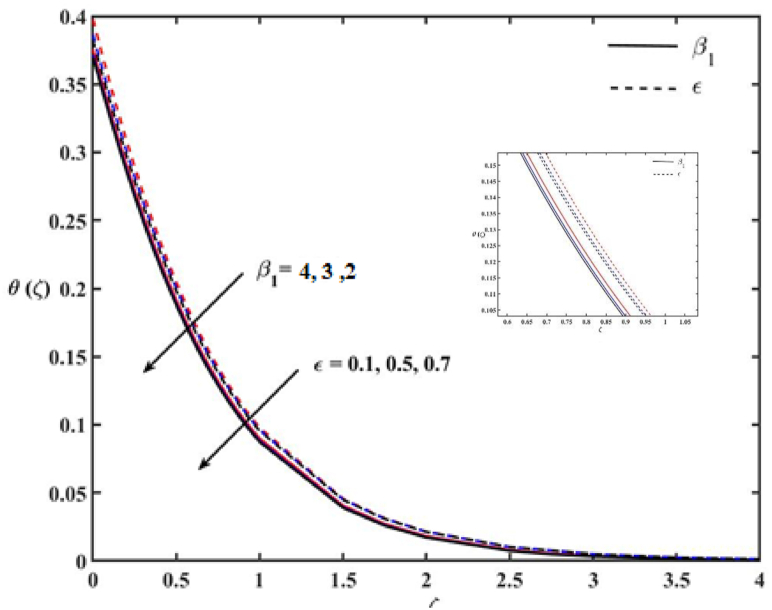
Fig. 6 indicates the impacts of N and k₁ on the temperature profile Ɵ(ζ). The increase in N enhances Ɵ(ζ). The heat transfer rate reduces with higher k₁. Hence, to enhance cooling from the stretching surface, the radiation parameter must be fixed low. A slight decrement in Ɵ(ζ) is observed with higher porous medium parameter in the catalytic surface. The impacts of α and Q₁ on Ɵ(ζ) are shown in Fig. 7. The temperature profile enhances when Q₁ > 0 and reduces when Q₁ < 0. The heat generation parameter increases the temperature of the fluid molecules; consequently, the thermal boundary layer thickness enhances and the heat absorption parameter observes the temperature from the liquid molecules and reduces the thermal boundary layer thickness. The parameter α shows a considerable impact on Ɵ(ζ). The behavior of Ɵ(ζ) is directly proportional to the heat of reaction parameter. The rising value of α increases the thermal boundary thickness. Fig. 8 displays the impacts of Q₂ and β on Ɵ(ζ). The impact of Q₂ on the temperature profile is similar to Q_1, but it is interesting to note that a good variation in thermal boundary layer is observed with Q_1. The variation of Q₂ does not show significant variation on the thermal boundary layer. The thermal boundary decreased with the increase of β. The impacts of β₁ and Ɛ on Ɵ(ζ) are exhibited in Fig. 9. It can be seen that an increase in β₁ implicating the higher viscosity of fluid, causes an increase in Ɵ(ζ) as a result of developing an ascending thermal boundary layer. With a larger value of the activation energy parameter (Ɛ), the thickness of the thermal boundary layer decreased slightly.

Fig. 6.

Effects of N and k₁ on temperature profile.

Fig. 7.

Effects of Q₁ and α on temperature profile.

Fig. 8.

Effects of Q₂ and β on temperature profile.

Fig. 9.

Effects of Ɛ and β₁ on temperature profile.

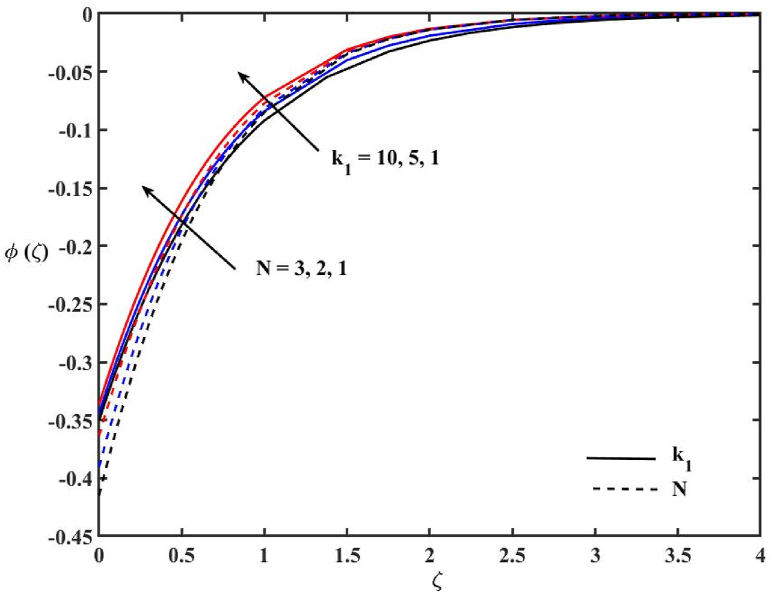
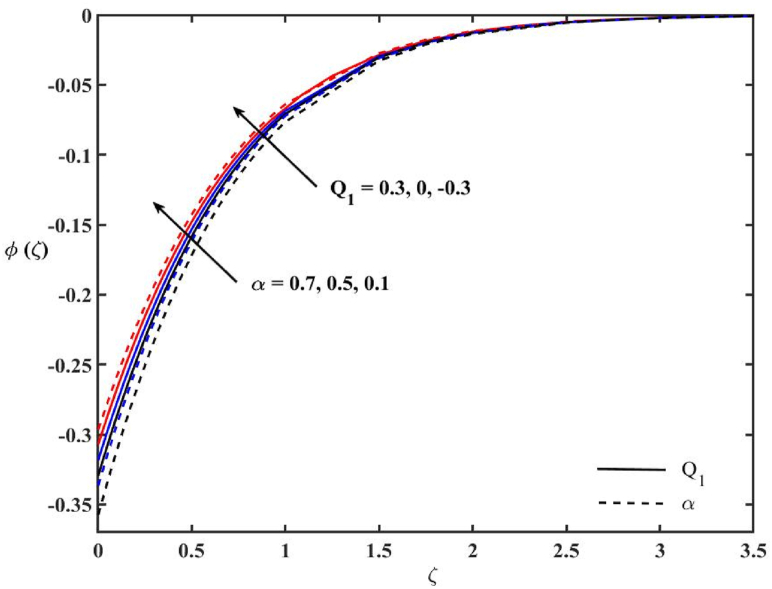
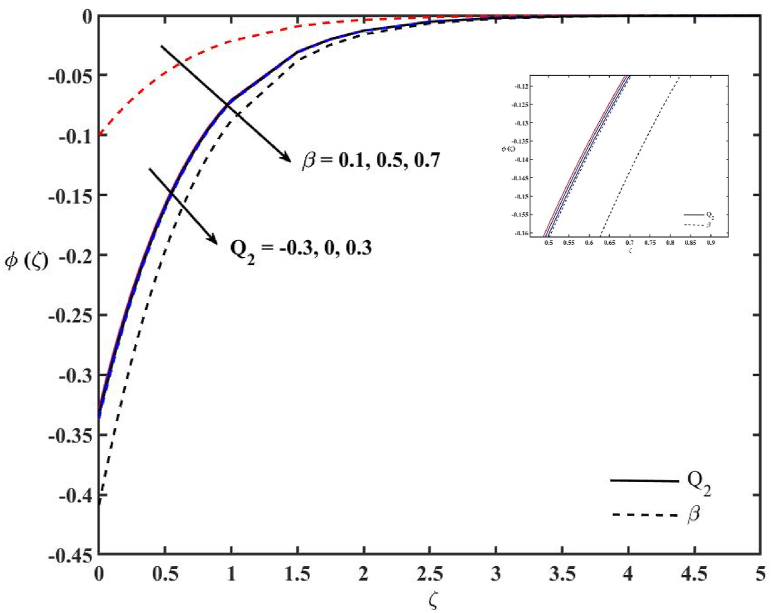
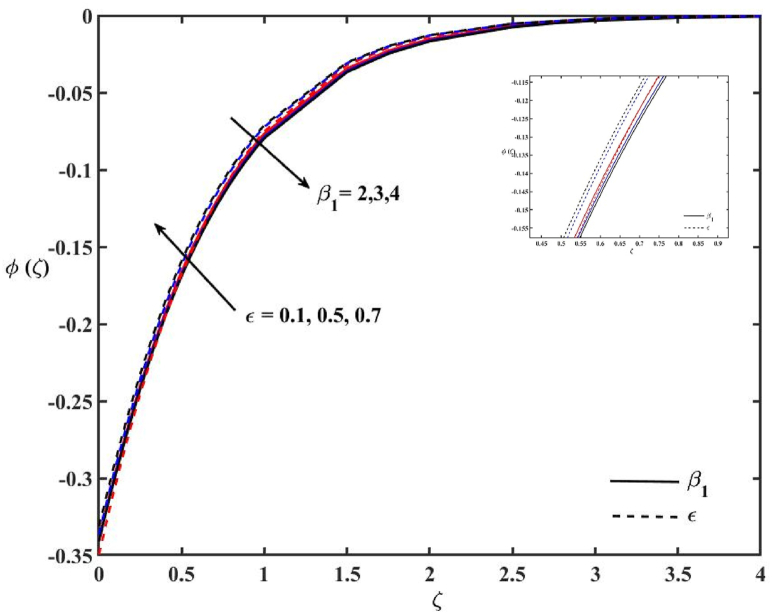
The impacts of N and k₁ on concentration profile φ (ζ) are demonstrated in Fig. 10. It is noted that both N and k₁ raise the concentration profile and reduce the thickness of the concentration boundary layer. Fig. 11 portrays the impacts of Q₁ and α on the concentration profile. The concentration profile increases with α. It is also noted that the concentration profile is higher in the presence of heat generation and lower in the presence of heat absorption. The combined impact of α with heat generation decreases the thickness of the concentration boundary layer. The impacts of β and Q₂ on the concentration profile is examined in Fig. 12. One may note that the temperature dependent heat generation/absorption parameter does not have significant impacts on the concentration profile. The concentration boundary layer increases with the increase of β. Fig. 13 is plotted to show the impacts of β₁ and Ɛ on the concentration profile. It is observed that the increase in β₁ reduces the concentration profile, while Ɛ enhances the concentration profile.

Fig. 10.

Effects of N and k₁ on concentration profile.

Fig. 11.

Effects of Q₁ and α on concentration profile.

Fig. 12.

Effects of Q₂ and β on concentration profile.

Fig. 13.

Effects of Ɛ and β₁ on concentration profile.

The variations of skin friction coefficient, non-dimensional wall temperature, and non-dimensional wall concentration are depicted in Fig. 14, Fig. 15, Fig. 16 respectively. The skin friction coefficient enhances with the increase of k₁,β₁, λ_c1, β and Ɛ; reduces with λ_t1, λ_t2, λ_c2, N and α (Fig. 14). The increasing values of λ_t1, λ_t2, λ_c2, α increase the non-dimensional wall temperature. The non-dimensional wall temperature decreases with β_1, N, λ_c1, β, k₁ and Ɛ (Fig. 15). The non-dimensional wall concentration rises with the rising values of α, λ_t1, λ_t2, and λ_c2 while it decreases with β, Ɛ, β_1, N,k₁ and λ_c1 (Fig. 16).

6. Conclusion

The nonlinear mixed convection flow of Casson liquid over a stretching surface is investigated numerically in a porous medium. The Arrhenius kinetics impact is considered at the boundary. The heat and mass transfer are analysed in the presence of space and temperature dependent heat generation/absorption and thermal radiation. The similarity solutions are obtained through the Runge-Kutta Fhelberg method along with the shooting technique. The key findings of the present study are:

• •Enhancing the radiation parameter, space and temperature dependent heat generation, heat of reaction, and activation energy accelerate the velocity profile, while the velocity profile decelerates with the increase of the porous medium parameter, space and temperature dependent heat absorption, reaction rate constant, and Casson parameters in the presence of nonlinear heat and mass transfer and Arrhenius kinetics.
• •The temperature profile increases with the increase of radiation, space and temperature dependent heat generation, heat of reaction, and Casson parameters and reduces with the porous medium parameter, space and temperature dependent heat absorption parameter, reaction rate, and activation energy parameters.
• •The concentration profile intensifies with the increase of the porous medium parameter, the radiation parameter, space dependent heat generation, heat of reaction, and activation energy, while it reduces with the reaction rate constant, and the Casson parameter.
• •The skin friction coefficient enhances with the porous medium parameter, Casson parameter, first order concentration buoyancy, reaction rate, and activation energy parameter and reduces with linear and nonlinear mixed convection due to temperature, and nonlinear convection due to concentration, radiation, and heat of reaction parameters.
• •The increasing values of linear and nonlinear mixed convection due to temperature and nonlinear convection due to concentration and heat of reaction increases the non-dimensional wall temperature.
• •The non-dimensional wall concentration rises with the rising values of heat of reaction, linear convection and nonlinear mixed convection due to temperature, and nonlinear convection due to concentration parameters.

The current study focused on the heat transmission from an exothermic process to the fluid surrounding it, which drives the convection flow of Casson fluid in a porous Darcian medium. The future directions of the present study are: the researchers may consider the flow of various non-Newtonian fluids, which is purely driven by the heat supplied to the fluid by an exothermic reaction.

Author contribution statement

N. Vishnu Ganesh; Qasem Al-Mdallal: Conceived and designed the experiments; Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper. Kalaivanan Raja; Reena K: Analysed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of competing interest

None.

Nomenclature

C

concentration (kg/m³)

C_w

concentration of the sheet (kg/m³)

$C_{\infty }$

concentration far away from the sheet (kg/m³)

C_f

local skin friction coefficient

c_p

Specific heat capacity (J/kg K)

D

molecular diffusivity (m²/s)

E

the activation energy (kcal/mol)

g₁

acceleration due to gravity (m/s²)

k

thermal conductivity (W/m K)

k_ab

coefficient of mean absorption

k_p

permeability of the porous medium

$k_1$

porous medium parameter

$N$

radiation parameter

p

pressure (kg m⁻¹s⁻²)

Pr

Prandtl number

Q_r

exothermicity of a reaction

Q₁

space dependent heat generation/absorption parameter

Q₂

temperature dependent heat generation/absorption parameter

q_r

radiative heat flux

R

gas constant

Re_x^1/2

Reynolds number

$Sc$

Schmidt number

T

local temperature of the fluid (K)

T_w

temperature of the sheet (K)

$T_{\infty }$

temperature of the fluid far away from the sheet (K)

$uandv$

velocity component in x and y direction (m/s)

u_w

velocity of stretching sheet (m/s)

x,y

coordinates along and perpendicular to the sheet (m)

X

reactant

Y

produce species

Greeksymbols

$\alpha$

heat of reaction

β

reaction rate

β₁

Casson parameter

β_t1

first order thermal expansion coefficient

β_t2

second order thermal expansion coefficient

β_c1

first order solutal coefficient

β_c2

second order solutal coefficient

σ_sb

constant of Stefan-Boltzmann

$\epsilon$

activation energy

$\rho$

density (kg/m³)

g

dimensionless velocity

$\theta$

$\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}$

$\phi$

$\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$

$\zeta$

$\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}$

$\vartheta$

$\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y}(m^2/\sec )$

${\tau }_w$

$\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}(\mathrm{N}/\mathrm{m}$²)

${\lambda }_{t1}$

$\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{d}\mathrm{u}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}$

${\lambda }_{t2}$

$\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{d}\mathrm{u}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}$

${\lambda }_{c1}$

mixed convection parameter due to concentration

${\lambda }_{c2}$

$\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{d}\mathrm{u}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$