Local $\alpha$-fractal interpolation function

Abstract

Constructions of the (global) fractal interpolation functions on standard function spaces got a lot of attention in the last centuries. Motivated by the newly introduced local fractal functions corresponding to a local iterated functions system which is the generalization of the traditional iterated functions system we construct the local non-affine $\alpha$- fractal functions in this article. A few examples of the graphs of these functions are provided. A fractal operator which takes the classical function to its local fractal counterpart is defined and some of its properties are also studied.

Introduction

Fractal functions are used as an alternative tool for interpolation and approximation purposes. It was first introduced by Barnsley [1] such that the graph of this function is the attractor of some iterated function system (IFS). Fractal functions usually are non-smooth functions and they interpolate a set of given data, for example, $\{(x_i,y_i)\in {\mathbb{R}}^2:x_i<x_{i+1},i=1,2,\cdots ,K\}$, which is quite different from the traditional interpolation techniques, where one can only produce piece-wise differentiable interpolation functions. Fractal interpolation functions are used in many diverse areas, like data analysis, image compression, signal processing etc [17–21]. For instance, in [19] Fractal functions are used to predict the seven-day moving average of daily positive cases due to COVID-19, for the upcoming three months from December 13, 2021, of six countries including India.

Motivated by the work of Barnsley [1], Navascués [3] defined a special kind of fractal function known as $\alpha$-fractal function. These functions not only interpolate but also approximate any continuous function defined on compact intervals of $\mathbb{R}$. By choosing the base function (see Sect. 2.3) as a nowhere differentiable function ( like, a Weierstrass function [16]) one can have non-smooth analogues of a continuous function. In consecutive papers [9–14], fractal dimension of $\alpha$-fractal function is also studied.

In a more general and flexible setting Masssopust [6] defined local fractal functions, which are fixed points of a particular class of Read-Bajactarević (RB) operators defined on the space of all bounded functions. The author also showed that the graphs of these local fractal functions are attractors of a specific local IFS. Massopust also defined local fractal functions on unbounded domains and derived conditions so that local fractal functions are elements of various standard function spaces like Lebesgue spaces, the smoothness spaces, the homogeneous Hölder spaces, the Sobolev spaces, Besov and Triebel-Lizorkin spaces (see [6–8]).

In this paper, we construct a generalised version of $\alpha$-fractal functions through the lens of local fractal functions. These local $\alpha$-fractal functions interpolate as well as approximate bounded functions on compact intervals of $\mathbb{R}$.

This paper is structured as the following. In Sect. 2 first, we introduce iterated function systems and define the attractor of an IFS, then we provide the construction of fractal interpolation functions and $\alpha$-fractal functions, also a brief summary of local fractal functions is given. In Sect. 3, we give the construction of the local $\alpha$-fractal function, provide some examples and also define an operator attached to local $\alpha$-fractal functions and study some properties of this operator.

Preliminaries

Iterated function system

Let X be a topological space and ${\beta }_i:X\to X$ $(i=1,2,\cdots ,K;K\in \mathbb{N})$ are continuous functions. The space X with the functions ${\beta }_i$ is called an iterated function system or IFS and it is denoted by $\{X;{\beta }_i:i=1,2,\cdots ,K\}$. Let $H_X$ be the set of all non-empty compact subsets of X. Define the Hutchinson operator $Q:H_X\to H_X$ by

$$\begin{array}{c}\hfill Q(S)=\bigcup _{i=1}^K{\beta }_i(S)\end{array}$$ 1

$S\in H_X$. When X is a metric space with metric $d_X$, we can define a metric $d_H$ on the space $H_X$ by,

$$\begin{array}{c}\hfill d_H(S_1,S_2)=inf\{ϵ\ge 0:S_1\subset N(S_2,ϵ),S_2\subset N(S_1,ϵ)\}\end{array}$$ 2

for $S_1,S_2\in H_X$, where

$$\begin{array}{c}\hfill N(S,ϵ)=\{x\in X:d_X(x,s)\le ϵ\text{for some}s\in S\}.\end{array}$$ 3

When $(X,d_X)$ is complete then $(H_X,d_H)$ is also complete. The IFS $\{X;{\beta }_i:i=1,2,\cdots ,K\}$ is called hyperbolic if the maps ${\beta }_i$’s are contractions, that is, there exists ${\theta }_i\in [0,1)$ such that

$$\begin{array}{c}\hfill d_X({\beta }_i(x),{\beta }_i(y))\le {\theta }_i{d}_X(x,y)\end{array}$$ 4

And in that case, Q is also a contraction map on the complete metric space $(H_X,d_H)$ [15]. A set $B\in H_X$ is called an attractor of the IFS $\{X;{\beta }_i:i=1,2,\cdots ,K\}$, if

$$\begin{array}{c}\hfill Q(B)=B.\end{array}$$ 5

When Q is a contraction on the complete metric space $(H_X,d_H)$ by the Banach fixed point theorem there exists a unique set $B\in H_X$ such that $Q(B)=B$ i.e. B is the unique attractor of the associated IFS $\{X;{\beta }_i:i=1,2,\cdots ,K\}$.

Fractal interpolation function

Let $\{x_i:i=0,1,\cdots ,K\}\subset \mathbb{R}$, where $K\in \mathbb{N}$, be such that $x_i<x_{i+1},\forall i\in \{0,1,\cdots ,K-1\}.$ Let $A=[x_0,x_K]$ be a closed and bounded interval. Let $\{(x_i,y_i):i=0,1,\cdots ,K\}$ be a set of data points. Setting $J_i=[x_{i-1},x_i]$, define $L_i:A\to J_i$ be such that,

$$\begin{array}{c}\hfill L_i(x_0)=x_{i-1},L_i(x_K)=x_i\end{array}$$ 6

and

$$\begin{array}{c}\hfill |L_i(c)-L_i(d)|\le l|c-d|\end{array}$$ 7

where $l\in [0,1)$ and for all $c,d\in A$ and $i=1,2,\cdots ,K$. Let ${\alpha }_i\in (-1,1)$ and continuous maps $F_i:A\times \mathbb{R}\to \mathbb{R}$ be such that

$$\begin{array}{c}\hfill F_i(x_0,y_0)=y_{i-1},F_i(x_K,y_K)=y_i\end{array}$$ 8

and

$$\begin{array}{c}\hfill |F_i(c,d_1)-F_i(c,d_2)|\le |{\alpha }_i||d_1-d_2|\end{array}$$ 9

for all $i=1,2,\cdots ,K$ and $c\in A$ and $d_1,d_2\in \mathbb{R}$. Define the maps $w_i:A\times \mathbb{R}\to J_i\times \mathbb{R}$ by

$$\begin{array}{c}\hfill w_i(x,y)=(L_i(x),F_i(x,y)),(x,y)\in A\times \mathbb{R}.\end{array}$$ 10

Let $\mathcal{G}=\{g:A\to \mathbb{R}\mid g\text{is continuous and}g(x_0)=y_0,g(x_N)=y_N\}.$ $\mathcal{G}$ forms a complete metric space with respect to the sup metric

$d_{\infty }(g_1,g_2)=sup\{|g_1(x)-g_2(x)|:x\in A\}$.

Theorem 1

[Barnsley [1]] The IFS $\left\{,A,\times ,\mathbb{R},;,w_i,:,i,=,1,,,2,,,\cdots ,,,K,\right\}$ has a unique attractor G, which is the graph of a continuous function $\widehat{f}:A\to \mathbb{R}$ such that $\widehat{f}(x_i)=y_i,i=0,1,\cdots ,K$.

Following is an example of a fractal interpolation function.

Example 1

Let $\{(i,sin(6\ast i))\mid i=0,1/2,1\}$ be a data set. A FIF corresponding to this data set is given in Fig. 1.

Fig. 1.

FIF corresponding to the data set $\{(i,sin(6\ast i))\mid i=0,1/2,1\}$

Define an operator $T:\mathcal{G}\to \mathcal{G}$ by,

$$\begin{array}{c}\hfill Tg(x)=F_i(L_i^{-1}(x),g\circ L_i^{-1}(x)),x\in J_i,\text{where}i=1,2,\cdots ,K.\end{array}$$ 11

Then T is a contraction on $\mathcal{G}$, i.e for $g_1,g_2\in \mathcal{G}$

$$\begin{array}{c}\hfill \Vert T{g}_1(x)-T{g}_2(x){\Vert \le |\alpha |}_{\infty }\Vert g_1(x)-g_2(x)\Vert ,\text{for all}x\in A,\end{array}$$ 12

where ${|\alpha |}_{\infty }:=max\{|{\alpha }_i|:i=1,2,\cdots ,K\}$. Since ${\alpha }_i\in (-1,1)$, ${|\alpha |}_{\infty }\in [0,1)$.

Again by Banach fixed point theorem, T being a contraction on the complete metric space $\mathcal{G}$, has a unique fixed point which is $\widehat{f}$ itself, i.e. $T(\widehat{f})=\widehat{f}$. $\widehat{f}$ is called a FIF corresponding to the data set $\{(x_i,y_i):i=0,1,\cdots ,K\}$.

One of the widely popular ways of defining a FIF is by choosing the maps $L_i$’s and $F_i$’s as the following,

$$\begin{array}{c}\hfill L_i(x)=a_{i}x+d_i,F_i(x,y)={\alpha }_{i}y+q_i(x),i=1,2,\cdots ,K\end{array}$$ 13

where the constants $a_i,d_i$ are determined by (6) and the maps $q_i:A\to \mathbb{R}$ are chosen continuous functions such that (8) holds. If we choose $q_i(x)$ to be linear then the corresponding FIF is called an Affine FIF (cf. [1, 2]).

Construction of $\alpha$-fractal function

Set $\mathcal{C}(A)$ as the space of all real valued continuous functions on A equipped with the sup norm ${\Vert g\Vert }_{\infty }=sup\{|g(x)|:x\in A\}$. Let $g\in \mathcal{C}(A)$. Navascués in [3, 4] took

$$\begin{array}{c}\hfill q_i(x)=g(L_i(x))-{\alpha }_i·b(x),i=1,2,\cdots ,K\end{array}$$ 14

where $b\in \mathcal{C}(A)$ with $b(x_0)=f(x_0),b(x_K)=f(x_K)$ and $b\ne g$. b is known as the base function.

Definition 1

[4] Let $g^{\alpha }$ be the continuous function whose graph is the attractor of the IFS (10), (13) and (14). Then, the function $g^{\alpha }$ is called the $\alpha$-fractal function associated to g with respect to the base function b(x) and the partition $\mathrm{\Delta }=(x_0<x_1<\cdots <x_K)$.

Following is an example of a $\alpha$-fractal function.

Example 2

The Fig. 2 represents a $\alpha$-fractal function corresponding to the function $sin(6x)$.

Fig. 2.

$\alpha$-Fractal function corresponding to $sin(6x)$

The choices made in (13) and (14), shapes T into a particular form as the following,

$$\begin{array}{c}\hfill Tg(x)=f(x)+{\alpha }_i·(g-b)\circ L_i^{-1}(x),x\in J_i,i=1,2,\cdots ,K.\end{array}$$ 15

Hence $g^{\alpha }$ satisfies the following self-referential equation

$$\begin{array}{c}\hfill g^{\alpha }(x)=f(x)+{\alpha }_i·(g-b)\circ L_i^{-1}(x),x\in J_i,i=1,2,\cdots ,K.\end{array}$$ 16

Construction of local fractal function

In this section, we introduce the construction, given by P. R. Massopust [6] of bounded local fractal functions. These functions are defined as the fixed points of a particular type of RB operators acting on the complete metric space of bounded functions.

For this purpose, let $\{Y_i:i=1,2,\cdots ,K\}$ be a family of nonempty connected subsets of a connected topological space Y. Suppose $\{{\lambda }_i:Y_i\to Y\mid i=1,2,\cdots ,K\}$ is a family of injective mappings with the property that $\{{\lambda }_i(Y_i):i=1,2,\cdots ,K\}$ forms a partition of Y. Now suppose that $(Z,d_Z)$ is a complete linear metric space and $B(Y,Z):=\{g:Y\to Z\mid g\text{is bounded}\},$ endowed with the sup metric $d(g_1,g_2)=sup\{d_Y(g_1(y),g_2(y)):y\in Y\}$.

For $i\in \{1,2,\cdots ,K\}$, define ${\gamma }_i:Y_i\times Z\to Z$ be a mapping such that $\exists r\in [0,1)$ and $\forall y\in Y_i$ and $\forall z_1,z_2\in Z$

$$\begin{array}{c}\hfill d_Z({\gamma }_i(y,z_1),{\gamma }_i(y,z_2))\le r·d_Z(z_1,z_2).\end{array}$$ 17

That is, ${\gamma }_i$ is uniformly contractive in the second variable.

Now we can define a RB operator $T:B(Y,Z)\to Z^Y$ by

$$\begin{array}{c}\hfill Th(y):=\sum _{i=1}^K{\gamma }_i({\lambda }_i^{-1}(y),h_i\circ {\lambda }_i^{-1}(y)){\chi }_{{\lambda }_i(Y_i)}(y)\end{array}$$ 18

   where $h_i:=h{\mid }_{Y_i}$ and

$$\begin{array}{c}\hfill {\chi }_M(y)=\left\{\begin{array}{cc}1,\hfill & y\in M\hfill \\ 0,\hfill & y\notin M.\hfill \end{array}\right)\end{array}$$

One can check that T is a well-defined contraction on the complete metric space B(Y, Z) and hence by the Banach Fixed Point Theorem T has, therefore, a unique fixed point $g$ in B(Y, Z). This unique fixed point is called a local fractal function $g=g_{\mathrm{\Phi }}$ (generated by T) [6].

Local $\alpha$-fractal function

Let $\{A_i:i=1,2,\cdots ,K\}$ be a collection of non-empty connected subsets of $A=[x_0,x_K]$ such that $x_0\in A_i,\forall i\in \{1,2,\cdots ,K\}$ and $x_K\in A_K.$

Also let, ${\lambda }_i:A_i\to A$ be injective maps with the following properties:

1. $\{{\lambda }_i(A_i):i=1,2,\cdots ,K\}$ forms a partition of A, i.e.

   • ${\bigcup }_{i=1}^N{\lambda }_i(A_i)=A$ and
   • ${\lambda }_i(A_i)\bigcap {\lambda }_j(A_j)=\mathrm{\varnothing }$.
2. $$\begin{array}{c}\hfill {\lambda }_i(x_0)=x_{i-1},\forall i=1,2,\cdots ,K\text{and}{\lambda }_K(x_K)=x_K\end{array}$$ 19

For $i\in \{1,2,\cdots ,K\}$, define ${\gamma }_i:A_i\times \mathbb{R}\to \mathbb{R}$ be a mapping for which $\exists r\in [0,1)$ such that, $\forall a\in A_i$ and $\forall b_1,b_2\in \mathbb{R}$

$$\begin{array}{c}\hfill |{\gamma }_i(a,b_1)-{\gamma }_i(a,b_2)|\le r|b_1-b_2|\end{array}$$ 20

that is, ${\gamma }_i$ is uniformly contractive in the second variable.

Set $B(A,\mathbb{R})=\{g:A\to \mathbb{R}\mid g\text{is bounded}\}$ and define a metric $d_{\infty }(f,g)={sup}_{x\in A}|f(x)-g(x)|$. Then $(B(A,\mathbb{R}),d_{\infty })$ is a complete metric space.

Define a RB operator $T:B(A,\mathbb{R})\to {\mathbb{R}}^A$ by

$$\begin{array}{c}\hfill Th(x):=\sum _{i=1}^K{\gamma }_i({\lambda }_i^{-1}(x),h_i\circ {\lambda }_i^{-1}(x)){\chi }_{{\lambda }_i(A_i)}(x),\end{array}$$ 21

where $h\in B(A,\mathbb{R})$,    ${\chi }_S(x)=\left\{\begin{array}{cc}1,\hfill & x\in S\hfill \\ 0,\hfill & x\notin S.\hfill \end{array}\right)$     and    $h_i:=h{\mid }_{A_i}$.

Note that T is well-defined and $T(B(A,\mathbb{R}))\subseteq B(A,\mathbb{R})$.

Also, for $h,g\in B(A,\mathbb{R})$

$$\begin{array}{cc}\hfill d_{\infty }(Th,Tg)=& \underset{x\in A}{sup}|Th-Tg|\hfill \\ \hfill =& \underset{i\in \{1,2,\cdots ,K\}}{sup}\hfill \\ \hfill & \underset{x\in {\lambda }_i(A_i)}{sup}|{\gamma }_i({\lambda }_i^{-1}(x),h_i\circ {\lambda }_i^{-1}(x))\hfill \\ \hfill & -{\gamma }_i({\lambda }_i^{-1}(x),g_i\circ {\lambda }_i^{-1}(x))|\hfill \\ \hfill \le & \underset{i\in \{1,2,\cdots ,K\}}{sup}\hfill \\ \hfill & \underset{x\in {\lambda }_i(A_i)}{sup}r|h_i\circ {\lambda }_i^{-1}(x)-g_i\circ {\lambda }_i^{-1}(x)|\hfill \\ \hfill \le & r\underset{i\in \{1,2,\cdots ,K\}}{sup}\hfill \\ \hfill & \underset{x\in {\lambda }_i(A_i)}{sup}|h_i\circ {\lambda }_i^{-1}(x)-g_i\circ {\lambda }_i^{-1}(x)|\hfill \\ \hfill \le & r\underset{x\in A}{sup}|h(x)-g(x)|\hfill \\ \hfill =& r{d}_{\infty }(h,g)\hfill \end{array}$$

which shows that T is a contraction on the complete metric space $B(A,\mathbb{R})$. Hence by Banach Fixed Point theorem there exists a unique $h\in B(A,\mathbb{R})$ such that $T(h)=h$, that is T has a unique fixed point $h$ in $B(A,\mathbb{R})$. This unique fixed point is called local fractal function $h=h_{\mathbf{T}}$ (generated by T).

Next, we would like to a particular form of the maps ${\gamma }_i$. Let the maps ${\gamma }_i:A_i\times \mathbb{R}\to \mathbb{R}$ be defined by the following,

$$\begin{array}{c}\hfill {\gamma }_i(x,y):=q_i(x)+{\alpha }_i(x)y,\end{array}$$ 22

where $q_i,{\alpha }_i\in B(A_i,\mathbb{R}),i\in \{1,2,\cdots ,K\}.$

Now, for $a\in A_i$ and $b_1,b_2\in \mathbb{R}$

$$\begin{array}{cc}\hfill |{\gamma }_i(a,b_1)-{\gamma }_i(a,b_2)|=& |{\alpha }_i(a)\times (b_1-b_2)|\hfill \\ \hfill \le & \Vert {\alpha }_i{\Vert }_{\infty ,A_i}|b_1-b_2|\hfill \\ \hfill \le & {|\alpha |}_{\infty }|b_1-b_2|\hfill \end{array}$$

where $\Vert {\alpha }_i{\Vert }_{\infty ,A_i}:=sup\{|{\alpha }_i(x)|:x\in A_i\}$ and ${|\alpha |}_{\infty }:=max\{|{\alpha }_i{|}_{\infty ,A_i}:i=1,2,\cdots ,K\}$. Hence for ${\gamma }_i$ to satisfy (20) we need ${|\alpha |}_{\infty }\in [0,1)$.

Continuing with this choice of ${\gamma }_i$’s, the operator T takes the following form

$$\begin{array}{c}\hfill Th=\sum _{i=1}^K(q_i\circ {\lambda }_i^{-1})·{\chi }_{{\lambda }_i(A_i)}+\sum _{i=1}^K({\alpha }_i\circ {\lambda }_i^{-1})·(h_i\circ {\lambda }_i^{-1})·{\chi }_{{\lambda }_i(A_i)}\end{array}$$ 23

Hence by Theorem 3 in [6] there exist a unique $h\in B(A,\mathbb{R})$ such that $T(h)=h$ i.e $h$ satisfies the self-referential equation

$$\begin{array}{c}\hfill h=\sum _{i=1}^K(q_i\circ {\lambda }_i^{-1})·{\chi }_{{\lambda }_i(A_i)}+\sum _{i=1}^K({\alpha }_i\circ {\lambda }_i^{-1})·(h_i\circ {\lambda }_i^{-1})·{\chi }_{{\lambda }_i(A_i)}\end{array}$$ 24

where $h_i=h{\mid }_{A_i}$.

This unique fixed point $h$ in (24) is called bounded local fractal function generated by T with respect to the set of functions $\{q_i\mid i=1,2,\cdots ,K\}$ and $\{{\alpha }_i\mid i=1,2,\cdots ,K\}$.

Let $\mathcal{H}:=\{g\in B(A,\mathbb{R})\mid g(x_0)=y_0\text{and}g(x_K)=y_K\}$. Then $(\mathcal{H},d_{\infty })$ is a complete metric space.

Now we would like to consider the functions $q_i$ in a special form,

$$\begin{array}{c}\hfill q_i(x):=g\circ {\lambda }_i(x)-{\alpha }_i(x)·b(x)\end{array}$$ 25

where $g,b\in \mathcal{H}$ are such that $g\ne b$ and $g(x_i)=y_i$ for $i=0,1,\cdots ,K$.

By this choice, it is clear that $q_i\in B(A_i,\mathbb{R})$ and hence the operator in (23) can be written in the following form,

$$\begin{array}{cc}\hfill Th=& \sum _{i=1}^K\{g-({\alpha }_i·b)\circ {\lambda }_i^{-1}\}·{\chi }_{{\lambda }_i(A_i)}\hfill \\ \hfill & +\sum _{i=1}^K({\alpha }_i\circ {\lambda }_i^{-1})·(h_i\circ {\lambda }_i^{-1})·{\chi }_{{\lambda }_i(A_i)}\hfill \\ \hfill =& \sum _{i=1}^{K}g·{\chi }_{{\lambda }_i(Ai)}\hfill \\ \hfill & +\sum _{i=1}^K\{({\alpha }_i·h_i)\circ {\lambda }_i^{-1}-({\alpha }_i·b)\circ {\lambda }_i^{-1}\}·{\chi }_{{\lambda }_i(Ai)}\hfill \\ \hfill =& g+\sum _{i=1}^K\{{\alpha }_i·(h_i-b)\circ {\lambda }_i^{-1}\}·{\chi }_{{\lambda }_i(A_i)}\hfill \\ \hfill \end{array}$$

or, equivalently

$$\begin{array}{c}\hfill Th=g+{\alpha }_i·(h_i-b)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\text{for}i=1,2,\cdots ,K.\end{array}$$ 26

Again by using (26) and (19), for $h\in \mathcal{H}$ we have

$$\begin{array}{cc}\hfill Th(x_0)& =g(x_0)+{\alpha }_1({\lambda }_1^{-1}(x_0))\hfill \\ \hfill & ·(h_1({\lambda }_1^{-1}(x_0))-b({\lambda }_1^{-1}(x_0)))\hfill \\ \hfill & =g(x_0)+{\alpha }_1(x_0)·(h_1(x_0)-b(x_0))\hfill \\ \hfill & =g(x_0)+{\alpha }_1(x_0)·(y_0-y_0)\hfill \\ \hfill & =g(x_0)\hfill \\ \hfill & =y_0.\hfill \end{array}$$

Similarly, it can be checked that $Th(x_K)=y_K$.

So we can consider T as an operator on $\mathcal{H}$ i.e. $T:\mathcal{H}\to \mathcal{H}$ is given by

$$\begin{array}{c}\hfill Th=g+{\alpha }_i·(h_i-b)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\text{for}i=1,2,\cdots ,K.\end{array}$$ 27

Hence T is a contraction mapping on the complete metric space $(\mathcal{H},d_{\infty })$. So T possesses a unique fixed point say $g^{\alpha }\in \mathcal{H}$.

Hence for fixed $g,b\in \mathcal{H}$ and for a selected collection of non-empty connected subsets $\mathbf{P}:=\{A_i\subseteq A:i=1,2,\cdots ,K\}$ and injective maps $\mathbf{F}:=\{{\lambda }_i:A_i\to A\mid i=1,2,\cdots ,K\}$ there is a unique $g^{\alpha }\in \mathcal{H}$ such that $T(g^{\alpha })=g^{\alpha }$ i.e. $g^{\alpha }$ satisfies the self-referential equation

$$\begin{array}{c}\hfill g^{\alpha }=g+{\alpha }_i·(g_i^{\alpha }-b)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\text{for}i=1,2,\cdots ,K.\end{array}$$ 28

where$g_i^{\alpha }=g^{\alpha }{\mid }_{A_i}$.

$g^{\alpha }$ will be called the local $\alpha$-fractal function associated to g with respect to b and $\mathbf{P},\mathbf{F}$.

Using (19) and since $g^{\alpha }\in \mathcal{H}$, $b\in \mathcal{H}$ and $g(x_i)=y_i,\forall i\in \{0,1,\cdots ,K\}$, we have for $i=0,1,\cdots ,K-1$

$$\begin{array}{cc}\hfill g^{\alpha }(x_i)=& g(x_i)+{\alpha }_{i+1}({\lambda }_{i+1}^{-1}(x_i))\hfill \\ \hfill & ·(g_{i+1}^{\alpha }({\lambda }_{i+1}^{-1}(x_i))-b({\lambda }_{i+1}^{-1}(x_i)))\hfill \\ \hfill =& g(x_i)+{\alpha }_{i+1}(x_0)·(g_{i+1}^{\alpha }(x_0)-b(x_0))\hfill \\ \hfill =& g(x_i)+{\alpha }_i(x_0)·(y_0-y_0)=g(x_i)=y_i\hfill \\ \hfill \text{and}\\ \hfill g^{\alpha }(x_K)=& g(x_K)+{\alpha }_K\left({\lambda }_K^{-1},(x_K)\right)\hfill \\ \hfill & ·(g_K^{\alpha }({\lambda }_K^{-1}(x_K))-b({\lambda }_K^{-1}(x_K)))\hfill \\ \hfill =& g(x_K)+{\alpha }_K(x_K)·(g_K^{\alpha }(x_K)-b(x_K))\hfill \\ \hfill =& g(x_K)+{\alpha }_i(x_K)·(y_K-y_K)=g(x_K)=y_K.\hfill \end{array}$$

This shows that $g^{\alpha }$ interpolates g at $\{x_i:i=0,1,\cdots ,K\}$.

Remark 1

If for all $i\in \{1,2,\cdots ,K\},{\alpha }_i\equiv 0$ that is ${|\alpha |}_{\infty }=0$, then (28) implies $g^{\alpha }=g$.

Theorem 2

Let $\{(x_i,y_i)\in \mathbb{R}\times \mathbb{R}:x_i<x_{i+1},i=0,1,\cdots ,K\}$ be a data set. Let $\mathbf{P}:=\{A_i\subseteq A:i=1,2,\cdots ,K\}$ be a collection of non-empty connected subsets and $\mathbf{F}:=\{{\lambda }_i:A_i\to A\mid i=1,2,\cdots ,K\}$ be a collection of injective maps with properties mentioned above. Let $g\in B(A,\mathbb{R})$ such that $g(x_i)=y_i,i=0,1,\cdots ,K$ be fixed. Let

$$\begin{array}{c}\hfill \alpha :=({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_K)\in {\times }_{i=1}^{K}B(A_i,\mathbb{R})\end{array}$$

be such that ${|\alpha |}_{\infty }\in [0,1)$. Also, let $b\in \mathcal{H}$ with $b\ne g$. Define $T:\mathcal{H}\to \mathcal{H}$ by

$$\begin{array}{c}\hfill Th=g+{\alpha }_i·(h_i-b)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\text{for}i=1,2,\cdots ,K.\end{array}$$

where $h_i:=h{\mid }_{A_i}$. Then T is a contraction on the complete metric space $\mathcal{H}$ and its unique fixed point $g^{\alpha }$ satisfies the self-referential equation

$$\begin{array}{c}\hfill g^{\alpha }=g+{\alpha }_i·(g_i^{\alpha }-b)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\text{for}i=1,2,\cdots ,K.\end{array}$$

where $g_i^{\alpha }=g^{\alpha }{\mid }_{A_i}$. Also $g^{\alpha }$ interpolates g at $\{x_i:i=0,1,\cdots ,K\}$.

Proof

The proof follows from the previous analysis. $\square$

A Local $\alpha$-fractal function corresponding to a continuous function is given in the following example.

Example 3

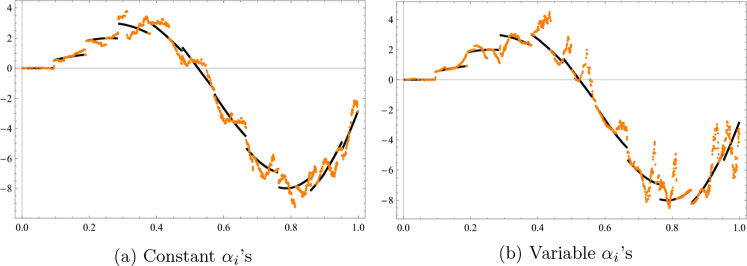
Let the data set be $\left\{,(,\frac{i}{16},,,sin,\frac{6·i}{16},),:\right)$ $\left(i,=,0,,,,1,,,\cdots ,,,,16,\right\}$. Let $A=[0,1].$ Let $A_i=[0,\frac{i}{16}]$ and ${\lambda }_i=\frac{x}{i}+\frac{i-1}{16},i=1,2,\cdots ,16$. Fix $g(x)=sin6x$. Then by choosing $b(x)=sin6·x$ the corresponding local $\alpha$-fractal function is shown in Fig. 3a and 3b with respect to the following scale vectors

Fig. 3.

The graph of $sin6x$ (black) and its corresponding local $\alpha$-fractal function (orange)

1. ${\alpha }_i=\left\{\begin{array}{cc}0.2,\hfill & i=odd\hfill \\ -0.2,\hfill & i=even;\hfill \end{array}\right)$

2. ${\alpha }_i(x)=\left\{\begin{array}{cc}0.5·sin60x,\hfill & i=1,5,9,13\hfill \\ exp-2x-1·0.5·sin60x,\hfill & i=2,6,10,14\hfill \\ 0.5·cos30x,\hfill & i=3,7,11,15\hfill \\ 0.5·sin40x,\hfill & i=4,8,12,16\hfill \end{array}\right)$

A Local $\alpha$-fractal function corresponding to a discontinuous function is given in the following example.

Example 4

Let the data set be $\left\{,(,\frac{i}{16},,,\lfloor \frac{10.5i}{16}\rfloor \right)$ $\left(,\ast ,sin,\frac{6i}{16},:,,i,=,0,,,,1,,,\cdots ,,,,16,\right\}$. Let $A=[0,1].$ Let $A_i=[0,\frac{i}{16}]$ and ${\lambda }_i=\frac{x}{i}+\frac{i-1}{16},i=1,2,\cdots ,16$. Fix $g(x)=\lfloor 10.5x\rfloor \ast sin6x$. Then by choosing $b(x)=10·sin6\ast x$ and the corresponding local $\alpha$-fractal function is shown in figure 4a and 4b with respect to the following scale vectors

Fig. 4.

The graph of $\lfloor 10.5x\rfloor \ast sin6x$ (black) and its corresponding local $\alpha$-fractal function (orange)

1. ${\alpha }_i=\left\{\begin{array}{cc}0.2,\hfill & i=odd\hfill \\ -0.2,\hfill & i=even,\hfill \end{array}\right)$

2. ${\alpha }_i(x)=\left\{\begin{array}{cc}0.5·sin60x,\hfill & i=1,5,9,13\hfill \\ exp-2x-1·0.5·sin60x,\hfill & i=2,6,10,14\hfill \\ 0.5·cos30x,\hfill & i=3,7,11,15\hfill \\ 0.5·sin40x,\hfill & i=4,8,12,16\hfill \end{array}\right)$

Remark 2

As we can see in the above examples that the local $\alpha$-fractal functions are discontinuous in both cases. This is not always the case though, for example, one simple way of getting a continuous local $\alpha$-fractal function is by choosing $K=1$ in the corresponding construction (see Sect. 3).

Again from (28) we have

$$\begin{array}{cc}\hfill g^{\alpha }& =g+{\alpha }_i·(g_i^{\alpha }-b)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \\ \hfill \text{Hence}{g}^{\alpha }-g& ={\alpha }_i·(g_i^{\alpha }-b)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \end{array}$$

which gives

$$\begin{array}{cc}\hfill \Vert g^{\alpha }-g{\Vert }_{\infty ,{\lambda }_i(A_i)}& =\Vert {\alpha }_i·(g_i^{\alpha }-b)\circ {\lambda }_i^{-1}{\Vert }_{\infty ,{\lambda }_i(A_i)}\hfill \\ \hfill & \le \Vert {\alpha }_i·(g_i^{\alpha }-b){\Vert }_{\infty ,A_i}\hfill \\ \hfill & =\Vert {\alpha }_i{\Vert }_{\infty ,A_i}·{\Vert (g_i^{\alpha }-b)\Vert }_{\infty ,A_i}\hfill \\ \hfill & \le {|\alpha |}_{\infty }·{\Vert (g^{\alpha }-b)\Vert }_{\infty ,A}\hfill \end{array}$$

since this is true for all $i\in \{1,2,\cdots ,K\}$ we can deduce that,

$$\begin{array}{cc}\hfill \Vert g^{\alpha }-g{\Vert }_{\infty ,A}& \le {|\alpha |}_{\infty }·{\Vert (g^{\alpha }-b)\Vert }_{\infty ,A}\hfill \\ \hfill & \le {|\alpha |}_{\infty }\left(\Vert ,g^{\alpha }-g,{\Vert }_{\infty ,A},+,{\Vert g-b\Vert }_{\infty ,A}\right)\hfill \end{array}$$

and hence

$$\begin{array}{c}\hfill \Vert {\mathcal{g}}^{\alpha }-g{\Vert }_{\infty ,A}\le \left(\frac{{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\right){\Vert g-b\Vert }_{\infty ,A}\end{array}$$ 29

Let us define an operator ${\mathcal{L}}^{\alpha }:\mathcal{H}\to \mathcal{H}$ by $g\hookrightarrow g^{\alpha }$, that is ${\mathcal{L}}^{\alpha }$ associates the local $\alpha$-fractal function $g^{\alpha }$ with g. Also, it is clear that ${\mathcal{L}}^{\alpha }={\mathcal{L}}_{b,\mathbf{P},\mathbf{F}}^{\alpha }$ depends on b and $\mathbf{P}$, $\mathbf{F}$.

Proposition 1

If b and $\mathbf{P}$, $\mathbf{F}$ are fixed then for all $g,f\in \mathcal{H}$

$$\begin{array}{c}\hfill \Vert {\mathcal{L}}^{\alpha }(g)-{\mathcal{L}}^{\alpha }(f){\Vert }_{\infty ,A}\le \left(\frac{1}{1-{|\alpha |}_{\infty }}\right){\Vert g-f\Vert }_{\infty ,A}\end{array}$$ 30

that is ${\mathcal{L}}^{\alpha }$ satisfies the Lipschitz condition on $\mathcal{H}$.

Proof

By the definition of ${\mathcal{L}}^{\alpha }$ and using (28), we have

$$\begin{array}{cc}\hfill {\mathcal{L}}^{\alpha }(g)& =g+{\alpha }_i·(g_i^{\alpha }-b)\circ {\lambda }_i^{-1}\text{on}{\lambda }_i(A_i),\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \\ \hfill {\mathcal{L}}^{\alpha }(f)& =f+{\alpha }_i·(f_i^{\alpha }-b)\circ {\lambda }_i^{-1}\text{on}{\lambda }_i(A_i),\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \end{array}$$

which gives

$$\begin{array}{cc}\hfill & {\mathcal{L}}^{\alpha }(g)-{\mathcal{L}}^{\alpha }(f)\hfill \\ \hfill & =(g-f)+{\alpha }_i·\left(g_i^{\alpha },-,f_i^{\alpha }\right)\circ {\lambda }_i^{-1}\text{on}{\lambda }_i(A_i),\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \end{array}$$

Hence

$$\begin{array}{cc}\hfill & \Vert {\mathcal{L}}^{\alpha }(g)-{\mathcal{L}}^{\alpha }(f){\Vert }_{\infty ,{\lambda }_i(A_i)}\hfill \\ \hfill & \le {\Vert g-f\Vert }_{\infty ,A}+{|\alpha |}_{\infty }·{\Vert g^{\alpha }-f^{\alpha }\Vert }_{\infty ,A}\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \end{array}$$

which in turn implies that

$$\begin{array}{c}\hfill \Vert {\mathcal{L}}^{\alpha }(g)-{\mathcal{L}}^{\alpha }(f){\Vert }_{\infty ,A}\le {\Vert g-f\Vert }_{\infty ,A}+{|\alpha |}_{\infty }·{\Vert g^{\alpha }-f^{\alpha }\Vert }_{\infty ,A}\end{array}$$

Hence

$$\begin{array}{c}\hfill \Vert {\mathcal{L}}^{\alpha }(g)-{\mathcal{L}}^{\alpha }(f){\Vert }_{\infty ,A}\le \left(\frac{1}{1-{|\alpha |}_{\infty }}\right){\Vert g-f\Vert }_{\infty ,A}\end{array}$$

$\square$

Theorem 3

The operator ${\mathcal{L}}^{\alpha }:\mathcal{H}\to \mathcal{H}$ is continuous on $\mathcal{H}$.

Proof

By proposition 1, we see that ${\mathcal{L}}^{\alpha }$ satisfies the Lipschitz condition on $\mathcal{H}$ and hence ${\mathcal{L}}^{\alpha }$ is continuous on $\mathcal{H}$. $\square$

Now, let us choose $b=g\circ u$ where $u\in B(A,A)$ and $u(x_0)=x_0$, $u(x_K)=x_K$, then the operator ${\mathcal{L}}^{\alpha }={\mathcal{L}}_{u,\mathbf{P},\mathbf{F}}^{\alpha }$, which assigns the local $\alpha$-fractal function $g^{\alpha }$ to g is linear, as $g,h\in \mathcal{H}$ implies

$$\begin{array}{cc}\hfill g^{\alpha }& =g+{\alpha }_i·(g_i^{\alpha }-g\circ u)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \\ \hfill h^{\alpha }& =h+{\alpha }_i·(h_i^{\alpha }-h\circ u)\circ {\lambda }_i^{-1},\text{on}{\lambda }_i(A_i),\hfill \\ \hfill & \text{for}i=1,2,\cdots ,K\hfill \end{array}$$

and for ${\lambda }_1,{\lambda }_2\in \mathbb{R}$, we have

$$\begin{array}{cc}\hfill & ({\lambda }_1{g}^{\alpha }+{\lambda }_2{h}^{\alpha })=({\lambda }_{1}g+{\lambda }_{2}h)\hfill \\ \hfill & +{\alpha }_i·\left[{\left({\lambda }_1,g^{\alpha },+,{\lambda }_2,h^{\alpha }\right)}_i,-,({\lambda }_1{g}^{\alpha }+{\lambda }_2{h}^{\alpha }),\circ ,u\right]\circ {\lambda }_i^{-1},\hfill \end{array}$$

$\text{for}i=1,2,\cdots ,K.$

Since the solution of the Eq. (28) is unique, for all ${\lambda }_1,{\lambda }_2\in \mathbb{R}$, we have

$$\begin{array}{c}\hfill {({\lambda }_{1}g+{\lambda }_{2}h)}^{\alpha }=({\lambda }_1{g}^{\alpha }+{\lambda }_2{h}^{\alpha }).\end{array}$$ 31

Again using $b=g\circ u$ in Eq. (29), we have

$$\begin{array}{cc}\hfill \Vert {\mathcal{L}}^{\alpha }(g)-g{\Vert }_{\infty ,A}& \le \left(\frac{{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\right){\Vert g-g\circ u\Vert }_{\infty ,A}\hfill \\ \hfill & \le \left(\frac{{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\right)\left[{\Vert g\Vert }_{\infty ,A},+,{\Vert g\circ u\Vert }_{\infty ,A}\right]\hfill \\ \hfill & \le \left(\frac{{2|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\right){\Vert g\Vert }_{\infty ,A}\hfill \end{array}$$

and consequently, we can derive the following

$$\begin{array}{cc}\hfill \Vert {\mathcal{L}}^{\alpha }(g){\Vert }_{\infty ,A}& \le \left[\left(\frac{{2|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\right),{\Vert g\Vert }_{\infty ,A},+,{\Vert g\Vert }_{\infty ,A}\right]\hfill \\ \hfill & \le \left(\frac{1+{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\right){\Vert g\Vert }_{\infty ,A}\hfill \end{array}$$

which in turn implies

$$\begin{array}{c}\hfill \Vert {\mathcal{L}}^{\alpha }{\Vert }_{\infty ,A}\le \left(\frac{1+{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\right).\end{array}$$ 32

It follows that the operator ${\mathcal{L}}^{\alpha }$ is a linear and bounded operator.

Theorem 4

Fixing the base function $b=g\circ u$, for $u\in B(A,A)$ and $u(x_0)=x_0$, $u(x_K)=x_K$, the operator ${\mathcal{L}}^{\alpha }:\mathcal{H}\to \mathcal{H}$ becomes linear and bounded.

Proof

This statement follows from the above considerations. $\square$

Conclusion and future directions

In this paper, we constructed the local $\alpha$-fractal function on a closed interval [a, b]. We provided a couple of examples of the local $\alpha$-fractal functions corresponding to a continuous function as well as a discontinuous function. Then we studied some properties of the fractal operator which assigns a function with its corresponding local $\alpha$-fractal function. By modifying the underlying conditions suitably one can define local $\alpha$-fractal functions in Lebesgue spaces, Sobolev spaces and other standard function spaces. One also expects to define local $\alpha$-fractal functions for functions defined on non-compact unbounded domains of $\mathbb{R}$. One might also generalise this paper by considering the scale-free fractal interpolation (see [5]). As mentioned in the introduction, Fractal interpolation functions are used in data analysis to interpolate real-world data sets that can not be interpolated by traditional polynomial interpolants. As the data sets involved are often discontinuous, so the local $\alpha$-fractal functions might be more suitable to study this kind of data as compared to classical fractal interpolation functions.

Author contribution statement

All the authors contributed equally to this work.

Funding

AB acknowledges the Council of Scientific & Industrial Research (CSIR), India, for the financial support under the scheme “JRF” (FileNo. 08/0155(12963)/2022-EMR-I). Md.NA acknowledges the Department of Science and Technology (DST), Govt. of India, for the financial support under the scheme “Fund for Improvement of S &T Infrastructure (FIST)” (File No. SR/FST/MS-I/2019/41).

Data Availability Statement

No data associated in the manuscript.

Declarations

Conflict of interest

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Ethics approval

This work did not contain any studies involving animal or human participants, nor did it take place on any private or protected areas. No specific permissions were required for corresponding locations.

Consent to participate

Not applicable.

Consent for publication

All authors have given consent to publish this work.

Code availability

Not applicable.