Stochastic Optimization of 3D Non-Cartesian Sampling Trajectory (SNOPY)

Abstract

Purpose:

Optimizing 3D k-space sampling trajectories is important for efficient MRI yet presents a challenging computational problem. This work proposes a generalized framework for optimizing 3D non-Cartesian sampling patterns via data-driven optimization.

Methods:

We built a differentiable simulation model to enable gradient-based methods for sampling trajectory optimization. The algorithm can simultaneously optimize multiple properties of sampling patterns, including image quality, hardware constraints (maximum slew rate and gradient strength), reduced peripheral nerve stimulation (PNS), and parameter-weighted contrast. The proposed method can either optimize the gradient waveform (spline-based freeform optimization) or optimize properties of given sampling trajectories (such as the rotation angle of radial trajectories). Notably, the method can optimize sampling trajectories synergistically with either model-based or learning-based reconstruction methods. We proposed several strategies to alleviate the severe non-convexity and huge computation demand posed by the large scale. The corresponding code is available as an open-source toolbox.

Results:

We applied the optimized trajectory to multiple applications including structural and functional imaging. In the simulation studies, the image quality of a 3D kooshball trajectory was improved from 0.29 to 0.22 (NRMSE) with SNOPY optimization. In the prospective studies, by optimizing the rotation angles of a stack-of-stars (SOS) trajectory, SNOPY reduced the NRMSE of reconstructed images from 1.19 to 0.97 compared to the best empirical method (RSOS-GR). Optimizing the gradient waveform of a rotational EPI trajectory improved participants’ rating of the PNS from ‘strong’ to ‘mild.’

Conclusion:

SNOPY provides an efficient data-driven and optimization-based method to tailor non-Cartesian sampling trajectories.

1 |. INTRODUCTION

Most magnetic resonance imaging systems sample data in the frequency domain (k-space) following prescribed sampling trajectories. Efficient sampling strategies can accelerate acquisition and improve image quality. Many well-designed sampling strategies and their variants, such as spiral, radial, CAIPIRINHA, and PROPELLER^1,2,3,4, have enabled MRI’s application to many areas^5,6,7,8. Sampling patterns in k-space are either located on the Cartesian raster or arbitrary locations (non-Cartesian sampling). This paper focuses on optimizing 3D non-Cartesian trajectories and introduces a generalized gradient-based optimization method for automatic trajectory design or tailoring.

The design of sampling patterns usually considers certain properties of k-space signals. For instance, the variable density (VD) spiral trajectory⁹ samples more densely in the central k-space where more energy is located. For higher spatial frequency regions, the VD spiral trajectory uses larger gradient strengths and slew rates to cover k-space as quickly as possible. Compared to 2D sampling, designing 3D sampling analytically is more challenging for several reasons. The number of parameters increases in 3D, and the parameter selection is more difficult due to the larger search space. For example, a 3D radial trajectory with 10000 spokes has 20000 degrees of freedom, while its 2D multi-slice counterpart with 200 spokes per slice has only 200 degrees of freedom. Additionally, analytical designs usually are based on the Shannon-Nyquist relationship^10,11,12 that might not fully consider properties of sensitivity maps and non-linear reconstruction methods. For 3D sampling patterns with high undersampling (acceleration) ratios, there are limited analytical tools for designing sampling patterns with an anisotropic FOV and resolution. The peripheral nerve stimulation (PNS) effect¹³ is also more severe in 3D imaging because of the additional spatial encoding gradient, further complicating manual designs. For these reasons, automatic designs of 3D sampling trajectories are crucial for efficient acquisition.

Many 3D sampling approaches exist. The ‘stack-of-2D’ strategy stacks 2D sampling patterns in the slice direction^6,12. This approach is easier to implement and enables slice-by-slice 2D reconstruction. Another design applies Cartesian sampling in the frequency-encoding direction and non-Cartesian sampling in the phase-encoding direction^14,15. However, these approaches do not fully explore the design space in three dimensions and may not perform as well as true 3D sampling trajectories¹⁶.

Recently, 3D SPARKLING¹⁶ proposes to optimize 3D sampling trajectories based on the goal of conforming to a given density while distributing samples as uniformly as possible¹⁷. That method demonstrated improved image quality compared to the ‘stack-of-2D-SPARKLING’ approach. In both 2D and 3D, the SPARKLING approach uses a pre-specified sampling density in k-space that is typically an isotropic radial function. This density function cannot readily capture distinct energy distributions of different imaging protocols, therefore adaptive density functions were recently proposed¹⁸. In SPARKLING, the PNS effects are not controlled explicitly, and the user may need to lower the slew rate to reduce PNS. SPARKLING optimizes the location of every sampling point, or the gradient waveform (freeform optimization), and cannot optimize parameters of existing sampling patterns.

In addition to analytical methods, learning-based methods have been investigated for designing trajectories. Since different anatomies have distinct energy distributions in the frequency domain, an algorithm may learn to optimize sampling trajectories from training datasets. Several studies have shown that different anatomies produce distinct optimized sampling patterns, and these optimized sampling trajectories can improve image quality^{19,20,21,22,23,24,25,26,27}. Some methods can optimize sampling trajectories with respect to specific reconstruction algorithms to further enhance reconstruction image quality^14,28. Several recent studies also applied learning-based approaches to 3D non-Cartesian trajectory design. J-MoDL¹⁴ proposes to learn sampling patterns and model-based deep learning reconstruction algorithms jointly. J-MoDL optimizes the sampling locations in the phase-encoding direction, to avoid the computation cost of non-uniform Fourier transform. PILOT/3D-FLAT^22,29 jointly optimizes freeform 3D non-Cartesian trajectories and a reconstruction neural network with gradient-based methods. These studies use the standard auto-differentiation approach to calculate the gradient used in optimization, which can be inaccurate and lead to sub-optimal optimization results²⁸.

This work extends our previous methods^20,28 and introduces a generalized Stochastic optimization framework for 3D NOn-Cartesian samPling trajectorY (SNOPY). The proposed method can automatically tailor given trajectories and learn k-space features from training datasets. We present several optimization objectives, including image quality, hardware constraints, PNS effect suppression and image contrast. Users can simultaneously optimize one or multiple characteristics of a given sampling trajectory. Similar to previous learning-based methods^14,20,21,22, the sampling trajectory can be jointly optimized with trainable reconstruction algorithms to improve image quality. The joint optimization approach can thus exploit the synergy between acquisition and reconstruction, and learn optimized trajectories specific for different anatomies and reconstruction methods^{14,20,28,30,31}. The algorithm can optimize various properties of a sampling trajectory, such as readout waveforms, or rotation angles of readout shots, making it more practical and applicable. We also introduced several techniques to improve efficiency, enabling large-scale 3D trajectory optimization. We tested the proposed methods with multiple imaging applications, including structural and functional imaging. These applications benefited from the SNOPY-optimized sampling trajectories in both simulation and prospective studies.

2 |. THEORY

This section describes the proposed gradient-based methods for trajectory optimization. We use the concept of differentiable programming to compute the descent gradient with respect to sampling trajectories required in the gradient-based methods. The sampling trajectory and reconstruction parameters are differentiable parameters, whose gradients can be computed by auto-differentiation. To learn or update these parameters, one may apply (stochastic) gradient descent algorithms. Fig. 1 illustrates the basic idea. The sampling trajectories can be optimized in conjunction with the parameters of learnable reconstruction algorithms so that the learned sampling trajectories and reconstruction methods are in synergy and produce high-quality images. The SNOPY algorithm combines several optimization objectives to ensure that the optimized sampling trajectories have desired properties. Sec. 2.1 delineates these objective functions. Sec. 2.3 shows that the proposed method is applicable to multiple scenarios with different parameterization strategies. For non-Cartesian sampling, the system model usually involves non-uniform fast Fourier transforms (NUFFT). Sec. 2.4 briefly describes an efficient and accurate way to calculate the gradient involving NUFFTs. Sec. 2.5 suggests several engineering approaches to make this large-scale optimization problem solvable and efficient.

FIGURE 1.

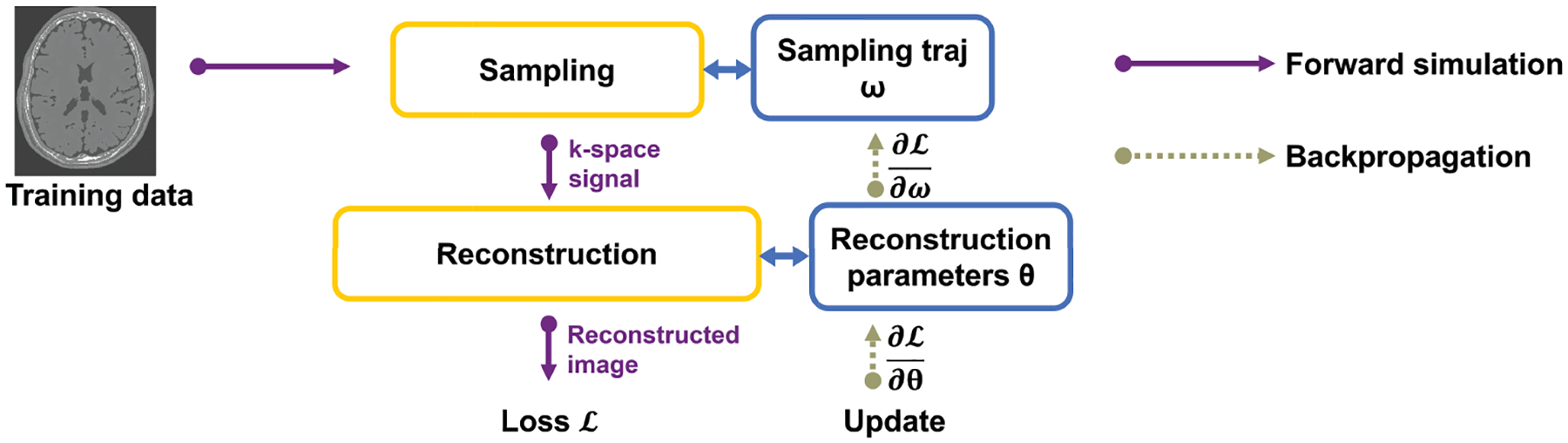
Diagram of SNOPY. The sampling trajectory (and possibly reconstruction parameters) are updated using gradient methods. The training/optimization process uses differentiable programming to obtain the gradient necessary for the update.

2.1 |. Optimization objectives

This section outlines the optimization objectives in SNOPY. As SNOPY is a stochastic gradient descent-like algorithm, the objective function, or loss function, is by default defined on a mini-batch of data. The final loss function can be a linear combination of following loss terms to ensure the optimized trajectory possesses multiple required properties.

2.1.1 |. Image quality

For many MRI applications, efficient acquisition and reconstruction aim to produce high-quality images. Consequently, the learning objective should encourage images reconstructed from sampled k-space signals to match the reference images. We formulate this similarity objective as the following image quality training loss:

$${ℒ}_{\text{recon}}=\ell \left(f_{\mathit{\theta },\mathit{\text{c}}}\left(\mathit{\text{A}}\left(\mathit{\omega }\left(\mathit{\text{c}}\right)\right)\mathit{\text{x}}+\mathit{\epsilon }\right)-\mathit{\text{x}}\right).$$ (1)

Here, $\mathit{\omega }\left(\mathit{\text{c}}\right)\in {ℝ}^{N_{\text{fe}}\times N_{\text{s}}\times N_{\text{d}}}$ denotes the trajectory to be optimized, with $N_{\text{s}}$ shots, $N_{\text{fe}}$ sampling points in each shot, and $N_{\text{d}}$ image dimensions. For 3D MRI, $N_{\text{d}}=3$. $\mathit{\epsilon }$ is simulated complex Gaussian noise. $\mathit{\text{A}}\left(\mathit{\omega }\right)$ is the forward system matrix for sampling trajectory $\mathit{\omega }\left(\mathit{\text{c}}\right)$³². $\mathit{\text{c}}$ denotes the parameterization coefficients of sampling trajectories $\mathit{\omega }$, which is introduced in Sec. 2.3. In this study, $\mathit{\text{A}}$ also incorporated multi-coil sensitivity information³³. $\mathit{\text{x}}$ denotes the reference image from the training set $𝒳$, which is typically reconstructed from fully-sampled signals. In addition to contrast-weighted imaging, if the training dataset $𝒳$ includes quantitative parameter maps, one may also simulate $\mathit{\text{x}}$ using the Bloch equation, and $\mathit{\text{A}}$ can subsequently consider imaging physics such as relaxation. $f_{\mathit{\theta },\mathit{\omega }}(\cdot )$ is the reconstruction algorithm to be delineated in Sec. 2.2. $\mathit{\theta }$ denotes the reconstruction algorithm’s parameters. It can be kernel weights in a convolutional neural network (CNN), or the regularizer coefficient in a model-based reconstruction method. The similarity term $\ell (\cdot )$ can be ${\ell }_1$ norm, ${\ell }_2$ norm, or a combination of both. There are also other ways to measure the distance between $\mathit{\text{x}}$ and $f_{\mathit{\theta },\mathit{\omega }}\left(\mathit{\text{A}}\left(\mathit{\omega }\right)\mathit{\text{x}}+\epsilon \right)$, such as the structural similarity index (SSIM³⁴). For simplicity, this work used a linear combination of ${\ell }_1$ norm and square-of-${\ell }_2$ norm, which is a common practice in deep learning-based image reconstruction³⁵.

2.1.2 |. Hardware limits

The gradient system of MR scanners has physical constraints, namely maximum gradient strength and slew rate. Ideally, we would like to enforce a set of constraints of the form

$${\Vert {\mathit{\text{g}}}_i\left[j,:\right]\Vert }_2\le g_{\text{max}},{\mathit{\text{g}}}_i={\mathit{\text{D}}}_1\mathit{\omega }\left[:,i,:\right]/\left(\gamma \Delta t\right)\in {ℝ}^{\left(N_{\text{fe}}-1\right)\times N_{\text{d}}},$$

for every shot $i=1,\dots ,N_{\text{s}}$ and time sample $j=1,\dots ,N_{\text{fe}}$, where $g_i$ denotes the gradient strength of the $i$ shot and $g_{\text{max}}$ denotes the desired gradient upper bound. One may use a Euclidean norm along the spatial axis so that any rotation of the sampling trajectory still obeys the constraint. Applying the penalty to each individual gradient axis is also feasible. A similar constraint is enforced on the Euclidean norm of the slew rate ${\mathit{\text{s}}}_i={\mathit{\text{D}}}_2\mathit{\omega }\left[:,i,:\right]/\left(\gamma \Delta t^2\right)$, where ${\mathit{\text{D}}}_1$ and ${\mathit{\text{D}}}_2$ denote first-order and second-order finite difference operators applied along the readout dimension. $\Delta t$ denotes the raster time interval and $\gamma$ denotes the gyromagnetic ratio.

To make the optimization more practical, we follow previous studies^20,22, and formulate the hardware constraint as a soft penalty term:

$${ℒ}_{\text{g}}=\sum _{i=1}^{N_{\text{s}}}\sum _{j=1}^{N_{\text{fe}}-1}{\varphi }_{g_{\text{max}}}\left({\Vert {\mathit{\text{g}}}_i\left[j,:\right]\Vert }_2\right)$$ (2)

$${ℒ}_{\text{s}}=\sum _{i=1}^{N_{\text{s}}}\sum _{j=1}^{N_{\text{fe}}-2}{\varphi }_{s_{\text{max}}}\left({\Vert {\mathit{\text{s}}}_i\left[j,:\right]\Vert }_2\right).$$ (3)

Here $\varphi$ is a penalty function, and we use a simple soft-thresholding function ${\varphi }_{\lambda }\left(\mathit{\text{x}}\right)=\text{max}\left(\left|\mathit{\text{x}}\right|-\lambda ,0\right)$, because it is sub-differentiable and easy to implement. It is possible to use more sophisticated functions. Since $\varphi$ here is a soft penalty and the optimization results may exceed the threshold, $s_{\text{max}}$ and $g_{\text{max}}$ can be slightly lower than the scanner’s actual physical limits to ensure that the optimization results are feasible on the scanner. Applying a sanity check before sequence programming is also useful. In addition to the soft-penalty approach, recent studies³⁶ also used projection-based methods.

2.1.3 |. Suppression of PNS effect

The additional gradient axis in 3D imaging can result in stronger peripheral nerve stimulation (PNS) effects compared to 2D imaging. To quantify possible PNS effects of candidate gradient waveforms, SNOPY uses a convolution model described in Ref. 37:

$${\mathit{\text{R}}}_{id}\left(t\right)=\frac{1}{s_{\text{min}}}\underset{0}{\overset{t}{\int }}\frac{{\mathit{\text{s}}}_{id}\left(\theta \right)c}{{(c+t-\theta )}^2}d\theta ,$$ (4)

where ${\mathit{\text{R}}}_{id}$ denotes the PNS effect of the gradient waveform from the $i$th shot and the $d$th dimension. ${\mathit{\text{s}}}_{id}$ is the slew rate of the $i$th shot in the $d$th dimension. $c$ (chronaxie) and $s_{\text{min}}$ (minimum stimulation slew rate) are scanner-specific parameters.

Likewise, we discretize the convolution model and use a soft penalty term as the following loss function:

$$\begin{gathered} {\mathit{\text{p}}}_{id}\left[j\right]=\sum _{k=1}^j\frac{{\mathit{\text{s}}}_{id}\left[k\right]c\Delta t}{s_{\text{min}}{(c+j\Delta t-k\Delta t)}^2}, \\ {ℒ}_{\text{pns}}=\sum _{i=1}^{N_{\text{s}}}\sum _{j=1}^{N_{\text{fe}}}{\varphi }_{p_{\text{max}}}\left({\left(\sum _{d=1}^{N_{\text{d}}}{\mathit{\text{p}}}_{id}{[j]}^2\right)}^{\frac{1}{2}}\right). \end{gathered}$$ (5)

Again, $\varphi$ denotes the soft-thresholding function, with PNS threshold $p_{\text{max}}$ (usually ≤ 80%³⁷). This model combines the 3 spatial axes via the sum-of-squares manner and does not consider anisotropic characteristics of PNS³⁸. The implementation may use an FFT (with zero padding) for efficient convolution.

2.1.4. |. Image contrast

In many applications, the optimized sampling trajectory should maintain certain parameter-weighted contrasts. For example, ideally the (gradient) echo time (TE) should be identical for each shot. Again, we replace this hard constraint with an echo time penalty. Other parameters, like repetition time (TR) and inversion time (TI), can be predetermined in the RF pulse design. Specifically, the corresponding loss function encourages the sampling trajectory to cross the k-space center at certain time points:

$${ℒ}_c=\sum _{\left\{i,j,d\right\}\in C}{\varphi }_0\left(\left|\mathit{\omega }\left[i,j,d\right]\right|\right),$$ (6)

where $\mathit{\text{c}}$ is a collection of gradient time points that are constrained to cross the k-space zero point. $\varphi$ is still a soft-thresholding function, with threshold 0.

The total loss function is a linear combination of the above terms

$$ℒ={\lambda }_{\mathit{\text{recon}}}{ℒ}_{\text{recon}}+{\lambda }_g{ℒ}_{\text{g}}+{\lambda }_s{ℒ}_{\text{s}}+{\lambda }_{\mathit{\text{pns}}}{ℒ}_{\text{pns}}+{\lambda }_c{ℒ}_{\text{c}}.$$

Note that not every term is required. For example, experiment 3.2.2 only used the ${ℒ}_{\text{recon}}$. Sec. 5 further discusses how to choose linear weights $\lambda \text{s}$.

2.2 |. Reconstruction

In (1), the reconstruction algorithm $f_{\mathit{\theta },\mathit{\omega }}(\cdot )$ can be various algorithms. Consider a typical cost function for regularized MR image reconstruction

$$\widehat{\mathit{\text{x}}}=\underset{\mathit{\text{x}}}{\text{arg\hspace{0.17em}min}}\parallel \mathit{\text{A}}\left(\mathit{\omega }\right)\mathit{\text{x}}-\mathit{\text{y}}{\parallel }_2^2+ℛ\left(\mathit{\text{x}}\right).$$ (7)

$ℛ\left(\mathit{\text{x}}\right)$ here can be a Tikhonov regularization $v\parallel \mathit{\text{x}}{\parallel }_2^2$ (CG-SENSE³⁹), a sparsity penalty $v\parallel \mathit{\text{Tx}}{\parallel }_1$ (compressed sensing⁴⁰, $\mathit{\text{T}}$ is a finite-difference operator), a roughness penalty $v\parallel \mathit{\text{Tx}}{\parallel }_2^2$ (penalized least squares, PLS), or a neural network (model-based deep learning, MoDL⁴¹). Sec. 4 shows that different reconstruction algorithms lead to distinct optimized sampling trajectories. In training, $\mathit{\text{y}}$ is retrospectively simulated as $\overline{\mathit{\text{y}}}=\mathit{\text{A}}\left(\mathit{\omega }\right)\mathit{\text{x}}+\mathit{\epsilon }$ (following (1)). In prospective studies, $\mathit{\text{y}}$ is the acquired k-space data.

To get a reconstruction estimation $\widehat{\mathit{\text{x}}}$, one may use iterative reconstruction algorithms. Specifically, the algorithm should be step-wise differentiable (or sub-differentiable) to enable differentiable programming. The backpropagation uses the chain rule to traverse every step of the iterative algorithm to calculate gradients with respect to variables such as $\mathit{\omega }$.

2.3 |. Parameterization

As is shown in Ref. 20, directly optimizing every k-space sampling location (or equivalently every gradient waveform time point) may lead to sub-optimal results. Additionally, in many applications, one may need to optimize certain properties of existing sampling patterns, such as the rotation angles of a multi-shot spiral trajectory, so that the optimized trajectory can be easily integrated into existing workflows. For these needs, we propose two parameterization strategies.

The first approach, spline-based freeform optimization, represents the sampling pattern using a linear basis, i.e., $\mathit{\omega }=\mathit{\text{Bc}}$, where $\mathit{\text{B}}$ is a matrix of samples of a basis such as quadratic B-spline kernels and $\mathit{\text{c}}$ denotes the coefficients to be optimized^20,22. This approach fully exploits the generality of a gradient system. Using a linear parameterization like B-splines reduces degrees of freedom and facilitates applying hardware constraints^20,42. Additionally, the parameterization can be combined with multi-scale optimization to avoid sub-optimal local minima and further improve optimization results^17,20,22. However, freeformly optimized trajectories could introduce implementation challenges. For example, some MRI systems can not store hundreds of different gradient waveforms.

The second approach is to optimize attributes $\mathit{\text{c}}$ of existing trajectories, where $\mathit{\omega }\left(\mathit{\text{c}}\right)$ is a differentiable function of the attributes $\mathit{\text{c}}$. For example, many applications use radial trajectories, where the rotation angles can be optimized. Suppose $\mathit{\text{s}}\in {ℝ}^{3\times N}$ is one radial sampling spoke, and consider an $M$-shot 3D radial trajectory,

$$\mathit{\omega }=\left[\begin{array}{ccc}{\mathit{\text{R}}}_1& \cdots & {\mathit{\text{R}}}_M\end{array}\right]{\mathit{\text{I}}}_M\otimes \mathit{\text{s}},$$ (8)

where ${\mathit{\text{R}}}_{\mathit{\text{i}}}\in {ℝ}^{3\times 3}$ denotes a rotation matrix, ${\mathit{\text{I}}}_M$ denotes an identity matrix of size $M$, and $\otimes$ denotes the Kronecker product. In this case, the list of ${\mathit{\text{R}}}_i$ is the coefficient to be optimized. This approach is easier to implement on scanners, and can work with existing workflows.

2.4 |. Efficient and accurate Jacobian calculation

In the similarity loss (1), the sampling trajectory is embedded in the forward system matrix $\mathit{\text{A}}$. The system matrix for non-Cartesian sampling usually includes NUFFT operators³². Updating the sampling trajectory in each optimization step requires the Jacobian, or the gradient with respect to the sampling trajectory. The NUFFT operator typically involves interpolation in the frequency domain, which is non-differentiable due to rounding operations. Several previous works used auto-differentiation (with sub-gradients) to calculate an approximate numerical gradient^22,29, but that approach is inaccurate and slow²⁸. We derived an efficient and accurate Jacobian approximation method²⁸. For example, the efficient Jacobian of a forward system model $\mathit{\text{A}}$ is:

$$\frac{\partial \mathit{\text{Ax}}}{\partial {\mathit{\omega }}^{\left[d\right]}}=-ı\text{diag}\left\{\mathit{\text{A}}\left(\mathit{\text{x}}\odot {\mathit{\text{r}}}^{\left[d\right]}\right)\right\},$$ (9)

where $d\in \left\{1,2,3\right\}$ denotes the spatial dimensions, ${\mathit{\text{r}}}^{\left[d\right]}$ denotes the Euclidean spatial grid, $\odot$ denotes the Hadamard product, and $\iota$ is the imaginary unit. Calculating this Jacobian simply uses another NUFFT, which is more efficient than the auto-differentiation approach. See Ref. 28 for more cases, such as $\frac{\partial {\mathit{\text{A}}}^{\prime }\mathit{\text{Ax}}}{\partial {\mathit{\omega }}^{\left[d\right]}}$ and the detailed derivation.

2.5 |. Efficient optimization

2.5.1 |. Optimizer

Generally, to optimize the sampling trajectory $\mathit{\omega }$ and other parameters (such as reconstruction parameters $\mathit{\theta }$) via stochastic gradient descent-like methods, each update takes a step (in the simplest form)

$$\begin{gathered} {\mathit{\theta }}^K={\mathit{\theta }}^{K-1}-{\eta }_{\mathit{\theta }}\frac{\partial ℒ}{\partial \mathit{\theta }}\left({\mathit{\omega }}^{K-1},{\mathit{\theta }}^{K-1}\right) \\ {\mathit{\omega }}^K={\mathit{\omega }}^{K-1}-{\eta }_{\mathit{\omega }}\frac{\partial ℒ}{\partial \mathit{\omega }}\left({\mathit{\omega }}^{K-1},{\mathit{\theta }}^{K-1}\right), \end{gathered}$$

where $ℒ$ is the loss function described in Section 2.1 and where ${\eta }_{\theta }$ and ${\eta }_{\mathit{\omega }}$ denote step-size parameters.

The optimization is highly non-convex and may suffer from sub-optimal local minima. We used stochastic gradient Langevin dynamics (SGLD)⁴³ as the optimizer to improve results and accelerate training. Each update of SGLD injects Gaussian noise into the gradient to introduce randomness

$$\begin{gathered} {\mathit{\theta }}^K={\mathit{\theta }}^{K-1}-{\eta }_{\theta }\frac{\partial ℒ}{\partial {\mathit{\theta }}^{K-1}}+\sqrt{2{\eta }_{\mathit{\theta }}}𝒩\left(0,1\right) \\ {\mathit{\omega }}^K={\mathit{\theta }}^{K-1}-{\eta }_{\mathit{\omega }}\frac{\partial ℒ}{\partial {\mathit{\omega }}^{K-1}}+\sqrt{2{\eta }_{\mathit{\omega }}}𝒩\left(0,1\right). \end{gathered}$$ (10)

Across most experiments, we observed that SGLD led to improved results and faster convergence compared with SGD or Adam⁴⁴. Fig. 2 shows a loss curve of SGLD and Adam of experiment 3.2.3.

FIGURE 2.

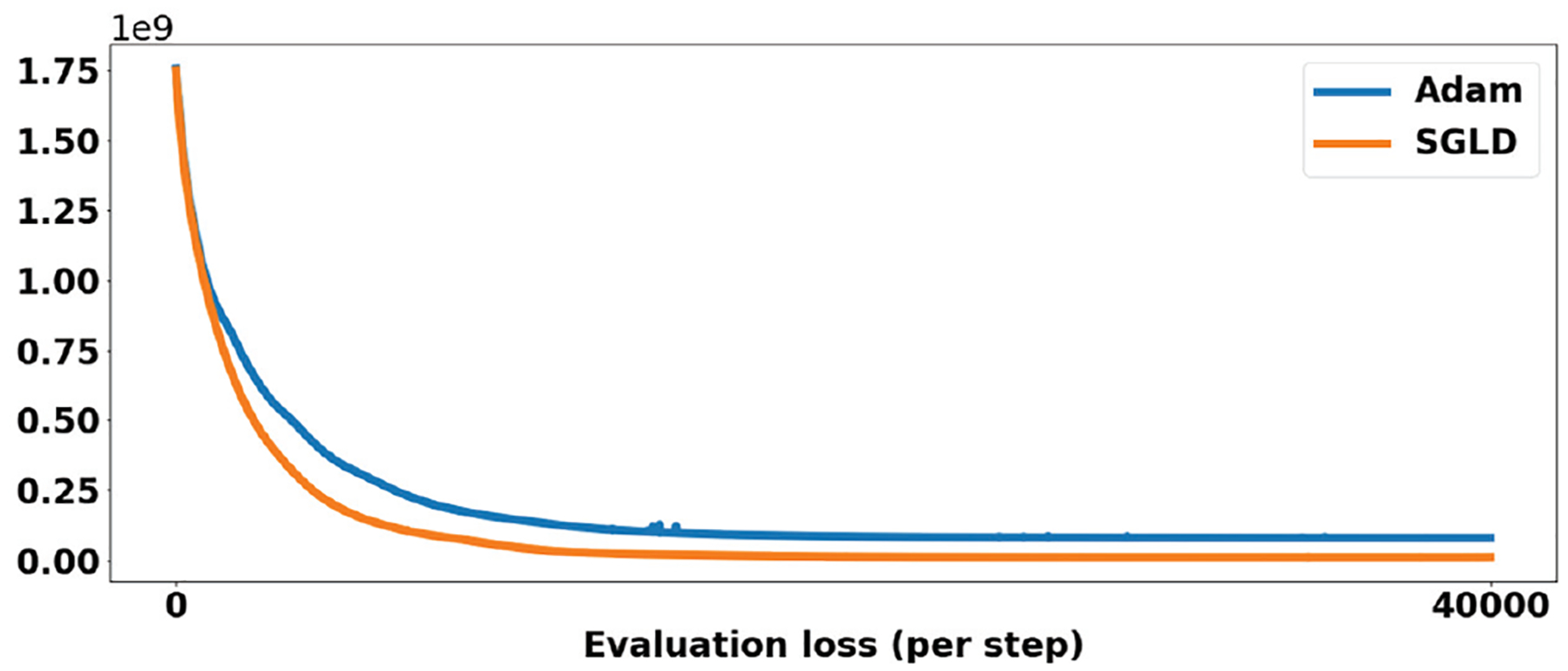
The evaluation loss curve for SGLD and Adam. The training process costs ~1 hrs.

2.5.2 |. Memory saving techniques

Due to the large dimension, the memory cost for naive 3D trajectory optimization would be prohibitively intensive. We developed several techniques to reduce memory use and accelerate training.

As discussed above, the efficient Jacobian approximation uses only 10% of the memory required by the standard auto-differentiation approach²⁸. We also used in-place operations in certain reconstruction steps, such as the conjugate gradient (CG) method, because with careful design it will not interrupt auto-differentiation. (See our open-source code^* for details.) The primary memory bottleneck relates to 3D NUFFT operators. One can pre-calculate the Toeplitz embedding kernel to save memory and accelerate computation^45,46. In the training phase, we used NUFFTs with lower accuracy, for instance, with a smaller oversampling ratio for gridding²⁸. Table 1 shows the incrementally improved efficiency achieved with these techniques. Without the proposed techniques, optimizing 3D trajectories would require hundreds of gigabytes of memory, which would be impractical for a single node. SNOPY enables solving this otherwise prohibitively large problem on a single GPU.

TABLE 1.

The memory/time use reduction brought by proposed techniques. Here we used a 2D 400×400 test case, and CG-SENSE reconstruction (20 iterations). ‘+’ means adding the technique to previous columns.

Plain	+Efficient Jacobian	+In-place ops	+Toeplitz embedding	+Low-res NUFFT
5.7GB / 10.4s	272MB / 1.9s	253MB / 1.6s	268MB / 0.4s	136MB / 0.2s

3 |. METHODS

3.1 |. Datasets

We used two publicly available datasets; both of them contain 3D multi-coil raw k-space data. SKM-TEA⁴⁷ is a 3D quantitative double-echo steady-state (qDESS⁴⁸) knee dataset. It was acquired by 3T GE MR750 scanners and 15/16-channel receiver coils. SKM-TEA includes 155 subjects. We used 132 for training, 10 for validation, and 13 for the test. Calgary brain datase⁴⁹ is a 3D brain T1w MP-RAGE⁵⁰ k-space dataset. It includes 67 available subjects, acquired by an MR750 scanner and 12-channel head coils. We used 50 volumes for training, 6 for validation, and 7 for testing. All sensitivity maps were calculated by ESPIRiT⁵¹.

3.2 |. Simulation experiments

We experimented with multiple scenarios to show the broad applicability of the proposed method. All the experiments used a node equipped with an Nvidia Tesla A40 GPU for training.

3.2.1 |. Optimizing 3D gradient waveform

We optimized the sampling trajectory with a 3D radial (‘kooshball’) initialization^52,53. As is described in 2.3, the experiment optimized the readout waveform of each shot with B-spline parameterization, to reduce the number of degrees of freedom and enable multi-scale optimization. The initial 3D radial trajectory had a 5.12 ms long readout (raster time = 4 μs) and 1024 shots (8× acceleration), using the rotation angle described in Ref. 16. The training used the SKM-TEA dataset. The retrospectively cropped FOV was 158×158×51 mm³ with 0.76×0.62×1.6 mm³ simulated resolution. The receiver bandwidth was ±125 kHz (dwell time = 4 μs). The training loss was

$$ℒ={ℒ}_{\text{recon}}+{10}^3{ℒ}_{\text{g}}+{10}^3{ℒ}_{\text{s}}+{ℒ}_{\text{pns}}.$$

The gradient strength $\left(g_{\text{max}}\right)$ and slew rate $\left(s_{\text{max}}\right)$ were 50 mT/m and 150 mT/m/ms (for individual axis). The PNS threshold $\left(p_{\text{max}}\right)$ was 80%. The simulated noise $\mathit{\epsilon }$ was 0. The batch size was 3. The learning rate ${\eta }_{\mathit{\omega }}$ decayed from 10⁻⁴ to 0 linearly. For multi-level optimization, we used 3 levels (with B-spline kernel widths = 32, 16, and 8), and each level used 200 epochs. The total training time was ~240 hrs. The trajectory was optimized with respect to several image reconstruction algorithms. We used a regularizer weight $v={10}^{-3}$ and 30 CG iterations for CG-SENSE and PLS. For learning-based reconstruction, we used the MoDL⁴¹ network that alternates between a neural network-based denoiser and data consistency updates. We used a 3D version of the denoising network⁵⁴, 20 CG iterations for the data consistency update, and 6 outer iterations. Similar to previous investigations^14,20, SNOPY jointly optimized the neural network’s parameters and the sampling trajectory using (10).

3.2.2 |. Optimizing rotation angles of stack-of-stars trajectory

This experiment optimized the rotation angles of a stack-of-stars trajectory, which is a widely used volumetric imaging sequence. The training used the Calgary brain dataset. We used PLS as the reconstruction method for simplicity, with $v={10}^{-3}$ and 30 iterations. The simulated noise $\mathit{\epsilon }$ was 0 and the batch size was 12. We used 200 epochs and a learning rate linearly decaying from 10⁻⁴ to 0. The FOV was retrospectively cropped to 256×218×32 mm³ with 1 mm³ resolution. We used 40 spokes per kz location (6× acceleration), and 1280 spokes in total. The readout length was 3.5 ms. The receiver bandwidth was ± 125 kHz (dwell time = 4 μs). The trajectory was a stack of 32 kz planes, hence SNOPY optimized 1280 rotation angles in this case.

Since optimizing rotation angles does not impact the gradient strength, slew rate, PNS, and image contrast, we only used the reconstruction loss $ℒ={ℒ}_{\text{recon}}$. We regarded the method (RSOS-GR) proposed in previous works¹² as the best empirical scheme. We applied 200 epochs with a linearly decaying learning rate from 10⁻³ to 0. The training cost ~20 hrs.

3.2.3 |. PNS suppression of 3D rotational EPI trajectory for functional imaging

The third application optimizes the rotation EPI (REPI) trajectory⁵⁵, which provides an efficient sampling strategy for fMRI. For high resolution (i.e., ≤1 mm), we found that subjects may experience strong PNS effects introduced by REPI. This experiment aimed to reduce the PNS effect of REPI while preserving the original image contrast. We optimized one shot of REPI, being parameterized by B-spline kernels (width=16). The optimized readout shot was rotated using the angle scheme similar to Ref. 55 for multi-shot acquisition.

We designed the REPI readout for an oscillating stead steady imaging (OSSI) sequence, a novel fMRI signal model that can improve the SNR^56,57. The FOV was 200×200×12 mm³, with 1 mm³ isotropic resolution, TR = 16 ms, and TE = 7.4 ms. The readout length was 10.6 ms. The receiver bandwidth was ±250 kHz (dwell time = 2 μs). The gradient strength $\left(g_{\text{max}}\right)$, and slew rate $\left(s_{\text{max}}\right)$ constraints were 58 mT/m and 200 mT/m/ms (3 axes combined).

To accelerate training, the loss term here excluded the reconstruction loss ${ℒ}_{\text{recon}}$:

$$ℒ={10}^{-2}{ℒ}_g+{10}^{-2}{ℒ}_s+{ℒ}_{\mathit{\text{pns}}}+{10}^2{ℒ}_c.$$

The training used 40,000 steps, with the learning rate decaying linearly from 10⁻⁴ to 0. The training cost ~1 hrs.

3.3 |. In-vivo experiments

We implemented the optimized trajectory prospectively on a GE UHP 3.0T scanner equipped with a Nova Medical 32-channel head coil. Participants gave informed consent under local IRB approval. Since the cache space in this MR system cannot load hundreds of distinct gradient waveforms, the experiment 3.2.1 was not implemented prospectively. Readers may refer to the corresponding 2D prospective studies²⁰ for image quality improvement and correction of eddy current effects. For experiment 3.2.2, we programmed the sampling trajectory with a 3D T1w fat-saturated GRE sequence⁵⁸, with TR/TE = 14/3.2 ms and FA = 20°. The experiment included 4 healthy subjects. For experiment 3.2.3, to rate the PNS effect, we asked 3 participants to score the nerve stimulation with a 5-point Likert scale from ‘mild tingling’ to ‘strong muscular twitch.’

3.4 |. Reproducible research

The code is publicly available^†. As an accompanying project, MIRTorch^‡ facilitates applying differentiable programming to MRI sampling and reconstruction.

4 |. RESULTS

For the spline-based freeform optimization experiment delineated in 3.2.1, Fig. 3 presents an example of the optimized trajectory, along with zoomed-in regions and plots of a single shot. Similar to the 2D case²⁰ and SPARKLING^16,17, the multi-level B-spline optimization generates a swirling trajectory that can cover more k-space in the fixed readout time, to reduce large gaps between sampling locations and, consequently, aliasing artifacts. Notably, the zoomed-in region highlights that different shots were automatically learned not to overlap with each other, which implicitly improved the sampling efficiency¹⁷. Fig. 4 displays point spread functions (PSFs) of trajectories jointly optimized with different reconstruction algorithms. To visualize the sampling density in different regions of k-space, we convolved the trajectory with a Gaussian kernel, and Fig. 4 shows the density of central profiles from different views. Compared with 3D kooshball, the SNOPY optimization led to fewer radial patterns in PSFs, corresponding to fewer streak artifacts in Fig. 5. Trajectories optimized with different reconstruction algorithms generated different PSFs and densities, which agrees with previous studies^28,30,31. Table 2 lists the quantitative reconstruction quality of different trajectories. The image quality metric is the average peak signal-to-noise ratio (PSNR) of the test set. SNOPY led to ~4 dB higher PSNR than the kooshball initialization. Fig. 5 includes examples of reconstructed images. Compared to kooshball, SNOPY’s reconstructed images have reduced artifacts and blurring. Though MoDL (and its variants) are well-performing NN-based reconstruction algorithms according to the open fastMRI reconstruction challenge⁵⁹, many important structures are distorted using the kooshball trajectory. Using the SNOPY-optimized trajectory, a simple model-based reconstruction (CG-SENSE) can reconstruct such structures. The gradient strength and the slew rate of optimized sampling trajectories are exhibited in the supplementary materials. SNOPY solves a non-convex problem; therefore, its results depend on the initialization. The supplementary materials compare optimization results with different initializations.

FIGURE 3.

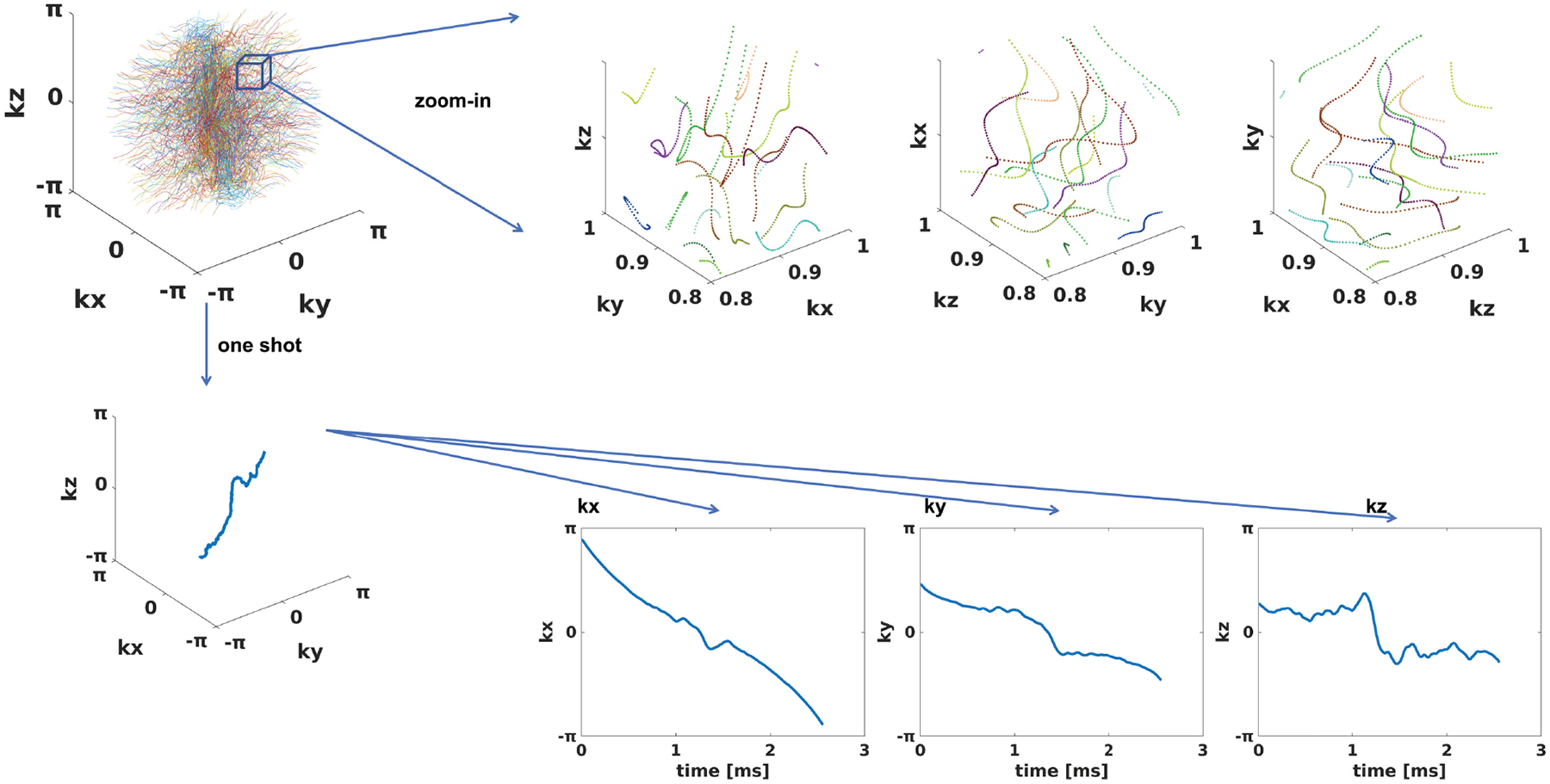
The optimized sampling trajectory of experiment 3.2.1. The training process involves the SKM-TEA dataset and CG-SENSE reconstruction. The upper row shows a zoomed-in region from different viewing perspectives. The lower row displays one shot from different perspectives.

FIGURE 4.

Visualization of the optimized trajectory in experiment 3.2.1. The upper subfigure displays PSFs (log-scaled, single-coil) of trajectories optimized with different reconstruction methods. The lower subfigure shows the density of sampling trajectories, obtained by convolving the sampling points with a Gaussian kernel. Three rows are central profiles from three perspectives.

FIGURE 5.

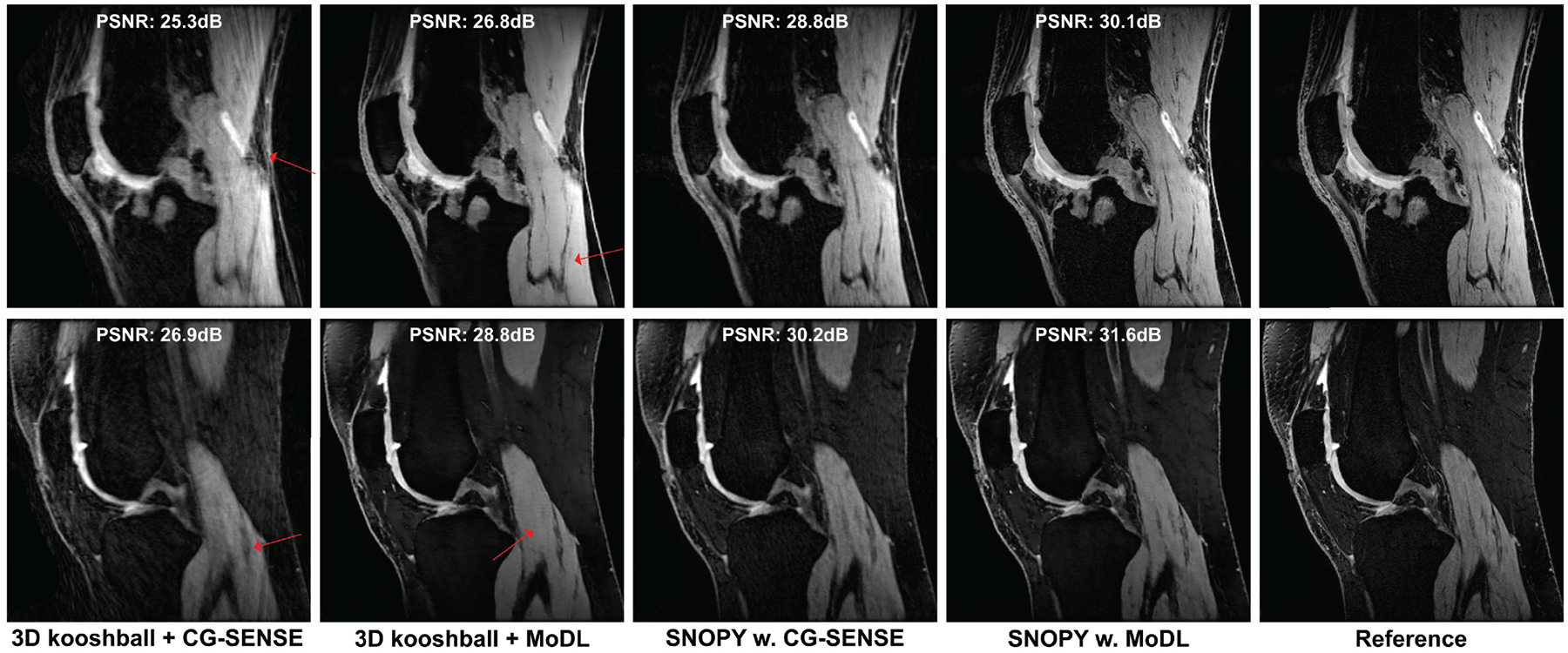
Examples of the reconstructed images for two knee slices in experiment 3.2.1.

TABLE 2.

The quantitative reconstruction quality (NRMSE) of the test set.

	CG-SENSE	PLS	MoDL
3D kooshball	28.2 dB	28.2 dB	30.1 dB
SNOPY	32.3 dB	32.4 dB	33.6 dB

For experiment 3.2.2, Fig. 6 shows the PSF of the optimized and RSOS-GR schemes¹². For the in-plane $\left(x-y\right)$ PSF, the SNOPY rotation shows noticeably reduced streak-like patterns. In the $y-z$ direction, SNOPY optimization leads to a narrower central lobe and suppressed aliasing artifacts. The prospective in-vivo experiments also support this theoretical finding. In Fig. 6, the example slices (reconstructed by PLS) from prospective studies show that SNOPY reduced streaking artifacts. The average PSNR of SNOPY and RSOS-GR for the 4 participants were 39.23 dB and 37.84 dB, respectively. Supplementary materials show the rotation angles before and after SNOPY optimization.

FIGURE 6.

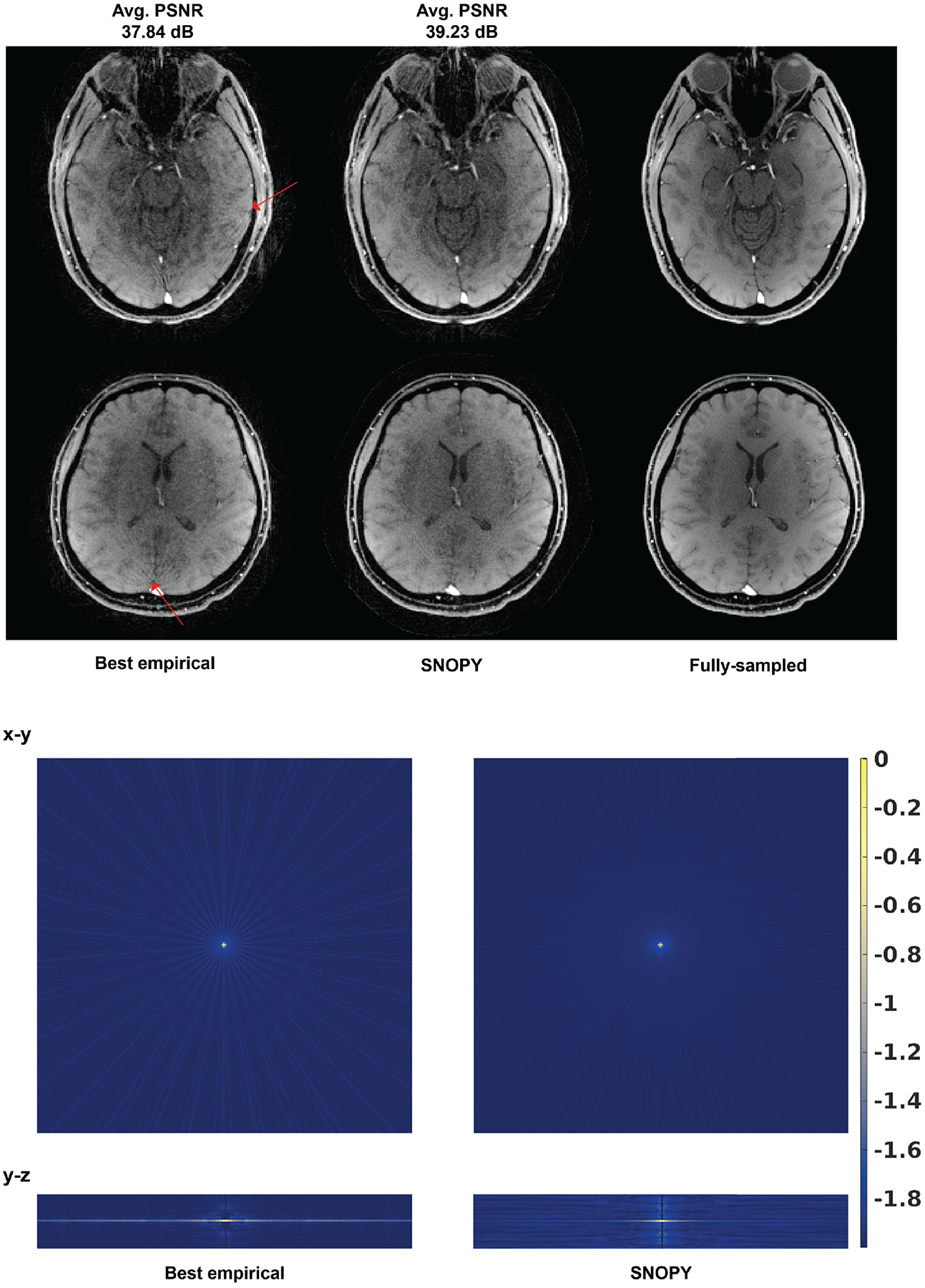
Prospective results of 3.2.2, optimizing the rotation angles of the stack-of-stars (6× acceleration). ‘Best empirical’ uses the design from a previous study¹². The upper subfigure shows two slices from prospective in-vivo experiments. The reconstruction algorithm was PLS. Avg. PSNR is the average PSNR of the 4 subjects compared to the fully sampled reference. The lower subfigure shows the log-scaled PSF (single-coil) of two trajectories.

In experiment 3.2.3, we tested three settings: unoptimized REPI, optimized with PNS threshold ($p_{\text{max}}$ in (5)) = 80%, and optimized with $p_{\text{max}}=70\text{\%}$. Fig. 7 shows one slice of reconstructed images by the CS-SENSE algorithm, as well as the subjective ratings of PNS. Though SNOPY suppressed the PNS effect, the image contrast was well preserved by the image contrast regularizer (6). Fig. 8 presents one shot before and after the optimization, and one plot of simulated PNS effects. The SNOPY optimization effectively reduced subjective PNS effects of given REPI readout gradients in both simulation and in-vivo experiments. Intuitively, SNOPY smoothed the trajectory to avoid a constantly high slew rate, preventing a strong PNS effect.

FIGURE 7.

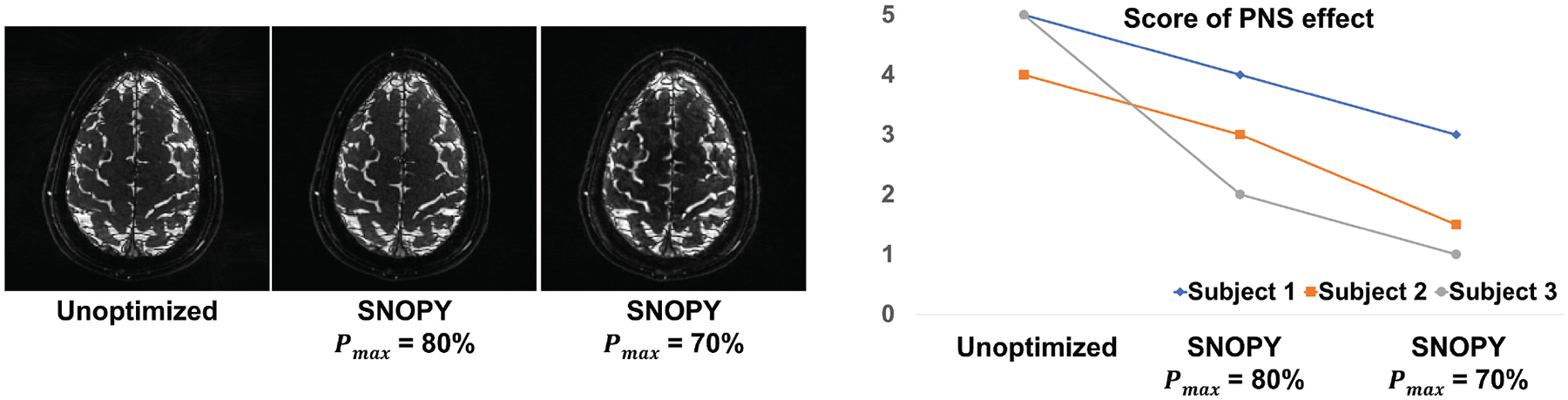
Prospective results of 3.2.3. We showed three different trajectories: the unoptimized REPI, as well as SNOPY-optimized with PNS thresholds of 80% and 70%. The left subfigure shows one slice of reconstructed images. The reconstruction used PLS and 120 shots (volume TR = 2s). The right subfigure shows subjective scores of the PNS effect.

FIGURE 8.

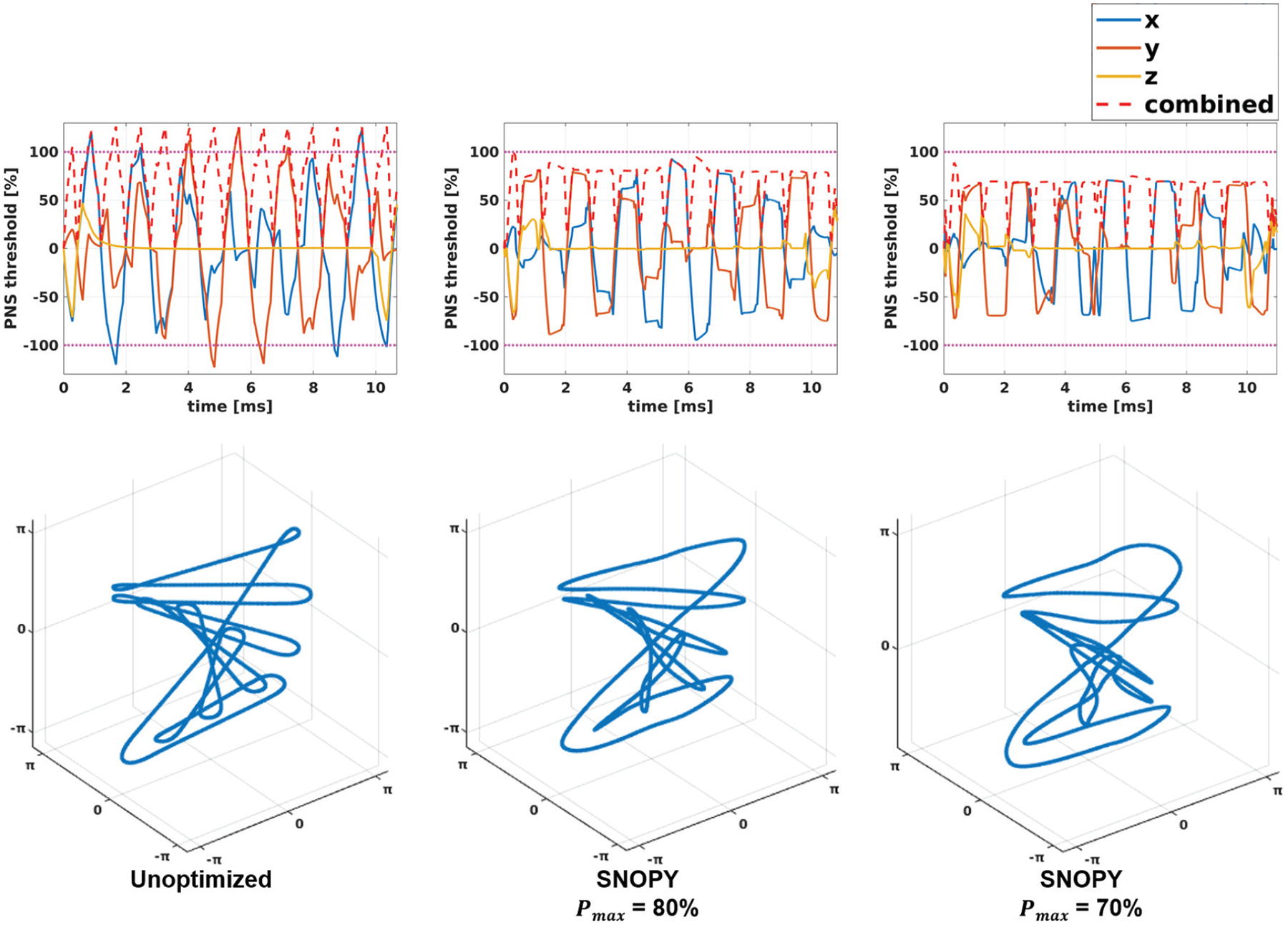
The first row of plots displays the PNS effect calculated by the convolution model (5) used in Experiment 3.2.3. The second row shows the corresponding readout trajectories before and after SNOPY optimization.

5 |. DISCUSSION

SNOPY presents a novel and intuitive approach to optimizing non-Cartesian sampling trajectories. Via differentiable programming, SNOPY enables the application of gradient-based and data-driven methods to trajectory design. Various applications and in-vivo experiments demonstrated the applicability and robustness of SNOPY and its 2D predecessor²⁰.

Experiments 3.2.1 and 3.2.2 used SNOPY to tailor sampling trajectories according to specific training datasets and reconstruction algorithms, by formulating reconstruction image quality as a training loss. One concern was whether the learned trajectories would overfit the training dataset. In experiment 3.2.2, the training set used an MP-RAGE sequence, while the prospective sequence was an RF-spoiled GRE. Similarly, 2D prospective and retrospective experiments²⁰ showed that trajectories learned with particular pulse sequences and hardware still improved the image quality of other sequences and hardware, and the NN-based reconstruction did not require fine-tuning with respect to prospective experiments. These empirical studies suggest that trajectory optimization is robust to moderate distribution shifts between training and inference. An intuitive explanation is that SNOPY can improve the PSF by reducing aliasing, and such improvements are universally beneficial. Future investigations will explore the robustness of SNOPY in more diverse settings, such as optimizing trajectories with healthy controls and prospectively testing them with pathological participants to examine image quality for pathologies. It will also be desirable to test SNOPY with different FOVs, resolutions, and ${\text{B}}_0$ strengths.

Our experiments demonstrated that iterative reconstruction with simple analytical regularizers, such as CG-SENSE, can benefit from the SNOPY-optimized sampling trajectories. As depicted in Fig. 3, CG-SENSE with SNOPY optimization can successfully reconstruct many anatomical structures that were blurred in the MoDL reconstruction without SNOPY trajectory. This result is consistent with previous studies²⁸, where compressed sensing algorithms with trajectory optimization also outperformed NN-based reconstruction. These findings indicate untapped potentials of model-based reconstruction by optimizing sampling trajectories.

MRI systems are prone to imperfections such as field inhomogeneity⁶⁰ and eddy currents⁶¹. Many correction approaches exist, such as ${\text{B}}_0$-informed reconstruction⁴⁵ and trajectory mapping^62,63. SNOPY-optimized trajectories are compatible with existing correction methods. For instance, we demonstrated the feasibility of implementing eddy currents correction for a 2D freeform optimized trajectory in Ref. 20. Additionally, incorporating system imperfections into the forward learning/optimization phase, such as off-resonance maps in the system model $\mathit{\text{A}}$ (as defined in (1)), may enhance the intrinsic robustness of the optimized trajectory. However, this approach requires the distribution of system imperfections, which is typically scanner-specific. To address this limitation, we plan to investigate prospective simulation approaches in future studies. The model mismatch may also happen at the digitization level: the training set typically consists of concrete discrete-space images, whereas real objects are continuous. This inverse crime is common in learning-based methods and may lead to suboptimal results. Future research should investigate strategies for mitigating this issue.

SNOPY uses a relatively simplified model of PNS. More precise models, such as Ref. 38, may lead to improved PNS suppression results. SNOPY can also incorporate other optimization objectives to encourage properties such as robustness to field inhomogeneity and reduction of acoustic noise.

The training process incorporates several loss terms, including image quality, PNS suppression, hardware limits, and image contrast. By combining these terms, the optimization can lead to trajectories that have multiple desired characteristics. One may alter the optimization results by controlling the coefficients. For example, with a larger coefficient of the hardware constraint loss, the trajectory will better conform to $s_{\text{max}}$ and $g_{\text{max}}$. The supplementary materials contain an example of optimization results using different combinations of weights. Setting the weights of several terms can be complicated. Empirically, the weight of soft constraints, including hardware (${ℒ}_{\text{g}}$ and ${ℒ}_{\text{s}}$), PNS suppression $\left({ℒ}_{\text{pns}}\right)$, and contrast $\left({ℒ}_{\text{c}}\right)$ can be tuned to a higher value if the optimized trajectory significantly violates these constraints. Additionally, the training losses may sometimes contradict each other, and the optimization process would get stuck in a local minimum. To address this, several empirical tricks have been employed. Similar to SPARKLING¹⁷, the constraint on maximum gradient strength can be relaxed using a higher receiver bandwidth. Bayesian optimization is another option for finding optimal loss weights, but may increase training time. Using SGLD can introduce randomness that helps escape local minima. In spline-based optimization, one can use a larger B-spline kernel width in the early stages of a coarse-to-fine search.

Trajectory optimization is a non-convex problem. SNOPY uses several methods, including effective Jacobian approximation, parameterization, multi-level optimization, and SGLD, to alleviate the non-convexity and achieve better optimization results. These methods were also found to be effective in previous studies^20,28. Initialization is also important for non-convex problems, as demonstrated in the supplementary materials. SNOPY can leverage existing knowledge of MR sampling as a benign initialization. For instance, our experiments used the widely accepted golden-angle stack-of-stars as optimization bases. The SNOPY algorithm can sequentially improve these skillfully designed trajectories to combine the best of both stochastic optimization and researchers’ insights.

SNOPY has a wide range of potential applications, including dynamic and quantitative imaging, particularly if large-scale quantitative datasets are available. These new applications may require task-specific optimization objectives in addition to the ones described in Sec. 2.1. In particular, if the reconstruction method is not easily differentiable, such as the MR fingerprinting reconstruction based on dictionary matching⁶⁴, one needs to design a surrogate objective for image quality.

Abbreviations:

MRI

magnetic resonance imaging

PSNR

peak signal-to-noise ratio