What drives performance in machine learning models for predicting heart failure outcome?

Abstract

Aims

The development of acute heart failure (AHF) is a critical decision point in the natural history of the disease and carries a dismal prognosis. The lack of appropriate risk-stratification tools at hospital discharge of AHF patients significantly limits clinical ability to precisely tailor patient-specific therapeutic regimen at this pivotal juncture. Machine learning-based strategies may improve risk stratification by incorporating analysis of high-dimensional patient data with multiple covariates and novel prediction methodologies. In the current study, we aimed at evaluating the drivers for success in prediction models and establishing an institute-tailored artificial Intelligence-based prediction model for real-time decision support.

Methods and results

We used a cohort of all 10 868 patients AHF patients admitted to a tertiary hospital during a 12 years period. A total of 372 covariates were collected from admission to the end of the hospitalization. We assessed model performance across two axes: (i) type of prediction method and (ii) type and number of covariates. The primary outcome was 1-year survival from hospital discharge. For the model-type axis, we experimented with seven different methods: logistic regression (LR) with either L₁ or L₂ regularization, random forest (RF), Cox proportional hazards model (Cox), extreme gradient boosting (XGBoost), a deep neural-net (NeuralNet) and an ensemble classifier of all the above methods. We were able to achieve an area under receiver operator curve (AUROC) prediction accuracy of more than 80% with most prediction models including L1/L2-LR (80.4%/80.3%), Cox (80.2%), XGBoost (80.5%), NeuralNet (80.4%). RF was inferior to other methods (78.8%), and the ensemble model was slightly superior (81.2%). The number of covariates was a significant modifier (P < 0.001) of prediction success, the use of multiplex-covariates preformed significantly better (AUROC 80.4% for L1-LR) compared with a set of known clinical covariates (AUROC 77.8%). Demographics followed by lab-tests and administrative data resulted in the largest gain in model performance.

Conclusions

The choice of the predictive modelling method is secondary to the multiplicity and type of covariates for predicting AHF prognosis. The application of a structured data pre-processing combined with the use of multiple-covariates results in an accurate, institute-tailored risk prediction in AHF

Graphical Abstract

Graphical Abstract.

Introduction

Despite the immense progress in cardiology in the last decades, heart failure is a growing pandemic worldwide. It is a leading cause of morbidity and mortality and a colossal economic burden on healthcare systems.^1–3 Acute heart failure (AHF) is the most common cause for hospitalization for adults (>65 years) in western societies.⁴ The prognosis of patients admitted with AHF is dismal, with 30% readmission rate and 5 to 15% mortality rate at 60 to 90 days post-discharge.^5,6 Nevertheless, AHF is a heterogenous syndrome with a variable prognosis and identifying patients for early events may have a broad impact on health care delivery.⁷ While in recent years, the armamentarium for mitigating high risk heart failure has been expanded, the lack of appropriate risk-stratification tools for AHF patients limits physician ability for tailoring the appropriate therapeutic and follow-up regimen. This limitation may contribute to the unacceptably high re-hospitalization rate and short-term mortality associated with AHF.^6,8

Advances in statistical machine learning (ML) method have led to an explosion of personalized risk scores based on a large number of patient-specific covariates. Many of these models were developed using electronic medical records (EMRs) of large patient populations. When assessing the value of these risk scores, several factors are often conflated: the use of large high-dimensional patient data derived from EMR, and the use of novel statistical methods for prediction. Such methods are often identified with the field of ML and include random-forest,⁹ gradient-boosted decision trees,¹⁰ sparse-regression methods such as least absolute shrinkage and selection operator¹¹ and deep-neural nets.¹²

Prediction based on hospitalization data is of major importance for supporting decisions related to optimizing patient discharge and examining the appropriate therapeutic strategy (e.g. eligibility for advanced heart failure device treatment and heart transplantation) and the surveillance schedule. In the current study, we used a single-centre cohort of AHF patients aiming at developing a clinically useful model for the prediction of mortality and HF re-hospitalization after hospital discharge. Toward this aim we evaluated the relative contribution of two axes of prediction drivers: (i) the type and number of covariates; (ii) The type of the prediction model including classical statistical models and ML-based methods.

Methods

Study population

We used a database of all patients admitted to the Rambam Medical Center, Haifa, Israel, with the primary diagnosis of AHF between September 2004 and December 2015. Eligible patients were those hospitalized with new-onset or worsening of preexisting heart failure as the primary cause of admission,^13–15 using the European Society of Cardiology criteria.¹⁶ The study was performed in accordance with the Declaration of Helsinki and approved by the institutional review committee on human research. Like most of the observational data in the healthcare domain, the patients’ data that used in our study were assembled from EMR. The basic characteristics of our cohort are detailed in Table 1.

Table 1.

Backgroud clinical characteristics of patients at development and validation cohorts

Variable	Value	Development	Validation	Missing
No. of patients		8520	2348
Demographics
Age, (years)		74.4 ± 12.1	74.3 ± 12.4	0
Gender (female)		49.4% (4209)	48.1% (1129)
BMI, Kg/m^2		29.9 ± 6.4	29.8 ± 6.4	8832
Comorbidities
Chronic renal failure (n)		33.4% (2843)	28.2% (662)	0
Valvular heart disease (n)		13.8% (1176)	12.9% (303)	0
AKI, % (n)		18.39% (1567)	21.97% (516)
Diabetes
COPD		52.6% (4483)	54.6% (1282)	0
Ischaemic heart disease		13.5% (1148)	15.1% (354)	0
Atrial fibrillation		22.3% (1899)	18.9% (443)	0
		41.7% (3556)	41.8% (981)	0
Smoking	not smoking	74.2% (6323)	70.4% (1654)
	past smoker	14.8% (1257)	14.5% (341)
	active smoker	11.0% (940)	15.0% (353)
Clinical parameters
Diastolic blood pressure, mmHg	Mean	68.6 ± 9.6	69.1 ± 9.6	2281
Systolic blood pressure, mmHg	Mean	131.2 ± 22.0	131.3 ± 19.5	2281
MAP, mmHg	Mean	89.5 ± 11.6	89.9 ± 11.3	2281
body temperature, celsius	First	37.1 ± 10.3	36.7 ± 0.4	2309
Estimated LVEF	Mean	44.3 ± 47.3	44.2 ± 19.5	6000
Lab tests
Albumin, g/dL		3.3 ± 0.5	3.2 ± 0.5	3672
BNP, ng/mL	First	1313.8 ± 1124.3	1112.3 ± 1011.4	5941
	Last	1306.1 ± 1118.6	1112.3 ± 1012.6	5941
BUN, mg/dL	Mean	36.0 ± 20.2	36.5 ± 21.0	2472
Creatinine, mg/dL	Mean	1.7 ± 1.1	1.6 ± 1.1	2473
RDW (%)	First	15.7 ± 1.9	16.1 ± 2.3	3496
Sodium, mmol/L
	Mean	138.3 ± 3.5	138.1 ± 3.7	2469
Haemoglobin, g/dL	First	11.6 ± 1.9	11.5 ± 2.0	2504
	Last	11.5 ± 1.8	11.4 ± 1.9	2498
Troponin, ng/mL	First	0.2 (1.5)	0.2 (1.1)	4088
HCT (%)	First	35.3 (5.7)	35.1 (5.9)	2502
Medical therapy
β-blockers (n)	Background	64.8% (5518)	78.7% (1849)	0
	In hospital	61.7% (5255)	88.4% (2075)	0
	Discharge	65.2% (5554)	83.3% (1955)	0
ACE inhibitors (n)	Background	60% (5114)	66.3% (1557)	0
Angiotensin receptor blocker, % (n)	In hospital	41.2% (3509)	49.6% (1165)	0
In hospital	15.5% (1322)	22.8% (536)	0
In hospital	17.9% (1522)	27.3% (642)	0
				MRA, % (n)
Furosemide, % (n)	Background	59.19% (5043)	68.44% (1607)	0
Target
1-year mortality, % (n)		30% (2552)	31.3% (736)	0

AKI, acute kidney injury; BMI, body mass index; BNP, brain natriuretic peptide; HCT-Hematocrit, MAP, mean arterial pressure, MRA, mineralocorticoid receptor antagonist; RDW, red cell distribution width.

Study outcomes

Study outcomes were predefined prior to data analysis. The primary outcome was 1 year mortality from hospital discharge. The secondary outcome was a composite of one year mortality or rehospitalization for AHF at 1 year. Analysis for the primary outcome is included in the main manuscript. Analysis for the secondary outcome is included in the Supplementary material online, supplementary data.

Data collection and preparation

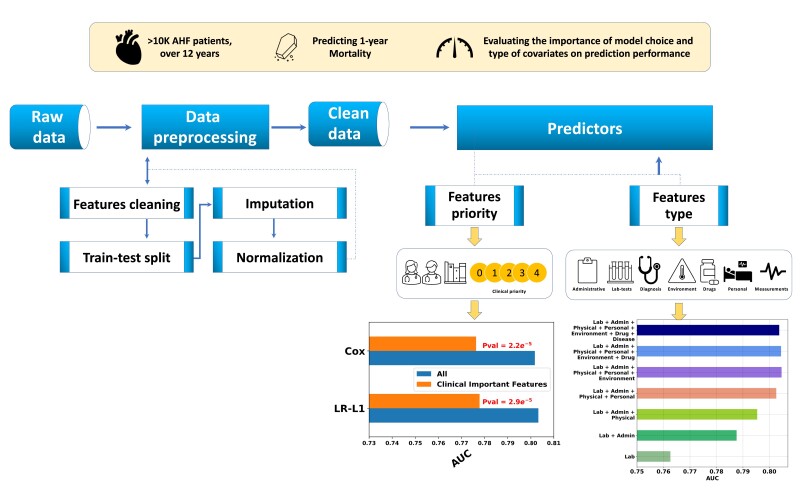
Using observational data (rather than prospective clinical research) is cheap, relatively easy to obtain and often provides a good representation of the real-world population of interest. However, it poses two major challenges that need to be addressed prior to the prediction efforts: wrong (noisy) data, and missing data. Below we describe how we handle these challenges. Overall, we used 372 covariates collected from admission to the end of the hospitalization including demographics, administrative data, lab tests, medical therapies, and echocardiographic data. A full list is available in the Supplementary material online, Table S8. A schematic representation of our data preparation pipeline is given in Figure 1.

Figure 1.

The suggested pipeline of the predicting process.

Data imputation and optimization

We searched for errors in the data by analyzing the distribution of each covariate in order to map outliers (e.g. mixture of [cm] and [m] in height data, swap between systolic blood pressure and diastolic blood pressure values), identify ill-calculated features (e.g. body mass index), and spot data points that are out of domain (e.g. text values in lab result feature). Then, each outlier was manually checked and fixed by the appropriate action, to ensure the data integrity. Covariates that were found to be too noisy or irrelevant were removed.

We addressed missingness by a two-stage process: indication and imputation. For each covariate with at least one missing value, we created a dummy variable to indicate which data-point was missing in the original data. Then, we imputed missing data¹⁷ using median imputation (see Supplementary material online, Table S2). We also experimented with multivariate imputation by chained equations (MICEs) imputation,^18–20 and found that the former achieved slightly better results (see Supplementary material online, Table S1). Therefore, we chose to use median imputation for all our analyses. Finally, the data were normalized using z-scoring: $\hat{x}=\frac{x-mean(X)}{std(X)}$. Some covariates (e.g. lab dates) were redefined to represent the number of days from admission, to ensure common domain.

Statistical analysis

We define the outcome y as a binary indicator of whether the patient died during a span of 1-year from hospital discharge. Given a set of patient covariates measured before and during hospitalization, denoted x, we estimated p(y|x), the probability of the outcome for a patient with the given set of covariates. The evaluation (test) set is temporally distinct from the set used to fit the model: 2004–2013 as train (model fitting) set, 2014–2015 as evaluation set.

Our aim was to assess model performance across two axes—(i) type of prediction method and (ii) type and number of covariates. For the model-type axis, we experimented with seven different methods for estimating p(y|x): logistic regression (LR) with either L₁ or L₂ regularization, random forest (RF), Cox proportional hazards model (Cox), extreme gradient boosting (XgBoost),¹⁰ a deep neural-net (NeuralNet), and an ensemble classifier (average of the LR- L₁, Cox proportional hazards model, XgBoost, and NeuralNet predictions). The LR, RF, and majority vote classifiers were implemented using the Sci-kit learn python package.²¹ The Cox model required regularization because of the large number of covariates. Since Cox model predicts time-to-event, and the other methods simply predict a probability of the event happening, we needed to slightly modify the way we use the Cox predictor for a direct comparison with the other models. See details below.

Transforming time-to-event prediction to binary prediction

We consider the difference between time-to-event analysis as performed by Cox regression and the rest of the models we use. Most predictors provide a probability that a sample is in a particular class (e.g. in the binary case, probability for mortality for a patient in the 1− year span from discharge), survival analysis does this and more. A time-to-event model provides the cumulative probability of a sample to have an event before (or at) a time t, where in our case t is the time from the baseline, to the event, measured in days.

Therefore, for an apples-to-apples comparison, we use the cumulative probability F(t) = P(T ≤ t) = 1 − S(t), where S(t) is the survival function, as given by the Cox analysis, and t is set to 365 days. This is exactly the probability for an event occurring during one year from the time of hospital discharge.

Neural network

We designed the neural network using a fully connected architecture. Each layer built from linear weights, a non-linear activation function (ReLU), and applying dropout during model fitting.²² We also added an L₁ regularization term on the weights of the first layer.

Covariate type and priority

In order to assess the relative contribution of choice of covariates, we conducted two analyses: using the type of the features and the clinical-priority of the features. From now on, we will refer to them as ‘Type’ models and ‘Priority’ models, respectively.

For the ‘Type’ analysis, we partitioned the covariates into seven types: Laboratory results (‘lab tests’), demographic (‘personal’), data related to administrative processes in the hospital such as relative time from admission to first blood test (‘admin’), patient comorbidities (‘disease’), drug related data, both prior to hospitalization, during hospitalization, and at discharge (‘drug’), physical measurements such as patient’s blood pressure (‘physical’), and environmental related features such as the season of admission (‘environment’). We ran each prediction method on every combination of the seven feature types outlined above, for a total of 2⁷ − 1 = 127 different sets of covariates per prediction method.

For the ‘Priority’ analysis, we used physicians’ expertise (heart failure cardiologists) to select for the most validated and established covariates both in terms of prediction ability and clinical prior knowledge.^23–26 Each covariate received a clinical-relevance score from 0 to 4, where 0 is ‘not relevant’ and 4 is ‘highly relevant’. Examples for priority 4 covariates are the last read of patient diastolic and systolic blood pressure, and examples for priority 0 covariates are whether the patient weight was recorded in admission. The full list of variables their subtype and the clinical priority is detailed in the Supplementary material online, Table S8. We use this clinical prior knowledge input to train our predictors as follows: The first model used only the most important clinical features (4), the next one used these together with the second most important ones, so we denote it 3+, and so on, where the last model used all the features, which we denote 0 + . Overall, for the Priority analysis, we evaluated five sets of covariates per prediction method.

Thus, in total we considered 127 + 5 = 132 sets of covariates, and seven prediction methods, giving a total of 132 × 7–7 = 917 models (we subtract 7 because the models fit on 0 + priority are identical to those fit using all Types of features). Each model’s hyper-parameters (e.g. level of regularization) was optimized for Area under receiver operator curve (AUROC) using 10-fold stratified cross-validation on the training set. The AUROC of different models was compared using the DeLong method for comparing areas under the ROC curve.^27,28 We emphasize that our goal is not to find the single most accurate model out of the 917—rather we wish to understand which factors account for better or worse model accuracy across the settings.

In addition to AUROC, we also give a decision curve analysis (net-benefit)²⁹ and report the following metrics, as suggest by Shameer et al.³⁰: sensitivity, specificity, negative predictive value (NPV), positive predictive value (PPV), accuracy, and Brier Score. See Supplementary material online, Table S9 for the full details.

Code availability

Full code is available in https://github.com/RomGutman/ADHF.

Results

A cohort of patients with a primary diagnosis of AHF admitted to a tertiary hospital during a period of 12 years was used in order to assess study outcomes. The cohort included 10 868 cases from which a total of 372 covariates were collected from admission to discharge. The training cohort consisted of 8520 cases and the validation cohort included 2348 cases.

The performance of the seven prediction models was evaluated across seven predetermined sets of covariates (demographic, physical examination, patient’s comorbidities, laboratory tests, drug therapy, environmental, and administrative) classified according to their clinical level of priority (indicated as low priority-0 to high priority-4). Heart failure clinicians identified 52 covariates as high priority level. The results on prediction model performances for predicting the primary outcome (1-year mortality) are presented over a total of 917 settings assessed on a temporally held-out dataset.

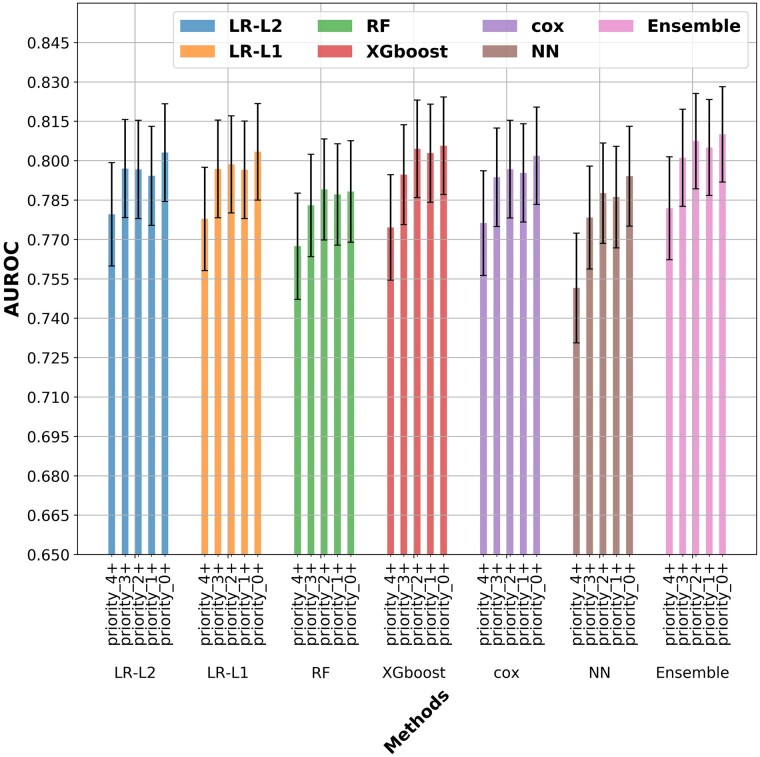
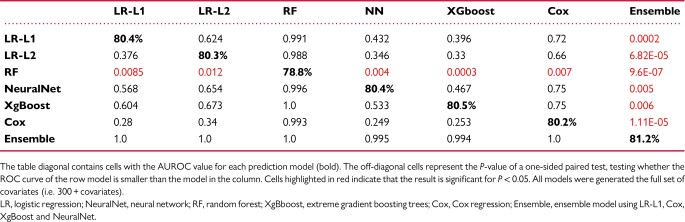
The models applied predicted one year mortality with a relatively high level of accuracy. Overall, the performance of the different methods was found to be comparable (Figure 2), with the exception of the RF model that significantly underperformed all other models (Table 2). Specifically, L1- and L2-regularized LR (80.4% and 80.3% AUROC, respectively), XgBoost (80.5%) and NeuralNet (80.4%) predicted the occurrence of one year mortality with essentially the same AUROC when using all covariates, whereas the RF (78.8%) performed slightly worse than other models and the ensemble model (81.2%) slightly better. The probable reason for RF to preform less than other models here may be related to overfitting of the training data. Importantly, Cox based model, which is not based on a ML paradigm, preformed similarly (80.2%).

Figure 2.

Prediction of the models based on the set of clinical covariates utilized. Area under receiver operator curve of the models used splitted by clinical priority of the variables. The confidence interval in this graph are the prediction interval for the area under receiver operator curve prediction. LR, logistic regression; NN, neuron network; RF, random forest; XgBoost, extreme gradient boosting trees; Cox, Cox regression; Majority Ensemble, ensemble model using LR-L1, Cox, XgBoost and NN.

Table 2.

Difference in predictive capacity for predicting the primary outcome between pairs of methods

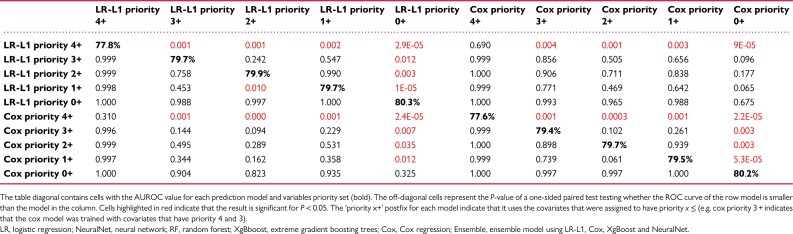
To further characterize the difference in the predictive capacity of the models a comparative analysis between pairs of models was conducted using the DeLong method for comparing areas under the ROC (AUROC) curve^27,28 (Table 2). A P-value for a one-sided test, i.e. whether model A has higher AUROC than model B, of all the pairs of methods when using the full set of covariates. The analysis demonstrate similar performance between the models despite the fact that the models we compare make vastly different assumptions about the outcome (linear vs. non-linear, sparse or not), and have a widely varying number of parameters (neural networks have 1.4 million parameters vs. 372 parameters for the LR models). To evaluate the contribution of the number of covariates and their clinical importance we evaluated the differential performance of each model according to the assigned priority of the clinical variables (Figure 2). A comparative analysis demonstrated that inclusion of low priority variables improved the predictive performance of the models even when comparing analyses based on priority 0 + compared to priority 1+ (Table 3).

Table 3.

Difference in prediction capacity according to the model used and the assigned clinical priority of the variables used

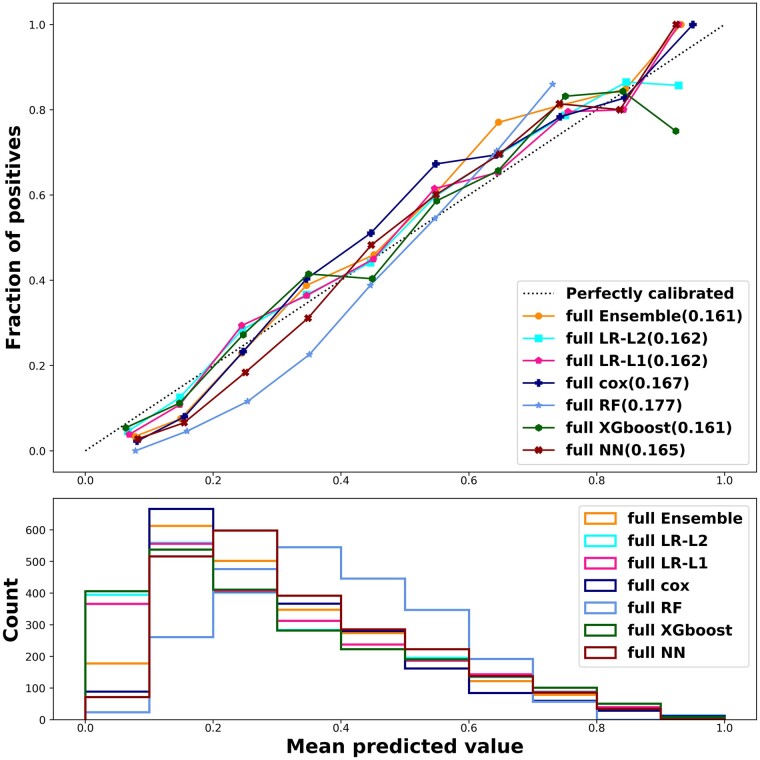
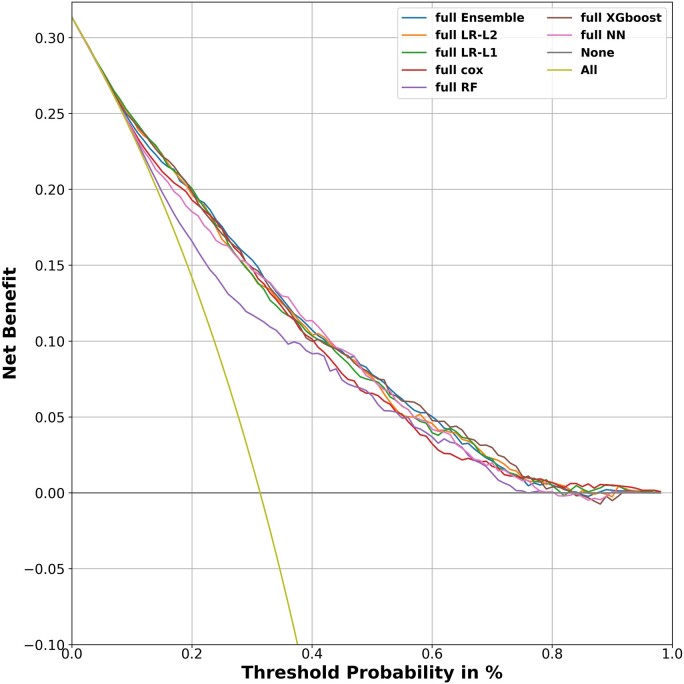
Calibration plots found a good calibration for most models with slight underestimation of the predicted risk for low risk patients using RF (Figure 3). To assess the clinical implication of the model in predicting mortality outcome for AHF patients, we carried out a net-benefit analysis (Figure 4).³¹ A reasonable threshold for 1 year mortality risk in heart failure patients that entails consideration of advanced therapies (e.g. Heart transplantation or mechanical circulatory support) is 20%.^32–34 All models give a significant net benefit and perform similarly across a wide range of decision thresholds. We further see that most models are indistinguishable in their net benefit, with RF again the only model with diminished performance compared to the other models. In addition, the sensitivity, specificity, NPV, PPV, and Brier score, for all models using the full set of covariates is detailed in Table 4. There are differences between the models in their sensitivity and PPV, but these are mostly the result of slightly different decision thresholds of the models, which disappear when using analyses that consider all possible thresholds such as AUROC and net benefit.

Figure 3.

Calibration plot. All models applied were reasonably calibrated (upper panel). Risk distribution of the patients evaluated using the prediction models delineates that most patients had a medium risk for the unified outcome—higher than that assessed for the 1 year mortality outcome (lower panel). The number in parentheses after each model indicates the brier score of each model. The ‘full’ prefix for each model is to indicate that it uses all the 300 + covariates. LR, logistic regression; NN, neuron network; RF, random forest; XGboost, extreme gradient boosting trees; Cox, Cox regression; Majority Ensemble, ensemble model using LR-L1, Cox, XGboost and NN.

Figure 4.

Net benefit of the prediction models. Net benefit allows to evaluate the clinical implication of the model in predicting mortality outcome. A threshold of 20% risk for mortality is considered significant for altering decisions regarding treatment strategies and patient’s categorization (Stage C vs. Stage D heart failure). All models give a significant net benefit with random forest being the least beneficial. The straight yellow line denotes the benefit of a model that predicts mortality for all patients. LR, logistic regression; NN, neuron network; RF, random forest; XGboost, extreme gradient boosting trees; Cox, Cox regression; Ensemble, ensemble model using LR-L1, Cox, xgboost and NN.

Table 4.

The metrics of the prediction models using all the features (variables) for predicting the primary outcome

	AUROC	Sensitivity	Specificity	PPV	NPV	Accuracy	Brier
Cox	80.18%	0.34	0.94	0.72	0.76	0.75	0.167
LR-L1	80.37%	0.44	0.91	0.69	0.78	0.76	0.162
LR-L2	80.29%	0.44	0.91	0.69	0.78	0.76	0.162
Ensemble	81.23%	0.42	0.92	0.71	0.78	0.76	0.161
NeuralNet	80.45%	0.45	0.90	0.68	0.78	0.76	0.165
RF	78.84%	0.51	0.86	0.63	0.79	0.75	0.177
XgBoost	80.49%	0.46	0.91	0.69	0.78	0.76	0.161

A threshold of 0.5 is used.

AUROC, area under receiver operator curve; NPV, negative predictive value; PPV, positive predictive value.

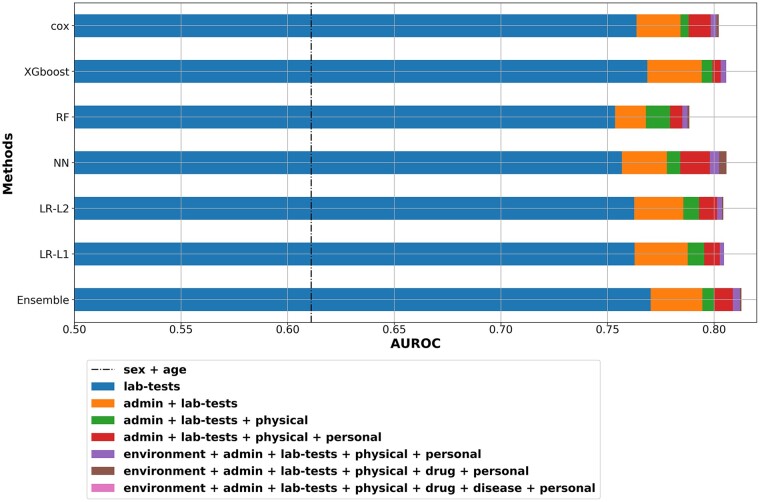
To estimate the relative cumulative contribution of different types of covariate, we analyzed their relative contribution to model performance. For this purpose, we conducted the analysis for the L1 LR model (Figure 5). Specifically, we ordered the types by the biggest gain each type gave over the previously added types, with the provision that age and sex are always included. Using only sex and age gives AUROC of no more than 61.6% (ranging from 56.3 to 61.6% across the other models). The addition of lab-test gives by far the biggest gain in performance, followed by adding administrative data (examples of administrative data is whether the patient had a previous AHF hospitalization in the previous years as indicated in the database, or whether a weight of the patient was recorded). We further see diminishing returns when adding two other types of information: personal (demographic data) and physical examination. On top of these, adding diseases (comorbidities), environmental and drug information gives essentially only modest gain in model performance. In Table 5, we summarize the most statistically significant covariates (P < 0.05) obtained when using L1 LR as the predictive model, applied to the full set of covariates.

Figure 5.

Area under receiver operator curve plot by types. The relative effect of the various variable types on the performance of the prediction model is delineated. Variable types that are not shown in the graph had a minor (or negative) contribution to the model’s performance. Sex and age contribution are represented by the dashed vertical line. Admin, administrative variables; lab-tests, laboratory tests; physical, physical examination; personal, demographic variables; drug, drug treatment; disease, comorbidities; LR, logistic regression; NN, neuron network; RF, random forest; XGboost, extreme gradient boosting trees; Cox, Cox regression; Majority Ensemble, ensemble model using LR-L1, cox, XGboost and NN.

Table 5.

Most significant variables predicting one year survival

Variable	Odds ratio	Std.Err	Z-value	P>|z|	[0.025	0.975]
Age	1.52	0.03	13.23	6.13E-40	1.43	1.61
Patient readmission	1.31	0.028	9.46	2.99E-21	1.24	1.38
Albumin	0.77	0.03	−8.76	1.92E-18	0.73	0.82
RDW(%)a	1.12	0.03	6.24	4.42E-10	1.13	1.26
Length of stay	1.24	0.04	5.49	3.95E-08	1.15	1.34
Last BNP	1.14	0.03	4.84	1.31E-06	1.08	1.2
Hyperlipidaemia	0.78	0.06	−4.33	1.49E-05	0.70	0.88
Statins at discharge	0.76	0.06	−4.14	3.42E-05	0.67	0.87
Missing weight measurement	1.32	0.07	4.05	5.05E-05	1.15	1.51
Sex (female)	0.80	0.06	−3.81	0.00014	0.72	0.9
Chloridea	0.90	0.03	−3.05	0.002	0.84	0.96
Furosemide (background)	1.21	0.07	2.85	0.004	1.06	1.38

BNP, brain natriuretic peptide; RDW, red blood cell distribution width.

First exams taken during hospitalization.

Discussion

The present study is aimed at understanding what drives success in mortality prediction based on a contemporary AHF hospitalization cohort utilizing a variety of ML methodologies. The study’s main finding is that the choice of the predictive modelling method is secondary to the choice and variety of covariates: most methods, including both classic methods such as Cox regression and newer methods such as gradient boosted trees, perform similarly when given the same set of covariates. The study also demonstrates that adding a large number of covariates, some of which are deemed less clinically relevant by clinical experts, results in a significant gain in accuracy, largely irrespective of the statistical method chosen. Finally, an additional finding of the study is that integrating non-clinical, administrative variables to demographic and laboratory variables significantly improves the predictive capabilities of the model.

In the current study, building prediction models with all available information resulted in a reliable prediction of 1-year mortality and rehospitalization using data gained solely from hospital EMR. Specifically, standard regularized linear methods such as LR and Cox regression were shown to be non-inferior to ML based methodologies. An important finding of the current study is that the use of multiple covariates is crucial for augmenting the prediction accuracy. On the priority front, we found that using 113 covariates (out of 372) that were set as high priority by clinical experts were inferior to using a multiple-covariates strategy (including variables deemed as non-significant, priority 0). These results were gained on future split of the data, which shows that data from the past can be used for accurate prediction.

Prediction of heart failure rehospitalization and mortality has been a long-standing challenge. Given the severe consequences associated with the disease many efforts were and are currently invested at improving the prediction the AHF prognosis, with limited success. Currently, there are two main prediction tasks that have been studied. First, for AHF patients, short-term prediction of rehospitalization, and in-hospital or 30 day mortality, mainly aiming to assess the quality of heart failure treatment during the hospitalization.³⁵ Second, for ambulatory chronic heart failure patient predicting 1-year and 3-year outcomes.^23,35–39 The clinical setting chosen for the present study, at patient discharge from acute hospitalization, is critical for choosing the appropriate therapeutic strategy (e.g. advanced therapies or Uptitration of heart failure medications) and for tailoring the surveillance programme and the medical therapy. While several models have been devised for risk stratifying heart failure patients at admission to hospital or ambulatory patients^24,40–42 none thus far have been developed for AHF patients at this critical decision point. The current study elucidates the relevant factors affecting AHF prognosis and the relative contribution of the factor-type to the risk stratification using an institution tailored methodology.

The main predictive variables in the study (listed in Table 5) include demographic, laboratory, drug therapy, and administrative factors. Age, albumin levels, and RDW have been described as predictive factors for mortality in general and heart failure mortality specifically.^43–48 Our study is in agreement with previous studies showing that discharge (or last) BNP is a stronger predictor of AHF prognosis than baseline BNP and provide a substantial tool for risk stratification.⁴⁹ In recent years, there is growing evidence that admission hypochloraemia is a marker for mortality and rehospitalization in chronic heart failure patients,⁵⁰ and the present study reiterates this finding and demonstrates that low plasma chloride levels at admission (more than low sodium levels) serve as a significant prognostic factor in AHF for predicting 1 year mortality. A key finding of the study is that administrative variables significantly boost the predictive performance of the evaluated models. Among those variables, while a history of recent AHF hospitalization is widely described as a prognostic factor,^51,52 factors such as length of stay and missing weight measurement are less established as risk markers and may be used to alert clinicians for the associated risks, serving as proxies for underlying patient characteristics.

The application of ML methodologies for predicting adverse events and outcomes based on electronic health records (EHRs) is a promising approach, highly relevant to acute exacerbation of chronic diseases such as heart failure.^42,53–55 The benefit of ML in predicting prognosis in the setting of heart failure is not yet established and its added advantage over traditional models is still controversial. In the study of Frizzell et al.,⁵⁶ use of a number of ML algorithms did not improve prediction of 30-day all-cause readmissions 30 days after discharge from a heart failure hospitalization compared with traditional LR models. Desai et al.⁵⁷ recently demonstrated that multiple ML methodologies have minimal benefit over traditional LR in the setting of chronic heart failure. However, the authors noted that ML approaches generally fared better when the models included numerous continuous variables such as laboratory tests.⁵⁷

A recent systematic review compared the results of LR and other ML methods, across different risk-scores using clinical data, found no evidence of superior performance of ML techniques in terms of AUROC.⁵⁸ More recent reviews have found and discussed similar finding regarding general benefit for using Deep-learning techniques.^59–61 Our findings generally agree, as we were unable to demonstrate any systematic benefit of ML methods in terms of AUROC, calibration or net benefit. Importantly, it remains to be determined whether ML can improve model calibration, which is considered as the ‘Achilles heel’ of predictive analytics, and specifically in heart failure (underestimating the risk for high-risk patients and overestimating the risk for low-risk patients).^62–64

The present study adds an important observation: using a very large and diverse set of covariates, many more than are used in classic risk scores, carries a significant benefit in terms of model discrimination regardless of the method used, without adversely affecting model calibration. This lesson is likely to be applicable not only for AHF outcome prediction but also for other chronic diseases undergoing acute decompensations with complex EHR data, such as inflammatory bowel disease and chronic obstructive pulmonary disease.

Unlike much of the above work, we propose not a single model but a framework for understanding what drives performance when building site-specific models. When building predictive models, there is usually a tradeoff between robustness and accuracy^65,66 In this work, we focus on the accuracy end of this tradeoff, where we are willing to use many hospital-specific and population-specific variables in order to boost accuracy at the site, with the possible price of building models which will not generalize well to other sites or populations. Thus, the limitation of using a large number of covariates is the adaptation and stability of the prediction model when applied to other EHRs in alternate institutions. For example, the typical time until a certain lab test is administered will very likely vary between hospitals. This means the models our framework yielded when applied to a specific population cannot and should not be used ‘as is’ in different environments. Rather, the structured framework for constructing models such as ours, each tailored to the patient population and practices of a specific hospital and a specific clinical scenario, should be used. Towards that end, we are sharing the code base used to construct and evaluate our models (https://github.com/RomGutman/ADHF). We also note that such predictors should be re-calibrated at some-future-point, as we cannot expect a model to be accurate for indefinitely long periods of time.

In conclusion, our study demonstrates that by applying ML strategies for optimal use of data, combined with the use of multiple covariates, we were able to reliably predict the outcome of a chronic disease such as heart failure based solely on hospitalization data during acute decompensation. However, we were unable to demonstrate a clear superiority of ML methods over the traditional Cox regression model (when used with a regularization factor). We believe that a similar multiple covariate strategy may be used as a disease and institute specific methodology for constructing decision support tools for risk stratification at discharge for patients with chronic diseases such as heart failure.

Supplementary material

Supplementary material is available at European Heart Journal – Digital Health online.

Funding

Funding support for this research was given by Yad Hanadiv Foundation, Israel Science Foundation, and the Council of Higher Education (Israel) for student funding.

Data availability

All data are included in the submission/manuscript file.