Abstract
Objective
When correcting for the “class imbalance” problem in medical data, the effects of resampling applied on classifier algorithms remain unclear. We examined the effect on performance over several combinations of classifiers and resampling ratios.
Materials and Methods
Multiple classification algorithms were trained on 7 resampled datasets: no correction, random undersampling, 4 ratios of Synthetic Minority Oversampling Technique (SMOTE), and random oversampling with the Adaptive Synthetic algorithm (ADASYN). Performance was evaluated in Area Under the Curve (AUC), precision, recall, Brier score, and calibration metrics. A case study on prediction modeling for 30-day unplanned readmissions in previously admitted Urology patients was presented.
Results
For most algorithms, using resampled data showed a significant increase in AUC and precision, ranging from 0.74 (CI: 0.69–0.79) to 0.93 (CI: 0.92–0.94), and 0.35 (CI: 0.12–0.58) to 0.86 (CI: 0.81–0.92) respectively. All classification algorithms showed significant increases in recall, and significant decreases in Brier score with distorted calibration overestimating positives.
Discussion
Imbalance correction resulted in an overall improved performance, yet poorly calibrated models. There can still be clinical utility due to a strong discriminating performance, specifically when predicting only low and high risk cases is clinically more relevant.
Conclusion
Resampling data resulted in increased performances in classification algorithms, yet produced an overestimation of positive predictions. Based on the findings from our case study, a thoughtful predefinition of the clinical prediction task may guide the use of resampling techniques in future studies aiming to improve clinical decision support tools.
Keywords: class imbalance, resampling, RUS, SMOTE, ADASYN, classification algorithms
INTRODUCTION
An underexposed and not widely known topic in machine learning is the “class imbalance” problem, meaning that there is an imbalance in the event outcome.1 While classification algorithms are frequently used for prediction models of binary outcomes in a clinical setting, these tend to learn based on the outcome class with the most observations: in medical sciences this is often the negative outcome.2 This may lead to an overestimation of predicting the most prevalent class in an imbalanced dataset, and developing algorithms which are less adequate for use in clinical setting.3,4 In medical data the outcome of interest is often much less prevalent opposed to the outcome not of interest (ie, negative outcome). For example in population screening for cancer or when predicting an adverse event following treatment. A severe imbalance would be that 0.1% of the patients have the outcome of interest, while 99.9% of the patients is negative for the outcome of interest. This would mean, that for every new prediction, the trained classification algorithm will predict a negative outcome with 99.9% accuracy.
In order to address the class imbalance problem, resampling can be applied to create a synthetic balanced dataset and thereby overcoming the class imbalance problem. The most common techniques are Random Under-Sampling (RUS), and Synthetic Minority Oversampling Technique (SMOTE).5,6 Oversampling synthesizes data based on the group of observations being positive on the specified outcome (ie, assuming the minor class), and undersampling by removing observations on the group being negative on specified outcome (ie, the major class). Also, sampling techniques are often used combining over- and undersampling methods to reach a well-balanced outcome in the dataset for the classification algorithm. There is no default ratio in which to resample data for each problem, despite that several clinical studies have shown that resampling can yield improved results with different ratios.7–10 Within classification algorithms there is a distinction between so-called weak and strong learners, where a weak learner is defined to be a classifier that can label examples better than random guessing, and a strong learner is a combination of weak learners. The latter option, also known as an ensemble based algorithm improves using findings from the weak learners and combining this into a classifier with strong accuracy.11–13
A recent study found that resampled data applied to logistic regression algorithms distorts model performance, with a notable impact in overestimations of positive predictions as opposed to the unsampled data.14 The effects of resampling using different ratios applied on classifier algorithms other than a logistic regression in a clinical scenario remain unclear.
OBJECTIVE
The aim of this study was to investigate the impact on model performance using different respective resampling ratios produced by over- and undersampling techniques applied to several classification algorithms. A case study on prediction modeling for 30-day readmissions in 7570 Urology patients with 757 (10%) unplanned readmissions was used as a typical unbalanced dataset. We hypothesized that: (1) correcting for class imbalance using resampling techniques improves model performance, and (2) resampling will improve model performance of more elaborate classification algorithms such as XGBoost, RandomForest, Neural Network, and Support Vector Machine.
MATERIALS AND METHODS
Case study: predicting the risk of a 30-day unplanned readmission
For this study, prediction models were developed to estimate the risk of a 30-day unplanned hospital readmission after discharge from the department of Urology. An unplanned hospital readmission was defined as where a patient, who was previously treated at the urology ward, had to return to the urology ward within 30 days of being discharged for an indication related to the original treatment. A prediction model could be used in clinical discharge management, and improve decision making whether to continue admission or safely discharge a patient. Previous study findings were applied on this case study, based on a former study we performed in predicting 30-day unplanned readmissions at Urology. In total, 7570 patients were available for inclusion, 757 of whom (10%) had an unplanned hospital readmission at Urology within 30-days. Patients having a clinical admission at Urology between January 2015 and October 2021 were included, only excluding patients who were deceased (n = 74) during clinical admission. Patient characteristics can be found in Table 1, and in detail under the “Feature” section in the Supplementary Materials. This retrospective cohort study was approved and registered with the institutional review board (METC).
Table 1.
Patient characteristics
| Unplanned readmission within 30 days |
||||
|---|---|---|---|---|
| Yes (N = 774) | No (N = 6796) | P value | Total (N = 7570) | |
| Charlson Comorbidity Index | ||||
| Mean (SD) | 1.48 (2.03) | 0.998 (1.74) | <.001 | 1.05 (1.77) |
| Median [Min, Max] | 0 [0, 10.0] | 0 [0, 11.0] | 0 [0, 11.0] | |
| Age | ||||
| Mean (SD) | 70.3 (15.7) | 64.4 (17.5) | <.001 | 65.0 (17.4) |
| Median [Min, Max] | 74.0 [20.0, 103] | 68.0 [13.0, 109] | 69.0 [13.0, 109] | |
| BMI | ||||
| Mean (SD) | 26.4 (5.48) | 25.9 (4.92) | .0181 | 26.0 (4.99) |
| Median [Min, Max] | 25.6 [13.3, 66.5] | 25.3 [13.3, 53.1] | 25.3 [13.3, 66.5] | |
| Systolic blood pressure | ||||
| Mean (SD) | 134 (17.2) | 131 (18.8) | <.001 | 131 (18.7) |
| Median [Min, Max] | 133 [93.0, 182] | 129 [85.0, 210] | 129 [85.0, 210] | |
| Diastolic blood pressure | ||||
| Mean (SD) | 74.5 (8.18) | 74.4 (9.04) | .644 | 74.4 (8.96) |
| Median [Min, Max] | 74.0 [53.0, 105] | 74.0 [44.0, 126] | 74.0 [44.0, 126] | |
| Creatinine blood | ||||
| Mean (SD) | 115 (90.9) | 95.5 (64.2) | <.001 | 97.5 (67.7) |
| Median [Min, Max] | 91.0 [37.0, 1260] | 83.0 [21.0, 1480] | 84.0 [21.0, 1480] | |
| Hemoglobin | ||||
| Mean (SD) | 7.67 (1.12) | 7.72 (1.22) | .246 | 7.71 (1.21) |
| Median [Min, Max] | 7.70 [4.10, 11.6] | 7.80 [4.00, 11.6] | 7.80 [4.00, 11.6] | |
| Clinical medication | ||||
| Mean (SD) | 51.7 (34.0) | 30.4 (25.7) | <.001 | 32.6 (27.4) |
| Median [Min, Max] | 44.0 [7.00, 227] | 22.0 [0, 267] | 24.0 [0, 267] | |
| Home medication | ||||
| Mean (SD) | 12.8 (8.47) | 8.07 (7.33) | <.001 | 8.55 (7.59) |
| Median [Min, Max] | 11.0 [0, 48.0] | 6.00 [0, 60.0] | 6.00 [0, 60.0] | |
| Clinical admissions last year | ||||
| Mean (SD) | 0.860 (1.52) | 0.311 (0.732) | <.001 | 0.367 (0.862) |
| Median [Min, Max] | 0 [0, 11.0] | 0 [0, 9.00] | 0 [0, 11.0] | |
| ED visits last 6 months | ||||
| Mean (SD) | 0.382 (0.890) | 0.144 (0.503) | <.001 | 0.169 (0.560) |
| Median [Min, Max] | 0 [0, 8.00] | 0 [0, 8.00] | 0 [0, 8.00] | |
| Length of stay | ||||
| Mean (SD) | 3.98 (5.44) | 2.21 (3.35) | <.001 | 2.39 (3.66) |
| Median [Min, Max] | 3.00 [0, 97.0] | 1.00 [0, 65.0] | 1.00 [0, 97.0] | |
| Sex | ||||
| Female | 153 (19.8%) | 2439 (35.9%) | <.001 | 2592 (34.2%) |
| Male | 621 (80.2%) | 4357 (64.1%) | 4978 (65.8%) | |
| History of smoking | ||||
| No | 656 (84.8%) | 5577 (82.1%) | .0702 | 6233 (82.3%) |
| Yes | 118 (15.2%) | 1219 (17.9%) | 1337 (17.7%) | |
| Use of alcohol | ||||
| No | 420 (54.3%) | 3308 (48.7%) | .00363 | 3728 (49.2%) |
| Yes | 354 (45.7%) | 3488 (51.3%) | 3842 (50.8%) | |
| Interpreter needed | ||||
| No | 738 (95.3%) | 6618 (97.4%) | .00183 | 7356 (97.2%) |
| Yes | 36 (4.7%) | 178 (2.6%) | 214 (2.8%) | |
| Fluency in Dutch | ||||
| No | 78 (10.1%) | 783 (11.5%) | .255 | 861 (11.4%) |
| Yes | 696 (89.9%) | 6013 (88.5%) | 6709 (88.6%) | |
| Uses a catheter at home | ||||
| No | 716 (92.5%) | 6563 (96.6%) | <.001 | 7279 (96.2%) |
| Yes | 58 (7.5%) | 233 (3.4%) | 291 (3.8%) | |
| Use of anticoagulants | ||||
| No | 116 (15.0%) | 2392 (35.2%) | <.001 | 2508 (33.1%) |
| Yes | 658 (85.0%) | 4404 (64.8%) | 5062 (66.9%) | |
| Use of NSAIDs | ||||
| No | 529 (68.3%) | 4697 (69.1%) | .692 | 5226 (69.0%) |
| Yes | 245 (31.7%) | 2099 (30.9%) | 2344 (31.0%) | |
| Use of corticosteroids | ||||
| No | 686 (88.6%) | 6533 (96.1%) | <.001 | 7219 (95.4%) |
| Yes | 88 (11.4%) | 263 (3.9%) | 351 (4.6%) | |
| Use of antipsychotics | ||||
| No | 715 (92.4%) | 6578 (96.8%) | <.001 | 7293 (96.3%) |
| Yes | 59 (7.6%) | 218 (3.2%) | 277 (3.7%) | |
| Use of ulcer medication | ||||
| No | 380 (49.1%) | 4086 (60.1%) | <.001 | 4466 (59.0%) |
| Yes | 394 (50.9%) | 2710 (39.9%) | 3104 (41.0%) | |
| Oncology | ||||
| Absent | 700 (90.4%) | 6358 (93.6%) | .0014 | 7058 (93.2%) |
| Present | 74 (9.6%) | 438 (6.4%) | 512 (6.8%) | |
| Medication | ||||
| No | 83 (10.7%) | 1793 (26.4%) | <.001 | 1876 (24.8%) |
| Yes | 691 (89.3%) | 5003 (73.6%) | 5694 (75.2%) | |
| Comorbidity | ||||
| Absent | 607 (78.4%) | 5995 (88.2%) | <.001 | 6602 (87.2%) |
| Present | 167 (21.6%) | 801 (11.8%) | 968 (12.8%) | |
| Surgery | ||||
| No | 354 (45.7%) | 4325 (63.6%) | <.001 | 4679 (61.8%) |
| Yes | 420 (54.3%) | 2471 (36.4%) | 2891 (38.2%) | |
P values calculated with Student’s t test for numeric variables and chi-squared test for categorical variables.
Data preprocessing
Missing values were imputed using multiple imputation by chained equations (MICE), and features with > 55% missing data were dropped. More information considering performed imputation and output can be found in the Supplementary Materials under the “Result of Imputing Missing Values with MICE” section.15 Over the original count of 53 features available, feature selection was carried out to identify and select those features contributing most to our outcome variable. Feature engineering (variable selection) was evaluated using a RandomForest algorithm to identify the predictive value for each feature, with the default set from 500 to 2500 to assure including most feature combinations.16 Based on 2 criteria, being: (1) feature had a good predictive value (≥10% importance), and (2) feature was expected to have clinical importance, 28 features were included. These consisted of patient characteristics, laboratory values, medication during admission, health care logistics (eg, length of stay or count of clinical admissions in the last 6 months), comorbidity, and type of surgery. More detailed information about the features can be found in the addendum under the “Features” section. Data were split into a train and a test set (70:30, respectively), and resampling was only performed on the training set to prevent information leakage to the test set.
Sampling methods
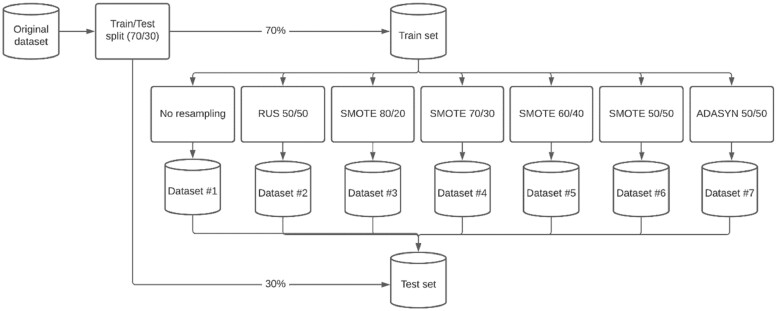
The original dataset had an outcome balance where 90% (6813 of 7570 patients) had no unplanned readmission (ie, the major group), compared to the remaining 10% (757 of 7570 patients) who did (ie, the minor group). The training set was resampled in order to generate 5 additional training sets. RUS was performed using the undersampling option of ROSE, and oversampling using SMOTE and ADASYN (Figure 1). The ratio of the outcome class was expressed in percentages of total observations, showing the major group first followed by the minor group.
Figure 1.
Process of under- and oversampling.
For this study, the outcome in the original train data was resampled in 5 additional training sets. Ratios and population size are specified in Table 2, with a flow-chart of the process setup in Figure 2.
Table 2.
Sampled datasets
| Dataset | Major–Minor | N |
|---|---|---|
| Original | 90%–10% | 7.570 |
| Train set | 90%–10% | 5.251 |
| Test set | 90%–10% | 2.319 |
| RUS | 50%–50% | 1.119 |
| SMOTE 20 | 80%–20% | 5.249 |
| SMOTE 30 | 70%–30% | 3.632 |
| SMOTE 40 | 60%–40% | 4.045 |
| SMOTE 50 | 50%–50% | 4.302 |
| ADASYN 50 | 50%–50% | 9.451 |
Figure 2.
Flowchart of resampling strategy.
Machine learning algorithms
The classification algorithms in our study were logistic regression (LR), decision trees (DT), XGBoost (XGB), RandomForest (RF), Neural Network (NN), and Support Vector Machine (SVM). For optimized performance, each algorithm was tuned with a 5-fold cross validation grid search on the original training data. Specified hyperparameters can be found per algorithm in the addendum under the “hyperparameter section.” Normalization was applied to LR, NN, and SVM.
Model performance evaluation
Model performance was evaluated according to the ABCD-framework for evaluation of a clinical prediction model, which includes discrimination with the Area Under the receiver operating Curve (AUC), precision (ie, Positive Predictive Value), recall (ie, sensitivity or True Positive Rate), calibration with a calibration curve, and the overall prediction error with the Brier score.17,18 Performance of the resampled datasets were calculated using a 5-fold cross-validation per dataset compared to original test set. In order to test for statistical significant differences of performance between the original train set and resampled datasets, evaluation metrics were calculated with 5-fold cross-validation, and tested using a dependent t test for paired samples. See the “Metric information” section in the addendum for more information concerning the evaluation metrics.
Software
Data preprocessing and sampling were performed using R Version 4.0.2, and R-studio Version 1.3.1073 (R-Studio, Boston, MA, USA). Modeling and evaluating the model performance were performed using Python version 3.9.8. with the scikit-learn version 1.1.1. All Python and R code will be made available immediately following publication to anyone who wishes to access the code, and access requests can be made to the corresponding author.
RESULTS
Our results show that resampling drastically improves model performance in AUC, precision, and recall in our case study. Specifically in XGB, RF, NN, and SVM, improvements in AUC and precision are observed as opposed to LR, and DT.
The performance in AUC on the original dataset ranged between 0.68 and 0.82 (CI: 0.64–0.85). A significant increase was observed in the resampled datasets in XGB, RF, NN, and SVM, with scores ranging from 0.74 (CI: 0.69–0.79), to 0.96 (CI: 0.95–0.96). No significant increase was observed in LR, and DT regardless of resampled data. Based on the original dataset, precision ranged from 0.00 to 0.67 (CI: 0–0.89), and improved on resampled data with scores ranging from 0.35 (CI: 0.12–0.58) to 0.88 (CI: 0.87–0.88) observed in NN and SVM, and decision trees. Significant increases in performance were mostly observed in DT, NN, and SVM. Irrespectively of resampled data, all classification algorithms showed a significant increase of performance in recall with scores ranging from 0.01 (CI: 0.00–0.01), to 0.92 (CI: 0.91–0.93) as opposed to the scores of the original dataset ranging from 0.00 and 0.19 (CI: 0–0.25). Brier scores showed an overall decrease in performance with scores ranging from 0.09 (CI: 0.07–0.10) to 0.21 (CI: 0.15–0.26), compared to the scores of the original dataset ranging from 0.07 to 0.09 (CI: 0.04–0.13). In comparison on performance in Brier scores, XGB, RF, NN, and SVM showed less decline as opposed to LR, and DT. A full overview of all scores and impact of resampled data can be found in Table 3 and Figure 3.
Table 3.
Differences in performance per algorithm, outcome, and dataset
| Metric (95% CI) | Original | RUS 50 | SMOTE 20 | SMOTE 30 | SMOTE 40 | SMOTE 50 | ADASYN 50 |
P values (compared to original) |
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RUS 50 | SMOTE 20 | SMOTE 30 | SMOTE 40 | SMOTE 50 | ADASYN 50 | ||||||||
| AUC | |||||||||||||
| LR | 0.77 (0.74; 0.8) | 0.77 (0.74; 0.8) | 0.77 (0.75; 0.79) | 0.77 (0.74; 0.79) | 0.77 (0.75; 0.79) | 0.77 (0.76; 0.79) | 0.82 (0.81; 0.83) | .980 | .859 | .847 | .942 | .787 | .005 |
| DT | 0.73 (0.69; 0.76) | 0.74 (0.72; 0.76) | 0.76 (0.74; 0.77) | 0.77 (0.75; 0.78) | 0.77 (0.74; 0.79) | 0.77 (0.75; 0.78) | 0.77 (0.75; 0.78) | .340 | .078 | .054 | .059 | .031 | .040 |
| XGB | 0.82 (0.79; 0.85) | 0.83 (0.80; 0.85) | 0.89 (0.88; 0.90) | 0.88 (0.86; 0.90) | 0.90 (0.89; 0.91) | 0.91 (0.90; 0.92) | 0.95 (0.95; 0.96) | .673 | .001 | .009 | .000 | .000 | .000 |
| RF | 0.82 (0.80; 0.85) | 0.83 (0.80; 0.86) | 0.91 (0.90; 0.92) | 0.90 (0.89; 0.92) | 0.92 (0.91; 0.93) | 0.93 (0.92; 0.94) | 0.96 (0.95; 0.96) | .531 | .000 | .000 | .000 | .000 | .000 |
| NN | 0.74 (0.71; 0.77) | 0.78 (0.75; 0.8) | 0.91 (0.9; 0.92) | 0.88 (0.86; 0.89) | 0.92 (0.91; 0.93) | 0.93 (0.92; 0.94) | 0.93 (0.93; 0.94) | .016 | .000 | .000 | .000 | .000 | .000 |
| SVM | 0.68 (0.64; 0.71) | 0.74 (0.69; 0.79) | 0.76 (0.75; 0.77) | 0.75 (0.74; 0.77) | 0.78 (0.76; 0.8) | 0.78 (0.77; 0.79) | 0.77 (0.76; 0.78) | .024 | .001 | .001 | .000 | .000 | .000 |
| Precision | |||||||||||||
| LR | 0.53 (0.37; 0.69) | 0.70 (0.65; 0.75) | 0.58 (0.52; 0.65) | 0.65 (0.61; 0.69) | 0.69 (0.66; 0.72) | 0.71 (0.68; 0.73) | 0.74 (0.73; 0.75) | .042 | .538 | .132 | .063 | .038 | .015 |
| DT | 0.25 (0.10; 0.40) | 0.68 (0.63; 0.72) | 0.56 (0.50; 0.61) | 0.59 (0.54; 0.63) | 0.65 (0.62; 0.67) | 0.71 (0.69; 0.72) | 0.68 (0.66; 0.71) | .000 | .000 | .000 | .000 | .000 | .000 |
| XGB | 0.67 (0.54; 0.8) | 0.74 (0.70; 0.79) | 0.75 (0.70; 0.79) | 0.74 (0.70; 0.78) | 0.78 (0.76; 0.81) | 0.80 (0.78; 0.82) | 0.86 (0.85; 0.87) | .249 | .296 | .298 | .100 | .049 | .010 |
| RF | 0.67 (0.44; 0.89) | 0.74 (0.69; 0.79) | 0.86 (0.81; 0.92) | 0.81 (0.78; 0.84) | 0.81 (0.79; 0.84) | 0.83 (0.81; 0.86) | 0.88 (0.87; 0.88) | .460 | .088 | .171 | .166 | .126 | .065 |
| NN | 0.45 (0.36; 0.54) | 0.70 (0.67; 0.74) | 0.77 (0.74; 0.8) | 0.75 (0.72; 0.77) | 0.82 (0.8; 0.84) | 0.85 (0.84; 0.87) | 0.86 (0.84; 0.87) | .000 | .000 | .000 | .000 | .000 | .000 |
| SVM | 0.00 (0; 0) | 0.65 (0.57; 0.72) | 0.35 (0.12; 0.58) | 0.62 (0.58; 0.67) | 0.65 (0.63; 0.67) | 0.69 (0.67; 0.71) | 0.67 (0.66; 0.69) | .000 | .007 | .000 | .000 | .000 | .000 |
| Recall | |||||||||||||
| LR | 0.09 (0.07; 0.12) | 0.66 (0.61; 0.7) | 0.20 (0.19; 0.22) | 0.36 (0.34; 0.39) | 0.54 (0.51; 0.57) | 0.72 (0.7; 0.73) | 0.77 (0.75; 0.78) | .000 | .000 | .000 | .000 | .000 | .000 |
| DT | 0.04 (0.01; 0.08) | 0.66 (0.59; 0.73) | 0.20 (0.13; 0.28) | 0.44 (0.28; 0.6) | 0.64 (0.59; 0.7) | 0.73 (0.7; 0.76) | 0.79 (0.74; 0.83) | .000 | .002 | .001 | .000 | .000 | .000 |
| XGB | 0.17 (0.13; 0.21) | 0.73 (0.70; 0.77) | 0.44 (0.40; 0.49) | 0.62 (0.59; 0.66) | 0.77 (0.75; 0.80) | 0.88 (0.86; 0.89) | 0.92 (0.91; 0.93) | .000 | .000 | .000 | .000 | .000 | .000 |
| RF | 0.08 (0.05; 0.11) | 0.73 (0.70; 0.77) | 0.39 (0.36; 0.42) | 0.58 (0.55; 0.61) | 0.77 (0.75; 0.78) | 0.88 (0.86; 0.89) | 0.91 (0.9; 0.92) | .000 | .000 | .000 | .000 | .000 | .000 |
| NN | 0.22 (0.18; 0.27) | 0.68 (0.64; 0.72) | 0.62 (0.6; 0.63) | 0.66 (0.63; 0.69) | 0.83 (0.8; 0.86) | 0.91 (0.89; 0.93) | 0.91 (0.9; 0.92) | .000 | .000 | .000 | .000 | .000 | .000 |
| SVM | 0.00 (0; 0) | 0.65 (0.59; 0.71) | 0.01 (0.0; 0.01) | 0.21 (0.19; 0.23) | 0.59 (0.56; 0.61) | 0.76 (0.74; 0.78) | 0.77 (0.76; 0.78) | .000 | .003 | .000 | .000 | .000 | .000 |
| Brier score | |||||||||||||
| LR | 0.08 (0.05; 0.11) | 0.20 (0.15; 0.24) | 0.13 (0.12; 0.15) | 0.17 (0.14; 0.2) | 0.19 (0.16; 0.22) | 0.19 (0.18; 0.21) | 0.17 (0.16; 0.19) | .000 | .000 | .000 | .000 | .000 | .000 |
| DT | 0.09 (0.05; 0.13) | 0.21 (0.14; 0.28) | 0.14 (0.06; 0.21) | 0.17 (0.01; 0.33) | 0.19 (0.13; 0.24) | 0.19 (0.16; 0.22) | 0.19 (0.15; 0.23) | .000 | .000 | .000 | .000 | .000 | .000 |
| XGB | 0.07 (0.04; 0.11) | 0.17 (0.14; 0.21) | 0.10 (0.06; 0.14) | 0.13 (0.09; 0.16) | 0.13 (0.1; 0.15) | 0.12 (0.11; 0.13) | 0.09 (0.07; 0.1) | .000 | .000 | .000 | .000 | .000 | .013 |
| RF | 0.08 (0.05; 0.11) | 0.17 (0.13; 0.21) | 0.10 (0.07; 0.13) | 0.12 (0.09; 0.15) | 0.12 (0.1; 0.14) | 0.12 (0.1; 0.13) | 0.09 (0.08; 0.11) | .000 | .000 | .000 | .000 | .000 | .001 |
| NN | 0.09 (0.04; 0.14) | 0.20 (0.15; 0.24) | 0.08 (0.07; 0.1) | 0.12 (0.09; 0.16) | 0.11 (0.08; 0.14) | 0.10 (0.08; 0.12) | 0.10 (0.09; 0.11) | .000 | .293 | .001 | .033 | .156 | .286 |
| SVM | 0.09 (0; 0) | 0.21 (0.15; 0.26) | 0.15 (0.15; 0.16) | 0.18 (0.16; 0.2) | 0.19 (0.16; 0.21) | 0.19 (0.18; 0.21) | 0.19 (0.18; 0.21) | .000 | .000 | .000 | .000 | .000 | .000 |
Note: Yellow marking indicates a significant difference compared to the original dataset.
Figure 3.
Evaluation metrics per learner.
The calibration curves show a similar effect leading to an overestimation of predicting positives as opposed to predicting negatives as seen in Figure 4. In most of the calibration overestimation of negatives was observed, showing that resampling techniques mainly create an overestimation on positives for our case of predicting 30-day unplanned readmission. In this scenario, there would be an abundance of patients with high positive prediction scores. Another effect observed is that all classification algorithms are affected in a similar manner of producing overestimates of positive predictions.
Figure 4.
Calibration curve plots per algorithm per sampled dataset.
DISCUSSION
Resampling data has a subtle yet substantial impact on performance of algorithms, producing more positive than negative predictions as compared to the original dataset. To our surprise, XGB, RF, NN, and SVM showed significant improved performances measured in AUC and precision when resampling compared to LR, and DT. For precision and recall, most algorithms showed a significant improvement in performance measured, let alone a notable difference when using resampled data. Another surprise was the improvement observed between 2 oversampling techniques set with the same 50-50 ratio, being ADASYN and SMOTE. Using ADASYN, improvements in precision and recall were seen in most models except for SVM and DT. Our results are in line with findings of previous studies, indicating that resampling data leads to similar results when applied to different data.3,11 Other studies show similarities in improved results by applying resampling, but not much drift in calibration, suggesting that the impact of resampling effects on calibration are more case-sensitive as compared to other evaluation metrics. Although distorting calibration, models trained on resampled data can still have clinical utility whereas the model can have poor calibration yet a strong discriminating performance. When correctly identifying cases with only low and high risk is important, as opposed to identifying cases across the range of all probability scores, the model can still benefit in performance from resampling data.19,20 Correcting the class imbalance problem with resampling for the case of 30-day unplanned readmissions, may yield more clinical utility as compared to no resampling. More clinical utility would be derived from improved performance in discriminative performance (ie, AUC), resulting in more accurate risk stratification of low and high risk patients, and possibly improving (safe) discharge management.
We acknowledge 2 limitations of this study. The first limitation is the limited use of different resampling algorithms, not using other options such as SMOTE Nominal and Continuous (NC), and borderline SMOTE. Although using another oversampling algorithm (ie, ADASYN) in this study, the limited choice may lead to a different effect on performance as compared to the techniques applied in this study. The second limitation is studying one clinical case, where we only observed the impact of sampling data over all trained algorithms with data of 30-day unplanned readmissions for patients in Urology. Performance might differ when applying resampling techniques to data in other clinical case scenarios, to investigate if the class imbalance problem might be less case-sensitive.
Future studies should aim at investigating other resampling techniques, in order to gain insight concerning the resampling techniques applied next to the overestimation of positives. Also, more than one clinical case should be analyzed in the same manner to investigate whether the class imbalance problem might be case-sensitive.
CONCLUSION
Our study highlights the importance of resampling techniques to overcome the class imbalance problem in a clinical scenario for prediction of unplanned readmission in urology patients. Resampling data results in increased performances in classification algorithms, yet produces an overestimation of positive predictions based on data in our case study. Based on our findings when using medical data from our case study, a thoughtful predefinition of the clinical prediction task, thereby balancing the importance of discrimination and calibration, may guide the use of resampling techniques in future studies aiming to improve clinical decision support tools.
Supplementary Material
Contributor Information
Koen Welvaars, Data Science Team, OLVG, Amsterdam, The Netherlands.
Jacobien H F Oosterhoff, Department of Engineering Systems & Services, Faculty Technology Policy and Management, Delft University of Technology, Delft, The Netherlands.
Michel P J van den Bekerom, Department of Orthopaedic Surgery, OLVG, Amsterdam, the Netherlands; Faculty of Behavioural and Movement Sciences, Vrije Universiteit, Amsterdam, the Netherlands.
Job N Doornberg, Department of Orthopaedic Surgery, UMCG, Groningen, the Netherlands.
Ernst P van Haarst, Department of Urology, OLVG, Amsterdam, the Netherlands.
OLVG Urology Consortium, and the Machine Learning Consortium:
J A van der Zee, G A van Andel, B W Lagerveld, M C Hovius, P C Kauer, L M S Boevé, A van der Kuit, W Mallee, and R Poolman
FUNDING
This work was supported by the OLVG Urology Consortium. The funders had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; and decision to submit the manuscript for publication.
AUTHOR CONTRIBUTIONS
KW had full access to all of the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis. Concept and design: All authors. Acquisition, analysis, modeling of data: KW. Interpretation of data: All authors. Drafting of the manuscript: All authors. Critical revision of the manuscript for important intellectual content: All authors. Statistical analysis: KW. Obtained funding: Not applicable. Administrative, technical, or material support: KW. Supervision: JHFO, EPvH, MPJvdB, and JND.
ETHICS APPROVAL
This study was approved by the independent Scientific Research Advisory Committee. The data was derived from the OLVG, Amsterdam, the Netherlands. The database is deidentified, and approval was granted by the institutional review board (METC).
STATEMENT OF HUMAN AND ANIMAL RIGHTS
This article does not contain any studies with animals performed by any of the authors.
INFORMED CONSENT
Informed consent was obtained from the independent Scientific Research Advisory Committee.
SUPPLEMENTARY MATERIAL
Supplementary material is available at JAMIA Open online.
CONFLICT OF INTEREST STATEMENT
All authors have no commercial associations (eg, consultancies, stock ownership, equity interest, patent/licensing arrangements, etc.) that might pose a conflict of interest in connection with the submitted article.
DATA AVAILABILITY
The 30-day unplanned readmissions from Urology dataset cannot be shared for ethical/privacy reasons.
Collaborators OLVG Urology Consortium: J.A. van der Zee, G.A. van Andel, B.W. Lagerveld, M.C. Hovius, P.C. Kauer, and L.M.S. Boevé
Collaborators Machine Learning Consortium: A. van der Kuit, W. Mallee, and R. Poolman
Investigation performed at OLVG Hospital, Amsterdam, the Netherlands.
REFERENCES
- 1. Megahed FM, Chen Y-J, Megahed A, et al. The class imbalance problem. Nat Methods 2021; 18 (11): 1270–2. [DOI] [PubMed] [Google Scholar]
- 2. Fernández A, García S, Galar M, et al. Learning from Imbalanced Data Sets. Cham: Springer International Publishing; 2018. doi: 10.1007/978-3-319-98074-4. [DOI] [Google Scholar]
- 3. Kim M, Hwang K-B.. An empirical evaluation of sampling methods for the classification of imbalanced data. PLoS One 2022; 17 (7): e0271260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Li D-C, Liu C-W, Hu SC.. A learning method for the class imbalance problem with medical data sets. Comput Biol Med 2010; 40 (5): 509–18. [DOI] [PubMed] [Google Scholar]
- 5. Fujiwara K, Huang Y, Hori K, et al. Over- and under-sampling approach for extremely imbalanced and small minority data problem in health record analysis. Front Public Health 2020; 8: 178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Zhang J, Chen L.. Clustering-based undersampling with random over sampling examples and support vector machine for imbalanced classification of breast cancer diagnosis. Comput Assist Surg (Abingdon) 2019; 24 (Suppl 2): 62–72. [DOI] [PubMed] [Google Scholar]
- 7. Lyashevska O, Malone F, MacCarthy E, et al. Class imbalance in gradient boosting classification algorithms: application to experimental stroke data. Stat Methods Med Res 2021; 30 (3): 916–25. [DOI] [PubMed] [Google Scholar]
- 8. Fotouhi S, Asadi S, Kattan MW.. A comprehensive data level analysis for cancer diagnosis on imbalanced data. J Biomed Inform 2019; 90: 103089. [DOI] [PubMed] [Google Scholar]
- 9. Gnip P, Vokorokos L, Drotár P.. Selective oversampling approach for strongly imbalanced data. PeerJ Comput Sci 2021; 7: e604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Blagus R, Lusa L.. SMOTE for high-dimensional class-imbalanced data. BMC Bioinformatics 2013; 14: 106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Pakhomov SVS, Finley G, McEwan R, et al. Corpus domain effects on distributional semantic modeling of medical terms. Bioinformatics 2016; 32 (23): 3635–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Liu L, Wu X, Li S, et al. Solving the class imbalance problem using ensemble algorithm: application of screening for aortic dissection. BMC Med Inform Decis Mak 2022; 22 (1): 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Sharma A, Verbeke WJMI.. Improving diagnosis of depression with XGBOOST machine learning model and a large biomarkers Dutch dataset (n = 11,081). Front Big Data 2020; 3: 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. van den Goorbergh R, van Smeden M, Timmerman D, et al. The harm of class imbalance corrections for risk prediction models: illustration and simulation using logistic regression. J Am Med Inform Assoc 2022; 29 (9): 1525–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Azur MJ, Stuart EA, Frangakis C, et al. Multiple imputation by chained equations: what is it and how does it work? Int J Methods Psychiatr Res 2011; 20 (1): 40–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Menze BH, Kelm BM, Masuch R, et al. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinformatics 2009; 10: 213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Steyerberg EW, Vergouwe Y.. Towards better clinical prediction models: seven steps for development and an ABCD for validation. Eur Heart J 2014; 35 (29): 1925–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Cox DR. Two further applications of a model for binary regression. Biometrika 1958; 45 (3–4): 562–5. [Google Scholar]
- 19. Ramezankhani A, Pournik O, Shahrabi J, et al. The impact of oversampling with SMOTE on the performance of 3 classifiers in prediction of type 2 diabetes. Med Decis Making 2016; 36 (1): 137–44. [DOI] [PubMed] [Google Scholar]
- 20. Koivu A, Sairanen M, Airola A, et al. Synthetic minority oversampling of vital statistics data with generative adversarial networks. J Am Med Inform Assoc 2020; 27 (11): 1667–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The 30-day unplanned readmissions from Urology dataset cannot be shared for ethical/privacy reasons.