Oxidation of Cysteine by Electrogenerated Hexacyanoferrate(III) in Microliter Droplets

Abstract

Chemical reactivity in droplets is often assumed to mimic reactivity in bulk, continuous water. Here, we study the catalytic oxidation of cysteine by electrogenerated hexacyanoferrate(III) in microliter droplets. These droplets are adsorbed onto glassy carbon macroelectrodes and placed into an immiscible 1,2-dichloroethane phase. We combined cyclic voltammetry, optical microscopy, and finite element simulations to quantify the apparent bimolecular rate constant, k_c,app, in microdroplets and bulk water. Statistical analyses reveal that the apparent bimolecular rate constant (k_c,app) values formicrodroplets are larger than those in the continuous phase. Reactant adsorption to the droplet boundary has previously been implicated as the cause of such rate accelerations. Finite element modeling of this system suggests that molecular adsorption to the liquid|liquid interface cannot alone account for our observations, implicating kinetics of the bimolecular reaction either at the boundary or throughout the microliter volume. Our results indicate that cysteine oxidation by electrogenerated hexacyanoferrate(III) can be accelerated within a microenvironment, which may have profound implications on understanding biological processes within a cell.

Graphical Abstract

INTRODUCTION

As an amino acid, cysteine plays a critical role in maintaining the cellular redox state and overall protein structure. Universal cellular redox processes, such as the formation of free radicals, can oxidize the sulfhydryl group in cysteine to form a dimerized product, cystine, which contains a disulfide bond. Gottlieb and co-workers have previously demonstrated cysteine’s key role in mitigating oxidative stress within the cell.¹ In cellulo, biomolecular cysteine oxidation occurs under confined conditions (most cells are sub-microliter). To demonstrate the importance of confinement on the protein structure, Pielak and co-workers previously showed that protein stability changes drastically in inverse micelles. Given that redox transformations between cysteine and cystine dictate a global tertiary protein structure within a cell, understanding bimolecular cysteine oxidation kinetics in confined spaces can elucidate how nature employs such environments.²

Aqueous droplets are model environments to study chemical reactions under confinement. Cooks et al. have reported extensively on enhanced reaction acceleration within electro-sprayed microdroplets.³ Griffiths and co-workers have used fluorescence spectroscopy to demonstrate that reaction acceleration occurs due to an adsorption mechanism, creating concentration gradients that drive reaction acceleration.⁴ Zare and co-workers have also demonstrated the unusual reactivity at the water|air phase boundary, where spontaneous reduction reactions (i.e., oxygen reduction⁵ and metal salt reduction⁶) are driven. Previously, our group has used electrochemical techniques to demonstrate a flavin adenine dinucleotide-dependent glucose dehydrogenase enzyme (FADGDH) rate enhancement in sub-femtoliter (<10⁻¹⁵ L) droplets.⁷ Rate acceleration has also been observed in microliter droplets. Leidenfrost droplets⁸ and acoustically levitated droplets⁹ have demonstrated modestly accelerated reaction rates a factor of 2−10 compared to bulk values. In these experiments, a microliter droplet is levitated, and chemical reactions within the droplet are traced using mass spectrometry.

Here, we develop electrochemical methods to study cysteine oxidation to cystine by electrogenerated hexacyanoferrate(III), shown in eqs 1 and 2. These types of reactions fall under a special type of coupled chemical reactions in voltammetry referred to as EC′, where “E” stands for the electrochemical reaction (eq 1) and “C” stands for the follow-up chemical reaction. The symbol associated with “C′” denotes that the initial electrochemical reactant is regenerated during the follow-up chemical reaction, as shown in eq 2. When the oxidation of hexacyanoferrate(II) is driven at the electrode surface, hexacyanoferrate(III) spontaneously oxidizes cysteine to form the dimerized product, cystine. We use optical micrographs to inform on the exact geometry of each droplet probed, and finite element modeling to simulate voltammograms that rigorously evaluate the apparent bimolecular rate constant, k_c,app. By assuming that the bimolecular rate constant is the only adjustable parameter, we demonstrate that k_c,app is statistically larger in microliter droplets compared to bulk, continuous water under similar conditions. This set of experiments highlights the power of coupling experimental electrochemistry and microscopy with simulation to elucidate accelerated reaction rates in microliter volumes. Finally, we explore the effect of adsorption to the liquid|liquid interface by adding adsorption to the finite element simulations. These results in small volumes highlight how biologically relevant reaction mechanisms that involve electron transfer may behave differently within a cell.

$$E\text{ Fe}{\left(\text{CN}\right)}_6^{4-}-e^{-}\stackrel{k^0\left( \text{cm}\cdot {\text{s}}^{-1}\right)}{\to }\text{Fe}{\left(\text{CN}\right)}_6^{3-}$$ (1)

$$C^{\prime }2\text{Fe}{\left(\text{CN}\right)}_6^{3-}+2{\text{C}}_3{\text{H}}_7{\text{NO}}_2\text{S}\stackrel{k_c\left({\text{M}}^{-1}\cdot {\text{s}}^{-1}\right)}{\to }2\text{Fe}{\left(\text{CN}\right)}_6^{4-}+2{\text{H}}^{+}+{\text{C}}_6{\text{H}}_{12}{\text{N}}_2{\text{O}}_4{\text{S}}_2$$ (2)

MATERIALS AND METHODS

Chemicals and Materials.

Potassium hexacyanoferrate(II) trihydrate (ferrocyanide, ≥99.95%) and potassium hexacyanoferrate(III) (ferricyanide, 99.98%) were purchased from Sigma-Aldrich and used without further purification. Phosphate buffer (PB) was prepared in-house using sodium phosphate dibasic anhydrous from Fisher Chemical and sodium phosphate monobasic from EM Science. Potassium chloride was purchased from Fischer Chemical. Hydro-chloric acid (36.5% HCl, 99.999%) was obtained from Alfa Aeser, and sodium hydroxide (NaOH) was obtained from Sigma Aldrich. Nanopure water (Millipore Milli-Q, 18.20 MΩ cm⁻¹) was used to prepare all aqueous solutions. 1,2-Dichloroethane (DCE) was obtained from Alfa Aesar. Tetrabutylammonium perchlorate (TBAP, ≥99.0%) was obtained from Sigma-Aldrich. Carbon macroelectrodes (r = 1.5 mm) and silver/silver chloride (Ag/AgCl) reference electrodes were obtained from CH Instruments (CHI, Austin, TX). In the droplet-confined experiments, a salt bridge composed of 3% agarose and 1 M KCl in a glass tube was used to connect the aqueous reference electrode to the organic (DCE) phase to protect the integrity of the reference. Before each new measurement, the working electrode was rinsed with acetone and nanopure water, polished with 0.3 μm alumina powder, then rinsed again with nanopure water and acetone, and dried with compressed air for ~15 s. In our experience, there is no difference in voltammetry when polishing with 0.05 μm versus 0.3 μm alumina particles.

Instrumentation.

All stock solutions were sonicated by a bench sonicator from VWR. All cyclic voltammetry experiments were performed with a CHI 601E potentiostat. A digital microscope from Park Systems was controlled by a PC for image collection, and measurement software from CoolingTech or ImageJ (NIH, Public Domain) was used to determine droplet geometry.

Experimental Section.

A glassy carbon electrode was used because it is not very catalytic toward cysteine oxidation. The oxidation of cysteine to cystine liberates proton and can be made more favorable in alkaline environments. Choosing a suitable buffer pH and concentration required consideration of the homogeneous and heterogeneous kinetics and solubilities. Although a favorable chemical reaction between hexacyanoferrate(III) and cysteine is preferred, the kinetics for the direct electrochemical oxidation of cysteine must be slow such that there is a window for the electrochemical measurement where the chemical oxidation of cysteine occurs when the electrochemical oxidation does not. This condition is necessary to drive EC′ reactions. At high pH, the electrochemical oxidation is favorable, limiting the electrochemical window (Figure S1a); however, at low pH, the chemical oxidation is sluggish (Figure S1b). Thus, a slightly acidic pH (6.3−6.5) was used for all measurements (Figure S1c). The buffer concentration used was 50 mM, and 0.5 M KCl was added to minimize iR drop. KCl was chosen because the transference numbers between K⁺ and Cl⁻ are similar and minimize junction potentials. Given the amount of the supporting electrolyte used in this study (>100 mM salt), we do not expect the charge of cysteine at various pH values to influence the voltammetric response shown in Figure S1.

It should also be noted that cysteine is a zwitterion and its maximum solubility is reached far away from its isoelectric point (pH = 5). The oxidation product, cystine, also has limited solubility at near neutral pH (0.5 mM for pH 7¹⁰). We used 0.5 mM hexacyanoferrate(II) and 5 mM cysteine, where the low absolute concentrations limited product formation under solubility constraints, but the high cysteine concentration reduced diffusional limitations to the reaction (Figure S2). A moderate scan rate of 0.1 V/s was employed, avoiding slow scan rates (creates more product) and fast scan rates, which have higher capacitive currents (scaling proportionally with the scan rate) and time scales that beat out the follow-up chemical step. Voltammetry windows were chosen to ensure that the faradaic process of interest could be observed at its mass transfer limitation but without the direct oxidation of cysteine.

All these optimizations were necessary to ensure relatively reproducible voltammograms. Given the complexity of the system, simulations were fit to the forward sweep for each voltammogram. Simulations for a return sweep are provided throughout the Supporting Information, but the local cystine concentration exceeds solubility on the return sweep, and so, they were not used for fitting. By using high amounts of salt relative to analyte, the voltammetric control experiments (no cysteine) showed a difference in peak potential near the expected ~60 mV, indicating very little iR drop within the system. Thus, our presented voltammograms are not corrected for iR.

Comparable values and mechanism for the oxidation of cysteine by electrogenerated hexacyanoferrate(III) were taken from a previous report by Compton and co-workers.¹¹

Simulation.

COMSOL Multiphysics 5.5 and 5.6 were used to compare computational transients to experimental data. When fitting experimental data to simulation to find the k_c,app, the experimental data were adjusted such that the foot of the wave overlaid the simulation before adjusting the k_c parameter. Importantly, in these simulations, k_c and the droplet geometry (observed in optical microscopy) are the only adjustable parameters. A detailed discussion on the performed simulation is provided in the Supporting Information, including information on the important computational parameters of the model and Figure S5. The finite element model accounts for changes in the geometry that may give rise to changes in the mass transfer coefficient. All reaction rates reported were evaluated using a finite element model that accounts for each droplet’s geometry. In these simulations, the only adjustable parameter is the reaction rate.

COMSOL Multiphysics 5.6 was also used to simulate the effect of reactant adsorption to the droplet boundary. This model introduces adjustable parameters to the simulation, all of which are discussed in detail in the Supporting Information (Figures S6 and S7).

RESULTS AND DISCUSSION

Cyclic voltammetry provides a powerful electroanalytical tool to study reaction mechanisms.¹² As a model system, we chose to study the apparent bimolecular rate constant (k_c,app) for the reaction between hexacyanoferrate(III) and cysteine. Hexacyanoferrate(II) is oxidized to hexacyanoferrate(III) at the electrode, when it is biased at oxidizing potentials (E⁰′ = 0.22 V vs Ag/AgCl). Hexacyanoferrate(III) is then reduced back to hexacyanoferrate(II) by cysteine, which dimerizes to cystine as a result of the chemical oxidation.¹¹ This mechanism is illustrated in Figure 1a. When confined to a microliter droplet, the reaction is similar; however, electroneutrality must be maintained to drive a sustained current. In our experiments, the perchlorate anion will transfer into and out of the microdroplet to maintain electroneutrality (Figure 1b). The technique presented here is applicable to electrochemical reactions with a follow-up chemical step if all reactants and products are selectively soluble in the aqueous phase and not the continuous oil phase.

Figure 1.

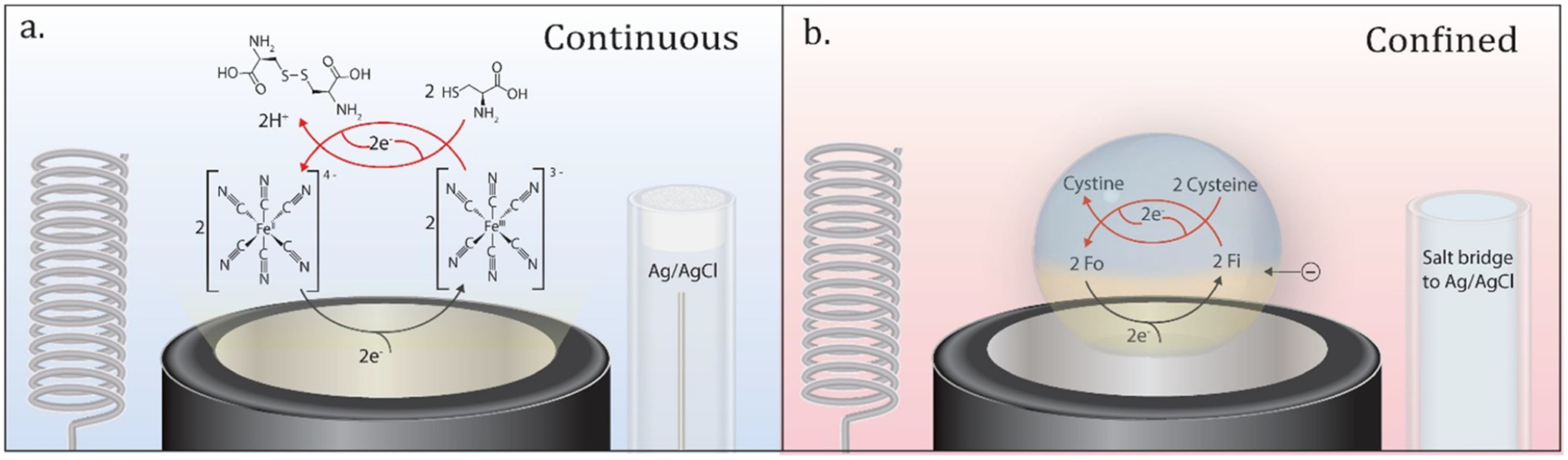
Schematic illustration of the continuous system and the confined system. (a) The continuous solution is composed of phosphate buffer and potassium chloride. The silver/silver chloride reference electrode and platinum coil counter electrode are in direct contact with the solution. (b) The confined solution is a 1 μL droplet of phosphate buffer and potassium chloride. The droplet is submerged in 1,2-dichloroethane with 0.5 M tetrabutylammonium perchlorate. The platinum coil counter electrode and salt bridge are in direct contact with 1,2-dichloroethane, and the salt bridge connects the reference electrode to the solution. Fi = hexacyanoferrate(III), Fo = hexacyanoferrate(II).

As demonstrated in Figure 2a, the electrochemical anodic current (proportional to hexacyanoferrate(II) concentration) is enhanced by the EC′ mechanism, as it is regenerated near (within 20 μm, vide infra) the electrode by the chemical reaction and can undergo further electron transfer with the electrode surface. The electrochemical cathodic current (proportional to hexacyanoferrate(III) concentration) is largely eliminated because any hexacyanoferrate(III) produced at the surface is consumed by the follow-up chemical reaction. This elimination manifests itself in the cyclic voltammogram as no cathodic peak on the return sweep. A similar response is observed in the microliter droplet system; however, in this system, the half-wave potential (E1/2) shifts to ~0.2 V vs Ag/AgCl. This potential is reproducibly ca. 20 mV less positive than in the bulk system (Figure 2b). The shift in the E_1/2 may be due to liquid junction potentials introduced by having the aqueous reference electrode/salt bridge in the non-aqueous phase.¹³ We note that these observed small shifts are on the order expected from changes in ion transference numbers but are difficult to characterize as they exist in a complex, multiphase system. Such recorded shifts in the E_1/2 do not distort voltammetry or have any influence on kinetics of the system and are simply accounted for by shifting the assigned equilibrium potential for the hexacyanoferrate (II/III) couple in the simulation to match the experimentally observed half-wave potential.

Figure 2.

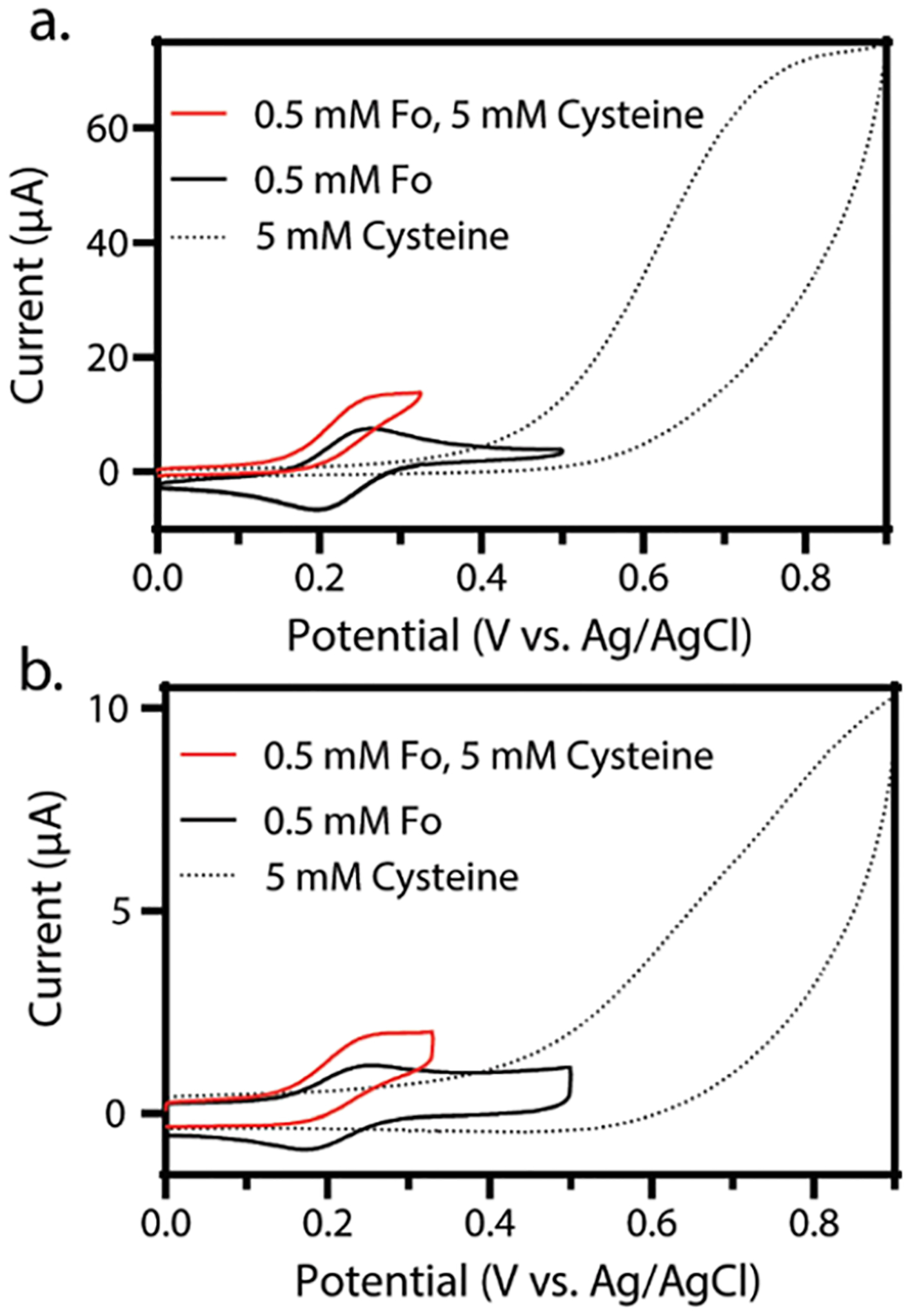
Overlaid cyclic voltammograms showing the voltammetry of hexacyanoferrate(II) (black), cysteine (black dotted), and hexacyanoferrate(II) in the presence of cysteine (red) in 50 mM PB, 0.5 M KCl (pH = 6.4). (a) Bulk, continuous water—cyclic voltammetry of 0.5 mM hexacyanoferrate(II) (black), 5 mM cysteine (black dots), and 0.5 mM hexacyanoferrate(II) and 5 mM cysteine (red). (b) Microliter water droplet—cyclic voltammetry of 0.5 mM hexacyanoferrate(II) (black), 5 mM cysteine (black dots), and 0.5 mM hexacyanoferrate(II) and 5 mM cysteine (red). For all voltammograms in this figure, three electrodes were used: working, reference, and counter electrodes of glassy carbon, Ag/AgCl, and platinum coil, respectively. The scan rate for all experiments is 0.1 V/s, and in line with IUPAC convention, the anodic current is plotted as positive.

The cyclic voltammograms were simulated using finite element simulations where the rate constant (k_c,app) was the only adjustable parameter. Figure 3a shows the response for the reaction between 0.5 mM hexacyanoferrate(III) and 5 mM cysteine, where the experimental data is overlaid with the simulated fit for the bulk, continuous solution (5 milliliters). The average rate was determined to be 309 ± 89 M⁻¹ s⁻¹. This rate, while specific to the experimental conditions, has reasonable agreement with previous studies that have determined the bimolecular rate constant under various conditions.^11,14 We also note that the rates presented in this study are used only for comparison between the bulk and confined systems, where experimental conditions and analyses are the same. To test the effects of confinement, 1 μL of the bulk solution was pipetted onto a glassy carbon electrode and submerged in 1,2-dichloroethane with 0.5 M tetrabutylammonium perchlorate, a salt used to maintain electroneutrality during the electrochemical reaction within the droplet (illustrated in Figure 1b). Images of the droplet reactor submerged in DCE were collected by a digital microscope for each experiment. The geometry of the droplet was measured by ImageJ or CoolingTech software using the electrode diameter (d = 3 mm) as the calibration measurement (Figure 3b). The electrochemical experiment correlated to the micrograph in Figure 3b is shown in Figure 3c, and the simulation is overlaid with the experimental data. Under these voltammetric conditions, we have no evidence that the three-phase boundary moves during the experiment. Using the optically determined geometry, finite element simulations allowed access to the apparent bimolecular rate constant: 490 ± 128 M⁻¹ s⁻¹, a value statistically higher than the constant calculated in the bulk solution (Figure 3d). Using COMSOL Multiphysics allows us to account for the special geometry of our system (e.g., droplet size and curvature). Data from panel 3d includes the k_c,app extracted from all measurements obtained from the same stock solution (each measurement is shown in Figures S2 and S3), which results in relatively large error bars, though statistical significance between the bulk and confined kinetics parameters is conserved (see Supporting Information, Figure S4 for discussion on microscopy error).

Figure 3.

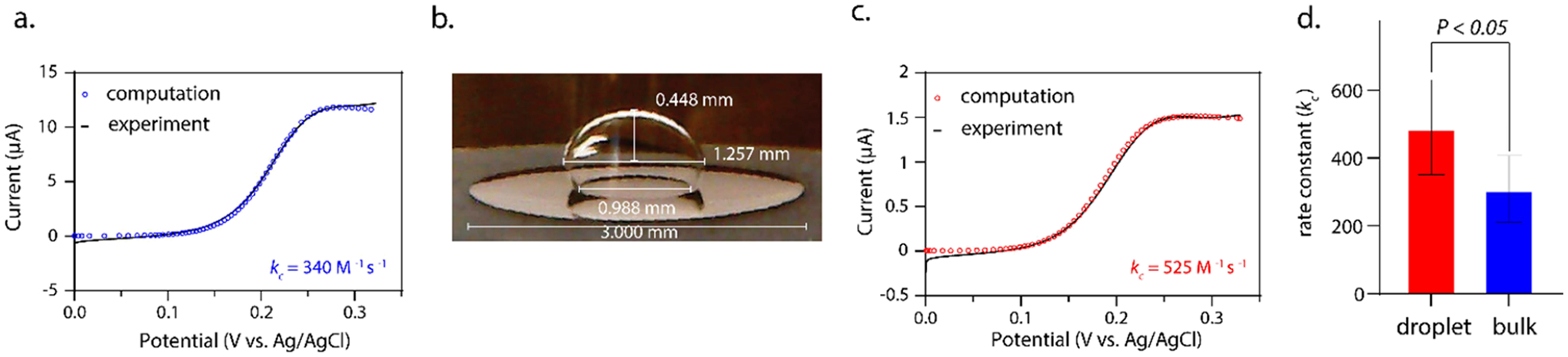
(a) Representative voltammogram (black) of 0.5 mM hexacyanoferrate(II) and 5 mM cysteine in a solution of 50 mM phosphate buffer and 0.5 M KCl (pH = 6.3). The simulated fit is overlaid (blue circles), where the k_c value is the only adjustable parameter and is set to 340 M⁻¹ s⁻¹ (scan rate = 0.1 V/s). (b) Image and measurement of a 1 μL pipetted droplet containing 0.5 mM hexacyanoferrate(II) and 5 mM cysteine in 50 mM phosphate buffer and 0.5 M KCl (pH = 6.3). The droplet is submerged in 0.5 M TBAP in DCE. (c) Voltammogram of the droplet system shown in panel b. The simulated fit is overlaid (red circles), where the k_c value is the only adjustable parameter and is set to 525 M⁻¹ s⁻¹ (scan rate = 0.1 V/s). (d) Bar graph showing the determined rate constants for the bulk (blue, 309 ± 89) and droplet-confined (red, 490 ± 128) system (N = 6, each). For all voltammetry in this figure, three electrodes were used with a working, reference, and counter electrode of glassy carbon (r = 1.5 mm), Ag/AgCl, and platinum coil, respectively. In line with IUPAC convention, the anodic current is plotted as positive.

To minimize the complications from experimental conditions, we chose to study the 0.5:5 mM ratio of ferrocyanide to cysteine in 50 mM buffer (see Methods for additional details). Finite element modeling allows for the quantification of reactant and product concentrations at the electrode surface through each timepoint of the measurement. This system minimized pH changes and cystine precipitation ^10,15 at the electrode surface over the duration of the experiment. To quantify kinetic parameters, we only fit data in the forward voltammetric scan. The simulation indicates that cystine reaches its solubility limitation at timescales beyond the first voltammetric sweep. Because the oxidation of cysteine will release a proton, one may be concerned with pH changes at the electrode surface during voltammetry. Our finite element model allows for the quantification of the pH change at the surface of the electrode in the presence of buffer during a voltammetric sweep. From simulation, we expect the pH at the electrode surface to change by a maximum of 6 × 10⁻⁵ pHunits (a value under the precision of the pH meter in most laboratories) for the droplet system shown in Figure 3. Under these buffered conditions, we do not expect the pH of the droplet to change during a voltammetric sweep. These simulations are shown in Supporting Information Figure S5.

These data suggest an average enhancement of about 1.5× in one microliter-confined volumes. Our results are similar to observations for other reported reactions in microliter volumes, where reaction rates are accelerated by a factor of 2−10.⁹ Cooks and co-workers have demonstrated the role partial solvation plays at the droplet|air interface. In our experiments, the phase boundary is between two immiscible electrolyte solutions. However, the solvation of molecules at the surface—and molecular orientation—may play a role in the accelerated reactions measured in this study. Previously, Aoki et al. have explored convection within microliter droplets.¹⁶ Voltammograms in various droplet systems in the absence of the EC′reaction have shown no obvious signs of convection (Figure S6). At this time, it is unclear whether or not comparable compounds (e.g., homocysteine, glutathione, and methionine) behave in a similar manner. An investigation into these compounds will be the topic of a future study.

Previously, we demonstrated that homogeneous reaction rates are inversely related to water droplet size.⁷ Whereas in nanodroplet experiments mixing is fast and the electrode contact radius does not play a significant role in the response, in the experiments reported here, the electrochemical response depends on the contact radius, as demonstrated in the Supporting Information (Figure S7d). Because of the correlation with microscopy, the rate constant can be the only adjustable parameter allowing for rigorous quantification (Figure S7). Thus, it is difficult to perform stochastic electrochemical experiments to rigorously probe the homogeneous reaction rate as a function of water droplet size because for sub-femtoliter droplets, the contact radius cannot be rigorously measured.

Throughout this article, the only adjustable parameter has been the apparent bimolecular rate constant. We call the rate constant “apparent” because it is the only parameter we control to fit the experimental voltammograms. In reality, it is apparent because we do not completely understand the physical cause of the observed accelerated rate. Previously, Griffiths and co-workers⁴ and Wilson et al.¹⁷ have independently demonstrated the importance of reactant adsorption to the liquid|liquid interface to accelerate chemical reactions. Cooks et al. have also demonstrated the importance of solvation at the interface.¹⁸ Given these results, we were curious whether or not a finite element model that accounts for adsorption may offer more insights into the mechanism of rate enhancement. In this section, our intent is not to robustly quantify mechanistic parameters but rather to offer another pathway by which the current response can be increased. For these simulations, the bulk bimolecular apparent rate constant (k_c,app = 309 M⁻¹ s⁻¹) is a constant and is not treated as an adjustable parameter. Figure 4a shows the simulated geometry with the concentrations of volumetric cysteine (in the droplet) and surface cysteine (on the liquid|liquid interface). We use the term “volumetric” to describe freely diffusing species in the droplet that are not adsorbed to any interface. We chose to represent data at 4 s into the simulated voltammetry because this is where the voltammetry is at the mass transfer limitation. This finite element model takes into consideration cysteine adsorption and diffusion on the droplet surface and the bimolecular rate of adsorbed cysteine with volumetric electrogenerated hexacyanoferrate(III), where the surface reaction occurs simultaneously with the reaction shown in eq 2. The new surface reactions can be described by the following equations:

$${\text{C}}_3{\text{H}}_7{\text{NO}}_2\text{S}\stackrel{K_{\text{eq}}}{\leftrightarrow }{\text{C}}_3{\text{H}}_7{\text{NO}}_2{\text{S}}_{(\text{ads})}$$ (3)

$$2\text{Fe}{\left(\text{CN}\right)}_6^{3-}+2{\text{C}}_3{\text{H}}_7{\text{NO}}_2{\text{S}}_{(\text{ads})}\stackrel{k_{c,\text{ surf }}\left({\text{M}}^{-1}\cdot {\text{s}}^{-1}\right)}{\to }2\text{Fe}{\left(\text{CN}\right)}_6^{4-}+2{\text{H}}^{+}+{\text{C}}_6{\text{H}}_{12}{\text{N}}_2{\text{O}}_4{\text{S}}_2$$ (4)

where K_eq is the equilibrium constant. In our simulation, we use a value of 1000 for K_eq given previously published literature on adsorption and desorption rates of molecules to a liquidl liquid interface.¹⁷ We validated our model’s surface adsorption by demonstrating the surface coverage versus bulk concentration follows what one would expect for Langmuir binding behavior (see Supporting Information Figure S8). We also validated that the electrochemical voltammetry of hexacyanoferrate (II/III) is not affected by the adsorption of cysteine (without the follow-up chemical reaction), and the peak current simulated matched that expected by the Randles−Sevcik equation (Figure S9). We do not treat adsorption of hexacyanoferrate (II/III) because we have seen no electrochemical evidence of this in previous investigations.¹⁹ Furthermore, Zare demonstrated that negatively charged molecules do not adsorb to the water|oil interface²⁰ because the interface is negatively charged.²¹ Figure 4b shows that the enhanced current could be partially explained by invoking adsorption and reactivity at the liquid|liquid interface. The observed droplet voltammetry (k_c,app = 490 M⁻¹ s⁻¹) could be predicted by instead invoking a high surface concentration (2 × 10⁻⁴ mol/m²) of cysteine that reacts with hexacyanoferrate(III) by a kinetic constant (kc,surf) 2 orders of magnitude higher (36,000 M⁻¹ s⁻¹) at the boundary than kinetics inside the droplet (309 M⁻¹ s⁻¹). When adding the adsorption to the model, we introduced more adjustable parameters (adsorption kinetics, surface concentration, surface diffusion, and so on). As such, this model signifies the role adsorption and boundary reactivity may play, manifesting in the observable current enhancement, and a thorough quantitative understanding of adjustable parameters will be the topic of a future investigation. An exciting frontier of measurement science is translating biochemical measurements to the single-cell level. Recently, nanoelectrodes have allowed for the quantification of metabolites within single cells.^22,23 How cells use adsorption effects to influence chemical kinetics is an enticing question for future inquiry.^{4–7,20,24,25}

Figure 4.

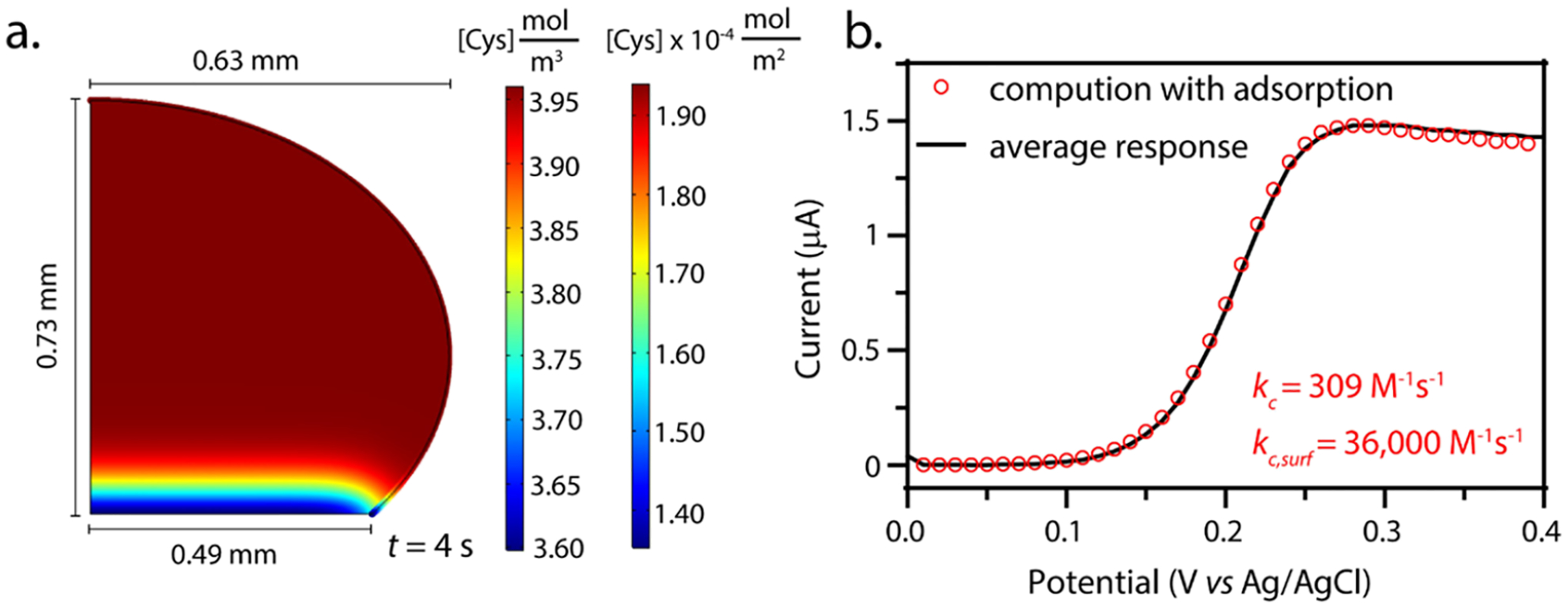
(a) 2D plot of the simulated droplet geometry from the photograph in Figure 3b. The domain coloring shows the concentration of cysteine (mol/m³) in the droplet and the boundary coloring shows the surface concentration of the adsorbed cysteine (mol/m²) at 4 s. The thickness of the adsorbed layer gradient is exaggerated for visibility and is not to scale with the rest of the geometry. (b) Simulated voltammetry for the adsorption model (red circles) overlaid with a voltammogram of the average response (k_c,app = 490 M⁻¹ s⁻¹) in the confined system (black line). For the adsorption model fit, the k_c value was set at 309 M⁻¹ s⁻¹ (average bulk measurement) and kc,surf was adjusted to 36,000 M⁻¹ s⁻¹ (scan rate = 0.1 V/s).

CONCLUSIONS

In sum, we have studied the oxidation of cysteine by electrogenerated hexacyanoferrate(III) in microliter water droplets. By coupling electrochemical measurements with optical micrographs and finite element simulations, we were able to extract the apparent homogeneous rate constants (k_c,app) in microliter water droplets and compare those rate constants to reactions in bulk, continuous water. Optical micrographs were necessary to obtain the geometry of the system for finite element analysis. Our results indicate that electrocatalysis is accelerated in the microenvironment, where we found the rate constants in microliter water droplets to be statistically higher (by ~1.5×) than rate constants in bulk water. These findings may suggest that the oxidation of cysteine, a reaction of particular importance in biology, proceeds quite differently inside a cell than inside a scintillation vial. Importantly, our findings add to a growing precedent spanning various analytical techniques (e.g., fluorescence and mass spectrometry) that chemical reactivity changes under confinement. Here, we propose a finite element model that shows that adsorption and faster bimolecular kinetics at the liquid|liquid boundary can account for the observed current enhancement.