Abstract

The addition of binders to energetic materials is known to complicate the thermal decomposition process of such materials. To assess this effect, the present work studied the thermal decomposition of cyclotrimethylene trinitramine (RDX)/hydroxy-terminated polybutadiene (HTPB) mixtures and of pure RDX over the temperature range of 2000–3500 K by combining the classical reaction and first-principles molecular dynamics methods. The incorporation of HTPB as a binder was found to significantly reduce the decomposition rate of RDX. At 3500 K, the decay rate constant of RDX in the RDX/HTPB system is 2.0141 × 1012 s–1, while it is 2.7723 × 1012 s–1 in the pure RDX system. However, the binder HTPB had little effect on the initial decomposition mechanism, which involved the rupture of N–NO2 bonds to produce NO2. The HTPB was predicted to undergo dehydrogenation and chain breaking. The free H resulting from these processes was predicted to react with low-molecular-weight intermediates generated by the RDX, resulting in greater equilibrium quantities of the final products H2O and H2 being obtained from the mixed system compared with pure RDX. HTPB-chain fragments were also found to combine with the primary RDX decomposition product NO2 to inhibit the formation of N2 and CO2.
1. Introduction
Cyclotrimethylene trinitramine (RDX) is a high-energy nitramine explosive that exhibits exceptional detonation performance and has many military and civilian applications.1,2 Even so, explosives based solely on RDX have several shortcomings, such as poor safety performance and difficulty in forming. For these reasons, binders are often added to reduce the sensitivity of the explosive while also improving the molding and mechanical properties. Unfortunately, the thermal decomposition mechanisms associated with these multicomponent explosives are more complex. Specifically, the intermediate and final products generated during thermal decomposition may oxidize the polymeric binders in mixed explosives, thus affecting the detonation performance. Consequently, further study of the thermal decomposition behaviors, reaction mechanisms, and sensitivities of these materials is required. Even so, the thermal decomposition of explosives is extremely rapid and so it is often difficult to assess the associated reactions in detail experimentally. Molecular dynamics simulation offers an alternative approach to elucidating the thermal decomposition mechanisms of high explosives on the atomic level. In this regard, first-principles and classical reaction molecular dynamics are especially helpful.3−6
In terms of classical reactive molecular dynamics research, Strachan et al.7 first used reactive molecular dynamics calculations based on the ReaxFF force field to simulate the thermal decomposition of RDX at different temperatures and densities in 2005. This prior work indicated that the cleavage of N–N bonds to generate NO2 is the primary reaction during the early stage of thermal decomposition. The production of CO and CO2 was also found to be largely determined by density. At low and high densities, CO and CO2 were shown to be the main products, respectively, although density evidently had little effect on the production of N2 and H2O. In 2017, Peng et al.8 also used ReaxFF reaction molecular dynamics method to study the thermal decomposition mechanism of RDX and its derivatives at high temperature. The results showed that the first step of RDX pyrolysis was the cleavage of the N–NO2 bonds to generate NO2, followed by the loss of side chains or ring opening. The intermediates NO2 and NO were also determined to undergo secondary reactions to form N2 such that the end products were N2, H2O, and CO2. The molecular dynamics of the thermal decomposition of RDX have been extensively studied but, because RDX is commonly used in mixed explosives, simulations of the thermal decomposition of such mixtures would be more valuable with regard to practical applications.9−12 In 2006, Zhang13 used the ReaxFF reaction molecular dynamics method to compare the thermal decomposition characteristics of RDX with and without a polyurethane binder. The results showed that the addition of the binder significantly reduced the thermal decomposition rate of RDX, although the products of decomposition were basically the same.
First-principles molecular dynamics calculations can accurately describe chemical reactions, while the density functional tight binding (DFTB) method improves the calculation speed and is widely used in the study of the thermal decomposition mechanism of explosives.14,15 In 2002, Manaa et al.16 used first-principles molecular dynamics calculations based on the self-consistent charge density functional tight binding method (SCC-DFTB) to model the reaction of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX) at 3500 K and predicted the rates of formation of typical products such as H2O, CO2, and N2. In 2019, He et al.17 studied the electronic properties and thermal decomposition behavior of an HMX/hydroxy-terminated polybutadiene (HTPB) plastic-bonded explosive using the first-principles molecular dynamics method based on SCC-DFTB. The results showed that the electrostatic interaction between the nitro group oxygen atoms of the HMX and hydroxyl butyrate groups of the HTPB significantly stabilized the surfaces of the HMX crystals. The incorporation of HTPB therefore inhibited the thermal decomposition of the HMX. The HTPB binder was also found to be highly stable such that the majority of polymer chains were predicted to remain intact following the reaction.
Currently, classical reaction molecular dynamics and first-principles molecular dynamics methods have been widely used to investigate the initial reaction paths and product formation of RDX and other explosives, which have provided a detailed understanding of their thermal decomposition mechanism. However, most explosives used in practice are mixed materials, and there is a lack of research on their thermal decomposition mechanism. Furthermore, there is a deficiency in a systematic analysis of the possible reactions that may occur between explosives and adhesives and their impact on the resulting products. Therefore, further research on the thermal decomposition mechanism of mixed explosives is necessary to ensure their safe use and promote their development.
On this basis, the present study employed the classical reaction molecular dynamics method based on the ReaxFF-lg reaction force field and the first-principles molecular dynamics method in conjunction with SCC-DFTB theory to simulate the thermal decomposition of RDX/HTPB explosives at high temperatures. The thermal decomposition characteristics of pure RDX and of RDX/HTPB were assessed at 3500, 3000, 2500, and 2000 K using classical reaction molecular dynamics, while the thermal decomposition of RDX/HTPB at 3000 K was modeled based on first-principles molecular dynamics. In this manner, the effect of HTPB on the decomposition of RDX was examined.
2. Computational Models and Methods
2.1. Construction of Computational Models
The properties of α-RDX are the most stable at room temperature, and the crystal structure of this compound (a = 11.443 Å, b = 10.611 Å, c = 13.156 Å, α = β = γ = 90°) has been determined based on X-ray diffraction data.18 HTPB is a homopolymer containing cis-1,4, trans-1,4, and trans-1,2 double bonds and, in the present work, was assumed to be based on a trans-1,4 monomer. In this model, the terminal groups were saturated with −H to construct a single-chain structure with n = 8 having the molecular formula C32H50O2. Figure 1 shows the classical reaction molecular dynamics model derived for RDX/HTPB. This model was generated by first using the Material Studio (MS) program to construct a 3 × 2 × 2 supercell structure based on the RDX cell, after which a 5 ps temperature and pressure relaxation was performed under regular ensemble NVT and constant temperature and pressure ensemble NPT conditions, respectively, to obtain a stable structure at 300 K and 0 GPa. This stable structure was subsequently expanded four times along the b direction. The PACKMOL program19 was then used to place 33 HTPB chains into a box of appropriate size to produce an HTPB system having a reasonable stacking mode via optimization calculations. Following this, the 10 and 50 ps relaxations were performed under NVT and NPT ensemble conditions, respectively. The resulting HTPB system was placed 10 Å away from the RDX supercell along the b direction of the supercell in the MS and then compressed at a specific speed along this same direction until there was no significant gap between the two systems and no mutual extrusion. Finally, the RDX/HTPB hybrid system was optimized at a temperature of 300 K to build a computational system having a reasonable density.
Figure 1.
Classical reaction molecular dynamics model of the RDX/HTPB system.
Figure 2 provides the first-principles molecular dynamics calculation model employed for the RDX/HTPB analysis. Based on the computing power required for this method, a 1 × 2 × 1 cell expansion was performed along the a, b, and c directions of an RDX single cell to obtain a supercell containing 16 RDX molecules (equivalent to 336 atoms). Two HTPB chains with a number of 8 were subsequently added along the [001] crystal plane. The conjugate gradient (CG) method in the CP2K package20 was used to optimize the cell parameters and conformation of the RDX/HTPB model so as to obtain a stable structure based on the DFTB process. The convergence criteria comprised a maximum geometric displacement near 20,000 steps of less than 0.003 b, a root mean square of less than 0.0015 b, a force component change of less than 0.00045 hartree/b, and a maximum root-mean-square force of less than 0.0003 hartree/b. Using these criteria in conjunction with a temperature and pressure of 300 K and 0 GPa, the RDX/HTPB model was calculated for 2 ps under NVT and NPT ensemble conditions, respectively, with a time step of 0.2 fs so as to further optimize the internal stress and allow the system to reach equilibrium. The equilibrium parameters determined for the RDX/HTPB system were a = 10.756 Å, b = 20.674 Å, c = 28.047 Å, α = 90°, β = 90°, and γ = 90°.
Figure 2.
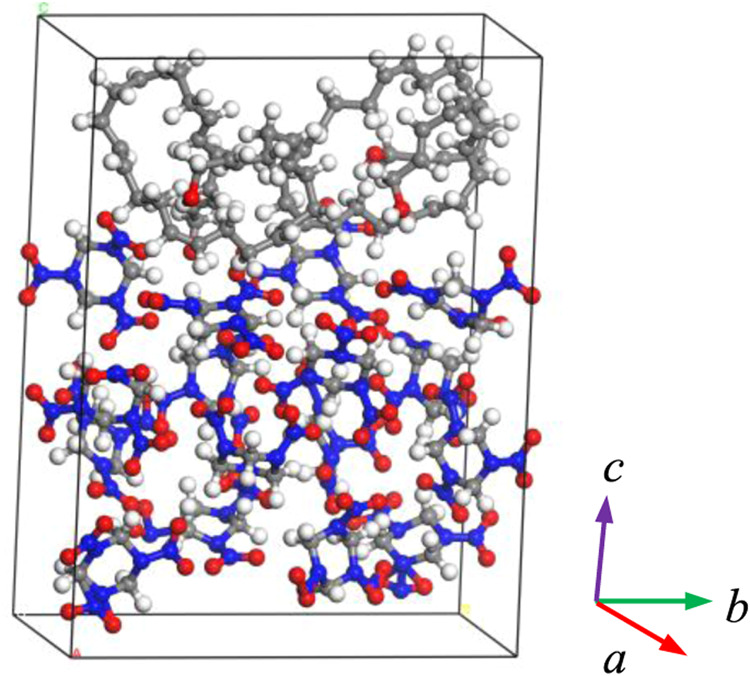
First-principles molecular dynamics model of the RDX/HTPB system.
2.2. Computational Methods and Parameters
2.2.1. Classical Molecular Dynamics Method
The force field is a function used in classical molecular dynamics simulations to describe intermolecular forces and can determine the accuracy of the calculation results. With the development of various applications for molecular dynamics, these functions have become increasingly complex. Traditional molecular dynamics methods are able to model the evolution of a system over time but cannot simulate bond cleavage and so are unable to model chemical reactions. For this reason, force field functions capable of describing chemical reactions have been developed, including the ReaxFF function based on the theory of bond order as proposed by van Duin et al.21 in 2001. This method has been widely used to simulate the chemical reactions of explosives. In these simulations, the breaking and forming of chemical bonds are determined by the bond lengths between atoms and the parameters of the force field function are fitted according to the results of first-principles calculations, such that the ReaxFF force field can provide approximately the same level of accuracy as quantum mechanics. In addition, the calculation costs associated with the force field method are low and so calculations involving millions of atoms are possible. The long-range interactions between molecules were subsequently incorporated into the ReaxFF function by adding dispersion forces to give the improved ReaxFF-lg force field function. The latter is able to describe crystal structures more accurately and so was used in the present work to simulate the chemical reactions of RDX/HTPB mixtures at high temperatures. Because research by Liu et al.22 has confirmed that the predicted RDX structures obtained using the ReaxFF-lg force field approach are generally consistent with experimental data, this paper assumes that this method is applicable to the analysis of RDX.
To verify the applicability of the ReaxFF-lg force field function to modeling of the HTPB binder, the radial distribution function, g(r), for HTPB following relaxation was determined and compared with the literature value. Figure 3 shows the radial distribution function obtained for HTPB after relaxation, while Table 1 compares the peak positions in this calculated function with the literature values. It can be seen from these results that the radial distribution function predicted using the ReaxFF-lg method was consistent with the literature data. This agreement indicates that the ReaxFF-lg force field is a suitable means of performing molecular dynamics calculations for HTPB.
Figure 3.
Radial distribution function determined for HTPB at 300 K.
Table 1. Comparison of the Peak Positions in the Calculated HTPB Radial Distribution Function with Reference Values.
| HTPB | C–H (Å) | C=C (Å) | C–C (Å) |
|---|---|---|---|
| reference23 | 1.13 | 1.37 | 1.53 |
| ReaxFF-lg | 0.96 | 1.35 | 1.52 |
The classical reaction molecular dynamics calculations were carried out using the large-scale atomic/molecular massively parallel simulator (LAMMPS) program. After obtaining the equilibrium structure for the RDX/HTPB and RDX systems, the NVE microcanonical ensemble and Berendsen thermal bath processes were employed to rapidly increase the temperature of each system to 2000, 2500, 3000, or 3500 K after which the resulting chemical reactions were analyzed using a time step of 0.1 fs. The cleavage of bonds during the chemical reactions was assessed by setting the cutoff radius of atomic pair bond orders to 0.3.24
2.2.2. First-Principles Molecular Dynamics Methods
Because the results of classical molecular dynamics simulations are greatly affected by the force field used, the accuracy obtained from such calculations is lower than that from first-principles molecular dynamics methods based on the Schrödinger equation or density functional theory (DFT). In the work reported herein, the CP2K first-principles molecular dynamics software package was used to calculate the thermal decomposition behavior of the RDX/HTPB system at high temperatures. CP2K is an ab initio molecular dynamics simulation package that was first developed by the Max Planck Research Center in Germany in 2000. This software is primarily used to calculate the atomic and molecular dynamics of solids, liquids, macromolecules, crystals, and biological systems. In the case of the present calculations, the interatomic forces were determined using the SCC-DFTB method, which is a tight binding approach based on the DFT. This method is able to accurately estimate the molecular structures associated with specific periodic boundary conditions and to describe the chemical bond reactions and weak interaction between molecules.
During the present first-principles molecular dynamics calculations, the RDX/HTPB system was rapidly heated to 3000 K using a Nose–Hoover thermal bath in NVT ensemble conditions. The self-consistent convergence accuracy was set to 10–5 au, the integration time step was 0.2 fs, and the total computation time was 5 ps. The molecular movement track was recorded at 0.2 fs intervals to allow a subsequent analysis of the reaction mechanism, associated species, and bond-breaking statistics. The atomic positions at each time interval were processed to obtain snapshots, species information, and bond-level files.
3. Results and Discussion
3.1. Evolution of Potential Energy and Number of Species
Using the classical molecular dynamics method, the potential energy values for the RDX/HTPB system over time at different temperatures were obtained and are plotted in Figure 4. These data demonstrate that, at all temperatures, the potential energy rapidly increased to a peak value in a very short time, and the higher the temperature is, the higher the peak value of potential energy is, and the maximum value of potential energy is reached at 3500 K. Subsequently, the potential energy decreased rapidly and then more slowly to produce an equilibrium in the late stage of the reaction. The shape of these plots can be attributed to the rapid absorption of heat from the reaction and the primary decomposition reaction in the early stage, which increased the potential energy. With the accumulation of heat, secondary thermal decomposition reactions began to occur in the system to generate a large number of intermediate and final products along with significant heat. The potential energy of the system thus decreased rapidly and finally produced an equilibrium. In the case of the RDX/HTPB system, the time spans required for the potential energy to reach the maximum value at 3500, 3000, 2500, and 2000 K were determined to be 1.16, 1.22, 1.4, and 1.62 ps, respectively. Thus, higher temperatures were associated with shorter time intervals. That is, a higher temperature caused the potential energy to decrease more rapidly and so shortened the time required to reach equilibrium.
Figure 4.
Potential energy values for the RDX/HTPB system at various temperatures as functions of time.
Figure 5 plots the number of species for the RDX/HTPB system over time at different temperatures. It is evident that, at the beginning of the reaction, the system contained two kinds of molecules. However, as the thermal decomposition reactions progressed, the number of molecules in the system increased rapidly to a maximum, after which secondary reactions consumed many of the small molecules and the number of species began to decline. Eventually, a dynamic equilibrium was achieved. The RDX/HTPB system exhibited the maximum number of species at 3.52, 8.36, 13.09, and 44.66 ps for temperatures of 3500, 3000, 2500, and 2000 K, respectively. Therefore, as expected, higher temperatures produced faster reaction rates. Note also that, at a relatively low temperature of 2000 K, fewer secondary reactions would be expected and so the number of species did not exhibit a downward trend after reaching the peak. Both the potential energy and species number data sets also indicate that the thermal decomposition reactions of the RDX/HTPB system were essentially complete by 100 ps.
Figure 5.
Total species values for the RDX/HTPB system at various temperatures as functions of time.
3.2. Decay Rate of RDX Molecules in a Mixed System
Analyzing the results obtained from the classical reaction molecular dynamics calculations provided data regarding the RDX quantities over time in the RDX/HTPB and RDX systems at different temperatures, as shown in Figure 6. The number of RDX molecules in both systems can be seen to have decreased rapidly after the reaction started, with more rapid decomposition at higher temperatures and complete decomposition within 100 ps. In the case of the RDX/HTPB system, the time intervals required for the complete decomposition of the RDX at 3500, 3000, 2500, and 2000 K were found to be 1.41, 2.95, 9.59, and 35.95 ps, respectively. These data also indicate that the decomposition of RDX in RDX/HTPB would be expected to occur more slowly than that of pure RDX at all temperatures.
Figure 6.
Quantities of RDX molecules for two systems as functions of time in RDX/HTPB and pure RDX systems.
The decay of nitramine explosives during thermal decomposition can be summarized by the equation
| 1 |
where C0 is the initial number of RDX molecules, C(t) is the number of RDX molecules at time t, and k is the decay rate constant (1012 s–1). The data in Figure 6 for the RDX/HTPB and pure RDX systems were fit using this equation, and the resulting values for k are summarized in Table 2. It is apparent from these results that the value of k increased along with the temperature. In addition, for a given temperature, the extent to which the RDX in the RDX/HTPB system decomposed was significantly lower than that in the pure RDX. These results confirm that the addition of a relatively small amount of HTPB to RDX as a binder would be expected to reduce the decomposition rate of the explosive.
Table 2. Rate Constants for RDX Decay in RDX/HTPB and Pure RDX Systems at Different Temperatures.
| system | temperature (K) | decay rate k (1012 s–1) |
|---|---|---|
| RDX/HTPB | 2000 | 0.2813 |
| 2500 | 0.8230 | |
| 3000 | 1.5619 | |
| 3500 | 2.0141 | |
| only RDX | 2000 | 0.6222 |
| 2500 | 1.3147 | |
| 3000 | 2.1260 | |
| 3500 | 2.7723 |
3.3. Decomposition Pathways of RDX Molecules in a Mixed System
Studying the initial decomposition of an energetic material can provide an improved understanding of the reaction mechanism. In the present work, the initial decomposition reaction path of RDX molecules in the RDX/HTPB system at high temperatures was assessed. The bond order files for the first 10 ps of classical reaction molecular dynamics calculations were counted, and all RDX reactions with a reaction frequency of greater than 2 were analyzed. Table 3 provides the initial decomposition reactions and reaction durations for RDX molecules in the RDX/HTPB system at various temperatures.
Table 3. Parameters for the Single-Molecule Decomposition Reaction of RDX in the RDX/HTPB System at Different Temperatures.
| T (K) | frequencies | reaction time (ps) | primary reaction |
|---|---|---|---|
| 3500 | 592 | 0.03–1.6 | C3H6N6O6 → NO2 + C3H6N5O4 |
| 9 | 0.2–1.23 | C3H6N6O6 → 2NO2 + C3H6N4O2 | |
| 7 | 0.34–1.28 | C3H6N6O6 → HNO2 + C3H5N5O4 | |
| 3 | 0.38–0.49 | C3H6N6O6 → O + C3H6N6O5 | |
| 9 | 0.63–2.16 | C3H6N6O6 → NO3 + C3H6N5O3 | |
| 2 | 0.69–0.75 | C3H6N6O6 → NO2 + HNO2 + C3H5N4O2 | |
| 2 | 1.21–2.11 | C3H6N6O6 → N2O5 + C3H6N4O | |
| 2 | 1.26–1.47 | C3H6N6O6 → NO + C3H6N5O5 | |
| 5 | 1.78–2.03 | C3H6N6O6 → N2O4 + C3H6N4O2 | |
| 3000 | 633 | 0.02–2.8 | C3H6N6O6 → NO2 + C3H6N5O4 |
| 3 | 0.2–0.36 | C3H6N6O6 → O + C3H6N6O5 | |
| 8 | 0.46–2.04 | C3H6N6O6 → 2NO2 + C3H6N4O2 | |
| 13 | 0.55–2.7 | C3H6N6O6 → NO3 + C3H6N5O3 | |
| 2 | 0.64–3.02 | C3H6N6O6 → NO2 + HO + C3H5N5O3 | |
| 2 | 0.69–1.57 | C3H6N6O6 → NO2 + HNO2 + C3H5N4O2 | |
| 9 | 0.72–1.52 | C3H6N6O6 → HNO2 + C3H5N5O4 | |
| 3 | 1.4–4.26 | C3H6N6O6 → HNO3 + C3H5N5O3 | |
| 2500 | 807 | 0.08–7.75 | C3H6N6O6 → NO2 + C3H6N5O4 |
| 18 | 0.38–7.22 | C3H6N6O6 → HNO2 + C3H5N5O4 | |
| 9 | 0.52–3.39 | C3H6N6O6 → NO3 + C3H6N5O3 | |
| 5 | 0.88–3.85 | C3H6N6O6 → 2NO2 + C3H6N4O2 | |
| 2 | 1.05–1.27 | C3H6N6O6 → CH2N2O2 + C2H4N4O4 | |
| 2 | 4.04–6.87 | C3H6N6O6 → HNO3 + C3H5N5O3 | |
| 2000 | 867 | 0.11–9.95 | C3H6N6O6 → NO2 + C3H6N5O4 |
| 4 | 0.63–3.78 | C3H6N6O6 → 2NO2 + C3H6N4O2 | |
| 11 | 0.76–8.32 | C3H6N6O6 → NO3 + C3H6N5O3 | |
| 2 | 2.03–2.36 | C3H6N6O6 → NO2 + HNO2 + C3H5N4O2 | |
| 20 | 2.7–9.95 | C3H6N6O6 → N2O4 + C3H6N4O2 | |
| 6 | 3.15–9.09 | C3H6N6O6 → HN2O4 + C3H5N4O2 | |
| 13 | 3.45–9.77 | C3H6N6O6 → HNO2 + C3H5N5O4 | |
| 2 | 9.13–9.84 | C3H6N6O6 → HNO3 + C3H5N5O3 |
It can be seen from Table 3 that four single-molecule decomposition reaction pathways were determined for RDX in RDX/HTPB at high temperatures. These were
| 2 |
| 3 |
| 4 |
| 5 |
For all four temperatures, the cleavage of the N–NO2 bond to generate NO2 (that is, reaction 2) was found to occur as the first step of decomposition and with the highest frequency. However, higher temperatures were determined to reduce the frequency of this reaction. This trend is attributed to the greater frequency of collisions between molecules at higher temperatures that, in turn, increases the number of multimolecule polymerization reactions and decreases the frequency of monomolecular decomposition reactions. In reaction 3, both N–NO2 bonds in the RDX ring are broken. Reaction 4 indicates that each nitro group can interact with the oxygen atom on an adjacent nitro group. Reaction 5 represents the transfer of a hydrogen from the RDX ring to the nitro group after which the N–NOHO bond breaks to form HNO2. At 3500 K, the frequency of these four monomolecular decomposition reactions decreased in the order of (2) > (3) = (4) > (5), meaning that the hydrogen transfer reaction was the least likely to occur. At 3000 K, the order was (2) > (4) > (5) > (3) such that the removal of two NO2 molecules was less likely than the hydrogen transfer reaction. At 2500 K, the order was (2) > (5) > (4) > (3). Again, the frequency of the hydrogen transfer reaction was greater than that of the reaction removing two NO2. At 2000 K, the order was (2) > (5) > (4) > (3) although the reaction C3H6N6O6 → N2O4 + C3H6N4O2 was also relatively likely to occur. Thus, a lower temperature would be expected to increase the probability of the N–NO2 bond breaking after hydrogen transfer while reducing the rate at which two N–NO2 bonds are broken simultaneously.
The initial decomposition mechanism for RDX in the RDX/HTPB system was obtained by analyzing the results of calculations based on classical reaction molecular dynamics. More details were obtained by assessing a total of six decomposition pathways by processing the results of first-principles molecular dynamics calculations, as shown in Figure 7. In the first path, taking the RDX molecule labeled ① as an example, the initial thermal decomposition pathway involves breaking of a N–NO2 bond of the molecule at 0.126 ps with the simultaneous generation of NO2 and is very rapid. Subsequently, at 0.168 ps, a C–N bond breaks and a ring opening reaction occurs. Finally, at 0.28 ps, the C–N bond nearest to a remaining NO2 breaks to provide two intermediate products: CH2N2O2 and C2H4N3O2. The reactions involved in this mechanism are therefore
| 6 |
| 7 |
In the second decomposition pathway, taking the RDX molecule labeled ② as an example, a N–NO2 bond breaks at 0.268 ps to generate NO2. At 0.30 ps, a C–N bond ruptures and ring opening occurs, after which a second C–N bond breaks at 0.308 ps. Note that this bond is at a different site from the C–N bond-breaking position in the first path. This process generates the intermediate products C2H4N and CH2N4O4 and can be expressed as
| 8 |
Using the RDX molecule labeled as ③ to represent the third decomposition pathway, the first step is the cleavage of the N–NO2 bond at 0.056 ps to generate NO2. At 0.122 ps, a second N–NO2 bond breaks to again produce NO2. Following this, a C–N bond breaks and ring opening occurs at 0.142 ps. In addition, a H atom is lost from an alkyl group and reacts with a NO2 to generate HNO2. At 0.380 ps, a second C–N bond ruptures to produce two intermediate products: C2H3N2 and CH2N2O2. This reaction path is relatively complex but can be summarized as
| 9 |
| 10 |
| 11 |
In the fourth decomposition pathway involving RDX molecule ④, a N–NO2 bond breaks at 0.208 ps to generate NO2 after which, at 0.260 ps, a C–N bond breaks and the ring opens. At this point, a −NO2 group combines with a H atom generated by another RDX molecule. The fifth decomposition path involving RDX molecule ⑤ begins with the rupture of a C–N bond to open the ring at 0.018 ps, followed by the breaking of a N–N bond and another C–N bond almost simultaneously at 0.048 ps, generating C2H4N3O2, CH2N2O2, and NO2. In the sixth decomposition pathway, taking RDX molecule ⑥ as an example, a C–N bond breaks to open the ring at 0.19 ps, after which a N–N bond breaks to generate NO2 at 0.21 ps. A second C–N bond ruptures at 0.226 ps to produce C2H4N and CH2N3O4.
Figure 7.
Six possible pathways for the decomposition of RDX in the RDX/HTPB system.
The monomolecular decomposition pathways obtained from the initial molecular dynamics calculations indicate that the majority of RDX molecules would be expected to first undergo N–NO2 bond breaking followed by the cleavage of a C–N bond to produce ring opening and the breaking of a second N–NO2 bond. The latter two processes compete with one another. Following ring opening, a H atom either from the same molecule or another molecule will be attracted by a remaining −NO2 group. It is also evident that, in some cases, the process will begin with the cleavage of a C–N bond after which a N–N bond will break. The time interval between these two steps is very small and so NO2 will also be produced quickly. These results are generally consistent with those obtained from classical reaction molecular dynamics.
3.4. Reaction between RDX and HTPB
The results of first-principles molecular dynamics calculations for the RDX/HTPB system were analyzed to examine the decomposition reactions of HTPB molecules. The outcome of this analysis is presented in Figure 8. The HTPB chains were found to primarily undergo dehydrogenation reactions as well as rupture of the carbon backbones. The low-molecular-weight products obtained from such reactions could potentially react with the RDX decomposition products, thus affecting the end products from the decomposition of the mixed explosive.
Figure 8.
Decomposition reactions of HTPB molecules.
Figure 9 summarizes the results of the first-principles calculations for the RDX/HTPB system at 3000 K. Several reactions, as presented here, were determined to occur between the small molecules generated by RDX decomposition and the decomposition products of the HTPB during the later stages of the decomposition process. In reaction 1, a H atom detaches from an HTPB chain at 0.45 ps and, at 0.47 ps, combines with the RDX decomposition product NO to form HNO as an intermediate. He et al.17 also found that the O atoms in nitro groups in HMX decomposition products will readily bond with H atoms from HTPB to generate intermediates such as HONO, OH, and HNO, which may then be converted to H2O, NO, and NO2. In the case of reaction 2, NO2 is released from an RDX molecule at 0.15 ps after which, at 0.16 ps, this molecule approaches an HTPB molecule. At 0.20 ps, the NO2 reacts with the broken HTPB chain to form a new C–N bond. This same type of reaction was also evident in the classical molecular dynamics simulations.
Figure 9.
Reactions between RDX and HTPB.
3.5. Main Thermal Decomposition Products
The RDX/HTPB mixed system will generate a large number of low-molecular-weight products during thermal decomposition reactions. Figure 10 plots the amounts of the primary product NO2 generated over time in both the RDX/HTPB and pure RDX systems. During the initial stage of the reaction, the N–NO2 bonds in RDX molecules were initially broken to generate a large quantity of NO2 and so the amount of this product increased rapidly. Subsequently, NO2 participated in various secondary reactions and so the concentration of NO2 decayed. In both systems, higher temperatures accelerated this decrease in the amount of NO2. As can be seen from the expanded view of the graph, the rate of increase was greater in the case of the pure RDX and the peak quantity was higher compared with the RDX/HTPB. These results can possibly be attributed to the reaction of a portion of the NO2 with HTPB in the latter system.
Figure 10.
Quantity of the primary product NO2 as a function of time for the RDX/HTPB and pure RDX systems at various temperatures.
Figure 11 plots the quantities of various final products obtained for the RDX/HTPB and pure RDX systems. As can be seen from the figure, significant amounts of H2O, H2, CO2, and N2 were generated. N2 was obtained primarily from the conversion of NO2 and NO based on secondary reactions. It is also apparent that the amount of N2 eventually reached an equilibrium value. At all temperatures, the rate of increase in the amount of N2 was higher in the pure RDX system as was the quantity at equilibrium. These results are ascribed to the reactions of carbon-chain fragments produced by HTPB decomposition with some NO2 or NO in the RDX/HTPB system. In contrast, the quantities of H2O and H2 were found to increase over time and the growth rates and equilibrium quantities of both products were greater in the case of the RDX/HTPB system. Previous studies have demonstrated that the HTPB alkyl groups in the RDX/HTPB system will undergo numerous dehydrogenation reactions, leading to the generation of more H2O and H2 compared with pure RDX. The amount of CO2 increased continuously until equilibrium, and higher temperatures increased the rate at which this product was obtained. Following ring opening of the RDX molecule, a variety of carbon-chain fragments were generated that eventually formed CO2. Because the RDX/HTPB system contained many such chains, the generation of CO2 was hindered and the growth rate was significantly lower than that for the pure RDX.
Figure 11.

Quantities of the main decomposition products as functions of time for the RDX/HTPB and pure RDX systems at various temperatures.
4. Conclusions
A classical reactive molecular dynamics method based on the ReaxFF-lg force field and a first-principles molecular dynamics method based on SCC-DFTB theory were used to simulate the thermal decomposition of an RDX/HTPB mixed explosive. Details of the reactions of both RDX and HTPB during the thermal decomposition process were analyzed. The effects of HTPB on the RDX thermal decomposition rate and on product formation were also examined. The results show that the presence of a small amount of HTPB will significantly reduce the RDX decomposition rate. During the initial stage of the reaction, N–NO2 bonds are broken to generate NO2 from the RDX/HTPB system at various temperatures, but lower temperatures promote hydrogen transfer reactions. After N–NO2 bond breaking, the rupture of a C–N bond induces ring opening and this step competes with the breaking of a N–N bond. Under high-temperature conditions, HTPB primarily undergoes dehydrogenation and chain breaking. Free H will subsequently react with the RDX decomposition products, and the broken HTPB chains will also combine with NO2. The reaction between HTPB and RDX leads to greater equilibrium quantities of the final products H2O and H2 than are obtained from pure RDX but less N2 and CO2. The thermal decomposition reactions of the mixed explosive systems are evidently complicated, and so it is important to develop detailed reaction mechanisms to ensure the safe use and storage of these energetic materials.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant 11832006).
The authors declare no competing financial interest.
References
- Wang C.; Zhang C.; Xue X. Pressure and Polymorph Dependent Thermal Decomposition Mechanism of Molecular Materials: A Case of 1, 3, 5,-Trinitro-1, 3, 5,-triazine. J. Phys. Chem. A 2022, 126, 463–472. 10.1021/acs.jpca.1c08171. [DOI] [PubMed] [Google Scholar]
- Ravaji B.; Wilkerson J. W. Effects of crystallography on hot-spot formation in porous RDX single crystals. Extreme Mech. Lett. 2021, 42, 101112 10.1016/j.eml.2020.101112. [DOI] [Google Scholar]
- Raabe D.Computational Materials Science: The Simulation of Materials Microstructures and Properties; Wiley-VCH Verlag GmbH, 1998. [Google Scholar]
- Wang F.; Chen L.; Geng D.; Lu J.; Wu J. Effect of density on the thermal decomposition mechanism of ε-CL-20: a ReaxFF reactive molecular dynamics simulation study. Phys. Chem. Chem. Phys. 2018, 20, 22600–22609. 10.1039/C8CP03010C. [DOI] [PubMed] [Google Scholar]
- Mei Z.; An Q.; Zhao F. Q.; Xu S. Y.; Ju X. H. Reactive molecular dynamics simulation of thermal decomposition for nano-aluminized explosives[J]. Phys. Chem. Chem. Phys. 2018, 20, 29341–29350. 10.1039/C8CP05006F. [DOI] [PubMed] [Google Scholar]
- She C.; Jin S.; Chen S.; Li L.; Shu Q.; Chen Y.; Wang J.; Wu N.; Chen M.; Chen K. Reactive molecular dynamics simulation of thermal decomposition for nano-FOX-7. Appl. Phys. A: Mater. Sci. Process. 2021, 127, 881 10.1007/s00339-021-05018-2. [DOI] [Google Scholar]
- Strachan A.; Kober E. M.; Van Duin A. C.; Oxgaard J.; Goddard W. A. III Thermal decomposition of RDX from reactive molecular dynamics. J. Chem. Phys. 2005, 122, 054502 10.1063/1.1831277. [DOI] [PubMed] [Google Scholar]
- Peng L. J.; Yao Q.; Wang J. B.; Li Z. R.; Zhu Q.; Li X. Y. Pyrolysis of RDX and its derivatives via reactive molecular dynamics simulations. J. Chem. Phys. 2017, 33, 745–754. (in Chinese) 10.3866/PKU.WHXB201701161. [DOI] [Google Scholar]
- Chen F.; Cheng X. Thermal decomposition behaviour of hexahydro-1,3,5-trinitro-1,3,5-triazine (RDX) under shock velocities by molecular dynamics simulation. J. At. Mol. Sci. 2016, 33, 315–319. [Google Scholar]
- Gump J. C.; Peiris S. M. Comparison of Reaction Kinetics of I-RDX and RDX at High Pressure. AIP Conf. Proc. 2006, 845, 1069–1072. 10.1063/1.2263507. [DOI] [Google Scholar]
- Feng S.; Guo F.; Yuan C.; Cheng X.; Wang Y.; Zhang H.; Chen J.; Su L. Effect of neutron irradiation on structure and decomposition of α-RDX: A ReaxFF molecular dynamics study. Comput. Theor. Chem. 2023, 1219, 113965 10.1016/j.comptc.2022.113965. [DOI] [Google Scholar]
- Zhao Y.; Zhao F. Q.; Xu S. Y.; Ju X. H. Molecular reaction dynamics simulation of thermal decomposition for aluminiferous RDX composites. Comput. Mater. Sci. 2020, 177, 109556 10.1016/j.commatsci.2020.109556. [DOI] [Google Scholar]
- Zhang L.; Zybin S. V.; Van Duin A. C.; Dasgupta S.; Goddard W. A. III Thermal Decomposition of Energetic Materials by ReaxFF Reactive Molecular Dynamics. AIP Conf. Proc. 2006, 845, 589–592. 10.1063/1.2263391. [DOI] [Google Scholar]
- Xu J.; Zhao J.; Sun L. Thermal decomposition behaviour of RDX by first-principles molecular dynamics simulation. Mol. Simul. 2008, 34, 961–965. 10.1080/08927020802162892. [DOI] [Google Scholar]
- Guo D.; An Q.; Zybin S. V.; Goddard W. A. III; Huang F.; Tang B. The co-crystal of TNT/CL-20 leads to decreased sensitivity toward thermal decomposition from first principles based reactive molecular dynamics. J. Mater. Chem. A 2015, 3, 5409–5419. 10.1039/C4TA06858K. [DOI] [Google Scholar]
- Manaa M. R.; Fried L. E.; Melius C. F.; Elstner M.; Frauenheim T. Decomposition of HMX at extreme conditions: A molecular dynamics simulation. J. Phys. Chem. A 2002, 106, 9024–9029. 10.1021/jp025668+. [DOI] [Google Scholar]
- He Z. H.; Huang Y. Y.; Ji G. F.; Chen J.; Wu Q. Electron properties and thermal decomposition behaviors for HMX/HTPB plastic-bonded explosives. J. Phys. Chem. C 2019, 123, 23791–23799. 10.1021/acs.jpcc.9b04759. [DOI] [Google Scholar]
- Woińska M.; Grabowsky S.; Dominiak P. M.; Woźniak K.; Jayatilaka D. Hydrogen atoms can be located accurately and precisely by x-ray crystallography. Sci. Adv. 2016, 2, e1600192 10.1126/sciadv.1600192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- CP2K Developer Group . CP2K Home Page. http://www.cp2k.org/.
- van Duin A. C. T.; Dasgupta S.; Lorant F.; Goddard W. A. ReaxFF: a reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. 10.1021/jp004368u. [DOI] [Google Scholar]
- Liu L.; Liu Y.; Zybin S. V.; Sun H.; Goddard W. A. III ReaxFF-lg: Correction of the ReaxFF reactive force field for London dispersion, with applications to the equations of state for energetic materials. J. Phys. Chem. A 2011, 115, 11016–11022. 10.1021/jp201599t. [DOI] [PubMed] [Google Scholar]
- Fröhlich M. G.; Sewell T. D.; Thompson D. L. Molecular dynamics simulations of shock waves in hydroxyl-terminated polybutadiene melts: mechanical and structural responses. J. Phys. Chem. A 2014, 140, 024902 10.1063/1.4853695. [DOI] [PubMed] [Google Scholar]
- Yang Z.; He Y. H. Pyrolysis of octanitrocubane via molecular dynamics simulations. Acta Phys.-Chim. Sin. 2016, 32, 921–928. 10.3866/PKU.WHXB201512251. [DOI] [Google Scholar]












