Regional Neuroanatomic Effects on Brain Age Inferred Using Magnetic Resonance Imaging and Ridge Regression

Abstract

The biological age of the brain differs from its chronological age (CA) and can be used as biomarker of neural/cognitive disease processes and as predictor of mortality. Brain age (BA) is often estimated from magnetic resonance images (MRIs) using machine learning (ML) that rarely indicates how regional brain features contribute to BA. Leveraging an aggregate training sample of 3 418 healthy controls (HCs), we describe a ridge regression model that quantifies each region’s contribution to BA. After model testing on an independent sample of 651 HCs, we compute the coefficient of partial determination ${\overline{R}}_p^2$ for each regional brain volume to quantify its contribution to BA. Model performance is also evaluated using the correlation $r$ between chronological and biological ages, the mean absolute error ($MAE$ ) and mean squared error ($MSE$) of BA estimates. On training data, $r=0.92$, $MSE=70.94$ years, $MAE=6.57$ years, and ${\overline{R}}^2=0.81$; on test data, $r=0.90$, $MSE=81.96$ years, $MAE=7.00$ years, and ${\overline{R}}^2=0.79$. The regions whose volumes contribute most to BA are the nucleus accumbens (${\overline{R}}_p^2=7.27\mathrm{\%}$), inferior temporal gyrus (${\overline{R}}_p^2=4.03\mathrm{\%}$), thalamus (${\overline{R}}_p^2=3.61\mathrm{\%}$), brainstem (${\overline{R}}_p^2=3.29\mathrm{\%}$), posterior lateral sulcus (${\overline{R}}_p^2=3.22\mathrm{\%}$), caudate nucleus (${\overline{R}}_p^2=3.05\mathrm{\%}$), orbital gyrus (${\overline{R}}_p^2=2.96\mathrm{\%}$), and precentral gyrus (${\overline{R}}_p^2=2.80\mathrm{\%}$). Our ridge regression, although outperformed by the most sophisticated ML approaches, identifies the importance and relative contribution of each brain structure to overall BA. Aside from its interpretability and quasi-mechanistic insights, our model can be used to validate future ML approaches for BA estimation.

Magnetic resonance imaging (MRI) brain scans have been leveraged to estimate brain age ($BA$) in living humans (1) using statistical models (2). The difference between chronological age ($CA$) and $BA$, often called age gap ($AG$), reflects atypical brain aging (3). The utility of $BA$ and $AG$ to capture phenotypic aging has been explored in Alzheimer’s disease, traumatic brain injury, and in other conditions where these measures parallel changes in neuroanatomy and cognitive functioning (4,5). Classical statistical models (eg, multivariate and univariate regression, general linear models, etc.) and machine learning (ML) techniques have been used to predict $BA$ from brain MRIs (2). When calibrating such techniques, an immediate goal is to minimize $AG$ (model error) in reference cohorts of healthy controls (HCs). In contrast to standard statistical models, ML techniques cannot typically provide neuroanatomical interpretability and specificity, in the sense that most ML cannot reveal aging-related regional alterations in brain structure or their contributions to $BA$ (1). This is of particular concern for researchers attempting to extend the use of ML to diseases and clinical conditions whose pathoanatomical deviations from typical aging may feature both global and focal alterations (6,7). Since the macroscale structural covariance of the brain is relatively high (8), methods are needed to quantify the unique contributions of distinct brain regions, while accounting for the statistical covariance and interaction between regions. Furthermore, interpretable statistical models of neuroanatomical contributions to BA can be useful as reference models when validating interpretable ML approaches (9,10). To address these needs, we implement, test, and validate a ridge regression model that uses brain MRIs to identify, quantify, and interpret the specific contributions of distinct neuroanatomical structures to BA while accounting for their covariance.

Method

Participants

Participant demographics are summarized in Table 1. Briefly, our training set includes n = 3 418 HCs aged 22–95 years, comprising 513 participants from the Alzheimer’s Disease Neuroimaging Initiative (ADNI), 508 from the Human Connectome Project Aging (HCP-A), 1 112 from HCP Young Adults (YA), and 1 285 from the UK Biobank (UKBB). The test set for the trained model includes n = 651 HCs aged 18–88 years, selected from the Cambridge Centre for Ageing and Neuroscience (Cam-CAN) repository. The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment and early Alzheimer’s disease. MRI acquisition protocols for HCP-A and HCP-YA have been described previously (11,12). For UKBB data, our study uses preprocessed images generated by a UKBB pipeline whose output included FreeSurfer reconstructions (13). Cam-CAN data were obtained from the repository at http://www.mrc-cbu.cam.ac.uk/datasets/camcan/ (14,15). The test data set was used not only to validate our predicted ages against $CA$ but also to quantify the ability of $BA$ to capture cognitive functioning phenotype. Thirteen cognitive measures assessing emotional processing, executive functioning, memory, and motor functioning were obtained from the Cam-CAN repository ((14,15); Supplementary Table 2).

Table 1.

Participant Demographics for (A) Training Data and (B) Testing Data

		$CA$ (y)				Sex Ratio	FreeSurfer Version
Data Source	$n$ *	min	max	$\mu$ †	$\sigma$ ‡	M:F	5.3.0	6.0.0	7.1.1
(A) Training data
ADNI	513	56	95	75.1	7.2	0.46	0	260	253
HCP-A	508	36	80	55.8	12.0	0.42	0	309	199
HCP-YA	1 112	22	37	28.8	3.7	0.46	1 112	0	0
UKBB	1 285	45	83	62.7	10.1	0.47	0	1 285	0
all	3 418	22	95	52.6	19.3	0.46	1 112	1 854	452
(B) Testing data
Cam-CAN	651	18	88	54.2	18.6	0.496	0	0	651

Notes: $CA$ = chronological age; Cam-CAN = Cambridge Centre for Ageing and Neuroscience; F = female; HCP-A = Human Connectome Project Aging; HCP-YA = Human Connectome Project Young Adult; M = male; max = maximum; min = minimum; UKBB = UK Biobank. Listed are the sample size $n$, the min, max, mean $\mu$, and standard deviation $\sigma$ of the sample $CA$, the M:F ratio, and FreeSurfer version used for preprocessing.

*$n$ = sample size

^† $\mu$ = mean $CA$ of sample

^‡ $\sigma$ = standard deviation of $CA$ of sample

Image Processing

All cortical reconstructions of T₁-weighted MRIs were obtained using FreeSurfer with enhancement to improve segmentation accuracy (16). For ADNI, HCP-A, and Cam-CAN participants, FreeSurfer versions 7.1.1 and 6.0.0 were used with T₂-weighted enhancement (Table 1). For HCP-YA, T₂-enhanced FreeSurfer reconstructions were obtained from the HCP repository (https://www.humanconnectome.org/study/hcp-young-adult). For UKBB, FreeSurfer reconstructions were obtained from the UKBB repository (https://www.ukbiobank.ac.uk/). These reconstructions had been enhanced using fluid-attenuated inversion recovery MRIs, rather than T₂-weighted MRIs. We used the connectogram processing pipeline of Irimia et al. (17) to compile FreeSurfer-generated regional brain measures and to normalize subject measures by total intracranial volume.

Number of Regional Features

The 4 regional brain feature types quantified by FreeSurfer and included here are volume (165 values, one for each structure), surface area, mean cortical thickness, and mean curvature (148 values for each of the latter 3). Because left and right brain features are collinear (8), their values were averaged across hemispheres. Structural collinearity between different regions’ feature variables motivated the use of a regularization technique, as described further below. Let $m$ denotes the number of regional features available for each subject after this averaging. For volumes, one obtains $m=(165-1)/2+1=83$ regional volumes for each subject. To account for the brainstem (which is not in either hemisphere), a factor of 1 is subtracted from the numerator above and then added to the fraction to obtain $m$. When averaging surface area, mean cortical thickness, or mean curvature across hemispheres, one must account for the fact that FreeSurfer does not compute these measures for the subcortex, cerebellum, or brainstem. Thus, $m$ is equal to $148/2=74$ for each of these feature types. Our analysis also explored the unique combination of two or more feature types.

Covariate Adjustments

In what follows, a statistical model is implemented separately for each feature type; in other words, age is predicted separately using regional volumes, surface areas, etc. First, we regressed out the confounding effects of sex, cohort, FreeSurfer version, and the cohort × $CA$ interaction. Then, ridge regressions were implemented both across sexes and for each sex. Both procedures are described in the Supplementary Material.

Ridge Regression Model Training

We used the fitrlinear function in MATLAB R2019a to fit a ridge regression model $\mathit{C}\mathit{A}\mathbf{=}\mathit{X}\widehat{\mathit{\beta }}\mathbf{+}\mathit{\epsilon }$, where $\widehat{\mathit{\beta }}$ is the empirical estimate of $\mathit{\beta }$. The objective function of the ridge regression (see Supplementary Table 1) involves $\lambda$ (a regularization parameter) and the $L^2$ (Euclidean) norm $||\cdot |{|}_2$of both $\mathit{C}\mathit{A}\mathbf{-}\mathit{X}\mathit{\beta }$ and $\mathit{\beta }$. The objective function has a first term quantifying the mean squared loss of the model and a second one that is proportional to the squared magnitudes of the regression coefficients. Minimization of the objective function considers not only the model’s fit to the data but also the cumulative sum of regression coefficients, such that larger coefficients are penalized. The objective function is minimized using a least-squares Bayesian optimization learner, 50 iterations for hyperparameter optimization, and 10-fold cross validation. Data are repartitioned in each round of cross-validation to increase model robustness by reducing statistical noise due to random partitioning. We also implement least absolute shrinkage and selection operator (LASSO) regression, which differs from ridge regression in its objective function for computing $\widehat{\mathit{\beta }}$, and which involves the $L^1$ norm of both $\mathit{C}\mathit{A}\mathbf{-}\mathit{X}\mathit{\beta }$ and $\mathit{\beta }$ (see Supplementary Table 1). The estimated $\widehat{\mathit{\beta }}$ of LASSO regression lacks a closed-form solution. Because LASSO regression coefficients may be set to zero, computing LASSO $R_p^2$ values and comparing them to those obtained using ridge regression can be misleading. For this reason, $R_p^2$ values were not compared across ridge and LASSO regressions. For both, we computed $\widehat{\mathit{B}\mathit{A}}\mathbf{=}\mathit{X}\widehat{\mathit{\beta }}$, and$\widehat{\mathit{A}\mathit{G}}\mathbf{=}\widehat{\mathit{B}\mathit{A}}\mathbf{-}\mathit{C}\mathit{A}$.

$CA$ Bias Correction

Due to regression to the mean, $AG$s estimated using ridge regression exhibit a $CA$-dependent bias (18). For this reason, on average, subjects with $CA$s younger than the mean $CA$ of the sample have positive $AG$s, whereas subjects with $CA$s older than the mean $CA$ of the sample have negative $AG$s. Due to the profile of linear regression’s influence functions (19), mean $AG$ magnitudes become larger with increases in the absolute difference between subjects’ $CA$s and the sample mean $CA$. Among the available methods to adjust predicted ages for this bias (20,21), we used a zero-correlation constraint method previously described (22). In the first step, this fits a simple linear regression model$\widehat{\mathit{A}\mathit{G}}=a+b\mathit{C}\mathit{A}+\mathit{\epsilon }$. $AGs$ can then be adjusted by scaling down $\mathit{C}\mathit{A}$ (21) to obtain${\widehat{\mathit{A}\mathit{G}}}_B=\widehat{\mathit{A}\mathit{G}}-(a+b\mathit{C}\mathit{A})$, where the subscript of ${\widehat{\mathit{A}\mathit{G}}}_B$ indicates that $AG$s have been adjusted according to this approach. The zero-correlation constraint method (22) can be used to convert ${\widehat{\mathit{A}\mathit{G}}}_B$ values into $AG$s that are adjusted by scaling up $\widehat{\mathit{B}\mathit{A}}$ (20), to obtain the vector of zero correlation constraint-corrected age gaps ${\widehat{\mathit{A}\mathit{G}}}_C$, whose formula is provided in Supplementary Table 1. Corrected ${\widehat{\mathit{B}\mathit{A}}}_{\mathrm{C}}$ values can then be computed as ${\widehat{\mathit{B}\mathit{A}}}_C={\widehat{\mathit{A}\mathit{G}}}_C+\mathit{C}\mathit{A}$. This procedure was applied to all models considered.

Performance Statistics

To assess model performance, we compute Pearson’s product-moment correlation coefficient $r(\mathit{C}\mathit{A},\widehat{\mathit{B}\mathit{A}})$, the mean squared error ($MSE$), the mean absolute error ($MAE$), and the adjusted coefficient of determination ${\overline{R}}^2$ (here, the bar denotes adjustment; Supplementary Table 1). Each statistic was computed for both uncorrected $\widehat{\mathit{B}\mathit{A}}$ values and for $CA$ bias-corrected ${\widehat{\mathit{B}\mathit{A}}}_{\mathrm{C}}$ values.

Brain Regions’ Contributions to Brain Age

To estimate the unique variance explained by each feature (ie, brain structure), we compute that feature’s adjusted coefficient of partial determination${\overline{R}}_p^2$, which is expressed as a percentage of ${\overline{R}}^2$ for the full model (Supplementary Table 1). When used as subscripts, $f$ and $r$ stand for full and reduced, respectively. For each structure $j$, this model is defined after removing the column vector of ${\mathit{f}}_j$ from ${\mathit{X}}_f$. This yields an $n\times m$ reduced design matrix ${\mathit{X}}_r$ that is used in place of $\mathit{X}$ to fit the reduced ridge regression model and to compute $SS{E}_r$. For comparison, we also computed the unadjusted$R_p^2$ (Supplementary Table 1). Adjusted${\overline{R}}_p^2$ values are plotted on the cortical surface and on the surfaces of subcortical structures using the ENIGMA Toolbox (23).

Model Testing

To validate our models and evaluate their robustness, we estimate the $BA$s of participants in an independent test data set from the Cam-CAN repository. We use the same covariate correction procedure described above, yielding a test design matrix ${\mathit{X}}_t$ for these data ($t$ stands for test). $BA$s and bias-corrected $CA$s are computed as previously described. To test the ability of estimated $BA$s to reflect cognitive phenotypes, we calculate the statistical significance of Spearman’s rank correlation coefficient$\rho$ quantifying the relationship between cognitive measures and (each of) $B{A}_C$, $A{G}_C$, and $CA$. A Bonferroni correction for multiple comparisons is applied to control the false discovery rate.

Results

Model Fit to Chronological Age

Four separate models were trained, each using only regional volumes, surface areas, mean cortical thicknesses, or mean curvatures, respectively. Performance statistics are listed for all models in Table 2A. Excluding models which suffered from extreme regression to the mean, the volumetric model typically performed best in terms of the 4 computed performance statistics. Exceptions are the following: (a) the test set for the $CA$ bias-corrected sex-combined model (where mean thickness performed best); (b) the training set for the uncorrected female model as well as both (c) the training and (d) test sets for the $CA$ bias-corrected female model (mean curvature performing best in these 3 cases). Whereas we considered models using each unique combination of feature types (12 in total), all these models suffered from extreme regression to the mean, and therefore all these combined models were excluded from further analysis for simplicity and brevity. Unregularized linear regression models were also computed to assess whether the presence of $CA$-dependent bias was of concern beyond models that involved regularization. However, this bias was also found in the unregularized model, leading us to conclude that regularization itself does not imply this bias. We chose to perform further analysis on our sex-agnostic volumetric model, as this was the best-performing model (which incidentally also included all subjects). This model achieved $r=0.92$, $MSE=70.94$ years, $MAE=6.57$ years, and ${\overline{R}}^2=0.81$ on the training data. The $CA$ bias-corrected $BA$s and $AG$s of subjects in the training set are plotted against $CA$s in Supplementary Figure 1. Performance statistics are listed in Table 2B for all models evaluated on test data. On our sex-combined test sample, the volumetric model achieved $r=0.90$, $MSE=81.96$ years, $MAE=7.00$ years, and ${\overline{R}}^2=0.79$. The $CA$ bias-corrected $BA$s and $AG$s of subjects in the test set are plotted against $CA$s in Figure 1. The LASSO regression model was found to suffer from extreme regression to the mean for all metric types considered. Bias-correcting these results yields overfit predictions. Although seeming to have nearly perfect performance ($r\simeq 1$, ${\overline{R}}^2\simeq 1$;$MSE,MAE\simeq 0$), these models are in fact uninformative and lacking in utility. In addition, whereas LASSO does perform pseudo-feature selection, our goal was to compute feature-level contributions to overall model performance. This would have confounded our ability to compute leave-one-out reduced models, as many features would have been effectively selected out of the full model, thus removing our ability to compute ${\overline{R}}_p^2$ values for the corresponding regions. For these reasons, ridge regression was preferred over this family of models, and the latter were not considered for further analysis.

Table 2.

Ridge Regression Performance Statistics in the (A) Training Data Set and (B) Test Data Set

				$\widehat{\mathit{B}\mathit{A}}$
				Uncorrected model				Corrected model
Measure	$m$ *	Sex	$n$ †	$r$ ‡	${\overline{R}}^2$ §	$MSE$ ‖ (y2)	$MAE$ ¶ (y)	$r$ ‡	${\overline{R}}^2$ §	$MSE$ ‖ (y2)	$MAE$ ¶ (y)
(A) Training data
Volume	83	m&f	3 418	0.90	0.82	69.36	6.66	0.92	0.81	70.94	6.57
		m	1 565	0.93	0.87	57.52	6.16	0.94	0.87	57.03	6.01
		f	1 853	0.69	0.05	340.33	16.10	1.00	1.00	0.01	0.08
Surface area	74	m&f	3 418	0.82	0.67	123.61	8.89	0.86	0.67	125.30	8.88
		m	1 565	0.54	0.05	405.97	17.77	1.00	1.00	0.01	0.08
		f	1 853	0.45	0.04	341.59	16.11	1.00	1.00	0.01	0.08
Mean thickness	74	m&f	3 418	0.88	0.78	85.25	7.27	0.90	0.77	87.40	7.28
		m	1 565	0.70	0.05	405.39	17.76	1.00	1.00	0.01	0.06
		f	1 853	0.59	0.04	341.52	16.12	1.00	1.00	0.01	0.06
Mean curvature	74	m&f	3 418	0.88	0.77	86.39	7.43	0.90	0.77	86.34	7.37
		m	1 565	0.89	0.80	84.39	7.33	0.91	0.81	82.21	7.17
		f	1 853	0.87	0.77	83.38	7.24	0.90	0.77	82.69	7.19
(B) Testing data
Volume	83	m&f	651	0.86	0.74	100.60	8.25	0.90	0.79	81.96	7.00
		m	332	0.87	0.68	147.30	9.62	0.93	0.88	54.16	5.63
		f	328	0.78	0.25	354.41	16.17	1.00	1.00	0.00	0.04
Surface area	74	m&f	651	0.54	0.36	247.95	12.87	0.70	0.08	356.13	14.85
		m	332	0.57	0.22	342.20	16.00	1.00	1.00	0.01	0.07
		f	328	0.50	0.22	354.98	16.19	1.00	1.00	0.01	0.06
Mean thickness	74	m&f	651	0.70	0.55	175.69	10.89	0.91	0.82	71.82	6.89
		m	332	0.39	0.22	342.67	16.01	1.00	1.00	0.02	0.08
		f	328	0.42	0.22	355.73	16.20	1.00	1.00	0.01	0.07
Mean curvature	74	m&f	651	0.76	0.57	166.42	10.62	0.86	0.68	123.19	8.74
		m	332	0.76	0.29	309.64	14.44	0.90	0.81	80.96	6.92
		f	328	0.74	0.36	291.80	13.71	0.91	0.84	71.82	6.89

Notes: $BA$ = biological age; f = female; m = male. Twelve models were fit, one for each combination of brain measure types (volume, surface area, mean thickness, and mean curvature) and sex-dependent model type (ie, males-only model, females-only model, and the sex-agnostic model with sex effects regressed out). Fitted values of $\widehat{\mathit{\beta }}$ were used to estimate $BA$ in the Cam-CAN independent test set.

*$m$ = number of model features

^† $n$ = sample size

^‡ $r$ = Pearson product-moment correlation coefficient between $\mathit{C}\mathit{A}$ and $\widehat{\mathit{B}\mathit{A}}$

^§ ${\overline{R}}^2$ = coefficient of determination

^‖ $MSE$ = mean squared error

^¶ $MAE$ = mean absolute error

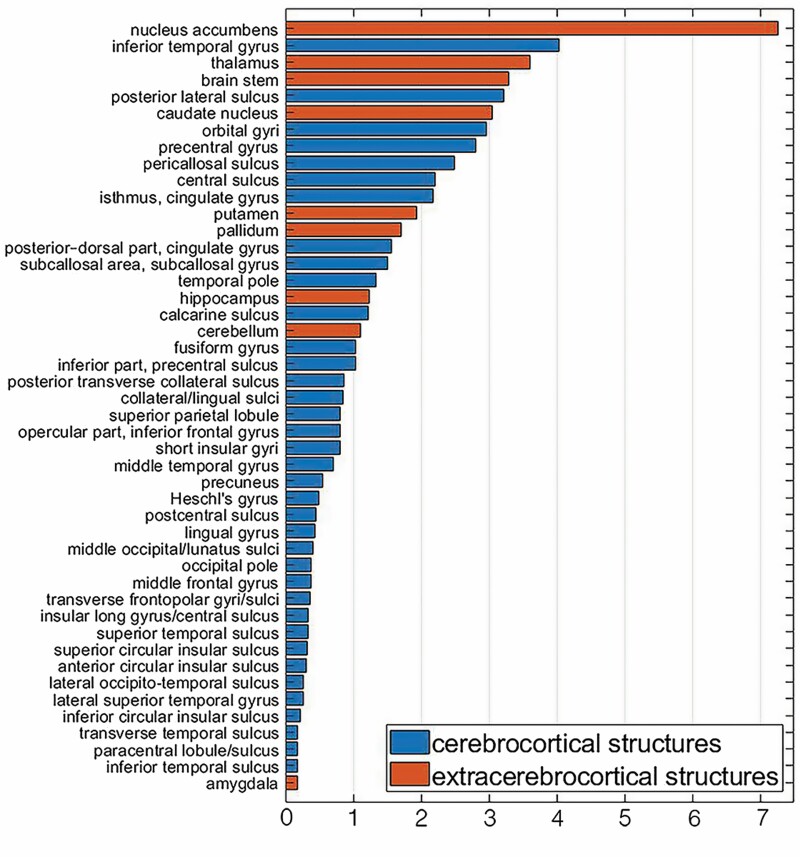
Figure 1.

Adjusted coefficients of coefficient of partial determination ${\overline{R}}_p^2$ for the 46 structures with the largest ${\overline{R}}_p^2$ values included in the sex-agnostic ridge regression model estimating age using regional volumes. Plotted are adjusted ${\overline{R}}_p^2$ values, expressed as percentages of the total variance ${\overline{R}}^2$ explained by the full model that includes all predictors (regions or structures). Cortical structures are plotted in darker hues (blue online); extra-cerebral structures, including the subcortex, cerebellum, and brainstem, are plotted in lighter hues (orange online).

Individual Feature Contribution

For each feature in the sex-agnostic volumetric model, adjusted partial coefficients of determination ${\overline{R}}_p^2$ values are tabulated (Supplementary Tables 1 and 3), depicted in bar plots (Figure 1, Supplementary Figure 2), and mapped on brain surfaces (Figure 2). To summarize, 8 structures are associated with the 10% largest $R_p^2$ values: the nucleus accumbens(${\overline{R}}_p^2=7.27\mathrm{\%}$), inferior temporal gyrus (${\overline{R}}_p^2=4.03\mathrm{\%}$), thalamus (${\overline{R}}_p^2=3.61\mathrm{\%}$), brainstem (${\overline{R}}_p^2=3.29\mathrm{\%}$), posterior lateral sulcus (${\overline{R}}_p^2=3.22\mathrm{\%}$), caudate nucleus (${\overline{R}}_p^2=3.05\mathrm{\%}$), orbital gyri (${\overline{R}}_p^2=2.96\mathrm{\%}$), and precentral gyrus (${\overline{R}}_p^2=2.80\mathrm{\%}$). In addition, 12 regions exhibit negative ${\overline{R}}_p^2$ values due to adjustments for changes in the number of features across distinct models.

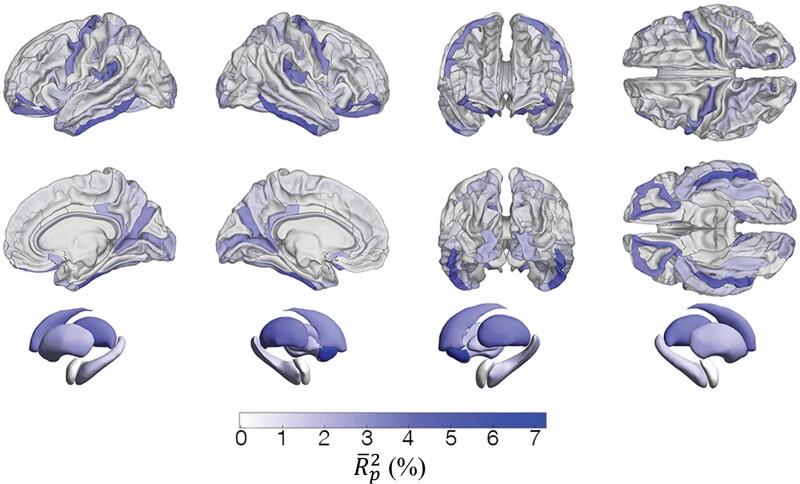
Figure 2.

Surface overlays of region- and structure-specific adjusted coefficients of partial determination ${\overline{R}}_p^2$ obtained using a sex-agnostic ridge regression model to estimate age using regional volumes. (A) ${\overline{R}}_p^2$ values for the 148 gyral/sulcal structures of the cerebral cortex (74 structures per hemisphere). (B) ${\overline{R}}_p^2$ values for the 7 subcortical structures included in the model.

Correlations With Cognitive Measures

Supplementary Table 4 lists Spearman’s rank correlation coefficients $\rho$ between each cognitive measure and each of $B{A}_c$, $A{G}_c$, and $CA$. After Bonferroni correction for multiple comparisons, we obtained a corrected α value of 0.0013 corresponding to an uncorrected significance threshold α = 0.05. Significant correlations were found between both $CA$ and $B{A}_C$ and the cognitive measures for each of the following tasks: emotional memory, fluid intelligence, hotel task (quantifying multitasking), unfamiliar face recognition, famous face recognition, picture priming, tip-of-the-tongue, visual short-term memory, force matching, motor learning, and reaction time choice and simple tasks. For the proverbs task, the cognitive outcome measure was significantly correlated only with $CA$. $A{G}_c$ values were not significantly correlated with any cognitive measures. Correlations with $CA$ were stronger than those with $B{A}_C$ across all participants, regardless of their $AG$.

Discussion

Motivation and Purpose

The primary reason for our development and implementation of the ridge regression model presented here is the current paucity of models that can provide insight into the relative contributions of distinct brain regions to BA. In recent years, ML models have become better and better at BA estimation, whether using Gaussian process regression (5), support vector regression (24), U-Nets (10), or other approaches. Such models can achieve $MAE$s as low as $\sim$4 years (2,10) without the need for complex and computationally intensive preprocessing to segment and parcel the brain. However, few models provide insights into the relative contributions of distinct regions to BA (25). By contrast, our ridge regression model is interpretable due to our ability to identify and quantify the relative contributions of various neuroanatomic structures to BA (albeit at the price of computationally intensive brain segmentation and parcellation). Another tradeoff of regression models is that, whereas they are typically easier to understand than many state-of-the-art ML models, they are also less sophisticated. Considering this, it is perhaps unsurprising that our model’s bias-corrected $MAE$ is only $\sim$6 years, whereas some ML models achieve $MAE$s as low as $\sim$4 years (2,10). Nevertheless, despite its inferior BA estimation ability in our aggregate data set, our model remains valuable for its original intended purpose of providing neuroanatomic interpretability. Because the theoretical framework of regression is well understood, our model can also be valuable for validating interpretable ML models currently being developed to provide interpretability based on salience maps or on other strategies (25,26). In one scenario, the developers of interpretable ML models may choose to train their models on data different from ours. In this case, our model can provide a reference specification of regional contributions to BA based on training using an independent data set. In the alternative scenario, ML model developers may choose to train and/or validate their models on the same data used here, since these data are freely available. In this second scenario, our model could be even more valuable because the insights provided by interpretable ML models can be compared to ours without the confound of different data sets being used for training. Thus, although a lower $MAE$is desirable for a model as long as BA estimates are accurate, providing neuroanatomic insight in a reference HC cohort remains as desirable; our study is arguably most valuable because it provides the latter.

Interpretation

For any neuroanatomic structure, the partial coefficient of determination ${\overline{R}}_p^2$ conveys how much variance the full model explains that is not already explained by a reduced model that excludes the structure in question. Thus, if that structure has a relatively large ${\overline{R}}_p^2$ compared to other structures, then the structure in question has a relatively large amount of unique covariance with $CA$ that is not shared with the covariance of all other regions. In this study, the nucleus accumbens exhibits the largest ${\overline{R}}_p^2$ value, corresponding to 7.27% of the covariance explained by the full model (Supplementary Table 3). This is nearly twice as much covariance as that explained by the region with the second largest ${\overline{R}}_p^2$, that is, by the inferior temporal gyrus (${\overline{R}}_p^2=4.03\mathrm{\%}$). In addition, 8 of the 9 extra-cerebrocortical structures in the model are among the top 19 ($\sim$23%) of 83 regions, sorted by ${\overline{R}}_p^2$ in descending order (Supplementary Table 3, Figure 1). Several studies have evaluated the age-related volume trajectories of the nucleus accumbens and of other subcortical structures (27–29). Possibly due to factors pertaining to neurodevelopmental profile (30), cytoarchitecture (31), susceptibility to disease (32), and/or anatomic location, these structures may be exposed to different age-related processes, in both kind and quantity, resulting in aging trajectories that are distinct from those observed across the cerebral cortex. Partly due to the large amount of unique covariance in volume between these structures and $CA$ (as quantified by ${\overline{R}}_p^2$), pathological processes may affect the aging trajectories of these regions—and therefore their estimated $BA$s—more strongly than the trajectories of other structures, for which our model yields smaller ${\overline{R}}_p^2$ values. Importantly, we did not observe a significant relationship between a region’s mean volume and its ${\overline{R}}_p^2$ (Spearman’s rank correlation coefficient $\rho =-0.19$, p = .9), indicating that the variance in regional volumes does not explain variance in ${\overline{R}}_p^2$ to a significant extent. This suggests that a brain region’s size is not critical in determining that region’s contribution to BA. In other words, BA depends far more on the biological ages of a few structures whose contributions to overall BA are larger than expected given their physical size.

There may be more than one cause for the relatively high contributions of subcortical structures to $BA$, and our findings may reflect the relative sensitivity of subcortical structures to aging-related disease processes. Such sensitivity could translate into the prominent role played by neuroanatomic changes across subcortical structures in determining $BA$. For example, excessive atrophy of the nucleus accumbens has been implicated in Parkinson’s disease (33–36), schizophrenia (36,37), Alzheimer’s disease (36,38), Huntington’s disease (36,39), frontotemporal dementia (40), and other conditions. Since our model was only tested on HCs, the potential utility and applicability on cohorts with disease is hypothetical. However, because the nucleus accumbens (which has the highest $R_p^2$ among all considered regions) has been implicated functionally in all these diseases, our model could be useful for assessing atypical aging in this structure. Future studies should clarify the extent to which the role of the basal ganglia in determining $BA$ reflects typical aging rather than neuropathological processes targeting the subcortex. Interpretable models like ours should also be used to quantify how brain structures change with disease-related brain aging, and to determine whether disease-related changes in structures which are important for $BA$ estimation can result in commensurate disease-related increases in $BA$.

Among cortical structures, the most prominent contributors to BA are localized to orbitofrontal cortex, to the medial aspect of the occipital and parietal lobes, to the inferolateral portion of the temporal lobe (inferior temporal gyrus) and to the precentral gyrus. This pattern is consistent with previous research that mapped the most significant structural differences between typical aging and Alzheimer’s disease (41). Notably, however, aside from the inferior temporal gyrus, the contributions of other temporal structures to BA are relatively weak in this large HC cohort. This is perhaps surprising given the relevance of broad areas across the lateral and medial aspects of the temporal lobe to neurodegeneration. For this reason, future studies should investigate these structures’ contributions to BA in neurodegenerative disease to clarify their importance in modifying BA above and beyond typical aging processes.

Model Selection, Parsimony, and Other Considerations

Of note, our model is not fully parsimonious because 12 regions exhibit adjusted ${\overline{R}}_p^2$ values that are negative. Although $R^2$ is always positive, adjusted ${\overline{R}}_p^2$ values can be negative (see the Method section) and adjusting $R_p^2$ is recommended to correct for the effect of $R^2$ increasing spuriously when a new predictor variable is added to a model (42). The fact that 12 structures have negative ${\overline{R}}_p^2$ values after adjustment conveys that these structures do not uniquely improve model performance. This is likely because each of these regions covaries with others to such an extent that the variance explained by the former is also explained collectively by the latter. For all 12 structures, $R_p^2$ is relatively quite low, often by more than an order of magnitude than the mean $R_p^2$. All adjusted ${\overline{R}}_p^2$ values that are negative are also very near zero, such that their signs may be unusually sensitive to noise in the training data and to model stochasticity arising from optimization of hyperparameters such as the regularization parameter $\lambda$, even though regularization serves to alleviate this effect. If model selection was implemented, many structures with negative adjusted ${\overline{R}}_p^2$ values would be removed from the model, such that no data on their relative importance would be provided despite potential interest by researchers studying these structures. Additionally, since these structures explain very little variance, their removal would likely improve model performance very marginally at considerable computational cost, which is not our objective. For all these reasons, we report all ${\overline{R}}_p^2$ here to provide the reader with insight on the relative prominence of all regions. This sidesteps the task of model selection in our setting, where the complex covariance structure of the data suggests that model selection, required to achieve parsimony, is accordingly difficult despite being of very limited practical utility.

Inspection of Supplementary Table 3 reveals that, occasionally, the sign of the multivariate regression coefficient ${\widehat{\beta }}_j$ describing the relationship between predictor $j$ and the response variable ($CA$) is positive despite the expected negative sign of the univariate regression coefficient $\widehat{\beta }$ between these quantities. In the latter case, a negative $\widehat{\beta }$ indicates that, on average, regional volume decreases with age in cross-section, as reported elsewhere (43–45). In our model, the multivariate regression coefficient ${\widehat{\beta }}_j$ is not always negative because ${\widehat{\beta }}_j$ conveys the conditional effect of a predictor (regional brain volume) on the response ($BA$) in the presence of all other predictors. In a multivariate model, a predictor’s conditional effect on the response differs from its unconditional effect because the conditional effect depends on the covariance between predictors, whereas the unconditional effect depends on the correlation between the single predictor and the response. In a univariate model, the sign of $\widehat{\beta }$ is that of the correlation coefficient $r$ because $\widehat{\beta }=r(s_y/s_x)$, where $s_y$ and $s_x$ are the variances of the response and predictor variables, respectively. In a multivariate model, however, the sign of ${\widehat{\beta }}_j$ is additionally dependent on the covariance between predictors. Occasionally, this covariance is strong enough to affect the sign of ${\widehat{\beta }}_j$, such that ${\widehat{\beta }}_j$ and the corresponding univariate $\widehat{\beta }$ have different signs.

In settings like ours, bias corrections must be interpreted carefully. For example, as Table 2 indicates, surface area and cortical thickness might both appear to predict $CA$ almost perfectly after bias correction. One could draw this incorrect conclusion because (a) the $MAE$s and $MSE$s of the models based on these measures are considerably smaller than those of the model predicting $BA$ using regional volumes, and because (b) the $r$ and ${\overline{R}}^2$ values of the former 2 models are very close to 1. However, prior to bias correction, the area and thickness models exhibit very large $MAE$s and $MSE$s, as well as $r$ and ${\overline{R}}^2$ values that are much smaller than those of the models based on volume and curvature (Table 2). Thus, the improvements in performance statistics ($MAE$, $MSE$, $r$, and ${\overline{R}}^2$) exhibited by the models for surface area and thickness can be attributed to the bias correction procedure. Specifically, before bias correction, $BA$s estimated using cortical surface area or thickness are predicted almost entirely by the sample mean $CA$. Similarly, after bias correction, $BA$s estimated using mean surface area or thickness are predicted almost entirely by $CA$s. Ultimately, each type of metric (volume, mean curvature, surface area, mean cortical thickness) can predict age only to the extent to which the metric type in question reflects variability in ages across the sample. Whereas volume and mean curvature are relatively sensitive to age, surface area and mean cortical thickness are not. This explains why the former 2 metrics provide BA estimation models that are more useful than those provided by the latter. These considerations highlight the importance of interpreting bias correction results properly in the context of regression models.

Correlations With Cognition

Spearman’s rank correlations between cognitive measures and age exhibit no significant differences when computed using $BA$ versus $CA$. Because we trained and tested our model on HCs, this is unsurprising because the model is fit by minimizing an objective function that includes $AG$, that is, the difference between $BA$ and $CA$. In addition, we obtained high correlation between $BA$ and $CA$, and the correlations between neuroanatomic measures and $BA$ are therefore expected to be similar to those between neuroanatomic measures and $CA$. By contrast, correlations between $AG$ and cognitive measures are expected to be weak, since bias correction ensures that $AG$s are centered around 0 for all $CA$s. Nevertheless, our model could be useful for estimating $BA$ and $AG$ in diseased cohorts whose members have much larger $AG$s than HCs (4,5). In such cohorts, systematic changes in $BA$ due to disease may correlate more strongly with cognitive changes that with $CA$. Thus, correlations between $BA$ and cognitive measures can be leveraged to forecast cognitive decline for individuals based on their $AG$s. Our modeling approach is particularly useful for this purpose since it can facilitate quantifying how various regions’ ${\overline{R}}_p^2$ values (ie, brain regions’ relative importance in estimating $BA$) change with disease.

Limitations

Because our model quantifies the contributions of distinct neuroanatomic structures to BA, our implementation required the segmentation of these structures using specialized software (eg, FreeSurfer). Thus, although more interpretable than black-box ML implementations, our ridge regression model may not be as attractive from a translational or clinical standpoint due to its dependence on computationally intensive preprocessing of MRIs to obtain regional segmentations. Additionally, our model’s interpretability is counterbalanced by the fact that its best $MAE$ (6.57 years) is relatively large compared to the $MAE$s of the best existing ML models, which are smaller than ours by $\sim$2 years (2,28). However, we emphasize that the motivation for our study is to provide neuroanatomic interpretability in the context of a standard statistical framework that is well understood, rather than to outperform existing ML models of BA.

Large samples like ours are often aggregated across open-access neuroimaging cohorts and data repositories. This often leads to the need for data curation and harmonization with respect to sources of variance arising from the inclusion of data from different studies, scanners, sequence parameters, etc. In this study, we included training from 3 major imaging consortia (HCP, ADNI, and UKBB), and the statistical effects of cohort and sub-cohort (eg, HCP Young Adult vs HCP Aging) were regressed out prior to further analysis (see the Method section). However, we acknowledge that the heterogeneity of our aggregate data set is not fully captured by a linear model, and that residual variance due to residual heterogeneity may persist.

As already stated in the context of model selection, noise can have notable effects in multivariate models like ours and dimensionality reduction approaches (eg, principal or independent component analysis) can help to exclude predictors from a regression model if their presence is redundant. These and similar methods, however, often require data standardization and may reduce interpretability by abstracting features into principal or independent components. In addition, these methods can also introduce additional hyperparameters, and may even require subjective modeling decisions. For example, in principal and independent component analysis, one must select and discard components whose presence reflects noise in the data. This selection, however, can be arbitrary because it is not always clear which components correspond to noise versus weak signal.

In the full model, 12 predictors do not explain variance above and beyond variance explained by all other predictors together. However, these 12 predictors’ contributions to the model are also very small, suggesting that their inclusion does not have substantial effects either. Because these predictors presumably covary with others already in the model, model selection can be arbitrary and subjective. For example, suppose that 2 predictors covary substantially, such that including only one increases the amount of variance explained by the model, whereas including both does not. The choice of the predictor to remove can be subjective, partly because different researchers may be interested in including and studying the effects of different predictors. To avoid such arbitrary decisions and to report results comprehensively, we included all predictors in this study. However, the drawback of such inclusion is that the full model is not parsimonious, a limitation that we acknowledge. Future studies should further investigate the relative prominence of neuroanatomic predictors in estimating BA, as well as how these predictors covary.

Conclusion

We introduced an interpretable model for $BA$ estimation using ridge regression. Using ${\overline{R}}_p^2$ to quantify unique neuroanatomic contributions to $BA$, we found that the nucleus accumbens, inferior temporal gyrus, and thalamus uniquely explain considerably more variance in $CA$than most others brain structures. Some 12 structures do not explain any variance above and beyond that explained by all the other structures, likely due to multicollinearity among predictors. Whether using standard statistical models or ML models, future studies should improve BA estimates while providing neuroanatomic interpretability. Additionally, the potential utility of other brain features implicated in aging, such as myelination measures (46), metrics of white matter connectivity or hyperintensity (47), and β-amyloid and tau measures obtained from positron emission tomography (48,49) should be explored. Whereas macroscale neuroanatomic features can be used to estimate $BA$, microanatomic and metabolic brain feature changes with age should also be considered. Further investigation is required to clarify whether our model has utility in detecting atypical aging as a result of disease processes. If it does, the clinical utility of ML models that detect and even predict atypical brain aging due to disease should be compared against models like ours, which are standard in quantitative biology and therefore well understood by biostatisticians. Usefully, our study provides insight into how brain features covary with age, and this can be useful for interpreting other models. Finally, our model may be useful for identifying brain regions that contribute to the BA s of diseased individuals to an extent greater than expected in HCs.

Funding

This work was supported by the National Institutes of Health grant R01 NS 100973 to A.I., by the US Department of Defense contract W81XWH-18-1-0413 to A.I., by a Hanson-Thorell Family Research Scholarship, and by the James J. and Sue Femino Foundation. Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The ADNI grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California. Data for this study were provided, in part, by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University. Research reported in this publication was also supported by the National Institute on Aging of the National Institutes of Health under Award Number U01 AG 052564. Cam-CAN funding was provided by the UK Biotechnology and Biological Sciences Research Council (grant number BB/H008217/1), together with support from the UK Medical Research Council and University of Cambridge, UK. The content of this study is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or of the University of Southern California. The funding sources had no role in study design, in the collection, analysis, and interpretation of data, in the writing of the report, or in the decision to submit the article for publication.

Conflict of Interest

None declared.