Genetic mechanisms determining grain number distribution along the spike and their effect on yield components in wheat

Abstract

The number of wheat grains is one of the major determinants of yield. Many quantitative trait loci (QTLs) and some causal genes such as GNI-A1 and WAPO-A1 that are associated with grain number per spike (GNS) have been identified, but the underlying mechanisms remain largely unknown. We analyzed QTLs for grain number and other related traits using 188 doubled haploid lines derived from the Japanese high-yield variety, Kitahonami, as a parent to elucidate the genetic mechanism determining grain number. The major QTLs for grain number at the apical, central, and basal parts of the spike were identified in different chromosomal regions. We considered GNI-A1 and WAPO-A1 as candidate genes controlling grain number at the central and basal parts of the spike, respectively. Kitahonami had the favorable 105Y allele of GNI-A1 and WAPO-A1b allele and unfavorable alleles of QTLs for grain number at the apical part of spikes. Pyramiding the favorable alleles of these QTLs significantly increased GNS without significantly reducing thousand-grain weight (TGW). In contrast, the accumulation of favorable alleles of QTLs for TGW significantly decreased GNS, whereas days to heading positively correlated with GNS. Late heading increased the spikelet number per spike, resulting in a higher GNS. Pyramiding of the QTLs for TGW and days to heading also altered the GNS. In conclusion, GNS is a complex trait controlled by many QTLs, and it is essential for breeding to design.

Supplementary Information

The online version contains supplementary material available at 10.1007/s11032-021-01255-8.

Introduction

Wheat is one of the most important crops, providing 20% of the food calories and protein consumed by the human population worldwide (FAOSTAT 2018). Increases in wheat grain yield are desired because of the increasing demands imposed by a growing human population, while areas suitable for growing wheat decrease. Many components are associated with grain yield, such as spikes per unit area, grain number per spike (GNS), and average grain weight, which usually result in better heritability (Zhang et al. 2018). Understanding the genes and gene networks associated with grain yield components is needed to increase the wheat grain yield.

The number of grains is more plastic than seed morphology, and wheat yield is apparently more closely related to grain number than grain weight (Fischer 2011; Sadras and Slafer 2012). The GNS is determined by several factors, such as spikelet number per spike (SNS) and the fertility of each floret (Sreenivasulu and Schnurbusch 2012; Guo and Schnurbusch 2015). The GNI-A1 gene, which encodes an HD-Zip I transcription factor and is located on the long arm of chromosome 2A, contributes to floret fertility in wheat (Sakuma et al. 2019). A non-synonymous SNP within a highly conserved homeodomain results in lost or attenuated function. The reduced function allele of GNI-A1 increases floret and grain number, especially at the central part of the spike. Quantitative trait loci (QTL) for grain-setting rates in apical and basal spikelets (Guo et al. 2015) suggest that the genetic mechanism of the grain-setting rate differs among various parts of the spike. Recent QTL analysis and genome-wide association studies (GWAS) have identified wheat ortholog of apo1 (WAPO1/TaAPO1), which is located on the long arm of chromosome 7A, as a candidate gene controlling SNS (Kuzay et al. 2019; Muqaddasi et al. 2019). H1, H2, and H3 haplotypes of WAPO-A1 have been identified in hexaploid and tetraploid wheat (Kuzay et al. 2019). Plants with the WAPO-A1b allele (H2 haplotype), which has an amino acid substitution in the F-box, have a higher SNS than those with the other two haplotypes. More of the WAPO-A1b allele is expressed than the WAPO-A1a allele, which has a deletion in the promoter region. The frequency of the WAPO-A1b allele in modern cultivars is higher (83.2%) than that in landraces (51.0%), suggesting that the WAPO-A1b allele has been favored through recent breeding.

Although GNS and grain weight are major components that determine grain yield, grain number and weight negatively correlate (Griffiths et al. 2015; Zhai et al. 2018). The Hap6 allele of GNI-A1, which has two copies of GNI-A1 and a non-synonymous mutation, increases grain weight without reducing grain number in tetraploid wheat (Golan et al. 2019). Considerable effort has been directed towards identifying QTLs for grain size and weight in wheat using bi-parental populations and GWAS (Gegas et al. 2010; Zanke et al. 2015; Guan et al. 2018; Mangini et al. 2018; Yang et al. 2020). Homology-based approaches have resulted in cloned and characterized candidate genes for grain size and weight (Jiang et al. 2011; Jiang et al. 2015; Su et al. 2011; Cao et al. 2020). Nonetheless, whether these QTLs and genes affect grain number remains obscure.

Favorable alleles of QTLs for yield-related traits should accumulate during long-term breeding programs. For example, the Japanese high-yield variety, Kitahonami, which is a leading cultivar in Hokkaido, Japan, has the reduced function allele of GNI-A1 (Sakuma et al. 2019). However, whether the high grain yield in Kitahonami is due to GNI-A1 alone or other genes remains unknown. In addition, the genetic mechanism determining grain number, including the trade-off between grain number and weight, is still largely unknown. To address these issues, we analyzed QTLs for yield-related traits, such as GNS and TGW using a doubled haploid population derived from a cross between Kitahonami and Shunyou. The genetic mechanisms that determine grain number are discussed based on the present findings.

Materials and methods

Plant materials

We investigated 188 F₁ derived doubled haploid lines (DHLs) derived from a cross between Shunyou and Kitahonami (Ishikawa et al. 2020). Traits were evaluated in 192 accessions including two replicates of the parental varieties. Field uniformity was validated using the two parental and Kinuhime, Yukiharuka, Hatsumochi, Satonosora, Ayahikari, and Yumeshiho varieties.

Trait evaluations

The experimental design consisted of three blocks for each of the 72 plots. The validation varieties were grown in each block, but each evaluation accession was planted only once. All materials were cultivated during the 2016–2017, 2017–2018, and 2018–2019 growing seasons in Tsukuba, Ibaraki, Japan (36.0°N, 140.1°E). Seeds were sowed on November 8, 2016, November 7, 2017, and November 7, 2018. Each plot consisted of 28 plants seeded at intervals of 5 cm in the 2016–2017 season and 15 plants seeded at 10-cm intervals during the 2017–2018 and 2018–2019 seasons.

The heading dates of the accessions recorded for all experimental plots were converted into days to heading after sowing (DH). The mean SNS, GNS, whole grain weight per spike (GWS) in five spikes, and total grain number at three parts of each spike were calculated. Apical, central, and basal parts of spike were divided according to Table S1, which were illustrated in Fig. S1. In order to evaluate grain number without being affected by spikelet numbers, we also analyzed grain number per spikelet (GNSP) at the three parts of each spike.

Genotyping GNI-1 and WAPO-A1

We genotyped GNI-A1 using the KASP assay with the following primers:

FAM, 5′-TCGCCGTGTGGTTCCAGT-3′; HEX, 5′-TCGCCGTGTGGTTCCAGA-3′; and 5′-GTACGCCAGTGTGAGTGTGTAT-3′. The KASP assay proceeded in a 5-μL reaction volume containing KASP master mix (2.5 μL), KASP primer assay mix (0.07 μL), and 2 μL of DNA template (10 ng/μL). The cycling conditions for GNI-A1 amplification were 94 °C for 15 min, 10 cycles of 94 °C for 20 s, and 61–55 °C in increments of − 0.6 °C per cycle for 1 min, followed by 29 cycles of 94 °C for 20 s and 55 °C for 1 min. Fluorescent end points were read using a CFX 384 (Bio-Rad Laboratories Inc., Hercules, CA, USA). Genotypes were called using CFX manager 3.1 software (Bio-Rad Laboratories Inc.) in allele discrimination mode. We genotyped WAPO-A1 using the primer pair WAPO1_pro_F and WAPO1_pro_R, which was also used to identify the WAPO-A1a allele (Kuzay et al. 2019). We amplified DNA by PCR using a T100 thermal cycler (Bio-Rad Laboratories Inc.) and GoTaq DNA polymerase (Promega Corp., Madison, WI, USA). The PCR conditions were as follows: denaturation at 95 °C for 1 min, followed by 35 cycles of 95 °C for 30 s, and 58 °C for 30 s, extension at 72 °C for 30 s, and then 72 °C for 5 min. The amplicons were separated by 2.0% agarose gel and visualized using SYBR Safe DNA Gel Stain (Invitrogen, Carlsbad, CA, USA). We sequenced WAPO-A1 using the primers, 5′-TTAGGACAATAGGAGAGACCATTGTTCA-3′ and 5′-GCGGCGGGACCTGGGAT-3′. Thirty-three PCR cycles proceeded using PrimeSTAR® GXL DNA Polymerase (Takara Bio Inc., Kusatsu, Japan) as follows: denaturation at 95 °C for 1 min, 32 cycles at 98 °C for 30 s, 60 °C for 30 s, and 30 s at 68 °C, and then 68 °C for 5 min. Sequences were determined using a 3730xl DNA Analyzer and BigDye Terminator version 3.1 (both from Applied Biosystems, Waltham, MA USA).

Map construction and QTL analysis

We constructed a linkage map using genotype data from Ishikawa et al. (2020) and MapDisto v2.1.0.1 (Lorieux 2012). Linkage groups were identified using a minimum logarithm of odds (LOD) score of 4 and a maximum recombination fraction of 0.30. Recombination fractions were converted into centimorgan (cM) map distances using the Kosambi mapping function. The physical positions of the markers were estimated by a BLAST search of marker sequences against the International Wheat Genome Sequencing Consortium (IWGSC) CS reference sequences (Appels et al. 2018). Table S2 lists the genetic and physical positions of the markers. We applied inclusive composite interval mapping (ICIM) using IciMapping software (http://www.isbreeding.net/software/). A model was created with a mapping step of 1.0 cM and a LOD significance threshold determined by 1,000 permutation tests with significance set at p = 0.05. Values for positive and negative additive effects were derived from Shunyou and Kitahonami. We defined the same QTL as the QTLs with overlapping confidence intervals.

Statistical analysis

The uniformity of the experimental field was examined using check varieties and analysis of variance (ANOVA) with the lm function in R. Marker-based heritability was estimated using the heritability package in R. A kinship matrix among DHLs was constructed using the kinship function in the statgenGWAS package with the IBS method. The significance of correlation coefficients was evaluated using the cor.mtest function in the corrplot package. P values for correlation coefficients were obtained by multiple comparison tests of all pairs of traits. The significance of each genotype was evaluated using ANOVA and Tukey–Kramer tests using the glht function in the multcomp package.

Gene annotation and expression profiles

Genes around QTLs were listed using IWGSC functional annotations (https://wheat-urgi.versailles.inra.fr/Seq-Repository/Annotations). The numbers of transcripts per million (tpm) of these genes were obtained from Wheat Expression Browser (http://www.wheat-expression.com, Ramirez-Gonzalez et al. 2018; Borrill et al. 2016).

Results

Phenotypic evaluation of 11 yield-related traits

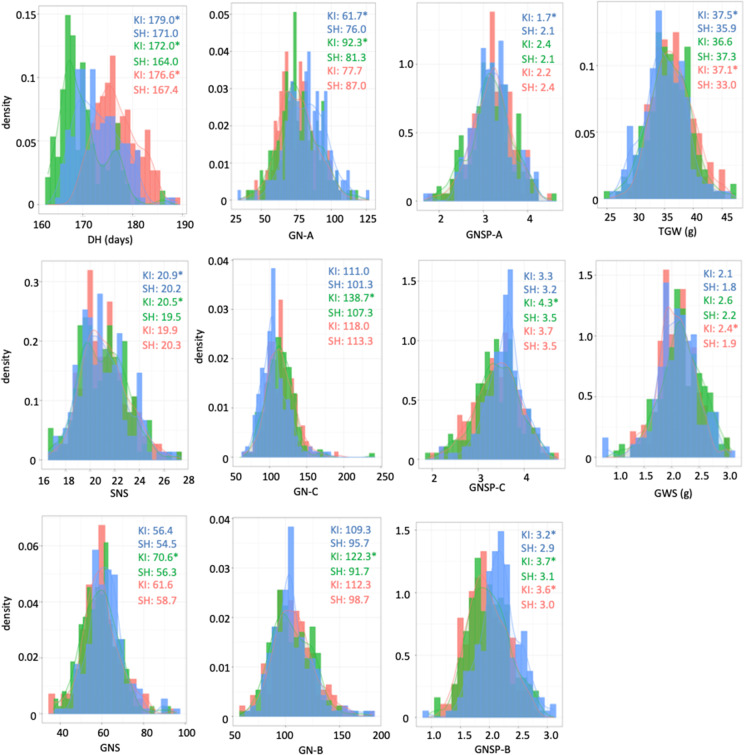
We cultivated Kitahonami and Shunyou plants in the field for three growing seasons and compared 11 yield-related traits and grain number between them. Since the three field blocks hardly significantly differ during the three seasons (p > 0.05, Table S3), we did not correct trait values. Kitahonami headed significantly later than Shunyou during the three seasons (Fig. 1) and tended to have higher SNS, GNS, and TGW, although the difference was not significant in one or two growing seasons. The central and basal parts of the Kitahonami spike contained more, whereas the apical part contained less grains than the Shunyou spike. Since GWS was dependent on both GNS and TGW, the higher GNS and TGW contributed to the higher GWS and also probably to the higher grain yield in Kitahonami.

Fig. 1.

Distributions of 11 traits across growing seasons. Blue, green, and red, 2016–2017, 2017–2018, and 2018–2019 seasons, respectively. *P < 0.05 statistically significant between Kitahonami and Shunyou. DH, days to heading; GN-A, total grain number at apical parts of five spikes; GN-B, total grain number at basal parts of five spikes; GN-C, total grain number at central parts of five spikes; GNS, grain number per spike; GNSP-A, grain number per spikelet at apical parts of spike; GNSP-B, grain number per spikelet at basal parts of spike; GNSP-C, grain number per spikelet at central part of spike; GWS, grain weight per spike; KI, Kitahonami; SH, Shunyou; SNS, spikelet number per spike; TGW, thousand grain weight

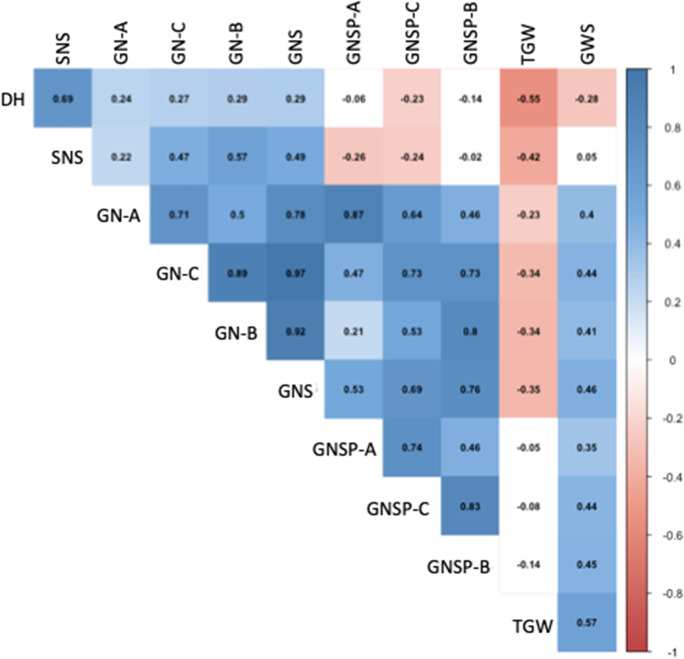
We calculated correlation coefficients of the 11 traits using 188 DHLs for three growing seasons to determine relationships between the 11 traits measured in this study (Figs. 2 and S2). Many traits significantly correlated with DH. Correlations were moderately positive and negative between SNS and DH and between TGW and DH, respectively, for the three growing seasons. The mean values of DH and GWS significantly and negatively correlated only during the 2017–2018 season. The 2017–2018 season showed different correlations between DH and the other traits than in the other seasons. No significant correlation was found between DH and GNS during the 2017–2018 season. The GWS significantly and positively correlated with GNS and TGW, although GNS and TGW significantly and negatively correlated. Unlike GNS, GNSP at each part of the spike did not significantly correlate with TGW.

Fig. 2.

Correlation coefficients of mean values for three growing seasons between 11 traits. Colored boxes, correlation coefficients are significant at 0.05 (Fig. S2 shows correlation coefficients for each growing season). DH, days to heading; GN-A, total grain number at apical parts of five spikes; GN-B, total grain number at basal parts of five spikes; GN-C, total grain number at central parts of five spikes; GNS, grain number per spike; GNSP-A, grain number per spikelet at apical parts of spike; GNSP-B, grain number per spikelet at basal parts of spike; GNSP-C, grain number per spikelet at central part of spike; GWS, grain weight per spike; SNS, spikelet number per spike; TGW, thousand grain weight

Heritability estimates of traits

We calculated marker-based estimates of heritability for the 11 traits (Table 1). Among the yield-related traits, the heritability of SNS and TGW was the highest (0.87). The heritability was higher for GNS (0.71) than DH (0.56), and that of GWS and DH was similar (0.57). The grain number was more heritable at the basal than that at the central and apical parts of the spike.

Table 1.

Marker-based estimates of trait heritability

Trait	va1	ve2	h23	conf.int4
DH	15.19	11.94	0.56	0.46	0.66
SNS	5.37	0.81	0.87	0.83	0.91
GN-A	129.32	105.39	0.55	0.44	0.66
GN-C	246.10	181.64	0.58	0.47	0.68
GN-B	342.39	163.04	0.68	0.58	0.77
GNS	85.39	34.97	0.71	0.62	0.79
GNSP-A	0.07	0.06	0.53	0.43	0.64
GNSP-C	0.13	0.09	0.60	0.50	0.69
GNSP-B	0.13	0.10	0.57	0.46	0.67
TGW	24.65	3.78	0.87	0.82	0.91
GWS	0.09	0.07	0.57	0.46	0.68

¹Restricted maximum likelihood (REML) estimate of the genetic variance

²REML estimate of the residual variance

³h2 plug-in estimate of heritability

⁴95% confidence interval for heritability

QTL analysis of yield-related traits

We analyzed the QTLs of the 11 traits using inclusive composite interval mapping of additive (ICIM-ADD). Table S4 and Table 2 respectively show and summarize all QTLs with significant LOD scores (p < 0.05) and mean values for the three growing seasons.

Table 2.

Summary of QTLs for 11 traits

Chromosome	GNS	GN-A	GN-C	GN-B	SNS	GNSP-A	GNSP-C	GNSP-B	TGW	GWS	DH
1A		1 (1)							4 (2)
1B
1D				1 (1)				1 (1)
2A	4 (2)	3 (2)	5 (2)	5 (2)	6 (3)	4 (1)	4 (1)	3 (1)	4 (1)		1 (1)
2B										3 (3)
2D	2 (1)	2 (1)	1 (1)	3 (1)	4 (1)			1 (1)	2 (1)		4 (1)
3A									3 (1)
3B	1 (1)		1 (1)			1 (1)
3D
4A	1 (1)		1 (1)	4 (2)	2 (1)			1 (1)	7 (2)		4 (1)
4B					3 (2)		1 (1)
4D											1 (1)
5A	1 (1)	4 (1)	1 (1)	3 (1)	1 (1)	4 (2)	1 (1)	1 (1)			1 (1)
5B
5D		2 (1)				2 (1)	2 (1)		4 (1)		2 (2)
6A					2 (2)						4 (1)
6B					2 (1)	2 (2)
6D	1 (1)		4 (1)	1 (1)			2 (1)		4 (2)		4 (2)
7A		4 (2)		5 (3)	4 (1)	5 (2)		2 (1)		1 (1)
7B									1 (1)
7D		1 (1)	1 (1)	1 (1)	2 (1)	1 (1)	1 (1)		4 (1)		5 (2)
total	10 (7)	17 (9)	14 (8)	23 (12)	26 (13)	19 (10)	11 (6)	9 (6)	33 (12)	4 (4)	29 (12)

Numbers in parentheses, number of QTLs with overlapping confidence intervals that are in fact the same QTL

Grain number per spike (GNS)

We identified QTLs for GNS on chromosomes 2A, 2D, 3B, 4A, 5A, and 6D. Seven QTLs were identified when QTLs with overlapping confidence intervals were the same QTL. The phenotypic variation explained (PVE) ranged from 3.8 to 14.3%, and the QTL on chromosome 2A had the highest PVE. No QTLs were detected during all seasons, and the QTL on chromosome 2A was the only significant QTL that was detected in two seasons.

Grain number at the basal, central, and apical parts of spikes (GN-B, GN-C, GN-A)

Compared with GNS, QTLs for total grain number at each part of five spikes were abundant (23, 14, and 17 QTLs for total grain numbers at the basal [GN-B], central [GN-C], and apical [GN-A] parts, respectively). We detected QTLs with the highest PVE for GN-B, GN-C, and GN-A on chromosomes 7A, 2A, and 5A. QTLs on chromosome 2A were detected for GN-B, GN-C, and GN-A. The QTL for GN-C was detected in this region for three growing seasons, whereas those for GN-A and GN-B in this region were found for one or two growing seasons. The QTL for GN-B that was identified on chromosome 7A had the highest PVE among the QTLs for GN-B (10.8% to 17.0%). The Kitahonami allele of this QTL increased GN-C and GN-B (negative additive effect). The QTLs for GN-A identified on chromosomes 5A and 7A were detected for three growing seasons, and the QTL for GN-A on chromosome 5A had the highest PVE (8.8 to 12.9%). These QTLs were named qGN-A-5A and qGN-A-7A, respectively. The Shunyou alleles of the QTLs on chromosomes 5A and 7A were increased in GN-A.

Spikelet number per spike (SNS)

In total, 26 QTLs for SNS were found on chromosomes 2A, 2D, 4A, 4 B, 5A, 6A, 7A, and 7D. Thirteen QTLs with overlapping confidence intervals were in fact the same QTL. The PVE ranged from 2.6 to 21.4% and was the highest (16.3 to 23.1%) on chromosome 2D. The QTLs located on chromosomes 2A, 2D, and 7A were detected during all growing seasons. The Shunyou allele of the QTL on chromosome 2A and the Kitahonami allele of the QTLs on chromosomes 2D and 7A increased SNS. The QTLs located on chromosomes 2A and 2D were discovered in the Ppd-A1 and Ppd-D1 regions, respectively, as the QTL for DH (see below).

Grain number per spikelet (GNSP)

To evaluate grain number without being affected by spikelet numbers, we also analyzed GNSP. Nineteen QTLs for GNSP-A, 11 for GNSP-C, and 14 for GNSP-B were detected on 13 chromosomes. The highest PVE of the QTLs for GNSP-C (24.0 to 43.3%) and GNSP-B (14.9 to 23.0%) was chromosome 2A, which was near GNI-A1. The QTLs for GNSP-C and GNSP-B on chromosome 2A were detected during all three growing seasons. The highest PVE of the QTL for GNSP-A was chromosome 5A (7.5 to 15.3%). The QTLs for GNSP-A on chromosomes 5A and 7A were also detected during all three growing seasons. The Kitahonami allele of the QTLs for GNSP-C and GNSP-B on chromosome 2A increased GNSP, whereas the Kitahonami allele of the QTL for GNSP-A on chromosome 5A decreased GNSP.

Thousand grain weight (TGW)

In total, 33 QTLs for TGW were identified on chromosomes 1A, 2A, 2D, 3A, 4A, 5D, 6D, 7 B, and 7D. Twelve QTLs with overlapping confidence intervals were in fact the same QTL. The PVE ranged from 3.0 to 13.1%, with the highest being for the QTL on chromosome 6D. The QTLs for TGW on chromosomes 1A, 2A, 4A, 5D, 6D, and 7D were identified for the three growing seasons. Three QTLs on chromosomes 4A, 6D, and 7D with a high PVE were named qTGW-4A, qTGW-6D, and qTGW-7D, respectively. The Shunyou allele of qTGW-4A and qTGW-6D and the Kitahonami allele of qTGW-7D increased TGW.

Grain weight per spike (GWS)

Four QTLs for GWS were found on chromosomes 2B and 7A. The PVE of these QTLs ranged from 6.5 to 8.7%, and that located on chromosome 2B was the highest. Although the QTLs located on chromosome 2B were detected during two growing seasons, the positions of the QTLs slightly differed between the growing seasons. In addition, two QTLs with opposing additive effects were located near each other on chromosome 2B during the 2017–2018 season.

Days to heading (DH)

We detected 29 QTLs for DH on chromosomes 2A, 2D, 4A, 4D, 5A, 5D, 6A, 6D, and 7D. Twelve QTLs with overlapping confidence intervals were in fact the same QTL. The PVE ranged 1.6 to 39.1%, and QTLs with the highest PVE were located on chromosomes 2A and 2D, which were discovered in the Ppd-A1 and Ppd-D1 regions, respectively. The QTLs located on chromosomes 2A and 2D exerted positive and negative additive effects, respectively, and those located on chromosomes 2A, 2D, 4A, 6A, 6D, and 7D were detected during all growing seasons.

Quantitative trait loci located near known genes associated with yield

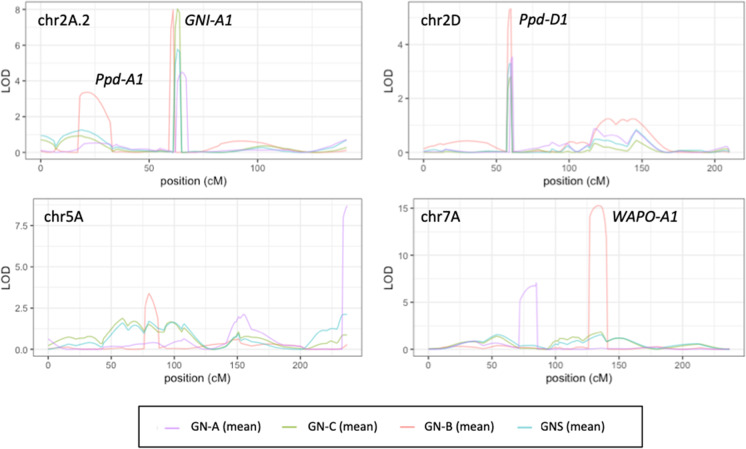
Significant QTLs for various traits were detected in the chromosomal region near genes that are associated with yield (Figs. 3, S3 and S4). The QTLs for grain number were found mainly in the GNI-A1 region. Kitahonami had the 105Y allele of GNI-A1, which produces a higher GNS (Sakuma et al. 2019). The KASP marker, which distinguished the 105Y and 105 N variants of GNI-A1, revealed that Shunyou had the 105 N allele of GNI-A1 (data not shown). The Kitahonami allele of GNI-A1 increased GN in the three parts of the spike, especially in the central part. The QTLs for GNSP-A and GNSP-C were detected in the GNI-A1 region, indicating that the higher grain number in Kitahonami was due to increased GNS by the 105Y allele of GNI-A1. Shunyou and Kitahonami had the WAPO-A1a and WAPO-A1b alleles, respectively (data not shown). The WAPO-A1b allele increased SNS and GN-B but decreased GNSP-A. The QTLs for SNS, GN-B, TGW, and DH were found in the Ppd-A1 and Ppd-D1 regions. Kitahonami and Shunyou had the Ppd-A1a and Ppd-D1a alleles, respectively, which conferred early heading phenotypes.

Fig. 3.

Detection of QTLs for grain number per spike (GNS) and total grain number at apical (GN-A), central (GN-C), and basal (GN-B) parts of five spikes. QTL likelihood curve of LOD score for GNS, GN-A, GN-C, and GN-B on linkage groups of 2A.2, 2D, 5A, and 7A. “Mean” indicate mean values of each trait for three growing seasons (Fig. S3 shows LOD curves of each growing season)

Candidate genes for qGNSP-A-5A and qGNSP-A-7A

We mapped qGNSP-A-5A between snp2947 and tarc0637 (Table S4). We respectively assigned snp2947 and tarc0637 to physical positions of 688.32 and 689.92 Mbp in the CS reference genome sequence (Table S2). However, the range of candidate genes for qGNSP-5A possibly extended to the distal end of chromosome 5A. The 21.45 Mbp region between snp2947 and the distal end contained 302 high-confidence genes (Table S5). We mapped qGNSP-A-7A between snp4426 and wmc83, which were respectively assigned to the physical positions of 84.75 and 89.97 Mbp in the CS reference genome sequence. The 5.22 Mbp region contained 55 high-confidence genes (Table S6), among which TraesCS7A02G136600 was specifically expressed in the spike (Fig. S6). TraesCS7A02G136600 encodes a COBRA-like protein, which is homologous to OsBC1L5 (Os06g0685100).

Pyramiding effect of QTLs for grain number and TGW

To analyze the pyramiding effects of favorable alleles of GN and TGW QTLs on GNS, we compared GNS, TGW, and GWS among lines with different number of favorable alleles for GNS and TGW (Fig. 4). Three GN QTLs (GNI-A1, WAPO-A1, and qGNSP-A-5A) with the highest PVE in the three parts of the spike were selected as the QTLs for grain number. Both GNS and GWS increased as pyramiding favorable alleles for GNS, whereas TGW did not significantly differ among the number of favorable alleles for GNS. More QTLs were found for GN-A than for GN-C and GN-B. Pyramiding of the two favorable alleles for GN-A significantly increased GN-A and GNSP-A (Fig. S5). None of GNSP-C, GNSP-B, and TGW significantly differed among the lines with different number of favorable alleles for GN-A. As the QTLs for TGW, qTGW-6D (tarc1335), qTGW-4A (Wx-B1), and qTGW-7D (tarc0372) with a high PVE were selected. As pyramiding favorable alleles for TGW, TGW increased but GNS decreased. The GWS did not significantly differ among lines with one or more favorable alleles for TGW. We compared GNS, TGW, and GWS among the four characteristic combinations of the two respective QTLs for GNS and TGW to determine their effects (Fig. 5). The TGW did not significantly differ between lines with various allele combinations of GNS and the same allele combination of TGW. In contrast, GNS was higher in lines with a favorable than an unfavorable allele combination of TGW QTLs. The lowest value of GWS among the eight lines with favorable alleles of both GNS and TGW QTLs (2.22 g) was much higher than that of lines with the other allele combinations (1.09–1.78 g).

Fig. 4.

Comparison of grain number per spike (GNS), thousand grain weight (TGW), and grain weight per spike (GWS) among lines with different number of respective favorable alleles for GNS and TGW. Genotypes of GNI-A1, WAPO-A1, and qGNSP-A-5A (snp2947) were used for GNS, and those of qTGW-6D (tarc1335), qTGW-4A (Wx-B1), and qTGW-7D (tarc0372) were used for TGW. Doubled haploid lines without any missing data were used. Top and bottom are 75% and 25% quartiles, respectively. Thick horizontal line, median (50% quartile). Whiskers represent minimum and maximum values excluding outliers. Mean values with same letters do not significantly differ (P > 0.05, Tukey–Kramer HSD tests)

Fig. 5.

Comparison of grain number per spike (GNS), thousand grain weight (TGW), and grain weight per spike (GWS) between allele combinations of QTLs for GNS and TGW. Bold letters indicate favorable allele for each gene or QTL. Top, 75% quartile; bottom, 25% quartile. Thick horizontal line, median (50% quartile). Whiskers represent minimum and maximum values excluding outliers. Mean values with same letters do not significantly differ (P > 0.05, Tukey–Kramer HSD tests). K, Kitahonami; S, Shunyou

Relationships between DH and the other traits

Correlations between DH and the other grain yield traits were significant during the three growing seasons (Figs. 2 and S2). The SNS and TGW were the most positively and negatively correlated with DH, respectively. Five chromosomal regions, including chromosomes 4A, 6D, and 7D, coincided with QTLs for both DH and TGW (Fig. S4). However, these QTLs had different effects on DH and TGW. For example, the QTL for DH on chromosome 2D (Ppd-D1) had the highest PVE, but Ppd-D1 had a low PVE for the TGW QTL (Table S4). Lines with two or three favorable alleles for TGW headed earlier than those with zero or one favorable alleles for TGW (Fig. S7). The SNS also decreased as the QTLs for favorable alleles for TGW increased, although this did not reach statistical significance. The QTLs for DH, the Ppd-A1, Ppd-D1, and qDH-7D (same as qTGW-7D, tarc0372) with a high PVE were selected. The DH and SNS significantly decreased (Fig. S8), and GNS also decreased as alleles conferring early heading accumulated, although the effect on GNS was smaller than that of DH and SNS. In contrast, TGW significantly increased as alleles that confer early heading accumulated.

Discussion

Many QTLs for yield-related traits have been detected in wheat (reviewed in Cao et al. 2020). The GNI-A1 and WAPO-A1 genes have recently been identified as candidates that determine grain number and SNS, respectively (Sakuma et al. 2017; Kuzay et al. 2019; Muqaaddasi et al. 2019). However, the genetic mechanism that determines grain number is largely unknown. Therefore, we analyzed QTLs for grain number and other yield-related traits using DHLs derived from Shunyou and the high-yielding Kitahonami variety. We discuss the genetic mechanism that determines grain number based on our results.

Different genetic mechanisms control grain number in three parts of spike

We detected QTLs for GNS and SNS in the GNI-A1 and WAPO-A1 regions, respectively. Kitahonami had the 105Y allele of GNI-A1 and WAPO-A1b, which elevated GNS and SNS, respectively. The 105Y allele of GNI-A1 increased GNSP mainly at the basal and central parts of the spike (Sakuma et al. 2019). First, we compared grain number and GNSP at the apical, central, and basal parts of the spike between Kitahonami and Shunyou. The GN and GNSP were higher at the central and basal parts of the spike in Kitahonami and in the apical part of Shunyou (Fig. 1). The QTLs for GN in the three parts with the highest LOD and PVE were detected in different chromosomal regions (Figs. 3 and S3, and Table S4). The QTL for GN-C with the highest LOD and PVE was identified in the GNI-A1 region. We found that GNI-A1 was not a major QTL for GN-A and GN-B. The major QTLs for GN-B and GN-A were identified in the WAPO-A1 region and the long arm of chromosome 5A (qGNSP-A-5A), respectively. The major QTLs for GNSP-A and GNSP-C were detected in the same chromosomal region as the QTLs for GN-A and GN-C, respectively, whereas WAPO-A1 was not identified as a QTL for GNSP-B. These findings indicated that the higher GNSP at the apical and central parts of the spike mainly contributed to higher GN-A and GN-C. Unlike the apical and central parts of the spike, spikelet number rather than GNSP affected GN at the basal part of the spike in the DHLs. A GWAS found that the four markers on chromosomes 1A, 5A, 3B, and 7B had the most pronounced effects on grain number in apical and basal spikelets (Guo et al. 2015) and were located on chromosomal regions where we identified QTLs for GNSP-A and GNSP-B. To the best of our knowledge, a QTL for GNS was not found in the qGNSP-A-5A and qGNSP-A-7A regions, implying that these QTLs are detectable only by measuring the grain number in each part of the spike. The qGNSP-A-5A region contains 302 high-confidence genes in the CS reference sequence v1.1 (Table S5). Shunyou and Kitahonami have awned and awnletted varieties, respectively. The QTL for the awn phenotype was identified in the same region as qGNSP-5A (data not shown). The dominant awn inhibitor gene, B1 (TraesCS5A02G542800), which is located on 698.52 Mbp of chromosome 5A (Haung et al. 2020; DeWitt et al. 2020), is probably the candidate gene for the awnletted phenotype in Kitahonami. Misexpression of B1 was considered to be the cause of awn inhibition. The constitutive overexpression of B1 also reduces fertility. On the other hand, Rebetzke et al. (2016) found that awns decreased the number of fertile spikelets and floret fertility; thus, whether B1 is the candidate gene for qGNSP-A-5A is unknown. The qGNSP-A-7A was mapped between 84.74 and 89.97 Mbp in the CS reference genome sequence. The 5.22 Mbp region contained 56 high-confidence genes (Table S6). TraesCS7A02G136600 was expressed specifically in the spike and encoded COBRA-like protein (Fig. S6 and Table S6). TraesCS7A02G136600 shares homology with the OsBC1L genes, which have a range of functions and participate in various developmental processes in rice (Dai et al. 2009). No osbc1l5/osbc1l5 homozygous plants were obtained because of defective male gametophytes. Therefore, the COBRA-like protein possibly contributed to the different fertility in the apical parts of the spike between Shunyou and Kitahonami. Further studies of gene expression and variant detection are needed to identify candidate genes for qGNSP-A-5A and qGNSP-A-7A. To determine whether pyramiding these QTLs increases GNS, we compared the GNS among lines with different number of favorable alleles for this trait (Fig. 5). The accumulation of favorable alleles of QTLs for GN-A, GN-C, and GN-B increased GNS. Lines with favorable alleles of both qGN-A-5A and qGN-A-7A had a higher GN-A and GNSP-A than those with no or one favorable allele (Fig. S4). To summarize these results, the genetic mechanism controlling grain number differed among the three parts of the spike, and the pyramiding of favorable alleles of these QTLs for GN increased GNS.

Unilateral effect of TGW QTLs on GNS can explain negative correlation between grain number and weight

Although TGW and GNS are primary determinants of grain yield, they negatively correlate (Jia et al. 2013; Shukla et al. 2015; Quintero et al. 2018). The present study also found a significant negative correlation between TGW and GNS (− 0.24 to − 0.4; Figs. 1 and S2). Thus, the effects of QTLs for GNS and TGW on each trait are important to understand. An allele of GNI-A1 (Hap6) is associated with a higher grain weight without reducing grain number in tetraploid wheat (Golan et al. 2019). We did not detect QTLs for TGW on the GNI-A1 region (Table S4) and found that the 105Y allele of GNI-A1 increased GNS without changing TGW, which was consistent with the results described by in Sakuma et al. (2019). The other QTLs for grain number, such as WAPO-A1, qGN-A-5A, and qGN-A-7A, did not coincide with the QTLs for TGW. Furthermore, TGW did not significantly change when favorable alleles of these QTLs accumulated (Fig. 5). The heritability of TGW was the highest among the 11 traits examined in this study (0.87), and six regions were identified as the QTLs for TGW during all three growing seasons (Tables 2 and S4). Compared with the other traits, more QTLs were detected during the three growing seasons. Only qTGW-7D coincided with known QTLs for TGW, which has been frequently identified (Mir et al. 2012; Kumar et al. 2016). As favorable alleles of TGW QTLs accumulated, TGW increased, but GNS decreased (Fig. 5). In contrast, TGW did not significantly differ among DHLs with favorable alleles of GNS QTLs. The accumulation of favorable alleles of QTLs for GNS can increase GWS without significantly reducing TGW. The 105Y allele of GNI-A1 can increase grain yield by 10–30% due to increasing GNS (Sakuma et al. 2019). Therefore, grain yield in Kitahonami can be improved by introducing the Shunyou alleles qGN-A-5A and qGN-A-7A. Additionally, the DHLs with favorable alleles of QTLs for both grain number and TGW generally yielded a higher GWS (Fig. 5). Thus, the genotype of these DHLs might be ideal for a higher GWS.

Days to heading is important trait for determining grain number and TGW

Days to heading often correlated with other yield-related traits (Figs. 2 and S2). In particular, negative correlations were closer with TGW (− 0.45 to − 0.55). The QTLs for DH coincided with the QTLs for TGW (Figs. 4 and S5). Among the six QTLs for TGW detected in all growing seasons, five regions were consistent with the QTLs for DH. Accumulation of the favorable alleles of TGW QTLs accelerated heading time, and the accumulation of alleles that confer early heading increased TGW (Figs. S7 and S8). A shortening of DH is generally associated with a longer interval between heading to maturation (Kajimura et al. 2011; Royo et al. 2016). The TGW was predicted to increase in plants with earlier heading due to a longer grain-filling period (Joudi et al. 2014; Baillot et al. 2018). Since QTLs with a high PVE differed between DH and TGW (Table S4), the mechanism of the negative correlation between DH and TGW could not be explained by the grain filling period. The function of the QTLs for TGW should be investigated to elucidate the effect of QTLs for TGW on DH. We found a close positive correlation between DH and SNS (0.62 to 0.69). An increase in SNS was considered to be due to an extended spike development period due to delayed heading time (Shaw et al 2018). Therefore, heading time plays a central role in determining both SNS and TGW. Since a higher SNS and GNS were associated, the trade-off between grain number and TGW might be established indirectly through the timing of heading. However, there was a QTL on chromosome 5D for DH, TGW, and GNS, and the QTL showed additive effects in the same direction for both TGW and GNS. Thus, it was suggested that the QTL could be valuable for breeding to simultaneously increase TGW and GNS despite slight effect on DH. Furthermore, there were some TGW QTL (chromosomes 3A and 4A) that were independent of DH and GNS and some QTLs for grain number such as GNI-A1 and qGNSP-A-5A that were independent of DH and TGW. These QTLs are also useful for breeding to increase either TGW or GNS without significant effects on the other traits. Compared with the grain number and TGW, the correlation between GNSP and DH was either weak or not significant, and GNSP-A did not significantly correlate with DH and TGW in any of the three growing seasons. Thus, the QTLs for GNSP such as GNI-A1 and qGNSP-A-5A are important; they are less susceptible to other traits and can increase grain yield. Heading occurred earlier during the 2017–2018 season than the other two seasons, probably because the temperature was 2–4 °C higher in March and April 2018 than in 2017 and 2019. Kitahonami had a higher GNS but a lower TGW during the 2017–2018 season compared with the other two growing seasons (Fig. 1). On the other hand, Shunyou had a higher TGW during the 2017–2018, than in the other seasons, and the difference in GNS in Shunyou among the three seasons was smaller than that in Kitahonami. The DH negatively correlated with GNSP-C and GNSP-B in the 2017–2018 season, but did not significantly correlate with grain number during the 2017–2018 season. These results indicated that higher temperatures during the reproductive phase might alter the effect of DH on the grain number. However, the tendencies of grain number and GNSP in the DHLs among the three growing seasons did not match those of Shunyou and Kitahonami. Thus, varietal differences in environmental changes might be genotype-dependent.

The present study found that Kitahonami had both the 105Y allele of GNI-A1 and the WAPO-A1b allele, which contributed to a higher GNS. We also identified different genetic mechanisms that control grain number in parts of the spike, and that GNS was determined by a combination of various yield-related QTLs (Fig. S9). The 105Y allele of GNI-A1 is at least essential for a higher grain yield, since it had less of a negative effect on the other yield-related traits investigated herein. Our findings also showed that grain number and GNSP were more variable in Kitahonami than Shunyou during the three growing seasons. Therefore, not only high, but also stable yields should be focused. Elucidating the genetic mechanism determining grain number will facilitate the design of suitable allele combinations of yield-related QTLs for stable high-yielding varieties.

Supplementary Information

Below is the link to the electronic supplementary material.

Abbreviations

DH

Days to heading

DHL

Doubled haploid lines

GN-A

Total grain number at apical parts of five spikes

GN-B

Total grain number at basal parts of five spikes

GN-C

Total grain number at central parts of five spikes

GNS

Grain number per spike

GNSP-A

Grain number per spikelet at apical parts of spike

GNSP-B

Grain number per spikelet at basal parts of spike

GNSP-C

Grain number per spikelet at central part of spike

GWS

Grain weight per spike

QTL

Quantitative trait loci

TGW

Thousand grain weight

SNS

Spikelet number per spike

Author contribution

NM, GI, HK, MT, CO, and MF conducted field evaluations; KN developed the DHLs; NM and GI analyzed data; and NM and GI wrote the manuscript. All authors read the manuscript.

Data availability

Not applicable.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.