A bioinspired 3D-printable flexure joint with cellular mechanical metamaterial architecture for soft robotic hands

Abstract

Compliant flexure joints have been widely used for cable-driven soft robotic hands and grippers due to their safe interaction with humans and objects. This paper presents a soft and compliant revolute flexure joint based on the auxetic cellular mechanical metamaterials with a heterogeneous structure. The heterogeneous architecture of the proposed metamaterial flexure joint (MFJ), which is inspired by the human finger joints, provides mechanically tunable multi-stiffness bending motion and large range of bending angle in comparison to conventional flexure joints. The multi-level variation of the joint stiffness over the range of bending motion can be tuned through the geometrical parameters of the cellular mechanical metamaterial unit cells. The proposed flexure joints are 3D printed with single flexible material in monolithic fashion using a standard benchtop 3D printer. The application of the MFJ is demonstrated in robotic in-hand manipulation and grasping thin and deformable objects such as wires and cables. The results show the capability and advantages of the proposed MFJ in soft robotic grippers and highly functional bionic hands.

1. Introduction

Compliant flexure joints are mechanisms that transfer force, motion, or energy through elastic deformation of their flexure elements, resulting in relative motion between two links[1]. Comparing to traditional joints, the compliant joints are hinge-less and can be fabricated as a monolithic structure, which reduces friction, wear, and backlash in the mechanism and enables compact and lightweight design[2]. In soft robotic applications, the compliant flexure joints are manufactured with soft and flexible materials. The inherent material compliance in addition to compliant flexure joint designs provides safer, cheaper, and simpler mechanisms (and consequently simpler control structures) compared to their rigid counterparts[3]. Due to these advantages, compliant flexure joints, in particular revolute pairs, have been widely used for soft robotic fingers with applications in robotic grippers/hands and anthropomorphic hand prostheses[4-6].

The most commonly used flexure-based compliant revolute joints for soft robotic fingers are single-axis single-flexure notch-type joints with rectangular, right-circular corner-filleted, or circular/elliptical shapes[6-8]. Altering the geometrical parameters of these joints will result in different stiffness values. These designs are fabricated using molding or 3D printing of flexible materials. The continuum and homogeneous structure of these joints makes them easy to design, model, and fabricate. However, this also results in a single constant stiffness for the whole range of rotation, lacking the advantages of the joints with stiffness variation along their range of motion in providing multiple characteristics, such as more stable grasp at high stiffness range, safer interactions and higher conformability at low stiffness range, and high impact absorption capability at quasi-zero stiffness range[9,10].

The conventional flexure joints also have a limited range of motion. To increase their range of motion, they require a large notch in their structure, which will make them prone to undesired out-of-rotational-axis motions. Compensating the out-of-axis motion through increasing the flexure stiffness will result in high stiffness all through the range of motion as they can only provide a constant stiffness for the whole range of rotation.

In this work, we investigated utilizing cellular mechanical metamaterials in design of the compliant flexure joints. Cellular mechanical materials, also known as architectured materials, are a class of artificial materials that can provide different mechanical properties mainly based on their structure/architecture, rather than the constitutive base material characteristics[11,12]. They consist of unit cells distributed in periodic or non-periodic fashion. The geometrical parameters of the unit cells and their spatial distribution/configuration can be altered to achieve the desired mechanical properties or functional behavior. The inherent heterogeneous structure of cellular mechanical metamaterials provides the ability to locally tune the mechanical properties, including stiffness, that cannot be afforded by homogeneous structures[13,14]. Therefore, the compliant flexure joints based on cellular mechanical metamaterials can potentially address the aforementioned limitations of the conventional flexure joints.

The applications of cellular mechanical metamaterials in compliant flexure joints and soft robotic fingers have been investigated in only a limited number of studies. The three-dimensional (3D) unit cells with dual material have been used in a soft robotic gripper[15]; however, the structure of the 3D-designed cellular fingers cannot provide the large range of bending angle, and additionally the bending stiffness of the finger joints has not been investigated. A soft robotic gripper with compliant cell stacks has been used for part handling[16] although the unit cells only considered at the surface of the gripper for the shape adaptation, not in the joint structure. Other soft robotic gripper designs based on mechanical metamaterial have been proposed[17,18], which have a large deformation capacity but only provide a single constant bending stiffness all through the range of motion. The properties of the most common soft flexure joint are summarized in Table 1.

Table 1.

Comparing mechanical properties and performance of the state-of-the-art passive flexure joints and the proposed metamaterial flexure joint

References	Fabrication method	Material	Actuation	Range of bending motion	Variable stiffness over the range of motion?
[5]	3D printing	TPU	Cable driven	~80°	Yes – but not mechanically tunable
[6]	Molding	Polyurethanes (IE90A)	Cable driven	~70°	Yes – but just the torsional stiffness
[8]	3D printing	TPU	Cable driven	90°	No
[15]	3D printing	TPU-PLA	Cable driven	-	No
[18]	3D printing	Flexible photocurable polymers	Cable driven	~45°	No
[25]	Multi-material 3D printing	Elastomer (Agilus30) and Polymer	Shape memory alloy	~90°	-
[26]	3D printing	TPU	Cable driven	-	No
[27]	3D printing	TPU-PLA	Pneumatic driven	100° @60 mm length of joint	No
Our design	3D printing	TPU	Cable driven	95° @30 mm length of joint	Yes

TPU: Thermoplastic polyurethane

In this paper, we propose a revolute flexure joint based on the auxetic cellular mechanical metamaterials with a heterogeneous structure. The heterogeneous structure of the proposed soft, compliant flexure joint enables: (i) Large range of rotation without requiring a large notch in the structure; and (ii) tunable multi-level bending stiffness. The type of unit cells considered in the structure of the joint has auxetic properties, which expand laterally when stretched longitudinally[19]. In addition, the geometrical parameters of these unit cells are different in the inner and outer sides of the joint. These result in large expansion and contraction of the joint under tension and compression forces, respectively, producing large range of joint rotation similar to human finger joint.

The multi-level bending stiffness of the proposed flexure joint is due to the multi-stage internal self-contact of the unit cells, and the interaction between inner and outer sides of the joint, which provides a mechanically tunable joint based on the passive mechanical metamaterials. The desired stiffness behavior can be encoded in the joint structure through changing the geometrical parameters of the unit cells. Therefore, the bending stiffness variation does not require external stimulus similar to field-responsive or active mechanical metamaterials[17,20]; however, the encoded stiffness behavior cannot be altered after fabrication. The capabilities of the proposed metamaterial flexure joints (MFJs) have been demonstrated through applications in soft robotic grasping and manipulation.

2. MFJ design

Here, the design of the proposed flexure-based revolute joint and its mechanical metamaterial architecture have been presented. The overall architecture of the proposed MFJ is inspired by the human finger joints, which have large expansion in the extension (outer) side and large contraction in the flexion (inner) side, as shown in Figure 1A. Three-dimensional model of the proposed flexure joint, as shown in Figure 1B, consists of auxetic re-entrant unit cells in its mechanical metamaterial architecture. While re-entrant type auxetic unit cells are mainly investigated under compression force conditions[12,19] (for energy absorption applications), here we use them for bending dominant situation.

Figure 1.

Metamaterial flexure joint design. (A) Human finger; (B) 3D CAD model; (C) architecture of the auxetic unit cells in the joint structure and geometrical parameters of a single unit cell; (D) FE simulation of the bending behavior of the auxetic unit cell; (E) FE simulation of the joint; (F) 3D-printed joint when force applied through the tendon cable.

Figure 1C shows the 2D model of the MFJ and the tunable geometrical parameters of the joint where w is the length of re-entrant struts, t is the thickness of struts, l is the length of the vertical struts, δ is the thickness of horizontal struts, and θ is the re-entrant angle. The value of θ should be <90° to represent an auxetic behavior[11]. In this architecture, the unit cells of the flexion and extension sides of the joint are decoupled to ensure maximum contraction and expansion in the flexion and extension sides of the joint. The geometrical parameters of the flexion and extension sides of the joint can be different to provide different bending stiffness behaviors. In addition, the number of unit cells in the joint structure varies depending on the values of geometrical parameters.

Figure 1D–F shows the mechanical behavior of a single auxetic-type unit cell and the flexure joint, which consists of multiple unit cells under bending loading through finite element (FE) simulations and experiments. The bending loading is applied through the tendon cable, which results in the expansion and contraction of the re-entrant unit cells in the extension (outer) and flexion (inner) sides of the flexure joint, respectively.

3. Materials and methods

3.1. Material and fabrication

The MFJs were fabricated using 3D printing of flexible filaments with fused deposition modeling 3D printers. The soft and flexible material was thermoplastic polyurethane with shore hardness 87A (eSUN eLastic, Shenzhen eSUN Industrial Co., Ltd). The 3D printer was the FlashForge Dreamer, a commercially available benchtop 3D printer with an open-source software (FlashPrint) for slicing the STL files and preparing the files for 3D printing. The setting considered for the 3D printing includes the extrusion speed of 60 mm/s, travel speed of 80 mm/s, and nozzle temperature of 220°C.

3.2. Bending angle measurement

In order to measure the bending angle of the MFJs when tendon cable force is applied, some markers (black dots) are placed on the top side of the joints, and videos are recorded to extract the position and orientation of the markers. The videos are analyzed using Tracker software, an open-source analysis software for video recordings[21]. The software has a feature of auto-tracking the position of a selected pixel in the video and gets its coordinate over time.

3.3. Force testing

To evaluate the bending stiffness of the joint using cable actuation, the tendon cable is attached to a single-axis force testing machine (Mecmesin Ltd, England). The tendon cable force is measured using the load cell (Mecmesin MultiTest-i Load cell, max 100 N) attached to the force testing machine.

3.4. Actuation and control system

The actuation of soft robotic fingers with MFJs is tendon cable-driven, wrapped around small spools, and connected to the geared DC motors (6V HPCB Micro Metal Gearmotor, Pololu Inc.)[5]. A potentiometer is attached to the shaft of each motor to measure the position of the shaft. All motors are controlled with a custom-designed PCB with microcontroller board, which is based on Atmel 8-bit ATmega2560 and Freescale MC33926 H-bridge motor driver with embedded current sensor.

4. Results and discussion

4.1. Characteristics of the MFJ

Here, the characteristics of the proposed MFJ have been investigated and compared with the conventional flexure joints commonly used in soft robotic fingers.

4.1.1. Multi-stiffness behavior

To compare the stiffness characteristics of the MFJ with conventional flexure joint, a sample notch-type conventional flexure joint with right-circular corner-filleted was fabricated, and its stiffness properties were evaluated, as shown in Figure 2A. The bending stiffness plot of this joint was approximately constant all through the range of the bending motion. As a result, it could be approximated with a single torsional spring with a constant bending stiffness. Altering the geometrical tuning parameters of these joints only changed the constant value of the bending stiffness.

Figure 2.

Comparing stiffness characteristics of: (A) Conventional flexure joint commonly used in soft robotic fingers; (B) the proposed metamaterial flexure joint.

Figure 2B shows a sample MFJ and its stiffness plot. The force vs. bending angle off the joint and its corresponding stiffness plot show three stages of stiffness variation: at stage I, the exerted force through the tendon cable tries to bend the flexion side unit cells and when the cells start bending; at stage II, the re-entrant unit cells are moving inward, resulting in contraction of flexion side unit cells and stretching of extension side unit cells; and finally at stage III, the densification of the flexion side unit cells starts happening, and further stretching of extension side unit cells occurs, which results in higher stiffness at this stage.

The bending and stretch/contraction in the flexion and extension side unit cells of the joint in addition to interaction between them lead to the multi-level stiffness variation of the MFJ, which can be considered a combination of multiple torsional and linear springs. The validation of the proposed spring equivalent model of the MFJ will be proposed in future works.

In the proposed MFJ design, it is assumed that all the unit cells at each flexion and extension sides are the same, but there is no limitation in using unit cells with different geometrical parameters at each side of the joint, whereas the structural integrity of the joint is satisfied[10].

In the MFJ, the geometrical parameters of the unit cells in the flexion and extension sides dictate the stiffness values at each stage of the stiffness variation. Therefore, multi-stiffness behavior of the MFJ can be tuned through altering the geometrical parameters of the unit cells.

4.1.2. Large range of bending motion

The large range of bending motion of the MFJ is mainly due to the auxetic characteristics of the re-entrant unit cells used in its architecture, which is also known as negative Poisson ratio[11]. The structures with auxetic unit cells contract under compression and expand under tension. In the MFJ, the re-entrant auxetic cells enables the large contraction under compression loading and large expansion under tension loading, which results in the large range of bending motion. In addition, the inward contraction of the re-entrant unit cells of the flexion side of the joint and their densification creates a pivot point for the applied force that results in further stretching of the extension side of the joint. Therefore, for the same length of the joint, the maximum range of motion of MFJ is higher than that of conventional flexure joints without the need for large notch as required in the conventional flexure joints (as shown in Figure 2A). The range of the MFJs depends on the geometrical parameters of the constituent unit cells as discussed in the following section.

4.2. The effect of unit cell geometrical parameters on MFJ characteristics

As MFJ architecture consists of unit cells, altering their geometrical parameters will result in different multi-level stiffness variation and range of bending motion. It should be noted that the mechanical property of the base material also provides an extra design freedom of the MFJ. Using different flexible materials for 3D printing can be considered in the case that we want to change the overall stiffness of the flexure joint. In this study, we mainly focused on developing metamaterial structures for the flexure joints that through manipulating the geometrical parameters of the structure, the local mechanical properties of the joint can be altered, which results in the desired characteristics. As shown in Figure 1C, the geometrical parameters of the unit cells include the length of the re-entrant struts (w), the thickness of the re-entrant struts (δ), the thickness of vertical struts (t), the length of the vertical struts (l), and the re-entrant angle (θ). The range of these parameters are constrained with the desired size of the joint, including length (L), width (W), and depth (D), and the geometrical relation between them to ensure that the joint is realizable with the tuning parameters. Therefore, the bending stiffness of the MFJ can be represented as:

Figure 3 represents the effect of the length of the joint (Figure 3A and B), the re-entrant angle (Figure 3C and D), and the thickness of the vertical struts (Figure 3E and F) on the stiffness values at different stages of the bending motion of the MFJ. The joint with L = 25 mm, θ = 60°, and t = 0.5 mm is used in all plots for the sake of comparison, highlighting the effect of different tuning parameters.

Figure 3.

The effect of different geometrical tuning parameters on the bending stiffness (force vs. bending angle) and range of motion of the metamaterial flexure joint. (A and B) the effect of length of the joint (L); (C and D) the effect of angle of re-entrant unit cell (θ); (E and F) the effect of thickness of re-entrant strut (t). The yellow dashed line with L = 25 mm, θ = 60°, and t = 0.5 mm is shown in all plots for the comparison between plots without cluttering.

The force versus bending angle plots of different geometrical parameters of the joint and auxetic unit cells show three linear regions corresponding to three approximately constant stiffness values as shown on the plots with the unit of N/rad. In the first regions, the joint starts deflection, then at the second region, the lower slope plateau region where the struts are bending until they start getting in contact with each other. At the third region, the unit cells are densifying, and unit cells of flexion side of the joint are moving inward and making a pivot point and lever that further displacement of the tendon cable will result in further expansion of the extension side of the joint and large bending angle (even more than 90°). The MFJ can also produce single linear stiffness behavior similar to the conventional flexure joints. Depending on the tuning parameters of the unit cells of the joint, the bending stiffness values of each of these three regions are different. As a result, the bending stiffness can be represented in the following form:

Where , and are corresponding to the stiffness values of the regions I, II and III (as shown in Figure 2B) at the bending angle ranges of [0, α_I], [α_I, α_II], and [α_II, α_III], respectively. This provides a structurally programmable flexure joint for different applications that require variable stiffness at different ranges of the bending angle.

4.3. Encoding motion in the soft robotic finger

The soft robotic fingers consist of multiple MFJ s that can provide different motion trajectory depending on the bending stiffness of the joints. As each MFJ enables multiple tunable stiffness’s at different bending angle ranges, the combination of multiple MFJs provides an ample design space and flexibility for producing a wide range of trajectories in the soft robotic fingers. This also results in a variety of grasping behaviors and versatile kinematic of soft robotic hands not affordable with conventional flexure joints.

Considering the tendon-driven under-actuated robotic finger with n MFJs and single tendon cable, the Cartesian coordination of the fingertip position, (x,y), representing the trajectory of the robotic finger, is as follows:

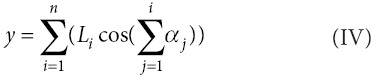
Where L_i and α_j are the length and bending angle of the joint j, respectively, as shown in Figure 1.

When force F is applied on the tendon cable, the displacement of the tendon cable will result in the bending of the joints and depending on the stiffness of the joints, leading to different motion trajectory. Considering the bending stiffness of the joint j as K_j and assuming uniform force along the tendon cable and negligible friction between tendon cable and the joints, the motion trajectory of the fingertip can be represented as:

The bending stiffness’s of the joints, K_j, in turn, is function of the geometrical parameters of the unit cells as discussed in Equation I. As a result, different motion trajectories can be encoded in the structure of the soft robotic finger through tuning the parameters of the MFJs. In addition, because of the multi-stiffness behavior of the MFJs, the motion trajectory of the finger can have different behavior at different ranges on the bending angle of the joints. These characteristics of the MFJs enable encoding of complex motions in the architecture of soft robotic fingers with application in robotic grasping and manipulation.

4.4. Applications of MFJs in robotic grasping and manipulation

Considering the two main characteristics of the MFJs, that is, multi-stiffness behavior and large range of bending motion, in this section, the capability of the MFJs is demonstrated through two applications: in-hand manipulation of a wooden cube with specific trajectory and grasping of linear objects with small diameter.

4.4.1. In-hand manipulation

In-hand manipulation is defined as the ability to reposition or reorient an object with respect to the hand frame[22]. In robotic hands with underactuated fingers, the in-hand manipulation capability of the hand is limited due to the limited number of active joints. In cable-driven soft robotic hands with conventional flexure joints, since the stiffness of the joint is constant, the trajectory of the object manipulation is the same in the whole range of the joint bending motion. In soft robotic hands with MFJs, due to the structurally programmable variable stiffness of the joints, it can perform more complex in-hand manipulation tasks. Since the bending stiffness varies at different range of the bending motion, the object will follow different trajectory at different range of the joint bending angles similar to externally stimulated soft actuators with variable stiffness[23]. To demonstrate this capability of the MFJs, a two-fingered soft robotic hand with conventional and MFJ s is used for in-hand manipulation of a wooden cube.

As shown in Figure 4A and Videoclip S1, in the robotic hand with conventional flexure joints, the joints of both fingers are the same. Therefore, after grasping the wooden cube, it will move in approximately vertical direction. For the robotic hand with MFJs, different architecture of the joints is used in the left and right fingers of the robotic hand in such a way that their stiffness behavior is similar in a specific range of the bending motion and then it will be different. As a result, the trajectory of the object is similar to the fingers with conventional flexure joints (Figure 4A) up to the range that the stiffness values are similar and then it will produce different trajectory due to the variation in stiffness values. For this purpose, we consider the first finger joints with the geometrical parameters of L = 25 mm, t = 0.5 mm, and θ = 60° and the second finger with re-entrant angle is 50°, and all the other parameters are the same. The stiffness behavior of these two joints is shown in Figure 3C where they have similar stiffness at the first 15 degrees of the bending angle and then the joint with re-entrant angle of 50° has higher stiffness. With this architecture of the fingers, as shown in Figure 4B and Videoclip S1, from the time lapse 1 to 6, the trajectory is similar to the robotic hand with conventional flexure joints and then due to the changes in the stiffness of the joints, the trajectory of the wooden cube will change, and the object will move toward the finger with lower stiffness joints. This example shows that more complex motions can be encoded in the robotic grippers with MFJs.

Figure 4.

In-hand manipulation of a wooden block and its trajectory using two-fingered robotic fingers with: (A) conventional flexure joints; (B) metamaterial flexure joints.

4.4.2. Grasping linear objects

The second application focuses on demonstration of the large bending angle of the MFJs through grasping linear objects with small diameters. In robotic community, objects such as ropes, rods, strings, and cables are referred to as linear objects[24]. At present, most of the robotic hands/grippers are using pinch-type grip for grasping and manipulation of the linear objects as they are not able to grasp linear objects with small diameter using power grasp. As a result, a high force pinch grip is required to manipulate the linear objects for performing a task, such as making a knot. Human hand uses power grasp for grasping linear objects (Figure 5A) and due to distributed forces on the objects, low force grasps are sufficient for stable grasping without slipping. This problem is more prominent in soft robotic hands since due to the compliance of the structure, they cannot exert a high level of pinch forces.

Figure 5.

Demonstration of metamaterial flexure joints (MFJs) with large bending angle through grasping linear objects. (A) How human hand grasps linear objects; (B) trajectory of the soft robotic finger with three MFJs with different geometrical parameters; (C) close-up image of a soft robotic finger with large bending angle of the proximal interphalangeal joint grasping a 0.3-mm wire; (D) grasping a fishing line with diameter of 0.6 mm; (E) pulling the blind rope with a diameter of 2 mm; (F) grasping and striping a wire with diameter of 0.3 mm; and (G) holding a rope with 3 mm diameter with a 1-kg weight attached to that.

To demonstrate the advantage of the MFJs in grasping linear objects with small diameter, which requires large bending angle of the finger joint, an anthropomorphic 5-fingered soft robotic hand[5] is fabricated where each finger consists of three MFJs with different tuning parameters. The proximal interphalangeal (PIP) joint of the fingers of the robotic hand has a MFJ with maximum bending angle of 110° similar to human finger. The metacarpophalangeal (MCP) and distal interphalangeal (DIP) joints of these fingers have higher stiffness in comparison to the PIP joint. The resultant trajectory of this architecture of the finger is similar to human hand for grasping linear objects with small diameter, as shown in Figure 5B and 5C.

The performance of the robotic hand in grasping three different linear objects is shown in Figure 5 and Videoclip S2, including a fishing line with diameter of 0.6 mm (Figure 5D), blind rope with diameter of 2 mm (Figure 5E), and also a wire with diameter of 0.3 mm (Figure 5F). Since the stiffness of the joint is nonlinear, the stiffness level is much higher at the end of the range of the bending angle, which results in firm power grasping, and it will not be easily opened because of the external force of grasping the objects. For instance, for pulling the rope with high force, the robotic hand should be able to not only grasp the rope but also hold it with high force. This is demonstrated in Figure 5G where the soft robotic hand can hold a rope with a 1-kg weight attached to that, showing the advantages of MFJs with large bending angle and variable stiffness.

5. Conclusions and future works

This paper presents a heterogeneous architecture of the cellular mechanical metamaterial for flexure-based revolute joints using 2D-designed auxetic unit cells. The proposed architecture enables soft flexure joint with large range of rotation without requiring a large notch in the structure and also provides tunable multi-level bending stiffness behavior. These characteristics of the MFJs enable the design of soft robotic fingers with complex pre-programmed motions and highly functional soft robotic hands for grasping wide range of objects without the need for bulky actuators or complex control systems.

The future work will focus on inverse design of the MFJs to obtain the geometrical parameters of the joints for a desired motion of the fingers. The main challenge in the inverse design is developing a general model of the MFJ. Since developing a theoretical model that is reliable is difficult because of the large deformation and large number of self-contacts in the MFJ, data-driven models can be developed using FE simulations or real-world experiments.

Funding

This project is funded by the Valma Angliss Trust and the University of Melbourne.

Conflict of Interest

The authors have declared that no competing interests exist.

Author Contributions

Conceptualization: Alireza Mohammadi, Elnaz Hajizadeh

Formal analysis: Alireza Mohammadi

Methodology: Alireza Mohammadi, Elnaz Hajizadeh

Supervision: Peter Choong, Denny Oetomo, Ying Tan

Validation: Alireza Mohammadi

Visualization: Alireza Mohammadi

Writing – original draft: Alireza Mohammadi

Writing – review & editing: Alireza Mohammadi, Ying Tan, Denny Oetomo

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data

All relevant data are within the manuscript or supplementary files.