Derivation and Validation of a Simplified Clinical Prediction Rule for Identifying Children at Increased Risk for Clinically Important Traumatic Brain Injuries Following Minor Blunt Head Trauma

Abstract

Objective

To develop a simplified clinical prediction tool for identifying children with clinically important traumatic brain injuries (ciTBIs) after minor blunt head trauma by applying machine learning to the previously reported Pediatric Emergency Care Applied Research Network dataset.

Study design

The deidentified dataset consisted of 43 399 patients <18 years old who presented with blunt head trauma to 1 of 25 pediatric emergency departments between June 2004 and September 2006. We divided the dataset into derivation (training) and validation (testing) subsets; 4 machine learning algorithms were optimized using the training set. Fitted models used the test set to predict ciTBI and these predictions were compared statistically with the a priori (no information) rate.

Results

None of the 4 machine learning models was superior to the no information rate. Children without clinical evidence of a skull fracture and with Glasgow Coma Scale scores of 15 were at the lowest risk for ciTBIs (0.48%; 95% CI 0.42%-0.55%).

Conclusions

Machine learning algorithms were unable to produce a more accurate prediction tool for ciTBI among children with minor blunt head trauma beyond the absence of clinical evidence of skull fractures and having Glasgow Coma Scale scores of 15.

Pediatric blunt head trauma accounts for approximately 52 000 deaths, 275 000 hospital admissions, and more than 650 000 emergency department visits each year in the US.¹ Although cranial computed tomography (CT) remains the standard imaging modality used to diagnose intracranial injury in acute settings,^2,3 radiation-induced malignancy remains an important risk from CT-associated ionizing radiation.4, 5, 6, 7, 8, 9 Children with apparently minor blunt head trauma (ie, those with Glasgow Coma Scale [GCS] scores ≥14) frequently are assessed using CT scans in the US. However, it is rare that neurosurgical intervention is needed in children who are neurologically normal.¹⁰ The concept of CT minimization has been widely studied and is the basis behind the development of clinical prediction rules for intracranial injury in children who have sustained blunt head trauma.¹¹

In 2007, the Pediatric Emergency Care Applied Research Network (PECARN) conducted a study of ∼42 000 children with minor blunt head trauma to develop a clinical prediction rule to identify children at low-risk of clinically important traumatic brain injuries (ciTBIs).¹⁰ Two age-dependent rules were derived: one for children younger than age 2 years and another for those 2 years and older (Table I).

Table I.

PECARN head injury prediction variables

	Age <2 years	Age ≥2 years
1.	GCS <15 or AMS	GCS <15 or AMS
2.	Palpable/suspected skull fracture	Signs of basilar skull fracture
3.	History of LOC ≥5 s	History of any LOC
4.	Severe MOI∗	Severe MOI∗
5.	Acting abnormally per parent	Severe headache
6.	Tempero/parietal/occipital scalp hematoma	History of emesis

AMS, altered mental status; LOC, loss of consciousness; MOI, mechanism of injury.

^∗Severe mechanism defined by motor vehicle crash with patient ejection, death of another passenger, or rollover; pedestrian or bicyclist without helmet struck by a motorized vehicle; fall >3 feet for those <2 years or fall >5 feet for patients ≥2 years; or head struck by a high-impact object.

Although previous studies including but not limited to PECARN have relied on traditional multivariable statistical methods and single recursive computer algorithms,10, 11, 12, 13 more recent research regarding prediction rules has focused on the use of artificial intelligence (AI).14, 15, 16, 17, 18, 19 Machine learning, a subset of AI, is a vital part of the digital revolution, with potential to influence clinical prediction rules and medicine.^20,21 Although a previous study used one machine learning algorithm with the intention of improving on the PECARN ciTBI prediction rules, no study to date has applied multiple algorithms or defined experimental methodologies.²² The objective of this study was to determine whether the application of multiple machine learning algorithms evaluated by an a priori, defined, experimental study design could produce a predictive model of ciTBI in children with blunt head trauma that added information to a no information, majority class predictor.

Methods

With this idea in mind, we trained Logistic Regression, Classification and Regression Tree, Random Forest, and Generalized Boosted Machine algorithms with low-risk subsets of the PECARN head trauma dataset (defined as those with no clinical evidence of skull fracture on initial physical examination and a GCS score of 14 or 15) and statistically compared each model's predictions with the majority outcome to matched hold out test subsets.

This study followed the STROBE (STrengthening the Reporting of OBservational studies in Epidemiology) guidelines for the reporting of observational studies.

The dataset used in this study was compiled by PECARN and included patients ≤18 years of age who presented with head trauma to 1 of 25 network pediatric emergency departments between June 2004 to September 2006. The details of data collection, predictive parameters (features), inclusion/exclusion criteria, and outcome (presence of ciTBI), were previously reported.¹⁰ The deidentified dataset was available to the public and was downloaded from the PECARN Web site (www.pecarn.org).

All data-related operations were performed in the R environment using the RStudio IDE.²³ Datasets were downloaded in .csv format. Number of subjects, data types, missing data, descriptive statistics and configuration of predictive variables, configuration of the response variable, and final selection of predictive variables were performed before graphical and data analysis.24, 25, 26

Missing data were handled in several ways. Children whose outcome (presence or absence of ciTBI) was missing in the original dataset were excluded from the analysis. Features missing in 10% or more of patients were assessed for clinical relevance: features with near-zero variation and general demographic descriptions were dropped. Parental assessment of the child's behavior following the incident was removed because 36% of the responses were missing. Important features were identified by univariable analysis using the χ² test (categorical features) and t test (continuous features) to detect significantly different distributions (P < .05) between children with ciTBI and those without. In those cases in which patients were missing entries for statistically significant features, the missing data points were imputed.²⁷

The final, complete, dataset of patients with GCS scores ≥14 and no clinical evidence of skull fractures (removed because of known high association with ciTBI) was randomly divided 2:1 into derivation (training) and validation (testing) sets.²⁸ The distribution of predictive variables and ciTBI rates in these sets was compared by χ² and t test.

Model Development

General Conditions. All models were constructed using 5-fold cross-validation with the holdout fold used to measure the performance of each model. Comparisons between predicted and actual outcomes were determined from receiver operating characteristic curves with algorithms optimized to maximize the rate for the absence of ciTBI which, by definition, minimized false-positive predictions.

Algorithm Selection. The classical algorithms from the 2 broad classes of machine learning models were selected for this study: parametric and nonparametric. Parametric algorithms make strong assumptions about the shape of the decision boundary. The classical parametric models assume a linear boundary and produce slopes and intercepts. The advantages of these models include simplicity, speed, and the need for less training data than nonparametric models. The accuracy of these models is influenced by collinearity among the predictive features, the number of features included in the model, missing data, and the requirement that the decision boundary must be linear.

Logistic regression was selected because it is the classic parametric classifier.²⁹ This algorithm generates a linear decision boundary by computing slopes for each parameter as well as an intercept. Nonparametric algorithms make no assumption about the structure of the decision boundary. Decision trees are the most widely employed nonparametric models for classification. These models consist of parent nodes (the initial distribution of outcomes), child nodes (the resulting subsets of data after a split), and leaves (the end points where no additional splits occur). Decision trees can be divided into 2 groups: single-decision trees and tree ensembles. Single-decision trees provide one complete tree. These models are visually simple and are not affected by collinearity, missing data, or boundary configuration. Accuracy of single tree models is affected by small variations in datasets, which lead to model instability and the need for strong predictors. The most widely used single tree algorithm is the Classification and Regression Tree (RPART), which provides an optimized, single decision tree.³⁰ This model is tuned by determining the optimum depth of the tree. Ensemble tree methods produce a large number of decision trees. The trees are “polled” and the resulting votes determine the class assignment for an unknown patient. The random forest algorithm produces a large number of trees. The model is tuned by determining how many randomly selected variables are used for determining the split of each node of each tree and how many trees the model will contain.³¹ This algorithm has the same advantages as the single decision tree. In addition, it is not as unstable as a single tree and works well with datasets where strong predictors are lacking. Unlike the random forest algorithm, in which each tree is developed independently of the other trees, the generalized boosted machine is an ensemble tree algorithm in which the misclassified subjects from the previous tree are overweighted in the next successive tree.³² This model has many tuning parameters, including the node size for each tree and the number of trees in the ensemble.

Model Comparisons

The fitted model of each algorithm was used to classify the patients in the validation set. The no information model was defined by the ciTBI rate in the validation set. Classifying those patients predicted to not have ciTBI as the low-risk population, the false-negative rates were compared among the models including the no information model by χ² test. Models significantly different from the no information model, defined by P values <.05, were considered for further evaluation.

Results

Details of the development of the complete dataset are shown in Figure 1. The complete dataset contained 43 399 observations, 125 variables, and 763 patients with ciTBIs; 20 patients were missing outcome data. After we removed those patients with missing outcome data, the prevalence rate of ciTBI in the complete dataset was 1.76%.

Figure 1.

Overview of original dataset and data subsets used in the study.

Patients were grouped by outcome, and missing data were evaluated. At least 10% of those patients with ciTBIs were missing a response to 1 or more of the following clinical variables: acting normally to parent (36%), duration of loss of consciousness (30%), neurologic deficit (22%), history of seizure (19%), amnesia (18%), history of loss of consciousness (17%), headache in the emergency department (15%), history of emesis (14%), and race (10%). Three clinical variables were removed: acting abnormally to parent, duration of loss of consciousness, and race. A bivariate comparison of the rates of occurrence for each of the remaining variables was significantly different between children with and without ciTBIs (Table II). Because removal of patients with missing data reduced the prevalence rate of ciTBI in the resulting dataset to 0.88%, missing values for these variables were imputed by random sampling using the probability distribution for each variable in either the ciTBI present or ciTBI absent groups. For each variable–group dyad, 5 datasets were imputed, assessed for comparability, and pooled into a single complete dataset that was used to replace the missing values. A final list of all the variables used for model development is shown in Table III.

Table II.

Bivariate comparison of clinical variables missing from more than 10% of responses for patients with and without ciTBI^∗

Rates of	ciTBI present (n = 763)	ciTBI absent (n = 42 616)
Amnesia	0.559	0.169
History of emesis	0.332	0.132
Headache in the ED	0.72	0.444
History of LOC	0.639	0.115
Neurologic deficit	0.194	0.0136
History of seizure	0.0984	0.0129

ED, emergency department.

^∗All rates are significantly different (P < .0001 by χ² test).

Table III.

Predictive variables used in model development

GCS score

Injury mechanism

Amnesia of event

History of loss of consciousness

History of seizure

When seizure occurred

Seizure duration

Headache

History of emesis

Intubated during examination

Paralyzed during examination

Pharmacologically sedated during examination

Altered mental status: agitated

Altered mental status: sleepy

Altered mental status: slow to respond

Altered mental status: repetitive questioning in ED

Altered mental status: other signs

Bulging fontanelle

Scalp hematoma

Size of hematoma

Injury above clavicle

Neurologic deficit

Sensory deficit

Cranial nerve deficit

Reflex abnormality

Non-head injury

Suspicion for intoxication

Sex

Observed in ED

Rates of ciTBI in Patients with GCS Scores ≥14

Of the 381 patients with GCS scores ≥14 and clinical evidence of skull fractures, 67 (14.9%) had ciTBIs. Of the 1230 patients with GCS scores of 14 and no clinical evidence of skull fractures, 77 (6.2%) had ciTBIs. Of the 39 876 patients without clinical evidence of skull fractures and GCS scores of 15, 192 (0.48%) had ciTBIs. For those patients without clinical evidence of skull fractures, the rates of ciTBI for the group with GCS scores of 14 and the group with GCS scores of 15 were significantly different (χ² = 604.02, P < .0001). As a result of this difference, patients without clinical evidence of skull fractures and GCS scores of 14 or 15 were modeled separately.

No Clinical Evidence of Skull Fracture and GCS Scores of 14

Derivation and Validation Subsets. To avoid overfitting the predictive models, those patients with no clinical evidence of skull fracture and a GCS score of 14 were randomly divided into a derivation subset, used to train the models, and a validation subset, used to compare the quality of the models. The derivation subset contained 812 patients and the validation subset contained 418 patients. The rate of ciTBI was 6.3% in the derivation subset and 6.2% in the validation subset. There were no significant differences in the rates or mean values of the 18 variables contained in the derivation and validation subsets.

Model Development and Evaluation. The algorithms were trained using the derivation subset and the fitted models were used to predict a low-risk group for ciTBI from the validation subset. The no information model was defined by the majority classifier in the validation subset. The results are shown in Table IV. None of the machine learning models were superior to the no information model.

Table IV.

Comparison of the no information model and machine learning algorithms as predictors of ciTBI in children with no clinical evidence of skull fractures and GCS scores of 14 or 15

Models	GCS score of 14				GCS score of 15
	True negative	False negative	ciTBI rate	P value	True negative	False negative	ciTBI rate	P value
No information	392	26	0.062	1	13 492	65	0.00479	1
Logistic regression	389	26	0.063	1	13 492	65	0.00479	1
Classification and regression tree	389	26	0.063	1	13 492	65	0.00479	1
Random forest	389	26	0.063	1	13 492	65	0.00479	1
Generalized boosted model	392	26	0.062	1	13 492	65	0.00479	1

No Clinical Evidence of Skull Fracture and GCS Scores of 15

Derivation and Validation Subsets. A similar approach was taken with those children who had a GCS score of 15 and no clinical evidence of skull fracture. The randomly assigned derivation subset contained 26 319 patients and the validation subset contained 13 557 patients. The rates of ciTBI in the derivation subset and validation subset were both 0.48%. There were no significant differences in the rates or mean values of the 18 clinical variables contained in the derivation and validation subsets.

Model Development and Evaluation. As with the previous group, algorithms were trained to predict a low-risk group for ciTBI with the derivation subset and were tested using the validation subset. The results are shown in Table IV. None of the machine learning models were superior to the no information model.

GCS Score as a Predictor of ciTBI

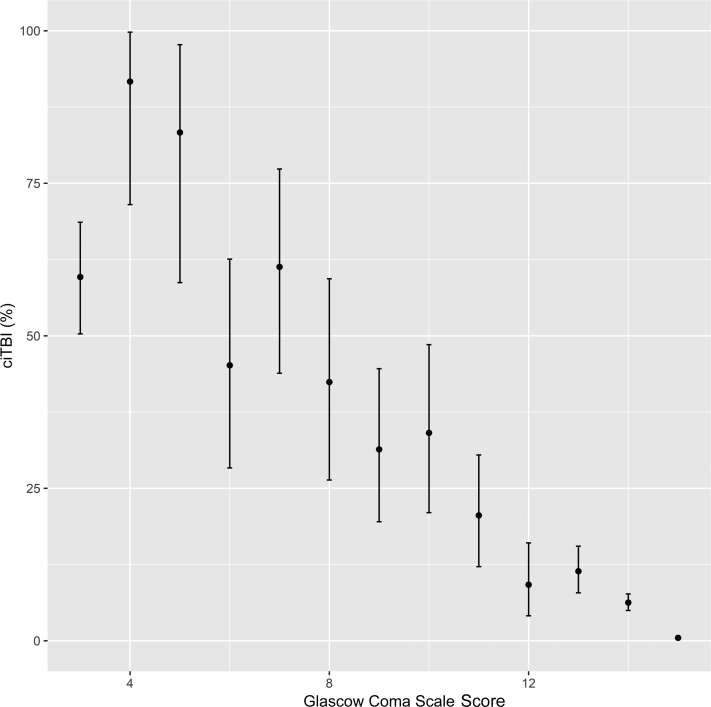
None of the features listed in Table III produced a model that surpassed the GCS score as a predictor of ciTBI in this population of children with minor blunt head trauma and no clinical evidence of skull fracture. The removal of all patients with clinically evident skull fractures produced a subset of 41 852 patients, 486 (1.2%) of whom had ciTBIs. The distribution of patients by GCS scores, the ciTBI rates, the associated CIs, and the strong inverse relationship between GCS and ciTBI are shown in Figure 2. For those patients without clinical evidence of skull fractures and GCS scores of 15, the rate of ciTBI was 0.48% (95% CI 0.42%-0.55%). Using these criteria, 39 876 children (91.9%) of those patients in the PECARN dataset with known outcomes were classified as low-risk.

Figure 2.

Relationship between ciTBI rates and GCS scores in 41 852 children with blunt head trauma and no clinical evidence of skull fracture.

Discussion

In this study, we were unable to produce a machine learning model that was superior to a no information model based on the absence of clinically evident skull fracture on physical examination and a GCS score of 14 or 15. Previous studies have reported low-risk predictive models for ciTBI using the PECARN head injury data and single classification tree algorithms.^10,22 Unlike the current study, each of the previous studies explored the use of only a single modeling technique. The original study used the greedy algorithm of Breiman et al, a top-down method that optimizes one node at a time, to develop a single decision tree.³³ Bertsmias and Dunn trained a single-decision tree using an algorithm that fits all the nodes simultaneously.³⁴ Although both studies used sensitivity and specificity as measures of model efficiency, neither compared overall false-negative predicted rates with the no information rate of ciTBI or calculated the area under receiver operating characteristic curves.

The present study treated all children with GCS scores ≤13 or clinical evidence of a skull fracture as high-risk. Several features make the current study unique: patients with GCS scores of 14 and 15 were treated as separate groups; 4 different machine learning algorithms, including the original single-tree model, were tested; and the predicted ciTBI rates in the low-risk groups of each model were compared with the no information rate using the validation set. By these methods, no algorithm produced a superior model to the clinical evidence of skull fracture/GCS score alone. When the GCS score was used as the only predictor, the predicted ciTBI rate in the GCS score of 14 group without clinical evidence of skull fracture was significantly greater than the rate in children with GCS scores of 15 (6.26% vs 0.48%, P < .001). Moreover, >90% of the children included in the entire dataset fell into the low-risk category defined as those children without clinical evidence of a skull fracture and a GCS score of 15.

As tree-based algorithms were used in the previous studies, the fitted models produced multiple terminal nodes with differing predicted rates of ciTBI. Many of the nodes with the lowest rates of ciTBI contained <0.1% of the sample and were derived from nodal splits of <1% of the total sample, limiting the utility of the model.¹⁰ Because the area under the receiver operating characteristic curve was not calculated for either model, overall performance is difficult to compare. The current study identifies the risk of ciTBI in all children, regardless of GCS score, with clinical evidence of skull fractures (17.6%; 95% CI 13.9%-21.6%) and it identifies a low-risk group with GCS scores of 15 and no clinical evidence of skull fractures (0.48%, 95% CI 0.42%-0.55%).

All predictive models are subject to 2 major limitations. Overfitting occurs when the model is overly complex and predicts the derivation data nearly perfectly. Overfit models perform poorly when given new data. The risk of overfitting can be reduced by cross-validation during training and by holding out a validation set for the final determination of model error. Both techniques were employed in the present study.

The second limitation of predictive models is generalizability. Applying models in a clinical situation implies that new patients resemble the sample group and that the clinical factors of new patients would be identically distributed as the predictors in the derivation set. This second requirement becomes increasingly hard to fulfill as the number of predictors increases and as the interobserver error increases for subjectively based predictors. The model presented here relies on 2 predictors: clinical evidence of skull fractures and GCS score. Although both factors are subject to interobserver differences among clinicians, at least one study suggests that there is a high level of interobserver agreement of clinical variables among children with blunt head trauma.³⁵

In conclusion, within a population of children with blunt head trauma seen in pediatric emergency departments, those without clinical evidence of skull fractures and with GCS scores of 15 were at low-risk for ciTBI. The rate is sufficiently low that routine imaging may be avoided after a period of observation, if access to follow-up and other clinical factors support this approach. Although AI research and machine learning algorithms have the potential to transform many aspects of medicine, the resulting models are only as good as the data inputs. Future studies need to surpass statistically the false-negative rates of ciTBI achieved with the predictive variables of a normal GCS score and no clinical evidence of skull fracture, as a rule-based predictive model.