Fitting stochastic epidemic models to gene genealogies using linear noise approximation

Abstract

Phylodynamics is a set of population genetics tools that aim at reconstructing demographic history of a population based on molecular sequences of individuals sampled from the population of interest. One important task in phylodynamics is to estimate changes in (effective) population size. When applied to infectious disease sequences such estimation of population size trajectories can provide information about changes in the number of infections. To model changes in the number of infected individuals, current phylodynamic methods use non-parametric approaches (e.g., Bayesian curve-fitting based on change-point models or Gaussian process priors), parametric approaches (e.g., based on differential equations), and stochastic modeling in conjunction with likelihood-free Bayesian methods. The first class of methods yields results that are hard to interpret epidemiologically. The second class of methods provides estimates of important epidemiological parameters, such as infection and removal/recovery rates, but ignores variation in the dynamics of infectious disease spread. The third class of methods is the most advantageous statistically, but relies on computationally intensive particle filtering techniques that limits its applications. We propose a Bayesian model that combines phylodynamic inference and stochastic epidemic models, and achieves computational tractability by using a linear noise approximation (LNA) — a technique that allows us to approximate probability densities of stochastic epidemic model trajectories. LNA opens the door for using modern Markov chain Monte Carlo tools to approximate the joint posterior distribution of the disease transmission parameters and of high dimensional vectors describing unobserved changes in the stochastic epidemic model compartment sizes (e.g., numbers of infectious and susceptible individuals). In a simulation study, we show that our method can successfully recover parameters of stochastic epidemic models. We apply our estimation technique to Ebola genealogies estimated using viral genetic data from the 2014 epidemic in Sierra Leone and Liberia.

1. Introduction

Phylodynamics is an area at the intersection of phylogenetics and population genetics that studies how epidemiological, immunological, and evolutionary processes affect viral genealogies/phylogenies constructed based on molecular sequences sampled from the population of interest (Grenfell et al., 2004; Volz, Koelle and Bedford, 2013). Phylodynamics is especially useful in infectious disease modeling because genetic data provide a source of information that is complementary to the traditional disease case count data. Here we are interested in inferring parameters governing infectious disease dynamics from the genealogy/phylogeny estimated from infectious disease agent molecular sequences collected during the disease outbreak. Working in a Bayesian framework, we develop an efficient Markov chain Monte Carlo (MCMC) algorithm that allows us to work with stochastic models of infectious disease dynamics, properly accounting for stochastic nature of the dynamics.

Infectious disease phylodynamics methods handle densely and sparsely sampled outbreaks differently (but see (Smith, Ionides and King, 2017; Vaughan et al., 2019) for potentially universal methods). In a densely sampled outbreak scenario, it is possible to simultaneously infer infectious disease dynamics parameters and a transmission network (Ypma, van Ballegooijen and Wallinga, 2013; Jombart et al., 2014; Klinkenberg et al., 2017). When an outbreak is sampled sparsely, a setting we are interested in this paper, it is impossible to determine who infected whom, so additional modeling is needed to connect sampled hosts to the unobserved population dynamics. Currently, learning about population-level infectious disease dynamics from a sparse sample of molecular sequences can be accomplished using three general strategies. The first strategy relies on the coalescent theory — a set of population genetics tools that specify probability models for genealogies relating individuals randomly sampled from the population of interest (Kingman, 1982; Griffiths and Tavaré, 1994; Donnelly and Tavare, 1995). Using a subset of these models (Griffiths and Tavaré, 1994), it is possible to estimate changes in effective population size — the number of breeding individuals in an idealized population that evolves according to a Wright-Fisher model (Wright, 1931). Such reconstruction can be done assuming parametric (Kuhner, Yamato and Felsenstein, 1998; Drummond et al., 2002) or nonparametric (Drummond et al., 2002, 2005; Minin, Bloomquist and Suchard, 2008; Palacios and Minin, 2013; Gill et al., 2013) functional forms of the effective population size trajectory. In the context of infectious disease phylodynamics, nonparametric inference is the norm and the estimated effective population size is often interpreted as the effective number of infections or the effective number of infectious individuals. However, reconstructed effective population size trajectories are not easy to interpret and estimation of parameters of disease dynamics is difficult to accomplish if one wishes to maintain statistical rigor (Pybus et al., 2001; Frost and Volz, 2010).

Another way to learn about infectious disease dynamics from molecular sequences is to model explicitly events that occur during the infectious disease spread and to link these events to the genealogy/phylogeny of sampled individuals using birth-death processes. For example, a Susceptible-Infectious-Removed (SIR) model includes two possible events: infections and removals (e.g., recoveries and deaths), represented by births and deaths in the corresponding birth-death model (Stadler et al., 2013; Kühnert et al., 2014). Other SIR-like models (e.g., SI and SIS models) differ by the number and types of the events that are needed to accurately describe natural history of the infectious disease (Leventhal et al., 2013).

Structured coalescent models provide the third strategy of inferring parameters governing spread of an infectious disease (Volz et al., 2009; Volz, 2012; Dearlove and Wilson, 2013). These models assume infectious disease agent genetic data have been obtained from a random sample of infected individuals, allowing for serial sampling over time. Although similar to the birth-death modeling framework, the structured coalescent models have two advantages. First, one does not have to keep track, analytically or computationally, of extinct and not sampled genetic lineages. Second, the density of the genealogy can be obtained given the population level information about status of individuals: for example, in the SIR model it is sufficient to know the numbers of susceptible, $\left(S\right(t\left)\right)$, infectious, $\left(I\right(t\left)\right)$, and recovered, $\left(R\right(t\left)\right)$, individuals at each time point $t$. The second advantage comes with two caveats: 1) such densities can be obtained only approximately and 2) evaluating densities of genealogies is not straightforward and involves numerical solutions of differential equations. Even in cases when these caveats are manageable, the density of the assumed stochastic epidemic model population trajectory remains computationally intractable. One way around this intractability assumes a deterministic model of infectious disease dynamics (Volz et al., 2009; Volz, 2012; Volz and Pond, 2014), which potentially leads to overconfidence in estimation of model parameters. Particle filter MCMC offers another solution (Rasmussen, Ratmann and Koelle, 2011; Rasmussen, Volz and Koelle, 2014).

In this paper, we develop methods that allow us to bypass particle filter MCMC with the help of a linear noise approximation (LNA). LNA is a low order correction of the deterministic ordinary differential equation describing the asymptotic mean trajectories of compartmental models of population dynamics defined as Markov jump processes (e.g., chemical reaction models and SIR-like models of infectious disease dynamics) (Kurtz, 1970, 1971; Van Kampen and Reinhardt, 1983). LNA can also be viewed as a first order Taylor approximation of Markov population dynamics models represented by stochastic differential equations (Giagos, 2010; Wallace, 2010). A key feature of the LNA method is that it approximates the transition density of a stochastic population model with a Gaussian density (Komorowski et al., 2009).

Inspired by recent applications of LNA to analysis of Google Flu Trends data (Fearnhead, Giagos and Sherlock, 2014) and disease case counts (Buckingham-Jeffery, Isham and House, 2018), we develop a Bayesian framework that combines LNA for stochastic models of infectious disease dynamics with structured coalescent models for genealogies of infectious disease agent genetic samples. Our approach yields a latent Gaussian Markov model that closely resembles a Gaussian state-space model. We use this resemblance to develop an efficient MCMC algorithm that combines high dimensional elliptical slice sampler updates (Murray, Adams and MacKay, 2010) with low dimensional Metropolis-Hastings (MH) moves. Using simulations, we demonstrate that this algorithm can handle reasonably complex models, including an SIR model with a time-varying infection rate. We apply this SIR model to a recent Ebola outbreak in West Africa. Our analysis of data from Liberia and Sierra Leone illuminates significant changes in the Ebola infection rate over time, likely caused by the public health response measures and increased awareness of the outbreak in the population.

2. Methodology

2.1. Genealogy as data

We start with $n$ infectious disease agent molecular sequences obtained from infected individuals sampled uniformly at random from the total infected population. Further, we assume that a phylogenetic tree, or genealogy, g relating these sequences has been estimated in such a way that the tree branch lengths respect the known sequence sampling times. Such estimation can be performed with, for example, BEAST — a software package for Bayesian phylogenetic inference (Suchard et al., 2018). The genealogy is represented by a tree structure with its nodes containing two sources of temporal information: coalescent and sampling times. The coalescent times correspond to the internal nodes of the tree, which are defined as the times at which two lineages in the tree are merged into a common ancestor. The sampling times, corresponding to the tips of the tree, are the times at which molecular sequences were sampled. Note that sampling times are observed directly, while coalescent times are estimated from molecular sequences during phylogenetic reconstruction.

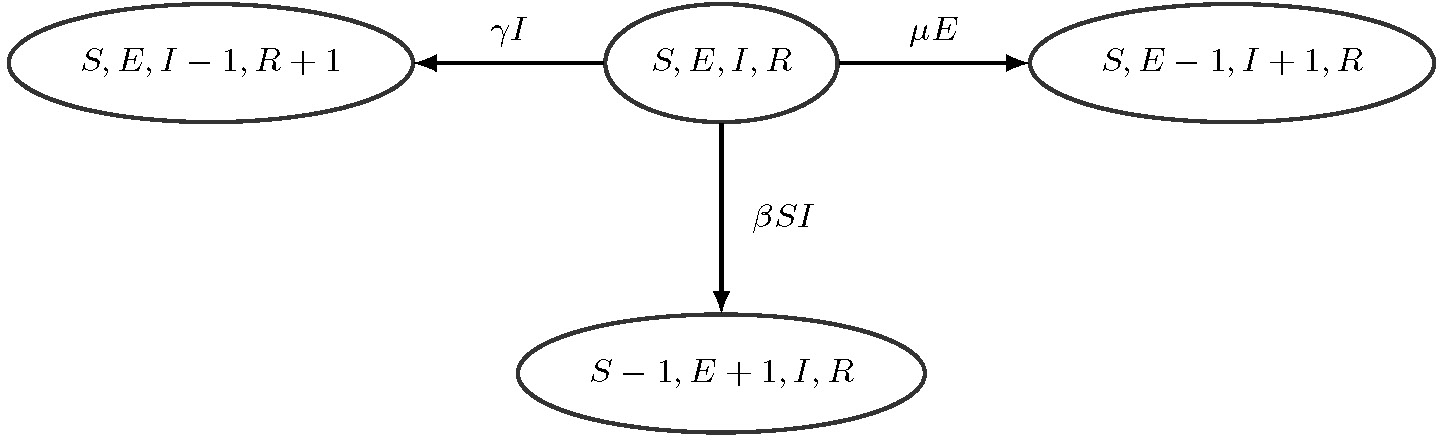
To perform inference about infectious disease dynamics using the above genealogy we need a probability model that relates the genealogy and infectious disease dynamics model parameters. We assume that the infectious disease is spreading through the population according to the SIR model — a canonical compartmental model that at each time point $t$ tracks the number of susceptible individuals $S\left(t\right)$, number of infected/infectious individuals $I\left(t\right)$, and number of removed individuals $R\left(t\right)$ (Bailey, 1975; Anderson and May, 1992). We assume that the population is closed so $S\left(t\right)+I\left(t\right)+R\left(t\right)=N$ for all times $t$, where $N$ is the population size that we assume to be known. This constraint implies that vector $\mathbf{X}\left(t\right)=\left(S\right(t),I(t\left)\right)$ is sufficient to keep track of the population state at time $t$. We follow common practice and model $\mathbf{X}\left(t\right)$ as a Markov jump process (MJP) with allowable instantaneous jumps shown in Figure 1 (O’Neill and Roberts, 1999). The assumed MJP process $\mathbf{X}\left(t\right)$ is inhomogeneous, because we allow the infection rate $\beta \left(t\right)$ and removal rate $\gamma \left(t\right)$ to be time-varying.

FIGURE 1.

SIR Markov jump process. From the current state with the counts S, I, R, the population can transition to state $S-1$, $I+1,R$ (an infection event) with rate $\beta (t)SI$ or to state $S$, $I-1,R+1$ (a removal event) with rate $\gamma (t)I$. No other instantaneous transitions are allowed.

The structured coalescent models assume that only coalescent times ${c_1<c}_2<\cdots <c_{n-1}$ provide information about the population dynamics. These times are modeled as jumps of an inhomogeneous pure death process with rate $\lambda \left(t\right)$, where each “death” event corresponds to coalescence of two lineages and $\lambda \left(t\right)$ is called a coalescent rate. Then the density of the genealogy, which serves as a likelihood in our work, is written as

$$\mathrm{P}\mathrm{r}(\mathbf{g})\propto \prod _{k=2}^n \lambda \left(c_{k-1}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\int }_{c_{k-1}}^{c_k} \lambda (\tau )\mathrm{d}\tau \right),$$

where $c_n$ denotes the most recent sequence sampling time. The dependence of coalescent rate on the assumed population dynamics can be complicated and mathematically intractable, but luckily approximations exist for some specific cases. For the SIR model the approximate coalescent rate can be obtained via the following formula:

$$\lambda (t)=\lambda (l(t),\beta (t),\mathbf{X}(t))=\left(\begin{array}{c}l(t)\\ 2\end{array}\right)\frac{2\beta (t)S(t)}{I(t)},$$ (1)

where $l(t)$ is the number of lineages present at time $t$ (Rasmussen, Ratmann and Koelle, 2011; Volz, Koelle and Bedford, 2013). The coalescent rate in the SIR model can be interpreted as the rate of infection events between sampled lineages present at time $t:\lambda (t)\approx \left(\begin{array}{c}l(t)\\ 2\end{array}\right)/\left(\begin{array}{c}I(t)\\ 2\end{array}\right)\cdot \beta (t)S(t)I(t)$, where $\beta (t)S(t)I(t)$ is the total infection rate in the population and $\left(\begin{array}{c}l(t)\\ 2\end{array}\right)/\left(\begin{array}{c}I(t)\\ 2\end{array}\right)$ corresponds to the probability that the infection occurs between lineages present at time $t$. Note that when the number of susceptibles is not changing significantly relative to the total population size (i.e., $S(t)\approx N$) and infection rate is constant (i.e., $\beta (t)=\beta$), the structured coalescent reduces to the classical Kingman’s coalescent, where we interpret $I(t)/(2\beta N)$ as the effective population size trajectory (Kingman, 1982). It is possible to find approximate coalescence rate for general compartmental models, but closed form expressions exist only for a few models with a low number of compartments (e.g., SI, SIR) (Volz et al., 2009; Volz, 2012; Dearlove and Wilson, 2013).

Since we allow sequences to be sampled at different times ${s_1<s_2<\cdots <s}_m=c_n$, some inter-coalescent times are censored. To deal with this censoring algebraically, each inter-coalesecent interval $\left[c_{k-1},c_k\right)$ is partitioned by the sampling events into $i_k$ sub-intervals: ${ℐ}_{0,k},\dots ,{ℐ}_{i_k-1,k}$. The intervals that start with a coalescent event are defined as ${ℐ}_{0,k}=\left[c_{k-1},\mathrm{m}\mathrm{i}\mathrm{n}\left\{c_k,s_j\right\}\right)$, for $s_j>c_{k-1}$ and $k=2,\dots ,n$. Let the number of lineages in each interval ${ℐ}_{i,k}$ be $l_{i,k}$. Then the number of lineages at each time point $t$ can be written as $l(t)={\sum }_{k=2}^n {\sum }_{i=0}^{i_{k-1}} 1_{\left\{t\in I_{i,k}\right\}}{l}_{i,k}$. If the interval ${ℐ}_{i,k}$ ends with a coalescent time, the number of lineages in the next interval will be decreased by 1. If the interval ends with a sampling event $s_i$, then the number of lineages in the next interval is increased by $n_i$ — the number of sequences sampled at time $s_i$. Figure 2.1 shows an example of a genealogy with labeled coalescent times, sampling times, number of lineages, and the corresponding intervals.

FIGURE 2.

Example of a genealogy. Black solid lines show the genealogy structure. The colescent times $c_1,\dots ,c_4$ and sampling times $s_1,\dots ,s_4$ are labeled with vertical dashed lines. The number of lineages $l_{i,k}$ is given in each intervals ${ℐ}_{i,k}$.

We are now ready to connect the SIR model and a genealogy with serially sampled tips with the help of a structured coalescent density/likelihood. First we discretize the time interval between the time to the most recent common ancestor $c_1$ (time corresponding to the root of the tree) and the most recent sampling time $s_m$ using a regular grid $t_0<t_1<\cdots <t_T$ ($t_0<c_1$ and $t_T>s_m$) Using this grid, we discretize the latent epidemic trajectory by assuming that $\mathbf{X}(t)={\sum }_{j=1}^T {\mathbf{X}}_{j-1}{\mathbf{1}}_{\left[t_{j-1},t_j\right)}(t)$, where ${\mathbf{X}}_j=\left(S_j,I_j\right)$ is a column vector. Similarly, we discretize the infectious disease dynamics parameter vector trajectory $\mathbf{\theta }(t)=(\beta (t),\gamma (t))$ so that $\mathbf{\theta }(t)={\sum }_{j=1}^T {\mathbf{\theta }}_{j-1}{\mathbf{1}}_{\left[t_{j-1},t_j\right)}(t)$, where ${\mathbf{\theta }}_j=\left({\beta }_j,{\gamma }_j\right)$ is also a column vector. We collect latent variables ${\mathbf{X}}_j\mathrm{s}$ and parameters ${\mathbf{\theta }}_j\mathrm{s}$ into matrices ${\mathbf{X}}_{0:T}$ and ${\mathbf{\theta }}_{0:T}$ respectively. The SIR structured coalescent density/likelihood then becomes

$$\begin{array}{l}\text{Pr}(\mathbf{g}\mid {\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T})\propto \prod _{k=2}^n(\begin{array}{c}l(c_{k-1})\\ 2\end{array})\frac{2\beta (c_{k-1})S(c_{k-1})}{I(c_{k-1})}\hfill \\ \text{exp}\left(-\sum _{i=0}^{i_k-1}\underset{{ℐ}_{i,k}}{\int }\left(\begin{array}{c}{l}_{i,k}\\ 2\end{array}\right)\frac{2\beta (\tau )S(\tau )}{I(\tau )}\text{d}\tau \right).\hfill \end{array}$$ (2)

Since $S(t)$, $I(t)$, and $\beta (t)$ are piecewise constant functions, the integrals in the above formula are readily available in closed form and are fast to compute.

2.2. Bayesian data augmentation

2.2.1. Posterior distribution

Given genealogy $\mathbf{g}$, our goal is to infer the latent SIR population dynamic ${\mathbf{X}}_{0:T}$ and rate parameters ${\mathit{\theta }}_{0:T}$ over time grid $t_0<t_1<\cdots <t_T$. Let $\mathrm{P}\mathrm{r}\left({\mathbf{X}}_0\right)$ and $\mathrm{P}\mathrm{r}\left({\mathit{\theta }}_{0:T}\right)$ denote the prior densities for the initial compartment states and the SIR parameters respectively. The posterior distribution for the population trajectory ${\mathbf{X}}_{0:T}$ and parameters ${\mathit{\theta }}_{0:T}$ given observed genealogy $\mathbf{g}$ is

$$\begin{array}{l}\mathrm{P}\mathrm{r}\left({\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T}\mid \mathbf{g}\right)\propto \mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T}\right)\mathrm{P}\mathrm{r}\left({\mathbf{X}}_{1:T}\mid {\mathbf{X}}_0,{\mathit{\theta }}_{0:T}\right)\\ \mathrm{Pr}\left({\mathit{\theta }}_{0:T}\right)\mathrm{Pr}\left({\mathbf{X}}_0\right),\end{array}$$ (3)

where $\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T}\right)$ is the structured coalescent likelihood introduced in Section 2.1 and $\mathrm{P}\mathrm{r}\left({\mathbf{X}}_{1:T}\mid {\mathbf{X}}_0,{\mathit{\theta }}_{0:T}\right)$ is the likelihood function for discrete observations of trajectory ${\mathbf{X}}_{1:T}$ given the initial value ${\mathbf{X}}_0$:

$$\mathrm{Pr}({\mathbf{X}}_{1:T}\mid {\mathbf{X}}_0,{\theta }_{0:T})=\prod _{i=1}^T\mathrm{Pr}({\mathbf{X}}_i\mid {\mathbf{X}}_{i-1},{\mathit{\theta }}_{i-1}),$$ (4)

where the factorization comes from the assumed Markov property of the disease dynamics. However, the SIR transition density $\mathrm{P}\mathrm{r}\left({\mathbf{X}}_i\mid {\mathbf{X}}_{i-1},{\mathit{\theta }}_{i-1}\right)$ becomes intractable as population size $N$ grows large, making it difficult to perform likelihood-based inference for outbreaks in large populations.

2.2.2. Linear noise approximation

To furnish a feasible computation strategy for large populations, we use a linear noise approximation (LNA) method, in which the computationally intractable transition probability $\mathrm{P}\mathrm{r}\left({\mathbf{X}}_i\mid {\mathbf{X}}_{i-1},{\mathit{\theta }}_{i-1}\right)$ is approximated using a closed form Gaussian transition density (Kurtz, 1970, 1971; Komorowski et al., 2009).

The LNA method replaces the MJP discrete state space with a continuous state space of $\mathbf{X}(t)$ to approximate the counts of at time $t$, under the following constraints: $S(t)>0,I(t)>0$ and $S(t)+I(t)\le N$. To briefly explain how this approximation is obtained, we will need additional notation.

The SIR MJP instantaneous transitions, depicted in Figure 1, are encoded in an effect matrix

$$\mathbf{A}=\left(\begin{array}{cc}\text{susceptible}& \text{infected}\\ -1& 1\\ 0& -1\end{array}\right)\underset{\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{v}\mathrm{a}\mathrm{l}.}{\mathrm{i}\mathrm{n}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$$ (5)

Each row in matrix (5) represents a type of transition event and each column corresponds to a change in the susceptible and infected populations. Next, we define a rate vector $\mathbf{h}$ and a rate matrix $\mathbf{H}$:

$$\mathbf{h}(\mathbf{X}(t),\mathit{\theta }(t))=\left(\begin{array}{c}\beta (t)S(t)I(t)\\ \gamma (t)I(t)\end{array}\right),\mathbf{H}=\left(\begin{array}{cc}\beta (t)S(t)I(t)& 0\\ 0& \gamma (t)I(t)\end{array}\right).$$ (6)

The above notation, as well as subsequent developments based on it, can be generalized to other epidemic models and, more generally, to a large class of density dependent stochastic processes, such as chemical reaction and gene regulation models (Wilkinson, 2011). See Section A-1 in the Appendix for more details on this generalization.

Consider a transition from ${\mathbf{X}}_{i-1}$ at time $t_{i-1}$ to ${\mathbf{X}}_i$ at $t_i$. Recall that we assume that the SIR rates $\mathit{\theta }(t)$ take constant values ${\mathit{\theta }}_{i-1}$ in $\left[t_{i-1},t_i\right)$. The LNA represents the value of the next state ${\mathbf{X}}_i$ as ${\mathbf{X}}_i=\mathit{\eta }\left(t_i\right)+\mathbf{M}\left(t_i\right)$, where $\mathit{\eta }\left(t_i\right)$ is a deterministic component and $\mathbf{M}\left(t_i\right)$ is a stochastic component. The deterministic component $\mathit{\eta }\left(t_i\right)$ can be obtained by solving the standard SIR ODE that in our notation can be written as

$$\mathrm{d}\mathit{\eta }\left(t\right)={\mathbf{A}}^T\mathbf{h}\left(\mathit{\eta }\left(t\right),{\mathit{\theta }}_{i-1}\right)\mathrm{d}t,t\in \left[t_{i-1},t_i\right].$$ (7)

The stochastic part $\mathbf{M}\left(t_i\right)$ corresponds to the solution of the following SDE at time $t_i$

$$\mathrm{d}\mathbf{M}(t)=\mathbf{F}\left(\mathit{\eta }(t),{\mathit{\theta }}_{i-1}\right)\mathbf{M}(t)\mathrm{d}t+\sqrt{{\mathbf{A}}^T\mathbf{H}\left(\mathit{\eta }(t),{\mathit{\theta }}_{i-1}\right)\mathbf{A}}\mathrm{d}{\mathbf{W}}_t,t\in \left[t_{i-1},t_i\right],$$ (8)

where $\mathbf{F}\left(\mathit{\eta }(t),{\mathit{\theta }}_{i-1}\right):={\left.\frac{\partial {\mathbf{A}}^T\mathbf{h}\left(\mathbf{X}(t),{\mathit{\theta }}_{i-1}\right)}{\partial \mathbf{X}}\right|}_{\mathbf{X}=\mathit{\eta }(t)}$ is the Jacobian matrix of the deterministic part ${\mathbf{A}}^T\mathbf{h}\left(\mathbf{X}(t),{\mathit{\theta }}_{i-1}\right)$ in (7) evaluated at $\mathit{\eta }(t)$. The solution of SDE (8), $\mathbf{M}(t)$, is a Gaussian process and can be recovered by solving two ordinary differential equations governing the mean function $\mathbf{m}(t):=\mathbf{E}[\mathbf{M}(t)]$ and covariance function $\mathbf{\Phi }(t):=\mathbf{V}\mathbf{a}\mathbf{r}(\mathbf{M}(t))$:

$$\mathrm{d}\mathbf{m}(t)=\mathbf{F}\left(\mathit{\eta }(t),{\mathit{\theta }}_{i-1}\right)\mathbf{m}(t)\mathrm{d}t$$ (9)

$$\begin{array}{l}\mathrm{d}\mathbf{\Phi }(t)=\left(\mathbf{F}\left(\mathit{\eta }(t),{\mathit{\theta }}_{i-1}\right)\mathbf{\Phi }(t)+\mathbf{\Phi }(t){\mathbf{F}}^T\left(\mathit{\eta }(t),{\mathit{\theta }}_{i-1}\right)\right.\\ \left.+{\mathbf{A}}^T\mathbf{H}\left(\mathit{\eta }(t),{\mathit{\theta }}_{i-1}\right)\mathbf{A}\right)\mathrm{d}t,\end{array}$$ (10)

for $t\in \left[t_{i-1},t_i\right]$. A heuristic derivation of LNA, based on (Wallace, 2010), is given in Section A-2 of the Appendix. Let ${\mathit{\eta }}_{t_{i-1}},{\mathbf{m}}_{t_{i-1}},{\mathbf{\Phi }}_{t_{i-1}}$ denote the initial values of $\mathit{\eta }(t)$, $\mathbf{m}(t)$, $\mathbf{\Phi }(t)$ at time $t_{i-1}$ in differential equations (7), (9), and (10) respectively. There are two options for choosing these initial conditions: the non-restarting LNA of Komorowski et al. (2009) and the restarting LNA of Fearnhead, Giagos and Sherlock (2014). In this paper, we will use the non-restarting LNA by Komorowski et al. (2009) since it allows us to isolate the effect of adding stochasticity to the ODE method as the mean population trajectory of the non-restarting LNA is the trajectory from the ODE method. The non-restarting LNA has the following choice of initial conditions:

1. ${\mathit{\eta }}_{t_{i-1}}=\mathit{\eta }\left(t_{i-1}\right)$, where $\mathit{\eta }\left(t_{i-1}\right)$ was obtained by solving the ODE (7) using parameter vector ${\mathit{\theta }}_{i-2}$ over the interval $\left[t_{i-2},t_{i-1}\right]$,

2. ${\mathbf{m}}_{t_{i-1}}={\mathbf{X}}_{i-1}-\mathit{\eta }\left(t_{i-1}\right)$,

3. ${\mathbf{\Phi }}_{t_{i-1}}=\mathbf{0}$.

Solving the system of ODEs (7), (9), (10), we obtain $\mathit{\eta }\left(t_i\right),\mathbf{m}\left(t_i\right)$, and $\mathbf{\Phi }\left(t_i\right)$. The solution $\mathbf{m}\left(t_i\right)$ will be a function of the initial value ${\mathbf{X}}_{i-1}-\mathit{\eta }\left(t_{i-1}\right)$, the interval length $\mathrm{\Delta }{t}_i:=t_i-t_{i-1}$ and the SIR rates ${\mathit{\theta }}_{i-1}$. To make this dependence explicit, we write $\mathbf{m}\left(t_i\right):=\mathit{\mu }\left({\mathbf{X}}_{i-1}-\mathit{\eta }\left(t_{i-1}\right),\mathrm{\Delta }{t}_i,{\mathit{\theta }}_{i-1}\right)$. Since (9) is a first order homogeneous linear ODE, the solution $\mathit{\mu }\left({\mathbf{X}}_{i-1}-\mathit{\eta }\left(t_{i-1}\right),\mathrm{\Delta }{t}_i,{\mathit{\theta }}_{i-1}\right)$ is a linear function of ${\mathbf{X}}_{i-1}-\mathit{\eta }\left(t_{i-1}\right)$. Hence, the transition from ${\mathbf{X}}_{i-1}$ to ${\mathbf{X}}_i$ follows the following Gaussian distribution:

$${\mathbf{X}}_i\mid {\mathbf{X}}_{i-1},{\mathit{\theta }}_{i-1}\sim 𝒩\left(\mathit{\eta }\left(t_i\right)+\mathit{\mu }\left({\mathbf{X}}_{i-1}-\mathit{\eta }\left(t_{i-1}\right),\mathrm{\Delta }{t}_i,{\mathit{\theta }}_{i-1}\right),\mathbf{\Phi }\left(t_i\right)\right).$$ (11)

To summarize, the derived conditional Gaussian densities $\mathrm{P}\mathrm{r}\left({\mathbf{X}}_i\mid {\mathbf{X}}_{i-1},{\mathit{\theta }}_{i-1}\right)$ allow us to compute the density of the latent SIR trajectory (4). As a result, our augmented posterior distribution of ${\mathbf{X}}_{0:T}$ and ${\mathit{\theta }}_{0:T}$, shown in equation (3), can be computed up to proportionality constant and approximated via “standard” (not particle filter) MCMC approaches.

2.3. Reparameterization, priors, and MCMC algorithm

2.3.1. Reparameterizing SIR rates

We have experimented with multiple parameterizations of our inhomogeneous SIR model and found that the following parameterization works best with our proposed MCMC algorithm for approximating the posterior distribution (3). First, recall that we allow SIR rates to vary with time. Since it is much more likely for the infection rate to be time variable, we are going to assume a constant removal/recovery rate $\gamma$. This leaves us with the following parameters: infection rates on a grid $\mathit{\beta }$, removal rate $\gamma$, and initial SIR state ${\mathbf{X}}_0=\left(S_0,I_0\right)$. Since we are interested in modeling an emerging infectious disease outbreak, we set the initial counts of susceptibles to $S_0=N-I_0$. Initial counts of infected individuals, $I_0$, is assumed to be low and treated as an unknown parameter with a lognormal prior distribution. Instead of the time-varying infection rate $\beta (t)$, we parameterize our SIR model with a time-varying basic reproduction number $R_0(t)=[\beta (t)N]/\gamma$. The reproduction number is interpreted as the average number of cases that one case generates over its infectious period in a completely susceptible population. Since our infection rate changes in a piecewise manner, the basic reproduction number varies over time in a piecewise manner too:

$$R_0(t)=\sum _{i=1}^T{R}_{0_{i-1}}{\mathbf{1}}_{[t_{i-1},t_i)}(t),$$ (12)

where $R_{0_i}=\left[{\beta }_{i}N\right]/\gamma$ is the reproduction number corresponding to the time interval $\left[t_{i-1},t_i\right)$. Let $R_0=R_{0_0}$ be the initial basic reproductive number and ${\delta }_i=\mathrm{l}\mathrm{o}\mathrm{g}\left(R_{0_i}/R_{0_{i-1}}\right)/\sigma$ be a normalized log ratio of $R_0(t)$ over two successive time intervals. Then, interval-specific basic reproduction numbers can be written as

$$R_{0_i}=R_0(t,{\mathit{\delta }}_{1:T},\sigma )=R_0\exp \left(\sum _{k=1}^i\sigma {\delta }_k\right),\text{for}i=1,\dots ,T,$$ (13)

where we assume a priori that ${\delta }_i\mathrm{s}$ are independent standard normal random variables.

This construction implies that log-transformed piecewise constant reproduction numbers, $\mathrm{l}\mathrm{o}\mathrm{g}\left(R_{0_i}\right)$s, a priori follow a first order Gaussian Markov random field (GMRF) with standard deviation $\sigma$ that controls the a priori smoothness of $R_0(t)$ trajectory (Rue, 2001; Rue and Held, 2005). In addition to speeding MCMC convergence, working with $R_0(t)$ is convenient, because this trajectory is dimensionless and retains its interpretation when one changes the population size $N$. The initial $R_0$ is assigned a lognormal $\left(a_1,b_1\right)$ prior. We use a lognormal $\left(a_2,b_2\right)$ prior for the inverse of standard deviation $1/\sigma$.

2.3.2. Grid size and prior for GMRF standard deviation

The number of grid intervals $T$ can be thought of as a tuning parameter in our model. Increasing $T$ linearly increases complexity of the coalescent likelihood and $R_0(t)$ prior density calculations, suggesting that keeping $T$ small is prudent from a computational point of view. However, if the chosen $T$ is too small, we may miss large changes of the latent numbers of susceptible and infectious individuals and changes of the basic reproduction number. We recommend choosing $T$ large enough to capture these changes, possibly experimenting with multiple grid sizes. We recommend setting the prior distribution for $\sigma$ in conjunction with $T$, for example, by controlling the probability that $R_0(t)$ a priori stays within a reasonable range.

2.3.3. Reparameterizing SIR latent trajectories

We reparameterize the latent SIR trajectory ${\mathbf{X}}_{1:T}$ with a sequence of independent Gaussian random variables ${\mathit{\xi }}_{1:T}$, following a non-centered parameterization framework of Papaspiliopoulos, Roberts and Sköld (2007). According to formula (11), conditional on ${\mathbf{X}}_{i-1},{\mathbf{X}}_i$ can be written as

$${\mathbf{X}}_i=\mathit{\eta }\left(t_i\right)+\mathit{\mu }\left({\mathbf{X}}_{i-1}-\mathit{\eta }\left(t_{i-1}\right),\mathrm{\Delta }{t}_i,{\mathit{\theta }}_{i-1}\right)+{\mathbf{\Phi }}_i^{1/2}{\mathit{\xi }}_i,$$ (14)

where ${\mathit{\xi }}_i\stackrel{\text{iid}}{\sim }𝒩(0,\mathbf{I})$ for $i=1,\dots ,T$ and $\mathbf{I}$ is a $2\times 2$ identity matrix. In our parameterization, we will treat ${\mathit{\xi }}_{1:T}$ as random latent variables and the SIR latent trajectory ${\mathbf{X}}_{1:T}$ as a deterministic transformation of ${\mathit{\xi }}_{1:T}$. More details about our non-centered parameterization of ${\mathbf{X}}_{1:T}$ can be found in Section A-3 of the Appendix.

2.3.4. MCMC algorithm

Using our new parameterization, we are now interested in the posterior distribution of the initial number of infected individuals, $I_0$, removal rate, $\gamma$, the initial basic reproduction number, $R_0$, standardized vectors, ${\mathit{\delta }}_{1:T}$ and ${\mathit{\xi }}_{1:T}$, and GMRF standard deviation, $\sigma$:

$$\begin{array}{l}\mathrm{P}\mathrm{r}\left(I_0,R_0,\gamma ,{\mathit{\delta }}_{1:T},{\mathit{\xi }}_{1:T},\sigma \mid \mathbf{g}\right)\propto \mathrm{P}\mathrm{r}\left(\mathbf{g}\mid I_0,R_0,\gamma ,{\mathit{\delta }}_{1:T},{\mathit{\xi }}_{1:T},\sigma \right)\mathrm{P}\mathrm{r}\left(I_0\right)\\ \mathrm{P}\mathrm{r}\left(R_0\right)\mathrm{P}\mathrm{r}(\gamma )\mathrm{P}\mathrm{r}\left({\mathit{\delta }}_{1:T}\right)\mathrm{P}\mathrm{r}\left({\mathit{\xi }}_{1:T}\right)\mathrm{P}\mathrm{r}(\sigma )\\ \propto \mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T}\right)\mathrm{P}\mathrm{r}\left(I_0\right)\mathrm{P}\mathrm{r}\left(R_0\right)\mathrm{P}\mathrm{r}(\gamma )\\ \mathrm{P}\mathrm{r}\left({\mathit{\delta }}_{1:T}\right)\mathrm{P}\mathrm{r}\left({\mathit{\xi }}_{1:T}\right)\mathrm{P}\mathrm{r}(\sigma ).\end{array}$$

The latent variables ${\mathbf{X}}_{0:T}$ and parameter vector ${\mathit{\theta }}_{0:T}$ are deterministic functions of new parameters $I_0$, $\gamma$, $R_0,{\mathit{\delta }}_{1:T}$, ${\mathit{\xi }}_{1:T}$, and $\sigma$. We use the following MCMC with block updates to approximate this posterior distribution. We update high dimensional vector $\mathbf{U}=\left(\mathrm{l}\mathrm{o}\mathrm{g}\left(R_0\right),{\mathit{\delta }}_{1:T},\mathrm{l}\mathrm{o}\mathrm{g}(\sigma )\right)$ using the efficient elliptical slice sampler (Murray, Adams and MacKay, 2010). Vector ${\mathit{\xi }}_{1:T}$ is updated the same way in a separate step. Initial number of invected individuals $I_0$ and removal rate $\gamma$ are updated using univariate Metropolis steps. The full procedure is described in Algorithm 2, which together with details of the elliptical slice sampler can be found in Section A-4.1 of the Appendix. After MCMC is done, we report posterior summaries using natural parameterization. For example, we report posterior medians and 95% Bayesian credible intervals (BCIs) of the piecewise latent reproduction number trajectory, $R_{0_i}$, for $i=0,\dots ,T$, and latent trajectory ${\mathbf{X}}_{0:T}$.

2.3.5. Implementation

Our R package called LNAPhylodyn provides an implementation of our MCMC algorithm. The package code is publicly available at https://github.com/MingweiWilliamTang/LNAphyloDyn. This repository also contains scripts that should allow one to reproduce key numerical results in this manuscript. The PhyDyn simulation example is also included in https://github.com/MingweiWilliamTang/LNAphyloDyn/blob/master/inst/SIR_phydyn_example.xml.

3. Simulation experiments

3.1. Simulations based on single genealogy realizations

In this section, we use simulated genealogies to assess performance of our LNA-based method and to compare it with an ODE-based method, where we replace equation (14) with its simplified version: ${\mathbf{X}}_i=\mathit{\eta }\left(t_i\right)$. Under our assumption of a fixed and known genealogy and constant $R_0$, our ODE-based method closely resembles previously developed methods by Volz et al. (2009) and Volz and Siveroni (2018). To compare ODE-based and LNA-based models in a Bayesian nonparametric setting, we equip the ODE model with the GMRF prior for time-varying $R_0(t)$, described in Section 2.3.1. We use the same MCMC algorithm for both LNA-based and ODE-based models, except we do not have a separate step to update latent vector ${\mathit{\xi }}_{1:T}$ (equivalently, ${\mathbf{X}}_{0:T}$) in the ODE-based inference. See Algorithm 3 in the Appendix for a more detailed description of the ODE-based MCMC.

The simulation protocol consists of two steps. First, given the population size $N$ and pre-specified parameters $\gamma ,I_0$, and $R_0(t)$, we simulate one realization of the SIR population trajectory based on the MJP using the Gillespie algorithm (Gillespie, 1977). Next, we generate realistic lineage sampling times and simulate coalescent times from the distribution specified by density (2) using a thinning algorithm by Palacios and Minin (2013). We specified several sampling times spanning the time of the epidemic. The number of sampled sequences at each sampling time in each scenario is set to be approximately proportional to the true prevalence. More details are given in Appendix Section A-5.1.

We test LNA-based and ODE-based methods under three “true” $R_0(t)$ trajectories over the time interval [0, 90]:

1. Constant (CONST) $R_0(t)$. $R_0(t)=2.2$ for $t\in \left[\mathrm{0,90}\right]$. Recovery rate $\gamma =0.2$. Initial counts of infected individuals $I_0=1$. Total population size is $N=\mathrm{100,000}$. The total number of sampled sequences is 1022.

2. Stepwise decreasing (SD) $R_0(t)$. $R_0(t)=2,t\in [\mathrm{0,30})$, $R_0(t)=1,t\in [\mathrm{30,60})$ and $R_0(t)=0.6,t\in [60,90]$. Recovery rate $\gamma =0.2$. Initial counts of infected individuals $I_0=1$. Total population size $N=\mathrm{1,000,000}$. The total number of sampled sequences is 342.

3. Non-monotonic $(\mathrm{N}\mathrm{M})R_0(t)$. $R_0(t)=1.4\times {1.015}^{0.5t},t\in \left[\mathrm{0,30}\right]$, $R_0(t)=1.750\times {0.975}^{t-30},t\in \left[\mathrm{30,80}\right]$ and $R_0(t)=0.4583,t\in \left[\mathrm{80,90}\right]$. Recovery rate $\gamma =0.3$. Initial counts of infected individuals $I_0=3$. Total population size $N=\mathrm{1,000,000}$. The total number of sampled sequences is 442.

For all simulations, we use lognormal (1, 1) prior for $I_0$. The parameters of the lognormal priors for the initial $R_0$ and inverse standard deviation $1/\sigma$ are set to $a_1=0.7,b_1=0.5$ and $a_2=3,b_2=0.2$ respectively, in such a way that a priori $R_0(t)$ trajectory stays within a reasonable range of [0, 5] with 0.9 probability. We assign an informative prior for $\gamma$ in each simulation scenario, assuming that prior information about this parameter is available: (1) CONST: $\gamma \sim \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(-\mathrm{1.7,0.1})$, (2) SD: $\gamma \sim \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(-\mathrm{1.7,0.1})$, (3) NM: $\gamma \sim \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(-\mathrm{1.2,0.1})$. We set the grid size to $T=36$, with $t_i-t_{i-1}=2.5$ for $i=1,\dots ,36$. As a result, each scenario has 72 latent variables that keep track of latent numbers of infectious and removed individuals, ${\mathbf{X}}_{1:36}$, and 36 parameters that describe changes in the basic reproduction number, ${\mathit{\delta }}_{1:36}$, plus parameters $R_0$, $I_0,\gamma$, and $\sigma$. For both LNA-based and ODE-based methods, we use 1,000,000 MCMC iterations. All MCMC chains appeared to converge (trace plots are shown in Section A-5.4.1 of the Appendix). The effective sample sizes of all unknown quantities were above 400 (See Table A-1 for more details).

The first row of Figure 3 shows point-wise posterior medians and 95% BCIs for the basic reproduction number trajectory, $R_0(t)$. Our LNA-based method performs well in capturing the continuous dynamics of $R_0(t)$. Though our approach may not perfectly catch the discontinuous changes in $R_0$ in the SD scenario, the method provides BCIs that are able to capture most of the $R_0(t)$ trajectory. The ODE-based method yields similar results in the CONST case and the $\mathrm{S}\mathrm{D}$ case, but underestimates the magnitude of the decrease in $R_0(t)$ toward the end of the epidemic.

FIGURE 3.

Analysis of 3 simulation scenarios. Columns correspond to CONST, SD, and NM simulated $R_0(t)$ trajectories. The first row shows the estimated $R_0(t)$ trajectories for the 3 scenarios, with the black solid lines representing the truth, the red dashed lines depicting the posterior median and the red-shaded area showing the 95% BCIs for the LNA-based method. For the ODE-based method, the posterior median is plotted in blue dotted lines, with blue shading showing the 95% BCIs. The second row corresponds to the estimation for the removal rate γ. Posterior density curves from the LNA are shown in red lines and the posterior density for ODE is plotted in blue lines, compared with prior density curve in green lines. The bottom two figures shows the estimated trajectory of $S(t)$ and $I(t)$ respectively.

The second row in Figure 3 shows posterior summaries of removal rate $\gamma$. Both LNA-based and ODE-based methods provide good estimates in the CONST scenario, with posterior modes centered at the true value and higher posterior densities at truth when compared with the prior. In the SD and NM scenarios with the time varying $R_0(t)$, the posterior estimates from the LNA-based method and ODE-based method, though still centered at the truth, do not differ much from the prior distribution.

Posterior summaries of $S(t)$ and $I(t)$ are depicted in the third and fourth rows of Figure 3. The two methods produce similar results in the CONST and SD scenario, as both of them have narrow BCIs covering the true trajectories. However, in the NM case, while the LNA-based method manages to recover the latent SIR trajectory trend, the BCIs from the ODE-based method fail to cover the true prevalence trajectory in the middle and at the end of the epidemic. Somewhat counterintuitively, LNA-based method produces BCIs for the latent trajectories, $S(t)$ and $I(t)$, that are narrower than its ODE counterparts. We suspect this is a result of the ODE-based method poor estimation of the basic reproduction number trajectory at the end of the epidemic.

3.2. Frequentist properties of posterior summaries

In this Section, we design a simulation study based on repeatedly simulating SIR trajectories using MJP with pre-specified parameters. We report simulations based on the non-monotonic $R_0(t)$ trajectory scenario in Section 3.1 with the same parameter setup, except the parameters of the lognormal prior for the initial $R_0$ are set to $a_1=0.7,b_1=0.3$. Results of repeatedly simulating SIR trajectories with constant and monotonic $R_0(t)$ trajectories are reported in Appendix Section A-5.3. Simulating SIR dynamics under low initial number of infected individuals $I_0$ can end up with low prevalence trajectories that end at the beginning of the epidemic, or trajectories having unrealistically high prevalence, which are less likely to be observed during real infectious disease outbreaks. Therefore, while simulating SIR trajectories we reject such “unreasonable” realizations to arrive at 100 simulated trajectories. The details of the rejection criteria are given in Section A-5.2 of the Appendix. For each simulated SIR trajectory, a realization of a genealogy is generated using the structured coalescent process. We use both LNA-based and ODE-based models to approximate the posterior distribution of model parameters and latent variables for each genealogy. In addition to the informative prior for removal rate $\gamma$, used in Section 3.1, we use a weaker prior $\gamma \sim \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(-1.2,0.25)$ to probe prior sensitivity of both LNA-based and ODE-based methods.

We use three metrics to evaluate models based on their estimates of $R_0(t)$ and $I(t)$: average error of point estimates (posterior medians), width of credible intervals, and frequentist coverage of credible intervals. Since the value of $R_0(t)$ is greater than 0 and usually upper-bounded by 20 (i.e, it stays within the same order of magnitude), we will measure accuracy using an unnormalized mean absolute error (MAE):

$$\text{MAE}=\frac{1}{T+1}\sum _T^{i=0}\left|{\widehat{R}}_{0_i}-R_0(t_i)\right|,$$ (15)

where ${\hat{R}}_{0_i}$ is the posterior median of $R_0\left(t_i\right)$. In contrast, $I(t)$ varies from one at the beginning of the epidemic to thousands at the peak, so to evaluate accuracy of prevalence estimation we use the mean relative absolute error (MRAE):

$$\text{MRAE}=\frac{1}{T+1}\sum _T^{i=0}\frac{\left|{\widehat{I}}_i-I(t_i)\right|}{I(t_i)+1},$$ (16)

where ${\hat{I}}_i$ is the posterior median of $\mathrm{I}\left(t_i\right)$. We assess precision of $R_0(t)$ estimation based on the mean credible interval width (MCIW):

$$\text{MCIW}=\frac{1}{T+1}\sum _{i=0}^T\left[{\widehat{R}}_{0_i}^{0.975}-{\widehat{R}}_{0_i}^{0.025}\right],$$ (17)

where ${\hat{R}}_{0_i}^{0.025}$ and ${\hat{R}}_{0_i}^{0.975}$ denote the lower and upper bounds of the 95% BCI for $R_{0_i}$. Similar as our measure of accuracy, precision of $I(t)$ estimation is quantified via mean relative credible interval width (MRCIW):

$$\text{MRCIW}=\frac{1}{T+1}\sum _{i=0}^T\frac{{\widehat{I}}_i^{0.975}-{\widehat{I}}_i^{0.025}}{I(t_i)+1}$$ (18)

where ${\hat{I}}_i^{0.025}$ and ${\hat{I}}_i^{0.975}$ specify the lower and upper bounds of the 95% BCI of $I\left(t_i\right)$. In addition, we compute the “envelope” (ENV) — a measure of coverage of BCIs the true trajectory — for $R_0(t)$ and $I(t)$ as follows:

$$\mathrm{E}\mathrm{N}\mathrm{V}-{\mathrm{R}}_0=\frac{1}{T+1}\sum _{i=0}^T \mathbb{1}\left({\hat{R}}_{0_i}^{0.025}\le R_0\left(t_i\right)\le {\hat{R}}_{0_i}^{0.975}\right),$$

$$\mathrm{E}\mathrm{N}\mathrm{V}-\mathrm{I}=\frac{1}{T+1}\sum _{i=0}^T \mathbb{1}\left({\hat{I}}_i^{0.025}\le I\left(t_i\right)\le I_i^{0.975}\right).$$

Sampling distribution boxplots of $R_0(t)$ posterior summaries are depicted in the left three plots of Figure 4. The LNA-based method yields lower MAE than the ODE-based method under both informative and weakly informative priors for the removal rate $\gamma$. As a trade-off, the MCIWs produced by the LNA-method are generally higher, as expected since the LNA-based method incorporates the stochasticity in the population dynamics. With less bias and wider BCIs, the LNA-based method BCIs result in better $R_0(t)$ coverage than ODE-based BCIs, as shown by the envelope boxplots. Informative prior for the removal rate $\gamma$ helps both LNA-based and ODE-based methods to estimate $R_0(t)$.

FIGURE 4.

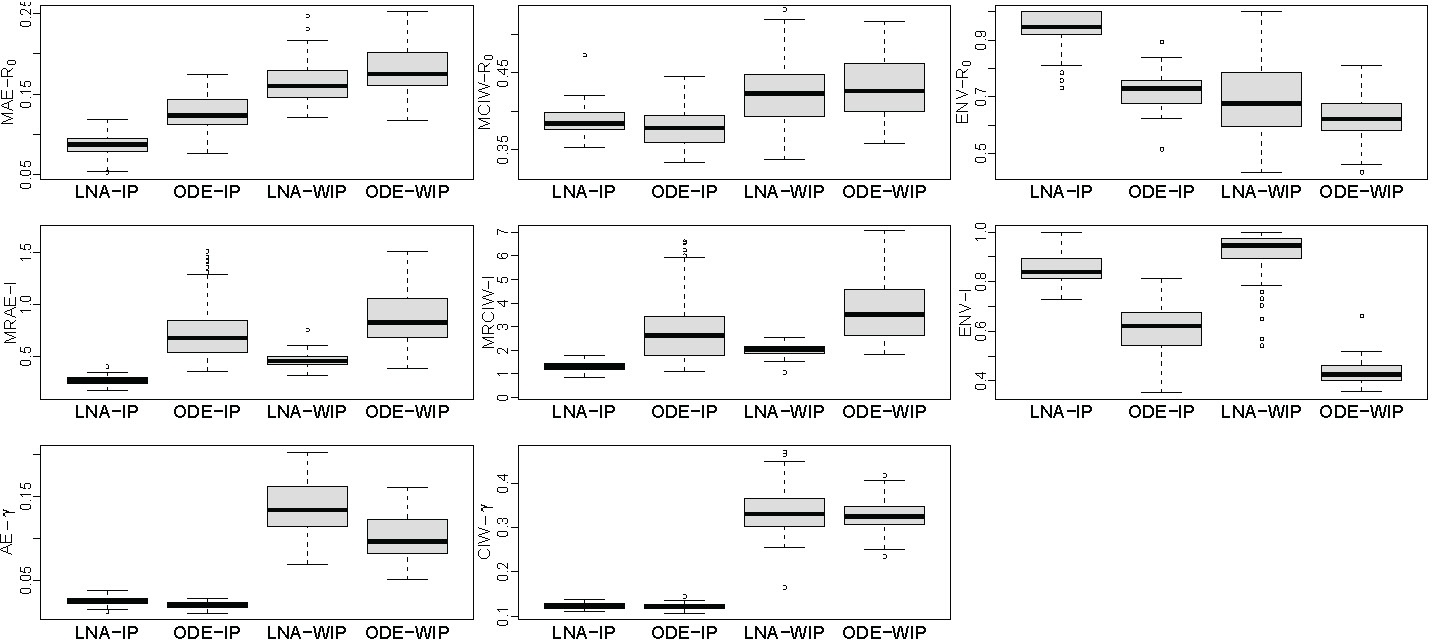
Borplots comparing performance of LNA-based and ODE-based methods using 100 simulated genealogies under informative prior (IP) and weakly informative prior (WIP) for removal rate $\gamma$. The first row shows mean absolute error (MAE), mean credible interval width (MCIW), and enevolope $\left(ENV-R_0\right)for{R}_0(t)$ trajectory. The second row depiets mean relative absolute error (MRAE), mean relative credible interval width (MRCIW), and enelope (ENV-1) for $I(t)$ (prevalence) trajectory (ENV-I). The last two plots show the absolute error (AE) and Bayesian credible intereval (BCI) width for $\gamma$.

Sampling distribution boxplots of $I(t)$ posterior summaries, shown in Figure 4, are similar to the $R_0(t)$ results, with the LNA-based method generally having lower MRAEs, higher MRCIWs and a better coverage/envelope than the ODE-based method. Again, somewhat counterintuitively, the MRCIWs for the LNA-based method are smaller than the ODE counterparts. This is likely caused by significant bias in $R_0(t)$ estimation by the ODE-based method. The contrast between results of informative and weakly informative prior is a little different from $R_0(t)$ estimation results, because the LNA-bnsed method is estimating $I(t)$ better than $R_0(t)$ under the weakly informative prior.

We also report the absolute error (AE) and 95% BCI widths for removal rate $\gamma$ in Figure 4. The LNA-based method yields slightly higher AEs than the ODE method. Under the informative prior, both LNA-based and ODE-based methods have coverage of 95% BCIs equal to 1.0. However, coverage of LNA-based method drops to 0.65 under the weakly informative prior, while the ODE-based method’s 95% BCI coverage becomes 0.99.

In conclusion, the ODE-based method tends to be biased and overconfident when estimating basic reproduction number $R_0(t)$ and prevalence $I(t)$. By modeling stochasticity of the population trajectory dynamics, our LNA-based method produces more accurate and less precise estimators of $R_0(t)$ and $I(t)$ that enjoy good frequentist properties. However, the ODE-based method does better in estimating the recovery rate $\gamma$, which is only weakly identifiable.

3.3. Additional simulations and validation

We perform the same repeated simulations for the constant and stepwise decreasing $R_0(t)$ scenarios under the same parameter setup as in Section 3.1 and report the corresponding frequentist properties of the posterior summaries in Figures A-5 and A-6. Both LNA-based and ODE-based methods results are similar to the results from the non-monotonic $R_0(t)$ simulation scenario, but the differences between LNA-based and ODE-based methods are less pronounced than in the non-monotonic $R_0(t)$ scenario.

Theoretically, both structured coalescent models and LNA are designed to work for epidemics in large populations. We test performance of LNA-based and ODE-based methods in a relatively small population with the size of $N=1,000$. For simplicity, we use a constant $R_0(t)$ simulation scenario. Assuming that $R_0$ is constant also allows us to compare our method to the BEAST 2 PhyDyn module that implements the ODE-based approach. PhyDyn can handle a wide range of different compartmental models of infectious disease dynamics, but we use only a simple SIR model in this comparison. This simulation study shows that our implementations of both LNA-based and ODE-based approaches perform reasonably in this small population setting, but PhyDyn does do as well. However, we find that the disagreement between our ODE implementation and PhyDyn is artifact of the small population size setting, which leads to the outbreak to be densely sampled. In Appendix Section A-9, we demonstrate that our ODE-based method implementation agrees with $\mathrm{R}$ package PhyDynR (a predecessor of BEAST 2 PhyDyn) under a setup with a large population size, but the two implementations disagree under a small population size setting.

4. Analysis of Ebola outbreak in West Africa

We apply our LNA-based method to the Ebola genealogies reconstructed from molecular data collected in Sierra Leone and Liberia during the 2014–2015 epidemic in West Africa (Dudas et al., 2017). We use a Sierra Leone genealogy, depicted in the top left plot of Figure 5, which was estimated from 1010 Ebola virus full genomes sampled from 2014-05-25 to 2015-09-12 in 15 cities. The Liberia genealogy, shown in the top left plot of Figure 6, was estimated from a smaller number of samples: 205 Ebola virus full genomes sampled from 2014-06-20 to 2015-02-14. The original sequence data and the reconstructed genealogies are publicly available at https://github.com/ebov/space-time.

FIGURE 5.

Analysis of the genealogy relating Ebola virus sequences collected in Sierra Leone. Top top left plot depicts the Ebola genealogy. The top right plot shows the estimated $R_0(t)$, with the red dashed line showing the posterior median and the salmon shaded area showing the 95% BCIs of the LNA-based method. The posterior median based on the ODE-based method is plotted as the blue dotted line with blue shading corresponding to the 95% BCIs. The medium left figure shows prior and posterior densities of the mean infection period $1/\gamma$. The prior density is shown in green, while the posterior densities based on LNA and ODE are plotted in red and blue respectively. The medium right and the bottom left figures show the estimated trajectory of $S(t)$ and $I(t)$, using the same legend as in top right plot. The bottom right plot shows the predicted median and 95% BCIs for weekly reported incidence together with the reported incidence from WHO shown as crosses.

FIGURE 6.

Analysis of the genealogy relating Ebola virus sequences collected in Liberia. See caption in Figure 5 for the explanation of the plots.

When Ebola virus infections were detected in West Africa in mid-Spring of 2014, various intervention measures were proposed and implemented to change behavior of individuals in the populations through which Ebola was spreading. Border closures, encouragement to reduce individual day-to-day mobility, and recommendations on changing burial practices were among the broad spectrum of interventions attempted by multiple countries. It is reasonable to expect that these intervention measures resulted in lowering the contact rates among members of the populations, which in turn reduced the infection rate, or equivalently the basic reproduction number.

When analyzing the Sierra Leone and Liberia genealogies, we rely on conclusions of Dudas et al. (2017) and assume the population in each country to be well mixed. Furthermore, we assume Ebola spread to follow SIR dynamics. For each country, the population size is specified based on its census population size in 2014, with $N=\mathrm{7,000,000}$ for Sierra Leone and $N=\mathrm{4,400,000}$ for Liberia. We investigated robustness to population size misspecification in Appendix Section A-8.2 and found that altering population size of Liberia by an order of magnitude in each direction did not appreciably change estimation results. As in our simulation study, we use the lognormal prior for $R_0$ with $a_1=0.7$ and $b_1=0.5$ and the lognormal prior for the inverse standard deviation $1/\sigma$ with $a_2=3,b_2=0.2$. Recall that this prior setting ensures that a priori $R_0(t)$ stays within a reasonable range of [0, 5] with probability 0.9. For removal rate $\gamma$, we use an informative lognormal prior with mean 3.4 and variance 0.2 based on previous studies (Towers, Patterson-Lomba and Castillo-Chavez, 2014). The parameter $1/\gamma$, interpreted as the length of the infectious period, is expected to be 8–18 days for each country a priori. The total time span for each genealogy is divided evenly into 40 intervals, which results in grid interval lengths, $\mathrm{\Delta }{t}_i\mathrm{s}$, to be 12.41 days for Sierra Leone and 6.9 days for Liberia. We experimented with two additional grid sizes for the Liberia analysis in Appendix Section A-7 and found that our results are not too sensitive to the choice of grid size.

We run the MCMC algorithm in Section 2.3 for 2,000,000 iterations with 9 parallel chains for Sierra Leone data and 750,000 iterations for Liberia data using a single chain. The posterior samples are obtained by discarding the first 100,000 iterations and saving every 30th iteration afterward. The trace plots in Section A-5.4.2 of the Appendix indicate the MCMC algorithm has converged and achieved good mixing in each case.

Figures 5 and 6 show results for Sierra Leone and Liberia respectively, with intervention events mapped onto the calendar time on the x-axis. Our LNA-based method estimates the initial $R_0$ in Sierra Leone during 2014–2015 to be 1.66, with 95% BCI of (1.31, 2.15). Similarly, $R_0$ in Liberia during 2014 –2015 has a point estimate 1.67 and a 95% BCI(1.29, 2.24). Our estimate of initial $R_0$ in Sierra Leone is consistent with the estimates of Stadler et al. (2014), who fitted multiple birth-death models to 72 sequences at the early stages of the outbreak. Our LNA-based method yields a slightly smaller estimate of the initial $R_0$ than methods based on susceptible-exposed-infectious-removed (SEIR) models. For example, Volz and Pond (2014) used a SEIR model with a constant $R_0$ and estimated it to be 2.40 (CI: (1.54, 3.87)). Althaus (2014) assumed an exponentially decaying $R_0(t)$ with an estimated initial $R_0$ of 2.52 (CI: (2.41, 2.67))The discrepancies between our and SEIR-based estimates are not unexpected, because SEIR models generally yield higher $R_0$ estimates than SIR models when applied to the same dataset (Wearing, Rohani and Keeling, 2005; Keeling and Rohani, 2011). Our estimated $R_0$ for Liberia is in agreement with results of Althaus (2014), who fitted a SEIR model to incidence data and arrived at an estimated $R_0$ of 1.59 (CI: (1.57, 1.60)).

The $R_0(t)$ dynamics in the two countries share a similar pattern: with (1) a decreasing trend that starts in Spring/Summer of 2014, (2) a stable/constant period until the end of September 2014 and (3) a final decrease below 1.0 (epidemic is contained) around November 2014. Since the number of susceptible individuals did not change significantly over the course of the epidemic, relative to the total population size, the basic and effective reproduction numbers, $R_0(t)=\beta (t)N/\gamma$ and $R_{\mathrm{e}\mathrm{f}\mathrm{f}}(t)=\beta (t)S(t)/\gamma$, are approximately equal. This allows us to compare our $R_0(t)$ estimation results with previously estimated changes in $R_{\mathrm{e}\mathrm{f}\mathrm{f}}(t)$. Our estimation of early $R_0(t)$ dynamics in Sierra Leone agrees with results of Stadler et al. (2013), who concluded that the effective reproduction number did not significantly decrease until mid June. Our estimated $R_0(t)$ trajectory suggests that later interventions, such as border closures and release of burial guides, may have been helpful in controlling the spread of the disease. The infectious period for Sierra Leone epidemic is estimated to be 10.8 days with a 95% BCI (7.6,15.6). For Liberia, the infection period has a point estimate of 9.8, with a 95% BCI (6.87, 14.05). The posterior median of the total number of infected individuals (final epidemic size) is 7,450 and its 95% BCI is (3495, 15518) for Sierra Leone, which is close to 8,706 total confirmed number of cases reported by (CDC). Liberia had a smaller epidemic than Sierra Leone, with estimated total infected individuals being 2,842 and a 95% BCI of (1296, 6173). These results are also in agreement with 3,163 total confirmed cases from CDC.

We perform an out-of-sample validation by comparing our results with weekly reported confirmed incidence in Sierra Leone and Liberia from the (2016) (WHO). The posterior predictive weekly incidence at time $t$, denoted by $\hat{N}(t)$, is approximated by

$$\hat{N}(t)=\hat{\beta }(t)\hat{S}(t)\hat{I}(t)\cdot \mathrm{\Delta }t$$ (19)

where $\hat{\beta }(t)$, $\hat{S}(t)$ and $\hat{I}(t)$ are the posterior estimates of the infection rate, number of susceptible and number of infected individuals at time $t$ respectively, and $\mathrm{\Delta }t:=7/365$ corresponds the time interval of one week. We plot the posterior predictive estimates of weekly incidence together with the corresponding weekly reported confirmed incidence. For both countries, our model-based incidence 95% BCIs cover the reported incidence counts from WHO, suggesting that our time varying SIR model can estimate incidence well from genetic data alone. We note that our estimated latent incidence should be greater than the reported incidence, because not all Ebola cases were reported and recorded. However, the discrepancy between latent and reported incidence should not be large, because Ebola reporting rate was high. For example, Scarpino et al. (2014) estimated that 83% of Ebola cases were reported.

We also report results from the ODE-based method and superimpose these results over LNA-based results on Figures 5 and 6. For the relatively small Liberia genealogy, the ODE-based and LNA-based methods yield similar parameter estimates. However, the larger Sierra Leone genealogy produces substantial differences between ODE-based and LNA-based estimates of the $R_0(t)$. The ODE-based method captures the decreasing trend of $R_0(t)$ in Spring and Summer of 2014, but provides narrow BCIs with unrealistic short term fluctuations in the basic reproduction number trajectory.

5. Discussion

In this paper, we propose a Bayesian phylodynamic inference method that can fit a stochastic epidemic model to an observed genealogy estimated from infectious disease genetic sequences sampled during an outbreak. Our statistical model can be viewed as semi-parametric: with (1) a parametric SIR model describing the infectious disease dynamics and (2) a non-parametric GMRF-based estimation of the time varying basic reproduction number. To the best of our knowledge, this is the first method combining a Bayesian nonparametric approach with a deterministic or stochastic SIR model for phylodynamic inference (although see (Xu, Kypraios and O’Neill, 2016) for a similar approach applied to more traditional epidemiological data). Our use of LNA allows us to devise an efficient MCMC algorithm to approximate high dimensional posterior distribution of model parameters and latent variables. Our LNA-based method produces posterior summaries with better frequentist properties than the state-of-the-art ODE-based method, underscoring the importance of working with stochastic models even in large populations. We showcase our method by applying it to the Ebola genealogies estimated from viral sequences collected in Sierra Leone and Liberia during the 2014–2015 outbreak. Our nonparametric estimates of $R_0(t)$ in Sierra Lione and Liberia suggest that the basic reproduction number decreased in two-stages, where the second stage brought it below 1.0 — a sign of epidemic containment. The second stage of $R_0\left(t\right)$ decrease closely follows in time implementation of interventions, pointing to their effectiveness.

Our method relies on the assumption that population is well-mixed and the population dynamics follow a SIR model. However, it may be desirable to be able to relax these assumptions. For example, in Ebola spread modeling some authors used a SEIR model that assumes a latent period during which an infected individual is not infectious (Althaus, 2014; Volz and Siveroni, 2018). Moreover, adding more compartments should allow us to partially relax the unrealistic assumption of homogeneous mixing. For example, stratifying compartments by age group would allow us to account for different contact rates between these groups. One future direction of this work is to generalize the LNA-based method to fit complicated compartmental epidemic models, including models with multi-stage infections like SEIR model and models with the population stratified by sex, age, geographic location, or other demographic variables. The structured coalescent likelihoods under these models may not have closed-form expressions. However, Volz (2012), Dearlove and Wilson (2013), and Müller, Rasmussen and Stadler (2017) propose several strategies to approximate structured coalescent likelihoods. Our LNA-based methodology is directly portable to these approximate structured coalescent likelihood approaches, but our current implementation lacks this generality. We hope to remedy this in our future work.

The experiments in Section 3.1 indicate that one has to pay close attention to parameter identifiability when fitting SIR models to genealogies or to sequence data directly. Identifiability may not be a problem under an assumption of a constant $R_0(t)$. However, the removal rate tends to be only weakly identifiable in the scenarios with a time-varying basic reproduction number, in which the estimation can be sensitive to the choice of priors. In Section 3.2 and Appendix Section A-6, we demonstrate that putting a weakly informative prior on the removal rate can cause bias not only in the estimation for removal rate, but also can lead to a failure in recovering the reproduction number and latent population dynamics. Therefore, successful inference of SIR model parameters using genealogical data should rely on a sound informative prior for the removal rate. This constraint is not a big shortcoming in situations where prior information about the removal rate, or mean length of the infectious period is available from patient hospitalization data (WHO Ebola Response Team, 2014).

Since parameter identifiability is a recurring problem in infectious disease modeling, integration of multiple sources of information is of great interest. Using particle filter MCMC, Rasmussen, Ratmann and Koelle (2011) demonstrated that jointly analyzing genealogy and incidence case counts considerably reduces the uncertainty in both estimation of latent population trajectory and SIR model parameters, compared with estimation based on a single source of information. We plan to use our LNA-based framework to perform similar integration of genealogical data and incidence time series. Another possible source of information is the distribution of genetic sequence sampling times. Karcher et al. (2016) proposed a preferential sampling approach that explicitly models dependence of the sampling times distribution on the effective population size. The authors demonstrated that accounting for preferential sampling helps decrease bias and results in more precise effective population size estimation. It would be interesting to incorporate preferential sampling into our LNA-based framework by assuming a probabilistic dependency between sampling times and latent prevalence $I(t)$.

Our method assumes a genealogy/phylogenetic tree is given to us. In reality, genealogies are not directly observed and need to be inferred from molecular sequences. Genealogy estimation remains one of the biggest computational bottlenecks in phylodynamics, with computational burden of such estimation being typically higher than the burden of phylodynamics methods that use the genealogy as input. Ideally, uncertainty in the genealogy should be handled by building a Bayesian hierarchical model and integrating over the space of genealogies using MCMC. In fact, implementations of such Bayesian hierarchical modeling already exist for nonparametric, birth-death, and ODE-based phylodynamic approaches (Drummond et al., 2005; Minin, Bloomquist and Suchard, 2008; Gill et al., 2013; Stadler et al., 2013; Volz and Siveroni, 2018). Therefore, an important future direction will be to extend our LNA framework to fitting stochastic epidemic models to molecular sequences instead of genealogies. Similarly to the structured coalescent model implementation of Volz and Siveroni (2018), the easiest way to achieve this will be integration of our LNA MCMC algorithm into popular open source phylogenetic/phylodynamic software packages, such as BEAST, BEAST2, and RevBayes (Suchard et al., 2018; Bouckaert et al., 2014; Höhna et al., 2016).

Appendix

for “Fitting stochastic epidemic models to gene genealogies using linear noise approximation”

by Mingwei Tang, Gytis Dudas, Trevor Bedford, Vladimir N. Minin

A-1. A general framework for stochastic kenetic models

A-1.1. Stochastic model generalization

In Section 2, we provide an example of the linear noise approximation (LNA) for the SIR model. The LNA framework can be also generalized to other types of the stochastic kinetic models in Infectious Disease Epidemiology and in Systems Biology. Here, we give a general representation of the stochastic kinetic model by viewing it as a reaction network system. The notation is based on the work of Fearnhead, Giagos and Sherlock (2014).

Let’s start with a reaction system with $d$ reactants ${𝒳}_1,\dots ,{𝒳}_d$ and $q$ reactions. Without loss of generality, each reaction is assumed to have a constant rate parameter ${\theta }_i$ for $i=1,\dots ,q$ and $\mathbf{\theta }=\left({\theta }_1,\dots ,{\theta }_q\right)$ denotes the rate vector of the system (this framework can be extended to handle stochastic kinetic models with time-varying rates as in Section 2 of the main text). The transition event in the ith reaction $(i=1,\dots ,q)$ has the following form:

$${\tilde{a}}_{i1}{𝒳}_1+\cdots +{\tilde{a}}_{id}{𝒳}_d\stackrel{{\theta }_i}{\to }{\bar{a}}_{i1}{𝒳}_1+\dots +{\bar{a}}_{i1}{𝒳}_d,$$ (A-1)

where ${\tilde{a}}_{ij}$ and ${\bar{a}}_{ij}$ are non-negative integers representing the number of ${𝒳}_j$ in the ith reaction equation. In a compartmental stochastic epidemic model, the coefficient ${\tilde{a}}_{ij}$ will be either 0 or 1. The transitions in the reaction system can be encoded in an effect matrix,

$$\mathbf{A}:=\left\{{\tilde{a}}_{ij}-{\bar{a}}_{ij}\right\}\in {\mathbb{Z}}^{q\times d},$$ (A-2)

with each row corresponding to a certain type of reaction event and each column representing the change in the counts of reactants. Let $X_j(t)$ denote counts/population of the ${𝒳}_j$ at $t$, and the population state at time t can be tracked by vector $\mathbf{X}(t):=\left(X_1(t),\dots ,X_d(t)\right)$. Let $h_i$ denote the reaction rate of the $i$ th reaction, where $h_i$ can be written as

$$h_i={\theta }_i\prod _{j=1}^d\left(\begin{array}{l}{X}_j\hfill \\ {\tilde{a}}_{ij}\hfill \end{array}\right).$$ (A-3)

Hence, following the same notation as in Section 2.2.1 of the main text, the rate vector $\mathbf{h}$ and the rate matrix $\mathbf{H}$ can be defined as

$$\mathbf{h}\left(\mathbf{X},\mathit{\theta }\right)={\left(h_1,\dots ,h_q\right)}^T,\mathbf{H}\left(\mathbf{X},\mathit{\theta }\right)=\mathrm{diag}\left(\mathbf{h}\left(\mathbf{X},\mathit{\theta }\right)\right).$$ (A-4)

Given the above notation, the deterministic ordinary differential equation model of the reaction system can be written as

$$\mathrm{d}\mathbf{X}={\mathbf{A}}^T\mathbf{h}(\mathbf{X},\mathit{\theta })\mathrm{d}t,\mathbf{X}(0)={\mathbf{x}}_0,$$ (A-5)

where ${\mathbf{x}}_0$ is a vector of initial counts of reactants ${𝒳}_1,\dots ,{𝒳}_d$.

FIGURE A-1.

SEIR Markov jump process. From the current state with the counts S, E, I, R, the population can transition to (1) state $S-1$, $E+1$, $I,R$ (an infection event) with rate $\beta$ SI or to (2) state $S$, $E-1$, $I+1,R$ (an event where infected individual becomes infectious) with rate $\mu E$ or to (S) state $S$, $E$, $I-1,R+1$ (a removal event) with rate $\gamma I$. No other instantaneous transitions are allowed.

A-1.1.1. Example: SEIR model

The above general representation of stochastic kinetic models can be directly applied to stochastic epidemic models. Here, we illustrate this on a Susceptible-Exposed-Infected-Recovery (SEIR) model. SEIR model is an extension of the SIR model that assumes a latent period called “Exposed”, in which an infected individual does not have the ability to infect others. The exposed individual will eventually become infectious with rate $\mu$. As in the SIR model, an infectious individual has removal/recovery rate $\gamma$. The transition events between different states of the SEIR model are depicted in Figure A-1.

Following the stochastic kinetic model representation, the SEIR model can be viewed as a reaction system of four reactants — susceptible, exposed, infected, and recovered individuals — and the following three “reactions”:

$$\text{Susceptible}+\text{Infected}\stackrel{\beta }{\to }\text{Exposed}+\text{Infected,}$$ (A-6)

$$\text{Exposed}\stackrel{\mu }{\to }\text{Infected,}$$ (A-7)

$$\text{Infected}\stackrel{\gamma }{\to }\text{Recovered}.$$ (A-8)

Since the recovered population never interacts with individuals in other compartments, we will only keep track of the counts of susceptible, exposed, and infectious individuals at time $t$, denoted by $S(t)$, $E(t)$, $I(t)$ respectively. The effect matrix $\mathbf{A}$ for the SEIR model can be written as:

$$\mathbf{A}=\left(\begin{array}{ccc}\text{Susceptible}& \text{Exposed}& \text{Infected}\\ -1& 1& 0\\ 0& -1& 1\\ 0& 0& -1\end{array}\right)\begin{array}{c}\text{reaction}\text{(A-6)}\\ \text{reaction}\text{(A-7)}\\ \text{reaction}\text{(A-8)}\end{array},$$ (A-9)

with columns representing compartments and rows representing reactant changes during reaction events.

If we let $\mathbf{X}(t)=(S(t),E(t),I(t))$ denote the state vector at time $t$, then the rate vector $\mathbf{h}$ for the SEIR model is

$$\mathbf{h}(\mathbf{X}(t),\mathit{\theta })=(\beta S(t)I(t),\mu E(t),\gamma I(t){)}^T.$$ (A-10)

A-2. Derivation of the linear noise approximation

A-2.1. SDE approximation for MJP

A stochastic way to approximate the MJP model is to use the Stochastic Differential Equation (SDE) approximation, also known as the chemical Langevin equation (CLE) (Gillespie, 2000). The SDE method can be viewed an approximation of the MJP at time $t$, obtained by applying a normal approximation to the Poisson distributed number of state transitions in a small interval of time $(t,t+\mathrm{\Delta }t)$ (Gillespie, 2000; Wallace, 2010). The deterministic part in SDE corresponds to the right hand side of ODE (7) and stochastic part is related to the variance of the system. The SDE for general stochastic kinetic models can be written as

$$\mathrm{d}\mathbf{X}(t)={\mathbf{A}}^T\mathbf{h}(\mathbf{X}(t),\mathit{\theta }(t))\mathrm{d}t+\sqrt{{\mathbf{A}}^T\mathbf{H}(\mathbf{X}(t),\mathit{\theta }(t))\mathbf{A}}\cdot \mathrm{d}{\mathbf{W}}_t,$$ (A-11)

where ${\mathbf{W}}_t$ denote a $d$ dimensional Wiener process and the square root $\sqrt{.}$ means the Cholesky triangle of the $d\times d$ covariance matrix.

A-2.2. LNA approximation of the SDE

Since in the main text we assume the rate $\mathit{\theta }(t)$ varies in a piecewise constant way, without loss of generality, we use the notation $\mathit{\theta }$ for the rate in a given time interval where the LNA is applied.

Theorem A-2.1

(Linear Noise Approximation for SDE). Let $\mathit{\eta }(t)$ be the solution of ordinary differential equation (7) with initial value ${\mathit{\eta }}_0$. Let $N$ be the system size, which is the total number of individuals in the system (In SIR model, $N$ will be the total population, i.e $N=S+I+R)$, $\mathit{\theta }=\left({\theta }_1,\dots ,{\theta }_q\right)$ denote the vector of rate parameters in $q$ reactions. Then the solution $\mathit{X}(t)$ of the SDE (A-11) satisfies the following equation

$$\begin{array}{l}\frac{1}{\sqrt{N}}\mathrm{d}(\mathbf{X}(t)-\mathit{\eta }(t))=\frac{1}{\sqrt{N}}(\mathbf{F}(\mathit{\eta }(t),\mathit{\theta })(\mathbf{X}(t)-\mathit{\eta }(t))+o(1))\mathrm{d}t+\\ \left(\frac{1}{\sqrt{N}}\sqrt{{\mathbf{A}}^T\mathbf{H}(\mathit{\eta }(t),\mathit{\theta })\mathbf{A}}+o(1)\right)\mathrm{d}{\mathbf{W}}_t,\end{array}$$ (A-12)

as $N\to +\mathrm{\infty }$.

Proof.

The following derivation is based on (Wallace, 2010).

We rescale both the compartment size and reaction rates as follows:

$$\tilde{\mathbf{X}}(t)=N^{-1}\cdot \mathbf{X}(t)$$ (A-13)

$${\tilde{\theta }}_i=N^{m_i-1}{\theta }_i,$$ (A-14)

where $m_i={\sum }_{j=1}^d {\tilde{a}}_{ij}$ is the sum of coeffcients in the left hand side of i-th reaction as in Section A-1. The transformed $\tilde{\mathbf{X}}(t)$ represents the proportion of individuals/reactants each compartment with respect to the total population size. Then we have $\mathbf{h}(\mathbf{X}(t),\mathit{\theta })=Nh(\tilde{\mathbf{X}}(t),\tilde{\mathit{\theta }})$ and $\mathbf{F}(\mathit{\eta }(t),\mathit{\theta })=\mathbf{F}(\tilde{\mathit{\eta }}(t),\tilde{\mathit{\theta }})$. Hence, the SDE (A-11) becomes

$$\mathrm{d}\tilde{\mathbf{X}}\left(t\right)={\mathbf{A}}^T\mathbf{h}\left(\tilde{\mathbf{X}}\left(t\right),\tilde{\mathit{\theta }}\right)\mathrm{d}t+\frac{1}{\sqrt{N}}\sqrt{{\mathbf{A}}^T\mathbf{H}(\tilde{\mathbf{X}}\left(t\right),\tilde{\mathit{\theta }})\mathbf{A}}\cdot \mathrm{d}{\mathbf{W}}_t.$$ (A-15)

Let $\tilde{\mathit{\eta }}(t)$ be the solution of the ODE

$$\mathrm{d}\tilde{\mathit{\eta }}\left(t\right)={\mathbf{A}}^T\mathbf{h}\left(\tilde{\mathit{\eta }}\left(t\right),\tilde{\mathit{\theta }}\right)\mathrm{d}t,$$ (A-16)

and we have $\mathit{\eta }(t)=N\tilde{\mathit{\eta }}(t)$, where $\mathit{\eta }(t)$ is the solution of the ODE (7). $\tilde{\mathit{\eta }}(t)$ can be viewed as a scaled version solution of ODE (7). Let $\mathit{\xi }(t)=\sqrt{N}(\tilde{\mathbf{X}}(t)-\tilde{\mathit{\eta }}(t))=\frac{1}{\sqrt{N}}(\mathbf{X}(t)-\mathit{\eta }(t))$ denote the scaled residual, then the rescaled compartment size vector $\tilde{\mathbf{X}}(t)$ can be written as

$$\tilde{\mathbf{X}}\left(t\right)=\frac{1}{\sqrt{N}}\mathit{\xi }\left(t\right)+\tilde{\mathit{\eta }}\left(t\right).$$ (A-17)

After using first order Taylor expansion of $\mathbf{h}(\tilde{\mathbf{X}}(t),\tilde{\mathit{\theta }})$ and $\mathbf{H}(\tilde{\mathbf{X}}(t),\tilde{\mathit{\theta }})$ around

$\tilde{\mathbf{X}}=\tilde{\mathbf{\eta }}(t)$, the SDE (A-15) becomes

$$\begin{array}{l}\mathrm{d}\tilde{\mathbf{X}}(t)={\mathbf{A}}^T\mathbf{h}\left(\tilde{\mathbf{\eta }}(t)+\frac{1}{\sqrt{N}}\mathit{\xi }(t),\tilde{\mathbf{\theta }}\right)\mathrm{d}t+\sqrt{{\mathbf{A}}^T\mathbf{H}\left(\tilde{\mathbf{\eta }}(t)+\frac{1}{\sqrt{N}}\mathit{\xi }(t),\tilde{\mathit{\theta }}\right)\mathbf{A}}\cdot \mathrm{d}{\mathbf{W}}_t\\ =\left({\mathbf{A}}^T\mathbf{h}(\tilde{\mathbf{\eta }}(t),\tilde{\mathbf{\theta }})+\mathbf{F}(\tilde{\mathbf{\eta }}(t),\tilde{\mathbf{\theta }})\cdot \frac{1}{\sqrt{N}}\mathit{\xi }(t)+𝒪\left(N^{-1}\right)\right)\mathrm{d}t\\ +\frac{1}{\sqrt{N}}\sqrt{{\mathbf{A}}^T\mathbf{H}(\tilde{\mathbf{\eta }}(t),\tilde{\mathit{\theta }})\mathbf{A}+𝒪(\frac{1}{\sqrt{N}})}\cdot \mathrm{d}{\mathbf{W}}_t\\ =\left({\mathbf{A}}^T\mathbf{h}(\tilde{\mathbf{\eta }}(t),\tilde{\mathit{\theta }})+\frac{1}{\sqrt{N}}\mathbf{F}(\tilde{\mathbf{\eta }}(t),\tilde{\mathit{\theta }})\cdot \mathit{\xi }(t)\right)\mathrm{d}t\\ +\frac{1}{\sqrt{N}}\sqrt{{\mathbf{A}}^T\mathbf{H}(\tilde{\mathbf{\eta }}(t),\tilde{\mathit{\theta }})\mathbf{A}}\cdot \mathrm{d}{\mathbf{W}}_t+o(N^{-1/2})\mathrm{d}{\mathbf{W}}_t+o\left(N^{-1}\right)\mathrm{d}t.\end{array}$$

where $\mathbf{F}(\tilde{\mathbf{\eta }}(t),\mathit{\theta }):={\left.\frac{\partial {\mathbf{A}}^T\mathbf{h}(\tilde{\mathbf{X}}(t),\mathit{\theta })}{\partial \tilde{\mathbf{X}}}\right|}_{\tilde{\mathbf{X}}=\tilde{\mathbf{\eta }}(t)}$ is the Jacobian matrix of the deterministic part ${\mathbf{A}}^T\mathbf{h}(\tilde{\mathbf{X}}(t),\mathit{\theta })$ in (7) at $\tilde{\mathbf{\eta }}(t)$. By subtracting (A-16) and multiplying by $\sqrt{N}$ on the two ends, the above equation becomes a differential equation with respect to $\mathit{\xi }$:

$$\text{d}\xi (t)=\mathbf{F}(\tilde{\mathit{\eta }}(t),\theta )\xi (t)\text{d}t+\sqrt{{\mathbf{A}}^T\mathbf{H}(\tilde{\mathit{\eta }}(t),\tilde{\theta })\mathbf{A}}\cdot \text{d}{\mathbf{W}}_t+o(N^{-1/2})\text{d}{\mathbf{W}}_t+o(N^{-1})\text{d}t\text{.}$$ (A-18)

After multiplying by $\sqrt{N}$, the above equation gives us (A-12).

Recall that $\mathbf{M}(t)$ is the solution of (8) with initial condition $\mathbf{M}(0)={\mathbf{X}}_0-{\mathbf{\eta }}_0$. We can use $\mathbf{\eta }(t)+\mathbf{M}(t)$ as an approximation of $\mathbf{X}(t)$. Based on the local Lipschitz property of $\mathbf{F}(\mathbf{\eta }(t),\mathit{\theta })$ with respect to $t$ and ${\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })$, $\mathbf{X}(t)$ can be approximated by $\mathbf{\eta }(t)+\mathbf{M}(t)$ with

$$\mathbf{X}\left(t\right)=\mathbf{\eta }\left(t\right)+\mathbf{M}\left(t\right)+o(N^{\frac{1}{2}}),$$ (A-19)

for fixed $t$ as system size $N\to +\mathrm{\infty }$.

A-2.3. Derivation of equations (9) and (10) in the main text

Lemma A-2.2 (Solution of linear ODE system).

Let $\mathbf{F}(t)\in {\mathbb{R}}^{d\times d}$ and $\mathbf{X}(t)\in {\mathbb{R}}^d$ be function of defined on $\{t:t\ge 0\}$ that satisfies the following linear ODE

$$\mathrm{d}\mathbf{X}(t)=\mathbf{F}(t)\mathbf{X}(t)\mathrm{d}t,{\mathbf{X}}_0={\mathbf{x}}_0.$$ (A-20)

For $t\ge 0$, the solution of (A-20) can be represented as

$$\mathbf{X}(t)=\mathbf{\Sigma }(t,0){\mathbf{x}}_0$$ (A-21)

where $\mathbf{\Sigma }(t,0)$ is the solution of ordinary differential equation in ${\mathbb{R}}^{d\times d}$

$$\mathrm{d}\mathbf{\Sigma }(t,0)=\mathbf{F}(t)\mathbf{\Sigma }(t,0)\mathrm{d}t,\mathbf{\Sigma }(0,0)=\mathbf{I}.$$ (A-22)

Lemma (A-2.2) gives the solution of linear ODE. Hence, the solution for the main text linear ODE 9 is on $\left[t_{i-1},t\right]$ will be

$$\mathbf{m}(t)=\mathbf{\Sigma }\left(t,t_{i-1}\right){\mathbf{m}}_{i-1},$$ (A-23)

where ${\mathbf{m}}_{i-1}$ is the initial state at $t_{i-1}$ and $\mathbf{\Sigma }\left(t,t_{i-1}\right)$ is the transition matrix by

$$\mathrm{d}\mathbf{\Sigma }\left(t,t_{i-1}\right)=\mathbf{F}\left(\mathit{\eta }\left(t\right),\mathit{\theta }\right)\mathbf{\Sigma }\left(t,t_{i-1}\right)\mathrm{d}t,\mathbf{\Sigma }\left(t_{i-1};t_{i-1}\right)=\mathbf{I},$$ (A-24)

and ${\mathbf{m}}_{i-1}$ is the initial value for $\mathbf{m}$ at time $t_{i-1}$.

Theorem A-2.3.

Let $\{\mathbf{M}(t){\}}_{t\ge 0}\in {\mathbb{R}}^d$ be stochastic process that satisfies the following stochastic differential equation,

$$\mathrm{d}\mathbf{M}\left(t\right)=\mathbf{F}\left(\mathbf{\eta }\left(t\right),\mathbf{\theta }\right)\mathbf{M}\left(t\right)\mathrm{d}t+\sqrt{{\mathbf{A}}^T\mathbf{H}\left(\mathbf{\eta }\left(t\right),\mathit{\theta }\right)\mathbf{A}}\mathrm{d}{\mathbf{W}}_t.$$ (A-25)

Then the solution of (A-25) is the Gaussian process

$$\mathbf{M}(t)=\mathbf{\Sigma }\left(t,t_0\right)\left(\mathbf{M}\left(t_0\right)+{\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right)\sqrt{{\mathbf{A}}^T\mathbf{H}(\mathit{\eta }(t),\mathit{\theta })\mathbf{A}}\mathrm{d}{\mathbf{W}}_s\right),$$ (A-26)

with mean process $\mathbf{m}(t):=\mathbf{E}\left[\mathbf{M}(t)\mid \mathbf{M}\left(t_0\right)\right]satisfies(9)andvarianceprocess\mathbf{\Phi }(t):=Var\left[\mathbf{M}(t)\mid \mathbf{M}\left(t_0\right)\right]$ satisfies (10).

Proof.

Define matrix function $\mathbf{\Sigma }\left(t,t_0\right)$ as (A-24). First we apply the linear transform $\tilde{\mathbf{M}}(t)={\mathbf{\Sigma }}^{-1}\left(t;t_0\right)\mathbf{M}(t)$. Based on Ito’s lemma, (A-25) can be simplified as a SDE of $\tilde{\mathbf{M}}(t)$:

$$\mathrm{d}\tilde{\mathbf{M}}\left(t\right)={\mathbf{\Sigma }}^{-1}\left(t;t_0\right)\sqrt{{\mathbf{A}}^T\mathbf{H}\left(\mathbf{\eta }\left(t\right),\mathit{\theta }\right)\mathbf{A}}\mathrm{d}{\mathbf{W}}_t,$$ (A-27)

with solution.

$$\tilde{\mathbf{M}}(t)=\tilde{\mathbf{M}}\left(t_0\right)+{\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s;t_0\right)\sqrt{{\mathbf{A}}^T\mathbf{H}(\mathit{\eta }(t),\mathit{\theta })\mathbf{A}}\cdot \mathrm{d}{\mathbf{W}}_s$$

Then the solution of $\mathbf{M}(t)$ is

$$\mathbf{M}(t)=\mathbf{\Sigma }\left(t,t_0\right)\left(\mathbf{M}\left(t_0\right)+{\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right)\sqrt{{\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{A}}\mathrm{d}{\mathbf{W}}_s\right).$$ (A-28)

$\mathbf{\Sigma }\left(t,t_0\right)\mathbf{M}\left(t_0\right)$ in (A-28) is a deterministic function of $t$. The integral ${\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right)\sqrt{{\mathbf{A}}^T\mathbf{H}(\eta (t))\mathbf{A}}\mathrm{d}{\mathbf{W}}_s$ in (A-28) should be Gaussian random variable with mean 0 since it is a linear combination of the increments of Brownian motion with different variance. Hence, the $\mathbf{M}(t)$ should be a Gaussian process. By taking the expectation of (A-28), the mean of $\mathbf{m}(t)=\mathbf{E}\left[{\mathbf{M}}_t\right]$ satisfies

$$\mathbf{m}\left(t\right)=\mathbf{\Sigma }\left(t,t_0\right)\mathbf{m}\left(t_0\right),$$ (A-29)

which corresponds to the solution of ODE (9).

For the variance process, from (A-28),

$$\mathbf{\Phi }(t)=\mathbf{\Sigma }\left(t,t_0\right){\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right){\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{A}{\mathbf{\Sigma }}^{-1}\left(s,t_0\right)\mathrm{d}s\cdot {\mathbf{\Sigma }}^T\left(t,t_0\right)$$ (A-30)

By differentiation with respect to $t$, (A-30) becomes

$$\begin{array}{l}\mathrm{d}\mathbf{\Phi }(t)=\mathrm{d}\mathbf{\Sigma }\left(t,t_0\right)\cdot {\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right){\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{A}{\mathbf{\Sigma }}^{-T}\left(s,t_0\right)\mathrm{d}s\cdot {\mathbf{\Sigma }}^T\left(t,t_0\right)\\ +\mathbf{\Sigma }\left(t,t_0\right)\cdot \mathrm{d}\left[{\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right){\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{A}{\mathbf{\Sigma }}^{-T}\left(s,t_0\right)\mathrm{d}s\right]\cdot {\mathbf{\Sigma }}^T\left(t,t_0\right)\\ +\mathbf{\Sigma }\left(t,t_0\right)\cdot {\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right){\mathbf{A}}^T\mathbf{H}(\mathit{\eta }(t),\mathit{\theta })\mathbf{A}{\mathbf{\Sigma }}^{-T}\left(s,t_0\right)\mathrm{d}s\cdot \mathrm{d}{\mathbf{\Sigma }}^T\left(t,t_0\right)\\ =\mathbf{F}(\mathbf{\eta }(t),\mathit{\theta })\cdot \mathbf{\Sigma }\left(t,t_0\right){\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right){\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{A}{\mathbf{\Sigma }}^{-T}\left(s,t_0\right)\mathrm{d}s\cdot {\mathbf{\Sigma }}^T\left(t,t_0\right)\mathrm{d}t\\ +\mathbf{\Sigma }\left(t,t_0\right)\cdot {\mathbf{\Sigma }}^{-1}\left(t,t_0\right){\mathbf{A}}^T\mathbf{H}(\mathit{\eta }(t),\mathit{\theta })\mathbf{A}{\mathbf{\Sigma }}^{-T}\left(t,t_0\right)\cdot {\mathbf{\Sigma }}^T\left(t,t_0\right)\cdot \mathrm{d}t\\ +\mathbf{\Sigma }\left(t,t_0\right)\cdot {\int }_{t_0}^t {\mathbf{\Sigma }}^{-1}\left(s,t_0\right){\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{A}{\mathbf{\Sigma }}^{-T}\left(s,t_0\right)\mathrm{d}s\cdot {\mathbf{\Sigma }}^T\left(t,t_0\right){\mathbf{F}}^T(\mathbf{\eta }(t),\mathit{\theta })\cdot \mathrm{d}t\\ =\left(\mathbf{F}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{\Phi }(t)+\mathbf{\Phi }(t){\mathbf{F}}^T(\mathbf{\eta }(t),\mathit{\theta })+{\mathbf{A}}^T\mathbf{H}(\mathbf{\eta }(t),\mathit{\theta })\mathbf{A}\right)\mathrm{d}t,\end{array}$$

which is the result in (10).

A-2.4. Relationship between LNA and other methods

The SDE approach can be viewed as a normal approximation based on a $\tau -$ leaping step for the MJP. The LNA can be derived either directly from Taylor expansion of the transition probability of the MJP or the Taylor expansion of the transition density of the SDE. The ODE solution can be considered as a limit of the mean trajectory of the MJP when system size $N$ goes to infinity. ODE solution can also be viewed as the deterministic part for SDE (A-11) and the mean process for LNA based on (A-36). Figure A-2.4 depicts relationships between different dynamical system representations as a diagram.

A-3. Non-centered parameterization

In LNA, the latent trajectory $\mathbf{X}(t)$ is decomposed into the deterministic part $\eta (t)$ plus a stochastic part $\mathbf{M}(t)$ that follows a multivariate Gaussian distribution with mean 0. However, the population size at the i-th time interval ${\mathbf{X}}_i$ depends on rate parameter $\mathbf{\theta }$ and is correlated with other population sizes ${\mathbf{X}}_j$s in the trajectory, leading to mixing issues for the MCMC chain, especially when we introduce multiple change points for reproduction number $R_0$.

FIGURE A-2.

The relationship between different dynamical system representations.

Here we take the idea of non-centered parameterization from Papaspiliopoulos, Roberts and Sköld (2007, 2003) and reparameterize the latent trajectrory in terms of residuals ${\mathbf{X}}_i-{\mathbf{\eta }}_i$ for $i=1,\dots ,T$. Given rate parameters ${\mathbf{\theta }}_{i-1}$, ODE solution ${\eta }_{0:T}$, fundamental matrix $\mathbf{\Sigma }\left(t_i,t_{i-1}\right)$ and variance matrix ${\mathrm{\Phi }}_i$ in (10), the trajectory ${\mathbf{X}}_{0:T}$ can be parameterized using standard Gaussian noise ${\mathit{\xi }}_{1:T}$ based on the following iterative equations:

$${\mathbf{X}}_0={\mathit{\eta }}_0,$$ (A-31)

$$\begin{array}{l}{\mathbf{X}}_i=\mathit{\mu }({\mathbf{X}}_{i-1}-\mathit{\eta }(t_{i-1}),\mathrm{\Delta }{t}_i,{\mathit{\theta }}_{i-1})+{\mathit{\eta }}_i+{\mathbf{\Phi }}_i^{1/2}{\mathit{\xi }}_i,\\ =\mathbf{\Sigma }(t_i,t_{i-1})({\mathbf{X}}_{i-1}-{\mathit{\eta }}_{i-1})+{\mathit{\eta }}_i+{\mathbf{\Phi }}_i^{1/2}{\mathit{\xi }}_i,\text{for}i=1,\dots ,T\text{.}\end{array}$$ (A-32)

Let ${\mathbf{M}}_i:={\mathbf{X}}_i-{\eta }_i$ denote the residual in grid cell $i$. Based on (A-32), the residual process satisfies

$${\mathbf{M}}_1={\mathbf{\Phi }}_1^{1/2}{\mathit{\xi }}_1$$ (A-33)

$${\mathbf{M}}_i=\mathbf{\Sigma }(t_{i-1},t_i){\mathbf{M}}_{i-1}+{\mathbf{\Phi }}_i^{1/2}{\mathit{\xi }}_i,i=2,\dots ,T.$$ (A-34)

Then ${\mathbf{M}}_{0:T}$ can be viewed as a Gaussian Markov random field with mean $0$ that follows the Markov property on a chain graph. Let ${\mathbf{\Sigma }}_i$ be the abbreviated notation of $\mathbf{\Sigma }\left(t_i,t_{i-1}\right)$ and ${\mathbf{P}}_i={\mathbf{\Phi }}_i^{1/2}$. From (A-34), ${\mathbf{M}}_i$ can be written as

$$\begin{array}{l}{\mathbf{M}}_i={\mathbf{\Sigma }}_{i-1}{\mathbf{M}}_{i-1}+{\mathbf{P}}_i{\mathit{\xi }}_i\\ ={\mathbf{\Sigma }}_{i-1}\left({\mathbf{\Sigma }}_{i-2}{\mathbf{M}}_{i-2}+{\mathbf{P}}_{i-1}{\mathit{\xi }}_{i-1}\right)+{\mathbf{P}}_i{\mathit{\xi }}_i\\ ={\mathbf{\Sigma }}_{i-1}{\mathbf{\Sigma }}_{i-2}{\mathbf{M}}_{i-2}+{\mathbf{\Sigma }}_{i-1}{\mathbf{P}}_{i-1}{\mathit{\xi }}_{i-1}+{\mathbf{P}}_i{\mathit{\xi }}_i\\ ={\mathbf{\Sigma }}_{i-1}{\mathbf{\Sigma }}_{i-2}\cdots {\mathbf{\Sigma }}_1{\mathbf{P}}_1{\mathit{\xi }}_1+\cdots +{\mathbf{P}}_i{\mathit{\xi }}_i\\ =\sum _{k=1}^i (\prod _{j=k}^{i-1} {\mathbf{\Sigma }}_j){\mathbf{P}}_k{\mathit{\xi }}_k.\end{array}$$

Since ${\mathbf{\Sigma }}_i$ and ${\mathbf{P}}_i$ are governed by rate parameters ${\mathbf{\theta }}_{i-1}$ and initial value ${\mathbf{X}}_0$, then we define the transform matrix $\mathbf{L}\left({\mathbf{X}}_0,{\mathbf{\theta }}_{0:T}\right)\in {\mathbb{R}}^{2T\times 2T}$,

$$\mathbf{L}\left({\mathbf{X}}_0,{\mathit{\theta }}_{0:T}\right)=\left(\begin{array}{cccccc}{\mathbf{P}}_1& 0& 0& \cdots & 0& 0\\ {\mathbf{\Sigma }}_1{\mathbf{P}}_1& {\mathbf{P}}_2& 0& \cdots & 0& 0\\ {\mathbf{\Sigma }}_2{\mathbf{\Sigma }}_1{\mathbf{P}}_1& {\mathbf{\Sigma }}_2{\mathbf{P}}_2& {\mathbf{P}}_3& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \ddots & \cdots & \cdots \\ {\mathbf{\Sigma }}_{T-2}\cdots {\mathbf{\Sigma }}_1{\mathbf{P}}_1& {\mathbf{\Sigma }}_{T-2}\cdots {\mathbf{\Sigma }}_2{\mathbf{P}}_2& {\mathbf{\Sigma }}_{T-2}\cdots {\mathbf{\Sigma }}_2{\mathbf{P}}_3& \cdots & {\mathbf{P}}_{T-1}& 0\\ {\mathbf{\Sigma }}_{T-1}\cdots {\mathbf{\Sigma }}_1{\mathbf{P}}_1& {\mathbf{\Sigma }}_{T-1}\cdots {\mathbf{\Sigma }}_2{\mathbf{P}}_2& {\mathbf{\Sigma }}_{T-1}\cdots {\mathbf{\Sigma }}_3{\mathbf{P}}_3& \cdots & {\mathbf{\Sigma }}_{T-1}{\mathbf{P}}_{T-1}& {\mathbf{P}}_T\end{array}\right)$$

A linear relationship between ${\mathbf{X}}_{1:T}$ and the reparameterized noise ${\mathit{\xi }}_{1:T}$ can be established with the help of the above transform matrix $\mathbf{L}$,

$$\left(\begin{array}{c}{\mathbf{X}}_1\\ ⋮\\ {\mathbf{X}}_T\end{array}\right)=\left(\begin{array}{c}{\mathit{\eta }}_1\\ ⋮\\ {\mathit{\eta }}_T\end{array}\right)+\mathbf{L}\left({\mathbf{X}}_0,{\mathbf{\theta }}_{0:T}\right)\left(\begin{array}{c}{\mathit{\xi }}_1\\ ⋮\\ {\mathit{\xi }}_T\end{array}\right).$$ (A-36)

Instead of directly updating ${\mathbf{X}}_{1:T}$, we will apply the above transform and update the Gaussian noise ${\mathit{\xi }}_{1:T}$ instead. The MCMC approach will focus on sampling parameter $I_0$, $R_0$, $\gamma$, ${\mathit{\delta }}_{1:T}$, ${\mathit{\xi }}_{1:T},\sigma$ with the posterior likelihood

$$\begin{array}{l}\mathrm{P}\mathrm{r}\left(I_0,R_0,\gamma ,{\mathit{\delta }}_{1:T},{\mathit{\xi }}_{1:T},\sigma \mid \mathbf{g}\right)\\ \propto \mathrm{P}\mathrm{r}\left(\mathbf{g}\mid I_0,R_0,\gamma ,{\mathit{\delta }}_{1:T},{\mathit{\xi }}_{1:T},\sigma \right)\mathrm{P}\mathrm{r}\left(I_0\right)\mathrm{P}\mathrm{r}\left(R_0\right)\mathrm{P}\mathrm{r}(\gamma )\mathrm{P}\mathrm{r}\left({\mathit{\delta }}_{1:T}\right)\mathrm{P}\mathrm{r}\left({\mathit{\xi }}_{1:T}\right)\mathrm{P}\mathrm{r}(\sigma )\\ \propto \mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T}\right)\mathrm{P}\mathrm{r}\left(I_0\right)\mathrm{P}\mathrm{r}\left(R_0\right)\mathrm{P}\mathrm{r}(\gamma )\mathrm{P}\mathrm{r}\left({\mathit{\delta }}_{1:T}\right)\mathrm{P}\mathrm{r}\left({\mathit{\xi }}_{1:T}\right)\mathrm{P}\mathrm{r}(\sigma ).\end{array}$$

In summary, the transformation that allows us to move from parameterization in terms of ${\mathbf{X}}_{0:T},{\theta }_{0:T}$ to the parameterization in terms of $I_0$, $R_0$, $\gamma$, ${\mathit{\delta }}_{1:T}$, ${\mathit{\xi }}_{1:T},\sigma$ are based on the following equations:

1. $R_{0_i}:=R_0\left(t_i\right)=R_0\cdot \mathrm{e}\mathrm{x}\mathrm{p}({\prod }_{j=1}^i {\delta }_j\sigma )$ - a function of $R_0,{\mathit{\delta }}_{1:i}$ and $\sigma$.

2. ${\beta }_i:=\beta \left(t_i\right)=\frac{N{R}_0\left(t_i\right)}{\gamma }$ - a function of $R_0$, ${\mathit{\delta }}_{1:i},\sigma$ and $\gamma$.

3. ${\mathbf{\theta }}_i=\left({\beta }_i,\gamma \right)$ - a function of $R_0$, ${\mathit{\delta }}_{1:i},\sigma$ and $\gamma$.

4. ${\mathbf{\theta }}_{0:T}$ - a function of $R_0,{\mathit{\delta }}_{1:T},\sigma$ and $\gamma$.

5. ${\mathbf{X}}_0={\left(N,I_0\right)}^T$.

6. ${\mathbf{X}}_{1:T}={\mathit{\eta }}_{1:T}+\mathbf{L}\left({\mathbf{X}}_0,{\mathbf{\theta }}_{0:T}\right){\mathit{\xi }}_{1:T}$ - a function of $R_0$, ${\mathit{\delta }}_{1:T}$, $\sigma$, $\gamma ,I_0$ and ${\mathit{\xi }}_{1:T}$.

A-4. MCMC details

A-4.1. Elliptical slice sampler

FIGURE A-3.

Parameter dependency graph after reparameterization. The root nodes $I_0$, $\gamma$, $\sigma$, ${\delta }_{1:T}$, $R_0,\sigma$ outside the large box are parameters and latent variables after reparameterization, for which we assign prior distributions. The dash-dotted lines show deterministic relationships and the solid lines show the stochastic dependencies. The grey node denotes the observed data. The figure shows the dependency structure between the transformed parameters and original parameters ${\mathit{\theta }}_{0:T},{\mathbf{X}}_0$ and ${\mathbf{X}}_{0:T}$.

The elliptical slice sampler, proposed by Murray, Adams and MacKay (2010), aims at sampling from posterior distributions associated with probability models with a latent a priori zero-mean Gaussian random vector $\mathbf{X}\in {\mathbb{R}}^d$ with covariance $\mathrm{\Sigma }(\mathbf{\theta })$, i.e., $\mathbf{X}\sim 𝒩(0,\mathrm{\Sigma }(\mathbf{\theta }))$. We use $L(\mathbf{Y}\mid \mathbf{X},\mathbf{\theta })$ to denote the likelihood function for observed data $\mathbf{Y}\mathrm{g}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathbf{X}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathbf{\theta }.\mathrm{H}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e},\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{b}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathbf{X}$ given is

$$\mathrm{Pr}\left(\mathbf{X}∣\mathbf{Y},\mathbf{\theta }\right)\propto L\left(\mathbf{Y}∣\mathbf{X},\mathbf{\theta }\right)𝒩\left(\mathbf{X}∣0,\mathrm{\Sigma }\left(\mathbf{\theta }\right)\right)\pi \left(\mathbf{\theta }\right),$$

where $\pi (\mathbf{\theta })$ is the prior distribution for parameter $\mathbf{\theta }$. The goal of elliptical slice sampler is to obtain posterior samples of latent variable $\mathbf{X}$ from $p(\mathbf{X}\mid \mathbf{Y},\mathbf{\theta })$. The proposal step in elliptical sampling consists of two parts: (1) proposing an auxiliary random vector $\mathbf{Z}\in {\mathbb{R}}^d$ from distribution $𝒩(0,\mathrm{\Sigma }(\mathbf{\theta }))$, (2) proposing a variable $\alpha \in [0,2\pi ]$ as an angle parameter. In elliptical slice sampler, a new state $\left({\mathbf{X}}^{\prime },{\mathbf{Z}}^{\prime }\right)$ is proposed by rotating the previous state $(\mathbf{X},\mathbf{Z})$ with angle $\alpha$,

$${\mathbf{X}}^{\prime }=\mathbf{X}\cos (\alpha )+\mathbf{X}\sin (\alpha )$$ (A-37)

$${\mathit{Z}}^{\prime }=\mathit{Z}\sin (\alpha )-\mathit{Z}\cos (\alpha )$$ (A-38)

For any given $\alpha$, this transition leaves the joint prior probability invariant, i.e,

$$𝒩(\mathbf{X}\mid \mathbf{0},\mathrm{\Sigma })𝒩(\mathbf{Z}\mid \mathbf{0},\mathrm{\Sigma })=𝒩\left({\mathbf{X}}^{\prime }\mid \mathbf{0},\mathrm{\Sigma }\right)𝒩\left({\mathbf{Z}}^{\prime }\mid \mathbf{0},\mathrm{\Sigma }\right).$$

Hence, $\left({\mathbf{X}}^{\prime },{\mathbf{Z}}^{\prime }\right)$ are considered at the proposed state and the ratio and the propose transition probability from $(\mathbf{X},\mathbf{Z})$ to $\left({\mathbf{X}}^{\prime },{\mathbf{Z}}^{\prime }\right)$ should equal that from $\left({\mathbf{X}}^{\prime },{\mathbf{Z}}^{\prime }\right)$ to $(\mathbf{X},\mathbf{Z})$, i.e

$$\frac{\mathrm{P}\mathrm{r}\left(\left({\mathbf{X}}^{\prime },{\mathbf{Z}}^{\prime }\right)\to (\mathbf{X},\mathbf{Z})\right)}{\mathrm{P}\mathrm{r}\left((\mathbf{X},\mathbf{Z})\to \left({\mathbf{X}}^{\prime },{\mathbf{Z}}^{\prime }\right)\right)}=1.$$

The algorithm for elliptical slice sampler is given in Algorithm 1. Notice that iterations will stop only when a new sample is accepted. Hence, the elliptical slice sampler has acceptance rate 1, meaning that it will always update the latent random vector $\mathbf{X}$ at each MCMC iteration.

Algorithm 1.

Elliptical slice sampler for posterior distribution $\pi (\cdot \mid \mathbf{Y},\mathbf{\theta })$

1	Input: Latent variable from the previous iteration $\mathbf{X}\in {\mathbb{R}}^d$. Observed data $\mathbf{Y}$, previous updated parameter $\mathbf{X}$..
2	Output Updated latent variable value ${\mathbf{X}}^{\prime }$
3	Sample ellipse $\mathbf{Z}\sim 𝒩(0,\mathbf{\Sigma }(\mathbf{\theta }\left)\right)$
4	Compute log-likelihood threshold: sample $U\sim \mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}(0,1)$ and let
	$\tau \leftarrow \log L(\mathbf{Y}\mid \mathbf{X},\mathbf{\theta })+\log (U)$
5	Sample angle parameter $\alpha \sim \mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}[0,2\pi ]$ and $\left[{\alpha }_{\mathrm{m}\mathrm{i}\mathrm{n}},{\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]\leftarrow [\alpha -2\pi ,\alpha ]$
6	${\mathbf{X}}^{\prime }\leftarrow \mathbf{X}\cdot \mathrm{c}\mathrm{o}\mathrm{s}\alpha +\mathbf{Z}\cdot \mathrm{s}\mathrm{i}\mathrm{n}\alpha$
7	while $\mathrm{l}\mathrm{o}\mathrm{g}\left(L\left(\mathbf{Y}\mid {\mathbf{X}}^{\prime },\mathbf{\theta }\right)\right)<\tau$ do
8	if $\alpha <0$ then
9	${\alpha }_{\mathrm{m}\mathrm{i}\mathrm{n}}\leftarrow \alpha$
10	else
11	${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}\leftarrow \alpha$
12	Sample $\alpha \sim \mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\left({\alpha }_{\mathrm{m}\mathrm{i}\mathrm{n}},{\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$.
13	Make new proposal
	${\mathbf{X}}^{\prime }\leftarrow \mathbf{X}\cdot \cos \alpha +\mathbf{Z}\cdot \sin \alpha$
14	Return ${\mathbf{X}}^{\prime }$.

A-4.2. MCMC algorithm for the LNA-based SIR model

In this framework, the observed data are the genealogy g estimated from a sample of sequences from virus hosts. The sufficient statistics for SIR structured coalescent likelihood would be the coalescent times $𝒯$ and sampling times $𝒮$. The unknown parameters and the latent variables are

1. The initial number of infected individuals: $I_0$. The initial population is parameterized as ${\mathbf{X}}_0=\left(N,I_0\right)$, suppressing that $S_0=N-I_0$ and that there are no recovered individuals at time 0.

2. The initial basic reproduction number $R_0$.

3. The removal rate $\gamma$.

4. The hyperparameter $\sigma$ that controls the smoothness of $R_0(t)$ trajectory.

5. The parameters modeling the first order differences in $\mathrm{l}\mathrm{o}\mathrm{g}\left(R_0(t)\right):{\mathit{\delta }}_{1:T}$.

   Note that assuming ${\delta }_0=1$, the infection rate ${\beta }_i$ can be obtained as

   $${\beta }_i=\frac{\gamma }{N}\cdot R_0\exp \left(\sum _{k=0}^i\sigma {\delta }_k\right).$$ (A-39)

   The parameter ${\mathbf{\theta }}_{0:T}$ can be obtained from $R_0$, ${\mathit{\delta }}_{1:T},\gamma$ and $\sigma$.

6. Random noise for the population trajectory at $t_1,\dots ,t_T$, i.e. ${\mathit{\xi }}_{1:T}$, with ${\mathit{\xi }}_i{~}_{\text{iid}}𝒩(0,\mathbf{I})$ a priori. The latent SIR trajectories ${\mathbf{X}}_{0:T}$ can be recovered from ${\mathbf{\theta }}_{0:T},{\mathbf{X}}_0$ and random noise ${\mathit{\xi }}_{1:T}$.

The MCMC update for parameters and latent variables is given in Algorithm 2.

Algorithm 2.

Updating rule in the LNA-based MCMC algorithm

1:	Input: Parameter values from the previous interation $I_0$,$R_0$,$\gamma$,${\mathit{\delta }}_{1:T}$,$\sigma ,{\mathit{\xi }}_{1:T}$, geneology g. Proposal density $q_1(\cdot )$, $q_2(\cdot )$ for updating the initial number of infected individuals and the removal rate.
2:	Output Updated parameters values
3:	Calculate ${\mathbf{X}}_{0:T},{\mathbf{\theta }}_{0:T}$ based on $I_0$,$R_0$,$\gamma$,${\mathit{\delta }}_{1:T}$,$\sigma .{\mathit{\xi }}_{1:T}$.
4:	Propose $I_0^{\prime }$ based on $q_1\left(\cdot \mid I_0\right)$, then ${\mathbf{X}}_{0:T}$ will be deterministically updated to ${\mathbf{X}}_{0:T}^{\prime }$ according to $I_0^{\prime }$,$R_0$,$\gamma$,${\mathit{\delta }}_{1:T}$,$\sigma ,{\mathit{\xi }}_{1:T}$.
5:	Accept $\left(I_0^{\prime },{\mathbf{X}}_{\mathrm{D}:T}^{\prime }\right)$ with acceptance probability
	$$a\leftarrow \mathrm{m}\mathrm{i}\mathrm{n}\left(1,\frac{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T}^{\prime },{\mathbf{X}}_{0:T}^{\prime }\right)\mathrm{P}\mathrm{r}\left(I_0^{\prime }\right)q_1\left(I_0\mid I_0^{\prime }\right)}{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T},{\mathbf{X}}_{0:T}\right)\mathrm{P}\mathrm{r}\left(I_0\right)q_1\left(I_0^{\prime }\mid I_0\right)}\right).$$
6:	Propose ${\gamma }^{\prime }$ based on $q_2(\cdot \mid \gamma )$, then ${\mathbf{X}}_{0:T},{\mathbf{\theta }}_{0:T}$ will be deterministically updated to ${\mathbf{X}}_{\mathrm{D}:T}^{\prime },{\mathbf{\theta }}_{0:T}^{\prime }$ according to $I_0$,$R_0$,${\gamma }^{\prime }$,${\mathit{\delta }}_{1:T}$,$\sigma ,{\mathit{\xi }}_{1:T}$.
7:	Accept $\left({\gamma }^{\prime },{\mathbf{X}}_{0:T}^{\prime },{\mathit{\theta }}_{0:T}^{\prime }\right)$ with acceptance probability
	$$a\leftarrow \mathrm{m}\mathrm{i}\mathrm{n}\left(1,\frac{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T}^{\prime },{\mathbf{X}}_{0:T}^{\prime }\right)\mathrm{P}\mathrm{r}\left({\gamma }^{\prime }\right)q_2\left(\gamma \mid {\gamma }^{\prime }\right)}{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T},{\mathbf{X}}_{0:T}\right)\mathrm{P}\mathrm{r}\left(\gamma \right)q_2\left({\gamma }^{\prime }\mid \gamma \right)}\right).$$
8:	Let $\mathbf{U}=\left(\mathrm{l}\mathrm{o}\mathrm{g}\left(R_0\right),{\delta }_{1:T},\mathrm{l}\mathrm{o}\mathrm{g}\left(\sigma \right)\right)$, then $\mathbf{U}$ a priori follows a multivariate normal distribution. Use elliptical slice sampler to obtain ${\mathbf{U}}^{\prime }$ and get the updated $R_0^{\prime },{\delta }_{1:T}^{\prime }$ and ${\sigma }^{\prime }.{\mathbf{X}}_{\mathrm{D}:T}$ will be deterministically updated to ${\mathbf{X}}_{\mathrm{D}:T}^{\prime }$ according to $I_0$,$R_0^{\prime }$,$\gamma$,${\mathit{\delta }}_{1:T}^{\prime },{\sigma }^{\prime }$.
9:	Since ${\mathit{\xi }}_{1:T}$ a priori follows a multivariate normal distribution, we use the elliptical slice sampler to obtain ${\mathit{\xi }}_{1:T}^{\prime }.{\mathbf{X}}_{0:T}$ will be deterministically updated to ${\mathbf{X}}_{0:T}^{\prime }$ according to $I_0$,$R_0$,$\gamma$,${\mathit{\delta }}_{1:T}$,$\sigma ,{\mathit{\xi }}_{1:T}^{\prime }$.

A-4.3. MCMC algorithm for the ODE-based model

The MCMC algorithm for ODE-based method is similar to the LNA-based MCMC except there is no need to update the Gaussian noise ${\mathit{\xi }}_{1:T}$ in the population trajectory. The MCMC updates of parameters and latent variables is given in Algorithm 3.

Algorithm 3.

Updating rule in the ODE-based MCMC algorithm

1:	Input: Parameter values from the previous interation $I_0$,$R_0$,$\gamma$,${\mathit{\delta }}_{1:T},\sigma$, geneology g. Proposal density $q_1(\cdot \mid \cdot )$, $q_2(\cdot \mid \cdot )$ for updating the initial number of infected individuals and the removal rate.
2:	Output Updated parameters values
3:	Calculate ${\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T}$ based on $I_0$,$R_0$,$\gamma$,${\mathit{\delta }}_{1:T},\sigma$.
4:	Propose $I_0^{\prime }$ based on $q_1\left(\cdot \mid I_0\right)$, then ${\mathbf{X}}_{0:T}$ will be deterministically updated to ${\mathbf{X}}_{0:T}^{\prime }$ according to $I_0^{\prime }$,$R_0$,$\gamma$,${\mathit{\delta }}_{1:T},\sigma$ based on ODE integration.
5:	Accept $\left(I_0^{\prime },{\mathbf{X}}_{D:T}^{\prime }\right)$ with acceptance probability
	$$a\leftarrow \mathrm{m}\mathrm{i}\mathrm{n}\left(1,\frac{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T}^{\prime },{\mathbf{X}}_{0:T}^{\prime }\right)\mathrm{P}\mathrm{r}\left(I_0^{\prime }\right)q_1\left(I_0\mid I_0^{\prime }\right)}{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T},{\mathbf{X}}_{\mathrm{D}:T}\right)\mathrm{P}\mathrm{r}\left(I_0\right)q_1\left(I_0^{\prime }\mid I_0\right)}\right)$$
6:	Propose ${\gamma }^{\prime }$ based on $q_2\left(\cdot ∣\gamma \right)$, then ${\mathbf{X}}_{0:T},{\mathit{\theta }}_{0:T}$ will be deterministically updated to ${\mathbf{X}}_{\mathrm{D}:T}^{\prime },{\mathit{\theta }}_{0:T}^{\prime }$ according to $I_0$,$R_0$,${\gamma }^{\prime }$,${\mathit{\delta }}_{1:T},\sigma$
7:	Accept $\left({\gamma }^{\prime },{\mathbf{X}}_{0:T}^{\prime },{\mathit{\theta }}_{0:T}^{\prime }\right)$ with acceptance probability
	$$a\leftarrow \mathrm{m}\mathrm{i}\mathrm{n}\left(1,\frac{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T}^{\prime },{\mathbf{X}}_{0:T}^{\prime }\right)\mathrm{P}\mathrm{r}\left({\gamma }^{\prime }\right)q_2\left(\gamma \mid {\gamma }^{\prime }\right)}{\mathrm{P}\mathrm{r}\left(\mathbf{g}\mid {\mathit{\theta }}_{0:T},{\mathbf{X}}_{0:T}\right)\mathrm{P}\mathrm{r}\left(\gamma \right)q_2\left({\gamma }^{\prime }\mid \gamma \right)}\right).$$
8:	Let $\mathbf{U}=\left(\mathrm{l}\mathrm{o}\mathrm{g}\left(R_0\right),{\mathit{\delta }}_{1:T},\mathrm{l}\mathrm{o}\mathrm{g}\left(\sigma \right)\right)$, then $\mathbf{U}$ a priori follows a multivariate normal distribution. Use elliptical slice sampler of obtain ${\mathbf{U}}^{\prime }$ and get the updated $R_0^{\prime },{\mathit{\delta }}_{1:T}^{\prime }$ and ${\sigma }^{\prime }.$ ${\mathbf{X}}_{\mathrm{D}:T}$ will be deterministically updated to ${\mathbf{X}}_{0:T}^{\prime }$ according to $I_0$,$R_0^{\prime }$,$\gamma$,${\mathit{\delta }}_{1:T}^{\prime },{\sigma }^{\prime }$ based on ODE integration.

A-5. Details of the simulation study

A-5.1. Simulation details for Section 3.1 of the main text

Here we provide details for the specified sequence/lineage sampling times and number of samples in each simulation scenario:

1. CONST $R_0(t):$ Sampling times: $𝒮=\{5,10,50,70,80,90\}$, number of samples at each time: $\{2,20,300,300,200,200\}$.

2. SD $R_0(t):$: Sampling times: $𝒮=\{5,10,50,70,80,90\}$, number of samples at each time: $\{2,20,200,80,20,20\}$.

3. NM $R_0(t):$ Sampling times: $𝒮=\{5,30,50,70,80,90\}$, number of samples at each time: $\{2,50,250,100,20,20\}$.

Table A-1 shows effective sample sizes for the parameter $I_0$, $R_0,\gamma$ and $\sigma$ in Section 3.1, based on 1,000,000 MCMC iterations.

TABLE A-1.

Effective sample sizes for simulation studies in Section 3.1.

	CONST		SD		NM
parameter	LNA.ESS	ODE.ESS	LNA.ESS	ODE.ESS	LNA.ESS	ODE.ESS
I 0	891	1130	772	1132	992	1124
R 0	677	751	686	730	407	617
γ	678	1391	2375	1780	705	824
σ	922	882	807	805	406	594

A-5.2. Simulation details for Section 3.2 of the main text

The $R_0(t)$ trajectory in the simulations is set to

$$R_0(t)=\left\{\begin{array}{ll}1.4\times {1.015}^{t/2},t\in \left[0,30\right]& t\in \left[0,30\right),\\ 1.750\times {0.975}^{t-30}& t\in \left[30,80\right],\\ 0.494& t\in \left(80,90\right]\end{array}\right.$$ (A-40)

which is depicted in the left plot of Figure A-4. The initial number of infected individuals is $I_0=3$ and the removal rate is set to $\gamma =0.3$. The population size is fixed to $N=\mathrm{1,000,000}$. Epidemic trajectories are simulated using the SIR Markov jump process (MJP) and are accepted/rejected based on the following criteria:

1. Reject the SIR trajectories that ends before time 90. The number of infected individuals should never drop to 0 for $t\in \left[\mathrm{0,90}\right]$, i.e. ${\mathrm{m}\mathrm{i}\mathrm{n}}_{t\in \left[\mathrm{0,90}\right]} I(t)>0$.

2. Reject the SIR trajectories with extremely high maximum prevalence: the maximum prevalence should be less or equal than 12,000, i.e., ${\mathrm{m}\mathrm{a}\mathrm{x}}_{t\in \left[\mathrm{0,90}\right]} I(t)\le 12000$.

3. Reject SIR trajectories with extremely low maximum prevalence. The maximum prevalence should be greater or equal than 600, i.e., ${\mathrm{m}\mathrm{a}\mathrm{x}}_{t\in \left[\mathrm{0,90}\right]} I(t)\ge 600$.

The 100 simulated SIR prevalence trajectories are shown in the right plot of Figure A-4 and the trajectories used in Section 3.1 is highlighted in blue. We also plot the ODE trajectory under the same parameter setting.

A-5.3. Repeated simulations for CONST and SD scenarios

In this Section, we repeat the simulation scenario for CONST and SD scenarios in Section 3.1 100 times. We use the same parameter set up for $R_0(t)$ and $\gamma$. The initial number of infected $I_0$ is se to 3 instead of 1 so that most of the numbers of simulated infectious individuals will not reach 0 before $T=90$. As in Section A-5.2, we reject trajectories than end before 90. For the SD scenario, we also reject trajectories with ${\mathrm{m}\mathrm{a}\mathrm{x}}_{t\in \left[\mathrm{0,90}\right]} I(t)>4000$ and ${\mathrm{m}\mathrm{a}\mathrm{x}}_{t\in \left[\mathrm{0,90}\right]} I(t)<300$. We run the LNA-based and ODE-based methods assuming the informative prior on $\gamma$. The posterior summary boxplots for CONST and SD scenarios are presented in Figure A-5 and Figure A-6 respectively.

The LNA-based method results in wider BCIs and enjoys better frequentist coverage (envelope) properties than the ODE-based method, although differences between the two methods are less pronounced than their counterparts in the NM scenario. In terms of bias, LNA-based and ODE-based methods perform similarly in these simulations.

FIGURE A-4.

Repeated simulation setup. Left: $R_0(t)$ trajectory under which the population trajectories are simulated. Right: The 100 simulated prevalence trajectories using MJP, the ODE trajectory under the same parameter setup, the MJP trajectory in for simulation in Section 3.1.

FIGURE A-5.

Boxplots comparing performance of LNA-based and ODE-based methods using 100 simulated genealogies in CONST $R_0(t)$ scenario. The first three plots shows mean absolute error (MAE), mean credible interval width (MCIW) and envelope for $R_0(t)$ trajectory. The next three plots depict mean relative absolute error (MRAE), mean relative credible interval width (MRCIW), and envelope for $I(t)$ (prevalence) trajectory. The last two plots show the absolute error (AE) and Bayesian credible interval (BCI) width for $\gamma$.

FIGURE A-6.

Boxplots comparing performance of LNA-based and ODE-based methods using 100 simulated genealogies in SD $R_0(t)$ scenario. See caption in Figure A-5 for explanation of the plots.

FIGURE A-7.

MCMC trace plots of the log-posterior in the 3 simulation scenarios. Columns correspond to CONST, SD, and NM simulated $R_0(t)$ trajectories. The first row shows the LNA-based results and the second row shows the ODE-based results.

A-5.4. Trace plots and effective sample sizes

A-5.4.1. Trace plots for simulations from Section 3.1 of the main text

Figure A-7 shows the trace plots of the log-posterior for the LNA-based method and ODE-based method in the three simulation scenarios from Section 3.1. The effective sample sizes (ESSs) for all parameters are above 400.

A-5.4.2. Trace plots for Ebola data

Figures A-8 and A-9 show trace plots of parameters $R_0,I_0,\gamma ,\sigma$ for the LNA-based model and ODE-based model respectively applied to the Sierra Leone genealogy, with each color correspond to a parallel MCMC chain. Figures A-10 and A-11 show the analogous trace plots for the analysis of the Liberia genealogy. We also list posterior medians, 95% BCIs, and ESSs for each parameter in the MCMC algorithm in Table A-2.

FIGURE A-8.

Trace plots for $I_0$, $R_0,\gamma$, and $\sigma$ in the LNA-based MCMC runs applied to the Ebola genealogy in Sierra Leone and using 9 parallel chains. Top left: Initial number of infected $I_0$. Top right: initial basic reproduction number $R_0$. Bottom left: removal rate $\gamma$. Bottom right: smoothing parameter $\sigma$.

Table A-2 show the effective sample sizes in the MCMC algorithm using genealogy from Sierra Leone and Liberia.

A-6. Prior sensitivity analysis

A-6.1. Simulations based on single genealogy realizations

In Section 3.1, we put informative priors on the removal rate $\gamma$ and explore three different simulation scenarios. Although our LNA-based model successfully recovers the $R(t)$ dynamics and SIR trajectories, the posterior density of the removal rate is not too different from its prior in the SD and NM scenarios. In this section, we investigate sensitivity of our inferences to changes in the prior of the removal rate $\gamma$. For the same genealogies and parameter settings as in Section 3.1, we assign weakly informative priors to the removal rate $\gamma$

1. CONST $R_0(t)$ scenario: $\gamma \sim \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(-\mathrm{1.7,0.25})$,

2. SD $R_0(t)$ scenario: $\gamma \sim \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(-\mathrm{1.7,0.25})$,

3. NM $R_0(t)$ scenario: $\gamma \sim \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(-\mathrm{1.2,0.25})$.

FIGURE A-9.

Trace plots for the ODE-based MCMC algorithm applied to the Ebola genealogy in Sierra Leone. See caption in Figure A-8 for the explanation of the plots.

FIGURE A-10.

Trace plots for the LNA-based MCMC algorithm applied to the Ebola genealogy in Liberia. Top left: Initial number of infected $I_0.Topright:initialbasicreproductionnumber{R}_0$ Bottom left: removal rate $\gamma$. Bottom right: smoothing parameter $\sigma$.

FIGURE A-11.

Trace plots for the ODE-based MCMC algorithm applied to the Ebola data in Liberia. See caption in Figure A-10 for the explanation of the plots.

TABLE A-2.

Table for posterior medians, 95% BCIs, and ESSs for MCMC algorithms applied to Ebola data from Sierra Leone and Liberia.

		Sierra Leone				Liberia
		post med	95%BCI	ESS		post med	95%BCI	ESS
LNA	I 0	4.84	[1.35,13.71]	1408	I 0	3.49	[1.03, 9.95]	1630
	R 0	1.66	[1.31.2.15]	1011	R 0	1.67	[1.29,2.24]	942
	γ	33.61	[23.44,48.21]	2160	γ	37.21	[25.98,53.13]	1704
	ρ	15.19	[10.60,21.53]	953	ρ	14.83	[10.41,20.70]	870
ODE	I 0	2.63	[1.09,6.09]	2085	I 0	4.31	[1.89,9.27]	1236
	R 0	1.64	[1.29,2.13]	1253	R 0	1.83	[1.41.2.44]	796
	γ	38.00	[26.12.55.40]	2841	γ	38.31	[27.27.53.43]	1608
	ρ	12.13	[8.46,16.40]	1012	ρ	11.79	[9.78,19.20]	879

For each scenario, we fit a LNA-based model using 300,000 MCMC iterations. The first row in Figure A-12 shows the point-wise posterior medians and 95% BCIs for the basic reproduction number trajectories, $R_{\mathbf{0}}(t)$ Our LNA-based method performs well in the CONST and SD scenario. However, for NM scenario, the method fails to fully capture the increase and decrease trend at the beginning and the end of the epidemic. The second row in Figure A-12 depicts the prior and posterior densities of the removal rate $\gamma$. The LNA-based method estimates the removal rate with good precision in the CONST scenario. However, for SD and NM scenario, the removal rate posterior densities are similar to the prior densities, but shift to the right from the truth. Posterior summaries of $S(t)$ and $I(t)$ are given in the third and fourth row of Figure A-12. The LNA-based method performs well in recovering the truth in the CONST and SD scenarios. In the NM scenario, the true trajectories are still covered by the wide BCIs, but the model seems to underestimate the $S(t)$ and overestimate $I(t)$.

A-7. Grid sensitivity analysis

The number of grid cells $T$ can be viewed as a tuning parameter in our model. Throughout the main text, $T$ is set to be around 30 to 40 and with a lognormal (3, 0.2) prior for inverse of smoothing parameter $1/\sigma$. In this section, we investigate sensitivity to the choice of grid size $T$. We fit our LNA-based method to genealogy data constructed from virus sequences collected from Liberia using the same prior setup as in Section 4 under different choices of grid sizes:

1. $T=20$, grid interval length $\mathrm{\Delta }{t}_i=12.6$ days.

2. $T=40$, grid interval length $\mathrm{\Delta }{t}_i=6.3$ days (The grid setup in Section 4).

3. $T=80$, grid interval length $\mathrm{\Delta }{t}_i=3.2$ days.

For simplicity, we use the same prior setup for each parameter and fit LNA-based method to the Liberia genealogy. We run the MCMC algorithm for 1,000,000 iterations and discard the first 200,000 iterations. Posterior summaries, depicted in Figure A-13, show that the estimation results do change significantly when we change the grid size.

A-8. Performance under population size misspecification

A-8.1. Simulation study

In real applications, the census population size is usually not an accurate estimate of the true population size $N_{true}$. Hence, robustness to the misspecification of the population size is desirable. In this section, we repeat the simulation study in Section 3.2 with true population size $N_{true}=\mathrm{1,000,000}$ and fit LNA-based models under different population size misspecifications:

1. $N=\mathrm{200,000},N/N_{true}=1/5$,

2. $N=\mathrm{500,000},N/N_{true}=1/2$,

3. $N=\mathrm{1,000,000},N/N_{true}=1/2$, true population size used in Section 3.2,

4. $N=\mathrm{5,000,000},N/N_{true}=5$,

5. $N=\mathrm{10,000,000},N/N_{true}=10$.

FIGURE A-12.

Analysis of 3 simulation scenarios using the LNA-based method with weakly informative priors. Columns correspond to CONST, $SD$, and NM simulated $R_0(t)$ trajectories. The first row shows the estimated $R_0(t)$ trajectories for the 3 scenarios, with the black solid lines representing the truth, the red depicting the posterior medians and the red-shaded area showing the 95% BCIs for the LNA-based method. The second row corresponds to the estimation of the removal rate $\gamma$. Posterior density curves from the LNA-base method are shown in red lines compared with prior density curve in green lines. The bottom two rows show the estimated trajectories of $\gamma$ and $I(t)$ respectively.

FIGURE A-13.

Analysis of genealogy relating Ebola sequence data collected in Liberia using LNA-based method under different choices of grid size. Top left: basic reproduction number $R_0(t)$ posterior summaries. Top right: removal rate $\gamma$ posterior density. Bottom left: $S(t)$ posterior summaries. Bottom right: $I(t)$ posterior summaries. The results for $T=40$ in Section 4 are plotted in red. Green color corresponds to the result based on the coarser grid $(T=20)andthebluecolorisusedtoshowposteriorsummariesforthefinergrid(T=80)$.

FIGURE A-14.

Boxplots comparing the performance of LNA-based method under population size misspecification using 100 simulated genealogies. See caption in Figure 4 for the explanation of the plot.

To evaluate model performance, we use the same metrics defined in Section 3.2 and generate posterior summary boxplots in Figure A-14. The Figure shows that it is safe to overestimate the true population size, but underestimating it leads to poor statistical performance. We note that while basic reproduction number and recovery rate have been shown before to be robust to population size misspecification (Koepke et al., 2016; Fintzi et al., 2017), the latent variables generally do not enjoy such robustness. For example, the number of susceptible individuals does depend on the assumed population size. In our simulation, susceptible individuals do not deplete enough to change estimation of latent prevalence, but in other cases prevalence estimation can be affected by the population size misspecification.

A-8.2. Analysis of Liberia genealogy under different population size assumptions

We repeat LNA-based analysis of the Liberia genealogy under different population size assumptions. Recall that the census population size $N_{census}=\mathrm{4,400,000}$ is used in Section 4. We use our LNA-based method assuming the following population sizes:

1. $N=\mathrm{440,000},N/N_{census}=1/10$,

2. $N=\mathrm{44,000,000},N/N_{census}=10$.

FIGURE A-15.

Analysis of genealogy relating Ebola sequence data collected in Liberia using the LNA-based method under different total population specification. Top left: basic reproduction number $R_0(t)$ posterior summaries. Top right: mean infection period $1/\gamma$ posterior density. Bottom left: Disease prevalence $I(t)$ posterior summaries. The results for $N=N_{census}=4,400,000$ in Section 4 is plotted in red as, with green color corresponding to the results based on overestimating total population $(N=44,000,000)$ and the blue color plotting posterior summaries under an underestimated total population size $(N=440,000)$.

In conclusion, if the final epidemic size is relatively small compared with the true total population size, estimation results are robust to the misspecification of the population size, if the misspecification is not too severe. Intuitively, this makes sense, because when the number of susceptible individuals $S(t)$ is approximately equal to the total population size $N$, the coalescent rate is reduced to

$$\lambda (t)=\left(\begin{array}{c}l(t)\\ I\end{array}\right)\frac{2\beta (t)S(t)}{I(t)}\approx \frac{2R_0(t)\gamma }{I(t)},$$

which is invariant to the population size $N$.

A-9. Comparison with PhyDynR package

In this paper, we implement the SIR structured coalescent likelihood based on equation (2) that can be found in (Volz, 2012). We check our implementation of this likelihood by comparing it with the implementation from PhyDynR package (a predecessor of the BEAST 2 PhyDyn module). The comparison protocol consists of two steps. First, a genealogy is simulated under a deterministic ODE SIR population trajectory determined by the pre-specified parameters: $R_0=2,\gamma =0.15$ and $I_0=3$. We assume the constant basic reproduction number. Secondly, the basic reproduction number $R_0$ and removal rate $\gamma$ are estimated via the maximum likelihood method. Variances and standard deviations of parameter estimates are obtained from the inverse Hessian of the log-likelihood function. We repeat the experiment 100 times and report absolute errors (AEs) and standard deviation (SDs) for parameters $R_0$ and $\gamma$ respectively.

FIGURE A-16.

Comparison of SIR coalescent likelhhood implementations of our ODE method and PhyDynR package in a sparsely sampled outbreak (population size is 10, 000 and the number of sampled sequences is 150). The first row shows the absolute errors (AEs) and estimated standard deviation (SDs) for basic reproduction number $R_0$. The second row shows the $AEs$ and estimated SDs for removal rate $\gamma$.

We consider two scenarios:

1. A sparsely sampled outbreak, where the population size is $N=10,000$ and the number of sampled sequences is 150.

2. A densely sampled outbreak, where the population size is $N=1,000$ and the number of sampled sequences is 200.

Figures A-16 and A-17 show the AEs and SDs for parameters in scenarios 1 and 2 respectively, demonstrating that the two likelihood implementations agree in the sparsely sampled outbreak setting, but disagree when outbreaks are densely sampled. Since all coalescent-based methods assume sparse sampling, we do not think that the disagreement between our implementation and PhyDynR is concerning.

Figure A-17.

Comparison of SIR coalescent likelihood implementations of our ODE method and PhyDynR package in a sparsely sampled outbreak (population size is 1, 000 and the number of sampled sequences is 200). The first row shows the absolute errors (AEs) and estimated standard deviation (SDs) for basic reproduction number $R_0$. The second row shows the AEs and estimated SDs for removal rate $\gamma$.

A-10. Simulations under small population size

A-10.1. Simulations based on single genealogy realization

In this section, we perform simulation studies under a small population size $=1,000$. We simulate an epidemic with constant reproduction number $R_0(t)=2$ for $t\in [0,90]$. The initial number of infected is set to be $I_0=3$ and the recovery rate the is $\gamma =0.15$. First, we simulate one realization of the population trajectory, based on which a sequence of coalescent times are simulated using pre-specified sampling times.

For simplicity, we also assume a constant basic reproduction number in the inference, i.e. fixing ${\mathit{\delta }}_{1:T}=0$. We fit both LNA-based algorithm and ODE-based algorithm to simulated genealogy. Moreover, since the reproduction number is constant, we also use the ODE-based model implementation in PhyDyn package from (Volz and Siveroni, 2018). We use the same prior setup for basic reproduction number $R_0$ and initial number of infected $I_0$ as in Section 3 and an informative prior lognormal $(-1.9,0.1)$ is assigned for the recovery rate $\gamma$.

Posterior summaries of the one realization simulation is shown in Figure A-18. Note the there exist differences in the posterior summaries between our ODE-based method and PhyDyn. Such differences are likely to be caused by differences in the grid set up for the coalescent likelihood and different ODE solvers used by the two methods. The top two plots show the posterior densities of $R_0$ and $\gamma$. While both our ODE-based method and PhyDyn posteriors have small shifts from the truth, our LNA-based method yields a more flat density curve that has much higher density at the truth. The bottom two plots depict posterior summaries for the population trajectories. Compared with the results in Section 3.1, the BCIs for LNA based method in small population epidemic lose in coverage of the population trajectory. However, the BCIs and posteriors median generally capture the trend of the population dynamic. Our ODE-based implementation and PhyDyn seem to be over-confident and yield narrow BCIs that miss most of the true trajectories. The inconsistency between our ODE-based inference and BEAST2 PhyDyn results are present only in a densely sampled outbreak settings, as demonstrated in Section A-9 above.

A-10.2. Frequentist properties of posterior summaries

We simulate 100 realizations of the SIR trajectories under the same parameter setup in Section A-10.1. We keep all the simulated trajectories but only reject those ending before $t=90$. The 100 simulated trajectories are plotted in Figure A-19 in grey lines, with the corresponding ODE curve plotted in black. For each simulated trajectory, we simulate genealogy and apply the LNA-based method, our implementation of ODE-based method, and BEAST2 PhyDyn package to each genealogy under the same prior setup as in Section A-10.1 (Volz and Siveroni, 2018). The estimation $R_0$ and $\gamma$ is evaluated by absolute error (AE), BCI width (BCIW) and envelope defined in Section 3.2. We evaluate the estimation of prevalence $I\left(t\right)$ is based on MRAE, MRICW and ENV-I. Posterior summaries for repeated simulations are depicted in Figure A-20.

FIGURE A-18.

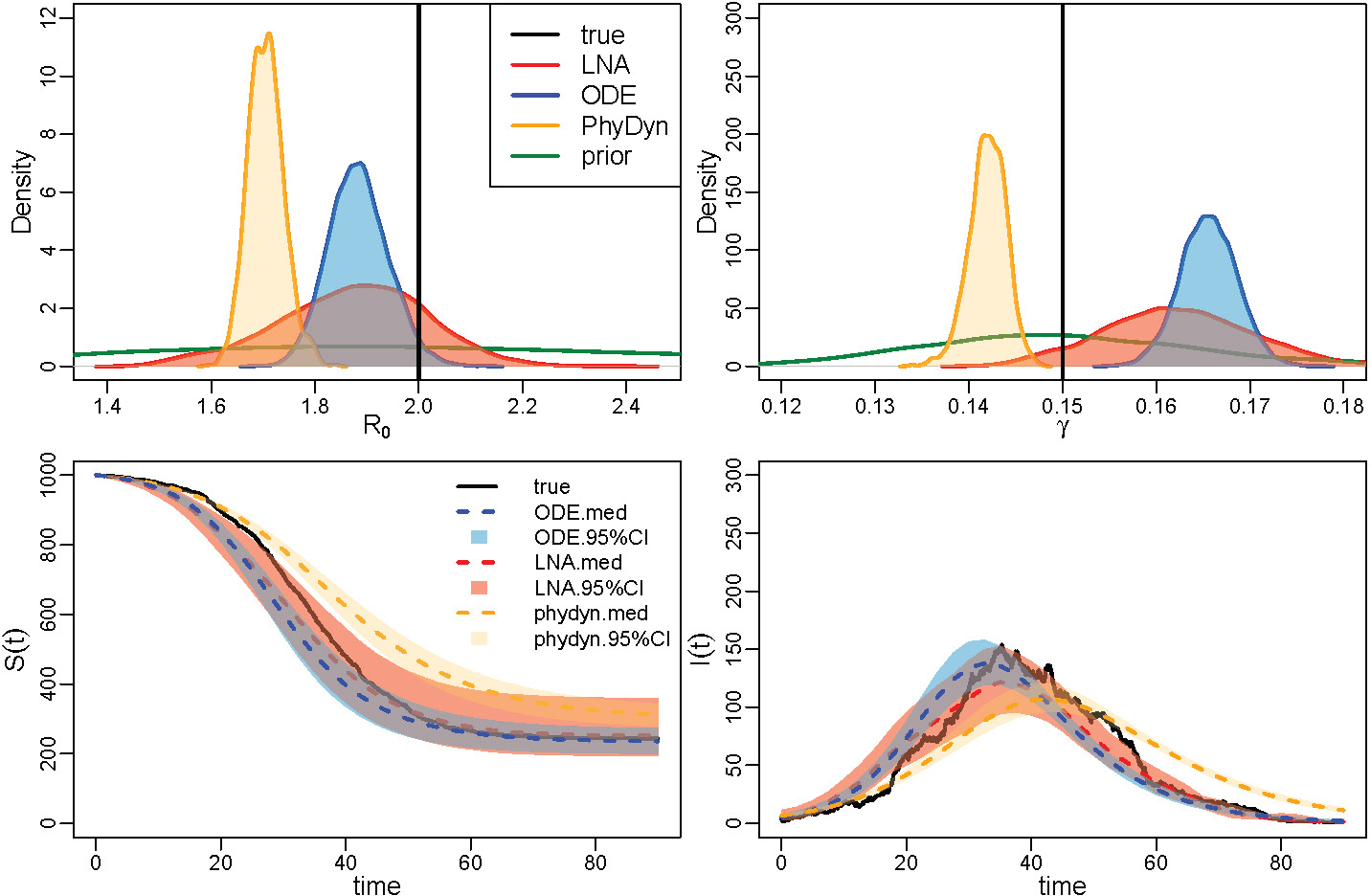
Analysis of LNA-based and ODE-based methods in the small population size setting. The first row shows the estimation results for basic reproduction number R₀ and removal rate γ respectively, with posterior density curve for LNA-based method plotted in red, our ODE-based implementation plotted in blue, and PhyDyn results plotted in orange. The second row shows posterior summaries for S(t) and I(t) trajectories with the same color scheme.

FIGURE A-19.

The 100 simulated prevalence trajectories using MJP and the ODE trajectory under the same parameter setup.

FIGURE A-20.

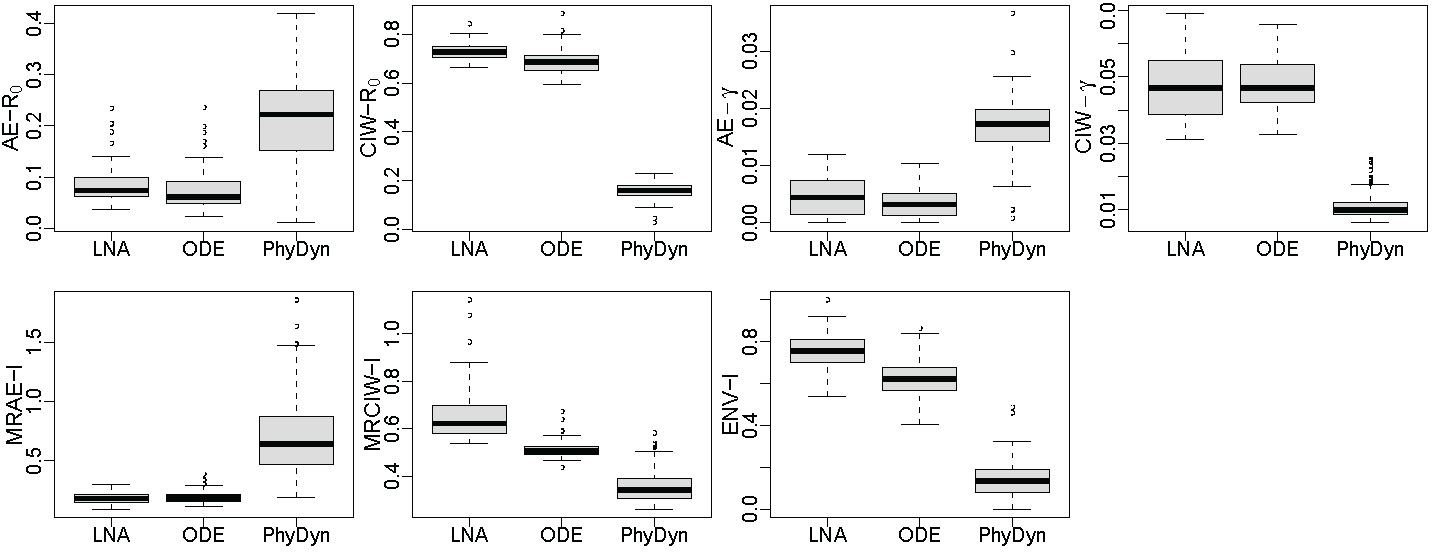
Boxplots comparing the performance of LNA-based, our implementation of the ODE-based method, and BEAST2 PhyDyn package implementation of the ODE-based method under population size $N=\mathrm{1,000}$ and using 100 simulated genealogies. First row: AE, CIW for $R_0$ (left two) AE, CIW for $\gamma$. Second row: MRAE, MRCIW and ENV-I for $I(t)$