Production-sharing of critical resources with dynamic demand under pandemic situation: The COVID-19 pandemic

Abstract

The COVID-19 virus’s high transmissibility has resulted in the virus’s rapid spread throughout the world, which has brought several repercussions, ranging from a lack of sanitary and medical products to the collapse of medical systems. Hence, governments attempt to re-plan the production of medical products and reallocate limited health resources to combat the pandemic. This paper addresses a multi-period production-inventory-sharing problem (PISP) to overcome such a circumstance, considering two consumable and reusable products. We introduce a new formulation to decide on production, inventory, delivery, and sharing quantities. The sharing will depend on net supply balance, allowable demand overload, unmet demand, and the reuse cycle of reusable products. Undeniably, the dynamic demand for products during pandemic situations must be reflected effectively in addressing the multi-period PISP. A bespoke compartmental susceptible-exposed-infectious-hospitalized-recovered-susceptible (SEIHRS) epidemiological model with a control policy is proposed, which also accounts for the influence of people’s behavioral response as a result of the knowledge of adequate precautions. An accelerated Benders decomposition-based algorithm with tailored valid inequalities is offered to solve the model. Finally, we consider a realistic case study – the COVID-19 pandemic in France – to examine the computational proficiency of the decomposition method. The computational results reveal that the proposed decomposition method coupled with effective valid inequalities can solve large-sized test problems in a reasonable computational time and 9.88 times faster than the commercial Gurobi solver. Moreover, the sharing mechanism reduces the total cost of the system and the unmet demand on the average up to 32.98% and 20.96%, respectively.

1. Introduction

The world has been experiencing severe disasters ranging from natural (e.g., hurricanes, floods, tornadoes, pandemics, etc.) to man-made disasters (e.g., terror, error, etc.). Recently, the world has been tolerating a crucial pandemic due to the emergence of the SARS-CoV-2 virus (COVID-19, hereafter) over the past three years. This has rapidly spread worldwide after initial exposure in China [1], [2], [3]. As of the beginning of the pandemic, all governments faced high demand for medical products/resources to control the virus’s spread and cure patients in critical situations. Hence, countries worldwide agreed to increase the production of medical products and equipment ranging from medical masks to ventilators, developing health protocols, raising awareness through social media, and correcting misconceptions [4], [5], [6]. They were also aware that such an action plan necessitates re-planing medical products’ production system and re-allocating/sharing limited health resources among different centers/regions to combat the pandemic as supply chain viability measures [7], [8], [9], [10], [11], [12]. The success of such an action plan highly depends on two main problems: a precise enough estimation of the demand for medical products; and an efficient logistics network to produce, stock, distribute, and share such products [13], [14], [15], [16].

As far as the estimation of the demand is concerned, there are various forecasting procedures, which can provide a precise prediction of the progression of the pandemic, including agent-based models [17], metrological and meta-population models [18], compartmental epidemiological models [19], [20], [21], [22], [23], [24], time-series methods [25], [26], machine learning [27], and deep learning approaches [28]. Except for compartmental epidemiological models, the other approaches are highly dependent on data availability, while in the early stages of a pandemic, data is either unavailable or unreliable [29]. Furthermore, long-standing data cannot be provided due to the emergence of new variants of the virus. Also, they cannot reflect various government policies, including better treatment or public awareness programs [30]. In this regard, these methods cannot consider a specific target to guarantee the achievement of sketched control policies, such as reducing the number of deaths or system costs [31]. However, to implement control policies, integrating compartmental epidemiological models with the optimal control problem (OCP) is a powerful approach, which can cope with a significant number of the listed barriers [32], [33], [34], [35], [36], [37]. More importantly, another advantage of epidemiological models is the possibility of computing an endemic equilibrium point by a dynamic optimization approach [38].

Despite all the advantages outlined for epidemiological models with OCP, researchers are less likely to utilize this approach due to the complexity of its implementation, especially in modeling the COVID-19 pandemic. What is more, although limited studies have applied this methodology, their findings cannot be used to plan logistics activities directly. Indeed, the considerations linked to their interaction with optimization models for logistics planning have not been taken into account because the presented models have only considered the aspect of epidemiology. As an illustration, we need a specific approach for identifying and estimating the demand for each piece of treatment equipment when trying to manage the supply, production, distribution, and sharing of items like ventilators, medical clothes, and ordinary and ICU beds.

Albeit a precise-enough estimation of demand aids in re-planning production and distribution decisions for medical products, it is nearly impossible to meet all demands due to limitations in proper infrastructures and facilities’ production capacity. As a result, a sharing system between healthcare facilities can significantly impact the effective utilization of available inventory. In this regard, there are various approaches to provide a sharing mechanism, including queuing theory [39], [40], [41], simulation [42], agent-based algorithms [43], dynamic optimization [44], game theory [45], and data envelopment analysis [46]. In contrast, optimization models have been less employed due to their complexity. Although limited studies have been conducted to provide ventilator and patient-sharing systems among healthcare facilities with the emergence of the COVID-19 pandemic, a broad range of concerns has been neglected in these studies that should be taken into account to increase their effectiveness. As an illustration, neglecting supply and production limitations can lead to serious doubts about the feasibility of the system’s results. Moreover, some medical equipment, such as ventilators and ICU beds, can be reused after an almost certain period as a lead time, which is about two weeks during the COVID-19 pandemic. So, this characteristic must be considered to update the inventory level in healthcare facilities, which may consequently affect the sharing decisions. What is more, a functional sharing system should provide the possibility that healthcare facilities can receive a certain amount of demand over their capacity. Such that they can fulfill this excess demand through service sharing instead of just accepting the demand based on a fixed capacity. In this regard, considering a broad range of factors are necessitated, including net supply balance, allowable demand overload, maximum sharing capacity, unmet demand, and adjusting inventory level relying on a reuse cycle for reusable equipment.

According to the above-mentioned description, we address the two problems (i.e., precise-enough estimation of the dynamic demand and planning an efficient logistics network to produce, distribute, and share medical products) through a comprehensive two-stage framework. In the first stage, we suggest a SEIHRS model with the OCP for controlling the dynamicity of the demands of consumable and reusable products. Through the OCP, various control policies, including raising awareness via spreading information and improving normal and critical treatments for hospitalized people, are examined. The second stage deals with modeling a new multi-period production-inventory-sharing problem (PISP), where a broad range of decisions are made, including supply, production, distribution, inventory, and sharing.

The contributions of this study are fivefold. First, we introduce a comprehensive optimization framework to combat a pandemic. Second, we develop a tailored SEIHRS model with a control policy to handle the demand dynamicity. Third, we formulate the multi-period PISP under the equipment reuse cycle. Fourth, we offer an accelerated Benders decomposition algorithm to solve the problem. Fifth, we render new valid inequalities in the context of the multi-period PISP, which are based on the real demand, the inventory levels, and the unmet demand. The proposed optimization framework is finally applied to a realistic case study of the COVID-19 pandemic in France for the first time.

The remainder of the paper is organized as follows. Section 2 offers a comprehensive investigation concerning associated studies in the literature. Section 3 presents the description of the SEIHRS epidemiological model with the OCP. Section 4 proposes the multi-period PISP formulation. Section 5 presents the valid inequalities along with an accelerated Benders decomposition algorithm. Section 6 describes the case study and provides computational results and a set of sensitivity analyses. Section 7 provides managerial insights and implications. Finally, this study is concluded, and future research directions are proposed in Section 8.

2. Literature review

The current study concentrates on two main phases: 1) disease progression modeling and 2) logistics planning, especially focused on sharing/re-allocating mechanisms, to offer a comprehensive framework to combat the COVID-19 pandemic. In the following, the relevant studies of the literature are reviewed and discussed to better position the current work and its contributions compared to the literature. First, Table 1 classifies the relevant papers according to different criteria. Next, the studies of each phase are separately discussed in the following subsections.

Table 1.

Classification of the relevant papers*.

Ref.	Phase 1			Phase 2			Characteristics									Sol.
	EM-wo-OCP	EM-w-OCP		Sup.	Prod.	Dist./	Demand				Resource		Inv.	Shr.	Re-use	Appr.
		Identical	Distinct			Shr.	Periodic	Overload	Unmet	Type	Type	Cap.	Cap.	Cap.
[49]	✓
[50]	✓
[51]	✓
[52]	✓
[53]	✓
[54]	✓
[55]	✓
[56]	✓
[57]	✓
[58]	✓
[59]	✓
[60]	✓
[61]	✓
[62]	✓
[63]	✓
[64]	✓
[65]	✓
[66]	✓
[67]	✓
[68]	✓
[69]		✓
[70]		✓
[71]		✓
[72]						✓	✓		✓	Stochastic	Single					HEU.
[73]						✓	✓		✓	Robust	Multi	✓				GRB.
[74]						✓	✓		✓	Stochastic	Single	✓	✓	✓		MH
[75]	✓				✓	✓	✓		✓	Dynamic	Multi	✓				CPlex
[76]	✓				✓	✓	✓		✓	Dynamic	Multi	✓				AnyLogic
[77]				✓		✓	✓			Stochastic			✓		✓	GRB.
This study			✓	✓	✓	✓	✓	✓	✓	Dynamic	Multi	✓	✓	✓	✓	BD

*EM-w/wo-OCP: Epidemiological model with/without OCP; Sup.: Supply; Prod.: Production; Dist.: Distribution; Shr.: Sharing; Inv.: Inventory; Cap.: Capacity; Sol. Appr.: Solution approach.

2.1. Phase 1—Disease progression modeling under the COVID-19 pandemic

Considering the advantages and disadvantages listed in the previous section for disease progression modeling methods, only studies that have used epidemiology models are examined in this section. Although the COVID-19 pandemic just emerged three years ago, a significant number of studies have been conducted to predict transmission dynamics and formulate disease progression via epidemiology models. In this regard, three review articles have been presented [29], [30], [47], [48], wherein epidemiological models such as susceptible-infected-recovered (SIR) and susceptible-exposed-infectious-recovered (SEIR) have been mostly employed. In this regard, the corresponding studies can be separated into two categories: the first category covers simply epidemiological models, while the second incorporates OCP into epidemiological models.

In the first category, Anand et al. [49] proposed a modified SIR model (MSIRM) with a case study in India, where infected individuals were tested and quarantined. Cooper et al. [50] proposed an MSIRM with a dynamic susceptible population, where the proposed model was examined on different datasets, including China, South Korea, India, Australia, Italy, and the USA. Chen et al. [51] addressed an MSIRM with a case study in China, in which recovery and transmission rates were time-dependent. Abou-Ismail [52] applied SIR and SEIR models and offered a susceptible-quarantined-quarantined-confirmed (SUQC) model. Wangping et al. [53] extended the SIR model with a case study in Italy, where the transmission rate was time-dependent, and the Markov Chain Monte Carlo method was employed to estimate the basic reproductive number. Ifguis et al. [54] applied the SIR model for a case study in Morocco. Calafiore et al. [55] developed an MSIRM based on a case study in Italy, where their contributions focused on determining the proper number of infected people and enhancing identification and prediction processes. He et al. [56] proposed a modified SEIR model (MSEIRM) with a case study in China, where a particle swarm optimization algorithm was used to adjust the SEIR’s parameters. Moreover, they examined the system’s behavior regarding seasonality and stochastic infections. Moreover, in order to forecast the basic reproduction number and pandemic spread rate, Liao et al. [57] developed an integrated strategy comprising a SIR model and a polynomial regression algorithm as a machine learning method. Indeed, the SIR model’s parameters were estimated using the machine learning algorithm. Similarly, Alanazi et al. [58] applied machine learning methods to estimate the parameters of a SIR model. Bagal et al. [59] applied the SIR model for analyzing various lockdown scenarios in India. Chen et al. [60] proposed a SIR model under an uncertain process by means of uncertain differential equations, where the proposed model was investigated in a case study of China. Kyurkchiev et al. [61] proposed new modifications for SIR and SEIR models, wherein intervention polynomial factor was applied to consider various scenarios for the contagious disease deployment. Zisad et al. [62] incorporated a neural network model into an SEIR model to enhance the prediction accuracy, where the neural network was utilized to predict the quarantined population.

Alenezi et al. [63] proposed a time-dependent SIR model for a case study in Kuwait. Hassen et al. [64] proposed an MSIRM called SIR-Poisson to forecast the number of infected individuals following a Poisson distribution. The accuracy of the proposed model was examined in Maghreb’s central regions, including Algeria, Tunisia, and Morocco. Prodanov [65] introduced an iterative approximation algorithm to estimate the parameters of the SIR model. Ala’raj et al. [78] applied ARIMA models to adjust the parameters of a modified susceptible-exposed-infected-recovered-deceased (SEIRD) model under time-dependent birth and death rates. What is more, Efimov and Ushirobira [66] proposed an MSEIRM by taking into account societal feedback on disease and confinement aspects as well as time-dependent parameters. Singh and Gupta [67] developed a generalized SIR model consisting of miscellaneous time-dependent patterns of emerging, peak amplitude, and dwindling. Also, they considered a logistic growth model to formulate infection spread. López and Rodo [68] proposed a time-dependent SEIR model for a case study in Spain and Italy, where infection spread during the latent period was considered under various proportions of containment.

In the second category, few studies have been conducted due to the complexity of reflecting OCP factors. Das and Samanta [69] suggested an MSIRM based on a fractional-order framework, in which OCP was applied to investigate the effectiveness of a social distance policy, where lockdown was one of the policy’s parts. Saha et al. [70] suggested a modified SEIRS model that accounts for the influence of information on adequate precautions on people’s behavioral responses. They used OCP to minimize disease burden by implementing two control policies: boosting disease awareness through information and improving treatment for hospitalized patients. Saha and Samanta [71] suggested an MSEIRM in which OCP was used to assess the efficacy of social distancing and proper hygiene policy on raising awareness.

Research gaps and questions According to the literature, increasing awareness about disease symptoms by spreading information and enhancing treatments to hospitalized patients in different stages of the COVID-19 pandemic substantially impacts medical products demand, including hydro-alcoholic gels, masks, medical clothes, ordinary and ICU beds, and ventilators. On this subject, the demand for each of the mentioned medical products is associated with a specified part of the target population. As an illustration, all susceptible individuals must use masks and hydro-alcoholic gels to prevent the spread of the virus regarding public health protocols. Also, hospitalized individuals in general wards need ordinary beds, and hospitalized individuals in ICUs require ICU beds and ventilators. Moreover, all hospitalized individuals in general wards and ICUs need medical clothes. Therefore, reflecting these concerns to formulate a realistic disease progression model is necessitated for identifying and estimating the demand for each piece of treatment equipment. Needless to say, sketching a meaningful interaction between the estimation phase of demand for mentioned products and the planning phase of logistics activities, including production, distribution, and sharing, is undeniable. Regarding the explained research gaps, the main research questions are (1) How can we estimate demands for different medical products according to changes in disease progression? (2) How can we use estimated demand to plan logistics activities? (3) Does considering dynamic demand lead to more accurate planning for logistics activities?

2.2. Phase 2—Logistics planning: sharing/re-allocating mechanisms

Resource re-allocation or sharing is a reputable concept that has applications in diverse domains, including judicial services [79], closed-loop supply chain [80], bike-sharing [81], and humanitarian logistics operations [82]. However, there are a limited number of studies in the context of mathematical modeling of sharing mechanisms in healthcare systems. It is interesting to know that these limited studies have also been formed due to the emergence of the COVID-19 pandemic.

As the first papers dealing with the COVID-19 pandemic issues, Mehrotra et al. [72] proposed a ventilator sharing framework to combat the COVID-19 pandemic under demand uncertainty, where a central agency allocated ventilators to various regions under safety stock and inventory levels. In the sharing process, surplus ventilators were returned to the central agency from the regions and redistributed by the central agency with and without lead time according to the demands of other regions in which demand uncertainty was handled by stochastic programming. Parker et al. [73] proposed two sets of mathematical models to redistribute the COVID-19 patients as demands, and beds and nurses as resources among healthcare facilities regarding inventory level. Also, a robust optimization approach handled the demand uncertainty, and the objective functions minimized the total surge capacity and nurse overflow. Blanco et al. [74] proposed a single product-sharing system among healthcare facilities in the COVID-19 pandemic regarding inventory and capacity levels, where a stochastic programming approach handled the demand uncertainty. Also, they examined four objective functions that stand for different aspects of the unmet demand. Rozhkov et al. [76] proposed a simulation model to analyze a production-inventory problem in a multi-layer supply chain system with perishable products during the COVID-19 pandemic, where two supply chain reactive strategies were considered, including order cancellation and excess inventory. On this subject, they modeled the pandemic dynamics and its disruptions by an agent-based forecast model as a separate system and analyzed its outcomes on the demand, supply, and capacities of the considered supply chain system. Li et al. [75] proposed an epidemiological model to formulate a coupled supply chain and disease network during the COVID-19 pandemic, where the proposed SEIHRS model worked alongside a production-inventory dynamic programming model. They considered four significant feedback functions to provide realistic circumstances of the COVID-19 pandemic and its disruptions, including disease-dependent capacity, disease-dependent demand, shortage-dependent transmission, and shortage-dependent fatality.

Research gaps and questions According to the literature, the supply and production of medical equipment have not been studied. Also, these plans are generally considered for one product type, while different products require different considerations. In this regard, some medical equipment, such as ventilators and ICU beds, can be reused after a certain period. So, this specification needs to be reflected to compute the inventory level of healthcare facilities and sharing decisions. Additionally, in real-world applications, sometimes healthcare facilities have a certain level of participation in the sharing process despite having excess capacity. Therefore, it seems necessary to consider a limited capacity for sharing process. What is more, a practical sharing system ought to allow healthcare facilities to accommodate some demand that exceeds their capacity so that they might share services to meet this surplus demand rather than simply accepting it based on a predetermined capacity. Regarding the explained research gaps, the main research questions are (1) How can we reduce health system costs and unmet demand by planning production, distribution, and sharing? (2) How does reusable products’ reuse cycle affect production to sharing decisions? (3) How do consumable and reusable products plan from production to distribution in a multi-period healthcare system?

Finally, with the intention of demonstrating research gaps and our contributions better, Table 1 is provided.

3. Epidemiological model

This section develops a SEIHRS epidemiological model with OCP (see Fig. 1 ) to estimate the demands of consumable and reusable products. As a new extension, hospitalized patients are separated into two groups. The first group represents the patients in general wards who need regular hospital beds and typical treatments. The second group comprises patients under severe conditions who require ICU beds, ventilators, and critical treatments. In addition, as the physical condition of the patients in the first group deteriorates, they are transferred to the second group. More importantly, in retrospect, people show different behavior towards minor and intense symptoms of corona disease. For example, most people do not pay attention to minor symptoms and postpone visiting physicians, while this is usually the opposite in relation to intense symptoms. In addition, as people become more aware of the consequences of delaying the start of needed treatment, this attitude usually changes. Furthermore, during the COVID-19 pandemic, due to the insufficient knowledge of scientists about the origin of this disease, many of the treatments used have been based on their experience with similar diseases in the past. Therefore, with the passage of time, conducting numerous clinical trials, increasing awareness of the complications of the disease, and how patients respond to the prescribed drugs, the treatments required in minor and intense conditions have been adjusted. Consequently, various control policies are considered to reflect such circumstances.

Fig. 1.

The proposed SEIHRS model.

3.1. Main assumptions and notations

The main assumptions to develop the SEIHRS epidemiological model are as follows: 1) As symptomatic infected population density rises, so does the accumulation of information, but over time it reaches saturation; 2) The recovery condition is not permanent and a number of recovered individuals return to the susceptible ones; 3) This model does not take into account the diseases’ natural histories, such as the incubation and latency periods; 4) Every member of the population engages in social interaction; 5) Every member of the population has the same health traits, such as immune response, immunity, etc.; and 6) All afflicted individuals are contagious and disseminate the illness among the susceptible individuals.

The list of the notations of the proposed mathematical model is provided as Table 2 .

Table 2.

Notations of the proposed SEIHRS model.

Notation	Description
Parameters
$\Delta$	Total population at the beginning of the pandemic
${\beta }_1/{\beta }_2$	Disease contagion rates per contact by asymptomatically/symptomatically infected individuals
${\beta }_3/{\beta }_4$	Disease contagion rates per contact by individuals hospitalized under normal/critical treatments
$d$	Natural death rate of individuals
${\delta }_1/{\delta }_2$	Particular death rate among asymptomatically/symptomatically infected individuals
${\delta }_3/{\delta }_4$	Particular death rate among individuals hospitalized under normal/critical treatments
$\rho$	Probability of being asymptomatically infected among exposed individuals
$c$	Probability of being hospitalized under critical treatments among symptomatically infected individuals
$\kappa$, $\eta$, $\omega$, ${\gamma }_1$, ${\gamma }_2$	Conversion rates from exposure to infected, asymptomatic to symptomatic, symptomatic to hospitalized, and normal and critical hospitalized to recovered individuals
$\xi$	Return rate of recovered individuals to be susceptible again
$a_0$	Depreciation rate of information in the course of time due to the physical fading of memory regarding sequels
$k$	Information interaction rate
$p$, $q$	Information growth rate and the unresponsiveness rate to information
Variables
State variables
$N\left(t\right)$	Total population at time $t$
$S\left(t\right)$	Number of susceptible individuals at time $t$
$E\left(t\right)$	Number of exposed individuals at time $t$
$A\left(t\right),I\left(t\right)$	Number of asymptomatically/symptomatically infected individuals at time $t$
$HN\left(t\right),HC\left(t\right)$	Number of hospitalized individuals under normal/critical treatments at time $t$
$R\left(t\right)$	Number of recovered individuals at time $t$
$Z\left(t\right)$	Awareness density because of the spread of information provided by social media platforms and educational campaigns concerning awareness programs to illustrate precaution measures ($Z\left(t\right)=0$ if lack of symptomatic infected individuals)
Control variables
$u_1$	Response intensity to the information
$u_2$	Awareness intensity of normal symptoms
$u_3$	Awareness intensity of intense symptoms
$u_4$	Response intensity to normal treatments
$u_5$	Response intensity to critical treatments

The susceptible people become exposed once they encounter infected individuals who are asymptomatic, symptomatic, or hospitalized under normal or critical treatments via the term $({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S$.

The exposed individuals are then divided into either asymptomatic or symptomatic segments regarding probabilistic $\rho$ and $(1-\rho )$, respectively if any disease symptoms have been recognized in the infected individuals [70]. Similarly, symptomatic individuals are separated into either normal or critical hospitalized people with probabilities $(1-c)$ and $c$, respectively, if they need supervised care in the hospital. Furthermore, the recovery condition is not permanent and a number of recovered individuals return to the susceptible segment, further with a constant rate $\xi$.

Although raising awareness persuades susceptible individuals to change their behavior and protect themselves from contagion, every person would not become cautious adequately forever due to various reasons ranging from financial matters to personality characteristics. Hence, a proportion of susceptible individuals adopt precautionary measures and alter their conventional habits, where these alterations depend not only on the number of susceptible individuals but also on the awareness density. Furthermore, the rate of information dissemination is solely determined by the number of symptomatic people. In this regard, let $u_{1}k$ be the rate at which the susceptible individuals’ behavior changes to prevent disease spread as a result of appropriate disease prevention proceedings (e.g., social distancing, cleanliness, and self-isolation). In addition, $\frac{pI}{1+qI}$ is a saturation function that represents how information grows among symptomatic infected individuals [70], [83].

3.2. The proposed SEIHRS model

The developed SEIHRS model for COVID-19 is a system dynamics model, where susceptible individuals acquire essential information concerning the disease and recommendations to avoid it. The infected individuals diverge into asymptomatic and symptomatic segments; however, due to the latency in the appearance of the symptoms, the possibility of converting asymptomatic individuals to symptomatic ones is considered. Additionally, symptomatic individuals are divided into minor and intense symptoms, which require normal and critical treatments. Furthermore, as the physical state of the patients in the first group deteriorates, they are transferred to the second group. Also, a number of hospitalized people can recover with necessary care, although they can become susceptible again due to the nature of the virus. Hence, the proposed system seeks to examine how to control the spread of the disease by investigating factors such as raising awareness about precautionary measures and offering better treatments. In this regard, the proposed SEIHRS model of Fig. 1 is mathematically formulated as the system of Eq. (1):

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}}& =& \Lambda -({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-dS+\xi R-u_{1}kSZS\left(0\right)>0,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}E}{\mathrm{d}t}}& =& ({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-(k+d)EE\left(0\right)\ge 0,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}A}{\mathrm{d}t}}& =& \kappa \rho E-\eta A-(d+{\delta }_1)AA\left(0\right)\ge 0,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}}& =& \kappa (1-\rho )E+\eta A-\omega I-(d+{\delta }_2)II\left(0\right)\ge 0,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}HN}{\mathrm{d}t}}& =& \omega (1-c)I-(d+{\delta }_3)HN-{\gamma }_{1}HN-\theta HNHN\left(0\right)\ge 0,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}HC}{\mathrm{d}t}}& =& \omega cI-(d+{\delta }_4)HC-{\gamma }_{2}HC+\theta HNHC\left(0\right)\ge 0,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}R}{\mathrm{d}t}}& =& {\gamma }_{1}HN+{\gamma }_{2}HC-\xi R-dR+u_{1}kSZR\left(0\right)\ge 0,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}Z}{dt}}& =& {\displaystyle \frac{pI}{1+qI}-a_{0}ZZ\left(0\right)\ge 0}\hfill \end{array}$$ (1)

This system represents the equilibrium of input and output flows at each state, which depends on time and simulates its fluctuation and dynamicity. In this regard, the first equation of the system (1) displays the number of susceptible people at time $t$. It calculates the difference between the total population, and the number of recovered individuals who return to susceptible ones, as the input flows; the number of susceptible individuals who become exposed, the number of susceptible individuals who die, and the number of susceptible individuals who follow health protocols, as the output flows. The second equation of the system (1) indicates the number of exposed people at time $t$. It calculates the difference between the number of susceptible individuals who become exposed, as the input flow; the number of exposed individuals who die, and the number of exposed individuals who become infected, as the output flows. The third equation of the system (1) indicates the number of asymptomatically infected people at time $t$. It computes the difference between the number of exposed individuals who become asymptomatically infected, as the input flow; the number of asymptomatically infected people who die naturally and unnaturally, and the number of asymptomatically infected people who become symptomatically infected, as the output flows. The fourth equation of the system (1) indicates the number of symptomatically infected people at time $t$. It calculates the difference between the number of exposed individuals who become symptomatically infected, and the number of asymptomatically infected people who become symptomatically infected, as the input flows; the number of symptomatically infected people who die naturally and unnaturally, and the number of symptomatically infected people who become hospitalized, as the output flows.

The fifth equation of the system (1) indicates the number of hospitalized individuals under normal treatments at time $t$. It calculates the difference between the number of symptomatically infected people who become hospitalized under normal treatments, as the input flow; the number of hospitalized individuals under normal treatments who die naturally and unnaturally, the number of hospitalized individuals under normal treatments who become recovered, and the number of hospitalized individuals under normal treatments who transfer to ICUs, as the output flows. The sixth equation of the system (1) indicates the number of hospitalized individuals under critical treatment at time $t$. It calculates the difference between the number of symptomatically infected people who become hospitalized under critical treatments, and the number of hospitalized individuals under normal treatments who transfer to ICUs, as the input flows; the number of hospitalized individuals under critical treatments who die naturally and unnaturally, and the number of hospitalized individuals under critical treatments who become recovered, as the output flows. The seventh equation of the system (1) indicates the number of recovered individuals at time $t$. It calculates the difference between the number of hospitalized individuals under normal and critical treatments who become recovered, and the number of susceptible individuals who follow health protocols, as the input flows; the number of recovered individuals who die naturally, and the number of recovered individuals who return to susceptible, as the output flows. Finally, the eighth equation of the system (1) indicates the awareness density at time $t$. It calculates the difference between the information growth, as the input flow, and the information depreciation, as the output flow.

For the calculation of the basic reproduction number ${\mathcal{R}}_0$ and the endemic equilibrium point, interested readers are referred to Appendix A. Furthermore, the stability analysis of the ${\mathcal{R}}_0$ equilibria is provided in Appendix B.

3.3. The optimal control problem – OCP

As discussed earlier, the main goal of the proposed SEIHRS model is to examine how to control the propagation of the disease by implementing a number of policies as control variables. Needless to say, managers are always looking for feedback from the system after the implementation of these interventions so that they can have precise control over them. In addition, it should not be forgotten that the implementation of these interventions always imposes costs on the system. This matter becomes more important when in the conditions of a pandemic; the available funds must be spent more obsessively. Therefore, an approach should be adopted that guarantees the achievement of the goal in addition to considering the mentioned limitations. However, the proposed SEIHRS model alone cannot provide the possibility of achieving the listed considerations. In this regard, OCP can be incorporated into the proposed system of equations (1) to determine control variables, satisfy the defined constraints of the devised system, and at the same time minimize the total costs of the system as a performance criterion.

In this regard, we considered two main policies, (1) raising awareness between susceptible and symptomatic infected people concerning minor and intense symptoms via spreading information, when the susceptible may observe precaution measures, and the symptomatic infected can seek treatment without disregarding their symptoms [70], and (2) improving normal and critical treatments for hospitalized individuals in general and ICU wards due to the increase of knowledge about virus behavior. In this regard and referring to Fig. 1, symptomatic infected individuals are divided into two categories. The first category visits medical centers with the mildest symptoms and receives normal treatment. The second category requires critical treatment due to ignoring the slightest symptoms, which exacerbates their health condition. This, in turn, leads to saturating general and ICU wards in medical centers. Therefore, let $\frac{{\epsilon }_1{u}_2\left(t\right)I}{1+{\zeta }_{1}I}$ and $\frac{{\epsilon }_2{u}_3\left(t\right)I}{1+{\zeta }_{2}I}$ be saturation functions for general and ICU wards, where ${\epsilon }_1$ and ${\epsilon }_2$ are acceptance rates of minor and severe symptoms by infected individuals with intensities $u_2$ and $u_3$ and saturation constants ${\zeta }_1^{-1}$ and ${\zeta }_2^{-1}$. Due to the unknown of COVID-19, treatments will be developed over time as more knowledge becomes available. This has an impact on disease progression and mortality rates. However, the ratio of patients to existing equipment is quite high, which leads to saturation in the system. In light of this reality, let $\frac{{\epsilon }_3{u}_4\left(t\right)HN}{1+{\zeta }_{3}HN}$ and $\frac{{\epsilon }_4{u}_5\left(t\right)HC}{1+{\zeta }_{4}HC}$ be saturation treatment functions, where ${\epsilon }_3$ and ${\epsilon }_4$ are normal and critical treatment rates with intensities $u_4$ and $u_5$ and saturation constants ${\zeta }_3^{-1}$ and ${\zeta }_4^{-1}$.

In this OCP, five control variables $u_i\left(t\right)$, $i=1,\dots ,5$ ($u_i\left(t\right)\in [0,1]$) are defined. In control variable $u_1\left(t\right)$, values 0 and 1 signify no reaction and the complete response of susceptible individuals to information, respectively. For control variables $u_2\left(t\right)$ and $u_3\left(t\right)$, value 0 signifies when a person is unaware of his or her normal or intense symptoms and does not seek medical advice, respectively; and value 1 represents complete awareness of symptoms. Finally, control variables $u_4\left(t\right)$ and $u_5\left(t\right)$, values 0 and 1 signify no response and complete response to normal and critical treatments in general and ICU wards, respectively. Hence, in order to determine the optimal response to minor and intense symptoms and optimal normal and critical treatments, an objective function is considered, which minimizes the system’s total costs including the cost of spreading awareness among susceptible and symptomatic infected individuals and the cost of normal and critical treatments in hospitals. The region of the control interventions can be defined as (2):

$$\begin{array}{ccc}\hfill \sqcap & =& \{u_1\left(t\right),u_2\left(t\right),u_3\left(t\right),u_4\left(t\right),u_5\left(t\right)\mid u_i\left(t\right)\in {[0,1]}^5,\hfill \\ \hfill i& =& 1,\dots ,5;t\in [0,T_f]\}\hfill \end{array}$$ (2)

where $T_f$ is the final time to implement the control policies, and $u_i\left(t\right)$ for $i=1,\dots ,5$ are bounded and measurable variables. Hence, with the intention of formulating the explained control policies, the following control problem is proposed with initial conditions $S\left(0\right)>0$, $E\left(0\right)\ge 0$, $A\left(0\right)\ge 0$, $I\left(0\right)\ge 0$, $HN\left(0\right)\ge 0$, $HC\left(0\right)\ge 0$, $R\left(0\right)\ge 0$ and $Z\left(0\right)\ge 0$.

$$\begin{array}{ccc}& & J[u_1\left(t\right),u_2\left(t\right),u_3\left(t\right),u_4\left(t\right),u_5\left(t\right)]\hfill \\ & & ={\int }_0^{T_f}[w_{1}I\left(t\right)+w_{2}HN\left(t\right)+w_{3}HC\left(t\right)+w_4{u}_1^2\left(t\right)\hfill \\ & & +w_5{u}_2^2\left(t\right)+w_6{u}_3^2\left(t\right)+w_7{u}_4^2\left(t\right)+w_8{u}_5^2\left(t\right)]\mathrm{d}t\hfill \end{array}$$ (3)

s.t.:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}}& =& \Lambda -({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-dS+\xi R-u_1\left(t\right)kSZ,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}E}{\mathrm{d}t}}& =& ({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-(k+d)E,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}A}{\mathrm{d}t}}& =& \kappa \rho E-(\eta +d+{\delta }_1)A,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}}& =& {\displaystyle \kappa (1-\rho )E+\eta A-(\omega +d+{\delta }_2)I-\frac{{\epsilon }_1{u}_2\left(t\right)I}{1+{\zeta }_{1}I}-\frac{{\epsilon }_2{u}_3\left(t\right)I}{1+{\zeta }_{2}I},}\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}HN}{\mathrm{d}t}}& =& {\displaystyle \omega (1-c)I-(d+{\delta }_3+{\gamma }_1+\theta )HN+\frac{{\epsilon }_1{u}_2\left(t\right)I}{1+{\zeta }_{1}I}-\frac{{\epsilon }_3{u}_4\left(t\right)HN}{1+{\zeta }_{3}HN},}\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}HC}{\mathrm{d}t}}& =& {\displaystyle \omega cI-(d+{\delta }_4+{\gamma }_2)HC+\theta HN+\frac{{\epsilon }_2{u}_3\left(t\right)I}{1+{\zeta }_{2}I}-\frac{{\epsilon }_4{u}_5\left(t\right)HC}{1+{\zeta }_{4}HC},}\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}R}{\mathrm{d}t}}& =& {\displaystyle {\gamma }_{1}HN+{\gamma }_{2}HC-\xi R-dR+u_1\left(t\right)kSZ+\frac{{\epsilon }_3{u}_4\left(t\right)HN}{1+{\zeta }_{3}HN}+\frac{{\epsilon }_4{u}_5\left(t\right)HC}{1+{\zeta }_{4}HC},}\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}Z}{dt}}& =& {\displaystyle \frac{pI}{1+qI}-a_{0}Z}\hfill \end{array}$$ (4)

The first term in the objective function (3) calculates the cost when symptomatic infected individuals consult a medical professional concerning normal and intense symptoms and seek necessary medical care without disregarding symptoms. The second and the third terms calculate the costs of hospitalized people in general and ICU wards, respectively. The fourth term calculates the cost of spreading awareness among susceptible individuals. The fifth and sixth terms compute the productivity loss due to mild or intense illness, respectively. Finally, the seventh and eighth terms calculate the opportunity loss, such as productivity loss, resulting from hospitalization to general and ICU wards, respectively. Remarkably, the square of the control variable reveals the intensity of side effects of awareness programs and treatment policies [31], [32], [38], [84], [85]. The positive parameters $w_i$, $i=1,\dots ,8$ are importance weights and balance the units of the integrand.

Theorem 3

The control system(3)and(4)has optimal control variables such that$J(u_1^{*},u_2^{*},u_3^{*},u_4^{*},u_5^{*})=\min \left[J(u_1,u_2,u_3,u_4,u_5)\right]$.

Proof

A mathematical proof has been provided in Appendix C. □

Finally, Appendix D provides the way to obtain optimal control variables. Noteworthy, as far as the pandemic is not over, $S\left(t\right)$, $A\left(t\right)$, $I\left(t\right)$, $HN\left(t\right)$, and $HC\left(t\right)$ help to estimate the demand of medical products corresponding to each segment of the population. For instance, considering the COVID-19 pandemic, the demands for hydro-alcoholic gels and masks over time can be estimated by $S\left(t\right)$; $HN\left(t\right)+HC\left(t\right)$ can represent the demand for medical clothes over time; the demand for ordinary beds over time can be estimated by $HN\left(t\right)$; and finally, the demands for ICU beds and ventilators over time can be estimated by $HC\left(t\right)$. More importantly, at the endemic equilibrium point, the demand for the above-mentioned products and equipment can be estimated using obtained optimal state variables ($S^{*}$, $H{N}^{*}+H{C}^{*}$, $H{N}^{*}$, and $H{C}^{*}$) resulting from the optimal system.

4. The proposed PISP model

This section formulates a logistics network that includes a set of suppliers and manufacturers that provide medical products and equipment, as well as a set of demand points/hospitals (hereafter, we only use the term hospitals as the demand and cure points of the population). The manufacturers and hospitals are clustered in a given number of regions, in such a way that the hospitals of a given region receive medical products and equipment from the manufacturers located in the same region. A set of medical products and equipment are considered, which are divided into consumable and reusable products. Manufacturers produce medical products and equipment using raw materials provided by suppliers and distribute them only among the hospitals of their corresponding region. Due to demand fluctuations and capacity limitations in manufacturers and suppliers, hospitals might encounter shortages. Hence, an applicable sharing system among hospitals in each region is developed, wherein hospitals with surplus products can transfer the extra portion to the hospitals with extra demands. In addition, hospitals can receive a higher percentage of their patients’ actual demands and respond to them through the sharing system. More importantly, a lead time is defined for reusable products according to their occupancy times in ICU wards. This is indeed in line with real-world practice, where these products become free and reusable over a certain period of time, and they will be reconsidered as available inventory.

Before entering the details of the proposed mathematical model, assumptions and necessary notations are described.

4.1. Assumptions and notations

The main assumptions of the defined problem are as follows: 1) The capacity of suppliers, manufacturers, and hospitals is limited; 2) The sharing capacity of any hospital, and the total sharing capacity over all regions are limited; 3) ICU beds and ventilators can be reused after a certain period as the occupancy time; 4) The shortage of medical products in hospitals is allowable, which is reflected by unmet demand; 5) Hospitals with surplus inventory can transfer the extra portion to hospitals with extra demands; 6) Hospital’s unmet demand is met using the net supply balance and sharing from other hospitals; 7) Hospitals with extra inventory cannot receive products from the sharing process; 8) The sharing approach enables hospitals to get a greater proportion of their patients’ actual demands and address them; and 9) The demand for medical products in hospitals is uncertain and has a dynamic pattern, which is estimated by the developed SEIHRS model with OCP.

The list of the notations of the proposed mathematical model is provided as Table 3 .

Table 3.

Notations of the proposed multi-period PISP model.

Notation	Description
Sets & Indices
$m,m^{\prime }\in M$	Set of nodes, including manufacturers and hospitals in all regions
$K$ & $H$	Set of manufacturers and hospitals in all regions
$K_i\left(m\right)$	Subsets of manufacturers in region $i$; $K=\bigcup _i{K}_i\left(m\right)$
$H_i\left(m\right)$	Subsets of hospitals in region $i$; $H=\bigcup _i{H}_i\left(m\right)$
$j\in J$	set of suppliers of raw materials
$p\in P$	Set of medical products, including two sets of consumable $P^{\prime }$ (hydro-alcoholic gel, mask, medical clothes, and ordinary beds) and reusable $P^{″}$ (ICU beds and ventilator)
$t\in T$	Set of time periods
Parameters
$L$	Lead-time periods as the occupancy time, at which the reusable products are reconsidered as available inventory
${\gamma }_p$	Conversion rate of raw materials to manufacture product $p$
$D_{pmt}$	Demand for product $p$ in hospital $m$ at period $t$
$U_{pj}$	Capacity limitation for product $p$ at supplier $j$
$Q_{pm}$	Capacity limitation for product $p$ at manufacturer $m$
$O{C}_j$	Ordering cost of product $p$ at supplier $j$
$S{C}_{pm}$	Production cost of product $p$ at manufacturer $m$
$P{C}_{pm}$	Unit production cost of product $p$ at manufacturer $m$
$T{C}_{pjm}$	Transportation cost per unit of product $p$ from supplier $j$ to manufacturer $m$
$CU$	Unit cost of unmet demand at hospitals
$I_{pm}^0$	Initial inventory of product $p$ at manufacturer/hospital $m$ at the beginning of the planning horizon
$I{C}_{pm}$	Unit inventory holding cost of product $p$ at manufacturer/hospital $m$
$I_{pm}^{\max }$	Maximum inventory capacity for product $p$ at manufacturer/hospital $m$
$G_{pm}^{\max }$	Maximum sharing capacity for product $p$ at hospital $m$
$T{Q}_p$	Total sharing capacity for product $p$ over all regions
${\mu }_p$	Allowed demand surplus (%) for product $p$ at hospitals that can be met through the sharing system
$T{C}_{pm{m}^{\prime }}$	Unit transportation cost of product $p$ shared among hospitals $m$ and $m^{\prime }$ during the sharing process
Decision variables
$w_{jt}$	1 if an order is placed to supplier $j$ at period $t$; 0 otherwise
$y_{pmt}$	1 if product $p$ is set up for production in manufacturer $m$ at period $t$
$b_{pmt}$	Net service balance of product $p$ in hospital $m$ at the beginning of period $t$ before transferring the products in the sharing process; $b_{pmt}=b_{pmt}^{+}+b_{pmt}^{-}$, where $b_{pmt}^{+}$ and $b_{pmt}^{-}$ are positive and negative parts of net service balance $b_{pmt}$ (i.e., $b_{pmt}^{+}=\max \{0,b_{pmt}\}$ and $b_{pmt}^{-}$ = $\min \{0,b_{pmt}\}$)
$v_m$	1 if $b_{pmt}>0$; 0 otherwise
$x_{pmt}$	Production quantity of product $p$ in manufacturer $m$ in period $t$
$u_{pjmt}$	Quantity of raw material for product $p$ transferred from supplier $j$ to manufacturer $m$ in period $t$
$q_{m{m}^{\prime }}^{pt}$	Quantity of product $p$ transferred from manufacturer $m$ to hospital $m^{\prime }$ at the beginning of period $t$
$I_{pmt}$	Inventory of product $p$ in node $m$ at the end of period $t$
$g_{pmt}$	Available quantity of product $p$ to be supplied by hospital $m$ in period $t$ to satisfy its internal demand and external sharing
$s_{m{m}^{\prime }}^{pt}$	Quantity of product $p$ shared from hospital $m$ to hospital $m^{\prime }$ in period $t$; $s_{mm}^{pt}=0$ and $s_{m{m}^{\prime }}^{pt}=-s_{m^{\prime }m}^{pt}$, where ${\left(s_{m{m}^{\prime }}^{pt}\right)}^{+}$ and ${\left(s_{m{m}^{\prime }}^{pt}\right)}^{-}$ are the positive and negative parts of shared products (i.e., ${\left(s_{m{m}^{\prime }}^{pt}\right)}^{+}=\max \{0,s_{m{m}^{\prime }}^{pt}\}$ and ${\left(s_{m{m}^{\prime }}^{pt}\right)}^{-}=\min \{0,s_{m{m}^{\prime }}^{pt}\}$ for $m\ne m^{\prime }$)
$S_{pmt}$	Amount of unmet demand of product $p$ in hospital $m$ at the end of period $t$
$S_{\max }$	Maximum unmet demand among all hospitals

4.2. The PISP formulation

This section proposes the multi-period PISP formulation as a mixed-integer linear programming model using the notations described in Table 3, where the demand for consumable and reusable products are estimated from the proposed SEIHRS model (4).

4.2.1. Objective function

The objective function of the multi-period PISP formulation is presented as (5) which minimizes the total costs of the system.

$$\begin{array}{ccc}\hfill \min Z& =& \sum _{j\in J}\sum _{t\in T}O{C}_j{w}_{jt}+\sum _{p\in P}\sum _{m\in K}\sum _{t\in T}S{C}_{pm}{y}_{pmt}+\sum _{p\in P}\sum _{j\in J}\sum _{m\in K}\sum _{t\in T}T{C}_{pjm}{u}_{pjmt}\hfill \\ & & +\sum _{p\in P}\sum _{m\in K}\sum _{t\in T}P{C}_{pm}{x}_{pmt}+\sum _{p\in P}\sum _{m\in K}\sum _{m^{\prime }\in H}\sum _{t\in T}T{C}_{pm{m}^{\prime }}{q}_{m{m}^{\prime }}^{pt}\hfill \\ & & +\sum _{p\in P}\sum _{m\in H}\sum _{m^{\prime }\in H}\sum _{t\in T}T{C}_{pm{m}^{\prime }}{s}_{m{m}^{\prime }}^{pt}+\sum _{p\in P}\sum _{m\in K\cup H}\sum _{t\in T}I{C}_{pm}{I}_{pmt}+CU\times S_{max}\hfill \end{array}$$ (5)

The objective function (5) includes eight different terms including: 1) fixed ordering costs for suppliers, 2) fixed production setup costs at manufacturers, 3) variable transportation costs between suppliers and manufacturers, 4) variable production costs at manufacturers, 5) variable transportation costs between manufacturers and hospitals, 6) variable sharing costs among hospitals, 7) variable inventory holding costs at manufacturers and hospitals, and 8) unmet demand costs, respectively.

4.2.2. Constraints

In the following, the constraints of the proposed multi-period PISP model are explained. The first set of constraints, i.e. (6)–(12), formulate the amount of unmet demand as well as the amount of raw materials and products among suppliers, manufacturers, and hospitals.

$$S_{max}\ge S_{pmt}\forall p\in P,m\in H,t\in T$$ (6)

$$\sum _{m\in K}{u}_{pjmt}\le U_{pj}{w}_{jt}\forall j\in J,p\in P,t\in T$$ (7)

$$\sum _{j\in J}{u}_{pjmt}={\gamma }_p{x}_{pmt}\forall p\in P,m\in K,t\in T$$ (8)

$$x_{pmt}\le Q_{pm}{y}_{pmt}\forall p\in P,m\in K,t\in T$$ (9)

$$\sum _{m^{\prime }\in H_i\left(m\right)}{q}_{m{m}^{\prime }}^{pt}\le x_{pm,t-1}+I_{pm,t-1}\forall i\in I,p\in P,m\in K_i\left(m\right),t\in T$$ (10)

$$g_{pmt}+\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m{m}^{\prime }}^{pt}\right)}^{+}\le \sum _{m^{\prime }\in K_i\left(m\right)}{q}_{m^{\prime }m}^{pt}\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (11)

$$\sum _{m\in K_i\left(m\right)}{q}_{m{m}^{\prime }}^{pt}\le G_{p{m}^{\prime }}^{max}\forall i\in I,p\in P,m^{\prime }\in H_i\left(m\right),t\in T$$ (12)

In this regard, constraint (6) calculates the maximum unmet demand among all hospitals. Constraint (7) represents supplier capacities and ensures that only suppliers that have already set up can supply raw materials. Constraint (8) represents the balance of raw materials quantity transferred from suppliers to manufacturers and the production quantity in manufacturers. Next, constraint (9) guarantees the production capacity of manufacturers for each product type at each period. Furthermore, constraint (10) ensures that the production quantity transferred from each manufacturer to hospitals at the beginning of each period can not exceed the production quantity of the previous period and the inventory at the beginning of the preceding period. In addition, constraint (11) ensures that supplied and shared products via each hospital during each period cannot exceed the amount of product delivered to that hospital. Finally, constraint (12) guarantees that the delivery quantity of any type of product from all manufacturers to each hospital in each period cannot exceed the hospital’s maximum supply capacity.

The second set of constraints, i.e. (13)–(17), monitor the inventory level of different products at manufacturers and hospitals.

$$I_{pmt}=I_{pm,t-1}+x_{pm,t-1}-\sum _{m^{\prime }\in H_i\left(m\right)}{q}_{m{m}^{\prime }}^{pt}\forall i\in I,p\in P,m\in K_i\left(m\right),t\in T$$ (13)

$$I_{pmt}\le I_{pm}^{max}\forall p\in P,m\in M,t\in T$$ (14)

$$\begin{array}{ccc}\hfill I_{pmt}& =& I_{pm,t-1}+\sum _{m^{\prime }\in K_i\left(m\right)}{q}_{m^{\prime }m}^{pt}-g_{pm,t-1}+\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m^{\prime }m}^{p,t-1}\right)}^{-}\hfill \\ & & -\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m{m}^{\prime }}^{p,t-1}\right)}^{+}\forall i\in I,p\in P^{\prime },m\in H_i\left(m\right),t\in T\hfill \end{array}$$ (15)

$$\begin{array}{ccc}\hfill I_{pmt}& =& I_{pm,t-1}+\sum _{m^{\prime }\in K_i\left(m\right)}{q}_{m^{\prime }m}^{pt}-g_{pm,t-1}+\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m^{\prime }m}^{p,t-1}\right)}^{-}\hfill \\ & & -\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m{m}^{\prime }}^{p,t-1}\right)}^{+}\forall i\in I,p\in P^{″},m\in H_i\left(m\right),t\in T;1<t\le L\hfill \end{array}$$ (16)

$$\begin{array}{ccc}\hfill I_{pmt}& =& I_{pm,t-1}+\sum _{m^{\prime }\in K_i\left(m\right)}{q}_{m^{\prime }m}^{pt}-g_{pm,t-1}+g_{pm,t-L}+\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m^{\prime }m}^{p,t-1}\right)}^{-}\hfill \\ & & -\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m{m}^{\prime }}^{p,t-1}\right)}^{+}\forall i\in I,p\in P^{″},m\in H_i\left(m\right),t\in T;L<t\hfill \end{array}$$ (17)

In this regard, constraint (13) represents product inventory in each manufacturer at the beginning of each period. Constraint (14) represents the storage capacity of facilitates, including manufacturers and hospitals, for each product type and period. Constraint (15) represents product inventory in each hospital at the beginning of each period for the consumable products. Constraint (16) represents product inventory in each hospital at the beginning of periods 2 to $L$ for the reusable products. Constraint (17) represents product inventory in each hospital from the beginning of period $L$-onwards for reusable products regarding the reuse cycle.

The rest of the constraints, i.e. (18)–(28), are defined to form the sharing system.

$$D_{pmt}\le (1+{\mu }_p)g_{pmt}\forall p\in P,m\in H_i\left(m\right),t\in T$$ (18)

$$\sum _{m\in H}{g}_{pmt}\le T{Q}_p\forall p\in P,t\in T$$ (19)

$$g_{pmt}\le I_{pmt}\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (20)

$$b_{pmt}=g_{pmt}-D_{pmt}\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (21)

$$S_{pmt}=-b_{pmt}-\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{s}_{m^{\prime }m}^{pt}\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (22)

$$b_{pmt}^{+}\le T{Q}_p{v}_m\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (23)

$$b_{pmt}^{-}\ge T{Q}_p(v_m-1)\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (24)

$$\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}{\left(s_{m{m}^{\prime }}^{pt}\right)}^{+}\le b_{pmt}^{+}\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (25)

$$b_{pmt}^{+}\ge {\left(s_{m{m}^{\prime }}^{pt}\right)}^{+}\forall i\in I,p\in P,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }$$ (26)

$$b_{pmt}^{-}\le {\left(s_{m{m}^{\prime }}^{pt}\right)}^{-}\forall i\in I,p\in P,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }$$ (27)

$${\left(s_{m{m}^{\prime }}^{pt}\right)}^{+}\le G_{pm}^{max}\forall i\in I,p\in P,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }$$ (28)

For this aim, constraint (18) ensures that each hospital’s demand for each product type in each period is met by the amount of hospital supply and the allowable demand overload ratio. Constraint (19) guarantees that all hospitals’ total available supply for any product cannot exceed the total supply capacity of that hospital. Constraint (20) guarantees that the supply quantity of each product type in each period via each hospital cannot exceed the hospital inventory at the beginning of the period. Constraint (21) represents the net supply balance of each product in each hospital before sharing. Constraint (22) states that each hospital’s unmet demand for any product is met using the net supply balance and product sharing from other hospitals. Constraints (23) and (24) impose that only one of $b_{pmt}^{+}$ and $b_{pmt}^{-}$ becomes nonzero. Constraint (25) guarantees that the total product transferred from each hospital to other hospitals should not exceed that hospital’s maximum transferable capacity. Constraint (26) ensures that each hospital with extra supply can offer an outgoing capacity transfer. Constraint (27) ensures that a hospital with extra supply can not receive an incoming capacity transfer. Constraint (28) prevents product sharing across regions. Finally, constraints (29) determine the types of decision variables.

$$\begin{array}{c}{u}_{pjmt},x_{pmt},q_{m{m}^{\prime }}^{pt},I_{pmt},g_{pmt},b_{pmt}^{+},{\left(s_{m{m}^{\prime }}^{pt}\right)}^{+},S_{pmt},S_{max}\ge 0\hfill \\ s_{m{m}^{\prime }}^{pt},b_{pmt}\in \mathrm{I}\mathrm{R}\hfill \\ b_{pmt}^{-},{\left(s_{m{m}^{\prime }}^{pt}\right)}^{-}\le 0\hfill \\ v_m,w_{jt},y_{pmt}\in \{0,1\}\hfill \end{array}$$ (29)

5. Benders decomposition

This section offers an accelerated Benders decomposition (ABD) algorithm [86] to solve the proposed PISP model. Benders decomposition divides the original problem into a master problem and several sub-problems such that each of which is generally easier to solve than the original problem. The sub-problems’ variables are estimated by applying linear programming duality. The remaining variables are in the master problem, as well as an artificial variable that describes a lower bound (upper bound) on the sub-problems’ objective function for a minimization (maximization) problem. Afterward, a cutting plane algorithm solves the resultant model, where the values of the master problem’s variables are first determined. Then, the sub-problems are solved with these variables determined at each iteration. A feasibility cut is added to the master problem if the sub-problems are infeasible and unbounded; else, an optimality cut is added. If sub-problems are feasible, an upper bound can be obtained, and if the optimal solution is obtained by solving the master problem, a lower bound can be obtained. The process is repeated until an optimal solution is detected or the optimality gap falls below a specified threshold. What is more, in order to enhance Benders decomposition’s performance, a number of acceleration methods are applied.

5.1. Valid inequalities

This section introduces a set of new valid inequalities that can be applied to strengthen the linear programming relaxation of the PISP formulation. The first class of inequalities depends on the products’ type (i.e., consumable and reusable). Three factors are considered in the valid inequalities for consumable products (i.e., Inequality (30)): inventory level, unmet demand quantity, and aggregated demand at hospitals. In addition to these factors, the valid inequalities of reusable products (i.e., Inequalities (31) and (32)) encompass the released inventory level due to the reuse cycle.

$$\begin{array}{ccc}& & \sum _{m\in H_i\left(m\right)}{I}_{pmh}+\sum _{m\in H_i\left(m\right)}{S}_{pmt}\ge \sum _{m\in H_i\left(m\right)}\sum _{\begin{array}{c}h\le t^{\prime }\le t\end{array}}\hfill \\ & & D_{pm{t}^{\prime }}(1-\sum _{m\in K_i\left(m\right)}\sum _{\begin{array}{c}h\le t^{\prime }\le t\end{array}}{y}_{pm{t}^{\prime }})\forall i\in I,p\in P^{\prime },t,h\in T;1\le h\le t\hfill \end{array}$$ (30)

$$\begin{array}{ccc}& & \sum _{m\in H_i\left(m\right)}{I}_{pmh}+\sum _{m\in H_i\left(m\right)}{S}_{pmt}\ge \sum _{m\in H_i\left(m\right)}\sum _{\begin{array}{c}h\le t^{\prime }\le t\end{array}}{D}_{pm{t}^{\prime }}(1-\sum _{m\in K_i\left(m\right)}\sum _{\begin{array}{c}h\le t^{\prime }\le t\end{array}}{y}_{pm{t}^{\prime }})\hfill \\ & & \forall i\in I,p\in P^{″},t,h\in T;1\le t\le L,1\le h\le t\hfill \end{array}$$ (31)

$$\begin{array}{ccc}& & \sum _{m\in H_i\left(m\right)}{I}_{pmh}+\sum _{m\in H_i\left(m\right)}{S}_{pmt}+\sum _{m\in H_i\left(m\right)}{D}_{pm,t-L}\ge \hfill \\ & & \sum _{m\in H_i\left(m\right)}\sum _{\begin{array}{c}h\le t^{\prime }\le t\end{array}}{D}_{pm{t}^{\prime }}(1-\sum _{m\in K_i\left(m\right)}\sum _{\begin{array}{c}h\le t^{\prime }\le t\end{array}}{y}_{pm{t}^{\prime }})\hfill \\ & & \forall i\in I,p\in P^{″},t,h\in T;L<t,L<h\le t\hfill \end{array}$$ (32)

Inequality (30) validates that the aggregated demand between periods $h$ to $t$ is typically fulfilled either from available inventory at hospitals through direct supply or sharing or from backlog if the required inventory is not available. Inequalities (31) and (32) represent a similar concept, except that after period $L$, the inventory level of reusable products is increased by the amount of demand at period $t-L$, which can be employed to fulfill demands through direct supply or sharing.

Moreover, since the primary master problem in this study only contains logical constraints upon $y_{pmt}$ and a limited number of optimality cuts, the master problem contributes to a supply chain with a restricted number of equipped suppliers and manufacturers in the initial iterations of the Benders algorithm. As a result, the lower bounds for early master problems are negligible. More importantly, only a tiny portion of demands can be fulfilled in sub-problems with few equipped facilities, imposing a high cost of unmet demand on the problem. In order to reduce this repercussion, the second class of inequalities is in charge of this task. In this regard, since suppliers provide raw materials to manufacturers and manufacturers make finished products, we must set up at least one supplier and manufacturer, which is guaranteed by inequalities (33) and (34). Finally, inequality (35) validates that the unmet demand of product $p$ in hospital $m$ during each period cannot exceed the product’s demand in that hospital.

$$\sum _{j\in J}\sum _{t\in T}{w}_{jt}\ge 1$$ (33)

$$\sum _{p\in P}\sum _{m\in K}\sum _{t\in T}{y}_{pmt}\ge 1$$ (34)

$$S_{pmt}\le D_{pmt}\forall p\in P,m\in H,t\in T$$ (35)

5.2. Knapsack inequalities

The knapsack inequality is added to the master problem to accelerate the branch-and-bound process in the solver. Indeed, the convergence speed of Benders decomposition can be improved by adding the following cuts, which assist progressive solvers like Gurobi in deriving a range of valid inequalities [87]. Consequently, the following cuts (36) are added in iteration $n+1$ of the master problem.

$$L{B}^n\le \sum _{j\in J}\sum _{t\in T}O{C}_j{w}_{jt}+\sum _{p\in P}\sum _{m\in K}\sum _{t\in T}S{C}_{pm}{y}_{pmt}+\zeta$$ (36)

where $L{B}^n$ signifies the best specified lower bound found so far, and $\zeta$ is an additional variable representing the total cost except ordering and setup costs. Finally, the PISP Benders reformulation is provided in Appendix F.

6. Computational experiments

This section presents the computational results of the devised framework to deal with pandemic situations under dynamic demand. For this aim, Section 6.1 designs a set of experiments based on a real case study, the COVID-19 pandemic in France. Next, Section 6.2 provides a comparative analysis between the proposed ABD algorithm and the Gorubi solver without (GRB) and with the valid inequalities (GRB_VI). The comparison between GRB and GRB_VI helps to investigate how much the valid inequalities have been effective in reducing the computational time of the Gurobi solver. Finally, a set of comprehensive sensitivity analyses are presented in Section 6.3 to investigate the behavior of the proposed PISP model to any changes in its input parameters.

6.1. Experimental design and case study

This section designs a set of experiments for evaluating the devised framework’s performance in dealing with the COVID-19 pandemic in France, where the demands of consumable and reusable products are determined using the proposed SEIHRS model. The experiments are derived from a real case study, the COVID-19 pandemic in France. In this case study, a set of six medical products and equipment are considered, which are divided into consumable and reusable products, including masks, hydro-alcoholic gel, medical clothes, and ordinary beds as consumable products, and ICU beds and ventilators as reusable ones. Among 13 metropolitan and 5 overseas regions of France, this case includes 12 regions, and each region has a given number of factories, hospitals, and population as depicted in Fig. 2 . Furthermore, there exist 12 suppliers to supply raw materials throughout France. For each region, we nominate a set of geographically dispersed hospitals throughout the region, and each may also integrate a set of other local/smaller hospitals. In the case of integrating multiple hospitals, the capacity of the representative hospital will be the sum of the capacity of integrated hospitals. Each main hospital or a group of hospitals is responsible for fulfilling the demand of a populated area under their coverage. Accordingly, the dynamic demand of products at each hospital (i.e., $D_{pmt}$) is obtained by running the proposed system dynamics model (4) for that area, where the total population and death rates are the mean values for covered populated areas, and the population is the sum of the populations in those areas. Moreover, we assume that the disease does not spread among different regions and the proposed SEIHRS model is executed separately for each region. Detailed information on all other parameters in the SEIHRS model and PISP formulation is provided in

Fig. 2.

The case study information on each region.

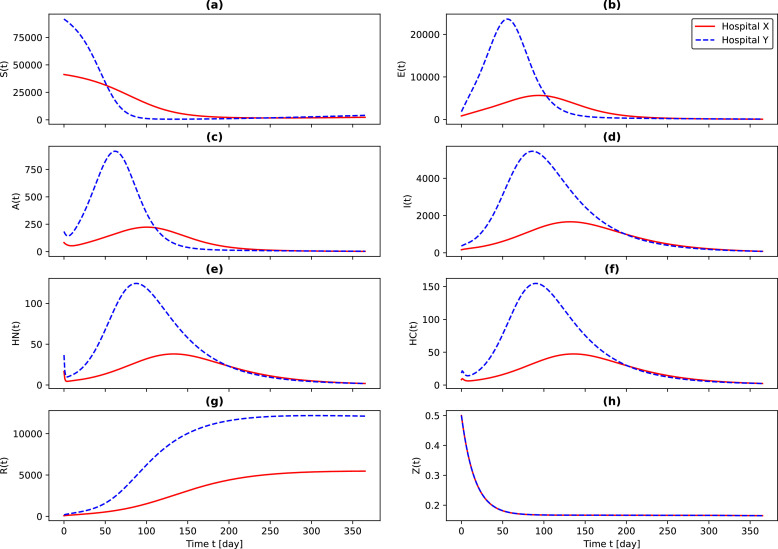
Figure 3 illustrates the outcomes of the SEIHRS model in determining the state variables for two distinct hospitals that belong to two different regions. It is worth mentioning that these results only represent the first peak of the disease. As can be observed, the dynamicity of the state variables in the two hospitals are significantly different, and they do not follow a specific distribution. These issues demonstrate the necessity of employing epidemiological-based system dynamics models (i.e., the SEIHRS model) to determine the demand. As a result, the policy-makers in each region should plan separately based on their production and sharing capacities. Needless to say, this knowledge leads to better utilization of the capacity. What is more, national policy-makers may also arrange to transfer excess capacity to other regions.

Fig. 3.

The outcomes of the SEIHRS model showing the dynamic demands.

Remarkably, since the basic reproduction number $R_0$ is obtained greater than 1 for the case study, the endemic equilibrium point of the pandemic cannot be obtained by solving the system of Eq. (A.6). Hence, it can be realized that the optimal values of the state variables cannot be used to estimate the demand for masks and hydro-alcoholic gels ($S^{*}$), ordinary beds ($H{N}^{*}$), ICU beds and ventilators ($H{C}^{*}$), and medical clothes ($H{N}^{*}+H{C}^{*}$). Therefore, the cumulative value of each of the state variables $\left(S\right(t),HN(t),HC(t),HN(t)+HC(t\left)\right)$ in a week represents the demand for medical products in each period of the PISP model.

To test the performance of the proposed ABD algorithm, a set of 25 test problems are derived from the case study, wherein the numbers of regions, suppliers, manufacturers, and hospitals are fixed, but the period increases from 4 weeks to 52 weeks. Since the SEIHRS model is run for each hospital for a time horizon of 365 days and it is also impossible and illogical to plan the PISP daily, each period of the PISP model represents a week and the demand of each period is the cumulative demand of the whole week.

The PISP model and the ABD algorithm were coded in Python 3 using the Gurobi library, and all experiments were done on a server containing four Intel XEON processors with 5 GB of RAM running at 2.3 GHz. Furthermore, two stopping criteria are considered when executing the accelerated Benders decomposition algorithm and the Gurobi solver: 1) a gap of 1% and 2) a CPU time of 7200s. For the ABD algorithm, the first criterion is the gap (%) between the obtained lower-bound and upper-bound at each iteration of the algorithm; and for the Gurobi solver, it is the gap (%) between the best-found solution and the current obtained solution.

6.2. Numerical results

This section provides a comparative analysis of the performance of the proposed ABD algorithm with the GRB and GRB_VI. Table 4 shows the results of this comparison for 25 test problems (i.e., column “$\left|T\right|$” as the number of periods), in terms of both objective function values (i.e., columns “Obj. Values”) and computational time (i.e., columns “Time (s)”). In columns “Obj. Values”, the values are proportional to the objective function value of the first test problem, which has been shown as “X” in Table 4.

Table 4.

ABD vs. GRB & GRB_VI and the impact of sharing.

$\left|T\right|$	Obj. values			Time (s)			Sharing impact (%)
	ABD	GRB	GRB_VI	ABD	GRB	GRB_VI	Obj.	$S_{\max }$
4	1.0X	1.0X	1.0X	9	28	18	15.71	25.99
6	2.0X	2.0X	2.0X	15	56	50	2.35	31.81
8	2.8X	2.8X	2.8X	74	1586	1220	$-$10.83	14.03
10	3.8X	3.8X	3.8X	56	750	623	$-$21.95	9.64
12	4.4X	4.4X	4.4X	129	2313	2005	$-$29.83	$-$9.77
14	5.3X	5.3X	5.3X	178	1548	1248	$-$35.08	$-$21.06
16	6.3X	6.3X	6.3X	412	5217	4350	$-$38.32	$-$29.07
18	6.9X	6.9X	6.9X	463	3560	3019	$-$40.61	$-$32.58
20	8.1X	33.4X	8.1X	558	7200*	2750	$-$42.02	$-$35.16
22	8.7X	8.7X	8.7X	623	5661	2572	$-$42.79	$-$35.31
24	9.3X	9.3X	9.3X	1131	6183	3334	$-$43.12	$-$35.20
26	10.3X	10.3X	10.3X	1228	6607	2873	$-$43.19	$-$36.44
28	11.5X	42.6X	11.5X	2002	7200*	6800	$-$42.94	$-$35.95
30	25.4X	44.8X	25.4X	2315	7200*	665	$-$42.50	$-$35.35
32	13.1X	47.3X	13.1X	2505	7200*	1316	$-$41.74	$-$34.68
34	27.9X	49.6X	27.9X	2580	7200*	1553	$-$40.95	$-$30.01
36	29.5X	52.0X	29.5X	2692	7200*	1661	$-$40.15	$-$29.22
38	35.1X	54.3X	35.1X	2858	7200*	1662	$-$39.26	$-$28.42
40	17.7X	56.7X	17.7X	3034	7200*	2044	$-$38.33	$-$27.61
42	59.1X	**	101.6X	3669	**	7200*	$-$37.36	$-$26.81
44	61.6X	**	104.5X	5413	**	7200*	$-$36.32	$-$26.03
46	64.1X	**	**	5665	**	**	$-$35.31	$-$25.28
48	66.6X	**	**	6029	**	**	$-$34.23	$-$24.55
50	69.0X	**	**	6743	**	**	$-$33.32	$-$23.85
52	71.5X	**	**	7126	**	**	$-$32.33	$-$23.21
						Average:	$-$32.98	$-$20.96

* Time limit of 7200 s reached.

** No feasible solution after 7200 s.

As can be seen in Table 4, all three methods have been able to obtain optimal solutions for test problems up to 26 time periods except the test problem with 20 periods; however, this has occurred in less computational efforts for the ABD algorithm compared to both GRB and GRB_VI. Furthermore, the GRB_VI has been also faster compared to the GRB in the mentioned test problems. In addition, the ABD algorithm has been able to obtain a gap of less than 1% for all test problems before reaching the maximum allowable CPU time of 7200s, even for larger test problems. It has also happened for the GRB_VI for almost all test problems except the last four test problems. Indeed, the proposed valid inequalities help the mathematical model to be solved faster, and they obtain better results under limited computational efforts. However, they are still ineffective when solving large-sized test problems for $\left|T\right|\ge 46$.

On the other hand, the GRB has been unable to obtain the optimal solution for test problems with 20 and $\ge 28$ periods, among which for test problems with $\left|T\right|\ge 42$ a feasible solution has not been even obtained within the limited computational effort of 7200s. It is also clear that there is a considerable difference between the computational time of GRB and GRB_VI compared to the ABD algorithm, which indicates the effectiveness of the proposed ABD algorithm in solving the PISP.

More importantly, to demonstrate the efficiency of the sharing mechanism, two critical evaluation criteria have been examined for all test problems, namely the total cost of the system and the maximum unmet demand. These evaluations have been reported in columns “Obj.” and “$S_{\max }$” under “Sharing impacts (%)”, respectively, where positive and negative values, respectively, show the increase and the decrease percentages in the corresponding values. For this aim, the ABD algorithm has been used to solve all test problems under two options: 1) sharing and 2) without sharing. In the second option, the parameter $G_{\max }$ is fixed to 0 to prohibit the hospitals from sharing products. As can be seen, the sharing mechanism reduces the total system costs and unmet demand in all test problems except for test problems with a smaller number of periods. For instance, the total cost of the system is increased by 15.71% and 2.35% for test problems $\left|T\right|=4$ and $\left|T\right|=6$, respectively. The unmet demand is also increased for test problems $\left|T\right|=\{4,6,8,10\}$. The reason for these exceptional increases in the total cost of the system goes back to the fact that in primer periods, the demand for medical products increases sharply up to period $t=10$ (when the peak of the pandemic occurs in most of the populated areas), consequently, the maximum unmet demand increases as well. In such situations, since the planning horizon is short, the system increases the inventory levels with the hope to fulfill the demand in all possible ways (i.e., direct or sharing fulfillment), while this increase is not that significant to absorb the effect of the unmet demand cost in the objective function. Therefore, the maximum unmet demand and the total cost of the system increase. However, when a higher number of periods are considered, the system allows for a significant increase in the inventory levels even in primary periods to fulfill the demand, as well as the fact that the extra inventory is allowed to be shared in further periods. In addition, this phenomenon indirectly decreases the total cost where the system prefers a higher transfer quantity of products in the lower frequency of supplier and manufacturer setups. Indeed, the system’s increase in transportation costs is more tolerable/affordable compared to the increase in setup costs.

Regardless of the system’s total cost increase, the sharing mechanism has led to a significant decrease of 32.98% and 20.96% on average in the total cost and the maximum unmet demand, respectively. Furthermore, these savings in the majority of the test problems are significantly more than the average reported savings. These maximum savings belong to test problems with $\left|T\right|\approx 24$. After a detailed investigation, we figured out that the maximum savings happen in test problems wherein the system experiences the pandemic’s peak demands. This, in turn, demonstrates the effectiveness and outstanding capabilities of the proposed framework to handle the sharp increase in demands whenever required.

Moreover, Table 5 provides a pairwise comparative analysis between the proposed ABD algorithm, the GRB, and the GRB_VI, in terms of both the objective function gap (%) and the computational time ratio. In columns “Obj. Values”, negative values indicate that the first algorithm has obtained a lower objective function compared to the second algorithm (i.e., first algorithm vs. the second algorithm) under a limited computational time of 7200s. In column “Time (ratio)”, the values represent how many times the first algorithm is faster than the second algorithm. The column “ABD vs. GRB” of “Obj. Values” reveals that, under the limited computational time of 7200s, the proposed ABD algorithm can obtain much better solutions in terms of objective function values compared to GRB with an average of $-57$% (i.e., the solutions of ABD algorithm are 57% better than the solutions of GRB without valid inequalities). Looking at column “ABD vs. GRB_VI” in “Obj. Values” figures out that both ABD and GRB_VI obtain the optimal solutions for test problems with $\left|T\right|=\{4-40\}$, but with a much less computational time for the ABD algorithm. For two test problems $\left|T\right|=\{42,44\}$, the GRB_VI has not been able to obtain the optimal solution, but its best-found solutions compared to the optimal solutions of ABD are in gaps of 41.82% and 41.04%, respectively.

Table 5.

Comparison between ABD & GRB & GRB_VI.

$\left|T\right|$	Obj. values (%)			Time (ratio)
	ABD vs. GRB	ABD vs. GRB_VI	GRB_VI vs. GRB	ABD vs. GRB	ABD vs. GRB_VI	GRB_VI vs. GRB
4	0.00	0.00	0.00	3.16	2.02	1.56
6	0.00	0.00	0.00	3.73	3.33	1.12
8	0.00	0.00	0.00	21.43	16.49	1.30
10	0.00	0.00	0.00	13.40	11.13	1.20
12	0.00	0.00	0.00	17.93	15.54	1.15
14	0.00	0.00	0.00	8.70	7.01	1.24
16	0.00	0.00	0.00	12.66	10.56	1.20
18	0.00	0.00	0.00	7.69	6.52	1.18
20	$-$75.91	0.00	$-$75.91	*	4.93	*
22	0.00	0.00	0.00	9.09	4.13	2.20
24	0.00	0.00	0.00	5.47	2.95	1.85
26	0.00	0.00	0.00	5.38	2.34	2.30
28	$-$72.89	0.00	$-$72.89	*	3.40	*
30	$-$43.34	0.00	$-$43.34	*	13.29	*
32	$-$72.25	0.00	$-$72.25	*	22.73	*
34	$-$43.88	0.00	$-$43.88	*	24.79	*
36	$-$43.28	0.00	$-$43.28	*	25.75	*
38	$-$35.45	0.00	$-$35.45	*	24.69	*
40	$-$68.81	0.00	$-$68.81	*	28.60	*
42	**	$-$41.82	*	**	*	*
44	**	$-$41.04	*	**	*	*
46	**	**	**	**	**	**
48	**	**	**	**	**	**
50	**	**	**	**	**	**
52	**	**	**	**	**	**
Average (in case of optimality of GRB):				9.88	7.46	1.48
Average (in case of optimality of GRB_VI):				N/A	12.12	N/A

* Time limit of 7200 s reached.

** No feasible solution after 7200 s.

Moreover, column “GRB_VI vs. GRB” in ‘Obj. Values” shows that the valid inequalities are indeed effective and help the GRB to obtain even optimal solutions for test problems $\left|T\right|=\{20,28-40\}$ under the limited computational time of 7200s. The columns “Time (ratio)” present interesting results on the speed of the three methods. As can be seen, the proposed ABD algorithm is always faster than GRB_VI, and GRB_VI is also faster than GRB. It is worth mentioning that the paired comparison between the two methods in terms of speed has been reported whenever both methods have reached the optimal solution under the limited computational time of 7200 s. In summary, for the test problems for which the GRB has obtained the optimal solution (i.e., $\left|T\right|=\{4-18,22-26\}$), it was observed that the ABD is on average 9.88 and 7.46 times faster than GRB and GRB_IV, respectively. Considering the same test problems, the GRB_VI is on average, 1.48 times faster than GRB. It reveals that the valid inequalities accelerate the GRB on the average up to 1.48 times faster when obtaining the optimal solutions. For another set of test problems (i.e., $\left|T\right|=\{4-40\}$) where the GRB_VI has obtained the optimal solution, the proposed ABD algorithm is, on average, 12.12 times faster than GRB_VI.

6.3. Sensitivity analyses

This section renders a broad range of sensitivity analyses to validate and illustrate the capabilities of the developed model and the solution approach. This investigation encompasses three main categories: 1) sensitivity of the objective function value, the inventory, and the sharing of products to input parameters, 2) inter-relation between the total demand, inventory, and sharing, and 3) capacity utilization. These three categories are explained in the following subsections, respectively.

6.3.1. Sensitivity to input parameters

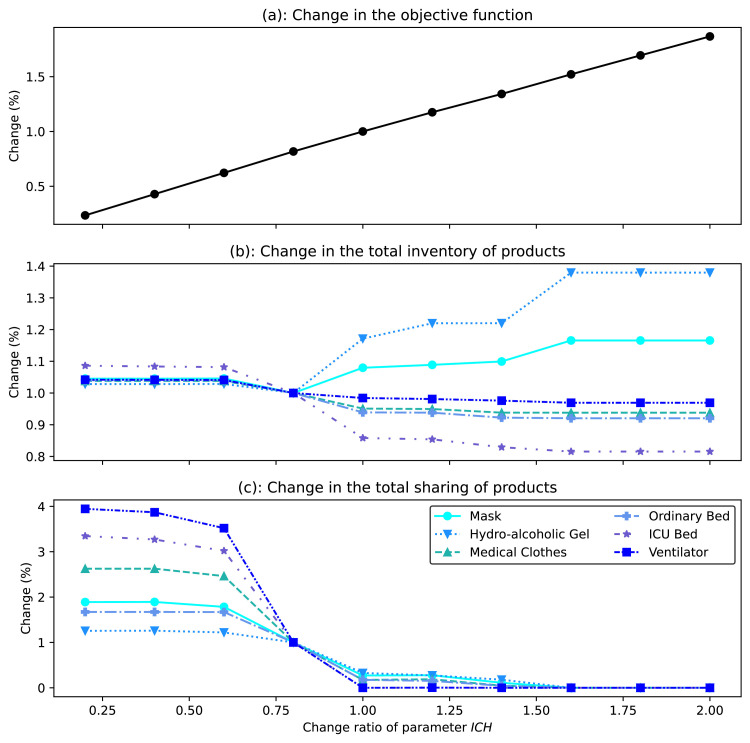
This section provides a broad sensitivity analysis of three main criteria including the objective function value (i.e., the total cost of the system), the total amounts of inventory, and sharing with respect to changes of certain input parameters including the cost of unmet demand ($CU$), the demand of products ($D$), maximum sharing capacity ($G_{\max }$), inventory holding cost ($ICH$), and allowable demand overload ratio ($\mu$).

Figure 4 shows how unmet demand cost affects the three mentioned criteria. Figure 4(a) indicates that if $CU$ increases, the total costs also increase. In fact, with a 35% of increase in the cost of unmet demand, it was observed that supply, manufacturing, distribution, and sharing expenses outweigh the overall cost of unmet demands. However, by increasing this cost from 35% to 60%, the costs of unmet demands surpass the system’s other expenses. Finally, by increasing this cost by more than 60%, the system reaches its maximum capacity and achieves a state of equilibrium. At this stage, a slight decrease can be seen in the system’s total cost. The reason for this decrease goes back to the fact that after increasing the cost of unmet demand higher than 60%, the last term of the objective function that calculates the total cost of the unmet demand (i.e., $CU\times S_{\max }$) becomes the dominant term of the objective function. Accordingly, the model puts a higher effort into minimizing this term. Therefore, a sudden fall happens in the maximum number of unmet demands ($S_{\max }$). This decrease is significant and, overall, leads to a decrease in the total cost of the system.

Fig. 4.

The impact of the cost of unmet demand on total cost, inventory, and sharing.

In terms of the changes in the total inventory of products in the system, Fig. 4(b) illustrates that as the cost of unmet demand increases, the system seeks to minimize mortality by increasing the production of hospital wards-related items such as medical clothes, ordinary beds, ICU beds, and ventilators. As a result, these items’ inventory levels increase. Simultaneously, individuals are attempting to take better care of themselves by observing public health, which is related to a rise in the usage of health products, such as masks and hydro-alcoholic gel, which will boost consumption and reduce the remaining inventory of these products. In connection with the changes in the total quantity of product sharing, Fig. 4(c) articulates that the sharing of all products has increased with the increase in the cost of unmet demand. This increase is entirely meaningful for ventilators and medical clothing. Indeed, the system decides to transfer the increased level of product inventory (seen in Fig. 4(b)) via sharing mechanism to fulfill the demand as much as possible to absorb the increase of unmet demand cost. Therefore, the system has attempted to fulfill demand by utilizing all available capacities. In addition, the considerable increase in the sharing of medical clothes is due to the demand for this product being impacted by hospitalized individuals in general and ICU wards.

Figure 5 shows how changes in demand $D$ affect the three criteria. As can be seen in Fig. 5(a), if $D$ increases, the total costs also increase. This trend is logical due to rising supply, production, distribution, and sharing expenses across various facilities. Also, Fig. 5(b) illustrates that the inventory of masks and hydro-alcoholic gels has reduced due to increased consumption of these products in response to rising demands. Other products – which are the essential products for curing patients – are facing an increase in their total inventory, which reflects the system’s behavior when the demand increases for such essential products. Indeed, the system produces more and stores more to fulfill the demand for essential products. For the reusable products (i.e., ICU beds and ventilators), the inventory also experiences a special increase, which is the return of these products to the utilization cycle. Finally, it might be claimed from Fig. 5(c) that there is an increasing-then-decreasing oscillation cycle in terms of the total sharing of products. Indeed, initially, the system strives to compensate for its lack of capacity by sharing, but once there is no more capacity to share, the system begins to boost product supply and production, resulting in less sharing.

Fig. 5.

The impact of demand on total cost, inventory, and sharing.

Figure 6 shows how changes in the maximum sharing capacity $G_{\max }$ affect the three concerned criteria. As can be seen in Fig. 6(a), raising the maximum sharing capacity lowers the total cost of the system. This trend has two primary explanations. The first is that as sharing capacity grows, more sharing is allowed through the system (see Fig. 6(c)). Consequently, the supplies and the productions are set up with lower frequency to effectively use the current capacity, mainly from the sharing mechanism. Another reason is that certain hospitals serve as intermediate distribution centers. In reality, due to the geographic structure of each region, hospitals in each region may either acquire products from manufacturers or distribute their excess products in the established sharing mechanism to other hospitals. This issue becomes even more pressing when this procedure lowers the cost of shipping items by eliminating the need to order products from manufacturers and allowing products to be moved between hospitals at significantly cheaper transportation costs (i.e., due to lower distance).

Fig. 6.

The impact of maximum sharing capacity on total cost, inventory, and sharing.

Moreover, as the sharing capacity rises in Fig. 6(b), the total inventory level also climbs because the system can now store more products and share them through the system. Also, as can be observed, the ventilator and ICU beds have greater inventory levels than other products being impacted by two reasons; first, these products are expensive to be produced, so the system attempts to store these products as much as affordable by the system; second; these products may be reused after a predefined lead time. When looking at Fig. 6(c), it is evident that as the capacity for sharing grows; more products are allowed to be shared since sharing is typically less expensive compared to manufacturing, especially for expensive products (e.g., beds and ventilators). In this regard, the bigger the capacity, the less the influence on the sharing of low-cost products (e.g., masks, hydro-alcoholic gels, and medical cloths) because the cost of manufacturing is affordable compared to the cost of sharing for these products.

Figure 7 shows how changes in the inventory holding cost $ICH$ impact the three mentioned criteria. As Fig. 7(a) depicts, the total cost of the system rises monotonically with the increase of $ICH$. This is because the cost of holding products in hospitals and the objective function have a direct linear connection. What is more in Fig. 7(b), when inventory holding costs rise, more expensive products (e.g., medical clothes, beds, and ventilators) will have lower inventory levels since the $ICH$ is a fraction of the production cost $PC$ (see Table G.8 ).

Fig. 7.

The impact of inventory holding cost at hospitals on total cost, inventory, and sharing.

Furthermore, for products with a lower production cost, the total inventory level rises. This pattern may be seen in hospitals that have greater holding costs. Indeed, they would prefer not to keep inventory in the system and instead use the sharing mechanism to satisfy their demand. On the other hand, this behavior enables other hospitals with lower holding costs to keep additional inventory to satisfy their demand. Finally, Fig. 7(a) illustrates that raising the cost of inventory in the hospital lowers product sharing. This is due to hospitals’ unwillingness to keep inventory to participate in the sharing process and preferring to get products only as much of their demand directly from the manufacturers.

Figure 8 illustrates the impact of allowable demand overload ratio $\mu$ on the three mentioned criteria. Based on Fig. 8(a), as the $\mu$ increases and consequently more and more amounts of products are allowed to be stored extra than the actual demand, the possibility of fulfilling demand surpluses through the sharing mechanism increases accordingly. As a result, the supply and production setups happen with a lower frequency, and their fixed setup costs decrease consequently. Furthermore, the transportation cost of direct transferring of products from manufacturers to hospitals decreases. All these result in lower total costs of the system. Moreover, Fig. 8(b) reveals that hospitals are more likely to employ the sharing mechanism and to decrease the total inventory of products as the overload ratio rises. As a result, hospitals strive to maintain their inventory levels to a minimum. In addition, when the allowable demand overload ratio rises in Fig. 8(c), the total sharing for all products intends to be increased. Remarkably, this trend is particularly apparent in consumable products because these products cannot be reused. As a result, since the inventory level of these products is derived from both production and sharing amounts, the excess demand is met entirely through the sharing system.

Fig. 8.

The impact of allowable demand overload ratio at hospitals on total cost, inventory, and sharing.

6.3.2. Inter-relation between cost, inventory, and sharing

This section seeks the inter-relation between the total demand and the total inventory and sharing of the products in the system. Indeed, the goal is to investigate how different hospitals manage the inventory level and the sharing of products based on their particular amount of demand. In this regard, Fig. 9 (a) depicts the quantity of total demand as well as the proportional level of total inventory and total sharing to the total demand over a period of 3 months (i.e., $\left|T\right|=12$), wherein the results of the even periods have been depicted for the sake of simplicity. As can be observed in Fig. 9(a)(a), there is a modest decrease in the total demand as the pandemic progresses, which is logical since we have only a single peak of demand at the early stages of the pandemic in our case study, and as long as the pandemic progresses, the demand decreases due to the control of the pandemic. In addition, due to a drop in the number of susceptible individuals after the pandemic peak, the inventory-to-demand ratio in Fig. 9(a)(b) for masks and hydro-alcoholic gels is falling. However, this ratio is higher for ICU beds and ventilators due to the rise in hospitalized individuals in general and ICU wards. As a result, the hospitals have attempted to fulfill the demand by storing more products. Furthermore, the sharing-to-demand ratio in Fig. 9(a)(c) indicates that the hospital is able to engage in the product-sharing procedure owing to the required inventory level.

Fig. 9.

Inter-relation between cost, inventory, and sharing.

In order to show how different hospitals manage their inventory and sharing, three different hospitals have been selected that behave differently in managing their inventory and sharing. The hospital of Fig. 9(b) refuses to engage in the sharing mechanism since no input (Fig. 9(b)(c)) and output (Fig. 9(b)(d)) sharing happens in this hospital. Consequently, the inventory level (Fig. 9(b)(b)) of the hospital remains at its minimum for the majority of the products. This indicates that the demand and the supply of products from manufacturers are in an implicit equilibrium. In a second hospital depicted in Fig. 9(c), the situation is different. In fact, this hospital faces an inventory shortage owing to high demand and the possibility of receiving surplus demand. In this situation, the hospital fulfills its demand (Fig. 9(c)(a)) simultaneously from its inventory (Fig. 9(c)(b)) as well as the input sharing (Fig. 9(c)(c)) coming from other hospitals, and it shares no products with others (Fig. 9(c)(d)). Finally, another hospital is available with excess products as Fig. 9(d). This hospital fulfills its demand (Fig. 9(d)(a)) only from its own inventory (Fig. 9(d)(b)) and shares the excess products with other hospitals (Fig. 9(d)(c)).

6.3.3. Supply and production capacity utilization

An interesting investigation in this study has been done in Fig. 10 to see how much of the supply and production capacities have been utilized over the first three months (i.e., $\left|T\right|=12$) of the pandemic.

Fig. 10.

The capacity utilization of suppliers and manufacturers.

For this curiosity, Fig. 10(a) depicts the percentage of suppliers that contributed to the fulfillment of the raw materials required to produce the medical products. As can be seen, from the early periods of the pandemic, at least 50% of the suppliers have been used, and this percentage goes up to full utilization of 100% from the sixth week of the pandemic (i.e., the moment that the pandemic approaches its peak). Furthermore, Fig. 10(b) and (c) depict the percentage of manufacturers that contributed to the production of medical products and their capacity percentage utilization, respectively. Knowing that manufacturers are involved in the system with an initial inventory, the whole number and the whole capacity of the manufacturers are not used in the early weeks of the pandemic; however, the involvement of the manufacturers increases as far as the pandemic progresses. Furthermore, Fig. 10(c) shows that the manufacturers do not always utilize their maximum production capacity for certain products (e.g., masks, hydro-alcoholic gels, medical clothes, and ordinary beds). However, they produce a higher rate of the more essential products (i.e., ICU beds and ventilators).

7. Managerial insights

Based on the findings of Section 6.3, this section provides a list of managerial insights for the health policy-makers to better plan for possible future health pandemics.

The first managerial implication of the proposed model relates to its ability to act as both business and mortality models. The behavior of the model changes by changing the unmet demand cost. Although the proposed model has a cost objective function, manipulating the unmet demand costs switches the proposed model from a cost-oriented model to a more mortality-oriented model. In fact, there is a turning point for this switch when increasing the unmet demand, the proposed model goes from cost-oriented planning to mortality-oriented planning. For the current case study, the switch happens when increasing the unmet demand cost up to 35%. Managers should also notice that increasing the unmet demand will also affect the level of inventory and sharing. Therefore, requirements should be met when switching the behavior of the model. In terms of the inventory of products, two different phenomena happen. As the cost of unmet demand increases, the system seeks to minimize mortality by increasing the production of hospital ward-related items such as medical clothes, ordinary beds, ICU beds, and ventilators. As a result, these items’ inventory levels increase. On the other hand, when experiencing a high unmet demand cost, individuals are attempting to take better care of themselves by observing public health, which is related to a rise in the usage of health products, such as masks and hydro-alcoholic gel, which will boost consumption and reduce the remaining inventory of these products.

Another important observation is the impact of demand variation on the sharing mechanism. We observed that the amount of sharing is a concave function of the demand. The results show that there are concave cycles in the total sharing amount of products when changing the demand. Initially, when increasing the demand, the system attempts to mitigate the risk of capacity shortage in some hospitals through sharing mechanism, but once the maximum sharing capacity is reached, the system begins to satisfy the demand by producing and supplying new products, which results in less sharing. This phenomenon highlights the impact of sharing mechanisms between hospitals to better respond to the surging product demand. As a matter of fact, sharing mechanisms provide both cost and responsiveness advantages. In terms of cost, sharing of products between neighboring hospitals reduces the transportation costs of transferring newly produced products from manufacturers to geographically far hospitals. On the other hand, this sharing mechanism helps to increase the responsiveness and agility of hospitals to their demands. In fact, due to usually less distance between neighboring hospitals compared to regional manufacturers, some hospitals can act as intermediate suppliers. In this situation, some hospitals should be allowed to store more products to respond to the shortage of farther hospitals more rapidly.

It is worth mentioning that the demand is not an independent parameter but a function of disease parameters in the epidemiological model. Any changes in these parameters would either increase or decrease the demand for products, under specific conditions. Table 6 shows how increasing the disease parameters increase (“+”) or decreases (“$-$”) the demand for products under specific conditions. Accordingly, any changes in disease parameters can be mapped to the changes in the objective function value, inventory, and sharing of products through the demand intermediate parameter. By manipulating the disease parameters, health policy-makers can change product demand and attempt better production-inventory-sharing planning.

Table 6.

Impact of disease parameters on the demand for products.

Demand for ...	${\beta }_1$	${\beta }_2$	${\beta }_3$	${\beta }_4$	$\zeta$	$\kappa$	$\eta$ (If ...)	$\rho$ (If ...)	$\omega$ (If ...)	$c$ & $\theta$ (If ...)	${\eta }_1\&{\eta }_2$
Demand for ...	${\beta }_1$	${\beta }_2$	${\beta }_3$	${\beta }_4$	$\zeta$	$\kappa$	$\eta$ (If ...)	$\rho$ (If ...)	$\omega$ (If ...)	$c$ & $\theta$ (If ...)	${\eta }_1\&{\eta }_2$
Masks & Hydro-alcoholic gel	$-$	$-$	$-$	$-$	+	$-$	$-$ (If ${\beta }_2>{\beta }_1$)	$-$ (${\beta }_1>{\beta }_2$)	$-$ (${\beta }_3,{\beta }_4>{\beta }_2$)	$-$ (${\beta }_4>{\beta }_3$)	+
							+ (${\beta }_2>{\beta }_1$)	+ (${\beta }_1<{\beta }_2$)	+ (${\beta }_3,{\beta }_4<{\beta }_2$)	+ (${\beta }_4<{\beta }_3$)
Medical clothes	+	+	+	+		+	+	$-$	+
Ordinary bed	+	+	+	+		+	+	$-$	+	$-$	$-$
ICU bed & Ventilator	+	+	+	+		+	+	$-$	+	$-$	$-$

We observed that as long as the inventory holding cost increases, the inventory level of less critical products (e.g., mask, hydro-alcoholic gel) increases while the inventory level of critical products (e.g., beds and ventilators) decreases. It was revealed if the unit inventory holding cost exceeds the unit of manufacturing setup cost, the inventory of critical products decreases. In this situation, the system also discourages the sharing mechanism (due to the lack of inventory), consequently leading to a higher level of unmet demand. Therefore, there is an important interplay between the inventory holding cost and the amount of product sharing. Accordingly, among different cost elements in the system, it is recommended to keep the inventory holding cost at its minimum level to encourage the sharing of products between hospitals. With this observation together with the role of intermediate supply of some hospitals, policy-makers may provide the geographically central hospitals with a higher inventory capacity and less inventory holding cost, and the farther hospitals (from the manufacturers) with less inventory holding capacity. This allows for storing more products in central hospitals with a lower inventory holding cost, and these hospitals share the excess product with farther ones. In this case, the distribution system goes from an isolated structure, where hospitals order and fulfill separately, to a more hierarchical and collaborative system, where hospitals order and fulfill collaboratively.

8. Conclusions

The COVID-19 pandemic has posed a variety of challenges to human civilizations, emphasizing the necessity for a decision-making framework to address them. In this study, we have presented a novel comprehensive framework that includes three phases of demand controlling, production-distribution-sharing planning, and solution methodology, wherein various specific concerns of the health pandemic have been reflected, particularly the COVID-19 pandemic. In the first phase, we proposed a SEIHRS epidemiological model with the optimal control problem for handling the dynamicity of the demands of consumable and reusable products. In the second phase, we have introduced and formulated a multi-period production-inventory-sharing problem in terms of a mixed-integer linear programming model. Finally, an accelerated Benders decomposition algorithm with a set of tailored valid inequalities has been proposed to solve the proposed model.

Although the framework has been partially adjusted to deal with the COVID-19 pandemic, it can surely be applied to deal with subsequent pandemics as well. The second phase, in particular, is a contrivance for planning supply, manufacturing, distribution, and sharing decisions that may be implemented directly or with minimal adjustments in a variety of populated areas. The computational results show that the proposed accelerated Benders decomposition algorithm is efficient in handling large-sized test problems. In this regard, it was observed that the proposed decomposition method coupled with effective valid inequalities could solve large-sized test problems in a reasonable computational time and 9.88 times faster than the Gurobi solver. In addition, the effectiveness of the valid inequalities was also reported that helping the proposed model to be solved 1.48 times faster using the Gurobi solver. Moreover, the sharing mechanism reduces the total cost of the system and the unmet demand, on average, up to 32.98% and 20.96%, respectively. Furthermore, the two parameters of maximum sharing capacity and allowable demand overload ratio are two valuable factors at hand for managers to regulate inventory and sharing decisions in the proposed sharing mechanism, which significantly influences the system’s total cost and unmet demand.

Some ideas for expanding the current study on the prediction and planning stages can be explored. The application of machine learning algorithms to estimate the parameters of the SEIHRS model during the prediction phase can improve demand prediction accuracy. The proposed SEIHRS model is a single-region-based model wherein the evolution of the pandemic in each region is modeled in isolation and no interaction between regions is considered. This assumption is similar to the situation when all regions are under a quarantine restriction and no inter-regional displacement or immigration happens. Therefore, as a new research direction, we propose to develop a multi-regional epidemiological model with inter-regional interactions [8].

In the planning phase, although we have planned the production, distribution, and sharing of the products according to the existing geographical borders for various regions, redistricting models may be applied to define regions, which also improves the efficacy of the sharing mechanism. Furthermore, the cost of unmet demand for all products is treated the same in this study, despite the fact that there is a substantial difference between the lack of ventilators and the absence of masks. As a result, using a cost function rather than a parameter can help improve the planning results.

Last but not least, developing an integrated optimization framework would be another research direction that is worthy of investigation. The current work considers that the disease parameters are constant during the planning horizon and no vaccination takes place. Therefore, a new framework can be developed to incorporate these two aspects. To do so, the proposed optimization model can be integrated with the SEIHRS model in an interactive way to develop a myopic model. In this model, the SEIHRS model and the optimization model interact in each period, and a vaccination rate can be added to the SEIHRS model. Furthermore, from one period to another, disease parameters can also vary.

CRediT authorship contribution statement

Behnam Vahdani: Formal analysis, Methodology, Project administration, Software, Validation, Supervision, Writing – review & editing. Mehrdad Mohammadi: Formal analysis, Methodology, Project administration, Software, Validation, Supervision, Writing – review & editing. Simon Thevenin: Formal analysis, Project administration, Validation, Supervision, Writing – review & editing. Patrick Meyer: Formal analysis, Project administration, Validation, Writing – review & editing, Supervision. Alexandre Dolgui: Formal analysis, Project administration, Validation, Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Basic reproduction number

In what follows, the basic reproduction number ${\mathcal{R}}_0$ and the endemic equilibrium point are calculated by solving the isoclines, where two equilibrium points can be considered including disease-free equilibrium point $E_0(S_0,0,0,0,0,0,0,0)=(\frac{\Lambda }{d},0,0,0,0,0,0,0)$ and endemic equilibrium point $E^{*}(S^{*},E^{*},A^{*},I^{*},H{N}^{*}$, $H{C}^{*},R^{*},Z^{*})$. The basic reproduction number ${\mathcal{R}}_0$ is an indicator for the study of contagious disease dynamics. If ${\mathcal{R}}_0\ge 1$, the outbreak is anticipated to continue, and the outbreak is going to end otherwise (i.e., ${\mathcal{R}}_0$ < 1). In order to calculate ${\mathcal{R}}_0$, we applied the proposed method by Van den Driessche and Watmough [88]. For this purpose, let $x\equiv (E,A,I,HN,HC)$ and constitute $\frac{dx}{dt}$, $\mathfrak{H}\left(x\right)$, and $v\left(x\right)$, where $\mathfrak{H}\left(x\right)$ refers to the segments in which new infection terms are introduced, and $v\left(x\right)$ refers to the remainder of the segments. Accordingly, we have:

$$\frac{dx}{dt}=\mathfrak{H}\left(x\right)-v\left(x\right)$$ (A.1)

$$\mathfrak{H}\left(x\right)=\left(\begin{array}{c}({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S\\ 0\\ 0\\ 0\\ 0\end{array}\right)$$ (A.2)

$$v\left(x\right)=\left(\begin{array}{c}(k+d)E\\ -k\rho E+(\eta +d+{\delta }_1)A\\ -k(1-\rho )E-\eta A+(\omega +d+{\delta }_2)I\\ -\omega (1-c)I+(d+{\delta }_3+{\gamma }_1+\theta )HN\\ -\omega cI+(d+{\delta }_4+{\gamma }_2)HC-\theta HN\end{array}\right)$$ (A.3)

In what follows, the equivalent linearized matrices of $\mathfrak{H}\left(x\right)$ and $v\left(x\right)$ at disease-free equilibrium $E_0=(S_0,0,0,0,0,0,0,0)$ can be constructed as (A.4) and (A.5), respectively.

$$F=\left(D\mathfrak{H}\left(x\right)\right)\left(E_0\right)=\left(\begin{array}{ccccc}0& {\beta }_1{S}_0& {\beta }_2{S}_0& {\beta }_3{S}_0& {\beta }_4{S}_0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)$$ (A.4)

$$V=\left(Dv\left(x\right)\right)\left(E_0\right)=\left(\begin{array}{ccccc}k+d& 0& 0& 0& 0\\ -\kappa \rho & \eta +d+{\delta }_1& 0& 0& 0\\ -\kappa (1-\rho )& -\eta & \omega +d+{\delta }_2& 0& 0\\ 0& 0& -\omega (1-c)& d+{\delta }_3+{\gamma }_1+\theta & 0\\ 0& 0& -\omega cI& -\theta & d+{\delta }_4+{\gamma }_2\end{array}\right)$$ (A.5)

Consequently, regarding matrices $F$ and $V$, the basic reproduction number is equal to the special vector of $F{V}^{-1}$. Moreover, the endemic equilibrium point is obtained by solving the system of Eq. (A.6).

$$\begin{array}{c}\Lambda -({\beta }_1{A}^{*}+{\beta }_2{I}^{*}+{\beta }_{3}H{N}^{*}+{\beta }_{4}H{C}^{*})S^{*}-d{S}^{*}+\xi R^{*}-u_{1}k{S}^{*}{Z}^{*}=0,\hfill \\ ({\beta }_1{A}^{*}+{\beta }_2{I}^{*}+{\beta }_{3}H{N}^{*}+{\beta }_{4}H{C}^{*})S^{*}-(k+d)E^{*}=0,\hfill \\ \kappa \rho E^{*}-(\eta +d+{\delta }_1)A^{*}=0,\hfill \\ \kappa (1-\rho )E^{*}+\eta A^{*}-(\omega +d+{\delta }_2)I^{*}=0,\hfill \\ \omega (1-c)I^{*}-(d+{\delta }_3+{\gamma }_1+\theta )H{N}^{*}=0,\hfill \\ \omega c{I}^{*}-(d+{\delta }_4+{\gamma }_2)H{C}^{*}+\theta H{N}^{*}=0,\hfill \\ {\gamma }_{1}H{N}^{*}+{\gamma }_{2}H{C}^{*}-\xi R^{*}-d{R}^{*}+u_{1}k{S}^{*}{Z}^{*}=0,\hfill \\ \frac{p{I}^{*}}{1+q{I}^{*}}-a_0{Z}^{*}=0\hfill \end{array}$$ (A.6)

After solving the system of Eq. (A.6), a unique equilibrium point is obtained when the basic reproduction number is greater than one ($R_0>1$). However, values smaller than one for the basic reproduction number ($R_0<1$) cause the non-occurrence of an endemic equilibrium. Therefore, the following statement can be deduced. The system of equations (1) has a disease-free equilibrium point $E_0(S_0,0,0,0,0,0,0,0,0)$ for any values of parameters. And for $R_0>1$, the system has a unique endemic equilibrium $E^{*}(S^{*},E^{*},A^{*},I^{*},$ $H{N}^{*},H{C}^{*},R^{*},Z^{*})$.

Appendix B. Stability analysis

Local and global stability conditions of the equilibria are analyzed as follows. For this aim, we analyze the local and global stability conditions for the disease-free equilibrium point. Let ${\alpha }_0=\kappa +d$, ${\alpha }_1=\eta +d+{\delta }_1$, ${\alpha }_2=\omega +d+{\delta }_2$, ${\alpha }_3=d+delt{a}_3+{\gamma }_1+\theta$, ${\alpha }_4=d+{\delta }_4+{\gamma }_2$. The Jacobian matrix $\overline{J}$ of system (1) is considered as follow:

$$\overline{J}=\left(\begin{array}{cccccccc}{\alpha }_{11}& 0& -{\beta }_{1}S& -{\beta }_{2}S& -{\beta }_{3}S& -{\beta }_{4}S& \zeta & -u_1\kappa S\\ {\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC& -{\alpha }_0& {\beta }_{1}S& {\beta }_{2}S& {\beta }_{3}S& {\beta }_{4}S& 0& 0\\ 0& \kappa \rho & -{\alpha }_1& 0& 0& 0& 0& 0\\ 0& \kappa (1-\rho )& \eta & -{\alpha }_2& 0& 0& 0& 0\\ 0& 0& 0& \omega (1-c)& -{\alpha }_3& 0& 0& 0\\ 0& 0& 0& \omega c& \theta & -{\alpha }_3& 0& 0\\ u_{1}kZ& 0& 0& 0& {\gamma }_1& {\gamma }_2& -(\xi +d)& u_{1}kS\\ 0& 0& 0& \frac{p}{{(1+qI)}^2}& 0& 0& 0& -a_0\end{array}\right)$$ (B.1)

where ${\alpha }_{11}=-({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)-d-u_{1}kZ$.

B1. Local stability of $E_0$

Jacobian matrix at the disease-free equilibrium point $E_0=(\Delta /d,0,0,0,0,0,0,0,0)$, which is shown by $\overline{J}|E_0$ is constructed and solved with Python to obtain eigenvalues of $\overline{J}|E_0$, where $S_0=\Delta /d$. In this regard, we have eight eigenvalues, where ${\lambda }_1=-d$, ${\lambda }_2=-(\xi +d)$, ${\lambda }_3=-a_0$, and other five eigenvalues can be obtained from the roots of the following equation:

$${\lambda }^5+Q_1{\lambda }^4+Q_2{\lambda }^3+Q_3{\lambda }^2+Q_4\lambda +Q_5=0$$ (B.2)

Regarding the values of parameters in Table G.8, by solving the above equation with Python, we can conclude that $Q_5$ is positive for $R_0<1$. So for $R_0<1$, the characteristic equation has roots with negative real parts only when $Q_2,Q_3,Q_4>0$, and we have the following theorem.

Theorem 1

Disease-free equilibrium point$E_0$of system(1)is locally asymptomatically stable for$R_0<1$when$Q_2,Q_3,Q_4>0$hold.

B2. Global stability of $E_0$

Theorem 2

Disease-free equilibrium point $E_0$ of the system (1) is globally asymptomatically stable when $p<d$ and $u_{1}k\Delta <a_{0}d$ hold.

Proof

Let us consider the Lyapunov function as follows:

$$V_1=(S-S_0-S_{0}ln\left(\frac{S}{S_0}\right))+E+A+I+HN+HC+R+Z$$ (B.3)

where $V_1$ is a positive definite function for all $(S,E,A,I,HN,HC,R,Z)$ other than the disease-free equilibrium point. Time derivative of $V_1$ along the solution of the system (1) is calculated as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{d}{V}_1}{\mathrm{d}t}}& =& {\displaystyle (1-\frac{S_0}{S})[\Lambda -({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-dS+\xi R-u_1\left(t\right)kSZ]}\hfill \\ & & +({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-d(E+A+I+HN+HC+R)-{\delta }_{1}A-{\delta }_{2}I\hfill \\ & & {\displaystyle -{\delta }_{3}HN-{\delta }_{4}HC-\xi R+u_{1}kSZ+\frac{pI}{1+qI}-a_{0}Z}\hfill \\ & =& {\displaystyle \Delta -d(E+A+I+HN+HC+R)-{\delta }_{1}A-{\delta }_{2}I-{\delta }_{3}HN-{\delta }_{4}HC-\frac{\Delta S_0}{S}+d{S}_0-\frac{\xi S_{0}R}{S}+u_{1}k{S}_{0}Z}\hfill \\ & & {\displaystyle +\frac{pI}{1+qI}-a_{0}Z\le (\frac{\Delta }{S}-d)(S-S_0)+(p-d)I+\frac{1}{d}(u_{1}k\Delta -a_{0}d)Z}\hfill \\ & =& {\displaystyle -\frac{d}{S}{(S-S_0)}^2+(p-d)I+\frac{1}{d}(u_{1}k\Delta -a_{0}d)Z}\hfill \end{array}$$ (B.4)

Therefore, $\frac{\mathrm{d}{V}_1}{\mathrm{d}t}<0$ when $p<d$ and $u_{1}k\Delta <a_{0}d$ hold. Also, $\frac{\mathrm{d}{V}_1}{\mathrm{d}t}=0$ when $S=S_0$ and $E=A=I=HN=HC=R=Z=0$. Regarding LaSalle’s invariance principle [89], $E_0$ is globally asymptomatically stable when $R_0<1$, and when the considered parametric limitations are satisfied. Similarly, the local and global stability of $E^{*}$ can be examined. □

Appendix C. Proof of Theorem 3

Proof

The optimal control interventions exist when the following conditions are satisfied:

• •The solution space of system dynamics (1) with control variables $u_i$, $i=1,\dots ,5$ in $\sqcap \ne \varphi$.
• •The state system is a linear function of control variables, whose coefficients depend on state variables and time, where set $\sqcap$ is convex and closed.
• •Integrand of (3): $L$ is convex on $\sqcap$ and $L(S,E,A,I,HN,HC,R,u_1,u_2,u_3,u_4,u_5)\ge f(u_1,u_2,u_3,u_4,u_5)$, where $f(u_1,u_2,u_3,u_4,u_5)$ is continuous, and $\parallel (u_1,u_2,u_3,u_4,u_5){\parallel }^{-}1f(u_1,u_2,u_3,u_4,u_5)$ $\to \infty$, when $\parallel (u_1,u_2,u_3,u_4,u_5)\parallel \to \infty$. Indeed, $\parallel .\parallel$ indicates the $L^5(0,T_f)$ norm.

Regarding system dynamics (1), the total population is $N=S+E+A+I+HN+HC+R$. Hence, $\frac{\mathrm{d}N}{\mathrm{d}t}=\Lambda -dN-{\delta }_{1}A-{\delta }_{2}I-{\delta }_{3}HN-{\delta }_{4}HC\le \Lambda -dN$, and $0<N\left(t\right)\le N\left(0\right)e^{-dt}+\frac{\Lambda }{d}(1-e^{-dt})$, where $N\left(0\right)=S\left(0\right)+E\left(0\right)+A\left(0\right)+I\left(0\right)+HN\left(0\right)+HC\left(0\right)+R\left(0\right)$. Also, when $t\to \infty$, we have $0<N\left(t\right)\le \frac{\lambda }{d}$. In addition, $\frac{\mathrm{d}Z}{\mathrm{d}t}=\frac{pI}{1+qI}-a_{0}Z\le pI-a_{0}Z$. So, $\frac{\mathrm{d}Z}{\mathrm{d}t}+a_{0}Z\le \frac{p\Lambda }{d}$, and $0<Z\left(t\right)\le Z\left(0\right)e^{-a_{0}t}+\frac{p\Lambda }{a_{0}d}(1-e^{-a_{0}t})$. Also, when $t\to \infty$, we have $0<Z\left(t\right)\le \frac{p\Lambda }{a_{0}d}$.

The solution of system dynamics (1) is bounded for each of the control variables in $\sqcap$, and the right-hand side functions are also locally Lipschitzian. The Picard Lindelöf theorem demonstrates that the first condition is met [90].

Regarding the definition, the control set $\sqcap$ is convex and closed. The second condition is likewise met because all of the equations in (1) are represented as linear equations in $u_i^{*},i=1,\dots ,5$, whose state variables are dependent on coefficients. Furthermore, the convex property of integrand $L(S,E,A,I,HN,HC,R,Z,u_1,u_2,u_3,u_4,u_5)$ is guaranteed by the quadratic nature of all control variables. Also, we have $L(S,E,A,I,HN,HC,R,u_1,u_2,u_3,u_4,u_5)=$ $w_{1}I+w_{2}HN+w_{3}HC+w_4{u}_1^2+w_5{u}_2^2+w_6{u}_3^2+w_7{u}_4^2+w_8{u}_5^2$ $\ge w_4{u}_1^2+w_5{u}_2^2+w_6{u}_3^2+w_7{u}_4^2+w_8{u}_5^2$.

Let $\overline{u}=\min (w_4,w_5,w_6,w_7,w_8)>0$ and $f(u_1,u_2,u_3,u_4,u_5)=$ $\overline{u}(u_1^2+u_2^2+u_3^2+u_4^2+u_5^2)$. Hence,

$L(S,E,A,I,HN,HC,R,Z,u_1,u_2,u_3,u_4,u_5)$ $\ge$ $f(u_1,u_2,u_3,u_4,u_5)$

In this regard, $f$ is continuous and $\parallel (u_1,u_2,u_3,u_4,u_5){\parallel }^{-1}f(u_1,u_2,u_3,u_4,u_5)\to \infty$, when $\parallel (u_1,u_2,u_3,u_4,u_5)\parallel \to \infty$. Hence, the third condition is also met. Therefore, we can conclude that there are control variables $u_i^{*}$, $i=1,\dots ,5$ with the condition $J(u_1^{*},u_2^{*},u_3^{*},u_4^{*},u_5^{*})=\min \left[J(u_1,u_2,u_3,u_4,u_5)\right]$ [38], [91]. □

Appendix D. Optimal control variables

In what follows, in order to obtain optimal control variables, the Hamiltonian function is formulated by introducing adjoint variables $\lambda =({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_8)\in R^8$, and minimized by applying Pontryagin’s Maximum Principle [92], which has been explained in Appendix E.

Theorem 4

If$S^{*}$,$E^{*}$,$A^{*}$,$I^{*}$,$H{N}^{*}$,$H{C}^{*}$,$R^{*}$,$Z^{*}$are optimal state variables, and$u_i^{*}$,$i=1,\dots ,5$are optimal control variables of system(3)and(4), there are adjoint variables$\lambda =({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_8)\in R^8$that satisfy the canonical system of Eq.(D.1):

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{d}{\lambda }_1}{\mathrm{d}t}}& =& {\lambda }_1({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC+d+u_{1}kZ)-\hfill \\ & & {\lambda }_2({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)-{\lambda }_7{u}_{1}kZ,\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{\lambda }_2}{\mathrm{d}t}}& =& {\lambda }_2(k+d)-{\lambda }_3\left(\kappa \rho \right)-{\lambda }_4\left(\kappa (1-\rho )\right),\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{\lambda }_3}{\mathrm{d}t}}& =& {\lambda }_1\left({\beta }_{1}S\right)-{\lambda }_2\left({\beta }_{1}S\right)+{\lambda }_3(\eta +d+{\delta }_1)-{\lambda }_4\left(\eta \right),\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{\lambda }_4}{\mathrm{d}t}}& =& {\displaystyle -w_1+{\lambda }_1\left({\beta }_{2}S\right)-{\lambda }_2\left({\beta }_{2}S\right)+{\lambda }_4(\omega +d+{\delta }_2+\frac{{\epsilon }_1{u}_2}{{(1+{\zeta }_{1}I)}^2}+\frac{{\epsilon }_2{u}_3}{{(1+{\zeta }_{2}I)}^2})-}\hfill \\ & & {\displaystyle {\lambda }_5(\omega (1-c)+\frac{{\epsilon }_1{u}_2}{{(1+{\zeta }_{1}I)}^2})-{\lambda }_6(\omega c+\frac{{\epsilon }_2{u}_3}{{(1+{\zeta }_{2}I)}^2})-{\lambda }_8\left(\frac{p}{{(1+qI)}^2}\right),}\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{\lambda }_5}{\mathrm{d}t}}& =& {\displaystyle -w_2+{\lambda }_1\left({\beta }_{3}S\right)-{\lambda }_2\left({\beta }_{3}S\right)+{\lambda }_5(d+{\delta }_3+{\gamma }_1+\theta +\frac{{\epsilon }_3{u}_4}{{(1+{\zeta }_{3}HN)}^2})-}\hfill \\ & & {\displaystyle {\lambda }_6\left(\theta \right)-{\lambda }_7({\gamma }_1+\frac{{\epsilon }_3{u}_4}{{(1+{\zeta }_{3}HN)}^2}),}\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{\lambda }_6}{\mathrm{d}t}}& =& {\displaystyle -w_3+{\lambda }_1\left({\beta }_{4}S\right)-{\lambda }_2\left({\beta }_{4}S\right)+{\lambda }_6(d+{\delta }_4+{\gamma }_2+\frac{{\epsilon }_4{u}_5}{{(1+{\zeta }_{4}HC)}^2})-}\hfill \\ & & {\displaystyle {\lambda }_7({\gamma }_2+\frac{{\epsilon }_4{u}_5}{{(1+{\zeta }_{4}HC)}^2}),}\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{\lambda }_7}{\mathrm{d}t}}& =& -{\lambda }_1\left(\xi \right)+{\lambda }_7(\xi +d),\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{\lambda }_8}{\mathrm{d}t}}& =& {\lambda }_1\left(u_{1}kS\right)-{\lambda }_7\left(u_{1}kS\right)+{\lambda }_8\left(a_0\right)\hfill \end{array}$$ (D.1)

Regarding the transversality conditions${\lambda }_i\left(T_f\right)=0$,$i=1,\dots ,8$, optimal control variables$u_i^{*}$,$i=1,\dots ,5$are obtained as:

$${\displaystyle u_1^{*}=\min \left\{\max \right\{0,\frac{k{S}^{*}{Z}^{*}({\lambda }_1-{\lambda }_7)}{2w_4}\},1\},}$$ (D.2)

$${\displaystyle u_2^{*}=\min \left\{\max \right\{0,\frac{{\displaystyle \frac{{\epsilon }_1{I}^{*}}{1+{\zeta }_1{I}^{*}}({\lambda }_4-{\lambda }_5)}}{2w_5}\},1\},}$$ (D.3)

$${\displaystyle u_3^{*}=\min \left\{\max \right\{0,\frac{{\displaystyle \frac{{\epsilon }_2{I}^{*}}{1+{\zeta }_2{I}^{*}}({\lambda }_4-{\lambda }_6)}}{2w_6}\},1\},}$$ (D.4)

$${\displaystyle u_4^{*}=\min \left\{\max \right\{0,\frac{{\displaystyle \frac{{\epsilon }_{3}H{N}^{*}}{1+{\zeta }_{3}H{N}^{*}}({\lambda }_5-{\lambda }_7)}}{2w_7}\},1\},}$$ (D.5)

$${\displaystyle u_5^{*}=\min \left\{\max \right\{0,\frac{{\displaystyle \frac{{\epsilon }_{4}H{C}^{*}}{1+{\zeta }_{4}H{C}^{*}}({\lambda }_6-{\lambda }_7)}}{2w_8}\},1\},}$$ (D.6)

Proof

Let $S^{*}$, $E^{*}$, $A^{*}$, $I^{*}$, $H{N}^{*}$, $H{C}^{*}$, $R^{*}$, $Z^{*}$ be optimal state variables, and $u_i^{*}$, $i=1,\dots ,5$ be optimal control variables of system (1) that minimize objective function (3). With the help of Pontryagin’s Maximum Principle and defined adjoint variables ${\lambda }_i$, $i=1,\dots ,8$, we have $\frac{\mathrm{d}{\lambda }_1}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }S}$, $\frac{\mathrm{d}{\lambda }_2}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }E}$, $\frac{\mathrm{d}{\lambda }_3}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }A}$, $\frac{\mathrm{d}{\lambda }_4}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }I}$, $\frac{\mathrm{d}{\lambda }_5}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }HN}$, $\frac{\mathrm{d}{\lambda }_6}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }HC}$, $\frac{\mathrm{d}{\lambda }_7}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }R}$, $\frac{\mathrm{d}{\lambda }_8}{\mathrm{d}t}=-\frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }Z}$, which lead to obtain Eq. (D.1). In regard to the transversality conditions ${\lambda }_i\left(T_f\right)=0$, $i=1,\dots ,8$ and optimality conditions, we have:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_1}|u_1=u_1^{*}}& =& 0\hfill \\ \hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_1}|u_1=u_1^{*}}& =& 2w_4{u}_1^{*}-{\lambda }_{1}kSZ+{\lambda }_{7}kSZ=0\hfill \\ \hfill u_1^{*}& =& {\displaystyle \frac{k{S}^{*}{Z}^{*}({\lambda }_1-{\lambda }_7)}{2w_4}}\hfill \end{array}$$ (D.7)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_2}|u_2=u_2^{*}}& =& 0\hfill \\ \hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_2}|u_2=u_2^{*}}& =& 2w_5{u}_2^{*}+{\lambda }_4(-{\epsilon }_{1}I/1+{\zeta }_{1}I)+{\lambda }_5({\epsilon }_{1}I/1+{\zeta }_{1}I)=0\hfill \\ \hfill u_2^{*}& =& {\displaystyle \frac{{\displaystyle \left(\frac{{\epsilon }_1{I}^{*}}{1+{\zeta }_1{I}^{*}}\right)({\lambda }_4-{\lambda }_5)}}{2w_5}}\hfill \end{array}$$ (D.8)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_3}|u_3=u_3^{*}}& =& 0\hfill \\ \hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_3}|u_3=u_3^{*}}& =& 2w_6{u}_3^{*}+{\lambda }_4(-{\epsilon }_{2}I/1+{\zeta }_{2}I)+{\lambda }_6({\epsilon }_{2}I/1+{\zeta }_{2}I)=0\hfill \\ \hfill u_3^{*}& =& {\displaystyle \frac{{\displaystyle \left(\frac{{\epsilon }_2{I}^{*}}{1+{\zeta }_2{I}^{*}}\right)({\lambda }_4-{\lambda }_6)}}{2w_6}}\hfill \end{array}$$ (D.9)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_4}|u_4=u_4^{*}}& =& 0\hfill \\ \hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_4}|u_4=u_4^{*}}& =& 2w_7{u}_4^{*}+{\lambda }_5(-{\epsilon }_{3}HN/1+{\zeta }_{3}HN)+{\lambda }_7({\epsilon }_{3}HN/1+{\zeta }_{3}HN)=0\hfill \\ \hfill u_4^{*}& =& {\displaystyle \frac{{\displaystyle \left(\frac{{\epsilon }_{3}H{N}^{*}}{1+{\zeta }_{3}H{N}^{*}}\right)({\lambda }_5-{\lambda }_7)}}{2w_7}}\hfill \end{array}$$ (D.10)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_5}|u_5=u_5^{*}}& =& 0\hfill \\ \hfill {\displaystyle \frac{\mathrm{\partial }\overline{H}}{\mathrm{\partial }{u}_5}|u_5=u_5^{*}}& =& 2w_8{u}_5^{*}+{\lambda }_6(-{\epsilon }_{4}HC/1+{\zeta }_{4}HC)+{\lambda }_7({\epsilon }_{4}HC/1+{\zeta }_{4}HC)=0\hfill \\ \hfill u_5^{*}& =& {\displaystyle \frac{{\displaystyle \left(\frac{{\epsilon }_{4}H{C}^{*}}{1+{\zeta }_{4}H{C}^{*}}\right)({\lambda }_6-{\lambda }_7)}}{2w_8}}\hfill \end{array}$$ (D.11)

Now, we can deduce the following optimal control variables from these observations and the properties of control set $\sqcap$:

$$u_1^{*}=\{\begin{array}{cc}0\hfill & {\displaystyle \text{if}\frac{k{S}^{*}{Z}^{*}({\lambda }_1-{\lambda }_7)}{2w_4}<0}\hfill \\ {\displaystyle \left[5pt\right]\frac{k{S}^{*}{Z}^{*}({\lambda }_1-{\lambda }_7)}{2w_4}}\hfill & {\displaystyle \text{if}0\le \frac{k{S}^{*}{Z}^{*}({\lambda }_1-{\lambda }_7)}{2w_4}\le 1}\hfill \\ \left[5pt\right]1\hfill & {\displaystyle \text{if}\frac{k{S}^{*}{Z}^{*}({\lambda }_1-{\lambda }_7)}{2w_4}>1}\hfill \end{array}$$ (D.12)

$$u_2^{*}=\{\begin{array}{cc}0\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_1{I}^{*}}{1+{\zeta }_1{I}^{*}}\right)({\lambda }_4-{\lambda }_5)}}{2w_5}<0}\hfill \\ {\displaystyle \left[5pt\right]\frac{{\displaystyle \left(\frac{{\epsilon }_1{I}^{*}}{1+{\zeta }_1{I}^{*}}\right)({\lambda }_4-{\lambda }_5)}}{2w_5}}\hfill & {\displaystyle \text{if}0\le \frac{{\displaystyle \left(\frac{{\epsilon }_1{I}^{*}}{1+{\zeta }_1{I}^{*}}\right)({\lambda }_4-{\lambda }_5)}}{2w_5}\le 1}\hfill \\ \left[5pt\right]1\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_1{I}^{*}}{1+{\zeta }_1{I}^{*}}\right)({\lambda }_4-{\lambda }_5)}}{2w_5}>1}\hfill \end{array}$$ (D.13)

$$u_3^{*}=\{\begin{array}{cc}0\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_2{I}^{*}}{1+{\zeta }_2{I}^{*}}\right)({\lambda }_4-{\lambda }_6)}}{2w_6}<0}\hfill \\ {\displaystyle \left[5pt\right]\frac{{\displaystyle \left(\frac{{\epsilon }_2{I}^{*}}{1+{\zeta }_2{I}^{*}}\right)({\lambda }_4-{\lambda }_6)}}{2w_6}}\hfill & {\displaystyle \text{if}0\le \frac{{\displaystyle \left(\frac{{\epsilon }_2{I}^{*}}{1+{\zeta }_2{I}^{*}}\right)({\lambda }_4-{\lambda }_6)}}{2w_6}\le 1}\hfill \\ \left[5pt\right]1\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_2{I}^{*}}{1+{\zeta }_2{I}^{*}}\right)({\lambda }_4-{\lambda }_6)}}{2w_6}>1}\hfill \end{array}$$ (D.14)

$$u_4^{*}=\{\begin{array}{cc}0\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_{3}H{N}^{*}}{1+{\zeta }_{3}H{N}^{*}}\right)({\lambda }_5-{\lambda }_7)}}{2w_7}<0}\hfill \\ {\displaystyle \left[5pt\right]\frac{{\displaystyle \left(\frac{{\epsilon }_{3}H{N}^{*}}{1+{\zeta }_{3}H{N}^{*}}\right)({\lambda }_5-{\lambda }_7)}}{2w_7}}\hfill & {\displaystyle \text{if}0\le \frac{{\displaystyle \left(\frac{{\epsilon }_{3}H{N}^{*}}{1+{\zeta }_{3}H{N}^{*}}\right)({\lambda }_5-{\lambda }_7)}}{2w_7}\le 1}\hfill \\ \left[5pt\right]1\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_{3}H{N}^{*}}{1+{\zeta }_{3}H{N}^{*}}\right)({\lambda }_5-{\lambda }_7)}}{2w_7}>1}\hfill \end{array}$$ (D.15)

$$u_5^{*}=\{\begin{array}{cc}0\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_{4}H{C}^{*}}{1+{\zeta }_{4}H{C}^{*}}\right)({\lambda }_6-{\lambda }_7)}}{2w_8}<0}\hfill \\ {\displaystyle \left[5pt\right]\frac{{\displaystyle \left(\frac{{\epsilon }_{4}H{C}^{*}}{1+{\zeta }_{4}H{C}^{*}}\right)({\lambda }_6-{\lambda }_7)}}{2w_8}}\hfill & {\displaystyle \text{if}0\le \frac{{\displaystyle \left(\frac{{\epsilon }_{4}H{C}^{*}}{1+{\zeta }_{4}H{C}^{*}}\right)({\lambda }_6-{\lambda }_7)}}{2w_8}\le 1}\hfill \\ \left[5pt\right]1\hfill & {\displaystyle \text{if}\frac{{\displaystyle \left(\frac{{\epsilon }_{4}H{C}^{*}}{1+{\zeta }_{4}H{C}^{*}}\right)({\lambda }_6-{\lambda }_7)}}{2w_8}>1}\hfill \end{array}$$ (D.16)

which is corresponding to (D.2)–(D.6). □

As mentioned earlier, Pontryagin’s Maximum Principle helps to obtain optimal controls $(u_1^{*},u_2^{*},u_3^{*},u_4^{*},u_5^{*})$. In this regard, the impacts of the application of one or all control variables to obtain the minimal cost have been examined one by one. So, the control system in Eqs. (3) and (4) is solved with respect to the mentioned parameters. On this subject, a number of combinations of control variables are reflected, including $[u_1,(u_1,u_2),(u_1,u_3),(u_1,u_4),(u_1,u_5),(u_1,u_2,u_3,u_4,u_5)]$. The computational simulation for all combinations is executed by Python. Next, the Forward-backward sweep method is employed to find the optimal control variables, where the optimal and adjoint state systems are solved by forward and backward in time, respectively. Afterward, in order to update the optimal controls by Hamiltonian for the optimality of the system, the steepest descent method is employed. This procedure carries on until the convergence [93].

Appendix E. Pontryagin’s maximum principle

Proof

We derived the necessary conditions for the optimal control problem for system (3) and (4) by using Pontryagin’s Maximum Principle [91], [92]. Let $\overline{H}$ be the Hamiltonian function, which is defined as (E.1) and (E.2):

$$\begin{array}{ccc}& & \overline{H}(S,E,A,I,HN,HC,R,Z,u_1,u_2,u_3,u_4,u_5,\lambda )\hfill \\ & & =L(S,E,A,I,HN,HC,R,Z,u_1,u_2,u_3,u_4,u_5)\hfill \\ & & {\displaystyle +{\lambda }_1\frac{\mathrm{d}S}{\mathrm{d}t}+{\lambda }_2\frac{\mathrm{d}E}{\mathrm{d}t}+{\lambda }_3\frac{\mathrm{d}A}{\mathrm{d}t}+{\lambda }_4\frac{\mathrm{d}I}{\mathrm{d}t}+{\lambda }_5\frac{\mathrm{d}HN}{\mathrm{d}t}+{\lambda }_6\frac{\mathrm{d}HC}{\mathrm{d}t}+{\lambda }_7\frac{\mathrm{d}R}{\mathrm{d}t}+{\lambda }_8\frac{\mathrm{d}Z}{\mathrm{d}t}}\hfill \end{array}$$ (E.1)

Hence,

$$\begin{array}{cc}\overline{H}=\hfill & w_{1}I+w_{2}HN+w_{3}HC+w_4{u}_1^2+w_5{u}_2^2+w_6{u}_3^2+w_7{u}_4^2+w_8{u}_5^2\hfill \\ & +{\lambda }_1[\Lambda -({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-dS+\xi R-u_1\left(t\right)kSZ]\hfill \\ & +{\lambda }_2[({\beta }_{1}A+{\beta }_{2}I+{\beta }_{3}HN+{\beta }_{4}HC)S-(k+d)E]\hfill \\ & +{\lambda }_3[\kappa \rho E-\eta A-(d+{\delta }_1)A]\hfill \\ & {\displaystyle +{\lambda }_4[\kappa (1-\rho )E+\eta A-\omega I-(d+{\delta }_2)I-\frac{{\epsilon }_1{u}_2\left(t\right)I}{1+{\zeta }_{1}I}-\frac{{\epsilon }_2{u}_3\left(t\right)I}{1+{\zeta }_{2}I}]}\hfill \\ & {\displaystyle +{\lambda }_5[\omega (1-c)I-(d+{\delta }_3)HN-{\gamma }_{1}HN-\theta HN+\frac{{\epsilon }_1{u}_2\left(t\right)I}{1+{\zeta }_{1}I}-\frac{{\epsilon }_3{u}_4\left(t\right)HN}{1+{\zeta }_{3}HN}]}\hfill \\ & {\displaystyle +{\lambda }_6[\omega cI-(d+{\delta }_4)HC-{\gamma }_{2}HC+\theta HN+\frac{{\epsilon }_2{u}_3\left(t\right)I}{1+{\zeta }_{2}I}-\frac{{\epsilon }_4{u}_5\left(t\right)HC}{1+{\zeta }_{4}HC}]}\hfill \\ & {\displaystyle +{\lambda }_7[{\gamma }_{1}HN+{\gamma }_{2}HC-\xi R-dR+u_{1}kSZ+\frac{{\epsilon }_3{u}_4\left(t\right)HN}{1+{\zeta }_{3}HN}+\frac{{\epsilon }_4{u}_5\left(t\right)HC}{1+{\zeta }_{4}HC}]}\hfill \\ & {\displaystyle +{\lambda }_8[\frac{pI}{1+qI}-a_{0}Z]}\hfill \end{array}$$ (E.2)

 □

Appendix F. The PISP Benders reformulation

Let ${\overline{w}}_{jt}$, ${\overline{y}}_{pmt}$, and ${\overline{v}}_m$ be the vectors of fixed $w_{jt}$, $y_{pmt}$, and $v_m$ variables, respectively. Based on the notation of Table F.7 , the Benders sub-problem can be written as follows:

$$\begin{array}{ccc}\hfill \min Z& =& \sum _{p\in P}\sum _{j\in J}\sum _{m\in K}\sum _{t\in T}T{C}_{pjm}{u}_{pjmt}+\sum _{p\in P}\sum _{m\in K}\sum _{t\in T}P{C}_{pm}{x}_{pmt}+\sum _{p\in P}\sum _{m\in K}\sum _{m^{\prime }\in H}\sum _{t\in T}T{C}_{pm{m}^{\prime }}{q}_{m{m}^{\prime }}^{pt}\hfill \\ & & +\sum _{p\in P}\sum _{m\in H}\sum _{m^{\prime }\in H}\sum _{t\in T}T{C}_{pm{m}^{\prime }}{s}_{m{m}^{\prime }}^{pt}+\sum _{p\in P}\sum _{m\in K\cup H}\sum _{t\in T}I{C}_{pm}{I}_{pmt}+CU\times S_{max}\hfill \end{array}$$ (F.1)

s.t.: Constraints (6), (8), (10)–(22), (25)–(29), and

$$\sum _{m\in K}{u}_{pjmt}\le U_{pj}{\overline{w}}_{jt}\forall j\in J,p\in P,t\in T$$ (F.2)

$$x_{pmt}\le Q_{pm}{\overline{y}}_{pmt}\forall p\in P,m\in K,t\in T$$ (F.3)

$$b_{pmt}^{+}\le T{Q}_p{\overline{v}}_m\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (F.4)

$$b_{pmt}^{-}\ge T{Q}_p({\overline{v}}_m-1)\forall i\in I,p\in P,m\in H_i\left(m\right),t\in T$$ (F.5)

Table F.7.

Vectors of the dual variables associated with the Benders sub-problem constraints.

Not.	Desc.	Not.	Desc.
$\mathbf{\alpha }$	$\{{\alpha }_{pmt}\ge 0|p\in P,m\in H,t\in T\}$	$\mathbf{\beta }$	$\{{\beta }_{jpt}\ge 0|j\in J,p\in P,t\in T\}$
$\mathbf{\Phi }$	$\{{\Phi }_{pmt}\in \mathbb{R}|p\in P,m\in H,t\in T\}$	$\mathbf{\eta }$	$\{{\eta }_{pmt}\ge 0|p\in P,m\in K,t\in T\}$
${\mathbf{\lambda }}_{\mathit{1}}$	$\{{\lambda }_{ipm,1}\ge 0|p\in P,i\in I,m\in K_i\left(m\right)\}$	$\mathbf{\lambda }$	$\{{\lambda }_{ipmt}\ge 0|p\in P,i\in I,m\in K_i\left(m\right),t\in T;t>1\}$
$\mathbf{\tau }$	$\{{\tau }_{ipmt}\ge 0|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$	${\mathbf{\pi }}_{\mathit{1}}$	$\{{\pi }_{ipm,1}\in \mathbb{R}|p\in P,i\in I,m\in K_i\left(m\right)\}$
$\mathbf{\pi }$	$\{{\pi }_{ipmt}\in \mathbb{R}|p\in P,i\in I,m\in K_i\left(m\right),t\in T;t>1\}$	$\mathbf{ϵ}$	$\{{ϵ}_{pmt}\ge 0|p\in P,m\in M,t\in T\}$
${\mathbf{\varphi }}_{\mathit{1}}$	$\{{\varphi }_{ipm,1}\in \mathbb{R}|p\in P,i\in I,m\in H_i\left(m\right)\}$	$\mathbf{\varphi }$	$\{{\varphi }_{ipmt}\in \mathbb{R}|p\in P^{\prime },i\in I,m\in H_i\left(m\right),t\in T;t>1\}$
${\mathbf{\varphi }}^{\prime }$	$\{{\varphi }_{ipmt}^{\prime }\in \mathbb{R}|p\in P^{″},i\in I,m\in H_i\left(m\right);1<t\le L\}$	${\mathbf{\varphi }}^{″}$	$\{{\varphi }_{ipmt}^{″}\in \mathbb{R}|p\in P^{″},i\in I,m\in H_i\left(m\right),t\in T;t>L\}$
$\mathbf{\Omega }$	$\{{\Omega }_{pmt}\ge 0|p\in P,m\in H,t\in T\}$	$\mathbf{\omega }$	$\{{\omega }_{pt}\ge 0|p\in P,t\in T\}$
$\mathcal{X}$	$\{{\mathcal{X}}_{ipmt}\ge 0|p\in P,i\in I{\mathbf{\varphi }}^{\prime }=,m\in H_i\left(m\right),t\in T\}$	$\mathcal{Y}$	$\{{\mathcal{Y}}_{ipmt}\ge 0|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$
$\mathcal{W}$	$\{{\mathcal{W}}_{ipmt}\in \mathbb{R}|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$	$\mathcal{R}$	$\{{\mathcal{R}}_{ipmt}\in \mathbb{R}|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$
$\mathcal{V}$	$\{{\mathcal{V}}_{ipmt}\ge 0|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$	${\mathcal{V}}^{\prime }$	$\{{\mathcal{V}}_{ipmt}^{\prime }\ge 0|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$
$\mathcal{Z}$	$\{{\mathcal{Z}}_{ipmt}\ge 0|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$	${\mathcal{Z}}^{\prime }$	$\{{\mathcal{Z}}_{ipmt}^{\prime }\ge 0|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$
${\mathcal{Z}}^{″}$	$\{{\mathcal{Z}}_{ipmt}^{″}\in \mathbb{R}|p\in P,i\in I,m\in H_i\left(m\right),t\in T\}$	$\mathcal{N}$	$\{{\mathcal{N}}_{ipm{m}^{\prime }t}\ge 0|p\in P,i\in I,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }\}$
${\mathcal{N}}^{\prime }$	$\{{\mathcal{N}}_{ipm{m}^{\prime }t}^{\prime }\ge 0|p\in P,i\in I,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }\}$	$\mathcal{M}$	$\{{\mathcal{M}}_{ipm{m}^{\prime }t}\in \mathbb{R}|p\in P,i\in I,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }\}$
${\mathcal{M}}^{\prime }$	$\{{\mathcal{M}}_{ipm{m}^{\prime }t}^{\prime }\in \mathbb{R}|p\in P,i\in I,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }\}$	${\mathcal{M}}^{″}$	$\{{\mathcal{M}}_{ipm{m}^{\prime }t}^{″}\ge 0|p\in P,i\in I,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }\}$
$\mathcal{H}$	$\{{\mathcal{H}}_{ipm{m}^{\prime }t}\ge 0|p\in P,i\in I,m,m^{\prime }\in H_i\left(m\right),t\in T;m\ne m^{\prime }\}$

The Benders master problem can be written as follows:

$$\min Z=\sum _{j\in J}\sum _{t\in T}O{C}_j{w}_{jt}+\sum _{p\in P}\sum _{m\in K}\sum _{t\in T}S{C}_{pm}{y}_{pmt}+\zeta$$ (F.6)

s.t.: Constraints (30)–(35) and (36), and

$$\begin{array}{cc}& -\sum _{p\in P}\sum _{m\in H}\sum _{t\in T}{D}_{pmt}{\alpha }_{pmt}-\sum _{j\in J}\sum _{m\in H}\sum _{t\in T}{U}_{pj}{w}_{jt}{\beta }_{jpt}-\sum _{p\in P}\sum _{m\in K}\sum _{t\in T}{Q}_{pm}{y}_{pmt}{\eta }_{pmt}\hfill \\ & +\sum _{i\in I}\sum _{m\in K_i\left(m\right)}\sum _{p\in P}{I}_{pm}^0({\pi }_{ipm,1}-{\lambda }_{ipm,1})-\sum _{p\in P}\sum _{m\in M}\sum _{t\in T}{I}_{pm}^{max}{ϵ}_{pmt}\hfill \\ & +\sum _{i\in I}\sum _{p\in P}\sum _{m\in H_i\left(m\right)}{I}_{pm}^0{\varphi }_{ipm,1}+\sum _{p\in P}\sum _{m\in H}\sum _{t\in T}{D}_{pmt}{\Omega }_{pmt}-\sum _{p\in P}\sum _{t\in T}T{Q}_p{\omega }_{pt}\hfill \\ & -\sum _{i\in I}\sum _{p\in P}\sum _{m^{\prime }\in H_i\left(m\right)}\sum _{t\in T}{G}_{p{m}^{\prime }}^{max}{\mathcal{X}}_{ip{m}^{\prime }t}+\sum _{i\in I}\sum _{p\in P}\sum _{m^{\prime }\in H_i\left(m\right)}\sum _{t\in T}{D}_{pmt}{\mathcal{W}}_{ipmt}\hfill \\ & -\sum _{i\in I}\sum _{p\in P}\sum _{m^{\prime }\in H_i\left(m\right)}\sum _{t\in T}T{Q}_p{v}_m{\mathcal{Z}}_{ipmt}+\sum _{i\in I}\sum _{p\in P}\sum _{m^{\prime }\in H_i\left(m\right)}\sum _{t\in T}T{Q}_p(v_m-1){\mathcal{Z}}_{ipmt}^{\prime }\hfill \\ & -\sum _{i\in I}\sum _{p\in P}\sum _{m\in H_i\left(m\right)}\sum _{\begin{array}{c}{m}^{\prime }\in H_i\left(m\right)\\ m^{\prime }\ne m\end{array}}\sum _{t\in T}{G}_{pm}^{max}{\mathcal{H}}_{ipm{m}^{\prime }t}\le \zeta \hfill \end{array}$$ (F.7)

$\forall (\mathbf{\alpha },\mathbf{\beta },\mathbf{\Phi },\mathbf{\eta },{\mathbf{\lambda }}_{\mathit{1}},\mathbf{\lambda },\mathbf{\tau },{\mathbf{\pi }}_{\mathit{1}},\mathbf{\pi },\mathbf{ϵ},{\mathbf{\varphi }}_{\mathit{1}},\mathbf{\varphi },{\mathbf{\varphi }}^{\prime },{\mathbf{\varphi }}^{″},\mathbf{\Omega },\mathbf{\omega },\mathcal{X},\mathcal{Y},\mathcal{W},\mathcal{R},\mathcal{V},{\mathcal{V}}^{\prime },\mathcal{Z},{\mathcal{Z}}^{\prime },{\mathcal{Z}}^{″},\mathcal{N},{\mathcal{N}}^{\prime },\mathcal{M},{\mathcal{M}}^{\prime },{\mathcal{M}}^{″},\mathcal{H})\in P_{\nabla }$

$$\zeta \ge 0$$ (F.8)

where $\nabla$ signifies the polyhedron specified by the constraints of the problem, and $P_{\nabla }$ implicates the set of extreme points of $\nabla$. Constraint (F.7) represents the optimality cut which can be generated consecutively in accordance with Bender’s sub-problem solution and the vectors of the dual variables.

Appendix G. Details of the case study’s data

Detailed information on all other parameters in the SEIHRS model and PISP formulation is provided in Table G.8. The majority of the parameters are based on real data except for the setup costs and the supply and production capacities which have been estimated based on expert opinion. Except for the death rates as well as the population in each set of populated areas, other parameters of the SEIHRS model are considered similar for the whole of France [52], [94], [95].

Table G.8.

Input data.

Parameter	Value	Parameter	Value	Parameter	Value
$I$	12	$\gamma$	[0.1,0.5]	$\omega$	0.02
$J$	12	$OC$ (€)	[15,000, 20,000]	${\gamma }_1$	0.5
$M$	233	$L$ (week)	2	${\gamma }_2$	0.3
$K$	33	${\beta }_1$	3.70E$-$11	$p$	0.01
$H$	200	${\beta }_2$	1.48E$-$10	$q$	1
$P$	6	${\beta }_3$	7,00E$-$12	$a_0$	0.06
$PC$ (€)	$[0.5,20,000]$	${\beta }_4$	7.00E$-$12	$c$	0.2
$SC$ (€)	$[500,5M]$	$\zeta$	3.00E$-$10	${ϵ}_1$	0.1
$TC$ (€ /100km)	$[5\%,10\%]\times PC$	$\kappa$	0.6	${ϵ}_2$	0.1
$IC$ (€)	$[5\%,20\%]\times PC$	$k$	0.002	${ϵ}_3$	0.9
$Q(\#)$	$[100,1M]$	$\varphi$	0.1	${ϵ}_4$	0.9
$I_{m\left(m\in K\right)}^{\max }(\#)$	$[20,10M]$	$\eta$	0.15	${\zeta }_1$	0.05
$I_{m(m\in H)}^{\max }(\#)$	$[4,10,000]$	${\delta }_1$	1.00E$-$04	${\zeta }_2$	0.05
$U(\#)$	$[3000,30,000]$	${\delta }_2$	5.00E$-$04	${\zeta }_3$	0.01
$G^{\max }(\#)$	$[400,20,000]$	${\delta }_3$	2.00E$-$04	${\zeta }_4$	0.01
$I^0(\#)$	$[10\%,20\%]\times I^{\max }$	${\delta }_4$	6.00E$-$04
$\mu (\%)$	[10,30]	$\theta$	0.2

Data availability

Data will be made available on request.