Abstract
Optimization of pump–probe signal requires a complete understanding of how signal scales with experimental factors. In simple systems, signal scales quadratically with molar absorptivity, and linearly with fluence, concentration, and path length. In practice, scaling factors weaken beyond certain thresholds (e.g., OD > 0.1) due to asymptotic limits related to optical density, fluence and path length. While computational models can accurately account for subdued scaling, quantitative explanations often appear quite technical in the literature. This Perspective aims to present a simpler understanding of the subject with concise formulas for estimating absolute magnitudes of signal under both ordinary and asymptotic scaling conditions. This formulation may be more appealing for spectroscopists seeking rough estimates of signal or relative comparisons. We identify scaling dependencies of signal with respect to experimental parameters and discuss applications for improving signal under broad conditions. We also review other signal enhancement methods, such as local-oscillator attenuation and plasmonic enhancement, and discuss respective benefits and challenges regarding asymptotic limits that signal cannot exceed.
Introduction
Ultrafast pump–probe spectroscopy is a powerful tool for measuring the structural dynamics and functions of molecules ranging between the millisecond and attosecond time scales.1−3 The technique consists of measuring the change in absorption of a probe pulse following a prior interaction with a pump pulse. Variations of the technique can differ by the number of independent variables resolved in a spectrum. In the simplest case, transient absorption spectroscopy resolves a spectrum as a function of the probe frequency and time delay between the pump and probe, enabling observation of how certain chemical species or populations change as a function of time. Transient absorption has seen a variety of applications, with examples ranging from photoinduced processes in molecular biology,4−6 polaritons in waveguides,7 and energy or charge transfer in nanostructures8,9 and photovoltaics.10
Time-resolved two-dimensional (2D) spectroscopy is another variation of the pump–probe technique that contains all the same information as transient absorption, while also adding more by resolving the spectrum as a function of both pump and probe frequencies. This enables disambiguation of combination bands, overtones, and Fermi resonances and allows for observing how populations evolve over time through correlations in frequency. Polarization schemes offer further insight into molecular structure through the relative orientation of modes.11 Applications of 2D spectroscopy are far reaching, with examples ranging from investigating protein folding motions,12−14 protein structure and dynamics,15,16 chemical reactions,17,18 solvent dynamics,19,20 mechanisms of charge separation and energy transfer in photosynthetic systems,21−25 and excitons in semiconductors.26
The improvement of signal-to-noise in pump–probe spectroscopy remains an ongoing challenge in order to expand the range of systems accessible by the technique.27 This requires a complete understanding of how signal scales with experimental factors. In the simplest case, signal scales quadratically with molar absorptivity and linearly with fluence, concentration, and path length. But conventional scaling laws do not account for asymptotic limits related to optical density, fluence, and path length. For example, the upper limit of signal for a two-level system under incoherent excitation is |ΔOD| ≤ OD, with equality corresponding to 100% transmission of the probe beam through the pumped sample. Furthermore, this upper limit is only valid for small optical densities (<0.1), but as we discuss later, increasing the optical density of a sample leads to higher attenuation of the pump beam and therefore weakens signal scaling factors. For example, increasing the optical density of a sample from 0.05 OD to 0.1 OD leads to a 1.9× increase in signal, but an increase from 0.5 OD to 1.0 OD merely leads to a 1.3× increase in signal. Accounting for solvent absorption and fluence further complicates scaling factors. Hence, conventional scaling laws are inadequate beyond a very limiting case of experimental conditions, and a more generalized formulation is necessary for accurately understanding how signal scales with experimental factors.
Early studies of photon echoes identified a nonlinear relationship between signal intensity and optical density due to accumulated attenuation of the excitation beams passing through the sample.28,29 Decades later, Jonas and co-workers explored the effect of optical density on signal both experimentally and theoretically through the use of beam propagation models based upon Maxwell’s equations30−32 or a modified form of Beer’s law to account for third-order response.33,34 In addition to high optical density, early studies of photon echoes also identified a nonlinear relationship between signal and intensity (or fluence).35 For a two-level system, the ratio of ground state to excited state oscillators cannot exceed unity due to competing processes of absorption and stimulated emission, which is the basis for fluence saturation.
Many of the formulas here build on previous work,36 including an approximation to another solution published by Cho et al.33 A number of publications have reported formulas for estimating relative quantities of signal, concentration, and cross sections but require a secondary measurement or calibrant to compute absolute quantities.34,37−40 Here we identify concise formulas for calculating absolute values of signal in cases of high optical density and/or high fluence given known quantities of molar absorptivity, concentration, path length, pulse energy, spectral bandwidth, line width, beam waist at focus, and optical density of the solvent. Furthermore, we analyze these formulas in the context of experimental strategies to enhance signal and identify asymptotic limits that signal cannot exceeded.
Following is the layout of the manuscript: Section 1 provides a quick review of Gaussian beams necessary for later formulas. Section 2 derives a model for optically dense samples while section 3 derives a model for high fluence measurements, and Section 4 derives a model suitable in both limits. Section 5 analyzes these formulas to identify trends for improving signal and recognizing asymptotic limits. Sections 6 and 7 review additional forms of signal enhancement including local oscillator attenuation and plasmonic enhancement, with discussion of how scaling laws and asymptotic limits apply in each case. Finally, Section 8 reviews a close relationship between temperature jumps and signal that is particularly relevant to aqueous samples excited in the infrared.
1. Gaussian Beams
The Gaussian beam is
a solution to the scalar wave equation that
assumes a laser beam primarily propagating in one direction ( ) and that the envelope slowly varies along
) and that the envelope slowly varies along  . An important feature of Gaussian beams
is that a point of focus must exist somewhere along the axis of propagation.
This captures the reality that infinitely collimated beams do not
exist. Rather, well-collimated beams are slowly converging, or diverging,
to, or from, a point of focus. Figure 1 illustrates a few common measures of Gaussian beams.
Siegman defines the spot size
. An important feature of Gaussian beams
is that a point of focus must exist somewhere along the axis of propagation.
This captures the reality that infinitely collimated beams do not
exist. Rather, well-collimated beams are slowly converging, or diverging,
to, or from, a point of focus. Figure 1 illustrates a few common measures of Gaussian beams.
Siegman defines the spot size as the radius of aperture that transmits
∼86% of the beam’s power.41Equation 1 provides
the formula for calculating the spot size in terms of the beam waist
as the radius of aperture that transmits
∼86% of the beam’s power.41Equation 1 provides
the formula for calculating the spot size in terms of the beam waist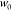 located at the focus
located at the focus  , and the Rayleigh length
, and the Rayleigh length at which the on-axis intensity of the beam
is 1/2 the intensity at the focus, or equivalently, where
at which the on-axis intensity of the beam
is 1/2 the intensity at the focus, or equivalently, where 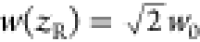 . And finally, sometimes it may be convenient
to reference the aperture diameter
. And finally, sometimes it may be convenient
to reference the aperture diameter that corresponds to ∼99% transmission
of the beam’s power. Note that Figure 1 is an equally valid model for both focused
and collimated laser beams.
that corresponds to ∼99% transmission
of the beam’s power. Note that Figure 1 is an equally valid model for both focused
and collimated laser beams.
| 1 |
Figure 1.
Characteristic measures
of a Gaussian beam, including spot size  , beam waist
, beam waist 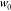 , Rayleigh length
, Rayleigh length 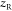 , and aperture diameter
, and aperture diameter  .
.
2. Competitive Absorber
The simplest model
for pump–probe signal assumes scaling
of ΔOD ∝ Fεa2ca , where F is the fluence
(energy/area) of the pump beam, εa and ca are the molar absorptivity and concentration of the
analyte, and
, where F is the fluence
(energy/area) of the pump beam, εa and ca are the molar absorptivity and concentration of the
analyte, and  is the path length of the sample. One shortcoming
of this model is the assumption that pump fluence stays constant as
the beam passes through the sample. As illustrated in Figure 2, this assumption is valid
in low OD samples (OD < 0.1) but inaccurate in higher OD samples
where increasing absorption of the pump beam leads to subdued scaling
in the signal. This effect is well-known and captured in models by
Jonas and co-workers but requires numeric integration.33 Here we present a shortened version of their
model based on Beer’s law that utilizes integral approximations
to generate a concise formula. For simplicity’s sake, our derivation
assumes a simple two-level system. We also note that similar shortened
formulas have recently appeared in literature.36,40
is the path length of the sample. One shortcoming
of this model is the assumption that pump fluence stays constant as
the beam passes through the sample. As illustrated in Figure 2, this assumption is valid
in low OD samples (OD < 0.1) but inaccurate in higher OD samples
where increasing absorption of the pump beam leads to subdued scaling
in the signal. This effect is well-known and captured in models by
Jonas and co-workers but requires numeric integration.33 Here we present a shortened version of their
model based on Beer’s law that utilizes integral approximations
to generate a concise formula. For simplicity’s sake, our derivation
assumes a simple two-level system. We also note that similar shortened
formulas have recently appeared in literature.36,40
Figure 2.
Plot of pump fluence as a function of the propagation depth into the sample in cases of low and high optical density.
We define signal, ΔOD, as the change in optical
density of
the probe pulse between pump “on” and “off”,
defined in eq 2. The
pump off optical density is simply equal to  . The pump on optical density is equal to
. The pump on optical density is equal to 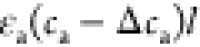 –
– 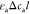 , where the first term accounts for absorption
from the pump depleted ground state and the second term accounts for
stimulated emission from the pump induced excited state. Hence, the
net change in optical density is equal to eq 3. One may multiply eq 3 by additional terms to account for auxiliary
effects like polarization, lifetime decay and rotational diffusion.11,33,38
, where the first term accounts for absorption
from the pump depleted ground state and the second term accounts for
stimulated emission from the pump induced excited state. Hence, the
net change in optical density is equal to eq 3. One may multiply eq 3 by additional terms to account for auxiliary
effects like polarization, lifetime decay and rotational diffusion.11,33,38
The factor of Δca in eq 3 is equal to the number
of pump photons absorbed by the sample divided by the volume of excitation.
In the low fluence limit, for a nonabsorbing solvent, the total number
of photons absorbed by the analyte is ΔNabs = Nres(1 – 10–OD), where Nres is the number of incident
photons resonant (overlapping) with the oscillator’s
line shape. For an absorbing solvent, ΔNabs is reduced by a factor of 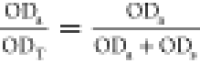 where ODa and ODs are optical densities of the analyte and solvent and ODT is the sum total of the two. Hence, the number of photons absorbed
by the analyte is
where ODa and ODs are optical densities of the analyte and solvent and ODT is the sum total of the two. Hence, the number of photons absorbed
by the analyte is 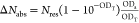 . We approximate the observation volume
as a cylinder with radius
. We approximate the observation volume
as a cylinder with radius  and path length
and path length  :
: 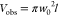 . Equation 4 combines ΔNabs and Vobs to estimate the average concentration of
analyte excited by the pump beam. Division by Avogadro’s number NA in eq 4 ensures Δca carries units
of molarity.
. Equation 4 combines ΔNabs and Vobs to estimate the average concentration of
analyte excited by the pump beam. Division by Avogadro’s number NA in eq 4 ensures Δca carries units
of molarity.
To calculate Nres,
we assume the pump
spectrum and oscillator line shape are both Gaussian, with FWHM denoted
by Δbw and Δlw, respectively. Furthermore,
we assume that Δbw ≫ Δlw,
which enables the approximation 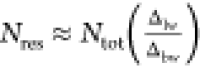 , where Ntot is the total number of pump photons. Ntot is related to the pump pulse energy by Ntot = Epump/hcν̃,
where h is Planck’s constant, c is the speed of light and ν̃ is the center frequency
of the pump spectrum. These expressions combine in eq 5 to estimate Nres.
, where Ntot is the total number of pump photons. Ntot is related to the pump pulse energy by Ntot = Epump/hcν̃,
where h is Planck’s constant, c is the speed of light and ν̃ is the center frequency
of the pump spectrum. These expressions combine in eq 5 to estimate Nres.
| 4 |
| 5 |
We recast ΔOD
into eq 6a based on
substitutions of Δca from eq 4 and Nres from eq 5. The formula is quite simple when factored in terms of the saturation
fluence; hence we have split a factor of ln(10)/ln(10) between eq 6a and eq 6c. The formula
says that ΔOD of the analyte is equal to the product of two
numbers. The first number,  , is effectively the optical density of
the analyte but adjusted for competing absorption of the pump light.
Notice how
, is effectively the optical density of
the analyte but adjusted for competing absorption of the pump light.
Notice how 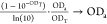 as ODT → 0. The term
“competitive” refers to any scenario in which ODT is significant due to competing absorption by the solvent
(ODs), the analyte (ODa), or both. The second
number, F̃/Fsat, is a measure of saturation induced by the pump beam. In fact, the
quantity approximates twice the relative change in population, F̃/Fsat ≈ 2Δca/ca, in the low
fluence and low OD limit.
as ODT → 0. The term
“competitive” refers to any scenario in which ODT is significant due to competing absorption by the solvent
(ODs), the analyte (ODa), or both. The second
number, F̃/Fsat, is a measure of saturation induced by the pump beam. In fact, the
quantity approximates twice the relative change in population, F̃/Fsat ≈ 2Δca/ca, in the low
fluence and low OD limit.
 |
6 |
We refer to the conventional scaling
law, ΔOD ∝ FεaOD, as
“linear” because
it assumes ΔOD is bilinear in optical density and fluence for
constant εa. Figure 3 compares signal scaling between the linear and competitive
absorber models. In each panel, we plot ΔOD vs OD while varying
OD as a function of ca, 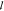 , or εa. As shown in panel
A, with respect to changes in concentration or path length, the two
models are similar below OD < 0.1 and then diverge with increasing
OD due to the asymptote imposed by competitive absorption of the pump
light. This stems from the factor of (1 – 10–OD) in eq 6a that accounts for the depletion
of the pump beam as it penetrates the sample, also illustrated in Figure 2. Above OD > 0.5,
the sample has absorbed >68% of the pump light and attempting to
increase
ΔOD by increasing path length or concentration of the analyte
returns dwindling gains. This trend agrees with prior observations
in the literature.33,40,42 The dependency on εa is similar to a higher order.
Because eq 6a scales as (1 – 10–εa)εa, ΔOD(εa) transitions between quadratic scaling below ODa < 0.1 to linear scaling above ODa > 0.5. Due to
the
impact of OD on signal scaling, we divide our discussion in section 5 into categories
of weak (OD < 0.1) and strong (OD > 0.5) absorption.
, or εa. As shown in panel
A, with respect to changes in concentration or path length, the two
models are similar below OD < 0.1 and then diverge with increasing
OD due to the asymptote imposed by competitive absorption of the pump
light. This stems from the factor of (1 – 10–OD) in eq 6a that accounts for the depletion
of the pump beam as it penetrates the sample, also illustrated in Figure 2. Above OD > 0.5,
the sample has absorbed >68% of the pump light and attempting to
increase
ΔOD by increasing path length or concentration of the analyte
returns dwindling gains. This trend agrees with prior observations
in the literature.33,40,42 The dependency on εa is similar to a higher order.
Because eq 6a scales as (1 – 10–εa)εa, ΔOD(εa) transitions between quadratic scaling below ODa < 0.1 to linear scaling above ODa > 0.5. Due to
the
impact of OD on signal scaling, we divide our discussion in section 5 into categories
of weak (OD < 0.1) and strong (OD > 0.5) absorption.
Figure 3.
Comparison of ΔOD scaling for linear and competitive absorbers. (A) Scaling with respect to OD as a function of concentration or path length. (B) Scaling with respect to OD as a function of analyte molar absorptivity.
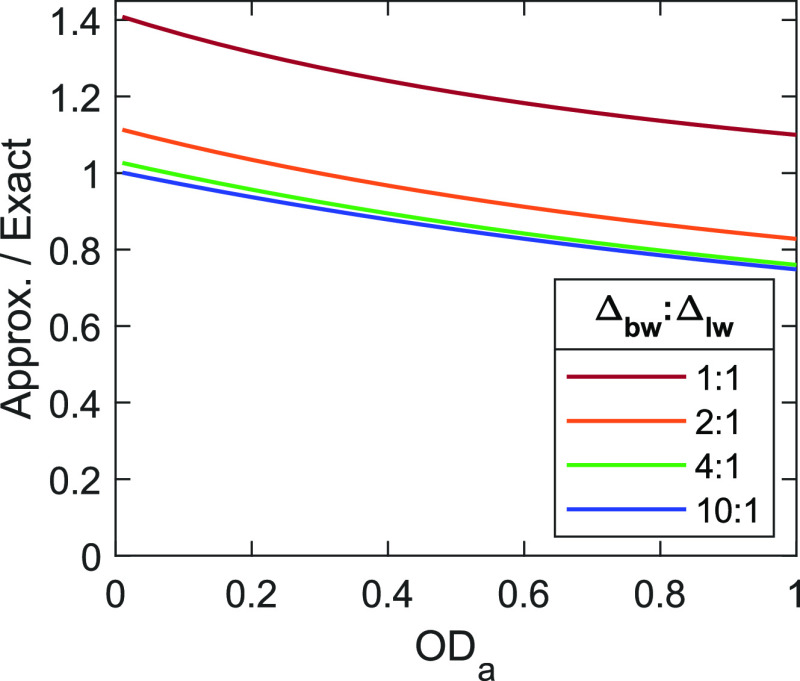
Figure 4 compares
ΔOD between the competitive absorber model in eq 6a, which is an approximate solution to Beer’s law,
to the exact solution derived by Jonas and co-workers, which models
experimental results with high accuracy.33 These results assume a two-level system in the low fluence limit,
pumped and probed by identically sized Gaussian beams. We find strong
agreement between the competitive absorber model and the Jonas model
(>90%) for systems with ODa < 0.3 measured by large
spectral bandwidths (2× line width or greater), and we still
find good agreement (>60%) in more extreme cases. The agreement
between
solutions is explainable through integral approximations. The exact
solution to Beer’s law is ΔOD = −log10(Pron/Pr) where Pron and Pr correspond to
eqs 9 and 10 in ref (33), integrated across X and Y and
evaluated at Z = 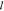 . First, we approximate the pump and probe
beams as averaged flat top beams, which eliminates all X and Y dependencies and simplifies ΔOD ≈
. First, we approximate the pump and probe
beams as averaged flat top beams, which eliminates all X and Y dependencies and simplifies ΔOD ≈  Δα dZ/ln(10). Then we approximate the integral in eq A7, ref (33), as the area of a triangle
such that Δα ≈ puα0 exp(−α0Z)2σΔbw evaluated
at the line shape peak, and a factor of 2 accounts for GSB + SE. And,
finally, the substitutions
Δα dZ/ln(10). Then we approximate the integral in eq A7, ref (33), as the area of a triangle
such that Δα ≈ puα0 exp(−α0Z)2σΔbw evaluated
at the line shape peak, and a factor of 2 accounts for GSB + SE. And,
finally, the substitutions  and Fsat = hcν̃/2σ and integration over Z yields the same expression as eq 6a. The
limiting estimate here is the triangle approximation of the spectral
overlap integral, which is valid at low ODa and
and Fsat = hcν̃/2σ and integration over Z yields the same expression as eq 6a. The
limiting estimate here is the triangle approximation of the spectral
overlap integral, which is valid at low ODa and  ≳ 3, but as seen in Figure 4, is prone to underestimate
absorption around the tails of the line shape at higher ODa and overestimate when the bandwidth of the pump spectrum is comparable
to the line width of the line shape.
≳ 3, but as seen in Figure 4, is prone to underestimate
absorption around the tails of the line shape at higher ODa and overestimate when the bandwidth of the pump spectrum is comparable
to the line width of the line shape.
Figure 4.
Comparison of ΔOD for the competitive absorber model computed by approximate and exact solutions to Beer’s law, as a function of optical density, for varying ratios of bandwidth to line width.
3. Saturable Absorber
The competitive absorber model is valid at low fluence for any optical density. Now we discuss the saturable absorber model, which is valid at low optical density for any incoherent excitation fluence. At low intensities, chromophores act as “linear” absorbers which means that, given an infinitesimally thin sample, the number of photons absorbed by the sample is linearly proportional to the number of photons incident upon it, i.e., the Beer–Lambert law. The linear absorber model works well at low intensities, typical of an FTIR light source, where just a small fraction of oscillators (<1%) absorb light. But given a sufficiently intense beam of light, the Beer–Lambert law predicts a sample could absorb more photons than are oscillators in solution. Therefore, the linear absorber model is unphysical at high intensities. Alternatively, the saturable absorber model accounts for saturation effects due to finite population and converges to the linear absorber model in the low intensity limit.
The saturable absorber model has two limiting cases. One for continuous wave, where the lifetime of the oscillator mode is much longer than the duration of the light source, and the other for ultrashort pulses with durations much shorter than the lifetime of oscillator mode.43 The model yields slightly different formulas in each limit and work in different units: intensity (energy/area/time) for the continuous wave case and fluence (energy/area) for the ultrafast case. Assuming a femtosecond light source, we restrict our analysis to the ultrafast limit.
The saturable absorption model asserts that optical density decays exponentially with fluence, as defined by eq 7a.43 As with the competitive absorber model before, only the resonant fluence, F̃, defined in eq 6b, is relevant here. We plot OD(F̃) versus F̃/Fsat in Figure 5. In the low fluence limit (F̃/Fsat ≲ 10–2), OD is constant, consistent with linear absorption, and then precipitously drops after F̃/Fsat ≈ 10–1 and approaches an asymptotic limit of OD = 0 above F̃/Fsat ≳ 5.
Figure 5.
Plot of absorption versus resonant fluence for a saturable absorber measured by an ultrafast pulse.
Equation 7b models ΔOD of a saturable absorber. In the high fluence limit, ΔOD → –OD, corresponding to 100% transmission of the pump sample. In the low fluence limit, all three models (competitive, saturable, and linear absorbers) converge to the same limit: ΔOD → −(F̃/Fsat)OD. These formulas suggest a strong connection between saturable absorption and pump–probe signal. Indeed, for a two-level system, the change in population follows a saturation curve. Therefore, the two subjects are closely related. While this point appears to have been understood several decades ago,44 the connection between the two subjects has rarely surfaced within the ultrafast community since. We hope to revive this perspective given the remarkably simple formulation it provides for computing ΔOD. One limitation with this formulation is it does not account for subdued scaling effects in high OD samples due to competitive absorption.
 |
7 |
According to eq 7b, the ratio 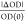 is a useful measure of saturation. Figure 6 plots this ratio
for both models as a function of F̃/Fsat. Not surprisingly, |ΔOD|/OD(0) is
linear in the weak fluence limit but appears increasingly nonlinear
at higher fluences. Generally speaking,
is a useful measure of saturation. Figure 6 plots this ratio
for both models as a function of F̃/Fsat. Not surprisingly, |ΔOD|/OD(0) is
linear in the weak fluence limit but appears increasingly nonlinear
at higher fluences. Generally speaking, 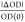 ≳ 0.3 appears unlikely for multilevel systems because up-pumping
will push population from ν = 1 into higher states to a point
where |ΔOD| of the 0–1 will actually decrease with additional
fluence.45 However, one way to avoid up-pumping
is positively chirping the pump pulse.46 Alternatively, when a pulse shaper is available, applying a mask
that removes pump light coincident with the 1–2 transition
(e.g., a sufficiently narrow Gaussian mask centered at the 0–1
transition, or a hole centered at the 1–2 band) prevents up-pumping
by disabling excitation to ν = 2 and higher.
≳ 0.3 appears unlikely for multilevel systems because up-pumping
will push population from ν = 1 into higher states to a point
where |ΔOD| of the 0–1 will actually decrease with additional
fluence.45 However, one way to avoid up-pumping
is positively chirping the pump pulse.46 Alternatively, when a pulse shaper is available, applying a mask
that removes pump light coincident with the 1–2 transition
(e.g., a sufficiently narrow Gaussian mask centered at the 0–1
transition, or a hole centered at the 1–2 band) prevents up-pumping
by disabling excitation to ν = 2 and higher.
Figure 6.

Pump–probe signal as a function of resonant fluence for a linear absorber and a saturable absorber. OD(0) is the linear absorbance measured in the weak fluence limit.
Sampling a few examples from literature, data reported
by both
Witte et al. for W(CO)6 in a regular pump–probe
experiment45 and Morichika et al. for plasmonic
enhancement of W(CO)6 in reflection mode,47 both equate to a saturable limit of  ≲ 0.3, which is attributed to the
up-pumping seen in both reports. Another convenient property of this
ratio is that
≲ 0.3, which is attributed to the
up-pumping seen in both reports. Another convenient property of this
ratio is that 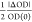 should approximate the factional change
in population, which appears confirmed by the data published by Witte
et al.45 Another interesting example is
azide in FDH, where
should approximate the factional change
in population, which appears confirmed by the data published by Witte
et al.45 Another interesting example is
azide in FDH, where 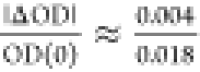 = 0.22, which implies a near-saturated
response in these experiments.48−50 While the effects of saturation
on measuring spectral diffusion have not been studied, for measurements
in the (τ1, TW, ω3) domain, it is unlikely that a 10% nonlinearity is going
to change spectral diffusion in any meaningful way.
= 0.22, which implies a near-saturated
response in these experiments.48−50 While the effects of saturation
on measuring spectral diffusion have not been studied, for measurements
in the (τ1, TW, ω3) domain, it is unlikely that a 10% nonlinearity is going
to change spectral diffusion in any meaningful way.
These examples
show that strong chromophores such as azide and
metal carbonyls have either already or nearly reached a saturation
point on standard 2D IR apparatuses and further increases in pump
fluence are unlikely to improve 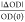 . On the other hand, some room remains for
fluence enhancement on weaker chromophores. For example, our recent
reports with MeSCN (ε ≈ 150 M–1 cm–1) have ratios of
. On the other hand, some room remains for
fluence enhancement on weaker chromophores. For example, our recent
reports with MeSCN (ε ≈ 150 M–1 cm–1) have ratios of  ≈ 0.01 and 0.05,51,52 which leaves room for ∼20× and ∼4× enhancement
by increasing the pump fluence.
≈ 0.01 and 0.05,51,52 which leaves room for ∼20× and ∼4× enhancement
by increasing the pump fluence.
Finally, it is worth noting the existence of Rabi oscillations. Upon excitation by a coherent light source, a two-level system well-isolated from dephasing and relaxation processes will oscillate in population between the ground and excited state as a function of fluence. The frequency of oscillation, known as the Rabi frequency ωR, is proportional to the product of the electric field amplitude and the transition dipole moment. Although the saturable absorber model assumes an incoherent pump source, the model is still appropriate for coherent light sources when ωR is smaller than the homogeneous line width because dephasing destroys the Rabi oscillation before it can significantly manifest.41
4. Saturable Competitive Absorber
The models reviewed up to this point are suitable for either high optical density or high fluence, but neither model is appropriate under both conditions. Here we derive a model suitable under both conditions which we call the saturable competitive absorber. The trick here is finding an expression that computes the change in population accounting for both saturation and high optical density. For the competitive absorber model, the change in ground state analyte from excitation by the pump beam at point z in the sample is Δca/ca = (1/2)(F̃/Fsat)10–OD where F̃ is the resonant fluence prior to entering the sample. This fails at high fluence because (F̃/Fsat)10–OD > 1 implies population inversion. To account for saturation, we replace the quantities F̃/Fsat and OD with their saturable counterparts from eqs 7a and 7b. Hence, Δca/ca = (1/2)(1 – f)10–f ·OD, where f = exp(−F̃/Fsat). This is consistent with the competitive absorber model in the low fluence limit, converging to (1/2)(F̃/Fsat)10–OD, and the saturable absorber model in the high fluence limit, converging to 1/2. Then, following eq 3, we compute ΔOD by integrating Δca = (ca/2)(1 – f)10–fcaεaz over z and multiplying by −2εa, which gives eq 8a. This formula converges to all expected limits: −ODa for F̃/Fsat ≫ 1, eq 6a for F̃/Fsat ≪ 1, eq 7b for ODT ≪ 1, and eq 7c for F̃/Fsat ≪ 1 and ODT ≪ 1.
 |
8 |
Figure 7 plots ΔOD as a function of optical density and fluence. The contours show that simultaneous increases in both optical density and fluence increase ΔOD, without an asymptote along the equidistant line. Higher fluence leads to more excitation, particularly toward the back end of high OD samples. Likewise, high optical density leads to more excitation. When possible, increasing both fluence and optical density could be a very potent strategy for improving signal, with the upper limit on signal only limited by the optical density of the sample. However, this could be problematic given line shape distortions are known to occur at high optical densities.31,32
Figure 7.
Contour plot of signal versus optical density and fluence for the saturable competitive absorber.
5. Conventional Methods of Enhancement
Analysis of the competitive absorber model in eq 6a shows that the pump–probe signal depends on several different variables. We refer to conventional methods of enhancement as any strategy that targets these variables. Table 1 summarizes how ΔOD scales with respect to each of these variables for the two limiting cases of weak absorption (OD < 0.1) and strong absorption (OD > 0.5). The section reviews each variable dependence in detail and discusses practical and theoretical limits related to signal enhancement.
Table 1. Scaling Dependencies of the Pump-Probe Signal (ΔOD) for the Competitive Absorber Model in the Low Fluence Limita.
| Low OD (<0.1)b | High OD (>0.5) | |
|---|---|---|
Inverse Beam Waist (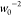
|
Quadratic | Quadratic |
| Analyte Molar Absorptivity(a) | Quadratic | Linear |
| Pump Energy (Resonant Bandwidth) | Linear | Linear |
| Concentration of Analyte(a) | Linear | Bounded-Exponential |
| Path Length(T) | Linear | Bounded-Exponential |
| Solvent Molar Absorptivity | Hyperbolic Decay | Hyperbolic Decay |
5.1. Decrease the Beam Waist/Increase the Mode Size
Equation 6a shows that ΔOD
scales as 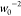 , and therefore decreasing the beam waist
, and therefore decreasing the beam waist  at the focus increases the pump–probe
signal quadratically. Assuming a Gaussian beam, Siegman approximates
the beam waist radius as eq 9 where f is the focal length, λ is
the center wavelength, and D is the diameter of aperture
at which 99% of light transmits just prior to reaching the focusing
optic.41 For example, using f = 50 mm parabolic mirrors, D = 20 mm irises, and
λ = 5 μm light, eq 9 expects a beam waist radius of
at the focus increases the pump–probe
signal quadratically. Assuming a Gaussian beam, Siegman approximates
the beam waist radius as eq 9 where f is the focal length, λ is
the center wavelength, and D is the diameter of aperture
at which 99% of light transmits just prior to reaching the focusing
optic.41 For example, using f = 50 mm parabolic mirrors, D = 20 mm irises, and
λ = 5 μm light, eq 9 expects a beam waist radius of 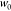 ≈ 12.5 μm. According to eq 9, there are only two ways
of decreasing the beam waist
≈ 12.5 μm. According to eq 9, there are only two ways
of decreasing the beam waist 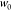 for a given wavelength: either reduce the
focal length or increase the diameter of the mode and aperture of
optics. These two quantities often limit each other through what is
known as the “f-number” of an optic.
for a given wavelength: either reduce the
focal length or increase the diameter of the mode and aperture of
optics. These two quantities often limit each other through what is
known as the “f-number” of an optic.
| 9 |
| 10 |
The f-number
(f/#), defined in eq 10, is equal to the focal length divided by the diameter
of the focusing optic. Note that the diameter of the optic does not
necessarily equal the aperture diameter D at which
99% of light transmits, but the smallest possible beam waist 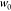 does appear when the two quantities are
equal. Assuming the two are equal, then according to eq 9, for a given wavelength, the only
way to reduce the beam waist
does appear when the two quantities are
equal. Assuming the two are equal, then according to eq 9, for a given wavelength, the only
way to reduce the beam waist 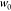 is to find an optic with a smaller f-number. Several vendors sell f/1 off-axis
parabolic mirrors and f/0.5 ZnSe aspherical lenses.
However, faster optics are unlikely due to manufacturing challenges.
is to find an optic with a smaller f-number. Several vendors sell f/1 off-axis
parabolic mirrors and f/0.5 ZnSe aspherical lenses.
However, faster optics are unlikely due to manufacturing challenges.
Regardless of the optic chosen, it is important to match the aperture
diameter D with the optic’s diameter of aperture
to achieve the smallest possible beam waist 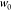 . We reiterate this point because, in our
experience, the output beams from OPA’s may have angular beam
spread which might require a telescope to collimate. Furthermore,
as later discussed in section 5.3, all “collimated” beams eventually diverge
after a finite distance which may be significant after a couple meters
of propagation. On the other hand, if a beam reaches the focusing
element with an aperture diameter D smaller than
the optic diameter, then eq 9 says that the beam waist
. We reiterate this point because, in our
experience, the output beams from OPA’s may have angular beam
spread which might require a telescope to collimate. Furthermore,
as later discussed in section 5.3, all “collimated” beams eventually diverge
after a finite distance which may be significant after a couple meters
of propagation. On the other hand, if a beam reaches the focusing
element with an aperture diameter D smaller than
the optic diameter, then eq 9 says that the beam waist 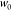 is unnecessarily large.
is unnecessarily large.
Note that eq 6a assumes matching mode sizes
between the pump and probe. Other factors that can inflate the beam
waist larger than predicted by eq 9 include spherical aberrations, wavefront distortion,
and anything that might affect the beam quality factor (M2).41,53 Spherical aberrations are eliminated
by replacing spherical optics with aspherical lenses or parabolic
mirrors. Nanometer deviations in optical surfaces imprint wavefront
distortions on laser beams. Manufacturers characterize surface flatness
using a monochromatic reference, e.g., λ/4, where λ is
usually 633 nm. Common values for surface flatness range from λ/2
≈ 300 nm to λ/10 ≈ 60 nm. It is important to recognize
that wavefront errors accumulate over optics, e.g., 16 reflections
off λ/2 mirrors add in quadrature to 300 nm ×  = 1.2 μm. Therefore, reducing the
number of optics, choosing optics with high surface flatness, and
keeping optics clean are simple strategies to mitigate wavefront distortion.
= 1.2 μm. Therefore, reducing the
number of optics, choosing optics with high surface flatness, and
keeping optics clean are simple strategies to mitigate wavefront distortion.
5.2. Choose an Analyte with a High Molar Absorptivity
Equation 6a shows that ΔOD scales quadratically with molar absorptivity εa in the weak absorption limit and linearly in the high absorption limit. In terms of general site-specific labels in proteins, the IR transparency window of water effectively limits the available chromophores to those listed in Table 2. See refs (2), (54), and (55) for further review on site-specific infrared labels. While azides are brighter than nitriles, their short vibrational lifetimes (∼1 ps) seriously limit their ability to report spectral diffusion.
Table 2. Site-Specific Infrared Labels Suitable for 2D IR Spectroscopy of Proteins, Including Molar Absorptivity εa and Vibrational Lifetime T1.
| Class | Unnatural Amino Acid | Isotopologue | Frequency (cm–1)c | εa (M–1 cm–1) | T1d (ps) | Ref |
|---|---|---|---|---|---|---|
| nitriles | 4-cyanophenylalanine | Phe-12C14N | ∼2237 | ∼180–220 | ∼4.1 | (56−58) |
| Phe-12C15N | ∼2210 | ∼0.9–2.2 | (56), (59) | |||
| Phe-13C14N | ∼2184 | ∼3.4–5.0 | (56), (59) | |||
| Phe-13C15Na | ∼2156 | ∼8–11 | (56), (58) | |||
| 4-cyanoselenophenylalanine | Phe-Se12C14Na | ∼2160 | ∼65 | ∼76 | (59) | |
| cyanocysteine | Cys-12C14N | ∼2150–2180 | ∼35–120 | ∼30–60 | (60−62) | |
| 5-cyanotryptophan | Trp-12C14N | ∼2210–2240 | ∼160 | ∼1.4 | (63), (64) | |
| azides | azidohomoalanine | Ala-14N3 | ∼2100–2140 | ∼300–400 | ∼1.0 | (65) |
| 4-azidophenylalanine | Phe-14N3b | ∼2120–2130 | ∼500–620 | ∼0.7 | (66), (67) | |
| 4-azidomethylphenylalanine | Phe-CH214N3a | ∼2110 | ∼310–370 | N/A | (67) |
Notably more expensive than other UAAs on this table and/or requires considerable synthesis.
Photoreactive with UVC light.
Bold entries: May require purging of CO2 to avoid chromatic dispersion.
Bold entries: Short vibrational lifetime limits spectral diffusion measurements.
5.3. Increase the Pump Energy
In the low fluence limit, eq 6a shows that ΔOD scales linearly with the energy per pump pulse, or more precisely, the spectral energy resonant with the analyte line shape. One approach to increasing pump energy is by improving the efficiency of mid-IR parametric amplifiers. An optical parametric amplifier works by splitting high frequency pump photons (ω3) into two lower energy photons, commonly referred to as the signal (ω2) and idler (ω1) where ω3 = ω2 + ω1.68 The photon conversion efficiency of an OPA, defined in eq 11, is the fraction of pump light split into lower energy fields. Given an input pump power P3(in) and input seed power much smaller than either the output signal power P2(out) or output idler power P1(out), the conversion efficiency is well-approximated by either of the latter two equalities in eq 11. Figure 8 illustrates typical photon conversion efficiency values for BBO and AgGaS2.69 Notice that power amplification stages, e.g., second pass in BBO or DFG in AgGaS2, tend to run upward of ∼30% while seed amplification stages, e.g., first pass in BBO, tend to run at ∼10%. Overall, the gross output power primarily comes from the power amplification stages (2nd pass in BBO and DFG in AgGaS2), so the total mid-IR photon conversion efficiency relative to the input Ti:sapphire pump is ∼(0.28)2 = 8%, which is typical in our experience (∼30 mW of mid-IR from ∼2200 mW of second pass pump). Beyond Ti:sapphire, some 2D IR groups have acquired 100 kHz Yb lasers with remarkable performance and applications.70−75
 |
11 |
Figure 8.
Typical photon conversion efficiency measured in near-IR BBO and mid-IR AgGaS2.
Note that ΔOD does not necessarily scale
with the power but,
rather, the energy or fluence per pump pulse. The distinction is significant
from an SNR standpoint when comparing lasers with equal average power
at different repetition rates. Consider, for example, a hypothetical
comparison between a 1 kHz and a 100 kHz laser with identical average
output powers. The 1 kHz laser yields a 100× larger signal owing
to a larger pulse energy. On the other hand, the 100 kHz laser reduces
noise first by a factor of 10× from 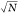 averaging, then by another factor of ∼10×
from reduction in shot-to-shot fluctuations associated with 1/f noise. Overall, the two lasers should exhibit comparable
values of SNR. In practice, the comparison is more complicated after
factoring in specifications known for commercially available lasers,
such as slightly higher average powers for 100 kHz systems, or implementation
of calibrated referencing schemes known to remove virtually all shot-to-shot
noise.51,76,77 And, finally,
we note that only the fraction of the frequency spectrum that is resonant
with the analyte line shape contributes to pump–probe signal,
which is important when comparing two different light sources with
different spectral bandwidths.
averaging, then by another factor of ∼10×
from reduction in shot-to-shot fluctuations associated with 1/f noise. Overall, the two lasers should exhibit comparable
values of SNR. In practice, the comparison is more complicated after
factoring in specifications known for commercially available lasers,
such as slightly higher average powers for 100 kHz systems, or implementation
of calibrated referencing schemes known to remove virtually all shot-to-shot
noise.51,76,77 And, finally,
we note that only the fraction of the frequency spectrum that is resonant
with the analyte line shape contributes to pump–probe signal,
which is important when comparing two different light sources with
different spectral bandwidths.
There are several sources of attenuation following the mid-IR light source, some of which are manageable. First is compounded reflection losses. For example, assuming gold mirror reflectivities of 98% for s-polarized light and 95% for p-polarized light, 15 reflections would accumulate 1 – 0.9815 = 26% power loss for s-polarized light and 1 – 0.9615 = 46% power loss for p-polarized light. Pulse shapers are known to attenuate pump light by 65–80%, depending on the circumstances. Taken altogether, for a typical 2D IR pulse shaping apparatus, one should expect the pump power at the sample to be 5–20% of the initial power measured at the mid-IR source.
The last source of attenuation worth noting is accidental divergence and/or long-range diffraction inherent to laser beams. Many 2D IR apparatuses propagate ∼5–8 m between the mid-IR source and sample cell. At these path lengths, small perturbations in the divergence angle might easily lead to major aperture losses in pump light. Furthermore, the diameter of the mode must be large enough to ensure the collimated range (twice the Rayleigh length) of the mode is long enough to reach the lens or parabolic mirror that focuses light into the sample. Equation 12 provides the formula for the collimated range of a Gaussian beam, borrowed from Siegman.41 Here λ is wavelength and D is the diameter of aperture for which 99% of light transmits at the two ends of the columnated range. For example, a 5 μm wavelength beam with diameter of aperture D = 10 mm can propagate 6 m before diverging larger than 10 mm again.
| 12 |
5.4. Increase the Analyte Concentration
Equation 6a shows that ΔOD scales linearly with ca in the weak absorption limit or bounded-exponentially in the strong absorption limit. For proteins incorporating a single, site-specific residue as an analyte reporter, the absolute upper limit for concentration is equal to the inverse volume of a single monomer of the protein. By estimating the volume of a protein from its molecule mass and density,78 and ignoring excess volume occupied by water between protein molecules, the maximum concentration of a crystalline protein in units of molarity is approximately equal to 1.37 (M·kDa)/m(kDa), where m is the protein mass in units of kDa. If one then assumes the void between crystalline molecules is ∼1/3 of the crystal volume, then 1.37 becomes 1 and a very handy rule of thumb is that the maximum concentration of a crystalline protein in molarity is equal to the inverse mass in kDa. A typical protein monomer weighs anywhere from 10 to 50 kDa, which suggests an upper limit of ca = 20–100 mM for crystalline protein. In practice, proteins start nucleating well before that point, which means the upper limit for a nonaggregate, solution phase measurement is somewhere between 0.1 and 10 mM, depending on the protein and experimental conditions.
5.5. Optimize the Path Length
Equation 6a shows that ΔOD scales linearly
with  in the weak absorption limit or bounded-exponentially
in the strong absorption limit. However, this does not account for
the overlap geometry. The Rayleigh length defines the distance at
which the pump intensity falls to 1/2 the peak intensity, and therefore
excitation of the analyte becomes negligible beyond a path length
of
in the weak absorption limit or bounded-exponentially
in the strong absorption limit. However, this does not account for
the overlap geometry. The Rayleigh length defines the distance at
which the pump intensity falls to 1/2 the peak intensity, and therefore
excitation of the analyte becomes negligible beyond a path length
of 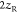 . Furthermore, the geometry of overlapping
pump and probe at a ∼30° angle shortens the observable
path length of excited analyte by a factor of 2. Hence, the Rayleigh
length
. Furthermore, the geometry of overlapping
pump and probe at a ∼30° angle shortens the observable
path length of excited analyte by a factor of 2. Hence, the Rayleigh
length 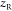 sets an upper limit signal dependency on
path length (Figure 9). For convenience, eq 13 provides a formula for computing the optimal path length in terms
of the beam waist and wavelength,41 or
alternatively, in terms of the focal length f and
aperture diameter D assuming M2 = 1. For example, given
sets an upper limit signal dependency on
path length (Figure 9). For convenience, eq 13 provides a formula for computing the optimal path length in terms
of the beam waist and wavelength,41 or
alternatively, in terms of the focal length f and
aperture diameter D assuming M2 = 1. For example, given  = 12 μm and λ = 4.7 μm, eq 13 estimates a Rayleigh
length of
= 12 μm and λ = 4.7 μm, eq 13 estimates a Rayleigh
length of 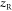 ≈ 100 μm.
≈ 100 μm.
| 13 |
Figure 9.
Plot illustrating the effective path length of the excitation volume relative to the Rayleigh length.
In practice, one may find that the optimal path
length is significantly
less than 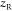 depending on the optics, beam geometry
and solvent. In the case of an absorbing solvent, one must consider
the intensity of probe or local-oscillator light necessary to fill
the well depth of the detector, which might further limit the path
length. Interestingly, if we assume
depending on the optics, beam geometry
and solvent. In the case of an absorbing solvent, one must consider
the intensity of probe or local-oscillator light necessary to fill
the well depth of the detector, which might further limit the path
length. Interestingly, if we assume 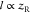 , then by eq 13
, then by eq 13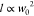 . In the limit of weak absorption, Table 1 shows
. In the limit of weak absorption, Table 1 shows 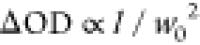 . Therefore, one should expect ΔOD
does not depend on the beam waist when ODT ≪ 1 and
. Therefore, one should expect ΔOD
does not depend on the beam waist when ODT ≪ 1 and 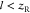 . In other words, given ODT ≪
1 and
. In other words, given ODT ≪
1 and 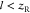 , ΔOD should not change with focusing
assuming the path length is proportional to the Rayleigh length
, ΔOD should not change with focusing
assuming the path length is proportional to the Rayleigh length 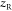 . Stated another way, ΔOD merely depends
on the energy of the pump pulse rather than the physical
dimensions of the observation volume, which is more intuitive. In
practice, independence of ΔOD on the beam waist is unlikely
merely because most samples have significant absorption from either
the analyte or solvent. In moderate to strongly absorbing samples,
the dependence of ΔOD on the inverse beam waist should be sublinear
assuming an optimized path length.
. Stated another way, ΔOD merely depends
on the energy of the pump pulse rather than the physical
dimensions of the observation volume, which is more intuitive. In
practice, independence of ΔOD on the beam waist is unlikely
merely because most samples have significant absorption from either
the analyte or solvent. In moderate to strongly absorbing samples,
the dependence of ΔOD on the inverse beam waist should be sublinear
assuming an optimized path length.
5.6. Choose a Solvent with a Low Absorptivity
The numerator of eq 6a scales bounded-exponentially
with the solvent absorptivity εscs and linearly in the denominator, the net effect approximating
a hyperbolic decay. Figure 10 displays ΔOD versus path length for varying values
of solvent absorptivity εscs, with ΔOD normalized to the Rayleigh length value for
easier assessment. Stars denote points at which 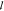 = 1/εscs.
The results show that signal reaches 90% or more of the asymptotic
limit at path lengths equal to the inverse absorptivity of the solvent.
More generally, extending path lengths longer than ODT =
1 will yield diminishing gains because additional excitation is negligible
beyond 90% attenuation of the pump beam. The necessity for low solvent
molar absorptivity often limits the measurable frequency range for
dilute analytes dissolved in water to between 2000 and 2600 cm–1. In that region the water bend+libration combination
band peaks at 2100 cm–1 with εs ≈ 3.1 M–1 cm–1,79 corresponding to εscs ≈ 170 cm–1. In that
region the optimal path length for a dilute analyte would be ∼60
μm.
= 1/εscs.
The results show that signal reaches 90% or more of the asymptotic
limit at path lengths equal to the inverse absorptivity of the solvent.
More generally, extending path lengths longer than ODT =
1 will yield diminishing gains because additional excitation is negligible
beyond 90% attenuation of the pump beam. The necessity for low solvent
molar absorptivity often limits the measurable frequency range for
dilute analytes dissolved in water to between 2000 and 2600 cm–1. In that region the water bend+libration combination
band peaks at 2100 cm–1 with εs ≈ 3.1 M–1 cm–1,79 corresponding to εscs ≈ 170 cm–1. In that
region the optimal path length for a dilute analyte would be ∼60
μm.
Figure 10.
Plot of ΔOD versus path length for various solvent absorptivities. Asterisks identify points at which the path length is equal to the inverse solvent absorptivity.
6. Enhancement by Local Oscillator Attenuation
Recognizing ΔOD as a heterodyned signal enables a clever
form of signal enhancement by interference of light. From a theoretical
standpoint, spectroscopists understand pump–probe signals more
accurately as the third-order nonlinear response of the sample. The
electric field of the third order response is Esig ∝ χ(3)IpumpEprobe where χ(3) is
the third-order susceptibility of the sample, Ipump is the intensity of the pump, and 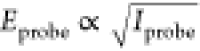 is the electric field of the probe.80 At the detector, the nonlinear signal interferes
with the local-oscillator field ELO such
that the total intensity is
is the electric field of the probe.80 At the detector, the nonlinear signal interferes
with the local-oscillator field ELO such
that the total intensity is 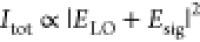 ∝
∝ 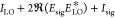 ≈
≈ 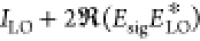 . Then ΔOD =
. Then ΔOD =  =
= 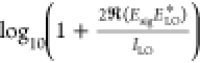 ≈
≈ 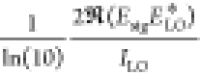 and using
and using 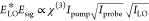 , we find ΔOD in eq 14.
, we find ΔOD in eq 14.
| 14 |
Therefore, accounting
for local oscillator attenuation just requires
multiplying ΔOD by 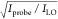 . For the pump–probe geometry, Iprobe = ILO restricts
that factor to
. For the pump–probe geometry, Iprobe = ILO restricts
that factor to 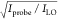 = 1. In four-wave-mixing, this factor is
variable and enables enhancement of ΔOD when using equally strong
pump and probe fields with a weak local oscillator field. However,
it is possible to use this enhancement in the pump–probe geometry
if one attenuates the probe after the sample where
the probe beam then acts as the local oscillator. This strategy has
been implemented in a variety of ways which work by selectively attenuating
the local-oscillator field faster than the signal field after the
sample, including a simple postsample polarizer,81 a Sagnac interferometer,82 or
some form of attenuated reflection.83 In
practice, the primary limitation with local-oscillator attenuation
is the heterodyned signal reaches a value too small for the well depth
of a detector which leads to increasing noise.
= 1. In four-wave-mixing, this factor is
variable and enables enhancement of ΔOD when using equally strong
pump and probe fields with a weak local oscillator field. However,
it is possible to use this enhancement in the pump–probe geometry
if one attenuates the probe after the sample where
the probe beam then acts as the local oscillator. This strategy has
been implemented in a variety of ways which work by selectively attenuating
the local-oscillator field faster than the signal field after the
sample, including a simple postsample polarizer,81 a Sagnac interferometer,82 or
some form of attenuated reflection.83 In
practice, the primary limitation with local-oscillator attenuation
is the heterodyned signal reaches a value too small for the well depth
of a detector which leads to increasing noise.
7. Enhancement by Plasmonics
Surface enhanced spectroscopies work by massively enhancing the electric field around the surface of small metal structures (nm to μm). The field enhancement arises from the collective oscillation of free metal electrons in response to an incident laser beam while trapped in a metal structure comparable in size to the wavelength of light. The term “plasmon”, which refers to the quantization of the oscillating electrons, stems from the observation that conduction band electrons are well-modeled as a confined gas but act as charged particles in the presence of an electric field and, hence, behave something like plasma.
Spectroscopists understand linear spectroscopy as two consecutive interactions between an oscillator and light: (1) incident light excites the oscillator, and in response, (2) the oscillator emits a “signal” that destructively interferes with the incident light, which appears as absorption.11 Plasmonic enhancement of linear spectra consists of four interactions: (1) incident light excites a surface plasmon on the metal structure, (2) the near-field of the surface plasmon excites the oscillator, (3) the oscillator emits a signal that interferes with the surface plasmon (known as “back action”), and (4) the surface plasmon, driven partially by the back action, emits a signal that interferes with the incident light. Though other interaction pathways among the incident light, plasmon, and oscillator do occur, the magnitude of enhanced signal from this four-step pathway is largest by at least an order of magnitude.84 The interaction pathway for 2D IR similarly involves a plasmon excitation and subsequent near-field interaction with the oscillator for each of the three incident fields, followed by the back action of the third-order response onto the plasmon.85,86 Plasmonic enhancement does come at the cost of scattering and absorption of the incident fields, and the range of enhancement only extends a few tens of nanometers from the surface into the sample.87−89 That being said, the enhancements in signal can be tremendous for analytes near enough to the surface.
In 2013, Donaldson and Hamm first reported a 102 enhancement of 2D IR signal from thiol-functionalized gold nanoparticles.90 In 2015, Selig, Siffels and Rezus reported a ∼104 enhancement of 2D IR signal using randomly spaced micron-long gold nanoantennas, lithographically deposited on CaF2.91 Shortly thereafter, Kraak and Hamm found that sputtering a 1–3 nm gold layer on the surface of an ATR prism enhanced the 2D IR signal of monolayers by 50–450 fold.92,93 Since then, additional studies have been reported on regularly spaced nanoantennas94−97 and trimer nanoantennas98,99 yielding 104–105 enhancement. Other studies have shown that combining plasmonic enhancement with an attenuated reflection geometry (SEAR-2D IR) enables an added mechanism for enhancement by means of local oscillator attenuation.47,86,100,101 In fact, Morichika et al. reported a 107 enhancement of 2D IR signal by detecting the back scattering off of gold nanoantenna arrays.47 With the exception of Donaldson and Hamm’s gold nanoparticles, virtually all surface enhanced 2D IR experiments reported to date are of thin film samples where the surface density of chromophores is comparatively high relative to mM bulk samples. Unfortunately for bulk samples, the enhancement only extends a few tens of nanometers from the surface into the sample,87−89 which effectively reduces the path length of bulk measurements by a few orders of magnitude. This questions the applicability of plasmonics to conventional bulk systems, particularly given the lack of demonstration thus far.
One complication introduced by plasmonic enhancement in both linear and nonlinear measurements is a Fano-like line shape.85,102 The origin of this phenomenon is from two complementary phase delays: the first is acquired between the incident field that excites the plasmon and the near-field response that excites the oscillator; the second is acquired by the complement back action process.84−86 This effect is prominent when the size of the metal particle is comparable to the wavelength of light, such as in micron sized nanoantennas,47,84,85,91,94,96,99,103 but appears negligible in reports using 1–3 nm gold particles deposited by sputtering.92,93,101 As pointed out by Chuntonov and Rubtsov, the plasmonic Fano resonance only occurs along the probe axis and is well-modeled by classical electromagnetic theory.85 This can be explained by the 2D IR signal carrying a ±ϕ1 ∓ ϕ2 + ϕ3 phase dependence such that the phase delay cancels along the pump axis but remains along the probe axis.85,86 In fact, Tek and Hamm have shown how the Fano interference can be corrected by simply applying a zero-order phase shift along the probe axis.104
One unanswered question regarding plasmonic enhancement is whether signal enhancement comes at the cost of enhanced temperature jump of the surroundings from absorption of the pump. Since plasmonic enhancement would apply to the pump field as well, one might expect that solvents such as water should be subjected to enhanced absorption of pump light per unit volume near the surface, which would cause a larger jump in solvent temperature as discussed below in section 8. More careful measurements of surface enhanced IR spectroscopy on aqueous proteins, particularly at the high intensities required by 2D IR, are needed to quantify this effect.
8. Temperature Jump Consideration
Signal enhancement by higher pump fluence is an attractive strategy for weaker chromophores. However, in systems with an absorbing solvent, this presents a dilemma where enhancing signal by increasing fluence also increases the amount of light absorbed by the solvent and thereby leads to an abrupt change in temperature of the solvent surrounding the analyte. The abrupt change in temperature induced by the pump pulse(s), known as the temperature jump, manifests as fluence and time-delay dependent artifacts in pump–probe spectra as a result of temperature dependent properties such as the index of refraction, dynamics, and other line shape features more generally.71,105
If the absorptivity of the solvent is much larger than the
analyte
(εscs ≫ εaca) and εs is
approximately constant throughout the pump spectrum, e.g., water at
2100 cm–1, then the heat absorbed by the solvent
is equal to the energy of the pump pulse times the fraction of light
absorbed by the solvent, q = Epump(1 – 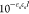 ). The temperature jump, ΔT, following vibrational relaxation of the absorbed light
is related to the specific heat capacity C and mass m of the solvent by q = mCΔT. The time scale of thermal diffusion out
of the excitation volume is on the order of hundreds of microseconds
to milliseconds,106 so ΔT does not relax prior to the arrival of the probe pulse. Therefore, m = ρVex where ρ
is the density of the solvent and
). The temperature jump, ΔT, following vibrational relaxation of the absorbed light
is related to the specific heat capacity C and mass m of the solvent by q = mCΔT. The time scale of thermal diffusion out
of the excitation volume is on the order of hundreds of microseconds
to milliseconds,106 so ΔT does not relax prior to the arrival of the probe pulse. Therefore, m = ρVex where ρ
is the density of the solvent and 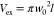 is the pump excitation volume. These expressions
combine to form an estimate of ΔT due to absorption
of the pump light by the solvent in eq 15.
is the pump excitation volume. These expressions
combine to form an estimate of ΔT due to absorption
of the pump light by the solvent in eq 15.
| 15 |
Comparing eqs 6a and 15, it is notable
that ΔOD and ΔT scale
identically in terms of the inverse beam waist and pump energy, hence,
the trade-off between ΔOD and ΔT as a
function of pump fluence. Equation 15 assumes a flat top beam profile and uniform excitation
as a function of propagation depth. The fluence of a Gaussian beam
at r = 0 is about ∼2× higher than the average
fluence of the averaged flat top beam. Therefore, the maximum temperature
jump within the sample, located at the front of the sample and center
of the pump beam, is 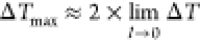 =
= 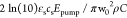 . It is possible to curb the temperature
jump by using a pulse shaper to band narrow the pump spectrum around
the analyte line shape, which reduces unnecessary absorption from
the solvent. Of course, band narrowing comes with a trade-off in time
resolution. As an example, consider the temperature jump of a dilute
cyano oscillator in an aqueous sample with Epump = 1 μJ, εs = 3.1 M–1 cm–1, cs = 55 M,
. It is possible to curb the temperature
jump by using a pulse shaper to band narrow the pump spectrum around
the analyte line shape, which reduces unnecessary absorption from
the solvent. Of course, band narrowing comes with a trade-off in time
resolution. As an example, consider the temperature jump of a dilute
cyano oscillator in an aqueous sample with Epump = 1 μJ, εs = 3.1 M–1 cm–1, cs = 55 M, 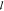 = 50 μm,
= 50 μm, 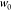 = 12.5 μm, ρ = 1 g/cm3, and C = 4.186 J/g·K yields ΔT ≈ 8 K.
= 12.5 μm, ρ = 1 g/cm3, and C = 4.186 J/g·K yields ΔT ≈ 8 K.
9. Summary
We have reviewed several different formulas for computing the absolute magnitude of pump–probe signal over a range of conditions known to complicate signal scaling laws. Figure 11 summarizes the various regimes in which each model is valid. The saturable competitive model is suitable in every case of fluence and optical density. In the limiting case of low (total) optical density, the model simplifies to the competitive absorber model. In the limiting case of low resonant fluence, the model simplifies to the saturable absorber model. And finally, in the limiting case of both low total optical density and low resonant fluence, the model simplifies to the linear absorber model.
Figure 11.
Four models of pump–probe signal under varying conditions of relative resonant fluence and total optical density. Quantities necessary to evaluate these formulas include the analyte optical density (ODa), total optical density (ODT), the fraction of pump fluence resonant with the analyte line shape (F̃), and the saturation fluence of the analyte (Fsat).
Evaluating these models requires knowledge of at least four experimental quantities, each of which we have reduced to some combination of the analyte molar absorptivity, concentration, path length, pulse energy, spectral bandwidth, line shape width, beam waist at focus, and the optical density of the solvent. We analyzed functional relationships between the pump–probe signal and these quantities and discussed practical limitations and trade-offs with respect to each. Several optical calculations were reviewed such as estimating the columnated range of a beam to identify the limit of propagation or the beam waist and Rayleigh length of a focused beam to estimate fluence and the maximum useful path length. We also reviewed other unconventional methods of increasing pump–probe signals, including various forms of local-oscillator attenuation and, more recently, plasmonic enhancement. Estimations of solvent heat absorption by the pump pulse suggest samples containing strongly absorbing solvents like water could have significant temperature jumps that may limit high fluence strategies including plasmonic enhancement.
Acknowledgments
The research in this publication was supported by funding from the National Institute of General Medical Sciences of the National Institutes of Health under award number R21GM143710. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Biographies

Kevin C. Robben is a postdoctoral scholar at the University of Iowa. He earned a B.S. in 2016 at Kansas State University and a Ph.D. in 2022 at the University of Iowa. His research focuses on the development and applications of two-dimensional infrared spectroscopy.

Christopher M. Cheatum is a Professor of Chemistry and Associate Dean in the College of Liberal Arts and Sciences at the University of Iowa. He earned a B.S. in Chemistry from the University of New Mexico in 1995 where he did undergraduate research with Mark Ondrias. He was a graduate student with F. Fleming Crim at the University of Wisconsin—Madison where he earned a Ph.D. in Physical Chemistry in 2001. He then did postdoctoral research in the group of Andrei Tokmakoff at MIT until 2003, when he started his independent career at the University of Iowa. His research focuses on the development and application of two-dimensional infrared spectroscopy, and his group’s primary interests have involved studies of enzyme dynamics.
The authors declare no competing financial interest.
Originally published ASAP May 18, 2023; Section 3 revised June 1, 2023.
References
- Ghosh A.; Ostrander J. S.; Zanni M. T. Watching Proteins Wiggle: Mapping Structures with Two Dimensional Infrared Spectroscopy. Chem. Rev. 2017, 117 (16), 10726–10759. 10.1021/acs.chemrev.6b00582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tumbic G. W.; Hossan M. Y.; Thielges M. C. Protein Dynamics by Two-Dimensional Infrared Spectroscopy. Annual Review of Analytical Chemistry 2021, 14, 299–321. 10.1146/annurev-anchem-091520-091009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuller F. D.; Ogilvie J. P. Experimental Implementations of Two-Dimensional Fourier Transform Electronic Spectroscopy. Annu. Rev. Phys. Chem. 2015, 66, 667–690. 10.1146/annurev-physchem-040513-103623. [DOI] [PubMed] [Google Scholar]
- Polli D.; Altoe P.; Weingart O.; Spillane K. M.; Manzoni C.; Brida D.; Tomasello G.; Orlandi G.; Kukura P.; Mathies R. A.; Garavelli M.; Cerullo G. Conical intersection dynamics of the primary photoisomerization event in vision. Nature 2010, 467 (7314), 440–U88. 10.1038/nature09346. [DOI] [PubMed] [Google Scholar]
- Ruban A. V.; Berera R.; Ilioaia C.; van Stokkum I. H. M.; Kennis J. T. M.; Pascal A. A.; van Amerongen H.; Robert B.; Horton P.; van Grondelle R. Identification of a mechanism of photoprotective energy dissipation in higher plants. Nature 2007, 450 (7169), 575–U22. 10.1038/nature06262. [DOI] [PubMed] [Google Scholar]
- Crespo-Hernandez C. E.; Cohen B.; Kohler B. Base stacking controls excited-state dynamics in A-T DNA. Nature 2005, 436 (7054), 1141–1144. 10.1038/nature03933. [DOI] [PubMed] [Google Scholar]
- Gunter G.; Anappara A. A.; Hees J.; Sell A.; Biasiol G.; Sorba L.; De Liberato S.; Ciuti C.; Tredicucci A.; Leitenstorfer A.; Huber R. Sub-cycle switch-on of ultrastrong light-matter interaction. Nature 2009, 458 (7235), 178–181. 10.1038/nature07838. [DOI] [PubMed] [Google Scholar]
- Klimov V. I.; Ivanov S. A.; Nanda J.; Achermann M.; Bezel I.; McGuire J. A.; Piryatinski A. Single-exciton optical gain in semiconductor nanocrystals. Nature 2007, 447 (7143), 441–446. 10.1038/nature05839. [DOI] [PubMed] [Google Scholar]
- Wu K.; Chen J.; McBride J. R.; Lian T. Efficient hot-electron transfer by a plasmon-induced interfacial charge-transfer transition. Science 2015, 349 (6248), 632–635. 10.1126/science.aac5443. [DOI] [PubMed] [Google Scholar]
- Gelinas S.; Rao A.; Kumar A.; Smith S. L.; Chin A. W.; Clark J.; van der Poll T. S.; Bazan G. C.; Friend R. H. Ultrafast Long-Range Charge Separation in Organic Semiconductor Photovoltaic Diodes. Science 2014, 343 (6170), 512–516. 10.1126/science.1246249. [DOI] [PubMed] [Google Scholar]
- Hamm P.; Zanni M. T.. Concepts and methods of 2d infrared spectroscopy; Cambridge University Press: Cambridge, New York, 2011; p ix, 286 pp. [Google Scholar]
- Chung H. S.; Ganim Z.; Smith A. W.; Jones K. C.; Tokmakoff A. Transient 2D IR spectroscopy of ubiquitin unfolding dynamics. Biophys. J. 2007, 104, 207a–207a. 10.1073/pnas.0700959104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strasfeld D. B.; Ling Y. L.; Shim S. H.; Zanni M. T. Tracking fiber formation in human islet amyloid polypeptide with automated 2D-IR Spectroscopy. J. Am. Chem. Soc. 2008, 130 (21), 6698. 10.1021/ja801483n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim S. H.; Gupta R.; Ling Y. L.; Strasfeld D. B.; Raleigh D. P.; Zanni M. T. Two-dimensional IR spectroscopy and isotope labeling defines the pathway of amyloid formation with residue-specific resolution. P Natl. Acad. Sci. USA 2009, 106 (16), 6614–6619. 10.1073/pnas.0805957106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh A.; Qiu J.; DeGrado W. F.; Hochstrasser R. M. Tidal surge in the M2 proton channel, sensed by 2D IR spectroscopy. P Natl. Acad. Sci. USA 2011, 108 (15), 6115–6120. 10.1073/pnas.1103027108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle D. A.; Cabral J. M.; Pfuetzner R. A.; Kuo A. L.; Gulbis J. M.; Cohen S. L.; Chait B. T.; MacKinnon R. The structure of the potassium channel: Molecular basis of K+ conduction and selectivity. Science 1998, 280 (5360), 69–77. 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- Ruetzel S.; Diekmann M.; Nuernberger P.; Walter C.; Engels B.; Brixner T. Multidimensional spectroscopy of photoreactivity. P Natl. Acad. Sci. USA 2014, 111 (13), 4764–4769. 10.1073/pnas.1323792111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahms F.; Fingerhut B. P.; Nibbering E. T. J.; Pines E.; Elsaesser T. Large-amplitude transfer motion of hydrated excess protons mapped by ultrafast 2D IR spectroscopy. Science 2017, 357 (6350), 491–494. 10.1126/science.aan5144. [DOI] [PubMed] [Google Scholar]
- Ramasesha K.; De Marco L.; Mandal A.; Tokmakoff A. Water vibrations have strongly mixed intra-and intermolecular character. Nature Chem. 2013, 5 (11), 935–940. 10.1038/nchem.1757. [DOI] [PubMed] [Google Scholar]
- Jansen T. L.; Knoester J. Waiting time dynamics in two-dimensional infrared spectroscopy. Acc. Chem. Res. 2009, 42 (9), 1405–11. 10.1021/ar900025a. [DOI] [PubMed] [Google Scholar]
- Engel G. S.; Calhoun T. R.; Read E. L.; Ahn T. K.; Mancal T.; Cheng Y. C.; Blankenship R. E.; Fleming G. R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446 (7137), 782–786. 10.1038/nature05678. [DOI] [PubMed] [Google Scholar]
- Calhoun T. R.; Ginsberg N. S.; Schlau-Cohen G. S.; Cheng Y. C.; Ballottari M.; Bassi R.; Fleming G. R. Quantum Coherence Enabled Determination of the Energy Landscape in Light-Harvesting Complex II. J. Phys. Chem. B 2009, 113 (51), 16291–16295. 10.1021/jp908300c. [DOI] [PubMed] [Google Scholar]
- Fuller F. D.; Pan J.; Gelzinis A.; Butkus V.; Senlik S. S.; Wilcox D. E.; Yocum C. F.; Valkunas L.; Abramavicius D.; Ogilvie J. P. Vibronic coherence in oxygenic photosynthesis. Nat. Chem. 2014, 6 (8), 706–711. 10.1038/nchem.2005. [DOI] [PubMed] [Google Scholar]
- Halpin A.; Johnson P. J. M.; Tempelaar R.; Murphy R. S.; Knoester J.; Jansen T. L. C.; Miller R. J. D. Two-dimensional spectroscopy of a molecular dimer unveils the effects of vibronic coupling on exciton coherences. Nat. Chem. 2014, 6 (3), 196–201. 10.1038/nchem.1834. [DOI] [PubMed] [Google Scholar]
- Thyrhaug E.; Tempelaar R.; Alcocer M. J. P.; Zidek K.; Bina D.; Knoester J.; Jansen T. L. C.; Zigmantas D. Identification and characterization of diverse coherences in the Fenna-Matthews-Olson complex. Nat. Chem. 2018, 10 (7), 780–786. 10.1038/s41557-018-0060-5. [DOI] [PubMed] [Google Scholar]
- Stone K. W.; Gundogdu K.; Turner D. B.; Li X. Q.; Cundiff S. T.; Nelson K. A. Two-Quantum 2D FT Electronic Spectroscopy of Biexcitons in GaAs Quantum Wells. Science 2009, 324 (5931), 1169–1173. 10.1126/science.1170274. [DOI] [PubMed] [Google Scholar]
- Maiuri M.; Garavelli M.; Cerullo G. Ultrafast Spectroscopy: State of the Art and Open Challenges. J. Am. Chem. Soc. 2020, 142 (1), 3–15. 10.1021/jacs.9b10533. [DOI] [PubMed] [Google Scholar]
- Friedberg R.; Hartmann S. R. Superradiant Damping and Absorption. Phys. Lett. A 1971, 37 (4), 285. 10.1016/0375-9601(71)90672-4. [DOI] [Google Scholar]
- Compaan A.; Abella I. D. Evidence of Strong Optical Super-Radiant Damping in Ruby. Phys. Rev. Lett. 1971, 27 (1), 23. 10.1103/PhysRevLett.27.23. [DOI] [Google Scholar]
- Belabas N.; Jonas D. M. Fourier algorithm for four-wave-mixing signals from optically dense systems with memory. Opt. Lett. 2004, 29 (15), 1811–1813. 10.1364/OL.29.001811. [DOI] [PubMed] [Google Scholar]
- Yetzbacher M. K.; Belabas N.; Kitney K. A.; Jonas D. M. Propagation, beam geometry, and detection distortions of peak shapes in two-dimensional Fourier transform spectra. J. Chem. Phys. 2007, 126 (4), 044511. 10.1063/1.2426337. [DOI] [PubMed] [Google Scholar]
- Spencer A. P.; Li H.; Cundiff S. T.; Jonas D. M. Pulse Propagation Effects in Optical 2D Fourier-Transform Spectroscopy: Theory. J. Phys. Chem. A 2015, 119 (17), 3936–3960. 10.1021/acs.jpca.5b00001. [DOI] [PubMed] [Google Scholar]
- Cho B.; Tiwari V.; Hill R. J.; Peters W. K.; Courtney T. L.; Spencer A. P.; Jonas D. M. Absolute Measurement of Femtosecond Pump-Probe Signal Strength. J. Phys. Chem. A 2013, 117 (29), 6332–6345. 10.1021/jp4019662. [DOI] [PubMed] [Google Scholar]
- Cho B.; Tiwari V.; Jonas D. M. Simultaneous All-Optical Determination of Molecular Concentration and Extinction Coefficient. Anal. Chem. 2013, 85 (11), 5514–5521. 10.1021/ac400656r. [DOI] [PubMed] [Google Scholar]
- Compaan A.; Lambert L. Q.; Abella I. D. Photon-Echo Dependence on Intensity. Phys. Rev. Lett. 1968, 20 (20), 1089. 10.1103/PhysRevLett.20.1089. [DOI] [Google Scholar]
- Robben K. C.Improvements in the Sensitivity of 2D IR Measurements by Edge-Pixel Referencing, Model Fitting, and Signal Enhancement Methods. Thesis; University of Iowa, 2022.
- Germann G. J.; Rakestraw D. J. Multiplex Spectroscopy - Determining the Transition Moments and Absolute Concentrations of Molecular-Species. Science 1994, 264 (5166), 1750–1753. 10.1126/science.264.5166.1750. [DOI] [PubMed] [Google Scholar]
- Grechko M.; Zanni M. T. Quantification of transition dipole strengths using 1D and 2D spectroscopy for the identification of molecular structures via exciton delocalization: Application to alpha-helices. J. Chem. Phys. 2012, 137 (18), 184202. 10.1063/1.4764861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunkelberger E. B.; Grechko M.; Zanni M. T. Transition Dipoles from 1D and 2D Infrared Spectroscopy Help Reveal the Secondary Structures of Proteins: Application to Amyloids. J. Phys. Chem. B 2015, 119 (44), 14065–14075. 10.1021/acs.jpcb.5b07706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donaldson P. M. Spectrophotometric Concentration Analysis Without Molar Absorption Coefficients by Two-Dimensional-Infrared and Fourier Transform Infrared Spectroscopy. Anal. Chem. 2022, 94 (51), 17988–17999. 10.1021/acs.analchem.2c04287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegman A. E.Lasers; University Science Books: Mill Valley, CA, 1986. [Google Scholar]
- Xiong W.; Strasfeld D. B.; Shim S. H.; Zanni M. T. Automated 2D IR spectrometer mitigates the influence of high optical densities. Vib Spectrosc 2009, 50 (1), 136–142. 10.1016/j.vibspec.2008.10.010. [DOI] [Google Scholar]
- Svelto O.Principles of lasers; Plenum Press: New York, 1976; p x, 376 pp. [Google Scholar]
- Heilweil E. J.; Cavanagh R. R.; Stephenson J. C. Population Relaxation of Co(V = 1) Vibrations in Solution Phase Metal-Carbonyl-Complexes. Chem. Phys. Lett. 1987, 134 (2), 181–188. 10.1016/0009-2614(87)87118-X. [DOI] [Google Scholar]
- Witte T.; Yeston J. S.; Motzkus M.; Heilweil E. J.; Kompa K. L. Femtosecond infrared coherent excitation of liquid phase vibrational population distributions (v > 5). Chem. Phys. Lett. 2004, 392 (1–3), 156–161. 10.1016/j.cplett.2004.05.052. [DOI] [Google Scholar]
- Kleiman V. D.; Arrivo S. M.; Melinger J. S.; Heilweil E. J. Controlling condensed-phase vibrational excitation with tailored infrared pulses. Chem. Phys. 1998, 233 (2–3), 207–216. 10.1016/S0301-0104(97)00367-4. [DOI] [Google Scholar]
- Morichika I.; Kusa F.; Takegami A.; Sakurai A.; Ashihara S. Antenna-Enhanced Nonlinear Infrared Spectroscopy in Reflection Geometry. J. Phys. Chem. C 2017, 121 (21), 11643–11649. 10.1021/acs.jpcc.7b01798. [DOI] [Google Scholar]
- Pagano P.; Guo Q.; Kohen A.; Cheatum C. M. Oscillatory Enzyme Dynamics Revealed by Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. Lett. 2016, 7 (13), 2507–2511. 10.1021/acs.jpclett.6b01154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagano P.; Guo Q.; Ranasinghe C.; Schroeder E.; Robben K.; Hase F.; Ye H.; Wickersham K.; Aspuru-Guzik A.; Major D. T. Oscillatory active-site motions correlate with kinetic isotope effects in formate dehydrogenase. ACS catalysis 2019, 9 (12), 11199–11206. 10.1021/acscatal.9b03345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranasinghe C.; Pagano P.; Sapienza P. J.; Lee A. L.; Kohen A.; Cheatum C. M. Isotopic labeling of formate dehydrogenase perturbs the protein dynamics. J. Phys. Chem. B 2019, 123 (49), 10403–10409. 10.1021/acs.jpcb.9b08426. [DOI] [PubMed] [Google Scholar]
- Robben K. C.; Cheatum C. M. Edge-pixel referencing suppresses correlated baseline noise in heterodyned spectroscopies. J. Chem. Phys. 2020, 152 (9), 094201 10.1063/1.5134987. [DOI] [PubMed] [Google Scholar]
- Robben K. C.; Cheatum C. M. Least-Squares Fitting of Multidimensional Spectra to Kubo Line-Shape Models. J. Phys. Chem. B 2021, 125, 12876. 10.1021/acs.jpcb.1c08764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecht E.Optics, 5 ed.; Pearson Education, Inc.: Boston, 2017; p vi, 714 pp. [Google Scholar]
- Ma J. Q.; Pazos I. M.; Zhang W. K.; Culik R. M.; Gai F. Site-Specific Infrared Probes of Proteins. Annu. Rev. Phys. Chem. 2015, 66, 357–377. 10.1146/annurev-physchem-040214-121802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blasiak B.; Londergan C. H.; Webb L. J.; Cho M. Vibrational Probes: From Small Molecule Solvatochromism Theory and Experiments to Applications in Complex Systems. Acc. Chem. Res. 2017, 50 (4), 968–976. 10.1021/acs.accounts.7b00002. [DOI] [PubMed] [Google Scholar]
- Rodgers J. M.; Zhang W. K.; Bazewicz C. G.; Chen J. X.; Brewer S. H.; Gai F. Kinetic Isotope Effect Provides Insight into the Vibrational Relaxation Mechanism of Aromatic Molecules: Application to Cyano-phenylalanine. J. Phys. Chem. Lett. 2016, 7 (7), 1281–1287. 10.1021/acs.jpclett.6b00325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Getahun Z.; Huang C. Y.; Wang T.; De Leon B.; DeGrado W. F.; Gai F. Using nitrile-derivatized amino acids as infrared probes of local environment. J. Am. Chem. Soc. 2003, 125 (2), 405–411. 10.1021/ja0285262. [DOI] [PubMed] [Google Scholar]
- Le Sueur A. L.; Ramos S.; Ellefsen J. D.; Cook S.; Thielges M. C. Evaluation of p-(C-13,N-15-Cyano)phenylalanine as an Extended Time Scale 2D IR Probe of Proteins. Anal. Chem. 2017, 89 (10), 5254–5260. 10.1021/acs.analchem.6b04650. [DOI] [PubMed] [Google Scholar]
- Ramos S.; Scott K. J.; Horness R. E.; Le Sueur A. L.; Thielges M. C. Extended timescale 2D IR probes of proteins: p-cyanoselenophenylalanine. Phys. Chem. Chem. Phys. 2017, 19 (15), 10081–10086. 10.1039/C7CP00403F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fafarman A. T.; Webb L. J.; Chuang J. I.; Boxer S. G. Site-specific conversion of cysteine thiols into thiocyanate creates an IR probe for electric fields in proteins. J. Am. Chem. Soc. 2006, 128 (41), 13356–13357. 10.1021/ja0650403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalton S. R.; Vienneau A. R.; Burstein S. R.; Xu R. J.; Linse S.; Londergan C. H. Cyanylated Cysteine Reports Site-Specific Changes at Protein-Protein-Binding Interfaces Without Perturbation. Biochemistry 2018, 57 (26), 3702–3712. 10.1021/acs.biochem.8b00283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt-Engler J. M.; Zangl R.; Guldan P.; Morgner N.; Bredenbeck J. Exploring the 2D-IR repertoire of the–SCN label to study site-resolved dynamics and solvation in the calcium sensor protein calmodulin. Phys. Chem. Chem. Phys. 2020, 22 (10), 5463–5475. 10.1039/C9CP06808B. [DOI] [PubMed] [Google Scholar]
- van Wilderen L. J. G. W.; Brunst H.; Gustmann H.; Wachtveitl J.; Broos J.; Bredenbeck J. Cyano-tryptophans as dual infrared and fluorescence spectroscopic labels to assess structural dynamics in proteins. Phys. Chem. Chem. Phys. 2018, 20 (30), 19906–19915. 10.1039/C8CP00846A. [DOI] [PubMed] [Google Scholar]
- Waegele M. M.; Tucker M. J.; Gai F. 5-Cyanotryptophan as an infrared probe of local hydration status of proteins. Chem. Phys. Lett. 2009, 478 (4–6), 249–253. 10.1016/j.cplett.2009.07.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloem R.; Koziol K.; Waldauer S. A.; Buchli B.; Walser R.; Samatanga B.; Jelesarov I.; Hamm P. Ligand Binding Studied by 2D IR Spectroscopy Using the Azidohomoalanine Label. J. Phys. Chem. B 2012, 116 (46), 13705–13712. 10.1021/jp3095209. [DOI] [PubMed] [Google Scholar]
- Thielges M. C.; Axup J. Y.; Wong D.; Lee H. S.; Chung J. K.; Schultz P. G.; Fayer M. D. Two-dimensional IR spectroscopy of protein dynamics using two vibrational labels: A site-specific genetically encoded unnatural amino acid and an active site ligand. J. Phys. Chem. B 2011, 115 (38), 11294–11304. 10.1021/jp206986v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazewicz C. G.; Liskov M. T.; Hines K. J.; Brewer S. H. Sensitive, Site-Specific, and Stable Vibrational Probe of Local Protein Environments: 4-Azidomethyl-L-Phenylalanine. J. Phys. Chem. B 2013, 117 (30), 8987–8993. 10.1021/jp4052598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyd R. W.Nonlinear optics, 4th ed.; Academic Press, an imprint of Elsevier: San Diego, 2019. [Google Scholar]
- Manzoni C.; Cerullo G. Design criteria for ultrafast optical parametric amplifiers. J. Opt. 2016, 18 (10), 103501. 10.1088/2040-8978/18/10/103501. [DOI] [Google Scholar]
- Luther B. M.; Tracy K. M.; Gerrity M.; Brown S.; Krummel A. T. 2D IR spectroscopy at 100 kHz utilizing a Mid-IR OPCPA laser source. Opt. Express 2016, 24 (4), 4117–4127. 10.1364/OE.24.004117. [DOI] [PubMed] [Google Scholar]
- Farrell K. M.; Ostrander J. S.; Jones A. C.; Yakami B. R.; Dicke S. S.; Middleton C. T.; Hamm P.; Zanni M. T. Shot-to-shot 2D IR spectroscopy at 100 kHz using a Yb laser and custom-designed electronics. Opt. Express 2020, 28 (22), 33584–33602. 10.1364/OE.409360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kearns N. M.; Mehlenbacher R. D.; Jones A. C.; Zanni M. T. Broadband 2D electronic spectrometer using white light and pulse shaping: noise and signal evaluation at 1 and 100 kHz. Opt. Express 2017, 25 (7), 7869–7883. 10.1364/OE.25.007869. [DOI] [PubMed] [Google Scholar]
- Hamm P. Transient 2D IR spectroscopy from micro- to milliseconds. J. Chem. Phys. 2021, 154 (10), 104201. 10.1063/5.0045294. [DOI] [PubMed] [Google Scholar]
- Donaldson P.; Greetham G.; Shaw D.; Parker A.; Towrie M. A 100 kHz pulse shaping 2D-IR spectrometer based on dual Yb: KGW amplifiers. J. Phys. Chem. A 2018, 122 (3), 780–787. 10.1021/acs.jpca.7b10259. [DOI] [PubMed] [Google Scholar]
- Greetham G. M.; Donaldson P. M.; Nation C.; Sazanovich I. V.; Clark I. P.; Shaw D. J.; Parker A. W.; Towrie M. A 100 kHz time-resolved multiple-probe femtosecond to second infrared absorption spectrometer. Applied spectroscopy 2016, 70 (4), 645–653. 10.1177/0003702816631302. [DOI] [PubMed] [Google Scholar]
- Feng Y.; Vinogradov I.; Ge N. H. General noise suppression scheme with reference detection in heterodyne nonlinear spectroscopy. Opt. Express 2017, 25 (21), 26262–26279. 10.1364/OE.25.026262. [DOI] [PubMed] [Google Scholar]
- Feng Y.; Vinogradov I.; Ge N. H. Optimized noise reduction scheme for heterodyne spectroscopy using array detectors. Opt. Express 2019, 27 (15), 20323–20346. 10.1364/OE.27.020323. [DOI] [PubMed] [Google Scholar]
- Erickson H. P. Size and Shape of Protein Molecules at the Nanometer Level Determined by Sedimentation, Gel Filtration, and Electron Microscopy. Biol. Proced Online 2009, 11 (1), 32–51. 10.1007/s12575-009-9008-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verma P. K.; Kundu A.; Puretz M. S.; Dhoonmoon C.; Chegwidden O. S.; Londergan C. H.; Cho M. The Bend plus Libration Combination Band Is an Intrinsic, Collective, and Strongly Solute-Dependent Reporter on the Hydrogen Bonding Network of Liquid Water. J. Phys. Chem. B 2018, 122 (9), 2587–2599. 10.1021/acs.jpcb.7b09641. [DOI] [PubMed] [Google Scholar]
- Mukamel S. Multidimensional femtosecond correlation spectroscopies of electronic and vibrational excitations. Annu. Rev. Phys. Chem. 2000, 51 (1), 691–729. 10.1146/annurev.physchem.51.1.691. [DOI] [PubMed] [Google Scholar]
- Xiong W.; Zanni M. T. Signal enhancement and background cancellation in collinear two-dimensional spectroscopies. Opt. Lett. 2008, 33 (12), 1371–1373. 10.1364/OL.33.001371. [DOI] [PubMed] [Google Scholar]
- Courtney T. L.; Park S. D.; Hill R. J.; Cho B.; Jonas D. M. Enhanced interferometric detection in two-dimensional spectroscopy with a Sagnac interferometer. Opt. Lett. 2014, 39 (3), 513–516. 10.1364/OL.39.000513. [DOI] [PubMed] [Google Scholar]
- Nishida J.; Yan C.; Fayer M. D. Enhanced nonlinear spectroscopy for monolayers and thin films in near-Brewster’s angle reflection pump-probe geometry. J. Chem. Phys. 2017, 146 (9), 094201. 10.1063/1.4977508. [DOI] [Google Scholar]
- Rezus Y. L. A.; Selig O. Impact of local-field effects on the plasmonic enhancement of vibrational signals by infrared nanoantennas. Opt. Express 2016, 24 (11), 12202. 10.1364/OE.24.012202. [DOI] [PubMed] [Google Scholar]
- Chuntonov L.; Rubtsov I. V. Surface-enhanced ultrafast two-dimensional vibrational spectroscopy with engineered plasmonic nano-antennas. J. Chem. Phys. 2020, 153 (5), 050902. 10.1063/5.0013956. [DOI] [PubMed] [Google Scholar]
- Gandman A.; Mackin R.; Cohn B.; Rubtsov I. V.; Chuntonov L. Two-Dimensional Fano Lineshapes in Ultrafast Vibrational Spectroscopy of Thin Molecular Layers on Plasmonic Arrays. J. Phys. Chem. Lett. 2017, 8 (14), 3341–3346. 10.1021/acs.jpclett.7b01490. [DOI] [PubMed] [Google Scholar]
- Neubrech F.; Huck C.; Weber K.; Pucci A.; Giessen H. Surface-Enhanced Infrared Spectroscopy Using Resonant Nanoantennas. Chem. Rev. 2017, 117 (7), 5110–5145. 10.1021/acs.chemrev.6b00743. [DOI] [PubMed] [Google Scholar]
- Simpkins B. S.; Long J. P.; Glembocki O. J.; Guo J.; Caldwell J. D.; Owrutsky J. C. Pitch-dependent resonances and near-field coupling in infrared nanoantenna arrays. Opt. Express 2012, 20 (25), 27725–27739. 10.1364/OE.20.027725. [DOI] [PubMed] [Google Scholar]
- Weber D.; Albella P.; Alonso-Gonzalez P.; Neubrech F.; Gui H.; Nagao T.; Hillenbrand R.; Aizpurua J.; Pucci A. Longitudinal and transverse coupling in infrared gold nanoantenna arrays: long range versus short range interaction regimes. Opt. Express 2011, 19 (16), 15047–15061. 10.1364/OE.19.015047. [DOI] [PubMed] [Google Scholar]
- Donaldson P. M.; Hamm P. Gold Nanoparticle Capping Layers: Structure, Dynamics, and Surface Enhancement Measured Using 2D-IR Spectroscopy. Angew. Chem. Int. Edit 2013, 52 (2), 634–638. 10.1002/anie.201204973. [DOI] [PubMed] [Google Scholar]
- Selig O.; Siffels R.; Rezus Y. L. A. Ultrasensitive Ultrafast Vibrational Spectroscopy Employing the Near Field of Gold Nanoantennas. Phys. Rev. Lett. 2015, 114 (23), 233004. 10.1103/PhysRevLett.114.233004. [DOI] [PubMed] [Google Scholar]
- Kraack J. P.; Kaech A.; Hamm P. Surface Enhancement in Ultrafast 2D ATR IR Spectroscopy at the Metal-Liquid Interface. J. Phys. Chem. C 2016, 120 (6), 3350–3359. 10.1021/acs.jpcc.5b11051. [DOI] [Google Scholar]
- Kraack J. P.; Hamm P. Vibrational ladder-climbing in surface-enhanced, ultrafast infrared spectroscopy. Phys. Chem. Chem. Phys. 2016, 18 (24), 16088–16093. 10.1039/C6CP02589G. [DOI] [PubMed] [Google Scholar]
- Kusa F.; Morichika I.; Takegami A.; Ashihara S. Enhanced ultrafast infrared spectroscopy using coupled nanoantenna arrays. Opt. Express 2017, 25 (11), 12896–12907. 10.1364/OE.25.012896. [DOI] [PubMed] [Google Scholar]
- Mackin R. T.; Cohn B.; Chuntonov L.; Rubtsov I. V. Intense-field interaction regime with weak laser pulses and localized plasmonic enhancement: Reference-free demonstration by 3rd-and 5th-order infrared spectroscopies. J. Chem. Phys. 2019, 151 (12), 121103. 10.1063/1.5120531. [DOI] [PubMed] [Google Scholar]
- Mackin R. T.; Cohn B.; Gandman A.; Leger J. D.; Chuntonov L.; Rubtsov I. V. Surface-Enhanced Dual-Frequency Two-Dimensional Vibrational Spectroscopy of Thin Layers at an Interface. J. Phys. Chem. C 2018, 122 (20), 11015–11023. 10.1021/acs.jpcc.8b02436. [DOI] [Google Scholar]
- Cohn B.; Prasad A. K.; Chuntonov L. Communication: Probing the interaction of infrared antenna arrays and molecular films with ultrafast quantum dynamics. J. Chem. Phys. 2018, 148 (13), 131101. 10.1063/1.5025600. [DOI] [PubMed] [Google Scholar]
- Cohn B.; Engelman B.; Goldner A.; Chuntonov L. Two-Dimensional Infrared Spectroscopy with Local Plasmonic Fields of a Trimer Gap-Antenna Array. J. Phys. Chem. Lett. 2018, 9 (16), 4596–4601. 10.1021/acs.jpclett.8b01937. [DOI] [PubMed] [Google Scholar]
- Mackin R. T.; Cohn B.; Engelman B.; Goldner A.; Rubtsov I. V.; Chuntonov L. Plasmonic Trimers for Dual-Frequency Surface-Enhanced Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. C 2019, 123 (40), 24731–24739. 10.1021/acs.jpcc.9b07045. [DOI] [Google Scholar]
- Ostrander J. S.; Lomont J. P.; Rich K. L.; Saraswat V.; Feingold B. R.; Petti M. K.; Birdsall E. R.; Arnold M. S.; Zanni M. T. Monolayer Sensitivity Enables a 2D IR Spectroscopic Immuno-biosensor for Studying Protein Structures: Application to Amyloid Polymorphs. J. Phys. Chem. Lett. 2019, 10 (14), 3836–3842. 10.1021/acs.jpclett.9b01267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petti M. K.; Ostrander J. S.; Saraswat V.; Birdsall E. R.; Rich K. L.; Lomont J. P.; Arnold M. S.; Zanni M. T. Enhancing the signal strength of surface sensitive 2D IR spectroscopy. J. Chem. Phys. 2019, 150 (2), 024707. 10.1063/1.5065511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe A.; Sinther M.; Fahsold G.; Pucci A. The correlation between film thickness and adsorbate line shape in surface enhanced infrared absorption. J. Chem. Phys. 2003, 119 (9), 4887–4890. 10.1063/1.1597232. [DOI] [Google Scholar]
- Dong L. L.; Yang X.; Zhang C.; Cerjan B.; Zhou L. N.; Tseng M. L.; Zhang Y.; Alabastri A.; Nordlander P.; Halas N. J. Nanogapped Au Antennas for Ultrasensitive Surface-Enhanced Infrared Absorption Spectroscopy. Nano Lett. 2017, 17 (9), 5768–5774. 10.1021/acs.nanolett.7b02736. [DOI] [PubMed] [Google Scholar]
- Tek G.; Hamm P. A Correction Scheme for Fano Line Shapes in Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. Lett. 2020, 11 (15), 6185–6190. 10.1021/acs.jpclett.0c01752. [DOI] [PubMed] [Google Scholar]
- Whaley-Mayda L.; Penwell S. B.; Tokmakoff A. Fluorescence-Encoded Infrared Spectroscopy: Ultrafast Vibrational Spectroscopy on Small Ensembles of Molecules in Solution. J. Phys. Chem. Lett. 2019, 10 (8), 1967. 10.1021/acs.jpclett.9b00748. [DOI] [PubMed] [Google Scholar]
- Ashwood B.; Lewis N. H. C.; Sanstead P. J.; Tokmakoff A. Temperature-Jump 2D IR Spectroscopy with Intensity-Modulated CW Optical Heating. J. Phys. Chem. B 2020, 124 (39), 8665–8677. 10.1021/acs.jpcb.0c07177. [DOI] [PMC free article] [PubMed] [Google Scholar]