Abstract
Precise segmentation of subcortical structures from infant brain magnetic resonance (MR) images plays an essential role in studying early subcortical structural and functional developmental patterns and diagnosis of related brain disorders. However, due to the dynamic appearance changes, low tissue contrast, and tiny subcortical size in infant brain MR images, infant subcortical segmentation is a challenging task. In this paper, we propose a context-guided, attention-based, coarse-to-fine deep framework to precisely segment the infant subcortical structures. At the coarse stage, we aim to directly predict the signed distance maps (SDMs) from multi-modal intensity images, including T1w, T2w, and the ratio of T1w and T2w images, with an SDM-Unet, which can leverage the spatial context information, including the structural position information and the shape information of the target structure, to generate high-quality SDMs. At the fine stage, the predicted SDMs, which encode spatial-context information of each subcortical structure, are integrated with the multi-modal intensity images as the input to a multi-source and multi-path attention Unet (M2A-Unet) for achieving refined segmentation. Both the 3D spatial and channel attention blocks are added to guide the M2A-Unet to focus more on the important subregions and channels. We additionally incorporate the inner and outer subcortical boundaries as extra labels to help precisely estimate the ambiguous boundaries. We validate our method on an infant MR image dataset and on an unrelated neonatal MR image dataset. Compared to eleven state-of-the-art methods, the proposed framework consistently achieves higher segmentation accuracy in both qualitative and quantitative evaluations of infant MR images and also exhibits good generalizability in the neonatal dataset.
Keywords: Infant, Subcortical segmentation, Brain, MRI
1. Introduction
The brain subcortex controls diverse cognitive and motor functions (Calabresi et al., 2014; Grossberg, 2009; Richard et al., 2013; Scimeca and Badre, 2012) and its abnormality has been reliably linked to affective dysfunctions and disorders (Ecker et al., 2015; Risacher et al., 2009; Tremblay et al., 2015). To perform subcortical related neuroimaging studies (Gilmore et al., 2012; Li et al., 2019a), accurate segmentation of subcortical structures from magnetic resonance (MR) images plays a fundamental role. However, manually delineating each subcortical structure on the low contrast infant brain MR images is expertise needed, hard to reproduce, and extremely time-consuming. Hence, many automatic subcortical segmentation methods have been proposed (Jenkinson et al., 2012; Zöllei et al., 2020). Particularly, deep learning-based methods recently exhibited a dominant performance in medical image segmentation, e.g., infant-dedicated brain tissue segmentation methods (Wang et al., 2018b; Zeng and Zheng, 2018), top-ranked methods in the iSeg2019 challenge (Multi-Site Infant Brain Segmentation Algorithms), i.e., xflz, CU_SIAT, and RB (Sun et al., 2021), nnUnet (one of the state-of-the-art medical image segmentation methods) (Isensee et al., 2021), and modality-aware medical image segmentation methods (Dou et al., 2020; Zhang et al., 2021; Zhu et al., 2021; Zou and Dou, 2020), and achieved tremendous successes by effectively learning the high-level semantic features. However, the existing deep learning-based subcortical segmentation methods (Dolz et al., 2018; Liu et al., 2020; Wu et al., 2019a; 2019b) only perform well on adult brain MR images. Due to the dynamic appearance changes, low tissue contrast, and tiny size of subcortical structures in infant brain MR images (Li et al., 2019b), as shown in Fig. 1, automatic infant subcortical segmentation is still a challenging task (Zöllei et al., 2020), especially in distinguishing the boundary voxels, limiting the neuroimaging studies of the early subcortical development (Li et al., 2019a; Qiu et al., 2013; Serag et al., 2011) and related brain disorders (Courchesne et al., 2001). Therefore, fully automatic infant-dedicated subcortical segmentation methods with high accuracy (particularly for the structural boundaries) are critically needed.
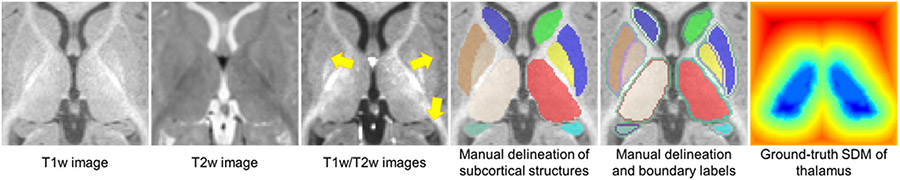
Fig. 1.
A 6-month subject’s T1w image, T2w image, T1w/T2w image, manual delineation map of 12 subcortical structures, manual delineation map with inner and outer boundaries, and the ground-truth signed distance map (SDM) of the thalamus. Due to the low tissue contrast of the 6-month infant brain MR images, the subcortical boundaries are ambiguous in the T1w image and T2w image, while the T1w/T2w image has the enhanced tissue contrast, and thus the boundaries are more distinguishable (pointed by yellow arrows). We performed the commonly used Euclidean distance transforms to create the subcortical ground-truth SDMs from the manual delineation maps.
To handle above-mentioned challenges and well segment the infant subcortical structures with ambiguous boundaries and large shape variances, in addition to the traditional multi-modal MR images (T1w and T2w), more information is needed, such as the myelin content information and spatial context information (e.g., distance maps with shape and position information). In detail, as shown in Fig. 1, the intensity ratio of T1w and T2w images (T1w/T2w), indicating the myelin content and reflecting somewhat iron content within the structures (Shams et al., 2019), has improved tissue contrast (Glasser and Van Essen, 2011; Misaki et al., 2015), especially for the iron-rich subcortical structures (Yoshida et al., 2021). Thus, T1w/T2w images already have been applied in characterizing the subcortical structures (Uddin et al., 2018) and measuring the myelin content within the early postnatal phase (Lee et al., 2015). Meanwhile, T1w/T2w images could also help eliminate the intensity inhomogeneity, due to the anti-correlated low-frequency variations within gray matter and white matter (Van Essen et al., 2013). Therefore, it is valuable to introduce the T1w/T2w ratio image with enhanced information into the infant subcortical segmentation, along with the T1w and T2w images. Previous works (Wang et al., 2018a; 2018b; Zeng and Zheng, 2018) proposed context-guided neural networks for tissue segmentation by introducing distance maps, which encode the spatial information, including position, shape, and relationship among different regions of interest. To make better use of the spatial context information, (Xue et al., 2019) took the signed distance maps (SDMs) as the primary target to supervise the network to learn the context information by directly predicting SDMs, while obtaining the segmentation maps based on the predicted SDMs through Heaviside function, making it possible to achieve enhanced segmentation accuracy. Attributed to the relatively stable position and shape of each subcortical structure, it could be particularly beneficial for subcortical segmentation by introducing distance maps as anatomical guidance. Besides, attention mechanisms, including channel and spatial attention, were commonly used to help the deep neural networks automatically focus on the most important channels and regions, which also have achieved many successes in medical image segmentation (Oktay et al., 2018; Roy et al., 2018; Wang et al., 2020). Similarly, such effective attention mechanisms can also be leveraged to help the subcortical segmentation network focus on the most efficacious channels and relevant subregions, which could boost the segmentation accuracy and reduce the outliers within the irrelevant subregions with similar intensity to the subcortical structures, especially on infant brain MR images with extremely low tissue contrast.
Motivated by these works, in this paper, we propose a context-guided, attention-based, coarse-to-fine deep neural framework, which intends to leverage the SDMs as spatial context information, including the relative position information and the shape information of the subcortical structures, to achieve accurate 3D subcortical segmentation in infant brain MR images. Specifically, at the coarse stage, we devise an SDM learning Unet (SDM-Unet) to directly predict high-quality SDM of each subcortical structure from the multi-modal MR images, including the T1w images, T2w images, and the ratio of T1w and T2w images (T1w/T2w) with enhanced structural contrast, by exploiting the subcortical spatial-context information (encoded in the ground-truth SDMs). Meanwhile, we introduced a Correntropy-based loss (Chen et al., 2016) into the SDM-Unet to enhance the training stability by providing the improved robustness to outliers. At the fine stage, we designed a multi-source and multi-path attention Unet (M2A-Unet) to effectively utilize the spatial context information (encoded in the previously predicted SDMs), alongside the multi-modal information, to further finetune the subcortical segmentations under both spatial and channel attention mechanisms. Besides, to well segment the challenging ambiguous subcortical boundaries, both inner and outer boundaries of each subcortical structure are delineated as extra boundary labels to force the M2A-Unet pay more attention to the boundary regions.
Overall, the main contribution of this paper can be summarized in four-fold:
We design a novel 3D context-guided attention-based framework with two stages to accurately segment infant subcortical structures. Specifically, the coarse stage SDM-Unet is trained to directly predict SDMs to provide the anatomical guidance for the fine stage; then, the fine stage M2A-Unet path-wisely incorporates the generated SDMs to achieve the refined segmentation maps;
We leverage both spatial and channel attention mechanisms to guide the M2A-Unet to focus on the important regions and feature maps to mitigate the dynamic and heterogeneous intensity changes in infant brain MR images to achieve final segmentation;
We delineate the structure-specific inner edges and uniform outer edge as extra boundary labels, and make the proposed M2A-Unet pay more attention to the ambiguous boundaries of subcortical structures;
The T1w/T2w images with enhanced tissue contrast, in addition to the original T1w and T2w images, were induced to provide extra information to help distinguish the subcortical structures.
Of note, our preliminary conference work (Chen et al., 2020), which is the first of using spatial context information to guide the infant subcortical segmentation, achieved encouraging performance at two age points (i.e., 6-month and 12-month). However, it is still challenging to effectively segment diverse subcortical structures at various ages due to the extremely tiny sizes (e.g., 0-month), noisy intensity images with severe partial volume effect and dynamic myelination in infant brain MR images. To better address these issues, in this paper, we have extended the previously presented conference version (Chen et al., 2020) as follows and achieved good subcortical segmentation accuracy on images across the first two postnatal years:
We added both spatial and channel attention mechanisms in our framework;
We adopted the inner and outer boundaries as extra labels for each subcortical structure;
We enlarged the applicable age range of our method to all ages in the first two postnatal years (from 0-month to 26-month);
We increased the label number from 6 to 12 (6 subcortical structures in each hemisphere) and simultaneously segmented the structures within each hemisphere;
We added more technical details and comprehensive analyses and systematically performed the ablation study;
We systematically verified the generalizability and domain adaptation ability of our trained framework on an unrelated neonatal dataset.
It should be noted that due to the doubled number of segmentation labels, which severely increases the segmentation difficulty, and the reorganized training and testing datasets, the segmentation results of this work are not directly comparable to that in our preliminary conference work with fewer labels.
The rest of the paper is organized as follows. Section II briefly reviews previous studies on subcortical segmentation, context-guided image segmentation, and attention mechanisms. Then, the proposed method is described in detail in Section III, followed by the experiments and results in Section IV. Finally, we conclude the paper in Section V.
2. Related work
2.1. Subcortical segmentation
As an essential step in various neuroimaging studies and related disease diagnoses, automatic subcortical segmentation has been explored in previous literature. A subcortical segmentation method is provided in the commonly used medical image analysis toolbox FSL (Jenkinson et al., 2012), which utilizes the Bayesian framework to differentiate the subcortical structures based on the low-level features, i.e., intensity and boundary. Similarly, the infant FreeSurfer pipeline (Zöllei et al., 2020) can provide infant subcortical segmentation based on an intensity adaptive version of a traditional Bayesian multi-atlas algorithm (Iglesias et al., 2013; Sabuncu et al., 2010). However, due to the low tissue contrast and dynamic appearance in infant brain MR images, such low-level features are noisy and fuzzy, which are thus not enough to accurately perform the infant subcortical segmentation.
Motivated by the recent success of the convolutional neural networks (CNNs) in semantic segmentation tasks, many efforts have been put into learning-based subcortical segmentation methods. In (Dolz et al., 2018), the authors proposed a 3D fully convolutional network for subcortical segmentation, which embedded intermediate-layer outputs in the final segmentation prediction to help the proposed network learn the local and global context. (Wu et al., 2019b) introduced a multi-atlas strategy to guide the training of a CNN segmentation network. Specifically, several randomly selected images are considered as template images and are affinely aligned to the target images. Then, during the training, multiple template patches are automatically chosen and input with the target patch to obtain the segmentation. Soon after, (Wu et al., 2019a) proposed an enhanced version by adding a 2D fine-stage segmentation network, which simultaneously segments the brain MR slices from three directions through three independent U-nets and fuses the outputs to get the refined segmentation. (Liu et al., 2020) proposed a U-net-like network, named -net, for subcortical segmentation and introduced a densely convolutional LSTM module (DC-LSTM), serially stacked to effectively aggregate features learned at each level, to progressively enrich low-level feature maps with high-level context. However, existing methods are all proposed for adult brain subcortical segmentation and perform poorly on infant brain MR images, due to the low tissue contrast, dynamic appearance changes, and tiny brain size in infants. Although, in the iSeg2019 challenge (Multi-Site Infant Brain Segmentation Algorithms) (Sun et al., 2021), the top-ranked methods, i.e., xflz, CU_SIAT, and RB, obtained trust-worth results in infant brain tissue segmentation, the infant subcortical segmentation is more challenging due to the tripled label classes for both left and right hemisphere. Hence, accurate infant subcortical segmentation methods remain challenging and need further investigation.
2.2. Context-guided medical image segmentation
Given a specific region within an image, the distance transform, also named level-set function, can transform the value of each pixel/voxel into the shortest distance to this region’s boundary to produce a distance map as spatial context information. Inspired by this, plenty of context-guided methods have been proposed to leverage distance maps as additional context information to deliver improved performance (Fabbri et al., 2008; Jones et al., 2006). For medical image segmentation tasks, in (Criminisi et al., 2008), the authors combined the distance transform with an efficient searching method to produce spatially smooth and contrast-sensitive segmentation labels, which was successfully performed on torso segmentation. In (Li et al., 2010), a distance regularization term was designed to help stabilize the level set function to maintain a reasonable shape, which achieved good performance on bladder segmentation. The random forest algorithms were also favorably integrated with geodesic distance transform for accurate organ segmentation (Kontschieder et al., 2013). Meanwhile, to deal with the MR images with intensity inhomogeneity, distance transform was also introduced to provide spatial context information and conformed with the intensity inhomogeneity correction methods to build the energy functions to generate accurate segmentation (Li et al., 2011; Zhang et al., 2015).
Recently, many context-guided CNN-based frameworks have been proposed for medical image segmentation and achieved many successes, especially for the infant brain (Wang et al., 2018a; 2018b; Zeng and Zheng, 2018). This type of methods utilizes the spatial context information included in the distance maps to generate the segmentation labels with enhanced accuracy (Park et al., 2019), which is highly effective for segmenting the structures with relatively stable position and shape. In (Wang et al., 2018b), the authors constructed SDMs with respect to the boundaries of different tissue types as anatomical guidance and jointly input them with T1w and T2w images. Similarly, (Zeng and Zheng, 2018) proposed a multi-stage network, which computed distance maps for each brain tissue based on the segmentations obtained from the first stage and applied them as input to achieve the refined segmentation in the second stage. To provide more context information, (Wang et al., 2018a) proposed a DeepIGeoS network to calculate the distance maps based on the geodesic distance transformation, instead of the commonly used Euclidean distance transform. However, these methods typically perform traditional segmentation networks (without considering the context information) to generate intermediate segmentation results for calculating distance maps during inference. Due to the low tissue contrast and dynamic appearance changes, it is extremely challenging to obtain valid intermediate infant subcortical segmentations for distance map calculation, and thus the segmentation errors would be accumulated in the constructed distance maps, degrading the performance of such context-guided methods in segmenting infant subcortex. In (Xue et al., 2019), the authors proposed a regression-based network to directly predict the signed distance map (SDM). Then, one can apply the Heaviside function to transform the obtained SDMs into segmentations. The biggest advance is the proposed network can learn the spatial context information contained from the ground-truth SDMs to improve the segmentation accuracy. In (Xue et al., 2019), to improve the training robustness of the proposed network, the ordinarily used loss was replaced by the loss to penalize the differences between the predicted SDMs and the ground-truth SDMs during training. Although, the robustness is increased, due to the non-differentiable issue of loss at zero, the training process could be unstable in multi-class segmentation tasks (Ren et al., 2015), making it unsuitable for the subcortical segmentation task. However, to the best of our knowledge, there is still an absence of an end-to-end distance transform-based coarse-to-fine deep framework, which could be remarkably beneficial for accurate infant brain subcortical segmentation.
2.3. Attention mechanisms in medical image analysis
To validly unearth salient subregions in intricate scenes, e.g., excavating the subcortical structures from the whole brain MR images, attention mechanisms are introduced to adaptively re-weight features learned by the networks and have presented superior advancements in many medical image analysis tasks, including classification, segmentation, and parcellation (Guo and Yuan, 2019; Li et al., 2022; Roy et al., 2018), due to their flexible incorporation with existing deep learning methods. The attention mechanisms are commonly performed on different aspects, resulting in three main categories, i.e., 1) channel attention, 2) spatial attention, and 3) channel and spatial attention.
Channel attention.
In CNNs, the learned feature maps are organized in a multi-channel manner, each of which usually illustrates different learned objects (Chen et al., 2017). Inspired by this, channel attention is generally applied to adaptively adjust the weight of each channel to help the network divert attention to the most important objects. In the presentation of SENet (Hu et al., 2018), the authors first introduced channel attention to help improve representation ability, within which a squeeze-and-excitation (SE) block was proposed to integrate global information and capture relationships between each channel. In (Zhang et al., 2018), the authors continuously improved the SE-block by introducing a semantic encoding loss, which can exploit the global contextual information to enhance the segmentation performance.
Spatial attention.
Different from channel attention, spatial attention mechanisms focus on selectively highlighting the relevant subregions within the learned feature maps. In (Oktay et al., 2018), the authors proposed an attention-Unet for medical image segmentation, introducing an attention gate block to guide the network to pay more attention to important regions, while suppress the activation of features within the irrelevant areas. Recently, self-attention methods have shown dominant performance, which performs a spatial attention mechanism to capture global information. Inspired by this, (Wang et al., 2020) introduced self-attention into medical image segmentation and proposed a non-local Unet, which can aggregate long-range information gradually by using the non-local information with flexible global aggregation blocks.
Channel and spatial attention.
In order to combine the advantages of both channel attention and spatial attention, many efforts have been made to perform them together under different strategies. To focus on essential regions as well as enhance informative channels, (Woo et al., 2018) proposed the convolutional block attention module (CBAM), which tandem connects the channel attention block and spatial attention block. Due to the global pooling, which is generally used in the spatial attention block, the pixel-wise spatial information is ignored, which could poorly influence the medical image segmentation. Thus, (Roy et al., 2018) proposed spatial and channel SE blocks (scSE) to densely provide spatial weights to complement channel attention and supervise the network focusing on critical subregions.
The above-mentioned attention mechanisms can help the network focus on the most relevant features and areas, which could be highly beneficial for the complex infant subcortical segmentation task.
3. Method
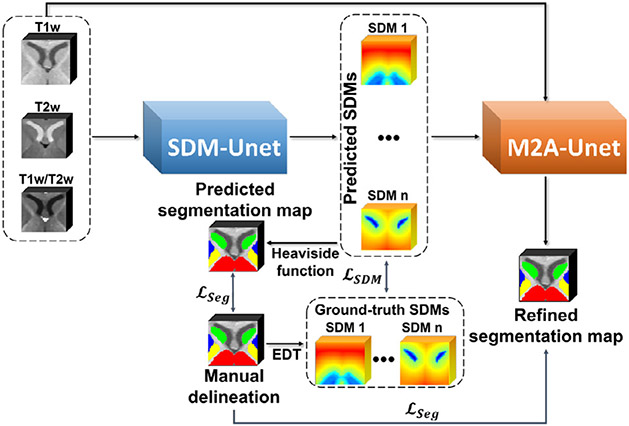
In Fig. 2, our framework, including two subnetworks for two stages, are illustrated. We will detailedly introduce each stage and its corresponding network in the following.
Fig. 2.
A schematic illustration of the proposed framework with the coarse stage network (SDM-Unet) and the fine stage network (M2A-Unet).
3.1. Coarse stage SDM-Unet
This section presents the coarse stage SDM learning Unet (SDM-Unet), which can leverage the position and shape context information included in the ground-truth SDMs to force the network learning to predict high-quality SDMs. In doing so, the predicted high-quality SDMs can further help achieve superior segmentation performance in the fine stage.
3.1.1. Generation of ground-truth SDMs
Given a manually delineated label map of subcortical structures, we can calculate the SDM of each specific structure through the following formula, which is a mapping from to :
| (1) |
where and are the coordinate of any voxel in the label map and the subcortical structure boundary , respectively. The regions inside (negative) and outside (positive) a subcortical structure are respectively denoted by and . In this work, all the subcortical SDMs are created using the Euclidean distance transforms (EDT).
3.1.2. Transformation from SDMs to segmentation maps
During training, in addition to supervise the similarity between the ground truth and predicted SDMs, we can introduce a segmentation loss to penalize the differences between the manual delineations and the predicted segmentation maps (converted from the predicted SDMs) to fully leverage the informative manual delineations, thus further improving the performance of the proposed SDM-Unet. Specifically, we can precisely convert the SDMs to the segmentation maps through the Heaviside function. However, the Heaviside function is non-differentiable, making it impossible to be directly performed in training. Therefore, we exploit a smooth approximation of the Heaviside function (Ito, 1994) to transform the predicted SDMs to the segmentation maps to build the segmentation loss, and the smooth approximation of the Heaviside function is defined as follows:
| (2) |
where and respectively denote the predicted SDM and segmentation map belonging to the -th class, and is the approximation parameter (a larger gives a closer approximation).
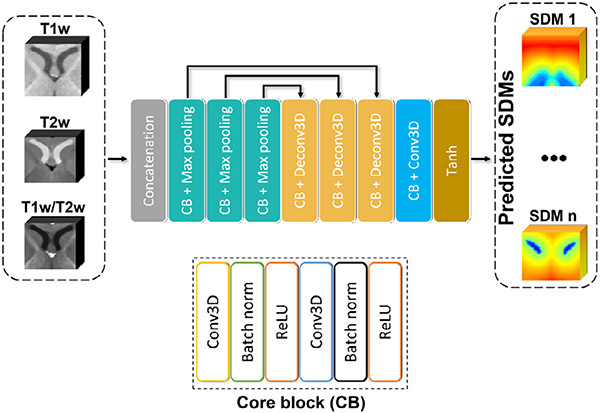
3.1.3. SDM-Unet Architecture
The architecture of the proposed SDM-Unet is shown in Fig. 3, which inputs multi-modal MR images (T1w, T2w, and T1w/T2w images) in a multi-channel manner and outputs the estimated SDMs for each subcortical structure. The SDM-Unet has an encoder-decoder structure. There are three encoding blocks in the encoder part, each of which repetitively takes the form of a combination of a core block (CB) and max pooling. The CB has a form of Conv3D-BN-ReLU-Conv3D-BN-ReLU. Conv3D denotes the 3D convolution layer, BN denotes the batch normalization, and ReLU denotes the rectified linear unit. Similarly, there are also three decoding blocks in decoder part, each taking the form of CB-DeConv3D. The DeConv3D denotes the traditional transposed convolution. Skip connections between each pair of encoding and the decoding blocks are added to help recover essential low-level features.
Fig. 3.
The architecture of the proposed SDM-Unet at the coarse stage.
3.1.4. SDM-Unet Loss function
There are two terms in the loss function of the proposed SDM-Unet, i.e., SDM learning loss and segmentation loss.
SDM learning loss.
First, we introduce the SDM learning loss term, which encourages the SDM-Unet to predict the SDMs from the original multi-modal MR images as similar as the ground-truth SDMs. The commonly used loss term for learning the SDMs is the loss, instead of loss, to enhance the robustness to outliers (Xue et al., 2019). However, the loss is non-differentiable at zero, severely influencing the training stability.
To overcome the limitation of loss and alleviate the degradation caused by outliers, we adopt the Correntropy-based loss (Closs) (Chen et al., 2016) as the SDM learning loss to penalize the differences between the estimated SDMs and the ground-truth SDMs. Closs is a maximum Correntropy criterion (MCC) based loss function, which has been successfully applied in signal processing and machine learning areas to improve the robustness against outliers. In detail, along with the increase of error e (the difference between source and target images), the derivative of loss exhibits a linear increase, making it extremely sensitive to outliers. On the contrary, when facing outliers, the derivative of Closs gets closer to zero, suggesting its remarkedly robustness to outliers. Meanwhile, compared to the loss, the Closs is differentiable everywhere (Liu et al., 2007), making the Closs-based SDM learning loss more stable in training.
In detail, for a segmentation task with H-class, the Closs-based SDM learning loss is defined as follows:
| (3) |
where is the tunable kernel bandwidth, and respectively represent the estimated SDM and ground-truth SDM belonging to the -th class.
Segmentation loss.
Once we transformed the predicted SDMs to segmentation maps by performing the Eq (2), we utilized the Dice loss (Milletari et al., 2016) to build the segmentation loss, which can measure the overlapping between the predicted segmentation maps and the manual delineation maps to further supervise the network training. For voxels, the Segmentation loss is defined as:
| (4) |
where, and respectively denote the -th voxel in the -th class manual delineation and predicted segmentation map.
Joint SDM-Unet loss.
By integrating two loss terms, we can have the joint loss function for SDM-Unet :
| (5) |
where is the weight parameter. We can minimize the joint SDM-Unet loss to stably train the proposed SDM-Unet to generate high-quality SDMs, and use the achieved SDMs as the spatial context information to help the following M2A-Unet refine the segmentation results.
3.2. Fine stage M2A-Unet
To further improve the segmentation accuracy, we propose a multi-source and multi-path attention Unet (M2A-Unet), which can fully leverage the context information generated by SDM-Unet to increase the segmentation accuracy.
3.2.1. Boundary-identified segmentation maps
It is worth noting that the subcortical structures are blurred with each other, as well as the fuzzy boundaries between the GM/WM, due to the low tissue contrast in infant MR images. Therefore, the identification of boundaries is more important than that of inner regions in infant subcortical segmentation. To supervise the proposed network to pay more attention to the boundaries of each subcortical structure, we delineated the inner boundary and outer boundary for each subcortical structure and assigned structure-specific labels for each inner boundary and a uniform label for the outer boundary, as shown in Fig. 1. By adding boundary labels to the manual delineations, the M2A-Unet can be trained to directly estimate both the inner and outer boundaries of each subcortical structure. Meanwhile, the performance of the M2A-Unet could be further improved by learning to match up the boundary labels with the boundaries of SDMs to better leverage the ample context information included in SDMs. Thus, the M2A-Unet can accurately achieve the refined subcortical segmentation maps by well capturing the boundaries.
3.2.2. 3D Attention blocks
To guide the proposed M2A-Unet to pay more attention to the beneficial subregions and feature maps while disregarding irrelevant parts, inspired by the recent progress in attention-based medical image segmentation (Roy et al., 2018), we extend both the spatial and channel attention blocks into 3D and path-wisely introduce them into our M2A-Unet to further enhance the accuracy of the refined segmentation, which are detailed below.
Spatial attention block (SAB).
The SAB spatially recalibrates the feature maps , outputted by the previous encoding or decoding blocks, along with the input channel and generates the spatially re-weighted feature maps along the output channel , where H, W, and D are the spatial height, width, and depth, respectively. In detail, for the feature maps , where corresponds to the spatial location at (, , ) on each channel, the SAB outputs a projection tensor through a convolution layer with the weight , and . Activated by the sigmoid function , the projection is rescaled to [0,1], and the spatially recalibrated is
| (6) |
This pixel-wise SAB block highlights more corresponding subregions and ignores immaterial regions along all channels by adjusting the magnitude of each .
Channel attention block (CAB).
The CAB recalibrates feature maps , where , in a channel-wise manner and outputs the re-weighted . Specifically, a global average pooling block is performed on each channel to aggregate information in each feature map as follows,
| (7) |
where . Then, a combination of the embedded global information vector is transformed through two fully connected (FC) layers with a ReLU operator,
| (8) |
where and , and the channel attention bottleneck parameter . Similar to the SAB, by passing through the sigmoid activation layer, the CAB outputs the resultant feature maps
| (9) |
Therefore, the higher value of means the -th channel is more important, and the trained network can ignore the futile channels adaptively and emphatically underline the more important ones to help improve the final segmentation of the subcortical structures in the low contrast infant brain MR images.
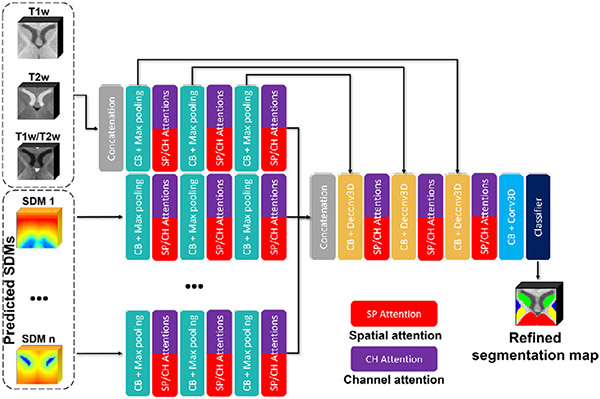
3.2.3. M2A-Unet Architecture
To sufficiently exploit both multi-modal appearance information and the spatial context information, we simultaneously feed both the multi-modal intensity images and the generated high-quality SDMs into the proposed M2A-Unet through different encoding paths, which is shown in Fig. 4 and detailed as follows.
Fig. 4.
The architecture of the proposed M2A-Unet at the fine stage.
There are two parts included in the input of the M2A-Unet: a) the multi-modal MR images are still input into one encoding path in a multi-channel manner; b) the SDMs predicted by the SDM-Unet are separately fed through different encoding paths. Specifically, unlike the multi-modal MR images, the SDMs contain spatial context information of each specific subcortical structure. Therefore, to effectively integrate the subcortical spatial context information, we construct individual encoding paths for the SDMs of each subcortical structure, making it possible to fully leverage all SDMs to extract more high-level features. Besides, similar to the SDM-Unet, we keep using three encoding blocks for each encoding path.
Meanwhile, to better leverage both SAB and CAB, following the suggestions of (Roy et al., 2018), we also organized the SABs and CABs parallelly and added them after each encoding and decoding block. A max-out mechanism was performed to efficiently fuse the complementary information extracted by each pair of SAB and CAB:
| (10) |
Finally, due to the (H + 1) encoding paths included in the M2A-Unet, it could be significantly complex to implement the skip connections for each encoding path. Therefore, as the multi-modal MR images accommodate exhaustive intensity information, we just linked the skip connections for the encoding blocks belonging to the encoding path of the multi-modal MR images to lessen the complexity of the proposed M2A-Unet and recover more useful details.
3.2.4. M2A-Unet Loss function
Herein, we still use the aforementioned Dice loss for the M2A-Unet training. It is worth noting that different from the SDM-Unet, by introducing the boundary labels, the total number of labels is 26, i.e., 12 structural labels, 12 inner boundary labels, 1 outer boundary label, and 1 background:
| (11) |
4. Experiments
4.1. Dataset and experimental setup
UNC/UMN Baby Connectome Project (BCP).
To sufficiently evaluate the proposed framework, we randomly selected 48 infant MRI scans from the UNC/UMN Baby Connectome Project (BCP) (Howell et al., 2019). The 48 scans belong to 4 age groups (12 scans per age group) from birth to two postnatal years (i.e., 0M-3M, 6M, 12M, 18M-24M). Each scan includes both T1w and T2w images with a resolution of 0.8 × 0.8 × 0.8 mm3. For each scan, we performed the FLIRT in FSL (Jenkinson et al., 2012) to linearly align T2w image onto the T1w image. Then, the T1w/T2w image was calculated by voxel-wisely dividing the T1w image by the T2w image. We also performed the N3 (Sled et al., 1998) on T1w and T2w images to correct intensity inhomogeneity. 1 scan from each age group are randomly selected to perform the histogram matching based on the intensity.
To generate reliable manual subcortical labels as ground-truth, we first took advantage of our proposed infant-dedicated 4D brain atlas (Chen et al., 2022) (including the subcortical labels) to generate the initial subcortical segmentations by warping the age-specific atlas subcortical labels to each individual scan using ANTs registration toolbox (Avants et al., 2009). Specifically, as the subcortical structures are established during the third trimester, it is possible to accurately propagate the subcortical labels from each age-specific atlas to individual scans from the BCP dataset. Second, two trained experts (each expert has more than 4 years of experience in infant brain MR image segmentation) performed manual correction based on the obtained initial automatic subcortical segmentations to correct segmentation errors based on T1w, T2w, and the T1w/T2w ratio images using ITK-SNAP software (Yushkevich et al., 2016) under the guidance of an experienced neuroradiologist, as we have done for data in MICCAI Grand Challenges iSeg 2017 and 2019 (Sun et al., 2021; Wang et al., 2019). For example, for each suspicious label, we first localized it in the 3 canonical views, i.e., axial, sagittal, and coronal views. Then, we determined its correct label based on the three images (T1w, T2w, and T1w/T2w) by considering 3 views together. We also filled the holes and removed the bulges with the help of surface rendering. In general, for the 12M, 18M, and 24M scans, it took 2 days to correct one scan, while the correction of the 0M, 3M, and 6M scans took almost 3 days per scan due to the low tissue contrast. In sum, the subcortical structures of all 48 scans were manually delineated into bilaterally symmetric 12 classes (each hemisphere includes the thalamus, caudate, putamen, pallidum, hippocampus, and amygdala). To simplify the network of M2A-Unet, we merged the 12 subcortical structures into six classes and calculated the corresponding ground-truth SDMs, which were used as the ground-truth to train the coarse-stage SDM-Unet and fed into M2A-Unet to generate refined subcortical segmentations.
Due to the distinct age-specific tissue contrast and appearance of the infant brain MR images within each age group, we trained networks for each age group, respectively. To validate our method, given an age group, a stratified 6-fold cross-validation strategy is employed, and each fold consists of 10 training images and 2 testing images. We performed the ablation study and selected hyper-parameters based on 6-month images.
We used a Linux workstation (Intel Xeon E5-2650 CPU (8 cores 16 threads) and NVIDIA TITAN Xp 12 GB GPUs) to train and test the proposed framework, which was implemented using TensorFlow 1.15. Parameters of SDM-Unet and M2A-Unet are experimentally set as: learning rate of Adam optimizer = 0.0001, kernel size of each network = 4, stride = 2, , and . , which is enough to guarantee the accuracy of the predicted segmentation map. The segmentation was performed in a patch-wise manner, with a patch size of 32 × 32 × 32. To avoid confusing the left and right structures during the patch-based training, we only performed random rotation and random scaling as data augmentation by utilizing the preprocessing strategies provided by the TensorFlow.Keras.preprocessing package, while avoiding flipping.
We compared the proposed method with the following methods: two commonly used software packages FIRST in FSL (Jenkinson et al., 2012) and Infant FreeSurfur (InfantFS) (Zöllei et al., 2020); state-of-the-art deep learning segmentation methods, including SA-net (Xue et al., 2019) (regarding as the baseline in the ablation study), V-net (Milletari et al., 2016), LiviaNet (Dolz et al., 2018), three top-ranked methods, i.e., xflz, CU_SIAT, and RB, in the iSeg2019 challenge (Multi-Site Infant Brain Segmentation Algorithms) (Sun et al., 2021), -net (Liu et al., 2020), nnUnet (Isensee et al., 2021), and MAML (an extension of nnUnet with dedicated framework for multi-modal medical images) (Zhang et al., 2021). For the learning-based methods, we experimentally set the learning rate and epoch numbers, respectively. In detail, the learning rates of V-net, LiviaNet, and -net were set to 0.0001, while the learning rates of SA-net, nnUnet, and MAML were set to 0.001. The learning rates for the xflz, CU_SIAT, and SmartDSP were set to 0.0002. The epoch numbers of each competing method were enlarged, and an early stop strategy was applied to ensure the convergence of each method during training. For the patch-based methods, their patch sizes were also set to a patch size of 32 × 32 × 32. To ensure a fair comparison, we also used the three MR modalities as multi-channel input to train and test each deep learning-based competing method.
The segmentation results were quantitatively evaluated by the Dice similarity coefficient (DSC) and average symmetric surface distance (ASSD) (mean and standard deviation). The DSC values mainly evaluate the overlapping between the ground-truth labels and the estimated labels, while the ASSD measures the surface distance between each pair of labels, which is more sensitive to the outliers.
developing Human Connectome Project (dHCP).
To evaluate the generalizability and the domain adaptation capability of the trained framework, we further introduced the developing Human Connectome Project (dHCP) dataset (Makropoulos et al., 2018) (including neonatal subjects with multi-modal brain imaging data (between 23–44 weeks post-menstrual age (PMA))), which were acquired by different scanners with different protocols. The dHCP dataset provides both T1w and T2w images with a resolution of 0.5 × 0.5 × 0.5 mm3. We randomly selected 5 scans with the age of around 33 weeks PMA and 5 scans with the age of more than 40 weeks PMA to perform the domain adaptation test and generalizability test, respectively. Similar to generating the ground-truth segmentation maps of the BCP dataset, we also warped the subcortical labels from our infant-dedicated 4D brain atlas (Chen et al., 2022) to the 10 dHCP scans using ANTs registration toolbox (Avants et al., 2009) as initial label maps. Then, each label map was manually-corrected by the same experts under the same procedures. For the generalizability test, we directly performed the trained 0M-3M framework to segment the 5 dHCP scans with the age of more than 40 weeks PMA. To verify the domain adaptation capability, we performed 5 fold cross-validation using the leave-one-out strategy. Note that all 10 scans were preprocessed by histogram-matching to the same BCP scan as mentioned above.
4.2. Results on BCP infant dataset
In this section, we qualitatively and quantitatively performed experiments on the BCP datasets to validate the performance of the proposed framework on infant subcortical segmentation, compared to other competing methods. Meanwhile, a comprehensive ablation study is provided to verify the effectiveness of each component newly added in the proposed framework. Finally, a hyper-parameter selection is included to detail the choosing of suitable hyper-parameters.
4.2.1. Qualitative comparison
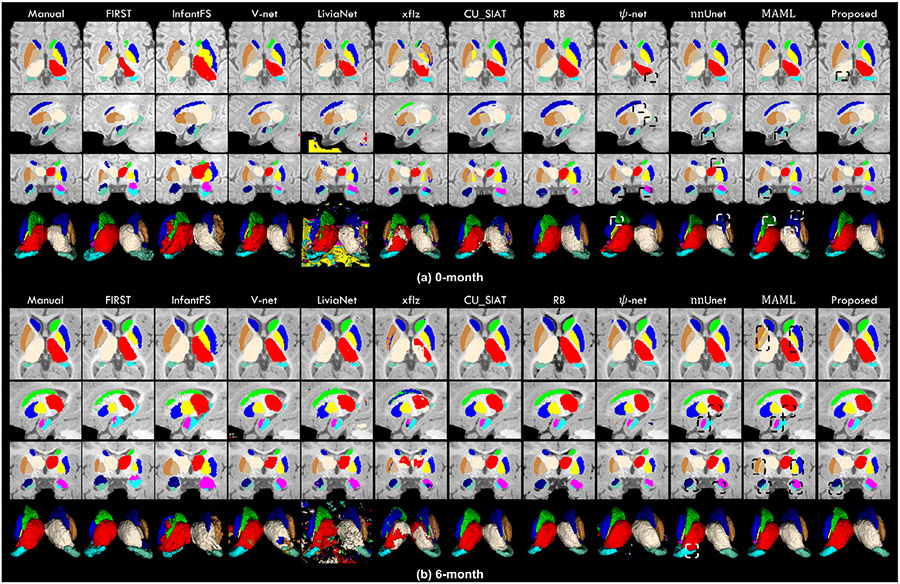
In Fig. 5, to evaluate the segmentation performance of our framework, we visually compared the segmentation results obtained by our method and other five competing methods on two randomly selected images from 0-month (Fig. 5 (a)) and 6-month (Fig. 5 (b)) age groups, respectively. In Fig. 5, the first column is the manual delineation, which is used as the ground-truth. The first 3 rows are 3 typical slices from 3 canonical views, i.e., axial, sagittal, and coronal views, respectively. The last row is mesh surfaces.
Fig. 5.
Visual comparison of the segmentation results of the 12 subcortical structures on both 0-month and 6-month T1w images, obtained from manual delineation and eleven automatic methods. Some differences are marked by boxes for evaluating convenience.
Markedly, we can find that the segmentations achieved by the proposed framework exhibit overall higher consistency with the manual delineations. Meanwhile, potentially attributed to the delineated structural inner and outer boundary labels, in our segmentation results, the boundaries of each subcortical structure are smoother than the results obtained by other competing methods. It is worth noting that by sufficiently leveraging the informative SDMs as spatial context, our framework can be trained to effectively learn the position, shape, and interstructural relationship of each subcortical structure, which leads to an accurate segmentation free of outliers. In comparison, some competing methods segmented both the 0-month and 6-month images poorly with lots of overshoots, missing voxels, and outliers, which may severely influence the practical applications and needs further post-processing. The others erroneously assigned the left-side labels to the right-side structures in both scans. In fact, due to the similar intensity between the left and right subcortical structures, all competing methods, although not obvious in Fig. 5, suffered from the missing assignments of the left and right labels. Potentially attributing to the spatial information included in the SDMs, by feeding the high-quality SDMs into the M2A-Unet, along with the original discrete structural labels, our framework can learn the shape, position, and relationships between the left and right subcortical structures to help identify the left and right labels, making our framework successfully survived this harmful issue. Finally, compared to other competing methods, the proposed framework can segment the amygdala and hippocampus much more precisely. Of note, the amygdala is the smallest subcortical structure, and the hippocampus has the most complicated shape. Thus, the above-mentioned results suggest that our framework can well segment each subcortical structure on infant brain MR images, making it highly useful in investigating the early development of the subcortex.
4.2.2. Quantitative comparison
In this subsection, we quantitatively compared the proposed framework with other competing methods, and summarized the values of DSC and ASSD of each subcortical label in Table 1 and Table 2, respectively. From Table 1 and Table 2, we have three observations.
Table 1.
The DSC (in %) values of the 12 subcortical structures of each age group.
| Age | Structure | FIRST | InfantFS | V-Net | LiviaNet | xflz | CU_SIAT | RB | -net | nnUnet | MAML | Our method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0M-3M | Thalamus_L | 83.5 ± 3.1 | 72.2 ± 4.3 | 80.5 ± 3.7 | 81.9 ± 3.0 | 82.3 ± 2.8 | 82.7 ± 2.3 | 83.4 ± 3.5 | 86.5 ± 6.7 | 92.4 ± 1.3 | 92.7 ± 1.1 | 94.5 ± 1.0 |
| Caudate_L | 65.3 ± 9.8 | 74.1 ± 9.1 | 76.9 ± 6.2 | 80.7 ± 2.4 | 80.8 ± 2.2 | 73.1 ± 7.2 | 83.4 ± 2.2 | 83.9 ± 5.4 | 87.3 ± 4.1 | 88.4 ± 3.3 | 90.9 ± 1.5 | |
| Putamen_L | 72.3 ± 4.2 | 71.3 ± 8.1 | 78.9 ± 3.4 | 80.9 ± 6.4 | 79.1 ± 5.8 | 83.2 ± 2.8 | 79.8 ± 7.0 | 82.3 ± 8.8 | 89.1 ± 3.6 | 89.7 ± 3.0 | 91.7 ± 1.7 | |
| Pallidum_L | 71.4 ± 8.2 | 68.7 ± 5.2 | 75.8 ± 6.4 | 71.8 ± 5.3 | 77.2 ± 4.0 | 77.6 ± 3.7 | 81.8 ± 2.9 | 79.2 ± 6.5 | 83.0 ± 6.6 | 83.7 ± 6.3 | 86.1 ± 3.1 | |
| Hippocampus_L | 68.9 ± 4.2 | 64.2 ± 9.9 | 73.0 ± 4.8 | 73.7 ± 5.4 | 72.7 ± 5.9 | 70.3 ± 7.5 | 85.0 ± 3.6 | 75.0 ± 6.6 | 84.2 ± 5.3 | 84.7 ± 4.9 | 88.4 ± 2.8 | |
| Amygdala_L | 55.0 ± 7.6 | 62.3 ± 6.8 | 73.6 ± 5.5 | 68.1 ± 5.1 | 62.8 ± 4.2 | 73.9 ± 4.5 | 79.4 ± 2.8 | 77.2 ± 7.9 | 81.8 ± 1.3 | 82.7 ± 6.8 | 86.9 ± 3.2 | |
| Thalamus_R | 81.9 ± 3.8 | 72.3 ± 3.5 | 82.3 ± 5.8 | 80.0 ± 6.9 | 84.0 ± 3.0 | 82.0 ± 2.7 | 83.3 ± 2.6 | 85.2 ± 6.1 | 91.5 ± 2.2 | 92.6 ± 1.7 | 95.0 ± 1.0 | |
| Caudate_R | 68.9 ± 8.2 | 75.0 ± 6.3 | 78.8 ± 4.9 | 80.3 ± 5.2 | 79.1 ± 4.1 | 70.1 ± 6.7 | 81.0 ± 4.6 | 81.2 ± 4.1 | 86.6 ± 3.8 | 88.9 ± 2.9 | 91.0 ± 1.6 | |
| Putamen_R | 76.3 ± 3.4 | 72.0 ± 2.5 | 78.9 ± 4.0 | 81.2 ± 4.1 | 78.3 ± 2.8 | 86.1 ± 1.9 | 77.4 ± 7.9 | 76.4 ± 7.8 | 86.3 ± 4.5 | 87.6 ± 3.6 | 91.8 ± 1.5 | |
| Pallidum_R | 72.9 ± 6.5 | 70.4 ± 5.9 | 75.9 ± 5.3 | 75.8 ± 8.0 | 75.3 ± 7.1 | 80.4 ± 3.4 | 82.6 ± 2.1 | 78.7 ± 5.7 | 81.0 ± 4.9 | 82.2 ± 3.1 | 85.9 ± 2.2 | |
| Hippocampus_R | 63.0 ± 6.2 | 67.4 ± 4.8 | 71.6 ± 8.3 | 73.9 ± 9.2 | 73.8 ± 3.4 | 66.1 ± 6.9 | 85.9 ± 4.0 | 77.6 ± 8.7 | 81.8 ± 4.3 | 83.7 ± 3.6 | 88.2 ± 1.6 | |
| Amygdala_R | 53.7 ± 7.3 | 61.9 ± 6.2 | 67.9 ± 9.7 | 65.4 ± 5.3 | 61.3 ± 3.8 | 70.2 ± 3.1 | 80.7 ± 4.2 | 75.5 ± 9.2 | 79.9 ± 7.4 | 81.8 ± 6.9 | 85.5 ± 5.6 | |
| 6M | Thalamus_L | 83.1 ± 1.9 | 87.6 ± 2.7 | 89.4 ± 2.6 | 88.0 ± 1.3 | 87.4 ± 2.8 | 90.7 ± 1.6 | 92.6 ± 1.4 | 90.1 ± 1.0 | 93.9 ± 1.5 | 94.2 ± 1.2 | 96.3 ± 0.5 |
| Caudate_L | 84.9 ± 1.7 | 88.1 ± 1.7 | 85.9 ± 3.0 | 86.9 ± 1.9 | 90.4 ± 2.4 | 90.3 ± 1.6 | 90.1 ± 2.7 | 86.2 ± 4.6 | 91.2 ± 1.7 | 91.6 ± 1.5 | 94.7 ± 0.7 | |
| Putamen_L | 74.7 ± 3.3 | 78.0 ± 4.6 | 81.8 ± 3.1 | 86.9 ± 2.2 | 87.8 ± 3.5 | 82.0 ± 4.3 | 89.7 ± 2.4 | 86.6 ± 3.3 | 90.1 ± 1.1 | 90.9 ± 1.0 | 93.4 ± 0.9 | |
| Pallidum_L | 76.5 ± 3.0 | 79.8 ± 6.2 | 82.8 ± 4.6 | 86.6 ± 1.6 | 89.1 ± 3.3 | 82.8 ± 3.2 | 89.4 ± 3.3 | 85.3 ± 4.1 | 90.5 ± 1.8 | 91.2 ± 1.4 | 92.7 ± 1.5 | |
| Hippocampus_L | 64.0 ± 4.8 | 72.2 ± 6.9 | 78.5 ± 6.2 | 81.1 ± 3.2 | 82.5 ± 4.6 | 79.1 ± 4.0 | 80.1 ± 4.9 | 83.1 ± 6.6 | 86.2 ± 4.0 | 87.0 ± 3.2 | 90.5 ± 1.4 | |
| Amygdala_L | 49.2 ± 4.3 | 57.9 ± 3.7 | 78.1 ± 3.1 | 81.1 ± 2.7 | 80.4 ± 3.2 | 83.3 ± 3.5 | 80.8 ± 2.8 | 82.6 ± 1.9 | 82.9 ± 3.3 | 83.9 ± 1.9 | 89.2 ± 2.0 | |
| Thalamus_R | 84.9 ± 1.8 | 87.3 ± 4.3 | 89.3 ± 1.7 | 85.7 ± 2.3 | 90.0 ± 2.4 | 89.9 ± 3.0 | 91.9 ± 2.8 | 89.7 ± 3.0 | 93.8 ± 1.7 | 94.1 ± 1.3 | 96.2 ± 0.4 | |
| Caudate_R | 84.5 ± 1.9 | 87.3 ± 2.4 | 87.9 ± 1.2 | 87.9 ± 1.0 | 88.7 ± 3.6 | 88.4 ± 2.9 | 90.8 ± 3.7 | 86.4 ± 4.2 | 90.4 ± 1.9 | 91.0 ± 1.1 | 94.2 ± 1.0 | |
| Putamen_R | 73.4 ± 3.9 | 76.7 ± 7.3 | 81.9 ± 3.2 | 85.6 ± 2.7 | 85.5 ± 4.3 | 83.7 ± 5.4 | 88.8 ± 2.5 | 85.1 ± 2.1 | 89.4 ± 2.0 | 90.2 ± 1.4 | 93.9 ± 1.1 | |
| Pallidum_R | 80.7 ± 2.3 | 79.8 ± 5.8 | 78.3 ± 3.8 | 86.8 ± 3.7 | 87.5 ± 3.7 | 83.3 ± 3.7 | 89.6 ± 3.3 | 86.7 ± 2.6 | 90.2 ± 2.6 | 90.8 ± 2.2 | 92.3 ± 1.4 | |
| Hippocampus_R | 67.2 ± 3.9 | 77.8 ± 6.3 | 78.7 ± 2.6 | 81.9 ± 4.1 | 83.7 ± 2.6 | 86.5 ± 2.8 | 80.5 ± 4.7 | 84.0 ± 3.1 | 86.5 ± 3.1 | 86.7 ± 3.3 | 90.7 ± 1.2 | |
| Amygdala_R | 50.8 ± 4.4 | 58.1 ± 3.9 | 77.2 ± 3.7 | 78.6 ± 3.3 | 76.3 ± 4.0 | 82.4 ± 1.5 | 77.7 ± 6.6 | 80.2 ± 2.2 | 83.4 ± 3.9 | 84.6 ± 3.7 | 88.8 ± 2.1 | |
| 12M | Thalamus_L | 86.8 ± 2.9 | 88.5 ± 3.6 | 89.5 ± 3.3 | 91.0 ± 1.0 | 90.1 ± 1.8 | 92.0 ± 0.8 | 93.9 ± 1.9 | 93.6 ± 1.4 | 94.1 ± 1.7 | 94.0 ± 1.5 | 96.3 ± 0.8 |
| Caudate_L | 85.3 ± 2.1 | 84.9 ± 3.7 | 88.2 ± 3.7 | 91.2 ± 1.5 | 88.2 ± 1.5 | 92.4 ± 1.1 | 92.9 ± 1.6 | 92.1 ± 1.8 | 92.8 ± 1.9 | 93.1 ± 1.3 | 94.8 ± 1.1 | |
| Putamen_L | 80.0 ± 3.2 | 83.4 ± 2.9 | 88.3 ± 2.9 | 89.7 ± 1.5 | 89.2 ± 1.2 | 85.9 ± 3.6 | 92.3 ± 2.3 | 90.5 ± 1.9 | 92.6 ± 2.0 | 92.5 ± 2.2 | 95.7 ± 1.4 | |
| Pallidum_L | 81.8 ± 2.5 | 82.8 ± 2.6 | 88.6 ± 3.6 | 92.3 ± 1.1 | 86.1 ± 3.1 | 90.0 ± 2.3 | 92.1 ± 1.9 | 93.7 ± 1.6 | 93.6 ± 1.4 | 93.9 ± 1.5 | 95.2 ± 1.0 | |
| Hippocampus_L | 82.2 ± 2.4 | 79.3 ± 5.5 | 85.8 ± 3.9 | 87.9 ± 2.3 | 84.5 ± 5.1 | 86.1 ± 3.4 | 88.1 ± 2.3 | 88.5 ± 2.1 | 88.9 ± 1.9 | 88.7 ± 1.5 | 91.8 ± 1.6 | |
| Amygdala_L | 54.5 ± 6.5 | 56.7 ± 5.7 | 74.1 ± 4.8 | 74.5 ± 5.8 | 78.9 ± 3.6 | 85.4 ± 4.6 | 84.8 ± 3.0 | 86.3 ± 3.6 | 87.4 ± 1.9 | 87.6 ± 1.5 | 89.6 ± 1.7 | |
| Thalamus_R | 87.9 ± 2.3 | 89.2 ± 1.5 | 88.7 ± 2.8 | 89.9 ± 1.4 | 91.5 ± 2.0 | 90.3 ± 1.4 | 92.4 ± 1.5 | 92.9 ± 1.1 | 93.5 ± 1.2 | 93.4 ± 0.8 | 96.0 ± 1.0 | |
| Caudate_R | 89.3 ± 1.8 | 88.9 ± 2.8 | 90.0 ± 2.4 | 89.9 ± 2.2 | 91.3 ± 1.7 | 90.7 ± 1.5 | 92.6 ± 3.3 | 93.1 ± 1.3 | 94.0 ± 1.1 | 94.3 ± 1.1 | 95.4 ± 1.1 | |
| Putamen_R | 87.8 ± 1.4 | 86.1 ± 5.2 | 88.8 ± 3.2 | 89.2 ± 2.5 | 88.4 ± 1.9 | 90.1 ± 1.8 | 93.3 ± 1.9 | 93.5 ± 1.7 | 93.9 ± 1.4 | 93.9 ± 1.5 | 95.1 ± 1.2 | |
| Pallidum_R | 83.9 ± 2.5 | 82.1 ± 3.8 | 87.0 ± 3.8 | 90.6 ± 1.9 | 89.2 ± 2.2 | 89.6 ± 2.8 | 89.8 ± 2.1 | 90.3 ± 2.3 | 90.1 ± 3.0 | 90.5 ± 2.0 | 94.8 ± 1.2 | |
| Hippocampus_R | 78.7 ± 4.9 | 78.1 ± 7.3 | 82.7 ± 3.6 | 84.3 ± 3.7 | 87.2 ± 3.6 | 86.6 ± 4.3 | 88.6 ± 1.7 | 85.4 ± 2.0 | 87.9 ± 2.1 | 87.7 ± 1.3 | 90.1 ± 2.3 | |
| Amygdala_R | 57.7 ± 5.1 | 60.7 ± 4.2 | 73.2 ± 3.7 | 73.1 ± 4.3 | 81.2 ± 4.5 | 87.5 ± 5.3 | 86.4 ± 2.4 | 87.5 ± 2.6 | 86.7 ± 3.1 | 87.2 ± 1.1 | 89.0 ± 2.4 | |
| 18M-24M | Thalamus_L | 89.2 ± 0.8 | 88.7 ± 1.1 | 91.5 ± 2.2 | 92.4 ± 1.5 | 92.5 ± 2.6 | 93.3 ± 2.0 | 94.1 ± 1.6 | 93.7 ± 1.6 | 94.2 ± 1.9 | 93.9 ± 1.8 | 96.6 ± 0.4 |
| Caudate_L | 86.0 ± 2.9 | 87.2 ± 1.3 | 90.4 ± 2.6 | 90.9 ± 1.8 | 89.4 ± 3.8 | 92.0 ± 1.6 | 93.0 ± 0.9 | 92.7 ± 0.9 | 93.2 ± 0.6 | 93.7 ± 0.7 | 95.0 ± 1.5 | |
| Putamen_L | 89.3 ± 2.3 | 82.0 ± 3.3 | 91.4 ± 2.0 | 92.9 ± 1.3 | 89.2 ± 2.1 | 88.0 ± 3.2 | 91.8 ± 2.7 | 92.3 ± 1.6 | 92.9 ± 1.8 | 92.5 ± 1.9 | 95.2 ± 1.7 | |
| Pallidum_L | 86.4 ± 2.7 | 85.7 ± 2.9 | 91.4 ± 1.9 | 92.0 ± 2.1 | 87.1 ± 3.3 | 92.8 ± 1.8 | 92.8 ± 2.3 | 92.2 ± 1.9 | 93.4 ± 1.9 | 93.4 ± 1.2 | 94.9 ± 1.6 | |
| Hippocampus_L | 82.0 ± 2.0 | 81.6 ± 3.1 | 85.9 ± 2.9 | 88.3 ± 2.2 | 87.8 ± 3.7 | 90.3 ± 1.8 | 89.8 ± 2.0 | 89.4 ± 1.9 | 90.6 ± 1.5 | 90.7 ± 1.1 | 92.2 ± 1.3 | |
| Amygdala_L | 62.6 ± 6.9 | 61.7 ± 7.1 | 78.8 ± 5.9 | 76.7 ± 6.0 | 80.6 ± 2.9 | 85.7 ± 3.0 | 84.1 ± 4.8 | 87.9 ± 2.9 | 86.8 ± 2.2 | 88.1 ± 1.0 | 89.7 ± 2.1 | |
| Thalamus_R | 88.0 ± 1.3 | 89.1 ± 1.1 | 90.6 ± 2.6 | 91.4 ± 1.6 | 91.2 ± 2.3 | 93.4 ± 1.3 | 93.9 ± 1.2 | 94.2 ± 1.0 | 94.4 ± 1.2 | 94.0 ± 1.6 | 96.5 ± 0.7 | |
| Caudate_R | 90.0 ± 2.2 | 89.5 ± 2.1 | 90.4 ± 2.8 | 91.7 ± 0.9 | 91.1 ± 2.0 | 92.9 ± 2.3 | 90.6 ± 2.8 | 91.9 ± 1.2 | 92.4 ± 1.1 | 93.2 ± 1.3 | 95.2 ± 1.2 | |
| Putamen_R | 89.2 ± 1.3 | 87.1 ± 3.2 | 91.2 ± 1.9 | 91.5 ± 1.4 | 88.6 ± 4.1 | 87.3 ± 2.8 | 90.9 ± 3.1 | 92.4 ± 2.7 | 92.3 ± 1.7 | 92.8 ± 1.5 | 94.4 ± 1.3 | |
| Pallidum_R | 88.0 ± 2.2 | 85.5 ± 3.1 | 89.3 ± 2.9 | 91.0 ± 1.5 | 89.7 ± 2.4 | 90.4 ± 2.0 | 91.8 ± 1.8 | 91.1 ± 3.1 | 91.2 ± 3.3 | 91.9 ± 2.6 | 92.9 ± 1.1 | |
| Hippocampus_R | 82.4 ± 5.6 | 77.6 ± 3.2 | 83.2 ± 2.2 | 85.5 ± 3.4 | 85.3 ± 4.1 | 87.3 ± 2.2 | 88.8 ± 1.2 | 86.2 ± 2.8 | 89.1 ± 1.8 | 88.5 ± 3.1 | 90.7 ± 1.9 | |
| Amygdala_R | 60.8 ± 4.6 | 61.5 ± 3.5 | 79.0 ± 4.7 | 76.0 ± 3.7 | 81.2 ± 6.2 | 86.4 ± 3.9 | 82.4 ± 4.3 | 87.4 ± 3.6 | 86.4 ± 3.8 | 86.2 ± 2.5 | 89.4 ± 1.6 |
Table 2.
The ASSD (in mm) values of the 12 subcortical structures of each age group.
| Age | Structure | FIRST | InfantFS | V-Net | LiviaNet | xflz | CU_SIAT | RB | -net | nnUnet | MAML | Our method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0M-3M | Thalamus_L | 0.79 ± 0.19 | 2.47 ± 0.55 | 0.74 ± 0.29 | 7.36 ± 3.24 | 0.73 ± 0.31 | 2.13 ± 0.50 | 0.34 ± 0.14 | 0.42 ± 0.19 | 0.25 ± 0.07 | 0.26 ± 0.08 | 0.19 ± 0.04 |
| Caudate_L | 0.47 ± 0.16 | 0.52 ± 0.25 | 0.38 ± 0.15 | 5.72 ± 1.75 | 0.65 ± 0.21 | 2.02 ± 0.35 | 0.21 ± 0.09 | 0.11 ± 0.02 | 0.10 ± 0.02 | 0.13 ± 0.04 | 0.06 ± 0.01 | |
| Putamen_L | 0.62 ± 0.17 | 2.44 ± 0.50 | 0.29 ± 0.19 | 5.34 ± 2.03 | 1.26 ± 0.44 | 2.28 ± 0.39 | 0.27 ± 0.13 | 0.17 ± 0.02 | 0.16 ± 0.05 | 0.15 ± 0.05 | 0.11 ± 0.02 | |
| Pallidum_L | 0.27 ± 0.12 | 1.72 ± 0.42 | 0.50 ± 0.01 | 3.03 ± 1.52 | 0.84 ± 0.34 | 1.85 ± 0.27 | 0.25 ± 0.09 | 0.13 ± 0.03 | 0.13 ± 0.04 | 0.10 ± 0.03 | 0.07 ± 0.01 | |
| Hippocampus_L | 0.36 ± 0.21 | 0.88 ± 0.43 | 0.45 ± 0.14 | 6.70 ± 1.03 | 1.47 ± 0.51 | 2.20 ± 0.44 | 0.32 ± 0.10 | 0.29 ± 0.11 | 0.17 ± 0.05 | 0.14 ± 0.04 | 0.10 ± 0.01 | |
| Amygdala_L | 0.62 ± 0.26 | 0.45 ± 0.11 | 0.23 ± 0.11 | 2.56 ± 0.90 | 1.18 ± 0.37 | 1.11 ± 0.19 | 0.23 ± 0.12 | 0.16 ± 0.03 | 0.13 ± 0.03 | 0.10 ± 0.02 | 0.07 ± 0.01 | |
| Thalamus_R | 0.75 ± 0.17 | 2.69 ± 0.60 | 0.60 ± 0.16 | 5.63 ± 1.09 | 0.82 ± 0.34 | 1.87 ± 0.41 | 0.29 ± 0.08 | 0.09 ± 0.01 | 0.12 ± 0.04 | 0.08 ± 0.01 | 0.05 ± 0.01 | |
| Caudate_R | 0.25 ± 0.10 | 0.62 ± 0.21 | 0.36 ± 0.14 | 2.80 ± 0.96 | 0.80 ± 0.25 | 2.13 ± 0.38 | 0.28 ± 0.13 | 0.05 ± 0.01 | 0.06 ± 0.03 | 0.05 ± 0.03 | 0.03 ± 0.01 | |
| Putamen_R | 0.75 ± 0.03 | 2.90 ± 0.40 | 0.31 ± 0.12 | 5.86 ± 1.96 | 1.41 ± 0.38 | 2.16 ± 0.28 | 0.23 ± 0.11 | 0.15 ± 0.04 | 0.14 ± 0.04 | 0.13 ± 0.03 | 0.08 ± 0.01 | |
| Pallidum_R | 0.30 ± 0.12 | 1.40 ± 0.36 | 0.52 ± 0.19 | 3.02 ± 1.03 | 0.74 ± 0.26 | 2.03 ± 0.21 | 0.24 ± 0.13 | 0.19 ± 0.03 | 0.17 ± 0.07 | 0.15 ± 0.04 | 0.10 ± 0.02 | |
| Hippocampus_R | 0.50 ± 0.23 | 0.84 ± 0.47 | 0.34 ± 0.16 | 4.26 ± 1.07 | 1.50 ± 0.64 | 2.41 ± 0.35 | 0.28 ± 0.11 | 0.15 ± 0.03 | 0.12 ± 0.03 | 0.10 ± 0.03 | 0.08 ± 0.02 | |
| Amygdala_R | 0.46 ± 0.21 | 0.38 ± 0.12 | 0.28 ± 0.13 | 1.73 ± 0.83 | 1.37 ± 0.39 | 1.42 ± 0.24 | 0.18 ± 0.08 | 0.12 ± 0.01 | 0.11 ± 0.02 | 0.08 ± 0.02 | 0.06 ± 0.01 | |
| 6M | Thalamus_L | 0.64 ± 0.18 | 0.61 ± 0.18 | 2.87 ± 0.98 | 6.63 ± 1.91 | 1.33 ± 0.34 | 0.45 ± 0.15 | 0.36 ± 0.10 | 0.24 ± 0.02 | 0.19 ± 0.04 | 0.14 ± 0.03 | 0.10 ± 0.02 |
| Caudate_L | 0.44 ± 0.11 | 0.33 ± 0.12 | 1.24 ± 0.41 | 1.44 ± 0.48 | 0.52 ± 0.17 | 0.43 ± 0.17 | 0.31 ± 0.12 | 0.10 ± 0.02 | 0.09 ± 0.03 | 0.08 ± 0.03 | 0.04 ± 0.01 | |
| Putamen_L | 0.47 ± 0.16 | 0.45 ± 0.15 | 0.88 ± 0.19 | 2.86 ± 1.29 | 0.55 ± 0.21 | 0.33 ± 0.10 | 0.22 ± 0.09 | 0.18 ± 0.03 | 0.14 ± 0.04 | 0.13 ± 0.02 | 0.11 ± 0.02 | |
| Pallidum_L | 0.31 ± 0.19 | 0.55 ± 0.21 | 0.30 ± 0.14 | 1.97 ± 0.84 | 0.35 ± 0.11 | 0.37 ± 0.17 | 0.27 ± 0.08 | 0.14 ± 0.05 | 0.12 ± 0.04 | 0.12 ± 0.03 | 0.06 ± 0.01 | |
| Hippocampus_L | 0.69 ± 0.31 | 0.44 ± 0.21 | 2.17 ± 0.91 | 3.22 ± 1.26 | 0.86 ± 0.38 | 1.03 ± 0.30 | 0.19 ± 0.09 | 0.14 ± 0.03 | 0.11 ± 0.03 | 0.15 ± 0.04 | 0.08 ± 0.02 | |
| Amygdala_L | 1.15 ± 0.62 | 0.66 ± 0.30 | 2.93 ± 1.06 | 1.86 ± 1.02 | 0.48 ± 0.27 | 0.95 ± 0.43 | 0.24 ± 0.10 | 0.13 ± 0.02 | 0.12 ± 0.03 | 0.11 ± 0.02 | 0.06 ± 0.01 | |
| Thalamus_R | 0.61 ± 0.19 | 0.62 ± 0.20 | 2.34 ± 0.83 | 4.76 ± 1.91 | 1.41 ± 0.55 | 0.57 ± 0.18 | 0.29 ± 0.14 | 0.19 ± 0.02 | 0.15 ± 0.02 | 0.14 ± 0.02 | 0.09 ± 0.01 | |
| Caudate_R | 0.60 ± 0.13 | 0.37 ± 0.18 | 1.35 ± 0.53 | 1.06 ± 0.46 | 0.64 ± 0.24 | 0.45 ± 0.20 | 0.24 ± 0.11 | 0.08 ± 0.03 | 0.09 ± 0.04 | 0.09 ± 0.03 | 0.04 ± 0.01 | |
| Putamen_R | 0.43 ± 0.15 | 0.46 ± 0.11 | 1.04 ± 0.30 | 3.73 ± 1.33 | 0.46 ± 0.18 | 0.36 ± 0.14 | 0.18 ± 0.07 | 0.14 ± 0.02 | 0.17 ± 0.04 | 0.16 ± 0.04 | 0.10 ± 0.01 | |
| Pallidum_R | 0.23 ± 0.06 | 0.66 ± 0.24 | 0.26 ± 0.15 | 1.59 ± 0.81 | 0.33 ± 0.11 | 0.44 ± 0.22 | 0.20 ± 0.10 | 0.16 ± 0.04 | 0.13 ± 0.02 | 0.09 ± 0.03 | 0.07 ± 0.01 | |
| Hippocampus_R | 0.72 ± 0.46 | 0.53 ± 0.24 | 2.50 ± 1.16 | 2.95 ± 1.05 | 0.79 ± 0.26 | 0.98 ± 0.27 | 0.17 ± 0.08 | 0.19 ± 0.06 | 0.15 ± 0.04 | 0.11 ± 0.03 | 0.07 ± 0.02 | |
| Amygdala_R | 1.55 ± 0.56 | 0.53 ± 0.24 | 2.90 ± 1.53 | 3.31 ± 1.02 | 0.50 ± 0.23 | 0.97 ± 0.48 | 0.25 ± 0.11 | 0.16 ± 0.06 | 0.14 ± 0.04 | 0.14 ± 0.03 | 0.07 ± 0.01 | |
| 12M | Thalamus_L | 0.34 ± 0.13 | 0.58 ± 0.23 | 1.17 ± 0.41 | 5.32 ± 1.03 | 0.37 ± 0.17 | 0.27 ± 0.09 | 0.23 ± 0.07 | 0.28 ± 0.02 | 0.18 ± 0.05 | 0.16 ± 0.05 | 0.10 ± 0.02 |
| Caudate_L | 0.37 ± 0.17 | 0.24 ± 0.12 | 0.74 ± 0.31 | 1.90 ± 0.58 | 0.31 ± 0.12 | 0.51 ± 0.28 | 0.21 ± 0.08 | 0.07 ± 0.01 | 0.08 ± 0.02 | 0.07 ± 0.02 | 0.04 ± 0.01 | |
| Putamen_L | 0.36 ± 0.16 | 0.33 ± 0.17 | 0.54 ± 0.18 | 1.00 ± 0.51 | 0.58 ± 0.22 | 0.65 ± 0.32 | 0.19 ± 0.07 | 0.22 ± 0.06 | 0.18 ± 0.05 | 0.20 ± 0.05 | 0.07 ± 0.01 | |
| Pallidum_L | 0.19 ± 0.08 | 0.24 ± 0.10 | 0.20 ± 0.11 | 3.59 ± 1.37 | 0.27 ± 0.13 | 0.30 ± 0.15 | 0.21 ± 0.08 | 0.16 ± 0.03 | 0.22 ± 0.06 | 0.19 ± 0.04 | 0.04 ± 0.01 | |
| Hippocampus_L | 0.49 ± 0.19 | 0.29 ± 0.12 | 0.38 ± 0.18 | 4.32 ± 1.34 | 0.60 ± 0.26 | 0.58 ± 0.32 | 0.25 ± 0.13 | 0.20 ± 0.08 | 0.19 ± 0.05 | 0.21 ± 0.06 | 0.08 ± 0.02 | |
| Amygdala_L | 0.57 ± 0.26 | 0.55 ± 0.20 | 0.13 ± 0.05 | 1.31 ± 0.69 | 0.44 ± 0.18 | 0.40 ± 0.14 | 0.20 ± 0.07 | 0.17 ± 0.05 | 0.18 ± 0.03 | 0.17 ± 0.03 | 0.09 ± 0.02 | |
| Thalamus_R | 0.27 ± 0.11 | 0.51 ± 0.15 | 1.00 ± 0.66 | 4.31 ± 1.05 | 0.41 ± 0.20 | 0.24 ± 0.06 | 0.27 ± 0.11 | 0.21 ± 0.07 | 0.16 ± 0.04 | 0.16 ± 0.03 | 0.05 ± 0.01 | |
| Caudate_R | 0.45 ± 0.18 | 0.28 ± 0.12 | 0.71 ± 0.29 | 1.93 ± 0.46 | 0.47 ± 0.24 | 0.55 ± 0.23 | 0.19 ± 0.11 | 0.05 ± 0.01 | 0.06 ± 0.02 | 0.05 ± 0.01 | 0.04 ± 0.01 | |
| Putamen_R | 0.27 ± 0.10 | 0.30 ± 0.11 | 0.82 ± 0.43 | 1.58 ± 0.85 | 0.55 ± 0.22 | 0.46 ± 0.20 | 0.23 ± 0.10 | 0.15 ± 0.04 | 0.17 ± 0.05 | 0.17 ± 0.04 | 0.05 ± 0.01 | |
| Pallidum_R | 0.21 ± 0.08 | 0.28 ± 0.12 | 0.18 ± 0.10 | 3.40 ± 1.72 | 0.34 ± 0.14 | 0.41 ± 0.14 | 0.17 ± 0.07 | 0.14 ± 0.03 | 0.15 ± 0.05 | 0.14 ± 0.06 | 0.04 ± 0.01 | |
| Hippocampus_R | 0.39 ± 0.25 | 0.24 ± 0.11 | 0.62 ± 0.38 | 3.56 ± 1.43 | 0.66 ± 0.23 | 0.62 ± 0.37 | 0.19 ± 0.08 | 0.16 ± 0.06 | 0.17 ± 0.07 | 0.16 ± 0.04 | 0.06 ± 0.01 | |
| Amygdala_R | 0.48 ± 0.23 | 0.42 ± 0.18 | 0.12 ± 0.04 | 1.51 ± 0.81 | 0.42 ± 0.13 | 0.45 ± 0.12 | 0.22 ± 0.08 | 0.16 ± 0.04 | 0.18 ± 0.03 | 0.17 ± 0.03 | 0.07 ± 0.02 | |
| 18M-24M | Thalamus_L | 0.24 ± 0.09 | 0.46 ± 0.17 | 0.43 ± 0.14 | 3.57 ± 0.63 | 0.23 ± 0.11 | 0.26 ± 0.11 | 0.21 ± 0.6 | 0.08 ± 0.02 | 0.13 ± 0.04 | 0.15 ± 0.05 | 0.05 ± 0.02 |
| Caudate_L | 0.16 ± 0.05 | 0.23 ± 0.10 | 0.43 ± 0.26 | 0.64 ± 0.32 | 0.56 ± 0.17 | 0.55 ± 0.18 | 0.16 ± 0.03 | 0.05 ± 0.01 | 0.05 ± 0.01 | 0.04 ± 0.01 | 0.03 ± 0.01 | |
| Putamen_L | 0.18 ± 0.07 | 0.41 ± 0.12 | 0.14 ± 0.03 | 1.56 ± 0.41 | 0.43 ± 0.15 | 0.51 ± 0.26 | 0.17 ± 0.07 | 0.10 ± 0.03 | 0.09 ± 0.03 | 0.11 ± 0.04 | 0.08 ± 0.02 | |
| Pallidum_L | 0.20 ± 0.05 | 0.28 ± 0.09 | 0.08 ± 0.02 | 1.23 ± 0.84 | 0.32 ± 0.13 | 0.22 ± 0.10 | 0.14 ± 0.05 | 0.05 ± 0.01 | 0.06 ± 0.02 | 0.07 ± 0.02 | 0.05 ± 0.01 | |
| Hippocampus_L | 0.27 ± 0.10 | 0.39 ± 0.17 | 0.15 ± 0.11 | 2.51 ± 0.94 | 0.37 ± 0.16 | 0.44 ± 0.14 | 0.20 ± 0.09 | 0.10 ± 0.04 | 0.12 ± 0.04 | 0.11 ± 0.03 | 0.10 ± 0.04 | |
| Amygdala_L | 0.45 ± 0.14 | 0.67 ± 0.20 | 0.16 ± 0.10 | 1.62 ± 0.63 | 0.29 ± 0.12 | 0.36 ± 0.16 | 0.17 ± 0.06 | 0.08 ± 0.01 | 0.10 ± 0.02 | 0.09 ± 0.02 | 0.09 ± 0.02 | |
| Thalamus_R | 0.22 ± 0.09 | 0.41 ± 0.15 | 0.37 ± 0.19 | 2.64 ± 0.58 | 0.24 ± 0.14 | 0.25 ± 0.13 | 0.23 ± 0.07 | 0.07 ± 0.01 | 0.12 ± 0.03 | 0.09 ± 0.03 | 0.05 ± 0.01 | |
| Caudate_R | 0.18 ± 0.07 | 0.19 ± 0.09 | 0.45 ± 0.19 | 0.69 ± 0.31 | 0.49 ± 0.17 | 0.60 ± 0.22 | 0.16 ± 0.05 | 0.04 ± 0.01 | 0.06 ± 0.02 | 0.05 ± 0.02 | 0.02 ± 0.01 | |
| Putamen_R | 0.16 ± 0.06 | 0.43 ± 0.12 | 0.12 ± 0.03 | 1.36 ± 0.35 | 0.35 ± 0.16 | 0.47 ± 0.21 | 0.20 ± 0.09 | 0.10 ± 0.03 | 0.07 ± 0.02 | 0.06 ± 0.02 | 0.06 ± 0.01 | |
| Pallidum_R | 0.22 ± 0.05 | 0.31 ± 0.13 | 0.09 ± 0.01 | 1.07 ± 0.68 | 0.24 ± 0.11 | 0.27 ± 0.08 | 0.17 ± 0.06 | 0.06 ± 0.01 | 0.08 ± 0.02 | 0.07 ± 0.02 | 0.06 ± 0.01 | |
| Hippocampus_R | 0.28 ± 0.10 | 0.47 ± 0.13 | 0.15 ± 0.10 | 4.65 ± 2.33 | 0.41 ± 0.26 | 0.42 ± 0.13 | 0.21 ± 0.07 | 0.11 ± 0.02 | 0.09 ± 0.03 | 0.12 ± 0.04 | 0.07 ± 0.02 | |
| Amygdala_R | 0.40 ± 0.13 | 0.36 ± 0.10 | 0.11 ± 0.04 | 1.49 ± 0.52 | 0.33 ± 0.17 | 0.33 ± 0.09 | 0.20 ± 0.10 | 0.05 ± 0.01 | 0.08 ± 0.04 | 0.07 ± 0.02 | 0.05 ± 0.01 |
First, compared to the competing methods, our framework has higher DSC values for all 12 subcortical structures in all four age groups and also achieves improved ASSD values on the vast majority of subcortical structures across the age groups examined. In comparison, LiviaNet obtained relatively high DSC values, but its performance on the ASSD metric is poor, which could be attributed to the countless outliers, as illustrated in Fig. 5. The superior performance on both metrics suggesting that our coarse-to-fine framework can effectively exploit the spatial information to refine the segmentation and reduce outliers.
Second, our framework performs much better in segmenting 0-month and 6-month images, while the others cannot segment the images acquired during these age ranges very well, especially for the hippocampus and amygdala. Note that it is very challenging to obtain promising segmentation on images acquired within the first several months of age, due to the extremely small structural sizes and extremely low tissue contrast. These results imply that the proposed framework has successfully learned to exploit the spatial context information included in the SDMs to extenuate the severe influence from low tissue contrast and accurately segment the infant subcortex. Moreover, it also validates that by introducing both the spatial and channel attention blocks, the proposed framework can pay more attention to vital regions and channels and ignore the less relevant information, helping enhance the utilization of the noisy intensity images and SDMs to further amend the aforementioned discords in infant brain MR images.
Third, although the competing methods, such as the -net, nnUnet, and MAML, have obvious improvements in segmenting the images acquired after 12-month, and achieve lower ASSD values in the segmentation of the amygdala at 24-month, our framework still outperforms the others in both DSC and ASSD metrics for all 12 subcortical structures at 12-month and 11 structures at 24-month (except for the left amygdala with slightly lower accuracy). As the 24-month brain MR images have a similar appearance and contrast to the adult brain MR image, this result further implies that incorporating the SDM of each specific subcortical structure can not only remedy the issue of the low tissue contrast to accurately segment the infant subcortex but also is highly valuable for the adult brain subcortical segmentation.
In summary, compared to competing methods, our method achieved the mean DSC with a remarkable improvement by 2.6% (from 89.8% to 92.4%, p – value = 3.6e−4) and the mean ASSD significantly reduced almost 42% (from 0.12 mm to 0.07 mm, p – value = 3.4e−3), which strongly suggests the superior performance of our method on the challenge infant subcortical segmentation task.
4.2.3. Ablation study
In this subsection, we regarded the SA-net (Xue et al., 2019) as the baseline and performed an ablation study to evaluate the effectiveness of the multi-modal images and robust loss function of the proposed SDM-Unet, including:
1) using only T1w images and replacing Closs with the norm (SDM-Unet + T1w Closs + (SA-net));
2) using only T1w images (SDM-Unet + T1w);
3) using both T1w and T2w images (SDM-Unet + T1w, T2w);
4) using both T1w, T2w, and T1w/T2w images (SDM-Unet + T1w,T2w,T1w/T2w).
Additionally, to indicate the effectiveness of attention blocks and boundary labels in the proposed M2A-Unet, we performed additional ablation studies on the performance of our framework as follows,
5) removing boundary labels (BL) and all attention blocks (Att) (Proposed - BL - Att);
6) removing boundary labels (Proposed - BL).
The ablation study was carried out on the 6-month infant images with the lowest tissue contrast in terms of both DSC and ASSD metrics, which are summarized in Table 3. The SDM-Unet is designed to estimate the SDMs of the 6 bilaterally symmetric subcortical structures. Therefore, we merged the results of our framework into 6 classes.
Table 3.
The ablation study of the bilaterally merged 6 subcortical structures within 6-month age group in terms of DSC (in %) and ASSD (in mm).
| Thalamus |
Caudate |
Putamen |
Pallidum |
Hippocampus |
Amygdala |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DSC | ASSD | DSC | ASSD | DSC | ASSD | DSC | ASSD | DSC | ASSD | DSC | ASSD | |
| SDM-Unet + T1 - Closs + (SA-net) | 91.5 ± 2.1 | 0.39 ± 0.13 | 89.8 ± 1.6 | 0.27 ± 0.08 | 88.5 ± 2.7 | 0.34 ± 0.09 | 87.1 ± 2.8 | 0.56 ± 0.24 | 86.2 ± 3.1 | 0.53 ± 0.20 | 81.3 ± 2.9 | 0.50 ± 0.14 |
| SDM-Unet + T1 | 92.1 ± 1.6 | 0.37 ± 0.15 | 89.3 ± 1.5 | 0.32 ± 0.11 | 88.9 ± 2.2 | 0.35 ± 0.10 | 88.1 ± 2.6 | 0.49 ± 0.17 | 86.6 ± 3.9 | 0.51 ± 0.22 | 81.9 ± 3.1 | 0.44 ± 0.17 |
| SDM-Unet + T1,T2 | 93.3 ± 0.8 | 0.28 ± 0.11 | 90.6 ± 1.1 | 0.30 ± 0.08 | 91.2 ± 2.0 | 0.24 ± 0.06 | 90.9 ± 1.4 | 0.24 ± 0.07 | 88.3 ± 2.1 | 0.37 ± 0.10 | 83.7 ± 2.4 | 0.32 ± 0.12 |
| SDM-Unet + T1,T2,T1/T2 | 93.8 ± 0.3 | 0.21 ± 0.09 | 92.2 ± 0.7 | 0.26 ± 0.07 | 91.9 ± 1.4 | 0.20 ± 0.05 | 90.7 ± 1.3 | 0.23 ± 0.08 | 88.8 ± 1.7 | 0.33 ± 0.11 | 85.2 ± 2.7 | 0.27 ± 0.09 |
| Proposed - BL - Att | 94.9 ± 0.5 | 0.16 ± 0.05 | 92.9 ± 0.6 | 0.13 ± 0.03 | 92.8 ± 1.2 | 0.15 ± 0.04 | 91.9 ± 1.2 | 0.17 ± 0.05 | 89.9 ± 1.6 | 0.20 ± 0.06 | 88.1 ± 2.8 | 0.17 ± 0.06 |
| Proposed - BL | 95.9 ± 0.4 | 0.14 ± 0.03 | 93.8 ± 0.7 | 0.10 ± 0.02 | 93.1 ± 1.3 | 0.12 ± 0.03 | 92.2 ± 1.1 | 0.15 ± 0.03 | 90.4 ± 1.7 | 0.16 ± 0.02 | 88.7 ± 2.4 | 0.13 ± 0.02 |
| Proposed | 96.3 ± 0.5 | 0.09 ± 0.02 | 94.3 ± 0.9 | 0.04 ± 0.01 | 93.7 ± 1.0 | 0.10 ± 0.02 | 92.5 ± 1.5 | 0.07 ± 0.01 | 90.6 ± 1.3 | 0.07 ± 0.02 | 89.0 ± 2.1 | 0.06 ± 0.01 |
From Table 3, we can find that our SDM-Unet with the robust Closs term achieved improved performance, compared to the baseline SA-net, which can further strengthen the performance of the fine stage M2A-Unet. Moreover, by taking advantage of the extra information provided by the multi-model images, especially the T1w/T2w images, the performance of the proposed framework upgrades obviously. By introducing the fine stage M2A-Unet, both DSC and ASSD metrics improved significantly, suggesting a positive effect of exerting the proposed M2A-UNet. Such improvements could be caused by directly inputting the SDMs with multiple encoding paths, which allows the auspicious learning of the spatial context information. Besides, by inducing both spatial and channel attention blocks, the performance of the proposed framework is further enhanced, highlighting the effectiveness of the attention blocks and the importance of the features learned by different encoding paths. Last of all, the proposed framework trained with labels including boundary delineations consistently yields better performance, suggesting the significance of guiding the network to focus on precisely segmenting the boundaries of subcortical structures.
4.2.4. Selection of hyper-parameters
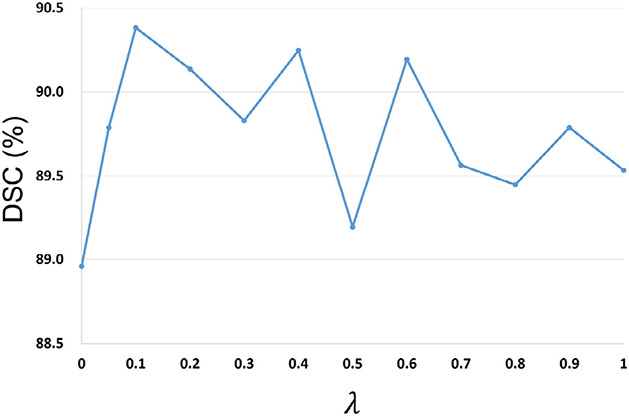
Our framework includes two hyper-parameters, i.e., as the loss weight parameter and the kernel bandwidth in the coarse-stage SDM-Unet, which could influence the segmentation accuracy. Specifically, appropriately choosing can help mitigate the bad influence of outliers to enhance the training stability. 6-month infant images are the most difficult to segment due to their lowest tissue contrast. Therefore, carefully tuning in segmenting 6-month infant images could help enhance the segmentation accuracy. In contrast, scans within other age ranges have better tissue contrast, making their segmentation relatively easier and less sensitive to . On the other hand, a suitable is used to help Closs well measure the similarity between the ground-truth SDMs and the generated SDMs. As the ground-truth SDMs of scans within different age ranges have similar distributions, the proper values for models of different age groups should be similar. Thus, we can select the proper value during the model training for one age group and conveniently apply it to other training models. In sum, we performed the selection of hyper-parameters on the 6-month infant images in terms of DSC metric. To choose a suitable , we first removed the and performed the SDM-Unet on the 6-month scans. Then, the was added with different values of to testify the trade-off between two loss terms. The DSC ratios of SDM-Unet with different kernel sizes and loss weight parameters are shown in Fig. 6 and Fig. 7, respectively.
Fig. 6.
DSC ratios of SDM-Unet with different kernel sizes .
Fig. 7.
DSC ratios of SDM-Unet with different loss weight parameters .
As shown in Fig. 6, if the values of were too small, our framework performed poorly. Along with the increase of , the DSC ratio kept increasing and finally tended to be stable, as the was approximately equivalent to the classic MSE with an infinite . Therefore, was set to 0.8.
As shown in Fig. 7, it is obvious that by adding the , the performance of the SDM-Unet can be further improved; while if is too large, the could dominate the loss function, making the suboptimized. Based on the above results, we set to 0.1.
4.3. Results on unrelated dHCP neonatal dataset
4.3.1. Qualitative comparison
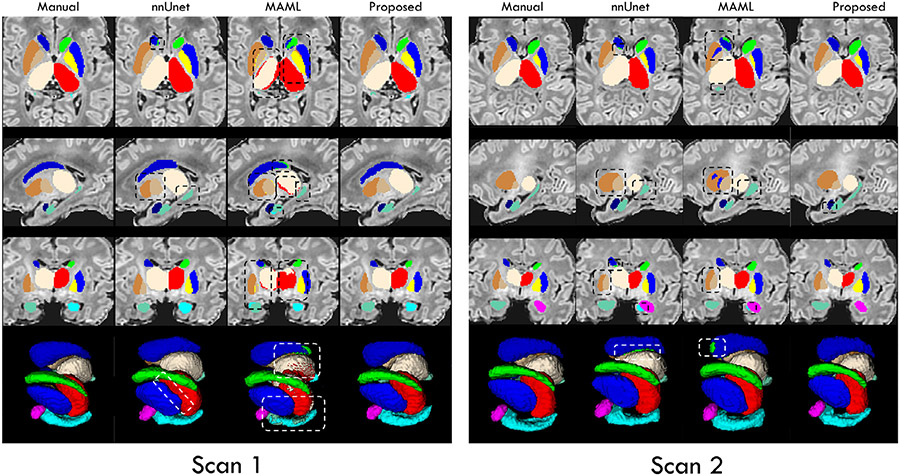
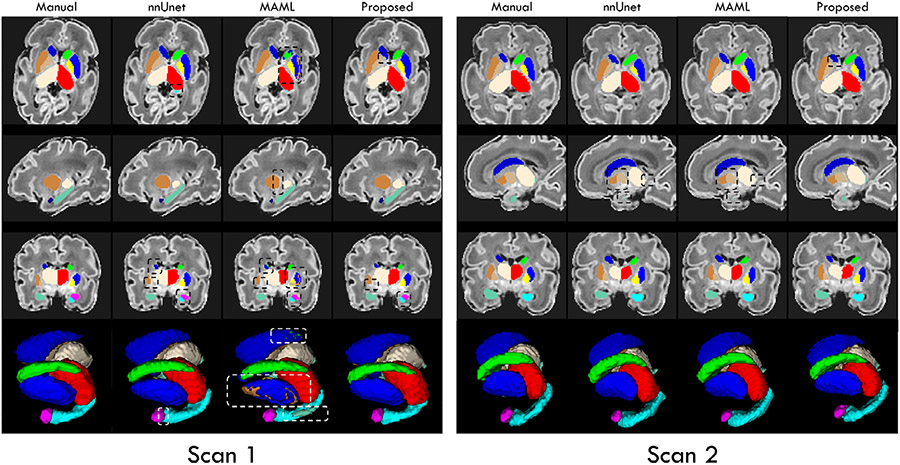
In Figs. 8 and 9, to verify the generalizability and domain adaptation ability of our framework, we qualitatively compared the segmentation results achieved by our trained framework and the state-of-the-art methods on 4 dHCP scans with the age of around 33 weeks and more than 40 weeks PMA, respectively. The first 3 rows illustrate the labels of subcortical structures in 3 canonical views, i.e., axial, sagittal, and coronal views, respectively. The mesh surfaces are shown in the last row.
Fig. 8.
Visual comparison of the segmentation results of the 12 subcortical structures on dHCP scans with age of more than 40 weeks PMA, obtained by directly applying our trained framework and the trained state-of-the-art methods. Some differences are marked by boxes for evaluating convenience.
Fig. 9.
Visual comparison of the segmentation results of the 12 subcortical structures on dHCP scans with age of around 33 weeks PMA, obtained by fine-tuning our trained framework and the trained state-of-the-art methods. Some differences are marked by boxes for evaluating convenience.
Generalizability.
Markedly, from Fig. 8, we can find that the segmentation maps achieved by our trained framework exhibit much better accuracy with significantly more complete segmentation of each subcortical structure, compared to the trained nnUNet and MAML. Particularly, our framework still obtained segmentation maps without any outliers, while the results from nnUNet and MAML contain a large number of missing labeled voxels, which obviously confused the left and right subcortical structures. Finally, nnUNet and MAML segmented the subcortical structures with obvious overshoots, especially for the thalamus and hippocampus. On the contrary, our trained framework can still well segment the hippocampus with a complicated shape. Therefore, these results further verified the great generalizability of the proposed framework, which could be attributed to the introduced anatomical context information.
Domain adaptation.
From Fig. 9, we can observe that after fine-tuning on the dHCP dataset, our trained framework can achieve significantly improved segmentations of each subcortical structure on the premature birth scans, compared to the trained nnUNet and MAML. On the contrary, similar to Fig. 8, the results from MAML existed the miss-assigned labels to the left and right subcortical structures. Besides, nnUNet and MAML segmented the subcortical structures with distinct missing labels, such as the thalamus and hippocampus. Oppositely, the results of our trained framework are much more consistent with the manual-corrected labels. Thus, by performing a simple fine-tuning procedure, our framework can again guarantee satisfied segmentation results on the out-of-domain brain MR images, making it applicable for other practical tasks.
4.3.2. Quantitative comparison
In Tables 4 and 5, we respectively presented the DSC ratio and ASSD values of the dHCP scans with the age of around 33 weeks and more than 40 weeks PMA to quantitatively evaluate the generalizability and domain adaptation ability of our framework, compared to the state-of-the-art nnUNet and MAML methods.
Table 4. Generalizability.
the DSC (in %) and ASSD (in mm) values of the 12 subcortical structures on dHCP scans with age of around 40 weeks PMA.
| nnUnet |
MAML |
Our method |
||||
|---|---|---|---|---|---|---|
| Structure | DSC | ASSD | DSC | ASSD | DSC | ASSD |
| Thalamus_L | 86.2 ± 2.3 | 0.59 ± 0.17 | 88.6 ± 1.7 | 0.46 ± 0.13 | 91.1 ± 2.6 | 0.22 ± 0.05 |
| Caudate_L | 68.6 ± 6.1 | 0.70 ± 0.16 | 75.5 ± 3.8 | 0.60 ± 0.22 | 84.6 ± 3.3 | 0.14 ± 0.04 |
| Putamen_L | 69.6 ± 4.4 | 0.87 ± 0.29 | 75.0 ± 5.2 | 0.65 ± 0.19 | 85.1 ± 2.8 | 0.10 ± 0.03 |
| Pallidum_L | 71.1 ± 5.5 | 0.28 ± 0.10 | 79.9 ± 3.2 | 0.23 ± 0.04 | 84.5 ± 2.2 | 0.13 ± 0.05 |
| Hippocampus_L | 74.9 ± 2.6 | 0.57 ± 0.14 | 71.4 ± 2.4 | 0.71 ± 0.19 | 82.4 ± 3.5 | 0.16 ± 0.04 |
| Amygdala_L | 72.4 ± 4.3 | 0.20 ± 0.04 | 79.7 ± 3.6 | 0.13 ± 0.03 | 82.8 ± 2.4 | 0.13 ± 0.02 |
| Thalamus_R | 85.3 ± 2.1 | 0.63 ± 0.19 | 87.6 ± 2.2 | 0.38 ± 0.08 | 91.4 ± 2.9 | 0.25 ± 0.06 |
| Caudate_R | 69.4 ± 2.3 | 0.53 ± 0.21 | 74.4 ± 4.2 | 0.55 ± 0.16 | 84.2 ± 3.4 | 0.19 ± 0.04 |
| Putamen_R | 67.2 ± 6.0 | 0.72 ± 0.16 | 73.2 ± 6.6 | 0.57 ± 0.17 | 86.3 ± 2.7 | 0.12 ± 0.02 |
| Pallidum_R | 70.0 ± 4.1 | 0.58 ± 0.15 | 81.6 ± 3.0 | 0.31 ± 0.07 | 83.9 ± 2.7 | 0.15 ± 0.05 |
| Hippocampus_R | 76.7 ± 3.2 | 0.62 ± 0.13 | 72.3 ± 3.1 | 0.66 ± 0.13 | 84.0 ± 2.8 | 0.14 ± 0.03 |
| Amygdala_R | 75.0 ± 5.1 | 0.18 ± 0.04 | 78.1 ± 4.3 | 0.14 ± 0.04 | 81.9 ± 2.5 | 0.11 ± 0.03 |
Table 5. Domain adaptation ability.
the DSC (in %) and ASSD (in mm) values of the 12 subcortical structures on dHCP scans with age of around 33 weeks PMA.
| nnUnet |
MAML |
Our method |
||||
|---|---|---|---|---|---|---|
| Structure | DSC | ASSD | DSC | ASSD | DSC | ASSD |
| Thalamus_L | 91.7 ± 2.0 | 0.23 ± 0.04 | 90.9 ± 2.2 | 0.26 ± 0.05 | 94.7 ± 1.5 | 0.14 ± 0.04 |
| Caudate_L | 86.4 ± 4.0 | 0.10 ± 0.05 | 85.3 ± 5.3 | 0.15 ± 0.06 | 90.6 ± 2.9 | 0.08 ± 0.02 |
| Putamen_L | 90.5 ± 2.1 | 0.12 ± 0.03 | 86.7 ± 3.0 | 0.17 ± 0.05 | 93.1 ± 2.2 | 0.10 ± 0.03 |
| Pallidum_L | 85.2 ± 3.4 | 0.17 ± 0.06 | 82.7 ± 4.8 | 0.29 ± 0.09 | 87.7 ± 3.0 | 0.14 ± 0.06 |
| Hippocampus_L | 80.9 ± 3.6 | 0.18 ± 0.07 | 78.2 ± 4.3 | 0.20 ± 0.06 | 86.1 ± 2.5 | 0.11 ± 0.03 |
| Amygdala_L | 84.5 ± 4.3 | 0.09 ± 0.03 | 80.2 ± 7.7 | 0.11 ± 0.05 | 87.8 ± 2.4 | 0.07 ± 0.02 |
| Thalamus_R | 91.0 ± 2.5 | 0.20 ± 0.04 | 91.3 ± 1.7 | 0.19 ± 0.03 | 93.9 ± 1.7 | 0.16 ± 0.04 |
| Caudate_R | 87.2 ± 3.8 | 0.12 ± 0.05 | 87.4 ± 3.6 | 0.13 ± 0.03 | 92.0 ± 1.8 | 0.10 ± 0.03 |
| Putamen_R | 91.0 ± 1.8 | 0.08 ± 0.03 | 88.6 ± 3.9 | 0.19 ± 0.06 | 92.7 ± 2.3 | 0.12 ± 0.02 |
| Pallidum_R | 85.4 ± 2.9 | 0.18 ± 0.05 | 81.3 ± 4.9 | 0.28 ± 0.07 | 86.8 ± 3.4 | 0.14 ± 0.04 |
| Hippocampus_R | 82.1 ± 4.1 | 0.17 ± 0.08 | 81.0 ± 3.7 | 0.16 ± 0.04 | 88.0 ± 2.8 | 0.09 ± 0.02 |
| Amygdala_R | 83.7 ± 3.5 | 0.08 ± 0.02 | 82.5 ± 6.8 | 0.09 ± 0.04 | 86.3 ± 2.6 | 0.08 ± 0.02 |
Generalizability.
From Table 4, we can observe that after histogram matching, our framework still consistently performed well on the out-of-domain dHCP dataset, which exhibited overall superior performance on each subcortical structure in both DSC ratio and ASSD values, compared to the competing methods. In detail, the DSC ratio increased 7.1% (from 78.1% to 85.2%, p – value = 5.1e−3) and ASSD values reduced 66.8% (from 0.45 mm to 0.15 mm, p – value = 6.5e−5), which could be attributed to the well learned features from SDMs. These results further testified the remarked generalizability of our framework in neonatal datasets.
Domain adaptation.
In Table 5, by implementing the fine-tuning on the dHCP scans with age of around 33 weeks PMA, our framework still mostly outperformed the competing methods (except for the ASSD value of Pallidum_R), where the DSC ratio increased 3.4% (from 86.6% to 90.0%, p – value = 7.2e−4) and ASSD values reduced 21% (from 0.14 mm to 0.11 mm, p – value = 5.9e−4). To sum up, our framework presented a good domain adaptation ability on limited labeled scans as ground-truth.
5. Conclusion and future works
In this work, we propose a novel spatial context-guided, coarse-to-fine, attention-based deep neural framework to precisely segment the 12 subcortical structures in infant brain MR images in an end-to-end manner. At the coarse stage, to cope with the extremely low tissue contrast in infant brain MR images, we took advantage of the spatial context information contained in the ground-truth SDMs by directly predicting SDMs from the multi-modal MR images, including T1w, T2w, and contrast-enhanced T1w/T2w ratio images. To improve the robustness to the outliers and enhance the training stability, we introduced the Correntropy-based loss to robustly measure the similarity between the predicted SDMs and ground-truth SDMs. At the fine stage, to sufficiently exploit the multi-modal MR images and the predicted informative SDMs, we further designed a multi-source and multi-path attention Unet (M2A-Unet) to effectively leverage the appearance information (multi-modal MR images) and the spatial context information (predicted SDMs) to refine the segmentation. In particular, both spatial and channel attentions mechanisms were deployed in the proposed M2A-Unet to help highlight the most relevant subregions and feature maps, thus mitigating the bad influence of the low tissue contrast and dynamic appearance changes. Besides, the inner and outer boundaries of each subcortical structure were delineated to help supervise the M2A-Unet to pay more attention to the ambiguous structural boundaries. Comprehensive experimental results illustrate that the segmentation accuracy of each subcortical structure achieved by our framework is remarkably higher than six state-of-the-art methods. Meanwhile, our framework also shows good generalizability and domain adaptation ability in segmenting neonatal brain MR images.
Although trust-worthy results were achieved by our method of segmenting both neonatal and infant brain subcortical structures, simply fusing multiple modalities in the later stages or fusing each modality as an input channel could lead to sub-optimal results. To more effectively leverage the multi-modality and context information to deliver enhanced results, inspired by the recent successes achieved by the contrastive learning methods, which disentangle the multimodal images into factors with separate meanings, we will explore such methods and introduce them in our future works on infant subcortical segmentation tasks.
Acknowledgment
This work was partially supported by NIH grants (NIH: MH116225, NIH: MH117943, NIH: MH109773, NIH: MH123202, NIH: AG075582, and NIH: NS128534). This work also utilizes approaches developed by an NIH grant (NIH: 1U01MH110274) and the efforts of the UNC/UMN Baby Connectome Project Consortium.
Footnotes
Data and Code Availability Statement
The UNC/UMN Baby Connectome Project (BCP) dataset and the developing Human Connectome Project (dHCP) dataset that support the findings of this study are publicly available. We will make the codes publicly available after the approval of the manuscript for publication.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
Credit authorship contribution statement
Liangjun Chen: Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing – original draft, Visualization. Zhengwang Wu: Methodology, Software, Investigation, Data curation, Writing – review & editing. Fenqiang Zhao: Writing – review & editing. Ya Wang: Writing – review & editing. Weili Lin: Resources, Funding acquisition. Li Wang: Methodology, Writing – review & editing, Resources, Funding acquisition. Gang Li: Conceptualization, Methodology, Investigation, Writing – review & editing, Resources, Supervision, Project administration, Funding acquisition.
Data availability
Data will be made available on request.
References
- Avants BB, Tustison N, Song G, 2009. Advanced normalization tools (ants). Insight j 2 (365), 1–35. [Google Scholar]
- Calabresi P, Picconi B, Tozzi A, Ghiglieri V, Di Filippo M, 2014. Direct and indirect pathways of basal ganglia: a critical reappraisal. Nat. Neurosci 17 (8), 1022–1030. [DOI] [PubMed] [Google Scholar]
- Chen L, Qu H, Zhao J, Chen B, Principe JC, 2016. Efficient and robust deep learning with correntropy-induced loss function. Neural Computing and Applications 27 (4), 1019–1031. [Google Scholar]
- Chen L, Wu Z, Hu D, Wang Y, Mo Z, Wang L, Lin W, Shen D, Li G, Consortium UBCP, et al. , 2020. A deep spatial context guided framework for infant brain subcortical segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 646–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, Wu Z, Hu D, Wang Y, Zhao F, Zhong T, Lin W, Wang L, Li G, 2022. A 4d infant brain volumetric atlas based on the unc/umn baby connectome project (bcp) cohort. Neuroimage 253, 119097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, Zhang H, Xiao J, Nie L, Shao J, Liu W, Chua T-S, 2017. Sca-cnn: Spatial and channel-wise attention in convolutional networks for image captioning. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 5659–5667. [Google Scholar]
- Courchesne E, Karns C, Davis H, Ziccardi R, Carper R, Tigue Z, Chisum H, Moses P, Pierce K, Lord C, et al. , 2001. Unusual brain growth patterns in early life in patients with autistic disorder: an MRI study. Neurology 57 (2), 245–254. [DOI] [PubMed] [Google Scholar]
- Criminisi A, Sharp T, Blake A, 2008. Geos: Geodesic image segmentation. In: European Conference on Computer Vision. Springer, pp. 99–112. [Google Scholar]
- Dolz J, Desrosiers C, Ayed IB, 2018. 3D fully convolutional networks for subcortical segmentation in MRI: a large-scale study. Neuroimage 170, 456–470. [DOI] [PubMed] [Google Scholar]
- Dou Q, Liu Q, Heng PA, Glocker B, 2020. Unpaired multi-modal segmentation via knowledge distillation. IEEE Trans Med Imaging 39 (7), 2415–2425. [DOI] [PubMed] [Google Scholar]
- Ecker C, Bookheimer SY, Murphy DG, 2015. Neuroimaging in autism spectrum disorder: brain structure and function across the lifespan. The Lancet Neurology 14 (11), 1121–1134. [DOI] [PubMed] [Google Scholar]
- Fabbri R, Costa LDF, Torelli JC, Bruno OM, 2008. 2D euclidean distance transform algorithms: acomparative survey. ACM Computing Surveys (CSUR) 40 (1), 1–44. [Google Scholar]
- Gilmore JH, Shi F, Woolson SL, Knickmeyer RC, Short SJ, Lin W, Zhu H, Hamer RM, Styner M, Shen D, 2012. Longitudinal development of cortical and subcortical gray matter from birth to 2 years. Cerebral cortex 22 (11), 2478–2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Van Essen DC, 2011. Mapping human cortical areas in vivo based on myelin content as revealed by t1- and t2-weighted MRI. J. Neurosci 31 (32), 11597–11616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossberg S, 2009. Cortical and subcortical predictive dynamics and learning during perception, cognition, emotion and action. Philosophical Transactions of the Royal Society B: Biological Sciences 364 (1521), 1223–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X, Yuan Y, 2019. Triple anet: Adaptive abnormal-aware attention network for wce image classification. In: International conference on medical image computing and computer-assisted intervention. Springer, pp. 293–301. [Google Scholar]
- Howell BR, Styner MA, Gao W, Yap P-T, Wang L, Baluyot K, Yacoub E, Chen G, Potts T, Salzwedel A, Li G, 2019. The UNC/UMN baby connectome project (BCP): an overview of the study design and protocol development. Neuroimage 185, 891–905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J, Shen L, Sun G, 2018. Squeeze-and-excitation networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 7132–7141. [Google Scholar]
- Iglesias JE, Sabuncu MR, Van Leemput K, Initiative ADN, et al. , 2013. Improved inference in bayesian segmentation using monte carlo sampling: application to hippocampal subfield volumetry. Med Image Anal 17 (7), 766–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isensee F, Jaeger PF, Kohl SA, Petersen J, Maier-Hein KH, 2021. Nnu-net: a self--configuring method for deep learning-based biomedical image segmentation. Nat. Methods 18 (2), 203–211. [DOI] [PubMed] [Google Scholar]
- Ito Y, 1994. Approximation capability of layered neural networks with sigmoid units on two layers. Neural Comput 6 (6), 1233–1243. [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TE, et al. , 2012. FSL. Neuroimage 62 (2), 782–790. [DOI] [PubMed] [Google Scholar]
- Jones MW, Baerentzen JA, Sramek M, 2006. 3D distance fields: a survey of techniques and applications. IEEE Trans Vis Comput Graph 12 (4), 581–599. [DOI] [PubMed] [Google Scholar]
- Kontschieder P, Kohli P, Shotton J, Criminisi A, 2013. Geof: Geodesic forests for learning coupled predictors. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 65–72. [Google Scholar]
- Lee K, Cherel M, Budin F, Gilmore J, Consing KZ, Rasmussen J, Wadhwa PD, Entringer S, Glasser MF, Van Essen DC, et al. , 2015. Early postnatal myelin content estimate of white matter via t1w/t2w ratio. In: Medical Imaging 2015: Biomedical Applications in Molecular, Structural, and Functional Imaging, Vol. 9417. International Society for Optics and Photonics, p. 94171R. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Huang R, Ding Z, Gatenby JC, Metaxas DN, Gore JC, 2011. A level set method for image segmentation in the presence of intensity inhomogeneities with application to mri. IEEE Trans. Image Process 20 (7), 2007–2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Xu C, Gui C, Fox MD, 2010. Distance regularized level set evolution and its application to image segmentation. IEEE Trans. Image Process 19 (12), 3243–3254. [DOI] [PubMed] [Google Scholar]
- Li G, Chen M-H, Li G, Wu D, Lian C, Sun Q, Shen D, Wang L, 2019. A longitudinal MRI study of amygdala and hippocampal subfields for infants with risk of autism. In: GLMI. Springer, pp. 164–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Wang L, Yap P-T, Wang F, Wu Z, Meng Y, Dong P, Kim J, Shi F, Rekik I, Lin W, 2019. Computational neuroanatomy of baby brains: a review. Neuroimage 185, 906–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Tan J, Wang P, Liu H, Li Z, Wang W, 2022. Anatomically constrained squeeze-and-excitation graph attention network for cortical surface parcellation. Comput. Biol. Med 140, 105113. [DOI] [PubMed] [Google Scholar]
- Liu L, Hu X, Zhu L, Fu C-W, Qin J, Heng P-A, 2020. -Net: stacking densely convolutional LSTMs for subcortical brain structure segmentation. IEEE Trans Med Imaging. [DOI] [PubMed] [Google Scholar]
- Liu W, Pokharel PP, Príncipe JC, 2007. Correntropy: properties and applications in non-gaussian signal processing. IEEE Trans. Signal Process 55 (11), 5286–5298. [Google Scholar]
- Makropoulos A, Robinson EC, Schuh A, Wright R, Fitzgibbon S, Bozek J, Counsell SJ, Steinweg J, Vecchiato K, Passerat-Palmbach J, et al. , 2018. The developing human connectome project: a minimal processing pipeline for neonatal cortical surface reconstruction. Neuroimage 173, 88–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milletari F, Navab N, Ahmadi S-A, 2016. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In: 3DV. IEEE, pp. 565–571. [Google Scholar]
- Misaki M, Savitz J, Zotev V, Phillips R, Yuan H, Young KD, Drevets WC, Bodurka J, 2015. Contrast enhancement by combining t 1-and t 2-weighted structural brain mr images. Magn Reson Med 74 (6), 1609–1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oktay O, Schlemper J, Folgoc LL, Lee M, Heinrich M, Misawa K, Mori K, McDonagh S, Hammerla NY, Kainz B, et al. , 2018. Attention u-net: learning where to look for the pancreas. arXiv preprint arXiv:1804.03999. [Google Scholar]
- Park JJ, Florence P, Straub J, Newcombe R, Lovegrove S, 2019. Deepsdf: Learning continuous signed distance functions for shape representation. In: CVPR, pp. 165–174. [Google Scholar]
- Qiu A, Fortier MV, Bai J, Zhang X, Chong Y-S, Kwek K, Saw S-M, Godfrey KM, Gluckman PD, Meaney MJ, 2013. Morphology and microstructure of subcortical structures at birth: a large-scale asian neonatal neuroimaging study. Neuroimage 65, 315–323. [DOI] [PubMed] [Google Scholar]
- Ren S, He K, Girshick R, Sun J, 2015. Faster R-CNN: Towards real-time object detection with region proposal networks. In: NeurIPS, pp. 91–99. [DOI] [PubMed] [Google Scholar]
- Richard JM, Castro DC, DiFeliceantonio AG, Robinson MJ, Berridge KC, 2013. Mapping brain circuits of reward and motivation: in the footsteps of ann kelley. Neuroscience & Biobehavioral Reviews 37 (9), 1919–1931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risacher SL, Saykin AJ, Wes JD, Shen L, Firpi HA, McDonald BC, 2009. Baseline mri predictors of conversion from mci to probable ad in the adni cohort. Curr Alzheimer Res 6 (4), 347–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy AG, Navab N, Wachinger C, 2018. Recalibrating fully convolutional networks with spatial and channel ǣqueeze and excitationǥ blocks. IEEE Trans Med Imaging 38 (2), 540–549. [DOI] [PubMed] [Google Scholar]
- Sabuncu MR, Yeo BT, Van Leemput K, Fischl B, Golland P, 2010. A generative model for image segmentation based on label fusion. IEEE Trans Med Imaging 29 (10), 1714–1729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scimeca JM, Badre D, 2012. Striatal contributions to declarative memory retrieval. Neuron 75 (3), 380–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serag A, Aljabar P, Counsell S, Boardman J, Hajnal JV, Rueckert D, 2011. Tracking developmental changes in subcortical structures of the preterm brain using multi-modal MRI. In: ISBI. IEEE, pp. 349–352. [Google Scholar]
- Shams Z, Norris DG, Marques JP, 2019. A comparison of in vivo mri based cortical myelin mapping using t1w/t2w and r1 mapping at 3t. PLoS ONE 14 (7), e0218089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC, 1998. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging 17 (1), 87–97. [DOI] [PubMed] [Google Scholar]
- Sun Y, Gao K, Wu Z, Li G, Zong X, Lei Z, Wei Y, Ma J, Yang X, Feng X, et al. , 2021. Multi-site infant brain segmentation algorithms: the iseg-2019 challenge. IEEE Trans Med Imaging 40 (5), 1363–1376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay L, Worbe Y, Thobois S, Sgambato-Faure V, Féger J, 2015. Selective dysfunction of basal ganglia subterritories: from movement to behavioral disorders. Movement Disorders 30 (9), 1155–1170. [DOI] [PubMed] [Google Scholar]
- Uddin MN, Figley TD, Marrie RA, Figley CR, Group CS, 2018. Can t1w/t2w ratio be used as a myelin-specific measure in subcortical structures? comparisons between fse-based t1w/t2w ratios, grase-based t1w/t2w ratios and multi-echo grase-based myelin water fractions. NMR Biomed 31 (3), e3868. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium W-MH, et al. , 2013. The wu-minn human connectome project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G, Zuluaga MA, Li W, Pratt R, Patel PA, Aertsen M, Doel T, David AL, Deprest J, Ourselin S, et al. , 2018. Deepigeos: a deep interactive geodesic framework for medical image segmentation. IEEE Trans Pattern Anal Mach Intell 41 (7), 1559–1572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Li G, Shi F, Cao X, Lian C, Nie D, Liu M, Zhang H, Li G, Wu Z, et al. , 2018. Volume-based analysis of 6-month-old infant brain MRI for autism biomarker identification and early diagnosis. In: MICCAI. Springer, pp. 411–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Nie D, Li G, Puybareau É, Dolz J, Zhang Q, Wang F, Xia J, Wu Z, Chen J-W, et al. , 2019. Benchmark on automatic six-month-old infant brain segmentation algorithms: the iseg-2017 challenge. IEEE Trans Med Imaging 38 (9), 2219–2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Zou N, Shen D, Ji S, 2020. Non-local u-nets for biomedical image segmentation. In: Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 34, pp. 6315–6322. [Google Scholar]
- Woo S, Park J, Lee J-Y, Kweon IS, 2018. Cbam: Convolutional block attention module. In: Proceedings of the European conference on computer vision (ECCV), pp. 3–19. [Google Scholar]
- Wu J, Zhang Y, Tang X, 2019. A joint 3D + 2D fully convolutional framework for subcortical segmentation. In: MICCAI. Springer, pp. 301–309. [Google Scholar]
- Wu J, Zhang Y, Tang X, 2019. A multi-atlas guided 3d fully convolutional network for mri-based subcortical segmentation. In: 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019). IEEE, pp. 705–708. [Google Scholar]
- Xue Y, Tang H, Qiao Z, Gong G, Yin Y, Qian Z, Huang C, Fan W, Huang X, 2019. Shape-aware organ segmentation by predicting signed distance maps. arXiv preprint arXiv:1912.03849. [Google Scholar]
- Yoshida A, Frank QY, David KY, Leopold DA, Hikosaka O, 2021. Visualization of iron-rich subcortical structures in non-human primates in vivo by quantitative susceptibility mapping at 3t mri. Neuroimage 241, 118429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich PA, Gao Y, Gerig G, 2016. Itk-snap: An interactive tool for semi-automatic segmentation of multi-modality biomedical images. In: 2016 38th annual international conference of the IEEE engineering in medicine and biology society (EMBC). IEEE, pp. 3342–3345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng G, Zheng G, 2018. Multi-stream 3d fcn with multi-scale deep supervision for multi-modality isointense infant brain mr image segmentation. In: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). IEEE, pp. 136–140. [Google Scholar]
- Zhang H, Dana K, Shi J, Zhang Z, Wang X, Tyagi A, Agrawal A, 2018. Context encoding for semantic segmentation. In: Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pp. 7151–7160. [Google Scholar]
- Zhang K, Zhang L, Lam K-M, Zhang D, 2015. A level set approach to image segmentation with intensity inhomogeneity. IEEE Trans Cybern 46 (2), 546–557. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Yang J, Tian J, Shi Z, Zhong C, Zhang Y, He Z, 2021. Modality-aware mutual learning for multi-modal medical image segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 589–599. [Google Scholar]
- Zhu L, Yang K, Zhang M, Chan LL, Ng TK, Ooi BC, 2021. Semi-supervised unpaired multi-modal learning for label-efficient medical image segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 394–404. [Google Scholar]
- Zöllei L, Iglesias JE, Ou Y, Grant PE, Fischl B, 2020. Infant freesurfer: an automated segmentation and surface extraction pipeline for t1-weighted neuroimaging data of infants 0–2 years. Neuroimage 218, 116946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou X, Dou Q, 2020. Domain knowledge driven multi-modal segmentation of anatomical brain barriers to cancer spread. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 16–26. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.