Evaluation of the treatment options for COVID-19 patients using generalized hesitant fuzzy- multi criteria decision making techniques

Abstract

The breakout of the pandemic COVID-19 has affected numerous countries and territories worldwide. As COVID-19 specific medicines yet to be invented, at present the treatment is case specific, hence identification and evaluation of different prevalent treatment options based on various criteria and attributes are very important not only from the point of view of present pandemic but also for futuristic pandemic preparedness. The present study focuses on identifying, evaluation and ranking of treatment options using Multi Criteria Decision Making (MCDM). In this regard, the existing literature, doctors and scientist were interviewed to know the current treatment options in vogue and the scale of their importance with respect to the criteria. The criteria taken are side effect, regime cost, treatment duration, plasma stability, plasma turnover, time of suppression, ease of application, drug-drug interaction, compliance, fever, pneumonia, intensive care, organ failure, macrophage activation syndrome, hemophagocytic syndrome, pregnancy, kidney problem, age. This study extended Hesitant Fuzzy Set (HFS) to Generalized Hesitant Fuzzy Sets (GHFS). Generalized Hesitant Pentagonal Fuzzy Number (GHPFN) is developed. The properties of GHPFN are demonstrated. Two types of GHPFN has been described. The GHPFN (2nd type) along with MCDM tool Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) has been applied to rank the treatment options. The result of the study ranked ‘Hydroxychloroquine’ as the first alternative followed by, ‘Plasma Exchange’, ‘Tocilizumab’, ‘Remdesivir’ and ‘Favipravir’. To check the robustness and steadiness of the proposed methodology, comparative analysis and sensitivity analysis has been conducted.

1. Introduction

Human history has faced the onslaught of diseases since its inception. Most of these diseases have been caused by viruses which have been ever present in our environment. These viruses are ever mutating and every once in a while, when they come in contact with a large throng of individuals it affects the latter like wildfire. Even though medical science has progressed by heaps and bounds, it will never be able to keep pace with the ever changing nature of these viruses, mainly due to the various hosts it captures for procreating (see Table 1 ).

Table 1.

Literature Review on application of MCDM tools for COVID-19.

Authors	Method used	Applications	Findings
[Yildrim et al., 2020] [76]	Fuzzy PROMETHEE and VIKOR	1. Evaluation of COVID-19 treatment options.	a. Plasma exchange is the most preferred alternative.
[Mardaniet al. 2020] [77]	SWARA and WASPAS with Fuzzy HFS	1. Evaluation and ranking the complexity challenges of Digital Technology (DT) intervention to control the COVID-19 pandemic.	a. Health Information System ranked as the first factor.
[Zolfani et al., 2020] [78]	Grey based decision support along with Criteria Importance Through Inter-Criteria Correlation (CRITIC) and Combined Compromise Solution (CoCoSo)	1. Temporary location selection for hospital sector for COVID-19	a. Beykoz and Bakirkoy districts of Istanbul are the most favourable location.
Ghorui et al.(2020) (Proposed Model)	GHPFN (2nd type)-TOPSIS, comparative and Sensitivity analysis with three different ranking method and interchange of weights respectively	1. Ranking of different treatment options for COVID-19	a. Hydroxychloroquine is the most preferred treatment.
[Özkan et al., 2021] [79]	Fuzzy AHP along with Multi-Objective Optimization Method by Ratio Analysis	Evaluation of criteria and COVID-19 patients for intensive care unit admission in the era of pandemic	Evaluation of ICU admission criteria is the dominant factor.
[Hezer et al., 2021] [80]	Technique for Order Performance by Similarity to Ideal Solution (TOPSIS), Vise Kriterijumsa Optimizacija I Kompromisno Resenje (VIKOR) and Complex Proportional Assessment (COPRAS) methods.	Comparative analysis of TOPSIS, VIKOR and COPRAS methods for the COVID-19 Regional Safety Assessment	COPRAS provides the closest result to the DKG report while VIKOR gives the most distant result.
[De Andrade et al., 2022] [81]	Hybrid TOPSIS and VIKOR	The impact of social welfare and COVID-19 stringency on the perceived utility of food apps	Country social welfare and success in COVID-19 control negatively affect the perceived utility of the apps. Also, success in COVID-19 control and the perceived utility of food apps positively affect the proportion of unhealthy reviews, whereas social welfare has a negative impact.
[Adabavazeh et al., 2023] [82]	Best-Worst Method(BWM)	Identifying and prioritizing resilient health system units to tackle the COVID-19 pandemic	Appropriate intervention programs and protocols should be established by WHO for crisises.

Throughout history Coronaviruses have been causing outbreaks in humans and animals [1] such as the avian influenza outbreak in 1997, the Severe Acute Respiratory Syndrome (SARS) in 2003 [2] and the severe fever with thrombocytopenia syndrome (SFTS) in China in 2010 [3].

December 2019 was another stark example where the zoonotic transmission caused a population of approximately 11.9 million people in Wuhan, China to come to a standstill [4]. The coronavirus responsible for this was designated as Coronavirus Disease 2019 (COVID-19) by the World Health Organization [5]. It spread in two stages-the Imported transmission stage wherein the individuals who had a foreign travelling history carried the virus from the foreign country to the host country. The second stage was categorized as the Community transmission stage where the virus positive individuals spread it to the healthy individuals thereby infecting the entire community. This stage lead to mass hospitalization and death of patients all across the world.

This study seeks to identify, evaluate and rank the treatment options available for COVID-19 patients. Generalized Hesitant Fuzzy Multi Criteria Decision Making Techniques has been applied for the same. In this non-deterministic environment Fuzzy logic is the most reliable method.

1.1. Review of literature

1.1.1. Fuzzy set theory

Fuzzy sets theory is very popular for uncertainty modeling in different field of science, engineering and social science problems. The Fuzzy set concept is first introduced by the author of [6] and through this pioneering work a new area of uncertainty modeling with fuzzy theory has opened up. Since1965, several researchers contributed in the field of fuzzy set theory. From Fuzzy set the idea of fuzzy number [[7], [8], [9]] evolved which has become a tool to represent uncertain parameter where the data is not precisely known due to measurement difficulty, system behavior or lack of reliable data. There exists literature where researchers used different type of fuzzy number in their theoretical framework as well as for modeling real life problems. These literatures reveal the following type of fuzzy number:

Triangular fuzzy number [10,11], Trapezoidal fuzzy number [12,13], Pentagonal fuzzy number [14,15], Hexagonal fuzzy number [16,17], Heptagonal fuzzy number [18,19], Time dependent fuzzy number [20,21], Horizontal fuzzy number [22,23], Dense fuzzy number [24,25], Cloudy fuzzy number [26,27], Type 2 fuzzy number [28,29], Bell shaped fuzzy number [30,31] etc. Now the question arises if we want to take a fuzzy number then what will be its geometrical representation? What will be the membership function? If the decision maker takes a fuzzy membership which graphically resembles a pentagon then how their memberships function will be defined?

As per the linguistic variable set, we can take the different fuzzy parameters as follows:

Triangular fuzzy number: Low, Medium, High.

Trapezoidal fuzzy number: Low, Medium, Average, High.

Pentagonal fuzzy number: Very low, Low, Medium, High, Very high.

If a researcher wants to represent uncertain real life situation as a fuzzy number then which fuzzy number to use, capable of capturing the uncertainties in an elegant manner. The researcher can take a fuzzy number suitable to represent the research problem. From this point of view we considered pentagonal fuzzy number with its more generalized form [14,15,[32], [33], [34], [35]] as it is suitable for our uncertainty framework.

1.1.2. Generalized fuzzy number

In fuzzy sets the maximum value for degree of belongingness is 1. But this maximum degree of membership may vary from one decision maker to another if more than one decision maker is involved. In that context the concept of generalized fuzzy set concept comes. In statistical theory when we measure some quantity, the scale can be different from different measurement system. Similarly same concepts holds here when we take the opinion of different decision maker from their own viewpoint. That is like suppose the decision maker1 (DM1) opined that in a pond there is about 100 big fish but he is not fully confident (he give his confident level as 0.9 in [0,1] scale), in same question DM2 replies that in that pond there is about 100 big fish is there but he is not fully confident (he give his confident level as 0.8 in [0,1] scale). So for DM1 recommendation the fuzzy number is like $\left\{\widetilde{100};\omega \in \left[\mathrm{0,0.9}\right]\right\}$, and for DM1 recommendation the fuzzy number is like $\left\{\widetilde{100};\omega \in \left[\mathrm{0,0.8}\right]\right\}$. Several theoretical and application of that area is already done. The generalized fuzzy numbers have been first defined by the authors of [36]. It has become more popular in scientific community in theoretical and application fields such as management science [37], ranking [[38], [39], [40]], fault diagnosis [41], risk analysis [[42], [43], [44]], transportation problems [45], decision making [46], and pattern recognition [47] etc. For better understanding we recommended the papers [48,49].

1.1.3. Hesitant fuzzy number

Zadeh's fuzzy set theory [6] decision making with uncertain behavior is most popular. Several people has handle uncertainty in different areas by their own viewpoint followed by extension of fuzzy set theory and so on. In several real-life problems, it is not so easy thing to express its membership function due to several factor like increasing complexities as time goes by, time bounded factors, the impreciseness of the decision makers mind, and so many other related reasons. To deal with this matter, the author of [50] first proposed the idea of the Hesitant Fuzzy Set (HFS), where the membership degree value of an element for given fuzzy set, having different values.

The author of [50] also give brief idea how hesitant fuzzy set are connected with the other extended fuzzy sets concept like intuitionistic fuzzy set [51,52], type-2 fuzzy set [53,54] and fuzzy multi-set [55]. Therefore the extension of FSs, HFSs have demonstrated as easily reached and needful tools to depict the impreciseness and vagueness that occurred in real-life world problem. For more details the paper [[56], [57], [58], [59], [60], [61], [62], [63], [64], [65]] may be referred.

Since in decision making theory Hesitant fuzzy set can a key term so in multi criterion decision making problem it can be a good choice to deal the real problems. Several work is already publish in MCDM with Hesitant fuzzy uncertainly. The several methods for MCDM is tagged with Hesitant fuzzy uncertainty such as HF-AHP [66,67], HF-TOPSIS [68,69], HF-MOORA [70,71], HF-COPRAS [72,73], HF-VIKOR [74,75] etc.

1.2. Application of OR in pandemic

OR deals with optimal usage of available resources. During any pandemic as the situation is uncertain and complex, dissemination of information for awareness creation, improved man power management, decision making while implementing lockdown and unlock are of prime importance. OR techniques helps in identifying patients who has higher probability of hospitalization requirement. MCDM tools are very much helpful in this case. Anticipation and early detection of pandemic trend will enable administration to formulate strategies and managerial decision making. Evaluation of different treatment options depends on several criteria, hence MCDM based optimization technique is an useful tool in ranking the treatment options. The authors of [83] used data from the UK, USA, India, Germany, Singapore up to mid-April 2020 and applied predictive analytics tools to forecast COVID-19 growth rates at country-level. The authors of [84] highlighted opportunities for Operational Research to contribute for effective and efficient infectious disease management and improved health outcomes.

1.3. Objectives of this study

• •Identification of different treatment alternatives. Detailed questionnaires based on treatment and the criteria, data were collected from the experts.
• •Identification of criteria for application of these treatment options, assigning proper weightage to them based on their importance.
• •Development of GHPFN, defining its two types, the correspondence arithmetic operations, its examples, score functions and its application in our study.
• •GHPFN- TOPSIS approach is used to rank the treatment alternatives.
• •Ranking of treatment options using proposed model and checking the reliability and steadiness of the model through comparative analysis and sensitive analysis.

1.4. Novelties of the study

This research developed Generalized Hesitant Pentagonal Fuzzy Number (GHPFN) and illustrated its two types. The arithmetic operations, score functions for the two types are developed and shown in an elaborate way. This study used GHPFN (2nd type) for the linguistic rating given by the DMs. The GHPFN covers the level of confidence/hesitancy in a suitable way. The PFN incorporates the fuzziness in broader dimension as it describes the linguistic term in five numbers.

• i.)GHPFN methodology has been developed. The two types of GHPFN, their arithmetic operations, score functions and illustrated with examples.
• ii.)GHPFN- TOPSIS methodology is applied to evaluate and rank the treatment options.
• iii.)The selection of pertinent and relevant treatment options and the criteria has been done by the consultant doctors and scientist.
• iv.)The Opinion of the consultants are converted into GHPFN (2nd type).
• v.)Score function of Generalized Hesitant Triangular Fuzzy Number (GHTFN) has been developed and applied to obtain ranks for treatment options.
• vi.)Comparative analysis has been conducted between GHTFN, Generalized Hesitant Trapezoidal Fuzzy Number (GHTrFN) along with TOPSIS approach and the proposed model.
• vii.)Sensitivity analysis is conducted by interchange of criteria weights.

The remaining of the paper is organized in the following way: the sub-section 1.5 represents the structured framework of the study. Section 2 discusses elaborately about the treatment alternatives and the criteria. HFS, GHFN, GHPFN methodology, benefits of HFS over FS are covered in section 3. Section 4 illustrates the numerical study of the application, depicts the ranking of the treatment options. A comparative analysis is represented in Section 5. Section 6 covers the sensitivity analysis. Section 7 briefly discusses the findings of the study and conclusion is finally shown in section 8.

1.5. Framework of the study

Fig. 1 depicts the framework structure of the study.

Fig. 1.

Representation of framework for the study.

2. Description of the treatment options and the criteria

2.1. Remdesivir

Remdesivir shows a broad spectrum anti viral activity against Ebola virus (Nature, 531 (2016), pp. 381–385), Nipah virus (SciTransl Med, 11 (2019), p. eaau9242), respiratory syncitial virus and a large category of corona viruses including SARS CoV and MERS CoV (MBio, 9 (2018) e00221–e00218). Remdisivir, neucleotide analogue acts by blocking replication of viruses but its precise mechanism is still unknown. It has been observed that remdisivir-triphosphate resembles Adenosine triphosphate (ATP) molecule and competes with the nucleotide during the viral RNA synthesis leading to chain termination (Archives of Medical Research Volume 51, Issue 6, August 2020, Pages 585–586). This is a generalized mechanism of remdesivir against viral activity to cause a broad spectrum effect against various viral infections. It has been reported from Ebola trial that there is possible liver damage caused due to Remdesivir.

Side effects: Nausea, constipation, pain, bleeding, bruising of the skin, soreness, or swelling near the place where the medication was injected. Yellow eyes or skin; dark urine; or pain or discomfort in right upper stomach area can cause liver damage.

Treatment duration: 5 days (NIH Covid Treatment Guidelines)

Macrophage activation syndrome (MAS): Associated with decreased risk of MAS (PMID: 32422376)

Hemophagocytic syndrome (HS): No data available.

Pneumonia: yes.

Intensive care: yes.

Organ failure: can cause liver, kidney damage.

Age: adults above 12 y.

Pregnancy: well tolerated in pregnancy (PMID:32771381)

Drug interaction: 289 drugs are known to interact with Remdesivir.

2.2. Flavipiravir

Flavipiravir is a purine nucleic acid analog that has a similar mechanism of action to the antiherpesvirus drug acyclovir (doi: 10.1016/j.mjafi.2020.08.004) and has the property of not producing a resistant virus (PharmacolTher. 2020 May; 209: 107512). The drug interferes with viral replication by incorporating into the viral strand causing chain termination or viral mutagenesis. Flavipiravir is effective against a broad range of viruses specially influenza virus (PharmacolTher. 2020 May; 209: 107512).Favipiravir is contraindicated in pregnant women due to its teratogenicity and embryotoxicity in animals and also in patients with utricaria. Flavipiravir has shown promising result in early infection of SARS CoV2 leading to lower viral load and faster clinical recovery. In some cases Favipiravir is reported to stop “cytokine storm” preventing disease progression from moderate to severe form (Lancet Global health 2020, 8:e639).

Side effects: Hyperuricemia, diarrhoea, reduced neutrophil count, transaminitis, rash, nausea, vomiting. Also has teratogenic potential and embryotoxicity.

Treatment duration: Varied; 7 days/11 days/13 days (PMID: 32895599)

Macrophage activation syndrome (MAS): No data available.

HS: Associated with decreased risk of HS (DOI:https://doi.org/10.1016/j.jiac.2018.07.009.

Pneumonia: yes.

Intensive care: yes

organ failure: No.

Age: children and adults.

Pregnancy: unsafe during pregnancy.

Drug interaction: interacts with 284 drugs.

2.3. Tocilizumab

Tocilizumab is a genetically engineered humanised monoclonal antibody that competitively inhibits the binding of interleukin-6 (IL-6) to its receptor (IL-6R) (https://doi.org/10.2146/ajhp070449). Inhibition of IL-6R prevents IL-6 signal transduction to inflammatory mediators leading to T cell population expansion and B cell differentiation (Int J Antimicrob Agents. 2020 May; 55(5): 105954.). The SARS CoV2 virus activates the innate and adaptive arms of the immune system resulting to the release of large number of cytokines creating “cytokine storm”. IL-6 is one of the major inflammatory cytokine released on viral infection and plays a central role in acute inflammation. Inhibition of IL-6 signalling can prevent acute phase response. Tocilizumab appears to provide an additional option for combination treatment with other drugs. Since IL-6R inhibition has a distinct mechanism of action, some patients who do not respond to other agents or who have a partial response may respond to tocilizumab. (DOI: https://doi.org/10.1016/S2665-9913(20)30277-0 )

Side effects: Upper respiratory tract infections, nasopharyngitis, headache, high blood pressure, elevated total cholesterol levels and in some cases elevated levels of alanine transaminase. Less common side effects include dizziness, mild rashes, gastritis and mouth ulcer.

Treatment duration: Varied (DOI:https://doi.org/10.1016/S2665-9913(20)30173-9)

MAS: Associated with decreased risk of MAS (PMID: 27688774, PMID: 22398373)

HS: Associated with decreased risk of HS (PMID: 32321563)

Pneumonia: yes.

Intensive care: yes

organ failure: yes.

Age: above 2 years.

Pregnancy: This drug should be used during pregnancyonly if the benefit outweighs the risk.

2.4. Hydroxychloroquine

Chloroquine or hydroxycholoroqine in its unprotonated form diffuses through the cell membrane to the acidic vesicles in the cell called lysosomes. The drugs get trapped in these vesicles as a protonated form as it cannot diffuse out of the vesicles. The drug alters the acidic environment in the lysosome and, as a result, the cell cannot proceed with endocytosis, exosome release or phagolysosomal fusion (doi: 10.1016/j.ijantimicag.2020.106028). The spike (S) protein of SARS-CoV-2 is cleaved in the phagosome by host cell proteases, which can be inhibited owing to the increased pH in the lysosome as a result of HCQ accumulation (https://doi.org/10.1016/j.ijantimicag.2020.105932). HCQ may also interfere with the effective binding of the S protein by reducing the glycosylation of ACE2 receptor (https://doi.org/10.1016/j.ijantimicag.2020.105938). Considering minimum risk of use of HCQ against many other diseases, cost effectiveness and easy availability HCQ is presently recommended for treatment against COVID 19, especially in India.

Side effects: Nausea, stomach cramps, diarrhoea, headache, itching, reduced apetite, vomiting, chronic use can result in retinopathy,altered eye pigmentation, acne, anemia, bleaching of hair, blisters in mouth and eyes, cardiomyopathy, convulsions, vision difficulties, diminished reflexes, muscle paralysis,weakness or atrophy,tinnitus, skin inflammation and scaling, skin rash, vertigo, weight loss, and occasionally urinary incontinence.

Treatment duration: 10 days (PMID: 32205204)

MAS: Associated with decreased risk of MAS (PMID: 27688774, PMID: 22398373)

HS: Associated with decreased risk of HS (PMID: 29451069)

Pneumonia: yes.

Intensive care: yes

organ failure: No.

Age: above 2 years.

Pregnancy: can be used during pregnancy.

Drug interaction: interacts with 387 drugs.

2.5. Plasma exchange

Therapeutic Plasma exchange (TPE) is a procedure of removal of plasma from patient and replenishing it with plasma from healthy/cured individual. Recently, convalescent plasma donated from survivors of COVID-19 infection, has been shown as a promising and safe treatment. The convalescent plasma is used to passively transfer antibodies to a diseased person from a previously infected individual. The TPE dates back almost 100 years and have been used mostly during outbreaks like polio & ebola and pandemics like Spanish flu and now COVID19 (https://doi.org/10.1101/2020.05.12.20099879. 05.12.20099879.). The majority of COVID 19 patients who recovered from the disease develop circulating antibodies against SARS CoV2 virus. Several primate study showed these antibodies are protective against SARS CoV2 at least for weeks to months. TPE can be used prophylactically to prevent the disease or therapeutically to cure COVID patients. According to recent reports TPE is effective preferably with high antibody titters and administration prior to intubation and development of life-threatening inflammatory end organ failure.

Side effects: Fever, chills, urticaria, muscle cramps, or paresthesias.

Treatment duration: 2–3 h.

MAS: Successful against MAS.

HS: Successful against HS.

Pneumonia: yes.

Intensive care: yes

organ failure: No.

Age: above 2 years.

Pregnancy: can be used during pregnancy.

Drug interaction: NA.

3. Methodology

3.1. Hesitant Fuzzy numbers (HFN) and its extended approach to generalized hesitant Fuzzy numbers (GHFN)

HFS is one of the extensions of fuzzy sets theory. It was introduced by the author of [50] and is applicable when uncertainties and hesitancy exists in assigning the degree of membership of the elements. Decision making process involves the hesitancy or uncertainty of the decision makers in terms of preferences, thus HFS can be flexibly used to represent the preferences of decision makers, according to the authors [85]. The author of [49] defined hesitant fuzzy set as follows:

Definition 1

Assume a fixed set $X$, a hesitant fuzzy set (HFS)on $X$ is defined in terms of a function, which when applied to $X$ returns a subset of [0,1].

To make it simpler, the authors of reference [86] represented the HFS in mathematical symbol as follows:

$$F_h=\left(⟨x|\gamma \left(x\right)⟩|x\in X\right)\text{,}$$ (1)

Where $\gamma \left(x\right)$ denotes a set of some values in [0,1], which indicates the degree of membership of the element $x\in X$ to the set $F_h$. For convenience, $\gamma =\gamma \left(x\right)$, is called a hesitant fuzzy element (HFE).

Let three HFEs be represented by $\gamma ,{\gamma }^{1}and{\gamma }^2$, the following operational rules defined by the authors of [86] are:

$$\mathrm{a}.){\gamma }^{\prime }={\bigcup }_{\rho \epsilon \gamma }\left\{1-\rho \right\}$$ (2)

$$\mathrm{b}.){\gamma }^1\bigcup {\gamma }^2={\bigcup }_{{\rho }^1\epsilon {\gamma }^1{\rho }^2\epsilon {\gamma }^2}\max \left\{{\rho }^1,{\rho }^2\right\}$$ (3)

$$\mathrm{c}.){\gamma }^1\bigcap {\gamma }^2={\bigcup }_{{\rho }^1\epsilon {\gamma }^1{\rho }^2\epsilon {\gamma }^2}\min \left\{{\rho }^1,{\rho }^2\right\}$$ (4)

Let $\epsilon >0\text{,}$ assuming three HFEs $\gamma ,{\gamma }^{1}and{\gamma }^2$, the authors of references [[87], [88], [89]] introduced some arithmetic operations of hesitant fuzzy element as follows:

$$\mathrm{i}){\gamma }^{\epsilon }={\bigcup }_{\rho \epsilon \gamma }\left\{{\rho }^{\epsilon }\right\}$$ (5)

$$\mathrm{i}\mathrm{i})\epsilon \gamma ={\bigcup }_{\rho \epsilon \gamma }\left\{1-{\left(1-\rho \right)}^{\epsilon }\right\}$$ (6)

$$\mathrm{i}\mathrm{i}\mathrm{i}){\gamma }^1+{\gamma }^2={\bigcup }_{{\rho }^1\epsilon {\gamma }^1{\rho }^2\epsilon {\gamma }^2}\left\{{\rho }^1+{\rho }^2-{\rho }^1{\rho }^2\right\}$$ (7)

$$\mathrm{i}\mathrm{v}){\gamma }^1\times {\gamma }^2={\bigcup }_{{\rho }^1\epsilon {\gamma }^1{\rho }^2\epsilon {\gamma }^2}\left\{{\rho }^1{\rho }^2\right\}\text{.}$$ (8)

$$\mathrm{v}){\gamma }^1-{\gamma }^2={\bigcup }_{{\rho }^1\epsilon {\gamma }^1{\rho }^2\epsilon {\gamma }^2}\left\{{\rho }^{\bullet }\right\},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}$$

$${\rho }^{\bullet }=f\left(x\right)=\{\begin{array}{c}\frac{{\rho }^1-{\rho }^2}{1-{\rho }^2},if{\rho }^1\ge {\rho }^{2}and{\rho }^2\ne 1\\ 0,otherwise\end{array}$$

$$\mathrm{v}\mathrm{i})\frac{{\gamma }^1}{{\gamma }^2}={\bigcup }_{{\rho }^1\epsilon {\gamma }^1{\rho }^2\epsilon {\gamma }^2}\left\{{\rho }^{*}\right\},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}$$ (9)

$${\rho }^{*}=f\left(x\right)=\{\begin{array}{c}\frac{{\rho }^1}{{\rho }^2},if{\rho }^1\le {\rho }^{2}and{\rho }^2\ne 0\\ 1,otherwise\end{array}$$

3.1.1. Example of HFS in real life problem

HFS theory is applicable, when the decision expert are hesitant or uncertain about a particular event. Unlike fuzzy numbers, where one is restricted to a particular form. For example, in triangular fuzzy number (TFN), the uncertainty is described in three numbers, the middle value represents the maximum membership. In hesitant fuzzy numbers, the DMs can give rating or preference with no such restrictions. The HFS covers the hesitancy of the DM or group of DMs in true aspects. In our day to day life, we come across some real life problems, when we are not much sure or perfect of assigning crisp or fuzzy values in decision making.

Example 1

Recruitment of teachers or evaluation of teachers in institutions depend on numerous attributes of a teacher. Some criteria are conflicting. There are certain attributes of a teacher where the DMs may be a little hesitant to express their opinion in definite terms. Thus, the decision makers can express their opinions with the help of HFS.

Example 2

Identification of the risk factors for the occurrence of a particular disease, which depends on many factors. It becomes very tough for the experts to identify the exact reason, as the cause and the symptoms of the disease vary from person to person. Therefore HFS concepts can be used by decision makers to obtain the result.

The cases when we take according to Fig. 2 :

• (1)Hesitant Pentagonal fuzzy number:This is a set of different PFNs with different support interval on R instead of crisp values. Example of HPFN is: $\left\{\left(\mathrm{1,3,3,4,5}\right),\left(\mathrm{3,4,6,6,7}\right),\left(\mathrm{5,6,8,9,10}\right)\right\}\text{.}$.
• (2)Generalized Hesitant fuzzy number: It is a set of some different generalized fuzzy numbers in the set of real numbers R, which represents the possible membership functions of the element $x\in X\text{.}$ Different example of this form are generalized triangular hesitant fuzzy number (GTHFN), generalized trapezoidal hesitant fuzzy number (GTrHFN), generalized pentagonal hesitant fuzzy number (GPHFN) etc.
• (3)Generalized Pentagonal fuzzy number: In this form, the maximum membership need not to be 1. It can assume any value [0, 1]. If $f\left(x\right)=1$, then the generalized pentagonal fuzzy number (GPFN) is reduced to PFN.
• (4)Generalized Hesitant Pentagonal fuzzy number: A GHPFN is defined in this paper in two forms. In GHPFN (1st type), the number of PFN can be more than 1 but the membership function is restricted to 1. In GHPFN (2nd type), the PFN is restricted to 1 but the membership function can be more than 1. For detailed information about GHPFN and its types, please refer definition 3, 4 and 5.
• (5)Benefits of HFS rather than FS: HFS is useful in handling the complexities, hesitancy and uncertainties which arises in real life problem. Thus HFS enables the DMs to convey his hesitancy while assigning membership value in a mathematical way.

Definition 2

The authors of [89] defined ranking method for HFEs. For an HFE $\text{'}\rho \text{'}$, the score function denoted as

$$s_F\left(\gamma \right)=\frac{1}{\#h}\sum _{\rho \epsilon \gamma }\rho$$

where $\#h$ is the number of elements in $\gamma \text{.}$.

Suppose two HFEs ${\gamma }^{1}and{\gamma }^2\text{,}$ let $S\left({\gamma }^1\right)$ and $S\left({\gamma }^2\right)$, the scores of ${\gamma }^{1}and{\gamma }^2$, respectively

$$\left(1\right)\mathrm{I}\mathrm{f}S\left({\gamma }^1\right)>S\left({\gamma }^2\right),then{\gamma }^1>{\gamma }^2$$ (10)

$$\left(2\right)\mathrm{I}\mathrm{f}S\left({\gamma }^1\right)=S\left({\gamma }^2\right),then{\gamma }^1={\gamma }^2\text{.}$$ (11)

Pentagonal Fuzzy Number: A pentagonal fuzzy number (PFN) of a fuzzy set is represented as $P=\left({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4,{\mu }_5\right)$, where ${\mu }_i\epsilon \mathbf{R}\text{,}$ the set of real numbers such that ${\mu }_1\le {\mu }_2\le {\mu }_3\le {\mu }_4\le {\mu }_5$. The membership of PFN is denoted as:

$$P=f\left(x\right)=\{\begin{array}{c}0,forx\le {\mu }_1\\ \frac{\left(x-{\mu }_1\right)}{{\mu }_2-{\mu }_1},for{\mu }_1\le x\le {\mu }_2\\ \frac{\left(x-{\mu }_1\right)}{{\mu }_3-{\mu }_2},for{\mu }_2\le x\le {\mu }_3\\ 1forx={\mu }_3\\ \frac{\left({\mu }_4-x\right)}{{\mu }_4-{\mu }_3},for{\mu }_3\le x\le {\mu }_4\\ \frac{\left({\mu }_5-x\right)}{{\mu }_5-{\mu }_4},for{\mu }_4\le x\le {\mu }_5\\ 0forx\ge {\mu }_5\end{array}$$

Fig. 3 shows graphical representation of pentagonal fuzzy number (PFN)

Note 1

If in the closed interval [q,s], ${\mu }_{\hat{A}}\left(x\right)=1$, then the Pentagonal fuzzy number (PFN) is reduced to Trapezoidal fuzzy number (TrFN).

Note 2

If q = r = s, then the PFN is reduced to Triangular Fuzzy Number (TFN)

Remark: Fig. 3 denotes PFN, where $p<q<r<s<t$. The variable $\text{'}r\text{'}$ possess the maximum membership of 1. The variables $\text{'}q\text{'}and\text{'}s\text{'}$ achieve equal membership of 0.5, whereas the variables $\text{'}p\text{'}and\text{'}t\text{'}$ have 0 membership value. The membership increases from $\text{'}p\text{'}$, reaches the pick value at $\text{'}r\text{'}$ and then start declining till $\text{'}t\text{'}\text{.}$.

Arithmetic operation on PFN.

• 1.Addition: ($P+Q)=\left({\mu }_1+{\vartheta }_1,{\mu }_2+{\vartheta }_2,{\mu }_3+{\vartheta }_3,{\mu }_4+{\vartheta }_4,{\mu }_5+{\vartheta }_5\right)$.
• 2.Subtraction:($P-Q)=\left({\mu }_1-{\vartheta }_1,{\mu }_2-{\vartheta }_2,{\mu }_3-{\vartheta }_3,{\mu }_4-{\vartheta }_4,{\mu }_5-{\vartheta }_5\right)$.
• 3.Multiplication: ($P\times Q)=\left({\mu }_1{\vartheta }_1,{\mu }_2{\vartheta }_2,{\mu }_3{\vartheta }_3,{\mu }_4{\vartheta }_4,{\mu }_5{\vartheta }_5\right)$.
• 4.Scalar Multiplication: $aP=\left(a{\mu }_1,a{\mu }_2,{a\mu }_3,{a\mu }_4,{a\mu }_5\right)$.
• 5.Division: $\left(\frac{P}{Q}\right)=(\frac{{\mu }_1}{{\vartheta }_5}$, $\frac{{\mu }_2}{{\vartheta }_4}$, $\frac{{\mu }_3}{{\vartheta }_3},\frac{{\mu }_4}{{\vartheta }_2}$, $\frac{{\mu }_5}{{\vartheta }_1}$)
• 6.Inverse: $P^{-}=\left(\frac{1}{{\vartheta }_5},\frac{1}{{\vartheta }_4},\frac{1}{{\vartheta }_3},\frac{1}{{\vartheta }_2},\frac{1}{{\vartheta }_1}\right)$.

Remark: It should be noted that the resultant PFN after addition, subtraction and scalar multiplication is a PFN but the multiplication, division and inverse need not necessary be a PFN. For the time being, we use the approximated resultant as PFN for multiplication, division and inverse operation.

Fig. 2.

Representation of different types of fuzzy number as venn diagram.

Fig. 3.

Graphical representation of PFN.

3.1.1.1. Generalized hesitant pentagonal fuzzy numbers (GHPFN)

Definition 3

Let $\text{'}X\text{'}$ be a fixed set and $p_i,q_i,r_i,s_i,t_i\epsilon \mathfrak{R}$ such that $p_i\le q_i\le r_i\le s_i\le t_i\left(i\epsilon I_m=\left\{\mathrm{1,2},\dots ,m\right\}\right)\text{.}$ Then a pentagonal hesitant fuzzy set on $\text{'}X\text{'}$ is defined as:

$$\Psi =\left\{⟨x,\left(p_i,q_i,r_i,s_i,t_i\right):i\epsilon I_m⟩:x\epsilon X\right\}$$

Where {$\left(p_i,q_i,r_i,s_i,t_i\right):i\epsilon I_m\}$ is a set of different pentagonal fuzzy numbers denoting the set of real numbers, that represents the membership value of the element $x\epsilon X$.

Definition 4

Assume $\text{'}X\text{'}$ to be a fixed set, ${\alpha }_i\epsilon \left[\mathrm{0,1}\right]\left(i\epsilon I=\left\{\mathrm{1,2},..,m\right\}or\left\{\mathrm{1,2},\dots ,n\right\}or\dots ..\right)$ and $p_i,q_i,r_i,s_i,t_i\epsilon \mathfrak{R}$ such that the relation among them are $p_i\le q_i\le r_i\le s_i\le t_i\left(i\epsilon I\right)$. A GHPFN is then defined as:

$$\Psi =\left\{⟨x,\left(p_i,q_i,r_i,s_i,t_i\right);{\delta }_i:i\epsilon I⟩:x\epsilon X\right\}$$

Where $\left\{\left(p_i,q_i,r_i,s_i,t_i\right);{\delta }_i:i\epsilon I\right\}$ represents set of different GPFN in a set of real numbers, denoting the possible membership functions of the element $x\epsilon X$.

From the above definitions, we construct two particular forms of generalized hesitant pentagonal fuzzy numbers. In the first type of GHPFN, the membership function is fixed but the PFN can vary. In the second type, the PFN are considered to be fixed but the membership for a specific PFN can vary depending on the preference of DMs (see Table 3).

Definition 5

Let $\Psi =\left\{⟨x,\left(p_i,q_i,r_i,s_i,t_i\right);{\delta }_i:i\epsilon I⟩:x\epsilon X\right\}$ represents set of different GHPFN. If ${\delta }_i=\delta$ for all $i\epsilon I$, then GHPFN is reduced to single membership function for different GHPFN. This form of GHPFN is said to be 1st type. The example in Table 4 represents GHPFN of first type. Symbolically it can be expressed in the following way:

$${\beta }_{GHPFN}^a=⟨x,\left(p_i,q_i,r_i,s_i,t_i\right):i\epsilon I;\left\{\beta \right\}⟩$$

Remark: GHPFN can be used to describe the hesitancy or vagueness of a DM or group of DMs in different possible ways. Unlike the Generalized Hesitant Triangular Fuzzy Number(GHTFN) or Generalized Hesitant Trapezoidal Fuzzy Number(GHTrFN) which represents the impreciseness in three numbers or four numbers respectively, GHPFN considers five numbers and thus captures the uncertainty in better form.

Remark: Table 4 represents the GHPFN 1st type for linguistic terms. If we consider the term ‘High’, the PFN assigned by DMs are different but the degree of confidence for the particular terms is same for the DMs. The value 0.8 signifies, the DMs are highly confident about assigning a particular alternative with respect to the criteria.

Fig. 4 represents the GHPFN 1st type.

Note 3

The GHPFN 1st type considers same degree of hesitancy for different set of PFN. In this case the DMs preference for rating can be a different PFN but the degree of membership for a particular event is same. Table 4 and Fig. 4 captures the concept clearly. The diagram signifies that the PFN can be different by the DMs but their hesitancy/confidence $\text{'}\delta \text{'}$ of assigning that particular PFN for the linguistic term remains the same.

Definition 4

Let $\Psi =\left\{⟨x,\left(p_i,q_i,r_i,s_i,t_i\right);{\delta }_i:i\epsilon I⟩:x\epsilon X\right\}$ represents set of different GHPFN.If ${p=p}_i,{q=q}_i,r=r_i,s=s_i,{t=t}_i$ for all $i\epsilon I\text{,}$ then GPFN is reduced to single valued generalized hesitant pentagonal fuzzy number with different membership value. This form of GHPFN is said to be 2nd type. Symbolically it can be expressed as:

${\beta }_{1GHPFN}=⟨\left(p,q,r,s,t\right);\left\{{\beta }_i:{\beta }_i\epsilon \beta \left(x\right)\right\}⟩,\beta \left(x\right)$ isa set of some values in [0,1].

This is a special form of hesitant fuzzy set on the set of real numbers $\mathfrak{R}\text{.}$ The membership functions are defined as follows:

$$f^i\left(x\right)=\{\begin{array}{c}\left(x-p\right){\beta }_i/\left(q-p\right),p\le x<q\\ \left(x-q\right){\beta }_i/\left(r-q\right),q\le x<r\\ {\beta }_{i}x=r\\ \frac{\left(s-x\right){\beta }_i}{\left(s-r\right)}r<x\le s\\ \frac{\left(t-x\right){\beta }_i}{\left(t-s\right)}s<x\le t\\ 0Otherwise\end{array}$$

Remark: Table 5 express the GHPFN 2nd type for linguistic terms. The degree of hesitancy/confidence is different for DMs. If we consider the linguistic term ‘Very high’, the PFN assigned by DMs remain same but their level of hesitancy/confidence is different. The value ‘0.8’ implies highly confident, 0.5 implies average confident or hesitant (see Table 6).

Fig. 5 represents GHPFN 2nd type.

Note 4

In GHPFN 2nd type, the PFN remains one but the membership value or degree of hesitancy for DMs changes. Table 5 and Fig. 5 clearly depicts the concept. The figure signifies that the PFN generated by the DM is constant but the confidence ${{\prime \delta }_i}^{\prime }$ of assigning a particular PFN changes for different DMs depending on their individual hesitancy/confidence.

Table 3.

Linguistic term in PFN 1–9 scale.

Linguistic Terms	1-9 Scale	Pentagonal fuzzy number
Equally Important	1	(1,2,2,3,5)
Moderately Important	3	(3,4,5,6,7)
Strongly Important	5	(3,6,6,7,9)
Very Strongly Important	7	(5,6,7,8,9)
Absolutely Important	9	(7,8,9,9,10)
Moderately not Important	1/3	(1/7,1/6,1/5,1/4,1/3)
Strongly not Important	1/5	(1/9,1/7,1/6,1/6,1/3)
Very Strongly not Important	1/7	(1/9,1/8,1/7,1/6,1/5)
Absolutely not Important	1/9	(1/10,1/9,1/9,1/8,1/7)

Table 4.

Linguistic variables representing GHPFN (1st type).

Linguistic Terms	GHPFN (1st Type)
Very high	$⟨\left(4.4,4.5,4.7,4.9,5\right),\left(4.6,4.7,4.9,5,5.2\right);\left\{0.8\right\}⟩$
High	$⟨\left(\mathrm{3.5,3.7},3.9,4,4.1\right),\left(3.7,3.9,4,4.2,4.3\right);\left\{0.8\right\}⟩$
Average	$⟨\left(2.6,2.7,2.8,2.9,3\right),\left(2.9,3,3.1,3.2,3.3,3.4\right);\left\{0.5\right\}⟩$
Less	$⟨\left(1.9,2,2.1,2.2,2.3\right),\left(2,2.2,2.3,2.4,2.5\right);\left\{0.6\right\}⟩$
Very less	$⟨\left(1,1.3,1.5,1.6,1.7\right),\left(1.3,1.5,1.6,1.7,1.9\right);\left\{0.4\right\}⟩$

Fig. 4.

Representation of GHPFN 1st type.

Table 5.

Linguistic variables representing GHPFN (2nd Type).

Linguistic Terms	GHPFN (2nd Type)
Very high	$⟨\left(3.3,3.5,3.7,3.9,4\right);\left\{\mathrm{0.5,0.7},0.8\right\}⟩$
High	$⟨\left(2.7,2.9,3,3.1,3.3\right);\left\{0.8,0.4\right\}⟩$
Average	$⟨\left(2.2,2.3,2.5,2.7,2.9\right);\left\{0.5,0.6\right\}⟩$
Less	$⟨\left(1.6,1.7,2,2.2,2.3\right);\left\{0.4,0.9,0.5\right\}⟩$
Very less	$⟨\left(1,1.3,1.5,1.6,1.7\right);\left\{0.3,0.6\right\}⟩$

Table 6.

The criteria of the COVID-19 treatment, the importance of these criteria's in linguistic terms and GHPFN (2nd type).

Linguistic scale for evaluation	GHPFN (2nd type)	Criterion rating
Highly Important	$⟨\left(3.3,3.5,3.7,3.9,4\right);\left\{0.7,0.8\right\}⟩$	Plasma stability $\left(C_1\right)$
		Plasma turnover $\left(C_2\right)$
		Time of suppression $\left(C_3\right)$
		Drug-drug interaction $\left(C_4\right)$
		Compliance $\left(C_5\right)$
		Pneumonia $\left(C_6\right)$
		Intensive care $\left(C_7\right)$
		Organ failure $\left(C_8\right)$
		Macrophage activation syndrome $\left(C_9\right)$
		Hemophagocytic syndrome $\left(C_{10}\right)$
Important	$⟨\left(2.7,2.9,3,3.1,3.3\right);\left\{0.8,0.7\right\}⟩$	Pregnancy $\left(C_{11}\right)$
		GFR $\left(C_{12}\right)$
		Age $\left(C_{13}\right)$
		Side Effect $\left(C_{14}\right)$
		Fever $\left(C_{15}\right)$
Average	$⟨\left(2.2,2.3,2.5,2.7,2.9\right);\left\{0.5,0.6\right\}⟩$	Treatment Duration $\left(C_{16}\right)$
		Ease of application $\left(C_{17}\right)$
		Regime cost $\left(C_{18}\right)$

Fig. 5.

Representation of GHPFN 2nd type.

3.1.1.1.1. Arithmetic operations and score function on GHPFN (1st Type)

Note 5

The arithmetic operations on GHPFN (1st Type) is applicable only if the number of HPFN are equal given by the DMs.

Let ${\beta }_{GHPFN}^1=⟨\left(p_1,q_1,r_1,s_1,t_1\right),\left(p_2,q_2,r_2,s_2,t_2\right);\beta ⟩,{\beta }_{GHPFN}^2=⟨\left(p_3,q_3,r_3,s_3,t_3\right),\left(p_4,q_4,r_4,s_4,t_4\right);\beta ⟩and\epsilon \ge 0$. Then

• A.${\beta }_{GHPFN}^1+{\beta }_{GHPFN}^2=⟨\left(p_1+p_3,q_1+q_3,r_1+r_3,s_1+s_3,t_1+t_3\right),\left(p_2+p_4,q_2+q_4,r_2+r_4,s_2+s_4,t_2+t_4\right);\left\{\beta \right\}⟩$.
• B.${\beta }_{GHPFN}^1-{\beta }_{GHPFN}^2=⟨\left(p_1-t_3,q_1-s_3,r_1-r_3,s_1-q_3,t_1-p_3\right),\left(p_2-t_4,q_2-s_4,r_2-r_4,s_2-q_4,t_2-p_4\right);\left\{\beta \right\}⟩$.
• C.${\beta }_{GHPFN}^1\times {\beta }_{GHPFN}^2=\{\begin{array}{c}\left(p_1{p}_3,q_1{q}_3,r_1{r}_3,s_1{s}_3,t_1{t}_3\right),\left(p_2{p}_4,q_2{q}_4,r_2{r}_4,s_2{s}_4,t_2{t}_4\right);\\ \left\{\beta \right\}\left(t_1>0,t_2>0,t_3>0,t_4>0\right)\\ \left(p_1{t}_3,q_1{s}_3,r_1{r}_3,s_1{q}_3,t_1{p}_3\right),\left(p_2{t}_4,q_2{s}_4,r_2{r}_4,s_2{q}_4,t_2{p}_4\right);\\ \left\{\beta \right\}\left(t_1<0,t_2<0,t_3>0,t_4>0\right)\\ \left(t_1{t}_3,s_1{s}_3,r_1{r}_3,q_1{q}_3,p_1{p}_3\right),\left(t_2{t}_4,s_2{s}_4,r_2{r}_4,q_2{q}_4,p_2{p}_4\right);\\ \left\{\beta \right\}\left(t_1<0,t_2<0,t_3<0,t_4<0\right)\end{array}$.
• D.${\beta }_{GHPFN}^1÷{\beta }_{GHPFN}^2=\{\begin{array}{c}\left(p_1/t_3,q_1/s_3,r_1/r_3,s_1/q_3,t_1{/p}_3\right),\left(p_2/t_4,q_2/s_4,r_2/r_4,s_2/q_4,t_2{/p}_4\right);\\ \left\{\beta \right\}\left(t_1>0,t_2>0,t_3>0,t_4>0\right)\\ \left(t_1/t_3,s_1/s_3,r_1/r_3,q_1{/q}_3,p_1/p_3\right),\left(t_2/t_4,s_2/s_4,r_2/r_4,q_2{/q}_4,p_2/p_4\right);\\ \left\{\beta \right\}\left(t_1<0,t_2<0,t_3>0,t_4>0\right)\\ \left(t_1/p_3,s_1{/q}_3,r_1/r_3,q_1{/s}_3,p_1/t_3\right),\left(t_2/p_4,s_2{/q}_4,r_2/r_4,q_2{/s}_4,p_2/t_4\right);\\ \left\{\beta \right\}\left(t_1<0,t_2<0,t_3<0,t_4<0\right)\end{array}$.
• E.$\epsilon {\beta }_{GHPFN}^1=⟨\left(\epsilon p_1,\epsilon q_1,\epsilon r_1,\epsilon s_1,\epsilon t_1\right),\left(\epsilon p_2,\epsilon q_2,\epsilon r_2,\epsilon s_2,\epsilon t_2\right);\left\{1-{\left(1-\beta \right)}^{\epsilon }\right\}⟩$.
• F.${\left({\beta }_{GHPFN}^1\right)}^{\epsilon }=⟨\left(p_1^{\epsilon },q_1^{\epsilon },r_1^{\epsilon },s_1^{\epsilon },t_1^{\epsilon }\right),\left(p_2^{\epsilon },q_2^{\epsilon },r_2^{\epsilon },s_2^{\epsilon },t_2^{\epsilon }\right);\left\{{\beta }^{\epsilon }\right\}⟩$.

Example 1.Let ${\beta }_{GHPFN}=⟨\left(\mathrm{2.5,2.6,2.8,2.9,3}\right),\left(\mathrm{2.9,3,3.1,3.3,3.5}\right);\left\{0.8\right\}⟩,{\beta }_{GHPFN}^1=⟨\left(\mathrm{3.8,3.9,4,4.1,4.2}\right),\left(\mathrm{4.1,4.3,4.5,4.6,4.7}\right);\left\{0.8\right\}⟩,{\beta }_{GHPFN}^2=⟨\left(\mathrm{4.7,4.8,4.9,5,5.1}\right),\left(\mathrm{5.1,5.3,5.5,5.6,5.7}\right);\left\{0.8\right\}⟩\text{,}$ then

• a.${\beta }_{GHPFN}^1+{\beta }_{GHPFN}^2=⟨\left(\mathrm{8.5,8.7,8.9,9.1,9.3}\right),\left(\mathrm{9.2,9.6,10,10.2,10.4}\right);\left\{0.8\right\}⟩$.
• b.${\beta }_{GHPFN}^1-{\beta }_{GHPFN}^2=⟨\left(-1.3,-1.1,-0.9,-0.7,-0.5\right),\left(-1.6,-1.3,-1,-0.7,-0.4\right);\left\{0.8\right\}⟩$.
• c.${\beta }_{GHPFN}^1\times {\beta }_{GHPFN}^2=⟨\left(/\mathrm{17.86,18.72,19.6,20.5,21.42}\right),\left(\mathrm{20.91,22.79,24.75,25.76,26.79}\right);\left\{0.8\right\}⟩$.
• d.${\beta }_{GHPFN}^1÷{\beta }_{GHPFN}^2=⟨\left(\mathrm{0.74,0.78,0.82,0.85,0.90}\right),\left(\mathrm{0.72,0.77,0.82,0.87,0.92}\right);\left\{0.8\right\}⟩$.
• e.$3{\beta }_{GHPFN}=⟨\left(\mathrm{7.5,7.8,8.4,8.7,9}\right),\left(\mathrm{8.7,9,9.3,9.3,10.5}\right);\left\{0.992\right\}⟩$.
• f.${\left({\beta }_{GHPFN}\right)}^2=⟨\left(\mathrm{6.25,6.76,7.84,8.41,9}\right),\left(\mathrm{8.41,9,9.61,10.89,12.25}\right);\left\{0.64\right\}⟩$.

3.1.1.2. Score function on GHPFN (1st type)

The GHPFN captures the hesitancy of the decision expert. As compared to fuzzy numbers, where the opinions are restricted to a particular kind. HFS considers all the possible outcomes of DMs. Due to the existence of vagueness and insufficient knowledge about a specific data, HFNs concept can be considered helpful for DMs. In this paper, we developed GHPFN and represented its types. Once the DMs give preferential rating to the criteria and alternative in terms of GHPFN, it become important to see, the score values of HFS. In order to compare two HFS, score function is required. Score function can also be considered as an extension of defuzzification process which is required to get the ultimate ranking. Thus the next section represents some arithmetic operation of GHPFN and definition for score function.

Definition 5

Let ${\beta }_{GHPFN}^1=⟨\left(p_1,q_1,r_1,s_1,t_1\right),\left(p_2,q_2,r_2,s_2,t_2\right);{\beta }^1⟩$ be a GHPFN (1st type). Then the score function of ${\beta }_{GHPFN}^1$ is defined as $S\left({\beta }_{GHPFN}^1\right)=\frac{2{\left(r_1+r_2\right)}^2+{\left(s_1+s_2\right)}^2+{\left(t_1+t_2\right)}^2-{\left(p_1+p_2\right)}^2-{\left(q_1+q_2\right)}^2}{3\left(\#h\right)}\times {\beta }^1$.

Where, #h denotes the number of elements in ${\beta }_{GHPFN}^1\text{.}$.

3.1.1.2.1. Arithmetic operations and score function on GHPFN (2nd Type)

Let ${\beta }_{GHPFN}^1=⟨\left(p_1,q_1,r_1,s_1,t_1\right);{\beta }^1⟩,{\beta }_{GHPFN}^2=⟨\left(p_2,q_2,r_2,s_2,t_2\right);{\beta }^2⟩and\epsilon \ge 0$. Then,

• A.${\beta }_{GHPFN}^1+{\beta }_{GHPFN}^2=⟨\left(p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2,t_1+t_2\right);{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }_1^1+{\beta }_1^2-{\beta }_1^1.{\beta }_1^2\right\}⟩\text{;}$.
• B.${\beta }_{GHPFN}^1-{\beta }_{GHPFN}^2=⟨\left(p_1-t_2,q_1-s_2,r_1-r_2,s_1-q_2,t_1-p_2\right);{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }^{.}\right\}⟩$ where, ${\beta }^{.}=\{\begin{array}{c}\frac{{\beta }_1^1-{\beta }_1^2}{1-{\beta }_1^2}if{\beta }_1^1\ge {\beta }_1^{2}and{\beta }_1^2\ne 1\\ 0Otherwise\end{array}$.
• C.${\beta }_{GHPFN}^1\times {\beta }_{GHPFN}^2=\{\begin{array}{c}\left(p_1{p}_2,q_1{q}_2,r_1{r}_2,s_1{s}_2,t_1{t}_2\right);\\ ⟨{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }_1^1.{\beta }_1^2\right\}⟩\left(t_1>0,t_2>0\right)\\ \left(p_1{t}_2,q_1{s}_2,r_1{r}_2,s_1{q}_2,t_1{p}_2\right);\\ ⟨{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }_1^1.{\beta }_1^2\right\}⟩\left(t_1<0,t_2>0\right)\\ \left(t_1{t}_2,s_1{s}_2,r_1{r}_2,q_1{q}_2,p_1{p}_2\right);\\ ⟨{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }_1^1.{\beta }_1^2\right\}⟩\left(t_1<0,t_2<0\right)\\ \end{array}$.
• D.${\beta }_{GHPFN}^1÷{\beta }_{GHPFN}^2=\{\begin{array}{c}\left(p_1/t_2,q_1/s_2,r_1/r_2,s_1/q_2,t_1{/p}_2\right);\\ ⟨{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }^{*}\right\}⟩\left(t_1>0,t_2>0\right)\\ \left(t_1/t_2,s_1/s_2,r_1/r_2,q_1{/q}_2,p_1/p_2\right);\\ ⟨{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }^{*}\right\}⟩\left(t_1<0,t_2>0\right)\\ \left(t_1/p_2,s_1{/q}_2,r_1/r_2,q_1{/s}_2,p_1/t_2\right);\\ ⟨{\cup }_{{\beta }_1^1\epsilon {\beta }^1,{\beta }_1^2\epsilon {\beta }^2}\left\{{\beta }^{*}\right\}⟩\left(t_1<0,t_2<0\right)\end{array}$.

Where

$${\beta }^{*}=\{\begin{array}{c}\frac{{\beta }_1^1}{{\beta }_1^2},if{\beta }_1^1\le {\beta }_1^{2}and{\beta }_1^2\ne 0<0\\ 1,otherwise\end{array}$$

• E.$\epsilon {\beta }_{GHPFN}=⟨\left(\epsilon p,\epsilon q,\epsilon r,\epsilon s,\epsilon t\right);{\cup }_{\beta \epsilon \beta \left(x\right)}\left\{1-{\left(1-\beta \right)}^{\epsilon }\right\}⟩,\epsilon \ge 0$.
• F.${\left({\beta }_{GHPFN}\right)}^{\epsilon }=⟨\left(p^{\epsilon },q^{\epsilon },r^{\epsilon },s^{\epsilon },t^{\epsilon }\right);{\cup }_{\beta \epsilon \beta \left(x\right)}\left\{{\beta }^{\epsilon }\right\}⟩\left(\epsilon \ge 0\right)\text{.}$.

Example 2. Let ${\beta }_{GHPFN}=⟨\left(\mathrm{2.5,2.6,2.8,2.9,3}\right);\left\{\mathrm{0.8,0.7,0.6}\right\}⟩,{\beta }_{GHPFN}^1⟨\left(\mathrm{3.8,3.9,4,4.1,4.2}\right);\left\{0.3,\mathrm{0.4,0.6}\right\}⟩,{\beta }_{GHPFN}^2=⟨\left(\mathrm{4.7,4.8,4.9,5,5.1}\right);\left\{\mathrm{0.7,0.8}\right\}⟩\text{,}$ then

• a)${\beta }_{GHPFN}^1+{\beta }_{GHPFN}^2=⟨\left(\mathrm{8.5,8.7,8.9,9.1,9.3}\right);\left\{\mathrm{0.37,0.49,0.37,0.48,0.43,0.52}\right\}⟩$.
• b)${\beta }_{GHPFN}^1-{\beta }_{GHPFN}^2=⟨\left(-1.3,-1.1,-0.9,-0.7,-0.5\right);\left\{\mathrm{0,0,0,0,0,0}\right\}⟩$.
• c)${\beta }_{GHPFN}^1\times {\beta }_{GHPFN}^2=⟨\left(\mathrm{17.86,18.72,19.6,20.5,21.42}\right);\left\{\mathrm{0.21,0.24,0.28,0.32,0.42,0.48}\right\}⟩$.
• d)${\beta }_{GHPFN}^1÷{\beta }_{GHPFN}^2=⟨\left(\mathrm{0.74,0.78,0.82,0.85,0.89}\right);\left\{\mathrm{0.43,0.375,0.57,0.5,0.86,0.75}\right\}⟩$.
• e)$2{\beta }_{GHPFN}=⟨\left(\mathrm{5,5.2,5.6,5.8,6}\right);\left\{\mathrm{0.96,0.91,0.51}\right\}⟩$.
• f)${\left({\beta }_{GHPFN}\right)}^{0.5}=⟨\left(\mathrm{1.6,1.61,1.67,1.7,1.73}\right);\left\{\mathrm{0.89,0.84,0.77}\right\}⟩\left(\epsilon \ge 0\right)\text{.}$.

3.1.1.3. Score function of GHPFN (2nd type)

Definition 6

Let ${\beta }_{2GHPFN}=\left\{\left(p,q,r,s,t\right);\beta \left(x\right)\right\}$ be a GHPFN. Then the score function of ${\beta }_{2GHPFN}$ is defined as

$$S\left({\beta }_{2GHPFN}\right)=\frac{2r^2+s^2+t^2-p^2-q^2}{3\left(\#h\right)}\sum \beta$$ (13)

Where, #h denotes the number of elements in ${\beta }_{2GHPFN}\text{.}$.

3.2. GHPFN- TOPSIS approach

For the ranking of treatment options in COVID-19, the MCDM tool TOPSIS introduced by the authors of [90] is applied. The GHPFN-TOPSIS procedures is used in the following way:

• Step 1: Determination of alternatives and their preferential ratings in terms of GHPFN 2nd type.

Assuming a set of ‘j’ treatment options $T_1,T_2,\dots .,T_j$ and ‘k’ criteria $U_1,U_2,\dots .,U_k$. Let $D_1,D_2,\dots .,D_r$ be the number of decision experts. As there is no permanent specific medicine for COVID-19, the decision experts may be uncertain or imprecise about a particular treatment. Thus, the DMs assign HPFNs as his/her decision for the alternatives depending on different criteria.

• Step 2: Calculation of score values using equation (13)

• Step 3: Normalization of the score values, using the formula:

$${NZ}_{ef}=\frac{n_{ef}}{\sqrt{\sum _{e=1}^j{n}_{ef}^2}}e=\mathrm{1,2},\dots ,j;f=\mathrm{1,2},\dots .,k\text{;}$$ (14)

• Step 3. Determination of the weighted normalized matrix

$${WN}_{ef}=w_e{\times NZ}_{ef}e=\mathrm{1,2},\dots ,j;f=\mathrm{1,2},\dots .,k\text{;}$$ (15)

• Step 4. Calculation of the Positive Ideal Solution (${PIS}^{P+})$ and the Negative Ideal Solution $\left({NIS}^{P-}\right)$.

$$\begin{array}{c}\left({PIS}^{P+}\right)=\{\begin{array}{c}\underset{e}{\max }\left({WN}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\\ \underset{e}{\min }\left({VW}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\end{array}\\ \left({NIS}^{P-}\right)=\{\begin{array}{c}\underset{e}{\min }\left({WN}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\\ \underset{e}{\max }\left({WN}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\end{array}\end{array}\}$$ (16)

• Step 5. Computation of the distance measure between alternative $T_p$ and thePositive Ideal Solution (${PIS}^{P+})$.

$$D_e^{+}=\sqrt{{\sum _{f=1}^k\left({WN}_{ef}-T_f^{+}\right)}^2},e=\mathrm{1,2},\dots ,j$$ (17)

• Step 7. Computation of the distance measure between alternative $T_p$ andthe Negative Ideal Solution $\left({NIS}^{P-}\right)$.

$$D_e^{-}=\sqrt{{\sum _{f=1}^k\left({WN}_{ef}-T_f^{-}\right)}^2},e=\mathrm{1,2},\dots ,j$$ (18)

Where $D_e^{+}$ and $D_e^{-}$ denotes the distance measure of the individual alternative from the positive ideal solution(${PIS}^{P+})$ and negative ideal solution(${NIS}^{P-})$ respectively.

• Step 8. Calculation of the relative closeness $\left(R_e\right)$ of each option.

$$R_e=\frac{D_e^{-}}{D_e^{-}+D_e^{+}}$$ (19)

3.3. Pseudo code for the proposed research

The research model under consideration involving ‘j’ number of treatment options based on ‘k’ number of criteria is represented below. The input taken in our study are the preferential linguistic terms assigned by doctors and scientist. These terms are converted to GHPFN (2nd type) for obtaining the output i.e. the ranking of the treatment options.

j = Treatment options

k = Number of criteria

j*k = Size of the matrix.

Input: the preferential rating matrix in terms of GHPFN 2nd type.

Output: the ranking order of the treatments in the TOPSIS approach.

1. for(e = 1 to j, f = 1 to k)do.

2. Generate GHPFN 2nd type by DMs;

3. Generate score values $S\left({\beta }_{GHPFN}\right)=\frac{2r^2+s^2+t^2-p^2-q^2}{3\left(\#h\right)}\sum \beta \text{;}$.

4. Construct normalized score values ${NZ}_{ef}$;

5. Generate weighted normalized matrix ${WN}_{ef}=w_e{\times NZ}_{ef}\text{;}$.

6. Calculate (${PIS}^{P+})$ and (${NIS}^{P-})$.

$$\begin{array}{c}\left({PIS}^{P+}\right)=\{\begin{array}{c}\underset{e}{\max }\left({WN}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\\ \underset{e}{\min }\left({VW}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\end{array}\\ \left({NIS}^{P-}\right)=\{\begin{array}{c}\underset{e}{\min }\left({WN}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\\ \underset{e}{\max }\left({WN}_{ef}\right),\left(f=1,2,3,\dots ,k\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\end{array}\end{array}\}\text{;}$$

7. Calculate distance measure of each treatment options from (${PIS}^{P+})$ and (${NIS}^{P-})$.

$$D_e^{+}=\sqrt{{\sum _{f=1}^k\left({WN}_{ef}-T_f^{+}\right)}^2},D_e^{-}=\sqrt{{\sum _{f=1}^k\left({WN}_{ef}-T_f^{-}\right)}^2}\text{;}$$

8. Compute relative closeness $R_e$ = $\frac{D_e^{-}}{D_e^{-}+D_e^{+}}$;

9. end for.

4. Numerical application

Score function of GHPFN (2nd type) is used for the calculation of criteria weights.

The treatment options for COVID-19 which are selected as an alternative in this paper are as follows:

• 1.Plasma exchange
• 2.Tocilizumab
• 3.Remdesivir
• 4.Favipravir
• 5.Hydroxychloroquine

GHPFN (2nd type) with TOPSIS model applied to rank the treatment alternatives. The steps to calculate are as follows.

Step 1.A decision table is constructed by the team of experts for linguistic rating of the treatment alternatives with respect to the criteria. Table 7 represents the linguistic and its respective GHPFN (2nd type)

Table 7.

The GHPFN (2nd type) taken in empirical study.

Linguistic Terms	GHPFN (2nd Type)
Very high	$⟨\left(\mathrm{7,8,9,9,10}\right);\left\{0.8,0.9\right\}⟩$
High	$⟨\left(\mathrm{5,6,7,8,9}\right);\left\{0.7,0.9\right\}⟩$
Average	$⟨\left(\mathrm{3,6,6,7,8}\right);\left\{0.6,0.8\right\}⟩$
Low	$⟨\left(\mathrm{3,4,5,6,7}\right);\left\{\mathrm{0.7,0.8}\right\}⟩$
Very low	$⟨\left(1,\mathrm{2,2,3,5}\right);\left\{0.7,0.9\right\}⟩$

Step 2.The linguistic terms are converted to GHPFN (2nd type) using score function developed in equation (13). The decision Table 8, Table 9 represents it.

Table 8.

The linguistic terms are represented as score functions of GHPFN (2nd type).

Treatment	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$	$C_6$	$C_7$	$C_8$	$C_9$
Plasma Exchange	13.07	11	19.41	0	3.95	3.95	19.41	11	11
Tocilizumab	13.07	3.95	11	13.07	11	3.95	26.07	13.07	11
Remdesivir	13.07	13.07	26.07	11	19.41	19.41	26.07	3.95	11
Favipravir	13.07	19.41	11	13.07	13.07	13.07	3.95	3.95	11
Hydroxychloroquine	13.07	3.95	11	19.41	13.07	13.07	3.95	3.95	11

Table 9.

The linguistic terms are represented as score functions of GHPFN (2nd type).

Treatment	$C_{10}$	$C_{11}$	$C_{12}$	$C_{13}$	$C_{14}$	$C_{15}$	$C_{16}$	$C_{17}$	$C_{18}$
Plasma Exchange	11	19.41	3.95	19.41	13.07	3.95	13.07	3.95	26.07
Tocilizumab	11	19.41	3.95	13.07	19.41	3.95	13.07	3.95	26.07
Remdesivir	11	13.07	3.95	13.07	11	19.41	19.41	13.07	26.07
Favipravir	11	19.41	3.95	11	11	13.07	13.07	13.07	19.41
Hydroxychloroquine	11	19.41	3.95	11	19.41	13.07	19.41	19.41	3.95

Step 3. The normalized table is constructed using eq. (14) and represented in Table 10, Table 11 (see Table 2).

Table 10.

Representation of Normalized table.

Treatment	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$	$C_6$	$C_7$	$C_8$	$C_9$
Plasma Exchange	0.447	0.416	0.515	0.000	0.135	0.144	0.462	0.598	0.447
Tocilizumab	0.447	0.149	0.292	0.451	0.376	0.144	0.620	0.710	0.447
Remdesivir	0.447	0.494	0.692	0.380	0.664	0.709	0.620	0.215	0.447
Favipravir	0.447	0.734	0.292	0.451	0.447	0.477	0.094	0.215	0.447
Hydroxychloroquine	0.447	0.149	0.292	0.670	0.447	0.477	0.094	0.215	0.447

Table 11.

Representation of Normalized table.

Treatment	$C_{10}$	$C_{11}$	$C_{12}$	$C_{13}$	$C_{14}$	$C_{15}$	$C_{16}$	$C_{17}$	$C_{18}$
Plasma Exchange	0.447	0.474	0.447	0.626	0.383	0.144	0.367	0.144	0.529
Tocilizumab	0.447	0.474	0.447	0.422	0.568	0.144	0.367	0.144	0.529
Remdesivir	0.447	0.319	0.447	0.422	0.322	0.709	0.546	0.477	0.529
Favipravir	0.447	0.474	0.447	0.355	0.322	0.477	0.367	0.477	0.394
Hydroxychloroquine	0.447	0.474	0.447	0.355	0.568	0.477	0.546	0.709	0.080

Table 2.

Linguistic variables representing PFN.

Linguistic Terms	Pentagonal fuzzy number
Very high	(3.3, 3.5, 3.7, 3.9, 4)
High	(2.7, 2.9, 3, 3.1, 3.3)
Average	(2.2, 2.3, 2.5, 2.7, 2.9)
Less	(1.6, 1.7, 2, 2.2, 2.3)
Very less	(1, 1.3, 1.5, 1.6, 1.7)

Step 4. Calculation of weighted normalized matrix using eq. (15).

For calculation of weighted Normalized matrix, the weights of criteria obtained are represented in Table 12, Table 13 .

Table 12.

Representation of criteria weight.

Criteria	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$	$C_6$	$C_7$	$C_8$	$C_9$
Weights of criteria	0.496	0.496	0.496	0.496	0.496	0.496	0.496	0.496	0.496

Table 13.

Representation of criteria weight.

Criteria	$C_{10}$	$C_{11}$	$C_{12}$	$C_{13}$	$C_{14}$	$C_{15}$	$C_{16}$	$C_{17}$	$C_{18}$
Weights of criteria	0.496	0.319	0.319	0.319	0.319	0.319	0.185	0.185	0.185

Step 5. Determination of $\left({PIS}^{P+}\right)$ and $\left({NIS}^{P-}\right)$ using eq. (16).

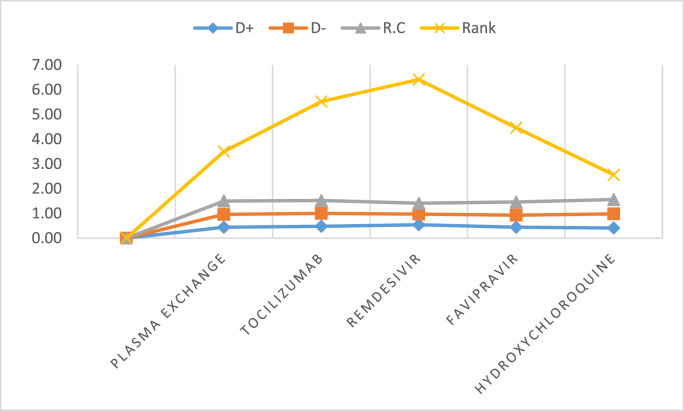
Step 6. Calculation of distance $D_e^{+}and{D}_e^{-}$ measure of each treatment option from $\left({PIS}^{P+}\right)$ and $\left({NIS}^{P-}\right)$ respectively. The final ranking of the treatments are done by finding out the relative closeness $\left(R_e\right)\text{.}$ The larger value of $\left(R_e\right)$ denotes the better alternative. Table 14 represents the distance measure, relative closeness and final ranking of the alternatives.

Table 14.

Calculation of distance measure, relative closeness and final ranking.

Treatment	D+	D-	R.C	Rank
Plasma Exchange	0.44	0.52	0.54	2
Tocilizumab	0.48	0.52	0.52	4
Remdisivir	0.54	0.43	0.44	5
Favipravir	0.44	0.49	0.53	3
Hydroxychloroquine	0.41	0.57	0.58	1

Fig. 6 illustrates the distance measure, relative closeness and ranking obtained by GHPFN- TOPSIS methodology.

Fig. 6.

Illustration of distance measure, relative closeness and ranking of the treatment alternatives.

5. Comparative analysis

In this section, we applied different form of generalized hesitant fuzzy numbers and noticed the changes in the ranking. Two different forms GHTFN and GHTrFN are used and the ranking so obtained are illustrated in table (15) and figure (7) .

• 1.GHTFN- In this form, three numbers are taken in the order-low, medium, high i.e. the TFN to represent a linguistic term remains one but the degree of hesitancy/confidence are multiple depending on the DMs. The GHTFN score function is developed in this paper in the way GHTrFN [91] and GHPFN introduced in this paper. GHTFN- TOPSIS approach is applied and ranks are obtained. The method used in this paper ranked ‘hydroxychloroquine’ as the best treatment option, ‘Plasma Exchange’ as the second one, ‘Favipravir’ the third, ‘Tocilizumab’ the fourth and ‘Remdesivir’ the bottom, whereas GHTFN ranked ‘tocilizumab’ the first followed by ‘plasma exchange, ‘hydroxychloroquine’, ‘remdesivir’ and ‘favipravir’.
• 2.GHTrFN- In Table 15, for obtaining R3 the concept of GHTrFN [91] has been used with TOPSIS methodology to rank the alternatives. The score function defined for GHTrFN [91] is used and the ranking so obtained under this method is depicted. This methodology ranked ‘Plasma exchange’ the first, followed by ‘Tocilizumab’, ‘Remdesivir’, ‘Hydroxychloroquine’ and ‘favipravir’.

Fig. 7.

Representation of ranking obtained under GHPFN, GHTFN and GHTrFN.

Table 15.

Ranking obtained under different methods.

Treatments	Rank (R1) obtained using GHPFN	Rank (R2) obtained using GHTFN	Rank (R3) obtained using GHTrFN
Plasma Exchange	2	2	1
Tocilizumab	4	1	4
Remdesivir	5	4	5
Favipravir	3	3	3
Hydroxychloroquine	1	1	2

Fig. 7 depicts the different ranking obtained using different form of generalized hesitant fuzzy numbers.

6. Sensitivity analysis

The sensitivity analysis has been conducted by interchanging of criteria weights. We considered three different cases and obtained ranking of treatment options. The ranking obtained under sensitivity analysis is been illustrated in Table 16 and Fig. 8 .

Table 16.

Ranking obtained under sensitivity analysis.

Treatment	Rank (i)	Rank (ii)	Rank (iii)
Plasma Exchange	3	2	2
Tocilizumab	4	3	3
Remdesivir	5	4	4
Favipravir	1	1	1
Hydroxychloroquine	2	1	2

Fig. 8.

Representation of rankings under sensitivity analysis.

7. Results and discussions

In the present study generalized pentagonal fuzzy number theory is applied for identification, application and ranking of 5 different treatment strategies of COVID-19 patients. After application of fore-said statistical methodology, HCQs has ranked first, followed by Plasma Exchange, Favipravir, Tocilizumab and Remdisivir. Thesubsequent sensitivity analysis depicted in Table 14 and Fig. 6 clearly indicates that Favipravir has ranked 1 and theage old drug HCQS has ranked 1 or 2 consistently irrespective of different criteria weights. The Convalescent Plasma Exchange therapyhas ranked 2 or 3in treatment modality scale.

The inflammatory response, in COVID patients, is indicated by the elevated immune-inflammatory biomarkers such as Procalcitonin, Ferritin, C-Reactive Protein (CRP), D-Dimer, Lactate Dehydrogenase and Interleukin-6 (IL-6) etc. These markers are used as severity indicators and even as prognostic factors. The use of Therapeutic Plasma Exchange has the theoretical ability to eliminate some of the pro-inflammatory substances and toxic substances of the sick individuals [92].

The important findings from several Chinese -Korean studies [94,[96], [97], [98]] European [93] and American research [95] works are in tandem with the results so obtained in this present work. There is convincing evidence in favour of Convalescent plasma exchange therapy, in its ability to reduce mortality in critically ill patients, by Increase in neutralizing antibody titre and improvement of clinical symptoms and laboratory reports without jeopardizing the safety profile.However the need of further conclusive studies cannot be denied.

8. Conclusion

In this study, we have introduced GHPFN, its arithmetic properties and score functions. The GHPFN- TOPSIS methodology has been utilized to rank the treatment alternatives available for COVID-19. Permanent medicines for the pandemic COVID-19 yet to invented, till now the existing drugs used for influenza, SARS has been used for treating COVID patients. The GHPFN (2nd type) score function is used to determine the weight of the criteria. The results obtained demonstrated ‘Hydroxychloroquine’ the first rank followed by, ‘Plasma Exchange’,‘Favipravir’, ‘Tocilizumab’ and ‘Remdesivir’. In this study, the HFS is extended to GHFS which is helpful in solving MCDM issues which are complicated. Thus the integrated approach of GHFS with MCDM technique provides efficiency to attain highest accuracy in the result. Comparative analysis has been conducted to check the validity of the proposed methodology. Sensitivity analysis has been discussed as how the ranking changes with the change in weight of the criteria. In future, the treatment options and criteria can be included depending on the availability. Different MCDM techniques such as the weighted Aggregated Sum Product Assessment (WASPAS), Election et ChoixTraduisant La Realite (ELECTRE) can be used in future for ranking of medicine selection and decision making problems.

Data availability

No data was used for the research described in the article.