Abstract
Zero-export photovoltaic systems are an option to transition to Smart Grids. They decarbonize the sector without affecting third parties. This paper proposes the analysis of a zero-export PVS with a green hydrogen generation and storage system. This configuration is feasible to apply by any self-generation entity; it allows the user to increase their resilience and independence from the electrical network. The technical issue is simplified because the grid supplies no power. The main challenge is finding an economic balance between the savings in electricity billing, proportional to the local electricity rate, and the complete system's investment, operation, and maintenance expenses. This manuscript presents the effects of the power sizing on the efficacy of economic savings in billing () and the effects of the cost reduction on the levelized cost of energy (LCOE) and a discounted payback period (DPP) based on net present value. In addition, this study established an analytical relationship between LCOE and DPP. The designed methodology proposes to size and selects systems to use and store green hydrogen from the zero-export photovoltaic system. The input data in the case study are obtained experimentally from the Autonomous University of the State of Quintana Roo, located on Mexico's southern border. The maximum power of the load is LPmax = 500 kW, and the average power is LPmean = 250 kW; the tariff of the electricity network operator has hourly conditions for a medium voltage demand. A suggested semi-empirical equation allows for determining the efficiency of the fuel cell and electrolyzer as a function of the local operating conditions and the nominal power of the components. The analytical strategy, the energy balance equations, and the identity functions that delimit the operating conditions are detailed to be generalized to other case studies. The results are obtained by a computer code programmed in C++ language. According to our boundary conditions, results show no significant savings generated by the installation of the hydrogen system when the zero-export photovoltaic system Power ≤ LPmax and DPP ≤ 20 years is possible only with LCOE ≤ 0.1 $/kWh. Specifically for the Mexico University case study, zero-export photovoltaic system cost must be less than 310 $/kW, fuel cell cost less than 395 $/kW, and electrolyzer cost less than 460 $/kW.
Keywords: Green hydrogen, Energy balance analysis, Sustainable buildings, Sizing tool
Abbreviations
- CFE
Mexico National Electricity Commission
- FC
Fuel Cell
- H2
Hydrogen
- PEME
Proton Exchange Membrane Electrolyzer
- PEMFC
Proton Exchange Membrane Fuel Cell
- PV
Photovoltaic
- RE
Renewable Energy
Nomenclature
Savings in Billing
Investment Cost
Load Factor
Total Energy Consumed to Electricity Rate
Electrolyzer Efficiency
Fuel Cell Efficiency
- CO&M
Annual Operation and Maintenance Cost
- CRep
Replacement Cost
- d
Real Interest Rate
- DPP
Discounted Payback Period
- G
Tariff to determine the deemed cost for energy generation: for a Base horary, for an intermediate horary and for a peak horary
- j
Sequential Year Analyzed
- k
LCOE Horizon Period
- kNPV
Net Present Value Horizon Period
- LCOE
Levelized Cost of Energy
- LPmax
Load Maximum Power
- LPmean
Load Average Power
- NPVj
Net Present Value
- PPVexp
Solar Available Power
- PPVmax
Solar Maximum Power
- εLoad
Electrical Load
- εPV
Photovoltaic Resource
Power Capacity Installed Deemed Cost
Energy Distribution Deemed Cost
Power Distribution Tariff
Maximum Demand Power Recorded
Peak Horary Maximum Demand Power Recorded
Electrolyzer Replacement Costs
Electrolyzer Investment Cost
Electrolyzer Annual Operating and Maintenance Cost
Hydrogen Storage Tank Energy Capacity
Hydrogen Storage Tank Energy Consumed
Hydrogen Storage Tank Energy Supplied
Hydrogen Storage Tank Energy Stored
Actual Billing
PEMFC Annual Operating and Maintenance Cost
Fuel Cell Replacement Costs
Fuel Cell Investment Cost
Hydrogen Storage Tank Investment Cost
Hydrogen Storage Tank Annual Operating and Maintenance Cost
Nominal Billing
Electrolyzer Installed Power
Electrolyzer Operational Power
Fuel Cell Installed Power
- Fuel Cell Operational Power
Fuel Cell Operational PowerPhotovoltaic Power
Inverter Replacement Costs
Photovoltaic Investment Cost
Photovoltaic Annual Operating and Maintenance Cost
Cost Reduction Factor of Hydrogen Systems
Cost Reduction Factor of Photovoltaic Systems
Energy Consumed and Billed
Tariff to Determine the Cost of Energy Transmission
1. Introduction
Basic facts and statistics show that annual energy-related CO2 emissions must decrease by over 70% by 2050 [1]. In this sense, Mexico urgently needs rapid decarbonization [2]. Therefore, one of the main objectives today is reducing anthropogenic emissions and achieving a green future in the medium term. Renewable energy (RE) is a viable alternative to sustainability. The use of RE sources such as solar [3], wind [4], and fuel cells [5] as clean energy production have significantly built up in many countries due to a viable option to meet the increasing energy demand and lessen greenhouse gases. However, RE sources depend highly on weather conditions like wind speed, solar irradiance, and seasonal and unpredictable nature [6]. These conditions necessitate energy storage to meet the current system demand. The most common types of backup energy are diesel engines and battery banks, but both are highly polluting.
Many photovoltaic systems are connected to the local electricity grid [7]. Solar panels are directly connected to the grid through inverters and bi-directional meters; the energy produced is utilized for self-consumption, the surplus is exported to the grid, and the deficit is imported. This option has significant economic advantages, but the interconnected grid mode affects the grid differently, including voltage and frequency stability and synchronization challenges. With very high photovoltaic penetration, a large amount of power would be injected into the distribution grid, leading to unacceptable energy quality. The hosting capacity concept can be applied to determine how many systems should be installed in the current network [8]. Therefore, there are technical regulations (standards) or other normative regulations where injecting current into the electrical network may be limited or denied by the network administrator.
On the other hand, in a zero-export photovoltaic system, the surplus is monitored to prevent injection into the grid. This exclusively self-consumption mode reduces faults and offers the user independence, quality, and resiliency advantages [9]. Furthermore, energy storage in the zero-export photovoltaic system increases the savings capacities; nevertheless, to break even the local electricity rate, all costs incurred by the project must be considered [10,11].
Using hydrogen (H2) generated by electrolysis (powered by RE) as a carbon-free energy vector presents an opportunity to decarbonize several industrial sectors [[12], [13], [14], [15], [16]] - such as chemical, steel, and transportation sectors-. This proposal would reach the goal of carbon neutrality by 2050; some analyses even indicate that H2 will have more active participation in our daily lives by 2030 [14]. Every day, more and more countries are committed to developing H2 energy and Fuel Cell (FC) technologies. Storing RE in the form of H2 is considered one of the most attractive energy storage routes, making RE storage possible because of its high energy density per mass and long-term storage capability [15]. Moreover, the surplus of the zero-export photovoltaic system can be converted to H2 by utilizing electrolysis (green hydrogen) [16], and the produced H2 can be stored for usage during high-energy demand periods.
However, this proposal presents some disadvantages as the infrastructure development needed and the current high costs for electrolyzers and FCs. Even so, as the efficiency of H2 technologies increases and their costs decrease [17], the adoption of H2 technologies will continue to grow. Sanchan et al. researched the techno-economic outlook in 2030 by considering an electrolytic H2 supply using solar photovoltaics (PV) installations, H2 and battery energy storage, proton exchange membrane electrolyzer (PEME), and gaseous H2 energy storage. Their findings show that 2.5 $/kg levelized H2 costs (LCOE = 0.075 $/kWh) occur for PV capital costs of 500 $/kW and 496 $/kW for electrolyzer systems [18]. Shaner et al. estimated the levelized cost for PV electricity-based electrolytic H2 to be 6.1 $/kg (LCOE = 0.183 $/kWh) when supplemented by grid electricity (priced at 0.07 $/kWh) and 12.1 $/kg (LCOE = 0.363 $/kWh) when electricity is sourced entirely from PV [19]. Mueller-Langer et al. evaluated different H2 production processes and suggested that electrolysis is unlikely to be competitive, primarily due to high electricity prices [20].
In this work, the main interest is determining DPP and LCOE as a function of different configurations of size and cost per unit of photovoltaic system power, electrolyzer power, fuel cell power, and cost per unit of hydrogen storage tank energy. The strategy employs a Mexican university's case study, with the installed PV's experimental data, electrical demand measurements, fuel cell and electrolyzer experimental polarization curves, and billing rate. The results are obtained using our computing algorithm programmed in C language and developed in Dev-C ++ (Company Free Software Foundation, Inc., version 5.11). Energy balance equations and operation index functions are detailed in the methodology, with different novelty points, mainly: beyond LCOE and net present value, DPP allows further analysis of the effects of the system costs. In addition, our approach implements experimental efficiency equations of the fuel cell and electrolyzer. Finally, the study is performed to size, analyze, and assess the feasibility of using real energy billed and Mexican weather data. Furthermore, the proposed methodological strategy allows it to be generalized to other distributed buildings and regions of the country.
2. Methodology
The numerical strategy consists of solving an energy balance in a steady state and analyzing the averages obtained in a representative period. The energy balance model is parameterized based on the power of the installed sub-systems and index functions that mathematically define the operating conditions. The input data are the local conditions: solar irradiance, electricity consumption profile, and rates for billing.
In this work, the parameterized model focuses on quantifying the energy that will be billed (Eq. (7)). Eq. (7) is used to numerically determine DPP by employing Eq. (9) in Eq. (10) and to determine (Eq. (8)) analytically, and LCOE (Eq. (11)). Equations (1)–(6) describe the model step by step.
2.1. Operating assumptions
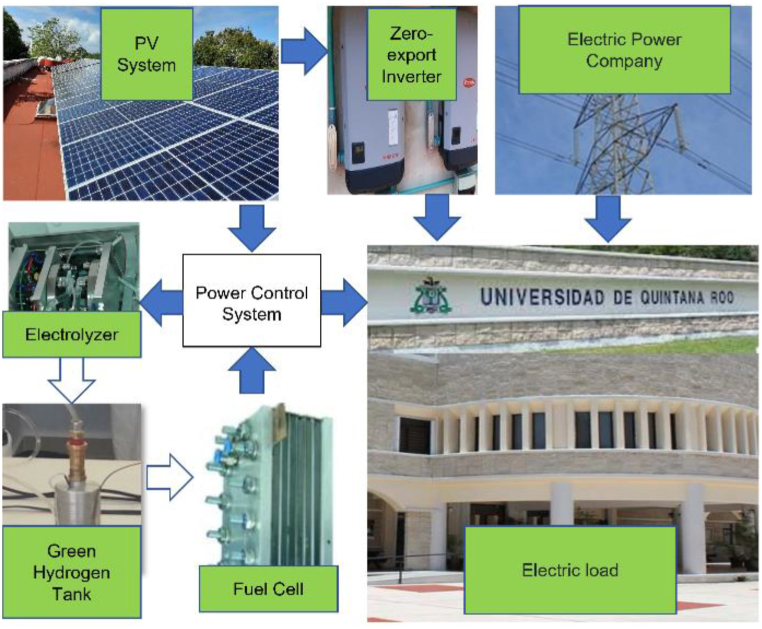
The electrical network is assumed to have a capacity large enough to satisfy the total electrical demand. The PV supplies energy directly to the electrical load; when surplus energy, H2 is generated through a PEME, and the H2 is stored in a high-pressure tank. When the PV system cannot meet the load, a proton exchange membrane fuel cell (PEMFC) provides part of the energy required. Fig. 1 shows a diagram of the proposed system.
Fig. 1.
Diagram of the zero-export photovoltaic system studied; the photos correspond to the experimental components of Quintana Roo University.
The effect of power size and cost of installed systems is studied parametrically. First, an energy balance model is applied in a stable state, with an hourly solution, analyzing the averages obtained in a predefined period in the boundary conditions. The results of this analysis are obtained using a computer code programmed in the C++ language. Then, the input data is defined annually: available photovoltaic resource (εPV), demanded electrical load (εLoad), and hourly rate of the electrical network.
2.2. Energy management strategy
An algebraic hourly energy balance of the input and output energy determines whether there is an energy surplus or deficit, as described by Eq. (1).
| (1) |
Analytical or numerical models can determine the εPV magnitude; in this work, εPV is defined by Eq. (12) that use normalized data obtained experimentally. It is important to note that the name of the index function is not a dependent variable. Nevertheless, Surplus and Deficit variables are critical magnitudes to determine the operational power of electrolyzer () and the fuel cell's operational power (). This influence is described by the indicator function on equations (2), (3)).
| (2) |
| (3) |
Where is the current energy stored in the hydrogen tank and is the maximum storage energy capacity of the tank. In equations (2), (3)), the first two conditions delimit the size of the installed power so that the local power of generation or consumption of H2 is not greater than the power of the installed equipment, specifically, the installed power of the PEME () and the installed power of the PEMFC (). In the third condition, in both functions, operational powers are limited to zero in function of the hydrogen tank level. In Eq. (2), if the tank is at maximum level (). In Eq. (3), if the tank is empty (). In order to parameterize , the storage energy balance in the tank of equation (4) is proposed.
| (4) |
Where is the energy supplied to the tank due to green hydrogen generated, which is a function of , the operation time, and the electrolyzer efficiency . is the energy consumed in the tank due to the consumption of green hydrogen; it is a function of and the fuel cell efficiency . It is important to note that the magnitudes and significantly differ from those of and . The experimental data of the efficiency of the fuel cell and electrolyzer, both developed in our laboratories, are implemented through the model described in Barbosa et al. [21], as indicated by equations (5), (6)), respectively,
| (5) |
| (6) |
The constant magnitudes of the equations are obtained experimentally [21]. Finally, the energy consumed and billed () is determined; the identity function of equation (7) defines this magnitude.
| (7) |
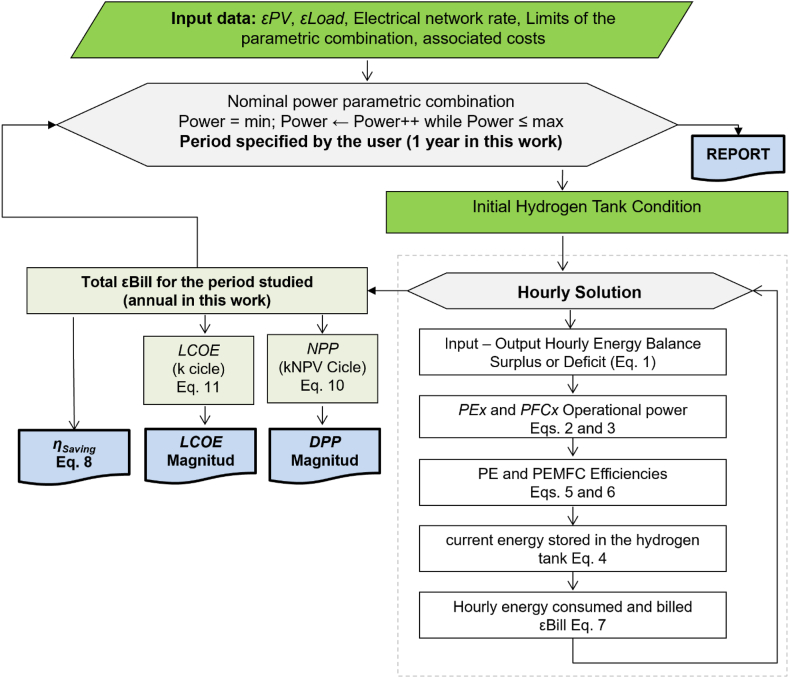
The first condition defines that, in any surplus condition, the local energy bill is zero. The second condition determines that the cell can operate jointly with the PV system if there is a deficit and energy is available in the hydrogen tank. Finally, the third condition defines that only the PV system operates if there is a deficit but insufficient energy in the hydrogen tank. Fig. 2 shows the general flowchart of the implemented algorithm.
Fig. 2.
General flow diagram of the algorithm employed.
2.3. Economic analysis
is determined by equation (8), which describes an economic savings rate in energy billing based on installed power and operating conditions.
| (8) |
is the nominal billing of the total , and is the actual billing. Then, the net present value (NPVj), eq. (9), determines the net cash flows [22].
| (9) |
Where kNPV is the defined period in years; j is the sequential year analyzed; is the investment cost, which considers the sum of all the components in year zero of the simulation. CO&M is the annual operation and maintenance cost; CRep is the replacement cost of the components; d is the real interest rate (which is a function of the nominal interest rate and the annual inflation rate); in this work, d = 5.0% [22,23]. Analytically, the magnitude of NPVj is positive when the sum of the cash flow is greater than the sum of the investment, CO&M, and CRep costs. DPP is determined numerically by the index function of Eq. (10),
| (10) |
Equations (9), (10)) provide the DPP numerical solution calculated in the finite range 1 ≤ j ≤ kNPV. kNPV typically corresponds to the useful life of the system. However, this work analyzes a horizon of kNPV = 200 years to widen the analysis scope.
LCOE is a widely used parameter to compare the cost of electricity generation systems [23]. LCOE is calculated as the sum of lifetime costs divided by the total energy produced during the same lifetime. These economic and energy magnitudes are also analyzed at a Present Net Cost. This work examines LCOE in US dollars on energy ($/kWh), as described in Eq. (11) [23].
| (11) |
In this work, for LCOE, the study horizon corresponds to the useful life of the system k = 20 years. Table 1 shows the specific costs used as base reference in our simulation [23]. It is important to note that column four, specifies where the cost reduction factor of hydrogen systems ( and PV systems ( are applied. The factors and are analyzed between 100 and 5% in 20 intervals of 5%.
Table 1.
Specific costs in the initial calculation (base reference) [23].
| Symbol | Description | Units | Fee |
|---|---|---|---|
| PEMFC investment cost, including balance of plant (BOP). | $/kW | (3947) | |
| PEMFC annual operating and maintenance cost. | $/kW | (118) | |
| PEMFC replacement costs occur every 5 years. | $/kW | (1815) | |
| Electrolyzer investment cost, including BOP. | $/kW | (4600) | |
| Electrolyzer annual operating and maintenance cost. | $/kW | (138) | |
| Electrolyzer replacement costs occur every 5 years. | $/kW | (1610) | |
| Hydrogen storage tank investment cost, including BOP. | $/kWh | (14.241) | |
| Hydrogen storage tank annual operating and maintenance cost. | $/kWh | (0.285) | |
| PV investment cost, including balance of system (BOS). Lifetime 20 years. | $/kW | (1547) | |
| PV annual operating and maintenance cost. | $/kW | (24) | |
| PV-Inverter replacement costs occur every 10 years. | $/kW | (80) |
3. Case study
is evaluated at hourly intervals and averaged to evaluate the system's global performance for a year on each possible configuration of the parametric combination of the nominal power of the subsystems, an average of the load power (LPmean), and maximum value of the load power (LPmax), listed in Table 2.
Table 2.
Limits of the parametric combination of the nominal powers.
| PPV (kW) | (kW) | (kW) | (kWh) | |
|---|---|---|---|---|
| Minimum | 0.4 LPmean | 0.05 LPmean | 0.05 LPmean | 0.4 LPmean |
| Maximum | 5.0 LPmax | 5.0 LPmax | 5.0 LPmax | 10 LPmax |
3.1. Solar resource (data in)
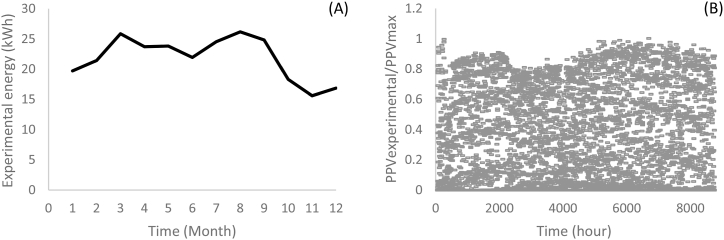
Primary energy data were experimentally obtained from an interconnected photovoltaic system at Quintana Roo University; its main technical characteristics are 355 monocrystalline modules of 415 Wp (CANADIAN SOLAR model: CS3W–410 W) and nine inverters of 15 KW 220 V (FRONIUS model SYMO 15.0–3208). The measurements determine average annual energy of 263 MWh. In addition, the hourly data of the available solar power (PPVexp) were normalized on the maximum solar power measured (PPVmax) to obtain a factor that allows parameterizing the simulated hourly energy in the installation, as presented in equation (12).
| εPV = (PPVexp / PPVmax) PPV (time) | (12) |
Where εPV is the hourly energy generated, parameterized by the simulated PV power (PPV). Fig. 3(A) shows the experimental energy generated monthly and Fig. 3(B) shows the factor resulting from the division PPVexp/PPVmax. In addition, a peak sun hour of 5.5 kWh/m2 per day is determined by experimental data.
Fig. 3.
Experiment solar resource used for simulation: actual monthly energy output 3(A) and hourly PPVexp/PPVmax rate 3(B).
3.2. Electrical load (data in)
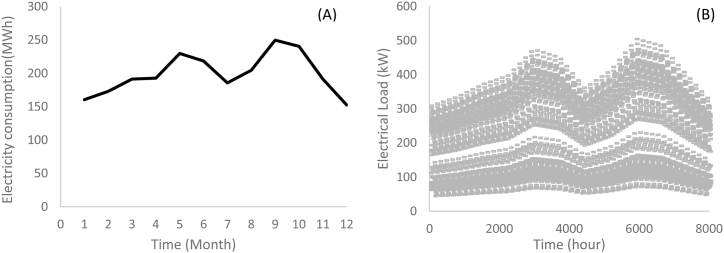
This work determined εLoad by an hourly measurement, carried out experimentally in a typical work week (outside of the pandemic), and adjusted annually by average monthly billing data over five years. Fig. 4(A) shows the monthly energy consumption and Fig. 4(B) shows the hourly power demanded. This information can identify LPmean = 250 kW and LPmax = 500 kW.
Fig. 4.
Average monthly electricity consumption 4(A) and electrical load 4(B).
3.3. Unit rates for energy bill (data in)
This investigation considered the Mexican National Electricity Commission (CFE) rate. Then, equation (13) presents the analytical function to determine the billing amount in the Great Demand in Medium Hourly Voltage rate.
| (13) |
is the tariff to determine the cost of energy transmission, is a constant charge multiplied directly by the total energy consumed, . G is a tariff to determine the deemed cost for energy generation, and there are three types: for a base horary, for an intermediate horary, and for a peak horary. Table 3 shows these timetables. , determined by equation (14), is the deemed cost for the energy distribution, and , determined by equation (15), is the deemed cost for the power capacity installed.
| (14) |
Where is the tariff per unit for power distribution, is the maximum demand power recorded in the studied period, is a constant denominated load factor in our studied region, . is determined by Eq. (15),
| (15) |
Where is the maximum demand power recorded in the studied period only at the peak horary. Table 3 shows the current unit rate for electricity in December 2021. The algorithm identifies the rate for each hour of the study year.
Table 3.
Mexico unit rates for the energy cost of equation (13) ($ US dollars).
| Symbol | Description | Units | Fee |
|---|---|---|---|
| The cost attributed to energy transmission | $/kWh | 0.0087 | |
| The cost attributed to the energy consumed at base horary: Summer schedule: Monday-Friday (0:00–6:00); Saturday (0:00–7:00), Sunday (0:00–19:00). Not Summer schedule: Monday-Friday (0:00–6:00); Saturday (0:00–8:00), Sunday (0:00–18:00). | $/kWh | 0.0557 | |
| The cost attributed to the energy consumed at intermediate horary: Summer schedule: Monday-Friday (6:00–20:00) and (22:00–24:00); Saturday (7:00–24:00), Sunday (19:00–24:00). Not Summer schedule: Monday-Friday (6:00–18:00) and (22:00–24:00); Saturday (8:00–19:00) and (21:00–24:00), Sunday (18:00–24:00). | $/kWh | 0.0932 | |
| The cost attributed to the energy consumed at peak horary: Summer schedule: Monday-Friday (20:00–22:00). Not Summer schedule: Monday-Friday (18:00–22:00); Saturday (19:00–21:00). | $/kWh | 0.1038 | |
| The cost attributed to energy distribution | $/kW | 4.9800 | |
| The cost attributed to power capacity demanded | $/kW | 17.4180 |
4. Results
The results are separated into five sections. Section 4.1 discusses the effect of sizing on savings in billing. According to equation (8), it is not a function of the cost of the system. Section 4.2 presents the results of LCOE and DPP as a function of the powers installed using current costs found in the literature (δH2SYS = 1.0; δPVSYS = 1.0). Section 4.3 analyzes the effect of reducing the photovoltaic system cost in the range 0.1 ≤ δPVSYS ≤ 1.0 @ δH2SYS = 1.0. It also analyzes the effect of reducing the cost of the hydrogen system in the range 0.1 ≤ δH2SYS ≤ 1.0 @ δPVSYS = 0.2. Then, section 4.4 presents the results of LCOE and DPP in the function of installed capacities using costs affected by δH2SYS = 0.1 and δPVSYS = 0.2. Finally, section 4.5 offers a sequence that generalizes the proposed analysis strategy.
4.1. Dependence on size
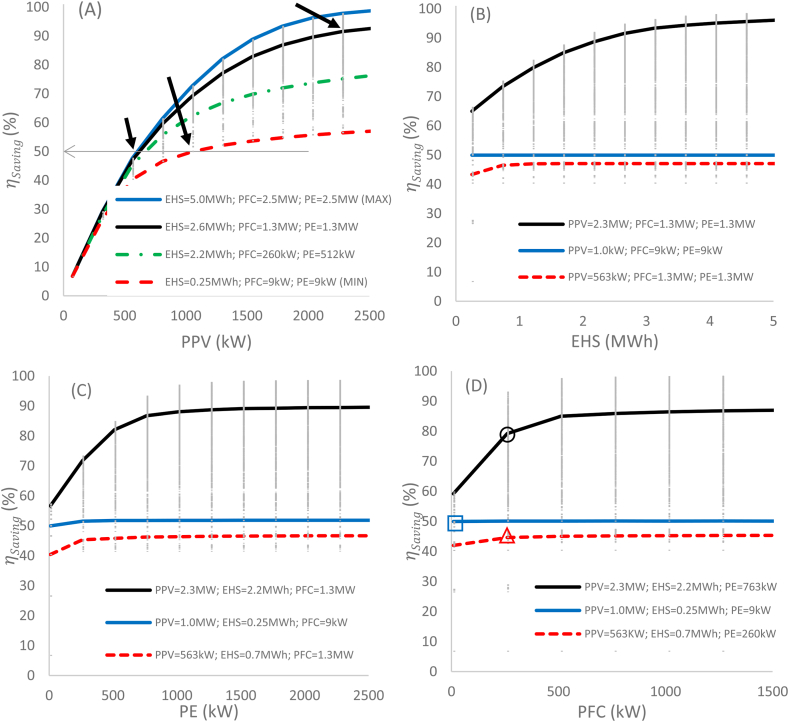
Fig. 5 shows the magnitude of (equation (8)) as a function of the powers of the installed systems. For Fig. 5(A), the difference between the red dotted line and the upper line (solid blue line) indicates the advantage of having an energy storage system to increase . The gap () of using or not using the green H2 storage system is at upper PPV magnitudes (PPV = 2.3 MW). Even in the PPV < 500 kW (LPmax condition), the H2 high-power condition is not significantly different from the H2 low-power condition () because there are no significant surpluses. The condition of the lower installed powers of the H2 components looks to be satisfying the load without the storage system. All the curves displayed in Fig. 5(A-D), exhibit that as the installed power increases, increases with a tendency to asymptotic maximum.
Fig. 5.
The behavior of depending on the installed powers: 5(A) PPV, 5(B) EHS, 5(C) PE, and 5(D) PFC.
In Fig. 5(A), arrows indicate three powers: PPV = 563 kW, PPV = 1.0 MW and PPV = 2.3 MW. The black, blue and red color selected lines have a sequence that begins with these three arrows and ends with Fig. 5(D). Then, the lines of Fig. 5(D) contain information selected from the previous graphs. In Fig. 5(D), three points are selected to analyze the LCOE trends: 1) Δ PPV = 563 kW; EHS = 0.70 MWh; PE = 260 kW; PFC = 260 kW; in which = 45%. 2) □ PPV = 1.0 MW; EHS = 0.25 MWh; PE = 9 kW; PFC = 9 kW; in which = 50%. 3) ○ PPV = 2.3 MW; EHS = 2.2 MWh; PE = 763 kW; PFC = 260 kW, where = 80%. These three points will be analyzed further on.
4.2. Economic analysis without a cost reduction factor
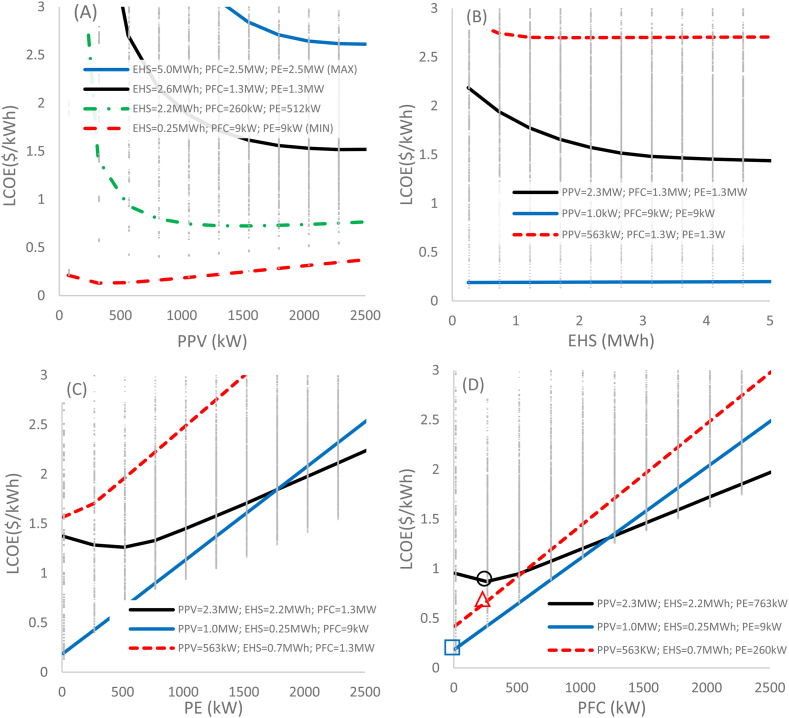
Fig. 6(A-D) shows the LCOE corresponding values for the powers, referring to Fig. 5(A-D). Again, colors, marks and sequence are the same as the previous, and it is coherent with Fig. 12. For all the curves displayed in Fig. 6(A-D), we can observe that the selected powers significantly modify LCOE, and there is no direct relationship between LCOE and .
Fig. 6.
The behavior of LCOE depending on the installed powers: 6(A) PPV, 6(B) EHS, 6(C) PE, and 6(D) PFC.
Fig. 12.
The behavior of LCOE depending on the installed powers: 12(A) EHS, 12(B) PE, and 12(D) PFC.
In Fig. 6(A), observing the red dotted line (EHS = 0.25 MWh; PFC = 9 kW and PE = 9 kW), a minimum in LCOE is identified at PPV = 260 kW. This value indicates that even with low power conditions in storage systems, LCOE has a minimum PPV = LPmean. In Fig. 6(D), with the same sequence of the points of Fig. 5(D), we can observe that LCOE Δ is higher than LCOE □ and the difference between LCOE Δ and LCOE ○ is significantly less than the difference between Δ and ○. There are some interesting trends in Fig. 6, but as seen below, cost reduction factors are necessary for a DPP lower than 20 years.
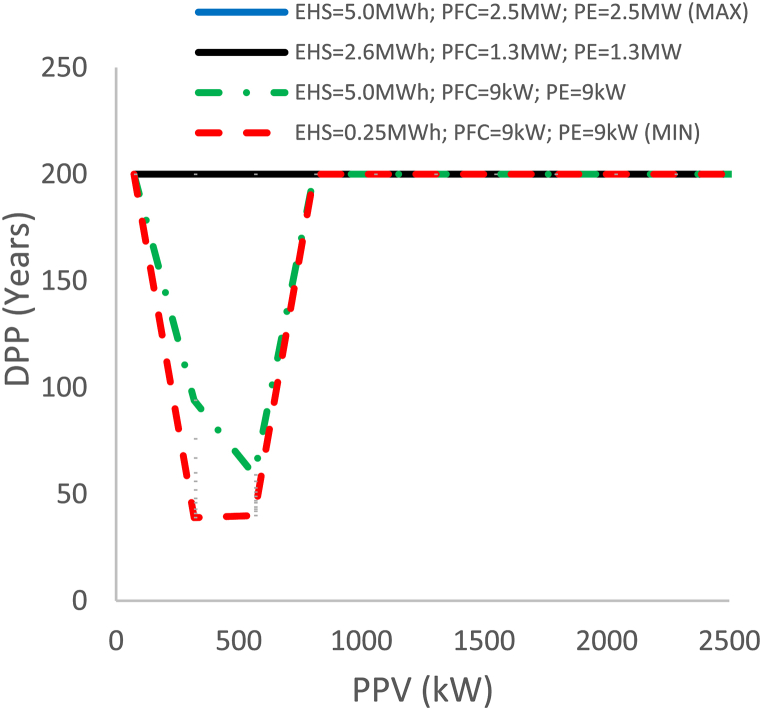
Fig. 7 shows the result of DPP as a function of PPV. In this sequence, because the results are out of the study range (DPP > 200 years), the behavior of DPP as a function of EHS, PE, and PFC is not presented.
Fig. 7.
DPP as a function of PPV.
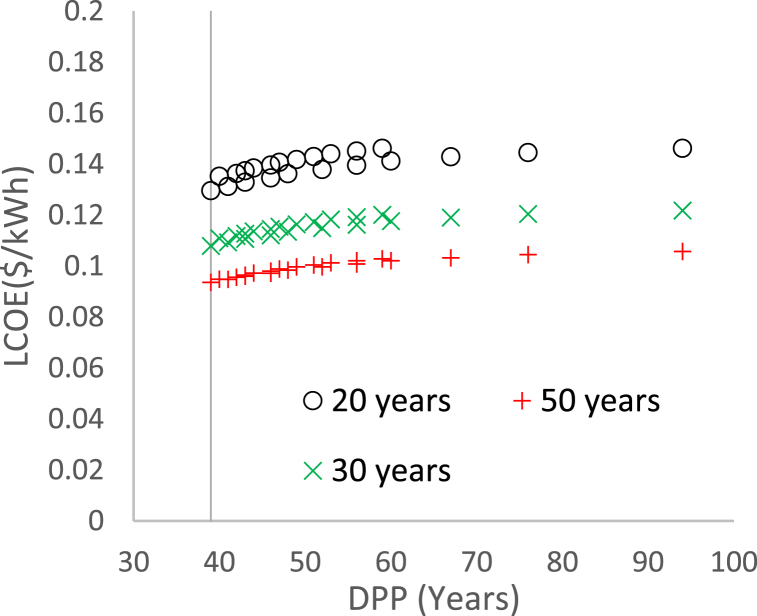
The numerical strategy to obtain DPP has been carried out for 1 year ≤ j ≤ 200 years. In Fig. 7, the powers selected in the black and blue lines have a value greater than 200 years, so there was no trend. We can see that PE = 9 kW and PFC = 9 kW (Minimum powers) can generate DPP < 200 years for the powers selected in the red and green lines. However, under current conditions, every system generates DPP > 40 years. Therefore, LCOE is determined in the period N, defined in equation (11), in Fig. 6, Fig. 7, N = 20 years. Fig. 8 presents LCOE as a function of the numerical DPP with three magnitudes: N = 20 years, N = 30 years, and N = 50 years.
Fig. 8.
LCOE as a function of DPP, with three different horizons: N = 20 years, N = 30 years, and N = 50 years.
In the graphs of Fig. 8, there is a definite trend. The most relevant observation is that no condition promotes DPP < 40 years. Also, the graph that the N increase promotes the reduction of LCOE magnitude.
4.3. Cost reduction factor effects
Fig. 9 shows the results for applying the δPVSYS factor; the gray points are for all the possibilities of the range of powers studied.
Fig. 9.
Effect of the discount rate on the cost of photovoltaic systems (δPVSYS): 9(A) is for LCOE, 9(B) presents DPP, and 9(C) presents the relationship between LCOE vs. DPP.
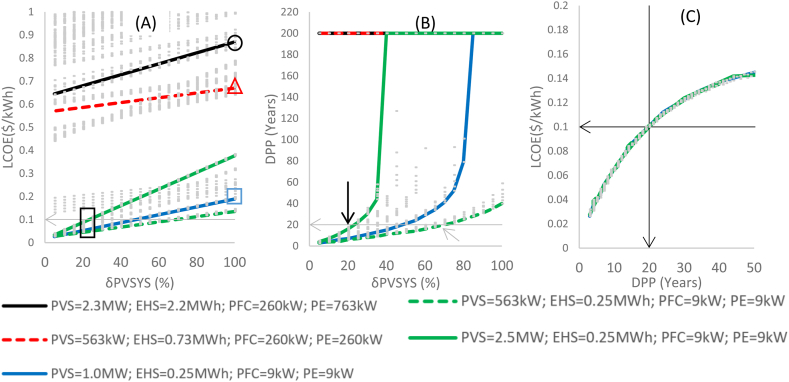
In Fig. 9(A), the same three points of Fig. 5(D) are indicated in δPVSYS = 100%. The slopes change significantly depending on the installed power. The black and red lines, which in this selection correspond to powers higher than the minimum (EHS > 0.25 MWh; PE > 9 kW; PFC > 9 kW), have a low slope of change in these two lines LCOE > 0.5$/kWh. Fig. 9(B) indicates that in the green dotted line, we can find DPP = 20 years @ δH2SYS = 70% (PV.Cinv = 1082 $/kW). With the solid green line option, we can find DPP = 20 years @ δH2SYS = 20% (PV.Cinv = 309 $/kW). The most important observation is that, despite δPVSYS, DPP < 20 years may only occur with systems with the lowest hydrogen production and storage capacity under current economic conditions. For example, in Fig. 9(C), we see DPP ≤ 20 years @ LCOE ≤ 0.1 $/kWh. Fig. 10 presents the effect of the factor δHYSYS @ δPVSYS = 20%.
Fig. 10.
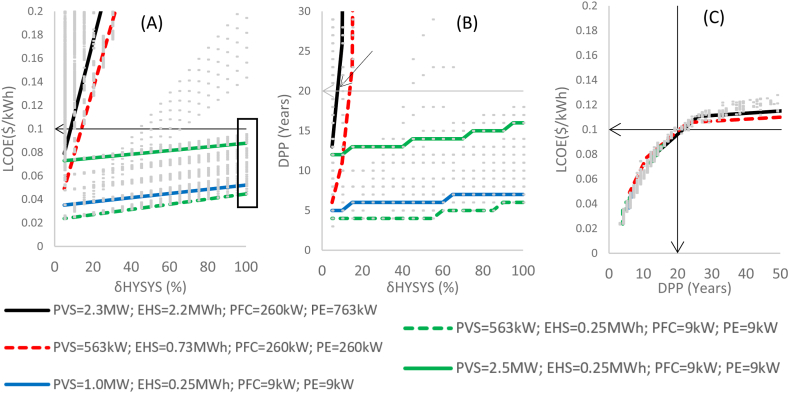
Effect of the discount rate on the cost of hydrogen systems (δHYSYS): 10(A) is for LCOE, 10(B) presents DPP, and 10(C) presents the relationship between LCOE vs. DPP.
In Fig. 10(A), the points δH2SYS = 100%, corresponding to Fig. 9(A), are indicated in the black rectangle. The black, blue, and dotted red curves correspond to the powers selected in the previous figures: 5(D), 6(D), and 9(A). Contrary to Fig. 9(A), the slopes of greater magnitude are for the black and red curves, which in this figure also correspond to the system EHS >0.25 MWh; PE > 9 kW; PFC > 9 kW. Fig. 10(C), as Fig. 9(C), show that DPP ≤ 20 years @ LCOE ≤ 0.1 $/kWh.
It is important to remember the reference points of Fig. 5(D): 1) the red dotted line in Fig. 10 refers to the red triangle Δ, which in Fig. 5(D) = 45%. 2) The blue line in Fig. 10 refers to the blue square □, which in Fig. 5(D) = 50%. 3) The black line in Fig. 10 refers to the black circle ○, which in Fig. 5(D) = 80%. In Fig. 10(B), the point of the black line is indicated to obtain DPP < 20 years @ δH2SYS = 10%, which corresponds: to FC.Cinv = 395 $/kW, HT.Cinv = 1.4 $/kWh, E.Cinv = 460$/kW. It is observed that the blue line generates DPP ≤ 20 years @ δH2SYS = 100%, even from δPVSYS ≤ 45%, see Fig. 9(B). In comparison, the red line requires that δH2SYS ≤ 15% for DPP ≤ 20 years.
4.4. Economic analysis with cost reduction factor applied
Fig. 11 presents the behavior of LCOE as a function of PPV, considering the factors δPVSYS = 20% and δHYSYS = 10%. It is worth pointing out the following observations: the dotted red line refers to the red triangle Δ of Fig. 5(D); the solid blue line refers to the blue square □ in Fig. 5(D); the black line refers to the black circle ○ in Fig. 5(D).
Fig. 11.
LCOE as a function of PPV considering δPVSYS = 20% and δHYSYS = 10%.
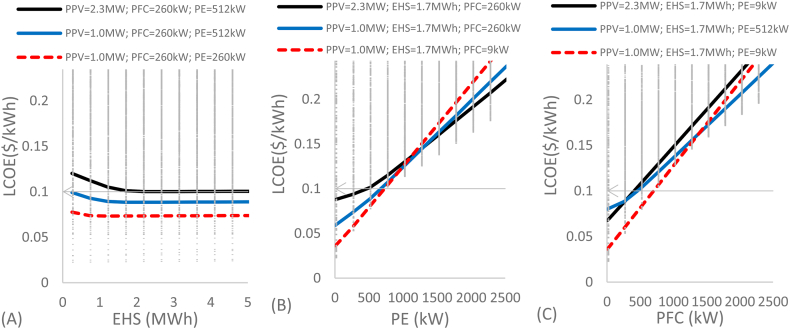
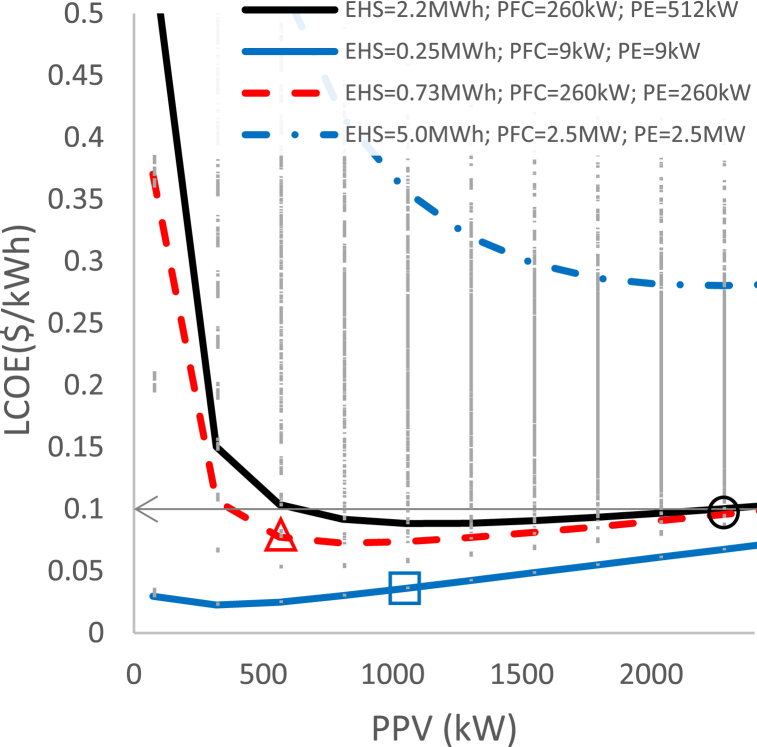
There is a minimum LCOE point for each selected system. For example, the powers of the blue dotted line (above), which in Fig. 5(D), could be identified with the highest magnitude of , have an LCOE > 0.25 $/kWh, which indicates DPP > 20 years. From PPV > 563 kW, the black line promotes LCOE ≤ 0.1 $/kWh. As seen before, low-power hydrogen systems (solid blue line) promote LCOE <0.1 $/kWh, and it is observed that LCOE increases as PPV increases. Likewise, it stands out that at PPV = 2.5 MW, there is little difference in the LCOE magnitude between the black and red lines. Fig. 12 presents the behavior of LCOE as a function of EHS 12(A), PE 12(B), and PFC 12(C). The selected powers are modified from the previous observations.
For all the curves displayed in Fig. 12(A-C), the analysis of the red line show: 1) the size of the EHS hydrogen tank does not modify the behavior of LCOE. 2) The PE and PFC powers significantly increase LCOE, determining that LCOE > 0.1 $/kWh @ PE > 763 kW and @ PFC >763 kW. For the system selected in the blue line, it is observed: 1) the results find a minimum value LCOE = 0.09 $/kWh @ EHS > 1.7 MWh. 2) the curve has a change in slope at PE = 512 kW and PFC = 260 kW. 3) LCOE > 0.1 $/kWh @ PE > 763 kW and @ PFC > 512 kW. For the black line, it is observed: 1) the curve finds a minimum value LCOE = 0.1 $/kWh @ EHS > 1.7 MWh. 2) LCOE > 0.1 $/kWh @ PE > 512 and @ PFC > 260 kW. We can select the systems that best fit our needs with these curves.
4.5. Generalized algorithm
According to the gathered experience, we proposed a general methodology, consisting of the following sequence of steps:
-
I.
The user defines the local conditions: local irradiance, electrical demand, and billing tariff. Then, input data is ideally defined per hour in an average year or year representative.
-
II.
An energy balance is applied in the period specified by the user. Then, using the function identity of Eq. (7), the energy that will be billed () is determined. This value depends on the operating powers and the level of the tank, determined by equation (2), which proposes the implementation of the experimental efficiency of the electrolyzer (Eq. (4)) and efficiency of the fuel cell (Eq. (3)), which use the identity functions of Eqs. (6), (5)). In this way, the analysis considers the effect of sizing dynamically and with greater certainty. is used in Equations (8), (11)).
-
III.
According to the billing rate defined, is determined by equation (8).
-
IV.
The user defines the costs of the system (Table 1) and the study horizon k (years). LCOE is determined by Eq. 11 and DPP by Eq. (10).
The results generate proper trend curves to assess the effect of size on savings at billing and levelized cost. Identifying a minimum magnitude or asymptote is possible in these curves. In addition, to the apparent analysis of trends, the users can select the systems that best fit their needs. For example, with systems indicated in the black circle of Fig. 11, in PPV = 2.3 MW, we have two possibilities: System A) PFC = 260 kW, PE = 260 kW, and EHS = 0.73 kWh. System B) PFC = 260 kW, PE = 512 kW and EHS = 2.2 MWh. Both systems provide LCOE = 0.1 $/kWh, which generates, according to Fig. 10(C), DPP = 20 years. However, system A, which costs $ 20.1 million, offers = 62.37%, while system B, which costs $ 22.4 million, offers = 75.12%.
5. Conclusions
This study proposes a new parametric dimensioning strategy. The energy balance model considers four index functions to evaluate the critical conditions of the hydrogen level contained in the tank and allows it to include the experimental efficiency of the fuel cell and electrolyzer. These models provide the effect that the size of the system has on the energy generated by the PV-H2 system and, consequently, on the billing savings, levelized cost of energy, and the discounted payback period. The overall pattern and sequence could apply to other applications of a zero-export photovoltaic system with green hydrogen storage. The generated curves are very useful for the user to identify trends and select the system that best meets the energy and economic needs. The results show that less than 20 years of DPP is only possible when LCOE is less than 0.1 $/kWh. For the specific case of study, regardless of the cost of the systems, we can note that when the PPV is not greater than the maximum power demand, there are no changes or significant savings generated by the installation of the hydrogen system. In this case study, with the current rate, to have LCOE ≤ 0.1 $/kWh, the cost of zero-export photovoltaic system must be below 310 $/kW, the fuel cell cost less than 395 $/kW, the electrolyzer $ 460/kW, and hydrogen tank at 1.4 $/kWh.
Author contribution statement
Romeli Barbosa: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Beatriz Escobar: Performed the experiments; Wrote the paper.
Victor M. Sánchez: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Jaime Ortegón: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors thank the National Council for Science and Technology, Mexico for the grant SENER-LENERSE 254667\.
References
- 1.Salah Salma I. Towards a sustainable energy future for Egypt: a systematic review of renewable energy sources, technologies, challenges, and recommendations. Clean. Eng. Technol. 2022;8 [Google Scholar]
- 2.Lu Shen J. Unravelling a large methane emission discrepancy in Mexico using satellite observations. Rem. Sens. Environ. 2021;260 [Google Scholar]
- 3.Benda Vítezslav, Cerná Ladislava. PV cells and modules – state of the art, limits and trends. Heliyon. 2020;6 doi: 10.1016/j.heliyon.2020.e05666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Xiao Ma L. The projection of Canadian wind energy potential in future scenarios using a convection-permitting regional climate model. Energy Rep. 2022;8:7176–7187. [Google Scholar]
- 5.Escobar-Yonoff Rony, Maestre-Cambronel Daniel, Charry Sebastián, Rincón-Montenegro Adriana, Portnoy Ivan. Performance assessment and economic perspectives of integrated PEM fuel cell and PEM electrolyzer for electric power generation. Heliyon. 2021;7 doi: 10.1016/j.heliyon.2021.e06506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Abu-Salih Bilal, Wongthongtham Pornpit, Morrison Greg, Coutinho Kevin, Al-Okaily Manaf, Huneiti Ammar. Short-term renewable energy consumption and generation forecasting: a case study of Western Australia. Heliyon. 2022;8 doi: 10.1016/j.heliyon.2022.e09152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barbose Galen L., Darghouth Naïm R. Lawrence Berkeley National Laboratory; Berkeley, CA: 2023. Tracking the Sun: Pricing and Design Trends for Distributed Photovoltaic Systems in the United States. [Google Scholar]
- 8.Mulenga Enock, Math H., Bollen J., Etherden Nicholas. A review of hosting capacity quantification methods for photovoltaics in low-voltage distribution grids. Int. J. Electr. Power Energy Syst. 2020;115 [Google Scholar]
- 9.Das C., Bass O., Kothapalli G., Mahmoud T., Habibi D. Overview of energy storage systems in distribution networks: placement, sizing, operation, and power quality. Renew. Sustain. Energy Rev. 2018;91:1205–1230. [Google Scholar]
- 10.Kumar Piyush, Malik Nitin, Garg Anjali. Comparative analysis of solar - battery storage sizing in net metering and zero export systems. Energy Sustain. Dev. 2022;69:41–50. [Google Scholar]
- 11.Seetharaman, Moorthy Krishna, Patwa Nitin, Saravanan, Gupta Yash. Breaking barriers in deployment of renewable energy. Heliyon. 2019;26 doi: 10.1016/j.heliyon.2019.e01166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kueppers M. Decarbonization pathways of worldwide energy systems–definition and modeling of archetypes. Appl. Energy. 2021;285 [Google Scholar]
- 13.Sasanpour Shima, Cao Karl-Kiên, Christian Gils Hans, Jochem Patrick. Strategic policy targets and the contribution of hydrogen in a 100% renewable European power system. Energy Rep. 2021;7:4595–4608. [Google Scholar]
- 14.Rubber Rodriguez H. Sizing of a fuel cell–battery backup system for a university building based on the probability of the power outages length. Energy Rep. 2022;8:708–722. [Google Scholar]
- 15.Mould Karen, Knott Fabio Silva Shane F., O'Regan Brian. A comparative analysis of biogas and hydrogen, and the impact of the certificates and blockchain new paradigms. Int. J. Hydrogen Energy. 2022;47:39303–39318. [Google Scholar]
- 16.Shiva Kumara S., Lim Hankwon. An overview of water electrolysis technologies for green hydrogen production. Energy Rep. 2022;8:13793–13813. [Google Scholar]
- 17.Gregor Brändle S. Estimating long-term global supply costs for low-carbon hydrogen. Appl. Energy. 2021;302 [Google Scholar]
- 18.Dharik Sanchan Mallapragada O. Can industrial-scale solar hydrogen supplied from commodity technologies Be cost competitive by 2030? Cell Rep. Phys. Sci. 2020;1 [Google Scholar]
- 19.Shaner M.R., Atwater H.A., Lewis N.S., McFarland E.W. A comparative technoeconomic analysis of renewable hydrogen production using solar energy. Energy Environ. Sci. 2016;9:2354–2371. [Google Scholar]
- 20.Mueller-Langer F., Tzimas E., Kaltschmitt M., Peteves S. Techno-economic assessment of hydrogen production processes for the hydrogen economy for the hydrogen economy for the short and medium term. Int. J. Hydrogen Energy. 2007;32:3797–37810. [Google Scholar]
- 21.Yunez-Cano A., Gonzalez-Huerta R., Tufiño-Velazquez M., Barbosa Romeli, Escobar B. Solar-hydrogen hybrid system integrated to a sustainable house in Mexico. Int. J. Hydrogen Energy. 2016;41:19539–19545. [Google Scholar]
- 22.Ma Haoyuan, Liu Zhan. Techno-economic assessment on a multi-stage compressed carbon dioxide energy storage system with liquid storage. Energy Rep. 2022;8:11740–11750. [Google Scholar]
- 23.Marocco P., et al. A study of the techno-economic feasibility of H2-based energy storage systems in remote areas. Energy Convers. Manag. 2020;211 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.