Emergence of division of labor in tissues through cell interactions and spatial cues

Summary

Most cell types in multicellular organisms can perform multiple functions. However, not all functions can be optimally performed simultaneously by the same cells. Functions incompatible at the level of individual cells can be performed at the cell population level, where cells divide labor and specialize in different functions. Division of labor can arise due to instruction by tissue environment or through self-organization. Here, we develop a computational framework to investigate the contribution of these mechanisms to division of labor within a cell-type population. By optimizing collective cellular task performance under trade-offs, we find that distinguishable expression patterns can emerge from cell-cell interactions versus instructive signals. We propose a method to construct ligand-receptor networks between specialist cells and use it to infer division-of-labor mechanisms from single-cell RNA sequencing (RNA-seq) and spatial transcriptomics data of stromal, epithelial, and immune cells. Our framework can be used to characterize the complexity of cell interactions within tissues.

Graphical abstract

Highlights

• •Division of labor theory predicts distinct, mechanism-dependent spatial patterns
• •Spatial proximity of specialist cells suggests involvement of cell interactions
• •Archetype crosstalk networks reveal patterns of interactions between specialist cells
• •Enterocytes and fibroblasts exemplify distinct division of labor strategies

Two of the mechanisms that can drive division of labor in tissues are external signaling gradients and cell-cell interactions. Theory for optimal task allocation explains how to distinguish between the two strategies in single-cell and spatial omics data. This is demonstrated for colon fibroblasts, intestinal enterocytes, lung fibroblasts, and macrophages.

Introduction

Many cell types in multicellular organisms are multifunctional: for example, epithelial cells perform sensory, secretory, transport, and defense functions. Moreover, some functions, such as transport and defense functions in epithelial cells, are bound by trade-offs: they cannot be optimized at the same time in the same cells. Division of labor is a common strategy to handle such functional trade-offs, but how it occurs within a given cell-type population remains largely unknown. Cells’ expression profiles provide an opportunity to characterize division of labor in tissues, to infer the functional constraints driving it, and to determine its underlying mechanisms.

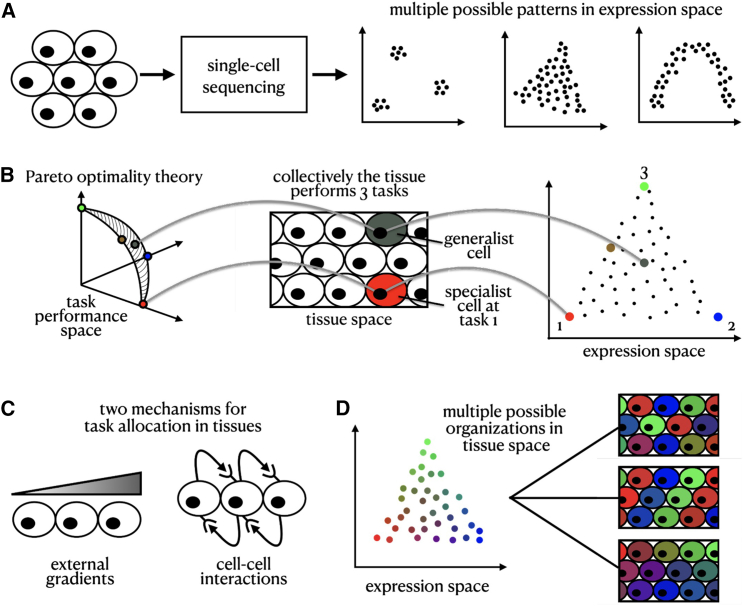
In particular, low-dimensional representations of patterns of cellular gene expression (Figure 1A) (“gene expression space”) can reflect not only distinct cell types as discrete clusters and dynamical processes, such as cell differentiation along continuous trajectories,^1,2,3,4 but also the collective optimization of task performance under trade-offs within a given cell type.^5,6,7,8 A theoretical framework based on Pareto optimality predicts that the optimal performance of a multitasker cell that faces trade-offs is achieved when its finite resources, including gene expression,⁹ are invested in performing these tasks, and thus a greater specialization in one task reduces specialization in another.^5,6,7,8 Geometrically, this means that expression is bounded inside a polytope whose vertices are expression profiles optimal at each task, called archetypes (Figure 1B). The Pareto optimality theory was recently extended to consider an ensemble of cells that are working as a collective to perform the tissue’s tasks.¹⁰ In the case of collective performance, theory predicts that cells form clusters in gene expression space where they either all concentrate at the polytope’s archetypes (specialists) or all assume an identical composition of task allocation (generalists) (Figure 1B).

Figure 1.

Pareto optimality framework

(A) Single-cell RNA sequencing data in expression space can reveal various low-dimensional structured patterns.

(B) Mapping of the representation of individual cells across task performance, tissue, and expression space.

(C) We consider two underlying mechanisms driving the allocation of tasks in the tissue: external signaling gradients and cell-cell interactions.

(D) Mapping patterns in tissue space with those in expression space is an ill-posed inverse problem—there are multiple possible tissue compositions consistent with a given expression configuration.

Task performance of cells in a tissue can be affected by exogenous, instructive factors, such as oxygen and nutrient levels or physical barriers that constrain cellular performance. In the case of instructive spatial gradients, a continuum of expression is generated inside the polytope such that the specialist cells optimal for each task are located in distinct positions in the tissue, where conditions are best for their performance.¹⁰ For example, variation in expression between individual hepatocytes in liver lobules¹¹ and intestinal enterocytes¹² can be explained by their spatial positioning in the tissue. However, the variability in expression between cells of other types within the same tissues, for example between fibroblasts in the developing mouse embryo, cannot be easily explained by their spatial position at the tissue scale.¹³

In addition to instructive constraints, cell-cell interactions, including contact-dependent and secreted signals, also regulate gene expression and coordinate cell performance^14,15 (Figure 1C) such that cells self-organize and use feedback interactions to regulate each other’s performance. This is well established in cell differentiation: for example, during development, the contact-dependent Delta-Notch pathway controls early neural versus epidermal cell-fate decisions.¹⁶ Morphogens, including the Bmp, Wnt, Hedgehog, and FGF, shape cells’ expression programs and differentiation into distinct cellular fates.^17,18 In tissue response to injury, secreted growth factors such as transforming growth factor β (TGF-$\beta$) drive fibroblasts to transition into myofibroblasts, which in turn regulate the wound-healing process.^19,20 Immune cells constantly sense the landscape of cytokines and chemokines produced by other cells to determine the nature of their response.²¹

While cell-cell communication is a key mechanism that governs cell differentiation, how cell-cell communication promotes division of labor within a given cell type remains unclear. Could a continuum within a polytope in gene expression space emerge when cells co-organize to control their task allocation? What would be the physical arrangement of cells in the tissue when their task allocation is controlled by cell-cell interactions locally or at longer ranges? Can we leverage the Pareto optimality framework to predict the spatial arrangements of cells in the tissue based on their gene expression profile (Figure 1D)?

Here, we develop and apply a theory that considers the optimal trade-off between tasks in the tissue when cells directly communicate their specializations to each other. Unlike instructive factors, where the conditions of performing tissue-wide tasks are guided extrinsically, in this framework, the cells use feedback interactions and self-organize to divide labor in an optimal way. The theory predicts a diversity of patterns both in tissue (physical) and gene expression spaces that emerge from different types of cell-cell interactions that are distinct from patterns that emerge from instructive signals. We apply the theory to single-cell RNA sequencing (scRNA-seq) and spatial transcriptomics data by comparing the spatial organization and expression patterns of mouse colon fibroblasts and intestinal mature enterocytes and by constructing ligand-receptor crosstalk networks across specialist cells from single-cell gene expression data of fibroblasts and macrophages. This framework can provide insights into whether expression patterns originate from instructive constraints or cell-cell interactions in diverse biological systems.

Results

Modeling cell-cell communication under the Pareto optimality framework generates a variety of patterns in tissue and gene expression space

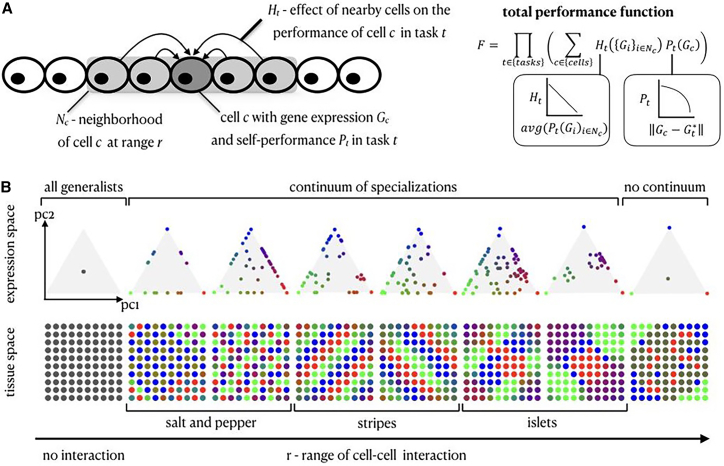
To model the Pareto-optimal expression profiles of cells in a tissue, we consider how cells collectively contribute to the tissue by performing several tasks. As was previously presented,^5,10 we model this trade-off by considering that each task, $\text{t}$, is best performed at an optimal expression profile, ${G_t}^{\ast }$ (or an optimal task allocation), and shows a parabolic decline in performance as cells move further away from ${G_t}^{\ast }$ in gene expression space. We define the total performance function of a tissue, $F$, as a product over the performance of all the tasks that need to be collectively performed by the cells in the tissue, summing over the contribution of each cell to the performance in each task¹⁰ (STAR Methods).

To model the effect of cell-cell interactions on optimal task allocation, we introduce an interaction term, $H_t$, which captures how a cell’s performance is influenced by the performance of its neighboring cells. We explore the effect of varying the range of the interaction by varying the size of the neighborhood of each cell ($N_c$). The contribution of each cell ($c$) to task $t$ is therefore the product of two components; a self-component, $P_t$, which is a function of cell $c$’s gene expression profile ($G_c$), and an interaction component, $H_t$, which is a function of the average $P_t$ of the neighboring cells of cell $c$ (Figure 2A).

Figure 2.

A variety of tissue and expression patterns emerge from the Pareto optimality framework with a cell-cell communication mechanism of lateral inhibition

(A) Theoretical framework of Pareto optimality with cell-cell interactions—cell $c$’s performance is affected by the performance of its neighboring cells in the tissue, $N_c$. The total performance function, $F$, is a product over the tasks, where the performance in each task is the sum over the contribution of all cells considering a self-component ($P_t$) and the effect of interaction with nearby cells ($H_t$).

(B) Simulation results of lateral inhibition in expression and tissue space. Varying the range of cellular interactions produces diverse tissue patterns akin to patterns observed in real tissues.

The interaction term, $H_t$, can generally represent different types of interactions, including positive and negative effects on performing the same task. Here, we focus on lateral inhibition, where a cell’s performance in task $t$ linearly declines if its neighboring cells exhibit high performance in the same task (Figure 2A; STAR Methods). We consider a representative example of a 2D spatial grid of 100 cells that need to perform three tasks and compute the expression profiles (or task allocations) of the cells that maximize $F$ (STAR Methods). While we focus on negative interactions in order to explore patterns that are distinct from patterns that emerge from an instructive smooth gradient, we also examine positive interactions, where the cells stimulate each other to perform the same task (Figure S2E; supplemental information). We discuss tissue dimensions, number of tasks, and other types of functional forms for the performance and interaction functions in the supplemental information (Figures S1 and S2).

In the absence of cell-cell interactions, the tissue reaches optimal performance when all cells are generalists, equally performing all tasks, but when interactions are present, the cells span multiple qualitatively distinct arrangements within the Pareto front in gene expression space (a triangle in the case of three tasks) and a diversity of spatial patterns in the tissue, depending on the range of interactions (Figure 2B). Specifically, short-range/direct interactions with nearest neighbors lead to the formation of a salt-and-pepper pattern in tissue space, where the cells are confined to the circumference of the polytope in gene expression space. Increasing the range of lateral inhibition interactions drives the cells to fill the polytope with a continuum of profiles spanning both specialist and generalist cells. At the other extreme, when all cells are mutually interacting irrespective of location, the optimal solution partitions the cells to specialists and generalists (no continuum). In tissue space, the model gives rise to a range of physical patterns often observed in tissues in development and homeostasis,²² including stripes and islets of the different specialist cells (Figure 2B). Another type of inhibitory interaction model, where one task inhibits a distinct task in neighboring cells, yielded similar results for long-range interactions but a distinct pattern for short-range ones (Figure S2D).

Both instructive gradients and cell-cell interactions can lead to continua of gene expression profiles but distinct spatial patterns

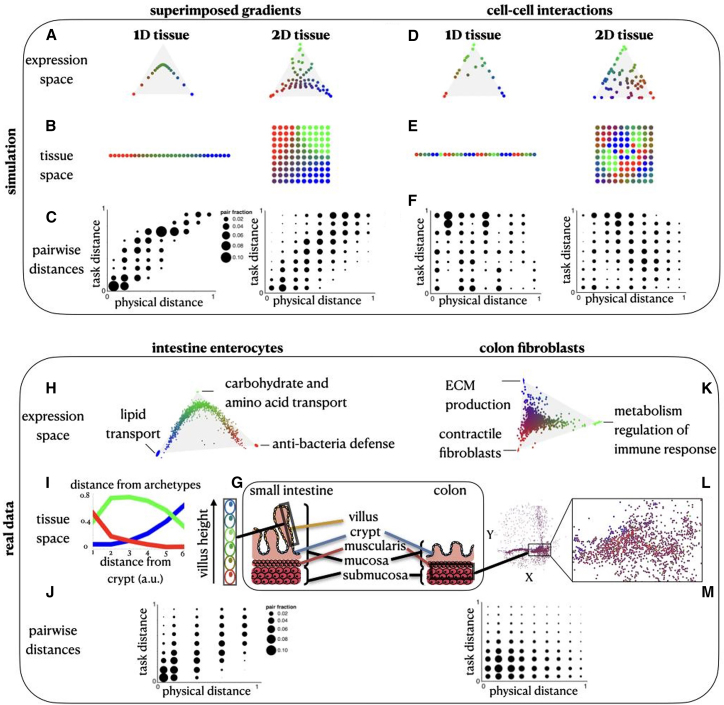
When simulating lateral inhibition of cell-cell interactions, a continuum of gene expression profiles can emerge (Figure 2B), similar to the continuum generated by external gradients (Figures 3A–3E; STAR Methods)¹⁰ but with a key difference in the spatial configuration of the cells. With instructive monotonic gradients, cells that are physically proximal within the tissue can exhibit many times, on average, similar expression profiles²³ and thus similar task allocation. In this case, specialist cells of distinct specializations are expected to be located far from each other within the tissue, and similarities in gene expression and physical proximity are congruent. Conversely, in a population of cells whose expression profiles are driven by lateral inhibition, different specialist cells can be close to each other in tissue space (Figures 3D and 3E) such that gene expression and tissue space can be incongruent. We demonstrate this quantitatively by comparing the distribution of pairwise distances of cells in tissue space (“physical distance”) and in task allocation space (“task distance”), where a cell’s task allocation is the normalized gene expression distance from each of the archetypes (Figures 3C and 3F). We then construct a null model for assessing the statistical significance of the physical locations of cells using random permutations (STAR Methods). Simulations with instructive monotonic gradients show a statistically significant Pearson correlation between pairwise distances in gene expression and physical spaces (Figures 3C and 3F; STAR Methods). When a combination of both instructive gradients and lateral inhibition governs the simulation, the Pearson correlation of physical and gene expression pairwise distances generally increases as the strength of the effect of the external signaling gradients increases (Figure S1C).

Figure 3.

Distinct spatial patterns emerge from external gradients and cell-cell interactions

(A and B) The Pareto-optimal solution of cells that are affected by an external gradient across a 1D and a 2D tissue in gene expression (A) and tissue (B) space.

(C) With external gradients, the pairwise expression distances (y axis) versus the pairwise physical distances (x axis) show high Pearson correlation (for 1D: corr = 0.88, p < 0.001, for 2D: corr = 0.72, p < 0.001).

(D and E) The Pareto-optimal solution of cells that are affected by cell-cell interactions in a 1D and a 2D tissue in gene expression (D) and tissue (E) space.

(F) With cell-cell interactions, the pairwise expression distances (y axis) versus the pairwise physical distances (x axis) are anticorrelated (in terms of Pearson correlation, for 1D, corr = −0.1, p = 0.002, for 2D, corr = −0.13, p < 0.001).

(G) Schematics of the colon tissue including the intestinal villi and the muscularis layer.

(H) Gene expression profile of enterocytes where the cells are colored by their task specializations (combinations of red, green, and blue colors representing the three tasks).

(I) Arrangements of enterocytes along the crypt-to-villus axis. The distance of the cells from each archetype is plotted as a function of the distance from the crypt.

(J) The pairwise distances in expression versus physical space of enterocytes show high Pearson correlation (corr = 0.67, p < 0.001).

(K) Gene expression profile of colon fibroblasts from Slide-seq data (Avraham-Davidi et al.²⁴), where the cells are colored by their task specializations. At the vertices (H,K) are ellipses that indicate STD of vertex position from bootstrapping.

(L) Spatial arrangements of the fibroblasts in the colon tissue.

(M) The pairwise distances in expression versus physical space of fibroblasts show negative Pearson correlation (corr = −0.1, p < 0.001).

Both intestinal enterocyte and colon fibroblast distributions show task specialization, but only enterocytes’ task allocation can be explained by a global instructive gradient

To test our predictions in the context of real biological systems, we turned to two datasets to infer whether the distribution of gene expression profiles is dominated by either instructive gradients or cell-cell interactions. The first system consists of mature enterocytes from the villus of the mouse small intestine, dissected into six regions using laser-capture microdissection and then dissociated and profiled by scRNA-seq.¹² Multiple nutrients and resource gradients were previously suggested to influence the expression profiles of enterocytes along the crypt-to-villus axis (Figures 3G and 3I). The second system consists of fibroblasts in the mouse colon assayed in situ using the spatial transcriptomics method Slide-seq²⁴ (Figures 3G and 3L).

Next, we test whether expression profiles of colon fibroblasts are governed by an instructive gradient, similar to enterocytes in the small intestine, and what the role of cell-cell interactions is in regulating their heterogeneity at steady state. As expected, enterocyte profiles follow a 1D continuum of expression bounded within a triangle in gene expression space, as previously shown,¹⁰ consistent with a trade-off in enterocytes between three tasks: lipid transport, carbohydrate and amino acid transport, and antibacterial defense (Figure 3H). Specialist enterocytes are found in distinct positions in the tip, middle, and bottom of the villus (STAR Methods). This pattern was observed among mature enterocytes that line the villus from the small intestine; enterocytes from other regions may show distinct patterns. Conversely, Slide-seq beads capturing fibroblasts span an expression continuum within a triangle (p < $10^{-4}$, based on the ParTI algorithm⁷). The genes enriched near each of the fibroblast archetypes suggest task specialization in extracellular matrix (ECM) production, contractile functions, and metabolism and regulation of immune response (Figure 3K; STAR Methods).

Unlike the gradual change in enterocyte profiles along the crypt-to-villus axis (Figure 3I), the distinct colon fibroblast archetypes are often close to each other in the tissue space (Figure 3L). Computing the expression and physical pairwise distances for both cell-type populations, we find a significant Pearson correlation for enterocytes, in line with the assumption of a dominant monotonic gradient along the villus axis, while the signature for fibroblasts is not consistent with monotonic spatial gradients alone (Figures 3J and 3M; STAR Methods). This distinction is observed even when we simulate in the Slide-seq data the coarse laser cutting dissection approach that was applied for enterocytes in the small intestine. This shows that the difference in correlation between physical and task distances observed for mature intestinal enterocytes and colon fibroblasts is not merely explained by the difference in experimental assays (Figures S3F and S3G). Although colon fibroblasts are known to be influenced by morphogenic signals such as Wnt produced by deep-crypt secretory cells,^25,26,27 the spatial mixture of fibroblast archetypes within the crypt suggests that fibroblasts are also influenced by additional mechanisms (Figure S3H). We next turn to examine whether cell-cell interactions between fibroblasts play a central role in regulating fibroblast heterogeneity.

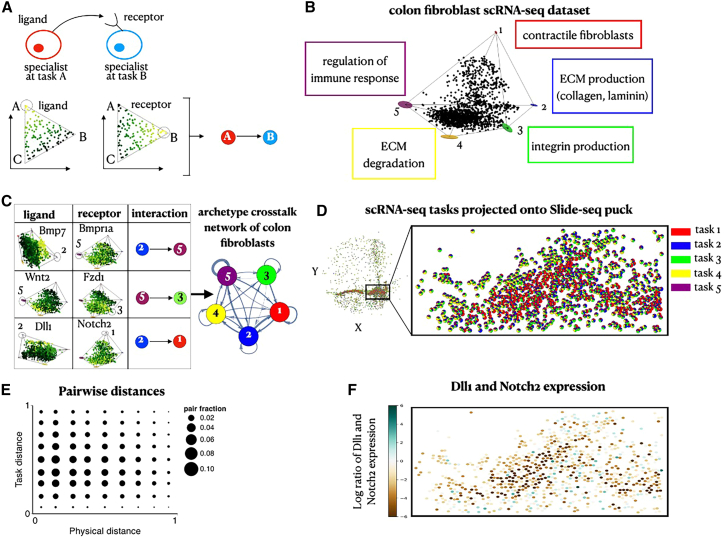
An archetype crosstalk network for colon fibroblasts highlights specific ligand-receptor interactions as potential mechanisms for optimal task allocation

To explore whether cell-cell interactions between fibroblasts play a role in fibroblast task specialization, we developed a method to construct crosstalk networks between archetypes of different specializations based on ligand-receptor interactions (Figure 4A; STAR Methods). Specifically, we construct a directed graph where vertices are the different archetypes, and a directed edge connects from archetype A to archetype B if a ligand whose expression is enriched toward archetype A in gene expression space has a corresponding receptor whose expression is enriched toward archetype B (Figure 4A; STAR Methods). Here, we consider interactions within the same cell-type population (e.g., fibroblasts) and their effect on task performance, although task performance of fibroblasts may be additionally affected by interaction with other cell types, which we do not consider.

Figure 4.

Inferring archetype crosstalk networks of colon fibroblasts based on ligand-receptor interactions

(A) Interactions between specialist cells are inferred from enrichments of ligands and their corresponding receptors. We use a directed edge to represent a pair of a ligand and its corresponding receptor that are enriched near each of the archetypes it connects.

(B) A projection of gene expression profiles of single-cell RNA sequencing (scRNA-seq) colon fibroblasts²⁸ on the first three PCs. Fibroblasts fill in a 5-vertex polytope (p < $10^{-4}$).

(C) A table showing examples of ligands and their respective receptors that are enriched near the archetypes. We plot the complete archetype crosstalk network inferred for the colon fibroblasts where the thickness of each edge corresponds to the number of ligand-receptor pairs enriched between its vertex archetypes.

(D and E) Using TACCO,²⁹ we compute a mapping from fibroblast cells assayed by scRNA-seq and Slide-seq beads based on their expression agreement. Using the mapping, we (D) infer the scRNA-seq task components for each bead (depicted in pie charts per bead) and (E) compute the corresponding correlation of pairwise task distances versus physical distances (corr = −0.05, p < ${10}^{-3}$).

(F) Projection of the scRNA-seq expression profiles onto the Slide-seq beads. To view the expression of Delta and Notch, we image their log ratio. Beads whose inferred Delta expression is greater/less than their Notch expression lean toward a turquoise/brown shade, respectively.

We first applied this approach to scRNA-seq data of mouse colon fibroblasts²⁸ (which detects receptor and ligand gene expression with higher sensitivity than Slide-seq). Colon fibroblast profiles span a 5-vertex expression polytope with five archetypes corresponding to fibroblast contractile functions, ECM production including collagen and laminin, integrin production, ECM degradation, and regulation of immune response (Figure 4B; STAR Methods). These archetypes are in line with fibroblast categories that were recently described.³⁰ Three of the five fibroblast archetypes inferred from scRNA-seq (ECM production, regulation of immune response, and fibroblast contractile functions) were similar to the three archetypes in Slide-seq data. Due to the larger depth of the single-cell data, we were able to detect two additional archetypes that fibroblasts specialize in. Interestingly, the Pareto optimality analysis reveals two distinct archetypes of collagen production and contractile functions, suggesting that there are two subpopulations performing myofibroblast functions.

The constructed archetype crosstalk network based on a database of ligand-receptor pairs³¹ shows that all colon fibroblast archetypes potentially interact with each other (Figures 4C and S5) (unlike enterocytes, discussed below). These interactions include secreted signaling molecules, such as Bmp, Wnt, and Fgf, which are known to be produced by fibroblasts in the colon and play a significant role in regulating tissue organization³² (Figure 4C). Interestingly, the ECM production and contractile fibroblast archetypes are enriched for Delta (Dll1) and Notch (Notch2) respectively, suggesting that fibroblasts may use contact-dependent signals and lateral inhibition to regulate their task specializations.

Next, we mapped the scRNA-seq data to Slide-seq data using TACCO (STAR Methods; Mages et al.²⁹), first by annotating Slide-seq beads with “fractions” of cell-type annotations and then projecting the scRNA-seq task annotations and expression profiles onto tissue space (Figures 4D and S4). Like the Slide-seq task annotations (Figure 3L), the scRNA-seq task annotations also present a clear boundary between the contractile fibroblast (red) and ECM-related (blue and yellow) archetypes and lack global smoothness of task annotations (Figure 4E; correlation [corr] = −0.05, p < ${10}^{-3}$), in support of mechanisms beyond (smooth) spatial signals controlling the behavior of cells. Notably, immune response fibroblasts are interspersed with contractile fibroblasts in space but are clearly separable as an archetype (Figure 4E). The projected expression of strong ligand-receptor interactions inferred from the scRNA-seq, such as the Dll1-Notch2 pair enriched in ECM production and contractile fibroblast archetypes, respectively, along the spatial boundary of these archetypes suggests the involvement of cellular interactions in setting the task allocations across the tissue (Figure 4F). The spatial proximity between ECM-producing cells and contractile specialists may be important, where performance of contractile functions may depend on the ability of the cells to attach to matrix factors produced by the ECM-producing cells. This is supported by the fact that contractile fibroblasts show enrichment of integrin (Itgb1), which serves as a receptor for collagen (Col1a1, Col1a2, Col4a1, Col4a5, Col4a16) and laminin (Lama5, Lamb1) produced by the ECM-producing cells. Additionally, the ECM-producing cells are enriched with expression of thrombospondin (Thbs1)—an adhesive glycoprotein that mediates cell-to-cell and cell-to-matrix interactions that can bind to integrin.

Archetype crosstalk networks can be used to dissect communication-driven tissue organization from non-spatial single-cell profiles

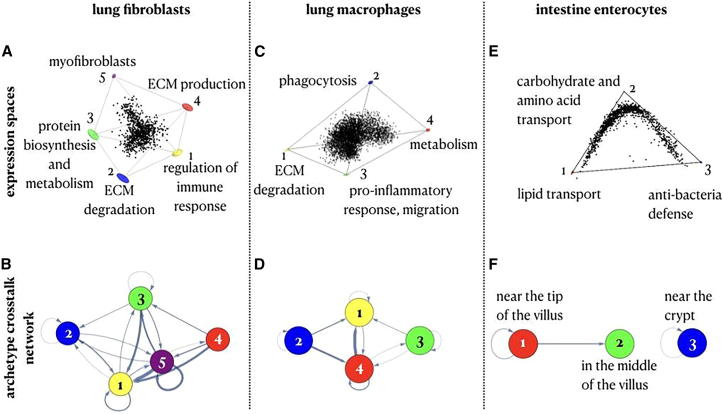
Even if positional information of the cells is not available, archetype crosstalk networks can highlight potential cell-cell interactions that regulate cell specialization. We demonstrate this for fibroblast and macrophage profiles from human lungs (data from Adams et al.³³). Lung fibroblasts span five archetypes that are overall similar to the five colon fibroblast archetypes above, with fibroblast contractile functions, ECM production, ECM degradation, and immune response regulation as distinct archetypes in both tissues. Specifically, lung fibroblasts specialize in (1) regulation of immune response (with enriched cytokines [CCL2], chemokines [CXCL2, CXCL3, CXCL8], and interleukins [IL-32, IL-33]); (2) ECM degradation (ADAMTS1, ADAMTS4, MMP14); (3) protein biosynthesis and metabolism, including collagen production; (4) ECM production and regulation; and (5) contractile fibroblast functions (Figure 5A; STAR Methods). Lung macrophages fill in a tetrahedron in expression space and trade off between ECM degradation, phagocytosis, metabolism of lipids, proteins, glucose and fatty acids, and pro-inflammatory response (Figure 5C; STAR Methods).

Figure 5.

Archetype crosstalk networks can help estimate the role of cell-cell interactions in shaping task allocation even without spatial information

(A) Human lung fibroblasts (from Adams et al.³³) fit in a 5-vertex polytope in expression space (p = 0.004) and show 5 archetypes that correspond to regulation of immune response, ECM degradation, protein biosynthesis and metabolism, ECM production, and myofibroblast specializations.

(B) Archetype crosstalk network of lung fibroblasts.

(C) Human lung macrophages (from Adams et al.³³) fit in a tetrahedron in expression space (p < 10⁻⁴) and show 4 archetypes that correspond to ECM degradation, phagocytosis, pro-inflammatory response, and metabolism specializations.

(D) Archetype crosstalk network of lung macrophages.

(E) Expression profile of intestine enterocytes (from Moor et al.¹²).

(F) Archetype crosstalk network of intestine enterocytes.

The archetype crosstalk networks for lung fibroblasts and macrophages show that both cell types exhibit strong connectivity between the different archetypes within each cell-type population (Figures 5B and 5D; see STAR Methods for a comparison between the connectivity in the archetype crosstalk networks with the connectivity in networks of non-specialist cells; Figures S5E–S5O). In contrast, in the intestinal enterocytes’ archetype crosstalk network, not all archetypes interact with each other, and the interactions are restricted to spatially proximal cells (Figures 5E and 5F; STAR Methods). Thus, even without spatial data, a pattern of strong connectivity between the different archetypes within a given cell-type population suggests that cell-cell interactions play an important role in regulating the division of labor between the cells.

Discussion

Cells work together in tissues and contribute to their collective function in homeostasis and their dysfunction in disease. They can influence each other’s performance both directly, e.g., through contact-dependent and secreted signals, and indirectly, through altering the environment by, e.g., consuming nutrients and thus changing exogenous factors that in turn directly affect cellular task performance. In this work, we studied how direct cell-cell communication shapes the distribution of cellular gene expression. Through simulations based on our theoretical framework and its application to real data, we conclude that self-organization mechanisms can explain a diversity of patterns in both task and tissue space. Additionally, we construct a framework for distinguishing the effects of cell-cell communication and instructive gradients by mapping ligand-receptor interactions between specialized cells.

Inferring the underlying mechanism for division of labor is a challenge since multiple potential mechanisms may result in the same phenotype. For example, in Delta-Notch interaction, a mechanism of local inhibition between archetypes, the model can reproduce the potential patterns when such interactions are observed. While there are many examples where Delta-Notch-like mechanisms are responsible for alternating patterns,³⁴ alternative mechanisms, including cell migration and proliferation, could also yield such diverse patterns. As comprehensive spatial transcriptomics data become more prevalent and extended to capture 3D tissue structure³⁵ and causation,³⁶ our framework can be used to better infer or narrow down the potential underlying mechanisms of collective cellular division of labor.

Our theory currently focuses on the principles underpinning the optimal division of labor of cells within a given cell-type population. Future work accounting for multiple different cell-type populations could depict a more holistic image of tissues, which would enable, for example, exploring how crosstalk between fibroblasts, epithelial, and immune cells in the colon regulates their heterogeneity and division of labor.

In this work, we focused on characterizing the division of labor among cells in a steady state of a developed tissue. Expanding the theoretical framework to consider Pareto optimality in a dynamical setting can provide insights into developmental strategies and their regulation. Another question that can be explored using the Pareto framework applied to time-resolved data is whether cells converge to specific specializations or whether the same cell can switch between different specializations when needed, for example in the context of epithelial mesenchymal transition, as was recently suggested.³⁷ Finally, our framework can be used to explore the transition of tissues to pathological states and, particularly, to study how the role of cell interactions in regulating fibroblast heterogeneity is reshaped in the context of fibrosis and cancer.

Limitations of the study

In our modeling approach, we focused on a specific choice of functional forms for the performance function and the interaction term. Other choices may give rise to other types of patterns, as we exemplify in additional analyses (Figure S2).

In this work, we compared direct interactions between cells with instructive smooth monotonic signals. However, instructive signals can be formed or altered in turn by cells, for example when a nutrient is consumed by particular cells in a large tissue mass. This case may lead to altered patterns, despite the fact that cells do not interact directly, and would require additional theoretical exploration.

Finally, we explored ligand-receptor secretion levels based on RNA data. However, intracellular RNA levels may not correctly reflect extracellular secreted protein. While similar ligand-receptor-based analysis has been successfully utilized in diverse biological settings,^14,38,39 and while there are examples of correlation between transcripts and their associated proteins,^40,41,42 levels of secretion do not necessarily correlate with RNA expression measures.^43,44,45

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Intestinal enterocytes single-cell RNA-sequencing	Moor et al. 201812	GEO: GSE109413
Colon fibroblast Slide-seq	Avraham-Davidi et al. 202224	https://singlecell.broadinstitute.org/single_cell/study/SCP2038
CellTalkDB ligand-receptor list	Shao et al. 202131	http://tcm.zju.edu.cn/celltalkdb
Colon fibroblast single-cell RNA-sequencing	Muhl et al. 202028	GEO: GSE150294
Human lung fibroblasts and macrophages single-cell RNA-sequencing	Adams et al. 202033	GEO: GSE136831
Data files used in this paper	This paper	https://zenodo.org/record/7569404#.ZBwyr-xByWB
Software and algorithms
Sanity	Breda, Zavolan, and van Nimwegen 202146	https://github.com/jmbreda/Sanity
ParTI	Hart et al. 20157	https://github.com/AlonLabWIS/ParTI
IGraphM	Horvat et al. 202247	http://szhorvat.net/pelican/igraphm-a-mathematica-interface-for-igraph.html
TACCO	Mages et al. 202329	https://github.com/simonwm/tacco
Resource website for the Mathematica code	This paper	https://github.com/miriadler/pareto_interactions
Resource website for the Python code	This paper	https://github.com/nitzanlab/pareto_interactions_py

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Mor Nitzan (mor.nitzan@mail.huji.ac.il).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

No experimental models were used in this study.

Method details

Pareto optimality framework with cell interactions

The Pareto optimality framework introduced in¹⁰ (set to allocate cells' gene expression toward a maximal, collective performance of the tissue) is formalized by the constrained maximization of the total performance function, F:

$$F=\prod _{t\in \left\{tasks\right\}}\left(\sum _{c\in \left\{cells\right\}}{P}_t\left(G_c\right)\right)$$

Where, $G_c$ is a vector of cell c’s gene expression, that is constrained to lie in the polytope whose vertices are the archetypes’ gene expression, that is ${\left\{G_t^{\ast }\right\}}_{t\in \left\{tasks\right\}}$. The performance of a cell for task t, $P_t\left(G_c\right)$, is computed as $P_t\left(G_c\right)=a_1-a_2{d}_{tc}^2\text{,}$ where $d_{tc}={\Vert G_c-G_t^{\ast }\Vert }_2$ (Euclidean distance of cell c from the archetype t) and $a_1,a_2$ are constant parameters introduced to avoid negative performance. In the main text (Figure 2B) we considered $a_1=2,a_2=1$. In Figure S2A we considered $a_1=1,a_2=\frac{1}{2}$ meaning that the performance function can be written as $P_t\left(G_c\right)=\frac{a_0-d_{tc}^2}{a_0}$ with $a_0=2$ which yielded similar results. Summation over the cells describes the equal, linear contribution of each cell’s performance in task t to the collective performance of task t. The product over the performance in each task expresses the need to excel in all tasks simultaneously.

To model the effect of a cell’s local environment, we consider cells arranged in an acyclic 1D or 2D grid. $N_c$, the set of cell c’s neighbors is set to be cells within order r (range) from c.

For interactions of lateral inhibition of the same task, we factor in $H_t\left({\left\{G_i\right\}}_{i\in N_c}\right)$, a diminishing factor ($\le 1$) introduced by the performance in task t of cell c’s neighbors:

$$F=\prod _{t\in \left\{tasks\right\}}\left(\sum _{c\in \left\{cells\right\}}{H}_t\left({\left\{G_i\right\}}_{i\in N_c}\right)P_t\left(G_c\right)\right)$$

For simplicity, we set $H_t$ to be: $H_t\left({\left\{G_i\right\}}_{i\in N_c}\right)=1-\frac{1}{N_c}\sum _{i\in N_c}{P}_t\left(G_i\right)$.

We implemented the optimization problem both in Python using the scipy.optimize.minimize function which uses Sequential Least Squares Programming (SLSQP) and in Mathematica using the NMaximize function. Examples, varying tissue dimensions, and number of tasks, are depicted in Figure S1.

Tissue and gene expression space with alternative models of performance and interactions

While our main model employed a quadratic performance function of the distance from the archetype and high performance of a task de-prioritizes the task’s allocation in the local region (inhibiting interactions) (Figure S2A), we also simulated alternative models of performance, interaction function and interaction relations for 100 cells organized in a 2D acyclic grid, optimized on three tasks (Figure S2).

We have previously shown¹⁰ that in the absence of cell-cell interactions or instructive signals, convex performance functions partition expression profiles to distinct specialist groups, whereas concave functions lead to generalist cells. In line with these results, in a model with interactions, when we set the performance function to decrease linearly with the distance away from the optimal expression profile ($P_t\left(G_c\right)=\frac{a_0-d_{tc}^{}}{a_0}$), no continuum in gene expression space arises and instead, cells form clusters of specialized cells (Figure S2B). The spatial organization depends on the range of interactions ranging from a salt and pepper pattern to islets of specialized cells.

In our main model, inhibition is a linear function of a cell’s neighbors’ performance in the task, however, this inhibition function can be modeled in other ways, for example, as decaying exponentially with neighbors’ contribution – $H_t\left({\left\{G_i\right\}}_{i\in N_c}\right)=\mathit{exp}\left\{-\rho \frac{1}{N_c}\sum _{i\in N_c}{P}_t\left(G_i\right)\right\}$, with $\rho =1.5$ (Figure S2C). In this case, a preference for expression of generalists emerges (Figure S2C).

While we focused mainly on lateral inhibition of the same task, that is, performance of neighbors in task A downweighs the cell’s performance in task A, other types of interactions can be considered. For example, we also considered inhibition across tasks in a cyclic manner, where performance of neighbors in task A down weighs the cell’s performance in task B, modeled as $H_t\left({\left\{G_i\right\}}_{i\in N_c}\right)=1-\frac{1}{N_c}{\sum }_{i\in N_c}{P}_{f\left(t\right)}\left(G_i\right)$ with $f\left(t\right)=(t+1)\mathit{mod}m$ for $m$ tasks (Figure S2D). In this case, for the parameter choice and functional forms we considered, long-range cyclic inhibitory interactions yield similar results as the lateral inhibition interactions we considered. However, short-range cyclic inhibitory interactions yield a distinct pattern, where the specialist cells occupy distinct positions in the tissue space similarly to the instructive signal case.

We also consider a positive interaction model, where performance of a task stimulates the same task in neighboring cells. We model this by considering the interaction term, $H_t\left({\left\{G_i\right\}}_{i\in N_c}\right)=\frac{1}{N_c}{\sum }_{i\in N_c}{P}_{f\left(t\right)}{\left(G_i\right)}^w$ with $w=4$ (Figure S2E). This model can yield distinct regions of specialists even at short interaction ranges.

Correspondence between expression and physical distances increases as instructive gradients dominate over interactions (and vice versa)

So far, our model accounted for either external gradients or interactions within the Pareto optimality framework. In practice, however, it is most likely that both mechanisms act simultaneously and jointly shape the gene expression space. We combine the two models and introduce a parameter to interpolate between the effect of external gradients and interactions in Figure S1C.

Quantification and statistical analysis

Correlation of expression and physical distances

We wish to compare the expression and tissue space optimized with external gradients or with interactions. For external gradients, we use the setup previously proposed in¹⁰ where:

$$F=\prod _{t\in \left\{tasks\right\}}\left(\sum _{c\in \left\{cells\right\}}{\varphi }_t\left(L_c\right)P_t\left(G_c\right)\right)$$

Where $L_c$ is cell c’s location within the tissue. ${\varphi }_t\left(L_c\right)$ is a coefficient defined by the external gradient that weighs cell c’s performance according to gradients at its location ($L_c$) in the tissue. Exact gradients set for 1D and 2D tissues are ${\varphi }_1\left(x\right)=x,{\varphi }_2\left(x\right)=1-x$, and ${\varphi }_1\left(x,y\right)=1-x,{\varphi }_2\left(x,y\right)=1-y,{\varphi }_3(x,y)=1$, respectively, and we use $P_t\left(G_c\right)=a_1-a_2{d}_{tc}$ for evaluating the performance in correspondence to the simulation in¹⁰ (Figures 3A and 3B).

To plot binned expression-vs-physical-distances, we bin (separately) cell-pairs’ task allocation distances and cell-pairs’ physical locations: (1) compute cell-to-cell Euclidean distance (expression or physical distances), (2) remove extreme distances (>99 percentile), (3) normalize (divide by max distance) to restrict to 0–1 range, and (4) divide into evenly-spaced bins (using 10 bins, for enterocytes, physical distances collapse into 5 bins due to low spatial resolution).

Then, for each (expression distance bin x physical distance bin), we plot a point of size corresponding to the fraction of cell pairs (number of pairs/total number of pairs) falling within this set of bins. Correlation values are computed between the Euclidean expression/physical distances and compared to null correlation values (1000 repeats) that are generated by permuting cells’ locations.

Intestinal enterocyte scRNA-seq analysis

We re-analyzed scRNA-seq data of mouse intestinal enterocytes (data from¹²) where we preprocessed and normalized the data and considered the triangle that encloses the data as was previously described in.¹⁰ See Table S1 for a full list of enriched genes near the enterocyte archetypes.

To plot the pairwise distances in expression and tissue space, we consider every pair of enterocytes in the data. For distance in expression space, we compute the Euclidean distance in task space between every pair of cells. For distance in spatial space, we consider the spatial height of the cells along the crypt-to-villus axis that was inferred by Moor et al.,¹² and compute the difference between the heights of every pair of cells.

The full list of enriched ligand-receptor pairs in the enterocytes data that were used to plot the archetype crosstalk network in Figure 5F can be found in Table S1.

Colon fibroblast Slide-seq data analysis

We analyzed Slide-seq data of mouse colon fibroblasts from Avraham-Davidi et al.,²⁴ where we considered fibroblasts as beads that received a fibroblast score higher than 0.5.²⁹ In the main text we focus on a specific slide from the dataset (puck #20), but we analyzed other slides included in the data and found similar results (see Figures S3A–S3D for results of another puck in the data). Puck #20 includes 2,559 fibroblasts that show expression in 13,520 genes. To preprocess the expression data, we used ‘Sanity’ – a recently developed method to normalize single-cell data and to infer the transcriptional activity of genes.⁴⁴ Following the Sanity normalization, we removed genes with low expression (log₁₀(average expression) < −11) and low expression variance (standard deviation <0.1) across beads, which left us with 1,047 genes. We note that these thresholds for selection of genes do not affect the distribution of expression profiles in expression space and analyzing all 13,520 genes yields similar results.

We next used the ParTI package in MATLAB to fit the fibroblast expression data to a polytope.⁷ We find that fibroblasts fit well within a triangle (p-val< $10^{-4}$, we also tested for 4 archetypes which yield a good fit with p-val = 0.001). We used ParTI to find genes that are enriched near the archetypes to infer the tasks the archetypes are specializing in. The enriched genes near the first myofibroblast archetype are: Malat1, Actg2, Myh11, Tpm1, Pdlim3, Acta2, Mylk, Cnn1, Smtn, Tagln, Des, Actb, mt-Nd4, Flna, Myl9. The enriched genes near the second ECM production archetype are: Col3a1, Col1a2, Gsn, Dcn, Sparc, Dpt. The enriched genes near the third metabolism/immune response archetype are: Lars2, Cmss1, Hexb, Camk1d, Tpm2. We find similar enriched genes in other pucks in the dataset (Figure S3D).

To plot the pairwise distances in expression and tissue space, we consider every pair of fibroblasts in the data. For distance in expression space, we compute the Euclidean distance in task space between every pair of cells. For distance in spatial space, we consider the spatial (x, y) coordinates of the cells from the Slide-seq data and compute the Euclidean spatial distance between every pair of cells.

Differences in assays used for colon fibroblasts and intestinal enterocytes do not explain differences in correlation between physical and task pairwise distances

To test whether the difference in spatial resolution between the experimental methods used to assay the colon fibroblasts²⁴ (assayed with Slide-seq) and the enterocytes along the intestine villus¹² (laser cut into six sections) are the reason for the different resulting correlation values of task and physical distances, we mimic the coarse dissectioning of enterocytes in the analysis of the fibroblasts. To this end, we identify the layers of the colon and infer the distance from the deep crypt layer using TACCO,²⁹ and then perform in silico dissection of the fibroblasts according to these distances into six bins (Figure S3F). When using the coarse spatial sectioning of the fibroblasts, we observe a very low Pearson correlation between the task and (new) physical distances (corr = 0.02, p-val = 0.037, Figure S3G).

Construction of archetype crosstalk networks

To construct archetype crosstalk networks from single-cell expression data, we first fit the data to a polytope. Once the polytope and archetypes are defined, we consider the genes that are enriched near the archetypes and use available ligand-receptor pairs datasets (we used CellTalkDB³¹) to search for enriched ligand-receptor pairs. We used the package IGraphM⁴⁷ in Mathematica 12.1.1.0 and the functions Graph, IGEdgeMap, IGEdgeProp to build a weighted directed graph where a directed edge from archetype A to archetype B represent an enriched ligand near archetype A and its corresponding receptor enriched near archetype B. The weights on the edges correspond to the number of ligand-receptor pairs that link the two archetypes.

Colon fibroblast scRNA-seq analysis

We analyzed scRNA-seq data of mouse colon fibroblasts from Muhl et al., 2020²⁸. The data includes 1,646 cells that show expression in 30,920 genes. Following the Sanity normalization, we removed genes with low expression (log₁₀(average expression) < −14) and low expression variance (standard deviation <0.1) across single cells, which left us with 8,479 genes. We next used the ParTI package in MATLAB to fit the fibroblast expression data to a polytope. We find that fibroblasts fit well within a 5-vertex polytope (p-val< $10^{-4}$, we also tested for 3 and 4 archetypes which yield a good fit with p-val< $10^{-4}$). We find hundreds of enriched genes near the 5 fibroblast archetypes (see Table S2 for the full table of enriched genes). The full list of enriched ligand-receptor pairs in the scRNA-seq colon fibroblasts data that were used to plot the archetype crosstalk network in Figure 4E can be found in Table S2.

Mapping fibroblast scRNA-seq to spatial positions

To further support the role of cell-cell interactions in guiding the spatial task allocations for colon fibroblasts, we map the high-quality single-cell data onto the fibroblast-dominated (probability fibroblast >0.5) Slide-seq beads. To this end, we deploy TACCO, mapping the Slide-seq data using single-cell data as a reference.²⁹ We use TACCO’s platform normalization booster to overcome platform biases and Optimal Transport to map solely based on gene expression similarity to the reference expression profiles. Using the cell-to-bead mapping, we compute the single-cell task allocation and the inferred expression per bead.

Human lung fibroblast and macrophage analysis

We analyzed single-cell RNA-seq data of human lung fibroblasts from Adams et al. 2020.³³ The data includes 1,051 cells from the control samples. Following the Sanity normalization, we removed genes with low expression (log₁₀(average expression) < −11) and low expression variance (standard deviation <0.05) across single cells, which left us with 6,934 genes. We also removed a small fraction of outlier cells that skewed the data that show low average expression (log₁₀(average expression) < −9.9), which left us with 945 cells.

The human lung macrophage data from Adams et al.³³ includes 25,142 cells (macrophages and monocytes). Due to the large number of cells, we randomly sampled 5,000 cells to carry on with the analysis. Following the Sanity normalization, we removed genes with low expression (log₁₀(average expression) < −11) and low expression variance (standard deviation <0.05) across single cells, which left us with 6,273 genes.

We used the ParTI package in Matlab to fit the fibroblast and macrophage datasets to a polytope. We find that the fibroblast data fits well in a 5-vertex polytope (p-val = 0.004 with the SISAL algorithm to find the archetypes, p-val = 0.067 with the PCHA algorithm to find the archetypes), and the macrophage data fits well in a tetrahedron (p-val<${10}^{ˆ}\text{-}4$ with the SISAL algorithm, p-val = 0.067 with the PCHA algorithm). We repeated the enrichment analysis using both PCHA and SISAL algorithms and found that the enriched genes near the archetypes were very similar using both algorithms suggesting that the results are robust to different methods of finding the archetypes’ positions.

Tables of full lists of enriched genes near the fibroblast and macrophage archetypes can be found in Tables S3 and S4. The full list of enriched ligand-receptor pairs in the lung fibroblasts and macrophages datasets that were used to plot the archetype crosstalk network in Figures 5B and 5D can be found in Table S5.

Enrichment of ligand-receptor interactions between archetypes

To test the degree to which the archetypes in the single-cell expression data we analyzed interact with each other through ligand-receptor interactions, we compare the connectivity between the archetypes to the connectivity between a different choice of points in the polytope. To that end, we consider points that are equally distant from each pair of archetypes which we refer to as midpoints. Considering data that fits well within a polytope with M archetypes (Figure S5E), the midpoints are the collection of arithmetic means over every set of M-1 points out the M archetypes (Figure S5F). We used the ParTI package in MATLAB to calculate the enriched genes with respect to the midpoints instead of the archetypes. We then constructed the crosstalk network as described above based on ligand-receptor pairs that are enriched near the midpoints. The resulting midpoint crosstalk networks for all three scRNA-seq datasets^28,33 (Figures S5H, S5K, and S5N) show that in comparison to the archetype crosstalk networks (Figures S5G, S5J, and S5M) the number and intensity of links between the vertices declines and not all points interact with each other. The overall number of enriched genes near the midpoints decreases compared to the archetypes. However, the decrease in the crosstalk network connectivity is not due to the decrease in enriched genes. Although the percentage of enriched ligands and receptors out of the total number of enriched genes is on the same order of magnitude (Figures S5G, S5H, S5J, S5K, S5M, and S5N), the number of enriched ligand-receptor pairs is significantly lower near the midpoints compared to the archetypes. This is also quantitatively shown when we compute the degree distribution of the two crosstalk networks (Figure S5I, S5L, and S5O).

Published: April 21, 2023

Data and code availability

• •This paper analyzes existing, publicly available data. The accession numbers for the datasets are listed in the key resources table.
• •All original code has been deposited at https://github.com/nitzanlab/pareto_interactions_py and https://github.com/miriadler/pareto_interactions and is publicly available as of the date of publication. DOIs are listed in the key resources table. All data files used in this paper are deposited at https://zenodo.org/record/7569404#.ZBwyr-xByWB.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.