Abstract
Real-time, three-dimensional (3D), passive acoustic mapping (PAM) of microbubble dynamics during transcranial focused ultrasound (FUS) is essential for optimal treatment outcomes. The angular spectrum approach (ASA) potentially offers a very efficient method to perform PAM, as it can reconstruct specific frequency bands pertinent to microbubble dynamics and may be extended to correct aberrations caused by the skull. Here we assesses experimentally the abilities of heterogeneous ASA (HASA) to perform trans-skull PAM. Our experimental investigations demonstrate that the 3D PAMs of a known 1 MHz source, constructed with HASA through an ex vivo human skull segment, reduced both the localization error (from 4.7±2.3 mm to 2.3±1.6 mm) and the number, size, and energy of spurious lobes caused by aberration, with modest additional computational expense. While further improvements in the localization errors are expected with arrays with denser elements and larger aperture, our analysis revealed that experimental constraints associated with the array pitch and aperture (here 1.8 mm and 2.5 cm, respectively) can be ameliorated by interpolation and peak finding techniques. Beyond the array characteristics, our analysis also indicated that errors in the registration (translation and rotation of ±5 mm and ±5°, respectively) of the skull segment to the array can led to peak localization errors of the order of a few wavelengths. Interestingly, errors in the spatially dependent speed of sound in the skull (±20 %) caused only sub-wavelength errors in the reconstructions, suggesting that registration is the most important determinant of point source localization accuracy. Collectively, our findings show that HASA can address source localization problems through the skull efficiently and accurately under realistic conditions, thereby creating unique opportunities for imaging and controlling the microbubble dynamics in the brain.
Keywords: Angular Spectrum Approach, Brain, Image-guided Treatment, Focused Ultrasound
I. Introduction
The skull presents a significant challenge for ultrasonic imaging of the brain, as its acoustic properties and complex geometry introduce distortions in the transmitted and received wavefields, and degrade the coherence of the resulting images. These skull aberrations particularly complicate source localization and quantification, which are problems of principal importance to the monitoring and guidance of microbubble-enhanced focused ultrasound (FUS) brain therapies [1]. The spectral content of the resultant microbubble echoes (acoustic cavitation) is known to be indicative of the bubbles’ dynamic behavior, and thus is a good proxy for their mechanical effects on the surrounding vessels [2]. Therefore, accurate knowledge of the location and nature of the cavitation during treatment is vital to ensure the safety and effectiveness of FUS treatments [3].
Real-time monitoring of cavitation during FUS therapy typically employs passive cavitation detection (PCD), in which one or a few receiving elements are used to detect acoustic emissions, and their frequency content may be analyzed to adjust the applied therapeutic levels [3]. However, such techniques either do not yield spatial information, or the spatial information is very limited and thus cannot provide high fidelity information about the origin of the signals and of this origin is at the desired location or elsewhere [4]. To address this problem, passive acoustic mapping (PAM) methods have been developed which use an array of sensors to beamform the recorded emissions and yield a spatial map of the cavitation activity. While many PAM implementations do not account for medium heterogeneity [5]-[10], recent works have incorporated aberration corrections due to the human skull into both frequency-domain [11], [12] and time-domain [13]-[18] formulations. However, methods for determining the appropriate phase and amplitude corrections for each element and each position of interest within the brain typically present challenges: experimentally, they either require each set of corrections to be determined via an invasive measurement [19], [20], or the recording of echoes for that purpose prior to therapy [21]. Simulation of the trans-skull propagation [17], [22], [23] can also provide these data, but is computationally expensive without more specialized (e.g., GPU) computing resources [11], [14], [15], [24], [25].
Another approach to PAM employs the spatial frequency domain angular spectrum approach (ASA), whose frequency selectivity and computational efficiency (more than one hundredfold faster than delay-and-sum in 3D) makes it well suited to the real-time, narrowband problem of interest [10]. We have recently extended ASA to account for nonuniformity of the medium and correct aberration in the resulting PAMs [26]. Although we demonstrated via numerical simulations that the heterogeneous ASA (HASA) allowed for the correction of skull-induced aberration with modest computational overhead, experimental evidence of the utility of this method for PAM is still missing.
In this manuscript we address this gap by assessing the ability of HASA to perform volumetric trans-skull PAM experimentally. Subsequently, we determine the relative influence of experimental uncertainties due to finite aperture effects, translational and rotational registration uncertainty, as well as those due to empirically-derived local material properties. Finally, we establish the requisite values for positional and sound speed errors for attaining accurate transcranial point source localization with the HASA.
II. Methods
A. Passive Acoustic Mapping with ASA/HASA
A brief overview of the derivation of ASA and HASA are presented here; for more specific details on the derivations and approximations employed, see Refs. [10], [26], [27].
1). Homogeneous ASA:
For a time harmonic pressure field where is the angular frequency, the angular spectrum is given by its 2D spatial Fourier transform
| (1) |
When applied to the homogeneous Helmholtz equation , the spatial Fourier transform gives an ordinary differential equation for the angular spectrum :
| (2) |
where , and is the (constant) speed of sound. If is measured at the plane , and if there are no reflected waves, then the solution of Eq. (2) is
| (3) |
If Eq. (3) is evaluated at successive parallel planes (at each depth of interest), a volumetric wavefield may be recovered.
2). Heterogeneous ASA:
For heterogeneous media where the sound speed changes in space slowly compared with the wavelength, then the ordinary differential equation for the angular spectrum becomes
| (4) |
Here, , , is a reference (average) sound speed, and * indicates two-dimensional convolution over the component wavenumbers and . An implicit solution of Eq. (4) may be obtained with a Green’s function technique, and numerical approximation allows computation of at arbitrary via
| (5) |
where . As long as the marching step size is much smaller than the wavelength (i.e., ), Eq. (5) enables calculation of the field in the heterogeneous medium analogously to Eq. (3) for the case of a uniform medium.
3). Passive Acoustic Mapping:
To compute the maps of acoustic intensity, the time series pressure from each element of the receiving array is recorded. Here is the position vector in the plane of the transducer, with the origin at its center. Next, the temporal Fourier transform (via MATLAB’s fft) is performed on the time series data to obtain . Then, the angular spectrum of at the measurement plane (i.e., transducer face) for each frequency of interest is computed by taking the spatial transform (via MATLAB’s fft2), denoted . Finally, the initial angular spectrum may be propagated via Eq. (3) through the homogeneous medium with sound speed , and the inverse transform is taken to obtain the intensity map:
| (6) |
In the case of heterogeneous medium, the bracketed term in Eq. (6) is replaced with the approximation Eq. (5) to give
| (7) |
where
| (8) |
see Fig. 1(a). In the two-dimensional case used for the simulation data sets, and both vanish.
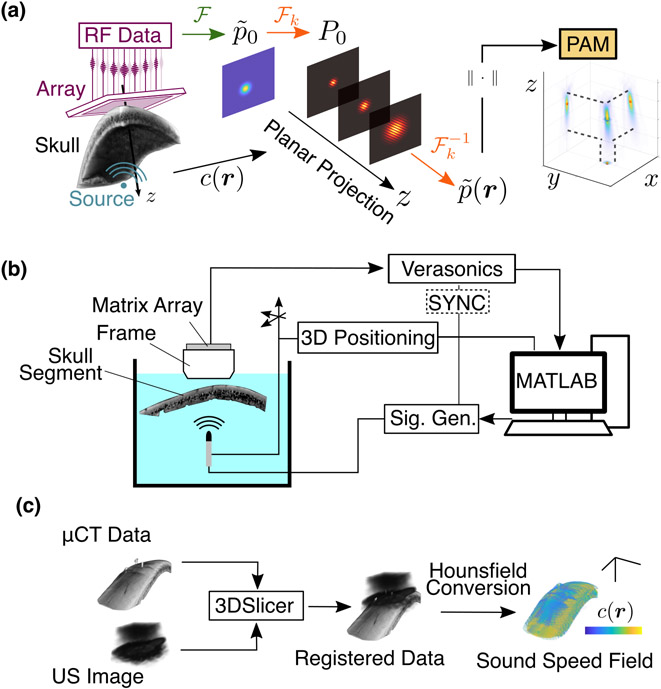
Fig. 1.
(a) PAM formation with aberration correction: RF signals are recorded from a source behind a skull. The data are beamformed in the spatial frequency domain using corrections from the known sound speed field with Eq. (5). (b) Experimental setup: Emissions from a known source are collected with a matrix array through a degassed human skull segment. (c) Sound speed registration: Using an acoustic image from the array and the micro-CT data, fiducial registration is used to obtain the transformation matrix. A semi-empirical model was used to convert the CT intensities to material properties.
B. Trans-skull Experiments
1). Experimental Setup:
To evaluate the ability of HASA to improve the accuracy and quality of the PAMs, we performed in vitro trans-skull experiments. A custom-built (Imasonic, Voray-sur-l’Ognon, France) matrix transducer array (13-by-13 elements, each with dimensions 1.5 mm-by-1.5 mm, with pitch 1.8 mm, center frequency 820 kHz, and 37 % fractional bandwidth) was positioned in a 3D printed frame to which a skull segment was affixed. The transducer was controlled with a 256-channel research ultrasound system (Verasonics, Kirkland, WA, USA) and custom MATLAB scripts. The segment of a human skull from the right parietal region (Skulls Unlimited, Oklahoma City, OK, USA) approximately 10 cm-by-5 cm-by-0.5 cm was degassed overnight (approximately 12 hours) prior to the measurements. The entire frame assembly was then placed in a tank of degassed de-ionized water.
To provide a source with a known truth position, a nearly omnidirectional (±3 dB expected across the transducer aperture) hydrophone (TC4038, Reson Slangerup, Denmark) was connected to an arbitrary waveform generator (Keysight, Santa Rosa, CA, USA). The hydrophone was excited with a 40-cycle windowed sine pulse at 1 MHz to mimic the narrowband emissions of acoustic emissions during transcranial FUS therapy [28]. The transmitted frequency, which is near the edge of the matrix array’s bandwidth, was chosen as the HASA correction is more valid for higher frequencies [26]. The acoustic emissions of the source were recorded passively by the matrix array, which was synchronized through an output trigger of the waveform generator. A three-axis positioning system (Velmex, Bloomfield, NY, USA) controlled and stored the position of the hydrophone relative to the array; see Fig. 1(b). Due to the limitations of array aperture and experimental geometry, the source position was constrained within an approximately 1 cm3 volume, about which source positions were evaluated; see Fig. 2(a).
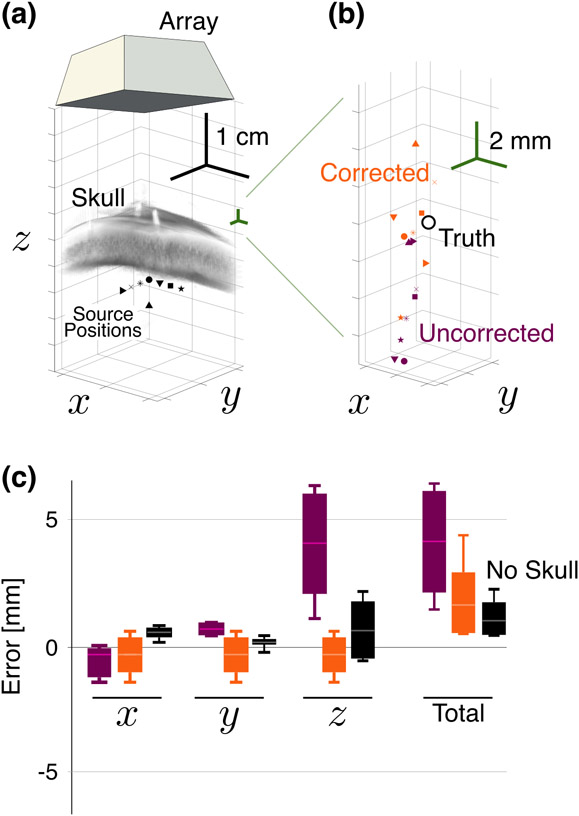
Fig. 2.
(a) Known source positions relative to the array and skull segment. (b) Recovered source posiutions relative to the truth position (white circle) for the corrected (orange) and uncorrected (purple) points. Shapes correspond to the positions in (a). (c) Error relative to truth over all positions in (a), with and without the correction, as well as the no-skull case. Boxes represent the middle 50th percentile for each, while the whiskers represent the maximum and minimum values. The notch indicates the median for each case.
2). Experimental Data Processing:
Given the relatively course discretization in space introduced by the pitch of the array, as well as its relatively narrow aperture, techniques to reduce aliasing and wraparound errors were applied. While the pitch is larger than the acoustic wavelength, the sound is incident almost normal to the array (i.e., ). Thus the transverse wavenumber components and are comparatively small, and the spatial sampling density is sufficiently high for reconstructions near the center of the array. Thus the initially measured distributions in the frequency domain were first interpolated 4× in both the - and -dimensions to give a computational spatial resolution of . The initial distribution was zero-padded in both the - and -directions to give a total grid size of 188-by-188. To reduce the high spatial frequency content induced by sharp transition due to the zero-padding, a Tukey window with cosine factor 0.25 was applied the measured . A step size of was used for all reconstructions. Finally to isolate the source in each experimental PAM, the map was smoothed with a 3D Gaussian filter (via MATLAB’s imgausfilt3 with standard deviations 0.2 pixels transverse and 0.4 pixels axially) and thresholded at an empirically determined threshold of 0.2 (−14 dB) to isolate regions. The region containing the highest intensity was taken to contain the source, and its centroid was taken as the source location; remaining volumetric regions (if any) were designated as sidelobes due to aberration. The “energy” of each region was defined as the integrated PAM intensity in the region.
Next, implementation of the correction [Eq. (5)] requires knowledge of the sound speed field relative to the array (such that the initial measurement plane coincides with ). To obtain the orientation of the skull segment within the holder, three small steel fiducial markers were placed in shallow (approximately 2 mm) recesses drilled into the outer surface. These markers are plainly visible in the micro-CT image. After placement in the frame, a volumetric plane wave image (±10° in 1° increment) was captured of the skull. The plane wave and micro-CT datasets were then imported into 3D Slicer [29], [30] and the fiducial registration [31] was performed using manually assigned locations of the markers in both the CT and ultrasound images (see Suppl. Fig. S-1). Finally, the full transformation matrix was applied to the sound speed map obtained from the CT data via semi-empircal Hounsfield scale conversion described previously [17], [32] [Fig. 1(c)]. The resulting 3D speed of sound matrix defines the for use in evaluation of the HASA PAM [Eq. (7)].
C. Trans-skull Simulations
Acoustic simulations were carried out in k-Wave [33]. Because the incident acoustic waves were less than the critical angle for skull bone (approximately 26° [34]), no elastic effects were included. To determine the skull densities and sound speeds, a micro-CT scan was taken of the skull segment with voxel size 91 μm (resampled to 200 μm for the computational grid). In addition to the local speed of sound, the spatially-dependent density and absorption coefficient of the bone were computed from the same conversion as for the experiments (Sec. II-B2). Power law absorption was modeled as . , with defined for the entire medium [36], as the spatial variation of this parameter is not possible in k-Wave.
All PAM reconstructions and data analysis scripts were written in MATLAB and run on a desktop workstation (Intel Xeon Gold 5120, 14 cores at 2.2 GHz and 64 GB memory) without parallel or graphical processing techniques. Simulations and associated reconstructions were performed in 2D for efficiency (60 mm by 80 mm, with 10 point perfectly matched layer). Thus, for the 2D reconstructions, the second transverse wavenumber was uniformly set to zero . Spatial grid spacing 200 μm and time step 62.5 ns were used for all simulations (CFL number ), and 813 time steps (50 μs) were simulated. The reference sound speed was taken to be the average value over the entire grid.
As both the aperture size and pitch affect the image resolution and quality, both were varied in the simulation. The experimental array had pitch , above the theoretical limit to preclude grating lobes (, which for 1 MHz requires . Though, as discussed previously, this requirement is more relaxed for near-axis targets). Thus for comparison, simulated arrays with a pitch of 0.5 mm were considered. Additionally, the experimental 2D array had an aperture 25.6 mm, and due to geometrical constraints of the experiment, required the source to be close to 40 mm (F# ~1.6). Since HASA in particular and PAM in general are improved for F# closer to 1 [26], simulated reconstructions also considered apertures of 64 elements at the experimental (1.8 mm) and ideal (0.5 mm) pitches, to determine the influence of aperture and pitch on the experimental results.
Finally, to evaluate the effect of experimental uncertainties, errors (relative to the exactly known simulation conditions) were introduced into the reconstructions. First, simulations with known skull positions were performed, and then the translational and rotational position of the skull was altered in the reconstruction to investigate the effect of imperfect registration. Rotational errors were introduced by rotating the (now 2D) speed matrix about a central pivot point, while translational errors were simulated by shifting the matrix in the axial direction. In addition to evaluating the effects of translational and rotational registration errors independently, translation and rotation errors were also combined to emulate realistic experimental conditions.
To determine the importance of the accuracy of the empirical skull speed of sound conversion (from the CT scan) used for the experiments, we also added errors in the skull sound speed, again compared to the known properties in the simulation. Proportional errors were introduced following , where and skull are the skull sound speeds in the simulation and reconstruction, respectively, and is the proportional error. The error in source localization in the HASA reconstruction with these perturbed sound speed fields served as a metric for sensitivity analysis.
III. Results
A. Experimental Aberration Correction
1). Source Localization Accuracy:
First, we assessed the ability of HASA to recover the source location through the skull, compared with the uncorrected ASA trans-skull results and reference free space conditions. The lateral errors in the recovered source position in all cases were relatively small for both ASA and HASA (Fig. 2): −0.4±0.8 mm/0.6±0.4 mm in directions for the corrected case, compared with −0.7±0.7 mm/0.9±0.2 mm in the uncorrected case, and 0.6±0.3 mm/0.2±0.2 mm when no skull was present. However in the axial direction, the errors were reduced more appreciably, from 4.5±2.4 mm without the correction to −0.2±2.7 mm with it, compared with 0.8±1.2 mm for the no-skull case. The mean total (i.e., radial) error when no correction was applied was 4.7±2.3 mm, and when the correction was used, the total error was reduced approximately by half to 2.3±1.6 mm, compared with 1.4±0.7 mm for the no-skull case. Directional errors as a function of the source position, from which significant trends did not emerge due to the limited available source positions, are shown in Suppl. Fig. (S-2).
2). PAM Quality:
Beyond the improvement in source localization, the HASA also offered improvement in the overall quality of the PAM. Figure 3 shows a typical experimental PAM and mean values for metrics of the quality of the maps. As expected in the no-skull case [Fig. 3(b), top row], the reconstructions are smooth, and the source position is evident—and coincides with the known source position. When the skull is inserted, but no correction applied, the field is distorted and side lobes are prominent [Fig. 3(b), middle row]. However, application of the correction [Fig. 3(b), bottom row] reduces the peak region volume as well as the relative PAM intensity of the side lobes.
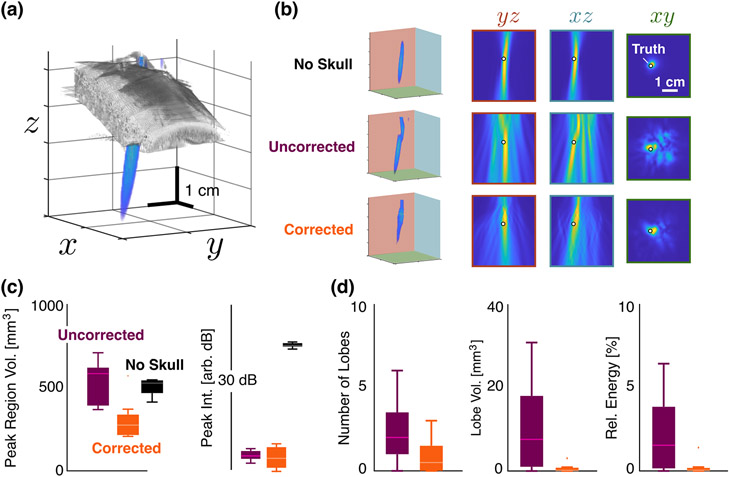
Fig. 3.
Comparison of PAM Quality. (a) Experimental reconstructed PAM relative to the position and size of the skull. (b) Reconstructed maps for positions (0, 5, 30) mm with no skull (top row), with the skull (i.e., uncorrected, middle row), and with the skull and correction (bottom row). The columns show the projections of the maps onto the indicated axes relative to the true position of the source (white circle). The 1 cm scale bar is constant for all PAMs. (c) Mean peak region volume and PAM intensities at the peak averaged over all positions for the no-skull (black), uncorrected (purple), and corrected (orange) cases. Scale bar in plane of top row is constant for all images. (d) Mean number, volume, and total energy within the side lobes averaged over all cases. No side lobes were present in the no skull case.
These effects persisted over all maps (i.e., those for each source location). Figure 3(c) indicates that the peak region volume was reduced significantly from the uncorrected case from 540±130 mm3 to 310±120 mm3—which led to improved accuracy in the peak location. While the no-skull case had a larger mean peak region volume (520±80 mm3), the lack of distortion resulted in accurate peak localization, as expected. Note that these peak region volumes reflect the 14 dB cutoff necessitated by the peak finding; for a cutoff of 3 dB, the peak region in the water path case were 29±20 % smaller than the corrected skull case (and 81±9 % smaller than the uncorrected skull case). The PAM intensities at the peak locations were comparable with and without the correction (within 0.2 dB in arbitrary units), and much lower than the no skull case (19 dB higher). This was consistent with the insertion loss (i.e., , where is the received pressure, and the 0 subscript indicates the no-skull case) found due to the skull (14 dB).
The use of the HASA to compute the PAMs did not change the order of the computational time. Reconstructions for the 4× interpolated, zero-padded initial condition yielded a reconstruction time of 2.76±0.12 s compared with 1.54±0.05 s for the uncorrected ASA for a single frequency. The final volume for these reconstructions had dimensions of 188-by-188-by-601 (21.2 × 106 total) voxels.
B. Trans-Skull Simulations
1). Effect of Receiver Aperture:
To investigate the influence of the data preprocessing and source localization routines that proved necessary for the experimental data, we performed numerical simulations. Reconstructions with HASA using the native dimension and resolution of the experimental array showed that the field suffered due to the low resolution and resulting errors in axial source localization [, Fig. 4(a)]. However, when the raw measurement (i.e., ) was interpolated 4× and smoothing and centroid peak finding employed (as was done for the experimental results) an improvement in source localization accuracy was observed [, Fig. 4(b)]; additionally the peak region area was reduced by 44 % and its peak intensity increased by 8%. The resulting axial FWHM in the corrected, interpolated case (3.0 cm) was consistent with that theoretically expected for this frequency and receiver geometry in the homogeneous medium case (approximately 3.1 cm) [6], [37]. Thus interpolation can help to improve accuracy when the array pitch falls below the strict requirement, and can provide useful improvement near the center of the array (i.e., as long as remains less than 1).
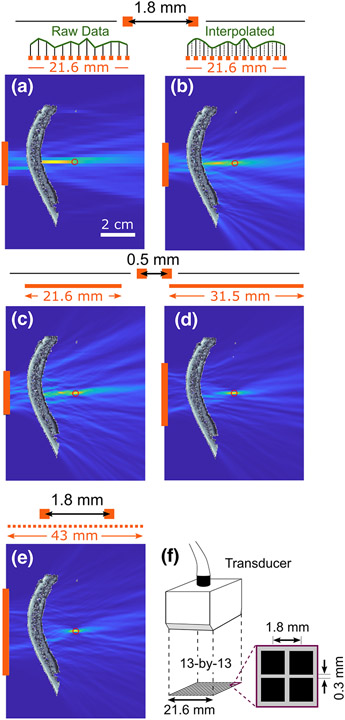
Fig. 4.
Effect of aperture and pitch on corrected reconstruction accuracy for a source at . (a) Reconstruction at a native resolution of the experimental array (13 elements, ). (b) Reconstruction with data recorded at native resolution of the array (13 elements, ), but interpolated 4×. (c) Reconstruction with a smaller pitch of , but with same aperture length (21.6 mm) as the experimental array. (d) Reconstruction with , and 64 total elements. (d) Reconstruction with smaller pitch of , but with the same aperture length (21.6 mm) as the experimental array. (d) Reconstruction with experimental pitch , but twice as many elements (26 in total). (f) Schematic of custom 2D array used in the experiments. Scale bar in (a) is applicable to subplots (a)–(e).
However, provided that grating lobes are prevented by closely-spaced elements, the localization is quite effective: Figure 4(c) shows that, even for the relatively high of the experimental geometry, subwavelength localization (error ) is possible if the element spacing is 0.5 mm (43 elements). The quality of the map is further improved (error , peak PAM intensity 48% higher) if the number of elements is increased to 64 as in Fig. 4(d). For near-axis targets, the effect of the aperture is seen to be of primary importance; even as the relatively coarse experimental pitch of the array [ Fig. 4(f)] is maintained, the resulting PAM is of improved quality when the aperture is made larger [compare 26 elements Fig. 4(e) with 13 elements Fig. 4(a); see also Suppl. Videos 1 & 2]. Together, our findings indicate that the aperture of the array should tailored to the imaging depth for PAM using HASA to be effective; this conclusion should also be applicable to all PAM algorithms.
2). Effect of Registration:
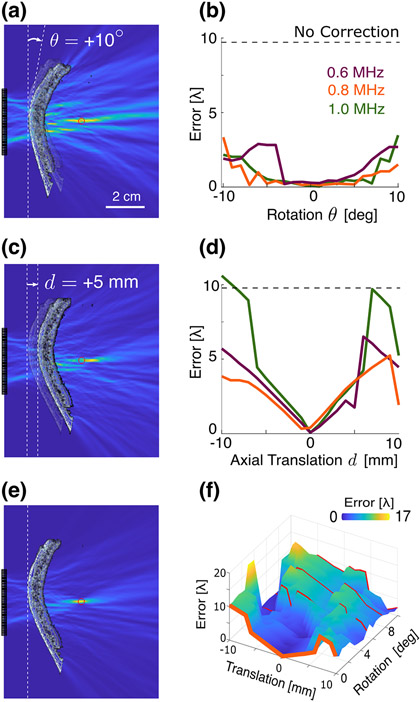
Following the quantification of the errors in source localization due to aperture constraints, we sought to quantify how the uncertainty in the positioning of the array and skull (i.e., registration error) affects source localization, through simulations in which the ground truth geometry was known. The influence of rotational registration errors on the resulting error in PAM source localization was less pronounced. Skull rotation errors as large as ±10° resulted in localization errors of less than [here the wavelength , where is the mean sound speed over the entire simulation domain, see Fig. 5(a-b)]. However, translational error had more pronounced effects on localization. Registration errors of ±5 mm resulted in errors on the order a few wavelengths, but the error approached that of the uncorrected case when the translation approached 1 cm [Fig. 5(c-d)]. No specific or strong trend was observed with respect to rotation registration error, whereas a clear linear trend appeared with either an increase or decrease in skull translation error. However, when translational and rotational errors were introduced simultaneously [Fig. 5(f)], the linear trend of translation was progressively lost. Finally, we found that the peak PAM intensity and region area, as well as the number and intensity of side lobes, exhibited trends within registration errors of ±2 mm and ±5 ° (see Suppl. Fig. S-3).
Fig. 5.
(a) 1 MHz source reconstruction with a 10° rotation error in the reconstruction. (b) Localization error as a function of the rotational registration error for the indicated frequencies, compared with the uncorrected ASA-PAM result (dashed line). (c) 1 MHz source reconstruction with a 5 mm translation error in the reconstruction. (d) Localization error as a function of the translational registration error, compared with the uncorrected ASA-PAM result (dashed line). (e) Trans-skull PAM reconstruction at 1 MHz with no registration error. (f) Localization error compared to the average wavelength as a function of the translational and rotational registration errors. Scale bar in (a) is applicable to subplots (a), (c), (e).
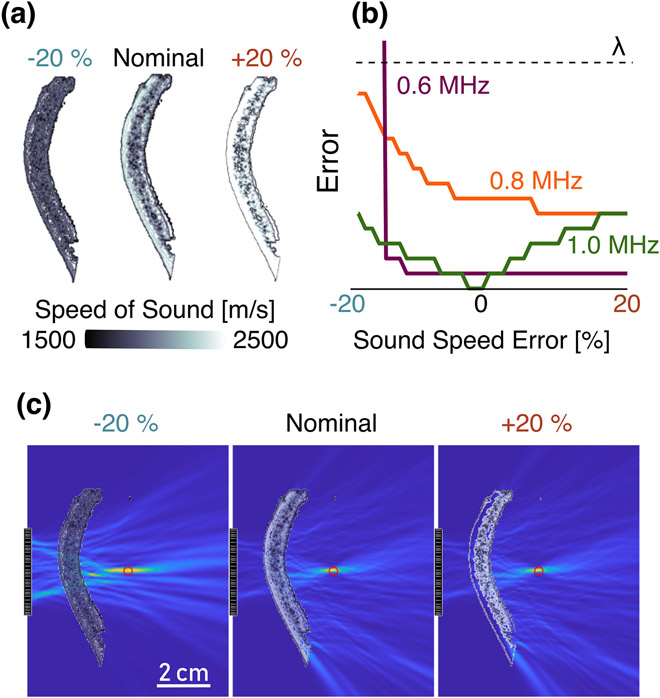
3). Effect of Sound Speed Errors:
Since the sound speed used for the correction was derived from an empirical relationship, we lastly investigated how any differences between the true and assumed local speed of sound within the skull influenced the resulting localization accuracy. The effect of scaled sound speed error on localization error in the resulting PAM was seen to be less dramatic than that of registration errors (Fig. 6). For instance, a ±20% error in sound speed amounts to less than half a wavelength of error in reconstruction. Results indicated that an increase in the assumed sound speed leads to larger peak intensities than in the true sound speed case, as the effective wavelength in the reconstruction was smaller, and thus the point spread function scaled accordingly. The localization error magnitudes were relatively modest for the inaccurate skull speeds of sound, most likely because the skull comprises only a fraction of the propagation medium. A full scaling of induces more systematic trends in the localization error, see Supplementary Material. This reduction in the PSF is also likely the reason that the error decreases slightly when the reconstructed sound speed is larger than ground truth [Fig. 6(b)].
Fig. 6.
(a) Sound speed profile of the skull segment used for the experiment and used in the simulations, derived from micro-CT scans. The sound speed values in the skull were then scaled by values from 0.8 to 1.2 (±20 %) from the nominal case. (b) Effect of sound speed error on PAM source localization error magnitude for the indicated frequencies, compared to the mean wavelength at 1 MHz. (c) HASA-PAMs formed at 1 MHz for the nominal and extreme case sound speeds. The 2 cm scale bar is constant for all PAMs.
IV. Discussion
In this paper we have demonstrated experimentally the ability of HASA to address the problem of volumetric trans-skull point source localization (Figs. 1 and 2). The inherent computational advantage of HASA is substantial, especially for volumetric PAM, and comparable to the uncorrected ASA (2.3 s vs 1.4 s). This allows reconstruction of full maps of the acoustic field (tens of millions of voxels) within a few seconds with no special computational resources. Such efficiency is of first importance for cavitation emissions–guided and –controlled therapies [8], [21], [38]-[41], and offers lower overhead than other augmentations to improve PAM quality [7], [42], [43] or efficiency [24], [44].
While our findings demonstrate that HASA is able to localize point sources through ex vivo human skull with reduced number, size, and energy of spurious lobes caused by aberration, we submit that the experimental array and setup employed in this study were sub-optimal for this application. Most notably, the relatively coarse pitch [Fig. 4(e)] meant that measurements were limited to frequencies for which aberration is less pronounced, and assumptions of the HASA (namely, that wavelength is short compared to the spatial gradient of the sound speed) are less strictly met; this is likely the reason that the transverse experimental errors were comparable in between ASA and HASA. Also, the relatively small experimental aperture necessitated more complex peak detection routines. Simulations showed that the interpolation can alleviate some of these effects [Fig. 4(a-b)], but a more extensive experimental vetting of the technique, at deeper targets and larger angles, would require an array with a larger aperture. While spatial upsampling of the initial condition creates a numerically dense array, the number and position of physical receivers must only be sufficient to provide a reasonable interpolation of the field. Hence, an array with wider aperture than the one used in our experiments but with the same pitch will result in robust localization and PAMs with still smaller side lobes [Fig. 4(e)] and access to more clinically relevant targets. Additionally, the availability of a larger bandwidth would enable more improved localization from higher-frequency signals (i.e., representative of higher harmonic or ultraharmonic components), for which the aberration will be more pronounced, and for which the HASA is a better approximation [26].
Despite the experimental limitations, HASA compares favorably to other PAM methods. Compared to time domain methods, its spatial resolution is equivalent for a given geometry [6], [37], [45]. While the available experimental array had degraded capabilities compared to the trans-skull corrections demonstrated with more expansive hemispherical arrays [8], [11], simulations indicate a modest increase of the aperture size will improve the HASA PAM quality [Fig. 4(d-e)]. The formulation employed here limits its use to planar measurements; thus while HASA results tracked with theoretical predictions for peak region dimensions [6], those for larger aperture hemispherical arrays will be inherently more compact (e.g., [8] reports −3 dB axes of 5.4 mm axially and 3.0 mm laterally for a map of source acticity at 306 kHz, compared with 8.8 mm axially and 1.4 mm laterally at here). Additionally, HASA has the same inherent spectral resolution as frequency domain PAM techniques [9], [46], but accounts for the skull and reduces the computational expense. Thus the high temporal resolution of HASA make it naturally suited for the problem of real-time therapeutic feedback and control [41]. Notably the inherent properties of this method may also create new opportunities for adaptive focusing which are not restricted to planar arrays.
Because correcting aberration with PAM requires knowledge of the acoustic environment, we next assessed the influence of registration error relative to the array, which is inherent to any practical implementation. Our simulations demonstrated that translational and rotational registration errors on the order of ±5 mm and ±5 ° (respectively), which are in line with reported registration accuracies [18], [47], yielded source localization errors on the order of a few wavelengths (Fig. 5). The trends in peak intensity and size seen as functions of the registration errors suggest that an optimization routine might enable iterative improvement of the experimental registration (Suppl. Fig. S-3). Additionally, analysis of sound speed field similarity as function of translation will inform the relative importance of registration accuracy in each dimension (Suppl. Fig. S-4).
While these errors were assessed explicitly for the HASA method, they may extend to uncertainty constraints applicable to other PAM methods [9]-[11], [17]. Further experiments with additional skull pieces and with other experimental effects such as transducer cross-talk [48] that were not considered in the simulations, will consolidate our findings and support the utility of the proposed method in the clinic.
V. Conclusion
In this work, we provided experimental evidence of the ability of HASA to perform spectrally-resolved and computationally efficient trans-skull source localization. HASA was seen to reduce the localization error and improve the quality of 3D PAMs, while retaining computation times of order 100 ns per voxel. Simulations showed that wider aperture and reduced experimental uncertainty would further improve the accuracy of the resulting PAMs. In sum our findings support the use of 3D HASA-PAM to map and characterize cavitation fields in the brain, with high potential for eventual therapeutic guidance.
Supplementary Material
Acknowledgments
This was supported by NIH/NCI Grant R37CA239039, and NSF/HMMI Grants 1933158 and 1830577.
Contributor Information
Scott Schoen, Jr, Woodruff School of Mechanical Engineering Georgia Institute of Technology Atlanta, GA USA.
Pradosh Dash, Woodruff School of Mechanical Engineering Georgia Institute of Technology Atlanta, GA USA.
Costas D. Arvanitis, Woodruff School of Mechanical Engineering and Coulter Department of Biomedical Engineering Georgia Institute of Technology and Emory University Atlanta, GA, USA.
References
- [1].Meng Y, Hynynen K, and Lipsman N, “Applications of focused ultrasound in the brain: from thermoablation to drug delivery,” Nature Reviews Neurology, vol. 17, no. 1, pp. 7–22, Jan. 2021. [DOI] [PubMed] [Google Scholar]
- [2].Aryal M, Arvanitis CD, Alexander PM, and McDannold N, “Ultrasound-mediated blood–brain barrier disruption for targeted drug delivery in the central nervous system,” Advanced Drug Delivery Reviews, vol. 72, pp. 94–109, Jun. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Jones RM and Hynynen K, “Advances in acoustic monitoring and control of focused ultrasound-mediated increases in blood-brain barrier permeability,” The British Journal of Radiology, vol. 92, no. 1096, p. 20180601, Feb. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Hu Z, Xu L, Chien C-Y, Yang Y, Gong Y, Ye D et al. , “Three-dimensional Transcranial Microbubble Cavitation Localization by Four Sensors,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, pp. 1–1, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Salgaonkar VA, Datta S, Holland CK, and Mast TD, “Passive cavitation imaging with ultrasound arrays,” The Journal of the Acoustical Society of America, vol. 126, no. 6, pp. 3071–3083, Dec. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Gyöngy M and Coussios C-C, “Passive cavitation mapping for localization and tracking of bubble dynamics,” The Journal of the Acoustical Society of America, vol. 128, no. 4, pp. EL175–EL180, Sep. 2010. [DOI] [PubMed] [Google Scholar]
- [7].Coviello C, Kozick R, Choi J, Gyöngy M, Jensen C, Smith PP et al. , “Passive acoustic mapping utilizing optimal beamforming in ultrasound therapy monitoring,” The Journal of the Acoustical Society of America, vol. 137, no. 5, pp. 2573–2585, May 2015. [DOI] [PubMed] [Google Scholar]
- [8].Jones RM, Deng L, Leung K, McMahon D, O’Reilly MA, and Hynynen K, “Three-dimensional transcranial microbubble imaging for guiding volumetric ultrasound-mediated blood-brain barrier opening,” Theranostics, vol. 8, no. 11, pp. 2909–2926, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Haworth KJ, Bader KB, Rich KT, Holland CK, and Mast TD, “Quantitative Frequency-Domain Passive Cavitation Imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 64, no. 1, pp. 177–191, Jan. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Arvanitis CD, Crake C, McDannold N, and Clement GT, “Passive Acoustic Mapping with the Angular Spectrum Method,” IEEE Transactions on Medical Imaging, vol. 36, no. 4, pp. 983–993, Apr. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Jones RM, O’Reilly MA, and Hynynen K, “Transcranial passive acoustic mapping with hemispherical sparse arrays using CT-based skull-specific aberration corrections: a simulation study,” Physics in Medicine & Biology, vol. 58, no. 14, p. 4981, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Treeby B, Lucka F, Martin E, and Cox BT, “Equivalent-Source Acoustic Holography for Projecting Measured Ultrasound Fields Through Complex Media,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 65, no. 10, pp. 1857–1864, Oct. 2018. [DOI] [PubMed] [Google Scholar]
- [13].O’Reilly MA and Hynynen K, “A super-resolution ultrasound method for brain vascular mapping,” Medical Physics, vol. 40, no. 11, p. 110701, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].O’Reilly MA, Jones RM, and Hynynen K, “Three-Dimensional Transcranial Ultrasound Imaging of Microbubble Clouds Using a Sparse Hemispherical Array,” IEEE Transactions on Biomedical Engineering, vol. 61, no. 4, pp. 1285–1294, Apr. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Jones RM and Hynynen K, “Comparison of analytical and numerical approaches for CT-based aberration correction in transcranial passive acoustic imaging,” Physics in Medicine and Biology, vol. 61, no. 1, pp. 23–36, Nov. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Deng L, O’Reilly MA, Jones RM, An R, and Hynynen K, “A multi-frequency sparse hemispherical ultrasound phased array for microbubble-mediated transcranial therapy and simultaneous cavitation mapping,” Physics in Medicine & Biology, vol. 61, no. 24, p. 8476, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Arvanitis CD, Clement GT, and McDannold N, “Transcranial Assessment and Visualization of Acoustic Cavitation: Modeling and Experimental Validation,” IEEE Transactions on Medical Imaging, vol. 34, no. 6, pp. 1270–1281, Jun. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Jones RM, O’Reilly MA, and Hynynen K, “Experimental demonstration of passive acoustic imaging in the human skull cavity using CT-based aberration corrections,” Medical Physics, vol. 42, no. 7, pp. 4385–4400, Jul. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Thomas J-L and Fink M, “Ultrasonic beam focusing through tissue inhomogeneities with a time reversal mirror: application to transskull therapy,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 43, no. 6, pp. 1122–1129, Nov. 1996. [Google Scholar]
- [20].Gâteau J, Marsac L, Pernot M, Aubry J, Tanter M, and Fink M, “Transcranial Ultrasonic Therapy Based on Time Reversal of Acoustically Induced Cavitation Bubble Signature,” IEEE Transactions on Biomedical Engineering, vol. 57, no. 1, pp. 134–144, Jan. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Jones RM, Huang Y, Meng Y, Scantlebury N, Schwartz ML, Lipsman N et al. , “Echo-Focusing in Transcranial Focused Ultrasound Thalamotomy for Essential Tremor: A Feasibility Study,” Movement Disorders, vol. 35, no. 12, pp. 2327–2333, Jul. 2020. [DOI] [PubMed] [Google Scholar]
- [22].Pinton GF, Dahl J, Rosenzweig S, and Trahey GE, “A heterogeneous nonlinear attenuating full- wave model of ultrasound,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 56, no. 3, pp. 474–488, Mar. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Top CB, White PJ, and McDannold NJ, “Nonthermal ablation of deep brain targets: A simulation study on a large animal model,” Medical Physics, vol. 43, no. 2, pp. 870–882, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Kamimura HAS, Wu S-Y, Grondin J, Ji R, Aurup C, Zheng W et al. , “Real-Time Passive Acoustic Mapping Using Sparse Matrix Multiplication,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 68, no. 1, pp. 164–177, Jan. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Kim P, Song JH, and Song T-K, “A new frequency domain passive acoustic mapping method using passive Hilbert beamforming to reduce the computational complexity of fast Fourier transform,” Ultrasonics, vol. 102, p. 106030, Mar. 2020. [DOI] [PubMed] [Google Scholar]
- [26].Schoen S Jr and Arvanitis CD, “Heterogeneous Angular Spectrum Method for Trans-Skull Imaging and Focusing,” IEEE Transactions on Medical Imaging, vol. 39, no. 5, pp. 1605–1614, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].—, “Acoustic source localization with the angular spectrum approach in continuously stratified media,” The Journal of the Acoustical Society of America, vol. 148, no. 4, pp. EL333–EL339, Oct. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Sun T, Samiotaki G, Wang S, Acosta C, Chen CC, and Konofagou EE, “Acoustic cavitation-based monitoring of the reversibility and permeability of ultrasound-induced blood-brain barrier opening,” Physics in Medicine and Biology, vol. 60, no. 23, pp. 9079–9094, Nov. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Kapur T, Pieper S, Fedorov A, Fillion-Robin J-C, Halle M, O’Donnell L et al. , “Increasing the impact of medical image computing using community-based open-access hackathons: The NA-MIC and 3D Slicer experience,” Medical Image Analysis, vol. 33, pp. 176–180, Oct. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Kikinis R, Pieper SD, and Vosburgh KG, “3D Slicer: A Platform for Subject-Specific Image Analysis, Visualization, and Clinical Support,” in Intraoperative Imaging and Image-Guided Therapy, Jolesz FA, Ed. New York, NY: Springer, 2014, pp. 277–289. [Google Scholar]
- [31].Horn BKP, “Closed-form solution of absolute orientation using unit quaternions,” JOSA A, vol. 4, no. 4, pp. 629–642, Apr. 1987. [Google Scholar]
- [32].Aubry J-F, Tanter M, Pernot M, Thomas J-L, and Fink M, “Experimental demonstration of noninvasive transskull adaptive focusing based on prior computed tomography scans,” The Journal of the Acoustical Society of America, vol. 113, no. 1, pp. 84–93, Jan. 2003. [DOI] [PubMed] [Google Scholar]
- [33].Treeby BE and Cox BT, “k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields,” Journal of Biomedical Optics, vol. 15, no. 2, p. 021314, Mar. 2010. [DOI] [PubMed] [Google Scholar]
- [34].Clement GT, White PJ, and Hynynen K, “Enhanced ultrasound transmission through the human skull using shear mode conversion,” The Journal of the Acoustical Society of America, vol. 115, no. 3, pp. 1356–1364, Feb. 2004. [DOI] [PubMed] [Google Scholar]
- [35].Treeby BE and Cox BT, “Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian,” The Journal of the Acoustical Society of America, vol. 127, no. 5, pp. 2741–2748, May 2010. [DOI] [PubMed] [Google Scholar]
- [36].Cobbold RSC, Foundations of Biomedical Ultrasound. Oxford University Press, 2007. [Google Scholar]
- [37].Gyöngy M and Coussios CC, “Passive Spatial Mapping of Inertial Cavitation During HIFU Exposure,” IEEE Transactions on Biomedical Engineering, vol. 57, no. 1, pp. 48–56, Jan. 2010. [DOI] [PubMed] [Google Scholar]
- [38].Coussios CC, Farny CH, Haar GT, and Roy RA, “Role of acoustic cavitation in the delivery and monitoring of cancer treatment by high-intensity focused ultrasound (HIFU),” International Journal of Hyperthermia, vol. 23, no. 2, pp. 105–120, Jan. 2007. [DOI] [PubMed] [Google Scholar]
- [39].Ebbini ES and Haar GT, “Ultrasound-guided therapeutic focused ultrasound: Current status and future directions,” International Journal of Hyperthermia, vol. 31, no. 2, pp. 77–89, Feb. 2015. [DOI] [PubMed] [Google Scholar]
- [40].Sun T, Zhang Y, Power C, Alexander PM, Sutton JT, Aryal M et al. , “Closed-loop control of targeted ultrasound drug delivery across the blood–brain/tumor barriers in a rat glioma model,” Proceedings of the National Academy of Sciences, vol. 114, no. 48, pp. E10281–E10290, Nov. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Patel A, Schoen SJ, and Arvanitis CD, “Closed-Loop Spatial and Temporal Control of Cavitation Activity With Passive Acoustic Mapping,” IEEE Transactions on Biomedical Engineering, vol. 66, no. 7, pp. 2022–2031, Jul. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Choi JJ, Carlisle RC, Coviello C, Seymour L, and Coussios C-C, “Non-invasive and real-time passive acoustic mapping of ultrasound-mediated drug delivery,” Physics in Medicine and Biology, vol. 59, no. 17, pp. 4861–4877, Aug. 2014. [DOI] [PubMed] [Google Scholar]
- [43].Crake C, Brinker ST, Coviello CM, Livingstone MS, and McDannold NJ, “A dual-mode hemispherical sparse array for 3D passive acoustic mapping and skull localization within a clinical MRI guided focused ultrasound device,” Physics in Medicine & Biology, vol. 63, no. 6, p. 065008, Mar. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Gray MD, Elbes D, Paverd C, Lyka E, Coviello CM, Cleveland RO et al. , “Dual-Array Passive Acoustic Mapping for Cavitation Imaging With Enhanced 2-D Resolution,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 68, no. 3, pp. 647–663, Mar. 2021. [DOI] [PubMed] [Google Scholar]
- [45].Norton SJ and Won IJ, “Time exposure acoustics,” IEEE Transactions on Geoscience and Remote Sensing, vol. 38, no. 3, pp. 1337–1343, May 2000. [Google Scholar]
- [46].Haworth KJ, Mast TD, Radhakrishnan K, Burgess MT, Kopechek JA, Huang S-L et al. , “Passive imaging with pulsed ultrasound insonations,” The Journal of the Acoustical Society of America, vol. 132, no. 1, pp. 544–553, Jul. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Batts A and Konofagou E, “Targeting Accuracy of Transcranial Power Cavitation Imaging for Blood-Brain Barrier Opening Using a Theranostic Phased Array,” in 2020 IEEE International Ultrasonics Symposium (IUS), Sep. 2020, pp. 1–3. [Google Scholar]
- [48].Martin E, Roberts M, and Treeby B, “Measurement and simulation of steered acoustic fields generated by a multielement array for therapeutic ultrasound,” JASA Express Letters, vol. 1, no. 1, p. 012001, Jan. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.