Prediction of Compound Plasma Concentration–Time Profiles in Mice Using Random Forest

Abstract

Pharmacokinetic (PK) parameters such as clearance (CL) and volume of distribution (Vd) have been the subject of previous in silico predictive models. However, having information of the concentration over time profile explicitly can provide additional value like time above MIC or AUC, etc., to understand both the efficacy and safety-related aspects of a compound. In this work, we developed machine learning models for plasma concentration–time profiles after both i.v. and p.o. dosing for a series of 17 in-house projects. For explanatory variables, MACCS Keys chemical descriptors as well as in silico and experimental in vitro PK parameters were used. The predictive accuracy of random forest (RF), message passing neural network, 2-compartment models using estimated CL and Vdss, and an average model (as a control experiment) was investigated using 5-fold cross-validation (5-fold CV) and leave-one-project-out validation (LOPO-V). The predictive accuracy of RF in 5-fold CV for i.v. and p.o. plasma concentration–time profiles was the best among the models studied, with an RMSE for i.v. dosing at 0.08, 1, and 8 h of 0.245, 0.474, and 0.462, respectively, and an RMSE for p.o. dosing at 0.25, 1, and 8 h of 0.500, 0.612, and 0.509, respectively. Furthermore, by investigating the importance of the in vitro PK parameters using the Gini index, we observed that the general prior knowledge in ADME research was reflected well in the respective feature importance of in vitro parameters such as predicted human Vd (hVd) for the initial distribution, mouse intrinsic CL and unbound fraction of mouse plasma for the elimination process, and Caco2 permeability for the absorption process. Also, this model is the first model that can predict twin peaks in the concentration–time profile much better than a baseline compartment model. Because of its combination of sufficient accuracy and speed of prediction, we found the model to be fit-for-purpose for practical lead optimization.

Introduction

Dose and exposure—and hence pharmacokinetics—play an important role in the development of new drugs.¹ Clinical trials (in particular in phase II) are a common point of failure in drug development, and improving the success rate of these requires the estimation of effective clinical dosages that produce the best drug effect profile, which is based on pharmacokinetics/pharmacodynamics (PK/PD) analysis.² Therefore, it is necessary to accurately predict human pharmacokinetic parameters from nonclinical experimental data before transitioning to human clinical trials.³ In general, the parameters that have a large effect on the blood concentration profile of a drug during intravenous administration (i.v.) are Vd, which quantifies the distribution of the drug inside the human body, and total body clearance (CL_tot), which describes the drug processing capacity within the body as a whole.

To predict CL_tot and Vd, many in silico models have been developed using machine learning algorithms paired with chemical structure descriptors.⁴⁻⁶ More recently, some studies using in vitro or in silico derived data as explanatory variables have also been published.⁷⁻⁹ The objectives of these were to predict rat PK parameters like the area under the plasma drug concentration–time curve for oral administration (AUC_p.o.) using in vitro, in silico, and physicochemical properties, namely, membrane permeation, free fraction, metabolic stability, solubility, pK_a, and lipophilicity. In the first study, the authors observed that drug exposure after i.v. administration can be predicted similarly well using hybrid models with in vitro- or in silico-predicted end points as inputs, with fold change errors of 2.28 and 2.08, respectively. The observed fold change errors (FCEs) for exposure after oral administration were higher, and the prediction from in vitro inputs performed significantly better in comparison to in silico-based models with FCEs of 3.49 and 2.40, respectively. In addition, the prediction errors for AUC_p.o. were generally higher than those for AUC_i.v., which the authors attributed to the higher complexity of oral bioavailability (BA).⁷ Moreover, the prediction accuracy from in vitro inputs performed significantly better in comparison to their in silico counterparts. In the second study, the predictivity of AUC_p.o. by machine learning models was generally improved by incorporating in vitro parameters as input features (R² values over 0.55). On the other hand, clearance prediction utilizing in vitro intrinsic clearance data in combination with the well-stirred model was found to perform substantially worse compared to machine learning approaches.⁸ In the final study, they compared the performance of various traditional machine learning algorithms and deep learning approaches, including graph convolutional neural networks, and also investigated time–concentration profiles. Although the predictability for each PK parameter (CL_tot, Vd, BA) was high (R² values over 0.55), they found that the prediction of AUC_p.o. was more difficult than that of AUC_i.v..⁹ Moreover, recently, the Life Intelligence Consortium, which is a Japanese pharmaceutical consortium, found that using not only in vitro and in silico but also in vivo parameters of different animal species was useful to predict human PK parameters.¹⁰ On the basis of these studies, to predict in vivo PK parameters, different input parameters should be used as explanatory variables to achieve the best model predictivity.

PK parameters such as CL_tot, Vd, and BA, which have been the subject of previous in silico models, can then be used for the prediction of dosing in clinical trials.¹ As long as we have these parameters, exposure–response analysis can be performed. However, when conducting a PK/PD analysis, information about the full time–concentration profile of a drug in vivo is considered to be more essential than the exposure–response analysis because it includes the subtle change due to time elapsed.¹¹ Historically, from antibacterial research, three PK/PD parameters that consider the concept of time are known to be important and have been used extensively since the 1980s:¹² the ratio of maximum concentration to minimum inhibitory concentration (MIC), ratio of area under the concentration–time curve to MIC, and time–concentration above MIC. Nowadays, this concept has been developed further such that, during PK/PD analysis, the whole time–concentration profile is used.^13,14

Traditionally, during PK/PD studies, the simulation of time–concentration profiles is performed with a compartment model using CL_tot and Vd as inputs.² However, the compartment model has several limitations. First, when using a one-compartment model, the elimination phase is depicted as a straight line, meaning that the distribution phase cannot be simulated. Second, when using the more complex two-compartment model, although we can describe the distribution phase, it requires double the number of input parameters. Moreover, despite the increase in complexity, this model cannot describe the redistribution of the drug from the deep tissue compartment.² Finally, when attempting to use physiologically based pharmacokinetic (PBPK) models with greater than three compartments, the total number of in vitro parameters required as input becomes unmanageble.² Consequently, it is not easy to use PBPK models in the early drug discovery stage.

In contrast to compartmental models, recently, a machine learning model, which uses Alchemite, for rat PK time–concentration profiles was developed that predicted intravenously (i.v.) and orally (p.o.) administrated data simultaneously.¹⁵ Overall, the authors found that the accuracy of the predicted PK time–concentration curves after i.v. dosing was good (R² median across time points of 0.82), but the prediction of curves after oral dosing was poor (R² median across time points of −0.78), perhaps as a result of the higher variability in p.o. dosing curve data.⁹ Hence, we can conclude that for the prediction of compound plasma concentration–time profiles, the investigation of machine learning models using predicted in vitro PK parameters is preferential to compartmental models.

From the viewpoint of animal species to be used for PK study, the rat is commonly used during in vivo PK/PD experiments as the rodent model, which may be the reason why the three aforementioned recent research focused on developing predictive PK model using rat data.⁷⁻⁹ On the other hand, it is also true that the mouse is known to be suitable.¹⁶ There are many reasons why mice may be considered better for PK/PD studies such as the small size, ease of handling, low cost, fast reproduction rate, and greater number of human disease models. From the viewpoint of the drug discovery process, one of the most important reasons is related to its smaller size. This is because the dosage of the drug (mg/kg) required to achieve a given exposure is directly linked to the amount of test compound synthesized. From a medicinal chemistry and economic standpoint, smaller is better because less time and material resources are required.

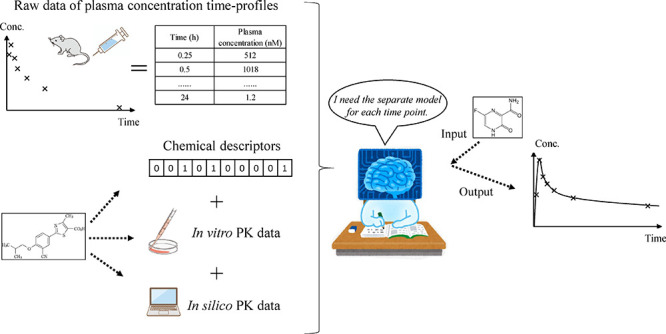
In this study, we developed separate machine learning models capable of predicting time–concentration profiles of small-molecule drugs in mice after both i.v. and p.o. administration, respectively. We decided to use the single task method to build the in silico model for the concentration at each time point. This is because the multitask learning can work under similar end points.¹⁷ In the concentration–time profiles, the values at the different times reflect the different phases of the drugs, namely, absorption, distribution, elimination phase, etc. Therefore, we anticipated that a tiny error in different time points could lead to a larger error in later time points. To this end, drug plasma concentrations for various time points after the initial administration were predicted separately as a single task, and predictions were subsequently combined.

Materials and Method

In Vitro Experiments

The in vitro data sets used in this study were obtained following the standard protocol described below.

To obtain mouse intrinsic clearance (mCLint), the source matrix was pooled mice liver microsomes (0.2 mg/mL), and the concentration of the test compound was 1 μM (n = 2). The reaction buffer was 100 mM potassium phosphate buffer (pH 7.4) containing 1.2 mM NADPH, and the incubation time was 25 min with NADPH at 37 °C. For the termination of incubation, 300 μL ice-cold acetonitrile was added to 100 μL reaction volume and mixed vigorously followed by centrifugation. The detection method was LC–MS/MS (API 4000, AB Sciex Pte. Ltd.), and the data were analyzed as the percentage of the parent compound remaining when calculating mCLint.

To obtain the unbound fraction of mouse plasma (mfu), the source matrix was pooled mice plasma. The concentration of the test compound was 1 μM (n = 2), and equilibrium dialysis was performed using a rapid equilibrium dialysis (RED) device (Thermo Fisher Scientific K.K.) in PBS buffer at pH 7.4. Incubation was performed at 37 °C for 6 h with constant shaking (400 rpm), and the samples from the buffer and plasma were collected separately. These two samples were measured by LC–MS/MS to calculate the free fraction of plasma.

To obtain Caco-2 permeability A to B (Caco-2), the cells were grown for 10 days in 37 °C in the incubator with 5% CO₂ supply and controlled humidity. The assay was performed in a 96-well plate (pH 7.4) in HBSS buffer containing 10 mM HEPES (1% DMSO), and the concentration of compounds was 2 μM (n = 2). Incubation was performed at 37 °C for 2.5 h (without shaking) under 5% CO₂ and 95% relative humidity. The detection method was LC–MS/MS. The Papp was calculated as Papp = [Va/(area × time)] × (LC–MS area of acceptor sample/LC–MS area of initial donor), where Va = volume of acceptor well (in milliliters) = 0.25, area = surface area of the membrane (in square centimeters), and time = time of incubation (in seconds) = 9000.

To obtain the solubility of compounds (Solubility), the test system was the JP 2nd Fluid for the disintegration test (pH 6.8), and the concentration of compounds was 200 μM containing 1% DMSO (n = 2). Incubation was 37 °C with shaking for 1 h. A spectrophotometer (SpectraMax M5, Molecular Devices, LLC) was used to detect the absorbance maxima, and the linearity range was set to five points from 2.5 to 200 μM (n = 1).

In Vivo Experimental PK Protocol

All experimental procedures used in this study were approved by the Animal Care and Use Committee of Teijin Institute for Bio-Medical Research. All efforts were made to minimize suffering. All PK data were obtained using the following standardized protocol: Briefly, the species of animals was CD-1 mouse, the sex of animals was male, and the age was 6 weeks at the start of dosing. In each experiment, three replicate animals were used. Cassette dosing was used with five compounds per animal. Each animal was fasted from 13 h before dosing to 4 h after dosing. Compound doses for i.v. and p.o. were 1 and 2 μmol/kg, respectively, and the dosing vehicle was 1/15 M NaH₂PO₄, 0.5% Tween 80, and 10% DMSO. The blood sampling time points were 5, 15, and 30 min and 1, 2, 4, 8, and 24 h for i.v. and 15 and 30 min and 1, 2, 4, 8, and 24 h for p.o. with a volume sample of 40 μL. The matrix was the plasma obtained by the centrifugation of the blood with an anticoagulant (heparin sodium). The detection method for plasma concentration was LC–MS/MS.

Data Set Preparation

In this study, we used mouse i.v. PK data obtained for 970 compounds as described above for 17 projects in TEIJIN Pharma’s in-house database. In addition, we used p.o. PK data obtained from the same 17 projects, which contained 871 compounds. Each compound’s project number is shown in Table 1. The number of unique compounds in a single project ranged from 1 to 212 for i.v. PK data and from 1 to 200 for p.o. PK data. The unit of measured concentration is nmol/L, and this is used as the original scale. The lowest limit of quantification (LLOQ) was 1 nmol/L, and values less than 1 nmol/L were considered as 0. When constructing models, all end points other than bioavailability (BA) were firstly log10 transformed.

Table 1. Number of Compounds for Each Project.

project ID	number of compounds for i.v.	(%)	number of compounds for p.o.	(%)
1	28	(2.9)	28	(3.2)
2	48	(4.9)	48	(5.5)
3	188	(19.4)	182	(20.9)
4	1	(0.1)	1	(0.1)
5	44	(4.5)	40	(4.6)
6	116	(12.0)	108	(12.4)
7	212	(21.9)	200	(23.0)
8	15	(1.5)	15	(1.7)
9	18	(1.9)	17	(2.0)
10	71	(7.3)	71	(8.2)
11	115	(11.9)	114	(13.1)
12	69	(7.1)	11	(1.3)
13	1	(0.1)	1	(0.1)
14	18	(1.9)	11	(1.3)
15	1	(0.1)	1	(0.1)
16	1	(0.1)	1	(0.1)
17	24	(2.5)	22	(2.5)
total	970	(100.0)	871	(100.0)

Standardization of Compound Representations

All simplified molecular-input line-entry system (SMILES) strings were obtained from an internal Teijin database. These were inputted by medicinal chemists considering their chirality. Before starting the process of model building, all structures were canonicalized using the RDKit (version 2020.09.01) components “RDKit Canon SMILES” and “Speedy SMILES De-salt” in KNIME (version 4.3.4).

Experimental Error

We next quantified the experimental error of plasma concentration measurements to provide a baseline model of the upper limit of prediction accuracy. To this end, for each experiment (n = 3 animals), the standard deviation was computed, and we recorded two times the median value of the standard deviation distribution across experiments. Overall, the average model (AVM) and experimental errors were regarded as points of lowest and highest practically achievable performances of our models, respectively. This was achieved by comparing both experimental errors and average predictions’ results to other models’ root mean square error (RMSE).¹⁸

Investigation of the In-House Data Set’s Distribution in Chemical Space Compared to Approved Drugs.

We investigated the chemical space present in the data set through using Uniform Manifold Approximation and Projection (UMAP).¹⁹ For the input, we calculated the similarity matrix with MACCS Keys chemical descriptors.²⁰ The distribution of Tanimoto similarity of 5-nearest neighborhood (5-NN) was calculated by MACCS Keys using the RDKit (version 2020.09.01) Chem functions.²¹ This was then compared with 2503 Food and Drug Administration (FDA)-approved drugs from DrugBank (version 5.1.8) using canonical SMILES obtained using the same process for in-house compounds as the input structure.²² In addition, we calculated inter-5-NN similarity between in-house compounds and FDA-approved drugs and assessed whether the distributions were significantly different using the Kolmogorov–Smirnov test. To do so, we utilized the scipy (version 1.7.0) library stats.ks_2samp function with the alternative option set to “two-sided”. For each compound, the 5-NN similarity was calculated using the RDkit (version 2020.09.01) BalkTanimotoSimilarity function and averaging the similarity of the top five most similar compounds.²¹

Machine Learning Model Generation

Method Overview

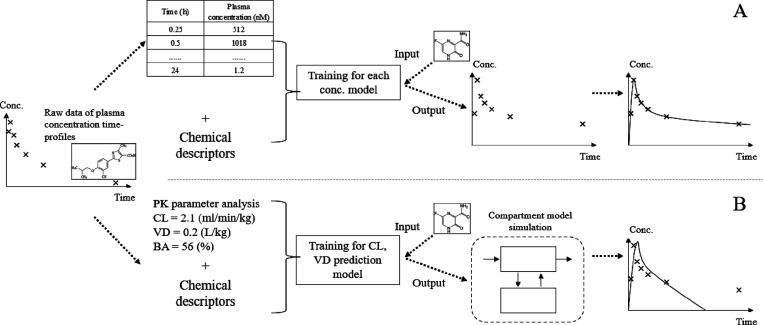
We developed a novel method to predict plasma concentration–time profiles in mice after both intravenous and oral administration of small molecules by optimizing machine learning models for plasma concentration at different time points and subsequently integrating the predictions as outlined in Figure 1.

Figure 1.

Overview of the workflow of this research. (A) We developed models to predict in-vivo concentration data using the compound structure (MACCS Keys) and both in silico and in vitro PK parameters. Separate models were built for each time point after compound administration. The predictions were subsequently combined to form a predicted time–concentration curve (see the section “Explanatory Variables” in “Materials and Method”). (B) The conventional compartmental model method to predict compound plasma concentration–time profiles (see the section “Baseline Compartmental Model” in “Materials and Method”). In the conventional method, CL and VD needed to be predicted, which was achieved using machine learning models built in this study, and then used as inputs of the compartmental model. Finally, plasma concentration–time profiles were obtained.

Explanatory Variables

Machine learning models were developed using combinations of two input descriptors: chemical structure (ECFP4 or MACCS Keys fingerprints) and both in vitro and in silico PK parameters. These are discussed separately below in sections “Chemical Structure Descriptors” and “PK Parameters”, respectively.

Chemical Structure Descriptors

For machine learning modeling, chemical descriptors and the chemical structure as graph were used. Regarding chemical descriptors, MACCS Keys²⁰ and ECFP6 (1024 bit, radius: 3)²³ were used, and for chemical graphs, canonical SMILES was used. These were calculated using the corresponding RDKit (version 2020.09.01) Chem functions,²¹ MACCS Keys, and AllChem.

PK Parameters

In this study, in addition to using chemical structural information in the form of descriptors, we also utilized the following in vitro PK parameters according to prior knowledge of ADME:^24,25in silico human Vd calculated by ADMET Predictor (hVd),²⁶in vitro mCLint, and mfu. These parameters were selected because of their known relation to the distribution and elimination process of compounds.

For models predicting compound plasma concentration–time profiles after p.o. administration, in addition to hVd, mCLint, and mfu, we also further utilized in vitro PK parameters known to be related to the absorption process, namely, in vitro Caco-2 permeability and solubility.

Machine Learning Models

In this study, we used a two-stage workflow to first generate and then evaluate the performance of machine learning models (see Figure 1A). First, we built separate machine learning models for predicting plasma concentrations after i.v. administration for a variety of time points postdosing. To this end, we utilized the following models: random forest (RF)²⁷ using chemical descriptors as input, the message passing neural network (MPNN)²⁸ using graphs as input, the 2-compartment model using predicted CL and steady-state Vd (VDss) by RF, and AVM.

Regarding RF, the Python (ver. 3.7.10) scikit-learn (version 0.24.2) library RandomForest Regressor function was used, and the parameters were set as defaults.

Regarding MPNN, the Python (ver. 3.7.10) Chemprop (version 1.3.1) library chemprop function was used, and the parameters were set as defaults.^28,29

For the AVM model, the concentration at every time point was simply predicted as the average concentration across all compounds. Specifically, in each case for 5-fold cross-validation (5-fold CV) and leave-one-project-out validation (LOPO-V), the values of the compounds other than those removed for the validation were used to calculate the average. This provided a baseline model of the lower limit of prediction accuracy.

Baseline Compartmental Model

For the baseline compartment model (CPM), first, we constructed RF models for CL and VDss using MACCS Keys and in vitro PK parameters using the same parameters used to construct the i.v. PK model, and then we used them as inputs for CPM (Figure 1B). An overview of the hypothesis and workflow used is shown in detail in Figure S1. Also, the accuracy of the RF model for CL and VDss used as input for CPM is shown in Table S1. These models utilize both the predicted PK parameters and physiological information required to use a two-compartment model. The estimated accuracies were deemed acceptable: RMSEs were within 0.3, and percentages of within 2-fold error were 70%. Hence, we concluded that this baseline model can be considered to be a reliable conventional model.

On the basis of RF performing best for i.v. models, we also chose this prediction method for the construction of p.o. models. Briefly, RF was selected because it obtained the highest predictive accuracy for i.v. data. Also, MACCS Keys were used as explanatory variables because they outperformed ECFP6 when used in i.v. RF models. Finally, CPM and AVM were compared with RF. During CPM for p.o. PK data, we predicted the compound’s BA by the RF model and used it as an input for CPM, as described in Figure S1.

Model Validation

The predictive performance of each model type was evaluated using 5-fold CV. The 5-fold CV was performed using the KFold function in scikit-learn (0.24.2) with parameters n_splits = 5 and shuffle = true. Furthermore, the best model (RF) was then also evaluated using LOPO-V. Within each fold of LOPO-V, data for one project were withheld (test set), which were subsequently predicted using models constructed using the data from all other projects (training set). For the i.v. PK model, this process was repeated across nine projects that had over 25 compounds, and the RMSEs and percentages within 2-, 3-, and 5-fold error were recorded. For the p.o. PK model, we also performed 5-fold CV, and the best model was evaluated using LOPO-V across eight projects having over 25 compounds.

Descriptor Importance Evaluation

We estimated the importance of each descriptor in RF models using the Python (version 3.7.10) scikit-learn (version 0.24.2) library feature_importances_ function to obtain Gini index values for each descriptor.

Metrics to Compare Each In Silico Model

To evaluate the predictive accuracy of models in this study, we calculated the RMSE, percentage within k-fold error (k = 2, 3, and 5), and R² coefficient of determination as the R² value. These are shown in eqs 1 and 2, where a_i, b_i, n, and i serve as the observed value, predicted value, number of samples, and an indicator function, respectively. Also, it is shown in eq 3, where SS_res means the sum of squares of residuals and SS_tot means the total sum of squares. Here, a_i and b_i are in the original scale. This calculation was performed in Microsoft Excel (version Office 365). For all parameters, RMSE values were computed using the log10 scale of the model predictions, except in the case of BA where the original scale was used. Finally, any values predicted to be lower than zero were considered as zero for the purpose of quantifying model accuracy. Throughout the manuscript, we will predominately use the RMSE metric as it can most easily be compared to the experimental error that provides an upper bound on model predictivity.

1

2

3

Results and Discussion

Analysis of the In-House Chemical Space Compared to Approved Drugs

Before developing machine learning models, we first investigated the distribution of the in-house compounds’ chemical space compared to FDA-approved drugs using MACCS Keys descriptors and the Tanimoto similarity. For visual interpretation, we investigated the UMAP using i.v. data sets that covered all of the compounds used in this study. Compared to the FDA-approved drugs, the compounds in projects 3, 6, 11, 12, and a part of 7 were located in distinctly different regions of chemical space (Figure S2A). Regarding intercompound similarity, the average 5NN similarity values between in-house compounds and FDA-approved drugs [0.696 ± 0.085 (i.v.), 0.698 ± 0.048 (p.o.)] were significantly smaller than the intrasimilarity of in-house compounds [0.879 ± 0.084 (i.v.), 0.874 ± 0.081 (p.o.)] (Figure S2B–E). The p value of the Kolmogorov–Smirnov test was lower than the limit of calculation for i.v. PK data, and that for p.o. PK data was 3.12e^–317. This suggested that both the i.v. and p.o. in-house compounds used in the present study have narrower and significantly different chemical space compared to FDA-approved drugs, although the number of compounds was totally different (2503 of FDA-approved drugs, 970 in-house compounds for p.o., and 871 in-house compounds for i.v.). Moreover, when using ECFP6 extended-connectivity fingerprints, similar results were identified as shown in Figure S3. This result was somewhat expected because in-house compounds are novel and were developed in distinct chemical series in each project.

Chemical Descriptor Selection in RF Using i.v. PK Data

To identify the optimal chemical descriptor to be used prior to the construction of the machine learning models, we first investigated the combination of either MACCS Keys or ECFP6 descriptors alongside in vitro PK parameters, either in isolation or when used together during modeling. To this end, we utilized an RF model built using i.v. PK data. Figure S4 shows the resulting 5-fold CV predictive accuracies of the combination of chemical descriptors and PK parameters. The RMSE of the model using only PK parameters was higher (from 0.614 at 2 h to 0.242 at 24 h). However, this performance was outperformed when PK parameters were combined with either MACCS Keys (from 0.569 at 2 h to 0.230 at 24 h) or ECFP6 chemical descriptors (from 0.557 at 2 h to 0.218 at 24 h). This indicates that the combination of chemical descriptors and PK parameters improves the predictive accuracy.

We identified MACCS Keys as the most suitable chemical descriptors (as opposed to ECFP6) for use in modeling in vivo concentration–time curves by initially modeling i.v. PK data using RF. The final decision was not based on predictive accuracy (RMSE) as the values in RF models built using MACCS Keys (average RMSE across all time points: 0.440) were similar to those of ECFP6 (average RMSE across all time points: 0.442, Figure S4). Instead, because in the present study we were oriented toward the practical usage of the models in the early drug discovery stage, the interpretability of the descriptors was paramount. Because originally MACCS Keys were optimized for substructure search,²⁰ the increased interpretability of MACCS Keys (166 descriptors relating to predefined substructural keys)²⁰ compared to ECFP6 (1024 hashed bits related to bonding connectivity and atom types,²³ the precise meaning of which changes depending on the training set compounds) will more easily allow predictions to be scrutinized when applied to various kinds of chemical series and help alleviate the need for PK experiments and shorten the DMTA cycle with large compound libraries where it is easier to filter by simpler chemical structures such as those from MACCS Keys.³⁰ Moreover, because of the drastically lower dimensionality of MACCS Keys descriptors, we could expect to more easily avoid overfitting during model building despite potential oversimplicity resulting from their low dimensionality.²⁰ Consequently, we decided to use MACCS Keys to build all subsequent machine learning models.

Intravenous PK Model Evaluation Using 5-Fold Cross-Validation

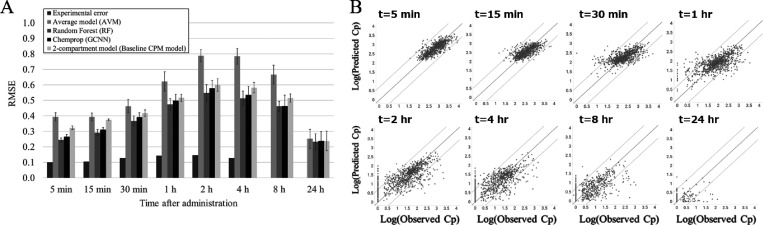
We next compared the predictive accuracy of several predictive algorithms for i.v. PK data by 5-fold CV when using MACCS Keys and in vitro PK parameters (hVd, mCLint, mfu) as descriptors. The RMSEs of RF, MPNN, and CPM models were lower than AVM and higher than the experimental error. When considering the error bars of 5-fold CV trials, that was not the case with 15 min for CPM and 24 h for all models. However, at all time points, the RMSEs of RF models were the lowest. For example, the RMSEs for AVM, RF, MPNN, and CPM were 0.622, 0.474, 0.498, and 0.516 at 1 h and 0.666, 0.462, 0.463, and 0.515 at 8 h (Figure 2A). Moreover, the percentages within n-fold error in RF were mostly the highest; those within 2-, 3-, and 5-fold error were 42.4, 60.6, and 76.9 for AVM; 63.0, 76.6, and 87.0 for RF; 55.9, 72.7, and 85.1 for MPNN; and 44.3, 69.7, and 86.9 for CPM at 1 h and 15.9, 32.1, and 83.1 for AVM; 62.6, 77.8, and 88.2 for RF; 59.1, 77.5, and 90.1 for MPNN; and 66.6, 77.4, 86.8 for CPM at 8 h (Table S2). The accuracy of the RF model for CL and VDss used as input for CPM is shown in Table S1. Figure 2B shows the observed plasma concentration and that predicted by the RF model for i.v. PK data. It can be seen that at the short time points like from 5 min to 1 h, the plots fitted to the line of unity well. In addition, at the longer time points such as from 2 to 24 h, most of the points were within the line of 5-fold errors. More precisely, although RMSEs at 4, 8, and 24 h were lower than that at 2 h, it might be derived from the numbers of LLOQ samples; i.e., within our methodology, these were still used during model training as 0 concentration (numbers of LLOQ samples: 0 at 5 min, 0 at 15 min, 1 at 30 min, 17 at 1 h, 129 at 2 h, 268 at 4 h, 530 at 8 h, and 894 at 24 h). Therefore, if the model simply predicted 0, lower RMSE values could result. From inspection of the plots, we concluded that this RF could predict i.v. PK time profile well except for 24 h. On the other hand, the relatively poor predictive accuracy for the CPM model observed is in agreement with the result of previously published results that showed that the accuracy of CPM using in vitro in vivo extrapolation (IVIVE) was inferior to machine learning methods when predicting PK data.³¹ On the basis of these results, as well as the practical advantage over MPNNs with a large number of hyperparameters,³² we decided to use the RF model in all subsequent analyses.

Figure 2.

Predictive accuracy (RMSE) of predictive i.v. models in the present study (A) and the observed plasma concentration versus that predicted by RF for both i.v. (B) data when using MACCS Keys and in vitro PK parameter descriptors during 5-fold CV. (A) RMSEs of all models and experimental error in each time points were compared. (B) Observed values (x axis) and RF model predicted values (y axis). The diagonal lines represent perfect prediction (y = x) and 5-times under and over prediction.

Per Os PK Model Evaluation Using 5-Fold Cross-Validation

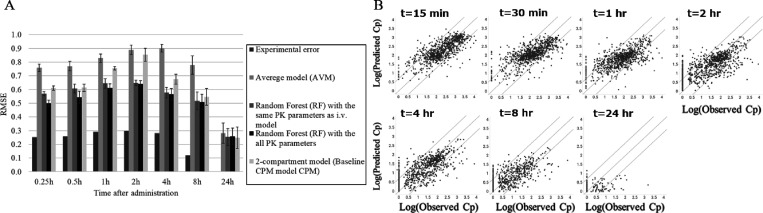
We next compared RF and CPM predictive algorithms for p.o. PK data by 5-fold CV when using MACCS Keys and in vitro PK parameters as descriptors (Figure 3A). The details of the resulting values are documented in Table S3, and the accuracy of the RF model for CL, VDss, and BA used as input for CPM is shown in Table S1. The RMSE of AVM, RF with i.v. PK parameters (hVd, mCLint, mfu), RF with all PK parameters (hVd, mCLint, mfu, Caco-2, Solubility), and CPM were 0.828, 0.644, 0.612, and 0.755 at 1 h and 0.779, 0.517, 0.509, and 0.538 at 8 h. The percentages of within 2-, 3-, and 5-fold error were 31.3, 46.3, and 63.9 for AVM; 43.9, 61.9, and 76.8 for RF with i.v. PK parameters; 45.2, 63.0, and 77.5 for RF with all PK parameters; and 40.8, 56.5, and 71.7 for CPM at 1 h and 16.0, 21.8, and 79.0 for AVM; 54.9, 71.1, and 83.8 for RF with i.v. PK parameters; 54.3, 71.1, and 85.1 for RF with all PK parameters; and 63.0, 73.2, and 84.5 for CPM at 8 h. As seen for the i.v. models, the RMSEs of RF and CPM models were lower than AVM and higher than the experimental error, and the percentages within n-fold errors were higher than AVM. However, when considering the error bars of 5-fold CV trials, that was not the case with 2 h for CPM and 24 h for all models. The difference of RMSE between AVM and CPM was not large, being less than 0.1 at 1, 2, and 4 h. The best model at all time points was RF when using MACCS Keys and all PK parameters. Figure 3B shows the observed plasma concentration and that predicted by the RF model for p.o. PK data (RF with all PK parameters). It can be seen that at the short time points from 15 min to 1 h, the plots fitted to the line of unity well. In addition, at the longer time points such as from 2 to 24 h, most of the points were within the line of 5-fold errors. More precisely, although RMSEs at 4, 8, and 24 h were lower than that at 2 h, it might be derived from the numbers of LLOQ samples; i.e., within our methodology, these were still used during model training as 0 concentration (numbers of LLOQ samples: 11 at 15 min, 26 at 30 min, 62 at 1 h, 133 at 2 h, 245 at 4 h, 447 at 8 h, and 799 at 24 h). Therefore, if the model simply predicted 0, lower RMSE values could result. From the inspection of the plots, we concluded that this RF could predict p.o. PK time profile well except for 24 h. Similar to the result for i.v. models, a relatively low predictive accuracy of CPM models was observed, and this is in agreement with previously published results showing that the accuracy of CPM using in vitro in vivo extrapolation (IVIVE) was inferior to machine learning methods when predicting PK data.³¹ Finally, the RMSE difference between the best p.o. model that used the additional PK variables Caco-2 and Solubility compared to the RF whose explanatory variables were the same as the i.v. model was larger at short time points (15 min to 1 h) compared to long time points (4 to 8 h). We concluded that RF with MACCS Keys using all available PK parameters was the best model.

Figure 3.

Predictive accuracy (RMSE) of predictive p.o. models in the present study (A) and the observed plasma concentration versus that predicted by RF for both p.o. (B) data when using MACCS Keys and in vitro PK parameter descriptors during 5-fold CV. (A) RMSEs of all models and experimental error in each time points were compared. (B) Observed values (x axis) and RF model predicted values (y axis). The diagonal lines represent perfect prediction (y = x) and 5-times under and over prediction.

Comparison of RF Models for Both i.v. and p.o. PK Data at Different Time Points Using 5-Fold Cross-Validation

We next compared the result of 5-fold CV between i.v. and p.o. models to investigate the relative performance of models. Regarding the RF model for i.v. PK data, at short time points (≤30 min), the RMSEs ranged from 0.245 to 0.367; however, at long time points (from 1 to 8 h), they ranged from 0.462 to 0.549 (Figure 2 and Table S1). This might reflect the difficulty of predicting the rate of elimination, which is the result of many processes including distribution, metabolism, and excretion, which has a larger impact to the plasma concentration–time profile at long time points after compound administration.³³ Regarding the p.o. PK data, RMSEs of AVM and the experimental errors were much higher than those of i.v. PK (Tables S2 and S3); i.e., at early time points (≤30 min), the experimental errors ranged from 0.251 to 0.258 for p.o. and 0.100 to 0.127 for i.v., and at the later time points (from 1 to 8 h), they ranged from 0.119 to 0.300 for p.o. and 0.000 to 0.146 for i.v. This suggests that compared to the i.v. PK data, p.o PK data were intrinsically harder to predict. Although the increased difficulty to accurately predict longer time points was the same as the i.v. case, the difference of RMSEs between the early and late time points was not so large. For example, for p.o. PK data, the RMSEs of RF from 0.25 to 8 h were all in the range of 0.500 to 0.642 (Figure 3 and Table S3). Overall, because of the higher experimental errors observed compared to i.v. administration (100% bioavailable), initial absorption processes and other factors such as first-pass liver metabolism make the task of predicting p.o. concentration–time profiles intrinsically more difficult.³³

Investigating the Applicability Domain Using Leave-One-Project-Out Validation

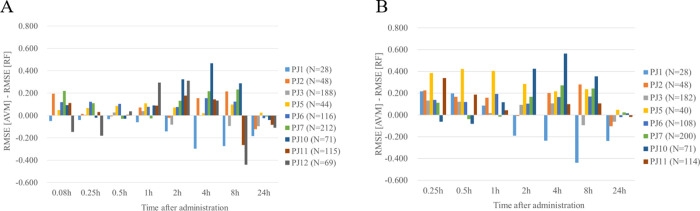
We next investigated the applicability domain of RF models to chemical series not seen during model optimization that resembles the application of the model also to new chemical series in the future. To this end, we predicted plasma concentration–time profiles during LOPO-V using the best p.o. and i.v. RF models. Figure 4A and Table S4A show the result of LOPO-V for i.v. PK data using RF. We compared the RMSE difference (RMSE [AVM] – RMSE [RF]), so a larger positive difference indicates an increasingly predictive RF model compared to its corresponding AVM during LOPO-V and vice versa. For time points ranging from 5 min to 8 h, the RMSE differences between AVM and RF were mostly positive (44 out of 63, 69.8%) across the nine projects analyzed. Some exceptions were observed for projects 2, 3, 5, 6, 7, and 10, but these were not less than −0.100. Moreover, for those of project 11 at time points other than 8 h, the RMSE difference was also not less than −0.100. However, the differences between AVM and RF for projects 1 and 12 were less than −0.100 at several time points, indicating poor predictivity of the RF models; i.e., the values for project 1 were −0.142 at 2 h, −0.297 at 4 h, and −0.273 at 8 h, and those for project 12 were −0.147 at 5 min, −0.180 at 15 min, and −0.440 at 8 h. Overall, as the majority of RMSE differences were positive, we conclude that this i.v. PK model will be able to be applied for many projects. However, in reality, we acknowledge that this model will not be able to predict all of the compound plasma concentration–time profiles for any projects as the applicability domain is still limited by the training data.

Figure 4.

RMSE difference between AVM and RF models (AVM minus RF) for both i.v. (A) and p.o. (B) when using MACCS Keys and in vitro PK parameter descriptors during LOPO-V. The difference of RMSE between AVM and RF as an “RMSE of AVM minus RMSE of RF” for (A) i.v. PK and (B) p.o. PK. In panel A, only projects 1, 2, 3, 5, 6, 7, 10, 11, and 12 that had more than 25 compounds in the RF model under the LOPO-V were evaluated. In panel B, this corresponded to only evaluating projects 1, 2, 3, 5, 6, 7, 10, and 11. Most projects in many time points had positive values.

We next analyzed p.o. RF models and compared them with i.v. RF models. Figure 4B and Table S4B show the result of LOPO-V for p.o. PK data using RF. The absolute value of RMSE of RF p.o. models was larger than that of i.v. models; i.e., the RMSEs in RF models’ LOPO-V through all projects were in the range of 0.335–0.752 (i.v. from 15 min to 8 h) and 0.624–0.837 (p.o. from 15 min to 8 h). On the other hand, for time points ranging from 15 min to 8 h, the RMSE differences between AVM and RF were mostly positive (39 out of 48, 81.3%), and those of projects 2, 3, 5, 6, 7, and 10 were not less than −0.100. However, the differences between AVM and RF for project 1 were less than −0.100 at several time points; i.e., those values for project 1 were −0.189 at 2 h, −0.234 at 4 h, and −0.438 at 8 h. Hence, it can also be concluded that this PK model for p.o. will be able to be applied for many projects.

Regarding average predictivity through all projects for i.v., the RMSEs were 0.335 (at 5 min), 0.403 (at 15 min), 0.467 (at 30 min), 0.575 (at 1 h), 0.752 (at 2 h), 0.698 (at 4 h), 0.685 (at 8 h), and 0.269 (at 24 h). Especially for the earliest time point as t_5min, the RMSE was observed as 0.335 ± 0.059, and this was lower than the other time points except for 24 h. Also, regarding the average predictivity through all projects for p.o., the RMSEs were 0.624 (at 15 min), 0.685 (at 30 min),0.765 (at 1 h), 0.837 (at 2 h), 0.760 (at 4 h), 0.690 (at 8 h), and 0.282 (at 24 h). Especially for around t_max such as 15 and 30 min, the RMSEs were observed as 0.624 ± 0.097 (at 15 min) and 0.685 ± 0.121 (at 30 min), and those were lower than the other time points except for 24 h. Hence, we can conclude that from the viewpoint of fit-for-purpose, this model could be more useful for the prediction of plasma concentration at the earlier time points.

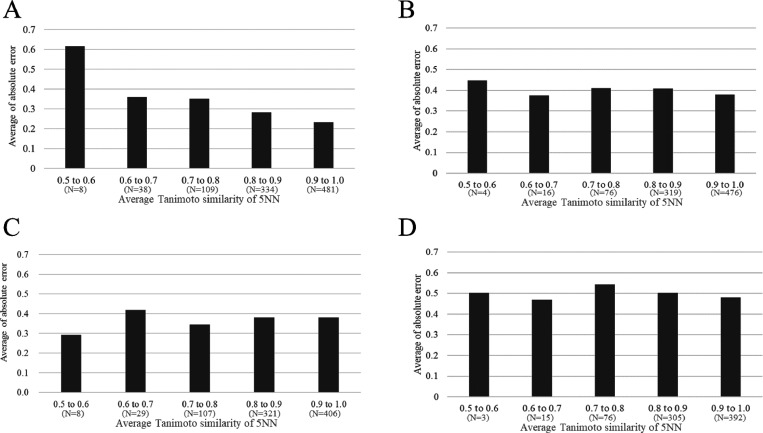
Evaluation of Model Applicability Domain Using Tanimoto Similarity

The results of LOPO-V analysis suggested that the PK of a few projects could not be correctly predicted (Figure 4), and then we can see the difference of the distribution in the chemical space of the in-house data set from FDA-approved drugs using UMAP (Figure S2A). Therefore, we next analyzed whether this was related to the chemical similarity of each project to the model training set. To this end, we investigated the relationship between the test set 5NN Tanimoto similarity to the model training set and the absolute prediction errors. Figure 5 shows the relationship between absolute errors for predicted values by RF model in 5-fold CV and LOPO-V and the 5NN Tanimoto similarity to the training set using MACCS Keys. It can be seen that for i.v. PK data prediction in 5-fold CV, the 5NN Tanimoto similarity was negatively correlated with the absolute error (i.e., test set compounds more similar to the training set were predicted better; Figure 5A). More specifically, for each 5NN Tanimoto similarity range analyzed, the average absolute error across the similarity bins analyzed decreased as follows: 0.615 (0.5 to 0.6, n = 8), 0.359 (0.6 to 0.7, n = 38), 0.351 (0.7 to 0.8, n = 109), 0.282 (0.8 to 0.9, n = 334), and 0.232 (0.9 to 1.0, n = 481). This is consistent with the concept of a chemical similarity based applicability domain.³⁴ This trend was also observed in LOPO-V: 0.448 (0.5 to 0.6, n = 4), 0.375 (0.6 to 0.7, n = 16), 0.409 (0.7 to 0.8, n = 76), 0.408 (0.8 to 0.9, n = 319), and 0.380 (0.9 to 1.0, n = 476) (Figure 5B). This analysis suggested that we could judge whether a compound, whose i.v. plasma concentration–time profile we want to predict, can be predicted with confidence by calculating the 5NN Tanimoto similarity with the model’s training data sets.

Figure 5.

The relationship between the average 5NN Tanimoto similarity relative to the model training set and average of absolute error predicted by RF during i.v. for both 5-fold CV (A) and LOPO-V (B) and then p.o. for both 5-fold CV (C) and LOPO-V (D). This figure shows that for the i.v. PK model, we can judge the predictability beforehand. On the other hand, it is difficult to do it for the p.o. PK model. N in the parenthesis means the number of sample in each bin.

We next evaluated the 5NN Tanimoto similarity applicability domain for the RF model trained on p.o. PK data. However, in contrast to the i.v. model, we could not find any correlation between the 5-NN Tanimoto similarity and absolute errors in 5-fold CV and LOPO-V (Figure 5C,D). We postulate three potential reasons for this. First, the predictability of the RF model for p.o. PK data was not as good as that for i.v. PK data (Figures 2 and 3). Second, the contribution of MACCS Keys in the RF model for p.o. PK data was much smaller than that for i.v. PK data across all the time points analyzed (Figure 6). This second point is pertinent because if a model does not utilize chemical structure information to make predictions, then its applicability domain will naturally not be influenced by chemical similarity. The third one is that, in LOPO-V, some compounds whose project included a small number of compounds were removed. This might lead to a decrease in the applicability domain of the LOPO-V model compared to the 5-CV model.

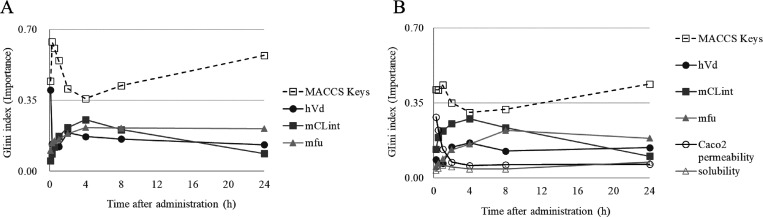
Figure 6.

Feature importance by GINI index of MACCS Keys and in vitro PK parameters across different time points. (A) This plot shows the Gini index shift of each time point for the i.v. RF model. (B) This plot shows the Gini index shift of each time point for the p.o. RF model.

We conclude that for the i.v. model, the predictability of novel compounds is related to their chemical similarity to the model training set. However, for the p.o. model, this was not the case, and therefore, future work is required to elucidate and enlarge its applicability domain before it can be used with confidence to predict the PK of novel compounds.

Analysis of Feature Importance by Administration Route and Time Point

We next utilized the Gini index to investigate the importance of each descriptor for both i.v. and p.o. PK model predictions and as a function of time, the results of which are shown in Figure 6A. In the RF model for i.v. administration, the sum of the Gini index across MACCS Key descriptors was higher than each individual in vitro PK parameter; the average of the Gini index of MACCS Keys through all time points was 0.500. The highest Gini indices of MACCS Keys observed were 0.035 (sum of all MACCS Keys Gini = 0.445) at 5 min, 0.034 (sum of all MACCS Keys Gini = 0.546) at 1 h, and 0.014 (sum of all MACCS Keys Gini = 0.358) at 4 h. The substructure with the highest Gini was different from each other. Therefore, overall, no single substructure influenced our models to a great extent. The highest Gini indices of the in vitro PK parameters at each time point were 0.401 (hVd at 5 min), 0.140 (mfu at 15 min), 0.150 (mfu at 30 min), 0.172 (mCLint at 1 h), 0.216 (mCLint at 2 h), 0.255 (mCLint at 4 h), 0.213 (mfu at 8 h), and 0.210 (mfu at 24 h). Focusing on the PK parameters, at 5 min, the importance of hVd was 3.9 and 7.8 times higher than mCLint and mfu, respectively, suggesting that the volume of distribution is a critical factor for predicting i.v. PK data.²³ However, the importance of hVd decreased from earlier to later time points, whereas that of mCLint and mfu increased. For example, at 5 min, values were 0.401 (hVd), 0.051 (mCLint), and 0.103 (mfu), and at 8 h, these were 0.159 (hVd), 0.206 (mCLint), and 0.213 (mfu). This might reflect the increased importance of processes including distribution, metabolism, and excretion at later time points.

In the RF model for p.o. PK data, we also investigated the feature importance of each descriptor for model prediction, shown in Figure 6B. Again, we observed that the sum of the Gini indices across MACCS Keys descriptors was higher than each individual PK parameter; the average of the Gini index of MACCS Keys through all time points was 0.381. The highest Gini indices of MACCS Keys observed were 0.042 (sum of all MACCS Keys GINI = 0.412) at 15 min, 0.030 (sum of all MACCS Keys GINI = 0.433) at 1 h, and 0.032 (sum of all MACCS Keys GINI = 0.305) at 4 h. The substructure with the highest Gini was also different from each other. Therefore, overall, no single substructure influenced our models to a great extent. The highest Gini indices of the in vitro PK parameters at each time point were 0.284 (Caco2 at 15 min), 0.222 (Caco2 at 30 min), 0.219 (mCLint at 1 h), 0.253 (mCLint at 2 h), 0.276 (mCLint at 4 h), 0.233 (mCLint at 8 h), and 0.185 (mfu at 24 h). However, the contribution of chemical structure (described by MACCS Keys) for the prediction of compound plasma concentration–time profiles was much lower than in case of the i.v. model; the average of the sum of MACCS Keys Gini indices across all time points was 0.500 for i.v. compared to 0.381 for p.o. Focusing on the PK parameters, at 15 min, the importance of Caco2 permeability was 2.1 times higher than the next most important variable (mCLint). However, the importance of Caco2 permeability decreased from shorter to longer time points from 0.284 (at 15 min) to 0.063 (at 24 h). This suggests that Caco2 permeability could be helpful to predict the absorption process at earlier time points, and this is consistent with the general understanding of ADME in vitro screening.^35,36 On the other hand, although solubility was also considered to be an important factor, it was observed to have the lowest importance of all PK parameters investigated across all time points: 0.035 (15 min), 0.043 (30 min), 0.058 (1 h), 0.050 (2 h), 0.041 (4 h), 0.040 (8 h), and 0.073 (24 h).³⁷ A possible explanation for this was the fact that the vehicle for dosing solution in the present study was 1/15 M NaH₂PO₄, 0.5% Tween80, and 10% DMSO, and therefore, the true compound solubility was not reflected in the PK. In contrast to shorter-term time points, at 2 to 8 h, the importance of hVd, mCLint, and mfu was at least 1.8 times higher than Caco2 permeability (the next most important PK parameter). This suggests the increased importance of processes including distribution, metabolism, and excretion and the concurrent lowering of Caco2 importance at later time points. Given the good accuracy of the machine learning model, this suggests that these parameters contribute differently toward the efficient model abstraction of key absorption and distribution processes at different time points after administration, and this is generally consistent with prior knowledge in ADME research.³³

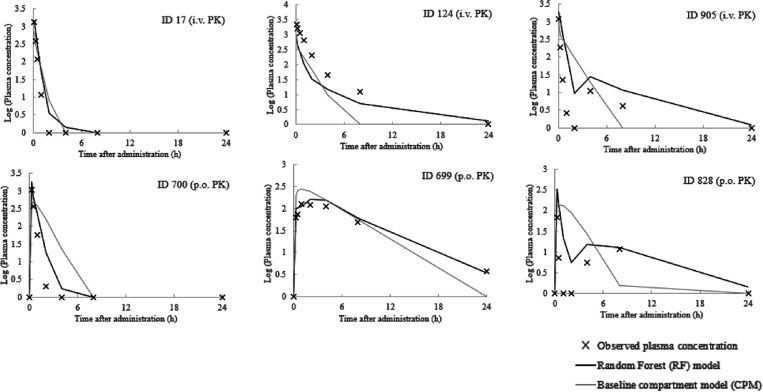
Case Study of Compound Plasma Concentration–Time Profiles Predicted by the RF Model

Finally, we aimed to investigate characteristics of integrated compound plasma concentration–time profiles predicted by the RF models in 5-fold CV to simulate their intended real-world project use. To this end, we sampled three representative concentration–time profiles that exhibited a short half-life, long half-life, or twin peaks behavior from the visual inspection of the plots. These corresponded to compound IDs 17, 124, and 905 for i.v. PK and 700, 699, and 828 for p.o. PK (Figure 7), respectively.

Figure 7.

Representative case studies of RF predicted compound plasma concentration–time profiles. The observed and predicted compound plasma concentration–time profiles. The number above each graph indicates the compound ID from which the data were derived. The profiles of compound IDs 17, 124, and 905 are from i.v. The lines were predicted by the best RF models using the descriptors hVd, mCLint, and mfu for i.v. and hVd, mCLint, mfu, Caco-2, and Solubility for p.o. PK data and the profiles of compound IDs 700, 699, and 828 are from p.o. data.

Before investigating the cases, to scrutinize the data set in 5-fold CV, we checked the project of each compound. This composition is shown in Table S5. Moreover, we calculated the 5NN between training and test in each fold, and the average value (and standard error) was observed for i.v. and p.o. as 0.854 ± 0.007 and 0.852 ± 0.005, respectively. It can be seen that the similar distribution of chemical space was sampled in the training and test data sets. Next, to grasp the overall predictivity of compound plasma concentration–time profiles, we calculated the R² value between the observed plasma concentration and predicted ones by the RF model in 5-fold CV plasma concentration through all of the times. The R² values for i.v. and p.o. were 0.725 and 0.752, respectively. When omitting LLOQ from the data, those values for i.v. and p.o. were 0.550 and 0.540, respectively. These values indicate that the overall PK time profiles predicted by the RF model can reflect the observed profiles well.

Regarding i.v. PK, the plasma concentration at 5 min was predicted well by both RF and CPM for most compounds (IDs 17, 124, and 905). However, the terminal phase was reproduced more accurately by RF compared to CPM (ID 124) with absolute prediction errors of 0.485 and 0.650 (at 4 h) and 0.398 and 1.103 (at 8 h) for RF and CPM, respectively. This might be a result of the greater predictivity of RF at 4 and 8 h compared to CPM (Figure 2A and Table S2). Also, this implied that the difficulties of predicting clearance in the CPM model (Table S1 and Figure S1) affected compound plasma concentration–time profiles to a considerable extent. Next, it was observed that the RF model could predict the plasma concentration–time profiles of some compounds with twin peaks (ID 905). The twin peak is a rare but well-characterized event that can be caused by enterohepatic circulation^38,39 or variable absorption partially related to P-gp expression.⁴⁰ Historically, the only way to predict or analyze this event was by preparing a special compartment model.^41,42 Furthermore, we scrutinized the number of twin peak in each project. The result is shown in Table S5A. Although the numbers of total twin peaks were less in i.v. than p.o. and most of the twin peaks are the compounds in project 2, one twin peak in project 8 was correctly predicted by the RF model. The ratio of the number of compounds predicted correctly to compounds with twin peaks was 41.7% (15 out of 36). Therefore, the RF model developed in the present study could greatly contribute to the prediction of such events.

Regarding p.o. PK data, the RF model could accurately predict the concentration at the short time points such as at 15 min (IDs 700, 699, and 828). This might be derived from the high feature importance assigned to Caco2 permeability (Figure 6B). On the other hand, CPM could not predict the earlier time points well such as for compound IDs 700 and 699 where absolute errors at 15 min of 0.216 and 0.413 (ID 700) and 0.186 and 0.487 (ID 699) were observed for RF and CPM, respectively. The worse performance of CPM here might be derived from difficulties estimating not only clearance but also bioavailability, which were used as inputs to the model. However, it is acknowledged that the estimation of bioavailability is very hard task because a large number of factors contribute to it such as absorption and both gastrointestinal and hepatic metabolism.⁴³ Finally, as seen for i.v. PK data, the twin peak could only be predicted by the RF model and not the CPM model (compound ID 828) after p.o. administration. We investigated the number of twin peak in each project. The result is shown in Table S5B. We could find the compounds whose twin peaks were correctly predicted by the RF model in most projects (project numbers 1, 2, 3, 5, 6, 7, 8, 10, 11, 12, and 17). The ratio of the number of compounds predicted correctly to compounds with twin peaks was 50.0% (73 out of 146).

We conclude that we observed good predictability of time–concentration of profiles, and moreover, this model could predict rare PK profile features such as twin peaks. This is one of the unique features of the RF models developed in the present study because each time point was predicted independently. This is a conceptual difference from previous studies that used time as one of the explanatory variables when predicting rat time–concentration profiles of compounds.⁹ Surely, we showed here good examples, and we never deny that there are samples that were not predicted correctly. As references, we show 50 examples in both i.v. and p.o. in Figures S5 and S6.

Conclusions

In conclusion, in this work, we derived the RF models for compound plasma concentration–time profiles in mice after i.v. and p.o. administration. We found that a combination of compound descriptors (MACCS Keys) and in vitro PK parameters gave the best predictivity. By means of applicability domain analysis, we identified that for the i.v. model, we could capture the relationship between 5-NN Tanimoto similarity and absolute prediction errors, hence making the user aware for which compounds one might expect high or low predictivity. By investigating the importance of the in vitro PK parameters using the Gini index, we observed that the general prior knowledge in ADME research was reflected well in the respective feature importance of in vitro parameters such as hVd for initial distribution; hVd, mCLint, and mfu for the elimination process; and Caco2 permeability for absorption process. This finding could be considered to support this model’s robustness as it reflects prior ADME understanding. Finally, we observed that when using machine learning models, twin peaks in the PK time profiles could be predicted. As far as we know, this is the first predictive PK model that can predict twin peaks. Although the predictivity of the model developed depended on each project, due to its combination of sufficient accuracy, interpretability, and speed of prediction, we found the model to be fit-for-purpose (for example, compound screening only with chemical structure or auxiliary information after performing in vitro assays) for practical lead optimization.

Glossary

Abbreviations

PK

pharmacokinetic

CL

clearance

VD

distribution

RF

random forest

5-fold CV

5-fold cross-validation

LOPO-V

leave-one-project-out cross-validation

PK/PD

pharmacokinetics/pharmacodynamics

CL_tot

total body clearance

i.v.

intravenous

p.o.

oral

VDss

steady-state Vd

MPNN

message passing neural network

mCLint

mouse intrinsic clearance

mfu

unbound fraction of mouse plasma

Caco-2

Caco-2 permeability A to B

Solubility

solubility of compounds

SMILES

simplified molecular-input line-entry system

NN

nearest neighborhood

hVd

human Vd calculated by ADMET Predictor

AVM

average mode

CPM

baseline compartment model

BA

bioavailability

RMSE

root mean square error

5NN

5-nearest-neighbor

h

hours

min

minutes

LLOQ

lowest limit of quantification

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author other than the in-house data set. All software used in this study was freely available.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.molpharmaceut.3c00071.

• Prediction of CL and VDss for the input of CPM by RF (Table S1); predictive accuracies of AVM, RF, MPNN, and CPM when predicting i.v. data; the RF model was the best model across all time points (Table S2); predictive accuracies of AVM, RF, and CPM when predicting p.o. data; RF models were the best model using all PK parameters and the second model using three PK parameters across all time points (Table S3); RF and AVM models in leave-one-project-out validation (LOPO-V) for i.v. (A) and p.o. (B) models of RF and AVM (Table S4); number of compounds in each project in 5-CV and compounds with twin peaks for i.v. (A) and p.o. (B) (Table S5); two-compartment model and its hypothesis (Figure S1); in-house compounds, which had PK data, had a narrower chemical space compared with FDA-approved drugs (Figure S2); in-house compounds, which had PK data, had a narrower chemical space compared with FDA-approved drugs using ECFP6 (Figure S3); predictive accuracy (RMSE) of RF models in the present study for i.v. PK data when using different combinations of MACCS Keys, ECFP6, and in vitro PK parameter descriptors during 5-Fold CV (Figure S4); picking up 50 compounds: i.v. observed (blue) and predicted (orange: RF model, green: baseline CPM model) compound plasma concentration–time profiles in mice with ID (Figure S5); and picking up 50 compounds: p.o. observed (blue) and predicted (orange: RF model, green: baseline CPM model) compound plasma concentration–time profiles in mice with ID (Figure S6) (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.