Optimal Filters for ERP Research I: A General Approach for Selecting Filter Settings

Abstract

Filtering plays an essential role in event-related potential (ERP) research, but filter settings are usually chosen on the basis of historical precedent, lab lore, or informal analyses. This reflects, in part, the lack of a well-reasoned, easily implemented method for identifying the optimal filter settings for a given type of ERP data. To fill this gap, we developed an approach that involves finding the filter settings that maximize the signal-to-noise ratio for a specific amplitude score (or minimizes the noise for a latency score) while minimizing waveform distortion. The signal is estimated by obtaining the amplitude score from the grand average ERP waveform (usually a difference waveform). The noise is estimated using the standardized measurement error of the single-subject scores. Waveform distortion is estimated by passing noise-free simulated data through the filters. This approach allows researchers to determine the most appropriate filter settings for their specific scoring methods, experimental designs, subject populations, recording setups, and scientific questions. We have provided a set of tools in ERPLAB Toolbox to make it easy for researchers to implement this approach with their own data.

1. Introduction

Filters are essential in research using event-related potentials (ERPs). At a minimum, a low-pass filter must be applied in hardware prior to digitizing the continuous EEG signal so that aliasing can be avoided (Picton et al., 2000). In addition, high-pass filters can significantly improve statistical power by reducing skin potentials (Kappenman & Luck, 2010), and low-pass filters can minimize muscle artifacts and induced electrical noise (Luck, 2014; de Cheveigné & Nelken, 2019). However, a strong filter may reduce the amplitude of the ERP component of interest as well as attenuating noise. Moreover, inappropriate filter settings can create temporal smearing, artifactual deflections, or bogus oscillations in the ERP waveform, potentially leading to erroneous conclusions (de Cheveigné & Nelken, 2019; Acunzo et al., 2012; Rousselet, 2012; Tanner et al., 2015, 2016; van Driel et al., 2021; VanRullen, 2011; Yeung et al., 2007).

What, then, are the ideal filter settings for a given study? Although some recommendations have been proposed (e.g., a bandpass of 0.1–30 Hz for most cognitive studies in neurotypical adults; Luck (2014)), the existing cognitive and affective ERP literature does not provide a clear, complete, and quantitatively justified answer to this question. In part, this is because different filter settings may be optimal for different experimental paradigms, participant populations, scoring methods, and scientific questions. As a result, the range of filter settings used in published ERP research varies widely across laboratories and often within a laboratory, presumably based on a combination of empirical testing, mathematical understanding (or misunderstanding) of filtering, and lab lore. The goal of the present paper is to provide a principled and straightforward approach for determining optimal filter settings. The approach is conceptually simple: A set of filters are evaluated, and the optimal filter is the one that maximizes the data quality while minimizing distortions of the ERP waveform. However, this requires methods for quantifying the data quality for a specific amplitude or latency score and methods for assessing waveform distortion. Our approach includes methods for each of these steps ¹. A companion paper (Zhang et al., under review) uses this approach to provide recommendations for seven commonly-used ERP components combined with four different scoring methods (mean amplitude, peak amplitude, peak latency, and 50 % area latency). That paper uses data from the ERP CORE (Compendium of Open Resources and Experiments;Kappenman et al. (2021)), which includes data from 40 young adults who performed six standardized paradigms that yielded seven commonly-studied ERP components. However, the recommendations that were developed for those data may not generalize to different populations of participants (e.g., infants), different recording setups (e.g., dry electrodes), or different experimental paradigms. The present paper therefore describes in detail how researchers can apply this approach to their own data. To make this approach easy to implement, we have also added new tools to version 9.20 and higher of ERPLAB Toolbox (Lopez-Calderon & Luck, 2014). Our approach can be implemented either through ERPLAB’s graphical user interface or through scripting, and we have also provided example scripts at https://osf.io/98kqp/. We have also provided a brief overview of the approach and a tutorial for implementing it in ERPLAB at https://github.com/lucklab/erplab/wiki/Selecting-Optimal-Filters-with-ERPLAB-Toolbox.

Our intention is for this paper to be useful for researchers from a broad variety of backgrounds, whether or not they have any technical expertise with signal processing. Consequently, the technical details have been emphasized in the main text and can be found in footnotes, supplementary materials, or the cited papers.

2. Review of basic filter properties

We first review the basic frequency-domain properties of the kinds of filters used most often in ERP research. Figure 1 shows the frequency response functions of several different filters along with their effects on an example averaged ERP waveform. Figure 1 a shows low-pass filters (which pass low frequencies and attenuate high frequencies), and Figure 1 b shows high-pass filters (which pass high frequencies and attenuate low frequencies). In the ERP waveforms, you can see that the low-pass filters mainly “smooth” the waveform, whereas the high-pass filters reduce the amplitude of the P3 wave ². These effects will be described in more detail in the next section.

Figure 1:

Frequency response functions for several filters and their application to a single-participant ERP waveform. The frequency response functions quantify the extent to which a given frequency is passed versus blocked by the filter. (a) Frequency response functions for low-pass filters. Two cutoff frequencies are shown (5 Hz and 20 Hz), combined with four roll-off slopes (12 dB/octave, 24 dB/octave, 36 dB/octave, and 48 dB/octave). (b) Frequency response functions for high-pass filters. Two cutoff frequencies are shown (0.1 Hz and 0.5 Hz), combined with four roll-off slopes (12 dB/octave, 24 dB/octave, 36 dB/octave, and 48 dB/octave). (c) Averaged ERP waveform with different half-amplitude low-pass filter cutoffs (no filter, 5 Hz, 10 Hz, and 20 Hz, all with slopes of 12 dB/octave). (d) The same averaged ERP waveform with different half-amplitude high-pass filter cutoffs (no filter, 0.1 Hz, 0.5 Hz, and 2 Hz, all with slopes of 12 dB/octave). Note that the filters used for (c) and (d) were applied to the continuous EEG data prior to epoching and averaging. All filters used here were noncausal Butterworth filters, and cutoff frequencies indicate the half-amplitude point. The waveforms in (c) and (d) were from the face condition in the ERP CORE N170 paradigm, Subject 40, CPz electrode site.

The frequency response functions characterize how the filters impact the frequency content of the data. The X axis is frequency, and the Y axis is gain. The gain indicates the extent to which a given frequency passes through the filter rather than being attenuated. A gain of 1.0 means that the frequency passes through completely (no filtering); a gain of 0.75 means that 75% of the signal at that frequency passes through the filter and that the signal is attenuated by 25% at that frequency; a gain of 0.0 means that the signal is completely attenuated at that frequency. The frequency response function of a filter is often summarized with the half-amplitude cutoff frequency, which is the frequency at which the gain is 0.5 and the signal is attenuated by 50% ³. The high-pass filters shown in Figure 1a have a half-amplitude cutoff at either 0.1 Hz or 0.5 Hz. The low-pass filters shown in Figure 1b have a half-amplitude cutoff at either 5 Hz or 20 Hz.

Filters are also characterized by their roll-offs, which specify how rapidly the gain changes as the frequency changes. This is often summarized by the slope of the filter at its steepest point, using logarithmic units of decibels of gain change per octave of frequency change (dB/octave). The filters in Figure 1 have roll-offs ranging from relatively shallow (12 dB/octave) to relatively steep (48 dB/octave). Researchers often assume that a steeper roll-off is better, because this means that most frequencies are either passed nearly completely (a gain near 1.0) or attenuated nearly completely (a gain near 0.0). However, as we will demonstrate in this paper, steeper roll-offs tend to produce greater waveshape distortion.

Filters can be either causal (unidirectional) or noncausal (bidirectional). Causal filters create a rightward shift in the waveform and are typically avoided except under specific conditions ⁴ (Rousselet, 2012; Woldorff, 1993). All filters used here were therefore noncausal.

3. Defining and quantifying the signal-to-noise ratio

Our approach to filter selection focuses on minimizing the noise in the filtered data, on maximizing the size of the signal relative to the noise (the signal-to-noise ratio or SNR), and on minimizing the waveform distortion produced by the filter. Although the concept of SNR has been used in ERP research for many decades, it is not simple to define and quantify either the signal or the noise in a way that is truly useful. This section therefore provides a new way of defining and quantifying the signal, the noise, and the SNR. We begin with an informal way of visualizing the effects of low-pass and high-pass filters on the signal and the noise. We then describe the classic definition of the SNR and its shortcomings for selecting optimal filters. The section ends by describing our new method for quantifying signal, noise, and SNR.

The signal portion of the SNR is usually framed in terms of the amplitude of the signal, so we will focus on ERP amplitudes for the next several sections. A slightly different approach is required for ERP latencies, as described in Section 6.

3.1. An informal visualization of the effects of filters on signal and noise

The logic behind applying high-pass and low-pass filters to EEG/ERP data is that some types of noise are confined to relatively low frequencies (e.g., skin potentials) whereas other types of noise are confined to relatively high frequencies (e.g., line noise and muscle artifacts). The signal of interest (i.e., the neural activity) typically has less power than the noise in the very low and very high frequencies, so attenuating these frequencies may reduce the noise more than it reduces the signal. This subsection provides visualizations of how filtering reduces both the signal and the noise.

To illustrate the loss of signal, Figure 1 c shows the effects of low-pass filters with different cutoffs ⁵ on the averaged ERP waveform from a single participant in the ERP CORE N170 paradigm (Kappenman et al., 2021). These filters “smoothed” out the high-frequency noise, but reducing the low-pass cutoff frequency all the way down to 5 Hz clearly reduced the amplitudes of the P1 and N1 waves. However, these low-pass filters had less impact on the amplitude of the P3 wave. In general, low-pass filters will decrease the amplitude of fast, narrow waves such as P1 and N1, with less impact on slow, broad waves such as P3 and N400. An intermediate amount of amplitude reduction will be produced for intermediate waves, such as the N2 family of components.

Figure 1 d shows the effects of high-pass filtering on the same averaged ERP waveform. As the cutoff frequency increased above 0.1 Hz, the amplitude of the P3 peak declined. However, the amplitude of the P1 peak was largely unaffected until the cutoff reached 2.0 Hz. In general, high-pass filters will decrease the amplitude of the longer-latency, broader waves but will have less impact on shorter-latency, narrower waves.

Although low-pass filters produce a clearly visible reduction in high-frequency noise in the averaged ERP waveforms (as in Figure 1 c), the noise reduction produced by high-pass filters is not usually obvious in the averaged ERP waveform (as in Figure 1 d). However, the effects of high-pass filtering on noise can be visualized by looking at the single-trial EEG epochs and at the standard error of the mean (SEM) at each point in the averaged ERP waveform. Figure 2 illustrates this using data from a participant in an active oddball task from the ERP CORE (Kappenman et al., 2021). Figure 2 a shows unfiltered single-trial EEG epochs and illustrates the fact that slow drifts in the EEG cause the single-trial EEG waveforms to tilt upward on some trials and downward on other trials. Because the epochs are baseline-corrected using the prestimulus period, the trial-to-trial variability in voltage increases progressively over the course of the epoch. In other words, the spread among the waveforms increases over the course of the epoch.

Figure 2:

Examples of single-trial EEG epochs, averaged ERP waveforms, and standardized measurement error (SME) values without filtering (top row) and after application of a high-pass filter with a half-amplitude cutoff at 0.5 Hz (bottom row). The SME was calculated for the mean amplitude in consecutive 100-ms time periods, for mean amplitude in the P3 measurement window (300–600 ms), and for peak amplitude in the P3 measurement window. The shaded region for the ERP waveforms reflects the standard error of the mean at each individual time point. The filter was a noncausal Butterworth filter with a slope of 12 dB/octave. The data were from the standard condition in the ERP CORE visual oddball paradigm, Subject 40, Pz electrode site.

This can also be seen by looking at the SEM at each time point of the averaged ERP waveform, as illustrated in Figure 2 b. The SEM increases progressively over the course of the epoch, just as the spread of single-trial EEG voltages increases over the course of the waveform. Note that the participant shown in Figure 2 had unusually large low-frequency drifts (relative to the other participants in the ERP CORE) to make the effects of slow voltage drifts obvious. However, virtually all participants exhibit increasing drift and increasing SEM over the course of the epoch. It is an inevitable consequence of using the prestimulus interval for baseline correction.

These low-frequency drifts can cause a dramatic reduction in statistical power, especially for later components that are farther away from the baseline period (Kappenman & Luck, 2010). This is because the drift will be random on the trials that are combined into an averaged ERP waveform, and the drifts will not average to zero unless an enormous number of trials are averaged together. This creates a random shift in each participant’s amplitude values, increasing the variance across participants.

Figure 2 d shows that the drift in the single-trial EEG can be dramatically reduced by applying a 0.5 Hz high-pass filter to the EEG. Figure 2 e shows that the filter reduces the SEM in the averaged waveform, especially later in the epoch. Thus, low-frequency drift is a threat to statistical power but can be minimized by high-pass filtering.

3.2. The classic definition of signal-to-noise ratio (SNR) and its limitations

Now that we have seen how filters can influence both the signal and the noise, we will take a closer look at how the signal-to-noise ratio (SNR) can be quantified. Classically, the SNR in ERP research is defined separately at each individual time point in the averaged ERP waveform. The signal is the amplitude of the averaged waveform at a given time point, and the noise is quantified by some measure of trial-to-trial variability at that time point (Picton et al., 2000). Each point in an averaged ERP waveform is the mean of the single-trial voltages at that time point, so the standard error of the mean (SEM) is a natural way to quantify the noise. Thus, the SNR at a given time point is the amplitude at that time point (the signal) divided by the SEM at that time point (the noise). The SEM is typically estimated as $\text{SD/}\sqrt{N}$, where SD is the standard deviation of the single-trial amplitudes at that time point and N is the number of trials being averaged together. Because the SEM is linearly related to $\sqrt{N}$, this definition of the SNR explains why the SNR of an averaged ERP waveform improves linearly with $\sqrt{N}$.

In Figures 2b and 2e, we could compute the SNR at each time point by dividing the amplitude of the averaged ERP at that time point by the SEM at that time point. However, the SNR at individual time points is not particularly useful in most ERP research, because most studies derive amplitude and latency scores from the pattern of voltages across multiple time points. For example, the size of mismatch negativity (MMN) component in the ERP CORE (Kappenman et al., 2021) was measured as the mean voltage from 125–225 ms in the deviant-minus-standard difference waves. Because this is the type of score that is typically entered into statistical analyses and used to test the hypotheses of a study, the SNR of a given score is much more important than the SNR at individual time points (except when mass univariate analyses are used ⁶). However, there is no simple mathematical relationship between the SNR of a score that is derived from multiple time points and the SNR at the individual time points.

In addition, the effect of a given filter will depend on what scoring method is being used (e.g., mean amplitude vs. peak amplitude). For example, when the mean voltage over a reasonably wide time window is used to score the amplitude of an ERP component, high-frequency noise has relatively little impact on the score. This is illustrated in Figure 3, which shows a simulated ERP waveform with and without high-frequency noise. The rapid upward and downward noise deflections within the measurement window cancel each other out, and the mean amplitude from 300–500 ms in the noisy waveform is similar to the mean amplitude from 300–500 ms in the clean waveform. However, the peak amplitude is strongly affected by the high-frequency noise. High-frequency noise will also have a substantial impact on peak latency scores. By contrast, low-frequency noise has a modest impact on peak latency scores but a large impact on mean amplitude and peak amplitude scores. Thus, when choosing a filter, it is essential to consider how the averaged ERP waveform will be scored and how the filter will impact the SNR of that specific score.

Figure 3:

Simulated ERP waveform without noise (a) and with high-frequency noise added (b). This high-frequency noise had very little impact on the mean amplitude during this window because the upward and downward noise deflections largely canceled each other. However, the noise had a large impact on the peak amplitude.

A partial solution to this problem is to define the signal as the mean voltage during the time window of interest and the noise as the standard deviation of the voltage across the points during the baseline period (e.g., Debener et al. (2008)^; Klug & Gramann (2021)). However, this is valid only for mean amplitude scores and does not apply to other scoring methods (e.g., peak amplitude, peak latency). In addition, there is no guarantee that the noise level will remain constant between the baseline period and the time window of interest. The noise might increase owing to low-frequency drifts (as in Figure 2 a), or it might decrease owing to stimulus-induced suppression of alpha-band activity (Klimesch, 2012). Thus, we need a means of quantifying the SNR that can apply to any scoring method and that directly reflects the noise that impacts the score of interest.

3.3. Using the standardized measurement error (SME) to estimate the SNR for ERP amplitude scores

A new definition of SNR that meets these criteria was recently proposed by Luck et al. (2021). The signal is straightforward: It can be estimated by the score itself (although a caveat to this will be described in Section 3.4). For example, when MMN peak amplitude is measured from a deviant-minus-standard difference wave, the signal is the measured peak amplitude. The noise can then be estimated as the standard error of measurement for that score.

This is a simple generalization of the method for computing the SNR at each individual time point, in which the SEM at a given time point was used to estimate the noise. When we make an averaged ERP waveform, the value at a given time point is the mean of the single-trial voltages at that time point. Because it is a mean, the standard error of measurement for this value is the standard error of the mean (the SEM). Thus, the SNR at a given time point is the mean across trials at that time point divided by the SEM at that time point.

However, when the signal of interest is a score that is based on the pattern of voltages across multiple time points, we need to estimate the standard error of measurement for that particular score. Luck et al. (2021) developed an approach for quantifying the standard error of measurement for ERP amplitude and latency scores, and the resulting estimate of the noise is called the standardized measurement error (SME) ⁷. Thus, the SNR for a given amplitude score can be quantified as the score divided by the SME for that score. We refer to this specific definition of SNR as SNR_SME. Although the SME can be estimated for both amplitude scores and latency scores, SNR_SME is primarily relevant for amplitude scores, and a different approach is needed for latency scores (see Section 6).

When the amplitude of an ERP component is scored as the mean voltage within a given time window in an averaged ERP waveform, Luck et al. (2021) demonstrated that the SME is equivalent to the SEM of the single-trial mean amplitude values from that time window. That is, the mean voltage across the time period is scored for each individual trial, and the usual formula for the SEM is applied to these values $\text{SD/}\sqrt{N}$ ⁸. When estimated using this simple analytic approach, the result is called the analytic SME or aSME. Unfortunately, this simple approach is not valid for other scoring methods, such as peak amplitude. For those scoring methods, Luck et al. (2021) developed a bootstrapping method for estimating the SME. The result is called the bootstrapped SME or bSME. Note that the SME assumes that the score of interest will be obtained from averaged ERPs, not from single trials. Some other yet-to-be-developed approach would be needed when single-trial scores are used as the dependent variable in statistical analyses.

The aSME is automatically computed by version 8.1 and later of ERPLAB Toolbox. Computing the bSME currently requires Matlab scripting, but the scripts are relatively simple, and example scripts are available at https://doi.org/10.18115/D58G91. In addition, the ERP CORE resource contains SME values and the code required to compute them for all seven ERP components (https://doi.org/10.18115/D5JW4R; see Zhang & Luck (2023)).

No matter how the SME is computed, it is an estimate of the standard error of measurement for the score of interest, and it can therefore be used as the noise term when computing the SNR_SME. For example, P3 amplitude in the ERP CORE visual oddball experiment was scored as the mean amplitude from 300–600 ms in the rare-minus-frequent difference waves. The SNR_SME for P3 amplitude for a given participant in this experiment is therefore this mean amplitude score for that participant divided by the SME of the score for that participant.

Using this approach, the SNR_SME can be estimated for both filtered and unfiltered data to determine the extent to which a given filter increases or decreases the signal-to-noise ratio. This is illustrated in the rightmost column of Figure 2. When P3 amplitude was scored as the mean amplitude from 300–600 ms in the unfiltered data, the score was 6.62 µV (see Figure 2 b) and the SME of this score was 2.90 µV (see Figure 2 c). The SNR_SME was therefore 6.62/2.90 or 2.28. When the peak amplitude was scored instead, the score was 11.74 µV and the SME of this score was 2.24 µV, yielding an SNR_SME of 11.74/2.24 or 5.24. After a 0.5 Hz high-pass filter was applied (Figures 2 d-f), the mean amplitude and peak amplitude scores were slightly smaller than before (4.50 µV and 9.05 µV, respectively). However, the SME values were reduced by a much greater amount (to 0.80 µV and 0.95 µV, respectively). Consequently, the SNR_SME was almost doubled by the filtering to 5.63 for mean amplitude and 9.53 for peak amplitude.

This example shows how we can determine which filter parameters lead to the best signal-to-noise ratio. To our knowledge, this is the first method that can quantify how filters impact the SNR of the actual amplitude scores that are used to test hypotheses in most cognitive and affective ERP experiments.

However, it is important to keep in mind that the SNR is not the only factor that should be considered when choosing a filter. In particular, the next section will show that a filter with a better SNR_SME may produce more waveform distortion than a filter with a worse SNR_SME. Thus, it is necessary to consider both the SNR_SME and the amount of waveform distortion when selecting a filter.

3.4. Improving the estimate of the signal

Although it is straightforward to use the amplitude score as the signal in the SNR_SME calculation, these scores are distorted by any noise in the averaged ERP waveform and are therefore an imperfect estimate of the signal. For example, as shown in Figure 3, high-frequency noise will cause the peak amplitude to be overestimated, which will then lead to an overestimate of the SNR_SME. Filtering out the high-frequency noise will decrease the peak amplitude, bringing it closer to the true value, but this might create the illusion that filtering has decreased the signal-to-noise ratio.

A simple solution to this problem is to obtain the score from the grand average ERP waveform, which typically has much less noise than the single-participant waveforms. This score could then be divided by the SME for a given participant to estimate the SNR_SME for that participant. To obtain a group SNR_SME, the score from the grand average would be divided by an aggregate of the single-participant SME values as described in Section 5.

Obtaining the score from the grand average is not a perfect solution, because some noise will remain in the grand average and contribute to the estimate of the signal. This residual noise is often negligible, but when substantial noise remains in the grand average an artificial ERP waveform can instead be used to estimate the signal (see Section 4). We found nearly identical results for the ERP CORE data when measuring the signal from the grand average or from artificial waveforms, so we used the grand average when calculating the SNR_SME in the present paper and in the companion paper (Zhang et al., under review).

Obtaining the score from the grand average is also an imperfect approach for nonlinear scoring methods, such as peak amplitude, because the mean of the single-participant peaks is not the same as the peak of the grand average waveform. For example, if the timing of an ERP component varies across participants, the peak amplitude of the grand average ERP waveform will be smaller than the average of the single-participant peaks (even in the absence of noise). However, the goal of the present procedure is not to determine the true SNR_SME, but instead to determine how the SNR_SME varies across different filter settings. The pattern of SNR_SME values across filters is typically not impacted by the nonlinearity problem, so measuring from the grand average typically works well in practice for determining the optimal filtering parameters.

3.5. Measuring from difference waves

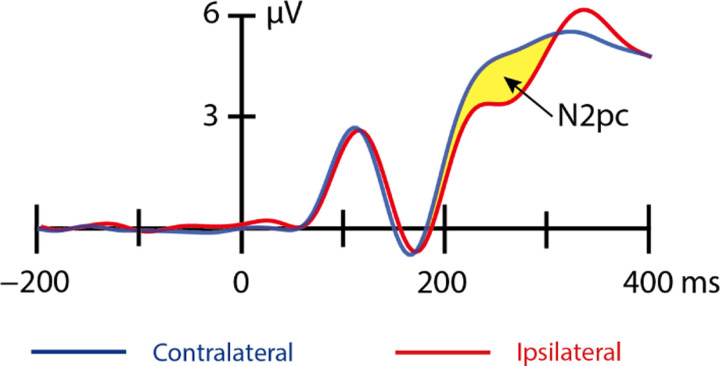
The vast majority of ERP experiments use multiple conditions to isolate a specific ERP component from the many overlapping components that contribute to the averaged ERP waveform (e.g., oddballs versus standards for P3 and MMN, faces versus cars for N170). In these cases, we recommend estimating both the signal and the SME from difference waves (e.g., oddballs-minus-standards, faces-minus-cars). The reasoning is illustrated in Figure 4, which shows the grand average ERP waveforms from the ERP CORE N2pc experiment (Kappenman et al., 2021). The N2pc component is defined as the difference between the waveform at electrode sites contralateral versus ipsilateral to the target location (indicated by yellow shading). Although this difference is approximately 1.5 µV, the N2pc is superimposed on a broad positivity arising from other ERP components, bringing the overall voltage up to approximately 5 µV. If we measured the signal from the contralateral and ipsilateral waveforms (the parent waveforms), we would get a value that is approximately three times as large as the actual 1.5 µV N2pc component. This would vastly overestimate the size of the signal. In addition, if we measured from the parent waveforms, a high-pass filter that reduced the broad positivity might appear to reduce the signal even if it had minimal impact on N2pc amplitude. Similarly, if we estimated the SME from the parent waveforms, our measure of the noise would also be distorted by the overlapping components.

Figure 4:

Grand average ERP waveforms from the ERP Core N2pc experiment. Separate waveforms are shown for trials where the target was contralateral to the electrode site and trials where the target was ipsilateral to the electrode site. The N2pc is defined as the difference in voltage between the contralateral and ipsilateral waveforms (denoted here by yellow shading).

By measuring the signal and the SME from the difference waveform, we can avoid these problems and more directly determine how different filters impact the signal of interest and the noise that impacts that signal. In addition, when the parent waveforms differ greatly in amplitude (e.g., the oddball and standard waveforms in a P3 experiment or the semantically related and unrelated waveforms in an N400 experiment), we might get very different signal and noise estimates for the two different waveforms. Measuring the signal and noise from the difference wave avoids this problem. However, there may be cases in which it makes sense to quantify the signal from parent waveforms rather than difference waveforms.

4. Assessing waveform distortion using artificial waveforms

Filters are a form of controlled distortion, and they inevitably “smear” the ERP signal in time, reducing the temporal resolution of the data (for an explanation, see Chapter 7 in Luck (2014)). Moreover, filters may produce artifactual peaks in the ERP waveform, which can lead researchers to draw wildly incorrect conclusions (Tanner et al., 2015, 2016). Consequently, a filter that is optimal in terms of SNR may be far from optimal in terms of waveform distortion. In this section, we will provide visualizations of these distortions and describe an approach that researchers can easily use to quantify the distortions produced by the filters they are considering for their own data.

The most straightforward way to assess the distortion produced by a filter is to pass an artificial waveform through the filter and compare the filtered and unfiltered versions of this waveform. Artificial waveforms must be used for this purpose because the true (i.e., noise-free) waveform is not usually known for real data, making it difficult to know if the filter is “revealing” the true waveform by eliminating noise or is instead creating a bogus effect that mischaracterizes the underlying brain activity (Yeung et al., 2007).

4.1. Creating simulated N170 and P3 effects

In this section, we provide examples using two artificial waveforms that simulate two of the effects observed in the ERP CORE: a) the larger N170 for faces than for cars in a visual discrimination paradigm, and b) the larger P3 for oddballs than for standards in a visual oddball paradigm. We have chosen these two effects because they span the gamut from a relatively early perceptual effect to a relatively late cognitive effect. These and most other ERP effects can be simulated with Gaussian and ex-Gaussian functions ⁹. Beginning in version 9.20, ERPLAB Toolbox provides a tool for using these and other functions to create artificial waveforms that simulate ERP components. Whereas this tool simulates averaged ERP waveforms, the SEREEGA toolbox (Krol et al., 2018) can be used to simulate single-trial EEG epochs that contain ERP-like effects ¹⁰.

Panels a and b of Figure 5 show the grand average N170 and P3 effects from the ERP CORE. The N170 paradigm involved a series of faces, cars, scrambled faces, and scrambled cars, and the N170 effect was defined as the faces-minus-cars difference. The P3 paradigm involved a sequence of rare and frequent letter categories, and the P3 effect was defined as the rare-minus-frequent difference. The N170 effect can be approximated by a negative-going Gaussian function with a mean of 129 ms and an SD of 14 ms. The P3 waveform is typically skewed to the right, and the ERP CORE P3 effect can be approximated by an ex-Gaussian function with a Gaussian mean of 310 ms, a Gaussian SD of 58 ms, and an exponential rate parameter (λ) of 2000 ms.

Figure 5:

Filter-induced distortions of real and simulated N170 and P3 components from the ERP CORE. (a) Grand average N170 difference wave and simulation with a Gaussian function (mean = 129 ms, SD = 14 ms, peak amplitude = −4.6 µV). (b) Grand average P3 difference wave and simulation with an ex-Gaussian function (mean = 310 ms, SD = 58 ms, λ = 2000 ms, peak amplitude =8.6 ). The artificial waveforms were preceded and followed by 1000 ms of zero values to avoid edge artifacts. (c, d) Effects of a 5 Hz low-pass filter on the real N170 and P3 waveforms, respectively. (e, f) Effects of a 5 Hz low-pass filter on the simulated N170 and P3 waveforms, respectively. (g, h) Effects of a 2 Hz high-pass filter on the real N170 and P3 waveforms, respectively. (i, j) Effects of a 2 Hz high-pass filter on the simulated N170 and P3 waveforms, respectively. All filters used here were noncausal Butterworth filters with a slope of 12 dB/octave, and cutoff frequencies indicate the half-amplitude point.

These simulated waveforms are overlaid on the observed grand average waveforms in Figures 5 a and 5 b. They are not a perfect fit, but they do a reasonable job of capturing the key properties of the N170 and P3 components, and most ERP components can be approximated by Gaussian and ex-Gaussian functions with appropriate parameters.

Because the true waveform is not known, it may be necessary to create several different artificial waveforms that reflect different possibilities for the true waveform. A filter can then be chosen that minimizes the waveform distortion for the entire set of simulated waveforms. In addition, some effects may consist of changes in multiple overlapping components. This can be approximated by creating simulations of the individual components and then summing them together.

The following subsections show how the real and simulated waveforms shown in Figure 5 are distorted by a low-pass filter and a high-pass filter. We have chosen relatively extreme cutoff frequencies for these examples to make the distortions obvious. We also provide examples of the distortions produced by more typical filters in Figures 6 and 7.

Figure 6:

Effects of different low-pass filter cutoffs (5, 10, 20, 30, 40, and 80 Hz) and roll-offs (12, 24, 36, and 48 dB/octave) on the simulated N170 and P3 waveforms. Note that the distortion is most notable for the lowest cutoff frequencies. All filters used here were noncausal Butterworth filters with a slope of 12 dB/octave, and cutoff frequencies indicate the half-amplitude point.

Figure 7:

Effects of different high-pass filter cutoffs (0.01, 0.05, 0.1, 0.5, 1, and 2 Hz) and roll-offs (12, 24, 36, and 48 dB/octave) on the simulated N170 and P3 waveforms. Note that the distortion is most notable for the highest cutoff frequencies. All filters used here were noncausal Butterworth filters with a slope of 12 dB/octave, and cutoff frequencies indicate the half-amplitude point. The embedded number in each panel is the artificial peak percentage (in %, shown in magenta for P3 and light blue for N170).

4.2. Effects of low-pass filtering on simulated ERPs

Panels c and d of Figure 5 show the results of applying a 5 Hz low-pass filter to the real N170 and P3 waveforms, and Panels e and f show the results of filtering the simulated versions of these waveforms. The filter reduced the amplitude of both the real and simulated N170 peaks, just as was observed for the P1 and N1 waves in Figure 1 b. Figure 5 e also shows that the filter “smeared out” the simulated N170, artificially creating an earlier onset time and a later offset time. This temporal smearing can also be seen with the real N170 in Figure 5 c and with the P1 and N1 waves in Figure 1 b. However, the other overlapping peaks in the real waveforms make it difficult to precisely determine the amount of smearing, and it is also impossible to know whether the smearing in the real waveforms is a filter-induced distortion or a revelation of the true time course of the effect. Only a simulated waveform provides ground truth and makes it possible to unambiguously assess the distortion produced by a filter.

As illustrated in Figures 5 d and 5 f, the 5 Hz low-pass filter had relatively little effect on the P3 wave. The filter reduced the peak amplitude slightly, and a slight smearing of the onset time was visible in the simulated P3 waveform. Thus, as described in Section 3.1 and shown in Figure 1 b, low-pass filters have a much larger effect on short-latency, narrow peaks such as the N170 than on long-latency, broad peaks such as the P3.

Figure 6 shows the effects of a variety of different low-pass filter cutoffs and roll-offs on the simulated N170 and P3 waveforms. When a relatively gentle roll-off of 12 dB/octave was used, the waveform distortion consisted of a progressively greater temporal smearing as the cutoff frequency declined, with minimal smearing when the cutoff was above 15 Hz. When steep roll-offs were used, however, the distortion of the simulated N170 also included opposite-polarity peaks on either side of the N170 (see, e.g., the cutoff of 10 Hz with a slope of 48 dB/octave). Thus, filtering N170 data with a steep slope might cause a researcher to reach the invalid conclusion that faces elicit a small, early, positive response as well as the typical N170 response. Filtering with a shallow slope avoids this problem. However, filters with shallow slopes still distort the onset and offset times of the waveform, especially with cutoff frequencies below 20 Hz. Whether these distortions are a significant problem depends on the nature of the scientific questions being asked and the analysis procedures being applied.

4.3. Effects of high-pass filtering on simulated ERPs

Panels g and h of Figure 5 show the results of applying a 2 Hz high-pass filter to the real N170 and P3 waveforms, respectively, and Panels i and j show the results of filtering the simulated versions of these waveforms. This filter did not produce any obvious distortion of the real N170 waveform, except for a modest reduction in peak amplitude, but the simulated waveform shows that the filter also produced opposite-polarity artificial peaks on each side of the simulated N170 wave. The other voltage deflections in the real data made it difficult to see these artifactual peaks.

The filter produced much greater distortion of the real and simulated P3 waves. In addition to dramatically reducing the peak amplitude of the P3, the filter produced an artifactual negative peak prior to the true peak. This was especially obvious for the artificial waveform but it was also visible in the real waveform. Thus, a researcher who used this filter might incorrectly conclude that the rare stimuli elicited a larger negativity than the frequent stimuli, peaking around 200 ms (for additional examples of invalid conclusions that may arise from filtering, see Tanner et al. (2015); Yeung et al. (2007)).

Figure 7 shows the effects of a variety of different high-pass filter cutoffs and roll-offs on the simulated N170 and P3 waveforms. The artifactual opposite-polarity peaks were minimal for cutoffs of 0.1 Hz or lower, but they became clearly visible at 0.5 Hz and increased progressively as the cutoff increased further. In addition, when a steep roll-off was used, an oscillating distortion was present. For example, with a cutoff at 2 Hz and a roll-off of 48 dB/octave, an artifactual negative peak was present immediately before the P3 peak, and an artifactual positive peak was present prior to this artifactual negative peak. Note also that the artifactual peaks for the P3 wave were more pronounced prior to the P3 peak than after the P3 peak. This is a result of the right skew in the simulated P3 waveform. The same asymmetry can be observed in the filter artifacts for the real P3 waveform in Figure 5 h. Thus, the typical pattern of waveform distortion produced by high-pass filters is an artifactual opposite-polarity peak prior to the true peak.

We quantified the size of the artifactual peaks produced by high-pass filters using the artifactual peak percentage, which reflects the amplitude of the artifactual peak produced by the filter relative to the amplitude at the peak of the true component after filtering. It was calculated as 100 times the absolute value of the peak voltage of the artifactual peak divided by the absolute value of the peak voltage of the true peak (after filtering). Consider, for example, the artificial P3 wave after high-pass filtering with a cutoff at 2 Hz and a slope of 12 dB/octave (Figure 7, upper right corner). The peak amplitude¹¹ of the artifactual peak was −1.466 µV, and the peak amplitude of the true peak was +2.789 µV, so the artifactual peak percentage was 100 × |−1.466 | / |2.789| = 52.56%. This value is shown for each filter setting in Figure 7.

The idea behind this approach is that a small artifactual peak is likely to be obscured by the background noise and have no impact on the conclusions drawn from a given study, but a large artifactual peak might be statistically significant and lead to a bogus conclusion. In addition, the artifactual peak might be considered to be substantial in size if it is relatively large compared to the other peaks in the waveform (such as the true peak after filtering). For example, the artifactual peak in the upper right corner of Figure 7 looks like a very substantial effect when compared with the rest of the waveform.

Although artificial peaks are mainly a problem for high-pass filters, Figure 6 shows that they may also occur for low-pass filters with a steep cutoff (see, e.g., the lower left panel in Figure 6). We therefore provide the artifactual peak percentage values for the low-pass filters in supplementary Table A.1.

5. Putting it all together to select an optimal filter

Now that we have described the individual elements of our approach for determining filter settings, we will discuss how they can be combined to select an optimal filter for an ERP amplitude score. Like most other analysis decisions that influence the results of a given experiment, the filter settings should be chosen a priori. This requires using previous studies to determine the appropriate settings for a given study of interest. This is straightforward when prior studies are available that are similar to the study of interest. When such prior studies are not available, reasonable filtering parameters can still be chosen as long as prior recordings are available that contain reasonably similar waveforms and noise levels. We have also added options in ERPLAB’s Channel Operations tools that allow users to add noise of various different types to prior data.

5.1. Example: Computing the SNR_SME for P3 mean amplitude

In this subsection, we will use the mean amplitude score for the P3 wave from the ERP CORE visual oddball paradigm to illustrate the process of computing the SNR_SME resulting from a broad range of filter settings. The following section shows how to combine this information with our metric of waveform distortion (artifactual peak percentage) to choose the optimal filter settings. A more complete analysis, including peak amplitude, peak latency, and 50% area latency scores, is provided in the companion paper (Zhang et al., under review).

The first step is to estimate the signal by obtaining the score of interest. For the P3 wave in the ERP CORE oddball experiment (Kappenman et al., 2021), this would be the mean amplitude from 300–600 ms at the Pz electrode site, measured from the rare-minus-frequent difference wave. It is usually best to obtain this score from the grand average ERP waveform (see Section 3.4). This score can then be obtained from the unfiltered data and from data that have been filtered with a variety of different cutoff frequencies. The result is shown in Figure 8. To create this figure, we filtered the continuous EEG (to avoid edge artifacts), using each combination of seven high-pass filter cutoffs (0, 0.01, 0.05, 0.1, 0.5, 1, and 2 Hz) and seven low-pass filter cutoffs (5, 10, 20, 30, 40, 80, and 115 Hz). We then epoched the EEG, computed averaged ERPs, computed the rare-minus-frequent difference wave, created a grand average across participants, and computed the mean voltage from 300–600 ms from the grand average difference wave. The result is the estimate of the signal after the attenuation produced by each filter. Figure 8 a shows the resulting mean amplitude scores for each low-pass/high-pass filter combination (see supplementary Figure A1 for the grand average waveforms from which the scores were obtained). Significant attenuation of the P3 was produced by high-pass cutoffs above 0.1 Hz, whereas low-pass filtering had very little effect on the signal.

Figure 8:

Demonstration of how the signal, noise, and signal-to-noise ratio (SNR) vary as a function of the filter settings for the P3 mean amplitude score from the ERP CORE visual oddball paradigm. (a) Signal: P3 mean amplitude score (from 300–600 ms at Pz) obtained from the grand average rare-minus-frequent difference wave. (b) Noise: Root mean square (RMS) of the single-participant standardized measurement error (SME) values for the P3 scores. Analytic SME values were obtained for each participant for the rare and frequent conditions for mean amplitude, and Equation 1 was applied to obtain the SME of the rare-minus-frequent difference for each participant. These SME values were then aggregated across participants using the RMS. (c) SNR: The signal divided by the noise for each filter setting. Note that filtering was applied to the continuous EEG prior to averaging with every combination of seven high-pass filter cutoffs (0, 0.01, 0.05, 0.1, 0.5, 1, and 2 Hz) and seven high-pass filter cutoffs (5, 10, 20, 30, 40, 80, and 115 Hz). All filters used here were noncausal Butterworth filters with a slope of 12 dB/octave, and cutoff frequencies indicate the half-amplitude point.

The second step is to estimate the noise by computing the SME for the score of interest. If the score is the mean amplitude over a fixed time window in the waveform from a given condition (e.g., the mean voltage from 300–600 ms for the oddball trials), the SME can be calculated directly by ERPLAB Toolbox. However, if a nonlinear score such as peak amplitude is being used, then bootstrapping is needed to estimate the SME. In addition, ERPLAB cannot directly compute the SME for mean amplitude scores obtained from difference waves (e.g., the mean voltage from 300–600 ms obtained from the rare-minus-frequent difference wave in the ERP CORE oddball experiment). However, it is straightforward when the score is a mean amplitude over a fixed time window to take the SME values provided by ERPLAB for the individual conditions and use them to compute the SME of the difference wave:

$$SM{E}_{A-B}\hspace{0.17em}=\sqrt{SM{E}_A^2\hspace{0.17em}+\hspace{0.17em}SM{E}_B^2}.$$ (1)

In this equation, $SM{E}_{A-B}$ is the SME of the difference between conditions A and B, and $SM{E}_A$ and $SM{E}_B$ are the SMEs of the two individual conditions. Note that this equation applies only when the score is the mean voltage across a time window. In addition, it applies only when the difference wave is between waveforms from separate trials (e.g., rare minus frequent for P3, unrelated minus related for N400), not when it is a difference between two electrode sites (e.g., contralateral minus ipsilateral for N2pc or lateralized readiness potential).

This gives us an estimate of the noise for a single participant, but it is typically more useful to quantify the noise for an entire group of participants. This could be accomplished by averaging the single-participant SME values. However, participants with particularly noisy data have an outsized effect on statistical power (Luck et al., 2021), so it is better to use the root mean square (RMS) of the single-participant SME values as the noise estimate for the group. The RMS is obtained by squaring each single-participant SME value, taking the mean of these squared values, and then taking the square root of this mean. Figure 8 b shows the resulting RMS(SME) values for a variety of filter cutoffs. The noise level decreased progressively as the high-pass cutoff increased. Thus, Figure 8 a shows that high-pass filtering decreased the signal, and Figure 8 b shows that it also decreased the noise. Next, we must determine the extent to which the attenuation of the noise by a given filter outweighs the attenuation of the signal. This is assessed by computing the SNR_SME.

The SNR_SME for a group of participants can be estimated by taking the score from the grand average (the estimated signal; Figure 8 a) and dividing it by the RMS of the single-participant SME values (the estimated noise; Figure 8 b). The SNR_SME for a variety of filter combinations is summarized in Figure 8 c. As shown in the figure, the low-pass filter had very little effect except when a 2 Hz high-pass filter was also applied. This is because mean amplitude scores are largely insensitive to high-frequency noise. However, the high-pass filter had a clear impact on the SNR_SME, with the largest SNR_SME obtained for the 0.5 Hz cutoff. For cutoffs below 0.5 Hz, the low-frequency noise was not attenuated as much, decreasing the SNR_SME. For cutoffs above 0.5 Hz, filtering decreased the amplitude of the P3 (the signal) more than it decreased the noise, so these filters also decreased the SNR_SME. However, low-pass filtering had little or no impact on the SNR_SME as long as the high-pass cutoff was below 1 Hz. The SNR values are also summarized in supplementary Figure A2, which also includes a denser sampling of high-pass cutoff frequencies between 0.1 and 1.0 Hz.

5.2. Example: Assessing waveform distortion for P3 mean amplitude and selecting a maximal artifactual amplitude percentage

It would be tempting to select a high-pass cutoff of 0.5 Hz on the basis of the results shown in Figure 8, but it is also necessary to assess the waveform distortion produced by the filters. This is accomplished by creating an artificial waveform and passing it through the filters. As we have already seen in Figure 7, the 0.5 Hz high-pass filter produced substantial distortion of the simulated P3 wave, including an artifactual negative peak that was 14% as large as the amplitude of the true peak (after filtering). The 0.1 Hz filter produced minimal waveform distortion, with an artifactual peak percentage of only 0.74%. You might, therefore, select a cutoff of 0.1 Hz, opting for minimal waveform distortion at the cost of a slightly lower SNR. Alternatively, you might decide that the 14% artifactual peak amplitude produced by the 0.5 Hz cutoff is negligible, and the greater SNR justifies selecting this cutoff. How could you make this decision in a rigorous, well-informed manner?

Deciding on a high-pass cutoff requires balancing the risk of a false positive (an artifactual peak that is large enough to be statistically significant) and the risk of a false negative (a true effect that is not statistically significant because of reduced SNR). This is analogous to the alpha criterion for statistical significance in traditional frequentist statistical analyses (typically 0.05); a lower alpha such as 0.01 reduces the risk of a false positive (a Type I error) but also decreases statistical power and increases the risk of a false negative (a Type II error). Generally, scientists are more concerned about false positives than false negatives and choose a relatively conservative criterion. The chosen criterion is usually arbitrary, but at least the risks are well defined.

For most ERP studies conducted in low-noise environments with highly cooperative participant populations, we propose a criterion of 5% for the artifactual peak percentage. That is, we recommend that researchers use the high-pass filter that produces the best SNR_SME while also producing an artifactual peak percentage of less than 5%. This amount of distortion would be like a 0.5 µV artifactual N2 preceding a 10 µV P3, a 0.4 µV artifactual P2 preceding an 8 µV N400, or a 0.1 µV artifactual P1 preceding a 2 µV N2pc. Such effects are unlikely to be statistically significant under typical conditions. If we increased the criterion to 10%, however, we might have a 1 µV artifactual N2, a 0.8 µV artifactual P2, or a 0.2 µV artifactual P1, which would have a good chance of being statistically significant ¹² and leading to a fundamentally incorrect conclusion. If we decreased the criterion to 1%, there would be almost no chance that the artifactual peaks would be significant, but we would also be choosing a filter that yields a poorer SNR and therefore lower statistical power. Thus, a maximal artifactual peak amplitude of 5% seems like a reasonable balance between false positives and false negatives.

However, we would like to stress that this 5% criterion is arbitrary, and it would not be straightforward to assess the actual probability that an artifactual effect of a given size would be statistically significant. However, the 5% criterion seems reasonably conservative without being overly strict for most ERP studies conducted in low-noise environments with highly cooperative participant populations. Under other conditions, it is likely that a more liberal criterion would be justified. For example, in studies with noisy EEG signals or an unusually small number of trials, an artifactual peak of 10% amplitude is much less likely to lead to a statistically significant effect, and the boost in SNR and statistical power produced by a high-pass cutoff that produces an artifactual peak percentage of 10% may therefore be well justified.

When the amplitude of an ERP component is being scored, the temporal smearing of the waveform produced by a low-pass filter is not usually a concern (unless it impacts the SNR). Thus, we do not recommend using the amount of latency distortion as a criterion for filter section when mean or peak amplitudes are being scored. However, this smearing could be an issue when the exact onset or offset latency of an effect is of theoretical relevance or when mass univariate statistical analyses are used. In those situations, the specific theoretical questions should drive the decision about how much latency distortion is acceptable ¹³. Section 6 considers the impact of low-pass filter settings on latency scores.

5.2.1. Example: Selecting optimal filter parameters for P3 mean amplitude

Now that we have computed the SNR_SME for a broad range of filter cutoffs and have selected a criterion for the maximal allowable artifactual peak percentage, we can finally select the optimal filter settings for the P3 mean amplitude score. A high-pass cutoff of 0.5 Hz produced the best SNR_SME, but the artifactual peak percentage of 14.0% for this cutoff exceeds our criterion of 5%. A lower cutoff of 0.1 Hz reduces the artifactual peak percentage to an acceptable level of 0.70%, with only a modest decline in SNR_SME. Figure A2 shows SNR_SME values and artifactual peak percentages for a denser sampling of cutoff frequencies, and it shows that a high-pass cutoff frequency of 0.2 Hz is the optimal value in terms of maximizing the SNR_SME while staying under the 5% criterion for the artifactual peak percentage (See Figure A2).

Because the low-pass cutoff had little effect on the SNR_SME when the high-pass cutoff was less than 1 Hz, no low-pass filtering would be necessary. However, there is also no harm in applying a mild low-pass filter (e.g., 30 Hz, 12 dB/octave), and such a low-pass filter will remove “fuzz” in plots of the waveforms that might make it difficult to visualize differences between conditions.

One could also assess the impact of different roll-off slopes on the SNR_SME and the waveform distortion, but a slope of 12 dB/octave is usually best in terms of minimizing waveform distortion (see Figures 6 and 7). For example, even a low-pass filter can produce an artifactual peak percentage that exceeds the 5% threshold when a steep slope is used (see supplementary Table A.1).

Thus, our recommendation for P3 mean amplitude scores in studies such as the ERP CORE is a half-amplitude high-pass cutoff at 0.2 Hz, optionally accompanied by a half-amplitude low-pass cutoff at 30 Hz (with slopes of 12 dB/octave). The companion paper provides recommendations for six other ERP components, and includes peak amplitude, peak latency, and 50% area latency scores in addition to mean amplitude scores.

6. Selecting optimal filter settings for latency scores

Under ordinary conditions, the kinds of filters typically used in ERP research can only decrease the amplitude of an ERP component¹⁴. As a result, filters tend to reduce the difference in amplitude between groups or conditions. This is illustrated in Figures 9 a and 9 b, which show a simulation of two conditions in which the P3 amplitude differs. In the unfiltered data (Figure 9 a), the peak amplitude differed by 0.5 µV between the two conditions. When a high-pass filter with a half-amplitude cutoff of 1 Hz was applied (Figure 9 b), the difference in amplitude between conditions was reduced to 0.24 µV. This is why our approach to determining optimal filtering parameters for amplitude scores involves quantifying the effects of filtering on the signal as well as the noise.

Figure 9:

Demonstration of how filters reduce amplitude differences but not latency differences. (a) Simulated P3 wave in two conditions, with a difference in peak amplitude of 0.5 µV between the conditions. (b) Same waveforms as in (a) after the application of a high-pass filter with a 1 Hz half-amplitude cutoff and a slope of 12 dB/octave. The filtering caused a reduction in the amplitude difference to 0.24 µV. (c) Simulated P3 wave in two conditions, with a difference in peak latency of 100 ms between the conditions. (d) Same waveforms as in (c) after the application of a high-pass filter with a 1 Hz half-amplitude cutoff and a slope of 12 dB/octave. The difference in latency between the two conditions is still 100 ms. The waveforms were created using ex-Gaussian functions with a standard deviation of 58 ms, a tau of 2000 ms, an amplitude of 0.5 µV or 1µV, and a Gaussian mean of 320 ms or 220 ms.

Filters do not typically have large effects on latency scores, and any observed effects may consist of an increase or a decrease depending on the shape of the waveform. Moreover, if a shift in latency does occur, the latency scores will typically be shifted equivalently across conditions. This is illustrated in Figures 9 c and 9 d, which show a simulation of two conditions in which the P3 latency differs. In the unfiltered data (Figure 9 c), the peak latency differed by 100 ms between the two conditions. When a high-pass filter with a half-amplitude cutoff of 1 Hz was applied (Figure 9 d), the peak latency was shifted leftward by 6.4 ms in both conditions, and the difference in peak latency between the two conditions remained 100 ms. Because filtering does not consistently reduce the difference in latency between groups or conditions, it is not typically necessary to consider the effects of filtering on the signal relative to the noise (SNR_SME) when selecting an optimal filter for latency scores ¹⁵. Instead, one can simply determine which filters yield the lowest noise (the smallest SME value), along with a consideration of waveform distortion.

6.1. Example: Selecting optimal filter parameters for P3 peak latency

In this subsection, we will use the peak latency score for the P3 wave from the ERP CORE visual oddball paradigm to illustrate our process of selecting filter parameters for latency scores. As in our analyses of P3 mean amplitude in Section 5, we filtered the continuous EEG with many combinations of low- and high-pass filters prior to creating the averaged ERPs. We then used bootstrapping (Luck et al., 2021) to obtain the SME for P3 peak latency, which was scored from the rare-minus-frequent difference wave as the peak latency between 300 and 600 ms at the Pz electrode site. We then aggregated across participants by computing the RMS of the single-participant SME values. The resulting RMS(SME) values are shown in Figure 10 (see Supplementary Figure A1 for the grand average waveforms).

Figure 10:

Noise defined by root mean square of the standardized measurement error values for P3 peak latency from the ERP CORE across a wide range of filter combinations. The continuous EEG was filtered prior to averaging with every combination of seven high-pass filter cutoffs (0, 0.01, 0.05, 0.1, 0.5, 1, and 2 Hz) and seven high-pass filter cutoffs (5, 10, 20, 30, 40, 80, and 115 Hz). All filters used here were noncausal Butterworth filters with a slope of 12 dB/octave, and cutoff frequencies indicate the half-amplitude point.

The high-pass cutoff frequency had relatively little impact on the RMS(SME) until the cutoff reached extreme values (1 Hz or greater). By contrast, the low-pass cutoff frequency had a large impact, with progressively smaller (better) RMS(SME) values as the cutoff frequency decreased. This is the opposite of the pattern that was observed for mean amplitude scores, where the high-pass cutoff had a large effect on the RMS(SME) and the low-pass cutoff had virtually no effect (see Figure 8 b). These opposite patterns reflect the fact that mean amplitude scores are strongly impacted by low-frequency noise but not by high-frequency noise, whereas peak latency scores are strongly impacted by high-frequency noise but not by low-frequency noise. This further reinforces the general point that the optimal filter settings depend on how the data will ultimately be scored.

The best RMS(SME) value was produced by the combination of a 0.5 Hz high-pass filter and a 5 Hz low-pass filter. However, it is also necessary to consider the waveform distortion produced by the filters. As shown in Figures 7 and A2, high-pass filters produce an artifactual amplitude percentage above our criterion of 5% for half-amplitude cutoffs above 0.2 Hz. We therefore recommend a high-pass cutoff of 0.2 Hz and a slope of 12 dB/octave (which yields an RMS(SME) value that is only slightly worse than the 0.5 Hz cutoff).

For the simulated P3 wave, low-pass filters produced minimal waveform distortion as long as the half-amplitude cutoff was at least 10 Hz (see Figure 6). We therefore recommend a low-pass cutoff of 10 Hz and a slope of 12 dB/octave, which significantly decreases the noise while producing minimal waveform distortion. Even with a 5 Hz cutoff, the only time-domain distortion was a mild decrease in P3 onset latency. It would therefore be reasonable to use a 5 Hz cutoff in studies where the absolute onset latency of the P3 wave is not of interest. Note that this is much lower than the low-pass cutoff frequency of 30 Hz that we previously recommended for general use in cognitive and affective research (Luck, 2014). This shows the value of using a formal procedure to determine the optimal filtering parameters.

7. Limitations and Future Directions

The present approach to filter selection has several strengths, including the use of objective and quantifiable properties of filters with respect to specific ERP effects and the scoring methods used to quantify them. However, subjective decisions are involved in selecting the shape of the artificial waveforms that are used to assess waveform distortion. In addition, the 5% artifactual peak percentage criterion, although reasonable, is somewhat arbitrary. Nonetheless, the present approach makes it possible to quantitatively assess both the benefits and costs of filtering.

Another important limitation of the present approach is that it is designed only for studies in which the scores are obtained from averaged ERP waveforms (because the SME is a measure of data quality for such scores). It is not designed for single-trial analyses, which can be quite valuable and are becoming increasingly common (Bürki et al., 2018; Heise et al., 2022; Volpert-Esmond et al., 2018; Winsler et al., 2018). However, there is good reason to believe that the present approach will work well for single-trial analyses in which mean amplitude is scored from single-trial EEG epochs and these single-trial scores are then entered into the statistical analyses. This scoring method is a linear operation, as is averaging across trials, and the filters typically used in ERP research also involve a linear or approximately linear operation. The order of operations does not matter for linear operations (Luck, 2014), so the effects of filtering should be the same whether the mean amplitude is measured before or after averaging. Thus, we conjecture that our filter selection approach will also be well suited for single-trial analyses using mean amplitude scores. However, additional research would be required to verify this conjecture.

The present approach is also not designed for mass univariate analyses, in which statistical comparisons between groups or conditions are made at a large number of individual time points and/or electrode sites, accompanied by an appropriate correction for multiple comparisons (Frossard & Renaud, 2022; Groppe et al., 2011; Maris & Oostenveld, 2007). As discussed in Section 3.2, the SNR for an individual time point can be estimated by simply dividing the voltage at that time point by the standard error of the mean (SEM) at that time point. Rather than using SNR_SME, this traditional SNR value could be used in selecting filter parameters. However, it is not obvious how one would combine SEM values across time points and/or electrode sites or how these SEM values would interact with the procedure for correcting for multiple comparisons. This is another avenue for future research.

Impact Statement:

Filtering can have a large impact on ERP data, influencing both statistical power and the validity of conclusions. However, there is no standardized, widely-used method for determining optimal filter settings for cognitive and affective ERP research. Here, we provide a straightforward method along with tools that will allow researchers to easily determine the most appropriate filter settings for their data.