Ultrafast dynamic machine vision with spatiotemporal photonic computing

Abstract

Ultrafast dynamic machine vision in the optical domain can provide unprecedented perspectives for high-performance computing. However, owing to the limited degrees of freedom, existing photonic computing approaches rely on the memory’s slow read/write operations to implement dynamic processing. Here, we propose a spatiotemporal photonic computing architecture to match the highly parallel spatial computing with high-speed temporal computing and achieve a three-dimensional spatiotemporal plane. A unified training framework is devised to optimize the physical system and the network model. The photonic processing speed of the benchmark video dataset is increased by 40-fold on a space-multiplexed system with 35-fold fewer parameters. A wavelength-multiplexed system realizes all-optical nonlinear computing of dynamic light field with a frame time of 3.57 nanoseconds. The proposed architecture paves the way for ultrafast advanced machine vision free from the limits of memory wall and will find applications in unmanned systems, autonomous driving, ultrafast science, etc.

A spatiotemporal photonic computing architecture breaks the memory wall and realizes nanosecond dynamic machine vision.

INTRODUCTION

Processing dynamic light fields at high speed has proven to be of vital importance in visual computing and scientific discovery. With the development of artificial neural networks (1, 2), machine learning–based electronic visual computing has achieved excellent performances in various applications (3, 4). The rapid implementation of dynamic visual computing such as tracking, detection, and recognition has become vital in time-varying scenarios, including autonomous driving (5) and intelligent robots (6). Unfortunately, the integration density of silicon transistors gradually approaches physical limits, thereby saturating the computational speed of electronic computers and electronic visual computing (7, 8). Besides visual computing, studying ultrafast light fields is also crucial for scientific research. Repetitive probing and continuous imaging support recording transient processes down to the nanosecond and picosecond levels (9–11). However, the reconstruction and analysis of ultrafast visual dynamics require digital transferring and postprocessing with electronic computers, which precludes real-time analysis and feedback control of the ultrafast phenomena (12).

Endowed with low-loss, parallel, ultrafast, and clock-free light propagation, photonic computing has been heralded as a prospective solution to alleviate the limitations of electronic computing and expedite light-field processing (13–17). Recently, researchers have validated the advantages of photonic computing in performing high-speed linear matrix operations with coherent photonic integrated circuits (18, 19), on-chip resonators (20), diffractive optical processors (21–25), photonic phase-change materials (26–28), dispersive optical delay lines (29), etc. It has also been demonstrated that light can be used for ubiquitous computing, including nonlinear neuron activation (30), nondeterministic polynomial-time hard (NP-hard) optimization (31, 32), equation solving (33), and integration as well as differentiation (34–36). On the basis of the linear and nonlinear optical computing paradigms, photonic neural networks have been constructed for machine vision tasks such as edge detection (37), image classification (25, 38), saliency detection (22), and human action recognition (25, 39). Despite recent advances, state-of-the-art photonic computing methods are incapable of processing ultrafast dynamic light fields. Currently, to process spatiotemporal light fields, dynamic inputs are usually computed sequentially in the spatial domain, while the spatial output at different time steps needs to be transmitted, stored, and further processed with digital electronics (25, 39). Although such a procedure exploits the advantage of high spatial parallelism of light propagation, digital transmission and read/write operations of memory pose severe limitations to inference speed, which impairs the merit of photonics for high-speed computing.

The incorporation of spatial and temporal photonic computing to eliminate the digital bottlenecks is promising for ultrafast light-field processing. This is because the spatiotemporal manipulation of light fields can overcome the limitations of spatial-only modulation (40, 41). Temporal information preprocessing with nonlinear reservoirs has been applied in vowel recognition (42), serial data classification (43), time-series prediction (44), etc. In addition, multi-mode fiber has also been used to build a nonlinear reservoir for single-image classification (45). However, these solutions apply only to spatial or temporal data. The limited degree of freedoms (DOFs) render these approaches ineffective in processing high-dimensional light fields. Another approach, that is, computational imaging, exploits the dimensional advantages of light and realizes high-speed imaging. For example, single-pixel imaging encodes the spatial data in the temporal dimension for fast and compressed imaging (46). The time-stretched serial time-encoded amplified imaging uses a dispersed supercontinuum laser pulse to spectrally capture and record the serialized image contents (9). However, without a computational model, these computational imaging methods only record the data and are unable to effectively compute and make decisions. Thus far, a general parametric photonic computing solution to process spatiotemporal light fields at high speed is still lacking, which restricts the rapid implementation of advanced machine vision architecture and real-time analysis of ultrafast visual dynamics. Technically, (i) owing to the inherent dimension mismatch of the spatial and temporal light fields, computing and converting between highly parallel spatial light fields and high-speed temporal optical dynamics remain challenging. (ii) The DOFs of spatial and temporal computing are limited; thus, there is a gap between the existing photonic computing methods and full-space spatiotemporal computing.

In this study, we propose and implement a spatiotemporal photonic computing (STPC) architecture for ultrafast dynamic machine vision. By co-optimizing a general STPC unit, the STPC extracts spatiotemporal information and makes predictions based on time-varying light fields. In essence, the STPC architecture comprises the spatial computing module, the spatiotemporal multiplexing module, and the temporal computing module. Specifically, (i) a spatial computing module involves a spatial modulator that performs per-point multiplication, convolution, etc. (ii) To effectively compute and convert between spatial and temporal optical dynamics, we devise spatial multiplexing (SMUX) and wavelength multiplexing (WMUX) modules to match the highly parallel spatial outputs and high-speed temporal inputs while adequately preserving content information. Spatial content is thus processed and mapped to parallel sequences of temporal dynamics spatially and spectrally, leading to the generation of a temporal computing–compatible spatiotemporal feature space. (iii) In the temporal computing module, to store and merge the fast-changing optical signals, an analog temporal buffer is constructed such that the information can be delayed and reproduced in the optical domain. Temporal matrix-vector multiplication (MVM) is then performed to build weighted connections in the time domain, which is co-designed with spatial computing modules to implement comprehensive computing in the entire spatiotemporal plane. The STPC architecture is enhanced with an experimental system learning method, which can optimize the parametric physical system along with the computational model and improves the accuracy of STPC by more than 80%. The experiments of the SMUX-STPC network showed superior performance on spiking sequence classification, human action recognition, and object motion tracking tasks. Compared with existing photonic computing methods, the SMUX-STPC system increases parameter efficiency and reduces inference time by more than one order of magnitude. A two-layer all-optical WMUX-STPC network with multivariate nonlinear activation function recognizes the ultrafast flashing sequences with nanoseconds frame time, free of memory read/write latencies. The STPC architecture bolsters high-performance photonic neural networks and enables real-time analysis of dynamic visual scenes beyond nanosecond time scales.

RESULTS

STPC architecture

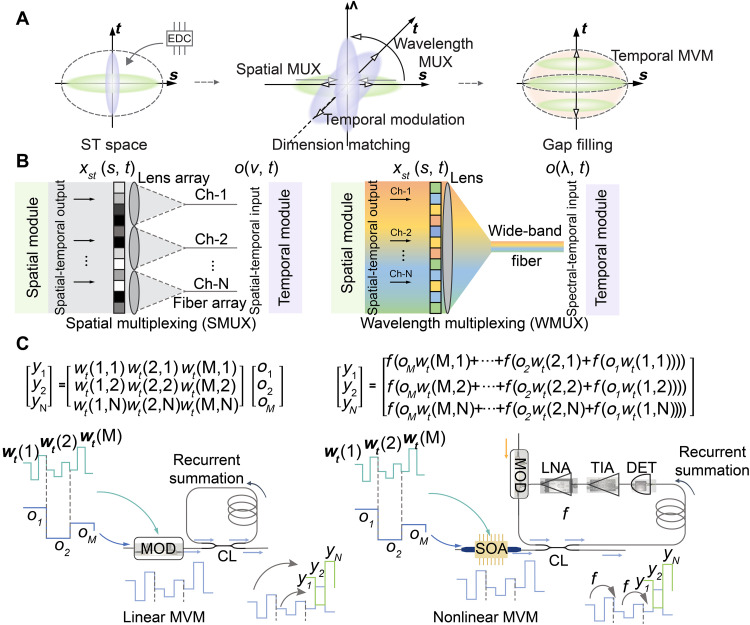
The STPC architecture is illustrated in Fig. 1A. Millisecond-to-nanosecond time-varying light fields from a dynamic scene propagates into the STPC network, which consists of cascaded blocks of STPC units, each with a spatial module and a temporal module connected by a multiplexing module. Through combinations of spatial and temporal operations, the STPC unit extracts information from the high-dimensional dynamic light fields and infers semantic information from the contents of the scene. The core STPC system is shown in the left panel of Fig. 1B, with the network model displayed on the right. The unfolded system is shown in Fig. 1C. Each STPC unit transforms the spatiotemporal input x_i(s, t) to the output y(s, t), where s, t are the spatial and temporal coordinates, respectively. The output y(s, t) is subsequently activated nonlinearly and fed into the next layer. There are three main procedures in each spatiotemporal (ST) layer: (i) spatial modulation in the spatial computing module, (ii) spatiotemporal multiplexing, and (iii) MVM in the temporal computing module. The input spatiotemporal light field x_i is a three-dimensional (3D, two spatial dimensions and one temporal dimension) stack. In the spatial computing module, x_i(s, t) is weighted with a spatial light modulator, such as a digital micromirror device (DMD), or a liquid crystal on silicon–based spatial light modulator to perform amplitude and/or phase modulation, that is

$$x_{st}(s,t)=w_s(s,t)x_i(s,t)$$ (1)

Fig. 1. STPC for ultrafast dynamic light-field processing.

(A) STPC architecture. Dynamic scene encoded on spatiotemporal light fields enters the STPC network consisting of STPC units. Each unit contains a spatial module and a temporal module connected by a multiplexing module. Decision-making is finally executed by the last STPC unit. (B) Core system of the STPC unit (left) and the corresponding network model (right). The input spatiotemporal light field x_i is modeled as a 3D (two spatial dimensions and one temporal dimension) stack. In the spatial module, a DMD performs spatial modulations and expands the stack in the time dimension. Spatial output x_st is spatially/spectrally multiplexed (MUX) into the temporal module (o). Through temporal modulations in the modulators (MOD) and buffering in the recurrent buffer, the temporal module performs weighted connection (MVM) in the time domain and produces the output y, which is activated by photonic nonlinearity (NL) and fed to the next layer. (C) Unfolded system of an STPC unit in time. The M/K spatiotemporal input slices are expanded K times in the spatial module, producing M output slices. The M slices are sequentially computed and recurrently merged in the N × M temporal MVM to produce the N final output slices. COL, collimator; FL, focusing lens; CL, 2 × 2 fiber coupler; SOA, semiconductor amplifier.

As shown in Fig. 1 (B and C), during the period of each input temporal slice, x_i(s, t) is sequentially modulated K times, such that the effective number of temporal slices in x_st(s, t) is K times that of x_i(s, t). Although we used element-wise weighting in spatial computing, it can also be generalized to other spatial computing models, such as convolution (47) and diffractive processing (25).

The spatially weighted results x_st(s, t) are then fed into the temporal channels. When spatial outputs transition into temporal channels, the mode diversity decreases drastically. Thus, directly coupling the spatial contents into the single-mode temporal channel leads to the loss of most of the information. Thus, we propose SMUX STPCs and WMUX STPCs to increase the information capacity (48), which coordinates between highly parallel spatial and high-speed temporal modules

$$o(u,t)=\int T(u,s)x_{st}(s,t)ds$$ (2)

where T(u, s) is the spatial-to-temporal transfer function, and u is in the multiplexing dimension, which is the space and wavelength for SMUX and WMUX, respectively. The details of SMUX and WMUX are presented in Fig. 2B.

Fig. 2. Implementation of multiplexing modules and temporal MVMs.

(A) Dimensionality of STPC. Left: Basic spatial and temporal modules with dimension mismatch and a gap in the spatiotemporal plane, which is usually alleviated with an EDC at the expense of speed bottlenecks. In the STPC, the spatiotemporal dimension mismatch is resolved with multiplexing techniques (middle), and the spatiotemporal gap is filled using the temporal MVM unit (right). (B) Implementation of spatial and wavelength multiplexing techniques that coordinate between spatial and temporal modules. In space-multiplexed (SMUX) STPC, the high-resolution output from the spatial module is divided into subdivisions. Light in each division is coupled into separate temporal fiber channels through a lens array. In wavelength-multiplexed (WMUX) STPC, spatial light is encoded on different wavelengths, and the multiwavelength optical signal is fed into a wide-band fiber channel. (C) Implementation of the linear (left) and nonlinear (right) MVM. Left: Each multiplier in the vector is multiplied by a column of multiplicands in the temporal modulator. The multiplied signals are then looped in the temporal buffer and recurrently added. Right: A nonlinear temporal MVM. The SOA performs temporal weighting. The detector (DET), amplifiers (transimpedance amplifier, TIA; voltage amplifier, LNA), and modulator (MOD) construct an OEO loop, which nonlinearly transforms the inputs in the temporal buffer. CL, 2 × 2 fiber coupler.

The temporal module then takes in the multiplexing outputs o(u, t), where a temporal MVM is constructed. Discretizing the time, the temporal operations can be formulated as

$$y(u,k\text{Δ}\mathrm{\tau })={\text{Σ}}_i{w}_t(k\text{Δ}\mathrm{\tau },i\text{Δ}\mathrm{t})o(u,i\text{Δ}t)$$ (3)

Specifically, temporal modulation is conducted to weigh the temporal inputs with an intensity modulator (MOD), producing w_t(kΔτ, iΔt)o(u, iΔt), with Δτ denoting the output sampling period and Δt indicating the recurrent period in the temporal buffer. The temporal buffer, constructed through waveguide extension and recurrent coupler (CL) connection, offers picosecond to millisecond buffering and merging of temporal signals. With i = 1,2,3, …, M and k = 1,2,3, …, N, Eq. 3 essentially formulates the multiplication between an M × 1 vector and an N × M matrix. An implementation of linear MVM and the extension to nonlinear MVM are presented in Fig. 2C. The dynamic light field y(u, t) is then nonlinearly activated using nonlinear optical effects such as the saturable gain effect of a semiconductor optical amplifier (SOA) and demultiplexed back into the spatiotemporal domain, which is fed into the subsequent ST computing units for further processing. Last, the characteristics of the light field are inferred, including the type of action and (non-)normality of the transient pattern.

Figure 2A shows the dimensionality of photonic computing. As shown in the left panel of Fig. 2A, basic spatial and temporal photonic computing modules are afflicted with (i) dimension mismatch and (ii) gap in the spatiotemporal plane. Electronic digital computing (EDC) can help alleviate these dimension issues; however, it also induces speed bottlenecks due to the read/write operations of the memory. STPC resolves these two issues in two ways, respectively. First, as shown in the middle panel of Fig. 2A, directly coupling the spatial light fields into the temporal channels would shrink the spatial information diversity (shaded arrow). The lost information could be recovered by stretching the shrunken spatial dimension and modulating the light field in the temporal dimension in SMUX-STPC. In the WMUX-STPC, the spatial dimension is rotated to the wavelength dimension such that the information can be accommodated in the temporal channel with a large optical bandwidth. Second, the photonic computing DOFs are limited. As shown in the left panel of Fig. 2A, a single spatial computing module (green ellipsoid) or temporal computing module (purple ellipsoid) could only process a temporal slice or a spatial slice, respectively, thus a gap between the single modules (inner dashed ellipsoid in the right panel of Fig. 2A) and the full ST plane (external dashed ellipsoid in the right panel of Fig. 2A). In this work, we propose the temporal MVM to connect the outputs from spatial computing modules at different time steps so that the computing DOFs are extended to the full spatiotemporal plane. With matched dimensions and fulfilled spatiotemporal plane, the STPC architecture can process dynamic light fields without memory read/write latency.

Figure 2B depicts the implementation of the SMUX and WMUX in the STPC. In SMUX-STPC, the input space is divided into subregions Ω_j, and the spatial features in each division are collectively coupled into a single-mode-fiber channel through the focusing lens, that is, o(j, t) = ∫_ΩjT(j, s)x_st(s, t)ds, with T(j, s) being the coupling coefficients from spatial location s to the jth temporal channel. The SMUX and high-speed modulation implemented by millions-of-pixel spatial light modulators convert spatial information spatiotemporally. The higher modulation rate and the more spatial channels, the more retained information. With a fixed modulation speed and spatial channel number, there is a trade-off between the processing time and the amount of information retained. In WMUX-STPC, the spatial features are encoded onto different wavelengths and multiplexed into a single temporal channel, that is, spatial-to-temporal transfer function T(j, s) = δ(s − s_j)T(s), and o(j, t) = ∫ δ(s − s_j)T(s)x_st(s, t)ds, with δ(s − s_j) being the Kronecker delta function that encodes the spatial features at s_j onto wavelength j and T(s) being the spatial coupling coefficient. With WMUX, abundant spatial contents can be conserved spectrally so that it supports the processing of ultrafast dynamics without additional high-speed spatial modulators.

Figure 2C illustrates the mathematical model of the temporal MVM, including the linear (left) and nonlinear (right) implementations. Denote the buffer transfer function as f(·), the general form of the temporal MVM can be formulated as y(u, k) = f{o_Mw_t(k, M) + … + f[w_t(k,2)o₂ + f[w_t(k,1)o₁)]} (k = 1, 2, …, N). In the linear implementation, the fiber loop is used as the buffer; thus, f(x) = x. The input series o₁, o₂, …, o_M is multiplied by vectors w_t(1), w_t(2), …, w_t(M) {w_t(j) = [w_t(j,1), w_t(j,2), …, w_t(j, N)]^T}, respectively, with the intensity MOD, forming o₁w_t(1), o₂w_t(2), …o_Mw_t(M) injected into the temporal buffer. Each time light cycles through the temporal buffer, the signal is recurrently merged, such that the output sums to y = o₁w_t(1) + o₂w_t(2) + … + o_Mw_t(M). The linear matrix multiplication performs coherent summation and thus supports complex matrix elements at a single wavelength. For signals at different wavelengths, the light intensities are summed so that the matrix elements are nonnegative real values. A nonlinear implementation of the temporal MVM is also shown in the right panel of Fig. 2C. The temporal weighting is performed by modulating the injection current of the SOA. In the recurrent buffer, an optical-electrical-optical (OEO) converter is constructed with a photodiode (PD), a transimpedance amplifier (TIA), a voltage amplifier [low-noise voltage amplifier (LNA)], and an intensity MOD. Thus, the temporal transfer function f(·) exhibits nonlinear behavior that is programmable by tuning the bias of the intensity modulator. When the intensity modulator is biased at its minimal output (the NULL point), f(x) = a · sin (b · x)², where a and b are system parameters depending on the input power and the loop gain coefficient. As nonlinear matrix multiplications are computed in terms of intensity, the elements of the nonlinear matrix elements are nonnegative as well. In addition, as the nonlinear buffer features a sinusoidal transfer function here, the matrix elements are thus nested in the sinusoidal function. In general, the proposed temporal MVM is a temporally reconfigurable recurrent neural network (49).

SMUX STPC network for high-speed dynamic scene analysis

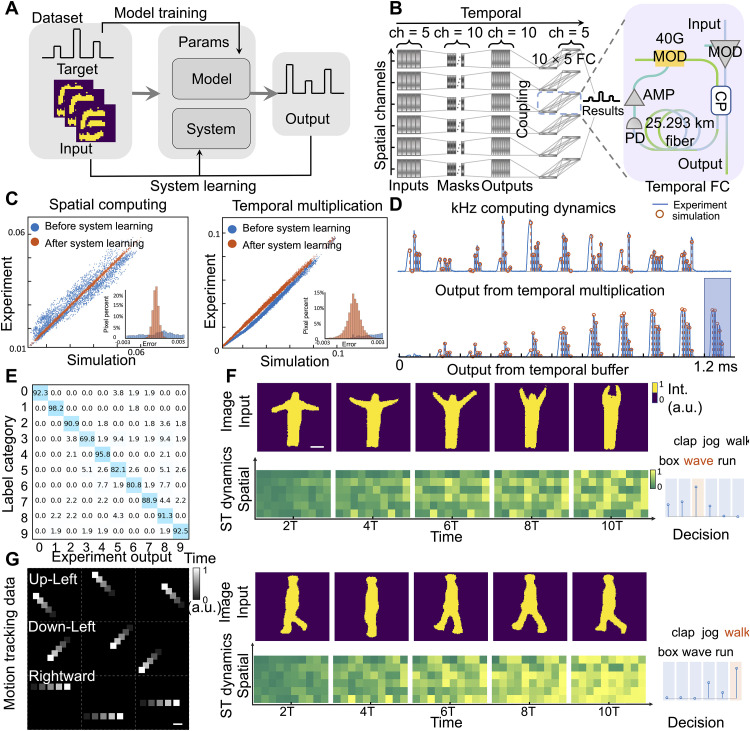
Figure 3A illustrates the learning process of the STPC physical experiments, including model training and system learning. The entire system consists of three parts: datasets with input and target pairs, an experimental system, and the experimental outputs. The experimental system contains the model parameters and system parameters. The model parameters include the weights of the STPC, which primarily involve the spatial computing masks and the temporal modulation weights. The system parameters characterize the transfer function of the experimental physical system with spatial and temporal modules that can be initially calibrated with random inputs. Given the training input and target pairs, we pretrain the system using the calibrated system parameters until convergence. Owing to the bias and noise in the calibration data, the experimental results deviate from the simulation. Here, we devise a system learning process to finely train the system parameters when the model parameters are fixed and the system parameters are updated to fit the experimental output with higher precision. After completing the system learning process, the system corresponds better with the numerical prediction, and we use the refined system parameters for the final training of the model parameters, which are subsequently used for the experiments.

Fig. 3. Space-multiplexed (SMUX) STPC network for high-speed dynamic scene analysis.

(A) Model training and system learning. The experimental system contains model parameters and system parameters. The model parameters configured in the STPC are learned with training input and target pairs, while the system parameters characterizing the transfer function of the physical system are learned with the experimental inputs and outputs to improve the system modeling fidelity. (B) An SMUX-STPC network consisting of six spatial divisions was designed to recognize high-speed video dynamics. Each division was spatially and temporally computed to infer the final results. (C) Spatial computing and temporal multiplication accuracy before (blue) and after (orange) system learning on spiking handwritten digits classification experiment. Inset shows the error distribution before and after system learning. (D) Kilohertz computing dynamics of the STPC system. The outputs from temporal multiplication were fed into and merged in the temporal buffer. The orange circles represent the simulation results, while the green line plots represent the experimental outputs. (E) Experimental confusion matrix of spiking handwritten digits classification. (F) Two samples from the human action recognition experiment. The first and the third rows show the input frames to the STPC network. The second and fourth rows show the spatiotemporal dynamics in the temporal buffer along with the final decision. (G) Examples in motion tracking dataset. Square objects were configured to move in three directions, up-left, down-left, and rightward. Scale bars, 1 mm. PD, photodiode; MOD, modulator; AMP, amplifier; CP, coupler; a.u., arbitrary units.

The proposed spatiotemporal architecture was validated using an SMUX-STPC network consisting of six SMUX divisions configured to recognize high-speed dynamics (Fig. 3B). In each division, every frame in the five-frame sequence is modulated with two spatial masks on the DMD working at a frame rate of 8024 frames per second (fps). Each spatial computing produced a temporal stack of 10 frames, summing to a spatiotemporal stack of dimension 6 × 10. The 6 × 10 outputs were then coupled into temporal channels. In the temporal module, multiplications were performed in a SOA by modulating its injection current. An OEO loop was constructed with a 25.293-km fiber ring, amplifiers (AMP, including a TIA and a low-noise amplifier), and intensity MOD to buffer and relay the inputs. Through the 10 × 5 temporal MVM in the temporal module, the 6 × 10 spatiotemporal outputs from the spatial module were transformed to a spatiotemporal stack of size 6 × 5, which was combined for the final inference results (details are provided in Materials and Methods).

Furthermore, the STPC network was experimentally tested on the dynamic version of the benchmarking handwritten digits classification task using the neuromorphic Modified National Institute of Standards and Technology database (N-MNIST) (50), which includes 10 classes of temporal spiking events. Each sample was preprocessed into a sequence of five spiking maps with a resolution of 541 × 541 DMD pixels (details are provided in Materials and Methods). To calibrate the system parameters, we first calibrated the DMD, SOA, and temporal buffer and used these measured transfer functions for the system simulation during the pre-training process (details of system calibration are provided in Materials and Methods). However, owing to the difference between the distributions of the calibration and dataset inputs, as well as the measurement noise present in the calibration process, the experimental outputs on 61 randomly selected training sequences obviously deviated from the simulations, as is shown by the blue data points in Fig. 3C. We further used these 61 randomly selected training sequences as the system learning subset to finely adjust the coupling matrix of the DMD and the system parameters of the SOA with the input data and the measured output. During system learning, the system parameters were updated using the gradient descent training method, targeting the captured experimental results (details are provided in Materials and Methods). After system learning and additional training, the experimental measurements corresponded better with the expected results (orange data points in Fig. 3C), and the relative error of spatial computing and temporal multiplication decreased from 12.05 to 1.20% and from 17.48 to 2.91%, that is, by 90.04 and 83.35%, respectively.

Figure 3D shows the evolution of the temporal buffer in temporal computing. In the first row, the output from temporal multiplication is displayed, which contains 10 coupled inputs, each weighted five times by SOA. In the temporal buffer, at each time step, the input light was merged with the buffered light in the temporal buffer. The merged light then passed through the buffer transfer function. There were 10 cycles of buffer and merge. At time step 11, the output was produced (shaded box). The constructed temporal buffer performed a 10 × 5 full connection at a frame rate of 8024 fps. The 6 × 5 spatiotemporal outputs were then spatially computed to classify the objects as one of the 10 digits. In the experiment, before system learning, the experimental accuracy degraded to 53.03% on the selected system learning subset, far below the training accuracy of 98.49%. After the system learning, we randomly selected 500 testing sequences from the testing set to evaluate the blind testing accuracy. The overall experimental accuracy was 88.4%, which agreed well with the simulation testing accuracy of 92.1%. The confusion matrix is shown in Fig. 3E. More than half of the categories were classified with more than 90% accuracy.

To further validate the capability of SMUX-STPC to recognize high-speed dynamic motion, we experimented with the KTH human-action video dataset (51). The dataset contained videos of six different actions, namely, boxing, clapping, waving, jogging, running, and walking, performed by 25 subjects. Videos were further decomposed into sequences of training and testing datasets and were fed into the constructed SMUX-STPC for recognition, with each input sequence consisting of five frames (details of preprocessing in Materials and Methods). On the basis of the content of the five-frame inputs, the STPC network determined the category. Figure 3G shows two inputs, “waving” and “walking,” and the corresponding spatiotemporal dynamics. For these two different classes, the spatiotemporal outputs in the first temporal step were highly similar, suggesting that single-frame images have limited diversity and that human action recognition based on a single image frame is challenging. As more frames were fed into the system, the unique features of the different motions began to accumulate. Even with the same STPC architecture, the recognition performances with dynamic inputs (five frames) outperform those of single-frame inputs by more the 10% (fig. S16), which implies the importance of the STPC architecture in dynamic light-field processing. After system learning, the experimental sequence accuracy increased from 48.49 to 80.45%, approaching a simulated accuracy of 86.81%. We also calculated the video accuracy voted by the winner-takes-all policy for all the frames of the same video. The experimental video accuracy of the STPC was 90.74% (successfully classified 49 of the 54 testing videos), which is the same as simulation video accuracy. The confusion matrix and video classification results are shown in fig. S4.

The high-speed SMUX-STPC network will revolutionize video-based real-world applications, for example, biological research (52). In biology, tracking cell movements is a fundamental procedure that helps with analyzing tissue development and diseases (53). To study the potential of SMUX-STPC on this problem, we constructed a motion tracking dataset comprising 704 cell-like square objects moving in three directions, up-left, down-left, and rightward (Materials and Methods). The examples from the dataset are shown in Fig. 3G. An SMUX-STPC network with spatial outputs of size 8 × 10 and temporal outputs of size 8 × 5 was trained to classify the object as one of the three categories. With sufficient spatial and temporal connections, the SMUX-STPC successfully classified the testing dataset with 100% accuracy in the experiment, corresponding well with the simulation. The complete testing datasets and the spatiotemporal dynamics are shown in movie S1.

We compare the SMUX-STPC system with a state-of-the-art photonic video processor (25) performing the same tasks on the KTH and motion tracking dataset. The results are shown in fig. S14 and section S1. Endowed with adequate trainable spatial and temporal connections, the SMUX-STPC architecture has competitive performances compared with the previously reported diffractive processor with 0.27 million parameters and five recurrent blocks while containing only 6.20- and 7.60-kilobyte parameters for the KTH recognition and motion tracking tasks, respectively, thus reducing the number of parameters by more than 35-fold compared with the 0.27-million-parameter benchmark. Furthermore, free from the limit of digital latency, the STPC system works at a frequency of 8024 Hz. With 10 spatial computes for the final inference, it has thus a speed of 802.4 sequences per second, which effectively increases the processing rate by more than 40 times compared with ~20 fps state-of-the-art speed (25, 39). The details of the system evaluations are provided in section S1.

WMUX all-optical nonlinear STPC network for nanosecond dynamic light-field analysis

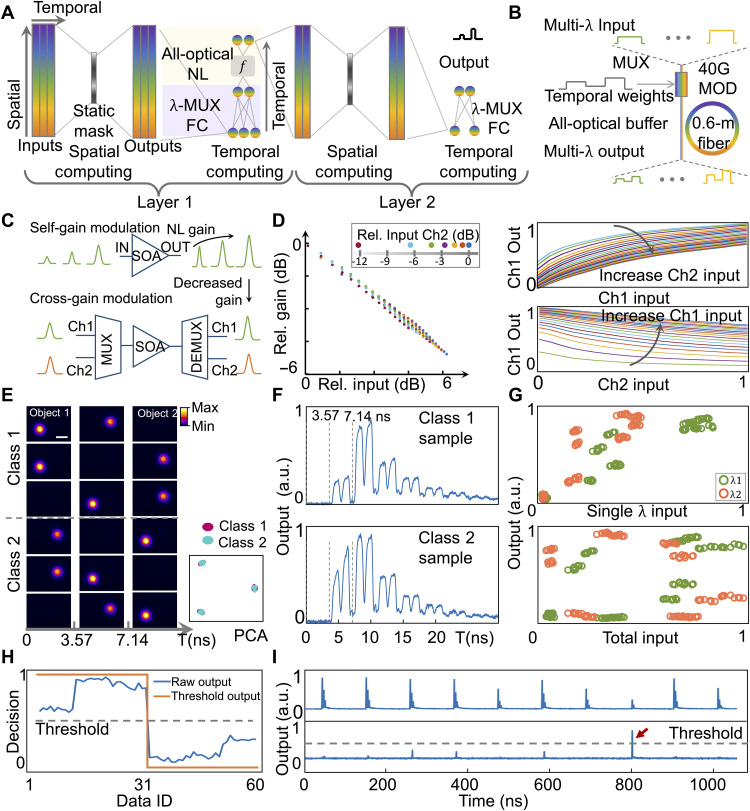
When the spatial inputs are encoded on different wavelengths, making use of a large spectral bandwidth, multiwavelength inputs can be multiplexed into the temporal channel without sacrificing spatial information. Thus, the structure of the WMUX-STPC is appropriate for processing ultrahigh-speed visual dynamics. To enable ultrafast spatiotemporal computing, a two-layer all-optical nonlinear WMUX-STPC network was constructed, as shown in Fig. 4A. In the spatial computing module, the spatial content was processed at the speed of light using a static spatial modulation mask on DMD. Subsequently, the spatial contents were squeezed into a single temporal fiber channel, and the weighted connection was temporally implemented with a 40-GHz modulator and a 0.6-m optical fiber buffer. All-optical nonlinearity between the two layers was realized through the nonlinear gain process of the stimulated emission. The details of the wavelength-multiplexed full connection are shown in Fig. 4B. The temporal dynamics were weighted and recurrently added in the all-optical buffer. At each time step, the spatial content was squeezed spatially and conserved spectrally. Thus, the spatial contents were computed in parallel by using the wideband optical modulators. Figure 4C illustrates the all-optical nonlinearity from the stimulated emission process of the SOA. The gain coefficient of the SOA is dependent on the input power and decreases with the increase of the input power. For self-gain modulation with input and output signals of the same wavelength, an increase in the input power leads to an increase in the output power but a decrease in the gain coefficient. For the multispectral inputs, an increased input power at one wavelength lowers the total gain of the SOA, resulting in a decrease in the output power at other wavelengths. In this work, self-gain modulation and cross-gain modulation effects are combined to construct a multivariate nonlinear neuron activation function, z_λi = g(y_λ1, …y_λN), where y_λi is the input power at wavelength λ_i, and z_λi is the output power at wavelength λ_i. Figure 4D shows the measured gain versus the input power, in which a highly nonlinear region was used in our experiment. We swept the input power of Ch1 and Ch2 and measured the output power of Ch1 (with Ch2 as the control channel). A gain coefficient dependent on the total input power was clearly observed (section S2). The self-modulation and cross-modulation effects of each wavelength channel were measured. The results are shown in the right panel of Fig. 4D. When increasing the input power of one wavelength, the output power at the corresponding channel will increase nonlinearly (top right panel in Fig. 4D), while the output at other channels will decrease nonlinearly (bottom right panel in Fig. 4D), as a result of the decreased total gain. Previously reported optical nonlinear neuron activation function models were univariate; that is, the output of a specific channel depends solely on its own input (30). Here, we develop a novel multivariate optical nonlinear activation function for multivariate STPC by modeling the self and mutual nonlinearity across multispectral channels.

Fig. 4. Wavelength-multiplexed (WMUX) all-optical nonlinear STPC network for nanosecond dynamic light-field analysis.

(A) Wavelength-multiplexed STPC network. The spatial light field was encoded on wavelengths and multiplexed (MUX) into a temporal channel. Different wavelength channels shared the multiplication weights and were recurrently added. Between layers, an all-optical nonlinear module took in the multispectral inputs, and the outputs were demultiplexed spatially after nonlinear activation. (B) Implementation of wavelength-multiplexed full connection. The multispectral spatial outputs were multiplexed into the temporal channel and modulated with a 40-GHz intensity modulator (MOD) and recurrently added in the temporal buffer consisting of a 0.6-m fiber ring. (C) Spectral nonlinearity of SOA, with nonlinear self-gain modulation and cross-gain modulation. (D) Left: Measured highly nonlinear region of SOA. Data points with the same color denote the same control power. Right: Measurement of self-gain modulation (top) and cross-gain modulation (bottom). (E) Slow motion of the ultrafast dataset captured by an InGaAs camera. Right: Low-dimensional manifold of the dataset, with PCA. (F) Layer 1 output temporal dynamics of class 1 and class 2 samples, with a 3.57-ns frame time. (G) Nonlinear activation. Outputs of different wavelengths as a function of the respective input (top) and as a function of total input (bottom). (H) Final output and classification results of the whole dataset. (I) Monitoring the continuous high-speed dynamics with a 10-MHz frame rate and a 3.57-ns frame time. Top: Temporal buffer output. Bottom: Output with a selection window. Scale bar, 3 mm.

We experimentally configured a high-speed dynamic scene consisting of two spherical objects flashing on and off at a nanosecond time scale (3.57 ns per frame) to validate the performance of the proposed method for high-speed processing. A dataset containing sequences of two objects with two different flashing orders was constructed (object 1 flashes first and object 2 flashes first). Every sequence comprises three frames, wherein one object flashes in a frame slot. There are 180 training data and 60 testing data, each with different flashing intensities. Experimentally, owing to the limited frame rate of existing cameras, it is difficult to capture the frequently and continuously flashing pattern and to discriminate the flashing order. As shown in Fig. 4E, dynamic datasets were slowed down and monitored using an InGaAs camera. A two-layer WMUX-STPC model was used to recognize the dynamics based on the previously calibrated parameters. Specifically, in each frame, the spatial input content was encoded on two different wavelengths. The spatial inputs were spatially weighted in amplitude using DMD. Thereafter, the signal was squeezed into one fiber channel by WMUX. In the temporal channel, the 3 × 2 and 2 × 2 temporal weighted connections were implemented with an intensity modulator and temporal buffer at layer 1 and layer 2 of the WMUX-STPC network. The multispectral output from the first layer entered the SOA and was activated nonlinearly, and the subsequent output was finally demultiplexed by a DWDM multiplexer and fed into the second spatiotemporal layer for the inference of the final computing results (details of the system are illustrated in Materials and Methods).

The sequences of the datasets were projected onto a two-dimensional (2D) manifold using principal components analysis (PCA; details in Materials and Methods) (right panel of Fig. 4E). The data from the two categories were distributed in three clusters and overlapped with each other, which are not linearly separable. The task is challenging because accurately identifying the category requires simultaneously determining the spatial location and temporal flashing order of the two objects. The output dynamics of class 1 (the third row of Fig. 4E) and class 2 (the sixth row of Fig. 4E) from the first layer of WMUX-STPC is visualized in Fig. 4F, the frame time is 3.57 ns, and the temporal weighting slots have a duration of 1.78 ns. Figure 4G shows the nonlinear activation outputs of the testing datasets. The output levels at different wavelengths are plotted against the input of their respective wavelengths (top) and total input (bottom). The multiwavelength input-output transfer function is highly nonlinear, as the output power levels depend on both the input power at the respective wavelength and the total input power (Fig. 4D). With a nonlinear multilayer architecture, the WMUX-STPC network successfully classified the entire testing dataset, which is consistent with the simulation. Comparatively, a one-layer WMUX-STPC network achieved only 84.4% testing accuracy (section S1 and fig. S15). The experimental results are shown in Fig. 4H. By setting an appropriate threshold (dashed line), the first half (class 1) and the second half (class 2) of the dataset are clearly distinguished. The complete experimental results are presented in fig. S10. The system was then configured to operate in continuous mode. The input sequences flashed at a high repetition rate of up to 10 MHz. Among the continuous series, only one of the sequences flashed differently, and the WMUX-STPC network successfully determined the outliers. This shows that the all-optical WMUX-STPC network is capable of real-time processing with a response time at the nanosecond level. The final output can be used for real-time feedback control of the system.

Nanosecond real-time processing is already competitive against state-of-the-art specially designed electronic systems, including event cameras and field-programmable gate arrays (FPGAs) with at least nanoseconds cycle time (section S1). To further increase the processing speed of the system, the round-trip delay of the temporal buffer in the WMUX-STPC can be minimized on a photonic integrated circuit platform. Through simulation on a low-loss silicon-nitride-on-insulator photonic platform, we numerically validated that a ring resonator with a 1.4-mm ring length would reduce the delay time to 10 ps (section S3). We also extracted matrix multiplication operations of similar dimensions and executed them on a standard central processing unit (CPU) and graphics processing unit (GPU) system. Each read-compute-write cycle consumes at least 4 and 20 μs on average (section S1). In summary, the proposed WMUX-STPC is three to five orders of magnitude faster than the CPU- and GPU-based general-purpose system and is also competitive against the specially optimized electronic system.

DISCUSSION

In this study, an STPC architecture is proposed and experimentally demonstrated for ultrafast dynamic machine vision. By codesigning the multiplexed spatiotemporal computing architecture and colearning the parametric physical system with the neural network model, fast and precise computing on spatially and temporally varying light fields becomes possible. The STPC comprehensively extracts content information in high-dimensional optical feature space and is free of the digital burden of transmission and storage; thus, it is promising for the high-speed analysis of complex visual scenes. We experimentally validated that the SMUX-STPC network can process daily visual scenes with similar performance to that of existing methods while having over an orders of magnitude improvement in speed and parameter efficiency. In addition, the WMUX-STPC network supports ultrahigh-speed photonic machine vision with multiwavelength inputs and permits discerning visual dynamics with frame times of nanoseconds to picoseconds. The introduction of multivariate all-optical nonlinearity effectively enhances the performances of the STPC network on linearly inseparable problems.

The SMUX-STPC system uses a high-speed modulator to stretch the spatial information in the temporal dimension; thus, a higher modulation speed can increase the inference speed and contribute to better information extraction. Currently, the upper speed limit of the DMD is tens of kilohertz, with millions of modulation pixels. With the advancement of high-speed spatial light modulators (54–56), the speed of SMUX-STPC would be further accelerated. Moreover, in the WMUX-STPC system, to increase the spatial resolution, the continuous wave (CW) laser sources can be upgraded with a supercontinuum source to allow for continuous sampling in the spatial optical domain (9). In the future, multimode fibers could also be used to enlarge the capacity of the temporal channels and provide alternative forms of nonlinearity (45). To scale up the STPC networks, the loop number in an all-optical buffer can be optimized by adjusting the coupling coefficients of the coupler (fig. S17). The noise induced by the amplifiers may be further controlled with quantization of analog-to-digital converters and digital-to-analog converters.

In state-of-the-art electronic computers, memory access is associated with latencies of more than 100 ns (57), which precludes real-time processing of dynamic events at the nanosecond time scale and inhibits the ultrafast implementation of artificial neural networks, as sequential data dependencies in the neural network architecture result in frequent read/write operations (58). The memory dependencies also block the access of existing photonic computing techniques to the full potential of light (a discussion of existing methods is provided in section S5). The STPC architecture eliminates the memory read/write burden by codesigning the computing, interfacing, and buffering modules in the spatiotemporal computational domain. Furthermore, with recent advancements in hundreds-of-gigahertz optical modulators and detectors (59–61), low-loss photonic integrated circuits, and ~100-GHz high-speed waveform generators, the temporal resolution of the STPC is expected to reach ~10 ps. The capability of high-speed and consecutive computing not only accelerates neural network computing but also underpins real-time analysis of nonrepetitive transient visual phenomena (62, 63), thereby enabling in situ feedback control of light-field dynamics over gigahertz frequency. The STPC architecture broadens the scope of photonic computing, paving the way for ultrafast advanced machine learning and transient experimental control in the optical domain.

MATERIALS AND METHODS

Experimental system

In the spatial module of the SMUX-STPC system, the temporal free-space input stack was processed using a high-speed DMD (DLP9500, Texas Instruments DLP). The output from the spatial module was then downsampled by being focused through a focusing lens and coupled into a single-mode fiber. In this manner, free-space inputs were spatially squeezed and extended temporally with high-speed spatial modulation and converted to guided-wave dynamics in the fiber. The polarization of light in the fiber was controlled with a polarization controller to align with the slow axis of the SOA (Thorlabs S9FC1004P) input. By modulating the injection current of the SOA, its gain coefficient was varied, and the input guided-wave dynamic sequence was temporally weighted. A quarter of the emitted light from the SOA is split out with a 1 × 2 fiber coupler and monitored by a photodiode (PD-1, Thorlabs DET08CFC/M). The remainder of the light entered the temporal buffer constructed by an OEO loop through a 2 × 2 fiber coupler. Within the temporal buffer, the light passed through the 25.293-km fiber as a temporal delay line. The delayed optical output was then detected by a photodiode (PD-2), and the photocurrent was amplified by a TIA (FEMTO DHPCA-100) and a low-noise voltage amplifier (LNA, AMI 351A-1-50-NI). The amplified electrical signal drove the intensity modulator (Thorlabs LN05S-FC), and the temporal dynamics were converted back to the optical domain with different wavelengths from those of the spatial module (1550 and 1568 nm, respectively), which was subsequently fed back to the input of the buffer. The round-trip delay of the entire temporal buffer is approximately 124.6 μs, which matches the 8024-Hz spatial computing frequency. In the fiber coupler, the recurrent signal was incoherently merged with the input signal from the spatial module. The temporal module effectively performed weighted connections, and the final outputs from the buffer were monitored using a photodiode outside the buffer (PD-3). The details of the system are shown in fig. S1.

In an all-optical nonlinear WMUX-STPC system, the dynamic input scene was encoded on multiwavelength inputs to the DMD. In the experiment, we used laser beam spots at 1550.12 and 1550.92 nm to simulate two spherical objects. The on-and-off states of the objects were controlled with 10-GHz electro-optical modulators. The inputs were spatially weighted on the DMD, squeezed into a single fiber, and amplified by an erbium-doped fiber amplifier (EDFA; Amonics AEDFA-PA-35). The spatial computing outputs from the EDFA were N_λ 3 × 1 vectors with three timeslots and N_λ wavelengths. Each entry of the vector corresponded to a time duration of 3.57 ns. Then, the multiwavelength temporal inputs were modulated with a 40-GHz broadband modulator with a pulse width of 1.78 ns. The recurrent temporal connection was performed in an all-optical buffer consisting of an all-pass ring resonator with a fiber ring of around 0.6-m length. The weighted optical connection parallelly implemented N_λ MVM on the 3 × 1 vectors with a 3 × 2 weight matrix. The outputs from the buffer were then selected with a high-speed modulator and were nonlinearly activated by the SOA (Thorlabs S9FC1004P) and demultiplexed before being injected into the second layer. The second layer performed a weighted connection, and the outputs were N_λ 2 × 1 vectors. With the detection of a PD, outputs of different wavelengths were summed, producing the final output of size 1 × 2, with the largest entry denoting the categories of the test sample. The high-speed system was controlled with a 5-GHz-bandwidth arbitrary wave generator (RIGOL DG70004) with 10-GHz drivers. The high-speed outputs were captured using a 10-GHz oscilloscope (Tektronix MSO64B). The details of the system are shown in fig. S2.

Dataset and preprocessing

N-MNIST dataset

The N-MNIST dataset (50) contains neuromorphic forms of handwritten digits captured by event cameras. It consists of 60,000 training samples and 10,000 testing samples. Each original sample is a spiking event series of ~5000 in length, with each entry in the series denoting the spiking position. The spiking events were first uniformly divided into 13 short image frames. For each frame, the spiking positions were grouped in a 2D plane and converted into a binary image with a resolution of 34 × 34. In the experiments, we selected the first five of the processed binary images and cropped 26 × 26 pixels from the center of the image, which were up-sampled to 541 × 541 and used for the evaluation in the experiments.

KTH human action dataset

The KTH dataset (51) contains 600 videos with a spatial resolution of 160 × 120, including six different types of natural actions (boxing, handclapping, handwaving, jogging, running, and walking) performed by 25 subjects in four different scenes. The same preprocessing method as (25) was used to extract the silhouette to accommodate the DMD used in the system. In the experiment, the first scene was selected for comparison with the existing methods, and the spatial resolution was rescaled to 541 × 541. Videos were divided into subsequences with a length of five and split into training and testing sets. The training set had 16 subjects, including 7680 subsequences, while the testing set had 9 subjects, including 2160 subsequences.

Motion tracking dataset

To validate a potential real-world use of the STPC network, we constructed a motion tracking dataset emulating the cell motion and performed the tracking task with it. The dataset contains 704 samples (674 for training and 30 for testing) moving in three directions, up-left, down-left, and rightward. Each sample contains five frames, where a 63 × 63 square object was randomly placed in the 541 × 541 grid initially and then moved toward one of the three directions. The interframe stepping distance is set to be 83 pixels for the rightward direction and 59 pixels for the up-left and down-left directions.

Flashing object dataset

The flashing object dataset constructed for nanosecond dynamic recognition contains two spherical objects flashing at different time steps. The dataset contains three frames, with the frame time being 3.57 ns, and one object flashes at a single frame. Examples of the six flashing patterns are shown in Fig. 4E. The relative flashing intensity of each object was randomly sampled from the range of 5.4 mW to 6.0 mW. The entire dataset contains 180 training data and 60 testing data. As shown in Fig. 4E, PCA (64) was performed on the testing dataset. Specifically, singular value decomposition was calculated on the basis of the centered dataset to obtain the projection matrix with which the data were projected onto a low-dimensional space.

Calibration of STPC units

In the SMUX-STPC system, the spatial computing modules can be numerically modeled as $o={\mid {\mathit{t}}_{\mathit{s}}^T({\mathit{w}}_{\mathit{s}}{\mathit{x}}_{\mathit{i}})+b_0\mid }^2$, where x_i denotes the input light fields, w_s denotes the spatial weights, t_s denotes the coupling coefficients, b₀ denotes the background, and o denotes the intensity of the light fields coupled to the optical fiber. In the experiment, t_s, w_s, and x_i had an effective dimension of 676 × 1. To calibrate the spatial coupling coefficient t_s, 3300 random binary spatial masks representing w_sx were projected onto the DMD. Each pixel value in the mask was drawn from independent and identically distributed Bernoulli distribution. The proportion of DMD pixels being in the “on” state varied from 30 to 57%. A neural network of the same form as the numerical model was then constructed. The collected (w_sx,o) pairs were fed into the constructed network to train the coefficient t_s. The learning batch size was set to 16; the learning rate was set to 0.000005, and the learning rate decayed by 1% every 5000 iterations. In addition, the network was trained using Adam optimizer (65). The training error decreased to less than 5% after 15 epochs of training. Figure S5 shows the convergence curve, converged phase, and amplitude of t_s.

The transfer function of the SOA is formulated as o′ = o · w_t(o, v), where o is the input to the SOA, v is the modulation voltage, and o′ is the output power. We swept the input-output relation of the SOA with different levels of input intensity o from 0 to 30 μW and swept the voltage v from 0 to 5 V. These points were selected as markers for the calibration of the function o^′ = φ(o, v_t), from which the complete function could be interpolated. The results are presented in fig. S6. For each control voltage level, the input gain coefficient decreased with an increase in the input power, which is a manifestation of the nonlinear saturable gain effects of the SOA.

In the experiment, the modulator was biased toward the NULL point. The characteristics of the temporal buffer can be modeled as o′′_t = a · sin [b · (o′′_t−1 + o′_t)]², where o′_t is the input intensity at time t, o′′_t−1 is the precedent recurrent intensity, and o′′_t is the current recurrent density at time t. In addition, a and b are the system parameters dependent on the driving laser power and amplifier gain coefficient, respectively. The system was calibrated by projecting light pulses onto a temporal buffer and measuring the decay dynamics of the cavity. The decay dynamics were then fitted to the transfer formula to obtain parameters a and b. Details of the calibration dynamics and the fitting results are shown in fig. S7.

In the WMUX-STPC system, the transfer dynamics of the spatial computing module are modeled as o = t_s(x_i, w_s), where x_i,o,w_s are the input light fields, output light, and spatial weights, respectively. Specifically, under different w_s levels, we swept the input light field x_i and measured the output intensity o. The measurement triplets (x_i,o,w_s) were further used for fitting the function o = t_s(x_i, w_s). The transfer characteristics of object 1 and object 2 are shown in fig. S8. Then, wideband multiplication was also validated. The wavelength of the input light varied from 1528 to 1566 nm, and the transmission coefficient was measured against the modulating voltages. Specifically, we measured the high-speed modulating characteristics at 1550.12 nm with 1.78-ns short pulses with amplitude varying between 0 and 2.1 V. In addition, the modulation output can be formulated as w_t(v) and o′ = o · w_t(v). The measurements are shown in fig. S9. Last, the nonlinear transfer function of the SOA was calibrated by measuring the self-gain modulation and cross-gain modulation nonlinearity. We denote the input intensity of different wavelengths with y_λ1, y_λ2, …,y_λN. The input intensity was swept from 0 to the maximal intensity (6 mW), and the outputs z_λ1, z_λ2, …,z_λN were measured. In the experiments, we measured the transfer function of two wavelengths, z_λ1 = g(y_λ1, y_λ2) and z_λ2 = g(y_λ2, y_λ1). The results are shown in Fig. 4D.

Neural network architectures and training methods

In the SMUX-STPC network, after calibration of the spatial computing module, temporal modulation module, and temporal buffer, the calibrated system parameters were used for pretraining the experimental system. In each of P spatial channels, the input image sequence consists of M/K frames, and each frame is spatially modulated by K spatial masks. The M spatial outputs are then coupled into the temporal buffer for spatiotemporal computing, forming temporal inputs $o_j={\mid {\mathit{t}}_{\mathit{s}}^{\mathit{T}}({\mathit{x}}_{\mathit{i}}\cdot {\mathit{w}}_{\mathit{s},\mathit{j}})+b_0\mid }^2$, where j = 1,2,3, …, M and w_s,j is the jth trainable spatial weight mask. Each value in the M outputs is modulated by N temporal voltage weights in the temporal computing module, v_j,k, k = 1,2,3, …N, and the inputs to the temporal buffer are o′_j,k = φ(o_j, v_j,k). In the temporal buffer, the dynamics is o′′_j,k = a · sin [b · (o′′_j−1,k + o′_j,k)]². In spiking sequence classification and human action recognition experiments, M, N, K, and P were set to 10, 5, 2, and 6, respectively. Through the first ST unit, we obtained 6 × 5 spatiotemporal outputs y_k = o′′_M,k, which were demultiplexed to a second ST unit simulated with an electronic linear layer, producing 10 × 1 and 6 × 1 output vectors, respectively, for final classification. In the motion tracking experiment, P was set to 8, and the output dimension was set to 3 × 1, while the other parameters were set the same as in the other two experiments. The source code of the numerical simulation was written in Python 3.7 using the PyTorch package on the Windows 10 platform with an Nvidia GeForce RTX 3070 GPU. During the training, the cross-entropy loss was used, and regularization terms were used to enhance the stability of the system and to maximize the signal-to-noise ratio in the experiments (details of training loss are presented in section S4). Adam optimizer was used for the training, and the training batch size was set to 16. In addition, the spatial learning rate was set to 0.01, and the temporal learning rate was set to 0.0001. Furthermore, training on the N-MNIST, KTH, and motion tracking datasets required 200, 100, and 2000 epochs, respectively, to converge.

In the WMUX-STPC network, the input sequential light field is the triplet (x_it0, x_it1, x_it2). x_it was fed into the spatial transfer function o_t = t_s(x_it, w_s), and the input light fields at different time slots share the same spatial weight w_s. The output triplet (o_t0, o_t1, o_t2) was then fed into the temporal multiplication unit (intensity modulator); thus, o′ = o · w_t(v), and the output o^′ from the temporal multiplication unit was recurrently added in the temporal buffer. The temporal output y was fed to the nonlinear activation function g(y₁, y₂). The final two outputs at wavelengths λ₁ and λ₂ were demultiplexed and fed to the second layer. In this manner, the first layer implements 3 × 2 temporal nonlinear computing, while the second layer implements 2 × 2 temporal computing without nonlinear activation. The final outputs were used to determine the category of dynamics. In the network training, the cross-entropy loss was used with the Adam optimizer (regularization loss is presented in section S4), with a learning rate of 0.0005, on the same platform as that of the SMUX-STPC network. The training took 200 epochs to converge.

Experimental system learning

In the experiment, the calibrated parameters were dependent on the calibration data. Owing to the discrepancy between the inference inputs and random calibration inputs, as well as the presence of system noise in the calibration, the accuracy of the calibrated transfer matrix is biased to the distribution of the calibration data; consequently, the system computing accuracy may not be the best for the inference inputs.

To enhance the system modeling accuracy, instead of simply using calibrated system parameters for the final experiments, we used a further step to learn the system parameters with trainable functions, which we termed system learning. From the perspective of machine learning, we regard the parameters that characterize the experimental system as variables that are trainable and, together with the model parameters (weights in the ST modules of STPC), comprise the entire set of parameters. As a result, the pretraining step is the process of learning the neural network model parameters, and the system learning is the process of learning the experimental system parameters. These two steps can be iteratively performed to asymptotically approach the best computational neural network model and most accurate system model collaboratively. Compared with existing photonic neural network training methods that update only the model parameters during the learning process (25, 66–68), the proposed system learning method constructed a unified trainable framework with both the experimental system parameters and computational model parameters, thus exploring the complete parametric space and achieving optimal convergence. A flowchart of the learning process of STPC is shown in fig. S3.

After pretraining, we extracted a subset of the training data and measured the experimental output to fine-train the system parameters. Specifically, we extracted a small portion of the training data (61 in spiking sequence classification, 42 in human action recognition, and 66 in motion tracking) as the system learning subset and measured the outputs from the spatial modules and the temporal multiplication modules. In spatial computing, the output $\widetilde{o_j}={\mid {\mathit{t}}_{\mathit{s}}^{\mathit{T}}({\mathit{x}}_{\mathit{i}}\cdot {\mathit{w}}_{\mathit{s},\mathit{j}})+b_0\mid }^2$is collected (the experimental measurements are denoted with a tilde), and we used the $(\widetilde{o_i},{\mathit{x}}_{\mathit{i}})$ pair to finely train the parameters (t_s, b₀). During the training, the learning rate was set to 0.000005, which decayed by 1% every 5000 iterations, and the batch size was set to 16. In addition, the training process converged after 500 epochs (fig. S5). We also collected SOA input and output pairs with experimental inputs $\tilde{o}{}^{\mathrm{\prime }}=\mathrm{\phi }(\tilde{o},\widetilde{v_t})$. We used the ($\tilde{o}{}^{\mathrm{\prime }},\tilde{o},\widetilde{v_t}$) triads to train the SOA calibrated markers with a learning rate of 0.0001 combined with a decay rate of 10% every 5000 iterations. The training process converged after 60 epochs (fig. S6). Furthermore, the system parameters from system learning were used for further training of the model parameters for 20 epochs, with the learning rate set to 0.0001. Last, the converged parameters were deployed in the experimental system.

Supplementary Materials

This PDF file includes:

Sections S1 to S5

Figs. S1 to S17

Table S1

Legend for movie S1

References

Other Supplementary Material for this manuscript includes the following:

Movie S1