A structured jet explains the extreme GRB 221009A

Abstract

Long-duration gamma-ray bursts (GRBs) are powerful cosmic explosions, signaling the death of massive stars. Among them, GRB 221009A is by far the brightest burst ever observed. Because of its enormous energy (E_iso ≈ 10⁵⁵ erg) and proximity (z ≈ 0.15), GRB 221009A is an exceptionally rare event that pushes the limits of our theories. We present multiwavelength observations covering the first 3 months of its afterglow evolution. The x-ray brightness decays as a power law with slope ≈t^−1.66, which is not consistent with standard predictions for jetted emission. We attribute this behavior to a shallow energy profile of the relativistic jet. A similar trend is observed in other energetic GRBs, suggesting that the most extreme explosions may be powered by structured jets launched by a common central engine.

The afterglow of GRB 221009A implies a shallow structured jet is produced in the most powerful stellar explosions.

INTRODUCTION

Gamma-ray bursts (GRBs) are sudden and brief flashes of high-energy radiation. Those lasting longer than a couple of seconds generally signal the death of very massive, rapidly rotating stars. With typical durations of 1 to 100 s (1) and isotropic-equivalent luminosities of 10⁵⁰ to 10⁵⁴ erg s⁻¹ (2), they are considered one of the most energetic explosions in the Universe. When their intense radiation reaches us, it is attenuated by the large distance scale it has traveled, ≈16 Gpc for the median GRB redshift z ∼ 2 (3). Moreover, most of the flux above gigaelectronvolt energies is suppressed by interactions with the extragalactic background light (4). Therefore, as observed at Earth, GRBs display fluences in the range 10⁻⁷ to 10⁻⁴ erg cm⁻² (1) and spectra up to the megaelectron volt or, less frequently, gigaelectronvolt range (5).

On 9 October 2022 at 13:16:59 UT (hereafter referred to as T₀), the Gamma-ray Burst Monitor (GBM) aboard Fermi (6), among other high-energy satellites [Konus-Wind, SRG, and GRBAlpha; (7, 8)], detected an unprecedented, extremely bright burst lasting hundreds of seconds. This burst, dubbed GRB 221009A, is the brightest GRB ever detected in nearly 55 years of operating gamma-ray observatories, with an observed fluence of ≈5 × 10⁻² erg cm⁻² in the 20-keV to 10-MeV band, more than an order of magnitude brighter than GRB 840304 and GRB 130427A (9), the previous record holders (Fig. 1). Its high-energy radiation was so intense that it disturbed Earth’s ionosphere (10).

Fig. 1. The extreme brightness of GRB 221009A.

(A) Top left: Histogram of gamma-ray fluence for Fermi (blue; 10 to 1000 keV) and BATSE (gray; 50 to 300 keV) GRBs compared to GRB 221009A. (B) Bottom left: Isotropic-equivalent gamma-ray energy (1 keV to 10 MeV) versus redshift for a sample of long-duration GRBs compiled from (44, 64). (C) Right: Observed x-ray afterglow light curves in the Swift XRT (03 to 10 keV) energy band for a sample of long-duration GRBs. GRB 221009A is the brightest x-ray afterglow ever observed.

The prompt gamma-ray phase was followed by longer-lived, nonthermal afterglow radiation, visible across nearly 19 decades in energy, from low-frequency radio up to the teraelectronvolt range, corresponding to the highest energy photon (18 TeV) ever detected from a GRB (11). The afterglow phase was exceptionally bright at all frequencies and at all times, surpassing the population of x-ray afterglows by over an order of magnitude (Fig. 1) and causing the Neil Gehrels Swift Observatory to send a trigger alert nearly an hour (T₀ + 55 min) after the initial gamma rays were detected for the first time (12).

The extraordinary properties of this GRB are only partially explained by its proximity to us. At a redshift of z = 0.1505 (13), its luminosity distance is ≈ 720 Mpc (14), a factor of ≳20 closer than the average GRB. However, even after correcting for distance effects, GRB 221009A remains one of the most luminous explosions to date, pushing the limits of our understanding in terms of both GRB energetics and the rate of events. Its isotropic-equivalent gamma-ray energy, E_γ,iso ≳ 3 × 10⁵⁴ erg measured over the 20-keV to 10-MeV energy range (15), is at the top of the GRB energy distribution (Fig. 1) and only sets a lower limit to the total (isotropic-equivalent) energy release. By including the blast-wave kinetic energy that is converted into afterglow radiation, as well as the contribution of the teraelectronvolt component, the isotropic-equivalent energy budget would easily surpass 10⁵⁵ erg, corresponding to ≳5 M ⊙ c². According to the GRB luminosity function (2), an event as bright as GRB 221009A occurs this close to Earth less than once in a century. If we factor in its long duration and total energy release, then our chance to observe a similar event is 1 in ≈ 1000 years (see Materials and Methods). The detection of GRB 221009A and other extraordinary events, such as GRB 130427A (9), seems therefore at odds with our basic expectations of how frequent the most energetic explosions are in the nearby Universe.

A key element for calculating the true energy release and rate of events is the geometry of the relativistic outflow. The outflow’s angular structure and collimation leave clear imprints in GRB afterglow light curves (16–19), and, therefore, we can constrain these properties through our multiwavelength campaign. In particular, if the outflow is collimated into narrow sharp-edged jets, then we should observe the afterglow flux rapidly falling off after the time of the “jet break,” i.e., when the inverse of the Lorentz factor of the outflow becomes comparable to the jet’s half-opening angle θ_j (19, 20). To search for the signature of collimation, we turn to the x-ray afterglow, which is unaffected by other components [e.g., supernova and reverse shock (RS)] and probes the nonthermal emission from electrons accelerated by the forward shock (FS), driven by the outflow into the surrounding medium (21).

RESULTS

The x-ray light curve features an initial power-law decay index of α_X,1 = −152 ± 0.01, steepening to α_X,2 = −1.66 ± 001 after t_b,X= 0.82 ± 0.07 days (see Fig. 2). The x-ray spectrum is well described by an absorbed power law with a time-variable spectral index, ranging from −0.65 ± 0.02 measured by Swift at 1 hour to −1.10 ± 0.17 measured by NuSTAR at 32 days. According to standard models of GRB jets (21, 22), this progressive softening is consistent with the passage of the cooling frequency v_c of the synchrotron spectrum. Therefore, the x-ray spectral shape can be used to constrain the density profile of the circumburst medium as ρ(r) ∝ r^−k where k < 4/3 (such that v_c decreases with time) and the energy distribution of the shock-accelerated electrons as N(E) ∝ E^−p where p ≈ 2.2 to 2.4. This value matches the spectral measurements of the early high-energy emission (23, 24), suggesting that the synchrotron component extends to the gigaelectronvolt range. Thus, we can use the high energy flux, assuming that it is afterglow-dominated, as a proxy for the blast-wave kinetic energy (25), obtaining E_K,iso≈ 10⁵⁵ (1 + Y) erg, where Y is the Compton parameter of the gigaelectronvolt-emitting electrons. A similarly high value is obtained by assuming a typical gamma-ray efficiency η_γ ≈ 20%.

Fig. 2. Multiwavelength light curve of GRB 221009A.

The XRT and XMM-Newton data represent the x-ray flux density at 1 keV, whereas the flux density from the NuSTAR observations is reported at 5 keV. OIR data represented as empty squares were compiled from General Coordinates Network circulars, whereas filled circles are data analyzed in this work. The OIR data are not corrected for Galactic extinction.

In the standard model, the GRB jet has a constant energy profile within its core of angular size θ_j. The energy then declines rapidly or goes to zero at angles beyond θ_j. The prediction for the post–jet-break decay is t^−p ≈ t^−2.2, which is inconsistent with the x-ray slope of −1.66 measured after t_b,X. If t_b,X is not the jet-break time t_j, then the uninterrupted power-law decay of the x-ray emission sets a lower limit t_j > 80 days for the jet-break time. The resulting limit on the jet opening angle, θ_j ≳ 15°, pushes the total collimation-corrected energy release to E_K ≳ 4 × 10⁵³ (t_j/80 days)^0.75 erg (see Materials and Methods), leading to an energy crisis for most models of GRB central engines (26, 27). However, at the time of the x-ray temporal break, the optical and infrared (hereafter, OIR) light curves are also seen to steepen. The OIR emission displays an initial shallow decay with α_OIR,1 = −0.88 ± 0.05, which steepens to α_OIR,2 = −1.42 ± 0.11 at around t_b,OIR = −0.63 ± 0.13  days (Fig. 2). The achromatic steepening of the x-ray and OIR light curves provides a strong indication of a geometrical effect, such as a jet break (19, 20), although the observed post-break decay rates are shallower than theoretical predictions. If GRB 221009A was followed by a supernova, like most long GRBs are, then the supernova contribution could cause an apparent flattening of the OIR light curve and mask the jet break. By assuming that a SN 1998bw–like transient contributes to the OIR emission, an afterglow decay rate as steep as −1.5 is consistent with the optical and near-IR data. This is close to the observed x-ray slopes, yet too shallow for a post–jet-break phase.

Additional evidence for geometrical effects comes from the late-time radio observations, which tend to favor a collimated outflow. The x-ray flux at 1 hour sets a lower limit of ≳10 mJy to the FS peak flux. As the shock cools down and passes from the x-rays to the radio band, the peak brightness remains constant in a uniform medium (28) or slowly decreases as F_v,max ∝ t^−α_k, with α_k < 1/4 in a stratified environment with k < 4/3. Either behavior would violate the observed radio limits of 0.4 mJy at 80 days unless the assumption of spherical symmetry breaks down, causing the peak flux to decrease more rapidly (20).

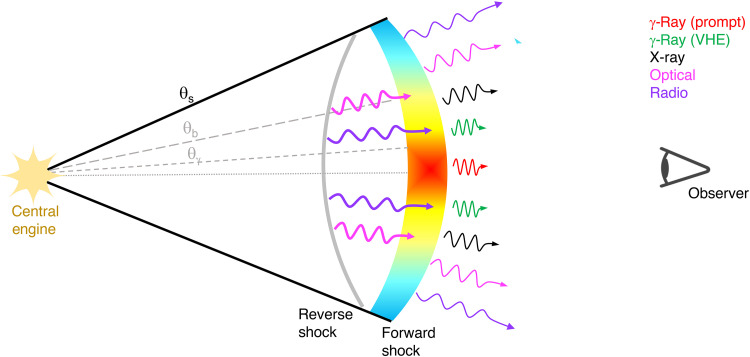
These different and apparently discordant observations can be reconciled if the afterglow emission is powered by a structured jet with a shallow angular energy profile (29–31), composed by an inner component of angular size θ_b with a shallow energy profile dE_K/dΩ ∝ θ^−a₁ and a slightly steeper lateral structure at θ > θ_b with dE_K/dΩ ∝ θ^−a₂, where a₁ < a₂ < 2 (see Fig. 3). This profile is motivated by the lack of a sharp jet break feature in the x-ray and OIR light curves and the energy crisis that would be implied for a jet with a steeper angular profile. Similar shallow angular profiles are seen in simulations of relativistic jets expanding in complex media (32).

Fig. 3. Schematic of the structured jet for GRB 221009A.

Emission from the FS and RS are produced by the jet out to its truncation angle θ_s. The angular structure of the jet, E_K/dΩ ∝ θ^−a, breaks slightly at θ_b, transitioning from a slope a₁ ∼ 0.75 to a₂ ∼ 1.15. The prompt gamma rays may be radiated from the central narrow core of aperture θ_γ, whereas the afterglow and very-high energy (VHE) gamma-rays could come from a wider angular structure.

A structured jet can account for the achromatic temporal break visible at x-ray and OIR wavelengths and explain their post-break slopes as emission from the lateral structure as it comes into view. For a₁ ∼ 0.75, a₂ ∼ 1.15, and a transition at θ_b ∼ 3°, this model yields initial temporal slopes of α_OIR,1 = −1.3 and α_X,1 = −1.55 that transition to α_OIR,2 = −1.47 and α_X,2 = −1.67 after ∼0.8 days. Although this does not capture the complexity of the early-time afterglow evolution, it provides a good description of the full x-ray light curve and the OIR dataset from 0.8 to 80 days (Fig. 4). Over this time period, the low-frequency radio counterpart is dominated by synchrotron emission from the ejecta decelerated by the RS. Emission from the RS is likely contributing to the optical light curve at t < 0.8 days, and responsible for its early shallow decay. The evolution of this component, however, does not follow standard prescriptions.

Fig. 4. Afterglow spectral evolution.

Multiepoch broad-band spectral energy distributions (SEDs) of GRB 221009A modeled by the combination (solid line) of FS and RS (dotted line); see Materials and Methods. The data are corrected for extinction and absorption.

DISCUSSION

The main advantage of the structured jet model is that it eases up the energetic requirements relative to the uniform jet, leading to E_K ≲ 8 × 10⁵² (t_j/80 days)^0.37 erg (see Materials and Methods), where t_j is the observed time when the jet edges become visible, causing a final steepening of the light curve (if still relativistic). Causal contact across the full jet surface will only be established once the jet edges are already subrelativistic, leaving no room for strong jet spreading before the observed x-ray light curve behavior segues into a nonrelativistic slope t^(4−3p)/2 (33) that resembles the pre-transition slope. In the structured jet model, the collimation-corrected energy remains at the boundary of the energy budget for a magnetar central engine (<10⁵³ erg for a rapidly rotating supramassive neutron star), requiring an unrealistically high efficiency inconverting the magnetar’s rotational output into gamma rays and blast-wave kinetic energy. The massive energy required to power GRB 221009A is consistent with a magneto-hydrodynamical process (34), extracting rotational energy from a rapidly spinning (a = 0.9) stellar mass (∼5 M_⊙) black hole (35).

The shallow structured jet model helps explain the lack of prominent jet breaks in some long GRBs (36). In particular, the family of bright bursts with very high-energy emission, including events like GRB 130427A, GRB 180720B, GRB 190114C, and GRB 190829A, shares the common property of long-lasting afterglows (Fig. 5) with late-time temporal decay indices between 1.4 and 1.7 (37–39), similar to GRB 221009A. A shallow angular structure may thus be a frequent feature of the most violent explosions. However, none of these bursts reached the high energy of GRB 221009A, which provides compelling evidence for revising the standard jet model in a massive star explosion.

Fig. 5. Long-lived x-ray light curves of bright GRBs.

A sample of bright long GRBs without a canonical jet break to late times is shown. For comparison, the dashed line shows the predicted late-time decay for a sharp-edged uniform jet.

A structured jet profile also affects the rate calculation. For GRB 221009A, we infer an angular size, θ_s ≳ 0.4 rad (see Materials and Methods), larger than that of the general GRB population, θ_j ≈ 0.1 rad. This would naively suggest that a similar event is θ_s/θ_j)² ≈ 16 times more likely to be detected than a regular GRB. If the intrinsic rate of highly energetic GRBs is significantly lower than the rate of typical GRBs, then the larger solid angle of the jet can explain the detection of GRB 221009A. However, this interpretation is not supported by the small viewing angle, θ_obs ≲ 0.01 rad, inferred from afterglow observations. Alternatively, if the rate of highly energetic GRBs is comparable to the rate of standard GRBs, then the large angular size of GRB 221009A is not consistent with the low rate of observed events (Fig. 1). A natural explanation for this contradiction is that the prompt gamma-ray radiation is produced only within a narrow range of the GRB jet (θ_γ ≪ θ_s) (40), due to a reduction in Lorentz factor Γ with angle.

This leads to an increased opacity to photon-photon annihilation, which, in turn, can suppress the emission beyond a critical value (41), and, for a wide range of dissipation and emission mechanism models, a smaller Lorentz factor also leads to a reduction in the gamma-ray production. One example is a decrease in the dissipation radius R_d ∝Γ² at which the gamma rays are emitted. Even a small reduction in Lorentz factor can lead the dissipation radius to be smaller than the photospheric radius, which decreases with Lorentz factor, trapping the gamma-ray radiation for angles away from the core. This would lower the total energy released in gamma rays by a factor (θ_s/θ_γ) ≳ 20 but still require a substantial radiative efficiency along the sight line, η_γ(θ_obs) ≳ 20%.

The suppression of gamma-ray emission above θ_γ would cause observers at θ_obs > θ_γ not to detect the prompt GRB emission and instead possibly identify such an event as an “orphan” afterglow. This may lead to a population of luminous orphan afterglows, which could be searched for in various transient surveys (42). The predicted rate of orphan afterglows differs by orders of magnitude between different jet models. However, as the jet angular structure shapes the early afterglow evolution (17), search strategies calibrated on a uniform jet model may not efficiently recover all the possible events. To constrain the rate of GRB 221009A–like transients and their gamma-ray beaming factor, transient classification schemes should be fine-tuned to a wide range of angular energy profiles.

MATERIALS AND METHODS

Energetics and rates

GRB 221009A triggered Fermi/GBM (6) on 2022-10-09 at 13:16:59 UT. The GRB displayed an initial short pulse (∼40 s) followed by a period of apparent quiescence and then a main emission episode consisting of two bright peaks, at T₀ + 225 s and T₀ + 260 s, respectively. A third, weaker peak is visible at T₀ + 520 s.

Because of the GRB’s immense brightness, the majority of satellites were saturated during the main emission episode. This prevents us from carrying out standard analysis without careful corrections (6, 7, 43). However, the burst fluence can be constrained using the Konus-Wind spectrum at the onset of the main pulse (T₀ + 180 to 200 s). This is described by a band function with α = −109, β = 2.6, and peak energy E_p ≈ 1 MeV. By applying this model to the entire GRB prompt phase, a fluence of ∼5.2 × 10² erg cm⁻² (20 keV to 10 MeV) (15) was derived between 0 and 700 s after the initial trigger. As the spectrum of the brightest peaks is likely harder than the spectrum at the onset, this value places a conservative lower bound to the true GRB fluence and already makes GRB 221009A the brightest GRB ever detected by over an order of magnitude (Table 1). On the basis of the fluence distribution of Fermi bursts (1), the expected probability of observing a similar event is less than 1 in 1000 years for a spatially homogeneous GRB population in Euclidean space (Fig. 6).

Table 1. Historical bright GRBs.

GRB	Observatory	Fluence (erg cm−2)	Energy band	Reference
840304	PVO, ICE, Vela 5B	2.8 × 10−3	5 keV to 3 MeV	(66)
130427A	Fermi, Swift	2.5 × 10−3	10 keV to 1 MeV	(9)
830801B	SIGNE 2 MP9	2.0 × 10−3	30 keV to 7.5 MeV	(67)
850624	PVO	2.0 × 10−3	5 keV to 3 MeV	(68)
940703A	BATSE, GRANAT, ULYSSES	1.6 × 10−3	100 keV to 1 MeV	(69)

Fig. 6. Fluence distribution of Fermi GRBs.

We have normalized the number of bursts for the mission lifetime, its duty cycle, and field of view (1). At large fluences (S ≳ 5 × 10⁻⁵ erg cm⁻²) the distribution has a slope consistent with the Euclidean one (−3/2), also shown for comparison (dashed line). The two most fluent GRBs are GRB 130427A (circle) and GRB 221009A (star).

At the redshift of z = 0.1505 (13), the observed fluence corresponds to an isotropic-equivalent energy of E_γ,iso ≳ 3 × 10⁵⁴ erg (1 keV to 10 MeV), among a short list of the most energetic GRBs to date (44) and very similar to GRB 160625B (45). Highly energetic (≳10⁵⁴) GRBs are intrinsically rare events. Swift has detected approximately 11 of them during its entire lifetime (46). As expected, most are in the redshift range 1 ≲ z ≲ 3, where the star formation (hence, the GRB rate) peaks. Assuming a constant GRB formation rate over this redshift interval, we compute an all-sky volumetric rate of energetic GRBs

$$R_{\mathrm{z}}\approx \frac{N_{54}}{V}\frac{4\mathrm{\pi }}{f_z{\text{Ω}}_{\mathrm{BAT}}}\frac{1}{\mathrm{ϵ}T}={0.014}_{-0006}^{\pm 0007}{\mathrm{Gpc}}^{-3}{\mathrm{year}}^{-1}$$ (1)

where N₅₄ ≈ 8 is the number of very energetic events detected within 1 ≲ z ≲ 3, the available volume is $V={\int }_1^3\frac{dV}{dz}\frac{dz}{1+z}\approx 300{\mathrm{Gpc}}^{-3}$, where $\frac{dV}{dz}$ is the comoving volume element (14), T ≈ 18 years is the current lifetime of the Swift mission, ε ≈ 78% is the duty cycle, and Ω_BAT ≈ 2.2 sr is the field of view of the Swift Burst Alert Telescope (BAT) with partial coding > 10%. As these are very energetic events, we use an efficiency f_z ≈ 0.8 for obtaining a redshift measurement.

If we assume that the GRB rate scales as the star formation rate (47), then the local rate of events is at least a factor of 10 lower, R_local ≈ 0.001 Gpc⁻³ year⁻¹, and the probability of seeing a GRB as energetic as GRB 221009A within z < 0.15 is only 1 in 1000 years. Growing evidence shows that metallicity has a primary role in driving the GRB formation, and this could further lower the local rate by a factor ≈ 2.

A similar conclusion is reached by comparing GRB 221009A to the distribution of isotropic-equivalent GRB luminosities (2). Using the burst peak photon flux (10 to 1000 keV) from the preliminary GBM analysis, 2385 ± 3 photons  s⁻¹ cm⁻² (48), and the Konus-Wind spectral parameters reported above, we derive a peak gamma-ray luminosity of L_{γ, iso} ≈ 9 × 10⁵² erg s⁻¹. In the simplest scenario, not including an evolution of the GRB rate with redshift or metallicity, we find that less than ≈ 0.1% of GRBs have luminosities comparable to GRB 221009A, which translates in an all-sky rate of once in a decade across the visible Universe. For a local GRB rate in the range 0.3 to 2 Gpc⁻³ year⁻¹, we derive that the rate of events as luminous as GRB 221009A is one every 300 to 1100 years within z ≲ 0.15. These independent analyses confirm that, due to its brightness and proximity to Earth, GRB 221009A is an exceptionally rare event.

Afterglow temporal evolution

We model the afterglow light curves with a series of power-law segments, F_v ∝ t^α. In the x-ray band, our best fit model (χ²/df ≈ 1.3 for 1679 df) is a broken power law with initial decay index α_X,1 = −1.52 ± 0.01, steepening to α_X,2 = −1.66 ± 0.01 after t_break,X = 0.82 ± 0.07 days. A single power-law slope provides a significantly worse description of the data (χ²/df ≈ 2.1).

The OIR light curve, combining the grizJHK and the MASTER C filters, displays an initial power-law decay of α_OIR,1 = −0.88 ± 0.05, which steepens to α_OIR,2 = −1.42 ± 0.11 at around t_break,OIR = 0.63 ± 0.13 days (χ²/df ≈ 1.3 for 95 df). At times t > 10 days, a slight deviation from this power law is observed (Fig. 2), possibly caused by the contribution from a supernova (49) or the underlying host galaxy. By performing a joint fit to the x-ray and OIR light curves, we derive a break time of t_break,XOIR = 0.79 ± 0.04 days (χ²/df ≈ 1.3 for 1775 df). This joint fit results in a slightly steeper initial OIR decay of α_OIR,1 = −0.92 ± 0.04, whereas the other best-fit slopes remain consistent with our previous values.

The afterglow behavior at radio energies is markedly different, suggesting that its evolution is decoupled from the higher energy data. Our dataset starts 6 days after the GRB trigger and follows the afterglow evolution up to 110 days in multiple frequencies. During the time interval of 6 to 41 days, we derive a power-law decay with slope −0.76 ± 0.08 at 16.7 GHz (Fig. 2), much shallower than the simultaneous OIR and x-ray light curves. A consistent behavior is observed at 21.2 GHz, whereas higher (>30-GHz) frequencies show a possible chromatic steepening after ≈30 days. A comparison with the lower frequency data (5.5 GHz) shows that the simple power-law model overpredicts the radio flux at t ≲ 1 day, requiring the presence of a temporal break at early times.

Afterglow spectral properties

X-rays

We model the afterglow spectra in each energy band (x-ray, OIR, and radio) using a simple power-law function, F_v ∝ v^β. The best fit was found by minimizing the Cash statistic within XSPEC v12.12.0. The effects of absorption were included using the XSPEC model tbabs^*ztbabs^*pow with fixed redshift z = 0.1505. The GRB sight line intercepts dense clouds along the Galactic plane, as shown by the bright dust scattering echoes at x-ray energies (12). We probed the absorbing column in the GRB direction by extracting multiple spectra of the ring located 6 arcmin from the GRB position at T₀ + 1.2 days (ObsID: 01126853005). They are well described by a power law with photon index Γ = ${4.3}_{-0.5}^{+0.6}$ and an absorbing column of N_H = ${2.1}_{-0.6}^{+0.2}\times {10}^{22}$ cm⁻². We used the latter value as our estimate of the Galactic hydrogen column density.

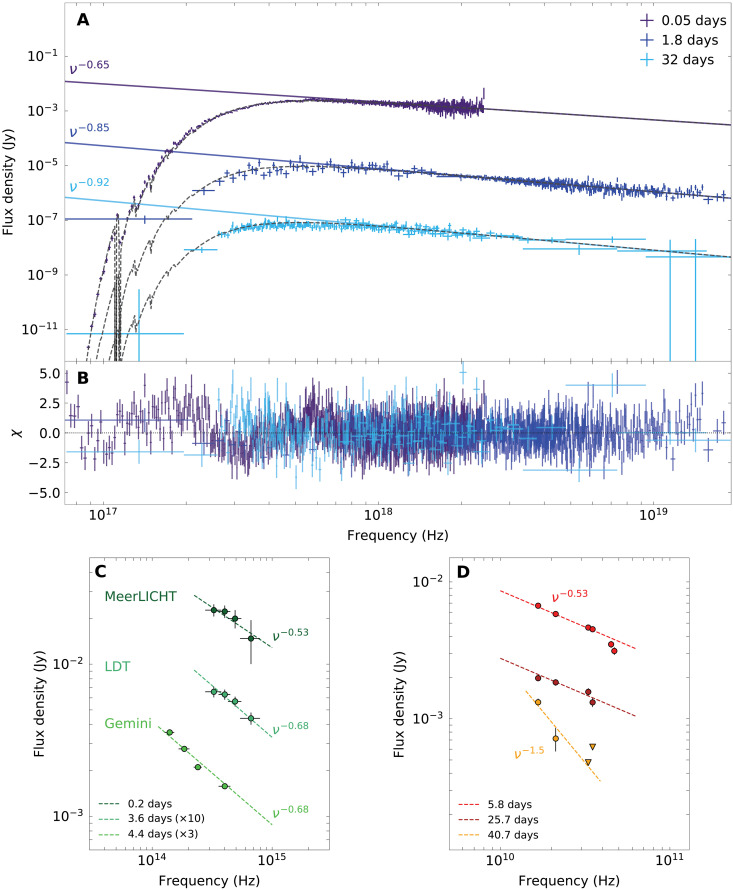
The soft x-ray spectra (0.3 to 10 keV) display an initial hard spectral index of β_X = −0.65 ± 0.02 at 1 hour, which is seen to soften with time to β_X = −0.85 ± 0.03 at 5 hours and β_X = −0.92 ± 0.01 at 32 days. A similar trend is measured in the NuSTAR data (3 to 79 keV), which also display a spectral softening between −0.81 ± 0.01 at 1.8 days and –1.10 ± 0.17 at 32 days. The latter value is consistent with the initial spectral index, β_BAT = −1.08 ± 0.03, determined by Swift BAT (12).

Optical and infrared

The OIR data were modeled within XSPEC using the model redden*zdust^*pow with fixed redshift z = 0.1505. Using a Galactic extinction of E(B − V) = 1.32 mag (50), we derive a negligible intrinsic extinction E(B − V)_z < 0.1 mag at the 3σ confidence level, a spectral index β_OIR = −0.53 ± 0.10 between 0.2 and 0.5 days, and a steeper index β_OIR = −0.68 ± 0.05 after 1.7 days (see Fig. 7). These values are consistent with the spectral index of the early (∼1 hour) x-ray afterglow.

Fig. 7. Multiepoch spectra and SEDs of GRB 221009A.

(A) Top: X-ray spectra of GRB 221009A fit an absorbed power-law model: Swift at 0.05 days, Swift and NuSTAR at 1.8 days, and XMM-Newton and NuSTAR at 32 days. (B) Middle: Residuals of the x-ray spectral fits. (C) Bottom left: Spectral energy distributions of the OIR data fit with a simple power-law model. The OIR data have been corrected for Galactic extinction E(B − V) = 1.32 mag (50). (D) Bottom right: Spectral energy distributions of the radio data (16.7 to 47 GHz).

Radio

Our dataset spans the frequency range between 5.5 and 47 GHz. Our second epoch (14.7 days after burst) was not included in the spectral analysis due to the large systematic uncertainty at higher frequencies. As shown in Fig. 7, the spectra at 5.8 and 25.7 days can be described by a power law with spectral index β_R = −0.53 ± 0.17. There is possible evidence for a turnover of the radio spectrum at 40.7 days, suggesting that the component powering the low-frequency radio emission is not contributing to the optical and x-ray flux.

Theoretical modeling

Standard jet model

We began by exploring the simple scenario of a relativistic fireball (21, 22, 28, 51) propagating into an ambient medium with density of the form ρ_ext(r) = A r^−k. The shock-accelerated electrons have an energy distribution of the form N(E) ∝ E^−p and cool via synchrotron radiation with a broadband spectrum described by three break frequencies: the cooling frequency v_c, the characteristic frequency v_m, and the self-absorption frequency v_a. We focus mainly on the properties of the x-ray and OIR afterglow, as our analysis shows that the radio emission is dominated by a different component.

Our observational constraints include (i) the notable spectral evolution of the optical and x-ray emission during the first 24 hours since the GRB and (ii) the nearly achromatic steepening of the optical and x-ray light curves at around 0.8 days. A simple explanation for the spectral and temporal evolution of the x-ray counterpart is the passage of the cooling break. The observed change in x-ray spectral index, Δβ_X = −0.46 ± 0.07 between 0.05 and 40 days, points to a decreasing cooling break. The synchrotron cooling frequency is expected to change with time as $v_{\mathrm{c}}\propto t^{\frac{3k-4}{2k-8}}$. This constraint implies k < 4/3 and rules out a wind-like environment with density profile k = 2 or steeper. However, if v_c ≲ v_X at 1 day, the x-ray temporal slope after the break, α_X = −1.66, would require a steep p = (2 − 4α_X)3 ≈ 2.88, hence a soft spectral index β_X = p/2 ≈ 1.4 inconsistent with the observed spectral shape by ≈5σ.

A possible solution could be to include a time-dependent evolution of the shock microphysical parameters (52–54): ε_e is the fraction of the burst kinetic energy E_K in electrons and ε_B is the fraction in magnetic fields. To explain the slope of the x-ray light curve after the break, we require that the time dependence of the microphysical parameters adds an additional t^−0.51 to the temporal decay above v_c (assuming p = 2.2). As the flux above v_c has a very shallow dependence on ε_B (${\propto }_B^{1/20}$ for p = 2.2), it is more practical to consider a time evolution of ε_e. We find that ε_e ∝ t^−0.425 would not only reproduce the x-ray temporal slope but also drive a fast evolution of the spectral peak toward lower frequencies, v_m ∝ t⁻²³⁵, severely overpredicting the observed radio flux. Moreover, it does not account for the nearly simultaneous steepening of the optical emission. We therefore conclude that the passage of the cooling break across the x-ray band can explain some of the observed properties (e.g., the spectral softening) but does not entirely account for the steep temporal decay.

A straightforward explanation for the nearly achromatic temporal break at 0.8 days is a geometrical effect (19, 20). The beamed geometry of the outflow causes the afterglow to decay at a faster rate once the jet edges become visible, with a change in temporal slope of Δα = (3 − k)/(4 − k) in the absence of lateral spreading, for a uniform sharp-edged (or “top-hat”) jet. To be consistent with the x-ray measurements of Δα_X = 0.14 ± 0.02, this model requires a steep density profile k ≈ 2.8 in disagreement with the limit k < 4/3 derived above.

If the temporal break at 0.8 days is not due to the collimation of the GRB outflow, then the required energetics to power the burst are challenging to reproduce. The x-ray light curve evolves as a power law up to at least 80 days after the trigger (at the time of writing).

Therefore, we can put an observational lower limit on t_j > 80 days, which leads to a lower limit on both the jet opening angle θ_j and the collimation-corrected energy of the GRB. Assuming k = 0 (uniform medium) and a redshift z = 0.1505, we derive

$$E_{\mathrm{K}}>4\times {10}^{53}\mathrm{erg}{\left(\frac{t_j}{80\mathrm{days}}\right)}^{3/4}{\left(\frac{1+z}{1.15}\right)}^{-3/4}{\left(\frac{E_{K,\mathrm{iso}}}{{10}^{55}\mathrm{erg}}\right)}^{3/4}{\left(\frac{n}{1{\mathrm{cm}}^{-3}}\right)}^{1/4}$$ (2)

where n is the circumburst density for a uniform medium. Such a high beaming corrected energy would be an outlier in the GRB energy distribution (Fig. 8) (35).

Fig. 8. Collimation corrected kinetic energy E_K versus prompt gamma-ray energy E_γ.

We have displayed a sample of long GRBs from the literature (35, 38). The empty red star displays the lowerlimit to the energy of GRB 221009A in the top-hat jet scenario and the filled red star in the structured jet case. The gray-shaded regions show a range of allowed values for magnetar central engines based on the mass of the neutron star (NS) (26, 65). The black lines show a gamma-ray efficiency of η_γ = 30 to 80%.

A structured jet

The standard assumption that GRB jets have a constant energy dE_K/dΩ within the core of the jet is likely an oversimplification, and a structured jet naturally arises as the GRB breaks out of its stellar environment (32, 55). Here, we consider a GRB jet with a broken power-law structure (Fig. 3) defined by

$$\frac{{dE}_{\mathrm{K}}}{d\text{Ω}}\propto \{\begin{array}{c}{\mathrm{\theta }}^{-a1}\mathrm{for}\mathrm{\theta }<{\mathrm{\theta }}_{\mathrm{b}}\\ {\mathrm{\theta }}^{-a2}\mathrm{for}{\mathrm{\theta }}_{\mathrm{b}}<\mathrm{\theta }<{\mathrm{\theta }}_{\mathrm{s}}\\ {\mathrm{\theta }}^{-a3}\mathrm{for}\mathrm{\theta }>{\mathrm{\theta }}_{\mathrm{s}}\end{array}$$ (3)

where a₁ < a₂ < 2, a₃ → ∞, and an observer angle θ_obs < θ_b. This jet is therefore composed of an initial shallow slope followed by a steeper lateral profile that becomes visible when Γ ≈ ${\mathrm{\theta }}_{\mathrm{b}}^{-1}$, where θ_b is the width of the initial shallow profile. In this case, the flux and frequency evolution is dictated by the lateral structure, leading to a shallow angular structure dominated emission (sASDE) phase [see tables 1 and 2 of (29)]. The flux evolution is initially the same as for a spherical outflow with an isotropic-equivalent energy corresponding to the value along the line of sight. This lasts up to a time, t_sph, when the Lorentz factor along the line of sight has decelerated to ${\mathrm{\theta }}_{\mathrm{obs}}^1$. At this point, the lateral structure becomes visible and the sASDE phase begins. In this regime, the flux in an interstellar medium environment is determined by

$$F_v\propto \{\begin{array}{c}t\frac{3(a+2p-2)}{(a-8)}\mathrm{for}{v}_{\mathrm{m}}<v<v_{\mathrm{c}}\\ t\frac{2(a+3p-2)}{a-8}\mathrm{for}{v}_{\mathrm{c}}<v\end{array}$$ (4)

This phase lasts until t_b ≈ 0.8 days, which is the time at which Γ = ${\mathrm{\theta }}_{\mathrm{b}}^{-1}$. For t > t_b, the flux evolves in a similar way (i.e., governed by Eq. 4) but with a₁ → a₂. For angles θ > θ_s, a steep jet break is expected at late times (t_j > 80 days) if the jet is still relativistic (33, 56).

We consider a scenario where t_sph < 1 hour, such that the temporal decay is provided by Eq. 4 for the entire time period of our observations (0.05 to 80 days). We find a solution for p = 2.2, k = 0, a₁ = 0.75, and a₂ = 1.15, which yields an initial pre-break slope of α_X,1 = 1.55 that steepens to α_X,2 = −1.67 after ∼ 0.8 days, assuming that v_c < v_X. The OIR slope after the break is α_OIR,2 = −1.47 for v_m < v_OIR < v_c, while the early OIR data (<1 day) are dominated by emission from a different component, likely an RS.

Motivated by this solution, we modeled the afterglow spectral energy distributions from radio to x-ray wavelengths with a phenomenological model combining two components, an FS and an RS. The FS closure relations are governed by the jet structure (Eq. 4).

The RS evolution in a structured outflow has not been sufficiently developed yet for inclusion in our study. We therefore adopt standard prescriptions of a thin-shell model parameterized by the power-law index g of the Lorentz factor distribution with radius Γ ∝ R^−g (57). Each component was allowed to have an independent electron spectral slope p and was parameterized by the locations of v_a, v_m, and v_c at a reference time of 1 day as well as the peak flux F_v,max at that time. The best fit was obtained by simple χ² minimization on the extinction-corrected afterglow data (Fig. 4).

We find that the FS reproduces the full x-ray light curve and the OIR data after 0.8 days (Fig. 4). In this model, the cooling break v_c,FS moves through the x-ray band, producing the observed spectral softening. The injection frequency v_m,FS is constrained to be close to the soft x-ray band at early times, as otherwise the FS severely overpredicts the radio emission at later times (>14 days). A jet model with a single slope for the power-law energy distribution dE_K/dΩ ∝ θ^−a with a ≈ 1 can reproduce these observations. However, a broken power-law energy structure is well motivated by simulations (32) of GRB jets, which display an evolution of the jet’s angular energy distribution from shallower to steeper slopes. For a jet with structure given by a₁ ≈ 0.75 and a₂ ≈ 1.15, we derive v_c,FS ≈ 1.7 × 10¹⁸ Hz, v_m,FS ≈ 3.6 × 10¹⁴ Hz, F_v,max,FS ≈ 5.9 mJy, and p ≈ 2.25. The self-absorption frequency v_a,FS ≲ 10¹⁰ Hz remains unconstrained.

Afterglow modeling depends on a large number of physical parameters, larger than the number of observed constraints. Many values of the physical parameters, varying over orders of magnitude, will produce nearly identical afterglow emission. Using fiducial values of E_K,iso = 10⁵⁵ erg, n = 1 cm⁻³, and θ_obs = 0.01 rad and inverting the values of F_v,max,FS, v_m,FS, and v_c,FS, we find a solution for ε_e = 0.17, ε_B = 4.4 × 10⁻⁶, and an electron participation fraction ξ_N = 0.015.

As expected, we find that the standard thin-shell RS is not capable of reproducing the phenomenology of a structured outflow. Even for large values of the parameter g ≳ 3, this model cannot account for the early optical emission and, at the same time, reproduce the shallow decay of the radio afterglow (Fig. 9). To capture this behavior, we require at least two separate RS components (Fig. 4), with the first RS dominating at <10 days capable of explaining the early radio and OIR data. Alternatively, ad hoc solutions such as energy injection and/or variability of the shock microphysics may be introduced to slow down the RS evolution.

Fig. 9. Multiepoch broad-band SEDs of GRB 221009A.

We have modeled the data by the combination (solid line) of an FS and an RS (dotted line). A single RS evolved following the thin-shell closure relations (57) cannot reproduce the early optical and late radio emission. The data are corrected for extinction and absorption.

Similar challenges were encountered in the modeling of other bright GRBs (58). For example, a two component model was explored in the case of GRB 030329A (40), GRB 130427A (59), and GRB 190829A (37, 60), whereas time-evolving microphysics were favored in the case of GRB 190114C (39). GRB 221009A adds to the growing sample of bursts deviating from the basic RS scenario and motivates further extension of the standard model by incorporating a broader set of jet angular structures.

Implications of a structured jet

Energetics

An advantage of the shallow structured jet scenario suggested above is that it reduces the energy requirements compared to steep jet models. The viewing angle to the burst θ_obs is directly related to the earliest time, t_sph, at which the afterglow begins evolving according to the inner (shallow) slope of the energy profile (i.e., E_K,iso ∝ θ^−a₁; see Eq. 4) and can be expressed as

$${\mathrm{\theta }}_{\mathrm{obs}}={\left(\frac{(3-k)E_{\mathrm{K},\mathrm{iso}}({\mathrm{\theta }}_{\mathrm{obs}})}{4\mathrm{\pi }A{2}^{3-k}{c}^{5-k}}\right)}^{\frac{1}{2k-8}}{t}_{\mathrm{sph}}^{\frac{3-k}{8-2k}}$$ (5)

which, for k = 0 (as favored by the spectral evolution), implies θ_obs ≲ 0.016 rad for t_sph < 0.05 days. For a shallow structured jet, the maximum polar angle of the jet viewable to an observer at θ_obs evolves in time according to

$$\mathrm{\theta }(t)={\mathrm{\theta }}_{\mathrm{obs}}\{\begin{array}{c}{(t/t_{\mathrm{sph}})}^{\frac{3-k}{8-2k-a_1}}\mathrm{for}{t}_{\mathrm{sph}}<t<t_{\mathrm{b}}\\ {(t_{\mathrm{b}}/t_{\mathrm{sph}})}^{\frac{3-k}{8-2k-a_1}(t/t_{\mathrm{b}})\frac{3-k}{8-2k-a2}}\mathrm{for}t>t_{\mathrm{b}}\end{array}$$ (6)

where we adopt a₁ = 0.75 and a₂ = 1.15. This is related to the angle θ_b below which E_K,iso evolves as θ^−a₁ and above which as θ^−a₂. Therefore, θ_b can be expressed as

$$\begin{array}{c}{\mathrm{\theta }}_{\mathrm{b}}={\left(\frac{(3-k)E_{\mathrm{K},\mathrm{iso}}({\mathrm{\theta }}_{obs})}{4\mathrm{\pi }A{2}^{3-k}{c}^{5-k}}\right)}^{\frac{1}{2k-8+a_1}}{t}_{\mathrm{b}}^{\frac{3-k}{8-2k-a_1}}{\mathrm{\theta }}_{\mathrm{obs}}^{\frac{a_1}{8-2k-a_1}}\\ =0.057\mathrm{rad}{\left(\frac{E_{\mathrm{K},\mathrm{iso}}}{{10}^{55}\mathrm{erg}}\right)}^{-0.14}{\left(\frac{n}{1{\mathrm{cm}}^{-3}}\right)}^{0.14}{\left(\frac{{\mathrm{\theta }}_{\mathrm{obs}}}{0.01}\right)}^{-0.10}{\left(\frac{t_{\mathrm{b}}}{0.8\mathrm{days}}\right)}^{0.4}{\left(\frac{1+z}{115}\right)}^{-0.4}\end{array}$$ (7)

As we do not observe a steep break (i.e., traditional jet break with F_v ∝ t^−p) in the light curve out to t_j > 80 days, we can set a lower limit to the opening angle θ_s (see Eq. 3) out to which the relation E_K,iso ∝ θ^−a₂ extends. This, in turn, allows us to derive a lower limit to the collimation-corrected kinetic energy in the jet E_K. Using θ_obs and θ_b, these relations are provided by

$${\mathrm{\theta }}_{\mathrm{s}}>\mathrm{\theta }(t)={\mathrm{\theta }}_{\mathrm{b}}{\left(\frac{t_j}{t_{\mathrm{b}}}\right)}^{\frac{3-k}{8-2k-a_2}}$$ (8)

$$E_{\mathrm{K}}=\frac{a_3-a_2}{(2-a_2)(a_3-2)}\mathrm{\theta }{(t)}^2{E}_{\mathrm{K},\mathrm{iso}}({\mathrm{\theta }}_{\mathrm{obs}}){\left(\frac{{\mathrm{\theta }}_{\mathrm{b}}}{{\mathrm{\theta }}_{\mathrm{obs}}}\right)}^{-a_1}{\left(\frac{\mathrm{\theta }(t)}{{\mathrm{\theta }}_{\mathrm{b}}}\right)}^{-a_2}$$ (9)

which, for θ(t) = θ_s, k = 0, a₁ = 0.75, a₂ = 1.15, and a₃ → ∞, becomes

$$\begin{array}{rl}& {\mathrm{\theta }}_{\mathrm{s}}>0.4\mathrm{rad}{\left(\frac{E_{\mathrm{K},\mathrm{iso}}}{{10}^{55}\mathrm{erg}}\right)}^{-0.14}{\left(\frac{n}{1{\mathrm{cm}}^{-3}}\right)}^{0.14}{\left(\frac{{\mathrm{\theta }}_{\mathrm{obs}}}{0.01}\right)}^{-0.10}\\ & {\left(\frac{t_{\mathrm{b}}}{0.8\mathrm{days}}\right)}^{-0.04}{\left(\frac{1+z}{1.15}\right)}^{0.04}{\left(\frac{t_{\mathrm{j}}}{80\mathrm{days}}\right)}^{0.44}\end{array}$$ (10)

$$\begin{array}{rl}{E}_{\mathrm{K}}& =8\times 10^{52}{\left(\frac{E_{\mathrm{K},\mathrm{iso}}}{{10}^{55}\mathrm{erg}}\right)}^{0.83}{\left(\frac{n}{1{\mathrm{cm}}^{-3}}\right)}^{0.17}{\left(\frac{{\mathrm{\theta }}_{\mathrm{obs}}}{0.01}\right)}^{062}{\left(\frac{t_{\mathrm{b}}}{0.8\mathrm{days}}\right)}^{0.14}\\ & {\left(\frac{t_{\mathrm{j}}}{80\mathrm{days}}\right)}^{0.37}{\left(\frac{1+z}{1.15}\right)}^{-0.51}\end{array}$$ (11)

Formally, this limit decreases for smaller viewing angles θ_obs. However, considering that t_sph has to be greater than the prompt duration of the GRB, θ_obs cannot decrease by much. The required energy is reduced compared to the standard jet case (4 × 10⁵³ erg). Furthermore, the energy has a shallower dependence on the time of the steep jet break $t_{\mathrm{j}}^{0.37}$ compared to $t_{\mathrm{j}}^{3/4}$ for a top-hat jet. In other words, as the length of time over which we do not observe a steep jet break increases, the more energetically favorable the structured jet model becomes.

A structured jet with extended wings will take even longer to establish causal contact across the jet surface than a top-hat jet, which can help to explain the lack of post–jet break dynamics observed for GRB 221009A and similar events. In the central engine frame, a relativistic sound wave traveling along the jet surface between edge and tip will move along with velocity β_θ = 1/(2Γ) for a jet with local shock Lorentz factor Γ. If Γ∝ θ^−a_1/2, then causal contact out to angle θ will occur once Γ(θ) = (1 − a₁/2)/(3θ) ≲ 1 (for example, θ = 0.4 rad, a₁ = 0.75, Γ = 0.52 < 1 shows a clear breakdown of the assumption of relativistic dynamics; a steepening to a jet structure slope a₂ at intermediate angle would lead to an even lower Γ). The nonrelativistic light curve slope above the cooling break (e.g., in the x-rays) is given by t^(4−3p)/2, which can be very similar to the relativistic slope of a shallow structured jet.

Rate of events

We have demonstrated that GRB 221009A stands out compared to other long-duration GRBs in terms of its both energetics and close proximity. The shallow flux decay in the x-ray and OIR until very late times is interpreted as evidence for a shallow jet structure. We therefore suggest that GRB 221009A and other nearby GRBs without steep jet breaks (GRB 130427A, GRB 180720B, GRB 190114C, and GRB 190829A) imply the existence of a subclass of energetic GRBs with shallow jet structures.

This subclass, due to their shallow angular profiles, has a different effective beaming compared to the typical GRB population, which affects their observed rate. On the one hand, the large inferred value of θ_s ≈ 0.4 rad derived for GRB 221009A in Eq. 10 is larger than typical opening angles derived for long GRBs, i.e., θ_j ≈ 0.1 rad, where jet breaks are easier to observe for energetic and narrow jets. This would suggest that even a relatively small intrinsic rate associated with the subpopulation of shallow jets might be overrepresented in the observed data, approximately by a factor of (θ_s/θ_j)² ≈ 16. However, the low derived value of the viewing angle to GRB 221009A, θ_obs ≲ 0.016 rad (Eq. 5), is in tension with this suggestion. In particular, because of the larger solid angles associated with greater viewing angles, for each burst like GRB 221009A that is viewed from ≲θ_obs, there should be (on average) ∼ 625 GRBs viewed from ≲ θ_s. If we take a shallow angular profile of the kinetic energy, E_K,iso ∝ θ^−a with a ≈ 0.9 between θ_obs and θ_s, then bursts viewed from ∼θ_s might be expected to have a gamma-ray fluence that is roughly 20 times smaller than that of GRB 221009A. In other words, if the observed rate of GRB 221009A is about 1 in 1000 years, then, roughly once in 1.5 year, we should be detecting bursts that are ∼20 times less fluent. As shown in Figs. 1 and 6, this is clearly in contradiction with Fermi and BATSE observations. This suggests that, even if GRB 221009A–like jets have shallow profiles extending up to large latitudes, their gamma-ray production might be restricted to a much narrower range (up to some θ_γ ≪ θ_s). Such a possibility is expected if there is even a relatively small reduction in the bulk Lorentz factor of the outflows with θ (61). Beniamini and Nakar (61) have argued that this is a limiting factor in the detectability of long GRBs based on various observational lines of evidence. To conclude, the intrinsic rate of GRB 221009A–like jets is strongly dependent on the effective opening angle for gamma-ray production, and, with only one well-constrained event of this type, the intrinsic rate of such bursts remains largely unconstrained. Nonetheless, if θ_γ ≪ θ_s as suggested by the discussion above, then there should be a large population of similar jets that would have produced little or no gamma rays, despite having been viewed from θ < θ_s and, therefore, corresponded to very bright and initially fast evolving afterglows in all wavelengths. The existence of these on-axis orphan afterglows of shallow jets can be constrained using transient surveys (62).

Assuming that the prompt GRB emission is produced in an optically thin region of the outflow, the dissipation radius inferred from the prompt emission variability timescale t can be compared to the photospheric radius to place a constraint on the minimum outflow Lorentz factor placing emission beyond the photospheric radius. Following (63), this requirement translates to Γ ≳ 505(E/10⁵⁵ erg)^1/5 (δt/0.1 s)^−2/5 for a jet of isotropic-equivalent energy E. The atypical jet structure inferred for GRB 221009A, with a very narrow core (a tip) embedded within shallow power-law profile, implies a far smaller jet surface area detectable in prompt emission. Assuming an inner jet Lorentz factor profile Γ = Γ_tip(θ/θ_j)^−a₁/2 and a₁ = 0.9, we find a maximum observer angle θ_γ ∼ 0.043(θ_j/10⁻²(E/10⁵⁵ erg)^−0.74(δt/0.1 s)^1.5(Γ_tip/750)^3.7 rad, assuming that the tip (i.e., the region of the jet at θ < θ_γ) is sufficiently fast in the first place. Thus, even if shallow power-law jets with narrow cores were intrinsically equally likely as “typical” top-hat jets with θ_j ∼ 0.1 rad, this already renders them about five times as rare. The intrinsic likelihood of producing a jet with a narrow core and shallow power-law structure further affects their expected rate, as do the energetics and initial baryon loading of the jet.

Supplementary Materials

This PDF file includes:

Supplementary Text

Tables S1 to S5

References