The strength of surgical knots involves a critical interplay between friction and elastoplasticity

Abstract

Knots are the weakest link in surgical sutures, serving as mechanical ligatures between filaments. Exceeding their safe operational limits can cause fatal complications. The empirical nature of present guidelines calls for a predictive understanding of the mechanisms underlying knot strength. We identify the primary ingredients dictating the mechanics of surgical sliding knots, highlighting the previously overlooked but critical effect of plasticity and its interplay with friction. The characterization of surgeon-tied knots reveals the relevant ranges of tightness and geometric features. Using model experiments coupled with finite element simulations, we uncover a robust master curve for the target knot strength versus the tying pre-tension, number of throws, and frictional properties. These findings could find applications in the training of surgeons and robotic-assisted surgical devices.

The strength of surgical knots exhibits a robust mechanism involving topology, geometry, friction, and elasto-plasticity.

INTRODUCTION

Surgery is a delicate craft in which high-quality suturing requires precision manual skills (1, 2). Knots are central to surgical procedures, where they are used as ligatures during suturing (3, 4). Knots are the weakest link in a suture (5, 6), with disastrous consequences when they fail if they fail (7, 8). A typical complication in surgery is wound dehiscence, whereby a previously sutured incision reopens, thus preventing wound healing (9). The related incisional hernia can be as high as 20% within the first year following midline laparotomy (10). In many common surgical procedures, suturing using monofilaments (versus braided ones) is advantageous for lower infection risks, albeit more challenging to ensure mechanical safety (11).

Surgeons tie sliding knots daily, consciously, or unwittingly (12); all intended flat knots tied in monofilaments capsize into a sliding conformation (13). Typical sliding knots consist of a series of half-hitches around a nearly straight filament segment under tension. A notation has been developed (5, 12, 14, 15) to describe these knot configurations: “S” denotes a sliding throw, and “||” or “×” indicates an identical or nonidentical subsequent throw, respectively. For example, S || S refers to the sliding granny knot with two identical throws, and S × S to the sliding square knot with two nonidentical throws. The more complex S || S × S configuration describes a sliding granny knot followed by a sliding square knot. This notation is used throughout.

Although a high variability of knot-tying techniques is found across surgeons (1), additional throws in a knot have been shown to consistently decreases spontaneous untying rates (5, 16, 17). Furthermore, the tying pre-tension applied by the surgeon to tighten each throw appears to depend more on individual perception than experience (18). Even if the importance of mechanical analysis of knots has long been recognized in the medical profession, existing guidelines for best practices are primarily empirical and historical, not relying on physics-based structural analyses (5). Despite their broad and practical relevance, the predictive understanding of the physical mechanisms underlying knots remains crude. Existing frameworks in the classic mathematical theory of knots or elastic rod theory (19) are limited to purely geometric abstractions (20–22) or loose physical knots (23, 24) and, thus, cannot capture the mechanical behavior of tight physical knots with their three-dimensional (3D) deformations and frictional contact (25–27). In addition to the fundamental challenges related to topology, geometry, 3D elasticity, contact, and frictional interactions, knotted surgical monofilaments also undergo elastoplastic deformation (28, 29). The consequences and potentials of plasticity in functional knots have, to the best of our knowledge, not been considered to date.

Here, we seek to establish physics-based operational and safety guidelines for the strength of surgical sliding knots, focusing on commercial polypropylene suturing monofilaments which are common in surgical practice. We develop a physical model system to study the resistance of the knot to slippage—the knot strength—by systematically varying the tying pre-tension, number of throws, and knot topology (|| versus × throws). Our data are consistent with a power law for the knot strength as a function of the applied pre-tension and a linear relation between the knot strength and the number of throws. In addition, we characterize knots tied by an experienced surgeon, finding that they intuitively leave a safety margin between the regimes where knots are too loose to be functional and the high-tension regime resulting in filament fracture. The influence of friction on knot safety is explored systematically, using finite element modeling(FEM) to simulate elastoplastic knots with varying frictional interactions. Last, we propose a normalization that collapses all the data onto a master curve, describing the knot strength of tight knots in all of the configurations we considered and a wide range of friction coefficients. Our analysis suggests a robust mechanism for the strength of these surgical knots.

RESULTS

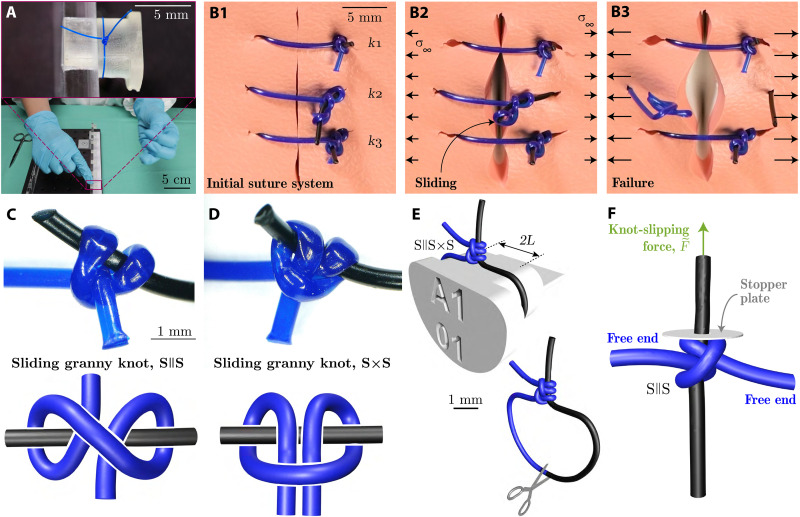
The photograph in Fig. 1A (and movie S1) shows a series of half-hitch throws tied by a surgeon in a polypropylene suturing filament (Prolene, Ethicon Inc., Johnson & Johnson). This monofilament of circular cross section and area, A, was used throughout the study in the diameters of 0.25 or 0.49 mm United States Pharmacopeia (USP) designation 3-0 and 1, respectively (30)]. The yield strength of as-received Prolene was determined from uniaxial stress-strain measurements to be σ_Y = 19.1 MPa [from the 0.1% offset yield point (31)]. Typically, multiple suturing knots allow binding tissue, sealing an accident tear or a surgical incision (11, 32). In Fig. 1 (B1 to B3) (and movie S2), we illustrate the typical surgical failure mode of wound dehiscence using a suturing practice pad with three stitches (S || S × S each) of different tightness. The outer knots k₁ and k₃ are tighter than the middle knot k₂. The system was loaded by gradually increasing the far-field uniaxial stress field of magnitude σ_∞. At a sufficiently large stress level, the filament of the middle knot, k₂, starts sliding (Fig. 1B2) until it completely slips out and, from then on, no longer fulfills its binding function (Fig. 1B3).

Fig. 1. Failure of surgical sliding knots.

(A) Photograph of the tying of a common sliding knot by an experienced surgeon in a Prolene polypropylene filament on a rigid support. (B1 to B3) Photographs illustrating knot safety and sliding for different levels of tightness of the S || S × S knot in a suture system on a practice pad, at increasing levels of the far-field stress, σ_∞. (C and D) Optical microscope image (top) and topological diagram (bottom) of the S || S (C), and S × S (D) sliding-knot topologies. (E) Schematic of the S || S × S knot tied around a 3D-printed pin and visualization of the cutting location in the suture loop. (F) FEM-computed configuration for a S || S knot tied with a pre-tension of $\tilde{T}=10.9$. The same configuration is implemented in the mechanical testing experiments to measure the slipping force, $\tilde{F}$, of the S || S knot (cf. Fig. 2).

In Fig. 1 (C and D), we present optical microscope images (top) of S || S and the S × S knots, tightened using a UTM (universal testing machine; Instron 5943), along with their topological diagram (bottom). The knots (surgeon- and machine-tied) were tied around rigid 3D-printed pins (stereolithography 3D printer: Form 2, Formlabs; Clear V4 resin), with a flat upper surface of width, 2L = 6 mm (Fig. 1E). This pin geometry was chosen on the basis of the common rule for skin closures (33), prescribing the distance between the needle’s entry point and the wound’s edge, L, to equal the thickness of the tissue, ranging from 1 to 4 mm in the human body. After the half-hitch (identical or nonidentical throw) was set manually in its loose configuration on the rigid pin, the two free extremities of the filament were clamped to the UTM. The protocol to tighten the knot to a set pre-tension, $\tilde{T}$, is described in Materials and Methods.

We characterized sliding knots by quantifying their slippage resistance as follows. The loop surrounding the pin was cut open (Fig. 1E), and the protruding sliding strand (extremity of the filament at the cut) was threaded through the hole of a rigid stopper plate, as schematized in Fig. 1F for the S || S knot. Then, the knotted configuration was pulled against this plate to measure the knot-slipping force, $\tilde{F}$. In this model system, the plate represents the bound tissue in the suturing system, where tractions may lead to wound dehiscence (Fig. 1B). Figure 2A1 presents the experimental setup, where the protruding (sliding) strand, previously part of the loop, was first slid through a clearance hole (0.30 − mm diameter for 3-0 USP filament) in a flat, rigid acrylic plate (4 − mm thickness). Using the UTM at the constant speed of 1 mm/s, the S || S knot is then pulled against the plate, blocking vertical translation, and eventually leading to the sliding mechanism (Fig. 2, A1 to A4). In Fig. 2B, we plot the resulting dimensionless slipping force $\tilde{F}=F/({\mathrm{\sigma }}_{Y}A)$ versus the normalized displacement $\tilde{\mathrm{\delta }}=\mathrm{\delta }/D$. Initially, $\tilde{F}$ increases as the vertical filament is pulled upward and the knotted filament is resisted by the stopper plate (Fig. 2A2). Past an initial transient, the force reaches a plateau, where the filament slides with a nearly constant slipping force (Fig. 2A3). This characteristic force, denoted nondimensionally as ${\tilde{F}}_0$, corresponds to the knot strength, ultimately, the cause of the knot’s untying (Fig. 2A4). Note that forces are nondimensionalized in units of σ_YA; applied dimensionless tensions greater than 1 involve plastic deformation of the straight filament strand.

Fig. 2. Mechanical tests of the strength of a S||S knot.

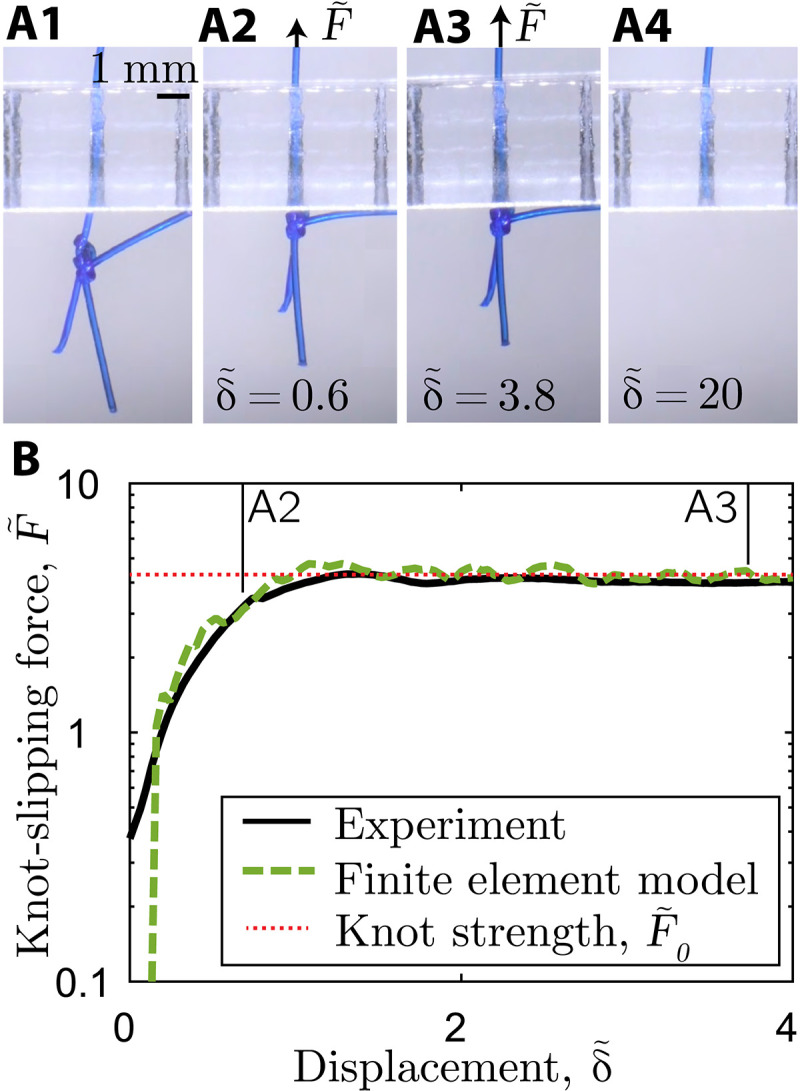
(A1 to A4) Sequence of photographs during mechanical testing, visualizing the sliding process of a previously tied knot that is pulled against a stopper plate to measure the slipping force, $\tilde{F}$. The frames are shown at increasing values of dimensionless displacement, $\tilde{\mathrm{\delta }}=\mathrm{\delta }/D$, of the vertically pulled filament. (B) Representative curves (experiments and FEM) of $\tilde{F}$ versus displacement, $\tilde{\mathrm{\delta }}$. The plateau of the curves defines the knot strength, ${\tilde{F}}_0$. The points A2 and A3 correspond to the photographs in (A2) to (A3). The S || S knot was tied to a pre-tension of $\tilde{T}=10.9$.

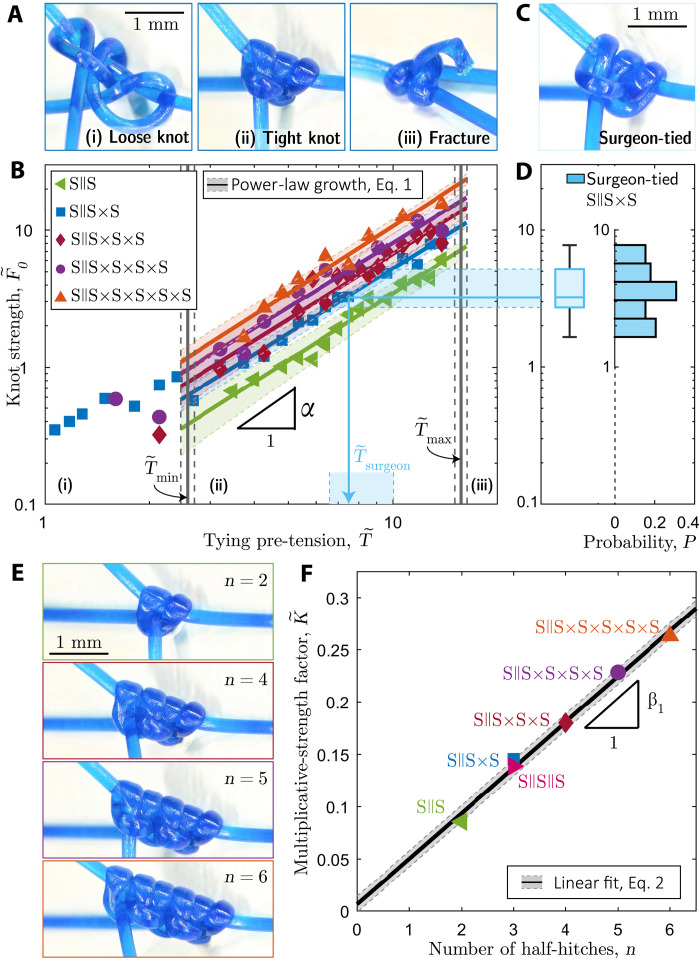
Next, we use the mechanical testing described above to characterize the knot strength, ${\tilde{F}}_0$, while systematically varying the tying pre-tension, $\tilde{T}$, and the number of throws, n. First, we focus on the S || S × S topology (n = 3), with each throw pre-tensioned equally. Different levels of $\tilde{T}$ lead to the three distinct regimes showcased in Fig. 3A: (i) loose knots ($\tilde{T}<T_{\min }$), (ii) tight knots ($T_{\min }\le \tilde{T}\le T_{\max }$), and (iii) filament fracture ($\tilde{T}>T_{\max }$). Loose and tight knots were distinguished quantitatively using volume measurements on the sliding granny knot. In fig. S1, we report results on the knot’s volume (measured from the convex hull of x-ray tomography data) as a function of $\tilde{T}$, demonstrating two distinct slopes. The transition between the two regimes is compatible with the convex hull computation applied on the ideal (purely geometric), tightest sliding granny knot, using the Ridgerunner algorithm (34). From this volumetric analysis, the minimum knot tying pre-tension is determined as ${\tilde{T}}_{\min }=T_{\min }/{\mathrm{\sigma }}_{Y}A=2.59\pm 0.14$ (leftmost vertical line in Fig. 3B), below which the knot is considered loose.

Fig. 3. Dependence of the knot strength on pre-tension and topology.

(A) Photographs of representative S || S × S knots tied with different values of pre-tension: (i) loose knot ($\tilde{T}=15$), (ii) tight knot ($\tilde{T}=8.5$), and (iii) fracture of the last throw ($\tilde{T}=20$). (B) Knot strength, ${\tilde{F}}_0$, versus tying pre-tension, $\tilde{T}$, for sliding knots with multiple throw. The solid lines represent the average power-law increase, and the corresponding shaded regions are the 65% confidence interval. The bounds of the intermediate region (ii), ${\tilde{T}}_{\min }$ and ${\tilde{T}}_{\max }$, are represented by vertical solid lines with their SD by the dashed lines. (C) Photograph of a surgeon-tied S || S × S knot. (D) Histogram and box plot of knot-strength measurements for surgeon-tied knots (S || S × S), with the mapping (shaded region) onto the experimental curve in (B). (E) Photographs of sliding knots with different numbers of throws, n = {2,4,5,6} ($\tilde{T}=8.5$). (F) Multiplicative-strength factor, $\tilde{K}$, cf. Eq. 1, of the fitted curves in (B) as a function of the number of throws, n. The linear fit to Eq. 2 and the corresponding 65% confidence interval are represented by the solid line and shaded region, respectively.

Beyond the onset of tight knots, in the intermediate region (ii), the knot strength follows

$${\tilde{F}}_0=\tilde{K}{\tilde{T}}^{\mathrm{\alpha }}$$ (1)

where the exponent α and the prefactor $\tilde{K}$ are two fitting parameters. Equation 1 provides an excellent fit to the data up to filament fracture. This upper limit is determined by rate- and temperature-dependent fracture tests on knotted Prolene filaments and represented by the rightmost vertical line at ${\tilde{T}}_{\max }=T_{\max }{\mathrm{\sigma }}_{Y}A=15.74\pm 0.63$ (fig. S2).

We turn to surgeon-tied knots, mapping their strength to the model experiments described above. Using the same monofilaments, topology (S || S × S), and rigid supports as in the model experiments, an experienced surgeon was instructed to hand-tie 38 knots, tightened identically to their routine suturing procedure. The level of pre-tension of the manually tied knots was unknown (see the representative knot in Fig. 3C). Using our experimental setup, the surgeon-tied knots were then tested for their strength, ${\tilde{F}}_0$, which, as presented in Fig. 3D, exhibits a nearly uniform histogram in the range, $1.7<{\tilde{F}}_0<7.7$. The probability distribution is summarized by the box plot with a median normalized strength of 3.2 and lower and upper quartiles at 2.7 and 5.2, respectively. Projecting the median knot strength and interquartile ranges (shaded region from Fig. 3D to Fig. 3B) onto the results from the model experiments on the S || S × S knot provides an estimate of the operating range of pre-tensions for surgeon-tied knots, ${\tilde{T}}_{\mathrm{surgeon}}\in [6.6-10]$. We find that ${\tilde{T}}_{\mathrm{surgeon}}\in [{\tilde{T}}_{\min },{\tilde{T}}_{\max }]$; the surgeon targets the middle of the intermediate regime (ii) for tight knots identified by our model experiments while leaving safety margins between loose knot configurations, ${\tilde{T}}_{\min }$, and filament fracture, ${\tilde{T}}_{\max }$.

Thus far, we focused on the S || S × S knot, the simplest configuration comprising the two sliding topologies of interest: S || S and S × S. However, surgeons typically tie more than three half-hitches for increased knot safety. To explore the effect of the number of throws, n, on knot strength, we return to the model experiments and investigate configurations with an initial S || S knot followed by different numbers of non-identical (×) throws (Fig. 3E). In Fig. 3B, we plot ${\tilde{F}}_0$ versus the tying pre-tension, $\tilde{T}$. These more complex knots with additional throws exhibit the same functional dependence, Eq. 1, as the simpler S || S × S topology, with α = 1.59 ± 0.03. The consistency of α across the different tested topologies is notable, considering the underlying geometric complexity. These robust results call for a detailed theoretical analysis, which is beyond the scope of the present study. The knot strength increases with n with a prefactor $\tilde{K}$, which we denote as a multiplicative-strength factor. In Fig. 3F, we plot the fitted value of $\tilde{K}$ versus n, finding the linear relation $\tilde{K}={\mathrm{\beta }}_{1}n$, with β₁ = 0.047 ± 0.003. All the fitted parameters are summarized in table S1.

In Fig. 3F, fig. S3, and table. S1, we show that the behavior according to Eq. 1 and the value of K are identical for the S || S × S and the S || S || S knots. In other words, these two topologies are equivalent regarding knot strength. Therefore, quantifying the mechanical performance of complex surgical knots with various topological combinations of multiple throws reduces to characterizing a single sliding knot (n = 2) with a single topology (e.g., S || S). Combining the above observations, we find that surgeon-tied sliding knots are in the tight regime, where the knot strength follows Eq. 1, with the same exponent, independently of the number of throws or the topological combination. The knot strength is described by a multiplicative-strength factor, $\tilde{K}$, which depends linearly on the number of throws, such that

$${\tilde{F}}_0={\mathrm{\beta }}_{1}n{\tilde{\mathrm{T}}}^{\mathrm{\alpha }}$$ (2)

We proceed by complementing the experimental results with fully 3D finite element modeling (FEM) simulations to gain physical insight into the underlying mechanism leading to the knot strength in the tight regime. We used the commercial package ABAQUS/EXPLICIT (Simulia, Dassault Systèmes) to simulate knotted filaments, probing physical quantities not accessible in the experiments, especially the reactions on the surface of the filament. The self-contact of the monofilaments was modeled using Amontons-Coulomb friction enforced through normal penalty forces, combined with tangential frictional forces, with a prescribed dynamic friction coefficient, μ = 0.20 ± 0.02 (fig. S4). On the basis of (35, 36), a 3D continuum-level constitutive model for elastic-viscoplastic mechanical behavior (specialized for uniaxial tension) was developed and implemented in the simulations (fig. S5 and table S2). The filaments used throughout this study undergo unknown deformation during manufacturing and packaging, leading to intrinsic curvature upon unpacking. To account for this (unknown) loading history in the simulations, we considered an effective residual bending stress, σ_R, applied on the initially straight model of the filament (fig. S6).

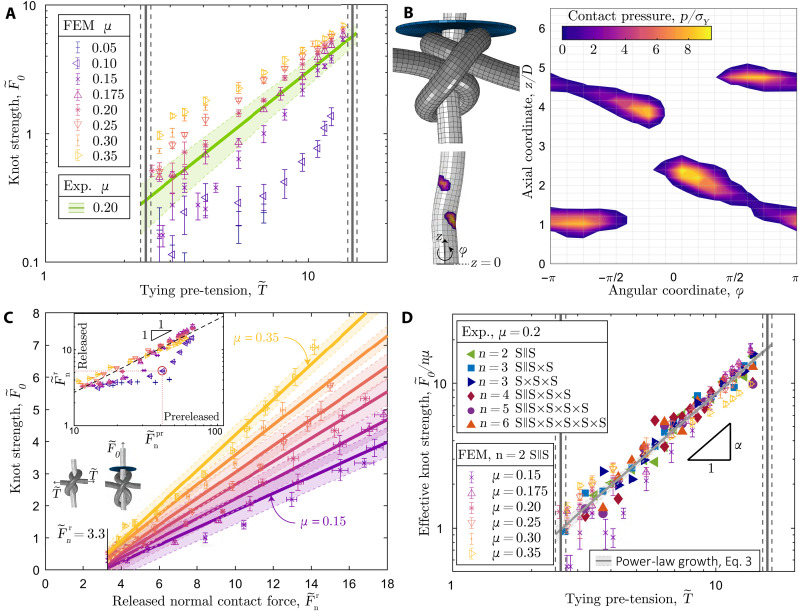
After calibrating the FEM simulations for uniaxial and bending deformations (Materials and Methods) of our filaments, we simulated S || S knots by applying a sequence of prescribed displacements and rotations to control the nodes located at each end and the central filament coordinate (see Materials and Methods and movie S5). For generality, the simulations were performed with a unit-diameter filament. The numerical configuration presented in Fig. 1F was tied with $\tilde{T}=10.9$. The corresponding force-displacement curve is shown in Fig. 2B (dashed line). Note that, at this stage, the FEM has no adjustable parameters; all material parameters and mechanical properties were determined independently. As a final validation step of the numerics, we compared the computed knot strength against experiments over the full range of $\tilde{T}$ in the tight knots regime (ii). In Fig. 4A, we replot the experimental ${\tilde{F}}_0$ data for the S || S knot with the solid line representing the corresponding fit from Fig. 3B. In the same plot, we juxtapose the FEM data computed using the experimentally measured kinematic friction coefficient, μ = 0.2 (* symbols). The agreement between experiments and FEM furthers the confidence in the numerical model and validates the choice for the nondimensionalization of the forces by σ_YA, noting that all simulations were performed assuming unit diameter. Last, we leveraged the FEM to vary μ systematically; the data in Fig. 4A reveals that the knot strength increases with μ.

Fig. 4. Analysis of surface tractions and master curve for knot strength.

(A) FEM-computed knot strength, ${\tilde{F}}_0$, versus tying pre-tension, $\tilde{T}$, for the S || S (n = 2) configuration, over a range of friction coefficients, μ ∈ [0.05 − 0.35]. The green line corresponds to the experimental fit of the data in Fig. 3B to Eq. 1; the shaded region represents the 65% confidence interval of the fit. The experimental value of the friction coefficient is μ = 0.2 (fig. S4). (B) Three-dimensional visualization of the S || S knot system ($\tilde{T}=95$) simulated using FEM (top). Contact pressure, p/σ_Y, visualized on the pulled 3D rod (bottom) and mapped in 2D along the axial coordinate, z/D, and the angular coordinate, ϕ(right). (C) Knot strength, ${\tilde{F}}_0$, versus released integrated normal contact force, ${\tilde{F}}_{\mathrm{n}}^{\mathrm{r}}$, for friction coefficients in the range, μ ∈ [0.15 − 0.35]; see legend in (A). Linear fit of the data (lines) and 65% confidence interval (shaded regions). Inset: Released normal contact force, ${\tilde{F}}_{\mathrm{n}}^{\mathrm{r}}$ versus the prereleased normal contact force, ${\tilde{F}}_{\mathrm{n}}^{\mathrm{pr}}$, for all the simulated values of μ; see legend in (A). Spring back (dilation) of the knots is observed for the datasets with μ = 0.05, 0.10, an example of which is shown in the adjacent FEM configuration corresponding to the red-circled data point (μ = 0.10, $\tilde{T}=6.8$). (D) Effective knot strength, ${\tilde{F}}_0/n\mathrm{\mu }$, versus $\tilde{T}$, combining all the experimental and numerical results obtained in this study.

Zooming into the inner workings of the knot, we used the FEM to compute the normalized contact pressure, p/σ_Y, between the half-hitches and the quasi-straight sliding filament. For the representative case of an S || S knot (n = 2) with $\tilde{T}=9.5$, Fig. 4B shows a 3D visualization of p/σ_Y and its projected 2D map, the latter focusing on the contacting regions. We distinguish two main contact domains related to the two half-hitches, with four distinct pressure hot spots. Integrating the local normal tractions over the entire surface of the knotted rod yields the integrated normal contact force, ${\tilde{F}}_{\mathrm{n}}=F_{\mathrm{n}}/{\mathrm{\sigma }}_{Y}A$. It is useful to define the prereleased configuration as the state when the pre-tension is still applied before freeing the ends and the released configuration when the ends have been freed for testing. Their respective renderings are shown in Fig. 4C (left and right, respectively). The inset in Fig. 4C plots the integrated normal contact force in the released versus that in the prereleased configurations, i.e., ${\tilde{F}}_{\mathrm{n}}^{\mathrm{r}}$ versus ${\tilde{F}}_{\mathrm{n}}^{\mathrm{pr}}$. For μ ≥ 0.15, we find ${\tilde{F}}_{\mathrm{n}}^{\mathrm{r}}\approx {\tilde{F}}_{\mathrm{n}}^{\mathrm{pr}}$ (dashed line), meaning that the released configuration maintains the normal contact force onto the sliding filament due to the plastic deformation accumulated during the pre-tensioning step. For μ < 0.15, ${\tilde{F}}_{\mathrm{n}}^{\mathrm{r}}<{\tilde{F}}_{\mathrm{n}}^{\mathrm{pr}}$ as the knot dilates (elastic springback) after the pre-tension is released with an insufficient level of plastic deformation. In these low-friction cases, the desired constricting geometry around the sliding filament is insufficient; consequently, the normal tractions in the released configuration are low. Thus, plasticity turns out to be crucial to prevent the complete unraveling of the knot, even for vanishing friction coefficients (μ = 0.05). The plastically bent filament guarantees the knot topology, while the same knots on a purely elastic rod would unravel (movie S3).

Focusing on the tight, nondilated configurations (μ ≥ 0.15), the data in Fig. 4C evidence that the global knot strength depends linearly on the integrated local normal force; ${\tilde{F}}_0\propto {\tilde{F}}_{\mathrm{n}}^{\mathrm{r}}$. Therefore, despite the strong underlying geometric nonlinearities, the Amontons-Coulomb friction law is at the source of this proportionality (as implemented in the FEM model), relating the total integrating tangential force, $\widetilde{F_{\mathrm{t}}}$, and hence the knot strength, to ${\tilde{F}}_{\mathrm{n}}^{\mathrm{r}}$. Combining the friction-related dependence with Eq. 2, the knot strength is expected to behave as

$${\tilde{F}}_0={\mathrm{\beta }}_{2}n\mathrm{\mu }{\tilde{T}}^{\mathrm{\alpha }}$$ (3)

with the prefactor ${\mathrm{\beta }}_2=\tilde{K}/(n\mathrm{\mu })=0.21\pm 0.07$ measured by fitting. In Fig. 4D, we plot ${\tilde{F}}_0/(n\mathrm{\mu })$ versus $\tilde{T}$ for the experimental data (n ∈ [2,6], from Fig. 2) together with the FEM data (n = 2 and μ ∈ [0.15,0.35]). Consistently with Eq. 3, the data collapse onto a master curve with α = 1.56 ± 0.23. These results confirm that the frictional interactions dictate the knot strength with the required normal contact forces ensured by the plastic deformation accumulated during pre-tensioning. As evidenced in Fig. 4C, note that the description of Eq. 3 is valid only for tight knots (above T_min). These findings call for future theoretical efforts to rationalize the measured values of α and β₂, which are independent of the filament diameter, the number of throws, and the friction coefficient (for μ ≥ 0.15), in the tension range of the tight-knots regime.

DISCUSSION

Our results on both surgeon-tied knots and model experiments, combined with FEM, enabled us to identify the ingredients dictating the strength of surgical sliding knots. In addition to topology, geometry, and elasticity, the interplay between plastic deformation and frictional interactions is crucial in a knotted monofilament. Our findings could be translated into practical guidelines on how to tie a safe surgical knot in a given suturing monofilament with friction coefficient, μ ≥ 015, and yield strength, σ_Y. The surgeon can adapt the filament caliber and the number of throws, or control the tying pre-tension to induce an appropriate level of plastic deformation and hence normal-contact pressures, which, through friction, establish a desired knot strength. Since we only considered dry conditions, the master curve of the effective knot strength is applicable to dry suturing environments. In the presence of fluids during surgical procedures, lower knot strengths are to be expected, which can be compensated by $\tilde{T}$ and n.

We hope that our investigation will raise awareness of the physical ingredients in surgical knots among experienced surgeons and will be valuable in the training of entry-level surgeons. Furthermore, our quantitative description of the mechanism underlying sliding knots could be implemented into emerging robotic-assisted surgical devices containing haptic feedback to target effective knot-tying at a level akin to an experienced surgeon (37).

MATERIALS AND METHODS

Experimental procedure for knot-tying in our physical model system

To reproducibly tie knots of well-defined pre-tension, we used the following protocol. Rigid 3D-printed pins were used as support for manually tying an initial half-hitch in its loose configuration. One end of the filament was kept straight by applying a slight tension (far below the yield strength), while the other end was wound around the straight filament segment. The manually applied tension should be just enough to keep the half-hitch in place before the two free filament extremities were clamped on the UTM. Then, the knots were tightened under displacement-controlled conditions, followed by a load-controlled holding step to account for any viscous material effects. The pulling speed was 1 mm/s (i.e., engineering strain rate $\dot{\mathrm{\epsilon }}=0.01/\mathrm{s}$) up to the set value of the tying pre-tension, $\tilde{T}$, and held constant for 100 s to account for any potential viscoelastic effects. Subsequently, the sample was unmounted from the UTM, and anotherhalf-hitch (identical or nonidentical throw) was added manually in its loose configuration, and then tightened with the UTM. This protocol was repeated for every additional throw (increasing n).

Threshold to define tight knots

As demonstrated in the main text, tight knots, compared to loose knots, exhibit higher knot strength due to the increased self-contact pressure between different segments of the filament. In general, the transition from loose to tight physical knots is a continuous process without an abrupt change in geometry or mechanical behavior (see fig. S1A). Still, we developed a method to define an approximate threshold separating the two regimes, combining a volumetric analysis based on x-ray micro–computed tomography (μCT) and a purely geometric rod model. We focus on the elementary, sliding granny knot, S || S, since knots with higher throw numbers are not necessary for the procedure described.

The notion of “tightest knot” is well-defined in the mathematical framework of ideal (geometric) knot theory: A prescribed diameter and arc length of an ideal filament enable the computation of the tightest knot shape for the maximal end-to-end shortening (21, 26). An ideal filament is characterized by an undeformable circular cross section, inextensible centerline, and vanishing bending stiffness (22). On the basis of this geometric theory of knots, we computed the shape of the tightest S || S knot using the software Ridgerunner, developed by Ashton et al. (34). This software iteratively increases the tightness of an initial (ansatz) knot geometry. The tightening algorithm is based on a C-language code for tightening ideal knots (38), combining a polygonal thickness version (39–41) with a constrained gradient descent. In our case, this ansatz was provided by the centerline coordinates of an FEM simulation of a loose knot. In fig. S1B, we present the tightest S || S knot configuration. The compactness of the resulting knot was characterized as the volume of the 3D convex hull [convhulln function in Matlab 2019, based on Qhull (42)], around the bulk knot, excluding the protruding filaments. The computed convex hull on the tightest sliding granny knot is represented as a semi-transparent envelope in fig. S1B and was measured to have a dimensionless volume of 4V_ideal/πD³ ≈ 32.3. A cylinder of diameter and height D (normalized volume, πD³/4) is used as the reference volume.

Next, we make use of 3D μCT images of physical knots to quantify their compactness as a function of the pre-tension applied to both throws. First, the S || S knots were machine-tied on monofilaments (Prolene 1 USP 0.49 mm in diameter) within the range of tying pre-tensions, $1.5\le \tilde{T}\le 6.8$. Second, as shown in the photograph in fig. S1A, the knots were mounted in an array of increasing pre-tensions, $\tilde{T}$, labeled (1) to (7). Then, the samples were slid along a narrow cylindrical sample holder (diameter, 14 mm) and scanned with the maximum spatial resolution of 4.9 μm (voxel size) using μCT imaging (μCT100, Scanco Medical).

In fig. S1C, we show the 3D reconstruction of the μCT-scanned tightest knot (7) with four protruding strands. To quantify only the volume of the knot, we excluded the four protruding strands by implementing the following cropping steps using MATLAB (Matlab 2019b, MathWorks). The 3D image consisted of grayscale values, representing the local material density of the voxels, ranging from 0 (nonoccupied voxels outside filament) to 1 (occupied voxels inside filament). The dataset was binarized using the voxel value 0.5 as the threshold. The gradient profile (gradient function in MATLAB), representing the change in the number of occupied voxels, was computed in each of the three spatial directions, {x, y, and z}. The gradient profile (along each spatial direction) exhibits peaks (gradient values larger than 25) at the transition between the bulk knot and either surrounding air or a single protruding strand. Beyond each peak location, the voxel values were set to 0 (nonoccupied voxels), such that the long protruding strands were cut off from the bulk knot, leaving a confined knot region. This technique was repeated by rotating the knot in each of the three spatial directions (incremental rotation angle: π/4 rad) and smoothly removing all protruding strands. Similar to the compactness measurement of the tightest ideal knot, we constructed the 3D convex hull on the bulk physical knot, as shown by the semi-transparent cover in fig. S1D.

In fig. S1E, we plot the volume measurements of the convex hull obtained from the μCT, 4V/πD³, as a function of the tying pre-tension, $\tilde{T}$. Each experimental data point is based on three scanned knot samples. We observe two regimes with different slopes, whose transition was determined by performing a linear fit to each of the two regions and determining the intersect, fitting seven consecutive data points in each regime. The uncertainty of each best fit is at the basis of the error analysis on the intersection point. The resulting onset of tight knots is given by the tying pre-tension, ${\tilde{T}}_{\min }=T_{\min }/{\mathrm{\sigma }}_{Y}A=2.59\pm 0.14$ (vertical line). At this tightness level, the experimental knot volume is 4V₀/πD³ ≈ 28.1 and corresponds to knot (7) in fig. S1A. The transition between the two regimes is compatible with the result of the tightest knot volume from the purely geometric model, 4V_ideal/πD³ ≈ 32.3, reported above and represented by the dotted horizontal line in fig. S1E. We conclude that the transition between the distinct behavior in volume reduction is an appropriate definition for the onset of tight knots. Note that the smaller convex hull volume of experimental knots at the transition compared to the purely geometric case is presumably due to cross-sectional elastoplastic deformations, which induce a decrease in volume for the same amount of confined arc length.

Note that since the knot tightness is dictated by the volume of each individual throw, the tight-knot onset depends only on the applied tying pre-tension. In the main text, we report a change in the knot strength behavior between lower and higher tying pre-tensions, i.e., between loose and tight knots. The transition between the two regimes corresponds to the transition tension determined using the critical knot volume described above, ${\tilde{T}}_{\min }$, further asserting the validity of the knot volume method to describe the onset of tight knots.

Material testing and fracture

All the experiments presented in the main text were performed at room temperature (21°C) and with constant engineering strain rate $\dot{\mathrm{\epsilon }}=0.01/\mathrm{s}$ for the knot tying and strength testing. Here, we describe the mechanical tests performed to quantify the material response, including fracture, aiming to evaluate the range of applicability of our results for different tying rates and operating room temperatures.

We tested the tensile properties of single-filament specimens following the ISO 11566 (43) standard, which is designed to avoid filament fracture at the clamps. In fig. S2 (A and B), we present schematic illustrations of the sample preparation procedure with either straight, unknotted (A), or knotted (B) monofilaments. Since the knotted case is used for fracture tests, an S || S knot was tied manually on the rigid pin (described in the main text). For both cases (A) and (B), the Prolene 3-0 USP filament was glued with epoxy on a rectangular polyvinyl chloride shim stock frame (thickness: 0.1 mm, outer dimensions of the frame: 70 × 20 mm²) with a gauge length of L = 50 mm. Besides setting reference length precisely, this technique also reinforces the filament at the ends by the epoxy layer, preventing fracture at the clamping due to stress concentration. Once the sample is clamped in a UTM (Instron 5943), the frame is cut along the y direction (orthogonal to the filament). Then, the mechanical response is measured by pulling along the axial direction of the filament (x direction in fig. S2, A and B) and recording the traction force throughout the imposed displacement.

In fig. S2C, we present the cyclic engineering stress-strain behavior (maximum strain, ε = 0.5) of the straight Prolene 3-0 USP filament at room temperature (21°C) as a function of the applied strain rate, ranging from $\dot{\mathrm{\epsilon }}=0.0025/\mathrm{s}$ to $\dot{\mathrm{\epsilon }}=0.16/\mathrm{s}$. Each curve shows the mean (solid line) and SD (shaded region) of three tests on five different Prolene 3-0 USP samples. We notice a slight increase in the stress quantities for higher strain rates. Still, despite the vast range of explored strain rates (variation of 6300%), the relative change in measured engineering stress at ε_eng = 0.5 is only 6.7%. The nominal fracture strength is determined by the maximum recorded engineering tensile force on straight filaments and represented by the blue box plots in fig. S2D. Similarly to the stress at ε_eng = 0.5, the fracture strength does not change considerably for different strain rates. Adding an S || S knot to the filament reduces the macroscopic fracture strength by 40 to 50% (see gray box plots), which is in agreement with the experimental observations reported in (6, 26, 28, 44), although the underlying mechanism remains poorly understood.

In fig. S2E, we present results for the engineering stress-strain response of filaments under cyclic loading (constant strain rate, $\dot{\mathrm{\epsilon }}=0.01/\mathrm{s}$) while controlling temperature. The tests were conducted at 21°, 37°, and 45°C, within clinically relevant temperature ranges. In the operating room, the temperature is crucial to avoid intraoperative hypothermia (core temperature < 35°C) (45, 46): in orthopedics, the room temperature is regulated to 16°C to reduce the infection risk (47); in obstetrics, the well-being of the newborn requires a temperature of 20° to 21°C (48); and in burn surgery, the operating room is heated to 30° − 40°C (49). Three tests on three different Prolene 3-0 USP samples were performed for each curve in fig. S2E. High reproducibility was achieved, as suggested by the small uncertainty regions (shaded region) around the average curve (solid curve). The Prolene filaments are somewhat temperature-dependent, exhibiting softening in their mechanical response to higher temperatures. Temperature dependence is less prominent in the nominal fracture strength of S || S-knotted filaments, plotted in fig. S2F as a function of the three temperature-regulated environments. The relative difference between the median values of the fracture strength at 21°C versus 45°C is only 3.6%.

As expected, the mechanical response of straight Prolene monofilaments exhibits some rate and temperature dependence. In the current case study, however, we are mostly concerned with the uncertainty of the macroscopic fracture strength in knotted samples since this fracture strength defines the upper boundary of applicable pre-tension during knot tightening. Relative changes of 12.3 and 6.1% are to be expected for the ranges of explored strain rates ($\dot{\mathrm{\epsilon }}=[0.0025-0.16]{\mathrm{s}}^{-1}$) and temperature (21° − 45°C), respectively. Therefore, given the vast ranges of parameters, the rate and temperature effects are relatively small. Consequently, for the study described in the main text, we consider the mean fracture strength with its SD, σ_c = 300.6 MPa ± 12.1 MPa, for the case of a strain rate, $\dot{\mathrm{\epsilon }}=0.01/\mathrm{s}$, and at room temperature (21°C). Last, the normalized maximal tying tension, ${\tilde{T}}_{\max }={\mathrm{\sigma }}_{\mathrm{c}}/{\mathrm{\sigma }}_Y=15.74\pm 0.63$, is considered as the upper force limit, corresponding to the vertical lines in Fig. 3B of the main text.

Topological effect on knot strength

In Fig. 1C of the main text, we visualized the two possible sliding knot topologies, S || S and S × S, comprising two consecutive half-hitches. Although the topologies differ, we are interested in the resulting knot performance for a given tying pre-tension. In fig. S3, we compare the knot strength, ${\tilde{F}}_0$, as a function of the tying pre-tension, $\tilde{T}$, between the S || S × S and the S || S || S knot. Note that the first two throws share the same topology for both cases to avoid contact effects from the underlying pin during tying. Unlike the log-log plots on knot strength in the main text, here, we use linear axes to better contrast the difference in the response of the two knots, especially for higher tying pre-tensions. Again, the knot-strength data are consistent with the functional increase described by Eq. 1 of the main text. We find that the knot strength is equivalent for the two-knot topologies throughout the whole range of tight knots. We conclude that the resistance to sliding of surgical sliding knots does not depend on the throw direction (identical versus nonidentical throws). Within this study, this observation enables us to reduce the complexity from various topological combinations to a single topology, e.g., S || S.

Frictional contact interaction

Inspired by the apparatus reported in (50), we have designed an experimental setup to measure the frictional properties of two filaments in sliding contact using an orthogonal-crossing configuration in dry conditions. The upper end of the first filament (Prolene 1 USP) was attached to a 50-N load cell of the UTM (Instron 5943), and a dead load of 100 g was attached at the other end of the filament. A second filament (Prolene 1 USP) was tightly coiled (10 turns) around a rigid acrylic post (square cross section of 20 × 20 mm² with rounded corners), as shown in the photograph of fig. S4A. The straight vertical filament was pressed by an annular ball bearing (external diameter: 30 mm) against the coiled filament with a normal load, F_n, using a mass-pulley system (not shown in the photograph). Next, the vertical filament was displaced upward at a speed of 1 mm/s, which is the same displacement velocity imposed in the knot untying experiments reported in the main text. In fig. S4B, we plot the measured tangential contact force, F_t, as a function of the applied normal force, F_n. We find a linear relationship between the two, as expected for Amontons-Coulomb friction behavior. The linear fit, F_t = μ_dF_n (solid line in fig. S4B), of the experimental data yields a dynamic friction coefficient, μ_d = 0.20 ± 0.02, in agreement with values reported in the literature for Prolene monofilaments (29).

Elastoplastic constitutive material model

During the tying and testing of surgical knots, the Prolene filament can undergo considerable plastic deformation. Quantitatively reproducing this mechanical behavior in the FEM simulations requires an appropriate constitutive material model for the elastoplastic behavior of the polymer filament. Before describing the plasticity model, we implemented in FEM, we must first characterize the constitutive response of the Prolene filaments experimentally.

In fig. S5A, we present results for the cyclic stress-strain behavior of a straight (unknotted) Prolene monofilament (1 USP, gauge length, L = 50 mm), plotting the axial true stress, α, versus true strain, ε. The tests were performed at the constant engineering strain rate of ${\dot{\mathrm{\epsilon }}}_{\mathrm{eng}}=0.01/\mathrm{s}$. For these characterization tests, we used the ISO11566 protocol for large-strain measurements. In the lower inset of fig. S5A, we show a schematic of the tested specimens prepared identically to those described in the “Material testing and fracture” section above. The plot in the upper inset of fig. S5A quantifies the dissipated energy density per cycle, W, measured from the area enclosed by each loading-unloading σ(ε) curve, for a particular cycle. We find that W decreases by ≈500% between the first and the second cycles before converging into a steady cycle. This seemingly large dissipated energy observed in the first cycle may be attributed to the unknown state of the material due to prior deformation history. We interpret the straightening of the intrinsically curved filament from the packaging and the preparation of the specimen for testing as the first loading cycle. To account for this first loading cycle, we will calibrate the constitutive model from the uniaxial tensile tests of a filament that has been preconditioned by prestretching it first to ε = 0.215 (i.e., after it has undergone the first cycle), and then unloaded for subsequent testing. In fig. S5B, we plot the σ(ε) experimental curves (solid lines) for the three subsequent loading-unloading cycles (2, 3, and 4); these data will be used to calibrate the elastoplastic constitutive model described next.

The 3D continuum-level constitutive model for elastic-viscoplastic mechanical behavior that we developed and implemented for the FEM simulations is based on (35, 36). Hence, only a summary of the relevant content underlying the model is provided here. Overall, the model includes isotropic hardening since the filaments only undergo one single loading cycle during the knot-tying and tightening process. Furthermore, the model is rate-dependent, a choice that is supported by the data presented in fig. S2. The total deformation gradient is decomposed into elastic and plastic parts

$$\mathbf{F}={\mathbf{F}}^e{\mathbf{F}}^p$$ (4)

We assume that plastic flow is incompressible, meaning that det F^p = J^p = 1, where J = det = F. The evolution equation for F^p is

$$\frac{\mathrm{d}{\mathbf{F}}^p}{\mathrm{dt}}={\mathbf{D}}^p{\mathbf{F}}^p$$ (5)

The flow rule may be written in the form

$${\mathbf{D}}^p=\sqrt{\frac{1}{2}}{\mathrm{\nu }}^p{\mathbf{N}}^p$$ (6)

where the equivalent plastic shear strain rate is

$${\mathrm{\nu }}^p={\mathrm{\nu }}_0{\left(\frac{\overline{\mathrm{\tau }}}{S}\right)}^{1/m}$$ (7)

the equivalent shear stress is

$$\overline{\mathrm{\tau }}=\sqrt{\frac{1}{2}({\mathbf{M}}_0^e:{\mathbf{M}}_0^e)}$$ (8)

and the direction of plastic flow is given by

$${\mathbf{N}}^p=\frac{{\mathbf{M}}_0^e}{\sqrt{2}\overline{\mathrm{\tau }}}$$ (9)

In the expressions above, the notation (•)₀ denotes the deviator of (•). The Mandel stress in Eq. 6 is given by the constitutive relation

$${\mathbf{M}}^e=2G{\mathbf{E}}^e+\mathrm{\lambda }(\mathrm{Tr}{\mathbf{E}}^e)\mathbf{1}=2G{\mathbf{E}}_0^e+K(\mathrm{Tr}{\mathbf{E}}^e)\mathbf{1}$$ (10)

where G, K, and λ = K − (2/3)G are the shear modulus, bulk modulus, and Lamé parameter, respectively. Note that the strain measure used is E^e = ln U^e, where U^e is the elastic stretch, F^e = R^eU^e, and accounts for large deformations. The Cauchy stress is related to the Mandel stress by

$$\mathbf{T}=J^{-1}{\mathbf{R}}^e{\mathbf{M}}^e{\mathbf{R}}^{e\mathrm{T}}$$ (11)

The strength model is given by an evolution equation for the deformation resistance S, which enters Eq. 4, taking the form

$$\dot{S}=h(S_{\mathrm{sat}}-S){\mathrm{\nu }}^p,S(t=0)=S_0$$ (12)

where S_sat is a saturation level for the deformation resistance, and h controls how quickly S approaches S_sat.

In summary, the elasto-viscoplastic model with isotropic hardening presented above involves the following material parameters, E, S₀, S_sat, h. Moreover, we define initial yield strength σ₀ as the initial condition for S. These parameters must be determined by fitting to the experimental data presented in fig. S5B, for the three consecutive loading and unloading cycles of a straight, unknotted, and prestretched Prolene monofilament.

The 3D constitutive model has been specialized for uniaxial tension, and the reduced model is implemented into MATLAB for the purpose of calibrating the parameters E, σ₀, S_sat, h. On the basis of the experimental data presented in fig. S5B, the built-in MATLAB function lsqnonlin was used to perform a nonlinear least-square optimization of the four parameters with a prescribed initial guess and lower and upper bounds, as summarized in table S2. The rate-sensitivity parameter was assumed as m = 0.08 to improve the numerical convergence of the optimization process. The shear strain rate was set to ν₀0001. Furthermore, we constrained the values of E using the initial slope of the test curves in the unloading region, which was measured to be ≈7000 MPa. Assuming material incompressibility, the shear modulus is related to the Young’s modulus by G = E/3. The optimization process yields the calibrated quantities presented in table S2, with the model fitted (dashed lines) to the experimental cyclic stress-strain curves (solid lines), as shown in fig. S5B.

Residual stress

The Prolene filament used throughout the experiments came originally packaged in a stadium-shaped spool (with straight sides of length 55 mm and semi-circular caps of radius 10 mm) and exhibits natural curvature upon unpacking. As is common in plasticity problems, this prior loading history affects any subsequent material response. To account for this (unknown) deformation history in the FEM simulations, we consider the effective residual bending stress, σ_R, as a predefined stress field on the initially straight reference configuration of the filament and treat it as an additional fitting parameter. We specify σ_R by assuming elastic-perfectly plastic (small) deformation of a beam with a circular cross section of diameter, D, with curvature κ(x) along the axial direction, x, of the beam, the axial strain in the bending direction, y, can be expressed as ε_xxxy.

For a fully plastic beam with yield strength, σ_Y, the cross section consists of two regions: the lower half, −D/2 ≤ y ≤ 0, with σ_xx = σ_Y and area, A₁; and the upper half, 0 ≤ y ≤ D/2, with σ_xx = −σ_Y and area, A₂. Thus, two regions of integration (A₁ and A₂) are considered to compute the bending moment:

$$M_p=-{\int }_{A_1}y{\mathrm{\sigma }}_Y{dA}_1-{\int }_{A_2}y(-{\mathrm{\sigma }}_Y){dA}_2=\frac{D^3{\mathrm{\sigma }}_Y}{6}$$ (13)

The residual stress is then expressed as the difference between the fully loaded and the elastically unloaded case,

$${\mathrm{\sigma }}_{xx}(\mathrm{unloaded})={\mathrm{\sigma }}_{xx}(\mathrm{loaded})-{\text{Δ}\mathrm{\sigma }}_{xx}$$ (14)

with the stress difference due to elastic spring-back,

$${\text{Δ}\mathrm{\sigma }}_{xx}=E{\text{Δ}\mathrm{\epsilon }}_{xx}=E({\mathrm{\kappa }}_{\mathrm{loaded}}-{\mathrm{\kappa }}_{\mathrm{unloaded}})y$$ (15)

Furthermore, from the moment-curvature relation, M_loaded = EI(κ_loaded − κ_unloaded), we get

$${\mathrm{\kappa }}_{\mathrm{loaded}}-{\mathrm{\kappa }}_{\mathrm{unloaded}}=\frac{M_{\mathrm{loaded}}}{EI}$$ (16)

Plugging Eq. 13 into Eq. 12 yields the axial stress difference

$${\text{Δ}\mathrm{\sigma }}_{xx}=-\frac{M_{p}y}{I}$$ (17)

where we considered loading to the fully plastic state (M_loaded ≡ M_p). Thus, Eq. 11 is written in the form

$${\mathrm{\sigma }}_{xx}(\mathrm{unloaded})={\mathrm{\sigma }}_{xx}(\mathrm{loaded})+\frac{M_{p}y}{I}$$ (18)

Considering a fully plastic deformation [σ_xx(loaded) = ± σ_Y], and plugging Eq. 10 into Eq. 15 gives the residual stress field as a function of the yield strength

$${\mathrm{\sigma }}_{R}y\{\begin{array}{c}(1+\frac{32y}{3\mathrm{\pi }D}){\mathrm{\sigma }}_Y\mathrm{for}y<0\\ (-1+\frac{32y}{3\mathrm{\pi }D}){\mathrm{\sigma }}_Y\mathrm{for}y<0\end{array}$$ (19)

In ABAQUS/EXPLICIT, the predefined stress field—Eq. 16—was applied on the initially straight reference configuration, σ_R(σ_Y = 0 MPa), of the filament of diameter, D_Fil = 0.49 mm (1 USP), and axial length,300 mm. Note that, whereas the calibration tests described next used this physical value of D_Fil, subsequent simulations (including all of those reported in the main text) were done with unit-diameter filaments for generality. The rod was meshed with reduced hybrid 3D solid elements (C3D8I) such that the number of elements along the axial direction was 200, with 26 elements per cross section. In fig. S6A, we show typical initial configurations of the filament for the different values σ_Y = {10,20,30} MPa; different values of σ_R relate to different natural curvatures of the filament.

Figure S6B presents a photograph of the apparatus developed to calibrate the parameters of our plasticity model. In this configuration, which we refer to as plastic capstan, we quantify the tension drop, ΔT, between the free end and the pulled end (displacement-controlled with 1 mm/s) of a Prolene monofilament (1 USP) passing through a grooved pin with the diameter in the range 0.5 mm ≤ D_Pin ≤ 9 mm. Given that the pin is mounted on an air-bearing, and the two constraining ball bearings minimize friction, the ensemble rotates as a frictionless gear when pulling the filament (movie S4). Hence, there is minimal sliding frictional dissipation; the dissipation is only due to plastic bending deformation of the filament around the pin, which causes the tension to drop between the two extremities. By contrast, in the classic capstan problem (50, 51), the tension drop is due to the friction interaction alone.

Using FEM, we simulate this same plastic capstan configuration for filaments subjected to residual bending stresses. The pin of diameter, D_Pin, and the gap walls were simulated as rigid bodies according to the fabrication tolerances of the pins, leaving a groove of depth D_Fil + 0.01 mm and width D_Fil + 0.11 mm. In fig. S6C, we present an FEM-computed configuration of the plastic capstan (D_Pin = 0.5 mm), color-coded by the equivalent plastic shear strain, γ^p, which increases along the filament from the free end (right) to the pulled end (left) as a result of the accumulated plastic deformation. A horizontal cut (purple dashed line) at the height of the pin exposes the in-plane profile of γ^p. In fig. S6D, we plot experimental and FEM data for the normalized tension difference, ΔT/(σ_YA), as a function of normalized curvature imposed by the pin of diameter D_Pin on the filament of diameter D_Fil: 2D_Fil/(D_Pin + D_Fil). Tuning the residual stresses allows for the calibration of the numerical model by matching its results to the experimental data to determine the fitting parameter. With the fitted value of σ_R(σ_Y = 30 ± 2MPa), we find that the FEM simulations accurately represent the experimental data across the full range. Note that the fitted yield strength is of the same order of magnitude as the experimentally determined 0.1% offset yield strength, σ_Y = 19.1 MPa (31).

Finite element modeling—Knot tying, tightening, and testing procedure

In the commercial package ABAQUS/EXPLICIT (Simulia, Dassault Systèmes), two initially straight filaments were implemented, each with unit diameter, D_Fil = 1. The filament (1) forming the two half-hitches was modeled with axial length, L₁ = 35D_Fil. The sliding filament (2) was chosen to be half as long. The two filaments were oriented such that their centerlines cross with a relative angle of 10°. Both filaments were meshed with 3D solid elements, enhanced with incompatible modes for bending (C3D8I). The number of elements along the axial direction was 230 for filament (1) and 115 for filament (2), with 40 elements per cross section in both cases. Two circular plates (5D_Fil in diameter, 0.1D_Fil in thickness) with a central clearance hole of diameter, 1.10D_Fil, were modeled as rigid bodies and aligned with the centerline axis of filament (2), leaving a relative distance 7D_Fil between the two plates.

The tying, tightening, and testing procedure described next is visualized in movie S5. In an initial step, the central region of filament (1), 0.25L₁ < L_center < 0.75L₁, was subject to the residual stress field σ_R(σ_Y = 30 ± 2MPa) since the filament extremities are not part of the knot. Mimicking the tying procedure of the surgeon, a dead load (Mg = 50 N) was applied to one of the extremities of filament (2), keeping the other end clamped. Next, by applying a sequence of prescribed displacements and rotations to control the nodes located at each end and the central coordinate of filament (1), two half-hitches were formed around filament (2), corresponding to the sliding granny knot. A similar tying protocol was introduced in (52), in the context of the clove hitch knot. Both knots share the same topology but differentiate by their application: A clove hitch knot attaches a rod to a rigid cylinder (typically larger than the rod diameter), whereas the sliding granny knot is a binding knot, connecting two rods (of equal diameters). We made use of the tying algorithm used in (52), with minor adaptations to tie the S || S knots.

After the S || S topology was set, both rigid plates were displaced, leaving a relative distance of 6D_Fil, to help keep filament (2) in place (in addition to the applied dead load) during the subsequent tightening step. Then, the two extremities of filament (1) were gradually loaded by the tying pre-tension of the same magnitude, $\tilde{T}$, but in opposite directions to yield a symmetric knot. Next, the pre-tensions were released symmetrically to free the ends of filament (1), while one of the two plates was displaced along the centerline axis of filament (2), away from the actual system since, subsequently, it is no longer needed. At this stage, the clamped boundary condition at the extremity of filament (2) was also released, such that the filament could be displaced with the constant unit speed 1 s⁻¹. Last, the S || S knot was pulled against the rigid stopper plate, and the slipping force, $\tilde{F}$, was measured.

Supplementary Materials

This PDF file includes:

Figs. S1 to S6

Tables S1 and S2

Legends for movies S1 to S5

Legend for data S1

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S5

Data S1