Risk estimation of lifted mask mandates and emerging variants using mathematical model

Abstract

Background

More than half of the population in Korea had a prior COVID-19 infection. In 2022, most nonpharmaceutical interventions, except mask-wearing indoors, had been lifted. And in 2023, the indoor mask mandates were eased.

Methods

We developed an age-structured compartmental model that distinguishes vaccination history, prior infection, and medical staff from the rest of the population. Contact patterns among hosts were separated based on age and location. We simulated scenarios with the lifting of the mask mandate all at once or sequentially according to the locations. Furthermore, we investigated the impact of a new variant assuming that it has higher transmissibility and risk of breakthrough infection.

Results

We found that the peak size of administered severe patients may not exceed 1100 when the mask mandate is lifted everywhere, and 800 if the mask mandate only remains in the hospital. If the mask mandate is lifted in a sequence (except hospital), then the peak size of administered severe patients may not exceed 650. Moreover, if the new variant has both higher transmissibility and immune reduction, the effective reproductive number of the new variant is approximately 3 times higher than that of the current variant, and additional interventions may be needed to keep the administered severe patients from exceeding 2,000, which is the critical level we set.

Conclusion

Our findings showed that the lifting of the mask mandate, except in hospitals, would be more manageable if implemented sequentially. Considering a new variant, we found that depending on the population immunity and transmissibility of the variant, wearing masks and other interventions may be necessary for controlling the disease.

1. Introduction

The Omicron variant has altered the course of the COVID-19 pandemic in Korea. The number of confirmed cases from February 1 to February 18, 2022 already exceeded the number of cumulative confirmed cases before February 1, 2022 [1]. During the first Omicron wave in 2022, the peak number of administered severe patients1 reached more than 1200 in mid-March, while the maximum capacity for the severe patients at the end of March was approximately 2000 [1,2]. As the number of cases skyrocketed, the number of PCR tests became insufficient. In turn, the Korean government changed the testing policy to include results from rapid antigen tests (RAT) conducted at medical clinics or hospitals. Since RAT has a lower accuracy than PCR and as symptoms become milder, unreported cases in Korea are expected [3]. Indeed, the Korea Disease Control and Prevention Agency performed antibody tests on 9901 randomly sampled people in August 2022 and found that there was a 19·15% difference between the case-confirmed ratio (38·50%) and N-antibody-positive ratio (57·65%), which is specifically induced after natural infection [4].

Even though the reported cases were high, nonpharmaceutical interventions (NPIs) were gradually eased due to the significantly milder symptoms and nationwide vaccination programs. Social distancing, which was the primary disease control strategy in Korea before vaccines and antiviral drugs were available, was lifted on April 18, 2022 [5]. Since then, wearing masks both outdoor and indoor has become noncompulsory [4]. Nevertheless, there are potential risks in easing NPIs. For example, at the end of 2021, the Korean government implemented a ‘return to normal’ policy, which gradually eases interventions. However, the number of administered severe patients at that time reached more than 1100 [6]. Careful consideration of many aspects such as vaccination, variants, booster shots, waning immunity, and age-specific factors is necessary to properly provide guidance to policymakers in decision-making.

Since the COVID-19 outbreak, policymakers have turned to mathematicians in predicting cases and crafting strategies that can mitigate the spread of infection [[7], [8], [9]]. There are numerous modelling studies considering COVID-19 variants [[10], [11], [12], [13], [14]]. However, only a few published works tackle the lifting of the mask mandate considering the Omicron variant. An evaluation of the different types of face masks has been proposed [15]. A limitation of their study is that vaccination was not incorporated. Vaccination and mask wearing were studied but the authors assumed that the population was well-mixed and that age-specific factors were not considered [16]. Age-structured models that consider vaccination were proposed [17,18]. However, unreported cases, booster shots, and specific variants were not considered.

In this study, we developed a model of COVID-19 to analyze the Omicron outbreak in Korea considering vaccination history (primary, booster, and updated booster shots), age structure that distinguishes the medical staff from the general population, breakthrough infections, unreported cases, seasonality, and NPIs. Since indoor mask wearing was the remaining mandatory NPI in Korea in 2022, we investigate the effect of lifting this policy in all locations. In the model, we quantify the effects of easing the mask protocol in school, work, other places, and hospital settings using contact rates between the different age groups. The model uses updated variant-specific vaccine effectiveness. Hence, scenarios on possible new variants can be studied. To the best of our knowledge, our work is the only age-structured mathematical model that considers updated booster shots and mask wearing. The proposed model can be applied not only to Korea, but also to other countries that have yet to remove all NPIs. As of December 2022 in the Western Pacific Region, China has the strictest mask mandates, which require wearing masks outdoors.

2. Methods

2.1. Mathematical modeling of COVID-19

In the model, we divided the population according to age, medical staff (MS) or non-MS, with or without prior infection, vaccination, and infection status. The epidemiological process follows a basic SEIR structure, in which the severity of the disease and unreported cases were added. Fig. 1 illustrates the flowchart of the mathematical model. There are 12 stages considering vaccine and prior infection: unvaccinated, $u$, vaccinated with primary doses within 180 days, $v$, vaccinated with primary doses after 180 days, $\hat{v}$, received a booster shot within 180 days, $b$, received a booster shot after 180 days, $\hat{b}$, and inoculated with an updated booster shot, $\tilde{b}$. The subscript ($pi$) indicates that the host had prior infection. Five age groups were considered: 0–19 ($Ⅰ$), 20–29 ($Ⅱ$), 30–49 ($Ⅲ$), 50–64 ($Ⅳ$), and 65+ ($Ⅴ$). Assuming that there are no underage or senior MS, then there are three MS groups: 20–29 MS (${Ⅱ}_{MS}$), 30–49 MS (${Ⅲ}_{MS}$), and 50–64 MS (${Ⅳ}_{MS}$). The initial time of our model simulation is August 15, 2022, and during this time, Korea was in the middle of an outbreak. Therefore, the initial state of the model is not a disease-free state. Details on the setting of the initial states of the model are described in the Supplementary material. We also consider the waning of immunity due to vaccination ($\omega$) and the waning of immunity from natural infection ($\zeta$). The system of equations describing the model is provided in the Supplementary material.

Fig. 1.

Flow diagram of the mathematical model of COVID-19 outbreak.

In Fig. 1, the force of infection to the susceptible age group $i\in AG$ in stage $x\in VG$, denoted as ${\lambda }_x^i$, is formulated as

$${\lambda }_x^i=\left(1-e_x\right){\delta }^i{m}_T\sum _{k\in VG}\sum _{j\in AG}h\left(c_1^{ij}+q_2{c}_2^{ij}+q_3{c}_3^{ij}+q_4{c}_4^{ij}+q_5{c}_5^{ij}\right)\left({I_k^j+\tilde{I}}_k^j\right)\text{,}$$ (1)

$$VG=\left\{u,v,\hat{v},b,\hat{b},\tilde{b},u_{pi},v_{pi},{\hat{v}}_{pi},b_{pi},{\hat{b}}_{pi},{\tilde{b}}_{pi}\right\},AG=\left\{Ⅰ,Ⅱ,{Ⅱ}_{MS},Ⅲ,{Ⅲ}_{MS},Ⅳ,{Ⅳ}_{MS},Ⅴ\right\}$$

In Equation (1), $e_x$ is the vaccine effectiveness against infection and reduces transmissibility of the disease, $c_n^{ij}$ indicates the average number of contacts from age group $i$ to $j$, and the subscript $n$ indicates the type of contact: 1 for household, 2 for school, 3 for work, 4 for other places, and 5 for hospital. The contact patterns $c_1$ to $c_4$ were aggregated and adjusted according to the age structure of our model, while $c_5$ was estimated assuming that one medical doctor and nurse (2 medical doctors and 3 nurses) have contact with an outpatient (inpatient) per day in Korea [[19], [20], [21], [22]]. The age-dependent relative susceptibility compared to age 0–19 (${\delta }^i$, i.e., ${\delta }^{Ⅰ}=1$) takes into account clinical susceptibility and other factors such as compliance with policy or behavior. The parameter $q_n$ ($n\in \left\{\mathrm{2,3,4,5}\right\}$) indicates the relative risk of contact from type $n$ compared to household contact ($c_1^{ij}$), $h$ is the probability of disease transmission through household contacts, and $m_T$ is the relative seasonality factor compared to the initial time, i.e., $m_1=1$. Eight parameters, $h$, ${\delta }^{Ⅱ}$, ${\delta }^{Ⅲ}$, ${\delta }^{Ⅳ}$, ${\delta }^{Ⅴ}$, $m_2$, $m_3$, and $m_4$, are determined using the Metropolis-Hastings algorithm, which is a Markov chain Monte Carlo method to estimate the distribution of unknown parameters by fitting to the cumulative confirmed cases of the five age groups from August 15 to November 30, 2022 (108 days) [1,23,24]. We assumed Gaussian additive noise and uniform prior distribution and sampled parameters as follows:

At iteration $i$ with $x_i$,

• 1.Generate $x^{*}$ from a proposal distribution, $x^{*}\sim q\left(x_i\right)$, $q$ is Gaussian
• 2.Accept or reject with acceptance rate $\alpha =\min \left[1,\frac{f\left(x^{*}|Y\right)}{f\left(x_i|Y\right)}\right]$.

Here, the likelihood function is $f\left(x_i|Y\right)=\int P\left(Y|x,{\sigma }_i\right)P\left({\sigma }_i\right)d{\sigma }_i\propto {\Vert Y-F\left(x_i\right)\Vert }^{-\frac{m}{2}}\text{,}$ where $F\left(x\right)$ is the model output, $\int \sum _i\sum _x{\rho }^i\alpha I_x^{i}dt$, $Y$ is the data with $m$ points, and $P$ is the prior. Detailed description is in the supporting information of the study of Clarke [23].

2.2. Scenario setting

In this study, we considered three phases (illustrated in Fig. 2). In the first phase (black arrow), we estimated the model parameters using age-dependent cumulative confirmed case data from August 15 to November 30, 2022 [1]. Then we extended our model simulation for 180 days to observe the impact of lifting the mask mandate (blue arrow) on the number of cases. For the extension, we used the estimated relative seasonality factor in the last phase ($m_4$). We set that if mask-wearing becomes nonmandatory in a certain location, then the transmission risk in that location ($q_1$ to $q_5$) increases 5-fold [25]. Finally, the simulation is extended further for another 3 years (orange arrow) to consider the effect of a new variant. We assume that the new variant has higher transmissibility and risk of breakthrough infections. We incorporate both risks as a single parameter, which we refer to as the variant varying factor ($VVF$), which reduces vaccine effectiveness and increases transmissibility and incorporated in the force of infection for the forecast simulations (${\bar{\lambda }}_x^i$) as follows:

$${\bar{\lambda }}_x^i=VVF\left(1-e_x\left(1-VVF\right)\right){\delta }^i{m}_4\sum _{k\in VG}\sum _{j\in AG}h\left(c_1^{ij}+q_2{c}_2^{ij}+q_3{c}_3^{ij}+q_4{c}_4^{ij}+q_5{c}_5^{ij}\right)\left({I_k^j+\tilde{I}}_k^j\right)\text{.}$$ (2)

In the analysis considering $VVF$, which modifies Equation (1), (2), we focused on the peak size of the administered severe patients and set the critical number at 2,000, which is near the maximum severe patient capacity in 2022 [1,2]. We also assumed that updated vaccines are administered as the new variant emerges and have relatively higher vaccine effectiveness (if the host does not have prior infection, then 0·8 against infection and 0·95 against severity, if does, then 0·9 against infection and 0·95 against severity) during this phase. Note that we did not consider the reduction of vaccine effectiveness against severity caused by a new variant.

Fig. 2.

Timeline of the study considering three phases.

3. Results

3.1. Data-fitting result

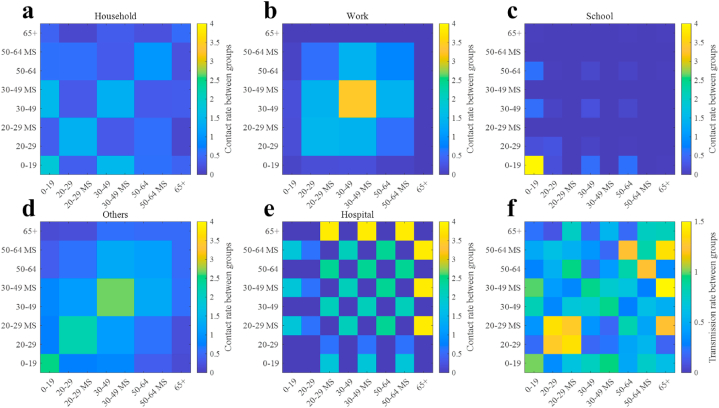
The modes of the obtained samples for $h$, ${\delta }^{Ⅱ}$, ${\delta }^{Ⅲ}$, ${\delta }^{Ⅳ}$, ${\delta }^{Ⅴ}$, $m_2$, $m_3$, and $m_4$ using the Metropolis-Hastings algorithm were used in the model. The corresponding values are 0·52, 1·72, 0·97, 1·53, 2·75, 0·93, 1·51, and 1·26, respectively. Fig. 3 shows the aggregated contact matrices and formulated transmission matrix among age groups using the estimated values. The transmission matrix in Fig. 3f shows a distinctive nonsymmetric shape, as it contains the age-dependent relative susceptibility (${\delta }^i$), e.g., ${\delta }^{i}h\left(c_1^{ij}+q_2{c}_2^{ij}+q_3{c}_3^{ij}+q_4{c}_4^{ij}+q_5{c}_5^{ij}\right)$; household ($c_1^{ij}$, Fig. 3a), work ($c_2^{ij}$, Fig. 3b), school ($c_3^{ij}$, Fig. 3c), others ($c_4^{ij}$, Fig. 3d), and hospital ($c_5^{ij}$, Fig. 3e). As the color gets closer to yellow, the more frequent the contact (Fig. 3a to e) or the higher the transmission rate (Fig. 3f).

Fig. 3.

The contract matrices between age groups in (a) household, (b) work, (c) school, and (d) other locations. Panel (f) shows the transmission rates between age groups calculated using matrices (a) to (e).

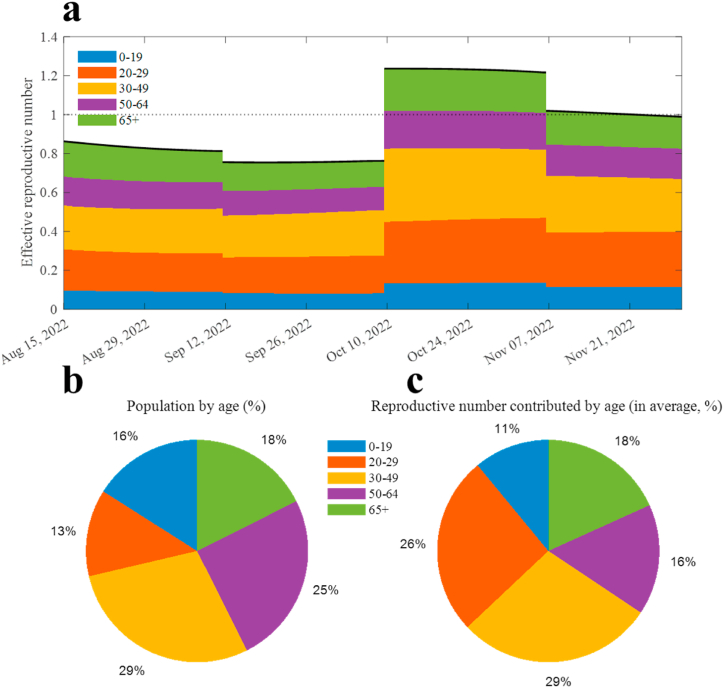
The fitted curves for the five age groups are displayed in Fig. 4, where Fig. 4a–e (Fig. 4f–j) indicate cumulative (daily) confirmed case number of age 0–19 ($Ⅰ$), 20–29 ($Ⅱ$), 30–49 ($Ⅲ$), 50–64 ($Ⅳ$), and 65+ ($Ⅴ$), respectively. Note that the MS results are included in their corresponding age groups (Fig. 4b–d and g–i). Fig. 5a shows the effective reproductive number ($R_t$) calculated using the next-generation method [26]. The filled areas indicate the age-related proportion ($R_t^i$), which is computed by taking the sum of the column entries of the next-generation matrix [26]. The formulation of the next-generation matrix is described in the Supplementary material. Moreover, Fig. 5b and c depict the proportion of the population and the average contribution of $R_t^i$ to $R_t$, respectively. The relative differences between the population proportion and the contribution of age groups 0–19, 20–29, 30–49, 50–64, and 65+ to the reproductive number were 5·01%p, −13·36%p, 0·10%p, 8·88%p, and 0·63%p, respectively, where the negative sign indicates that the group contributes to the transmission more relative to its population.

Fig. 4.

Data-fitting simulation results. Red squares and black curves indicate the data and model simulation results, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Fig. 5.

Reproductive number from the model simulation. (a) Effective reproductive number (dark curve); filled area indicates how much each age is dedicated to the value. (b) Proportion of the population by age. (c) Average proportion of the reproductive number contributed by age.

3.2. Near-future forecast with lifted mask mandate

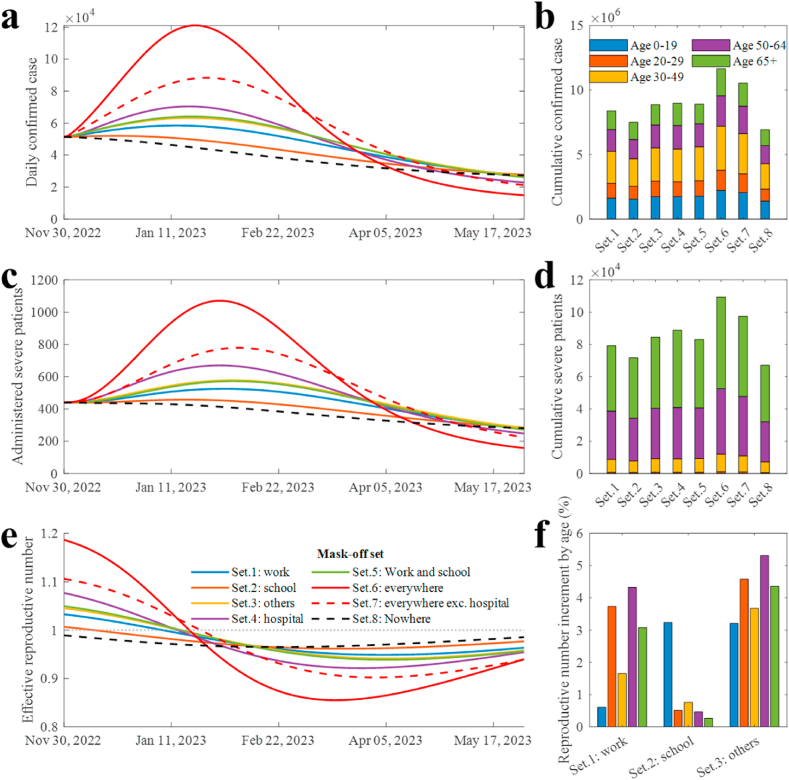
Fig. 6 shows the simulation results considering the lifting of the mask mandate in various places. Fig. 6a and b (Fig. 6c and d) display the daily and cumulative confirmed cases (administered severe patients), respectively. Excluding the masks-on scenario, removing masks in schools resulted in both the lowest number of cumulative confirmed cases (7,501,510) and severe patients (71,710). Taking off masks everywhere and except in hospitals had the first and second highest cumulative number of severe patients, respectively. The lifting of mask mandates in hospitals showed the highest number of confirmed cases and severe patients among the lifting mask mandates in single-place settings (set 1 to set 4). Adding the medical staff to their respective age groups, the confirmed cases (severe patients) in ages 0–19, 20–29, 30–49, 50–64, and 65+ in every scenario were approximately 19·59% (00·16%), 13·48% (00·80%), 29·02% (09·92%), 20·16% (37·22%), and 17·75% (51·90%), respectively. The effective reproductive numbers in each scenario are shown in Fig. 6e. The initial value of the reproductive number for scenarios 1 to 8 ranged from 0·99 to 1·19 Fig. 6f shows the age-dependent increment in the reproductive number in scenarios 1 to 3. If masks are taken off in school, the underage group has the highest increment (3·24%) of their reproductive number while the increments in other age groups were less than 1%.

Fig. 6.

Extended simulation results considering the lifted mask mandate. (a) Daily confirmed cases. (b) Cumulative confirmed cases of age groups in different scenarios. (c) Administered severe patients. (d) Cumulative severe patients of age groups in scenarios. (e) Effective reproductive number. (f) Age dependent transmissibility increment in different scenarios.

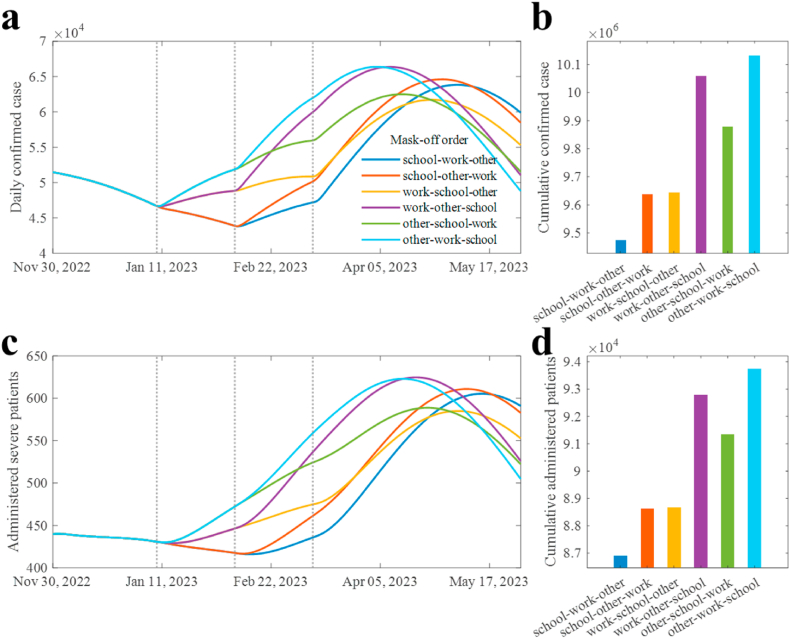
Furthermore, we investigated the effect on the number of cases of sequential lifting of the mask mandate in different locations (Fig. 7). In the simulations, we set that mask wearing in hospitals is mandatory. Lifting the policy in school, followed by the workplace, and then in other places (school-work-other) showed the least number of confirmed cases (Fig. 7a and b) and severe patients (Fig. 7c and d), while other-work-school had the greatest number of confirmed and severe patients. The other-work-school sequence resulted in 6·94% (7·89%) higher confirmed cases (severe patients) than when the order was school-work-other.

Fig. 7.

Extended simulation results with sequentially lifted mask mandate. (a) Daily confirmed cases. (b) Cumulative confirmed cases in scenarios. (c) Administered severe patients. (d) Cumulative severe patients in each scenario.

4. Far-future forecast with new variant

We extended the model simulation for 180 days from November 30, 2022 to forecast the number of cases considering the possible emergence of a new variant. The results are shown in Fig. 8. Assuming different mask-wearing policies, Fig. 8a to c display the heatmaps of the peak number of severe patients depending on the $VVF$ and the number of daily vaccinations. Contour lines are added to indicate the critical level of severe cases (2,000). Fig. 8d shows the contour lines with three distinctively filled areas: (1) best-case scenario (blue region), which does not require mask-wearing; (2) status-quo (green region), which requires hybrid mask-wearing, that is, masks may not be required in certain places; and (3) worst-case scenario (yellow area), which means the peak number of severe patients exceeds the critical level. Fig. 8e and f illustrate sampled simulation results from Fig. 8a to c, which are long-term predictions, to visualize the forecasted number of cases over time. If $VVF=0.35$, severe cases may reach more than 2,000, which means that additional NPIs are needed to control the spread of the disease. On the other hand, if $VVF=0.2$, the number of cases remains manageable even if the mask mandate is removed.

Fig. 8.

Peak size of administered severe patients in different settings. (a) When there is a mask mandate everywhere. (b) When the mask mandate is lifted in work and school. (c) When the mask mandate is lifted everywhere except the hospital. (d) Separable three areas using the contour lines from panels (a) to (c). Note that contour lines in (a) to (d) indicate the peak size of administered severe patients as 2000. (e) to (f) show the simulation results sampled from (a) to (c).

5. Discussions

Our model considers different factors affecting transmission and susceptibility to infection such as age, vaccination history, and prior infection. Moreover, the model separates the medical staff with the general population. A complex model requires more data, which would be challenging to be aggregated, but can render natural phenomena than simple a model [27]. The estimation of several model parameters was done using the up-to-date cumulative cases data. The recently available antibody test data provided key information on prior infections, which is needed in setting the initial state values for the simulations while in the middle of an outbreak. The results of the Metropolis-Hastings algorithm provide estimates, as well as uncertainties of the parameter estimates. A low prior infection ratio of seniors and a high susceptibility to infection shown by the model pose potential risks in the next wave. Moreover, a high contact rate between seniors and MS can be seen, which suggests that removing mask protocols in hospitals is not advisable given that the number of severe cases is still high [28].

On the other hand, a high prior infection proportion for those aged below 20 resulted in reduced infectivity. This suggests that wearing masks inside schools has less effect in reducing cases in the current situation, although it was known as a highly effective measure before omicron [29]. The transmissibility of the disease is reflected in the estimated relative seasonality factors ($m_T$), as it decreased from the middle of August to early October but later increased. This change can be attributed to the characteristics of the virus and seasonal social behavior. For example, there are more outdoor activities during summer months and more indoor activities during colder months. In Korea, since wearing masks indoors is the only remaining NPIs in 2022, the natural seasonality of the disease can be investigated. We expect that by incorporating this into the model, a more dynamic and realistic policy can be formulated.

Most of the severe cases were observed to have occurred in the older age groups (Fig. 6). Since seniors have more frequent contact with MS than the other age groups, our model simulations highlight the importance of mask wearing in hospitals. On the other hand, taking off masks in schools might be acceptable. We already observed that the underage group had the highest prior infection (73.40%, described in the Supplementary material) and low reproductive number (in Fig. 5). Moreover, the increment in the reproductive number in the underage is small and minimally affects the other age groups (Fig. 6f).

The lifting of mask mandates is possible and may be more manageable if the policy is relaxed sequentially. We found that if masks are removed in all locations at once except in hospitals, then the administered severe patients would reach 800. On the other hand, if the policy is relaxed in a sequence (school-work-other), then the number of severe patients are below 650 and decrease further.

Lifting mask mandates naturally increases the scale of an outbreak. If we consider a situation where a future variant occurs, the relaxed policy can increase the scale more than expected (in Fig. 8). If a highly transmissible new variant emerges, a risk of health system saturation is possible because of the high number of severe patients. We observed three possibilities depending on the VVF, vaccination rate, and threshold of severe patients. The critical $VVF$ value is approximately 0.3. Mask wearing may still be necessary if $VVF$ is higher than 0.23. For comparison, assuming that the population has 0.8 of the protection effect against infection, then the effective reproductive number will increase 3.24 fold if the new variant's VVF is 0.35 more, by Equation (2), $\left[\left\{1.35\times \left(1-0.8\times \left(1-0.35\right)\right)\right\}÷\left\{1\times \left(1-0.8\right)\right\}\right]=3.24$. It was found that the relative reproduction number of omicron compared to delta was 3·19, which would be similar to the previous example when $VVF$ was assumed to be 0.35 [29]. The $VVF$, which is proposed in this study can help policymakers develop a proactive intervention strategy when a new variant arises. When a more contagious variant becomes dominant, vaccination and mask-wearing may still be essential to reduce the number of severe cases. For example, if the number of daily-administered vaccines is 5000 (approximately 0.01% of the population) and $VVF$ is 0.32, then mask-wearing may not be enough. On the other hand, the outbreak may be controllable with mask-wearing if the number of daily-administered vaccines is 40,000. As the scale of vaccination increases, the disease becomes more manageable, although $VVF$ reduces vaccine effectiveness. Thus, efforts to reduce vaccine hesitancy in the older age group should be implemented, as this group has the highest proportion of severe cases.

In this study, we assumed that the N-positive proportion is the proportion of hosts who had prior infection. As with other serological tests, the N-positive immune response may not be detected if the infection was much earlier, which means that the actual proportion of the population with prior infection would be higher than the investigation results. Furthermore, we assumed that the N-positive rate of individuals aged 0–4 was the same as that of individuals aged 5–9. In the model parameter setting, the effectiveness of the updated vaccine is assumed due to the lack of studies. In initial states, the proportion of waned infection-induced immunity is set to 50%. We recognize that the contact matrix, N-positive rate for age 0–4, and effectiveness of updated vaccines can still be properly estimated but these can easily be modified in the model once the data become available. The control strategies proposed in this study are set based on several scenarios. For future work, one can apply control theory to our model, but this will require solving a very large system of nonlinear equations, that demands long computation time and rigorous mathematical analysis. The model may have to be simplified to do this.

6. Conclusion

In this study, we analyzed the risks related to lifting the mask mandate and new variants using an age-structured mathematical model. We found that removing the mask policy is possible while keeping the number of cases manageable. Notably, the results show that masks off in school can be implemented sooner. However, masks in hospitals should remain in place to protect older age groups. Possible new variants might cause the rise in infections and require stricter NPIs if the new variant has 30% higher transmissibility and immune reduction compared to the current omicron variant.

Simulations showed a hopeful perspective as we observed that the critical VVF is approximately 0.3, which was similarly recorded once in the past, when delta was replaced by omicron as the dominant variant, with the severity of omicron being significantly less than that of delta. Nevertheless, the potential risk is never zero, and prompt characterization of the new variant is vital, as it can guide the government to decide the proactive response. Although the model is formulated using Korean data, it is general enough that it can be applied to other countries that have yet to lift all their COVID-19 restrictions.

Author contribution statement

E.J acquired funding for this study. Y.K, J.L, and E.J conceived and designed the study. Y.K, R.M, and V.M analyzed the data and wrote the first draft. E.J, J.L, and Y.S improved the quality of the analysis and monitored the study progress. Y.K did data collection. All authors contributed data checking and processing. All authors reviewed the final version of the manuscript.

Funding

This paper is supported by the Korea National Research Foundation (NRF) grant funded by the Korean government (MEST) (NRF-2021M3E5E308120711). This paper is also supported by the Korea National Research Foundation (NRF) grant funded by the Korean government (MEST) (NRF-2021R1A2C100448711). This research was also supported by a fund (2022-03-008) by Research of Korea Disease Control and Prevention Agency.

Author contribution statement

Youngsuk Ko: conceived and designed the experiments; performed the experiments; analyzed and interpreted the data; contributed reagents, materials, analysis tools or data; wrote the paper.

Jacob Lee: conceived and designed the experiments.

Eunok Jung: conceived and designed the experiments; analyzed and interpreted the data; wrote the paper.

Renier Mendoza: analyzed and interpreted the data; wrote the paper.

Victoria Mendoza: analyzed and interpreted the data; wrote the paper.

Yubin Seo: analyzed and interpreted the data: wrote the paper.

Data availability statement

Data included in article/supp. material/referenced in article.

Additional information

Supplementary content related to this article has been published online at [URL].

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article.