A case study of an individual participant data meta-analysis of diagnostic accuracy showed that prediction regions represented heterogeneity well

Abstract

The diagnostic accuracy of a screening tool is often characterized by its sensitivity and specificity. An analysis of these measures must consider their intrinsic correlation. In the context of an individual participant data meta-analysis, heterogeneity is one of the main components of the analysis. When using a random-effects meta-analytic model, prediction regions provide deeper insight into the effect of heterogeneity on the variability of estimated accuracy measures across the entire studied population, not just the average. This study aimed to investigate heterogeneity via prediction regions in an individual participant data meta-analysis of the sensitivity and specificity of the Patient Health Questionnaire-9 for screening to detect major depression. From the total number of studies in the pool, four dates were selected containing roughly 25%, 50%, 75% and 100% of the total number of participants. A bivariate random-effects model was fitted to studies up to and including each of these dates to jointly estimate sensitivity and specificity. Two-dimensional prediction regions were plotted in ROC-space. Subgroup analyses were carried out on sex and age, regardless of the date of the study. The dataset comprised 17,436 participants from 58 primary studies of which 2322 (13.3%) presented cases of major depression. Point estimates of sensitivity and specificity did not differ importantly as more studies were added to the model. However, correlation of the measures increased. As expected, standard errors of the logit pooled TPR and FPR consistently decreased as more studies were used, while standard deviations of the random-effects did not decrease monotonically. Subgroup analysis by sex did not reveal important contributions for observed heterogeneity; however, the shape of the prediction regions differed. Subgroup analysis by age did not reveal meaningful contributions to the heterogeneity and the prediction regions were similar in shape. Prediction intervals and regions reveal previously unseen trends in a dataset. In the context of a meta-analysis of diagnostic test accuracy, prediction regions can display the range of accuracy measures in different populations and settings.

Introduction

Medical screening tests are used to identify possible disease before signs or symptoms present, such as HIV antibody testing, or to identify the presence of a condition that has not otherwise been identified, such as in depression screening. The accuracy of a screening test is evaluated by comparing against a reference standard that is thought to represent the true status of the target condition. Accuracy is typically characterized by sensitivity or true positive rate (TPR), which is the probability of a positive screen given that the patient has the condition, and 1-specificity or false positive rate (FPR), which is the probability of a positive screen given that the patient does not have the condition. When screening test results are ordinal or continuous, a threshold is set to classify test results as positive or negative.

Meta-analyses of test accuracy pool results from primary studies to attempt to overcome imprecision due to small samples, conduct subgroup analyses that were not feasible in the primary studies, and estimate variance within and between studies¹. Such meta-analyses must consider the intrinsic correlation between TPR and FPR across studies. This is because selecting a lower threshold for classifying positive screening results would simultaneously increase the TPR of the test but also its FPR while a higher threshold would have the opposite effect. The bivariate random effects model (BREM) is commonly used because it allows for simultaneous estimation of TPR and FPR with the random effects assumed to have a joint normal distribution².

The inter-study heterogeneity or variability of TPR and FPR is an important output from a meta-analysis and may be characterized by several different metrics. The most direct is the between-study variance, often denoted as ${\tau }^2$. However, given that this parameter ranges from zero to infinity, interpreting its value as “small” or “large” is difficult. Other approaches to characterize heterogeneity, such as Cochran’s $Q$ or $I^2$ have been shown to have important limitations as well. Cochran’s $Q$ has limited power with small numbers of studies and is overly sensitive with large numbers of studies³, whereas $I^2$ ranges from 0 to 1 and represents the proportion of observed variability attributable to heterogeneity but does not provide information about variation in sensitivity or specificity⁴.

Another way to describe heterogeneity is the prediction interval. This represents an estimated range of values that has a predetermined probability of containing the estimate of interest from a new study sampled from the same population as used to fit the model. The use of prediction intervals has important advantages in that it summarizes point estimates and variance components from the BREM as the interval considers overall mean estimates of TPR and FPR, their standard errors and between-study variance⁵. The Cochrane Handbook for Systematic Reviews of Diagnostic Test Accuracy regards the prediction interval as the best graphical depiction of the magnitude of heterogeneity⁶. In the bivariate case, prediction intervals for TPR and FPR are represented as regions in two-dimensional space where this set of values has a predetermined probability of containing a new two-dimensional vector of estimates from a new study comparable to those in the pool⁷.

The Patient Health Questionnaire-9 (PHQ-9) is a self-report depression symptom questionnaire that consists of nine items, each scored 0 to 3 (total possible score 0 to 27), that can be used for depression screening. A standard threshold score of 10 or greater has been shown to maximize the sum of sensitivity and specificity (TPR and 1-FPR)⁸. Meta-analyses assessing the diagnostic accuracy of the PHQ-9 and other similar screening questionnaires often report a confidence interval around pooled estimates of TPR and FPR^9,10. The confidence interval contains the true value of the mean measure, here the pooled estimate of TPR or FPR with probability 0.95. Consequently, other authors have argued that prediction intervals are more useful since they provide information on the range of possible accuracy values that may be encountered in a future study^11,12. Thus, a prediction interval and a confidence interval are not the same thing and serve different purposes. The confidence interval is a measure of precision that indicates how accurately we have estimated the pooled sensitivity or specificity based on the standard error and depends on the number of studies in the meta-analysis¹³. On the other hand, the prediction interval measures dispersion, is based on the standard deviation that shows how much the measures vary across different populations, and is not related to the number of studies in the analysis¹³. The prediction interval is more informative when it comes to heterogeneity, describing the extent of dispersion in the context of sensitivity or specificity¹³. A clinician using the results from a meta-analysis on the diagnostic accuracy of the PHQ-9 would have a better idea of how the diagnostic accuracy varied across studies, and indeed, how the PHQ-9 might be expected to perform in a new study, or setting such as the physician’s practice.

Because diagnostic accuracy is represented by the true positive rate (TPR) and the false positive rate (FPR), a prediction region is used rather than two prediction intervals. The region, which is elliptical in the logit space, takes into account the correlation between logit(TPR) and logit(FPR) which is reflected in the orientation and size of the minor axes of the prediction ellipse. The orientation of the ellipse relates to the “slope” linking logit(TPR) and logit(FPR) observations. The strength of the correlation is depicted by the width of the ellipses about their minor axis. Moreover, the prediction region makes explicit that some combinations of TPR and FPR are unlikely, whereas the two intervals do not.

Despite several sources suggesting that prediction intervals be used to quantify and describe heterogeneity and the range of accuracy values, they are still underused^11,12. The objective of the present study was to illustrate the use of prediction regions for TPR and FPR of the PHQ-9 as a numerical and graphical depiction of the heterogeneity in an individual participant meta-analysis (IPDMA) and investigate how these regions (1) change as more studies are included in the BREM, and (2) vary across subgroups.

Methods

This study is a secondary analysis of an IPDMA. For the main IPDMA registered in PROSPERO (CRD42014010673), a protocol was published¹⁴ and results have been reported⁸. The present analysis extends the work specified in the protocol by characterizing heterogeneity in the study pool via prediction regions constructed from the BREM, and using the region to describe the range of likely mean measures of TPR and FPR from an unseen study similar to those in the pool (with probability 0.95).

Description of dataset

For the original IPDMA, studies were eligible for inclusion if: (1) they included PHQ-9 scores, (2) they included major depression classification based on a validated diagnostic interview, (3) the time interval between administration of the PHQ-9 and the diagnostic interview was no more than 2 weeks, and (4) participants were at least 18-years old and recruited outside of psychiatric settings. The studies and data included in the dataset were selected from the results of an online search strategy from 2000 to 2016. Eligible studies were assessed independently by two investigators. For further details on the search and selection processes, refer to the published protocol¹⁴.

Data analysis for the present study

For each study in the PHQ-9 IPDMA dataset, generalized linear models were fitted to estimate TPR and FPR and their respective 95% CIs. From these, forest plots were produced for a qualitative assessment of heterogeneity. All analyses were completed in R¹⁵.

From the dataset, three dates were selected as “cutoff dates” (as reported in the “Date” column in Additional File 1). This approach was chosen to simulate how in reality more information becomes available on the topic over time and investigate the effects this accrual has on the heterogeneity of the study pool. The cutoff dates were selected so that participants in studies conducted up to and including each cutoff date comprised roughly 25%, 50% and 75% of the total number of participants. A BREM, as described in Additional File 2, was fitted for studies conducted up to and including each of the cutoff dates to jointly estimate TPR and FPR using the function “glmer” from the package “lme4”^15,16. As these measures are described in two-dimensional ROC-space, confidence and prediction regions are analyzed instead of their one-dimensional analogues: confidence, and prediction intervals. For each model, 95% confidence and prediction regions were constructed following the method described by Chew⁷ (for more details, refer to Additional File 2). At each cutoff date, the confidence region associated with the model was plotted as well as the individual measure estimates from the studies used for the fit. Similarly, prediction regions were plotted with the individual measure estimates of studies after the corresponding cutoff date to assess coverage. Finally, a BREM was fitted using data from all studies and 95% confidence and prediction regions were constructed in the same manner as above. To quantify the size of all prediction regions, we also estimated the area of the interval in logit space.

Prediction intervals for participant subgroups were also constructed to assess whether heterogeneity could be due to age or sex or participants. Subgroups were defined using binary sex categories and, separately, age quartiles.

Ethics approval and consent to participate

As this study involved only analysis of previously collected de-identified data and because all included studies were required to have obtained ethics approval and informed consent, the Research Ethics Committee of the Jewish General Hospital determined that ethics approval was not required.

Results

The final IPDMA dataset consisted of 58 primary studies, totaling 17,436 participants of which 2322 (13.3%) presented cases of major depression and 1794 (10.3% of total, 77.3% of cases) were correctly identified as cases using the standard PHQ-9 cutoff score of ≥ 10.

Main analysis

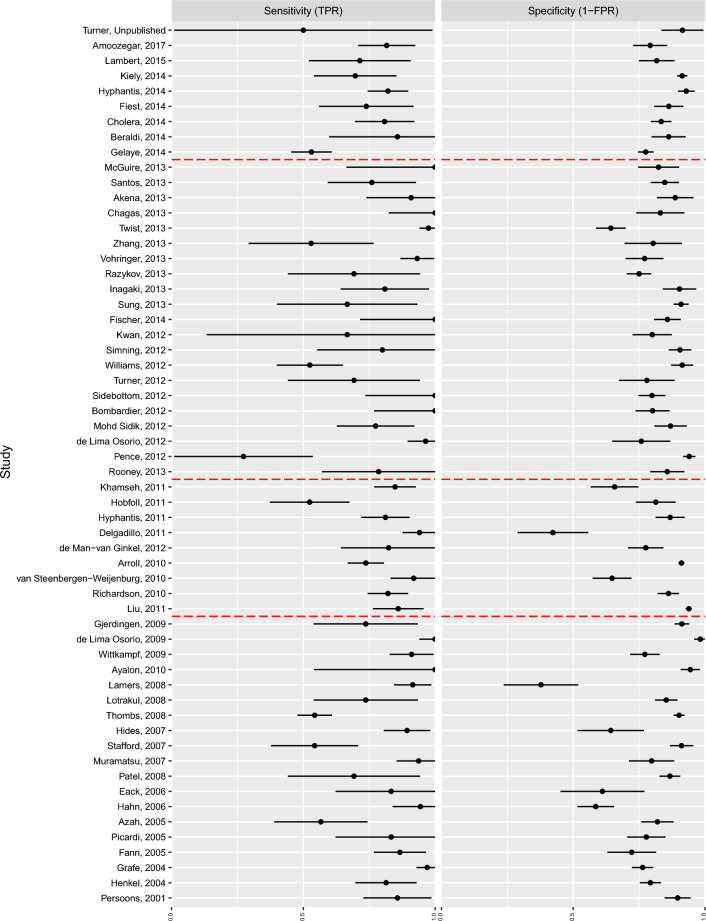
A summary of the individual participant data can be found in Additional File 1. The results of the generalized linear models per study for sensitivity and specificity (TPR and 1-FPR) can be seen in forest plots (Fig. 1). The presence of heterogeneity can be visually assessed in Fig. 1 Confidence intervals for specificity were much narrower than those for sensitivity.

Figure 1.

Forest plots of sensitivity (TPR) and specificity (1-FPR). (1) The dotted lines in the sensitivity forest plots indicate that the data from the study indicated a 100% true positive rate and a 0% false positive rate. This caused the sensitivity estimate to be 1 but the standard error was large enough to cover the whole interval $(0,1)$. (2) Red dot-dashed lines indicate the selected cutoff dates for the BREM. (3) Studies are sorted by the year in which the study started, while the label indicates the year in which they were published.)

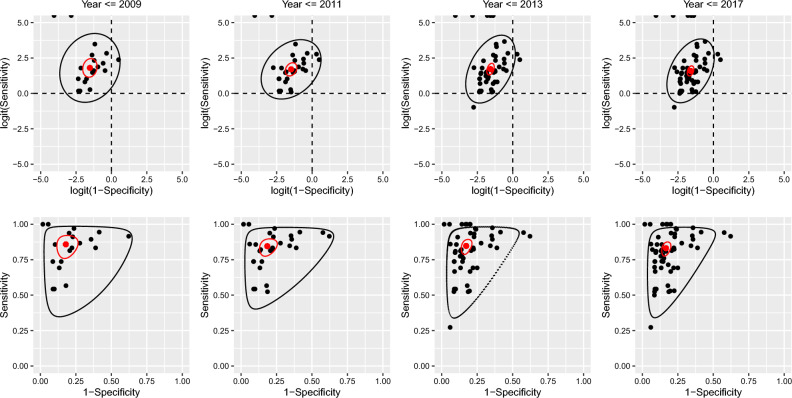
Studies published up to and including the cutoff dates of 2009, 2011 and 2013 included 19, 28 and 49 of the 58 available studies and 28.2%, 59.4% and 81.8% of total participants respectively. At the 2009 cutoff, the TPR and FPR were 0.86 and 0.18 (see Table 1). Increasing the number of studies at each cutoff date did not result in important differences in the pooled TPR and FPR, and the 95% confidence intervals for their estimates overlapped. As the number of studies increased, the standard error of the estimated pooled TPR and FPR decreased (not shown), and correspondingly, the confidence intervals and regions shrank as expected (see Table 1 and Fig. 2).

Table 1.

Summary of pooled FPR and TPR results from the BREM.

Time interval	Parameter	Estimate	95% CI
2001–2009	FPR (1 − specificity)	0.18	(0.12, 0.25)
	TPR (sensitivity)	0.86	(0.78, 0.92)
2001–2011	FPR (1 − specificity)	0.19	(0.14, 0.24)
	TPR (sensitivity)	0.85	(0.79, 0.89)
2001–2013	FPR (1 − specificity)	0.17	(0.14, 0.21)
	TPR (sensitivity)	0.85	(0.80, 0.89)
2001–2017	FPR (1 − specificity)	0.17	(0.14, 0.19)
	TPR (sensitivity)	0.83	(0.79, 0.87)

Figure 2.

Prediction and confidence regions through time (FPR = 1 − specificity, TPR = sensitivity). Black dots are the study specific estimates. The red dot is the pooled estimate. The black line indicates the prediction region. The red line is the confidence region. The top panel show the estimates and regions in logit-space, while the bottom panel are in the probability-space. (1) The change in the estimated correlation between sensitivity and 1 − specificity is reflected in the orientation and size of the minor axes of the prediction ellipses in the top row of figure. The orientation of the ellipses relates to the “slope” linking TPR and FPR observations. The strength of the correlation is depicted by the width of the ellipses about their minor axis.)

There was some evidence that between-study standard deviation estimates for FPR decreased from ${\widehat{\tau }}_0=0.87$ at the 2009 cutoff date, to ${\widehat{\tau }}_0=0.69$ when all studies were included (see Table 2), though confidence intervals largely overlapped. This decrease in the estimated variance component is reflected in the narrowing of the prediction region in ROC space along the FPR direction (see Fig. 2C*,D*). Correspondingly, the area of the prediction region decreased as more data was included (Table 2). The correlation estimates for the random effects increased (from 0.16 to 0.43) as more studies were included.

Table 2.

Summary of between study variances from the BREM*

Cutoff date	Parameter	Estimate	Correlation (${\widehat{\rho }}_{\tau }$)	Area of prediction region
2009	${\tau }_0$	0.87 (0.53, 1.18)	0.16 (− 0.46, 0.71)	22.83
	${\tau }_1$	0.99 (0.48, 1.42)
2011	${\tau }_0$	0.87 (0.59, 1.08)	0.32 (− 0.16, 0.71)	16.65
	${\tau }_1$	0.85 (0.54, 1.17)
2013	${\tau }_0$	0.71 (0.54, 0.88)	0.44 (0.13, 0.73)	13.51
	${\tau }_1$	0.98 (0.69, 1.26)
Full	${\tau }_0$	0.69 (0.54, 0.82)	0.43 (0.12, 0.71)	11.94
	${\tau }_1$	0.92 (0.67, 1.16)

*All estimates are on the logit scales. Confidence intervals for ${\tau }_0$, ${\tau }_1,and{\widehat{\rho }}_{\tau }$ were estimated using parametric bootstrap with 1000 replicates.

The change in the estimated correlation between logit(TPR) and logit(FPR) is reflected in the orientation and size of the minor axes of the prediction ellipses in the top row of Fig. 2. The orientation of the ellipses relates to the “slope” linking logit(TPR) and logit(FPR) observations. The strength of the correlation is depicted by the width of the ellipses about their minor axis.

Subgroup analyses

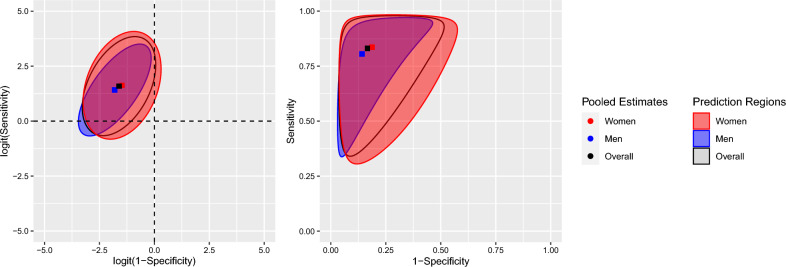
Female participants represented 57% of participants. For this subgroup, BREM estimates for TPR and FPR were 0.84 and 0.19. For the male subjects, BREM estimates were 0.80 and 0.14 for TPR and FPR respectively (see Table 3). Between-study standard deviation estimates were both higher in the female group than in the male. Estimated correlation of the random effects was greater in the male group (see Table 3 and Fig. 3). The area of the region (in logit space) for the female subgroup was larger than that in the males (see Table 3 and Fig. 3). Overall, there was no clear indication that sex meaningfully contributes to heterogeneity in the whole sample.

Table 3.

Summary of BREM by sex.

Subgroup	Parameter	Pooled estimate (95% CI)	Between study standard deviations* (95% CI)	${\widehat{\rho }}_{\tau }$ (95% CI)	Area of prediction region
Female	FPR	0.19 (0.16, 0.22)	0.73 (0.53, 0.88)	0.30 (− 0.08, 0.67)	14.58
	TPR	0.84 (0.79, 0.88)	1.00 (0.67, 1.29)
Male	FPR	0.14 (0.12, 0.17)	0.68 (0.49, 0.83)	0.69 (0.35, 100)	9.03
	TPR	0.80 (0.75, 0.85)	0.85 (0.49, 1.15)

*Standard deviations relate to the logit estimates. These are ${\tau }_0,{\tau }_{1.}$

Figure 3.

Prediction regions by sex subgroup (FPR = 1 − specificity, TPR = sensitivity).

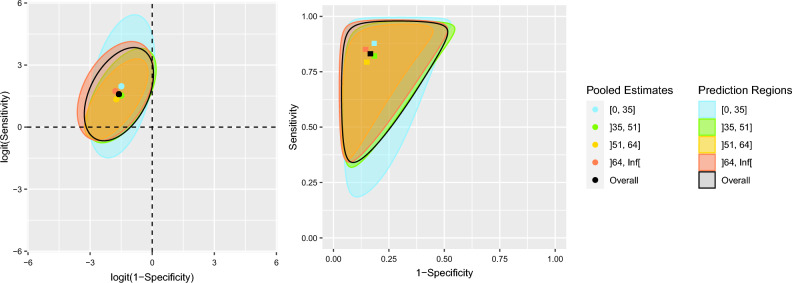
The quartiles for the age of participants were $Q_1=35$, $Q_2=51$, $Q_3=64$. Quantitative results of the BREM by age subgroup are presented in Table 4. Assessment of heterogeneity in these subgroups is summarized by the prediction regions in Fig. 4. In ROC space it can be observed that between-study standard deviation of FPR is not considerably different in any age subgroup ranging from 0.63 to 0.75. Between-study standard deviation of TPR is greatest among the group younger than 35 years (${\widehat{\tau }}_1=1.41$) and lowest for the group between 51 and 64 years old (${\widehat{\tau }}_1=0.80$). This comparison may also be observed by comparing the areas of their corresponding prediction regions. In logit-ROC space (Fig. 4A) it can be observed that the direction of correlation is similar across subgroups. The strength of the correlation, however, reaches a maximum in the age group between 51 and 64 years old (${\widehat{\rho }}_{\tau }=0.66$). No important contribution to the overall heterogeneity of the sample could be clearly identified from observing the prediction regions between the age subgroups.

Table 4.

Summary of BREM by age subgroup.

Age range*	Parameter	Pooled estimate (95% CI)	Between study standard deviations* (95% CI)	${\widehat{\rho }}_{\tau }$ (95% CI)	Area of prediction region
$\left[0,,,35\right]$	FPR	0.18 (0.15, 0.22)	0.66 (0.42, 0.86)	0.40 (− 0.08, 0.84)	18.31
	TPR	0.88 (0.80, 0.94)	1.41 (0.82, 2.02)
$\left(35,,,51\right]$	FPR	0.18 (0.15, 0.22)	0.68 (0.47, 0.86)	0.56 (0.15, 1.00)	11.43
	TPR	0.82 (0.76, 0.87)	0.93 (0.51, 1.30)
$\left(51,,,64\right]$	FPR	0.15 (0.12, 0.18)	0.63 (0.41, 0.80)	0.66 (0.20, 1.00)	8.24
	TPR	0.79 (0.73, 0.85)	0.80 (0.41, 1.14)
$(64,\infty )$	FPR	0.14 (0.11, 0.17)	0.75 (0.49, 0.95)	0.42 (− 0.13, 1.00)	15.18
	TPR	0.85 (0.78, 0.92)	0.98 (0.42, 1.49)

*The 25th, 50th and 75th percentiles were used to define the age ranges.

Figure 4.

Prediction regions by age subgroup (FPR = 1 − specificity, TPR = sensitivity).

Discussion

The present study aimed to characterize heterogeneity in an IPDMA of diagnostic test accuracy measures for the PHQ-9. The location of the overall estimates for TPR and FPR did not vary considerably as more studies were included. The size of the confidence region around the estimates shrank as more data were used in the model. The confidence region not only decreased in size but also changed shape as the correlation of the measures increased.

Prediction regions are one way to depict heterogeneity. Along the TPR axis, the prediction region changed erratically as more studies with differing estimates were included. Regarding FPR, the region consistently narrowed. This supports the initial inspection of the forest plots where sensitivity estimates (and therefore FPR), while scattered, showed less variability than the TPR estimates. The shape of the prediction region reflects the underlying positive correlation of these measures. Looking at Fig. 2D*, it can be observed that while a new study may estimate a high FPR (top-right corner of the prediction region), it is unlikely that the same study will simultaneously estimate a low TPR, say, below 0.5, as the coordinate in ROC-space would fall outside the 95% prediction region; this becomes more and more improbable as FPR increases. In the same way, a new study is unlikely to estimate low TPR and high FPR. The size of the prediction region is not guaranteed to decrease as more estimates are included, as seen in the 2013 cutoff (Fig. 2C*). The region updates, as more information becomes available on the location of individual estimates, to accurately represent the overall trends in the data.

Both confidence and prediction regions considering only the one-dimensional confidence/prediction intervals could be misleading, if interpreted naively. As an example, in Fig. 2D* the one-dimensional prediction intervals range from near 0 to almost 0.6 for FPR and from about 0.3 to 1 for TPR. However, if a clinician who administered the PHQ-9 wishes to consider the worst estimates for both accuracy measures i.e., 0.3 for TPR and 0.6 for FPR, this estimate is outside of the prediction region and the clinician could draw false conclusions from their assumptions.

The subgroup analyses aided in investigating possible sources of heterogeneity among the study pool. Prediction regions by subgroups can reveal some differences that might be hard to appreciate when only one-dimensional prediction intervals are used. Subgroup analysis by sex revealed no statistically significant differences between the point estimates of mean TPR and FPR between the female and male groups or when compared to overall population estimates; this coincides with the results of the main PHQ-9 IPDMA⁸. Both prediction regions for male and female groups span a comparable length parallel to either axis, although the shape of the ellipse in logit-ROC or the slanted border in ROC space differ between groups to some extent. This may be a depiction of the observed difference in the point estimates for correlation for both fixed and random effects between the female and male groups. The location of TPR and FPR estimates by age subgroup did not differ greatly from the overall population estimates. These regions were similar in size and shape: the largest region corresponding to the age group between 18 and 35 years old, being widest in the TPR direction, and the smallest corresponding to the 51 to 64 cohorts. While categorizing age has some downsides, it allowed us to present prediction regions by age category and improved interpretation of results.

The use of prediction intervals has been suggested in the literature as a complete summary of a random effects meta-analysis and a proper characterization of heterogeneity¹⁷. In meta-analyses that aim to estimate drug efficacy for a certain condition, prediction intervals provide information about its possible effects in a new, similar sample to the ones in the study pool. IntHout, Ioannidis, Rovers and Goeman report that prediction intervals which include the null value suggest that intervention effects could be null or even in the opposite direction of the intended effect¹¹. In a meta-analysis, reporting only a confidence interval around an overall pooled estimate may mask the possibility that, in some setting, treatments are ineffective¹². In the context of diagnostic accuracy, both TPR and FPR are sought to be different than 0.5. If either measure were to take on this value, the test would distinguish cases of major depression no better than a coin flip. Based on the prediction intervals in this study, it seems unlikely that in settings similar to the ones in the 58 studies available, both TPR and FPR are equal to 0.5. Prediction intervals have been reported to also aid in drawing conclusions from studies of varying size, instead of relying on the results of large studies¹⁸.

The present study had the advantage of access to a sizable data set of individual participant data collected from a large number of studies. The presence of heterogeneity was evident from preliminary analyses and later corroborated by graphical inspection of the prediction regions.

Conclusions

The use of prediction regions allowed us to shed light regarding previously unseen trends in the data. In the present analysis, the varying correlations between TPR and FPR as more studies were added to the model and across subgroups were of special interest as they had noticeable effects on the shape of the prediction regions. The present analysis used prediction regions to investigate heterogeneity in the study pool and revealed greater heterogeneity regarding TPR estimates as compared to FPR estimates. Prediction regions display the full range of variability in the data, which is essential for making predictions, and uncovering trends which may have been otherwise unknown to the researcher; thus, supporting the recommendation by authors of using prediction regions as the most adequate summary of the results of a meta-analysis.

Abbreviations

BREM

Bivariate random effects model

PHQ-9

Patient health questionnaire-9

IPDMA

Individual participant data meta-analysis

FPR

False positive rate (1 − specificity)

TPR

True positive rate (sensitivity)

Author contributions

A.L.M.V.L., P.M.B., Y.W., B.Levis, J.B., P.C., S.G., J.P.A.I., L.A.K., D.M., S.B.P., I.S., R.C.Z., B.D.T., and A.Benedetti were responsible for the study conception and design. J.B. and L.A.K. designed and conducted database searches to identify eligible studies. B.D.T., S.B.P., D.H.A., B.A., L.A., H.R.B., A.Beraldi, C.H.B., P.B., G.C., M.H.C., J.C.N.C., R.C., N.C., K.C., Y.C., J.M.G., J.D., J.R.F., F.H.F., D.F., B.G., F.G.S., C.G.G., B.J.H., M.Härter, U.H., L.H., S.E.H., M.Hudson, T.H., M.Inagaki, K.I., N.J., M.E.K., K.M.K., Y.K., F.L., S.I.L., M.L., S.R.L., B.Löwe, L.M., A.M., S.M.S., T.N.M., K.M., F.L.O., V.P., B.W.P., P.P., A.P., K.R., A.G.R., I.S.S., J.S., A.Sidebottom, A.Simning, L.S., S.C.S., P.L.L.T., A.T., C.M.v.d.F.C., H.C.v.W., P.A.V., J.W., M.A.W., K.W., M.Y., and Y.Z. contributed primary datasets that were included in this study. A.L.M.V.L., P.M.B., Y.W., B.Levis, B.D.T., Y.S., C.H., A.K., D.N., Z.N., M.Imran, D.B.R., K.E.R., N.S., and M.A. contributed to data extraction and coding for the meta-analysis. A.L.M.V.L., P.M.B., Y.W., B.D.T., and A.Benedetti contributed to the data analysis and interpretation. A.L.M.V.L., P.M.B., Y.W., B.D.T., and A.Benedetti contributed to drafting the manuscript. All authors provided a critical review and approved the final manuscript. ABenedetti is the guarantor; she had full access to all the data in the study and take responsibility for the integrity of the data and the accuracy of the data analyses. As all collected data had been previously anonymized, no consent for publication was required for this research.

Funding

This study was funded by the Canadian Institutes of Health Research (CIHR, KRS-134297). Mr. López Malo Vázquez de Lara was supported by the Mitacs Globalink Research Internship Program. Mr. Bhandari was supported by a studentship from the Research Institute of the McGill University Health Centre. Drs. Wu and Levis were supported by Fonds de recherche du Québec—Santé (FRQS) Postdoctoral Training Fellowships. Drs. Thombs and Benedetti were supported by a FRQS researcher salary award. Ms. Neupane was supported by G.R. Caverhill Fellowship from the Faculty of Medicine, McGill University. Ms. Rice was supported by a Vanier Canada Graduate Scholarship. Ms. Riehm and Ms. Saadat were supported by CIHR Frederick Banting and Charles Best Canada Graduate Scholarship master’s awards. The primary studies by Fiest et al. and Amoozegar et al. were supported by the Cumming School of Medicine, University of Calgary, and Alberta Health Services through the Calgary Health Trust, as well as the Hotchkiss Brain Institute. Dr. Patten was supported by a Senior Health Scholar award from Alberta Innovates Health Solutions. Dr. Jetté was supported by a Canada Research Chair in Neurological Health Services Research and an AIHS Population Health Investigator Award. Collection of data for the study by Arroll et al. was supported by a project grant from the Health Research Council of New Zealand. Data collection for the study by Ayalon et al. was supported from a grant from Lundbeck International. The primary study by Khamseh et al. was supported by a grant (M-288) from Tehran University of Medical Sciences. The primary study by Bombardier et al. was supported by the Department of Education, National Institute on Disability and Rehabilitation Research, Spinal Cord Injury Model Systems: University of Washington (Grant No. H133N060033), Baylor College of Medicine (Grant No. H133N060003), and University of Michigan (Grant No. H133N060032). Collection of data for the primary study by Kiely et al. was supported by National Health and Medical Research Council (Grant Number 1002160) and Safe Work Australia. Dr. Butterworth was supported by Australian Research Council Future Fellowship (FT130101444). Collection of data for the primary study by Zhang et al. was supported by the European Foundation for Study of Diabetes, the Chinese Diabetes Society, Lilly Foundation, Asia Diabetes Foundation and Liao Wun Yuk Diabetes Memorial Fund. Dr. Conwell received support from NIMH (R24MH071604) and the Centers for Disease Control and Prevention (R49 CE002093). Collection of data for the primary study by Delgadillo et al. was supported by grant from St. Anne’s Community Services, Leeds, United Kingdom. Collection of data for the primary study by Fann et al. was supported by Grant RO1 HD39415 from the US National Center for Medical Rehabilitation Research. The primary study by Fischer et al. was funded by the German Federal Ministry of Education and Research (01GY1150). Data for the primary study by Gelaye et al. was supported by grant from the NIH (T37 MD001449). Collection of data for the primary study by Gjerdingen et al. was supported by grants from the NIMH (R34 MH072925, K02 MH65919, P30 DK50456). The primary study by Eack et al. was funded by the NIMH (R24 MH56858). Collection of data for the primary study by Hobfoll et al. was made possible in part from grants from NIMH (RO1 MH073687) and the Ohio Board of Regents. Dr. Hall received support from a grant awarded by the Research and Development Administration Office, University of Macau (MYRG2015-00109-FSS). Collection of data provided by Drs. Härter and Reuter was supported by the Federal Ministry of Education and Research (Grants No. 01 GD 9802/4 and 01 GD 0101) and by the Federation of German Pension Insurance Institute. The primary study by Henkel et al. was funded by the German Ministry of Research and Education. The primary study by Hides et al. was funded by the Perpetual Trustees, Flora and Frank Leith Charitable Trust, Jack Brockhoff Foundation, Grosvenor Settlement, Sunshine Foundation and Danks Trust. Data for the study by Razykov et al. was collected by the Canadian Scleroderma Research Group, which was funded by the CIHR (FRN 83518), the Scleroderma Society of Canada, the Scleroderma Society of Ontario, the Scleroderma Society of Saskatchewan, Sclérodermie Québec, the Cure Scleroderma Foundation, Inova Diagnostics Inc., Euroimmun, FRQS, the Canadian Arthritis Network, and the Lady Davis Institute of Medical Research of the Jewish General Hospital, Montréal, QC. Dr. Hudson was supported by a FRQS Senior Investigator Award. Collection of data for the primary study by Hyphantis et al. (2014) was supported by grant from the National Strategic Reference Framework, European Union, and the Greek Ministry of Education, Lifelong Learning and Religious Affairs (ARISTEIA-ABREVIATE, 1259). The primary study by Inagaki et al. was supported by the Ministry of Health, Labour and Welfare, Japan. The primary study by Twist et al. was funded by the UK National Institute for Health Research under its Programme Grants for Applied Research Programme (Grant Reference Number RP-PG-0606-1142). The primary study by Lamers et al. was funded by the Netherlands Organisation for Health Research and development (Grant Number 945-03-047). The primary study by Liu et al. (2011) was funded by a grant from the National Health Research Institute, Republic of China (NHRI-EX97-9706PI). The primary study by Lotrakul et al. was supported by the Faculty of Medicine, Ramathibodi Hospital, Mahidol University, Bangkok, Thailand (Grant Number 49086). The primary studies by Osório et al. (2012) were funded by Reitoria de Pesquisa da Universidade de São Paulo (Grant Number 09.1.01689.17.7) and Banco Santander (Grant Number 10.1.01232.17.9). Dr. Osório was supported by Productivity Grants (PQ-CNPq-2-Number 301321/2016-7). Dr. Bernd Löwe received research grants from Pfizer, Germany, and from the medical faculty of the University of Heidelberg, Germany (Project 121/2000) for the study by Gräfe et al. Collection of data for the primary study by Williams et al. was supported by a NIMH grant to Dr. Marsh (RO1-MH069666). The primary study by Mohd Sidik et al. was funded under the Research University Grant Scheme from Universiti Putra Malaysia, Malaysia and the Postgraduate Research Student Support Accounts of the University of Auckland, New Zealand. The primary study by Santos et al. was funded by the National Program for Centers of Excellence (PRONEX/FAPERGS/CNPq, Brazil). The primary study by Muramatsu et al. (2007) was supported by an educational grant from Pfizer US Pharmaceutical Inc. Collection of primary data for the study by Pence et al. was provided by NIMH (R34MH084673). The primary study by Persoons et al. was partly funded by a grant from the Belgian Ministry of Public Health and Social Affairs and supported by a limited grant from Pfizer Belgium. The primary study by Picardi et al. was supported by funds for current research from the Italian Ministry of Health. The primary study by Rooney et al. was funded by the United Kingdom National Health Service Lothian Neuro-Oncology Endowment Fund. Dr. Shaaban was supported by funding from Universiti Sains Malaysia. The primary study by Sidebottom et al. was funded by a grant from the United States Department of Health and Human Services, Health Resources and Services Administration (Grant Number R40MC07840). Simning et al.’s research was supported in part by grants from the NIH (T32 GM07356), Agency for Healthcare Research and Quality (R36 HS018246), NIMH (R24 MH071604), and the National Center for Research Resources (TL1 RR024135). Dr. Stafford received PhD scholarship funding from the University of Melbourne. Collection of data for the studies by Turner et al. (2012) were funded by a bequest from Jennie Thomas through the Hunter Medical Research Institute. The study by van Steenbergen-Weijenburg et al. was funded by Innovatiefonds Zorgverzekeraars. The study by Wittkampf et al. was funded by The Netherlands Organization for Health Research and Development (ZonMw) Mental Health Program (nos. 100.003.005 and 100.002.021) and the Academic Medical Center/University of Amsterdam. Dr Vöhringer was supported by the Fund for Innovation and Competitiveness of the Chilean Ministry of Economy, Development and Tourism, through the Millennium Scientific Initiative (Grant Number IS130005). The primary study by Thombs et al. was done with data from the Heart and Soul Study. The Heart and Soul Study was funded by the Department of Veterans Epidemiology Merit Review Program, the Department of Veterans Affairs Health Services Research and Development service, the National Heart Lung and Blood Institute (R01 HL079235), the American Federation for Aging Research, the Robert Wood Johnson Foundation, and the Ischemia Research and Education Foundation.No other authors reported funding for primary studies or for their work on the present study.

Data availability

Requests to access data should be made to the corresponding author at andrea.benedetti@mcgill.ca.

Competing interests

All authors have completed the ICJME uniform disclosure form at www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: no support from any organisation for the submitted work; no financial relationships with any organisations that might have an interest in the submitted work in the previous three years with the following exceptions: Dr. Chan J CN is a steering committee member and/or consultant of Astra Zeneca, Bayer, Lilly, MSD and Pfizer. She has received sponsorships and honorarium for giving lectures and providing consultancy and her affiliated institution has received research grants from these companies. Dr. Hegerl declares that within the last three years, he was an advisory board member for Lundbeck and Servier; a consultant for Bayer Pharma; a speaker for Pharma and Servier; and received personal fees from Janssen Janssen and a research grant from Medice, all outside the submitted work. Dr. Inagaki declares that he has received a grant from Novartis Pharma, and personal fees from Meiji, Mochida, Takeda, Novartis, Yoshitomi, Pfizer, Eisai, Otsuka, MSD, Technomics, and Sumitomo Dainippon, all outside of the submitted work. Dr. Ismail declares that she has received honorarium for speaker fees for educational lectures for Sanofi, Sunovion, Janssen and Novo Nordisk. All authors declare no other relationships or activities that could appear to have influenced the submitted work. No funder had any role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; and decision to submit the manuscript for publication.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-023-36129-w.