Abstract
Purpose
The administration of safe, high-quality radiation therapy requires the systematic completion of a series of steps from computed tomography simulation, physician contouring, dosimetric treatment planning, pretreatment quality assurance, plan verification, and, ultimately, treatment delivery. Nevertheless, due consideration to the cumulative time required to complete each of these steps is often not given sufficient attention when determining patient start date. We set out to understand the systemic dynamics as to how varying patient arrival rate can affect treatment turnaround times using Monte Carlo simulations.
Methods and Materials
We developed a process model workflow for a single physician, single linear accelerator clinic that simulated arrival rates and processing times for patients undergoing radiation treatment using the AnyLogic Simulation Modeling software (AnyLogic 8 University edition, v8.7.9). We varied the new patient arrival rate from 1 to 10 patients per week to understand the effect of treatment turnaround times from simulation to treatment. We used processing-time estimates determined in prior focus studies for each of the required steps.
Results
Altering the number of patients simulated from 1 per week to 10 per week resulted in a corresponding increase in average processing time from simulation to treatment from 4 to 7 days. The maximum processing time for patients from simulation to treatment ranged from 6 to 12 days. To compare individual distributions, we used the Kolmogorov-Smirnov statistical test. We found that altering the arrival rate from 4 patients per week to 5 patients per week resulted in a statistically significant change in the distributions of processing times (P = .03).
Conclusions
The results of this simulation-based modeling study confirm the appropriateness of current staffing levels to ensure timely patient delivery while minimizing staff burnout. Simulation modeling can help guide staffing and workflow models to ensure timely treatment delivery while ensuring quality and safety.
Introduction
The administration of safe, high-quality radiation therapy requires the systematic completion of a sequence of steps: therapeutic (computed tomography [CT]) simulation, physician contouring, dosimetric treatment planning, pretreatment quality assurance, plan verification, and, ultimately, treatment delivery.1 This series is constrained by strict precedence relationships: the start of a task requires completion of a preceding step.
The optimal scheduling of patients involves an understanding of processing times of each individual step. We believe such an initiative is an important element of quality and safety. Although timely cancer care is important for optimal patient outcomes,2 overly ambitious turnaround times can result in burnout and medical errors.3 Although professional organizations have established guidelines for acceptable staffing levels for radiation oncology clinics,4 understanding the balance between the potentially competing factors is an important aspect for care delivery.
Estimates regarding reasonable processing times for each step in the treatment planning workflow have been previously established.5 Monte Carlo simulation modeling allows for evaluation of hypothetical scenarios that cannot be feasibly tested in real world settings. We used AnyLogic Simulation Modeling (AnyLogic 8 University edition, v8.7.9) software to develop a process modeling workflow to understand how changes in patient volume can affect total processing times for individual patients and to try to predict levels of patient volume that would result in strain on the clinic.
Methods and Materials
A process model simulation was developed using AnyLogic Software. A sequential process model was developed with a linearly defined precedence relationship. Details of AnyLogic modeling are described elsewhere.6 The schematic for the workflow model developed is shown in Fig. 1. Our clinic is an academically affiliated satellite center with a single physician, dosimetrist, and treatment machine. Physics support is provided by the primary academic center with at least 1 day a week of onsite coverage, with additional days to be coordinated as needed. For the purposes of this simulation study, we aggregated pretreatment quality assurance and plan-verification processing times into a single step.
Figure 1.
Overall schematic of workflow model.
Using processing times determined in our clinic, we tested our model clinic by varying the patient arrival rate (simulation rate) between 1 to 10 new patient simulations per week while holding our staffing levels constant. The simulation model was run for the entire calendar year 2022 (January 1, 2022 through December 31, 2022), and processing-time distributions of the last 100 patients who completed treatment in the virtual model were captured for analysis. Processing-time estimates were provided in hours, but the model was developed to account for an 8-hour workday or a 40-hour workweek. Events that were not completed during the business day would be queued to be completed the following day.
For the purposes of simulation modeling, we assumed that variation in processing times at each step followed a triangular distribution. A triangular distribution, abbreviated triangulara,m,b, models the randomness of a continuous variable observed within a strict range between minimum value (a) and maximum value (b), between which falls a mode or most likely value (m). For example, we estimated that patient contours might be completed in as little as 1 hour, are most likely to require 4 hours, and will take no more than 8 hours (1 business day), indicating triangular (1,4,8) to model the variation in contouring process completion times. We assumed that treatment planning, verification, and treatment delivery could be represented by the following distributions, respectively (in hours): triangular (2, 4, 16), triangular (8, 16, 60), and triangular (0.25,0.5,1). To account for the limitations of available staff, we defined a resource pool for physicians, dosimetry, physics, and machines (Fig. 1), which precludes more than 1 patient receiving service simultaneously at 3 of these steps. However, we established a resource pool of 2 for the treatment planning phase, as it is possible for the dosimetrist to simultaneously work on a second treatment plan during the process of plan optimization. In the case of verification, the resource pool allowed up to 2 patients to be in progress at any given moment, modeling the fact that the physicist and a radiation therapist can be completing their specific tasks concurrently. Statistical differences between the distributions of patient processing times were evaluated using the Kolmogorov-Smirnov test.
Results
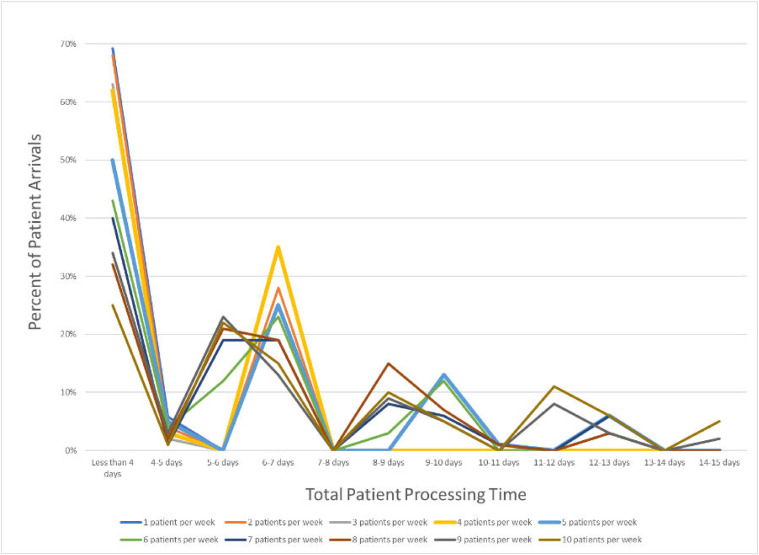
In this study, patient processing time is defined as total dwell time in the clinic, from the patient's arrival through to the completion of the first fraction of treatment. Average and maximum patients processing time at differing arrival rates is shown in Table 1. Altering the number of patients simulated from 1 to 10 patients per week resulted in a corresponding increase average processing time from 4 to 7 working days. The maximum processing time for patient from simulation to treatment increased from 6 to 14 working days. The distribution of the variation in processing times for each arrival rate is shown in Fig. 2. As an example, over 60% of patients complete treatment within 4 working days under the condition of 4 patient arrivals per week, but should such a patient require longer, the next most likely duration is 6 to 7 working days. These discontinuities are created by queuing, in that the first group represents patients who proceeded smoothly through the steps represented in Fig. 1, whereas members of the second group likely had to wait at pause once for capacity to clear in the step ahead.
Table 1.
Patient processing times at varying levels of patient arrival
| Patients per wk | Avg processing time (h) | Avg processing time (d) | Max processing time (h) | Max processing time (d) | KS test statistic | P value |
|---|---|---|---|---|---|---|
| 1 | 33.7 | 4 | 48.964 | 6.2 | - | - |
| 2 | 34.0 | 4 | 48.894 | 6.2 | 0.0854 | .9643 |
| 3 | 35.2 | 4 | 49.478 | 6.2 | 0.1 | .6994 |
| 4 | 35.3 | 4 | 49.26 | 6.2 | 0.08 | .9062 |
| 5 | 44.5 | 5 | 97.401 | 12.2 | 0.2 | .0366 |
| 6 | 43.8 | 5 | 96.874 | 12.2 | 0.09 | .8127 |
| 7 | 45.9 | 5 | 96.905 | 12.2 | 0.1 | .6994 |
| 8 | 47.4 | 5 | 112.681 | 14.1 | 0.1 | .6994 |
| 9 | 49.2 | 6 | 113.564 | 14.2 | 0.1147 | .5236 |
| 10 | 56.3 | 7 | 113.564 | 14.2 | 0.16 | .1545 |
Abbreviations: KS test = Kolmogorov-Smirnov statistical test.
Figure 2.
Distribution of processing time (percent of patients) under varying patient arrival rates.
To compare individual distributions at each level of patient arrival rate, we used the Kolmogorov-Smirnov statistical test and compared with the preceding distribution (2 patients per week compared with 1 patient per week, 3 patients per week compared with 2 patients per week, etc). We found that increasing the arrival rate from 4 patients per week to 5 patients per week resulted in the only significant change in the distributions of processing times (P = .03) as maximum processing time increased from approximately 6 days to 12 days, or from approximately 1 week to 2 weeks. No other significant changes in the distribution of processing times based on incremental increases to the arrival rate were observed (Table 1).
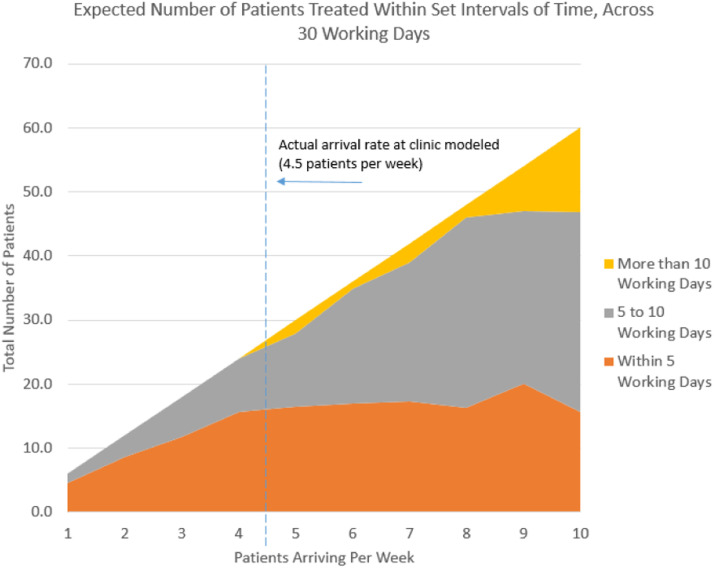
Maximum observed patient processing times are particularly significant in this setting. In the simulation, particularly long processing times can represent treatment activity that, in reality, would more likely be done outside of normal clinic hours. Thus, the longest processing times in these results are a proxy for what would be strain on the actual clinic. Using the results, Fig. 3 shows the count of patients expected over 30 days whose processing times fall within various intervals, including beyond 10 working days.
Figure 3.
Expected number of patients treated within set intervals of time across 30 working days.
Discussion
The results of this computer-based simulation study are consistent with our experience that patients can be treated within 1 to 2 weeks of CT simulation. Our facility treats approximately 250 patients per calendar year, corresponding to an arrival rate that is between 4 to 5 patients per week. Figure 3 highlights how our actual arrival rate is at an inflection point of observed distributional change. This study provides insight how the actual clinic is configured to handle a robust range of volume around its current observed load, but this robustness abruptly ends should arriving patients exceed 8 per week for any sustained amount of time.
A limitation of any simulation modeling study is that the results are inherently tied to the assumptions that are built into the model. We used our focus group data when constructing these assumptions and confirmed that actual turnaround times are consistent with those seen in the model. However, simulation modeling can only provide results based on the simulation logic and inputs into the model and thus does not account for external factors that affect processing times in reality. This computational model assumes that processing times are independent of workload, though diminishing returns would occur at high arrival rates. The model does not account for the “human” toll that would be associated with continual increased workload. Although our clinic will encounter specific weeks where there are 10 or more CT simulations, sustaining this rate consistently for a year would not be realistic.
Another limitation of our study is the assumption that processing time is independent of plan type and patient acuity. For example, a patient with a high medical acuity may warrant diversion of all departmental resources to allow immediate treatment. Additionally, patient start date can be delayed because of patient preference or coordination with complementary therapies. Such variation is not accounted for in our first-in-first-out processing model. Furthermore, the plan complexity could affect turnaround time. Nonetheless, we believe we have approximated this condition by constructing the model such that processing times follow a triangular distribution to account for the variability associated with plan complexity (3-dimensional conformal radiation therapy vs intensity modulated radiation therapy or volumetric arc therapy) over the course of a year. Overall, we believe that this limitation would not significantly affect the results of this simulation-based study.
We also recognize that our model is applicable only to our clinic model. However, it is feasible to model larger clinics by incorporating correspondingly larger resource pools with additional staffing and higher patient arrival rates. Nevertheless, it is reasonable to assume that a clinic of greater resources and complexity is still likely to have a “tipping point” in the face of increasing patient load. Additionally, we believe that the larger purpose of this study is to promote an open conversation about workflow processing times to reduce burnout associated with overly ambitious turnaround times.
Conclusions
We believe that this study demonstrates how simulation modeling can be used to study clinical operations of a Radiation-Oncology clinic. Furthermore, we hope that by evaluating system dynamics through simulation models, we can help promote open coversations among team members to reduce burnout.
Disclosures
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Sources of support: This work had no specific funding.
No patient or clinical information was used in this study. Data obtained from Monte-Carlo simulation is available upon request.
References
- 1.The American Society for Radiation Oncology. Safety is no accident: A framework for quality radiation oncology care. Available at:https://www.astro.org/Patient-Care-and-Research/Patient-Safety/Safety-is-no-Accident. Accessed June 7, 2022.
- 2.Hanna TP, King WD, Thibodeau S, et al. Mortality due to cancer treatment delay: Systematic review and meta-analysis. BMJ. 2020;371:m4087. doi: 10.1136/bmj.m4087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Patel RS, Bachu R, Adikey A, Malik M, Shah M. Factors related to physician burnout and its consequences: A review. Behav Sci. 2018;8:98. doi: 10.3390/bs8110098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.American College of Radiology. Personnel: Radiation oncology (revised 8-2-2022). Available at:https://accreditationsupport.acr.org/support/solutions/articles/11000049781-personnel-radiation-oncology-revised-8-2-2022-. Accessed March 27, 2023.
- 5.Chowdhry VK, Daniel Z, Hackett R. Departmental quality initiative to establish turnaround times from simulation to treatment. Tech Innov Patient Support Radiat Oncol. 2021;19:37–40. doi: 10.1016/j.tipsro.2021.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Borshchev Alexander. AnyLogic; Oakbrook Terrace, IL: 2022. The Big Book of Simulation Modeling: Multimethod Modeling With AnyLogic 8. [Google Scholar]