Epigenetics as a mediator of plasticity in cancer

Abstract

The concept of an epigenetic landscape describing potential cellular fates arising from pluripotent cells, first advanced by Conrad Waddington, has evolved in light of experiments showing non-deterministic outcomes of regulatory processes and mathematical methods for quantifying stochasticity. In this Review we discuss modern approaches to epigenetic and gene regulation landscapes and the associated ideas of entropy and attractor states, illustrating how their definitions are both more precise and relevant to understanding cancer etiology and the plasticity of cancerous states. We address the interplay between different types of regulatory landscapes, and how their changes underlie cancer progression. We also consider the roles of cellular aging and intrinsic and extrinsic stimuli in modulating cellular states, and how landscape alterations can be quantitatively mapped onto phenotypic outcomes, and thereby used in therapy development.

Graphical Abstract

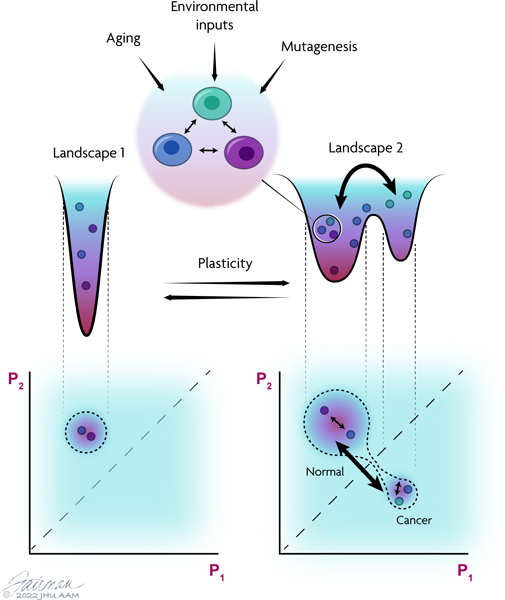
Summary sentence

A Review that discusses how epigenetic stochasticity can connect mutations and environmental perturbations to the phenotypic plasticity that drives tumor progression and therapeutic resistance.

Tumor cell heterogeneity and phenotypic plasticity have long been known to be principal drivers of invasion and metastasis (1). Complex and diverse behaviors displayed by cancer cells frequently involve coordinated expression of multiple genes, constituting programs that may be very distinct from those defining the phenotypes of the tissue of origin. Since oncogenic transformations are frequently accompanied by extensive mutagenesis, analysis of phenotypic heterogeneity displayed by cancer cell populations has typically been ascribed to the emergence of multiple genetically distinct clonal cell subpopulations within the same tumor (2). This genetic heterogeneity should be distinguished from phenotypic heterogeneity (i.e., emergence of stable phenotypic states in an isogenic population) and phenotypic plasticity (i.e., the ability of cells to adopt different phenotypic states transiently). Phenotypic plasticity is thought to underlie such complex phenotypic changes as epithelial-mesenchymal transition (EMT), drug resistance, and increased cell proliferation (3–6). Therefore, although genetic mutations may increase the probability of new phenotypic states, they may not completely define them and may not be strictly necessary for their emergence.

Elucidation of the interplay between epigenetic states and regulation of gene expression is crucial for our understanding of phenotypic plasticity. Multiple questions remain regarding coupling of these regulatory mechanisms. For example, since many regulators of gene expression may also have epigenetic modification capabilities, e.g., by recruiting DNA methylases and histone acetyltransferases, it is not clear whether epigenetic control might be viewed as a constituent part of transcriptional regulation, or it has independent and essential roles not fully predictable by the analysis of gene networks alone.

In this Review, we argue that epigenetic mechanisms can have several key functions that are frequently not evident from traditional quantitative approaches involving the analysis of transcriptional regulation or RNA and protein stability. In particular, epigenetic regulation may have a critical role in regulating variability of gene expression, accounting for variance in the current cellular states and emergence of new ones. Recent methodological advances now allow us to explicitly define and measure epigenetic landscapes that, along with gene regulation landscapes, can be used to much more precisely understand the etiology of cancer, and better understand the mechanisms underlying phenotypic plasticity and heterogeneity.

Theoretical approaches to describe genetic and epigenetic landscapes

Regulatory networks impose complex inter-dependencies on gene expression, which are commonly modeled using ordinary differential equations (ODEs) (Box 1, Equation 1). A related concept of “landscape” introduced by Waddington and further elaborated mathematically (7–10) has been instructed for simpler and well characterized systems, but has faced important challenges. In particular, molecular interactions constituting regulatory networks are frequently unknown and may be restricted by epigenetic mechanisms, such as DNA methylation. Furthermore, these interactions and networks are subject to biomolecular ‘noise’ or variability of molecular concentrations or alterations of molecular states (11–13), which are crucial for non-deterministic many-fate behaviors of the system. Although the Waddington landscape is frequently interpreted as the epigenetic landscape, these concepts may no longer be fully synonymous. Indeed, whereas previously the term “epigenetic” referred to any mechanism outside traditional gene expression control, today, it more commonly refers to a specific set of regulatory processes, affecting in particular DNA methylaiton and chromatin modifications.

Box 1. Mathematical analysis of stochastic biological systems.

Biological systems are governed by underlying interactions that could be described mathematically. These interactions can be stochastic due to the variability of the participating elements (molecular modifications, molecular and cellular numbers, etc.). The mathematical approach frequently used to capture stochastic interactions is the Langevin approximation based on the Ordinary Differential Equations (ODEs) describing temporal dynamics of variables $x_i$, using the function $f(\mathit{x})$ of the vector $\mathit{x}$ of all variables $x_j$_, with the added noise terms $\eta \left(x_i\right)$:

$$\frac{d{x}_i}{dt}=f_i\left(\mathit{x}\right)+{\eta }_i\left(x_i\right)$$ (1)

An alternative but equivalent description that is particularly useful for systems with very small values of $x_i$ that are expressed as whole numbers is to consider the dynamics of probabilities of $x_i$, rather than the dynamics of $x_i$ themselves. This is done using the so-called Master Equation based on the assumption that the underlying processes are Markovian (memoryless):

$$\frac{dP(x_i)}{dt}={\sum }_j{k}_{ij}P\left(x_j\right)$$ (2)

Unfortunately, other than for a few relatively simple systems, the mechanistic information that would define the functions $f(\mathit{x})$ and $k_{ij}$ is largely incomplete for most biological systems. Therefore, it is frequently hard to use these models for real biological systems to characterize their dynamic behavior and thus landscapes. Instead, it has proven easier to experimentally measure the distributions $P\left(x_i\right)$. Therefore, the problem can be inverted, i.e., reconstruct the underlying regulatory landscape from the knowledge of $P\left(x_i\right)$. The recipe for doing so is provided by statistical mechanics (Boltzmann-Gibbs distribution), and in particular the relationship between the energy $U\left(x_i\right)$ associated with a specific $x_i$ and the probability of this value of the variable (the energy here is quasi-potential, corresponding to measuring the energy in units of $k_{B}T$, i.e., the product of the boltzmann constant and temperature):

$$U\left(x_i\right)= -lnP\left(x_i\right)-ln\left({\sum }_j{e}^{-U(x_j)}\right)$$ (3)

If the distribution of different values that can be taken by variables x_i is constant (i.e., the landscape does not change) then the second term in (3) is constant and, since the energy $U\left(x_i\right)$ is only determined up to a constant, it can be omitted for the analysis of a constant landscape:

$$U\left(x_i\right) \simeq -lnP\left(x_i\right)$$ (4)

The relationship (3) can be used to directly define the energy (quasi-potential) landscape corresponding to the gene expression and epigenetic landscapes and to relate it to the entropy of the system, again up to a constant:

$$H\left(x\right)=-{{\displaystyle \sum }}_{i}P\left(x_i\right)logP\left(x_i\right) \simeq -{{\displaystyle \sum }}_{i}P\left(x_i\right) lnP\left(x_i\right) \simeq <U\left(x_i\right)>$$ (5)

This relationship, linking the entropy and average energy $<U>$ for a system, emphasizes the ‘global’ nature of the entropy measure, involving summation over multiple states. Thus, as illustrated in Fig.1, different landscapes may have the same entropy and thus cannot be uniquely distinguished using this function of the state. Conversely, the distributions captured by $P\left(x_i\right)$ and $U\left(x_i\right)$, can be more informative.

Finally, the mutual information is defined as the change of entropy (and thus the underlying landscape) of a state, $\Delta H\left(x\right)$, given a regulatory event or a signal. If the entropy decreases the mutual information is positive, which provides a measure of comparison between two distributions. Another important measure of dissimilarity between two distributions $P\left(x_i\right)$ and $Q\left(x_i\right)$ is the frequently used Kullback-Leibler (KL) divergence:

$$D_{KL}(\left.P\right|\left|Q\right.\text{)}={{\displaystyle \sum }}_{i}P\left(x_i\right)\text{log}\left(\frac{P\left(x_i\right)}{Q\left(x_i\right)}\right)$$ (6)

Mutual information is thus the KL divergence between the joint distribution of the variable values prior and following the event (or signal) and the product of their marginal distributions. A symmetrized version of the KL divergence of particular value in comparing epigenetic landscapes is the Jensen-Shannon distance, defined as:

$$\text{JSD}(P\parallel Q\text{)}=\frac{1}{2} D_{KL}\text{(P}\parallel \text{M)}+\frac{1}{2}{D}_{KL}\text{(}Q\parallel M\text{) where }M=\frac{1}{2}\left(P+Q\right)$$ (7)

The probabilistic nature of biochemical processes has been historically addressed in several ways. Most simply, added noise might be described by extending the ODE description using the Langevin approach (Box 1, Equation 1). However, this approach can break down if the number of molecules becomes very small, making the functions defining the ODE system behavior discontinuous. This consideration drove a conceptual quantum leap, akin to transition from classical to quantum mechanics in physics. In this new view, instead of describing the biological variables, such as molecular concentrations, one operates with the probabilities that system-defining variables take on certain values. This probabilistic dynamics is captured by the Master Equation, based on the Markovian assumption about the system dynamics (Box 1, Equation 2). However, while appearing superficially simple, such equations require advanced computational resources to solve or estimate, although some success has been achieved for simpler cases (14–16). A fundamental challenge facing both the Langevin and Master Equation approaches is the lack of complete knowledge of the mechanisms governing interactions between system variables. To date, relatively few biological networks have been fully characterized, and frequently this mechanistic characterization is only semi-quantitative. It is therefore difficult to theoretically or computationally predict the probability distributions of different molecular and cellular states. However, one can now directly experimentally estimate these probabilities (17–19) and thus attempt to solve an inverse problem of reconstructing the mechanisms underlying gene expression regulation and the corresponding genetic and epigenetic landscapes from experimental data.

The inferences based on experimentally obtained probability distributions can be put on a solid theoretical foundation that provide specific meanings to the notions of epigenetic and genetic landscapes, distinct from those implied by Waddington. Critical to this approach is the fundamental connection of potential energy and probability distributions provided by the Gibbs-Boltzmann approach (Box 1, Equations 3 and 4), which are particularly useful for definition and analysis of landscape attractors corresponding to specific coherent molecular, cellular, and phenotypic states. Specifically, this approach associates the probability of any outcome, e.g., gene expression or DNA methylation pattern and the corresponding phenotypic outcome, with a generically defined quasi-potential energy, a term adapted from physics to describe the origin of probability distributions of the possible cellular states (states with lower energy are occupied with higher probability; see Fig. 1A, and the definition in Box 1, Equation 3). This association allows one to define the corresponding genetic (gene expression) or epigenetic (e.g., DNA methylation markers) landscapes as the quasi-potential energy distributions. This landscape definition is consistent with the one implied by the Waddingtonian ODE approach, affording easy interpretation and visualization. The attractors within this landscape representation would be seen as the values of biological variables for which the local and global energy minima would be reached, thus constituting states with high relative probability values (Fig. 1A). The stability of the attractor is further defined by such landscape characteristics as the depth and width of the corresponding energy wells, and proximity, and thus accessibility, of other attractors (20). Increased variability or noise makes energy wells effectively more shallow, thus widening the distribution of biological variables (21). This allows cellular networks to explore multiple states across different attractors. The local energy (landscape) minima may be realized in different cells within a population or could only be accessible in specific developmental, physiological or pathological situations. Below we illustrate and discuss these and other important ideas, such as the entropy associated with the whole landscape and specific attrctor states, and the information associated with changes of this entropy (Box 1), particularly in the context of emergence and progression to cancer.

Figure 1. Gene expression and epigenetic landscapes control normal and cancer cell functions.

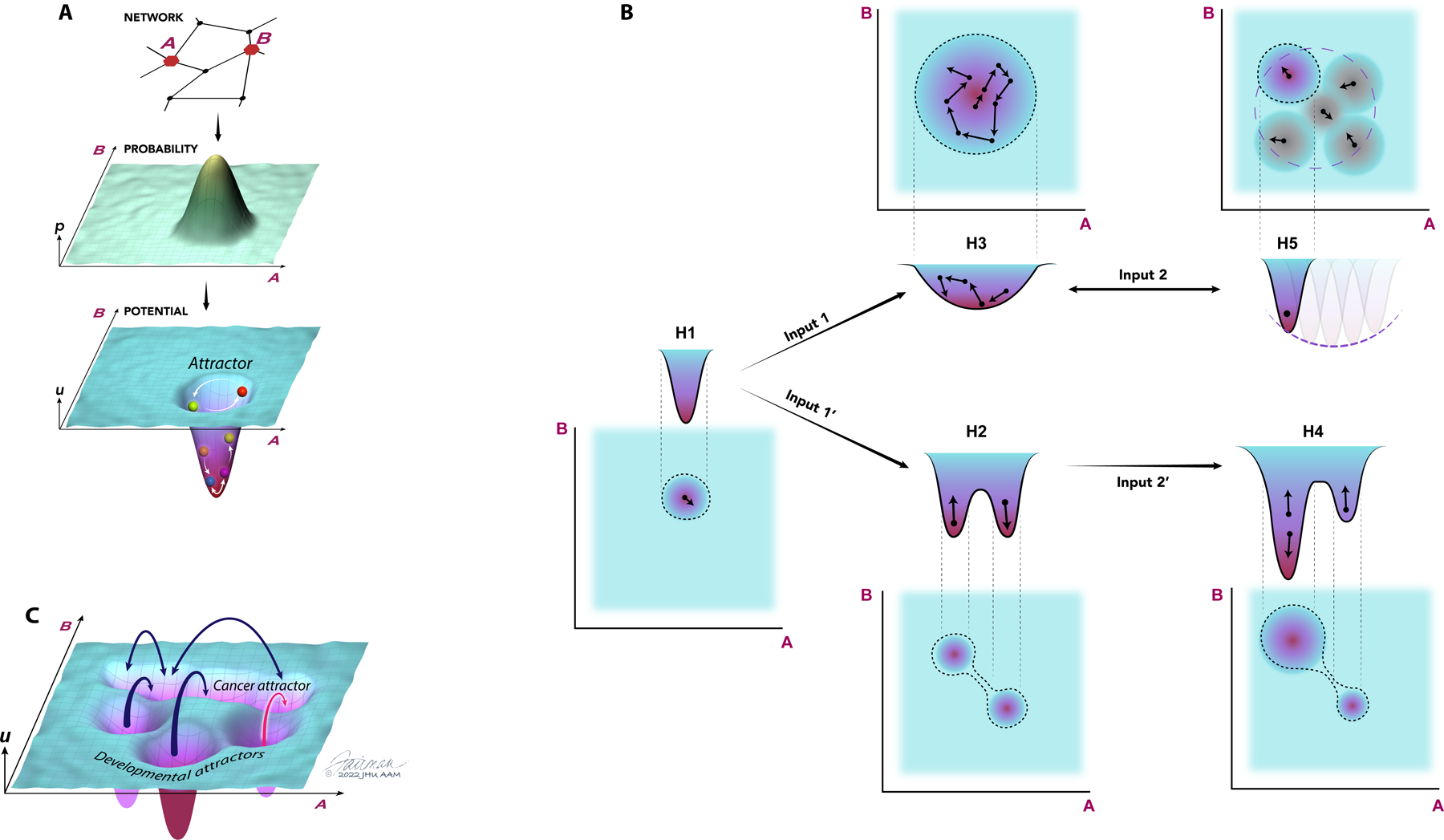
(A) Gene regulatory networks and availability of genes for expression can define the probabilistic distributions of proteins expressed within a cell population. In the example here, the network of interacting proteins that includes the molecules A and B (top) and the underlying epigenetic control determining the availability of the corresponding genes for expression define the distribution of expression of A and B (middle). This probability distribution can be experimentally measured and converted into a gene expression landscape by calculating the corresponding quasi-potential distribution (bottom, see Box). The epigenetic landscape can be similarly determined by experimentally measuring the probabilistic distributions of epi-alleles, DNA methylation marks at specific loci or by performing other measurements of epigenetic regulation across populations of cells and tissues, and then also converting these probability distributions into corresponding underlying quasi-potential landscapes. The landscape analysis allows conceptual accounting for abundance and dynamics of molecular species, shown here as a trajectory of particle inside a quasi-potential well, with the particle position defined by the current concentrations of A and B that can change probabilistically in time, with the quasi-potential wells interpreted as the landscape attractors. (B) Various scenarios of landscape alterations and the corresponding changes in the molecular distributions, shown as joint distributions of the molecules A and B and the corresponding entropies H1–5. Implementation of these scenarios in the context of carcinogens is extensively illustrated and discussed in the text. Oncogenic mutations of epigenetic modifiers and modulators or environmental inputs can lead to formation of new stable attractors with the overall entropy H2 greater than the original entropy H1 (H2>H1) generating phenotypic heterogeneity (Input 1’) or, alternatively, enlarge the existing attractor with the new entropy H3>H1, generating a more plastic state (phenotypic plasticity), with cells capable of stochastically and dynamically ‘exploring’ this attractor and thus transiently adopting different phenotypes. Note that in both cases entropy increases vs H1, and it is possible that H2=H3, thus making entropy less discriminating than the full landscape picture in the analysis of cell states. These new landscapes can be further altered by oncogenic and environmental inputs, so that one of the attractors becomes dominant (Inout 2’), associated with a lower entropy value (H4<H2), or, alternatively, with the narrowing of the wider (and more plastic) attractor (Inout 2, H5<H3). Again, it is possible that H4=H5, requiring the landscape analysis rather than entropy analysis alone for full characterization. The narrowing of the wide attractor due to either environmental or intrinsic inputs (Input 2) is frequently reversible and context dependent, further elaborating the more plastic overall state (transient nature of Input 2 described by a bidirectional arrow). The transiently occupied attractors can be simultaneously occupied by discerns cells in the population. Small arrows correspond to stochastic fluctuations of molecular concentrations within individual attractors. (C) Gene regulation and epigenetic landscapes of cancer cells can be complex and have multiple attractors, corresponding to distinct and stable cell states and phenotypes, which may be reshaped by oncogenic mutations, cell aging, environmental inputs and other perturbations, leading to mutual accessibility of the attractors, more plastic cell states and an increase in the phenotypic plasticity.

Landscape models of cancer

Gene regulatory landscapes can be evaluated from experimentally determined gene expression probability distributions, particularly those yielded by single cell RNA sequencing (scRNA-seq) data or from the analysis of multiple tissue samples (e.g., cancerous tissues from multiple patients) (Fig. 1A). The landscape attractors in these distributions correspond to groups of coordinately expressed genes and gene products, whose abundance and activity may be regulated by self-sustaining feedback interactions, endowing cells with specific phenotypic properties. Cancerous states may represent the genetic landscape attractors that are inaccessible in untransformed tissues but can be unmasked by oncogenic mutations (20, 22). This is exemplified by the emergence of the mesenchymal state in EMT (3). The Langevin ODE approach has been used to analyze a tri-stable regulatory circuit assumed to control epithelial-mesenchymal plasticity (23). Additionally, four attractor states have been proposed to control EMT, including metastatic, anti-metastatic, and two intermediate states (24). These studies illustrated putative feedback-based mechanisms of emergence of well-defined attractors in cancer-associated gene regulation landscapes. However, they were based primarily on theoretical modeling constructs that require experimental validation, whereas mechanisms, such as epigenetic regulation, may not have been included. Alternatively, the properties of experimentally measured regulatory landscapes can be inferred without imposing hypothetical mechanisms.

A key consequence of both the emergence of new attractors and elevated variability within the same attractors is the increase in the entropy of the underlying regulatory landscapes (Inputs 1 and 1’ in Fig. 1B, see Box 1). Indeed, it is consistently observed that the entropy of gene expression increases in cancer versus the corresponding non-cancerous tissue of origin, as e.g., revealed by examining gene expression data alone (25), or by integrating these data with protein interaction networks (to account for molecular interactions stabilizing the attractors) (26). A similar approach using protein-interaction networks and RNA-seq for multiple tissue samples, rather than single cells within the same sample, suggested that tumor progression is associated with increasing entropy (27). This approach was further used to link the entropy of gene expression to the pluripotency of underlying cell population (28), and to demonstrate that specific cell differentiation, in contrast to cancer emergence, could be represented by emergent attractors, associated with progressively lower variability and entropy. Consistent with this analysis, it was shown that cancer stemness may be inferred from increased entropy of the attractor defining a specific cell sub-population (28). Interestingly, this analysis revealed that decreased entropy was associated not only with cell fate-specifying molecular circuits, but also with specific cancer-related phenotypic states such as increased cell proliferation (22), implying correlated gene expression and molecular interaction of the components of the cell cycle, representing another example of a well-defined attractor in the gene expression landscape. However, this high proliferation attractor may not be fully stable, with recent studies suggesting that cells may stochastically transition into and out of a cell proliferation state (6, 29). Other studies further pointed to a transient rather than stable nature of other key cancer-associated phenotypes: drug resistance and EMT, indicating that they may be a consequence of phenotypic plasticity within a broader attractor state, potentially allowing these phenotypes to be transiently achieved (30–33). This broader attractor may be associated with a higher entropy stemness state, whereas each of the transiently visited phenotypic states may have much lower associated entropy, i.e., they can be considered sub-attractors that can be occupied by the cells either stochastically or in response to environmental inputs (34) (Inputs 1 and 2 in Fig. 1B).

These studies reveal that reasons for higher entropy in gene expression networks in cancer cells can be complex, because the same increase in entropy could be due to the emergence of new stable attractors in the cell population (phenotypic diversity, Input 1’ in Fig. 1B) or increased noisiness of the individual attractors that may already be present in the normal, pre-cancerous tissue or emerge due to cell de-differentiation (phenotypic plasticity, Input 1 in Fig. 1B). Furthermore, phenotypic plasticity can enable emergence of transiently stable, stochastically visited attractors that can nevertheless have important functional phenotypic characteristics, such as EMT, cell proliferation, and drug resistance (Input 2 in Fig. 1B). These phenotypes may be related to those occurring separately in normal development and tissue homeostasis, but might become mutually accessible in the context of a larger underlying attractor in the phenotypically plastic cancerous states (Fig. 1C). Thus, a more detailed landscape analysis is required to understand the mechanisms underlying the emergence and dynamics of cancerous cell populations. Furthermore, these studies leave the following questions open: what controls the availability of various transcriptional programs that enable diverse landscape attractors and what mechanisms regulate the transitions between different attractor states and thus the degree of plasticity of various phenotypes?

In contrast to gene regulation landscapes, in which variables, such as molecular concentrations, can be viewed as continuously adopting multiple values, epigenetic landscapes are essentially binary or “digital” in nature, e.g. the methylation patterns of specific CpG sites or the presence or absence of specific histone modifications. Nevertheless, the landscape analysis framework can also be used for these types of experimental data. For instance, epigenetic variation in the patterns of sets of four consecutive CpG sites display increasing stochasticity in aging fibroblasts and in cancer cells, within particular regions of the genome (35). The patterns of consecutive CpG sites, also known as epialleles, can thus be treated probabilistically, with their distributions within the same tumor estimated using a Bayesian model (36). The probability analysis lends itself to examination of entropy and information metrics (defined in Box 1), which was applied to several brain tumor and normal samples, revealing an increased methylation entropy of Alu repeat sequences (37). The epigenetic patterns of epialleles may display certain correlations, interpreted as specific attractor states in the underlying landscapes. Mechanistically, these correlated patterns may arise because DNA methylation at heritable (i.e. CpG) dinucleotides is affected by the state of the cell or location in the genome, as well as the nearest CpG neighbors, because DNA methyltransferase I, the enzyme that copies CpG from the parent to the daughter strand during DNA replication, resides at the replication fork, conferring a nonrandom methylation pattern to nearby CpG dinucleotides.

The underlying landscapes may be more formally defined recognizing the binary nature of the experimental data by exploiting the Ising model, introduced in the 1930’s for one-dimensional magnetic dipoles, whose binary states are also influenced by external forces and the nearest dipole neighbors (38). It also allowed a highly accurate computation of the Shannon normalized methylation entropy (NME) for DNA methylation. Furthermore, the Ising model enabled a more sophisticated analysis, such as the calculation of the Jensen-Shannon distance to evaluate the mutual information between two epigenomes, and thus to rank genomic features by their relative contribution to epigenetic landscape change (39). This more rigorous treatment revealed substantial entropy increases in the epigenetic landscapes of a variety of cancer types compared to matched normal tissues of origin (38). Importantly, it was found that an increase in disordered methylation patterns predicts poor clinical outcomes in chronic lymphocytic leukemia (40) and acute myelogenous leukemia (41). This recent progress has been striking because cancer epigenetics was thought to be computationally intractable due to being derived from “hundreds of landscapes” of normal tissue (42).

The increase in epigenetic landscape entropy observed in various cancers is accompanied by a greater variability in gene expression (43), thus linking epigenetic and gene regulation landscapes. A possible explanation for this linkage is that genetic programs accounting for new phenotypic properties can become accessible due to increased epigenetic variability, leading to the emergence of new gene regulation attractors. This hypothesis is supported by the observation that the increased variation in gene methylation and expression is often enriched in genomic regions that are larger than a single gene (43, 44), e.g., regions associated with EMT (43) or smaller domains, observed in pancreatic cancer (45), perhaps related to hypomethylated regions inferred for hematopoietic stem cells (46). Thus, epigenetic control of multiple genes needed to enable a specific phenotype could “loosen” and the corresponding genetic attractor may emerge and enable variable onset of a new phenotypic state in cell population. It was indeed found that the transition to the mesenchymal state depends on altered chromatin accessibility of the DNA regions incorporating EMT related genes (47). Furthermore, large heterochromatic domains related to developmentally regulated EMT (48) are topologically altered in colon cancer (49). These data suggest that a key cancer related phenotype is enabled by changes in both gene expression landscape (actualization of a cryptic attractor state) and epigenetic landscape (changes in DNA and histone markers that enable accessibility to the genetic information encoding components of this newly accessible genetic landscape attractor).

Together, these results suggest that a key condition for the emergence of a new attractor in the genetic landscape is the epigenetic re-organization of the corresponding genetic material, leading to increasing stochastic variability within the current attractor and increased probability of transition to a new state (21) (Input 1 in Fig. 1B). It is of interest therefore to explore the triggers of epigenetic and gene regulation landscape reorganization that occur during carcinogenesis, a task that is complicated by inter-dependencies of epigenetic and gene regulation mechanisms. Indeed, epigenetic modification, e.g., DNA methylation of gene regulatory sequences, can directly influence gene expression, and many transcription factors can recruit epigenetic regulators, suggesting substantial epigenetic and genetic landscape interdependence (Fig. 2). To provide more detailed insight into oncogenic processes that shape and are shaped by epigenetic and gene regulation landscapes, it will be instructive to examine the genetic and environmental inputs that can lead to precancerous and cancerous states.

Figure 2. Interplay between epigenetic and gene expression landscapes.

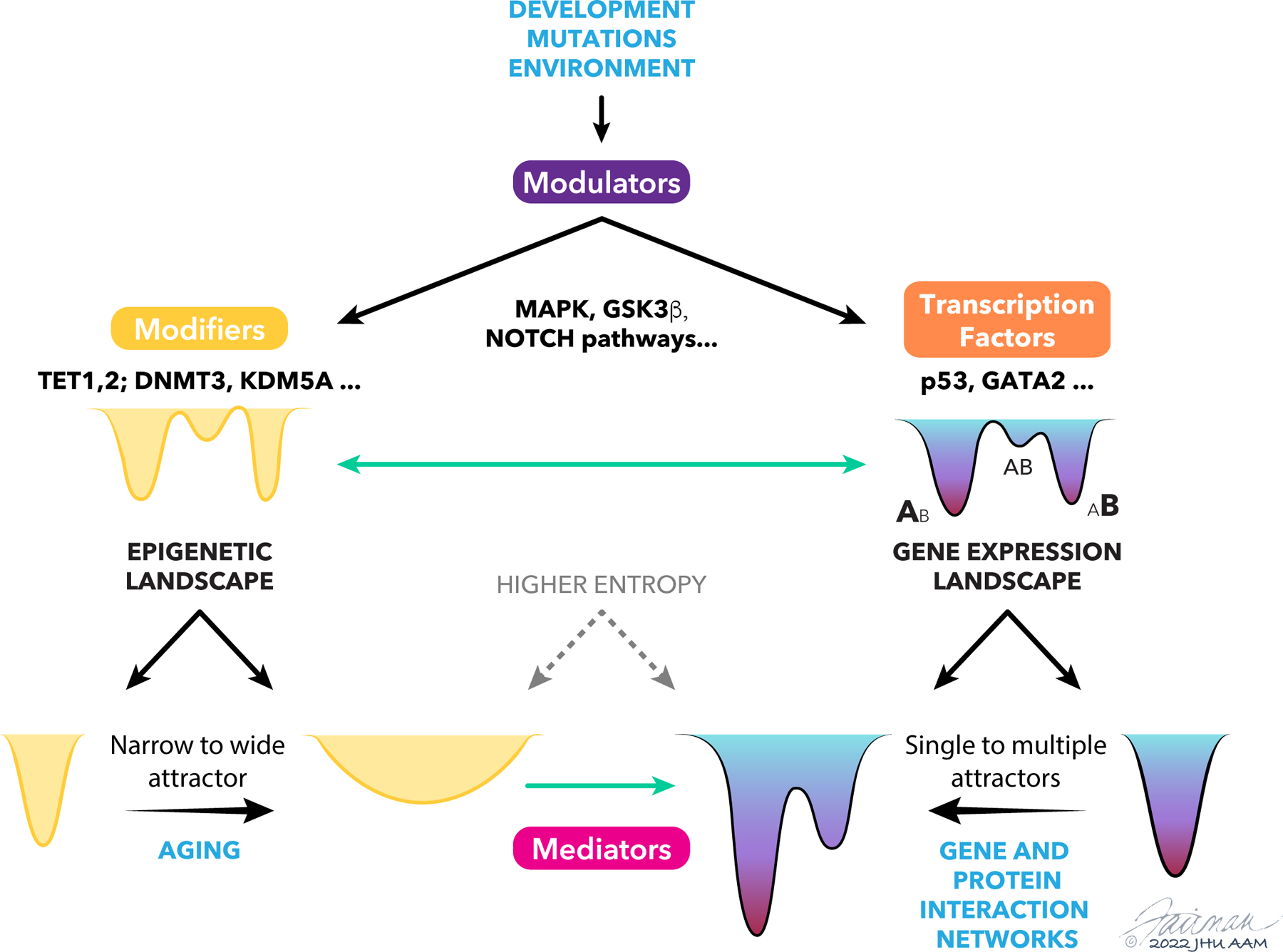
Developmental and environmental factors and genetic mutations can impact diverse modulators of epigenetic control and gene expression, such as signaling and cell communication networks, frequently leading to diversification of cell states. These modulators may directly impact modulators of epigenetic states, such as DNA demethylases, and gene expression, such as transcription factors, which also can directly interact with each other. Examples of these molecular regulators discussed in the text are shown here. The result is alterations of the epigenetic and gene regulation landscapes that are tightly coupled, e.g., through the action of mediators of epigenetic control, influencing accessibility of genes for regulation, and the magnitude and variability of gene expression. Certain additional inputs may be more specific to each of the landscapes, such as the epigenetic drift with cell aging primarily leading to a widening of the landscape attractors, higher plasticity and higher entropy of the state, and protein-protein interaction and gene regulatory networks, stabilizing various attractors and serving to decrease the plasticity and entropy.

Interplay between epigenetic and genetic landscapes

How can the large number of recurrent somatic mutations that drive carcinogenesis be connected to the pathways and genes responsible for cancer phenotypes (50)? Traditionally, this question has been addressed by analyzing the effects of various mutations on the magnitude of phenotypic changes, such as increased proliferation, in response to overexpression of diverse mitogenic regulators. What is currently less understood is how the increased variability (and thus entropy) of epigenetic and gene expression regulation is linked to cancer progression. Such analyses are now progressively enabled by the rank-ordering of oncogenic mutations using metrics such as Jensen-Shannon distance (Box 1, Equation 7), which establish the effect size and its importance in epigenetic control of cancer etiology (39).

The roles of mutations affecting molecules that directly (so-called, epigenetic modifiers) and indirectly (epigenetic modulators) control epigenetic landscape through their enzymatic functions (51) can be elucidated in cancerous states (Fig. 2). For example, in acute myelogenous leukemia (AML), driver mutations can affect both epigenetic modulator molecules [such as transcription factors and signaling pathways that can recruit epigenetic modifiers to specific gene targets (52)] and modifier molecules [such as the DNA demethylation-related gene TET2, which is directly mutated in a subset of AML patients (53)]. Analysis of epiallele distribution across AML patients with different driver mutations indicated an increase in the entropy of epiallele distribution, consistent with other cancers. Importantly, this analysis revealed a more fine-grained epigenetic landscape structure underlying entropy increase. In particular, epialleles commonly showed specific patterns for a subset of modulator mutations, whereas the distribution was much broader for modifier mutations. This study further indicated that tighter and more specific epiallele distributions were corelated with better clinical outcomes, whereas broader distributions were generally associated with poor clinical prognoses. Furthermore, higher epiallele diversity was associated with gene expression hypervariability and, thus, likely higher phenotypic and developmental plasticity. This result was consistent with an independent analysis of AML involving genetic rearrangement of the the histone methyltransferase gene KMT2A (also known as MLL) which, when compared to untransformed controls, also demonstrated a greatly increased epigenetic entropy (more specifically, NME) and high expression variability of genes implicated in AML etiology (54). Importanlty, animal models of AML revealed that epigenetic variability was a precursor of transformation to AML, pointing to the causal rather than correlative nature of the greater entropy states (53). Overall, these data suggest that mutations affecting particular regulatory pathways may result in adoption of specific genetic and epigenetic states (narrow and stable landscape attractors). Conversely, dysregulation of epigenetic modifiers can lead to a much broader epiallele distribution, which may result in broader, more ‘noisy’ attractors, phenotypic plasticity and poorer prognosis (Input 1 in Fig. 1B and Fig. 2). Indeed, a greater phenotypic plasticity enabled by a more global epigenetic dysregulation may enhance escape of cancer cells from various treatments and other pressures, including immune surveillance.

Whereas mutational alterations of some modulators can lead to emergence of specific attractor states, mutations of other modulator proteins may exert their effect indirectly, by regulating the broad specificity epigenetic modifiers, thus also leading to extensive epigenetic alterations, and broader, more plastic attractor states. For example, inhibition of DNA methylation was highly effective in AML patients harboring TP53 mutations (encoding the tumor suppressor p53), but had much lower effects in tumors with wild type TP53 (55). These results were supported by lung cancer xenograft studies and in vitro experiments (56), together suggesting that p53 is an epigenetic modulator that is critically important for epigenetic stability. Indeed, in ESCs, p53 restricts the expression of modifiers Dnmt3a and Dnmt3b thus inhibiting methylation, as well as regulating Tet1 and Tet2, making the loss of Trp53 a major driver of epigenetic heterogeneity (56, 57). Other genes commonly mutated in AML, WT1, IDH1 and IDH2 can also have more global effects on epigenetic landscapes, through inducing loss of TET2 function (58). These results suggest that, although epigenetic modifiers may not be mutated in specific tumors, in many cases the effect of modulator mutations can lead to changes in the methylation status of a large number of genes, similar to the effects of modifier mutations. The more specific, targeting effects of modifiers can be revealed through comparative gene expression analysis, e.g., by searching for enrichment of binding sites for specific transcription factors in the control regions of epigenetically variable genes. Enrichment of specific binding sites would suggest that a particular transcription factor can both recruit an epigenetic modifier to a particular gene and more directly control the expression of this gene, once it is epigenetically modified. This type of analysis yielded a number of putative modulator proteins, including GATA2, coupled to epiallele variation in many AML subtypes driven by distinct mutation events (53). Similar studies further suggested specific roles of NFKB1 and MYBL1 as modulator proteins, controlling the drug resistance phenotype in chronic lymphocytic leukemia (59).

Overall, these studies suggest the following refinement of our understanding of the interplay between genetic and epigenetic landscapes in the emergence of genetically driven cancers (Fig. 2). The effect of mutations in mediator and a subset of modulator genes may be broad, encompassing multiple genes across the genome and generating a high degree of epiallelic and genetic heterogeneity, which correlates with poor clinical outcome. The effect of mutations in another subset of modulators may be more specific, leading to emergence of less variable epiallele distributions and coordinated gene expression patterns, corresponding to a limited number of coupled attractors in genetic and epigenetic landscapes. In both cases, the entropy of epigenetic and genetic landscapes goes up, but for different reasons: in the former case, a more plastic state implies a noisy and relatively unstable attractor state, whereas in the latter case, increased entropy may correspond to the emergence and co-existence of new stable attractors in the genetic and epigenetic spaces (Fig 1B). This view implies that there may be different landscape paths to cancer, but the emergence of a more plastic, less defined attractor state may be particularly interesting to consider, because it may be related to both more pluripotent, stem cell-like states and increased plasticity of cancer cells.

Stabilization of attractor states by endogenous and exogenous inputs

Exogenous inputs.

Enhanced variability of both gene expression and epiallele abundance indicative of broad genetic and epigenetic attractors may permit cells to transiently achieve multiple alternative states that could be potentially further stabilized by additional inputs. For example, genetic perturbations of DNMT3A and DNMT3B dramatically increase genetic and epigenetic entropy in embryonic stem cells, whereas the effects on mean methylation were much more modest (60). Furthermore, several genes that are differentially controlled by this perturbation can promote cellular differentiation. Importantly, genetic perturbations of DNMT and TET genes revealed that the differentiated state is a separate attractor in the genetic landscape, and that this attractor exists dynamically, with cells reaching and leaving it according to the relative activities of DNMT and TET enzymes (61). These results are consistent with the current understanding of the importance of epigenetic regulation of induced pluripotency by the Yamanaka factors, particularly the increased expression of TET enzymes to stabilize this state (62). Critically, this differentiation attractor can also be regulated by modulators in the form of signaling pathways, particularly dual inhibition of MAPK signaling and GSK3β (63–65), suggesting that external signaling inputs can stabilize the differentiation state.

The insights from epigenetic regulation of stemness can elucidate how conditional attractors can emerge and be stabilized e.g., by exogenous signaling inputs in cancer (Input 2 in Fig. 1B). As an example of signaling attractor stabilization, it was found in two independent studies that paracrine signaling involving IGF-1 receptor activation or NOTCH pathway signaling can lead to an altered chromatin structure that is mediated by the histone demethylases KDM5A and KDM6A/B respectively, which in turn control the drug resistance phenotype (66). The acquisition of this phenotype was, in both cases, transient and stochastic, suggesting continuous transitions between distinct states associated with two or more attractors in the underlying landscape. The dynamic acquisition can be analyzed in substational detail in vivo, as was the case for AML in a genetically engineered mouse model (67).

Metaplasia.

The landscape-based analysis implies that a loss of stabilizing inputs, exogenous or endogenous, may make transitions to other available attractors more likely, maintaining a plastic state and metaplastic tissue composition. A particularly interesting example of this is found in kidney differentiation. WT1, a tissue specifying transcription factor that is critical for embryonic kidney development, can be seen as a molecule stabilizing the corresponding differentiation program attractor. Loss-of-function mutation of WT1 leading to a loss of DNA binding in the germline causes Denys-Drash syndrome with renal dysplasia (68). The resultant absence of WT1 in somatic cells leads to metaplastic trans-differentiation of early pronephric cells into other mesodermal elements such as skeletal muscle, fat and cartilage and generation of pre-neoplastic “intralobar nephrogenic rests,” relatively early in the developmental axis, increasing the risk of Wilms tumor development (69). WT1 also controls EMT, likely through interaction with the YAP transcriptional co-regulator in controlling E-cadherin expression (70), which may modulate the tissue organization and further influence the metaplastic state. Timed experimental activation of stem cell reprogramming factors in the developing mouse kidney can induce Wilms tumor in the absence of other perturbations, including absence of any WT1 mutations (71). This same effect arises from loss of imprinting (LOI) of IGF2 in Beckwith-Wiedemann syndrome, or sporadically in the general population, with hyperproliferation of developing nephrons also creating predisposition for Wilms tumor development. These results are consistent with losses of stabilizing control leading to a broad, variable and plastic landscape attractor, which can also decrease the probability of occupying the attractor corresponding to a stably differentiated nephron state (Figs. 1B and 3).

Figure 3. Connection between an epigenetic landscape and variable phenotypic outcomes.

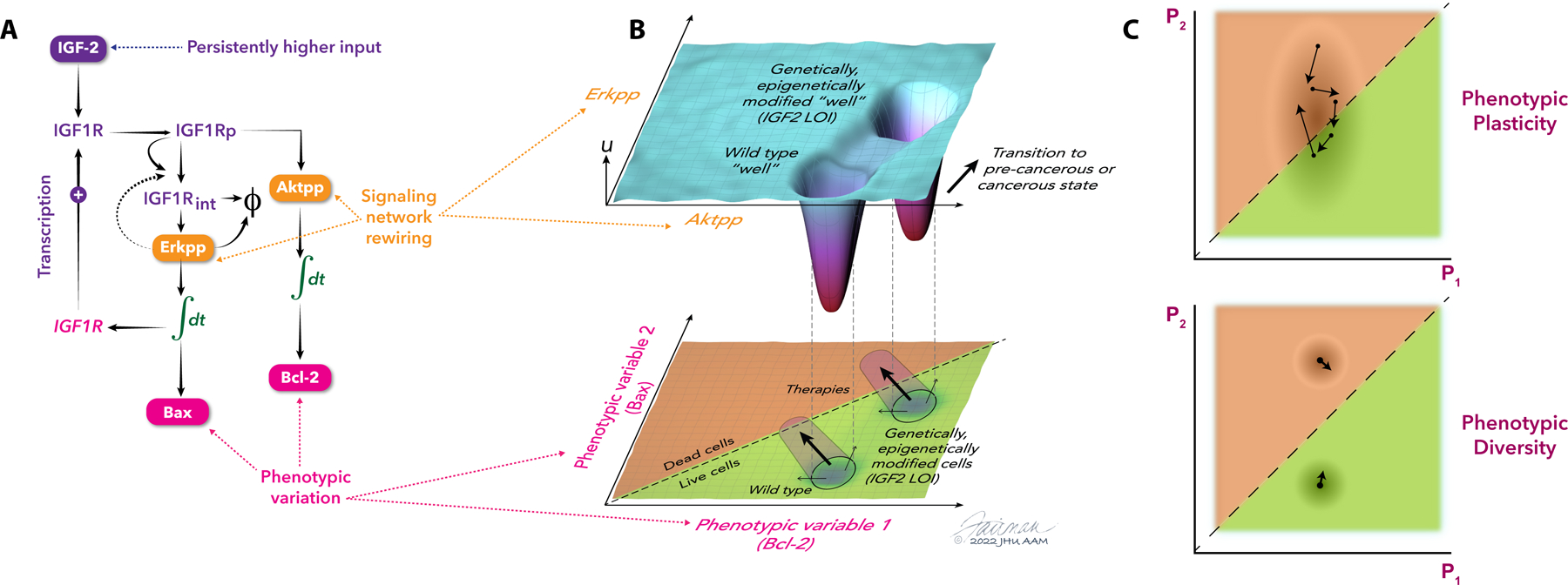
(A) An epigenetic alteration – loss of imprinting (LOI) of the insulin-like growth factor 2 gene (IGF2), implicated in Wilms tumor, doubling of the signaling input, can lead to rewiring of the signaling network activated by the IGF2 receptor IGF1R (depicted as IGF1Rp) through altered receptor trafficking (IGF1Rint), degradation (ϕ) and altered balance of activation of the downstream signaling pathways activating Erk (Erkpp) and Akt (Aktpp) kinases. Rebalancing of Erk and Akt activities translates into transcriptional upregulation of IGF1R, a higher proliferation rate but also rebalancing of pro- and anti-apoptotic protein abundances (BAX versus Bcl-2, respectively) leading to an increased propensity for cell death (113). The integral signs represent integration over time of signaling activities. (B) The landscape alterations that correspond to a change in phenotype (upper panel) is the altered expression and activity of signaling pathway molecules (and thus gene regulatory landscapes in the lower panel) in response to alteration of epigenetic landscapes (IGF2 loss of imprinting, LOI). This leads to emergence of a new attractor in addition to the wild type attractor, resulting in a mosaic wild type/LOI cell distribution in the tissue. This landscape alteration can be ‘mapped’ onto, for example, the apoptosis phenotype-defining network by a quantitative analysis of the dependence of the BCL family protein distributions on the signaling inputs, thus enabling a direct translation of the landscape alterations into phenotype distributions. In this example, the mapping can be visualized as wild type and LOI cell distributions mapped with respect to the areas of cell survival and death on the (BAX, Bcl-2) phenotypic plane, suggesting how treatments targeting LOI cells may be developed to spare the wild type cells. Arrows in the lower panel represent the effect of drugs, such as IGF1R inhibitors shifting the landscape and phenotypic distribution towards the boundary separating survival and death, with the red areas depicting the effect on the wild type and LOI cell populations. (C) A more general view of landscape mapping onto the apoptosis phenotypic plane. By analogy with Fig. 1B, one can contrast mapping of a large attractor versus two more limited attractors, representing the difference between a plastic and stochastic state (phenotypic plasticity) versus a state with two alternative stable attractors (phenotypic diversity). The more plastic state can allow cells to escape from the death area to the survival area even in the presence of a treatment (such as in (B)), by stochastically ‘exploring’ the available attractor, whereas a combination of more stable attractors (with the same overall entropy as the more plastic state) can allow for selective targeting by one but not the other attractor. Therefore, the treatment strategy suggested in (B) may benefit from the initial intervention stabilizing smaller attractors within a larger one and thus decreasing the plasticity of the state, particularly through epigenetic perturbations.

Metaplastic states do not need to involve processes that occur early in development or depend on reprogramming cues. Rather they may arise from stabilization of one of the mutually accessible attractors even in the mature adult tissue (Input 2’ in Fig. 1B). Acinar-ductal metaplasia (ADM; i.e., the process in which acinar cells in the pancreas differentiate into ductal cells) can occur in the untransformed adult pancreas as a part of the tissue repair process (72), but may also lead to pre-neoplastic lesions and, ultimately, progression to pancreatic ductal adenocarcinoma (PDAC) (73). In addition to ADM, which may occur as a normal adaptive process, de-stabilization of the attractor corresponding to the acinar cell type can lead to the emergence of pancreatic intra-epithelial neoplasms (PanINs). Furthermore, other cell types may also emerge in this process, e.g., tuft cells. This attractor destabilization may involve mutations of modulators KRAS and DPC4 (also known as SMAD4) and upregulation of KLF4 during inflammation or injury (74, 75), as well as changes in the epigenetic control of key regulators, such as AATK, as revealed by studies of a mouse model of ADM and pancreatic cancer (76).

Another example of an environmentally induced metaplastic process occurs in Barrett’s esophagus. In this case, the environmental stimulus (modulator) is acid reflux and inflammatory cytokine enrichment, which promote trans-differentiation of normal squamous epithelium of the esophagus into intestine-like columnar epithelium (77). Animal and human data suggest that, in this setting, the attractor corresponding to the esophageal cell type is compromised due to induction of intestinal-specific factors CDX1 and CDX2, which might be induced by inflammatory inputs and can self-stabilize due to auto-regulation (78). This process is associated with a bimodality in the DNA methylation distribution reflective of co-existence of esophageal and intestinal attractors, characteristic of this type of metaplasia (79). Trans-differentiation in this setting is again a major risk factor of ensuing development of esophageal adenocarcinoma.

Together, these observations suggest that metaplasia or alternative differentiation can be an important characteristic of pre-malignant tissue states. Consequently, the new states explored by the cells may not be random but frequently belong to closely related lineages (80), in agreement with the expectation that cells explore adjacent attractors along the underlying epigenetic and genetic landscapes, due to an increased stochasticity and thus entropy of the regulatory networks (Fig. 1C). Intriguingly, upregulation of epigenetic modifiers, such as ARID1A, is commonly observed both in the metaplastic states and multiple cancers (81–83). Tissue disorganization related to metaplasia as well as the common dysregulation of the EMT-MET program can further perturb local cell-cell interactions leading to hyperplasia and the onset of neoplastic growth (84–86).

Therefore, if these genetic or environmental inputs occur in tissues with a high potential for meta-plasticity, the occupancy of the attractors may change. The occupancy of the previously dominant attractors may become less likely, whereas pre-existing alternative attractors can be occupied with higher probabilities, leading to further metaplasia and potentially cancerous states (Fig. 1B). In another scenario, if epigenetic modulators are directly affected by genetic mutations or environmental inputs, even tissues with low initial plasticity can become more plastic and permit occupancy of previously inaccessible, cryptic attractors (Input 1’ in Fig. 1B). These attractors can become stable due to either internal feedback or additional stabilizing mutations, or can remain transient and stochastically visited, depending on the presence of an external cue. The higher degree of epigenetic plasticity and conditional, rather than stable, attractors can increase the corresponding phenotypic plasticity which can result in poor prognosis due to increased metastatic propensity, drug resistance, or immune escape. In this sense, stabilization of particular attractors, by reducing the plasticity of cell regulation, can make cancer progression more predictable and potentially increase the probability of success of personalized therapeutic interventions.

Attractor stability and aging

Stabilization of conditional attractors by an environmental cue enabled by dysregulated epigenetic control can occur through a variety of mechanisms, but particularly through activation of intracellular signaling networks. Indeed, new attractors, such as the mesenchymal cell state emerging in EMT, can be triggered by biochemical and biomechanical inputs from the microenvironment, and increased cell proliferation can be controlled by a progressive accumulation of growth factors and other ligands in the cellular milieu (87). Attractor stabilization may result in a decrease in entropy of gene expression and epiallele occurrence, which can be precisely quantified experimentally and used to evaluate the information carried by the signaling input (88) (see Box 1; information is defined as the decrease in entropy following an input). The entropy decrease is frequently modest, with only 1 bit of information about the signal amplitude commonly transferred in such events, on a cell-by-cell basis (89–96). Coordination of signaling between multiple cells can allow for an increase in this information transfer and thus further entropy decrease, although, since cellular communication is noisy, the effect may also not be very substantial (97). A further entropy decrease can occur if cells are engaged in response to the same input, but are not necessarily communicating (98).

One bit of information is sufficient to define a binary phenotypic outcome, such as cell death/survival, differentiation/self-renewal, or proliferation/migration. This binary outcome frequently reflects occupancy of alternative attractor states modulated by the signaling input (Inputs 2 and 2’ in Fig. 1B). In the context of cancer progression, multiple external cues can trigger signaling events, leading to diversification of cell responses through conditional occupancy of different attractors, as a function of the combinations of different cues (and their persistence) in a specific tumor location or the cues received by cancer cells during metastatic spread. Similar quantitative analysis can be used to gauge the effects of different mutations and drug treatments that can perturb the entropy of different attractors more specifically or the entropy associated with the overall epigenetic or genetic state more generally (93).

In contrast to the entropy decrease due to signaling inputs, entropy of a particular attractor and thus the associated phenotypic plasticity can also naturally increase due to epigenetic drift (Input 1 in Fig. 1B). Epigenetic drift occurs both in tissue culture and in vivo with increasing age of cells and organisms (99–102). In the context of hyper-proliferation associated with cancer, epigenetic drift is due to epimutations accumulating with the increasing number of cell divisions, which can happen at a high frequency (103). This increasing entropy of the epigenetic landscape is distinct from the recurrent changes in DNA methylation serving as a basis for the epigenetic clocks (104). Unlike the age related DNA hyper- or hypomethylation signatures at specific CpG sites, epigenetic drift is a reflection of increased DNA methylation variability which frequently occurs at loci related to malignancy and can be predictive of cancer emergence (105). One example of this site specificity is methylation at the locus encoding polycomb repressive complex-2 (PRC2, itself responsible for trimethylation of H3K27) (103). The entropy increase associated with epigenetic drift may also explain the emergence of a rare 5% subpopulation of bipotent-like breast cancer progenitor cells (106). Intra-tumor epigenetic drift may be dependent on the replication history of the individual clones, leading to a continually expanding spectrum of EMT identities in colorectal tumors (107). Overall, the landscape entropy is not static and can decrease and increase in a quantifiable fashion, even without genetic alterations, creating a more complex context for normal tissue function and progression to cancer.

Mapping regulatory landscapes onto phenotypic responses

Can quantitatively assessed changes in epigenetic and genetic landscapes inform selection of appropriate treatments? Since treatments are driven by disease specific phenotypes and alterations of lanscapes occur at the level of DNA modifications and molecular networks, it is important to consider in more detail how the specific phenotypes are controlled. In many cases, a phenotypic state is defined by a specific bio-molecular circuit. For instance, cell migration phenotypes are controlled by cytoskeleton reorganization, which in turn, is frequently controlled by a subset of Rho-family small GTPases (108, 109). Similarly, cell proliferation is phenotypically driven by the circuit involving regulation of cyclin-dependent kinases (110). It is therefore important to understand how the function of these specific, phenotype defining circuits may be influenced by the more global changes in cellular regulatory networks, as discussed below for the case of apoptosis.

Although the molecular circuits controlling apoptosis are complex, one can use the relative abundances of pro- and anti-apoptotic members of the BCL protein family controlling the phenotypic outcomes of either regulated cell death (relatively higher abundance of pro-apoptotic proteins, such as BAX) or cytoprotection (relatively higher abundance of anti-apoptotic proteins, such as Bcl2) (111, 112) (Fig. 3A). The equally matched abundance of pro- and anti-apoptotic proteins defines the boundary between these states within a phenotypic space (life versus death) onto which the epigenetic and genetic landscapes can be mapped (Fig. 3B). This mapping is based on biochemical input-output relatonships between the phenotype-defining molecules and the upstream genetic and epigenetic mediators, is a natural dimensionality reduction mechanism allowing the evaluation of effects of the underlying molecular network variability and regulation. In many circumstances, e.g., in the turnover of multiple epithelial tissues, the entropy associated with the underlying landscape and thus variability in the expression of apoptosis proteins can result in a subset of cells undergoing cell death even under homeostatic conditions. The distribution of cells across the epigenetic landscape can therefore define the fractions of cells displaying different phenotypes.

The mapping of signaling network activity onto this apoptosis-regulating circuit (Fig. 3B) can be established experimentally and visualized in 2D as the joint single cell distributions of BCL2-BAX pairs. The regulatory landscapes upstream of the phenotype-defining molecular circuit control the relative abundances of the proteins in these pairs, which can alter in response to an epigenetic change, such as LOI of IGF2 (113). The mis-regulation of the signaling inputs resulting from epigenetic alteration (particularly, the re-balancing of signaling through growth factor responsive ERK-MAPK and AKT pathways) is the key aspect of the newly emerging attractor state that translates into a new BCL2-BAX distribution, resulting in a higher propensity for cell death (Fig. 3C). Therefore, an epigenetic landscape change, in addition to promoting higher cell proliferation and tissue hyperplasia, creates a vulnerability (an increased propensity to undergo apoptosis) that can be exploited to selectively eliminate the cell population undergoing IGF2 LOI. These landscape perturbations cause the LOI cells but not wild type cells to cross the ‘death boundary’ (Fig. 3C), thus predicting the therapeutic window relevant to this pre-cancerous state for specific drugs, such as receptor tyrosine kinase inhibitors (113). This analysis highlights the direct translation of landscape concepts to the development of more targeted therapeutic approaches, particularly if an epigenetic alteration is considered an important therapeutic target (114).

This phenotypic mapping analysis can be further extended within the recently introduced framework of cellular archetypes in tissues (32, 33). Archetypes are defined as extreme phenotypic states spanning the available optimized phenotypic space and thus reflecting the available degrees of freedom of the phenotypic plasticity. The analysis of Wilms tumor patient samples revealed three archetypal phenotypic states, suggesting a more complex landscape distribution in vivo. More advanced stages of the disease, accompanied by emergence of IGF2 LOI, lead to a shift of cell population from a relatively uniform distribution across three archtypes: an epithelial and two mesenchymal states (one of which is also characterized by higher cell proliferation), towards a greater abundance of mesenchymal states versus the epithelial one (31). This result suggested a specific landscape change, potentially due to an increased expression of IGF2 promoting more aggressive cell behaviors related to cell proliferation and EMT. In spite of this more complex landscape structure, we suggest that phenotypic mapping analysis can still be employed to target specific cell states.

In general, measuring and mapping genetic and epigenetic landscapes onto phenotypic spaces can be an effective strategy to both infer the corresponding phenotypic diversity and target specific subpopulations defined by landscape attractors. Importantly, it can also elucidate the effects of phenotypic plasticity and guide corresponding treatment strategies. If mutations, epigenetic changes or environmental inputs leading to the emergence of pre-cancerous and cancerous states also increase the plasticity within emerging attractors, cell populations may be substantially less targetable due to a larger overlap with wild type attractors and faster escape from a vulnerable area of the attractor (Fig. 3C). This consideration both provides further interpretation for poor prognostic correlates of the more plastic tumor attractors and suggests that cancer treatment should reduce plasticity. More specifically, the clinical intervention would be aimed at reshaping the underlying landscape to first stabilize the cancer specific attractors by perturbing the attractor-defining pathways and molecular circuits, and then eliminate cells occupying these attractors, while minimizing the effect on untransformed cells.

Conclusions and future directions

The studies reviewed here support the utility of the genetic and epigenetic landscape approaches in our understanding of cancer etiology, ultimately allowing us to arrive at a more general and conceptual understanding of carcinogenesis. Importantly, this approach presents a detailed view of the system, which may focus on a specific attractor, but also a combination of multiple attractors and dynamic transitions between them. Conversely, entropy is frequently a less resolved and more global metric of the overall diversity of cell states. Both approaches are useful and frequently complementary. For example, the landscape view may be better at capturing the difference between an increase in phenotypic plasticity, i.e., the ability of cells (and their molecular networks) to dynamically ‘explore’ diverse states and corresponding phenotypes, from phenotypic diversity, i.e., stable occupancy of different attractors by different cells in the population (Fig. 3C). In both cases, the entropy of the tumor tissue may be higher compared to the parental wild-type tissue state, but the landscapes would be distinct, which can be a crucial level of resolution to determine prognosis and possible interventions. Nevertheless, entropy can still be a convenient metric, particularly in assessing the effects of signaling inputs, mutational and epigenetic perturbations or medical interventions. In particular, changes in entropy [assessed e.g., through different information theory-based measures (Box 1)] can quantitatively characterize the effects of these diverse inputs, or evaluate how long-term processes, such as cellular aging, may affect cellular landscapes.

New experimental approaches may also allow further analysis of causality versus correlation in the relationship between landscape alterations and the emergence of cancer states. For instance, new CRISPR methods can allow recruitment of specific epigenetic modifiers to a targeted locus within the genome and direct control of epigenetic and gene expression variability and attractor properties (30). Studies such as this, combined with further analysis of pre-cancerous states in patients and animal models involving specific perturbations of genetic and epigenetic mechanisms can provide further data to refine our understanding of cancer-specific lanscapes.

Within oncology applications, key advantages of the landscape and entropy concepts lie in an improvement of our understanding of cancer etiology and development of approaches to targeted and personalized cancer treatments. Indeed, more plastic attractors can allow cells to potentially rapidly adjust to both pharmacological and immune therapeutic interventions, as well as enable cells to dynamically switch between diverse phenotypic states required, e.g., for metastatic spread. Therefore, arguably, further approaches may focus on a combination of treatments that would not only attempt to eliminate specific cell sub-populations but also reduce the phenotypic plasticity of tumor cells. In developing these approaches, characterization of the underlying landscapes will be of particular importance. In these efforts, it will be important to refine our understanding of how the landscapes determined on the epigenetic and gene regulation levels can be quantitatively translated into the corresponding descriptions of the activity of the molecular circuits controlling specific phenotypes. Such phenotypic mapping can direct more specific drug development efforts and quantitatively establish the therapeutic windows of specific compounds.

In this Review we primarily focused on DNA methylation as a key epigenetic mechanism whose landscape and entropic analysis has already been performed in diverse biological systems. However, epigenetic control can occur on other levels, including through histone modifications. As rich data accounting for further levels of epigenetic control are gathered, an important challenge will be to understand whether extensive, landscape-based description of all levels of epigenetic and gene regulatory controls is necessary, or whether this complexity and data dimensionality can be reduced to a simpler measurement set. In these efforts, a key role may be played by various machine learning techniques to reveal mutual interdependencies of various molecular control mechanisms and their influences on phenotypic plasticity.