Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 May 24;39(22):7775–7782. doi: 10.1021/acs.langmuir.3c00616

Antibodies Adsorbed to the Air–Water Interface Form Soft Glasses

Caitlin V Wood †, Vladimir I Razinkov ‡, Wei Qi ‡, Christopher J Roberts †, Jan Vermant §, Eric M Furst †,*
PMCID: PMC10249626  PMID: 37222141

Abstract

graphic file with name la3c00616_0005.jpg

When monoclonal antibodies are exposed to an air–water interface, they form aggregates, which negatively impacts their performance. Until now, the detection and characterization of interfacial aggregation have been difficult. Here, we exploit the mechanical response imparted by interfacial adsorption by measuring the interfacial shear rheology of a model antibody, anti-streptavidin immunoglobulin-1 (AS-IgG1), at the air–water interface. Strong viscoelastic layers of AS-IgG1 form when the protein is adsorbed from the bulk solution. Creep experiments correlate the compliance of the interfacial protein layer with the subphase solution pH and bulk concentration. These, along with oscillatory strain amplitude and frequency sweeps, show that the viscoelastic behavior of the adsorbed layers is that of a soft glass with interfacial shear moduli on the order of 10–3 Pa m. Shifting the creep compliance curves under different applied stresses forms master curves consistent with stress–time superposition of soft interfacial glasses. The interfacial rheology results are discussed in the context of the interface-mediated aggregation of AS-IgG1.

Introduction

Non-native protein aggregation is a significant obstacle for the development and production of biologic therapies such as monoclonal antibodies (MAbs). Under physical, thermal, and chemical stresses, natively folded MAb protein monomers partially or fully unfold and form higher-molecular weight aggregates composed of protein subunits.1,2 Aggregation can reduce the effectiveness and yield of the drug and in some instances induce immunogenicity, which leads to drug resistance and other adverse patient events.3 The number, type, and formation mechanisms of aggregates that persist in any protein drug formulation must be understood and controlled.4 These issues are important because MAbs make up a growing class of biologics due to their potency, high binding specificity, and ability to be engineered for specific targets.5−7 MAb therapeutics are commercially available and undergoing clinical trials for the treatment of diseases that include cancers, viral infections, and autoimmune disorders.8−10

There are two broad protein aggregation pathways: those that occur in the bulk solution and interface-mediated routes. Their roles and importance change depending on the protein and solution conditions.11−13 Aggregation mechanisms in a bulk solution have been studied in detail;11,12,14 aggregation is also observed for MAb proteins in liquid formulations when the samples are agitated by stirring, shaking, or controlled isothermal interfacial compression–dilation (IICD) cycles, which is attributed to the formation and disappearance of an air–liquid interface. Investigators hypothesize that proteins partially or fully unfold and aggregate when exposed to vapor–liquid, liquid–liquid, or solid–liquid interfaces, or a combination of those interfaces (e.g., a three-phase contact line).15−22

Compared to aggregation in a bulk solution, surface-mediated aggregation is not as well understood, in part, because of the limited methods available to measure protein interactions and association at interfaces. In state-of-the-art studies, particles are detected in bulk solution using turbidity measurements and flow imaging microscopy after presumably desorbing from the interface.13,15,16,22 Compression and expansion experiments with tensiometry, including those employing a Langmuir–Pockels trough, or bubble or drop tensiometers, show that viscoelastic protein layers form at the interface and are compressible at low surface pressures and incompressible at high surface pressures.15,17,18,23 At high surface pressures, further compression leads to desorption of material from the interface and re-expansion allows protein to adsorb to the interface.18 As a result, the material properties measured from dilatational experiments are confounded with adsorption and desorption and mix changes in state variables with those of the mechanical properties.24

Shear rheology has been used to study proteins that act as foaming, emulsifying, and stabilizing agents25−27 and has recently been applied to pharmaceutical antibodies.28,29 An important and recent advance is a clear understanding of the operating windows of different interfacial rheometry techniques and the availability of new tools for a broad range of practitioners.30 In the work presented here, we show that interfacial shear rheology is a valuable tool for evaluating the formation and strength of protein layers at the air–water interface by a model MAb. During shear measurements, the size of the interfacial area is held constant, which greatly reduces the effects of adsorption and desorption when the interfacial area changes.

One difficulty of studying the shear rheology of adsorbed antibodies is their slow adsorption kinetics, which significantly lengthens the time required to prepare the interface for measurements. For example, the surface pressures of 1 mg/mL solutions of bovine serum albumin (66.5 kDa), β-lactoglobulin (36.8 kDa), and lysozyme (14.3 kDa) at the air–water interface each reach a regime of slow decrease within 1 h,27 whereas the surface pressure of different 1 mg/mL IgG (145 kDa) solutions at the air–water interface requires 4–5 h.23,28 We designed an experimental protocol, described later, to reach a consistent preparation of the interface prior to shear rheology measurements. Rheometry is performed using a double-wall-ring geometry with a stress-controlled rheometer.30 With this protocol, we evaluate the shear rheological properties of anti-streptavidin immunoglobulin gamma-1 (AS-IgG1) at the air interface using creep experiments and oscillatory strain amplitude and frequency sweeps. This work also examines the influence of solution pH and bulk protein concentration on the shear rheological properties as previous studies demonstrated that surface-mediated aggregation of AS-IgG1 depends on interprotein electrostatic interactions but is only weakly dependent on bulk concentration.13,31 The results of this work will be discussed within the context the mechanisms of protein aggregation at interfaces.

Experimental Section

Sample Preparation

pH 5 buffer is prepared by diluting acetic acid (Sigma-Aldrich, St. Louis, MO) to 20 mM in ultrapure water (resistivity of 18.2 MΩ cm, Advantage A10, MilliporeSigma, Billerica, MA) and titrating to pH 5 using a stock of a 5 M sodium hydroxide solution formed by dissolving sodium hydroxide pellets (Fisher Scientific, Waltham, MA) in ultrapure water. pH 6.5 buffer is prepared similarly by dissolving l-histidine monohydrochloride monohydrate (Sigma-Aldrich) to a concentration of 10 mM in ultrapure water. All buffers are filtered (0.22 μm polyvinylidene fluoride low-protein binding filters, Chemglass Life Sciences) before use. The pH and buffer conditions are selected to match prior work that studied bulk- and surface-mediated aggregation behavior and protein–protein interactions and the bulk solution viscosity of AS-IgG1.13,31,32

AS-IgG1 was provided by Amgen Inc. (Thousand Oaks, CA) as a monomeric stock solution (>98% monomer) at a concentration of 30 mg/mL. Stock solutions are dialyzed to the desired solution condition using Spectra/Por 7 dialysis tubing with a 10 kDa molecular weight cutoff (Spectrum Laboratories, Rancho Dominguez, CA) and filtered after dialysis. The pH of all final AS-IgG1 solutions is confirmed experimentally prior to use. Solution concentrations are determined using the ultraviolet absorbance (Cary 60, Agilent, Santa Clara, CA) at 280 nm using an extinction coefficient of 1.586 cm2/mg. Final protein concentrations of 0.1 and 1 mg/mL are achieved by gravimetric dilution.

Microbubble Tensiometry

The dynamic surface tension of an air–water interface is measured using a microtensiometer.13,33 Surface tension γ is calculated using the Young–Laplace equation

graphic file with name la3c00616_m001.jpg 1

where Δp is the pressure difference across the interface and R is the radius of the bubble. At the start of a measurement, a fresh interface is formed by increasing the pressure supplied to burst an existing bubble. A control loop in the controlling software program adjusts the pressure supplied to maintain a stable bubble size.

Accelerated Adsorption Protocol with a Langmuir–Pockels Trough

A rectangular Langmuir–Pockels (L–P) trough (720 mm × 75 mm, KSV Nima, Biolin Scientific, Gothenburg, Sweden) is used to compress the interface. The instrument consists of a polytetrafluoroethylene trough, two symmetrically placed moveable Delrin barriers that uniaxially compress or expand the surface area of the interface, a frame that supports the trough and controls the movement of the barriers, and an electromagnetic balance with a resolution of 0.1 μN/m that measures surface tension using a platinum Wilhelmy plate (KSV Nima). A sharp edge lines the perimeter of the trough to ensure pinning and prevent curvature of the interface. Before each experiment, the trough and barriers are rinsed with ultrapure water, wiped with precision wipes (Kimtech, Kimberly-Clark, Irving, TX) soaked with ethanol, rinsed at least three additional times with ultrapure water, and dried with compressed air. The Wilhelmy plate is cleaned by flame treatment after being rinsed with ethanol and acetone.

At the start of each accelerated test, the trough is filled with the desired protein solution, which requires ∼150 mL of the sample. Because proteins immediately begin adsorbing to the interface, the Wilhelmy plate is placed at the surface within 1 min of filling. Compression starts at a speed of 3 mm/min and continues until reaching the desired surface tension. Barrier movement then stops, and the surface area is held constant during the rheology measurements. All experiments are performed at room temperature.

Interfacial Shear Rheology

A double-wall-ring (DWR) geometry mounted on a DHR-3 rheometer (TA Instruments, New Castle, DE) is used to measure the shear rheology of the interface.34 The assembly consists of a Teflon cup and a platinum–iridium ring geometry that is attached to the rheometer and is the moving boundary. Because the interface is compressed prior to shear interfacial rheology measurements, the cup is placed in the center of the L–P trough. There are two openings on opposite ends of the cup that are oriented in the direction of barrier movement to ensure a homogeneous surface pressure inside and outside. Similarly, the ring has three openings to allow the surface pressure to equilibrate on both sides. Before use, the Teflon cup is cleaned in a manner identical to that used for the trough. The ring is rinsed several times with ethanol and ultrapure water.

At the start of an experiment, the trough and cup are filled with the desired sample solution and the ring is lowered and carefully positioned at the interface. After compression, the interface is allowed to recover for 10 min prior to shear rheology measurements. All experiments are performed at room temperature.

During measurements with surface shear rheometers, the total drag on the ring consists of not only contributions from the response of the complex fluid interface but also contributions from the velocity gradients in the subphase. The dimensionless Boussinesq number (Bq) is used to determine the importance of the surface drag relative to the bulk and is defined for a continuous shear flow as34

graphic file with name la3c00616_m002.jpg 2

where ηs is the surface shear viscosity in steady shear flow, η is the average bulk viscosity, V is a characteristic velocity, LI and Ls are the characteristic length scales over which the velocity decays at the interface and in the subphase, respectively, PI is the contact perimeter between the probe and the interface, and As is the contact area between the geometry and the subphase. One typically assumes that 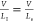Inline graphic.34 The ratio As/PI results in the geometry-dependent characteristic length scale a, which should be as small as possible.30 The outer radius of the ring used in this work is 24.5 mm, and the inner radius is 23.5 mm; the ring has three 5 mm gaps in the ring to facilitate a homogeneous surface pressure on the inside and outside. For oscillatory measurements and viscoelastic interfaces, the complex, frequency-dependent viscosity can be used to calculate Bq.35 If |Bq| ≫ 1, interfacial stresses dominate and the interfacial rheological properties can be simply calculated from shear measurements. In this work, |Bq| is always >100, indicating that surface stresses were dominating the measurements and subphase contributions could be neglected.

Creep Experiments

Creep experiments are performed to measure the compliance of the interface in response to an applied step stress. After accelerated arrest is achieved, a stress of 1 × 10–4 Pa m is applied for 200 s. Then, the stress is removed and the interface allowed to recover for 200 s. The process is repeated by applying and removing a stress that was 1 × 10–4 Pa m higher. Such cycles are continued until a viscous flow is observed, which is indicated by a linear compliance versus time. The interfacial creep compliance, Ji(t), is related to the applied stress, σ(t), and the measured strain, γ(t), by

graphic file with name la3c00616_m004.jpg 3

For a step stress represented by

graphic file with name la3c00616_m005.jpg 4

where H(t) is the Heaviside step function, eq 3 reduces to

graphic file with name la3c00616_m006.jpg 5

Dynamic Oscillatory Tests

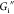Oscillatory strain amplitude and frequency sweeps are performed to evaluate the material response in terms of interfacial shear storage modulus Inline graphic and loss modulus Inline graphic. Strain amplitude sweeps are measured at a fixed frequency of 0.63 rad/s from 0.1% to 10%. Frequency sweeps are performed from 0.1 to 10 rad/s at a fixed strain amplitude of 0.52%, which is within the linear viscoelastic (LVE) regime. Data points in this report represent the average and standard deviation of four replicate measurements performed on two different days.

Results and Discussion

Adsorption Kinetics and Accelerated Adsorption Protocol

We measured the surface tension of an air–water interface during the adsorption of AS-IgG1 for two pH values and two bulk concentrations using a microbubble tensiometer33 and a Wilhelmy plate. For the former, the surface tension decreased and eventually approached a value of approximately 55 mN/m for bulk AS-IgG1 concentrations of 0.3–10.0 mg/mL (Figure 1a), in good agreement with measurements by pendant drop tensiometry for similar molecules.36

Figure 1.

Figure 1

Open in a new tab

Surface tension of AS-IgG1 at pH 5. (a) Surface tension of a constant-area interface measured with a microbubble tensiometer (bubble diameter of ∼80 μm). The solid black line is the apparent surface tension measured for 1 mg/mL on a Langmuir–Pockels trough using a Wilhelmy plate. (b) Scaled surface tension curves. The surface tension is normalized to that of the clean interface and time scaled by the coefficient k. The inset shows the dependence of the scaling coefficient on the bulk MAb concentration with a quadratic fit. The dashed line is the linear contribution. (c) Apparent surface tension of a Langmuir–Pockels trough used to identify an accelerated protocol for interfacial rheometry measurements. The surface area was compressed (dashed lines) at 3 mm/min until the surface tension reached 65 mN/m (black), 55 mN/m (red), or 45 (blue) mN/m. The surface area was held constant (solid lines) for 1 h following the end of the compression step.

The kinetics of adsorption are faster at higher bulk MAb concentrations, but each of the adsorption curves can be collapsed onto a master curve (Figure 1b) by scaling time with a coefficient k, an indication that the adsorption is irreversible and diffusion-limited, analogous to the kinetics of nanoparticle adsorption at interfaces.37 Empirically, the scaling coefficient is a function of the bulk MAb concentration by 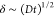Inline graphic. A quadratic contribution emerges at higher concentrations because significant adsorption occurs over a diffusion length Inline graphic that is initially smaller than the bubble radius, δ ≪ R (or for times t ≪ R2/D ≈ 36 s).38,39 Here, D = kT/6πahη is the Stokes–Einstein diffusivity of a MAb molecule with a hydrodynamic radius ah = 5 nm in a buffer with viscosity η = 10–3 Pa s.40 In each case, the adsorption kinetics gradually slow with time. Analogous to simulations of irreversible nanoparticle adsorption, we attribute the slowing rate of change in surface tension to the interface rapidly filling, together with the emergence of glassy-like dynamics of the adsorbed layer, which restricts spontaneous fluctuations of openings in the interface for arriving protein molecules.41

As the measurement with a Wilhelmy plate shows, the protein flux at the interface depends on geometry and decreases with interface curvature.33,42 A planar interface, which is required for shear rheology measurements, cannot reach the lower surface tension values associated with slower adsorption kinetics even after 13 h (see Figure 1a and the Supporting Information). However, we expect the surface tension should eventually reach a similar value. The curvature affects only the transport of mass to the interface, not the mechanism of adsorption. In addition to the impracticality of preparing the interface for this length of time prior to each rheology experiment, the measurement accuracy is affected by evaporation, which reduces the height of the sample in the trough and prevents the interface from pinning correctly to the sharp edge of the trough perimeter required to maintain a flat interface.43 To overcome this obstacle, we use a L–P trough to prepare consistent, reproducible interfaces for shear rheological measurements. Immediately after the addition of an AS-IgG1 sample to the bulk subphase, the trough barriers are moved to compress the interfacial area at a speed of 3 mm/min to reach 55 mN/m in approximately 30 min. During the preparation process, the surface tension of the interface decreases by a combination of AS-IgG1 adsorbing to the interface and the surface concentration increasing as the surface area decreases by the moving barriers.

The stability of the interface after this procedure and the suitability of 55 mN/m as an appropriate surface tension are evaluated by measuring the surface tension for 1 h after acceleration the protocol to 45, 55, and 65 mN/m (Figure 1c). The surface tension was stable at 55 mN/m, while the surface tension increased and decreased at 45 and 65 mN/m, respectively.

Creep Compliance of AS-IgG1 at the Interface

We plot the interfacial creep compliance for 1 mg/mL AS-IgG1 at pH 5 in Figure 2a for interfacial stresses of 1 × 10–4 to 1 × 10–3 Pa m. In the measurement series, the compliance at low stresses was small and, after an initial decaying oscillation caused by the instrument inertia, increased with a power law scaling with time as approximately Ji(t) ∼ t0.2. The low compliance indicates the formation of a strong, elastoviscoplastic layer. As the applied stress increases, the magnitude of the compliance also increases as the elastic response is lost, and plastic deformations occur. At a sufficiently high stress, the compliance undergoes a transition into a viscous flow regime, where Ji(t) ∼ t.

Figure 2.

Figure 2

Open in a new tab

Interfacial shear rheology of AS-IgG1 films. (a) Creep compliance Ji(t) measurements of AS-IgG1 interfacial layers at 1 mg/mL AS-IgG1 at pH 5 for interfacial stresses (σi) of 1.0 × 10–4 to 1.3 × 10–3 Pa m. Each curve represents an increment of 1 × 10–4 Pa m. (b) At 1 mg/mL at pH 6.5 (σi = 1.0 × 10–4 to 2.0 × 10–3 Pa m). (c) At 0.1 mg/mL at pH 5 (σi = 1.0 × 10–4 to 1.0 × 10–3 Pa m). (d) Stress–time superposition of 1 mg/mL AS-IgG1 at pH 5 data.

The strength of the interfacial layer may be influenced by electrostatic interactions between AS-IgG1 molecules. When the samples are subjected to the same step stress, the compliance of the AS-IgG1 layer is lower at pH 6.5 (Figure 2b) at the same bulk concentration. Also, at 1 mg/mL, the interfacial viscosity at high stress is 64 mPa m s for pH 6.5 and 9.2 mPa m s for pH 5. In bulk solution, the net protein–protein interactions of AS-IgG1 are less repulsive at pH 6.5 than at pH 5.32 This difference may facilitate denser packing of the AS-IgG1 molecules at the interface at the higher pH, which in turn leads to mechanically stronger films. The faster aggregation rates and larger resultant aggregates observed at pH 6.5 compared to pH 5 in IICD experiments also correlate with these results.13,31 At both pH 5 and 6.5, we measured the compliance of films formed at a lower bulk concentration, 0.1 mg/mL. The measurements for pH 5 at 0.1 mg/mL are shown in Figure 2c. They exhibit the same trends as measurements made at higher concentrations. At low stress, Ji(t) ∼ t0.2, and there is a transition to viscous behavior at high stress. The films formed at lower concentrations are weaker, as indicated by the higher compliances and lower stress to reach the viscous deformation. Data for pH 6.5 at 0.1 mg/mL are provided in the Supporting Information.

Oscillatory Shear Measurements

The initially elastic nature of AS-IgG1 layers on the interface was further characterized by oscillatory interfacial shear rheology in the linear viscoelastic (LVE) regime. Strain amplitude sweeps were performed at a fixed angular frequency of 0.63 rad/s for 0.1 and 1 mg/mL AS-IgG1 at pH 5 and 6.5 to determine the LVE regime of each condition (Figure 3a). 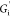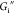As expected from the compliance, we measure a predominantly elastic or solid-like response; interfacial storage modulus Inline graphic is nearly an order of magnitude larger than interfacial loss modulus Inline graphic for each condition. The critical strain is between 2% and 3%. 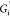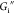Immediately beyond a critical strain amplitude, Inline graphic decreases and Inline graphic remains relatively constant with strain. The frequency dependence of Inline graphic and Inline graphic at a constant strain amplitude of 0.52%, which is within the LVE regime, is shown in Figure 3b. Like the results of the strain amplitude sweeps, a primarily elastic or solid-like response is observed over the frequency range. 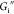Inline graphic increases with a weak power law dependence on frequency, while Inline graphic exhibits a slight decrease or is constant within the resolution of the measurement. Films at the higher concentration and pH have a higher modulus.

Figure 3.

Figure 3

Open in a new tab

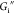Interfacial storage moduli Inline graphic (filled symbols) and loss moduli Inline graphic (empty symbols) for AS-IgG1 films. (a) Moduli as a function of strain at an angular frequency 0.63 rad/s. (b) Moduli as a function of frequency at 0.52% strain amplitude. Solid lines show the soft glassy rheology model fit to the frequency response of the 1 mg/mL, pH 6.5 data. Instrument inertial effects are expected above approximately 4 rad/s.

Soft Glassy Rheology of Antibody Films

Layers of protein adsorbed to the air–water interface form stiff, elastic films. The magnitudes of the measured viscoelastic moduli are on the order of 10–3 Pa m. 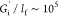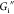Given that previous X-ray and neutron reflectivity measurements determined that MAb molecules adsorb to the air–water interface as a monolayer with a thickness of approximately lf ∼ 150 Å,28,44 the interfacial moduli then correspond to equivalent bulk moduli on the order of Inline graphic Pa. The strength of an AS-IgG1 layer is significant. Both Inline graphic and Inline graphic increase when the pH increases from 5 to 6.5 and when the bulk concentration increases from 0.1 to 1.0 mg/mL, again indicating stronger films at the higher pH and bulk concentrations. While the uncertainty in the measured shear rheological data is relatively large, which was likely a result of minute differences between the interfaces of different replicates (such as surface concentration) that could not be detected by surface tension measurements, these observations corroborate compliance measurements and the presence of an elastoviscoplastic interface.

There are two principal mechanisms through which AS-IgG1 could form strong solid-like structures at the interface. A high concentration of AS-IgG1 at the interface may be an amorphous densely packed system and sterically constrained such that rearrangements are frustrated, or AS-IgG1 at the interface may form a low-density network through strong interactions between adsorbed proteins. The latter, which describes a two-dimensional (2D) gel, typically exhibits an upturn in G″ immediately beyond the yield strain, a characteristic that is a consequence of how the network dissipates energy when it breaks.45 Notably, this feature is absent in the strain amplitude sweep of the AS-IgG1. The former mechanism describes a soft glass, which exhibits yield strains of a few percent, linear viscoelastic moduli with a power law dependence on frequency, and creep compliance with a power law behavior.46 All three of these features are present in the oscillatory and creep measurements, therefore suggesting that AS-IgG1 at the interface resembles a densely packed soft glass. This theory is supported by previous work that observed that MAbs orient into close-packed layers at the interface44,47 and is consistent with the characteristics of the adsorption kinetics discussed above.

The rheology of soft glasses is controlled by an initial elastic deformation and by plastic rearrangements when they are deformed strongly. Several model approaches exist to describe this elastoplastic behavior and for materials that flow, rather than fail, after leaving the elastic regime. The concept of stress-activated events and the coupling between rearrangements is captured by the soft glassy rheology (SGR) model, which moreover links the linear and nonlinear properties. The underlying energy landscape is described by an effective noise temperature x, which characterizes the rheological response of the material by the following relationships. When x > 3, the SGR model predicts a liquid-like response. When 1 < x < 3, the model predicts viscoelastic properties and shear thinning behavior. When x < 1, the model predicts that the system is in a glassy state.

The effective noise temperature is obtained by fitting the aging time and frequency dependence of the complex modulus to48,49

graphic file with name la3c00616_m022.jpg 6

where Gp is the elasticity of the mesoscopic elements and in the 2D case is an interfacial modulus, t is the aging time, and Γ(x) is the Γ function. Fitting of our data in Figure 3b gives an effective noise temperature x of 0.98 ± 0.02 for all conditions, indicating that the AS-IgG1 film is in a glassy state. The solid lines in the figure illustrate a representative fit to the data for 1 mg/mL AS-IgG1 at pH 6.5. The relatively small error of the fitted value reflects the sensitivity of eq 6 to the noise temperature. We show the interconversion between the creep compliance and oscillatory shear measurements in the Supporting Information.

The SGR model also suggests a stress–time superposition, which we discuss next. Let us remark here that this study does not capture aging, which is another hallmark of soft glasses. Aging of the protein films likely occurs on a time scale that is too slow to measure in the current experiments, possibly because of the accelerated adsorption protocol and the relatively high value of the noise temperature. For soft glassy carbon black layers spread at an octane–water interface, at least 0.5 h of waiting time was required between measurements to characterize rheological aging.49

Stress–Time Superposition of the Compliance

The time- and stress-dependent creep flows of soft glassy materials are often superimposed by normalizing the time scales of the imposed stress,50,51 which is consistent with the idea of stress-activated plastic events. This time–stress superposition is a generic feature of soft glassy materials and allows the deformation behavior of a material from a large range of aging times and stresses to be predicted by sampling a few short duration tests at select stresses. Consequently, we shift the data in Figure 2a by an empirical factor τ for each curve that superimposes the measured creep compliance with that from the lowest imposed interfacial stress (1 × 10–4 Pa m). The results of the superposition are shown in Figure 2d for 1 mg/mL at pH 5. Similar curves for the other conditions are provided in the Supporting Information. The successful application of superposition indicates that changes in applied stress influence the energy landscape of an interfacial layer. When the applied stress increases, mesoscopic elements have a stronger propensity to rearrange over energy barriers. When the applied stress decreases, fewer stress relaxation events take place. Such stress–time curves can be used to study or sample the energy landscape of a soft glassy system.52

We compare the time–stress master curves and shift factors for all four experimental data sets in Figure 4a. Each condition results in a unique master curve, which indicates that the energy landscape of AS-IgG1 at the interface depends on the solution pH and bulk concentration. This is most clearly seen by plotting 1/τ – 1 versus stress (Figure 4b). As the stress increases, 1/τ increases with a dependence on applied stress that is the reciprocal of the power law scaling of the compliance curves. A critical stress is eventually reached, above which 1/τ remains constant. At such high stresses, viscous flow is observed immediately. There is a clear order to the curves. A higher pH results in stiffer films, as does a higher bulk concentration. Each condition has a unique stress at which we observe the transition to purely viscous deformation: 6.5 × 10–4 Pa m for 0.1 mg/mL at pH 5, 7.0 × 10–4 Pa m for 0.1 mg/mL at pH 6.5, 1.2 × 10–3 Pa m for 1.0 mg/mL at pH 5, and 1.5 × 10–4 Pa m for 1.0 mg/mL at pH 6.5.

Figure 4.

Figure 4

Open in a new tab

(a) Master creep compliance curves and (b) time shift factors for 0.1 mg/mL AS-IgG1 at pH 5 (blue), 0.1 mg/mL AS-IgG1 at pH 6.5 (red), 1 mg/mL AS-IgG1 at pH 5 (orange), and 1 mg/mL AS-IgG1 at pH 6.5 (pink). The short time creep ringing of the compliance curves has been omitted for the sake of clarity. The logarithmic slope of 5 is the reciprocal of the compliance scaling exponent.

Correlation with Interface-Mediated Aggregation

Previous work used bulk solution measurements to evaluate the surface-mediated aggregation behavior of AS-IgG1 during isothermal interfacial compression–dilation (IICD) cycles and microbubble aeration.13,31 The solution pH had a significant influence on aggregation rates and the size and number of subvisible (>2 μm) particles. This effect was attributed to electrostatic interactions between the AS-IgG1 monomers and aggregates. When the overall net charge of the protein is lower, the net protein–protein interactions are less repulsive. However, those studies were unable to differentiate specific mechanistic step(s) that may be affected by electrostatic interactions (such as adsorption to the interface, aggregation and film formation on the interface, particle desorption from the interface, or a combination of these steps). Shear rheological measurements of the AS-IgG1 layer at the interface detect electrostatic effects on the strength of the material that, as shown by stress–time master curves, correlate with the previous results, indicating that electrostatic interactions impact at least the formation and structure of the AS-IgG1 layer. Because of the weakened electrostatic repulsions between the AS-IgG1 molecules at pH 6.5 compared to those at pH 5, AS-IgG1 may be able to pack into denser layers at the interface. In the context of the SGR model, the elastic elements are more rigid and have higher energy barriers for yielding and rearrangement.

Previous work also found a weaker (less than first-order) dependence of surface-mediated aggregation on the AS-IgG1 bulk solution concentration.13,15 This was attributed to saturation of AS-IgG1 on the interface, such that further increasing the AS-IgG1 concentration in bulk would not significantly increase the amount of AS-IgG1 that adsorbs to the interface. While shear rheological measurements in this work were performed after the interfaces were prepared to identical surface tensions (55 mN/m) with the accelerated protocol, the measurements detected that film strength correlated with bulk concentration, indicating that bulk concentration controls the formation and structure of the AS-IgG1 layer in a manner that went undetected by surface tension measurements. This highlights the importance of using complementary techniques to thoroughly investigate protein layers on interfaces. In most of this work, an increasing bulk concentration increased film strength in a manner similar to the effects of weakening repulsive protein interactions. Additionally, the bulk concentration is the dominant factor affecting the onset of viscous flow. Microbubble tensiometry experiments confirmed that adsorption of AS-IgG1 to air–water interfaces is faster at higher bulk concentrations. Clearly, the rate of accumulation on the interface affects the packing and rearrangement of AS-Ig1 molecules within the interfacial layer, which results in more rigid elements with higher energy barriers for yielding at higher bulk concentrations.

Aside from the correlations between protein formation and pH and bulk concentration, it is interesting to consider how such elastic, glassy layers could behave as they are rapidly compressed. Compressed elastic layers on a liquid interface are known to deform out of plane through the initial formation of wrinkles that then grow,53 and plastic deformation of glassy films can also localize as self-organized, parallel ridges.54 In the former case, an elastic layer with thickness h on a liquid should spontaneously wrinkle with a wavelength λ = 2π(B/K)1/4, where 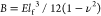Inline graphic is the bending stiffness for a film with Young’s modulus E = 2Gi(1 – ν)/lf and Poisson ratio ν and K = ρg. With ν values between 0.3 and 0.5, we find a wrinkling wavelength on the order of λ ∼ 10 μm, which is similar to the dimensions of particles formed in the IICD experiments.

Conclusions

This work demonstrated the importance of shear rheology in the understanding of therapeutic antibody aggregation at air–water interfaces. Employing a L–P trough to expedite the kinetic trapping of AS-IgG1 at the air interface, followed by shear measurements using a double-wall-ring geometry on a stress-controlled rheometer, enables precise control over the interfacial state and deformation dynamics and kinematics.

Oscillatory shear and creep compliance measurements reveal that soft glassy films form when AS-IgG1 adsorbs to the air–water interface. Importantly, the films are not gels or gel-like, at least in the sense that they do not form a percolated, interface-spanning network. Moreover, the realization that AS-IgG1 at the air–water interface is a soft glass reveals other characteristics that are shared by these materials. In the future, a similar superposition could be performed for creep compliance at different ages. This allows compliance after long aging times to be predicted from short aging experiments, which is powerful for understanding the behavior of therapeutic proteins that persist on the interface for long times during drug transportation and storage.

Acknowledgments

The authors acknowledge Amgen Inc. for providing AS-IgG1 and the European Soft Matter Infrastructure (EUSMI E181100203) for providing funding for this study. E.M.F. and C.J.R. acknowledge the Biomolecular Interaction Technologies Center (BITC) for financial support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.3c00616.

  • Additional figures and discussion, including kinetics of adsorption to a Langmuir–Pockels trough (Figure S1), creep compliance of AS-IgG1 at the air–water interface for 0.1 mg/mL AS-IgG1 at pH 6.5 (Figure S2), inertial limit of oscillatory measurement (Figure S3), comparison of creep and oscillatory measurements (Figure S4), creep superposition curves (Figure S5), and an illustration of rheological aging in soft glasses (Figure S6).

The authors declare no competing financial interest.

Supplementary Material

la3c00616_si_001.pdf (653.6KB, pdf)

References

  1. Wang W., Roberts C. J., Eds. Aggregation of Therapeutic Proteins; Wiley: New York, 2010. [Google Scholar]
  2. Amin S.; Barnett G. V.; Pathak J. A.; Roberts C. J.; Sarangapani P. S. Protein aggregation, particle formation, characterization & rheology. Curr. Opin. Colloid Interface Sci. 2014, 19, 438–449. 10.1016/j.cocis.2014.10.002. [DOI] [Google Scholar]
  3. Rosenberg A. S. Effects of protein aggregates: an immunologic perspective. AAPS journal 2006, 8, E501–E507. 10.1208/aapsj080359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Carpenter J. F.; Randolph T. W.; Jiskoot W.; Crommelin D. J.; Middaugh C. R.; Winter G.; Fan Y.-X.; Kirshner S.; Verthelyi D.; Kozlowski S.; et al. Overlooking subvisible particles in therapeutic protein products: Gaps that may compromise product quality. J. Pharm. Sci. 2009, 98, 1201–1205. 10.1002/jps.21530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Aggarwal S. What’s fueling the biotech engine—2012 to 2013. Nat. Biotechnol. 2014, 32, 32–39. 10.1038/nbt.2794. [DOI] [PubMed] [Google Scholar]
  6. Elvin J. G.; Couston R. G.; Van Der Walle C. F. Therapeutic antibodies: Market considerations, disease targets and bioprocessing. International journal of pharmaceutics 2013, 440, 83–98. 10.1016/j.ijpharm.2011.12.039. [DOI] [PubMed] [Google Scholar]
  7. Buss N. A.; Henderson S. J.; McFarlane M.; Shenton J. M.; De Haan L. Monoclonal antibody therapeutics: history and future. Current opinion in pharmacology 2012, 12, 615–622. 10.1016/j.coph.2012.08.001. [DOI] [PubMed] [Google Scholar]
  8. Reichert J. M. Antibodies to watch in 2016. MAbs 2016, 8, 197–204. 10.1080/19420862.2015.1125583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Reichert J. M. Antibodies to watch in 2013: Mid-year update. MAbs 2013, 5, 513–517. 10.4161/mabs.24990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Scolnik P. A. mAbs: a business perspective. MAbs 2009, 1, 179–184. 10.4161/mabs.1.2.7736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Barnett G. V.; Razinkov V. I.; Kerwin B. A.; Hillsley A.; Roberts C. J. Acetate-and citrate-specific ion effects on unfolding and temperature-dependent aggregation rates of anti-streptavidin IgG1. J. Pharm. Sci. 2016, 105, 1066–1073. 10.1016/j.xphs.2015.12.017. [DOI] [PubMed] [Google Scholar]
  12. Barnett G. V.; Razinkov V. I.; Kerwin B. A.; Laue T. M.; Woodka A. H.; Butler P. D.; Perevozchikova T.; Roberts C. J. Specific-ion effects on the aggregation mechanisms and protein–protein interactions for anti-streptavidin immunoglobulin gamma-1. J. Phys. Chem. B 2015, 119, 5793–5804. 10.1021/acs.jpcb.5b01881. [DOI] [PubMed] [Google Scholar]
  13. Wood C. V.; McEvoy S.; Razinkov V. I.; Qi W.; Furst E. M.; Roberts C. J. Kinetics and competing mechanisms of antibody aggregation via bulk-and surface-mediated pathways. J. Pharm. Sci. 2020, 109, 1449–1459. 10.1016/j.xphs.2020.01.005. [DOI] [PubMed] [Google Scholar]
  14. Brummitt R. K.; Nesta D. P.; Roberts C. J. Predicting accelerated aggregation rates for monoclonal antibody formulations, and challenges for low-temperature predictions. Journal of pharmaceutical sciences 2011, 100, 4234–4243. 10.1002/jps.22633. [DOI] [PubMed] [Google Scholar]
  15. Bee J. S.; Schwartz D. K.; Trabelsi S.; Freund E.; Stevenson J. L.; Carpenter J. F.; Randolph T. W. Production of particles of therapeutic proteins at the air–water interface during compression/dilation cycles. Soft Matter 2012, 8, 10329–10335. 10.1039/c2sm26184g. [DOI] [Google Scholar]
  16. Kiese S.; Papppenberger A.; Friess W.; Mahler H.-C. Shaken, not stirred: Mechanical stress testing of an IgG1 antibody. Journal of pharmaceutical sciences 2008, 97, 4347–4366. 10.1002/jps.21328. [DOI] [PubMed] [Google Scholar]
  17. Ghazvini S.; Kalonia C.; Volkin D. B.; Dhar P. Evaluating the role of the air-solution interface on the mechanism of subvisible particle formation caused by mechanical agitation for an IgG1 mAb. Journal of pharmaceutical sciences 2016, 105, 1643–1656. 10.1016/j.xphs.2016.02.027. [DOI] [PubMed] [Google Scholar]
  18. Lin G. L.; Pathak J. A.; Kim D. H.; Carlson M.; Riguero V.; Kim Y. J.; Buff J. S.; Fuller G. G. Interfacial dilatational deformation accelerates particle formation in monoclonal antibody solutions. Soft Matter 2016, 12, 3293–3302. 10.1039/C5SM02830B. [DOI] [PubMed] [Google Scholar]
  19. Perevozchikova T.; Nanda H.; Nesta D. P.; Roberts C. J. Protein adsorption, desorption, and aggregation mediated by solid-liquid interfaces. Journal of pharmaceutical sciences 2015, 104, 1946–1959. 10.1002/jps.24429. [DOI] [PubMed] [Google Scholar]
  20. McUmber A. C.; Larson N. R.; Randolph T. W.; Schwartz D. K. Molecular trajectories provide signatures of protein clustering and crowding at the oil/water interface. Langmuir 2015, 31, 5882–5890. 10.1021/acs.langmuir.5b00984. [DOI] [PubMed] [Google Scholar]
  21. Freer E. M.; Yim K. S.; Fuller G. G.; Radke C. J. Interfacial rheology of globular and flexible proteins at the hexadecane/water interface: comparison of shear and dilatation deformation. J. Phys. Chem. B 2004, 108, 3835–3844. 10.1021/jp037236k. [DOI] [Google Scholar]
  22. Mahler H.-C.; Müller R.; Frieβ W.; Delille A.; Matheus S. Induction and analysis of aggregates in a liquid IgG1-antibody formulation. Eur. J. Pharm. Biopharm. 2005, 59, 407–417. 10.1016/j.ejpb.2004.12.004. [DOI] [PubMed] [Google Scholar]
  23. Koepf E.; Schroeder R.; Brezesinski G.; Friess W. The film tells the story: Physical-chemical characteristics of IgG at the liquid-air interface. Eur. J. Pharm. Biopharm. 2017, 119, 396–407. 10.1016/j.ejpb.2017.07.006. [DOI] [PubMed] [Google Scholar]
  24. Jaensson N.; Vermant J. Tensiometry and rheology of complex interfaces. Curr. Opin. Colloid Interface Sci. 2018, 37, 136–150. 10.1016/j.cocis.2018.09.005. [DOI] [Google Scholar]
  25. Erni P.; Fischer P.; Windhab E. J.; Kusnezov V.; Stettin H.; Läuger J. Stress-and strain-controlled measurements of interfacial shear viscosity and viscoelasticity at liquid/liquid and gas/liquid interfaces. Review of scientific instruments 2003, 74, 4916–4924. 10.1063/1.1614433. [DOI] [Google Scholar]
  26. Felix M.; Romero A.; Vermant J.; Guerrero A. Interfacial properties of highly soluble crayfish protein derivatives. Colloids Surf., A 2016, 499, 10–17. 10.1016/j.colsurfa.2016.03.037. [DOI] [Google Scholar]
  27. Mitropoulos V.; Mütze A.; Fischer P. Mechanical properties of protein adsorption layers at the air/water and oil/water interface: A comparison in light of the thermodynamical stability of proteins. Advances in colloid and interface science 2014, 206, 195–206. 10.1016/j.cis.2013.11.004. [DOI] [PubMed] [Google Scholar]
  28. Tein Y. S.; Zhang Z.; Wagner N. J. Competitive surface activity of monoclonal antibodies and nonionic surfactants at the air–water interface determined by interfacial rheology and neutron reflectometry. Langmuir 2020, 36, 7814–7823. 10.1021/acs.langmuir.0c00797. [DOI] [PubMed] [Google Scholar]
  29. Mehta S. B.; Carpenter J. F.; Randolph T. W. Colloidal instability fosters agglomeration of subvisible particles created by rupture of gels of a monoclonal antibody formed at silicone oil-water interfaces. Journal of pharmaceutical sciences 2016, 105, 2338–2348. 10.1016/j.xphs.2016.06.010. [DOI] [PubMed] [Google Scholar]
  30. Renggli D.; Alicke A.; Ewoldt R. H.; Vermant J. Operating windows for oscillatory interfacial shear rheology. J. Rheol. 2020, 64, 141–160. 10.1122/1.5130620. [DOI] [Google Scholar]
  31. Wood C. V.; Razinkov V. I.; Qi W.; Furst E. M.; Roberts C. J. A rapid, small-volume approach to evaluate protein aggregation at air-water interfaces. J. Pharm. Sci. 2021, 110, 1083–1092. 10.1016/j.xphs.2020.11.024. [DOI] [PubMed] [Google Scholar]
  32. Woldeyes M.; Qi W.; Razinkov V.; Furst E.; Roberts C. How well do low- and high-concentration protein interactions predict solution viscosities of monoclonal antibodies?. J. Pharm. Sci. 2019, 108, 142. 10.1016/j.xphs.2018.07.007. [DOI] [PubMed] [Google Scholar]
  33. Alvarez N. J.; Walker L. M.; Anna S. L. A Microtensiometer to probe the effect of radius of curvature on surfactant transport to a spherical interface. Langmuir 2010, 26, 13310–13319. 10.1021/la101870m. [DOI] [PubMed] [Google Scholar]
  34. Vandebril S.; Franck A.; Fuller G.; Moldenaers P.; Vermant J. A double wall-ring geometry for interfacial shear rheometry. Rheol. Acta 2010, 49, 131–144. 10.1007/s00397-009-0407-3. [DOI] [Google Scholar]
  35. Reynaert S.; Brooks C.; Moldenaers P.; Vermant J.; Fuller G. Analysis of the magnetic rod interfacial stress rheometer. J. Rheol. 2008, 52, 261–285. 10.1122/1.2798238. [DOI] [Google Scholar]
  36. Kanthe A.; Ilott A.; Krause M.; Zheng S.; Li J.; Bu W.; Bera M. K.; Lin B.; Maldarelli C.; Tu R. S. No ordinary proteins: Adsorption and molecular orientation of monoclonal antibodies. Sci. Adv. 2021, 7, eabg2873 10.1126/sciadv.abg2873. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Nelson A.; Wang D.; Koynov K.; Isa L. A multiscale approach to the adsorption of core-shell nanoparticles at fluid interfaces. Soft Matter 2015, 11, 118–129. 10.1039/C4SM01881H. [DOI] [PubMed] [Google Scholar]
  38. Ward A. F.; Tordai L. Time-dependence of boundary tensions of solutions I. The role of diffusion in time-effects. J. Chem. Phys. 1946, 14, 453–461. 10.1063/1.1724167. [DOI] [Google Scholar]
  39. Fainerman V. B.; Makievski A. V.; Miller R. The analysis of dynamic surface tension of sodium alkyl sulphate solutions, based on asymptotic equations of adsorption kinetic theory. Colloids Surfaces A Physicochem. Eng. Asp. 1994, 87, 61–75. 10.1016/0927-7757(94)02747-1. [DOI] [Google Scholar]
  40. Yearley E. J.; Godfrin P. D.; Perevozchikova T.; Zhang H.; Falus P.; Porcar L.; Nagao M.; Curtis J. E.; Gawande P.; Taing R.; Zarraga I. E.; Wagner N. J.; Liu Y. Observation of small cluster formation in concentrated monoclonal antibody solutions and its implications to solution viscosity. Biophys. J. 2014, 106, 1763–1770. 10.1016/j.bpj.2014.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Schwenke K.; Isa L.; Del Gado E. Assembly of nanoparticles at liquid interfaces: Crowding and ordering. Langmuir 2014, 30, 3069–3074. 10.1021/la404254n. [DOI] [PubMed] [Google Scholar]
  42. Alvarez N. J.; Walker L. M.; Anna S. L. Diffusion-limited adsorption to a spherical geometry: The impact of curvature and competitive time scales. Phys. Rev. E 2010, 82, 011604. 10.1103/PhysRevE.82.011604. [DOI] [PubMed] [Google Scholar]
  43. Pepicelli M.; Verwijlen T.; Tervoort T.; Vermant J. Characterization and modelling of Langmuir interfaces with finite elasticity. Soft Matter 2017, 13, 5977. 10.1039/C7SM01100H. [DOI] [PubMed] [Google Scholar]
  44. Kanthe A. D.; Krause M. E.; Zheng S.; Ilott A.; Li J.; Bu W.; Bera M. K.; Lin B.; Maldarelli C.; Tu R. S. Armoring the interface with surfactants to prevent the adsorption of monoclonal antibodies. ACS Appl. Mater. Interfaces 2020, 12, 9977–9988. 10.1021/acsami.9b21979. [DOI] [PubMed] [Google Scholar]
  45. Alicke A.; Simon S.; Sjöblom J.; Vermant J. Assessing the interfacial activity of insoluble asphaltene layers: Interfacial rheology versus interfacial tension. Langmuir 2020, 36, 14942–14959. 10.1021/acs.langmuir.0c02234. [DOI] [PubMed] [Google Scholar]
  46. Fielding S. M.; Sollich P.; Cates M. E. Aging and rheology in soft materials. J. Rheol. 2000, 44, 323–369. 10.1122/1.551088. [DOI] [Google Scholar]
  47. Baszkin A.; Boissonnade M.; Kamyshny A.; Magdassi S. Native and hydrophobically modified human immunoglobulin g at the air/water interface: Sequential and competitive adsorption. J. Colloid Interface Sci. 2001, 239, 1–9. 10.1006/jcis.2001.7521. [DOI] [PubMed] [Google Scholar]
  48. Sollich P. In Molecular Gels: Materials with Self-Asembled Fibrillar Networks; Weiss R. G., Terech P., Eds.; Springer, 2006; Chapter 5, pp 161–192. [Google Scholar]
  49. Van Hooghten R.; Imperiali L.; Boeckx V.; Sharma R.; Vermant J. Rough nanoparticles at the oil-water interfaces: Their structure, rheology and applications. Soft Matter 2013, 9, 10791–10798. 10.1039/c3sm52089g. [DOI] [Google Scholar]
  50. Strum L. C. E. Physical aging in plastics and other glassy materials. Polym. Eng. Sci. 1977, 17, 165–173. 10.1002/pen.760170305. [DOI] [Google Scholar]
  51. Joshi Y. M.; Reddy G. R. K. Aging in a colloidal glass in creep flow: Time-stress superposition. Phys. Rev. E 2008, 77, 021501. 10.1103/PhysRevE.77.021501. [DOI] [PubMed] [Google Scholar]
  52. Nicolas A.; Ferrero E. E.; Martens K.; Barrat J. L. Deformation and flow of amorphous solids: Insights from elastoplastic models. Rev. Mod. Phys. 2018, 90, 45006. 10.1103/RevModPhys.90.045006. [DOI] [Google Scholar]
  53. Brau F.; Damman P.; Diamant H.; Witten T. A. Wrinkle to fold transition: Influence of the substrate response. Soft Matter 2013, 9, 8177–8186. 10.1039/c3sm50655j. [DOI] [Google Scholar]
  54. Cordella G.; Puosi F.; Tripodo A.; Leporini D.; Lemaître A. Plastic ridge formation in a compressed thin amorphous film. Phys. Rev. Mater. 2022, 6, L122601. 10.1103/PhysRevMaterials.6.L122601. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la3c00616_si_001.pdf (653.6KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES