Abstract
Objective.
Clinical outcomes of transperineal prostate interventions, such as biopsy, thermal ablations, and brachytherapy, depend on accurate needle placement for effectiveness. However, the accurate placement of a long needle, typically 150–200 mm in length, is challenging due to needle deviation induced by needle-tissue interaction. While several approaches for needle trajectory correction have been studied, many of them do not translate well to practical applications due to the use of specialized needles not yet approved for clinical use, or to relying on needle-tissue models that need to be tailored to individual patients.
Approach.
In this paper, we present a robot-assisted collaborative needle insertion method that only requires an actuated passive needle guide and a conventional needle. The method is designed to assist a physician inserting a needle manually through a needle guide. If the needle is deviated from the intended path, actuators shifts the needle radially in order to steer the needle trajectory and compensate for needle deviation adaptively. The needle guide is controlled by a new data-driven algorithm which does not require a priori information about needle or tissue properties. The method was evaluated in experiments with both in-vitro and ex-vivo phantoms.
Main results.
The experiments in ex-vivo tissue reported a mean final placement error of 0.36mm with a reduction of 96.25% of placement error when compared to insertions without the use of assistive correction.
Significance.
Presented results show that the proposed closed-loop formulation can be successfully used to correct needle deflection during collaborative manual insertion with potential to be easily translated into clinical application.
1. Introduction
Transperineal needle placement is widely performed for diagnosis and treatments of prostate cancer (PCa), including biopsy (Penzkofer et al. 2015), thermal ablations (de Marini et al. 2019, van Luijtelaar et al. 2019, Jones et al. 2008) and brachytherapy (Nguyen et al. 2012, King et al. 2021, Ragde et al. 2000). In those procedures, long 16–18 gauge needles are inserted into different areas in the prostate through the patient’s perineum to sample a tissue core from a suspected area or deliver treatment to a confirmed lesion. The clinical outcomes of these procedures rely on the final needle placement accuracy, and placement error may result in false negative biopsies (Robertson et al. 2014), or suboptimal treatment outcomes, i.e., post-treatment local tumor recurrence due to insufficient ablation/radiation, and side effects due to damage to adjacent critical structures (Bomers et al. 2020, Moreira et al. 2021).
To improve needle placement accuracy, several needle-guiding devices have been proposed and evaluated (Krieger et al. 2005, Stoianovici et al. 2017, Yakar et al. 2011, Tilak et al. 2015, Patel et al. 2019). Those devices are designed to mechanically guide a needle along the predefined path from outside the patient’s body while the physician is manually inserting it. However, those devices still do not offer consistent in-vivo needle placement accuracy largely due to needle deflection caused by various factors, such as asymmetric cutting forces at the needle tip, tissue-needle friction, puncture through membranes, and tissue deformation related to the presence of other anatomical structures (van Gerwen et al. 2012, Moreira et al. 2018), as illustrated by the example in Figure 1.
Figure 1.
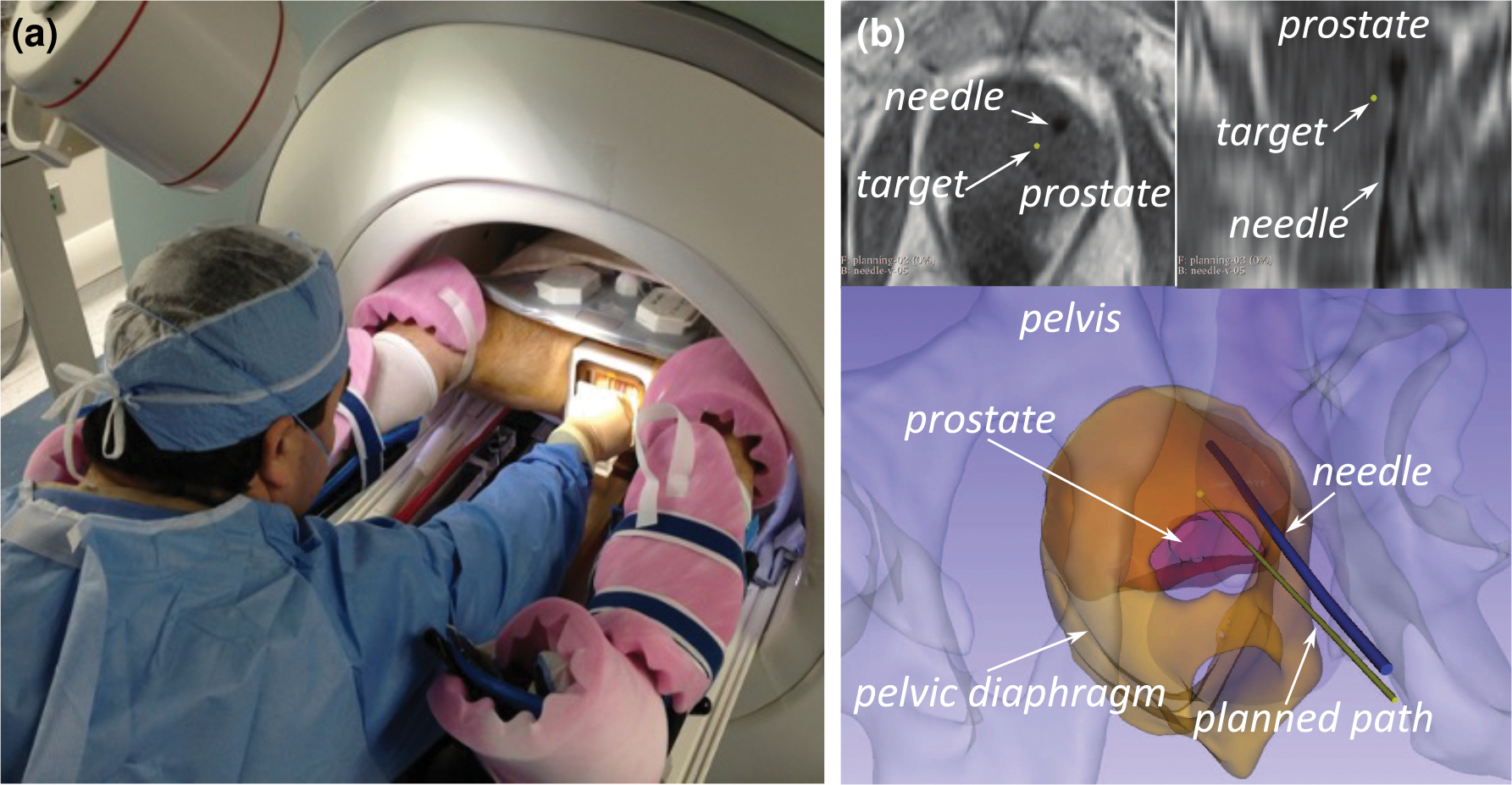
In-bore MRI-guided prostate biopsy as an example of transperineal prostate intervention. (a) The physician is inserting a biopsy needle through the patient’s perineum on the MRI table using a grid template. (b) Axial and reformatted coronal slices of T1-weighted MRI acquired after the needle placement (upper) and 3D models of the prostate and the planned and resultant needle path reconstructed from the image (lower). Interactions between the needle and layers of tissue cause it to deviate from the planned straight-line, resulting in the large targeting error.
There have been many efforts to model and predict needle deflection using different approaches such as mechanics-based models (Misra et al. 2010, Goksel et al. 2009), kinematic models (Webster III et al. 2006, Park et al. 2005, Favaro et al. 2020), and simulations with finite element models (FEM) (Hamzé et al. 2016, Duriez et al. 2009, Adagolodjo et al. 2019, Baksic et al. 2021). While those studies have demonstrated to accurately predict the tissue-needle interaction in a controlled environment, the clinical translation remains challenging for several reasons. Some of the models are computationally intensive and mostly suitable for preoperative planning. The pelvic anatomy and mechanical properties of the tissues involved in needle insertion vary significantly between individuals, making it extremely difficult to tailor those models to a specific patient. Without a model that accurately represents the patient, one cannot achieve an accurate prediction of needle deflection.
Another challenge in addressing the needle deflection issue is to steer the needle once it deviates from the intended path. Several computer- and robot-assisted systems have been proposed to compensate for needle deflection during insertion in soft tissue. The most common approaches are the steering of active (Konh et al. 2020, Pinzi et al. 2021, de Vries et al. 2021) or beveled flexible needles (Chevrie et al. 2018, Swaney et al. 2013), though obtaining regulatory clearance for a complex mechanical system that works inside the patient body is a major hurdle.
Some studies have focused on the correction of needle deflection using conventional rigid needles with a bevel tip (Wartenberg et al. 2018, Rossa et al. 2017). A bevel tip can generate a lateral reaction force to the tip when it is inserted, due to its asymmetric shape, resulting in the steering of the needle. To steer the needle in a desired direction, the needle is rotated about its axis to change the direction of the tip bevel. While this bevel-tip-based approach is more practical than the use of specially designed needles, it still has its own challenges. First, it requires a mechanism with an additional degree of freedom to rotate the needle. Second, the needle can only move in a circular trajectory, resulting in an under-actuated control problem. A recent clinical study has shown that the change of bevel tip orientation was insufficient to compensate for the extent of deflection observed in prostate biopsy procedures (Moreira et al. 2018).
One potential alternative to the aforementioned needle steering approaches is the use of radial displacement of the needle shaft. The idea comes from clinical experience in prostate biopsy procedures, where the physician places a finger or a diddler (a brachytherapy tool that resembles a crochet needle) in the space between the needle guide template and the patient’s perineum. They use it to push or pull the needle shaft in the horizontal and vertical directions to reorient and reposition the needle tip inside the tissue and correct small deflections from the desired path without retracting and reinserting the needle. Furthermore, radial displacements can be achieved with the same actuation mechanism used to position the needle guide (Figure 2). Hence the approach can be implemented using an existing needle guide as simple as 2 degree-of-freedom (DOF) (Song et al. 2013).
Figure 2.

A simple 2DOF device can be used to position a needle guide that simulates the function of a transperineal prostate grid template. The robot is placed in front of the patient’s perineum and moves the guide in the plane to reach the entry point planned from MRI images. In the pictured example (Song et al. 2013), the robot comprises a lead-screw-and-nut mechanism that transmits vertical and horizontal motion (blue arrows) to two crossbars. At the crosspoint of the bars, there is a passive needle guide for the manual insertion of the needle on the -axis direction.
So far, this method of conventional needle correction by radial displacement has received little consideration in robot-assisted procedures, except for a few works reported in the literature (Lehmann et al. 2018). The proposed approaches require complex modeling of the needle-tissue interaction forces and identification of tissue mechanical properties as it relies on the accurate prediction of needle bending and tissue deformation resulting from the radial displacement of the needle shaft.
From these observations, we proposed an insertion assist system based on needle radial displacement. The assist system corrects the needle trajectory using robotic horizontal and vertical displacement of the needle guide while the operator performs the insertion manually. Our method uses a data-driven strategy that relies on a simple local model updated online from the observed behavior of needle-tissue interactions to enable a simple yet robust closed-loop trajectory correction. Our rationale is that the simple adaptive local model does not depend on complex mechanical models that normally do not hold in real-world applications due to patient-specific tissue characteristics and anatomy, and thus it would be easily translated into clinical application. This method was implemented in a closed-loop control scheme using a robotic needle guide to radially displace the needle, and feedback of the current needle tip pose.
The primary contributions of this work are the proposal of an insertion assist system for manual needle insertion with collaborative robotic trajectory correction, the development of a data-driven method for estimation of the needle deflection without the use of a priori information of needle and tissue properties, its use in a Model Predictive Control (MPC) formulation for correction of the needle tip position using horizontal and vertical displacement of the needle guide, and experimental validation of this approach on a robotic device showing the accuracy improvements of the closed-loop control and its robustness to different tissue properties and inhomogeneity.
2. Methods
2.1. Assistive trajectory correction by radial displacement
In this study, we considered a 2DOF needle-guiding stage that simulates the function of a grid template widely used in transperineal prostate interventions, including biopsy, ablations, and brachytherapy. The stage is placed in front of the patient’s perineum where the needle is inserted and moves a passive needle guide radially to the needle axis to adjust the tip position. The needle is manually inserted by an operator.
The insertion is made in a stepwise manner, and between each manual insertion step, the robot moves the needle guide in the horizontal and vertical directions to correct any needle deflection from its straight trajectory path as depicted in Figure 3. By using a stepwise insertion, we eliminate error factors that are not related to the data-driven approach, such as the latency of the system. This allows a better evaluation of our method but does not represent a limitation of its use in a potential continuous insertion application in the future. In this work, the insertion steps were implemented with a button handled by the user to signal the conclusion of an insertion step. However, in our final design, this process will be automatic with the use of an MRI compatible encoder that reports the insertion length to the system as the needle is manually pushed, without the need of pressing any button.
Figure 3.

In the assisted needle insertion, the operator pushes the needle manually in the -axis direction. During insertion, however, the needle deflects from the straight-line planned path. Hence, the passive needle guide is automatically displaced in - and - directions, generating and input (left). As a result of the guide displacement, the needle tip is affected by a change on its current pose, described by the output , and realigned to the straight-line planned path (right).
The length of each insertion step was considered to be fixed and equal to 5mm, which was a feasible resolution for manual insertion with regular prostate biopsy needles. Their shafts exhibit evenly spaced marks that are often used by the physician as a visual guide to perform manual insertions at a given length.
In addition, for safety purposes, the displacement of the needle guide is restricted to a safe limit of 6mm around the initial entry point into the tissue. This limit was considered sufficient to prevent tissue damage and was chosen based on the reported needle tip deviation during puncture on a previous study with clinical cases (Moreira et al. 2018), which was measured comparing the device initial entry point and the final entry point measured in the MR images. The clinical study does not report any perineal adverse events and, to the best of our knowledge, no other study so far has characterized the amount of tissue damage caused by the needle displacement in transperineal prostate interventions. Considering the displacement values observed clinically from the reported study, and the natural elasticity of the skin and tissues of the perineum we believe that 6mm is a conservative estimate and that this safe limit could be even higher. However, more studies are required to better quantify a safe limit before increasing this value.
2.2. Data-driven estimated model
At the end of each insertion step, we used data consisting of the needle guide displacement and the resultant needle tip motion in the previous step to update our data-driven model. We implemented it using an adaptive approach with a Jacobian approximation to model the mathematical relationship between the needle guide displacement and the correspondent needle tip motion inside soft tissue. In this approach, we do not assume a priori knowledge of the tissue deformation and needle deflection, and use online data collected during the insertion to iteratively update our model to reflect the current behavior of the system. The system considered in this study can be described as:
| (1) |
where is the vector of needle guide positions with and corresponding to the current horizontal and vertical positions of the needle guide robot while is the needle insertion length, and is the vector of current needle tip pose with and corresponding to the tip positions in and coordinates of the robot, while and are the tip vertical and horizontal rotation angles (in radians) about the robot’s - and -axis, respectively.
Since the function defined in (1) is unknown, at each insertion step , we can estimate it with a first-order linear approximation so that:
| (2) |
where and are the measured variations of the needle base and the needle tip at a given insertion step.
Given that (2) is a linear approximation of an unknown non-linear relationship between and , it is considered to be a good representation of our system only at the vicinity of insertion step . Our strategy is to compensate the local nature of (2) by means of constant data-driven iterative updates that only rely on the needle tip and robot positions, which are easily measured during the procedure, and does not depend on any assumption on the underlying physics.
The Jacobian matrix for our approximated model is estimated with the algorithm proposed in (Alambeigi et al. 2018), and based on Broyden’s method (Nocedal & Wright 2006). The updated Jacobian estimate is obtained from its previous estimate and the measured variations in and recursively with
| (3) |
where is a constant parameter for the update rate of .
2.3. Automatic closed-loop trajectory correction
After each model update, we use the new estimated Jacobian in a Model Predictive Control (MPC) formulation to obtain the needle guide positions that will minimize the tip trajectory error over a prediction horizon .
The trajectory error is defined to be the difference between the current tip horizontal and vertical positions and a straight-line trajectory, that is,
| (4) |
with and being coordinates of the initial entry point of the needle into the tissue, and given by the needle tip pose at step . We chose not to include the insertion depth in the control error definition because the insertion is done manually without robotic assistance. Also, the depth error is not critical in a biopsy targeting application as the specimen is obtained from a 15–20mm long sample along the needle axis.
Hence, in our MPC, we use (2) to predict for the next H steps, considering to be constant and equal to the last estimated Jacobian matrix.
The control input is obtained with an optimization algorithm that searches for the sequence of next needle guide displacements that minimizes the objective function given by
| (5) |
where is just a weight vector to balance the sum of different magnitude elements, that is, millimeters and radians.
The control input is given by the first element of the obtained sequence and is applied to the needle guide robot. After it moves, the insertion step is finished and step begins. The cycle is repeated until the last insertion step is performed and the needle reaches its final length.
2.4. Experimental setup
To evaluate our approach, we designed and fabricated two types of phantoms, and developed a robotic needle guide system with closed-loop feedback. The software system was built using the Robotics Operational System version 2 (ROS2). The following sections summarizes our setup and experiments.
2.4.1. . System architecture:
The needle guiding system comprises a robotic needle guide, an electromagnetic (EM) tracking system with a sensorized needle, and computational modules for model estimation and MPC control implemented in a control computer (Ubuntu 20.04), as depicted in Figure 4a.
Figure 4.

System architecture. (a) Overall schematic of the system. (b) Software components present in the control computer. In blue, the ROS2 package implemented in this work.
Both the robotic needle guide and the EM tracking system communicate with the desktop through USB interface. The PLUSServer Toolkit (Lasso et al. 2014) is used to receive data from the EM tracking system and stream them to other software using the OpenIGTLink communication protocol (Tokuda et al. 2009). With this modular approach, the EM tracking system can be easily replaced by other types of needle sensors or image tracking modules in the future.
The software components are implemented using ROS2 Foxy (Macenski et al. 2022) in three separate packages (Fig 4b). The first package is a bridge for the OpenIGTLink communication between the EM tracker and ROS2 (Frank et al. 2017). The second package consists of ROS services and nodes that communicate with the robot hardware to command its motors and was developed in a previous work (Mareschal 2022). The third package implements the needle trajectory control.
For modularity purposes, the trajectory control was implemented with independent ROS nodes. The sensor processing node is responsible for processing the needle tracking data by filtering and registering the current needle tip pose to robot coordinates. The model estimation node estimates the Jacobian data-driven model as defined in (3). And finally, the model predictive control node defines the robot horizontal and vertical displacements to correct needle trajectory error as defined in Section 2.3. The MPC algorithm was implemented with the SciPy Optimization library to minimize the objective function (5) using Sequential Least Squares Programming (SLSQP) algorithm (Nocedal & Wright 2006) with the 6mm safe limit as bound constraints.
2.4.2. In-vitro and ex-vivo phantoms:
Ideally, we should use both needle and phantoms with realistic mechanical properties obtained from clinical studies (Podder et al. 2006). However, our study design was constrained by the 21-gauge EM sensorized needle used to obtain the real-time tip location for steering. This sensorized needle was thinner and more flexible than the clinical biopsy and brachytherapy needles (typically 18-gauge). To reproduce the magnitude of needle deviation observed in the clinical cases with 18-gauge needles (Moreira et al. 2018), we optimized the phantom specifically for the EM sensorized needle. This setup allows us to evaluate our method for future clinical application with 18-gauge needles while using the available 21-gauge EM sensorized needle.
We designed two different types of phantoms for testing purposes (Figure 5a). Firstly, we created in-vitro phantoms made of a combination of gel wax (Wick, American Crafts, Lindon, UT) and solid wax (Yankee Candle/Luminessence) at different ratios (see Table 1) to obtain homogeneous materials at different stiffness that could also be re-heat for reuse after multiple perforations. These phantoms allowed us to perform several tests in a controlled environment with reasonable repeatability for validation of our experimental setup and software implementation. The second type is an ex-vivo phantom composed of pork meat immersed in gelatin (600ml water and 34g jello, Kraft Heinz) so we could test our controller in an inhomogeneous material with close properties to real tissue. Both types of phantoms also embedded a piece of fabric on its surface (4-ply gauze dressing, Walgreen Co.) to serve as a layer of skin tissue and mimic the patient’s perineum.
Figure 5.

(a) Phantoms used to validate the proposed trajectory correction by radial displacement. The phantoms were placed in a plastic container with the fabric layer surface facing an opening through which needle insertions were performed. (b) 2 DOF needle guide robot used for experiments.
Table 1.
In-vitro phantoms composition
| Phantom | gel wax | solid wax |
|---|---|---|
|
| ||
| A | 750g | 22g (Yankee) |
| B | 750g | 45g (Yankee) |
| C | 750g | 90g (Luminessence) |
2.4.3. Needle guide robot:
The needle guide robot (Figure 5b) makes use of two 100mm linear stages (ET-100–11 eTrack, Newmark, Santa Margarita, CA, USA) mounted perpendicularly and controlled by a two-axis stepper motor controller (NCS-2AL, Newmark). They communicate to our ROS2 system via a USB interface using the manufacturer’s Linux API. Each stepper motor is responsible for an independent degree of freedom, being the vertical and horizontal movements of our needle correction strategy. An extension with a sliding rail was attached to the vertical linear stage in order to provide a guiding ledge for the needle manual insertion. At the end of the rail, a 3D-printed needle guide assures that the needle approaches the phantom at a right angle.
2.4.4. Needle tracking:
For tracking the current needle tip pose, we use the Aurora EM tracking system (NDI Digital, Waterloo, ON, Canada), combined with a beveled 21-gauge instrumented needle with a 5DOF magnetic sensor at its tip. The magnetic field generator is fixed in front of the tissue phantom (Figure 6), and distant enough from the needle guide robot so that its field is not disturbed by ferromagnetic components. The tracking accuracy of the Aurora 21-gauge needle is reported to be 0.70mm by the manufacturer and measurements of the needle tip pose are updated at a 40Hz rate. After fixation, a registration procedure with 252 reference points was performed to estimate the transformation from the Aurora coordinate frame to the robot coordinate frame. The resultant homogeneous matrix is used by the sensor processing node to convert the needle tip pose given in the tracking system reference frame to robot coordinates.
Figure 6.

Experimental setup used to evaluate our proposed method. The stage extremity is zoomed in to show the needle inserted through the passive needle guide and entering into the tissue phantom.
2.5. Experimental evaluation
2.5.1. Data-driven estimation:
The data-driven Jacobian estimation was evaluated using real needle insertions performed in in-vitro phantom C. The needle was inserted 100mm manually at 5mm steps, and at the end of each step, the robot would move the needle radially with random values within a safe limit range of maximum 6mm in each direction. For each insertion, we recorded the needle guide displacements at every step, and the corresponding needle tip poses captured by the Aurora tracking system. These data were processed offline to update and (2) was used to predict the needle tip behavior for the next insertion step in comparison to what was recorded by the EM tracking. We used an update rate of and two different initial Jacobians were tested: one that was obtained experimentally from a set of three shallow (20mm) insertions into in-vitro phantom B, and another that was arbitrarily defined to be . The purpose of testing two different is to verify that our method has no dependency on the Jacobian initialization, and hence there is no need to perform prior parameter identification for each patient or tissue type.
2.5.2. Needle placement accuracy:
The performance of the automatic closed-loop trajectory correction was evaluated against open-loop insertions by comparing the final needle placement error in a series of 5 insertions of each, using in-vitro phantom A. An open-loop insertion was defined as a single attempt insertion where the needle is initially aligned with the target using a static needle guide and then pushed manually without any adjustment until the tip reaches the planned depth.
The needle placement error was calculated as the Euclidean distance between the final needle tip position and a straight-line trajectory from the needle entry point. Both open- and closed-loop insertions were performed manually with 100mm total length and 5mm steps. We used an update rate of and an arbitrarily defined matrix for the estimator. For the MPC, we defined and for the prediction horizon based on preliminary insertions data. Since our data-driven model is a local linear approximation, the model holds only for a short-term prediction. Meanwhile, long-term prediction is necessary for better control performance. Therefore, the horizon size was optimized to balance the accuracy and the time range of prediction.
Additionally, we investigated changes in the controller performance for different stiffness tissues by repeating the experiment with phantoms B and C, and then for inhomogeneous tissue with the ex-vivo phantom. Phantoms A and B were made with a composition that resulted in needle deflections within the range of values more frequently observed when performing planned straight-line insertions with a needle guide in a clinical study (Moreira et al. 2018). However, we also wanted to test the proposed controller in a wider range of conditions to better characterize its performance and limitations. For that reason, we included tests in phantom C, which was made intentionally stiffer, as an extreme case that is less likely to happen in clinical practice.
3. Results
3.1. Data-driven estimation results
During stepwise needle insertions with random motions of the needle guide, our data-driven method was able to estimate the needle tip position, as depicted in Figure 7. The total RMS error of the estimated tip position obtained from our data-driven model was 0.52mm when using an experimentally obtained , and 0.88mm for an arbitrarily defined (Figure 8). Those results were comparable values with the Aurora sensor accuracy of 0.70mm, used as our ground truth.
Figure 7.

Estimation results using an arbitrary . (a) Random radial displacement applied at the needle guide. (b) Correspondent needle tip positions in robot coordinates. In blue, our model estimation. In red, actual values measured by the EM tracker.
Figure 8.

Data-driven model estimate errors for prediction of the needle tip position when using different initial Jacobians. (a) Experimentally obtained . (b) Arbitrarily defined
If we consider just the second half of the insertion that is, insertion length from 50 to 100mm, the RMS errors were 0.51mm, for the experimental , and 0.53mm for the arbitrary , showing that the model converges to similar prediction accuracy, regardless of the initial Jacobian estimate.
3.2. Needle placement accuracy results
3.2.1. Automatic closed-loop performance:
The plots in Figure 9 show the trajectory errors at each step for all insertions performed into phantom A. The mean final needle placement error with MPC correction was only 0.24 ± 0.10mm against 5.30 ± 0.60mm in open-loop. This represents a decrease of 95.47% in the final placement error when using the proposed data-driven control strategy.
Figure 9.

Trajectory errors for needle insertions into phantom A. In blue, 5 insertions in open-loop. In red, 5 insertions with closed-loop MPC control.
3.2.2. Influence of different tissue stiffness:
The same experiment was repeated for phantoms B and C and the results are presented in Table 2 for 5 trials each. The results show that the controller had a similar performance for phantoms A and B, hence being able to adapt to different tissue properties without a priori information about the needle and tissue mechanical properties. The same controller was also able to correct the needle deflection for phantom C, but with slightly inferior performance.
Table 2.
Mean final tip placement error [mm] for 100 mm length insertions into different stiffness phantoms
| Phantom | No correction | MPC correction | Error reduction |
|---|---|---|---|
|
| |||
| A | 5.30 ± 0.60 | 0.24 ± 0.10 | 95.47% |
| B | 6.51 ± 0.27 | 0.48 ± 0.17 | 92.26% |
| C | 8.70 ± 0.33 | 1.65 ± 0.48 | 81.03% |
3.2.3. Ex-vivo experiment:
The final placement error with closed-loop trajectory correction in the ex-vivo phantom after 5 insertions with 100mm length and 5mm steps was 0.34 ± 0.15mm while the mean final placement error without correction was 9.06 ± 0.42 mm. This represents a 96.25% reduction, which is similar to the performance obtained with phantoms A and B. One of the trials is depicted in Figure 10, which shows the radial motion performed by the needle guide in both horizontal and vertical directions, and the correspondent effect on the needle tip position. In this trial, the needle tip was successfully kept in the planned straight-line trajectory. From the results, our data-driven approach was also able to compensate for needle deflection during insertions in inhomogeneous tissue with the presence of different layers of muscle, fat, and ligaments.
Figure 10.

Example of a stepwise 100mm length needle insertion into ex-vivo phantom with (red) and without (blue) MPC closed-loop control. (a) Displacements applied at the needle guide. (b) Correspondent needle tip positions in both vertical and horizontal directions.
4. Discussion
Our data-driven model was able to capture the local relationship between the needle tip and needle guide displacement without previous knowledge of needle-tissue properties. The results from the data-driven estimation experiments show that even when we purposely used an arbitrary initial Jacobian , it did not have a significant impact on the model accuracy after a few updates.
As we can see from the plots for the arbitrary Jacobian (Figure 8b), errors were slightly higher at the beginning of the insertion, when there was still some residual influence of in the current estimate. These errors, however, were still reasonable with a maximum value inferior to 1.3mm, and after a few insertion steps, the estimated error was consistently inside the sensor accuracy range, and with similar values to the trial using an experimentally obtained initial Jacobian. Additionally, results depicted on Figure 8a suggest that we can successfully use data from previous patients as a starting point for our Jacobian estimate, since the experimental obtained with phantom B was successfully used for insertions on phantom C. From these results, we can conclude that the proposed approach does not require prior identification of tissue or patient parameters, which was one of our initial hypothesis.
The placement accuracy experiments showed that the data-driven MPC formulation was able to significantly reduce the needle trajectory error in closed-loop using horizontal and vertical displacement of the needle guide to adjust the needle tip position. Also, it was robust to different tissue stiffness and tissue inhomogeneity, with similar performance in different phantoms.
We noticed, however, a small decline in performance as we used a significantly stiffer tissue (phantom C). Investigating further, we identified that this specific combination of needle and tissue demanded that the needle guide move beyond the safe limit we had imposed to be able to correct the higher needle deflection. Consequently, the controller output was often saturated at its maximum, and not able to correct the deviation any further. To better quantify such effect, we used a metric defined as the percentage of insertion in which the controller was in its maximum limit (horizontal or vertical), and while it was 11%, 15% and 9% for phantoms A, B and ex-vivo respectively, for phantom C it was 43%.
This indicates that the performance of the proposed approach depends on a balance between the imposed safety limit and the system steerability, that is, the capability of influencing tip behavior through the displacement of the needle guide. It is already known that such steerability decreases with insertion depth (Lehmann et al. 2017). From our experiments, it was observed that steerability also depends on the relative stiffness of the needle against the tissue, and the rigidity of the skin at the entry point. As the rigidity of the entry point increases, it acts as a fulcrum, improving the steerability of the system, with specially greater effect at shallower insertion depths.
Additional tests under the same conditions as previous experiments performed in phantom A without the fabric layer on its surface presented final error placement of 0.80±0.62mm corresponding to only 89.06% error reduction against 95.47%, with 58% of the insertion performed with the control in saturation. These results confirm that the system steerability increases with a more rigid entry point.
As a consequence, we believe that the addition of a second needle guide fixed at the entry point and close to the patient’s perineum, similarly to the standard transperineal template guide (Penzkofer et al. 2015), could not only inscrease the overall system steerability but even prevent the risk of tissue damage and extend this approach to other clinical applications where the patient’s skin does not presents enough resistance to provide sufficient steerability while keeping the control actuation within the safe limit.
Nevertheless, considering the results of our ex-vivo experiments, the final mean placement error for insertions without correction (9.06±0.42mm) is similar to the values observed in clinical data from prostate interventions (Moreira et al. 2021). Previous studies show that smaller targeting errors result in better sensitivity of PCa detection in biopsies (Robertson et al. 2014). The significant (96.25%) error reduction obtained with the use of radial displacement for needle correction indicates that its use could substantially improve clinical outcomes.
It should be noted that our accuracy experiments compare the performance of the assist system against single attempt insertions, that is, open-loop insertions performed without trajectory correction by image guidance. Hence, while encouraging, the resulting accuracy improvement should not be interpreted as the overall improvement over clinical routine. The complete clinical procedure is performed in an iterative fashion, with frequent retraction and reinsertion of the needle to readjust its final placement, and the resultant final procedural error is likely smaller than the error from a single attempt insertion. Our approach, in contrast, has the potential to achieve accurate insertion in one attempt and eliminate the need for the iterative process, which leads to prolonged procedure time and unnecessary tissue damage.
This motivates further development to integrate our approach with an image-guided therapy framework based on previously developed MRI-guided prostate biopsy robots (Song et al. 2013, Patel et al. 2019). Since the radial displacement strategy does not require an additional DOF for needle rotation, it can be easily incorporated into devices already used in clinical studies, and even combined with a grid template for multiple-probe insertions, allowing its use in transperineal prostate cryoablation and brachytherapy applications.
Our plan for clinical translation is to replace the Aurora EM sensorized needle with a clinical 18-gauge biopsy or brachytherapy needle. For needle location feedback, we will use either a shape-sensing needle based on Fiber-Bragg-Grating (Borot de Battisti et al. 2016, Lezcano et al. 2022) or image-based needle tracking algorithm for real-time MRI. It is important to note that our accuracy evaluation is limited by the precision of the Aurora system, which is reported to be 0.70mm. Consequently, errors smaller than such value should be interpreted as a value smaller or equal to 0.70mm.
5. Conclusion
This paper proposed a novel method for correcting needle deflection using a data-driven approach instead of relying on mechanical based modeling of the needle-tissue interaction. It combines the online estimation of a Jacobian model and an MPC scheme that uses radial needle displacement to correct needle tip deflection during collaborative insertion.
It was experimentally validated on both in-vitro and inhomogeneous ex-vivo phantoms with encouraging results. They show that our insertion assist system achieved good performance, being able to reduce the final needle placement error by more than 96% when compared to the open-loop insertion for the ex-vivo phantom.
Also, to achieve similar steerability for different needle-tissue combinations, we intend to incorporate a second fixed needle guide to act as a rigid fulcrum at the needle entry point. We concluded from our tests that such improvement in the system design could increase its steerability while avoiding additional trauma to the patient. This could also expand the possible clinical applications of our approach to more delicate tissue.
In our experiments, we restricted the scenario to a straight trajectory control problem, but tissue deformation during needle insertion may cause the target to shift from its original position, resulting in a change in the aimed trajectory. We believe the presented method can be adjusted to moving targets if properly integrated with online tracking of the desired goal position. Such adjustments should be considered before moving forward to animal and clinical studies.
Acknowledgments
The study was funded in part by the National Institutes of Health (R01CA235134, R01EB020667, and P41EB028741). The content of the material is solely the responsibility of the authors and does not necessarily represent the official views of these agencies. The authors have confirmed that any identifiable participants in this study have given their consent for publication.
References
- Adagolodjo Y, Goffin L, De Mathelin M & Courtecuisse H (2019), ‘Robotic insertion of flexible needle in deformable structures using inverse finite-element simulation’, IEEE Transactions on Robotics 35(3). [Google Scholar]
- Alambeigi F, Wang Z, Hegeman R, Liu Y-H & Armand M (2018), ‘A robust data-driven approach for online learning and manipulation of unmodeled 3-D heterogeneous compliant objects’, IEEE Robotics and Automation Letters 3(4), 4140–4147. [Google Scholar]
- Baksic P, Courtecuisse H & Bayle B (2021), Shared control strategy for needle insertion into deformable tissue using inverse finite element simulation, in ‘Proc. IEEE International Conference on Robotics and Automation (ICRA)’, pp. 12442–12448. [Google Scholar]
- Bomers JG, Overduin CG, Jenniskens SF, Cornel EB, van Lin EN, Sedelaar JM & Fütterer JJ (2020), ‘Focal salvage MR imaging-guided cryoablation for localized prostate cancer recurrence after radiotherapy: 12-month follow-up’, Journal of Vascular and Interventional Radiology 31(1), 35–41. [DOI] [PubMed] [Google Scholar]
- Borot de Battisti M, Denis de Senneville B, Maenhout M, Lagendijk JJW, van Vulpen M, Hautvast G, Binnekamp D & Moerland MA (2016), ‘Fiber bragg gratings-based sensing for real-time needle tracking during MR-guided brachytherapy’, Medical Physics 43(10), 5288–5297. [DOI] [PubMed] [Google Scholar]
- Chevrie J, Shahriari N, Babel M, Krupa A & Misra S (2018), ‘Flexible needle steering in moving biological tissue with motion compensation using ultrasound and force feedback’, IEEE Robotics and Automation Letters 3(3), 2338–2345. [Google Scholar]
- de Marini P, Cazzato RL, Garnon J, Shaygi B, Koch G, Auloge P, Tricard T, Lang H & Gangi A (2019), ‘Percutaneous MR-guided prostate cancer cryoablation technical updates and literature review’, BJR—Open 1(1), 20180043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vries M, Sikorski J, Misra S & van den Dobbelsteen JJ (2021), ‘Axially rigid steerable needle with compliant active tip control’, PLOS ONE 16(12), 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duriez C, Guébert C, Marchal M, Cotin S & Grisoni L (2009), Interactive simulation of flexible needle insertions based on constraint models, in Yang G-Z, Hawkes D, Rueckert D, Noble A & Taylor C, eds, ‘Medical Image Computing and Computer-Assisted Intervention (MICCAI)’, Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 291–299. [DOI] [PubMed] [Google Scholar]
- Favaro A, Secoli R, Baena F. R. y. & Momi ED (2020), ‘Model-based robust pose estimation for a multi-segment, programmable bevel-tip steerable needle’, IEEE Robotics and Automation Letters 5(4), 6780–6787. [Google Scholar]
- Frank T, Krieger A, Leonard S, Patel NA & Tokuda J (2017), ‘ROS-IGTL-Bridge: an open network interface for image-guided therapy using the ROS environment’, International Journal of Computer Assisted Radiology and Surgery 12(8), 1452–1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goksel O, Dehghan E & Salcudean SE (2009), ‘Modeling and simulation of flexible needles’, Medical Engineering & Physics 31(9), 1069–1078. [DOI] [PubMed] [Google Scholar]
- Hamzé N, Peterlík I, Cotin S & Essert C (2016), ‘Preoperative trajectory planning for percutaneous procedures in deformable environments’, Computerized Medical Imaging and Graphics 47, 16–28. [DOI] [PubMed] [Google Scholar]
- Jones JS, Rewcastle JC, Donnelly BJ, Lugnani FM, Pisters LL & Katz AE (2008), ‘Whole gland primary prostate cryoablation: Initial results from the cryo on-line data registry’, Journal of Urology 180(2), 554–558. [DOI] [PubMed] [Google Scholar]
- King MT, Keyes M, Frank SJ, Crook JM, Butler WM, Rossi PJ, Cox BW, Showalter TN, Mourtada F, Potters L, Stock RG, Kollmeier MA, Zelefsky MJ, Davis BJ, Merrick GS & Orio PF (2021), ‘Low dose rate brachytherapy for primary treatment of localized prostate cancer: A systemic review and executive summary of an evidence-based consensus statement’, Brachytherapy 20(6), 1114–1129. [DOI] [PubMed] [Google Scholar]
- Konh B, Berkelman P & Karimi S (2020), Needle tip manipulation and control of a 3d steerable sma-activated flexible needle, in ‘IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob)’, pp. 903–909. [Google Scholar]
- Krieger A, Susil R, Menard C, Coleman J, Fichtinger G, Atalar E & Whitcomb L (2005), ‘Design of a novel MRI compatible manipulator for image guided prostate interventions’, IEEE Transactions on Biomedical Engineering 52(2), 306–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasso A, Heffter T, Rankin A, Pinter C, Ungi T & Fichtinger G (2014), ‘PLUS: Open-source toolkit for ultrasound-guided intervention systems’, IEEE Transactions on Biomedical Engineering 61(10), 2527–2537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann T, Rossa C, Usmani N, Sloboda R & Tavakoli M (2017), ‘Deflection modeling for a needle actuated by lateral force and axial rotation during insertion in soft phantom tissue’, Mechatronics 48, 42–53. [Google Scholar]
- Lehmann T, Sloboda R, Usmani N & Tavakoli M (2018), ‘Model-based needle steering in soft tissue via lateral needle actuation’, IEEE Robotics and Automation Letters 3(4), 3930–3936. [Google Scholar]
- Lezcano DA, Kim MJ, Iordachita II & Kim JS (2022), Toward FBG-sensorized needle shape prediction in tissue insertions, in ‘IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)’, pp. 3505–3511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macenski S, Foote T, Gerkey B, Lalancette C & Woodall W (2022), ‘Robot Operating System 2: Design, architecture, and uses in the wild’, Science Robotics 7(66), eabm6074. [DOI] [PubMed] [Google Scholar]
- Mareschal L (2022), Bench-top pre-clinical evaluation of adaptive needle steering for image-guided prostate intervention using shape sensing needle, Master’s thesis, École Polytechnique Fédérale de Lausanne, Switzerland. [Google Scholar]
- Misra S, Reed K, Schafer B, Ramesh K & Okamura A (2010), ‘Mechanics of flexible needles robotically steered through soft tissue’, The International Journal of Robotics Research 29(13), 1640–1660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreira P, Patel N, Wartenberg M, Li G, Tuncali K, Heffter T, Burdette EC, Iordachita I, Fischer GS, Hata N, Tempany CM & Tokuda J (2018), ‘Evaluation of robot-assisted MRI-guided prostate biopsy: needle path analysis during clinical trials’, Phys Med Biol 63(20), 20NT02. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreira P, Tuncali K, Tempany CM & Tokuda J (2021), ‘The impact of placement errors on the tumor coverage in MRI-guided focal cryoablation of prostate cancer’, Academic Radiology 28(6), 841–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen PL, Chen M-H, Zhang Y, Tempany CM, Cormack RA, Beard CJ, Hurwitz MD, Suh WW & D’Amico AV (2012), ‘Updated results of magnetic resonance imaging guided partial prostate brachytherapy for favorable risk prostate cancer: Implications for focal therapy’, Journal of Urology 188(4), 1151–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nocedal J & Wright SJ (2006), Numerical optimization, Springer Series in Operations Research and Financial Engineering, 2 edn, Springer-Verlag; New York. [Google Scholar]
- Park W, Kim JS, Zhou Y, Cowan N, Okamura A & Chirikjian G (2005), Diffusion-based motion planning for a nonholonomic flexible needle model, in ‘Proc. IEEE International Conference on Robotics and Automation (ICRA)’, pp. 4600–4605. [Google Scholar]
- Patel NA, Li G, Shang W, Wartenberg M, Heffter T, Burdette EC, Iordachita I, Tokuda J, Hata N, Tempany CM & Fischer GS (2019), ‘System integration and preliminary clinical evaluation of a robotic system for MRI-guided transperineal prostate biopsy’, Journal of Medical Robotics Research 04(02), 1950001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penzkofer T, Tuncali K, Fedorov A, Song S-E, Tokuda J, Fennessy FM, Vangel MG, Kibel AS, Mulkern RV, Wells WM, Hata N & Tempany CMC (2015), ‘Transperineal in-bore 3-T MR imaging–guided prostate biopsy: A prospective clinical observational study, Radiology 274(1), 170–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinzi M, Watts T, Secoli R, Galvan S & Baena F. R. y. (2021), ‘Path replanning for orientation-constrained needle steering’, IEEE Transactions on Biomedical Engineering 68(5), 1459–1466. [DOI] [PubMed] [Google Scholar]
- Podder T, Clark D, Sherman J, Fuller D, Messing E, Rubens D, Strang J, Brasacchio R, Liao L, Ng W-S & Yu Y (2006), ‘In vivo motion and force measurement of surgical needle intervention during prostate brachytherapy’, Medical Physics 33(8), 2915–2922. [DOI] [PubMed] [Google Scholar]
- Ragde H, Korb J, L., Elgamal AA, Grado GL & Nadir BS (2000), ‘Modern prostate brachytherapy. prostate specific antigen results in 219 patients with up to 12 years of observed follow-up’, Cancer 89(1), 135–141. [PubMed] [Google Scholar]
- Robertson NL, Hu Y, Ahmed HU, Freeman A, Barratt D & Emberton M (2014), ‘Prostate cancer risk inflation as a consequence of image-targeted biopsy of the prostate: a computer simulation study’, European Urology 65(3), 628–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossa C, Usmani N, Sloboda R & Tavakoli M (2017), ‘A hand-held assistant for semiautomated percutaneous needle steering’, IEEE Transactions on Biomedical Engineering 64(3), 637–648. [DOI] [PubMed] [Google Scholar]
- Song S-E, Tokuda J, Tuncali K, Tempany CM, Zhang E & Hata N (2013), ‘Development and preliminary evaluation of a motorized needle guide template for MRI-guided targeted prostate biopsy’, IEEE Transactions on Biomedical Engineering 60(11), 3019–3027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoianovici D, Kim C, Petrisor D, Jun C, Lim S, Ball MW, Ross A, Macura KJ & Allaf ME (2017), ‘MR safe robot, FDA clearance, safety and feasibility of prostate biopsy clinical trial’, IEEE/ASME Transactions on Mechatronics 22(1), 115–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swaney PJ, Burgner J, Gilbert HB & Webster RJ (2013), ‘A flexure-based steerable needle: High curvature with reduced tissue damage’, IEEE Transactions on Biomedical Engineering 60(4), 906–909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilak G, Tuncali K, Song S-E, Tokuda J, Olubiyi O, Fennessy F, Fedorov A, Penzkofer T, Tempany C & Hata N (2015), ‘3T MR-guided in-bore transperineal prostate biopsy: A comparison of robotic and manual needle-guidance templates’, Journal of Magnetic Resonance Imaging 42(1), 63–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokuda J, Fischer GS, Papademetris X, Yaniv Z, Ibanez L, Cheng P, Liu H, Blevins J, Arata J, Golby AJ, Kapur T, Pieper S, Burdette EC, Fichtinger G, Tempany CM & Hata N (2009), ‘OpenIGTLink: an open network protocol for image-guided therapy environment’, The International Journal of Medical Robotics and Computer Assisted Surgery 5(4), 423–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Gerwen DJ, J., D. & van den Dobbelsteen JJ (2012), ‘Needle-tissue interaction forces - A survey of experimental data’, Medical Engineering and Physics 34(6), 665–680. [DOI] [PubMed] [Google Scholar]
- van Luijtelaar A, Greenwood BM, Ahmed HU, Barqawi AB, Barret E, Bomers JGR, Brausi MA, Choyke PL, Cooperberg MR, Eggener S, Feller JF, Frauscher F, George AK, Hindley RG, Jenniskens SFM, Klotz L, Kovacs G, Lindner U, Loeb S, Margolis DJ, Marks LS, May S, Mcclure TD, Montironi R, Nour SG, Oto A, Polascik TJ, Rastinehad AR, De Reyke TM, Reijnen JS, de la Rosette JJMCH, Sedelaar JPM, Sperling DS, Walser EM, Ward JF, Villers A, Ghai S & Fütterer JJ (2019), ‘Focal laser ablation as clinical treatment of prostate cancer: Report from a Delphi consensus project’, World Journal of Urology 37(10), 2147–2153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wartenberg M, Schornak J, Gandomi K, Carvalho P, Nycz C, Patel N, Iordachita I, Tempany C, Hata N, Tokuda J & Fischer GS (2018), ‘Closed-loop active compensation for needle deflection and target shift during cooperatively controlled robotic needle insertion’, Ann Biomed Eng 46(10), 1582–1594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster III RJ, Kim JS, Cowan NJ, Chirikjian GS & Okamura AM (2006), ‘Nonholonomic modeling of needle steering’, The International Journal of Robotics Research 25(5–6), 509–525. [Google Scholar]
- Yakar D, Schouten MG, Bosboom DGH, Barentsz JO, Scheenen TWJ & Fütterer JJ (2011), ‘Feasibility of a pneumatically actuated MR-compatible robot for transrectal prostate biopsy guidance’, Radiology 260(1), 241–247. [DOI] [PubMed] [Google Scholar]


