Atomistic simulations modify interpretation of spin-label oximetry data. Part 1: intensified water–lipid interfacial resistances

Abstract

The role of membrane cholesterol in cellular function and dysfunction has been the subject of much inquiry. A few studies have suggested that cholesterol may slow oxygen diffusive transport, altering membrane physical properties and reducing oxygen permeability. The primary experimental technique used in recent years to study membrane oxygen transport is saturation-recovery electron paramagnetic resonance (EPR) oximetry, using spin-label probes targeted to specific regions of a lipid bilayer. The technique has been used, in particular, to assess the influence of cholesterol on oxygen transport and membrane permeability. The reliability of such EPR recordings at the water–lipid interface near the phospholipid headgroups has been challenged by all-atom molecular dynamics (MD) simulation data that show substantive agreement with spin-label probe measurements throughout much of the bilayer. This work uses further MD simulations, with an updated oxygen model, to determine the location of the maximum resistance to permeation and the rate-limiting barrier to oxygen permeation in 1-palmitoyl,2-oleoylphosphatidylcholine (POPC) and POPC/cholesterol bilayers at 25 and 35°C. The current simulations show a spike of resistance to permeation in the headgroup region that was not detected by EPR but was predicted in early theoretical work by Diamond and Katz. Published experimental nuclear magnetic resonance (NMR) oxygen measurements provide key validation of the MD models and indicate that the positions and relative magnitudes of the phosphatidylcholine resistance peaks are accurate. Consideration of the headgroup-region resistances predicts bilayer permeability coefficients lower than estimated in EPR studies, giving permeabilities lower than the permeability of unstirred water layers of the same thickness. Here, the permeability of POPC at 35°C is estimated to be 13 cm/s, compared with 10 cm/s for POPC/cholesterol and 118 cm/s for simulation water layers of similar thickness. The value for POPC is 12 times lower than estimated from EPR measurements, while the value for POPC/cholesterol is 5 times lower. These findings underscore the value of atomic resolution models for guiding the interpretation of experimental probe-based measurements.

1. Introduction

Cholesterol was first detected in organisms during the great oxygenation event. For that reason, cholesterol biosynthesis is hypothesized to have arisen as a protective response against oxygen (O₂) toxicity [1–3]. Indeed, membrane cholesterol is thought to protect the eye lens from oxidative damage and associated ocular cataract [4–6], by rigidifying the cell membrane and hindering oxygen transport [7]. However, cholesterol incorporation in membranes can also have adverse health effects. Dysregulation of cholesterol homeostasis has long been recognized as a hallmark of cancer, and numerous studies indicate that cholesterol (especially in mitochondria) promotes carcinogenesis [1,8–10]. Given that membrane cholesterol can reduce the rate of oxygen permeation [11,12], it is reasonable to suspect that cholesterol may contribute to intracellular hypoxia [13]. Hypoxia favors cancer cells because their response to it promotes survival by evading the apoptotic cell-death pathway [14–16].

The partitioning of oxygen toward hydrophobic media [17] has been suggested to enable rapid oxygen diffusion through the pulmonary surfactant membrane network present in alveoli [18,19]. Blood transport of oxygen is, in principle, facilitated by the hemoglobin contained within red blood cells (RBCs). Yet, upon absorption and release, oxygen must cross the RBC plasma membrane. Elevated RBC membrane cholesterol due to hypercholesterolemia has been reported to negatively influence the uptake and release of oxygen [20,21]. Biophysical studies to date [11,12,22–25] support the idea that membrane cholesterol content affects the distribution and dynamics of oxygen but do not fully explain why RBC oxygen uptake and release would be affected as strongly as observed experimentally [20,21]. Moreover, oxygen concentration gradients measured across mammalian (Chinese hamster ovary, CHO) cell plasma membranes are remarkably large and inflate further with increased membrane cholesterol content [13]. The meaning of these gradients with respect to membrane permeability has been a subject of debate [26,27].

Oxygen diffusive transport via lipid bilayers has been studied experimentally using fluorescence quenching [7,28–31], nuclear magnetic resonance (NMR) spectrometry [32,33], and electron paramagnetic resonance (EPR) oximetry [34–38]. Fluorescence measurements have low spatial resolution, relative to lipid bilayer depth, but have shown differential effects of cholesterol on oxygen diffusion in the lipid bilayer center versus the internal part of the membrane surface [Dumas 1997]. NMR oxygen measurements are achieved through chemical shift changes caused by nearby paramagnetic oxygen [33,39,40] but have a high detection limit and, thus, require sample exposure to O₂ pressures in the range of 20–50 bar [32,33,40,41]. High-resolution bilayer-depth-dependent oxygen concentration curves have been produced with ¹³C NMR [32,33], but application of the technique has been limited. Saturation-recovery EPR is sensitive to O₂ levels occurring in samples exposed to air at atmospheric pressure [23,42] and has moderate bilayer-depth resolution.

An EPR spin-label oxygen measurement technique has been employed in numerous studies, including several addressing the effects of cholesterol on oxygen transport as well as lipid phase separation [11,43–46]. The method uses lipid-conjugated spin-label probes to detect oxygen at various depths along a lipid bilayer [36,47], relying on differential spin-relaxation times for a radical electron in the presence and absence of oxygen [34,43]. Positional fluctuation of the spin-label moieties leads to a large estimated uncertainty of ±30% for bilayer oxygen permeability coefficients calculated from spin-labeled lipid measurements [11]. The depth location of the TEMPO-phosphocholine (T-PC) lipid conjugate used to measure oxygen in the bilayer headgroup region has been of particular concern, as earlier simulation work with POPC and POPC/cholesterol found strong agreement with EPR measurements throughout the bilayer, except in the headgroup region, where the simulation resistances were found to be much higher than experimental estimates [12,48]. A prior atomic resolution molecular dynamics simulation study by Kyrychenko and Ladokhin found the preferred depth position of the T-PC probe moiety (at 11 mol% in POPC) to be several angstroms below the lipid headgroups, toward the bilayer center [Kyrychenko 2013]. This finding suggests that the EPR technique may not measure oxygen accurately in the lipid–water interfacial regions.

The current work considers in detail the resistance distribution across the lipid bilayer, demonstrating that the headgroup resistances are critical determinants of the overall permeability. Specifically, we find that the maximal resistance to permeation and the rate-limiting barrier to oxygen permeation occurs in the headgroup region of POPC and POPC/cholesterol bilayers (not considering unstirred water layer effects). These findings will affect the interpretation of experimental EPR data relative to O₂ permeability and possibly also to the permeability of other gases of similar size, such as NO and CO. The work is motivated by a lack of detailed understanding of the local influence of cholesterol on the physical properties of lipid bilayers, which may give rise to global changes in membrane permeability and transmembrane concentration gradients.

2. Methods

2.1. Simulations

All simulations were conducted using the GPU-enabled molecular dynamics (MD) engine PMEMD-CUDA [49] of the AMBER biomolecular simulation software suite, version 14 [50]. The single precision fixed point (SPFP) model was used in compiling the PMEMD-CUDA code [49]. Simulation bilayers were built using the CHARMM-GUI online interface [51–53]. Two types of bilayer were constructed: POPC, with 64 POPC molecules per leaflet, and POPC/cholesterol (POPC/chol) in a 1:1 mole ratio, with 32 POPC and 32 cholesterol molecules per leaflet. All simulation systems were initially built with 35 TIP3P [54] water molecules per lipid. As in our previous work, O₂ molecules were subsequently introduced into the water layer by replacing water molecules [12]. The simulation system details are summarized in Table 1, and simulation snapshot images are shown in Fig. 1.

Table 1.

Simulation system compositions (number of molecules) and temperatures

System	POPCa	Cholesterola	Water	O2	T (K)
POPC, 25°C	64/64	0/0	4,440	40	298
POPC, 35°C	64/64	0/0	4,440	40	308
POPC/chol, 25°C	32/32	32/32	4,436	44	298
POPC/chol, 35°C	32/32	32/32	4,436	44	308

^aMolecules per leaflet.

Figure 1.

Simulation snapshot images of POPC (left) and POPC/chol (right) at 298 K. O₂ shown as red spheres and water molecules as reduced-size gray spheres. POPC headgroup carbons shown in green, tail carbons in gray, and cholesterol carbons in yellow. Other atoms colored by element, with N in blue, O in light red, and P in dark yellow. All H atoms hidden for clarity. Simulation periodic box boundaries shown with superimposed rectangles.

The following force fields were used: AMBER Lipid14 [55]; Lipid14 cholesterol extension [56]; and in-house molecular oxygen model with bond length 1.21Å [57], vibrational force constant 849.16 kcal/mol/Ų [58], and Lennard-Jones parameters equivalent to the carbonyl ester atom type (oC) in Lipid14 (radius R = 1.6500 Å and well depth ε = 0.140 kcal/mol) [59]. This O₂ model is updated relative to earlier work [12] and shows substantial improvement in the accuracy of lipid–water partitioning, which had been exaggerated by a factor of 2 or 3 [60].

Periodic boundary conditions were applied using particle mesh Ewald [61–63] to compute long-range electrostatic interactions, with a cutoff distance of 10 Å. Following energy minimization, heating, and volume equilibration, the lipids were allowed to mix for 320 ns of unrestrained molecular dynamics prior to production. The mixing phase and subsequent production were conducted in the NPT ensemble, using the Monte Carlo barostat to maintain a pressure of 1 bar and Langevin temperature control with a collision frequency of 1.0 ps⁻¹ to maintain a target temperature of either 298 K or 308 K (25°C or 35°C). These temperatures were chosen for direct comparison with EPR oximetry experimental data [11]. A timestep of 2 fs was employed throughout mixing and production, and the SHAKE algorithm was applied with a tolerance of 10⁻⁶ Å, restraining all bonds to hydrogen. Translational center of mass motion was removed every 1,000 steps (2 ps). Production simulations began 1 ns after adding oxygen to the premixed bilayers and continued without restraints for 190 ns. Coordinates and system information were recorded every picosecond.

2.2. Oxygen transport parameter and resistance to permeation calculations

The transport of oxygen through a lipid bilayer has been described by the diffusive permeation model [64,65] and the inhomogeneous solubility–diffusion model [66,67]. EPR oximetry measures the oxygen transport parameter, a function of both concentration and transbilayer diffusion of oxygen [11,34,42]. The technique relies on paramagnetic probes located at various depths, z, within the bilayer. Here, the z axis is perpendicular to the plane of the bilayer, with the bilayer center at z = 0 Å. Molecular oxygen, a paramagnetic species, can have a pronounced effect on electron spin-spin exchange (Heisenberg exchange) for an EPR probe, affecting its spin-lattice relaxation time from an excited state, T₁ [34,68–70]. The oxygen transport parameter, W(z), is calculated from the difference between the spin-lattice relaxation time in air vs. nitrogen environments at a given depth, z, within the bilayer:

$$W(z)=T_1^{-1}(air,z)-T_1^{-1}\left(N_2,z\right).$$ (1)

W(z) has been interpreted as the product of the depth-dependent oxygen concentration, C(z), and the depth-dependent diffusion coefficient, D(z), scaled by a constant, A, which depends on the probability of interaction between oxygen and the spin-label radical electron [34,42]:

$$W(z)=AC(z)D(z).$$ (2)

Here, A = 8πpr, where r is the interaction distance between oxygen and the probe electron and is taken to be 4.5 Å and where p is the probability that a collision will be detected and is assumed to equal one [42]. W(z) is generally expressed in per-microsecond units (μs⁻¹), and its reciprocal, W⁻¹(z), is a measure of resistance to oxygen permeation [11,42,71].

For comparison with EPR oximetry data, a simulation oxygen transport parameter, W_MD(z), can be calculated directly from C(z) and D(z) curves, as in a previous study by our group [12]:

$$W_{MD}(z)=A{X}_{P}C(z)D(z).$$ (3)

Here, X_p is the mole fraction of EPR probe used in experimental bilayer preparations. Relevant EPR experiments used 1 mol% of probe in POPC [11,72]. Thus, X_p is given the value 0.010 for pure POPC bilayers and 0.005 for 50% POPC/cholesterol [12]. For analysis, the simulation bilayer is divided into 1-Å thick slabs along the z axis, and c(z) is the fractional concentration of oxygen in a given slab—namely, the population of oxygen in that slab divided by the total population and by the slab volume [12]. W_MD(z) values were calculated over the whole of each production run.

Accurate and reliable calculation of depth-dependent diffusion coefficients in lipid bilayers continues to be a challenge in the field. For the current work, the depth-dependent diffusion coefficient, D(z), was approximated using an equation derived from the Einstein relation:

$$D(z)=\frac{1}{6t}\langle {\left(r_t-r_0\right)}^2\rangle .$$ (4)

This equation relates the mean square displacement of oxygen to the diffusion coefficient. For the purpose of comparison with EPR measurements, D(z) was calculated based on oxygen displacements in all three directions, assuming EPR probe relaxation is agnostic to the direction of O₂ motion. Here, 6 quantifies the number of degrees of freedom for movement in 3 dimensions (x, y, z); t = 1 ps is the time interval for displacements; r_t is the oxygen position at time t; and r₀ is the reference position. As in our earlier work [12] and consistent with the recommendation of Marrink and Berendsen [64], r₀ was reset every 1 ps. This method of estimating D(z) tends to overestimate D(z) in high-energy regions [73]. In addition, the depth position, z, of each displacement (r_t − r₀), was determined as the mean z-depth traversed during the time interval, producing additional error in high-energy regions due to positional averaging. In calculating D(z), the squared displacements were averaged over the duration of the production simulations.

2.3. Permeability coefficient calculations

The permeability coefficient, or permeability, is associated with the equations of flux under an imposed gradient [64]. Specifically, Fick’s law describes the flux, J, as directly proportional to the permeability and the solute concentration gradient, giving J = −PΔC [64]. The resistance to permeation or “resistance,” R, is generally defined as the reciprocal of the permeability, R = 1/P. In the inhomogeneous milieu of a lipid bilayer, the resistance to permeation varies with bilayer depth and can, thus, be expressed as a function of position along the z coordinate:

$$R(z)=C_w\left(\frac{1}{C(z)D(z)}\right),$$ (5)

and the permeability of a bilayer or membrane, P_M, can be calculated as the reciprocal of the integral of R(z) over the entire bilayer, within the boundaries z₁ and z₂:

$$P_M={\left[{\int }_{z_1}^{z_2}R(z)dz\right]}^{-1}={\left[C_w{\int }_{z_1}^{z_2}\left(\frac{1}{C(z)D(z)}\right)dz\right]}^{-1}.$$ (6)

Here, the depth-dependent concentration and diffusion coefficient product is normalized by the oxygen concentration in bulk water outside the bilayer, C_w [64]. In the current work, the integral was solved discretely as a Riemann sum, using 1-Å slabs within the bilayer boundaries, z₁ and z₂. Bilayer boundaries reported in EPR studies were employed in separate calculations, to enable comparison with EPR permeability estimates.

In this work, “integration-based” P_M values calculated using Eq. 6 are compared with values calculated using a “counting” technique described in our earlier work [74]. The technique relies on explicit tracking of O₂ molecule trajectories throughout a simulation. Specifically, events of O₂ molecule escape from the bilayer are recorded, following prior “entry” to the bilayer center plane (origin along the z axis). These escape events are tallied to calculate the escape frequency, Φ_esc, which is scaled by the average O₂ population in the water layer, N_w, and by an additional factor of 4 to account for possible entry from either bilayer leaflet (factor of 2) and possible escape via either leaflet (additional factor of 2) in the absence of a driving force. This scaling is necessary because P_M reflects the permeability of the whole bilayer and relates to unidirectional crossing of both leaflets. As with Eq. 6, the boundary positions, z₁ and z₂, can be varied and, in this context, function as thresholds on either side of the bilayer for counting escape events. The associated P_M equation for the counting technique is

$$P_M=\frac{{\Phi }_{esc}}{4N_w}.$$ (7)

2.4. Hydrophobic thickness calculation from experimental data

A hydrophobic thickness, or C2–C2 thickness, for POPC/chol at 298 K was calculated from published experimental NMR data, to assist with validation of the POPC/chol simulation model. For the simulation systems, the C2–C2 thickness was calculated as an average over all lipids and over the duration of the production simulations. To determine the POPC/chol C2–C2 thickness, d, from experimental NMR data, we used an expression derived from Ipsen’s method [75]:

$$d=d^0\left(1+\alpha \left(M_1-M_1^0\right)\right).$$ (8)

Here, d⁰ is a reference C2–C2 thickness for POPC without cholesterol; M⁰₁ = 47.0 × 10³ s⁻¹ is the value of the first moment of a POPC bilayer obtained by NMR; and M₁ is a moment dependent on the bilayer cholesterol content [75]. For the present comparison, M₁ was extrapolated for 50 mol% POPC/cholesterol (1:1 mole ratio), to give M₁ = 93.0 × 10³ s⁻¹. α is an expansivity constant with the value 5.8 × 10⁻⁶ s [75,76]. In the current study, a POPC C2–C2 thickness extrapolated to 298K from more recent small-angle neutron and X-ray scattering data, d⁰ = 29.0 Å [77], was used in place of the original estimate by Henriksen et al. of d⁰ = 25.8 Å [75]. The calculation yields POPC/chol C2–C2 thickness values at 298 K of d = 36.7 ± 0.5 Å based on NMR experimental data [75] and d = 36 ± 2 Å based on the current simulations.

3. Results and Discussion

3.1. Validation of bilayer physical properties

Lipid order parameter, bilayer thickness, and area per lipid values are reported here as a means of evaluating the physical properties of the simulation models. Comparison with experimental oxygen measurements, below, provides additional validation. Carbon-wise lipid order parameter curves show strong agreement with published nuclear magnetic resonance (NMR) spectrometry data for the sn-1 tail of POPC in bilayers composed of POPC or POPC/chol (SI Fig. 1). Due to limitations in the available data, comparisons are made with experimental measurements collected at similar, but not identical, temperatures.

Table 2 compares bilayer structural parameters calculated for each simulation system with biophysical experimental data. For POPC, the simulation data show a slight trend toward increased thickness (P–P and C2–C2) and decreased area per lipid, A_L, although the differences from experimental values are not significant. While quite small, these differences seem to be real because thickness and area per lipid are generally reciprocal properties and here are trending in opposite directions. Moreover, the two properties have been calculated using independent analysis techniques: thicknesses based on atomic positional histograms and areas using simulation box dimensions. They are, thus, not expected to be systematically correlated. Area per lipid and, to a lesser extent, bilayer thickness are predictive of solute permeability [78]. Therefore, the slight increase in thickness and decrease in area per lipid for the simulation model may introduce some error toward underestimation of oxygen permeability for POPC. However, this error may partially cancel error toward higher permeability due to exaggerated lipophilicity for the O₂ model [60,74]. Though the error ranges in Table 2 are generally larger for the simulation systems, strong agreement with experiment is evident for both bilayer compositions, at both temperatures studied.

Table 2.

Comparison of bilayer thickness and surface area per lipid, A_L, data for bilayers, based on molecular dynamics (MD) simulations and experiments [77,79,80].

Composition	T (K)	Technique	P–P (Å)a	C2–C2 (Å)b	AL (Å2)
POPC	298	MD	40 ± 3	30 ± 3	63 ± 1
		Expt.	39.4 ± 0.8	29.0 ± 0.6	63.5 ± 1.3
	308	MD	39 ± 3	29 ± 3	65 ± 1
		Expt.	38.8 ± 0.8	28.6 ± 0.6	65.0 ± 1.3
POPC/chol	298	MD	—	36.0 ± 2.0	—
		Expt.	—	36.7 ± 0.5	—

^aHeadgroup phosphorus to phosphorus distances (D_B or P–P).

^bTail carbon-2 to carbon-2 distances (C2–C2).

3.2. Application of the four-region model

Lipid bilayers are well-known to be inhomogeneous along the axis of permeation. The regular orientation of the amphiphilic lipids, relative to the plane of the bilayer, generates variation in polarity, density, and molecular dynamics. These variable properties modulate solute permeability, and it can be useful to delineate regions, based on bilayer structural features, where the physical properties are relatively homogeneous. More recent regional models [81,82] have divided the bilayer into three segments: the polar region, the hydrophobic region, and the interleaflet region. In the current study, the earlier four-region model of Marrink and Berendsen is adopted, as it additionally distinguishes a high-density headgroup region and a low-density headgroup region [64], which we find valuable for analyses related to oxygen solubility and diffusion.

The simulation images in Fig. 2 illustrate the four-region model, as applied to POPC and POPC/cholesterol bilayers. The regions are numbered I–IV and represent (I) low headgroup density, (II) high headgroup density, (III) high tail density, and (IV) low tail density. Label 5 indicates the MD bilayer boundaries, corresponding with the full span of the bilayer along the axis of permeation, between the outermost Region I borders for the two leaflets. The bilayer-depth positions used in this study to distinguish each of these regions at 298 K are provided in Table 3. The positions were determined from atomic positional histograms and calculated over the production simulations. The values reported in the table are distances along the bilayer normal, z-axis, where the bilayer midplane is located at z = 0 Å. The border of the low density headgroup region, I, demarcates the edge of the POPC choline nitrogen positional distribution, i.e., the farthest the choline nitrogen stretches into the flanking water. The beginning of the high density headgroup region, II, corresponds with the peak of the choline nitrogen positional distribution. For POPC at 298 K, this border occurs 22 Å from the bilayer midplane. Doubling this value gives the thickness value 44 Å, which compares favorably with the steric thickness D_B′ = 45.1 Å determined by X-ray diffraction for POPC at 30°C [80]. The high-density tail region, III, starts with the peak of the positional distribution for C2 of the oleoyl chain. The low-density tail region, IV, begins after the ninth carbon of the oleoyl chain, corresponding with a decrease in order parameter toward the bilayer midplane (Fig. 2 and SI Fig. 1). Further breakdown of these regions, in relation to EPR measurements, is included as Labels 6–8. Label 6 indicates the EPR region, corresponding with the full span of the bilayer considered in EPR experiments [11,23]. Near the outer edge of the EPR region, Label 7 marks the EPR headgroup segment, indicating the headgroup region considered in EPR experiments [11,23]. Label 8 marks the border between Regions I and II and corresponds with the highest density of the headgroup region.

Figure 2.

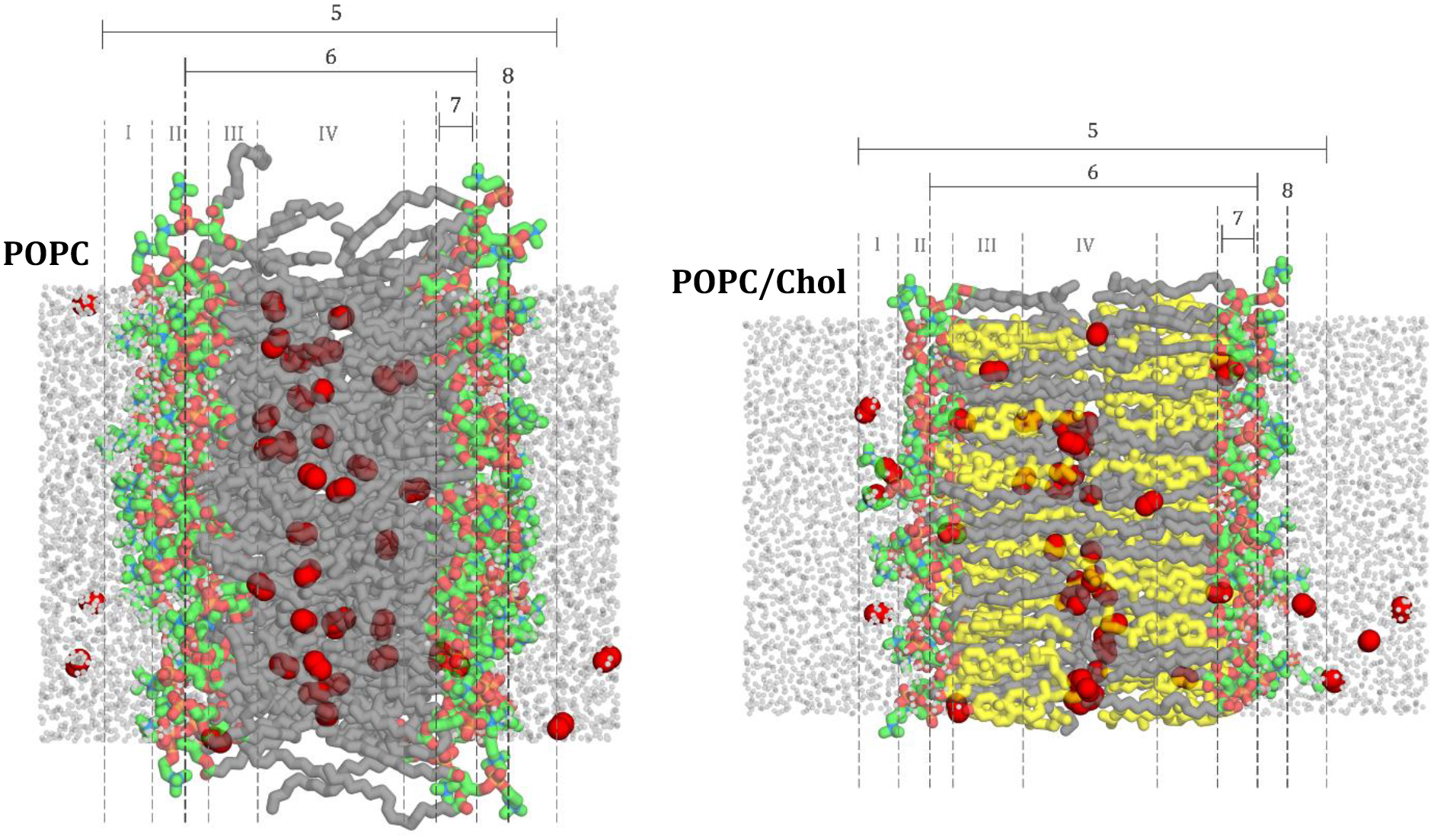
Positions used to distinguish bilayer regions (I–IV) at 298 K for representative (A) POPC bilayer and (B) POPC/chol bilayer. Region I denotes the low headgroup density, region II, denotes the high headgroup density, region III denotes high tail density and region IV denotes the low tail density. The MD simulation boundaries are denoted with label 5.

Table 3.

Positions used to distinguish bilayer regions (I–IV) and other features (5–8) at 298 K

Region/Label	Description	Distance from bilayer center (Å)
		POPC	POPC/chol
I	Low headgroup density	28	30
II	High headgroup density	22	25
III	High tail density	15	18
IV	Low tail density	9	8
5	MD boundaries: Z1, Z2	28	30
6	EPR region	18	21
7	EPR headgroup segment	13–18	16–21
8	Peak headgroup density	22	25

For regions, the outermost boundary is shown.

3.3. Comparison with experimental oxygen measurements (EPR)

To enable detailed comparison with EPR spin-label oxygen measurements, oxygen transport parameter curves, W_MD(z), and resistance to permeation curves, R(z) ≈ W_MD⁻¹(z), were calculated for the simulation systems, using Eq. 3 and its reciprocal. To recap, the oxygen transport parameter represents a scaled product of the local oxygen concentration and the local diffusion coefficient. MD curves for POPC and POPC/cholesterol are juxtaposed with experimental data in Figs. 3 and 4. Regardless of cholesterol content, the MD curves share several characteristics. In particular, the minimum oxygen transport parameter value and the maximum point of resistance to oxygen permeation occurs in the highest headgroup density region, at the boundary between Regions I and II (label 8). The resistance peak corresponds with the peak in the associated free energy curve and occurs near the minimum in the diffusion coefficient curve (SI Fig. 2, 3). The oxygen transport parameter maximum and the resistance to permeation minimum occur in the low tail density region between the leaflets (region IV).

Figure 3.

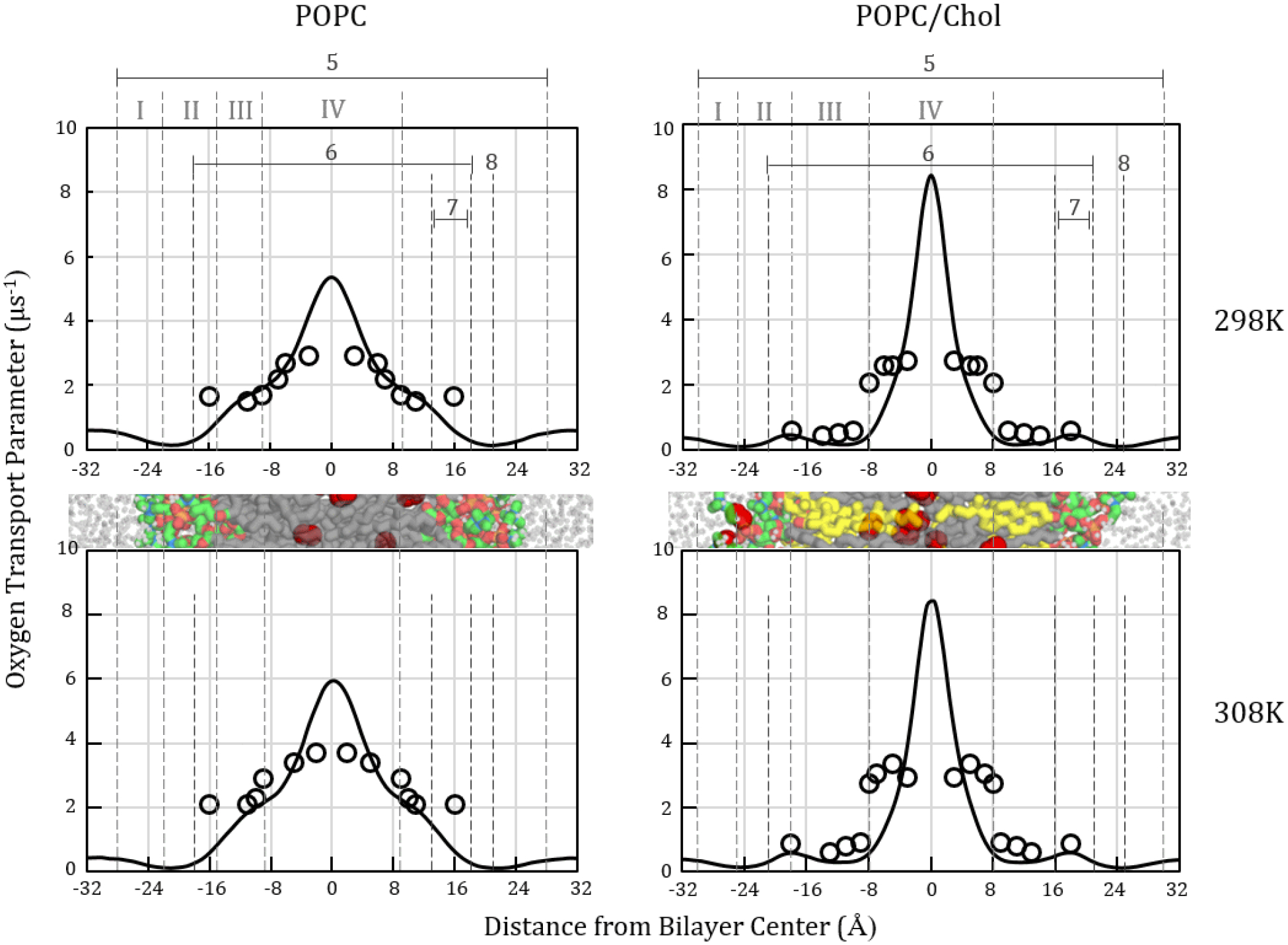
Oxygen transport parameter profiles, W(z), for POPC (left) and POPC/chol (right) calculated from MD simulations at 298 (top) and 308 K (bottom). Simulation-based curves shown as solid black lines. Published experimental EPR values [11,62] shown as hollow circles. Label 5 identifies the simulation bilayer thickness. Label 6 indicates the EPR thickness [11,62]. Label 8 identifies the MD peak resistance to oxygen permeation. Cropped bilayer images are juxtaposed with the plots to show corresponding structural features. Color scheme as in Fig. 1.

Figure 4.

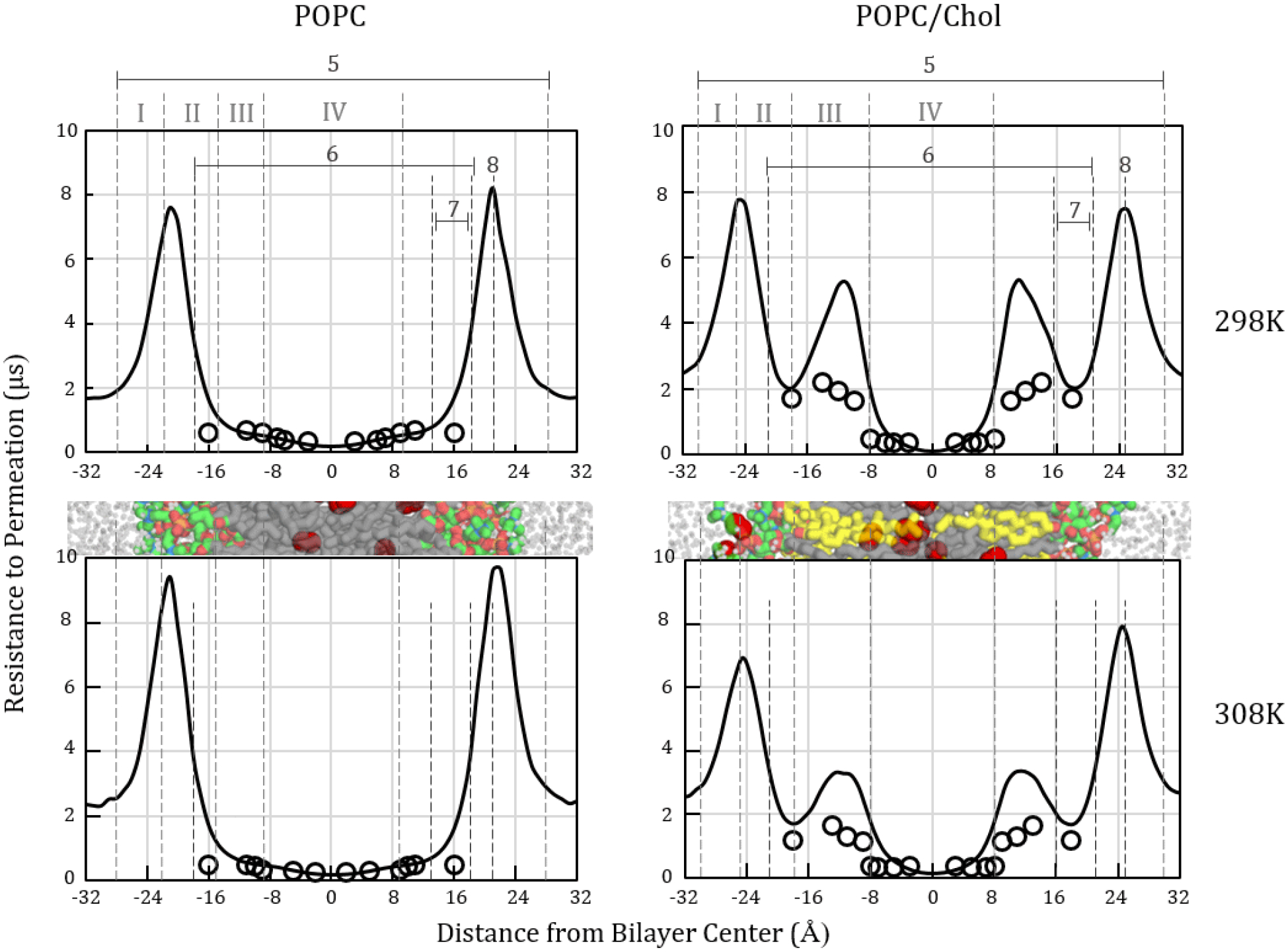
Oxygen resistance to permeation profiles, $W_{MD}^{-1}(z)$, calculated for POPC (left) and POPC/chol (right) from MD simulations at 298 (top) and 308 K (bottom). Each curve is the inverse of a corresponding oxygen transport parameter curve in Fig. 3. Simulation-based curves shown as solid black lines. Published experimental EPR data [11,62] shown as hollow circles. Label 5 identifies the simulation bilayer thickness. Label 6 indicates the EPR thickness [11,62]. Label 8 identifies the MD peak resistance to oxygen permeation. Cropped bilayer images are juxtaposed with the plots to show corresponding structural features. Color scheme as in Fig. 1.

The simulation oxygen transport parameter curves reflect more pronounced concentrating of oxygen toward the bilayer center than is detected with EPR. Two phenomena contribute to this difference: O₂ model accuracy and EPR probe positioning. First, the O₂ model used in this work shows exaggerated lipophilicity [60,74]. Thus, the MD oxygen transport parameter peak is expected to show systematic elevation in the hydrophobic region, relative to EPR.

The second factor contributing to the difference in MD and EPR oxygen transport parameter curve shapes in the interleaflet region is EPR probe positioning. In earlier work, we calculated discrete oxygen transport parameter points indicating the oxygen “signal” experienced by carbon atoms representing EPR probes covalently attached along the oleoyl chain [12]. Toward the center of the POPC bilayer, the discrete points deviate from the continuous MD oxygen transport parameter curve [12] because the tail carbons in the interleaflet region have broad positional distributions and sample bilayer depths with variable oxygen concentration. Prior atomistic MD simulation work using explicit spin-label probe moieties indicates that the probes have similarly broad positional distributions and are displaced somewhat, relative to the positions of the associated oleoyl tail carbons [83]. Experimental work also indicates that the lipid-conjugated EPR probes are highly mobile, contributing to substantial experimental uncertainty [11,38]. Thus, we attribute the difference in shape and peak height for EPR-based oxygen transport parameter curves, compared with MD simulation curves, partly to positional variation and associated averaging of oxygen concentrations.

Within the high- and low-tail-density regions (III and IV), the simulation oxygen transport parameter and resistance to permeation curves for POPC show strong agreement with the EPR experimental curves [11,23], except as noted. Most prominently, the curves differ in placing the peak resistance to permeation (lowest oxygen transport parameter) in the “headgroup” region. The simulations show pronounced peaks at the border between the low- and high-headgroup-density regions (I and II; label 8) on both sides of the bilayer. These peaks are much larger than the highest resistances observed with EPR. However, we note strong similarity in curve shape to published ¹³C nuclear magnetic resonance (NMR) experimental data [33], which we have plotted in Fig. 5 as C(z)/C_w and the inverse, C_w/C(z). This similarity substantially validates the MD oxygen transport parameter curve shape and interfacial resistance peak magnitude.

Figure 5.

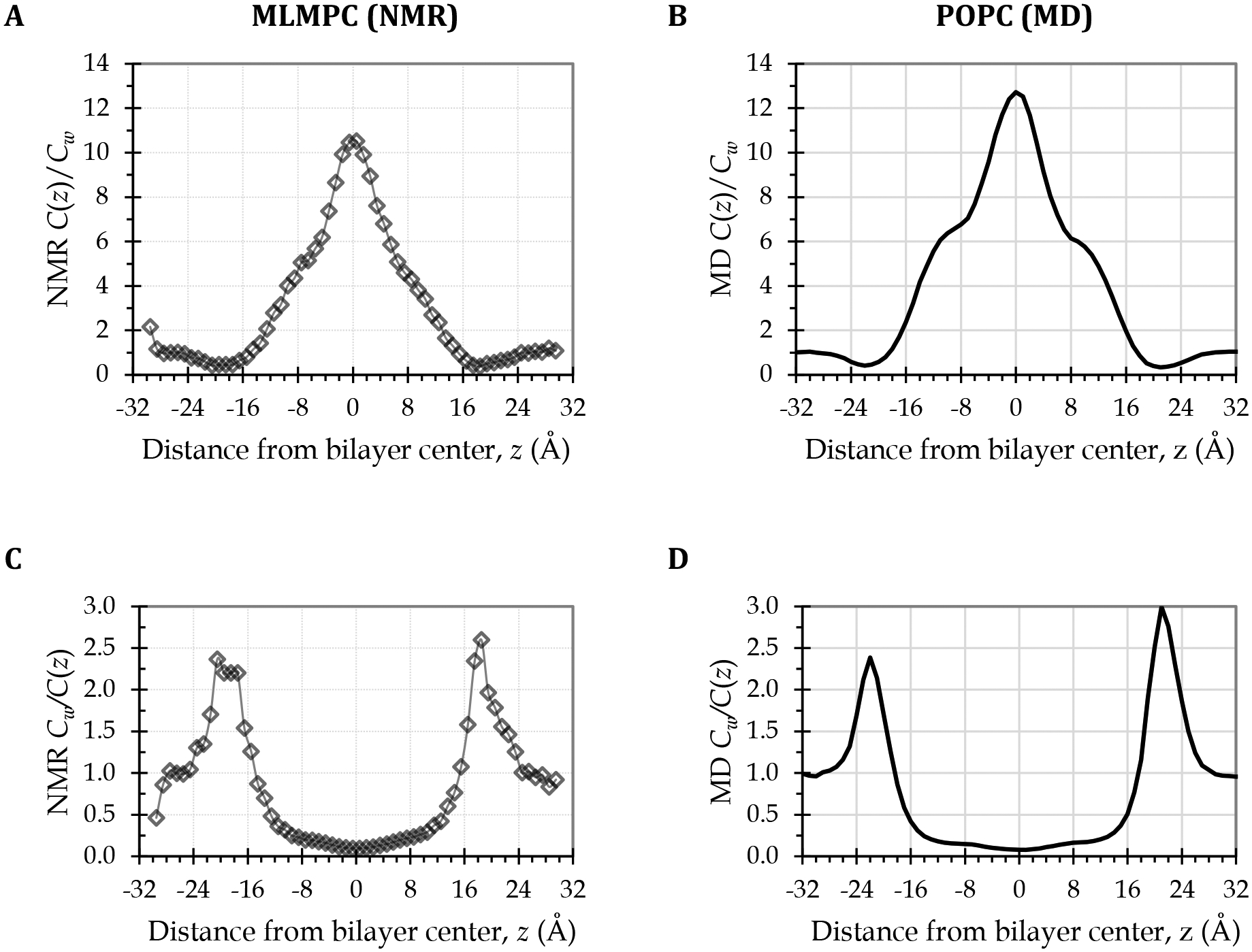
Strong interfacial resistances confirmed by comparing MD simulation curves for POPC (right) with curves derived from experimental NMR O₂ concentration data for a single-component phospholipid bilayer (left). (A) NMR-derived depth-dependent O₂ concentration curve for a bilayer of the phospholipid 1-myristelaidoyl-2-myristoylphosphatidylcholine (MLMPC) at 318 K [33], normalized to the average water layer O₂ concentration, to give C(z)/C_w, or the depth-dependent partition coefficient curve. (C) Inverse of the curve in panel A, equivalent to the O₂ concentration component of a resistance to permeation curve. (B) MD-derived C(z)/C_w curve for the POPC bilayer at 308 K. (D) Inverse of the curve in panel B, equivalent to the O₂ concentration component of the resistance to permeation curve in Fig. 4, lower left plot.

The strong intensification of resistance to permeation at the headgroup–water interface is consistent with the prediction of Diamond and Katz in seminal and widely appreciated theoretical work [66]. Diamond and Katz hypothesized that the region of lowest solubility should contribute disproportionately to the resistance. For a hydrophobic nonelectrolyte such as oxygen, they predicted the maximum resistance and the rate-limiting barrier to occur at the water–lipid interfaces, with interfacial resistances designated r′ and r″ in the following equation [66], which modifies Eq. 6:

$$P_M={\left[r^{\prime }+C_w{\int }_{z_1}^{z_2}\left(\frac{1}{C(z)D(z)}\right)dz+r^{″}\right]}^{-1}.$$ (9)

In spin-label EPR studies by Subczynski, Hyde, Kusumi, and coworkers, the interfacial resistances, r′ and r″, have been assumed to be estimated within the integral because of the inclusion of a spin-label probe targeted to the polar regions [11,42,84].

Diamond and Katz had proposed two possible resistance profiles for hydrophobic nonelectrolytes. Interestingly, the EPR resistance to permeation curves for POPC resemble one of the profiles, while the MD curves resemble the other. In the profile consistent with the EPR curves, the interfacial resistances are negligible. The resistance increases as the solute approaches the headgroup region but falls off just before passing the headgroups. In the profile consistent with the MD curves, an additional spike of resistance occurs at the water–lipid interface [66]. The agreement of the MD curve shape with the NMR-derived curves (Fig. 5) demonstrates that the strong interfacial resistance peaks predicted by the MD simulations are accurate and, thus, helps resolve the discrepancy between the MD and EPR profiles.

Apart from differences in the resistance peak intensity and position, the MD simulation and EPR resistance and oxygen transport parameter curves differ noticeably in the EPR headgroup segments (Label 7), near |z| = 16 Å. The EPR measurements in these segments used the tempocholine (T-PC) spin-label probe (structure shown in SI Fig. 4), with the intention of measuring oxygen in the polar headgroup region. The current work and our previous studies [12,48] support the hypothesis that the largely nonpolar T-PC probe resides primarily in a subheadgroup region and does not, in fact, probe the region of highest polarity and highest resistance, where the oxygen depth-dependent partition coefficient, K(z) = C(z)/C_w, is minimal. This hypothesis is additionally supported by a prior atomistic MD simulation study by Kyrychenko and Ladokhin [83]. There, the preferred depth position of the T-PC probe moiety under relatively dilute conditions (11 mol% in POPC) was found to be several angstroms below the lipid headgroups, toward the bilayer center [83]. To access this depth, the T-PC molecule assumes a “bent” conformation, with the tails oriented parallel to the POPC tails and the headgroup/probe moiety curved in a manner that brings the nitroxide spin-label into the tail region [83]. A similar bent conformation was observed in our simulations with a T-PC incorporation level of 1.6 mol% in POPC [48]. The EPR oximetry studies referenced here used 1 mol% T-PC [23]. If the T-PC probe, in fact, misses the targeted polar headgroup region, then the spin-label EPR oximetry technique will tend to underestimate the rate-limiting interfacial resistances.

The MD oxygen transport parameter curves for POPC show a subtle point of inflection around the border between regions III and IV, which corresponds with the position of the C9–10 cis double bond of the oleoyl tail. This inflection is likely averaged out in the EPR curves, due to probe positional variations. Unlike pure POPC, the POPC/cholesterol curves do not increase continuously in region III, which corresponds with the region spanned by the rigid cholesterol ring system. Rather, the oxygen transport parameter is very low in this region, and corresponding barriers are seen in the POPC/cholesterol resistance to permeation curves, $W_{MD}^{-1}(z)$ (Fig. 4, lower plots). These barriers correspond in approximate bilayer depth with the largest barriers observed by EPR [11], in Region III, which is the high tail order region and the cholesterol-ring-spanning region (Fig. 4). The magnitude of the simulation Region III barriers is about twice the magnitude of the EPR barriers. Likely sources of error in the simulations include force field inaccuracies and error in the diffusion coefficient profiles (SI Fig. 3) used to generate the curves. It is also possible that the EPR barriers are underestimated, due to local “melting” effects caused by placing bulky doxyl probes in high-order regions—as was noted in a fluorescence quenching study using bulky pyrene-based probes [85].

3.4. O₂ time progression and void-volume analysis

To enhance understanding of the physical-structural basis of the resistance to permeation patterns, we analyzed individual O₂ molecule time progression across the bilayer as well as O₂-sized void-volume patterns. The upper plots in Fig. 6 track the progression of individual O₂ molecules over time within the hydrated lipid bilayer systems at 298 K. These plots are juxtaposed with electron density curves calculated from the simulations (lower plots). Electron density is akin to atomic packing density and varies with bilayer depth. Vertical lines in Fig. 6 mark the positions of greatest electron density (blue line) and of highest resistance to permeation (black line). The headgroup-associated barriers diminish somewhat with incorporation of cholesterol, corresponding with reduced packing density in the headgroup regions of POPC/chol, relative to POPC. The reason is that the POPC headgroups are more sparsely distributed in POPC/chol. However, an additional barrier in the tail region arises in the cholesterol-rich bilayers, due to increased tail packing density along the rigid cholesterol ring system (yellow-shaded areas).

Figure 6.

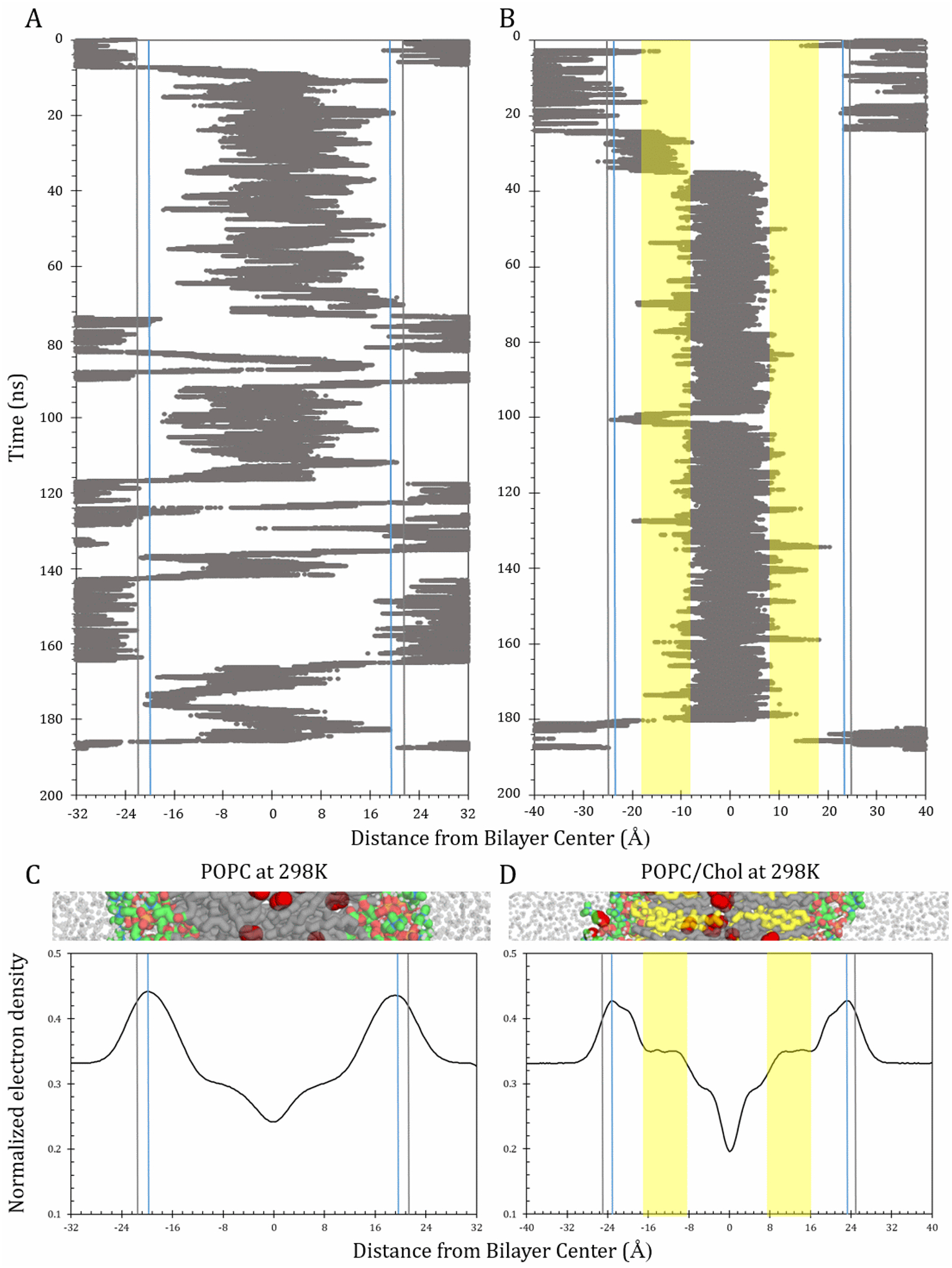
Time progression plots and electron density curves for POPC and POPC/chol at 298 K. Upper plots show a single representative O₂ molecule trajectory each for POPC (A) and POPC/chol (B), along the bilayer-depth dimension, z. Blue vertical lines denote the highest points of electron density, at 19.6 Å for POPC and 23.6 Å POPC/chol. Gray lines indicate the highest point of resistance to permeation, at 21 Å for POPC and 25Å for POPC/chol. Yellow areas in panel B denote the cholesterol-ring-spanning region (III). Lower plots show bilayer-depth-dependent electron density, normalized to give an area under the curve of 1, for POPC (C) and POPC/chol (D). Cropped bilayer images juxtaposed with plots to show corresponding structural features. Color scheme as in Fig. 2.

The time progression plots illuminate how the oxygen trajectory along the bilayer normal, z axis, is influenced by barriers and path effects. They additionally reflect the differential partitioning of oxygen toward the nonpolar bilayer interior in the POPC and POPC/chol systems. Finally, they underscore differences in the dynamics of oxygen movement within the systems, despite similar bilayer permeabilities. In both systems, the O₂ molecules tend to dwell primarily in the bilayer interior and make excursions into the surrounding water layers. The balance of time spent in the hydrophobic interior versus the water layer reflects partitioning toward the hydrophobic phase, due to greater relative solubility in nonpolar media. The time progression plots support the significance of the interfacial resistances for both POPC and POPC/chol, as the O₂ molecules tend to bounce back into the water layer when they encounter these headgroup-associated resistances.

In POPC, once past the interfacial resistance, the O₂ molecule moves quickly into the nonpolar tail region (III/IV). Over the course of the simulation, it makes several excursions into the water layer. The particular O₂ molecule depicted here escapes into the water layer 6 times during the 190-ns production simulation, including 5 full “crossing” events, in which the molecule enters on one side and escapes from the other. We emphasize that this is a stochastic process and, although the trajectory is similar to others in the POPC system, each molecule’s behavior is unique and does not directly represent the statistical ensemble that encompasses the behavior of all 40 O₂ molecules. It is also important to note that the water layers on either side of the bilayer are continuous with one another, due to the periodic boundary condition, such that an O₂ molecule leaving the simulation box on one side reenters it on the opposite side. Several such periodic “boundary crossing” events within the continuous water layer of the POPC system are visible in the time range 66–80 ns.

In the POPC/chol system, the high-solubility region is restricted to the narrower zone between the yellow-shaded, compacted areas dominated by cholesterol’s rigid rings (region III). Excursions out of this zone are relatively rare, and passage across the compacted areas is rapid. Transient dwelling of the representative O₂ molecule in the subheadgroup region between −23 Å and −10 Å is also visible (Fig. 6B).

In addition to time progression analysis, a void-volume analysis was used, with the goal of enhancing our understanding of the diffusion component of the resistance to permeation. Oxygen diffusional transport is thought to be facilitated by momentary voids, or empty spaces, among molecules [43,86,87]. Here, O₂-sized (or bigger) “cavities” were identified and quantified using KVFinder software [88], along with in-house scripts. Cavities were defined as regions of space outside the van der Waals radius of any atom with a volume equal to or greater than the threshold volume of 22.22 ų—the approximate volume of a single O₂ molecule. Our analysis has revealed that oxygen does not always use existing cavities in its translocation process (data not shown). Nonetheless, visualizing the pattern of cavity occurrence is useful for helping to understand the physical basis of the process.

The upper plots in Fig. 7 show cavities identified in representative simulation snapshots for POPC or POPC/chol simulated without O₂ at 298K. The cavities are shown as colored mesh volumes. It is important to note that these cavities are transient and fluctuate in position and volume throughout a simulation. Still, they enable visualization of the pattern of cavity occurrence, as influenced by the bilayer structure and lipid composition. Below each respective bilayer-cavity image is a corresponding histogram of the fractional volume occupied by cavities as a function of bilayer depth, calculated over 1 ns of simulation time (1000 frames at 1 ps per frame). This cavity volume fraction is the total volume of all cavities at a given bilayer depth, divided by the total volume at that depth—whether occupied by atoms or “empty.”

Figure 7.

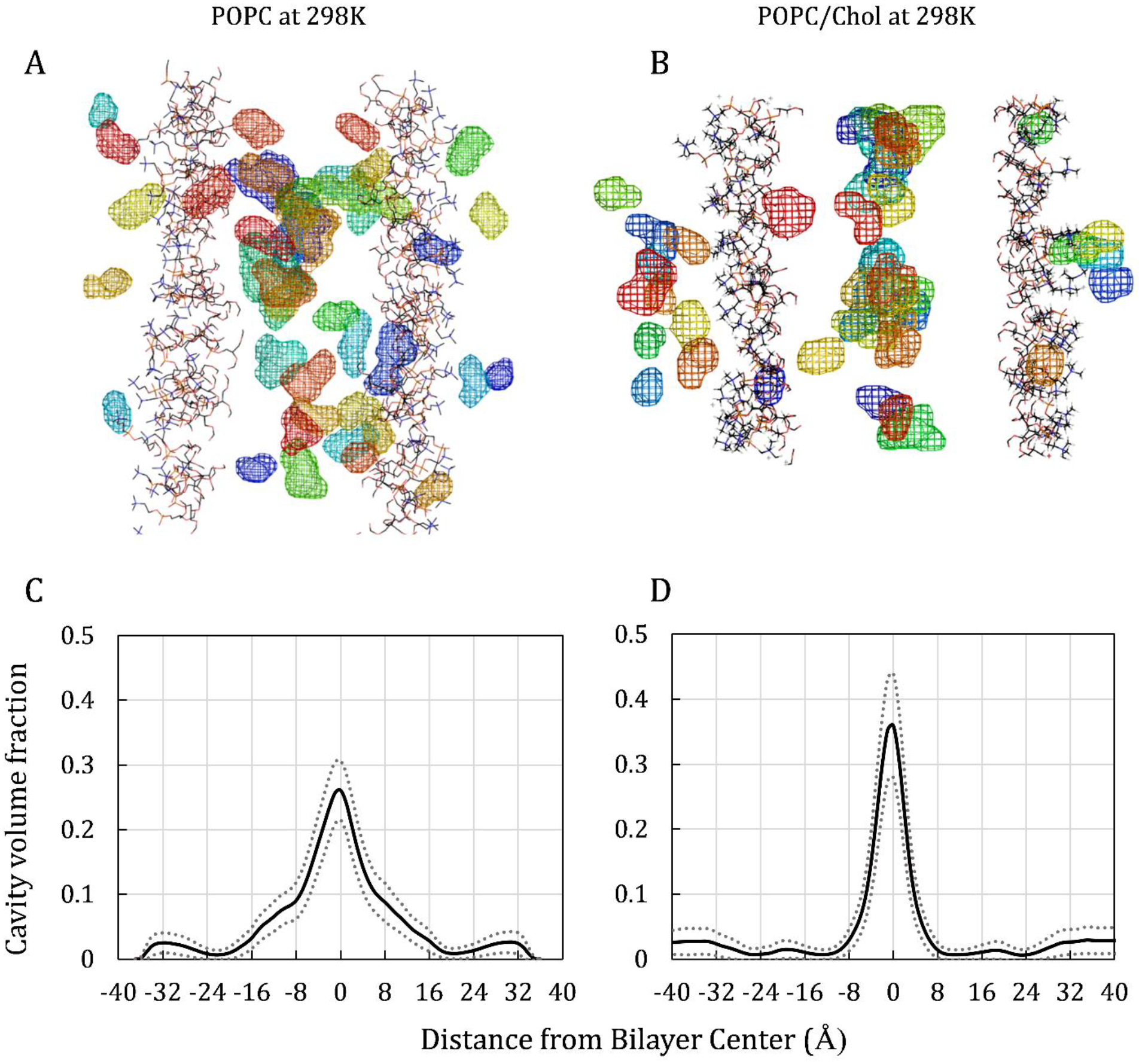
Cavity snapshots and volume fractions for POPC (left) and for POPC/chol (right). Upper images are simulation snapshots of cavity volumes. For clarity, only the lipid headgroups are shown, and all other atoms are hidden. Cavities are represented as mesh volumes, with colors indicating the distance from the viewer, according to “rainbow” order—with red closest to the viewer and dark blue farthest away. Lower plots show cavity volume fraction along the bilayer-depth dimension, z, for POPC (C) and POPC/chol (D). Cavity volume fraction is the fraction of the bilayer volume at a given depth that is identified as cavity volume. Dotted lines indicate the standard deviation for each curve.

In POPC, the bulk of the cavities occur in the lipid tail region, starting just below the headgroups and extending toward the bilayer center (midplane). The distribution in the POPC/chol system differs dramatically, with the bulk of the cavities occurring in a relatively narrow region near the midplane, at the interface between the two lipid layers. In addition, the peak height differs in the cavity volume fraction profiles (Fig. 7, lower plots), where the curve peaks at 0.35 for POPC/chol, versus 0.26 for POPC. We note, however, that the overlapping error ranges (dotted lines) indicate that the difference is not likely to be significant.

The cavity volume fraction curves bear strong resemblance to the respective oxygen transport parameter curves for POPC and POPC/chol (Fig. 3). This similarity in curve shape supports the established hypothesis that void availability contributes to the diffusive translocation of O₂. In particular, it is noteworthy that the POPC/chol cavity volume fraction curve shows small peaks in the subheadgroup area (region II/III boundary) that correspond with the positions of minor peaks in the POPC/chol oxygen transport parameter curves. These somewhat oxygen-enriched areas, near ±18 Å, coincide with the assumed average positions of the headgroup-targeted T-PC probes used in EPR experiments (Fig. 3).

Comparison of the cavity volume fraction profiles demonstrates a physical-mechanistic difference in the oxygen diffusion process in POPC and POPC/chol. In POPC, cavities abound in region III, providing putative pathways for oxygen solubility–diffusion. Conversely, in POPC/chol, the presence of the rigid cholesterol ring system in region III results in compaction and straightening of the lipid tails. The compaction is visible in the simulation electron density curve for POPC/chol, which reveals elevated atomic packing density in the cholesterol-ring-spanning region (Fig. 6D, yellow-shaded region) that is absent in the corresponding POPC curve (Fig. 6C). The straightening of the lipid tails in region III is apparent in the lipid order parameter curve (SI Fig. 1). Associated reduction in the cavity density, to just 0.6% to 2% of the volume, corresponds with the minor resistance to permeation peaks in region III for POPC/chol (Fig. 5, lower plots). Taken together, these data indicate that cholesterol presents a physical barrier to oxygen diffusion, due to lipid compaction. Even so, oxygen does cross the compacted regions, suggesting peristaltic-like movement of the lipids, to create spaces for oxygen to occupy transiently.

3.5. Bilayer permeability coefficient

To understand the influence of the interfacial resistances on the bilayer oxygen permeability coefficient, we calculated permeabilities using two general approaches. First, we estimated the permeability of a lipid bilayer as the inverse of the area under the resistance to permeation curve, applying the inhomogeneous solubility–diffusion model according to Eq. 6. We note that the underlying depth-dependent diffusion coefficient curves estimated in this study are expected to have low accuracy in more confined regions of the bilayer, such that we anticipated that these integration-based estimates would be qualitatively useful but quantitatively inaccurate. Therefore, we also applied a second, less model-dependent “counting” technique for estimating permeability coefficients (Eq. 7), developed in our earlier work and built upon an approach by de Groot and coworkers [74,89]. The technique relies on the relatively rapid permeation kinetics of oxygen, such that events of oxygen entry and escape from the bilayer can be tracked explicitly. This approach has yielded good reproducibility in other studies [48,74,90].

The effect of the interfacial resistances becomes clear by comparing permeability values estimated using the MD boundaries and the EPR boundaries. Table 4 provides the resulting oxygen permeability coefficients, calculated with both the solubility–diffusion (integration) technique and the counting technique. The counting technique yields large error for the “EPR region” estimates because of imprecision in the oxygen concentration adjacent to the EPR boundaries. Interestingly, the integration and counting techniques yield similar permeability values for the POPC bilayer, suggesting that the diffusion coefficient profiles are of sufficient accuracy to generate reasonable agreement across the techniques. For POPC/chol, the two techniques produce different estimates, as discussed further below.

Table 4.

Bilayer oxygen permeability, P_M, in cm/s

T echnique		POPC		POPC/chol
		298 K	308 K	298 K	308 K
EPR expt [11]	integration	100.37	157.40	37.42	49.70
EPR region, MD	integration	50 ± 5	63 ± 5	23 ± 3	33 ± 1
	counting	50 ± 10	80 ± 20	7 ± 1	15 ± 2
Full bilayer, MD	integration	11 ± 3	13 ± 5	10 ± 2	14 ± 1
	counting	9 ± 1	13 ± 1	5 ± 1	10 ± 1

MD values calculated using the integration technique (Eq. 6) or the counting technique (Eq. 7). Values in bold are best estimates, as established in this work.

Values are given as mean ± estimated standard deviation.

Regardless of the calculation technique, the simulation-based permeability coefficients strongly depend on the location of the boundaries. Using the EPR boundaries for POPC gives permeability values 4 to 6 times greater than using the MD boundaries. Part of the difference is due to the wider MD boundaries, as the permeability depends indirectly on the bilayer thickness. The proportion due to thickness should be less than a factor of 2, indicating that the interfacial resistances contribute an additional factor of 2 to 3 reduction, independent of thickness. This additional difference corresponds with the large interfacial resistance spikes, which are omitted in the “EPR region” estimates.

For POPC/chol, the headgroup resistance seems to be less dominant, as major resistance also occurs in the cholesterol ring-spanning region (III). The effect of boundary location is, likewise, much weaker for POPC/chol. Indeed, the boundary location effect can be explained by thickness alone for the counting-based estimates, while accounting for thickness leaves a factor of ~1.5 additional difference due to boundary location with the integration-based estimates.

For POPC, the integration technique yields permeability coefficients that are essentially the same (considering error bars) as those calculated using the counting technique. In contrast, the values estimated using the two techniques differ substantially for POPC/chol, especially within the EPR boundaries. The source of the differences for POPC/chol is not entirely clear. We have not ruled out error in the integration-based estimates due to inaccuracy in the underlying depth-dependent isotropic diffusion coefficient curves. However, the strong agreement of the POPC integration- and counting-based estimates suggests that the diffusion coefficient curves are likely not a major source of error, as cholesterol is expected to have little effect on depth-dependent diffusion coefficient profiles [12,25].

Since the permeability depends primarily on the free-energy landscape, one might suspect inaccuracy in the C(z)/C_w curve (free-energy antilog) used with the integration technique to generate the resistance to permeation curve. While the integration technique is sensitive to accuracy in the free-energy landscape, the counting technique depends only on the oxygen escape frequency and the average oxygen concentration in the water—a function of the partition coefficient. The free-energy profile is sensitive to sampling and equilibration. We are confident in the precision of the counting-based permeability coefficients, especially at 308 K, because of their consistency with our other work on POPC/chol bilayers at 310 K, where a more elaborate equilibration protocol and a longer sampling timeframe were used. However, it is likely that the integration technique does not fully capture the kinetics of oxygen transport in cholesterol-rich lipid bilayers because the inhomogeneous solubility–diffusion model underlying the technique may not be strictly valid here.

Namely, the inhomogeneous solubility–diffusion model assumes that the transition path can be defined as a function of a single transition coordinate [90], generally taken as the bilayer normal, or z-dimension. For the model to hold, it is necessary that only the z-component of the diffusion coefficient profile affects the permeation kinetics. In cholesterol-containing membranes, the assumed equivalency of the permeation path and the transition coordinate may not hold, due to inhomogeneous lateral distribution of the cholesterol molecules, as shown in Fig. 8. The uneven cholesterol distribution apparent here seems consistent with experimentally observed cholesterol clustering in somewhat more complex lipid mixtures [91]. It is likely that the inhomogeneously distributed cholesterol molecules influence the order of the phospholipids in their immediate local environment, such that the entire area of the bilayer is not equally permeable.

Figure 8.

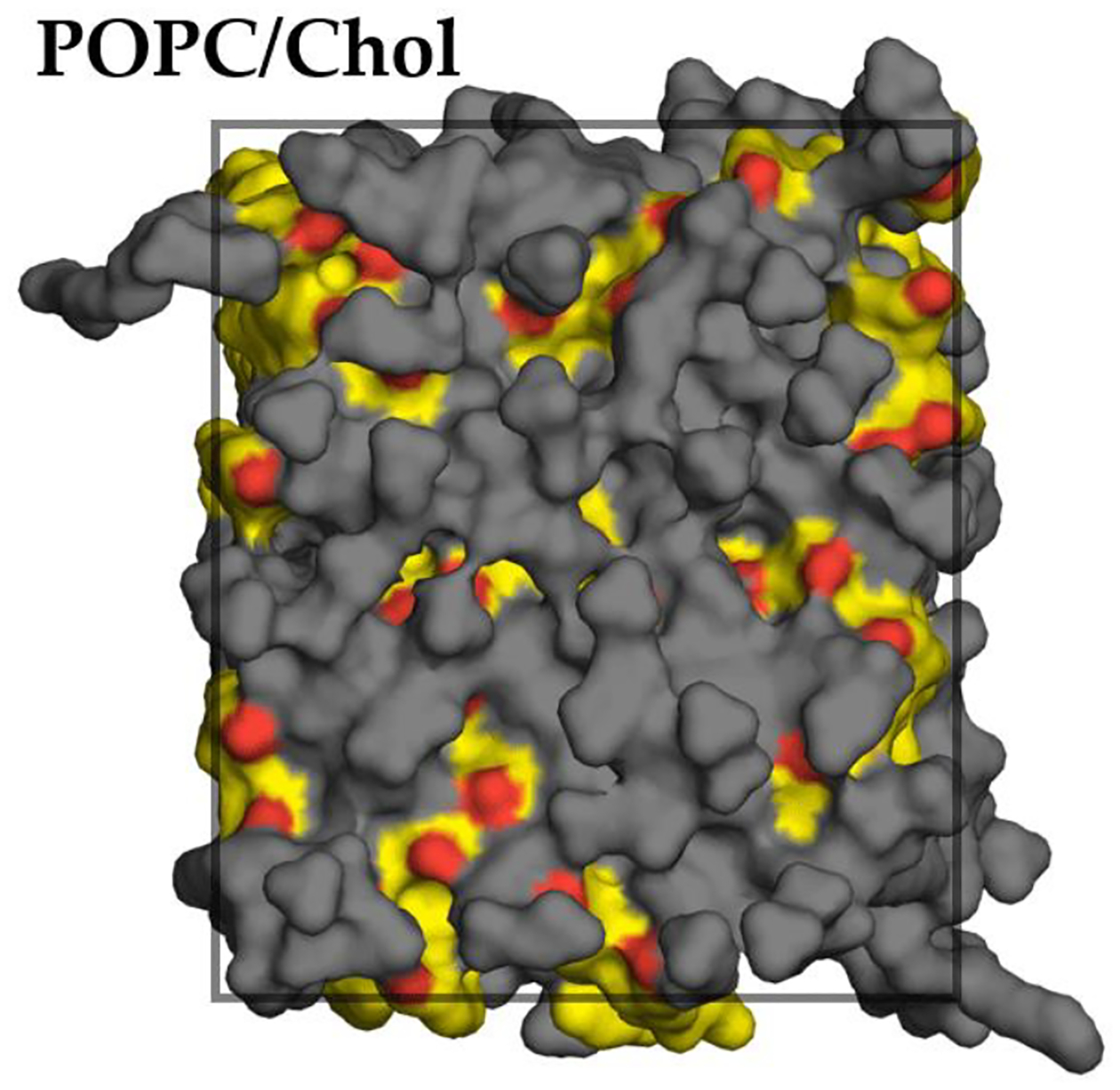
Inhomogeneous cholesterol distribution within the plane of a POPC/chol bilayer (top surface view of one leaflet for a simulation snapshot at 298 K). POPC molecules shown in gray, cholesterol molecules shown in yellow with red hydroxyl O atoms. All H atoms omitted for clarity. Approximate simulation box boundary indicated with superimposed rectangle.

Work on oxygen permeation pathways in mixed composition bilayers mimicking liquid-ordered and liquid-disordered domains found that O₂ molecules preferentially crossed the lipid leaflets at boundaries between more ordered and less ordered regions, primarily in zones where more than one lipid type was present [92]. After crossing one leaflet, the molecules tended to diffuse along the bilayer midplane, passing laterally through highly ordered regions with low permeability along the transition coordinate, before crossing the other leaflet. In a recent study, we visualized “void pathways” in POPC bilayers containing varying amounts of cholesterol [74]. The visualization indicated substantial path-dependence for oxygen escape from POPC/chol but not POPC bilayers. Specifically, transient void pathways spanning the bilayer leaflets were far more uniformly distributed and far more abundant in POPC than in POPC with 25% cholesterol, and the effect was even more marked with 50% cholesterol content. Importantly, the void pathways were not continuous from one leaflet to the other but seemed to require a transition along the midplane to cross the bilayer fully [74]. The cavity visualization in Fig. 7 is, similarly, suggestive of transition pathway discontinuity in POPC/chol, to a greater extent than in POPC. Collectively, these various sources of evidence point to the possible existence of discrete and discontinuous pathways across the lipid leaflets. Associated “access resistance” [93], or flux limitation related to “finding” an escape pathway via O₂ diffusion along the midplane, would help explain the large differences in the permeability estimates for POPC/chol using the counting and integration techniques.

If the diffusion pathway is discontinuous along the z-axis, a fundamental assumption of the inhomogeneous solubility–diffusion model underlying the integration technique (namely, equivalency of the transition pathway and the transition coordinate) may not hold in cholesterol-rich lipid bilayers, leading to errors in the permeability calculations for POPC/chol by a factor of 3 within the EPR boundaries and by a factor of 1.5–2 within the MD boundaries (Table 4). As such, a more complex transition coordinate may be required to capture fully the kinetics of oxygen permeation across cholesterol-rich bilayer systems.

More broadly, we note an anisotropic “lateral” diffusion effect along the midplane of lipid bilayers (region IV), which may be enhanced in bilayers incorporating 50 mol% cholesterol. Simulation work by Ghysels and coworkers identified anisotropy at the bilayer midplane, where radial (lateral) diffusion between the lipid leaflets is accelerated relative to transverse diffusion across the bilayer [82,92,94]. Fig. 6 demonstrates that oxygen molecules have much longer residence times between the lipid leaflets in POPC/chol than in POPC bilayers. If lateral diffusion is favored relative to transverse diffusion, a long residence time at the midplane will translate into extensive lateral movement.

The long residence times of the individual O₂ molecules also corresponds with enhanced partitioning of oxygen toward the bilayer midplane. As such, cholesterol-rich bilayers have a deep free-energy well at the bilayer midplane that seems to trap oxygen molecules (SI Fig. 2). It is common wisdom that, for most solutes, the influence of the free-energy landscape on the diffusion kinetics is limited only by free-energy barriers, where the free energy rises above its level in the bulk water layer. However, our work has consistently indicated that cholesterol reduces the permeability of lipid bilayers to oxygen, while also slightly reducing the magnitude of the headgroup barriers—the only barriers that rise above the water-layer reference free energy (SI Fig. 2). The representative O₂ molecule time progression plotted in Fig. 6 indicates that the depth of the well at the midplane of the POPC/chol bilayer must be sufficiently great to trap oxygen molecules and slow their progression across the bilayer. Such an effect was predicted in a recent theoretical work [94]. Namely, a deep free-energy well may yield a high permeability while also leading to longer crossing times at the molecular level.

The simulation permeability coefficients for the bilayers, P_M, are systematically lower than the experimental values. In contrast, simulation permeability coefficients for unstirred water layers, P_w, are systematically higher than experiment (Table 5). Combining the data gives P_M/P_w ratios near or above 1 based on experiment but much lower, near 0.1, based on the simulation estimates. Because the simulations systematically overestimate bilayer permeability, due to exaggerated lipophilicity of the oxygen model [60,74], the simulation P_M/P_w ratios are likely an upper limit. Therefore, the modeling suggests that lipid bilayers may be at least an order of magnitude less permeable than surrounding aqueous fluids. Incorporation of cholesterol at the level of 50 mol% further reduces the bilayer permeability by about 20% at 308 K. This magnitude of oxygen permeability reduction by cholesterol is consistent with our recent simulation work at 310 K (37°C) [74].

Table 5.

Comparison of bilayer permeability, P_M, with the permeability of water, P_w, at 308 K

Technique	Bilayer	PM (cm/s)	Pw (cm/s)	PM/Pw
EPR expt. [11]	POPC	157.40	69	2.3
	POPC/chol	49.70	60	0.8
Full bilayer, MD	POPC	12.9	118	0.109
	POPC/chol	9.8	110	0.089

P_w is the permeability of an unstirred water layer of the same thickness as the bilayer. Experimental P_w values calculated using the expression P_w = D_w/h, where D_w = 2.5 × 10⁻⁵ cm²/s at 308 K from published experimental data [95] and thicknesses h = 36 Å for POPC or h = 42 Å for POPC/chol. Simulation P_w values calculated using the counting technique with simulation boxes consisting entirely of water and O₂.

On the surface, the lower oxygen permeability of bilayers relative to surrounding water may seem to contradict the firmly established solubility–diffusion model (also known as Overton’s rule), which indicates that the membrane permeability of a molecule is directly proportional to its oil-water partition coefficient, or its membrane solubility. The general expression associated with Overton’s rule is a simplified form of Eq. 6, written as $P_M=\left(\frac{C_{oil}}{C_w}\right)\left(\frac{D_M}{h}\right)$, where C_oil/C_w is the oil–water partition coefficient, or the oil–water solubility ratio; D_M is the molecule’s diffusion coefficient in the lipid phase; and h is the thickness of the membrane. However, this expression is only strictly valid for a homogeneous membrane with negligible interfacial resistances [66].

Phospholipid membranes are amphiphilic and, therefore, inhomogeneous along the axis of permeation. Accounting for variations in the physical-structural environment along the bilayer depth is critical to accurate estimation of permeability, especially for nonpolar permeants. Therefore, the inhomogeneous solubility–diffusion model [64,66] is commonly used within the context of molecular-resolution study of membrane permeability. Applying the inhomogeneous solubility–diffusion model reveals that a lipid–water partition coefficient greater than 1, corresponding with a free-energy well in the lipid tail region, is insufficient to predict the overall bilayer permeability for a molecule, except in a relative sense. (Nonpolar oxygen has a greater bilayer permeability than polar water, and amphiphilic ethanol has an intermediate permeability [90].) Rather, the magnitude of free-energy rise above the free energy in the bulk (aqueous) phase dominates the permeation kinetics, which are largely independent of the depth of the free-energy well in the lipid phase [82,96]. For nonpolar molecules, the rate-limiting free-energy barriers are likely to occur at the periphery of the membrane, in the lipid–water interfacial regions, where the local partition coefficient and diffusion coefficient are lowest [66]. Therefore, a whole-membrane partition coefficient greater than 1 suggests relatively high bilayer permeability, but the actual permeability depends primarily on the interfacial resistances, corresponding with local minima in the partition coefficient profile for an inhomogeneous membrane. Therefore, the current finding that POPC and POPC/chol bilayers have permeabilities lower than the permeability of a water layer of equivalent thickness is congruent with the inhomogeneous solubility–diffusion model, which modifies Overton’s rule to account for chemical and physical variation along the axis of permeation.

An early simulation study estimated the oxygen permeability of a dipalmitoylphosphatidylcholine (DPPC) lipid bilayer to be 15 times more permeable at 350 K [86] than the current study estimates for POPC at 310 K. Apart from a temperature effect, which might account for a good portion of the difference [11], the spatial resolution of the current study is much greater (1 Å here vs. 3–8 Å in the earlier study), and the lipid force field used here is better developed and physically validated. Moreover, the oxygen permeability estimated in the earlier study has a very large uncertainty: 200 ± 500 cm/s [86]. Notably absent in that study are free-energy barriers in the headgroup regions, underscoring the significance of the interfacial barriers (resistances) to the overall permeability. The existence of headgroup-associated interfacial barriers is supported by other recent works using both molecular simulation [24,82,90,97] and experimental [33] techniques.

3.6. Limitations

The findings reported here are strongly supported by NMR and experimental membrane structural data. While they point to limitations of the EPR probe-based oximetry technique, the current study has not directly addressed the behavior of the lipid-linked spin labels. Part 2 of this work partially addresses this limitation, focusing on the dynamics of the T-PC headgroup probe through explicit modeling [98].

Further work will be necessary to determine whether the permeability of biological aqueous fluids (interstitial fluid and cytosol) is comparable to that of pure water [26]. Knowing the relative permeability of biological fluids and membranes will help to shed light on the pathway of oxygen diffusion within tissues and may reveal modulating compositional factors.

4. Conclusion

The molecular dynamics simulations featured in this study reveal strong, rate-limiting interfacial resistance peaks not captured in spin-label EPR oximetry studies of POPC and POPC/chol (50 mol% cholesterol) lipid bilayers. The physical properties of the bilayer models used in this study have been validated against experimental membrane structural data. It is found that the boundaries of the POPC lipid bilayer fall well outside the boundaries used to define the bilayer in EPR probe-based oximetry studies. The wider boundaries correspond with strong water–lipid interfacial resistances not detected with EPR probes. These interfacial resistances strongly impact the oxygen permeability coefficient for POPC but have less influence on the permeability coefficient for POPC/chol. The magnitude of the peaks is supported by probe-free experimental NMR measurements of oxygen, which additionally support a greater oxygen “sink” between the lipid leaflets than has been detected using EPR. In the current study, the permeability of POPC and POPC/chol is estimated to be well below the permeability of a water layer of equivalent thickness, with POPC/chol showing reduced permeability relative to POPC. Given that the solubility of oxygen in real biological aqueous fluids is likely to be lower than in pure water (see ref. [26]), the current work predicts that membranes present much more significant barriers to oxygen transport than has been understood from experimental studies alone. This work highlights the value of atomic resolution models for aiding in the interpretation of probe-based experimental measurements.