Deep Learning Reconstruction for Cardiac Magnetic Resonance Fingerprinting T₁ and T₂ Mapping

Abstract

Purpose:

To develop a deep learning method for rapidly reconstructing T₁ and T₂ maps from undersampled electrocardiogram (ECG) triggered cardiac Magnetic Resonance Fingerprinting (cMRF) images.

Methods:

A neural network was developed that outputs T₁ and T₂ values when given a measured cMRF signal timecourse and cardiac RR interval times recorded by an ECG. Over 8 million cMRF signals, corresponding to 4000 random cardiac rhythms, were simulated for training. The training signals were corrupted by simulated k-space undersampling artifacts and random phase shifts to promote robust learning. The deep learning reconstruction was evaluated in Monte Carlo simulations for a variety of cardiac rhythms and compared with dictionary-based pattern matching in 58 healthy subjects at 1.5T.

Results:

In simulations, the normalized root-mean-square-error (nRMSE) for T₁ was below 1% in myocardium, blood, and liver for all tested heart rates. For T₂, the nRMSE was below 4% for myocardium and liver and below 6% for blood for all heart rates. The difference in the mean myocardial T₁ or T₂ observed in vivo between dictionary matching and deep learning was 3.6ms for T₁ and −0.2ms for T₂. Whereas dictionary generation and pattern matching required more than 4 minutes per slice, the deep learning reconstruction only required 336ms.

Conclusion:

A neural network is introduced for reconstructing cMRF T₁ and T₂ maps directly from undersampled spiral images in under 400ms and is robust to arbitrary cardiac rhythms, which paves the way for rapid online display of cMRF maps.

Introduction

Quantitative MRI is a powerful tool for assessing cardiac health. Two clinically measured tissue properties are T₁ and T₂, which can be used for early detection and monitoring of fibrosis,¹ inflammation,² and edema,³ among other conditions. Cardiac Magnetic Resonance Fingerprinting (cMRF) is one technique for simultaneous T₁-T₂ mapping,^4,5 which uses a time-varying sequence, an undersampled spiral k-space trajectory, and pattern matching with a dictionary of simulated signals to estimate quantitative maps.

Although cMRF is efficient, as data are collected during one breathhold, the reconstruction time is long and prohibits real-time display of the maps. The major hurdle is that the subject’s cardiac rhythm dictates the sequence timings because the scan is electrocardiogram (ECG) triggered, and thus a new dictionary must be simulated after every acquisition. The dictionary simulation time increases if slice profile imperfections or other effects are modeled; both dictionary simulation and pattern matching take longer if additional properties (e.g., B₁⁺) beyond T₁ and T₂ are quantified.^6–8 A typical cMRF reconstruction for T₁-T₂ mapping requires 4 minutes for dictionary simulation (including corrections for slice profile and preparation pulse efficiency) and 10 seconds for pattern matching.

The combination of deep learning and MRF is gaining interest because of the potential for orders of magnitude reductions in computation time.^9–11 Previously, a neural network was proposed that reduces cMRF dictionary simulation time to one second and generalizes to arbitrary cardiac rhythms, which eliminates the need for time-consuming and scan-specific Bloch equation simulations.¹² However, this approach still generates a scan-specific dictionary that occupies memory (220MB). Measuring additional properties beyond T₁ and T₂ would require exponentially more memory and time and quickly become infeasible. In addition, the maps have quantization errors due to the discrete step sizes in the dictionary.

Neural networks have been proposed to directly quantify T₁ and T₂ from MRF images in non-cardiac applications, thereby bypassing dictionary simulation and pattern matching to reduce computation time and memory requirements. However, existing methods are not directly applicable to cMRF. Previous approaches have only considered scans with fixed sequence timings, whereas the cMRF sequence timings are determined by the subject’s cardiac rhythm.¹¹ Some existing neural network approaches cannot reconstruct maps from undersampled non-Cartesian data and require additional reconstruction steps.⁹ Other approaches require in vivo MRF datasets for training,¹⁰ which may be time-consuming and expensive to collect, and may not generalize to scenarios that are underrepresented in the training set.

In this work, a deep learning reconstruction is proposed for cMRF that directly outputs T₁ and T₂ maps from undersampled spiral images in under 400ms per slice without using a dictionary. The network is robust to arbitrary cardiac rhythms and eliminates the need for scan-specific Bloch equation simulations and pattern matching. The cMRF deep learning reconstruction is evaluated in simulations and compared with dictionary-based pattern matching using in vivo data acquired in 58 healthy subjects at 1.5T.

Methods

cMRF Sequence Parameters

The cMRF sequence has been described in previous work,¹³ although the breathhold duration here was reduced from 15 to 10 heartbeats. A FISP readout is used that is relatively insensitive to off-resonance due to the unbalanced gradient moment on the slice-select axis.¹⁴ Multiple preparation pulses are applied with the following pattern (which repeats twice): inversion (TI=21ms), no preparation, T₂-prep (30ms), T₂-prep (50ms), T₂-prep (80ms). The acquisition is ECG-triggered with a 250ms diastolic readout with 50 TRs collected each heartbeat and 500 TRs collected during the entire scan. Data are acquired using an undersampled spiral k-space trajectory with golden angle rotation¹⁵ that requires 48 interleaves to fully sample k-space.¹⁶ Other parameters include a 192×192 matrix, 300mm² field-of-view, 1.6×1.6×8.0mm³ resolution, and constant TR/TE 5.1/1.4ms.

Neural Network Architecture

Figure 1 shows a diagram of the proposed network. The network takes two inputs—the measured signal timecourse from one voxel and the cardiac RR interval times from the ECG. The timecourse is split into real and imaginary parts and concatenated with the RR interval times, resulting in a vector of length $2N+M$, where $N$ is the number of TRs and $M$ is the number of heartbeats. This study uses $N=500$ and $M=10$. The input is normalized by dividing the RR intervals (in milliseconds) by 1000 and dividing the signal by its $l_2$-norm. The network has 18 hidden layers with 300 nodes per layer. Skip connections are used every 4 layers beginning after the first, which avoids problems with vanishing gradients during training. Supporting Information Figures S1 and S2 provide justification for the number of hidden layers and use of skip connections. The final outputs are the T₁ and T₂ estimates for the given voxel.

Figure 1. Neural network for cMRF T₁ and T₂ map reconstruction.

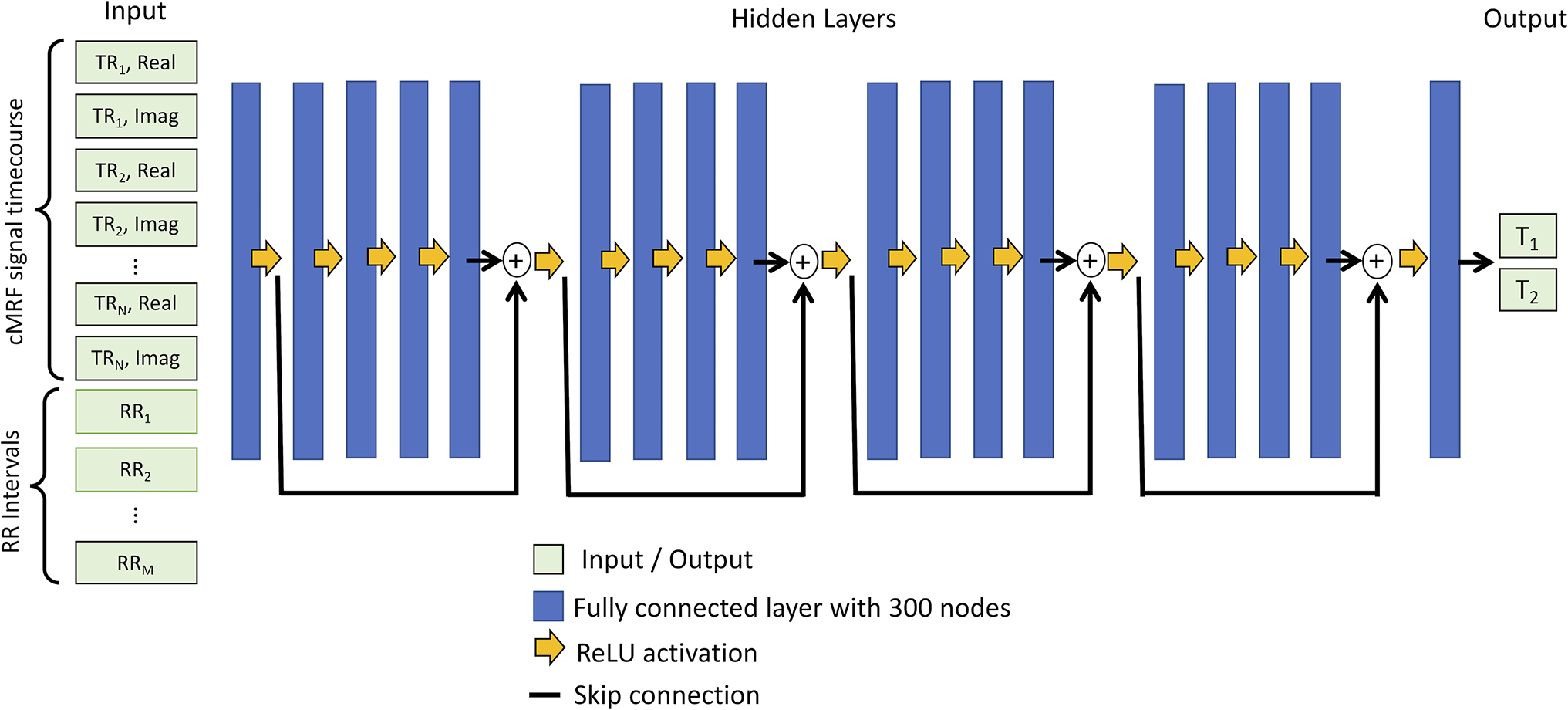
A neural network is used with 18 hidden layers with 300 nodes per layer (blue rectangles) and rectified linear unit (ReLU) activation functions (yellow arrows). Skip connections (black lines) are used every 4 layers. The inputs to the network are a measured cMRF signal timecourse concatenated with the cardiac RR interval times, and the outputs are the estimated T₁ and T₂ values. The network operations are performed independently for each voxel.

Neural Network Training

The training dataset consists of cMRF signals simulated using the Bloch equations, corresponding to 4000 randomly generated cardiac rhythms. Each cardiac rhythm has an average heart rate (HR) between 40–120 beats per minute (bpm), and random Gaussian noise with a standard deviation (SD) between 0–100% of the mean RR interval is added to the RR interval times to introduce variability. Adding noise with a large SD (i.e., near 100%) mimics ECG mis-triggering because it results in large timing variations between heartbeats. For each cardiac rhythm, 2000 signals were generated with T₁ and T₂ values selected from a uniform random distribution between 50–3000ms and 5–700ms, respectively. In total, 8 million (4000×2000) training signals were simulated including corrections for slice profile (assuming a 0.8ms duration sinc RF pulse with time-bandwidth product 2) and preparation pulse efficiency.^6,7

Although adding Gaussian noise to training data is common in machine learning to promote robust learning, non-Cartesian undersampling artifacts do not fall along a Gaussian distribution. Therefore, the network is trained using simulated cMRF signals corrupted with noise that mimics non-Cartesian aliasing, hereafter called “pseudo-noise” (Supporting Information Figure S3 compares neural networks trained with pseudo-noise versus Gaussian noise). A repository of pseudo-noise is generated before training (Supporting Information Figure S4). The pseudo-noise is meant to be agnostic to cardiac rhythm and image content. To create the repository, random T₁, T₂, and M₀ maps are synthesized where each voxel has a random value between 50–3000ms for T₁, 5–700ms for T₂, and 0–1 for M₀. A random cardiac rhythm is also generated with an average HR between 40–120bpm, with Gaussian noise having SD between 0–100% of the mean RR interval added to the RR interval times. Signals are simulated using the Bloch equations to yield a time series of reference images. Data acquisition is simulated using the spiral k-space sampling pattern, and undersampled images are gridded using the non-uniform fast Fourier Transform (NUFFT).¹⁷ The fully-sampled reference images are subtracted from the undersampled images. Each voxel in the resulting difference images is treated as an independent pseudo-noise sample and saved in the repository. For a 192×192 matrix, these steps result in 36,864 (192²) pseudo-noise samples. The complete repository contains 1.8 million pseudo-noise samples generated by repeating this process 50 times using random parameter maps and cardiac rhythms.

When training the network (Figure 2B), pseudo-noise samples are randomly selected from the repository every epoch and added to the simulated cMRF signals, similar to an approach described for contrast synthesis by Virtue, et al.¹⁸ Let $s\left(t\right)$ denote an arbitrary cMRF signal and $n\left(t\right)$ denote an arbitrary pseudo-noise sample. The pseudo-noise is randomly scaled by a factor $C$ so the SNR is between 0.2 and 1.0, which was empirically determined to be appropriate for the k-space trajectory employed in this study (Supporting Information Figure S5) and would need to be tuned for other trajectories. The SNR is defined as follows:

$$SNR=\frac{{‖s\left(t\right)‖}_2}{{‖n\left(t\right)‖}_2}$$ [Eq.1]

Figure 2. Generation of training data.

The network is trained using simulated cMRF signal timecourses. A pseudo-noise sample is randomly drawn from the repository (generation of pseudo-noise is described in Supporting Information Figure S4). The amplitude of the pseudo-noise is scaled by a factor C so the SNR of the noisy signal is between specific bounds (0.2–1.0 for this study). Random phase shifts ${\varphi }_1$ and ${\varphi }_2$ are applied to the cMRF signal and pseudo-noise, respectively. The pseudo-noise is added to the cMRF signal to yield the noisy signal that will be used for training.

Each cMRF signal is also multiplied by a random phase shift ${\varphi }_1$, and the pseudo-noise is multiplied by a different random phase shift ${\varphi }_2$. Phase shifts are performed because in vivo datasets have arbitrary phase due to factors such as receiver coil sensitivity profiles and off-resonance. Supporting Information Figure S6 compares the performance of networks trained with and without random phase shifts. The final cMRF signal used for training is denoted by $\tilde{s}\left(t\right)$.

$$\tilde{s}\left(t\right)=s\left(t\right)\cdot e^{i{\varphi }_1}+C\cdot n\left(t\right)\cdot e^{i{\varphi }_2}$$ [Eq.2]

A separate validation dataset was created by generating 400 random cardiac rhythms and simulating 500 cMRF signals for each rhythm corrupted by pseudo-noise and phase shifts. The neural network was implemented in PyTorch and trained for 5 epochs using an Adam optimizer with learning rate 10⁻⁴ and batch size 128. The network parameters with the smallest validation loss were saved. A normalized $l_1$ loss function (Equation 3) was used that was the sum of the relative errors in T₁ and T₂, where B is the batch size, $T_{1,i}^{net}$ and $T_{2,i}^{net}$ are the network estimates for T₁ and T₂, and $T_{1,i}^{ref}$ and $T_{2,i}^{ref}$ are the reference T₁ and T₂ values.

$$loss=\frac{1}{B}\sum _{i=1}^B\left(\frac{\left|T_{1,i}^{net}-T_{1,i}^{ref}\right|}{T_{1,i}^{ref}}+\frac{\left|T_{2,i}^{net}-T_{2,i}^{ref}\right|}{T_{1,i}^{ref}}\right)$$ [Eq.3]

Simulation Experiments

Monte Carlo simulations were performed using a digital cardiac phantom (MRXCAT)¹⁹ to evaluate the accuracy of the deep learning reconstruction. The phantom used myocardial T₁/T₂=1400/50ms, blood T₁/T₂=1950/280ms, and liver T₁/T₂=800/40ms. Datasets with different cardiac rhythms were simulated where the average HR was swept from 40 to 120bpm (step size 10bpm), and Gaussian noise was added to the RR interval times with SD 0%, 10%, 20%, 50%, 75%, and 100% of the mean RR interval to introduce heart rate variability. For each combination of average HR and noise level, 50 cMRF datasets with different cardiac rhythms were simulated by performing Bloch equation simulations, spiral k-space sampling, and gridding. The undersampled images and RR interval times were input to the neural network to reconstruct T₁ and T₂ maps. The mean T₁ and T₂ values were computed in the myocardial wall, left ventricular blood pool, and liver and are reported using normalized root mean square error (nRMSE).

In Vivo Experiments

cMRF scans from 58 healthy adult subjects were retrospectively collected in a HIPAA-compliant, IRB-approved study. The scans were performed on a 1.5T MRI scanner (MAGNETOM Aera, Siemens Healthineers, Germany) at a medial short-axis slice position during an end-expiration breathhold with a 192×192 matrix size, 300mm² field-of-view, and 1.6×1.6×8.0mm³ resolution. T₁ and T₂ maps were reconstructed in two ways: 1) using the Bloch equations to simulate a scan-specific dictionary and performing pattern matching as in previous cMRF work,¹³ hereafter called “dictionary matching”, and 2) using the deep learning reconstruction. The dictionary contained 23,345 entries with T₁ [10:10:2000, 2020:20:3000]ms and T₂ [4:2:100, 105:5:300, 320:20:500]ms. The mean T₁ and T₂ over the entire myocardial wall were compared between both reconstructions using a two-tailed Student’s t-test for pairwise comparisons, with p<0.05 considered statistically significant. The mean T₁ and T₂ were also compared using linear regression and Bland-Altman analyses.²⁰ Intrasubject variability for dictionary matching and deep learning were assessed by computing the SD in T₁ and T₂ over the myocardium for each subject. Intersubject variability was assessed by computing the coefficient of variation (CV), obtained by calculating the SD of the mean T₁ and T₂ measured for each subject and dividing by the group-averaged T₁ and T₂.

Results

Computation Time

Gridding required 30s and was required for both deep learning and dictionary matching reconstructions. The average time to quantify T₁ and T₂ maps from the gridded images using deep learning was 336ms. For comparison, simulating a scan-specific dictionary required 4 minutes, and pattern matching required an additional 10s. Each dictionary occupied 220MB of memory. The deep learning reconstruction does not utilize a dictionary, and the network parameters only occupied 7MB.

Simulation Experiments

Figure 3 shows results from the Monte Carlo simulations. The deep learning reconstruction was more accurate at estimating T₁ than T₂. The nRMSE for T₁ was generally below 1% for all tissue types (myocardium, blood, and liver). Note that a 1% error corresponds to a 14ms difference from the true T₁ of 1400ms in myocardium. The T₂ nRMSE was below 4% for myocardium and liver, and below 6% for blood. A 4% error corresponds to a 2ms difference from the true T₂ of 50ms in myocardium. The quantification accuracy for T₁ and T₂ was similar regardless of average HR or the variability of the cardiac rhythm.

Figure 3. Monte Carlo simulation results for (A) T₁ and (B) T₂ in myocardium, liver, and blood.

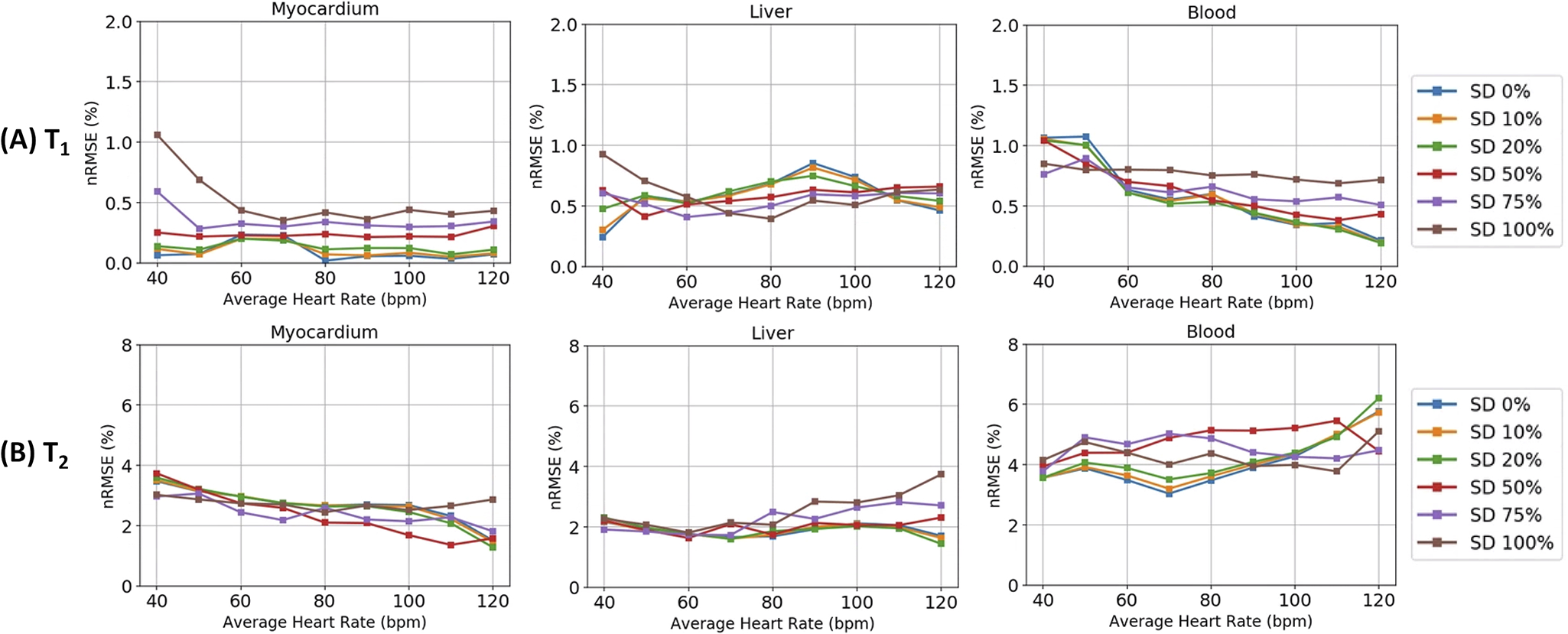
The different color lines refer to the standard deviation (SD) of Gaussian noise that is added to the RR interval times, with the SD given as a percentage of the mean RR interval. SD 0% refers to a constant heart rate, while SD 100% refers to a highly variable heart rate.

In Vivo Imaging

Maps from two representative subjects are shown in Figure 4. Subject A had a steady cardiac rhythm (mean RR 775±28ms), while Subject B had a variable cardiac rhythm (mean RR 77±215ms) with one missed ECG trigger during heartbeat 10. The maps in the myocardium were visually similar between the deep learning and dictionary matching reconstructions. There were differences in some areas, such as subcutaneous fat. Figure 5A shows the linear regression analysis between the mean myocardial T₁ and T₂ values from deep learning and dictionary matching. The measurements were strongly correlated, with R²=0.93 for T₁ and R²=0.95 for T₂. As seen in the Bland-Altman analysis (Figure 5B), the mean T₁ bias was 3.6ms with 95% limits of agreement (−18.9, 26.1)ms, and the mean T₂ bias was −0.2ms with 95% limits of agreement (−1.9, 1.5)ms. Using a paired t-test, the differences in the mean myocardial values between deep learning and dictionary matching were statistically significant for T₁ $(\mathrm{p}=0.019)$ and T₂ $(\mathrm{p}=0.038)$. Figure 5C compares the intrasubject standard deviations. The SD for T₁ was 106.9ms for dictionary matching and 110.2ms for deep learning, and the difference was statistically significant $(\mathrm{p}=0.013)$. The SD for T₂ was 6.8ms for dictionary matching and 7.3ms for deep learning, and the difference was statistically significant $(\mathrm{p}<0.0001)$. The intersubject variability was similar for both reconstructions. For T₁, the CV was 4.4% for dictionary matching and 4.5% for deep learning; for T₂, the CV was 9.1% for dictionary matching and 8.9% for deep learning.

Figure 4. cMRF T₁ and T₂ maps in two healthy subjects at 1.5T.

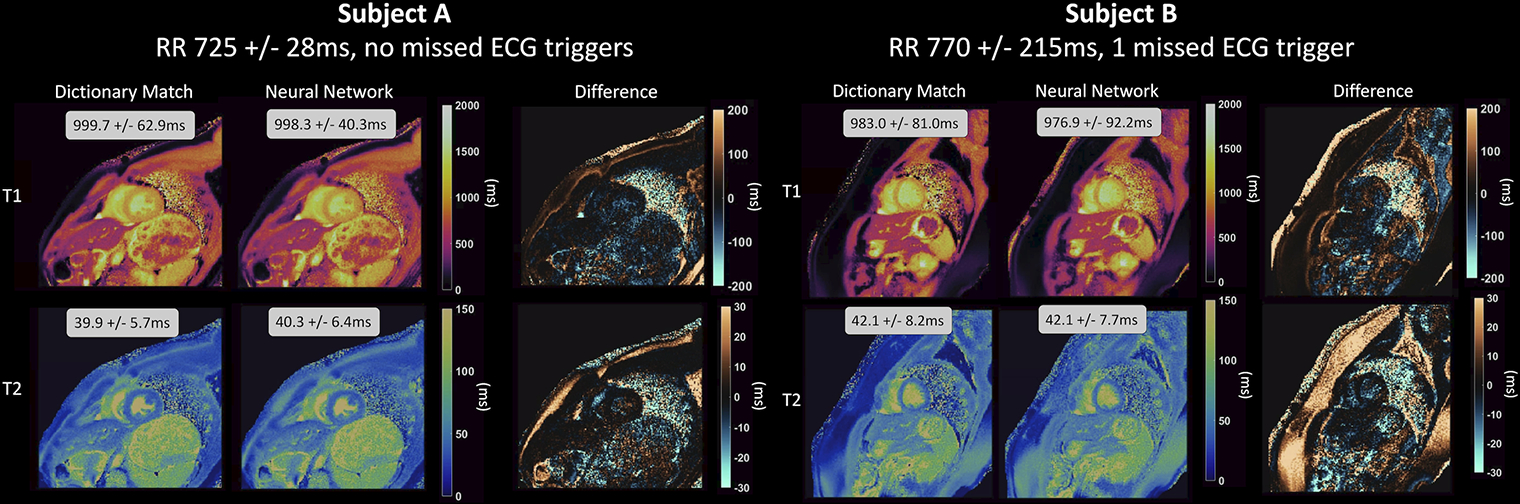
T₁ and T₂ maps are shown corresponding to dictionary-based pattern matching and the deep learning reconstruction, along with difference maps. Subject A had a steady cardiac rhythm, while Subject B had a variable cardiac rhythm with one missed ECG trigger. The mean and standard deviation in T₁ and T₂ over the entire myocardium are displayed as insets.

Figure 5. Analysis of the in vivo data.

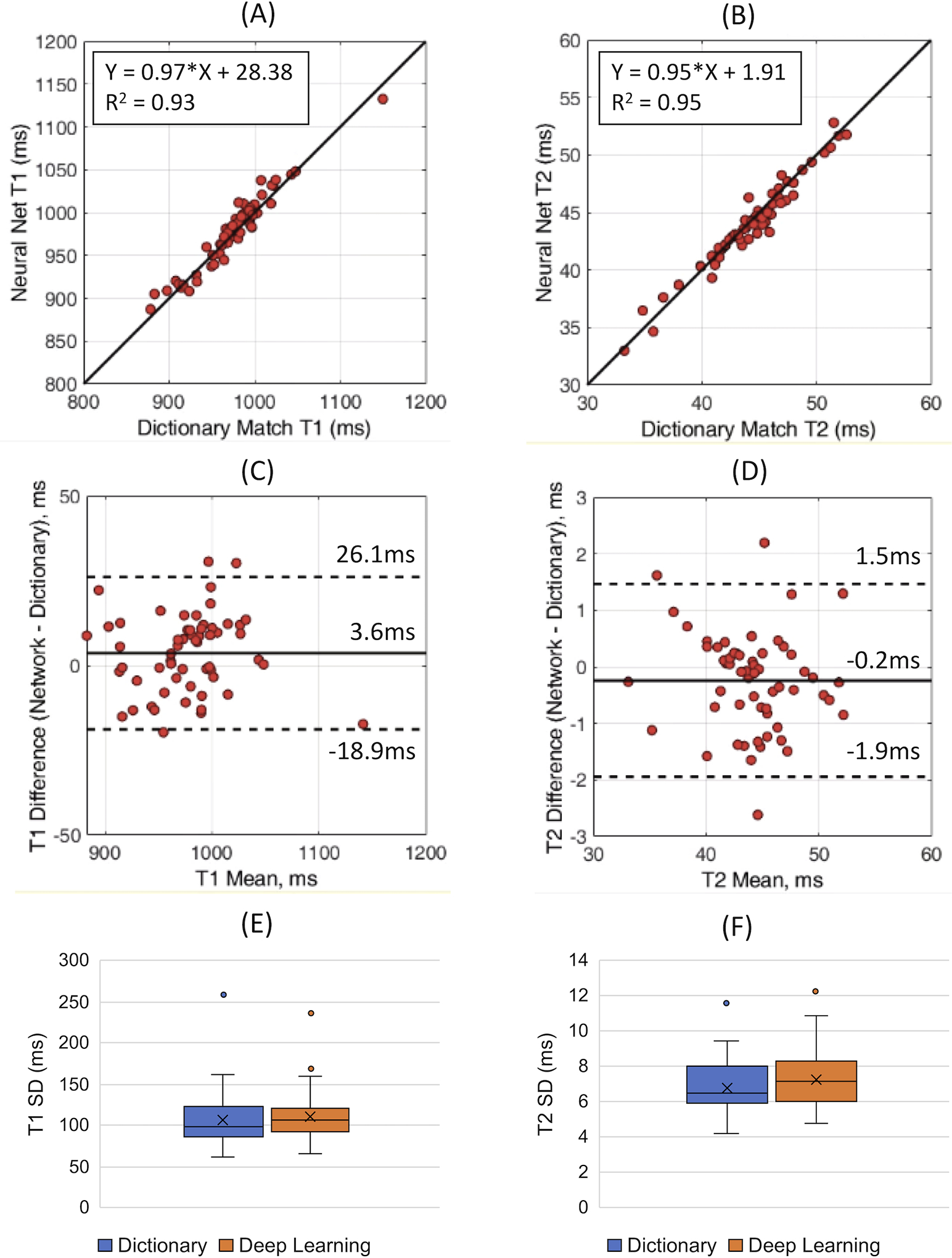
Linear regression plots are shown comparing the mean myocardial (A) T₁ and (B) T₂ values using dictionary matching and deep learning. Bland-Altman plots are shown comparing the mean myocardial (C) T₁ and (D) T₂. The solid line indicates the bias, and the dotted lines indicate the 95% limits of agreement. Boxplots comparing the intrasubject standard deviation (SD) for (E) T₁ and (F) T₂ in the myocardium are also presented.

Discussion

This study introduces a deep learning method for rapidly performing cMRF T₁ and T₂ quantification that is robust to arbitrary cardiac rhythms. A neural network was trained to directly output T₁ and T₂ maps from undersampled spiral cMRF images and cardiac RR interval timings. The deep learning reconstruction does not require Bloch equation simulations to create a dictionary or use pattern matching. The main advantage is the large reduction in computation time, which could enable real-time display of cMRF maps. The deep learning method takes less than 400ms per slice to reconstruct T₁/T₂ maps from cMRF images, which is more than a 700-fold speedup compared to dictionary matching. The deep learning reconstruction also requires less memory than dictionary matching. Whereas the dictionary occupies 220MB of memory, the network coefficients only occupy 7 MB. Although this study focuses on T₁ and T₂ quantification, the savings in computation time and memory may be more pronounced for applications seeking to measure additional tissue properties.

The deep learning reconstruction yielded accurate T₁ and T₂ estimates in simulations, with T₁ errors below 1% and T₂ errors below 6% regardless of the variability in the cardiac rhythms. In vivo, the deep learning reconstruction had similar accuracy and precision as dictionary matching. Although a statistically significant bias was observed in the mean and SD of the myocardial T₁ and T₂ values compared to dictionary matching, their magnitude was small (3.6ms difference in mean T₁ and −0.2ms difference in mean T₂).

There are several interesting features of the cMRF deep learning reconstruction. First, whereas dictionary matching leads to quantization errors because the T₁ and T₂ estimates are restricted to discrete values, the neural network produces continuous outputs. Supporting Information Figure S7 compares dictionary matching and deep learning in an example where the T₁ and T₂ values of a ground truth signal do not lie exactly on the T₁-T₂ grid used to populate the dictionary. Second, the network is trained for a fixed k-space undersampling pattern. To achieve the best performance, the network should be retrained if data are acquired with a different sampling pattern, as the distribution of aliasing artifacts would change (Supporting Information Figure S8).

Recently, other neural network approaches have been described for MRF and for cardiac parameter mapping. DRONE uses a 2-layer fully-connected network for MRF T₁ and T₂ quantification, although the sequence timings are fixed and non-Cartesian k-space undersampling is not taken into consideration.⁹ Cao, et al. have proposed a 4-layer fully-connected network and developed a method for simulating training data with non-Cartesian undersampling artifacts, although limited to MRF sequences with fixed timings.¹¹ Fang, et al. have developed a U-net for high-resolution spiral MRF in the brain. However, the network uses in vivo training data, which may be time-consuming and expensive to collect, and may not generalize to pathological scenarios underrepresented in the training set. In this study, a neural network is trained using simulated cMRF signals, which has the advantage that an arbitrarily large training set can be generated to improve performance. Also, whereas a U-net may introduce blurring, the network used here operates voxelwise and therefore does not induce spatial smoothing. Another recent technique is DeepBLESS, which is a deep learning reconstruction for simultaneous cardiac T₁-T₂ mapping using a non-fingerprinting sequence.²¹ Similar to this study, it is trained to be robust to arbitrary cardiac rhythms. However, highly undersampled radial images are first reconstructed using compressed sensing before being input to the network, which requires three minutes of additional computation time.

This study has several limitations. First, it is still necessary to grid the spiral k-space data, which requires 30s on a standard workstation using a CPU; thus, the computation bottleneck is now gridding rather than dictionary simulation. Gridding could be accelerated using parallel GPUs²² or by applying GRAPPA operator gridding (GROG) to shift the k-space data points onto a Cartesian grid,²³ although these approaches were not investigated here. Second, although the cMRF T₁ and T₂ estimation is robust to field inhomogeneities (Supporting Information Figure S9), no corrections were made for off-resonance blurring during the spiral readout, which can degrade spatial resolution and lead to fat signal contamination, especially near epicardial fat or in regions with intramyocardial fat (Supporting Information Figure S10). Third, both dictionary-based and deep learning cMRF reconstructions can be affected by partial volume artifacts (Supporting Information Figure S11). Fourth, B₁⁺ corrections were not considered. Fifth, no attempt was made to model the complicated spin history of flowing blood, and thus the blood T₁/T₂ estimates may not be reliable. Sixth, no post-contrast T₁/T₂ mapping was performed, although simulations suggest the network could be used for post-contrast data (Supporting Information Figure S12). Seventh, no comparison was made between deep learning cMRF and conventional T₁/T₂ mapping techniques, although prior work has compared dictionary-based cMRF with conventional mapping.¹³ Finally, the in vivo results were limited to healthy subjects, and additional validation of the deep learning cMRF reconstruction should be performed in patients with known cardiac pathologies.

In conclusion, this work introduces a deep learning method for reconstructing T₁ and T₂ maps from undersampled spiral cMRF images in less than 400ms per slice with similar accuracy and precision in vivo as dictionary matching. By eliminating the need for scan-specific dictionary generation and pattern matching, this approach may enable rapid at-the-scanner reconstructions and facilitate the clinical translation of cMRF.