GeoBind: segmentation of nucleic acid binding interface on protein surface with geometric deep learning

Abstract

Unveiling the nucleic acid binding sites of a protein helps reveal its regulatory functions in vivo. Current methods encode protein sites from the handcrafted features of their local neighbors and recognize them via a classification, which are limited in expressive ability. Here, we present GeoBind, a geometric deep learning method for predicting nucleic binding sites on protein surface in a segmentation manner. GeoBind takes the whole point clouds of protein surface as input and learns the high-level representation based on the aggregation of their neighbors in local reference frames. Testing GeoBind on benchmark datasets, we demonstrate GeoBind is superior to state-of-the-art predictors. Specific case studies are performed to show the powerful ability of GeoBind to explore molecular surfaces when deciphering proteins with multimer formation. To show the versatility of GeoBind, we further extend GeoBind to five other types of ligand binding sites prediction tasks and achieve competitive performances.

Graphical Abstract

Graphical Abstract.

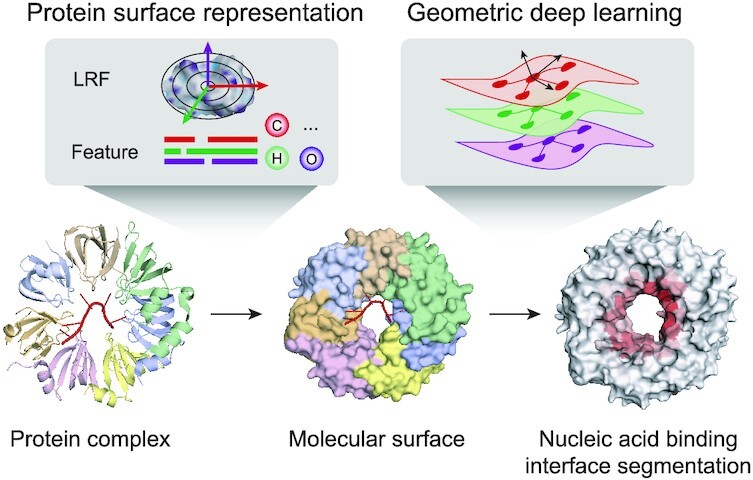
GeoBind: segmentation of nucleic acid binding interface on protein surface with geometric deep learning.

INTRODUCTION

Nucleic acid binding proteins (NBPs) play central roles in gene regulation, including transcription and alternative splicing (1,2). Accurate annotation of binding sites on NBPs remains one of the most challenging aspects of understanding nucleic acid interactions (3,4). It is still time-consuming and costly to determine the detailed binding patterns of nucleic acid-protein complexes experimentally. Fortunately, the impressive results achieved by AlphaFold (5) and RoseTTAFold (6) in protein folding prediction tasks demonstrate the power of machine learning, especially deep learning, in solving biological problems of structure determination. Thus, machine learning methods for predicting the binding sites on protein surface are desired.

Based on machine learning and deep learning methods, a number of NBP binding site predictors have been developed. In terms of the protein encoder paradigm, they can be briefly divided into two categories: primary sequence-based methods and tertiary structure-based methods. Most available predictors used sequence-based protein encoding strategies, ushering in a time when machine learning techniques were employed to predict nucleic acid binding sites, such as BindN (7), RNABindR (8), PRNA (9) and DRNAPred (10). Sequence-based descriptors encode binding residues as vectors and categorize them using a traditional classifier, such as random forest, support vector machine and naive Bayes. Due to the lack of protein spatial information, these predictors did not often perform effectively. As the development of deep learning and the richness of 3D protein structures, recent predictors integrated the structure information of protein into their models, e.g., PST-PRNA (11) based on 2D views, DeepRank on 3D grids (12), NucleicNet on space partitioning (13) and GraphBind (14) on local graph pattern of residues. However, these structure-based methods encode protein structures by simplifying the protein structure modeling, which have limitations in their ability to accurately represent the 3D structure of proteins and capture all the relevant information.

Geometric deep learning techniques have recently flourished in computer vision and graphics (15), allowing for the intrinsic modeling of non-Euclidean protein structures. Benefiting from this, geometric deep learning seeks to develop a non-Euclidean analogy of filtering and pooling operations on protein structures directly rather than considering them firstly in a 3D Euclidean space and then applying standard deep learning pipelines. Geometric deep learning has been shown effective in tasks related to protein structure modeling. For instance, AlphaFold and RoseTTAFold were designed for protein folding, EquiDock (16) and EquiBind (17) for protein–protein and protein-drug docking respectively, MaSIF (18) and dMaSIF (19) for protein-protein binding sites prediction, and ScanNet (20) for protein–antibody binding sites prediction. However, the usage of geometric deep learning technique in elucidating binding patterns between proteins and ligands, such as nucleic acids, metal ions and biologically relevant molecules, has not been well studied.

Here, we present GeoBind, a general framework for nucleic acid binding site segmentation on protein surfaces using geometric deep learning. We hypothesize that molecular surfaces imply fingerprints of interaction patterns between proteins and nucleic acids (18). In GeoBind, based on the 3D structure of a protein, we first compute the molecular surface and describe it as the basic formation of point clouds. The input features of point clouds are assigned with three kinds of feature descriptors (i.e., multiple sequence alignment (MSA) information, chemical environment and local curvature). They are learned to be a numerical task-specific vector by a series of quasi-geodesic convolutional layers. By constructing a local reference frame (LRF) on each point, the spatial information of point clouds is learned by a geometric neural network. Benefit from the pipeline, GeoBind is invariant to 3D rotations and translations. On two benchmark datasets, we show that GeoBind is superior to state-of-the-art methods. Taking full use of the concept of molecular surface, one advantage of GeoBind over existing methods is that GeoBind is able to analyze the surface of multimeric protein complex instead of being limited by the input of protein monomers. To demonstrate this advantage, we present two precise predictions in complexes, whereas the predictions are comparatively inaccurate in their corresponding individual components. Furthermore, we apply GeoBind to five other ligand-binding site prediction tasks. The results further demonstrate the versatility and scalability of GeoBind in protein representation learning.

MATERIALS AND METHODS

GeoBind overview

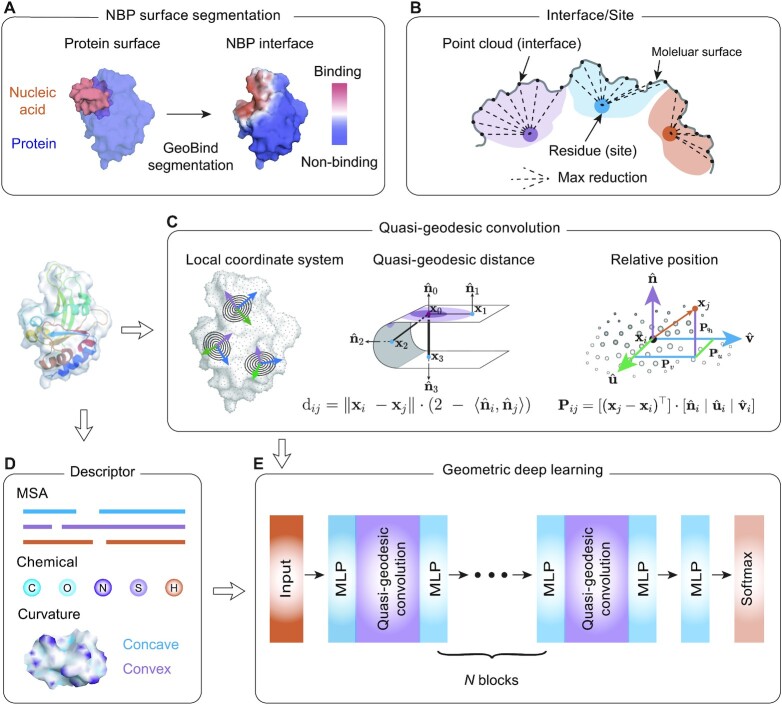
The overall framework of GeoBind is shown in Figure 1. Different from existing methods, GeoBind particularly approaches the challenge of predicting nucleic acid binding sites on protein surfaces in a segmentation manner (see Figure 1A). For GeoBind, two major processes are used sequentially, one focusing on preprocessing 3D protein structures, the other on model training and testing. In the following, we give a brief description of each procedure.

Figure 1.

Overflow of GeoBind. (A) An illustration of the NBP surface segmentation. GeoBind takes the whole protein surface as input and outputs the segmented surfaces with each point assigned a likelihood of being involved in nucleic acid binding events. (B) Definition of binding interface and site. Points located on the protein surface with a distance to nucleic acids less than a cutoff are considered binding interfaces. Binding sites refer to residues that close to nucleic acids according to a similar definition. The mapping from an interface score to a site score is achieved through a max pooling operator. (C) Left, an introduction to quasi-geodesic convolution. We assign each point on cloud with a LRF. GeoBind makes use of quasi-geodesic distance and relative position (computed by LRF) for geometric embedding. Middle, the geodesic distance between two points is estimated by their position and orientation. Right, the relative position of a point in the LRF refers to the projection of the point on three axes. (D) Each point is initialized with three types of descriptors, namely multiple sequence alignment (MSA), chemical environment and curvature information. (E) Basic architecture of GeoBind. GeoBind consists of four blocks which contain the quasi-geodesic convolutional layers. In each block, a Multi-Layer Perceptron (MLP) is set up before and after the quasi-geodesic convolutional layer for the pre- and post-encoder.

3D protein structure preprocessing

(1) Featurization. Given a structure of NBP complex which contains the 3D coordinates of atoms, we first compute its solvent excluded surface. The point cloud with 3D coordinates on the surface is the basic data frame used in GeoBind. Three kinds of features are computed for characterizing the primary representation of the molecular surfaces (i.e., MSA information, chemical environment and local curvature). In order to obtain the hierarchical representation of protein surface, a series of geometric convolutional networks are applied to aggregate the geodesic relationships of adjacent points. To achieve this, we construct a local reference frame (LRF) with respect to each point of cloud (see Figure 1D). (2) Binding interface and binding site definition. An interface is a point on the protein surface, and a binding interface is a point that is <3.0 Å away from any atom in the nucleic acid structure. Besides, we define protein surface interfaces in terms of binding sites or binding atoms. We find that defining the binding interface directly on the point cloud of the protein surface is the most effective and accurate definition (see Supplementary Figure S1). A binding site refers to a protein residue. The binding sites are annotated by BioLip (21). The binding preference of a site is calculated by max-pooling the interfaces generated by the site, as shown in Figure 1B.

Model architecture

The overall neural network architecture of GeoBind is shown in Figure 1E. GeoBind consists of four blocks which contain the quasi-geodesic convolutional layers. In each block, a Multi-Layer Perceptron (MLP) layer is respectively set for pre- and post-encoding the point presentation before and after the convolutional layer. To determine the interface score, an MLP layer followed by a Softmax function is applied after the last convolutional layer. The true interface labels and predicted interface scores provide the supervised information for optimizing the parameters of the proposed geometric deep learning model.

Datasets

The lists of nucleic acid-protein complexes (released up to March 2022) were downloaded from BioLip (21). Complex structures with a resolution higher than 8.0 Å were eliminated. Note that it is not a strict threshold given that the existing NBP structures are utilized as fully as possible. A higher resolution quality control will be applied in the following sequence clustering process. BioLip annotates the Chain ID of nucleic acid that interacts with protein, but not the Chain type (DNA or RNA). We added the annotation of nucleic acid chain type by searching the nucleobase types from PDB structures individually. Then, the complexes were divided into DBP dataset and RBP dataset according to their annotated nucleic acid chain type, resulting in redundant 13 864 DBPs and 22 908 RBPs, respectively. The redundant DBPs and RBPs were clustered using psi-cd-hit (22) program at sequence identity cutoff of 0.3. The protein with the best resolution structure in each cluster is chosen as the representative member. Sequence clustering resulted in 898 DBPs and 820 RBPs. Finally, the RBP and DBP sets were split into the training and testing datasets according to TM-score clustering results for depressing the structure similarity between them. Specifically, pair-wise matrix of TM-score for DBP set and RBP set were computed using TM-align algorithm (23). The training set and testing set were split by applying a hierarchical procedure using agglomerative clustering in Scikit-learn (24). As a result, 195 DBPs (denoted as DNA-195_Test) and 157 RBPs (denoted as RNA-157_Test) are selected for the purpose of testing. To avoid overfitting to the testing set, we have also set aside approximately 20% of the training set to construct a validation dataset, which will be used for hyperparameter tuning. Supplementary Table S1 provides detailed statistics of the binding and non-binding sites. We have included information on the distribution of protein length and protein structure resolution in our collected datasets in Supplementary Figure S2.

Problem formulation

GeoBind works on protein tertiary structure which is a set of atoms with 3D coordinates and atom types. Given a nucleic acid binding protein, we first compute the protein surface of protein based on the set of protein atoms. We collect residues that contribute to surface formation, while residues that fold into the interior structure are not considered. These surface sites are labeled by BioLiP as either binding or non-binding, denoted by: 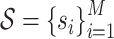, where M is the number of sites and s_i ∈ {0, 1} represents non-binding and binding sites, respectively. The protein surface is represented as a set of points, each of which is associated with a nucleic acid binding identity denoted by 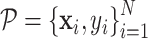. Here, N represents the number of points on the surface, 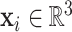indicates the 3D coordinate of the point, and y_i ∈ {0, 1} indicates whether the point is a binding interface. Specifically, a point x_i is labeled as a binding interface (y_i = 1) if there exists a ligand atom located within a distance of 3 Å from the point.

A set of point cloud with features can be thought of as a map 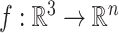. It assigns each point on protein surface with a n-dimensional vector. In GeoBind, we design a SE(3)-equivariant operator 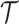to produce a new function 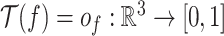that describes the point cloud with interface score 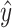. We parametrize 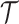using quasi-geodesic convolutional neural networks as described in Ref. (19).

To map the binding interface score to the binding site score in GeoBind, we utilize a max-pooling operator. Specifically, we calculate the binding site score 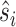for residue i by taking the maximum interface score 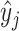among the surface points generated by residue i, denoted as R_i. The set R_i is determined by the generating solvent excluded surface, which is computed using the msms program (25). Supplementary Note S1 includes a comprehensive description of this problem formulation.

Oriented point cloud of protein surface

All proteins are protonated using program reduce (26) to add the missing hydrogen atoms. Then the classical solvent excluded surfaces (27) are triangulated using msms program with parameters of density of 3 and water probe radius of 1.5 Å. Then all protein meshes are resampled at a resolution of 1.2 Å using PyMESH (28) (available at https://github.com/PyMesh). Supplementary Figure S2d depicts how the number of data points relates to protein length, generated under five different sampling ratios.

As described in Problem formulation, the surface of a protein is represented by 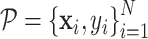. The normal 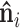of a reference point x_i on surface is computed by averaging the normal vectors of faces whose vertices contain the reference point x_i. Then, the surface of protein can be represented by .

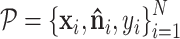Descriptors

Multiple sequence alignment (MSA) feature

The MSA information is of great significant in computational protein biotechnology. And it is a key intermediate step in predicting evolutionarily conserved properties such as tertiary structures, functional sites and interactions. We assign the MSA features to the point cloud according to the membership of points and residues. Specifically, the evolutionary score of a residue is assigned to the points of clouds generated by atoms in this residue. For a protein with the residue number of L, a profile hidden Markov model (HMM) matrix of shape L × 30 is computed by using the tool HHblits3 (29) searching against Uniclust30 (30) database. The HMM matrix consists of three kinds of information, i.e. 20 columns of observed frequencies for twenty kinds of amino acids in homologous sequences, 7 columns of transition frequencies and 3 columns of local diversities.

Chemical feature

In GeoBind, we do not utilize handcrafted protein physicochemical descriptors like electrostatics charge and hydropathy profile. Instead, we leverage a lightweight neural network to regress the physicochemical environment of protein surfaces using an atomic point cloud, as demonstrated in dMaSIF (19). In GeoBind, the chemical feature is represented as a 1 × 6 vector of one-hot encoding, with each element corresponding to one of six types of atoms (C, H, O, N, S, and others).

Geometric feature

For characterizing the geometric shape of a point cloud, the shape index around each point on the surface is described by the local curvature. It is defined with respect to the principal curvature κ₁, κ₂, κ₁ ≥ κ₂ as:

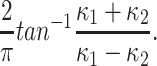(1)

After assigning the above features to the point cloud, we can represent the protein surface as: 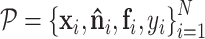, where .

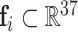Quasi-geodesic convolution

Quasi-geodesic distance

The computation of geodesic distance between each pair of points on a surface requires a high time cost. An alternative approximation defines the geodesic distance (Figure 1C, middle) between two points on a curved surface as:

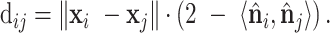(2)

To localize the filters in the convolutional layer, the geodesic distance is transformed by a smooth Gaussian window of σ = 12 Å which is defined as:

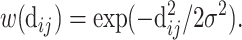(3)

Local reference frame (LRF)

For object recognition and surface registration task in 3D computer vision, a remarkable number of works introduced the LRF for designing 3D descriptors in order to reach model SE(3)-invariance (31–34). Recent works in structural biology have used the LRF for protein structure representation (16,17,19,35). The LRFs indicate the local orientations of a 3D object. As shown in Figure 1C, we build LRFs for all points on the protein surface. For any point x_i, a LRF is represented as 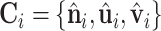to encode the relative positions between point x_i and its neighbors. The relative position P_ij between point x_i and x_j is a 3D vector and defined as:

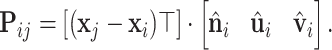(4)

Here, we give the details of generating the LRF of a point x_i: 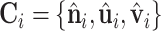. At first, 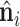is the normal vector of point x_i as described in oriented point cloud of surface. The normal vectors exhibit equivariance with respect to the SE(3) transformation of the protein. Then, we initialize the tangent vector 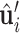, 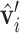using the orthonormal basis (36): 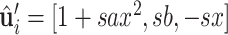, , 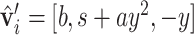where s = sign(z), a = −1/(s + z) and b = axy. Next, we orient (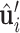, 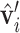) along the geometric gradient :

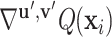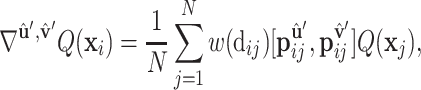(5)

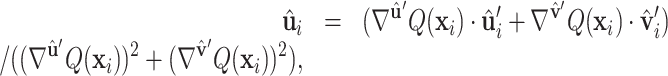(6)

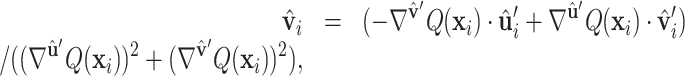(7)

where Q is a scalar field function on protein surface 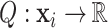, 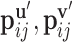are the relative positions of point x_j with respect to the orientation 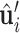and 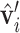within the initial LRF of point x_i. After building the LRF for each point, we can update the representation of protein as .

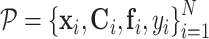Choice of the scalar field function

Generating a local reference frame (LRF) on a protein surface requires a scalar field function Q that is differentiable and equivariant to SE(3) transformation. In this study, we test five types of scalar field functions which have been acknowledged, i.e., BOARD (31), local curvature (37), STED, FLARE (32) and MLP (19). After comparing their performance in predicting DNA- and RNA-binding sites, we selected BOARD as our scalar function. For a point on the surface, BOARD computes the signed distances to the tangent plane of a point, based on a subset of points within a cutoff radius distance, and then averages them. The cutoff radius is the same as the size of the Gaussian window σ = 12 Å. The tangent plane of a point is determined by its normal vector. Supplementary Note S2 provides detailed descriptions of the other four scalar field functions.

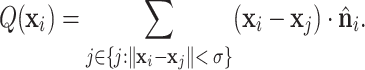(8)

Trainable convolution

Finally, we use quasi-geodesic convolution as the aggregation strategy for high-level representations of point clouds, which is defined as:

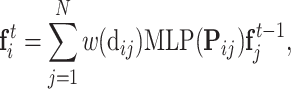(9)

where w(d_ij) is the smoothed distance between point x_i and x_j, 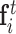is the feature of point x_i at the tth quasi-geodesic convolutional layer. The dimension of f_i is fixed at 64 for all quasi-geodesic convolutional layers. The MLP is a trainable multilayer perception for encoding the relative relations vector between point x_i and x_j. Specifically, the MLP layer consists of an input layer with 3 units (the dimension of the relative position vector P_ij), a hidden layer with 8 units, a ReLU non-linearity, and an output layer with 64 units. The output dimension of MLP(P_ij) is consistent with the dimension of 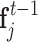, and the quasi-geodesic convolution operation involves element-wise multiplication of MLP(P_ij) and 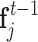using the Hadamard product.

Neural network architecture and training optimization

Neural network architecture

Details of the GeoBind architecture are shown in Supplementary Figure S3. The network of GeoBind consists of 4 blocks with one quasi-geodesic convolutional layer per block. For each block, an MLP (consists of two fully connected (FC) layers) layer is respectively set for pre- and post-encoding the point presentation before and after the quasi-geodesic convolutional layer. The number of feature channels increases to 64 in the first block and remains at that number throughout the series. A Leaky ReLU activation layer is followed after each FC layer. A batch normalization (38) layer is set after the pre- and post-encoding layers to accelerate the training of GeoBind. Following the fourth convolutional block, an MLP classifier, consisting of two FC layers followed by a Softmax layer, is set up to predict the likelihood 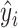that point x_i is a binding interface point or not. Finally, the max-pooling operator is used to aggregate the interface scores in order to determine the likelihood of a residue s_i to be a binding site:

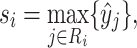(10)

where R_i denotes those surface points generated by residue i.

Optimization

For model optimization, a binary cross-entropy loss function is minimized via a back propagation algorithm using the ADAM (39) optimizer. For macro-molecule ligands, i.e., DNA, RNA, ATP and HEM (ATP, HEM and the following metal ion ligands are extended tasks introduced in results), the loss function is defined on the interface (point cloud) as:

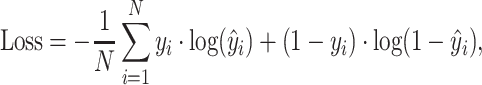(11)

where N is the number of points on surface, and y_i, 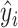stand for the true label and the probability of a point being a binding interface point. For metal ion ligands, i.e., Ca^{2 +}, Mn^{2 +} and Mg^{2 +}, the binding interfaces on surface are extremely few. Therefore, we first convert the interface score to site score according to Equation 10. Then the loss is defined on the sites (residues) as:

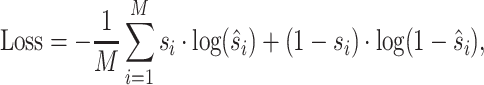(12)

where M is the number of residues forming the protein surface, and s_i, 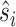stand for the true label and the probability of a site being a binding site.

Initially, the learning rate is set to 10⁻³. If the AUROC value does not improve in 5 epochs on the validation dataset, the learning rate decays by 10. We set an early stopping strategy for fast reaching the optimal model. Early stopping criterion is met if the AUROC value does not improve within 10 epochs. The batch size is set to 1 and we find that increasing the batch size does not significantly improve the performance.

Implementation and runtime

GeoBind is implemented by Python v3.7.12. Biopython v1.78 (40) is used to parse the PDB files. The quasi-geodesic neural network is achieved by PyTorch Geometric (PyG) v1.7.1 (41) based on the architecture of PyTorch v1.10.1 (42). The pair-wise distance of all points involved in quasi-geodesic distance and quasi-geodesic convolution is computed efficiently using KeOps v2.1 library (43,44). Other scientific computing and machine learning packages include NumPy v1.21.6 (45) and Scikit-learn v1.0.2 (24).

Experiments were conducted using a workstation with two Intel Xeon Gold 6226R processors @ 2.90 GHz and one NVIDIA RTX6000 GPU running on Ubuntu Linux 18.04. The pre-computation time for generating the featured point cloud from the PDB file depends on the length of the protein. The computation of the MSA feature (from HHM files by program HHblits3) is time-consuming. Thus, we accelerate the preprocessing of proteins in parallel using Slurm (46) system. The HHM files of all proteins for seven kinds of ligands are available for download at https://doi.org/10.5281/zenodo.7045931. Supplementary Figure S2c plots the running time of the precomputing time (excluding the time of generating the MSA feature) for proteins in RBP datasets. Training a model using a dataset consisting of 800 proteins typically requires approximately 10GB of memory and takes around 5 hours to complete for roughly 40 epochs.

Comparison methods

The comparing methods in this study are GraphBind (14), DRNApred (10), 3D Zernike descriptors (3DZD) (47), MaSIF-site (18), and dMaSIF-site (19). Supplementary Note S3 provides comprehensive descriptions of the implementation details of these methods.

RESULTS AND DISCUSSION

We respectively used the two NBP datasets (i.e., DNA-binding proteins (DBPs) and RNA-binding proteins (RBPs)) to train and test GeoBind and state-of-the-art methods. On account of the unbalanced data number between binding sites and non-binding sites, we use the area under the receiver operating characteristics curve (AUROC), the area under the precision-recall curve (AUPRC) and Matthew’s correlation coefficient (MCC) as the primary evaluation criteria (48). In addition, the results of the other criteria (i.e., recall, precision and F1-score) are tabulated in the Supplementary Tables.

GeoBind outperforms existing methods

To benchmark the effectiveness of GeoBind, we evaluate GeoBind and the other existing methods on the two compiled datasets. We compare GeoBind with five state-of-the-art methods, DRNApred (10), GraphBind (14), 3D Zernike descriptors (3DZD) (47), MaSIF-site (18) and dMaSIF-site (19). DRNApred and GraphBind are two predictors for identifying nucleic acid binding sites, with DRNApred being a sequence-based approach and GraphBind using structure-based methods. 3DZD, MaSIF-site, and dMaSIF-site are state-of-the-art surfaced-based approaches, but were originally developed to identify protein-protein binding sites. In this work, we have extended these surface-based methods to predict nucleic acid binding sites and demonstrate the effectiveness of our approach.

Overall evaluation

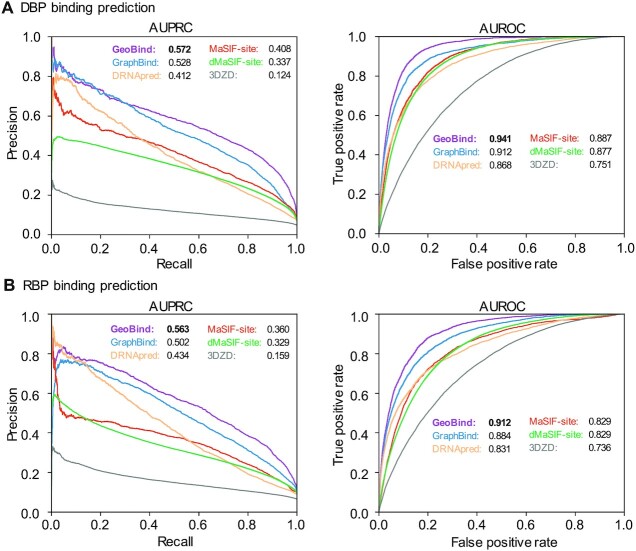
According to the results presented in Figure 2, GeoBind achieves impressive performance metrics on two different test datasets. Specifically, for DNA-195_Test, GeoBind achieves an AUPRC of 0.572 and an AUROC of 0.941, while for RNA-157_Test, GeoBind achieves an AUPRC of 0.563 and an AUROC of 0.912. These metrics demonstrate that GeoBind outperforms existing methods with substantial improvement. Notably, compared to the second best method, GeoBind achieves a 3.2% increase in AUROC and an 8.3% increase in AUPRC for DNA-195_Test, and a 3.2% increase in AUROC and a 12.2% increase in AUPRC for RNA-157_Test. Supplementary Table S2 provides more details of performances by comparison methods. In addition, GraphBind also achieves competitive performances caused by considering of the MSA information descriptor and structural context information. DRNApred also makes use of the MSA features for residue representation. However, due to the lack of structure information, the performance of DRNApred is overshadowed.

Figure 2.

Model performance of GeoBind and baseline methods. PR and ROC curves achieved by GeoBind and baseline methods on DNA-195_Test dataset (A), and on RNA-157_Test dataset (B).

Comparing with surface-based models

GeoBind was developed based on the prior knowledge that protein surfaces imply fingerprints of interaction patterns between proteins and nucleic acids. In order to demonstrate the advantage of GeoBind, we compared it with existing surface-based protein structure representation methods, such as 3DZD, MaSIF-site and dMaSIF-site, which were originally designed for predicting protein-protein binding sites. Since the core of these methods is to encode protein surfaces, they are extensible to predicting nucleic acid binding sites. The comparison results are shown in Figure 2. It is clearly shown that GeoBind outperforms these existing surface-based methods by a significant margin.

Furthermore, we observed that dMaSIF-site produces inferior results compared with GeoBind, e.g., with AUPRC values of 0.337 and 0.329 for DNA- and RNA-binding site predictions, respectively. These values are significantly lower than those achieved by GeoBind even without using the MSA feature. GeoBind without MSA achieves AUPRC values of 0.455 and 0.452 for DNA- and RNA-binding site predictions, as introduced in Section Ablation study. Since GeoBind and dMaSIF-site both embrace the quasi-geodesic convolutional framework, we investigated the details to understand the reason for the gap.

In addition to the carefully crafted designs in GeoBind, which includes accurate protein surface, features and LRF, we discovered that the difference in performance between GeoBind and dMaSIF-site can also be attributed to the optimization of model parameters. Specifically, dMaSIF employs a negative down-sampling strategy at the optimizing stage to address the issue of imbalanced numbers of binding and non-binding sites. Although this strategy helps the model focus on positive samples, it results in a large number of false positive recognitions, as reflected in the relative high recall and extremely low precision metrics achieved by dMaSIF-site (Supplementary Table S2). After replacing the loss function of dMaSIF-site with the one (Eq. 11) we used in GeoBind, dMaSIF-site achieves AUPRCs of 0.410 and 0.420 for DNA- and RNA-binding site predictions, respectively. Comparing the results with GeoBind without MSA features, we conclude that a problem-specific, manually designed approach performs better than general end-to-end learning in the segmentation of nucleic acid binding sites on the protein surface.

Extending to external benchmark dataset

In addition, we tested GeoBind on the benchmark datasets collected by GraphBind (14). The datasets in GraphBind were split based on the released time of PDB structures. More details about the data collection are listed in Supplementary Table S3. This experiment compared GeoBind with 8 existing DBP binding sites predictors and 7 DBP binding sites predictors. On the DBP dataset, GeoBind achieves MCC of 0.526 and AUROC of 0.940, outperforming the existing DBP predictors ranging from 5.1% to 50.2% of MCC, and from 1.4% to 19.0% of AUROC. On the RBP dataset, GeoBind achieves MCC of 0.373 and AUROC of 0.874, outperforming the existing RBP predictors ranging from 13.7% to 49.3% of MCC and from 2.3% to 24.1% of AUROC. Supplementary Table S4 provides more details about the comparison experiments.

Assessment of GeoBind on homologous unbound proteins

Proteins often undergo changes in their structures when transitioning from an unbound individual state to a bound state with nucleic acid (49). To assess this influence on our prediction, we tested GeoBind and three other comparing methods using an independent unbound testing dataset. We screened the Protein Data Bank (50) to retrieve the unbound formations of proteins without nucleic acids corresponding to the bound formations in the RNA-157_Test and DNA-179_Test datasets. We found 27 unbound RBP structures and 50 DBP structures compared to their bound counterparts. The rules for selecting the unbound benchmark are presented in Supplementary Note S4. Figure 3A shows the boxplot of TM-align scores for the bound and homologous unbound structures. Overall, GeoBind achieves an AUROC of 0.912 and 0.871 for predicting nucleic acid binding sites in the unbound DBPs and RBPs, respectively. Compared to the corresponding scores of 0.936 and 0.9, the prediction performance of GeoBind becomes slightly weaker when predicting nucleic acid binding sites in the unbound NBPs. We regard it is reasonable since the NBPs used to train GeoBind are all in nucleic acid-binding states. Although all the predictors demonstrate some difficulty in the prediction task for unbound proteins, GeoBind still achieves the best prediction performance.

Figure 3.

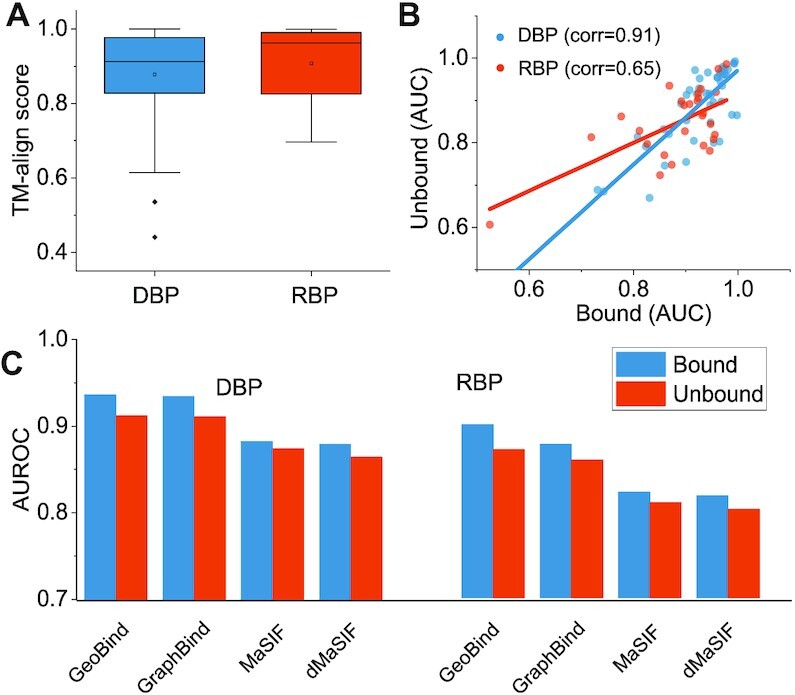
Evaluation on homologous unbound proteins. (A) Box-plots are used to display the TM-align scores between the bound and unbound forms in the collected datasets. (B) A comparison of the AUROCs predicted on unbound proteins versus those predicted on bound proteins using GeoBind. (C) The performance of GeoBind is compared with that of other state-of-the-art structure-based predictors.

Ablation study

A series of ablation studies are set up in this section to show how GeoBind is affected by each component in the proposed model. Ablation studies help to tune the model for optimal performance under the basic given architecture. For simplicity, an ablation study is conducted by changing only one criterion at one time. These experiments include feature contribution, scalar function choice, the depth of the network and the size of the Gaussian window.

Feature contribution to GeoBind

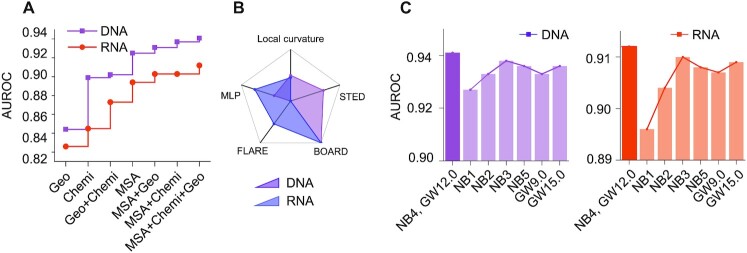
To investigate the contribution of features in GeoBind, we train and test the model successively by numerous subset feature space. As shown in Figure 4A (detailed results in Supplementary Table S5), the feature of MSA contributes the most to GeoBind, followed by chemical and curvature features sequentially. The results demonstrate that the shape of protein surface is fragile for protein functional pattern learning, which is consistent with the conclusion in MaSIF (18) and dMaSIF (19). Prior designed features, especially MSA features, still play a major role in understanding nucleic acid binding function for proteins. The MSA features are based on residues and are calculated by searching the primary sequences. The importance of MSA features is also identified with the evolutionary conservation property of NBP binding sites (51,52), which is known as the theory of nucleic acid binding motifs in the light of evolution (53,54).

Figure 4.

Ablation study of GeoBind. (A) GeoBind performance with different sub-sets of features. (B) GeoBind performance with different choice of scalar function that determines the LRF. The AUROC value is normalized to highlight their differences. (C) GeoBind performance effected by the neural network depths (number of blocks, NB) and radius size of the Gaussian window (GW).

Using LLM embeddings to replace MSA

Recently, some large language models (LLMs) at the scale of evolution are built up toward predictive and generative biological structure and function from protein sequences (55–57). They are pre-trained on large scale protein sequences, and then implemented as a protein embedding model for downstream tasks. This endeavor presents an alternative opportunity to investigate the LLM embedding features used for nucleic acid binding site prediction by replacing the handcrafted MSA features. In our study, we used the large pre-trained language model ESM-2 (55) to encode NBPs from our collected data into embedding features. We tried to vary the parameters of the ESM-2 model to create embedding features with different dimensions ranging from 320 to 5120. Then, we trained GeoBind on these embedding features, as well as the chemical and geometric features. The results are shown in Table 1. We found that GeoBind trained with the ESM-2 embedding features of 5120 dimensions obtains similar performance with the one trained with MSA features for predicting DNA-binding sites, but obtains lower performance for predicting RNA-binding sites. Moreover, the performance of the language-based GeoBind model improves gradually as we increase the scale of the ESM-2 model. Compared with MSA features with only 30 dimensions, the high-dimensional features of EMS-2 may not be well-suited to lightweight models such as the proposed GeoBind. Nevertheless, the experiments confirm that large pre-trained models have the great potentials in nucleic acid binding sites prediction tasks. This will be a valuable research direction to build up an LLM model with more complicated architectures and parameters.

Table 1.

Performance of GeoBind with LLM embeddings

		DBP		RBP
Feature source	Dim	AUROC	AUPRC	AUROC	AUPRC
esm2_t6_8M	320	0.914	0.483	0.874	0.455
esm2_t12_35M	480	0.915	0.513	0.867	0.477
esm2_t30_150M	640	0.931	0.557	0.886	0.506
esm2_t33_650M	1280	0.937	0.571	0.893	0.492
esm2_t48_15B	5120	0.940	0.582	0.897	0.472
MSA (HHblits)	30	0.941	0.572	0.912	0.563

Dim means the dimension of features.

Choice of scalar function for LRF

The LRF is the key module for achieving model SE(3)-equivariance. The tangent vectors in LRF require a scalar field function that determines the most descending orientations of points in the protein surface cloud. In this section, we explore five widely-used scalar field functions for choosing a better 3D representation, i.e. local curvature, STED (sum of total Euclidean distances), BOARD (31), FLARE (32) and MLP (19). The definitions of the five functions are given in Methods and Supplementary Note S2. Figure 4B shows the scaled AUROCs of GeoBind respectively based on the five scalar functions (the original results are listed in Supplementary Table S6). The top two functions for DBP's binding site prediction are BOARD and STED. The top two functions for RBP's binding site prediction are BOARD and FLARE. Based on the overall assessment, we choose BOARD as the baseline scalar field function in GeoBind.

Number of blocks and size of Gaussian window

As shown in Figure 4C (detailed results in Supplementary Table S7), GeoBind reaches the best performance when the number of blocks is set as 4. When the model depth is lower or higher than 4, the model is in a state of underfitting or overfitting. The best size of Gaussian window for both DNA- and RNA-binding site predictions is 12.0 Å.

GeoBind for segmentation of multimer surface

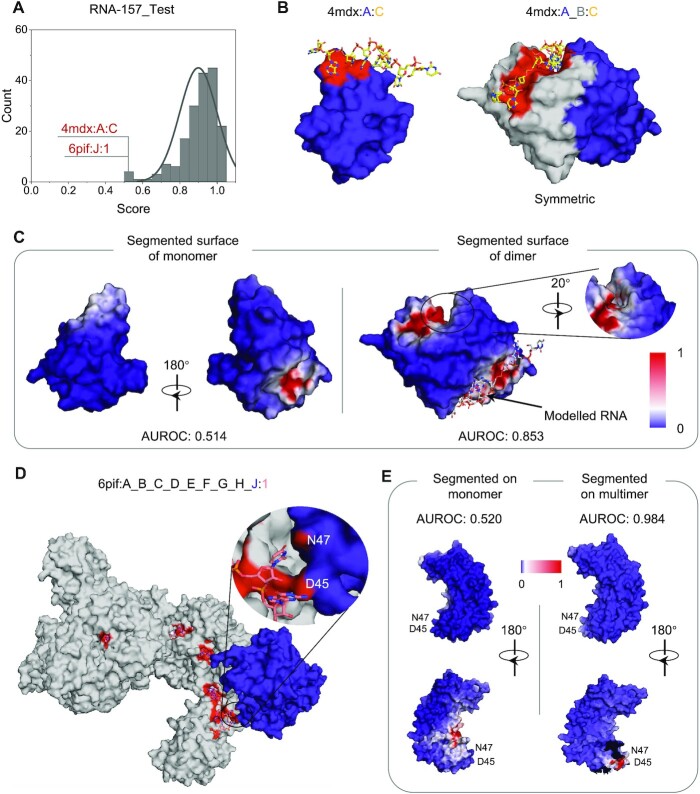
GeoBind is designed to make full use of the molecular surface concept, by taking both monomers and multimers as input. The AUROC distribution of 157 predicted RBPs in the testing set is shown in Figure 5A, while the distribution for DBPs can be found in Supplementary Figure S5. Although most proteins are well predicted, some proteins have an AUROC close to 0.5, indicating poor predictions. To understand the reasons behind these poor predictions, we present two examples and propose solutions.

Figure 5.

Case studies of RNA-binding proteins. (A) Distribution of AUROC values on 157 RBPs in the test dataset. Two cases are predicted with AUROC under 0.5. (B) MazF in a complex with an uncleavable RNA substrate (4mdx). Left is the MazF monomer (Chain A, in blue) binding to RNA. Right is two MazF subunits (Chain A in blue, Chain B in gray) that form a symmetrical dimer. The binding interface on the surface is colored in red. (C) The segmented surface of MazF monomer and dimer. The RNA in the crystal is colored in yellow. A modelled RNA is placed in the symmetric position in silver color. (D) The binding interface of v. cholerae TniQ-CasCade complex (PDB ID: 6pif). The TniQ.2 monomer (Chain: J, in RNA-157_Test dataset) is in blue. The other eight chains are colored in gray. The area of binding sites (N47 and D45) of TniQ.2 is amplified. (E) Left shows the segmented surface of TniQ.2 when GeoBind takes the surface of monomer as input. Right shows the segmented surface of TniQ.2 when GeoBind takes the surface of the multimer as input. The broken gap on the surface is where TniQ.2 attaches to other protein chains.

Figure 5B shows the structure of MazFs in complex with an uncleavable RNA substrate (PDB ID: 4mdx) (58). In this complex, there are two proteins forming into a homologous dimer binding to a RNA with sequence ‘UUdUACAUAA’. In order to avoid the biased assessment of models caused by sequence redundancy, Chain A is conserved when collecting datasets, while Chain B is abandoned. The binding interface of the monomer (Chain A) and dimer (Chains A and B) are shown in Figure 5C. The two MazFs jointly form an extensive dimeric interface. When GeoBind takes Chain A as input, namely monomer, only a portion of the dimeric interface is predicted with relative high probability on the segmented surface, resulting in an AUROC of 0.514. While we take the molecular surface of the dimer of MazFs as an input to GeoBind, the extensive dimeric interface binding to RNA is well segmented, resulting in an AUROC of 0.853. Besides, benefiting from the SE(3)-equivariant property of GeoBind, the symmetric pocket is predicted with high preference for binding to RNA. The ITC and filter-binding experiments suggest that this RNA can bind to any one of the two potential pockets without exhibiting any preference (58).

Another protein we showcase is the TniQ monomer in the V. cholerae TniQ-Cascade complex (PDB ID: 6pif:J:1) with a predicted AUROC of 0.52. The TniQ-Cascade complex is formed by one Cas8 monomer, six Cas7 monomers, one Cas6 monomer, one TniQ monomer (TniQ.2) and one CRISSPR RNA (crRNA), as shown in Figure 5D. Among these proteins, only TniQ.2 is in RNA-157_Test dataset. TniQ.1 monomer (Chain ID: I) in 6pif is dropped as it has no binding sites to crRNA according to the annotation by BioLip. The affiliation or homologous information of each monomer with the training or testing dataset is listed in Supplementary Table S10. when predicting the TniQ monomer using GeoBind, the segmented surface produces numerous false positive interfaces while failing to accurately identify the true positive interface around residues N47 and D45, as illustrated in the left panel of Figure 5E. GeoBind achieved an AUROC of 0.984 for TniQ.2 (Chain ID: J) when the entire surface of the complex was used as input. The two binding sites (N47, D45) were well-segmented, as shown in Figure 5E (right). Furthermore, for the complete complex containing Cas8, six Cas7s, Cas6, and TniQ (6pif:A_B_C_D_E_F_G_H_J:1), the predicted AUROC was 0.98. Note that some chains are in or homologous to the proteins in training dataset. The PSE files (open with PyMOL (59)) for generating the figures can be downloaded from https://github.com/zpliulab/GeoBind/tree/main/PSE/. The above cases suggest that protein interactions appear to influence the prediction of nucleic acid binding sites. The surface shapes and descriptors are changed along with conformation changes. Therefore, we suggest predicting the multimeric conformation of a protein rather than the monomer, whenever the multimeric conformation is available.

Extending GeoBind to the prediction of other types of ligands

GeoBind embeds a general framework for 3D protein structure encoding. It is therefore easy to extend GeoBind to predict other ligand binding sites. In this section, we apply GeoBind to other five ligands including two biologically relevant molecules (i.e., ATP and HEM) and three metal ions (i.e. Ca²⁺, Mn²⁺ and Mg²⁺). The dataset of ATP is collected by ATPBind (60) and the other four ligand datasets are collected by DELIA (61). The binding sites for the five ligands are annotated by BioLip (21). A description of the five datasets is listed in Supplementary Table S8. The hyper-parameters and details of GeoBind for training the ATP and HEM ligands are the same as GeoBind designed for nucleic acid binding prediction. For the three metal ion ligands, we fine-tune the model in two aspects for metal ion task-oriented learning. First, we set the probe radius to 0.5 Å instead of 1.5 Å (for macro-molecules) when computing the solvent excluded surface. We find some true sites binding to metal ion are buried into the surface of probe radius of 1.5 Å (See Supplementary Figure S4). Second, the loss function for GeoBind optimizing is computed on sites instead of interfaces due to the scarce of metal ion binding interface on protein surface.

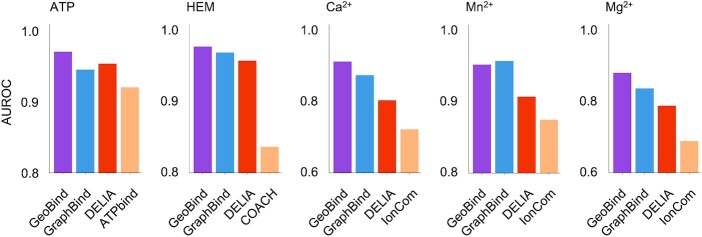
We also compare GeoBind with state-of-the-art programs, i.e. TargetS (62), S-SITE (63), COACH (63), IonCom (64), ATPBind (60) and DELIA (61). Figure 6 shows the comparison of AUROC values achieved by GeoBind with those achieved by the other existing methods. GeoBind ranks first in four of the five ligand-binding site predictions, outperforming the suboptimal method by 1.7% of ATP, 0.8% of HEM, 4.2% of Ca²⁺ and 5.1% of Mg²⁺, respectively. The detailed results of these experiments are listed in Supplementary Table S9. The results demonstrate the powerful representation learning ability of protein 3D structures and the advantage of our proposed method.

Figure 6.

Comparison of GeoBind with state-of-the-art methods on five types of ligands binding sites prediction tasks.

CONCLUSION

Here we described GeoBind, a geometric deep learning model for predicting nucleic acid binding sites on protein surface in the segmentation manner. On benchmark datasets, GeoBind outperformed state-of-the-art methods by a substantial margin. GeoBind discards the most handcrafted features representing protein surfaces, such as hydropathy and electrostatic charge. These features can be easily regressed by even a lightweight network through intrinsic atoms and their spatial arrangement (19). The only handcrafted feature GeoBind utilized is the MSA feature. A study of ablation showed that it improved the performance of models by around 4% of AUROC and 25% of AUPRC in GeoBind. It indicates the importance of the conservation property of nucleic binding motifs in the biological evolution process.

GeoBind uses the point cloud on the molecular surface as the basic frame to represent proteins, enabling it to predict proteins with multimeric formation. Our case studies demonstrate that the multimeric conformation alters the feature environment, leading to more precise binding interface segmentation on the molecular surface of multimers compared to monomers. Traditional protein encoding methods rely on the primary sequence or spatial arrangement of C_α skeleton, making it difficult to predict the functional sites of multimers. GeoBind offers a new alternative for analyzing the binding function of protein complexes. It is now available on our webserver http://www.zpliulab.cn/GeoBind for predicting nucleic and ligand binding sites.

DATA AVAILABILITY

The lists of seven kinds of ligand-binding proteins are available for download at https://github.com/zpliulab/GeoBind/Dataset. The pretrained models for seven kinds of ligands and available at https://github.com/zpliulab/GeoBind/Pretrained_Model. The PSE files (open with PyMOL) for molecular surface visualization in Fig. 4 are available at https://github.com/zpliulab/GeoBind/PSE/. The PDB files of NBP complexes are available for download at https://doi.org/10.5281/zenodo.7045931. GeoBind is open source and available at GitHub (https://github.com/zpliulab/GeoBind). For easy access, GeoBind is freely available online at our webserver http://www.zpliulab.cn/GeoBind. Source code and data are also in Zenodo: https://doi.org/10.5281/zenodo.7801930.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Key Research and Development Program of China [2020YFA0712402]; National Natural Science Foundation of China (NSFC) [61973190]; Fundamental Research Funds for the Central Universities [2022JC008]; Program of Qilu Young Scholars of Shandong University. Funding for open access charge: National Key Research and Development Program of China [2020YFA0712402]; National Natural Science Foundation of China (NSFC) [61973190].

Conflict of interest statement. None declared.