Highlights
-
•
Effects of equation of state on acoustic cavitation characteristics are assessed.
-
•
Peng–Robinson (PR) equation of state can accurately predict gas thermodynamics.
-
•
Gilmore-PR model predicts a stronger bubble collapse rather than Gilmore-vdW model.
-
•
The stronger the bubble collapse is, the differences between two models increase.
Keywords: Acoustic cavitation, Bubble collapse, Equation of state, Peng–Robinson equation, Van der Waals equation
Abstract
The cavitation dynamics of an air-vapor mixture bubble with ultrasonic excitation can be greatly affected by the equation of state (EOS) for the interior gases. To simulate the cavitation dynamics, the Gilmore-Akulichev equation was coupled with the Peng–Robinson (PR) EOS or the Van der Waals (vdW) EOS. In this study, the thermodynamic properties of air and water vapor predicted by the PR and vdW EOS were first compared, and the results showed that the PR EOS gives a more accurate estimation of the gases within the bubble due to the less deviation from the experimental values. Moreover, the acoustic cavitation characteristics predicted by the Gilmore-PR model were compared to the Gilmore-vdW model, including the bubble collapse strength, the temperature, pressure and number of water molecules within the bubble. The results indicated that a stronger bubble collapse was predicted by the Gilmore-PR model rather than the Gilmore-vdW model, with higher temperature and pressure, as well as more water molecules within the collapsing bubble. More importantly, it was found that the differences between both models increase at higher ultrasound amplitudes or lower ultrasound frequencies while decreasing as the initial bubble radius and the liquid parameters (e.g., surface tension, viscosity and temperature of the surrounding liquid) increase. This study might offer important insights into the effects of the EOS for interior gases on the cavitation bubble dynamics and the resultant acoustic cavitation-associated effects, contributing to further optimization of its applications in sonochemistry and biomedicine.
Nomenclature
- a (b)
Coefficients for the EOS
- Ah (Bh, Ch)
Constants in Henry’s law
- B (m)
Specific constants
Average velocity of molecules [K·mol·g−1]
- C0
Equilibrium speed of sound [m·s−1]
- Cl
Speed of speed at the bubble surface [m·s−1]
- cp
Heat capacity at constant pressure [J·m−3·K−1]
- cs
Transient concentration of molecules [mol·m−3]
- c∞
Concentration of dissolved gas [mol·m−3]
- Cv
Heat capacity at constant volume [J·K−1]
- D
Diffusion coefficient [m2·s−1]
- eth
Thermal energy of molecules [J]
- E
Energy inside a bubble [J·mol−1]
- f
Ultrasound frequency [Hz]
- fi
Degree of freedom of species i
- hw
Molecular enthalpy [J]
- H
Molar specific enthalpy [J·mol−1]
- k1 (k2)
Specific constants for the EOS
- kB
Boltzmann constant [J·K−1]
- KH
Henry’s constant
- Ldiff
Diffusion layer thickness
- Lth
Thermal boundary layer thickness
Mass flux of non-condensable gases [mol·s−1]
Evaporation–condensation rate of water [mol·s−1]
- M
Molar mass [kg·mol−1]
- n
Molar amount [mol]
- N
Number of particle [mole]
- P0
Static pressure [Pa]
- PA
Ultrasound amplitude [Pa]
- Pac
Driving acoustic pressure [Pa]
- Pin
Gas pressure inside bubble [Pa]
- Pw
Liquid pressure at the interface [Pa]
Heat exchange [W·m−3]
- R
Instantaneous bubble radius [μm]
- R0
Ambient bubble radius [μm]
- Rm
Compression ratio
- Rg
Universal gas constant [J·mol−1·K]
- t
Time [s]
- T
Temperature inside a bubble [K]
- T0
Ambient temperature [K]
- Ts
Interface temperature [K]
- V
Volume of the bubble [m3]
- Vm
Molar volume of the mixture [cm3·mol−1]
Greek symbols
- θη
Characteristic vibrational temperature [K]
- λ
Thermal conductivity [W·m−1·K]
- ε
Mass transport coefficient
- κ
Thermal diffusivity [m2·s−1]
- μ
Liquid viscosity [Pa·s]
- ρl
Density of the medium [kg·m−3]
- ρvap
Time-varying density [kg·m−3]
Saturated density of vapor [kg·m−3]
- σ
Surface tension of liquid water [N·m−1]
Subscript
- air
Air
- Ar
Argon
- c
Critical state
- i
Species
- mix
air-vapor mixture
- N2
Nitrogen
- O2
Oxygen
- tot
Total
- vap
Water vapor
Superscript
- ·
Time derivative
1. Introduction
Acoustic cavitation refers to the emergence, expansion, and violent collapse of small gas–vapor bubbles in liquid medium under sufficiently strong ultrasonic excitation [1]. At the end of violent collapse, extremely high temperature and pressure (up to thousands of Kelvins and hundreds of Megapascals) are reached inside the bubble, which plays an essential role in practical applications [2], [3], [4], [5]. These extreme conditions can further lead to the decomposition of the entrapped water molecules within the bubbles to form various free radicals, which have been extensively utilized in the chemical industry and environmental applications, such as extraction [6], distillation [7], ultrasonic cleaning [8], sonolysis [9], [10], etc. These cavitation-associated physical and chemical effects are closely related to the strength of acoustic cavitation in liquids. Therefore, gaining a deep understanding of the acoustic cavitation characteristics is of great significance, especially the extremely high temperature and pressure generated instantaneously within the violently-collapsing cavitation bubble.
Up to now, numerous experiments have been carried out to measure the temperature and pressure during the collapse of cavitation bubbles with ultrasonic excitation. Through the sonoluminescence experiment, Gaitan et al. [11] measured a maximum temperature of 6000 K and a maximum pressure even up to 2000 MPa during the bubble collapse at a frequency of 21 kHz. Similarly, it was also reported that the internal temperature is estimated to be between 5000 K and 20,000 K by fitting the experimental sonoluminescence spectra of a single bubble [12]. Moreover, Kanthale and Ashokkumar [13] examined multi-bubble sonoluminescence and sonochemistry, obtaining maximum temperatures of 10,300 K at 213 kHz and 700 K at 1056 kHz respectively. By using comparative rate thermometry, Suslick et al. [14] obtained that the temperature in the collapsing cavity of the alkane solutions is 5200 ± 650 K, and the pressure is 50 MPa. Overall, these studies provide experimental estimations of the temperature within a wide range of 700–20,000 K and the measured pressures are within the range of 50–2000 MPa. The obvious discrepancies in the experimentally measured temperature and pressure might be due to the different experimental methods and conditions. Additionally, acoustic cavitation of bubbles occurs at extremely short temporal scales (μs ∼ ms) and small spatial scales (μm ∼ mm). It can considerably increase the difficulty of experiments with high equipment requirements for more accurate measurements of the peak temperature and pressure at the end of violent bubble collapse.
In addition to the experimental measurements, the researchers have also conducted numerical predictions to further investigate the bubble dynamics as well as the time-varying temperature and pressure during acoustic cavitation, regardless of the experimental limitations. It was reported that Ahmed et al. [15] coupled the Keller–Miksis (KM) model with the ideal gas (IG) law, predicting the maximum temperatures up to 10,000 K and the maximum pressures up to the order of 1011 Pa. Then, Ferkous et al. [16] also coupled the KM model with the IG law and the peak values of the temperature and pressure within the collapsing cavity were estimated to be approximately 5000 K and 100 MPa, respectively. Moreover, Yasui [17] used the Van der Waals (vdW) equation of state (EOS) to study the non-equilibrium effects of evaporation and condensation at the cavitation bubble wall and predicted a maximum temperature of 104 K and a maximum pressure of 1010 Pa. Furthermore, the most developed Gilmore model was coupled with a van der Waals hard-core law to investigate the bubble dynamics in laser-induced cavitation [18], [19]. It was found that upon the first collapse, the collapsed bubble contained more vapor than gas and had a pressure of 13.5 GPa [19]. In addition, by coupling the Gilmore model with the Noble-Abel-Stiffend-Gas (NASG) EOS to simulate the dynamics of single-bubble cavitation, a maximum temperature inside the bubble of 104 K was estimated at the end of bubble collapse [20]. Most recently, Agrež et al. utilized the Gilmore-NASG model to calculate the cavitation bubble temporal evolution and pressure, which are well consistent with the experimental measurements [21]. In these numerical investigations, different bubble dynamics models (e.g., KM model and Gilmore model, etc.) and different equations of state (e.g., IG law, vdW EOS, and NASG EOS, etc.) were coupled to investigate the time-varying bubble dynamics of acoustic cavitation, consequently predicting the gas temperature and pressure within the bubble. Evidence from these theoretical results has established that there exist obvious deviations in the predicted results using numerical simulations as compared to the experimental data. This difference could be attributed to the inherent limitations of model simplifications and assumptions, the inconsistent parameter settings between experiments and simulations, as well as the potential errors in both experiments and simulations, etc. For an accurate simulation, the proper choice of the EOS to describe the gases within the cavitation bubble is crucial. It not only links the gas temperature, pressure and volume simultaneously, but also can readily obtain the thermodynamic properties of the gases that failed to be measured directly from experiments during the transient acoustic cavitation. More importantly, it has been proved that using the vdW EOS to estimate the state of the gases is more accurate than the IG law [22]. Compared to the vdW EOS, the Peng–Robinson (PR) EOS has more advantages in calculating vapor pressure, saturated liquid volumes, saturated vapor volumes and enthalpies of vaporization [23], [24]. Accordingly, it can be expected that choosing the PR EOS to estimate the thermodynamic properties of the gases within the cavitation bubble can provide more accurate results. However, little attention has been paid to combining the PR EOS with the cavitation model for predicting the acoustic cavitation characteristics with a high accuracy.
This study coupled the more accurate PR EOS with the most developed Gilmore model, i.e., a newly developed Gilmore-PR model, to accurately quantify the cavitation dynamics and the resultant temperature, pressure as well as number of gas molecules within the bubble, with a focus on the impacts of the EOS. Specifically, the Gilmore-Akulichev equation was respectively coupled with the PR and vdW EOS to numerically simulate the cavitation dynamics with considering the effects of mass and heat transfers. The thermodynamics of the interior mixed gases (i.e., water vapor and air) predicted by the two equations of state were first compared. Then, the differences in the acoustic cavitation characteristics (i.e., the bubble collapse strength, maximum gas temperature and pressure, as well as number of gas molecules within the bubble) between the two equations of state were comprehensively examined under various parameters, including the ultrasound amplitude, the ultrasound frequency, the initial bubble radius, as well as the surface tension, viscosity and temperature of the surrounding liquid.
2. Gilmore-PR model
Suppose that the bubble initially consists of water vapor (H2O) and air (78 % N2, 21% O2, 1% Ar) with only radial motions. Moreover, it is assumed that the bubble remains spherical throughout the whole cavitation process and does not break after the collapse [25]. Note that the bubbles may lose their spherical stability and exhibit non-spherical oscillations under certain conditions [26]. The non-spherical oscillations are neglected in the present work for the sake of simplification, similar to previous studies [15], [17], [20], [22]. Due to the geometrical symmetry of the bubble, it can be assumed that the internal temperature and pressure are spatially uniform. The effects of mass and heat transfers at the bubble interface are considered without chemical reactions.
2.1. Radial bubble motion
According to previous studies [27], [28], the Gilmore model and a newly developed bubble wall motion equation with the second-order Mach number are more suitable for investigating bubble oscillations with high Mach number. In this work, a relatively simple generalized Gilmore model is utilized to describe the radial bubble dynamics, which is given by [29]:
| (1) |
where R is the bubble radius and the dots represent the derivative with respect to time, H and Cl are the enthalpy and the sound speed at the bubble surface respectively, which are expressed as [30]:
| (2) |
| (3) |
in which ρl and C0 are the medium density and speed of sound in the medium, m and B are the specific constants whose values can be retrieved in the literature [31]. P0 is the static pressure and is the driving acoustic pressure where PA is the ultrasound amplitude and f is the ultrasound frequency. According to pressure equilibrium conditions, the following relationship between the liquid pressure at the interface Pw and the internal pressure Pin of bubble can be obtained:
| (4) |
in which μ and σ are the liquid viscosity and surface tension, respectively.
2.2. Peng-Robinson equation for interior gases
The internal pressure Pin is calculated from the IG law and the vdW EOS as presented in previous studies [32], [33]. In the present work, a more accurate PR EOS is used and its general form can be represented as [23]:
| (5) |
where Vm and T are the molar volume of the mixture and the temperature within the bubble, and Rg is the universal gas constant. k1 and k2 are specific constants for the EOS. Conveniently, the PR EOS (k1 = 2, k2 = −1) can readily reduce to the vdW EOS (k1 = k2 = 0). The coefficients amix and bmix are calculated in Appendix A.
2.3. Mass transport during bubble expansion and collapse
During acoustic cavitation, water vapor will evaporate or condense due to the dis-equilibrium between its partial pressure within the cavitation bubble and the pressure in the surrounding medium. The time-dependent change rate of water vapor at the wall of bubble is calculated by the following formula [34]:
| (6) |
| (7) |
where is the evaporation–condensation molar rate of water vapor. is mass transport coefficient, is the average velocity of molecules, and are the time-varying density and molar mass of water vapor. According to previous studies [35], [36], the temperature at the bubble wall is , where is the ambient temperature of the surrounding medium. The saturated density of vapor is expressed as [37]:
| (8) |
with = −2.03150240, = −2.68302940, = −5.38626492, = −17.2991605, = −44.7586581, = −63.9201063 and ϑ = (1-T0/Tc), where Tc = 647.37 K. Note that as the vapor partial pressure/temperature in the bubble reaches the water critical pressure/temperature, evaporation and condensation at the bubble wall are assumed to halt due to no clear distinction between liquid and gaseous phases [38].
The mass flux of non-condensable gases is given by the boundary layer theory and Fick’s law [39], [40], [41]:
| (9) |
| (10) |
where Di is the diffusion coefficient of gas species i (i.e., N2, O2 and Ar), is the concentration of dissolved gas, and is the transient concentration of molecules at the bubble wall. ntot is the number of total moles inside the bubble, ng is each non-condensable gas species mole inside the bubble and Henry’s constant KH can be calculated as follows [42]:
| (11) |
where Mi is the molar mass of each gas species i. The values of Ah, Bh, and Ch for gas species are given in Table 1 [43], [44], [45].
Table 1.
The alphabetical constants in Henry’s law.
2.4. Heat transfer at the bubble wall and gas temperature
Similar to mass transfer, the heat exchange and thickness of thermal boundary layer Lth are expressed by [40]:
| (12) |
where λmix and are the coefficients of thermal conductivity and diffusivity of an air-vapor mixture, respectively. The detailed calculating procedures are illustrated in Appendix B.
Furthermore, the overall equation governing the internal energy change of bubble is calculated by [39], [46], [47]:
| (13) |
| (14) |
in which E is the energy inside the bubble, is the change rate of bubble volume, hw,i is the molecular enthalpy, eth,i is the thermal energy of the molecule and is the rate of the molecular number change caused by mass diffusion. η is the number of the characteristic vibrational temperatures θη. and fi is the number rotational and translational degrees of freedom. Values of θη, and η, fi for gases are given in Table 2.
Table 2.
The constants for each gas species [40].
| Materials | θη (K) | η | fi |
|---|---|---|---|
| Water | 2295,5255,5400 | 3 | 6 |
| Nitrogen | 3350 | 1 | 5 |
| Oxygen | 2273 | 1 | 5 |
| Argon | / | / | 3 |
By combining Eqs. (12), (13), (14), the temperature change with respect to time inside the bubble is calculated by [39], [46], [47]:
| (15) |
| (16) |
where is the heat capacity of the air-vapor mixture.
In the simulation, the used physical parameters and their default values are given in Table 3 unless specified otherwise. The Runge-Kutta method is used for numerical integration of coupled ordinary differential equations.
Table 3.
Physical parameters.
| Parameters | Definition | Value | Unit |
|---|---|---|---|
| R0 | Initial bubble radius | 6 | μm |
| ρl | Ambient liquid density | 998.2 | kg·m−3 |
| C0 | Ambient liquid sound speed | 1482 | m·s−1 |
| σ | Surface tension | 0.073 | N·m−1 |
| μ | Viscosity | 0.001 | Pa·s |
| T0 | Ambient temperature | 293.15 | K |
| f | Ultrasound frequency | 45 | kHz |
| P0 | Static pressure | 1.01325 × 105 | Pa |
| PA | Ultrasound amplitude | 1.42 | atm |
| m | Empirical constant | 7 | / |
| B | Empirical constant | 3.1309× 108 | Pa |
| Rg | Universal gas constant | 8.314472 | J·mol−1·K |
| kB | Boltzmann constant | 1.38065 × 10-23 | J·K−1 |
| Accommodation coefficient | 0.4 | / | |
| Mvap | Molar mass of water vapor | 18.015268 × 10-3 | kg·mol−1 |
| Mair | Molar mass of air | 28.97 × 10-3 | kg·mol−1 |
| MN2 | Molar mass of nitrogen | 28 × 10-3 | kg·mol−1 |
| MO2 | Molar mass of oxygen | 31.9988 × 10-3 | kg·mol−1 |
| MAr | Molar mass of argon | 39.95 × 10-3 | kg·mol−1 |
3. Results and discussion
3.1. Pressure–temperature phase diagram for gases
The interior gases of the bubble are described by the EOS which directly determines the thermodynamic properties of the gases, consequently affecting the bubble dynamics as well as the resultant temperature, pressure and number of gas molecules within it [22]. As one of the commonly used equations to estimate the gases, the vdW EOS has a simple formula but it might result in the estimation with less accuracy. Comparatively, it is now well established that the PR EOS is one of the most potential and successful equations of state for liquid/gas thermodynamics and volumetric calculations for pure substances and mixtures [23], [24], [48], [49]. Each substance inside the air-vapor mixture bubble (i.e., water vapor, N2, O2, and Ar) has a different critical temperature, and the phase change is assumed to halt when the critical temperature is reached, according to previous studies [38], [50]. Therefore, we explore here how much the saturation pressures of the gases predicted by the PR and vdW EOS are different below the critical temperature of each gas, prior to investigating the acoustic cavitation characteristics of the air-vapor mixture bubble. The predicted pressure–temperature phase diagrams of the water vapor, N2, O2, and Ar by both PR and vdW EOS were compared, as shown in Fig. 1(a)−(d) respectively. The solid lines are the gas saturation curves for the PR (red) and vdW (black) EOS respectively, and the green point is the critical point. Compared to the vdW EOS, it is apparent that the saturation pressures of each gas predicted by the PR EOS are much closer to the experimental data of NIST (blue points) [51] within the whole temperature range. This evidence strongly suggests that the PR EOS can accurately predict the thermodynamic properties of the gases within the cavitation bubble. Moreover, the results also indicate that choosing the EOS could notably affect the predictions on the acoustic cavitation characteristics of the bubble due to the distinct differences in the thermodynamic properties of the interior gases estimated by the EOS. Therefore, the better PR EOS was selected to estimate the gases inside the bubble for a higher accuracy.
Fig. 1.
Pressure–temperature phase diagrams of (a) water vapor, (b) Nitrogen (N2), (c) Oxygen (O2), and (d) Argon (Ar) below the critical temperature of each gas, predicted by the Peng–Robinson (PR) (red line) and the Van der Waals (vdW) (black line) equations of state. The green point is the critical point. The experimental data of saturation pressure Psat (blue points) were obtained from the NIST [51].
3.2. Comparison of acoustic cavitation between two equations of state
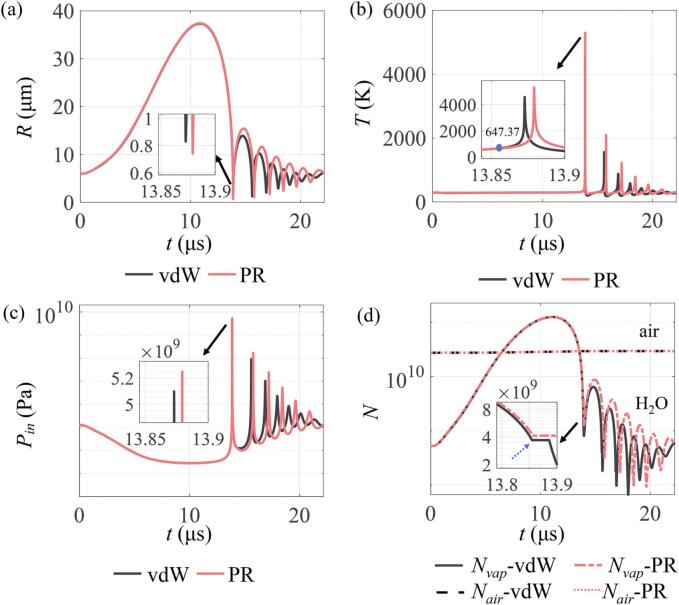
To examine the effects of the vdW and RP EOS on the acoustic cavitation of the air-vapor mixture bubble, the time-varying evolutions of the cavitation bubble radius, and the temperature, pressure, as well as number of gas molecules within it were first compared, as illustrated in Fig. 2. The simulation conditions were set as R0 = 6 µm, f = 45 kHz, PA = 1.42 atm, P0 = 1 atm, T0 = 293.15 K. As shown in Fig. 2(a), during the bubble expansion phase, no distinguishable difference can be observed between the two equations of state, resulting in the same maximum radius Rmax (approximately 37 µm). This result is in line with that reported by Ahmed et al. [15], who obtained a similar value for the maximum radius (about 40 µm) at PA = 1.42 atm and f = 40 kHz. More importantly, it means that choosing the EOS seems to exhibit little influence on the bubble dynamics at this stage. However, during the collapse stage, the minimum bubble radius obtained with the vdW EOS is larger than the one with the PR EOS, as shown in the inset of Fig. 2(a). This difference would lead to distinct estimations for the bubble collapse strength, which can be evaluated by several important indicators, such as the bubble wall velocity [52], compression ratio (Rmax/Rmin) [53], expansion ratio (Rmax/R0) [54], [55], relative expansion ratio (Rmax − R0)/R0 [56] and ratio of maximum oscillation radius to the collapse time () [57]. The compression ratio (Rmax/Rmin) was chosen here to characterize the bubble collapse strength. Accordingly, there is a larger compression ratio (Rm = Rmax/Rmin), in other words, the collapse strength predicted by the PR EOS would be stronger. Taking the vdW EOS as a reference, the relative difference in the compression ratio is up to 12%, which can significantly affect the temperature and pressure within the violent collapsing bubble.
Fig. 2.
Temporal evolutions of (a) bubble radius, (b) temperature, (c) pressure, and (d) number of gas molecules inside the bubble as predicted by the Peng–Robinson (PR) and the Van der Waals (vdW) EOS. Simulation conditions were set as R0 = 6 µm, f = 45 kHz and PA = 1.42 atm. Gas molecules include water vapor molecules and air molecules. Inset in each figure denotes the locally magnified part of bubble evolution around the end of collapse. The blue point represents the water critical temperature, and the position pointed by the blue dotted arrow corresponds to the time when the water critical temperature is located.
For the maximum temperature and pressure inside the collapsing bubble, the theoretical measurements are within the range of 6000 K and several thousand MPa under 1.5 atm of ultrasound amplitude [22]. As shown in Fig. 2(b) and (c), the maximum temperature and pressure predicted by the two equations of state are about 5000 K and 5000 MPa respectively, which are consistent with the theoretical measurement data [22]. Compared to the results using the vdW EOS, the maximum temperature predicted by the PR EOS exhibits an obvious increase (approximately 741 K), with a relative difference of 16%, as presented in Fig. 2(b). Similarly, it can be observed in Fig. 2(c) that the increment in the maximum pressure predicted by the PR EOS is up to 144 MPa (a relative difference of about 3%). Taken together, the predicted maxima of both temperature and pressure with the vdW EOS are smaller than those with the PR EOS, which are consistent with the results of the compression ratio. The larger the compression ratio is, the stronger the bubble collapse is and consequently the higher the peak values of temperature and pressure of collapsing bubble can get.
Furthermore, the most striking result to emerge from the Fig. 2(d) is that the number of water vapor molecules within the bubble greatly changes over time, taking the non-condensable air gas as a reference. These results strongly indicate that the effects of evaporation and condensation of water vapor at the wall of bubble are more significant than the diffusions of non-condensable gases. In addition, it has been demonstrated that water vapor has an important impact on the temperature and pressure at the moment of collapsing bubble [35], [58]. As a result, the present study mainly discusses the impacts of water molecules rather than the air molecules. Noticeably, the number of water vapor molecules predicted by the vdW EOS is apparently different from that predicted by the PR EOS. In particular, at the end of the collapse phase, the number of water vapor molecules trapped in the collapsing bubble is distinctly higher for the PR EOS compared to the vdW EOS. It might be explained that below the water critical temperature (647.37 K), more water vapor molecules are generated within the bubble via evaporation for the case of PR EOS relative to the vdW EOS, as illustrated by the inset of Fig. 2(b) and (d). Overall, these results confirm that choosing the EOS has an obvious influence on the simulation results, showing distinct differences in the acoustic cavitation characteristics, especially for the minimum bubble radius, the peak temperature and pressure, as well as the number of water vapor molecules within the bubble at the moment of transient collapse of the bubble.
3.3. Effects of mass and heat transfers
In addition to the mass transport mechanism (i.e., evaporation and condensation of water vapor), it has been found that the heat transfer on the bubble interface would also play a critical role in the acoustic cavitation process [59], [60]. Therefore, the effects of both mass and heat transfers on the acoustic cavitation characteristics of the air-vapor mixture bubble were elucidated based on the PR EOS. Specifically, the effects of mass and heat transfers on the evolution of the bubble radius, temperature, pressure and number of water vapor molecules were presented as a function of time, as shown in Fig. 3(a)–(d) respectively. The model only considering the heat transfer is denoted as Q, the model only considering the non-equilibrium evaporation and condensation is denoted as m, and the model considering both of them is denoted as m + Q (i.e., normal model).
Fig. 3.
(a) Bubble radius, (b) temperature, (c) pressure, and (d) number of water vapor molecules inside the bubble as a function of time with three models (with mass transfer, denoted as m (light yellow lines); with heat transfer (blue lines), denoted as Q; with mass and heat transfers (light grey lines), denoted as m + Q) based on the Peng–Robinson (PR) EOS. Simulation conditions were set as R0 = 6 µm, f = 45 kHz and PA = 1.42 atm. Inset in the figure denotes the magnified part of pressure inside the bubble evolution around the end of collapse.
As shown in Fig. 3(a), the maximum radius with the normal model is found to be largest. The decrease of the maximum bubble expansion in the other two models is due to the energy deficit. During the expansion, the bubble loses some work, which should be recovered by heat conduction and water evaporation towards the bubble interior. Therefore, once the heat transfer or mass transport is ignored for the sake of simplification, the less energy absorbed by the expanding bubble is not able to reach the maximum radius with the normal model. Moreover, according to the Ref. [59], heat conduction has a higher energetic influence on the energy inside the bubble compared to water evaporation during the bubble expansion. Consequently, Rmax in the model with heat transfer is greater than the model with mass transfer. To evaluate the bubble collapse strength in different cases, the values of the compression ratios are classified in an increasing order as follows: 40.92 for the model without heat transfer, 50.39 for the normal model and 51.31 for the model without mass transfer. These results evidently confirm that the bubble collapse predicted by the model without mass transfer is much stronger than those for the other two cases [59].
In Fig. 3(b)–(d), compared to the normal model, the model without mass transfer (blue lines) gives a higher peak temperature and pressure, while the number of water vapor molecules is obviously lower. In this case, less water vapor molecules within the bubble would decrease the heat capacity of the air-vapor mixture and results in an increase in temperature. Meanwhile, the bubble is easy to compress, and the pressure inside the bubble is substantially increased. On the other hand, when ignoring heat conduction through the bubble wall (light yellow lines), the peak temperature has the largest value since a huge amount of energy is prevented from being released when the bubble collapses without the heat transfer. Moreover, the corresponding peak pressure and the number of water vapor molecules inside the bubble have lower values as compared with the normal model (light grey lines). The bubble collapse strength in this case is much weaker than that predicted by the normal model due to a smaller compression ratio (40.92 vs. 50.39), resulting in a decrease in the internal pressure and less vapor molecules trapped inside the bubble.
Bearing in mind all these arguments, bubble cavitation characteristics are obviously different with or without considering mass and/or heat transfers. This indicates that the mass and heat transfers play a vital role in the acoustic cavitation. Furthermore, these results also highlight the necessity to consider the effects of mass and heat transfers while investigating the bubble acoustic cavitation, otherwise the simulated results might have a large deviation from the realistic results.
3.4. Parameters affecting the acoustic cavitation
3.4.1. Effects of the ultrasound amplitude
This section mainly investigated the effects of the ultrasound amplitude PA on the acoustic cavitation characteristics and the influences of the two equations of state were also compared. As indicated in Fig. 4(a), the compression ratio (Rm = Rmax/Rmin) for both equations of state increases with an increase in PA, which is consistent with the results of Merouani et al. [61]. They found that higher Rmax and lower Rmin (i.e., higher Rm) values were obtained when higher ultrasound amplitudes were applied. By contrast, the value of Rm is greater for the PR EOS compared to the vdW EOS. It can be explained that the two equations predict the same Rmax regardless of the variation of ultrasound amplitude, and the Rmin predicted by the PR EOS is always smaller than the one predicted by the vdW EOS (Fig. 2(a)). Moreover, the difference of Rm between the two equations of state gradually increases as PA increases and the relative difference in Rm is increased to 12% at 2 atm. For the maximum temperature Tmax inside the bubble, it shows that as PA increases, the Tmax predicted by the vdW EOS continues to increase, while it first increases and then slightly decreases as predicted by the PR EOS (Fig. 4(b)). In addition, it is apparent from Fig. 4(c) and (d) that both the maximum pressure Pmax and number of water vapor molecules inside the bubble at the end of collapse Nvap increase with the increase of PA using either the PR or vdW EOS. These increasing trends may be explained by the growth of Rm with an increase in PA, resulting in a more intense bubble collapse. This is in line with the results of the previous literatures [22], [52], [62], which found that as PA increases, the bubble collapse strength will be stronger.
Fig. 4.
Variations of (a) compression ratio Rm, (b) maximum temperature Tmax, (c) maximum pressure Pmax, and (d) number of water vapor molecules Nvap inside the bubble at the end of collapse with respect to the ultrasound amplitude PA. The effects of the Peng–Robinson (PR) and the Van der Waals (vdW) EOS on the acoustic cavitation characteristics at various PA were compared. Simulation conditions were set as R0 = 6 µm and f = 45 kHz.
It should be pointed out that the amount of water vapor trapped within the bubble predicted by the PR EOS is much larger at a higher PA than that predicted by the vdW EOS (Fig. 4(d)). At a higher PA, there are more water vapor molecules within the bubble for the PR EOS, which reduces the compression heating [38], [63]. This provides a possible explanation for the slight decrease of Tmax with the continuous increase of PA in the case of the PR EOS shown in Fig. 4(b).
Compared to the vdW EOS, the values of the Tmax, Pmax and Nvap in the PR EOS are considerably larger, probably due to a more intense bubble collapse predicted by the PR EOS (Fig. 4(a)). Meanwhile, what stands out in Fig. 4 is that the differences between the two equations of state increase as PA increases. Similar results have been reported in the work of Kerboua [22] who compared the effects of the IG and vdW EOS on the acoustic cavitation characteristics and found that the differences between the two models increase with the ultrasound amplitude increasing. Overall, the larger PA is, the stronger the acoustic cavitation effect is, and the greater the differences between the equations of state become.
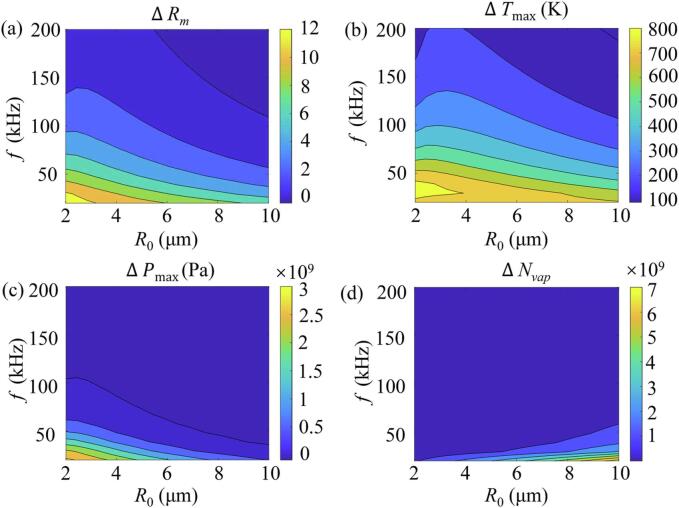
3.4.2. Effects of the initial bubble radius and the ultrasound frequency
Fig. 5 shows the contour plots of the differences of the acoustic cavitation characteristics predicted by the PR and vdW EOS as a function of the initial bubble radius R0 and ultrasound frequency f. It can be found in Fig. 5(a) that the difference of the compression ratios ΔRm increases with a decrease in the R0, f, or both of them. Moreover, when the R0 and f are smaller, it can be seen from Fig. 5(b) that the difference of the maximum temperatures ΔTmax is larger. Similarly, decreasing the f can also increase the difference of the maximum pressure ΔPmax but only exhibits a distinct effect at smaller values of the R0 and f (Fig. 5(c)). For the number of internal water vapor molecules at the final moment of bubble collapse, its difference ΔNvap between the PR and vdW EOS decreases with an increase in the f but increases with R0 increasing, and the effects were most pronounced only at larger R0 and lower f, as displayed in Fig. 5(d). Previous researches have established that the smaller R0 and/or f are beneficial to get the larger collapse pressure and stronger acoustic cavitation effects [22], [59]. Therefore, the results suggest that the increased differences of Tmax and Pmax between the two equations of state at lower R0, f, or both of them are closely and positively correlated with the stronger acoustic cavitation effects.
Fig. 5.
Contour plots of the differences between the Peng–Robinson (PR) and the Van der Waals (vdW) EOS with respect to various initial bubble radius R0 and frequencies f at PA = 1.42 atm, including the differences in (a) compression ratio ΔRm, (b) maximum temperature ΔTmax, (c) maximum pressure ΔPmax, and (d) number of water molecules ΔNvap inside the bubble at the end of collapse.
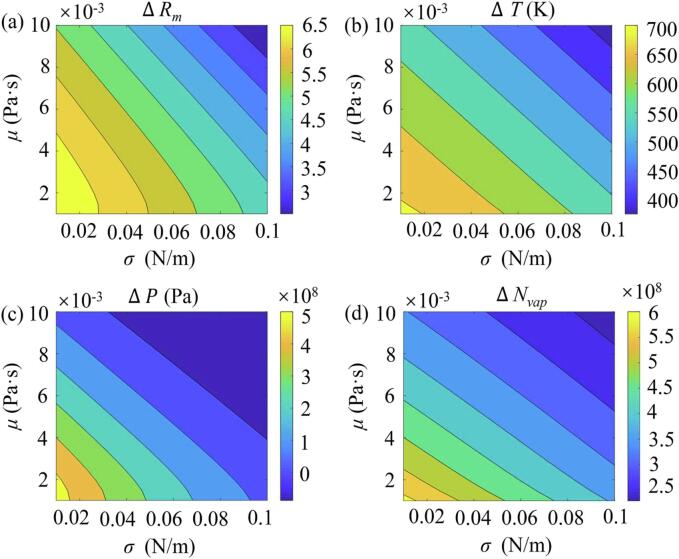
3.4.3. Effects of the surface tension and viscosity of the surrounding liquid
Contour plots of the differences of the acoustic cavitation characteristics predicted by the PR and vdW EOS as a function of the surface tension σ and viscosity μ of the surrounding liquid were plotted in Fig. 6. It has been demonstrated that increasing the σ or μ can lead to a weaker bubble collapse with reducing the acoustic cavitation effects [64], [65], [66]. Similarly, Fig. 6 shows that with increasing the σ, μ, or both of them, the differences between the two equations of state decrease due to the abated bubble collapse. Overall, these results suggest that the better PR EOS should be used to predict the acoustic cavitation characteristics of the bubble and can obtain stronger bubble collapse, higher collapse temperature and pressure, as well as more water molecules within the collapsing bubble as compared to the vdW EOS, especially for the cases at a lower σ and/or μ where the acoustic cavitation effects are much stronger.
Fig. 6.
Contour plots of the differences between the Peng–Robinson (PR) and the Van der Waals (vdW) EOS for the (a) compression ratio ΔRm, (b) maximum temperature, ΔTmax, (c) maximum pressure, ΔPmax, and (d) number of water molecules inside the bubble at the end of collapse ΔNvap with respect to various surface tension σ and the liquid viscosity μ. Simulation conditions were set as R0 = 6 µm, f = 45 kHz and PA = 1.42 atm.
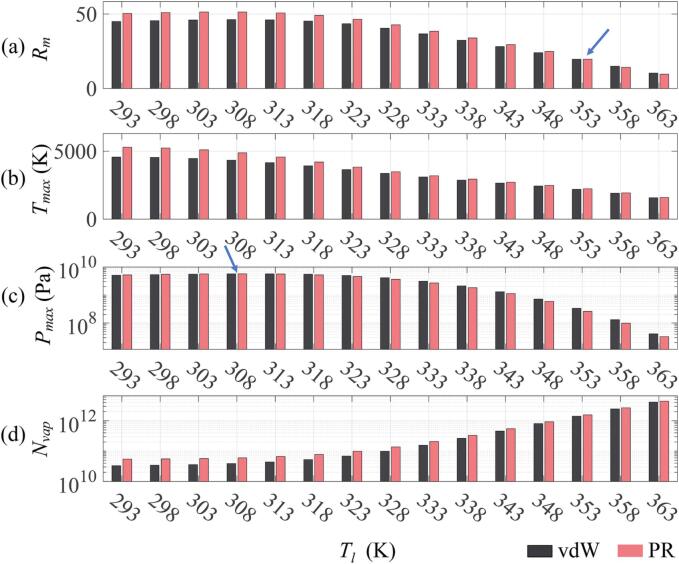
3.4.4. Effects of the liquid temperature
Fig. 7 displays the variations of the acoustic cavitation characteristics under different liquid temperatures Tl. From the obtained results, it is apparent that the liquid temperatures strongly affect the collapse strength of the cavitation bubble. Specifically, as shown in Fig. 7(a), when the liquid temperature Tl is small, the Rm predicted by the PR and vdW EOS both increase slightly and then decrease dramatically with increasing Tl. This is due to the growth rate of the predicted minimum bubble radius being larger than that of the maximum bubble radius at high liquid temperatures [67]. The resultant Tmax, Pmax and Nvap as function of Tl are presented in Fig. 7(b)–(d), respectively. It is evident that the Pmax exhibits the same variation trend as that of the Rm, the Tmax decreases while the Nvap increases with Tl increasing, which agree well with the variation trends reported in Refs. [38], [67]. The Rm is lower at higher Tl, leading to less violence of the bubble collapse, and consequently both Tmax and Pmax inside the bubble become smaller. The possible explanation for the increase of Nvap with Tl increasing is that the saturated water vapor pressure increases when the Tl increases (Fig. 1(a)), resulting in an increase in the evaporation rate of vapor at the expansion stage, and a decrease in the mass condensation rate at the collapse phase [67]. Consequently, the number of water vapor molecules trapped within the collapsing bubble increases.
Fig. 7.
Variations of (a) compression ratio Rm, (b) maximum temperature Tmax, (c) maximum pressure Pmax, and (d) number of water molecules Nvap inside the bubble at the end of collapse with respect to the liquid temperature Tl. The effects of the Peng–Robinson (PR) and the Van der Waals (vdW) EOS on the acoustic cavitation characteristics were compared at various Tl. Simulation conditions were set as R0 = 6 µm, f = 45 kHz and PA = 1.42 atm.
From Fig. 7(b) and (d), within the whole range of the Tl, the Tmax and Nvap calculated by the PR EOS are larger than those calculated by the vdW EOS. Nevertheless, it is noteworthy that when exceeding the liquid temperatures indicated by the blue arrows (Rm: Tl > 353 K, Pmax: Tl > 308 K), the Rm and Pmax predicted by the PR EOS are lower than those of the vdW EOS (Fig. 7(a) and (c)), which is well explained in Fig. 8. The minimum bubble radius Rmin predicted by the PR EOS is larger at higher liquid temperatures indicated by the blue arrow (Tl > 353 K), whereas the EOS has a negligible effect on the maximum bubble radius Rmax, as illustrated in Fig. 8(a). Accordingly, the PR EOS predicts smaller compression ratios (i.e., Rmax/Rmin) at higher liquid temperatures (Tl > 353 K) as compared to the vdW EOS, as shown in Fig. 7(a). On the other hand, ΔPin is the difference of the gas pressures inside the bubble at the time of R(t) = Rmin and Rmax, i.e., ΔPin = Pmax − PRmax, where PRmax is the pressure at R(t) = Rmax. It is obvious that both equations of state predict the same values of the PRmax for all Tl, whereas at higher liquid temperatures indicated by the blue arrow (Tl > 308 K), the values of ΔPin in the case of the PR EOS are lower than those in the case of the vdW EOS. In accordance with the expression of ΔPin, a lower Pmax will consequently be obtained with the PR EOS at a higher temperature as compared to the vdW EOS (Fig. 7(c)).
Fig. 8.
Variation curves of the (a) bubble radius and (b) pressure inside the bubble as a function of liquid temperature Tl, predicted by the Van der Waals (vdW) and the Peng–Robinson (PR) EOS. Rmax,: maximum bubble radius, Rmin: minimum bubble radius, PRmax: pressure inside the bubble at Rmax, ΔPin: the difference of the Pmax and PRmax. Simulation conditions were set as R0 = 6 µm, f = 45 kHz and PA = 1.42 atm.
4. Conclusion
This study set out to numerically investigate the acoustic cavitation characteristics of the air-vapor mixture bubble, by combining the Gilmore-Akulichev equation and the PR EOS (i.e., Gilmore-PR model). As compared to the experimental measurements, it can be found that the PR EOS can predict the gas thermodynamics for both air and water vapor more accurately than the vdW EOS. Moreover, the simulation results obtained with the more accurate PR EOS were also compared with those obtained using the vdW EOS to highlight the effects of the EOS. The results obtained with the two equations of state exhibit similar variation trends for the bubble compression ratio, the maximum temperature and pressure, as well as the number of water vapor molecules within the bubble, while varying the acoustic parameters (e.g., ultrasound amplitude and ultrasound frequency), the initial bubble radius and the liquid parameters (e.g., surface tension, viscosity and ambient temperature). However, it demonstrates that the differences between the results from the two equations of state increase at a higher ultrasound amplitude or a lower ultrasound frequency. By contrast, with the increase of the initial bubble radius and the liquid parameters, the differences between the two equations of state decrease. Compared to the vdW EOS, the PR EOS can predict a stronger bubble collapse, thus achieving higher internal temperature and pressure, as well as more water vapor molecules within the bubble.
The current study provides valuable insights into the impacts of the EOS on the acoustic cavitation characteristics of the bubble and might be contributing to further optimizing its utilization in sonochemistry and biomedicine. For instance, the coated microbubbles consist of C3F8 or C4F10 gases are commonly used in the biomedical applications, and the effects of the EOS for the interior gases as well as the influences of the mass and heat transfers on the bubble dynamics are usually ignored for simplification [68], [69], [70]. The current results suggest that choosing a proper equation describing the state of the C3F8 or C4F10 gases inside the cavitation bubble, and meanwhile considering the mass and heat transfers at the bubble wall are of great importance for accurately simulating the bubble dynamics. Furthermore, the comprehensive Gilmore-PR model developed in this work can also extend the prediction of the recently developed models for acoustic waves propagation properties in a bubbly liquid to higher Mach numbers [71], [72]. Specifically, at high driving acoustic pressures, the pressure-dependent attenuation and sound speed in a bubbly medium as well as the influences of the EOS on them can be accurately evaluated, which will gain better insights on the attenuation and sound speed phenomena of bubbly media. Nevertheless, the chemical reactions inside the bubble and the heat of reactions [59], as well as the interactions between bubbles [55], [73], [74] and the non-spherical bubble oscillations [26] are ignored, in the future, their effects on the acoustic cavitation characteristics of bubbles need to be investigated in detail.
CRediT authorship contribution statement
Dui Qin: Conceptualization, Methodology, Visualization, Writing – original draft, Writing – review & editing, Funding acquisition. Shuang Lei: Methodology, Software, Visualization, Writing – original draft, Writing – review & editing. Bo Chen: Visualization, Validation. Zhangyong Li: Writing – review & editing. Wei Wang: Writing – review & editing, Project administration, Resources. Xiaojuan Ji: Conceptualization, Project administration, Resources.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (11904042), the China Postdoctoral Science Foundation (2022MD723728) and the Science and Technology Research Program of Chongqing Municipal Education Commission (KJQN202000617).
Contributor Information
Dui Qin, Email: duiqin@cqupt.edu.cn.
Wei Wang, Email: wangw@cqupt.edu.cn.
Xiaojuan Ji, Email: jixiaojuan2003@163.com.
Appendix A. The coefficients of the vapor and air mixture
The values of coefficients amix and bmix of the mixtures are calculated by [75]:
| (A1) |
| (A2) |
in which xu (xv) and kuv are the mole fraction and interaction parameters, respectively. When the components have the same structure, the coefficient kuv is zero. In contrast, the coefficient kuv is non-zero in the calculations of phase-equilibrium for mixtures consisting of compounds with great differences in molecular shape and size [75]. In this Section, subscript u and v indicate that the water vapor and air components (i.e., N2, O2, Ar). Therefore, the coefficient kuv is zero and expressions (A.1), (A.2) are as follows:
| (A3) |
| (A4) |
where is the sum of the number of water vapor and air molecules within the bubble, i.e., .
For the coefficients of water vapor:
| (A5) |
For the coefficients of air:
| (A6) |
| (A7) |
where Rg is the universal gas constant and α is a function of reduced temperature for each component. The subscript c represents the critical condition. From the data in Ref. [23], the Van der Waal equation of state (vdW-EOS) has Ωa = 0.421875, Ωb = 0.1250, and the Ωa = 0.457240, Ωb = 0.0778 is set for the Peng–Robinson equation of state (PR-EOS). α = 1 used in the vdW-EOS, and the expression for α in the PR-EOS is written as:
| (A8) |
where is reduced temperature and is a function of the acentric factor w, which has the following form:
| (A9) |
The values of Pc, Tc, and w of each component are listed in Table A1 [76].
Table A1.
Values of critical and acentric factor for each of materials [76].
| Materials | Pc (bar) | Tc (K) | w |
|---|---|---|---|
| Water | 221.20 | 647.37 | 0.343 |
| Nitrogen | 33.90 | 126.20 | 0.037 |
| Oxygen | 50.43 | 154.58 | 0.020 |
| Argon | 48.70 | 150.58 | 0.000 |
Appendix B. The thermal diffusivity and conductivity of the vapor and air mixture
The thermal diffusivity κ of the vapor and air mixture can be expressed as [40]:
| (B1) |
| (B2) |
where cp, fi and kB are the heat capacity concentration of an air-vapor mixture, number of degrees of freedom for gas species i and Boltzmann constant, respectively. Ni/V is the molecular concentration, V = 4πR3 / 3 is the bubble volume and λmix is the thermal conductivity of the air-vapor mixture, which is given as follows [77]:
| (B3) |
where bmix is the coefficients of the air-vapor mixture and the is expressed as [78]:
| (B4) |
where is the number of total mole inside the bubble, and are the number of water vapor and air mole. The temperature-dependent of thermal conductivities of vapor and of air are described as follows [79]:
| (B5) |
where = 9.98 × 10-5 [W m−1 K−2], = 5.39 × 10-5 [W m−1 K−2], = −0.0119 [W m−1 K−1], = 0.0108 [W m−1 K−1].
Data availability
No data was used for the research described in the article.
References
- 1.Mason T.J., Lorimer J.P. Wiley-VCH Verlag GmbH; Weinheim: 2002. Applied sonochemistry: Uses of power ultrasound in chemistry and processing; pp. 25–60. [Google Scholar]
- 2.Suslick K.S., Flannigan D.J. Inside a collapsing bubble: sonoluminescence and the conditions during cavitation. Annu. Rev. Phys. Chem. 2008;59(1):659–683. doi: 10.1146/annurev.physchem.59.032607.093739. [DOI] [PubMed] [Google Scholar]
- 3.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Theoretical estimation of the temperature and pressure within collapsing acoustical bubbles. Ultrason. Sonochem. 2014;21(1):53–59. doi: 10.1016/j.ultsonch.2013.05.008. [DOI] [PubMed] [Google Scholar]
- 4.Dehane A., Merouani S., Hamdaoui O., Ashokkumar M. An alternative technique for determining the number density of acoustic cavitation bubbles in sonochemical reactors. Ultrason. Sonochem. 2022;82 doi: 10.1016/j.ultsonch.2021.105872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dehane A., Merouani S., Hamdaoui O. Theoretical investigation of the effect of ambient pressure on bubble sonochemistry: special focus on hydrogen and reactive radicals production. Chem. Phys. 2021;547 [Google Scholar]
- 6.Chemat F., Rombaut N., Sicaire A.-G., Meullemiestre A., Fabiano-Tixier A.-S., Abert-Vian M. Ultrasound assisted extraction of food and natural products. Mechanisms, techniques, combinations, protocols and applications. A review. Ultrason. Sonochem. 2017;34:540–560. doi: 10.1016/j.ultsonch.2016.06.035. [DOI] [PubMed] [Google Scholar]
- 7.Kiss A.A., Jobson M., Gao X. Reactive distillation: stepping up to the next level of process intensification. Ind. Eng. Chem. Res. 2018;58:5909–5918. [Google Scholar]
- 8.Yusof N.S.M., Babgi B., Alghamdi Y., Aksu M., Madhavan J., Ashokkumar M. Physical and chemical effects of acoustic cavitation in selected ultrasonic cleaning applications. Ultrason. Sonochem. 2016;29:568–576. doi: 10.1016/j.ultsonch.2015.06.013. [DOI] [PubMed] [Google Scholar]
- 9.Merouani S., Hamdaoui O., Saoudi F., Chiha M. Sonochemical degradation of Rhodamine B in aqueous phase: effects of additives. Chem. Eng. J. 2010;158:550–557. doi: 10.1016/j.jhazmat.2009.10.046. [DOI] [PubMed] [Google Scholar]
- 10.Chiha M., Hamdaoui O., Baup S., Gondrexon N. Sonolytic degradation of endocrine disrupting chemical 4-cumylphenol in water. Ultrason. Sonochem. 2011;18(5):943–950. doi: 10.1016/j.ultsonch.2010.12.014. [DOI] [PubMed] [Google Scholar]
- 11.Gaitan D.F., Crum L.A., Church C.C., Roy R.A. Sonoluminescence and bubble dynamics for a single, stable, cavitation bubble. J. Acoust. Soc. Am. 1992;91(6):3166–3183. [Google Scholar]
- 12.F.R. Young, Sonoluminescence, CRC press, Boca Raton, Florida, 2005. pp. preface and pp. 45–51.
- 13.Kanthale P., Ashokkumar M., Grieser F. Sonoluminescence, sonochemistry (H2O2 yield) and bubble dynamics: frequency and power effects. Ultrason. Sonochem. 2008;15(2):143–150. doi: 10.1016/j.ultsonch.2007.03.003. [DOI] [PubMed] [Google Scholar]
- 14.Suslick K.S., Hammerton D.A., Cline R.E. The sonochemical hot spot. J. Am. Chem. Soc. 1986;108:641–5642. [Google Scholar]
- 15.Ahmed Y., Man G., Trujillo F.J. A new pressure formulation for gas-compressibility dampening in bubble dynamics models. Ultrason. Sonochem. 2016;32:247–257. doi: 10.1016/j.ultsonch.2016.03.013. [DOI] [PubMed] [Google Scholar]
- 16.Ferkous H., Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Comprehensive experimental and numerical investigations of the effect of frequency and acoustic intensity on the sonolytic degradation of naphthol blue black in water. Ultrason. Sonochem. 2015;26:30–39. doi: 10.1016/j.ultsonch.2015.02.004. [DOI] [PubMed] [Google Scholar]
- 17.Yasui K. Effect of non-equilibrium evaporation and condensation on bubble dynamics near the sonoluminescence threshold. Ultrasonics. 1998;36(1-5):575–580. [Google Scholar]
- 18.Denner F., Schenke S. Modeling acoustic emissions and shock formation of cavitation bubbles. Phys. Fluids. 2023;35 [Google Scholar]
- 19.Liang X., Linz N., Freidank S., Paltauf G., Vogel A. Comprehensive analysis of spherical bubble oscillations and shock wave emission in laser-induced cavitation. J. Fluid. Mech. 2022;940:A5. [Google Scholar]
- 20.Denner F. The Gilmore-NASG model to predict single-bubble cavitation in compressible liquids. Ultrason. Sonochem. 2021;70 doi: 10.1016/j.ultsonch.2020.105307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Agrež V., Mur J., Petelin J. Near threshold nucleation and growth of cavitation bubbles generated with a picosecond laser. Ultrason. Sonochem. 2023;92 doi: 10.1016/j.ultsonch.2022.106243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kerboua K., Hamdaoui O. Computational study of state equation effect on single acoustic cavitation bubble's phenomenon. Ultrason. Sonochem. 2017;38:174–188. doi: 10.1016/j.ultsonch.2017.03.005. [DOI] [PubMed] [Google Scholar]
- 23.Zabaloy M.S., Vera J.H. The Peng-Robinson sequel. An analysis of the particulars of the second and third generations. Ind. Eng. Chem. Res. 1998;37:1591–1597. [Google Scholar]
- 24.Lopez-Echeverry J.S., Reif-Acherman S., Araujo-Lopez E. Peng-Robinson equation of state: 40 years through cubics. Fluid Phase Equilib. 2017;447:39–71. [Google Scholar]
- 25.Hilgenfeldt S., Brenner M.P., Grossmann S., Lohse D. Analysis of Rayleigh-Plesset dynamics for sonoluminescing bubbles. J. Fluid. Mech. 1998;365:171–204. [Google Scholar]
- 26.Klapcsik K., Hegedűs F. Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochem. 2019;54:256–273. doi: 10.1016/j.ultsonch.2019.01.031. [DOI] [PubMed] [Google Scholar]
- 27.Zilonova E., Solovchuk M., Sheu T.W.H. Bubble dynamics in viscoelastic soft tissue in high-intensity focal ultrasound thermal therapy. Ultrason. Sonochem. 2018;40:900–911. doi: 10.1016/j.ultsonch.2017.08.017. [DOI] [PubMed] [Google Scholar]
- 28.Zheng X., Wang X., Zhang Y. A single oscillating bubble in liquids with high Mach number. Ultrason. Sonochem. 2022;85 doi: 10.1016/j.ultsonch.2022.105985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gilmore F.R. California Institute of Technology; Pasadena, California: 1952. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid. Technical Report No. 26-24. [Google Scholar]
- 30.Church C.C. A theoretical study of cavitation generated by an extracorporeal shock wave lithotripter. J. Acoust. Soc. Am. 1989;86(1):215–227. doi: 10.1121/1.398328. [DOI] [PubMed] [Google Scholar]
- 31.Chavrier F., Chapelon J.Y., Gelet A., Cathignol D. Modeling of high-intensity focused ultrasound-induced lesions in the presence of cavitation bubbles. J. Acoust. Soc. Am. 2000;108(1):432–440. doi: 10.1121/1.429476. [DOI] [PubMed] [Google Scholar]
- 32.Sivasankar T., Moholkar V.S. Physical insights into the sonochemical degradation of recalcitrant organic pollutants with cavitation bubble dynamics. Ultrason. Sonochem. 2009;16(6):769–781. doi: 10.1016/j.ultsonch.2009.02.009. [DOI] [PubMed] [Google Scholar]
- 33.Hong S., Son G. Numerical modelling of acoustic cavitation threshold in water with non-condensable bubble nuclei. Ultrason. Sonochem. 2022;83 doi: 10.1016/j.ultsonch.2022.105932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Holzfuss J. Unstable diffusion and chemical dissociation of a single sonoluminescing bubble. Phys. Rev. E. 2005;71 doi: 10.1103/PhysRevE.71.026304. [DOI] [PubMed] [Google Scholar]
- 35.Pahk K.J., Gélat P., Kim H., Saffari N. Bubble dynamics in boiling histotripsy, Ultrasound. Med. Biol. 2018;44(12):2673–2696. doi: 10.1016/j.ultrasmedbio.2018.07.025. [DOI] [PubMed] [Google Scholar]
- 36.Kamath V., Prosperetti A., Egolfopoulos F.N. A theoretical study of sonoluminescence. J. Acoust. Soc. Am. 1993;94(1):248–260. [Google Scholar]
- 37.Wagner W., Pruß A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data. 1995;31(2002):387–535. [Google Scholar]
- 38.Lee G.L., Law M.C. Numerical modelling of single-bubble acoustic cavitation in water at saturation temperature. Chem. Eng. J. 2022;430 [Google Scholar]
- 39.Toegel R., Gompf B., Pecha R., Lohse D. Does water vapor prevent upscaling sonoluminescence? Phys. Rev. Lett. 2000;85:3165. doi: 10.1103/PhysRevLett.85.3165. [DOI] [PubMed] [Google Scholar]
- 40.Toegel R., Lohse D. Phase diagrams for sonoluminescing bubbles: a comparison between experiment and theory. J. Chem. phys. 2003;118:1863–1875. [Google Scholar]
- 41.Stricker L., Prosperetti A., Lohse D. Validation of an approximate model for the thermal behavior in acoustically driven bubbles. J. Acoust. Soc. Am. 2011;130(5):3243–3251. doi: 10.1121/1.3626132. [DOI] [PubMed] [Google Scholar]
- 42.Battino R., Rettich T.R., Tominaga T. The solubility of nitrogen and air in liquids. J. Phys. Chem. Ref. Data. 1984;13(2):563–600. [Google Scholar]
- 43.R. Battino, IUPAC Solubility Data Series. Nitrogen and Air, 10Oxford: Pergamon, 1982.
- 44.R. Battino, Solubility Data Series. Oxygen and ozone, 7Oxford: Pergamon, 1981.
- 45.Clever H. Pergamon Press; 4Oxford: 1980. IUPAC Solubility Data Series: Argon. [Google Scholar]
- 46.Samiei E., Shams M., Ebrahimi R. A novel numerical scheme for the investigation of surface tension effects on growth and collapse stages of cavitation bubbles. Eur. J. Mech. B-Fluid. 2011;30(1):41–50. [Google Scholar]
- 47.Chakma S., Moholkar V.S. Numerical simulation and investigation of system parameters of sonochemical process. Chin. J. Eng. 2013;2013:1–14. [Google Scholar]
- 48.Wilczek-Vera G., Vera J.H. Understanding cubic equations of state: A search for the hidden clues of their success. AIChE. J. 2015;61:2824–2831. [Google Scholar]
- 49.Valderrama J.O. The state of the cubic equations of state. Ind. Eng. Chem. Res. 2003;42(8):1603–1618. [Google Scholar]
- 50.An Y., Ying C. Model of single bubble sonoluminescence. Phys. Rev. E. 2005;71 doi: 10.1103/PhysRevE.71.036308. [DOI] [PubMed] [Google Scholar]
- 51.NIST, Thermophysical properties of fluid systems, Database, 2022.
- 52.Peng K., Qin F.G.F., Jiang R., Kang S. Interpreting the influence of liquid temperature on cavitation collapse intensity through bubble dynamic analysis. Ultrason. Sonochem. 2020;69 doi: 10.1016/j.ultsonch.2020.105253. [DOI] [PubMed] [Google Scholar]
- 53.Kanthale P.M., Brotchie A., Ashokkumar M., Grieser F. Experimental and theoretical investigations on sonoluminescence under dual frequency conditions. Ultrason. Sonochem. 2008;15:629–635. doi: 10.1016/j.ultsonch.2007.08.006. [DOI] [PubMed] [Google Scholar]
- 54.Wang X., Ning Z., Lv M., Yao J., Sun C. The enhanced effect of collapse strength of a dual-frequency driven bubble in 2-dimensional space. Results. Phys. 2021;29:104727. [Google Scholar]
- 55.Qin D., Zou Q., Zhong X., Zhang B., Li Z. Effects of medium viscoelasticity on bubble collapse strength of interacting polydisperse bubbles. Ultrason. Sonochem. 2023;95:106375. doi: 10.1016/j.ultsonch.2023.106375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kalmár C., Klapcsik K., Hegedűs F. Relationship between the radial dynamics and the chemical production of a harmonically driven spherical bubble. Ultrason. Sonochem. 2020;64:104989. doi: 10.1016/j.ultsonch.2020.104989. [DOI] [PubMed] [Google Scholar]
- 57.Kanthale P.M., Gogate P.R., Pandit A.B. Modeling aspects of dual frequency sonochemical reactors. Chem. Eng. J. 2007;127:71–79. [Google Scholar]
- 58.B.D. Storey, A.J. Szeri, Water vapour, sonoluminescence and sonochemistry, Proc. R. Soc. London A Math. Phys. Eng. Sci. 456 (2000) 1685–1709.
- 59.Dehane A., Merouani S., Hamdaoui O., Alghyamah A. A comprehensive numerical analysis of heat and mass transfer phenomenons during cavitation sono-process. Ultrason. Sonochem. 2021;73 doi: 10.1016/j.ultsonch.2021.105498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nazari-Mahroo H., Pasandideh K., Navid H.A., Sadighi-Bonabi R. Influence of liquid compressibility on the dynamics of single bubble sonoluminescence. Phys. Lett. A. 2018;382(30):1962–1967. [Google Scholar]
- 61.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Energy analysis during acoustic bubble oscillations: relationship between bubble energy and sonochemical parameters. Ultrasonics. 2014;54(1):227–232. doi: 10.1016/j.ultras.2013.04.014. [DOI] [PubMed] [Google Scholar]
- 62.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Computer simulation of chemical reactions occurring in collapsing acoustical bubble: dependence of free radicals production on operational conditions. Res. Chem. Int. 2015;41:881–897. [Google Scholar]
- 63.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Computational engineering study of hydrogen production via ultrasonic cavitation in water. Int. J. Hydrogen. Energy. 2016;41(2):832–844. [Google Scholar]
- 64.Sabzeghabae A.N., Devia-Cruz L.F., Gutierrez-Herrera E., Camacho-Lopez S., Aguilar G. Bubble dynamics of laser-induced cavitation in plasmonic gold nanorod solutions and the relative effect of surface tension and viscosity. Opt. Laser. Technol. 2021;134 [Google Scholar]
- 65.Wu H., Zhang T., Lai X., Yu H., Li D., Zheng H., Chen H., Ohl C.-D., Li Y. Influence of surface tension on dynamic characteristics of single bubble in free-field exposed to ultrasound. Micromachines. 2022;13:782. doi: 10.3390/mi13050782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wu H., Zheng H., Li Y., Ohl C.D., Yu H., Li D. Effects of surface tension on the dynamics of a single micro bubble near a rigid wall in an ultrasonic field. Ultrason. Sonochem. 2021;78 doi: 10.1016/j.ultsonch.2021.105735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Phan T.-H., Kadivar E., Nguyen V.-T., el Moctar O., Park W.-G. Thermodynamic effects on single cavitation bubble dynamics under various ambient temperature conditions. Phys. Fluids. 2022;34 [Google Scholar]
- 68.Sojahrood A.J., Haghi H., Shirazi N.R., Karshafian R., Kolios M.C. On the threshold of 1/2 order subharmonic emissions in the oscillations of ultrasonically excited bubbles. Ultrasonics. 2021;112:106363. doi: 10.1016/j.ultras.2021.106363. [DOI] [PubMed] [Google Scholar]
- 69.Sojahrood A.J., Haghi H., Karshafian R., Kolios M.C. Classification of the major nonlinear regimes of oscillations, oscillation properties, and mechanisms of wave energy dissipation in the nonlinear oscillations of coated and uncoated bubbles. Phys. Fluids. 2021;33 [Google Scholar]
- 70.Sojahrood A.J., Haghi H., Li Q., Porter T.M., Karshafian R., Kolios M.C. Nonlinear power loss in the oscillations of coated and uncoated bubbles: Role of thermal, radiation and encapsulating shell damping at various excitation pressures. Ultrason. Sonochem. 2020;66 doi: 10.1016/j.ultsonch.2020.105070. [DOI] [PubMed] [Google Scholar]
- 71.Louisnard O. A simple model of ultrasound propagation in a cavitating liquid. Part I: Theory, nonlinear attenuation and traveling wave generation. Ultrason. Sonochem. 2012;19:56–65. doi: 10.1016/j.ultsonch.2011.06.007. [DOI] [PubMed] [Google Scholar]
- 72.Sojahrood A.J., Li Q., Haghi H., Karshafian R., Porter T.M., Kolios M.C. Probing the pressure dependence of sound speed and attenuation in bubbly media: Experimental observations, a theoretical model and numerical calculations. Ultrason. Sonochem. 2023;95 doi: 10.1016/j.ultsonch.2023.106319. [DOI] [PubMed] [Google Scholar]
- 73.Qin D., Zou Q., Lei S., Wang W., Li Z. Nonlinear dynamics and acoustic emissions of interacting cavitation bubbles in viscoelastic tissues. Ultrason. Sonochem. 2021;78 doi: 10.1016/j.ultsonch.2021.105712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Qin D., Lei S., Wang X., Zhong X., Ji X., Li Z. Resonance behaviors of encapsulated microbubbles oscillating nonlinearly with ultrasonic excitation. Ultrason. Sonochem. 2023;94 doi: 10.1016/j.ultsonch.2023.106334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.A. Isaeva, I. Grushnikov, V. Dobrozhanskiy, Analysis of vapor-liquid equilibrium parameters of multicomponent hydrocarbon mixtures using cubic equations of state, SPE Russian Petroleum Technology Conference, Moscow, Russia, 2018.
- 76.Abbasi T., Abbasi S.A. Accidental risk of superheated liquids and a framework for predicting the superheat limit. J. Loss. Prevent. Proc. 2007;20(2):165–181. [Google Scholar]
- 77.Hirschfelder J.O., Curtiss C.F., Bird R.B. Wiley; New York: 1964. Molecular Theory of Gases and Liquids. [Google Scholar]
- 78.Poling B., Prausnitz J., O’Connell J. Mac Graw Hill; New York: 2004. The Properties of Gases and Liquids. [Google Scholar]
- 79.Yasui K. Effects of thermal conduction on bubble dynamics near the sonoluminescence threshold. J. Acoust. Soc. Am. 1995;98(5):2772–2782. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.