Abstract
The world has experienced an unprecedented global health crisis since 2020, the COVID-19 pandemic, which inflicted massive burdens on countries' healthcare systems. During the peaks of the pandemic, the shortages of intensive care unit (ICU) beds illustrated a critical vulnerability in the fight. Many individuals suffering the effects of COVID-19 had difficulty accessing ICU beds due to insufficient capacity. Unfortunately, it has been observed that many hospitals do not have enough ICU beds, and the ones with ICU capacity might not be accessible to all population strata. To remedy this going forward, field hospitals could be established to provide additional capacity in helping emergency health situations such as pandemics; however, location selection is a crucial decision ultimately for this purpose. As such, we consider finding new field hospital locations to serve the demand within certain travel-time thresholds, while accounting for the presence of vulnerable populations. A multi-objective mathematical model is proposed in this paper that maximizes the minimum accessibility and minimizes the travel time by integrating the Enhanced 2-Step Floating Catchment Area (E2SFCA) method and travel-time-constrained capacitated p-median model. This is performed to decide on the locations of field hospitals, while a sensitivity analysis addresses hospital capacity, demand level, and the number of field hospital locations. Four counties in Florida are selected to implement the proposed approach. Findings can be used to identify the ideal location(s) of capacity expansions concerning the fair distribution of field hospitals in terms of accessibility with a specific focus on vulnerable strata of the population.
Keywords: ICU bed Capacity, Field hospitals, Vulnerable populations, Spatial accessibility, Floating catchment area, Travel time constrained capacitated p-median model
1. Introduction
Since the beginning of 2020, the world has experienced an unprecedented global health crisis in the modern era, namely the COVID-19 pandemic, which affected societies and led to fundamental disruptions in all domains of human life, including those related to commuting, accessing services and goods, and communication. Albeit all countries tried to implement various prohibitive actions to halt the spread of the virus, such as quarantines, lockdowns, social distancing, and mandatory mask usage, many people have still suffered from devastating health and economic problems. Specifically, 623,470,447 people have been diagnosed as positive for COVID-19, and 6,551,678 have died globally as of October 2022 [1]. One of the major impacts of the pandemic has been the further deterioration of already existing inequalities among different communities concerning accessibility to resources, services, and goods. In particular, maintaining access to healthcare facilities and life-saving services provided at hospitals proved to be among the most critical concerns for the well-being of individuals experiencing the worst of the pandemic.
In terms of distance and capacity, spatial accessibility to healthcare resources is essential and should be provided equally for all population strata. Focusing on one dimension of this issue, unfortunately, there is a negative association between intensive care unit (ICU) access and the COVID-19 case fatality ratio [2], so ICU beds have played a critical role in saving lives during the pandemic [2]. Besides, problems in ICU access impacted other aspects of the pandemic. For example, areas with lower trust in medical experts due to discrepancies in ICU availability were found to be lower in vaccination support [3].
During the pandemic, healthcare systems were overwhelmed by the enormous demand for healthcare services. Many people had to be intubated and stayed for weeks at hospitals. In many unfortunate cases, people could not be admitted to the ICU beds due to insufficient capacity [4]. In some dire instances, hospitals with no beds to serve patients transferred COVID-19 patients to hospitals hundreds of miles away for treatment [5]. Many countries outside the U.S. experienced similar situations; in some states of Brazil, such as Amazonians, Pernambuco, Sao Paulo, and Rio de Janeiro, healthcare systems were about to collapse with no ICU availability for new patients [6]. In Sweden, ICU beds were near capacity [7], and in the U.S., 3 out of 5 hospitals exceeded 90% occupancy for at least two weeks during the third wave of the pandemic [8].
Some healthcare facilities, even though they have ICU admission capacity, may not be within reach for certain patients in need. In broader terms, the uneven geographical distribution of those resources could result in uneven accessibility. Several studies examine the accessibility to ICU beds during the pandemic and revealed discrepancies in access to healthcare resources among countries, counties, cities, and even neighborhoods. For example, in one study, the differences in access to ICUs among 14 European countries on national and regional levels were examined, and nonhomogeneous accessibility patterns were observed [9]. Germany had nation- and region-wide the highest accessibility scores, whereas other countries such as Sweden and France, have clustered services at the regional level. In another study, regional inequalities in healthcare access in the U.S. were identified [8]. Hospitals in the south and west of the U.S. were more likely to reach critical ICU capacity than those in the northeast. Hospitals in areas with the highest social vulnerability were more than twice as likely to reach capacity compared to those in the least vulnerable areas. Accessibility to ICU beds in rural areas was investigated in Davoodi et al. [10] for the U.S., and it was found that although 19% of the total population lived in rural areas, those areas comprised only 1% of the overall ICU beds in the country. The situation is perhaps more challenging considering that 10 million older adults live in rural areas with critical accessibility needs [11], and they were in one of the highest risk strata for COVID-19-inflicted direr health outcomes [12]. Disparities in access to healthcare resources among the 20 largest cities in Brazil were investigated and accordingly, ICU availability varied substantially between cities, and it was significantly lower among black and poor communities [13]. In another research, problems in accessibility to ICU space among Florida counties were analyzed [14]. According to this research, for North Florida rural areas, and zip codes with higher Latino or Hispanic populations, it was more probable to have lower access to ICU beds. At the lowest scale, segregation patterns and accessibility to hospital care differences among racial groups in Chicago Area were examined [15]. It was found that there was no significant difference in terms of the distribution of accessibility; however, there were travel cost-based accessibility differences. Therefore, many factors from the highest scale, such as the country people reside in, to personal factors such as income and age, have been found to play a significant role in ICU access. As the vulnerability (i.e., older age, poverty, racial segregation) increases, the above studies indicate that the likelihood of spatial accessibility to ICU decreases, which is directly linked to the limited availability of ICU supply.
Since the supply of ICU beds was scarce and not equally accessible during the peak phases of the pandemic, in line with the crisis standards [16], governments tried to expand their bed capacity. In some cases, ICU capacities of healthcare facilities were increased in situ [17,18] In others, the expansion was provided through constructing facilities such as new hospital buildings [19]. However, not all governments had such a dedicated and rapid response capability and were ready to build infrastructure similar to China [20]. Therefore, governments pursued other ideas such as structuring temporary medical centers by transforming spacious and accessible areas such as stadiums, fairgrounds, and exhibition centers into field hospitals [19]. For example, IFEMA Exhibition Center in Madrid was transformed into a temporary hospital [21], a field hospital in New York was deployed by the U.S. military [22], and Nightingale Hospital was situated at a conference center in London [23].
Field hospitals, which could serve as a practical capacity expansion alternative, and their location selection decision is the focus of this study. This would help better understand the COVID-19 pandemic from a spatial accessibility perspective. The current study contributes to the literature while investigating alternative locations by not only providing sufficient capacity expansion but also sustaining fairness in accessibility to the selected locations for all population strata. That is to say, the proposed methodology considers both the required number of ICU beds and possible distance-based demand preferences.
The novelty of this study is as follows: The fairness in accessibility has been considered using a max-min approach with the enhanced 2-step floating catchment area method (E2SFCA). This is the first modeling attempt in this context, to the authors' knowledge. Moreover, a travel-time-constrained capacitated p-median model is employed in the context of location selection of field hospitals that were salient and urgent during the pandemic. While utilizing median models (i.e., p-median and capacitated p-median models with travel time constraints) in this study, we aim to satisfy all the ICU bed demands within specified travel time limits with the minimum demand-weighted travel time. This has also not been done in this context, to the authors’ knowledge. Therefore, the resulting model is a novel interpretation of integrated accessibility and location selection models.
First, we focus on the existing situation in terms of ICU capacity and try to answer the following questions: Are there any disparities in spatial accessibility of ICU beds among different geographic areas? What is the burden on the existing facilities? Second, we search for alternative field hospital locations considering both maximin spatial accessibility and minimum demand-weighted travel time while satisfying facility capacities. We also impose travel limits for vulnerable populations considering income levels. We anticipate that our methodology and findings could provide support for planning interventions for emergent public health cases like COVID-19. These interventions could include identifying the spatial discrepancies in ICU access, determining possible locations of field hospitals or temporary healthcare facilities, and responding centrally by allocating capacity fairly.
The remainder of this paper is organized as follows. Section 2 introduces literature related to the location selection models and accessibility analysis in healthcare. Section 3 describes the study area and data sources that are used in this paper. Section 4 presents the methodology, which includes a tabu search-based regression model to estimate ICU demand; capacitated p-median model, E2SFCA method, proposed muti-objective model, and ε-constraint solution approach to determine field hospital locations considering fairness in terms of spatial accessibility. Section 5 presents the results of our analyses and related discussions. Section 6 is the conclusions.
2. Literature review
In disaster literature, temporary medical centers and field hospitals are viable alternatives for emergencies. Mass transport vehicles could be transformed into mobile hospitals [24], trucks could be repurposed as mobile emergency units [25], modular intensive care units could be designed [26], and additional service capacity could be set up in schools, sports complexes, parks, or prefabricated structures as field hospitals [27]. However, determining the placement of temporary medical facilities is a critical issue to consider and could be examined on different aspects such as effectiveness and fairness. In the former consideration, the location selection could be evaluated by the service capability or providing accessible service; in the latter consideration whether that service access is provided fairly.
The first consideration is usually a topic within the location selection domain. Several papers have considered related problems. Salman and Gul [27] proposed a multi-period mixed integer programming model to optimize capacity distribution and casualty transportation. Minimizing the total travel time and waiting time of casualties within the search-and-rescue period and the cost of deploying new field hospitals were the model's objectives. For determining the number and location of field hospitals and the allocation of disaster victims to those locations, a two-stage stochastic model was proposed by Aydin [28], which was a variation of the p-median model with capacity impositions. In Fereiduni and Shahanaghi [29], a p-robust approach was employed as a network design model in which location, allocation, and evacuation decisions were made, and emergency tents were considered temporary medical centers. In Oksuz and Satoglu [30], a two-stage stochastic programming model tried to determine the number and location of temporary medical centers. This model considered existing hospital locations, medical center capacities, causality classifications, and possible infrastructure damages while minimizing total setup and expected transport costs. In Barutcu and Ic [31], a VIKOR (multi-criteria optimization and consensus solution) model was employed for the determination of the locations of the field hospitals to be established after a probable earthquake by considering several criteria such as earthquake risk, population density, land area, distance to downtown, and other transportation alternatives.
The literature on location selection of temporary medical centers and field hospitals was further extended during the pandemic. In Zolfani et al. [32], to identify the locations of temporary COVID-19 hospitals, a gray-based decision support framework is developed, employing criteria importance through inter-criteria correlation (CRITIC) and combined compromise solution (CoCoSo) methods, with a case study of Istanbul, Turkey. The case study used ten criteria for technological, economic, environmental, and social aspects. Akpinar and Ilgin [33], a case study in Izmir, Turkey, identified the most suitable locations for COVID-19 field hospitals by fuzzy Choquet integral multi-criteria decision-making technique. The six main criteria used in the case study were accessibility, environmental, transportation, health center, population, and cost-related factors. In Aydin and Seker [34], a DELPHI-based multi-criteria decision-making (MCDM) framework was proposed to determine COVID-19 isolation hospitals, with a focus on Istanbul, Turkey. Some of the criteria used in the case study included land space, accessibility, geographical barriers, and population density. In Wang et al. [35], a decision support framework was developed using the fuzzy analytic hierarchy process (FAHP) and the weighted aggregated sum product assessment (WASPAS) model for the determination of temporary COVID-19 hospital locations in Ho Chi Minh City, Vietnam. In Kheybari et al. [36], a two-step hybrid approach was proposed. In the first step, an extensive set of relevant criteria was categorized into environmental, social, economic, and infrastructural dimensions along with a risk-averse best-worst method (BWM) to determine the optimal ranges of the criteria weights. This was followed by scoring the performances of the locations using mathematical modeling. A portfolio optimization model was proposed in the second step using the scores from the former one and the distance between the cities as parameters. The model was applied to a case study in Mazandaran, Iran. In Hassan et al. [37], the locations of COVID-19 field hospitals maximizing the number of patients were determined by solving a nonlinear binary constrained model-a variation of maximal covering problem-by a -discrete binary gaining-sharing knowledge-based metaheuristic algorithm. The method was applied to a case study of eight governorates in Upper Egypt. Most of the location selection models developed for COVID temporary medical centers and field hospitals used MCDM models. On the other hand, generic location selection models such as coverage and median models were also employed [37].
The second consideration, fairness, is usually studied under spatial accessibility literature. A widely used spatial accessibility technique, the floating catchment area (FCA) method and its variants are employed to measure accessibility values of various amenities and services such as jobs [38], libraries [39], urban fire service [40], parks [41], and schools [42]. Those methods are also used to measure spatial accessibility to health services and evaluate their fairness. Some examples of accessibility studies focusing on healthcare services are the examination of accessibility of primary care physicians [43], emergency medical services [44], healthcare providers [45], and high-tier hospitals [46]. Accessibility of healthcare services (e.g., ICU beds) and facilities during Covid-19 is also covered in the spatial accessibility literature. Park et al. analyzed daily changes in ICU accessibility by an enhanced two-step floating catchment area method and its relation to the case-fatality ratio [47]. ICU bed accessibility during Covid-19 is also studied by employing the E2SFCA method [48,49] and by employing the 3-step floating catchment area (3SFCA) method [14] and balanced floating catchment area (BFCA) method [13]. Sritart et al. evaluated spatial equity by analyzing the accessibility of public hospitals, physicians, and the number of ICU beds, by the two-step floating catchment area (2SFCA) method [50]. Park and Goldberg examined the spatial accessibility of ICU beds during Covid-19 from a stochastic perspective by employing Monte-Carlo simulation and an E2SFCA method [51]. Al-Omari et al. analyzed the accessibility of healthcare resources by an E2SFCA method [52]. Shen [53] analyzed the accessibility and equality of medical facilities by a kernel density two-step floating catchment area method.
These considerations are studied together in several studies. Shelter location selection with maximum equity [54], coverage and accessibility of emergency medical services [44], and equity of accessibility and demand coverage of medical facilities [55]. However, the location selection of field hospitals considering fairness has not been examined yet. Moreover, the fairness considerations for spatial accessibility are usually the standard deviation or variance [[56], [57], [58]], mean squared error [58], and Gini coefficient [42,44,53,58]. Though fairness could also be achieved by maximizing the minimum score [59], none of the prior studies employed that consideration for spatial accessibility optimization. Thus, our multi-objective optimization model integrates effectiveness and fairness considerations in the location selection of field hospitals by employing a modified median model with a maximin fairness objective.
3. Study area and data
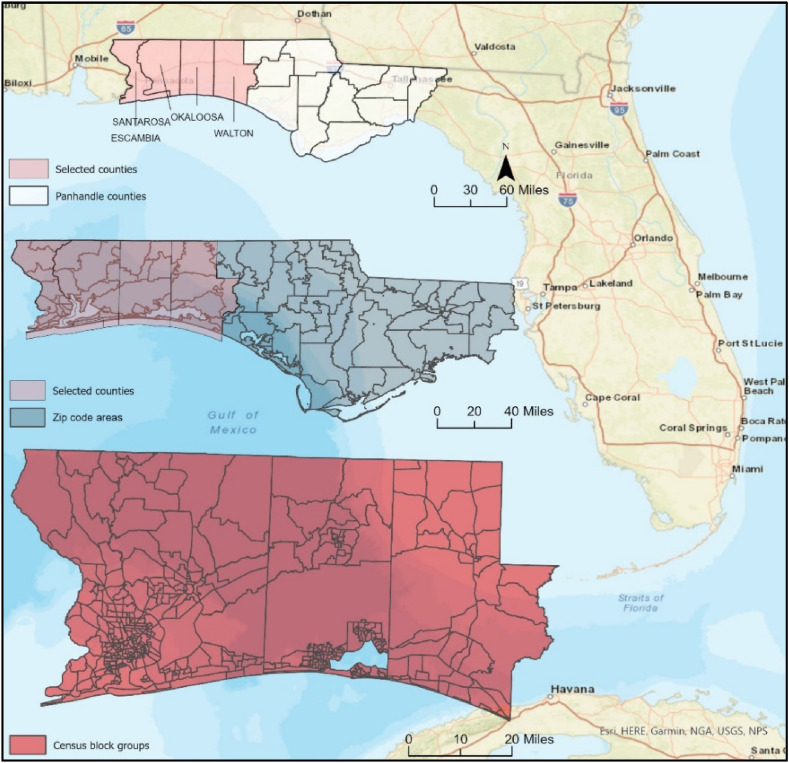
The U.S. is one of the most affected countries by the pandemic, with 88,027,926 cases and 1,012,816 deaths as of July 2022 [1]. Within the U.S., Florida is the third most populated state and ranks third after California and Texas in the total number of confirmed cases and deaths as of July 2022 [60]. Additionally, Florida has the second-highest aging (65 and older) population and the seventh-highest poverty rate in 2019 [61]. As aging populations are positively associated with greater healthcare needs [9], and poverty is negatively associated with ICU availability [13] the State of Florida, becomes an excellent test-bed. In Florida, we selected four counties in the Panhandle region. Three of them are urban counties Escambia, Santa Rosa, and Okaloosa and one is a rural county Walton, which has an additional negative correlation with ICU access [10,14]. We use the Florida Department of Health data which includes zip code area-level disaggregate data on COVID-19-positive cases. Moreover, other datasets (i.e., hospitals with ICU beds, their ICU bed capacities, and demographic characteristics at various levels including zip code and block group levels), are publicly available and utilized in this study.
Fig. 1 illustrates the study area's county, zip code, and block group boundaries. Since there is no ICU demand data at any disaggregate level, the available covid positive case counts are used to estimate the ICU demand. For this purpose, we collected the COVID-19 case data at the zip code level from the Florida COVID-19 Hub [62]. This data covers the period from the April 3, 2020 to the June 3, 2021, when the Florida Department of Health stopped sharing data at this level. Noting that for having a larger sample set for the regression analysis, zip code level COVID-19 positive cases for the overall Panhandle region are used. Then, the estimations are done for the selected subregion, which will be detailed in the methodology section. In addition, we gathered demographic and socioeconomic data at the zip code and block group levels from the American Community Survey (ACS) 2019 5-year estimates provided by the U.S. Census Bureau [63]. ACS data is also used to identify vulnerable block groups based on the poverty level. In this study, we considered the census block groups with more than 12.7% of the population below the poverty line as vulnerable communities. This threshold is the average poverty rate of Florida in 2019 [64].
Fig. 1.
Study area.
From the supply side, the hospitals' ICU bed capacities are collected from Ref. [65]. For possible field hospital locations, a comprehensive critical facility dataset for the region is gathered [66]. Among all the critical facilities, airports, community centers, fairgrounds, hospitals (with and without ICU capacities), emergency shelters, and stadiums are filtered as possible field hospital locations with the required power infrastructure and used as alternative locations during the COVID-19 pandemic [[67], [68], [69], [70]]. A further selection is done for space requirements. For the proposed 50 (low-capacity) and 75 (high-capacity) scenarios, space requirements are calculated by doubling the total ICU bed space −250 sq feet per ICU bed [71]- to cover parking and equipment storage needs. So at least 0.6 acres and 0.9 acres of available space are required for low and high-capacity scenarios respectively. It must be noted that the staffing requirements and equipment costs are not considered in this study. It is assumed that the required staff could be available with alternative scenarios such as employing former healthcare staff or qualified nursing and medical students [72] or shifting different specializations to intensive care [16].
In this setting, block group centroids are used to approximate the ICU demand origins, and selected critical facilities are used as possible field hospital locations. Thus, ICU demand estimates are calculated at the block group level. Travel times between origins (block group centroids) and destinations (existing and possible facility locations) are calculated by the Network Analyst toolbox of ArcGIS Pro [73].
4. Methodology
The proposed analysis has two parts. In the first part, the existing situation is investigated. The aim is to analyze the spatial accessibility levels of the block groups considering the existing facilities and their ICU bed capacities. Moreover, we also want to analyze the burden on existing hospitals when each origin can access the closest healthcare facility in the region without imposing capacity limitations. In the second part, considering varying demand rates (high-low), varying capacity limitations (high-low), and varying travel time limitations (considering vulnerable block groups), several scenarios are developed. For each scenario, the best (i.e., according to fairness and effectiveness) possible locations for the field hospitals in the region are searched.
Before the analysis of ICU bed accessibility and availability, the demand for ICU beds is required. The ICU demand for each census block group is estimated by developing a regression model considering socioeconomic and demographic characteristics of the zip code areas and positive COVID-19 case data at the zip code level as this is the finest level that both information is available. The model is then used to estimate the positive COVID-19 cases for a further disaggregated level, census block group. After predicting the number of positive COVID-19 cases at the census block group level, ICU demand for each block group is estimated by approximation and calibration. Though the study area consists of four counties, the case data for a larger sample (the Panhandle region) is used to overcome sampling size problems in linear modeling.
4.1. ICU demand estimation by tabu search-based linear regression
ICU bed occupancies for hospitals are available; however, it is impossible to know the origins of the patients that would need them. Therefore, ICU demand from each block group should be estimated to evaluate the accessibility of hospitals and locations of possible field hospitals. There are several studies in which ICU demand is calculated. For example, in Martin et al. [74], the ICU demand in England was calculated by first estimating the COVID-19 admissions by cohorts and then splitting the new COVID-19 patients in hospitals into wards and ICU beds. In Ritter et al. [75], ICU rates in several regions of Europe were modeled depending on positive rates, but the estimates were at aggregate levels.
Since we want to use socioeconomic and demographic variables not only to estimate ICU demand but also to investigate the current and possible situations in terms of economic vulnerability, we use regression modeling. In Lee et al. [76], multivariate logistic regression was applied to estimate the contributing factors to ICU admission in the Republic of Korea. Accordingly, being male, old aged, and living in Daegu city were the significant factors identified. However, their study was based on the actual case data unavailable for the proposed focus area of this study.
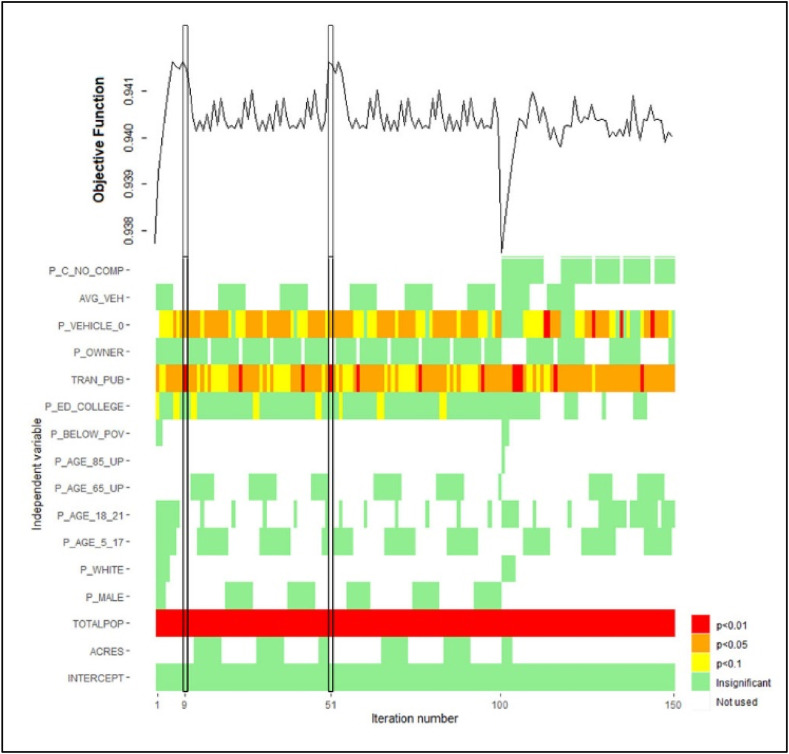
To estimate the ICU bed requirements, first, the number of COVID-19 cases per day per census block group must be predicted. There are already available data on the number of COVID-19 cases at the zip code level; however, such information is not available at the census block group level that is needed in this study. Therefore, a linear regression model has been developed to estimate the total number of COVID-19 cases (for the period starting from the April 3, 2020 to the June 3, 2021) at each census block group using the demographic and socioeconomic data. ACS 2019 provides a large group of data such as population (total and cohorts), number of households, gender, age, education, income, and mode of transport. To identify the best set of explanatory variables, we employed a tabu search-based optimization algorithm. Tabu-search is a metaheuristic technique proposed by Glover [77] for solving optimization problems. It is a stepwise local search procedure during which some moves are labeled as tabu, so being restricted. Thus, rather than applying a tabu move, the algorithm proceeds to an inferior solution until a termination criterion is satisfied. This tabu-search property could prevent the algorithm from being trapped at a local optimum, which is the main distinction from the greedy and improvement-type searching algorithms [78]. In this study, the tabu-search algorithm proposed in Ref. [79] is utilized to determine the best subset of independent variables that optimize the adjusted R2 value of regression models. The details of the tabu-search procedure and the variables used in the algorithm are given in Appendix since the focus of the paper is not the demand estimation part.
Consequently, we determine that the best model which consists of the total population, number of public transport users, percentage of occupied housing units having no vehicles, and percentage of the population with a college education, presented with decreasing significance levels in this order (see Table 1 ).
Table 1.
COVID case modeling.
| Descriptive Statistics | ||||
|
Variable |
Min |
Max |
Mean |
Std Dev. |
| Total COVID Cases | 47.00 | 7029.00 | 1543.54 | 1383.30 |
| Total population | 555.00 | 53703.00 | 14637.00 | 12902.19 |
| Transit users | 0.00 | 1141.00 | 50.06 | 135.17 |
| % No vehicle | 0.00 | 18.67 | 5.68 | 3.91 |
| % College education | 0.00 | 43.69 | 16.19 | 9.51 |
| (N = 100) |
||||
| Regression Model | ||||
|
Variable |
Estimate |
Std Error |
t statistics |
p-value |
| Intercept | 5.20 | 103.06 | 0.05 | 0.96 |
| Total population | 0.10 | 0.00 | 29.85 | 0.00 |
| Transit users | 0.90 | 0.31 | 2.91 | 0.01 |
| % No vehicle | 22.57 | 9.68 | 2.33 | 0.02 |
| % College education | −6.24 | 4.11 | −1.52 | 0.13 |
Multiple R-squared: 0.944, Adjusted R-squared: 0.942.
F-statistic: 400.3 on 4 and 95 DF, p-value: <2.2e-16.
Results show that the total population is the most significant variable and is positively associated with the number of positive cases. The percentages of occupied housing units with no vehicle available and the number of public transit users are influential factors in the number of COVID-19 cases. The percentage of the population with a college education is found to be negatively associated with the number of COVID-19 cases with a lower significance level. Consequently, the below model (M) is used to predict the total number of COVID-19 cases for the census block groups:
| (M) |
After estimating the total positive cases at the census block group level, the daily average is calculated by dividing the total estimated number of cases by the length of the period (427 days). The daily average is multiplied by a factor of 0.028, representing the rate of ICU requirement for positive cases. This factor is calculated by the multiplication of the estimated hospitalization rate (11.3%) of confirmed COVID-19 cases in the U.S. and the average ICU requirement rate for hospitalized COVID-19 patients (25%) [80,81]. The estimated hospitalization rate is calculated by dividing estimated cumulative hospitalizations per 100,000 people (1,093.9) [82] by the cumulative number of COVID-19 cases per 100,000 people (9,635.3) [83] for the period between May 2020–April 2021 in the U.S. This estimated number of ICU patients is used in the lower demand scenarios. For the high demand scenarios, the peak periods of the COVID-19 pandemic, the average daily estimation of ICU demand is calibrated by the highest rate in the U.S. during the pandemic as 86.8 ICU patients per million, which is recorded on the January 12, 2021 [84]. Finally, biweekly ICU demands (for both high and low demand levels) are calculated as this study a) does not consider patient transfers, b) the median stay of a patient is considered to be the demand estimation period, and c) the length of stay varies during the phases of the pandemic and from country to country [[85], [86], [87]].
4.2. Identification of field hospital locations by multi-objective mathematical modeling
The location selection decision of field hospitals to extend ICU capacity is put forward by two objectives in this study. One objective is the effectiveness of the selected locations, and the second one is the fairness of the spatial accessibility scores of the selected locations.
4.2.1. Effectiveness objective and median models
For the effectiveness objective, demand-weighted travel times are minimized concerning estimated demand and proposed capacities by a location model. Facility location decisions are important in designing a network that would achieve the desired service level (e.g., the maximum coverage available, and whole area coverage) with the minimum cost (e.g., facility construction, distance, travel). Among the facility location problems, discrete models constitute a significant category [88]. Discrete facility location models are used to select a subset of locations from a finite set of available locations [89]. The most common discrete location selection models in the literature are the center, covering, and median models. For center models, the aim is to find the facility locations that meet all the demands while having the minimum distance from the related demand points [90]. The most generic version is the p-center model where the maximum distance between a demand point and the closest point in a set of p-sites is minimized [91]. In covering models, generally, facilities must be within a certain distance or time of demand locations. In set covering problems, all demand is covered based on a service standard using a minimum number of facilities, whereas in maximal covering problems, the maximum number of demand points are covered with a limited set of service points [92]. Median models, on the other hand, aim to minimize the total or average weighted distance among facilities and demand points. The most common version of median models, p-median problems, optimizes the location of p facilities among a given set, to minimize the total cost of supplying the demand points [89]. Those generic models are widely used in different settings, such as service coverage for telecommunications and healthcare. In particular, p-median models are employed as a spatial optimization technique, with various large-scale implementations in different fields such as public health by sensor location selection for water quality [93], public services by school districting [94] and school allocation [95], finance by bank locations [96], and emergency service systems: determination of fire station locations [97], ambulance locations [98], shelter locations [[99], [100], [101]], and aid distribution [102].
The capacitated version of the p-median problem is also commonly employed. The objective of this problem is to minimize the total cost of locating a set of capacitated service/supply points and assigning the demand points to these service/supply points without violating the service/supply capacities [103]. Exact algorithms are proposed to solve the p-median [[104], [105], [106], [107]] and capacitated p-median [108] problems which are np-hard problems. For large-sized problems, heuristic algorithms such as clustering search [109], and variable neighborhood selection [110] and metaheuristic algorithms such as tabu-search [111,112], and genetic algorithm [[113], [114], [115]] are proposed. A very extensive literature review on capacitated and uncapacitated p-median problems with a bibliography is presented in Reese [116], and a review on metaheuristic solution techniques is presented in Mladenovic et al. [117].
p-Median and capacitated p-median models are also used in the healthcare sector, such as the determination of the healthcare center locations [118], emergency medical service locations [[119], [120], [121]], maternal hospital locations [122], organ transplant center locations [123,124]. Thus, we focus on the p-median model for this setting as being one of the widely used generic models to solve facility location problems. As opposed to the covering problem, the coverage distance for the p-median problem could be unrestricted, and the number of facilities to be located is known a priori, so doing a sensitivity analysis on the number of facilities to locate is eligible. In addition to the classic setting of p-median, we also applied travel time limits as a variation. As we aim to determine the locations with full-service coverage for varying travel time limits, the p-median model fits that purpose. As mentioned in Hillsman [125], it is not acceptable for any demand location to be so far from its closest facility, which in turn means ignoring the accessibility of the facilities, at least for some of the demand points. Besides, in ICU accessibility cases, it is not only critical for individuals but also an emergent public health issue. Thus, any assignment with a distance beyond the maximum, an undesirable case, could be eliminated by applying maximum distance constraints [106].
Accordingly, among the alternative supply points, p facilities are selected to minimize the overall cost of serving all the demand points [126], where each demand point must be served, and exactly a single supplier should provide this service. The following notation is used to formulate this problem:
Sets and parameters:
.
.
.
.
.
.
Decision variables:
.
.
Depending on the above notation, the following formulation is used for the p-median problem:
| (1) |
Subject to:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
in this formulation, the objective function [1] minimizes the demand-weighted travel times between the census block groups and the ICU facilities. Constraint [2] imposes that each block group i must exactly be assigned to one facility j. Constraint [3] ensures that exactly p facilities are selected from set S. Constraint [4] associates the decision variables and guarantees that if a block group is assigned to a facility, that facility is selected. Constraints [5,6] are the integrality constraints.
For the capacitated p-median case [[1], [2], [3],5,6], and [7] defines the formulation; where,
| (7) |
with [7], each facility imposes a capacity limit for demand assignments, where Q j is the capacity of facility j. One other variation is the distance-constrained model, in which the demand points are serviced by facilities within a predetermined range [127] or limiting the number of facilities to maintain [128]. According to the vulnerability consideration, a block group's maximum travel time is determined, thus, each block group has a limited set of available facility locations. Within this frame, the capacitated model is used to determine the best locations to provide additional capacity (field hospitals, ICU capacity assigned to the shelters and hospitals) by minimizing the overall demand-weighted travel time while obeying the capacity limitations of the facilities and the travel-time-constraints of the population block groups. Thus, equation set [8] is imposed; where,
| (8) |
Note that in this formulation, the costs other than the travel time such as the monetary cost of setting up field hospitals are not considered, since the proposed facilities are to be structured at or make use of existing infrastructure, and the costs of equipment required would be the same for all alternatives. Therefore, set-up costs would not affect the location selection decision.
4.2.2. Fairness objective and floating catchment area (FCA) models
The fairness objective in this study is based on the spatial accessibility scores of the ICU beds for the demand locations. Different than the effectiveness objective, the fairness objective is relative and based on travel time-based comparison for each demand and supply point. It is relative in such a way that there is no direct assignment of block groups to supply locations as in the model presented by Ref. [1]-(8). The preferences of block groups are represented by distance-based weights and each capacity is considered available for demand locations within travel time restrictions. The aim is to maximize the minimum spatial accessibility score which is calculated by a floating catchment area method. Floating catchment area models are gravity-based models to operationalize the relationship between supply and demand depending on the impedance (e.g., distance, travel cost, travel time) between them [129]. The enhanced 2-step floating catchment area (E2SFCA) is one of the most utilized spatial accessibility measurement methods in the accessibility literature. It is an improved version of a former 2-step floating catchment area method [130] to overcome its static operationalization of distance in which the supply locations within the maximum distance are evaluated as equally accessible [43]. The E2SFCA method consists of a relative representation of the distance (or any other cost e.g., travel time) between demand and supply locations by zoning the maximum catchment area and/or utilizing a distance decay function such as Gaussian, exponential, and inverse power functions [130].
Based on the varying catchment zones created there are two main steps. The first one is to calculate a supply-to-demand ratio in which each supplier's capacity is shared by the demand locations in reach of that supplier. In the second step, each demand location's accessibility score is calculated in which the relative distance-weighted supply amount in reach is evaluated. The enhancements are not limited to 2-step methods. There are 3-step methods that consider the competition among the suppliers; however, in this study, it is assumed that a competitive setting is not appropriate for the ICU context. According to this frame, the E2SFCA is utilized by the following equations with the notations presented in the previous section. As such, rather than distances, travel times are used in all formulations. Equation [9] is used to calculate travel time weights by a Gaussian decay function. For each origin and destination pair, a travel time weight is calculated. As travel time increases between locations the weight also decreases, and if travel time is beyond the specified maximum the weight is zero. After calculating travel time weights, in step 1, the supply-to-demand ratio for each supply point R j is calculated by dividing the supply amount by travel time-weighted demand figures as given in Equation [10]. In step 2, the accessibility score for each block group A i is calculated as the travel time-weighted supply-to-demand ratio as given in Equation [11].
| (9) |
- Step 1: Supply-to-demand ratio ):
(10) - Step 2: Accessibility index :
(11)
To select a given number of (p) field hospitals that maximize the minimum spatial accessibility score calculated by Ref. [9]-(11), the following mathematical model can be used:
| (12) |
| (13) |
| (14) |
| (15) |
The objective function [12] maximizes the minimum accessibility score . Constraint [13] restricts the number of field hospitals by p. Constraint [14] imposes that with the selected set of field hospitals, the accessibility score of each demand point is greater than or equal to the minimum score. Noting that supply-to-demand ratio Rj and travel time weight f(c ij ) are parameters of the model and are calculated by Ref. [9]-(10). Constraint [15] is for integrality.
4.2.3. Multi-objective model and ε-constraint solution approach
When the two models presented by Ref. [1]-(8) and [12]-(15) are integrated, the resulting model is a multi-objective mathematical model that minimizes [1] and maximizes [12] concerning the constraints [2]-(8) and [13]-(14). The integrated model responds to direct assignments (census block groups to shelters within capacity limitations) and relative assignments (optimizing the alternatives). However, the model with stated constraint sets does not eliminate the selection of a field hospital that has no direct assignments. Therefore, another constraint set [16] is imposed. If there is no direct assignment to a possible field hospital location, it cannot be selected.
| (16) |
There are several widely used multi-objective model optimization techniques such as the weighting method, and the ε-constraint solution approach. In the weighting approach, the weights of the objectives should be determined a priori which is not an easy task. Also, in the weighting method, the objectives needed to be scaled to reduce the influence of unscaled objectives on the solutions. Moreover, the weighting method is subject to miss efficient solutions. In the ε-constraint solution approach, one of the objectives is left as the objective of the model, and the other objectives are embedded as constraints. For each objective that is stated as a constraint, the problem is solved many times by revising the right-hand side (ε) of that objective to get the Pareto efficient solution space. By these properties, the ε-constraint solution approach does not have the stated shortcomings of the weighting approach [131].
In our modeling approach, the fairness objective is left as the objective of the model, and the effectiveness objective is added as a constraint. The resulting model consists of the objective function [17], constraint [18], and all the constraints stated before as follows:
| (17) |
| (18) |
In the objective function [17], the fairness objective is reduced by the effectiveness objective by multiplying with a sufficiently small positive constant ( to eliminate inefficient solutions, noting that the minimization objective is augmented with a negative sign to the maximization objective. The constraint [18] is the restriction by the effectiveness objective and the right-hand side is changed from the lower bound to the upper bound for each solution. The lower bounds are calculated by solving the model with the effectiveness objective only and the upper bounds are calculated by solving the model with the fairness objective and then solving for the effectiveness objective. In addition to this solution procedure, the minimum number for p is determined by solving the following covering model:
| (19) |
| (20) |
The methodology is applied to the case study area using a 2.7 GHz, AMD Ryzen Threadripper PRO personal computer with 256 GB memory. Data processing, travel time estimation, and visual representation are performed in ArcGIS Pro version 2.4. Regression models have been generated and solved in R whereas optimization models are coded in Python and solved by IBM CPLEX 20.1.0. The exact solutions are searched, and the best results with 1% mipgap are returned.
5. Results and discussion
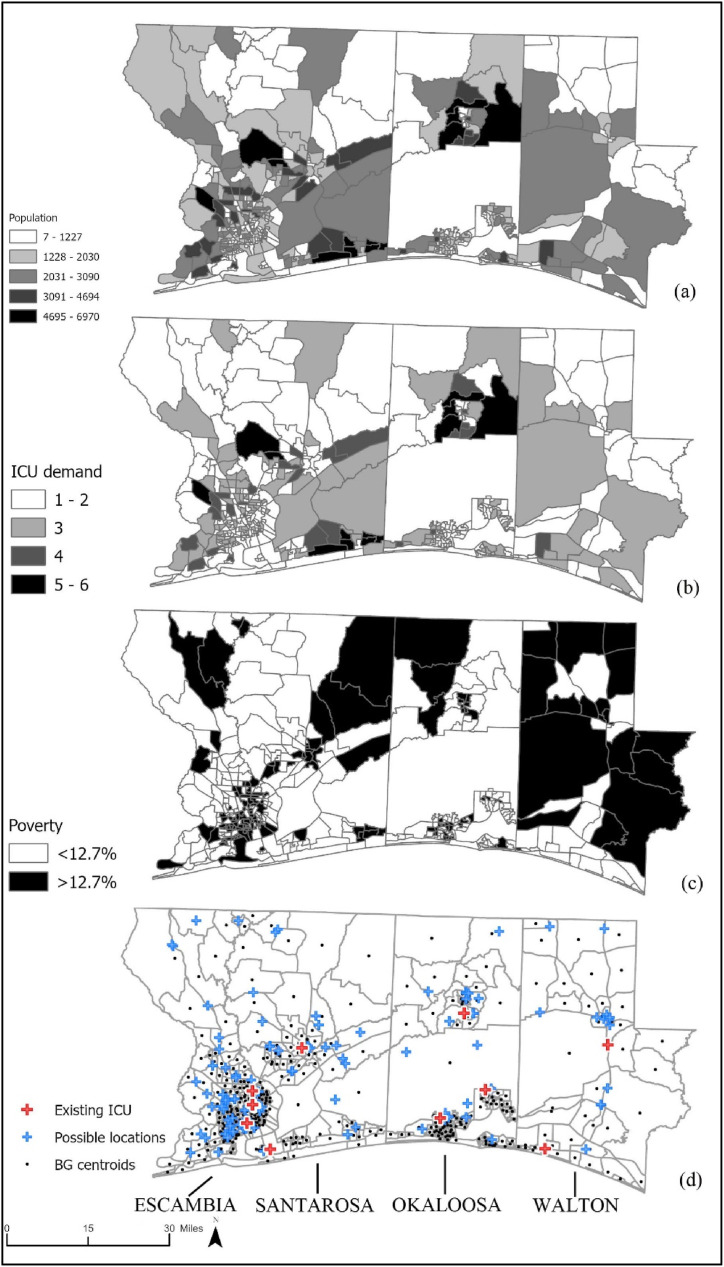
The regression model introduced in the previous section is used to predict the COVID-19 positive cases for 426 census block groups, and depending on the positive cases ICU demand for two weeks for each block group is calculated and presented in Fig. 2 b. Moreover, the vulnerable census block groups according to poverty level are depicted in Fig. 2c. According to the spatial distribution of the vulnerability, the clusters are mostly in Walton County which is a rural one. All four counties have existing ICU capacity (see Fig. 2d), but most of them are clustered in the populous west (Escambia County). In addition to the 11 existing facilities, there are 104 possible locations according to the considerations provided in Section 3. Moreover, if the capacity of an existing facility is less than the capacity of a new field hospital, an expansion option up to that capacity is defined as an alternative facility in the model.
Fig. 2.
(a) Population distribution (b) Predicted ICU demand-BG for 2 Weeks (c) Vulnerable populations-BG (d) Existing and possible ICU facility locations.
5.1. Accessibility in the current setting
In the existing situation, there are 11 hospitals with varying capacities. Considering the locations of the existing hospitals, the p-median model is applied by setting p as the maximum number of existing hospitals (p = 11). In this model no capacity restraints and travel time restrictions are imposed, thus all the demand points are assigned to their closest locations. The existing hospitals, their capacities, and the closest facility assignments are presented in Table 2 . It could be seen that in a case with estimated ICU demand, the existing capacity would be overwhelmed. The lowest capacity-to-demand rate is 12.2% (facility no: 4) observed in Walton County but the deficiency in absolute terms is highest in the most populous Escambia County (facility no: 2).
Table 2.
Existing ICU capacities and demand assignments.
| No | Hospital name | ICU capacity | ICU demand | % Met Demand | Unmet Demand |
|---|---|---|---|---|---|
| 1 | Select Specialty Hospital Pensacola | 8 | 16 | 50.0% | 8 |
| 2 | West Florida Hospital | 43 | 172 | 25.0% | 129 |
| 3 | Ascension Sacred Heart Emerald Coast | 22 | 63 | 34.9% | 41 |
| 4 | Healthmark Regional Medical Center | 6 | 49 | 12.2% | 43 |
| 5 | Santa Rosa Medical Center | 15 | 118 | 12.7% | 103 |
| 6 | Gulf Breeze Hospital | 10 | 73 | 13.7% | 63 |
| 7 | North Okaloosa Medical Center | 20 | 82 | 24.4% | 62 |
| 8 | Twin Cities Hospital | 15 | 56 | 26.8% | 41 |
| 9 | Fort Walton Beach Medical Center | 42 | 133 | 31.6% | 91 |
| 10 | Ascension Sacred Heart Pensacola | 61 | 72 | 84.7% | 11 |
| 11 | Baptist Hospital | 55 | 179 | 30.7% | 124 |
| OVERALL | 297 | 1013 | 29.3 | 716 |
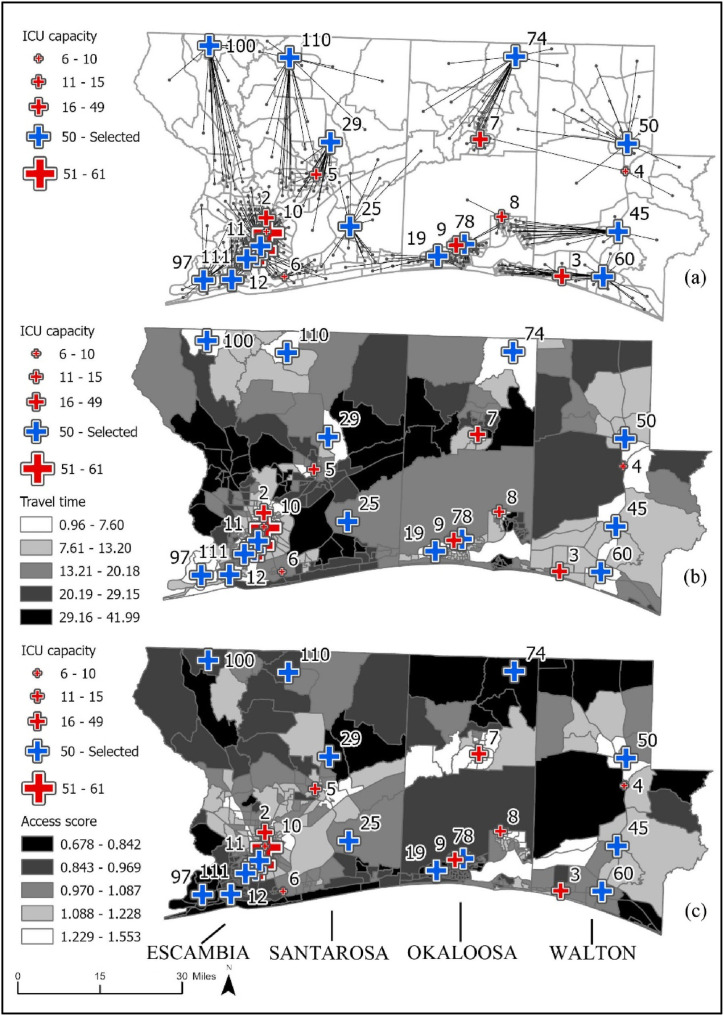
Moreover, even though people could access the hospitals, they do not have enough capacity to admit those patients; thus, they would have to travel more than they are in this case. Table 2 presents the hospital numbers matching Fig. 4, their capacities, the shortest facility-assigned demand, total travel time, and average travel time. If all these hospitals have had enough capacity to admit patients, the average travel time would have been 13.70 min per patient. Still, as mentioned, people in some block groups have to travel more than an hour up to 90 min to reach the closest hospital in the current situation. The most disadvantaged counties are Franklin and Liberty (see Fig. 3 ).
Fig. 4.
Location selection results for the representative setting (a) origin-destination pairs (b) travel times for the block groups (c) accessibility scores of the block groups.
Fig. 3.
Closest Facility Assignments with Existing Hospitals (a) Origin-Destination Links (b) Travel Time for p-Median Solution (c) Spatial Accessibility Scores without Travel Time Limits (d) Spatial Accessibility Scores with Travel Time Limits for Vulnerable Block Groups.
The shortest-distance assignments are depicted in Fig. 3a. For this assignment scheme, the travel distances are given in Fig. 3b. If there were enough capacity in the existing facilities, in terms of travel time, northern Escambia block groups have to travel more than 30 min. A similar pattern is observed for Walton block groups. Thus, at least for travel time consideration, those block groups require closer service. The paucity of services in the northern and eastern areas of the region is more obvious when spatial accessibility of ICU beds is calculated considering the existing facilities (see Fig. 3c). When travel time limits are imposed for the vulnerable census block groups the situation is direr for them. The minimum accessibility score drops to zero since for some block groups there are no facilities within the stated travel time limit (Fig. 3d). Time limits happen to create a gap between the lowest and highest accessibility scores as the E2SFCA method considers the available supply and the demand in reach. The time impositions limit some demand and some demand locations -the ones closer to the facilities-have higher access scores since they do not have to share the same capacity as before.
In the next section, the results of a sample scenario and proposed improvements are presented, and then the results of all scenarios are given.
5.2. Location selection of field hospitals in a representative setting
In this section, the proposed methodology is described in a sample scenario in which the capacity of proposed field hospitals is low (LC) as 50-ICU beds, and the demand for ICU beds is high (DH) as calibrated by the maximum amount observed during the pandemic (see Section 4.2) and the vulnerability of population block groups is not considered (VN), so in this scenario, only the overall travel time limitation is imposed as all block groups have to be assigned to facilities that are at most 60 min away. Therefore, this setting is a response to the existing situation presented in the previous section and depicted in Fig. 3a, b, and Fig. 3c.
First of all, the covering model is solved to determine the minimum number of facilities required to serve all demands (noting that existing facilities are considered open and preselected). Then with this input p, the capacitated p-median model is solved to determine the locations with the minimum demand-weighted travel time while assigning all demand to those facilities. This result is the optimum result for the effectiveness objective and the lower bound on the right-hand side (ε) for the ε-constraint solution approach.
The upper bound for the right-hand side (ε) is calculated by the lexicographic approach for the multi-objective problem, in which one objective is prioritized and the model is solved according to that objective. Then the result is used as a constraint and the model is solved according to the other objective. In our case, the fairness objective is prioritized by solving the capacitated p-median model with the fairness objective (maximizing the minimum accessibility score) and then the selected locations are used as constraints to the model, and the model is resolved according to the effectiveness objective (minimizing demand-weighted travel time).
After calculating the lower and upper bounds on the ε-constraint (for the effectiveness objective), the model is solved many times by changing the ε-value between the lower and upper bounds. The results provide the Pareto-efficient solution set in which the behavior of the model, the maximums, and the minimums could be inspected. The results for all scenarios for multiple p values are presented in the next section but the results for the representative setting are given in Table 3 .
Table 3.
Results for the representative setting.
| LC-DH-VN |
Spatial Access Score |
Travel Time (min) |
|||||
|---|---|---|---|---|---|---|---|
| Solution Method | p | Min | Max | Mean | MADa | Total | Avg |
| Existing (shortest distance assignment) | 11 | 0.0363 | 0.4006 | 0.2921 | 0.0549 | 13840.4 | 13.7 |
| Capacitated p-median (Effectiveness) | 26 | 0.2524 | 1.4071 | 1.0211 | 0.1646 | 9984.5 | 9.9 |
| Lexicographic (Fairness then Effectiveness) | 26 | 0.6783 | 1.6063 | 1.0320 | 0.1309 | 15474.2 | 15.3 |
| Epsilon constraint (Fairness and Effectiveness) | 26 | 0.6783 | 1.5532 | 1.0327 | 0.1297 | 15076.7 | 14.9 |
LC: low capacity; DH: high demand; VN: vulnerability not considered (no 30-min limits).
MAD: Mean absolute deviation.
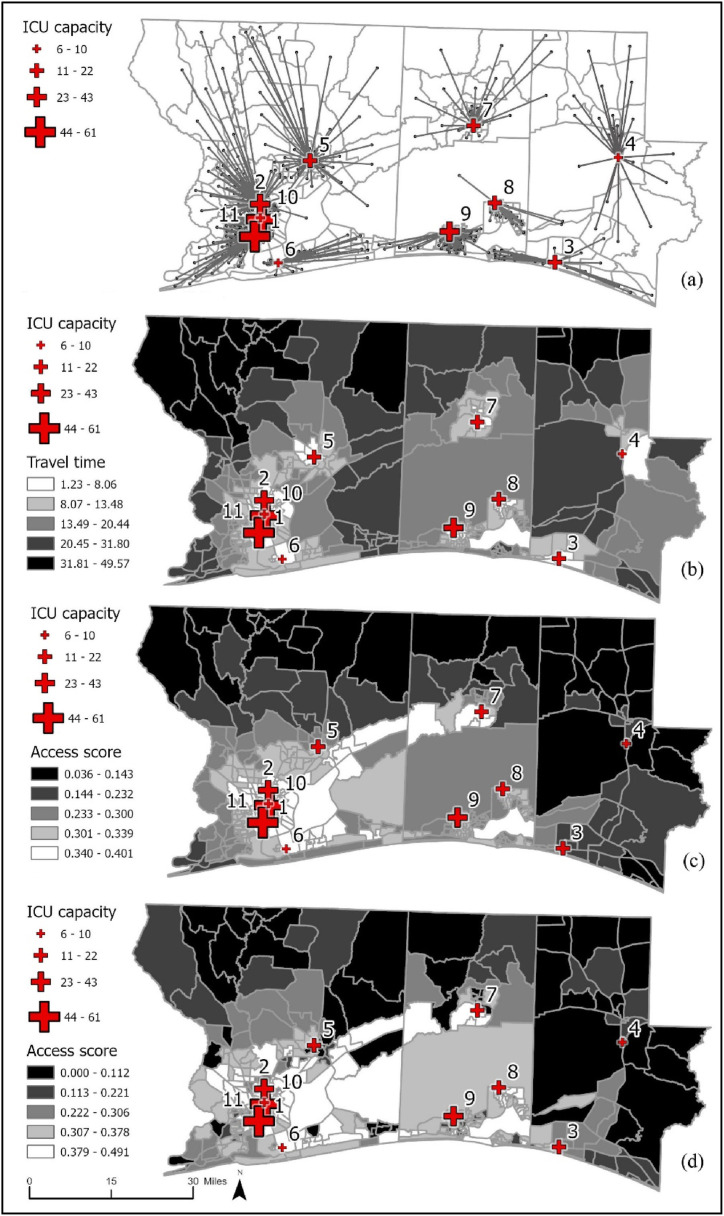
There are 11 hospitals in the existing situation with a minimum accessibility score of 0.0363. The travel time section presented for the current setting does not consider the capacities, so it is not feasible, but if the facilities had enough capacity to serve the closest demand, the total and average travel times would have been 13840.4 and 13.7 min respectively. According to the covering model, the minimum number of facilities to serve all demand is 26 (including the existing 11 hospitals). In this scenario, the minimum total travel time could be 9984.5 and the average could be 9.9 min. The total travel time calculated here is the lowest (best) value for the effectiveness objective and the lower bound on the ε-constraint. The effectiveness solution could yield a minimum accessibility score of 0.2524 which is significantly higher than the one in the current situation, but this is also due to the unsatisfactory capacity of the latter. After the median model solution with the effectiveness objective, the model is solved by the lexicographic approach (first solving according to the fairness objective then solving according to the effectiveness objective). This model gives the maximum (best) value for the fairness objective (0.6783) and the maximum (worst) value for the effectiveness objective and the upper bound on the ε-constraint. Finally, depending on the calculated lower and upper bounds on the ε-constraint, the model is solved several times with the fairness objective. The best spatial accessibility score is 0.6783 and the effectiveness objective is 15076.7 min. The accessibility score is significantly higher than the existing situation and the one calculated by the sole effectiveness objective, but the travel time is higher than those cases. The result of the ε-constraint model (the solution with the highest fairness objective) is depicted in Fig. 4.
According to the observed deficiencies in the northern and eastern parts of the region three of the new facilities are selected in the north (locations 74, 100, 110) and three of them are selected in the east of the region (locations 45, 50, 60). According to Fig. 4b, it could be observed that the travel times around those facilities are significantly reduced and the accessibility scores are increased. However, the lower access scores are again observed around the north of Okaloosa and Walton counties. This is due to the lower number of alternatives around those areas. Though all people are provided ICU capacity in the solutions, the number of alternatives is higher for some parts such as the south of Okaloosa County. It has to be mentioned that the results depend on the demand level, expansion capacity, vulnerability considerations, and the number of facilities proposed. In the next section, the results considering these factors are presented.
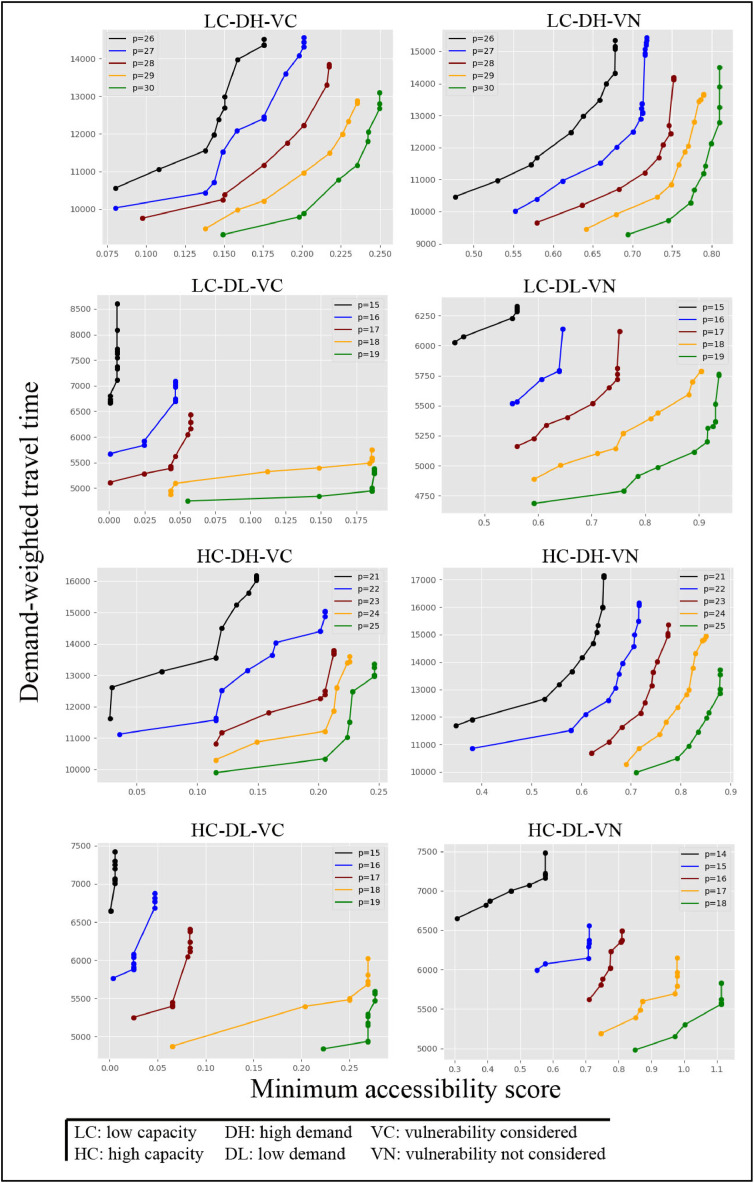
5.3. Locations selection of field hospitals in various scenarios
This section presents the results obtained by applying the proposed methodology for various scenarios and an overall evaluation. There are eight different scenarios based on the capacity level of proposed field hospitals, ICU demand level, and imposition of travel time limits considering vulnerable census block groups.
The capacity levels for the field hospitals are 50 ICU beds in low capacity (LC) scenarios and 75 ICU beds in high capacity (HC) scenarios. The ICU demand estimations with the model (M) are used in the low-demand (DL) scenarios (as the average demand for the period that the data was available) and calibrated (with the highest level observed in the U.S.) estimations in the high-demand (DH) scenarios. For the vulnerability consideration, as mentioned before, the poverty level is used, and for the scenarios in which vulnerability is considered (VC), it is imposed that a facility within a 30-min travel time must serve a vulnerable block group, and the overall travel time limit is 60 min. In the scenarios in which vulnerable block groups are not prioritized (VN), only the overall travel time limit of 60 min is imposed. In addition to the general scenario definitions, for each scenario, the minimum number of required facilities is determined, and four additional sub-scenarios (p, p+1, p+2, p+3, and p+4) are solved to observe robust selections.
The result of each setting is depicted in Fig. 5 . It could be observed that the effectiveness (travel time minimization) and fairness (maximum of minimum accessibility score) have the same payoff structure. A higher fairness objective requires higher travel-time assignments. This behavior of the model is significant and that is why we imposed the constraint set [16] which prohibits selecting a location without any demand assignment. If it is not imposed, to increase the spatial accessibility score the model could select locations with no direct demand assignments, especially for the scenarios with higher-than-minimum facility selections. So, spatial accessibility or fairness with more alternatives would cost higher travel times. One other observation from the results is the jumps in the accessibility score. Since the model tries to maximize the minimum score, for a real-life situation it is not possible to observe smooth transitions. The location alternatives are not distributed homogeneously. A selected location could increase the accessibility score of a specific block group significantly from minimum to above average. Moreover, vulnerability consideration (imposition of the 30-min time limit) exacerbates that structure. The curves under scenarios without vulnerability consideration (VN) are smoother, as the assignment alternatives are higher in those scenarios. As expected, as the number of facilities to select increases the tradeoff curves shift to the right, thus both the fairness and effectiveness objectives improve. On top of these, the fairness objective could be highly insensitive for some regions. That is to say, if a demand point has a very low accessibility score, and there are not any alternative locations in reach of that demand location, the minimum score could not be increased and it sticks to a value even more than enough facilities are selected for the region. To have meaningful results each demand point should be within the reach of several alternative facilities, which is the case in this study.
Fig. 5.
Results of ε-Constraint Solution Approach for Various p Values.
In Table 4 , all the results of the selected scenarios are presented. These are the solutions in which the highest fairness objective is obtained with the best effectiveness objective (lowest travel time). In each scenario, the minimum accessibility score increases, and travel time decreases as p increases.
Table 4.
Selected locations and selection percentages in scenarios.
| Scenario | p | Access score |
Travel time |
Location |
|||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | MAD | Total | Avg | ID | % | ||
| LC-DH-VC | 26 | 0.1755 | 2.1462 | 1.0019 | 0.4366 | 14355.87 | 14.17 | 97 | 100.0 |
| 27 | 0.2013 | 2.4093 | 1.0473 | 0.4685 | 14317.14 | 14.13 | 52 | 100.0 | |
| 28 | 0.2175 | 2.5364 | 1.0925 | 0.5009 | 13786.00 | 13.61 | 68 | 98.1 | |
| 29 | 0.2353 | 2.6491 | 1.1413 | 0.4980 | 12817.95 | 12.65 | 73 | 94.4 | |
| 30 | 0.2500 | 2.7423 | 1.1734 | 0.5191 | 12675.33 | 12.51 | 50 | 87.0 | |
| LC-DH-VN | 26 | 0.6783 | 1.5532 | 1.0327 | 0.1297 | 15076.68 | 14.88 | 97 | 100.0 |
| 27 | 0.7178 | 1.5206 | 1.0790 | 0.1434 | 15347.67 | 15.15 | 60 | 100.0 | |
| 28 | 0.7519 | 1.6322 | 1.1332 | 0.1406 | 14119.92 | 13.94 | 100 | 86.4 | |
| 29 | 0.7896 | 1.6791 | 1.1842 | 0.1571 | 13638.31 | 13.46 | 28 | 74.2 | |
| 30 | 0.8101 | 1.8853 | 1.2225 | 0.1642 | 13899.92 | 13.72 | 12 | 69.7 | |
| LC-DL-VC | 15 | 0.0055 | 2.8815 | 1.0957 | 0.4238 | 7107.31 | 15.83 | 73 | 85.2 |
| 16 | 0.0468 | 2.8976 | 1.2030 | 0.5111 | 6696.96 | 14.92 | 56 | 46.3 | |
| 17 | 0.0577 | 3.1326 | 1.3131 | 0.5272 | 6160.80 | 13.72 | 52 | 46.3 | |
| 18 | 0.1859 | 3.3983 | 1.4044 | 0.5712 | 5545.41 | 12.35 | 63 | 42.6 | |
| 19 | 0.1879 | 3.3983 | 1.5152 | 0.6096 | 5295.84 | 11.79 | 92 | 40.7 | |
| LC-DL-VN | 15 | 0.5604 | 1.7480 | 1.1066 | 0.1543 | 6285.14 | 14.00 | 33 | 48.1 |
| 16 | 0.6465 | 2.0702 | 1.2177 | 0.2073 | 6137.67 | 13.67 | 15 | 46.2 | |
| 17 | 0.7518 | 2.0508 | 1.3326 | 0.2226 | 6118.14 | 13.63 | 60 | 44.2 | |
| 18 | 0.9040 | 2.2566 | 1.4415 | 0.2276 | 5788.08 | 12.89 | 54 | 44.2 | |
| 19 | 0.9379 | 2.5447 | 1.5583 | 0.2350 | 5750.86 | 12.81 | 68 | 34.6 | |
| HC-DH-VC | 21 | 0.1488 | 2.5733 | 0.9943 | 0.4355 | 16027.30 | 15.82 | 68 | 100.0 |
| 22 | 0.2056 | 2.4917 | 1.0715 | 0.4731 | 14875.37 | 14.68 | 52 | 100.0 | |
| 23 | 0.2127 | 2.6365 | 1.1418 | 0.4999 | 13676.44 | 13.50 | 73 | 90.7 | |
| 24 | 0.2258 | 2.6670 | 1.2194 | 0.5669 | 13439.98 | 13.27 | 50 | 81.5 | |
| 25 | 0.2464 | 2.9685 | 1.2856 | 0.6146 | 12960.59 | 12.79 | 74 | 59.3 | |
| HC-DH-VN | 21 | 0.6447 | 1.4828 | 1.0364 | 0.1522 | 17083.84 | 16.86 | 60 | 95.2 |
| 22 | 0.7159 | 1.6007 | 1.1127 | 0.1526 | 16065.20 | 15.86 | 97 | 79.0 | |
| 23 | 0.7749 | 1.6201 | 1.1875 | 0.1595 | 15367.40 | 15.17 | 12 | 53.2 | |
| 24 | 0.8508 | 1.6830 | 1.2602 | 0.1610 | 14933.49 | 14.74 | 54 | 48.4 | |
| 25 | 0.8794 | 1.8074 | 1.3340 | 0.1688 | 13538.81 | 13.37 | 28 | 46.8 | |
| HC-DL-VC | 15 | 0.0055 | 4.1653 | 1.3147 | 0.5609 | 7011.36 | 15.62 | 73 | 80.8 |
| 16 | 0.0468 | 4.1653 | 1.4756 | 0.6941 | 6685.00 | 14.89 | 92 | 63.5 | |
| 17 | 0.0835 | 4.3279 | 1.6372 | 0.7367 | 6116.79 | 13.62 | 63 | 51.9 | |
| 18 | 0.2694 | 4.5025 | 1.7832 | 0.8522 | 5686.85 | 12.67 | 52 | 51.9 | |
| 19 | 0.2768 | 4.8459 | 1.9442 | 0.9530 | 5470.72 | 12.18 | 111 | 40.4 | |
| HC-DL-VN | 14 | 0.5766 | 2.0190 | 1.1623 | 0.2281 | 7162.30 | 15.95 | 54 | 46.5 |
| 15 | 0.7112 | 2.1482 | 1.3297 | 0.2249 | 6336.42 | 14.11 | 19 | 34.9 | |
| 16 | 0.8105 | 2.5093 | 1.4983 | 0.2519 | 6373.90 | 14.20 | 60 | 32.6 | |
| 17 | 0.9787 | 2.6293 | 1.6663 | 0.2440 | 5790.90 | 12.90 | 110 | 30.2 | |
| 18 | 1.1141 | 2.6934 | 1.8337 | 0.2456 | 5563.05 | 12.39 | 63 | 30.2 | |
LC: low capacity HC: high capacity; DH: high demand, DL: low demand.
VC: vulnerability considered, VN: vulnerability not considered.
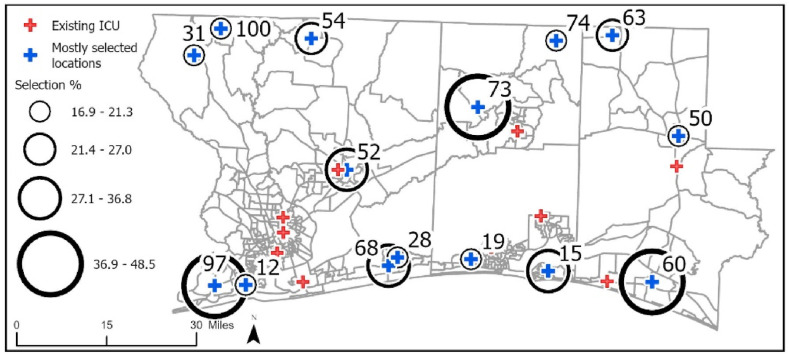
In terms of maximum, average accessibility, and mean absolute deviation (MAD), there are also patterns. The maximum travel time, average travel time and mean absolute deviation tend to increase as the number of alternatives increases (with exceptions). The deviation increase could be captured by the increases in the average. The increase in accessibility scores for some block groups would inevitably be higher due to geographic locations and this would increase with the provision of alternative locations. Table 4 also presents the 5 field hospital locations with the highest percentages of selection for each scenario. For example, for the LC-DH-VC scenario, the top 5 locations are location 97, location 52, location 68, location 73and location 50 with selection rates of 100%, 100%, 98.1%, 94.4%, and 87% respectively. That is to say in around 50 solutions with location 97 and location 52 are always selected, so they are prime alternatives considering this scenario.
Following this selection procedure, in Fig. 6 , the top 15 locations with the highest overall selection rates are depicted. Location 97 on the west Escambia, location 73 on the north Okaloosa, and location 60 on the south Walton are the ones with the highest selection rates. Since the southern coastal area is the most populous part of the region, location 60 and location 97 are mostly selected to respond to the lower accessibility scores due to high demand, and location 73 is to respond to the great deficiency in the northern part of the region.
Fig. 6.
Mostly selected locations.
There are several limitations of this study. One limitation of this study is that the models assumed static ICU demand. Hence, it happens simultaneously when no patient admission, treatment, and release relations were considered. We tried to match a high-demand scenario that overwhelms the healthcare system, which occurred in many parts of the world during the pandemic, and compared it with a lower-demand scenario. Still, consideration of dynamic demand is an exciting future direction of research. Secondly, the mode of transportation was not considered in the model. The modal choice would complicate the problem, and exact algorithms would not be capable of reasonable solutions if people were given multiple travel options. Also, the study area size is a constraining input. Exact solution procedures would not be capable of solving the models for larger study areas. As such, modal choice and application of heuristic algorithms would also be a future direction of this study. Although the methodology could easily be generalized and applied to other geographies, the results in this paper are specific to the selected area. Moreover, it should be mentioned that the floating catchment area optimization problems are highly sensitive to the spatial distribution of the demand and service locations. With the fairness objective employed in this study. Another limitation of the study is that staff and equipment were assumed to be available. Also, the focus of this study was to determine the locations that would increase accessibility for victims; however, staff availability and supply availability should also be considered for a more realistic case study.
6. Conclusions
In this paper, we addressed the location selection problem for field hospitals while evaluating the fairness in terms of spatial accessibility of people to ICU beds and effectiveness in terms of travel time to the facilities. For this purpose, first, we estimated the ICU demand of four counties in the Florida Panhandle at the census block groups level. For this estimation, the zip code level COVID-19 positive cases are used, and a tabu search-based optimization procedure is utilized to construct the best linear regression model. This was followed by the evaluation of the existing situation with a focus on the spatial accessibility scores calculated by the E2SFCA method and travel distances calculated by the p-median model. Then, our multi-objective model consisting of fairness and effectiveness objectives is solved by the ε-constraint approach for various scenarios. The results for each scenario and the overall results are presented and the tradeoff between the two objectives is discussed. The solution procedure could be used in location selection analyses and guide policymakers in regional-level decision-making to provide fair and effective services.
Author contributions
The authors confirm their contribution to the paper as follows: study conception and design: O.Alisan, M.B.Ulak, E.E.Ozguven., and M.W.Horner, data collection: O.Alisan, M.B.Ulak, E.E.Ozguven., and M.W.Horner, analysis and interpretation of results: O.Alisan, M.B.Ulak, E.E.Ozguven., and M.W.Horner, draft manuscript preparation: analysis and interpretation of results: O.Alisan, M.B.Ulak, E.E.Ozguven., and M.W.Horner. All authors reviewed the results and approved the final version of the manuscript.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
APPENDIX.
Table A1.
The Variables Used to Model Covid-19 Positive Cases
| Variable | Definition | Min | Mean | Max | Std |
|---|---|---|---|---|---|
| ACRES | Acreage | 2070.35 | 78960.71 | 483886.71 | 88124.02 |
| TOTALPOP | Total population | 555.00 | 14637.45 | 53703.00 | 12902.19 |
| P_MALE | Percentage of males | 42.94 | 51.74 | 74.03 | 5.87 |
| P_WHITE | Percentage of white people | 16.15 | 74.26 | 100.00 | 17.90 |
| P_AGE_5_17 | Percentage of population btw ages 5-17 | 4.77 | 14.56 | 24.07 | 3.67 |
| P_AGE_18_21 | Percentage of population btw ages 18-21 | 0.00 | 5.81 | 48.69 | 6.52 |
| P_AGE_65_UP | Percentage of population age 65+ | 0.26 | 17.61 | 36.38 | 5.91 |
| P_AGE_85_UP | Percentage of population age 85+ | 0.00 | 1.76 | 4.43 | 0.99 |
| P_BELOW_POV | Percentage of people below poverty level | 2.52 | 14.46 | 48.59 | 8.17 |
| P_ED_COLLEGE | Percentage of people with at least college degree | 0.00 | 16.19 | 43.69 | 9.51 |
| TRAN_PUB | Number of people using public transport to work | 0.00 | 50.06 | 1141.00 | 135.17 |
| P_OWNER | Percentage of owner occupied housing units | 0.00 | 68.72 | 96.91 | 18.22 |
| P_VEHICLE_0 | Percentage of occupied housing units with no car | 0.00 | 5.68 | 18.67 | 3.91 |
| AVG_VEH | Average number of vehicles per occupied housing unit | 1.25 | 1.82 | 2.20 | 0.19 |
| P_C_NO_COMP | Percentage of households that have no computer | 0.00 | 12.36 | 40.53 | 8.64 |
| Covid_case | Total number of positive COVID-19 cases | 47.00 | 1543.54 | 7029.00 | 1383.30 |
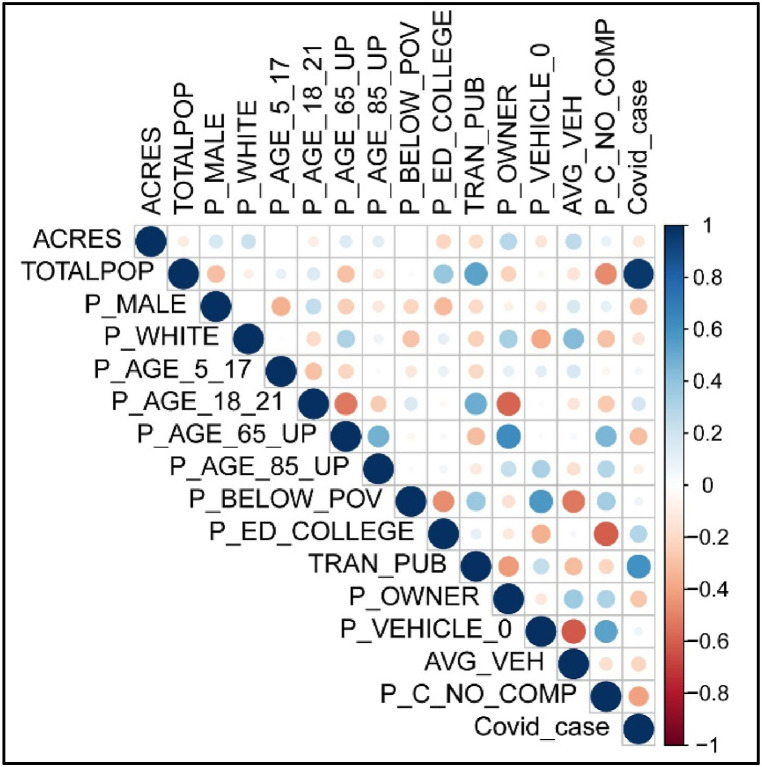
Fig. A1.
Correlation Plot of the Variables
Fig. A2.
Tabu Search Procedure
Fig. A3.
Tabu Search Results
Data availability
Data will be made available on request.
References
- 1.WHO Coronavirus (COVID-19) Dashboard WHO Coronavirus (COVID-19) Dashboard With Vaccination Data [Internet]. [cited 2022 Oct 19]. Available from: https://covid19.who.int/.
- 2.Puerta J.L., Torrego-Ellacuría M., Del Rey-Mejías Á., Bienzobas López C. Capacity and organisation of Madrid's community hospitals during first wave of COVID-19 pandemic. J Healthc Qual Res [Internet] 2022 Sep;37(5):275–282. doi: 10.1016/j.jhqr.2022.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Blanchard-Rohner G., Caprettini B., Rohner D., Voth H.J. Impact of COVID-19 and intensive care unit capacity on vaccination support: evidence from a two-leg representative survey in the United Kingdom. J Virus Erad. 2021;7(2) doi: 10.1016/j.jve.2021.100044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lack of ICU beds tied to thousands of excess COVID-19 deaths YaleNews [Internet]. [cited 2022 Sep 21]. Available from: https://news.yale.edu/2021/02/01/lack-icu-beds-tied-thousands-excess-covid-19-deaths.
- 5.Overwhelmed Hospitals Are Shipping COVID-19 Patients To Far-Off Cities NPR [Internet]. [cited 2022 Jul 15]. Available from: https://www.npr.org/2021/08/19/1029378744/hospital-beds-shortage-covid-coronavirus-states.
- 6.Palamim C.V.C., Marson F.A.L. Covid-19 – the availability of icu beds in Brazil during the onset of pandemic. Ann Glob Health. 2020;86(1):1–15. doi: 10.5334/aogh.3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Paterlini M. Covid-19: Sweden considers tougher restrictions as ICU beds near capacity. BMJ [Internet] 2020 doi: 10.1136/bmj.m4833. https://www.bmj.com/lookup/doi/10.1136/bmj.m4833 Dec 14;371:m4833. [DOI] [PubMed] [Google Scholar]
- 8.Tsai T.C., Jacobson B.H., Orav E.J., Jha A.K. Association of community-level social vulnerability with US acute care hospital intensive care unit capacity during COVID-19. Health Care Internet. 2022;10(1) doi: 10.1016/j.hjdsi.2021.100611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bauer J., Brüggmann D., Klingelhöfer D., Maier W., Schwettmann L., Weiss D.J., et al. Access to intensive care in 14 European countries: a spatial analysis of intensive care need and capacity in the light of COVID-19. Intensive Care Med [Internet] 2020;46(11):2026–2034. doi: 10.1007/s00134-020-06229-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Davoodi N.M., Healy M., Goldberg E.M. Rural America's hospitals are not prepared to protect older adults from a surge in COVID-19 cases. Gerontol Geriatr Med. 2020;6 doi: 10.1177/2333721420936168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Aldrich N., Benson W.F. Disaster preparedness and the chronic disease needs of vulnerable older adults. Prev. Chronic Dis. 2008;5(1) [PMC free article] [PubMed] [Google Scholar]
- 12.Pijls B.G., Jolani S., Atherley A., Derckx R.T., Dijkstra J.I.R., Franssen G.H.L., et al. Demographic risk factors for COVID-19 infection, severity, ICU admission and death: a meta-analysis of 59 studies. BMJ Open. 2021;11(1):1–10. doi: 10.1136/bmjopen-2020-044640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pereira R.H.M., Braga C.K.V., Servo L.M., Serra B., Amaral P., Gouveia N., et al. Geographic access to COVID-19 healthcare in Brazil using a balanced float catchment area approach. Soc. Sci. Med. 2021;273(February) doi: 10.1016/j.socscimed.2021.113773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim K., Ghorbanzadeh M., Horner M.W., Ozguven E.E. Identifying areas of potential critical healthcare shortages: a case study of spatial accessibility to ICU beds during the COVID-19 pandemic in Florida. Transport Pol. 2021;110(January):478–486. doi: 10.1016/j.tranpol.2021.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cromley G., Lin J. Examining the interplay between racial segregation patterns and access to hospital care. Environ. Plan. B Urban Anal. City Sci. 2022;0(0):1–13. [Google Scholar]
- 16.Kelen G.D., David Marcozzi, Marx J.J., Kachalia A. 2023. Criteria for Declaring Crisis Standards of Care: A Single, Uniform Model. New England Journal of Medicine [Internet]https://catalyst.nejm.org/doi/pdf/10.1056/CAT.22.0269 [cited 2023 Feb 9]; [Google Scholar]
- 17.Oakley C., Pascoe C., Balthazor D., Bennett D., Gautam N., Isaac J., et al. Assembly Line ICU: what the Long Shops taught us about managing surge capacity for COVID-19. BMJ Open Qual. 2020;9(4) doi: 10.1136/bmjoq-2020-001117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.O'Donoghue S.C., Donovan B., Anderson J., Foley J., Gillis J., Maloof K., et al. Doubling intensive care unit capacity by surging onto medical-surgical units during the COVID-19 pandemic. Dimens. Crit. Care Nurs. 2021;40(6):345–354. doi: 10.1097/DCC.0000000000000496. [DOI] [PubMed] [Google Scholar]
- 19.Winkelmann J., Webb E., Williams G.A., Hernández-Quevedo C., Maier C.B., Panteli D. European countries' responses in ensuring sufficient physical infrastructure and workforce capacity during the first COVID-19 wave. Health Policy (New York) [Internet] 2022;126(5):362–372. doi: 10.1016/j.healthpol.2021.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Phua J., Weng L., Ling L., Egi M., Lim C.M., Divatia J.V., et al. Intensive care management of coronavirus disease 2019 (COVID-19): challenges and recommendations. Lancet Respir Med [Internet] 2020;8(5):506–517. doi: 10.1016/S2213-2600(20)30161-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Candel F.J., Canora J., Zapatero A., Barba R., González Del Castillo J., García-Casasola G., et al. Temporary hospitals in times of the COVID pandemic. An example and a practical view. Rev. Española Quimioter. 2021;34(4):280–288. doi: 10.37201/req/041.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Clifton G.T., Pati R., Krammer F., Laing E.D., Broder C.C., Mendu D.R., et al. MMWR Morb Mortal Wkly Rep [Internet]; 2021. SARS-CoV-2 Infection Risk Among Active Duty Military Members Deployed to a Field Hospital — New York City, April 2020.https://www.cdc.gov/mmwr/volumes/70/wr/mm7009a3.htm Mar 5 [cited 2022 Sep 21];70(9):308–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Proudfoot A.G., O'Brien B., Schilling R., Gould D.W., McGlennan A., Wragg A., et al. Rapid establishment of a COVID-19 critical care unit in a convention centre: the Nightingale Hospital London experience. Intensive Care Med [Internet] 2021;47(3):349–351. doi: 10.1007/s00134-020-06334-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Blackwell T., Bosse M. Use of an innovative design mobile hospital in the medical response to hurricane katrina. Ann. Emerg. Med. 2007;49(5):580–588. doi: 10.1016/j.annemergmed.2006.06.037. [DOI] [PubMed] [Google Scholar]
- 25.Chen Z., He S., Li F., Yin J., Chen X. Mobile field hospitals, an effective way of dealing with COVID-19 in China: sharing our experience. Biosci Trends. 2020;14(3):212–214. doi: 10.5582/bst.2020.01110. [DOI] [PubMed] [Google Scholar]
- 26.Narayan S., Setlur R., Jahan N., Chatterjee K., Kanitkar M. Planning a modular intensive care unit for patients of the COVID-19 pandemic. Journal of Marine Medical Society. 2020;0(0):0. [Google Scholar]
- 27.Salman F.S., Gül S. Deployment of field hospitals in mass casualty incidents. Comput. Ind. Eng. 2014;74(1):37–51. [Google Scholar]
- 28.Aydin N. A stochastic mathematical model to locate field hospitals under disruption uncertainty for large-scale disaster preparedness. An Int. J. Optim. Control Theor. Appl. (IJOCTA) 2016;6(2):85–102. [Google Scholar]
- 29.Fereiduni M., Shahanaghi K. A robust optimization model for distribution and evacuation in the disaster response phase. Journal of Industrial Engineering International. 2017;13(1):117–141. [Google Scholar]
- 30.Oksuz M.K., Satoglu S.I. A two-stage stochastic model for location planning of temporary medical centers for disaster response. International Journal of Disaster Risk Reduction [Internet] 2020;44 doi: 10.1016/j.ijdrr.2019.101426. [DOI] [Google Scholar]
- 31.Barutcu I., Ic Y.T. Selecting the field hospital location for earthquakes: an application for Ankara Province in Turkey. International Journal of Emergency Services. 2022;11(1):168–187. [Google Scholar]
- 32.Zolfani S.H., Yazdani M., Torkayesh A.E., Derakhti A. Application of a gray-based decision support framework for location selection of a temporary hospital during COVID-19 pandemic. Symmetry (Basel) 2020;12(6) [Google Scholar]
- 33.Akpınar M.E., Ilgın M.A. Location selection for a Covid-19 field hospital using fuzzy choquet integral method. Gümüşhane Üniversitesi Sosyal Bilimler Enstitüsü Elektronik Dergisi [Internet] 2021;12(3):1095–1109. https://dergipark.org.tr/en/download/article-file/1782117 [Google Scholar]
- 34.Aydin N., Seker S. Determining the location of isolation hospitals for COVID-19 via Delphi-based MCDM method. Int. J. Intell. Syst. 2021;(January:3011–3034. doi: 10.1002/int.22410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang C.N., Chou C.C., Hsu H.P., Nguyen V.T., Nguyen V.T. Optimization model for selecting temporary hospital locations during COVID-19 pandemic. Comput. Mater. Continua (CMC) 2021;70(1):397–412. [Google Scholar]
- 36.Kheybari S., Ishizaka A., Salamirad A. A new hybrid risk-averse best-worst method and portfolio optimization to select temporary hospital locations for Covid-19 patients. Journal of the Operational Research Society [Internet] 2021;0(0):1–18. doi: 10.1080/01605682.2021.1993758. [DOI] [Google Scholar]
- 37.Hassan S.A., Alnowibet K., Agrawal P., Mohamed A.W. Optimum location of field hospitals for COVID-19: a nonlinear binary metaheuristic algorithm. Comput. Mater. Continua (CMC) 2021;68(1):1183–1202. [Google Scholar]
- 38.Wang F. Modeling commuting patterns in Chicago in a GIS environment: a job accessibility perspective. The Professional Geographer [Internet] 2000;52(1):120. https://www.tandfonline.com/doi/full/10.1111/0033-0124.00210 33. [Google Scholar]
- 39.Guo Y., Chan C.H., Yip P.S.F. Spatial variation in accessibility of libraries in Hong Kong. Libr. Inf. Sci. Res. 2017 Oct 1;39(4):319–329. [Google Scholar]
- 40.Xia Z., Li H., Chen Y., Yu W. Integrating spatial and non-spatial dimensions to measure urban fire service access. ISPRS Int. J. Geo-Inf. 2019 Mar 1;8(3) [Google Scholar]
- 41.Tan R., Wang R., Wang Y., Yi D., Chen Y., Cai W., et al. The Park city perspective study: revealing the park accessibility influenced by experiences of visitors under different travel modes. Front. Environ. Sci. 2022 Sep 14:10. [Google Scholar]
- 42.Han Z., Cui C., Kong Y., Li Q., Chen Y., Chen X. Improving educational equity by maximizing service coverage in rural Changyuan, China: an evaluation-optimization-validation framework based on spatial accessibility to schools. Appl. Geogr. 2023 Mar 1:152. [Google Scholar]
- 43.Luo W., Qi Y. An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health Place. 2009;15(4):1100–1107. doi: 10.1016/j.healthplace.2009.06.002. [DOI] [PubMed] [Google Scholar]
- 44.Li M., Wang F., Kwan M.P., Chen J., Wang J. Equalizing the spatial accessibility of emergency medical services in Shanghai: a trade-off perspective. Comput. Environ. Urban Syst. 2022 Mar 1:92. [Google Scholar]
- 45.Bauer J., Groneberg D.A. Measuring spatial accessibility of health care providers-introduction of a variable distance decay function within the floating catchment area (FCA) method. PLoS One. 2016 Jul 1;11(7) doi: 10.1371/journal.pone.0159148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Li C., Wang J. A hierarchical two-step floating catchment area analysis for high-tier hospital accessibility in an urban agglomeration region. J. Transport Geogr. 2022 Jun 1:102. [Google Scholar]
- 47.Park J., Michels A., Lyu F., Han S.Y., Wang S. vol. 154. Applied Geography [Internet]; USA: 2023 May. https://linkinghub.elsevier.com/retrieve/pii/S0143622823000607 (Daily Changes in Spatial Accessibility to ICU Beds and Their Relationship with the Case-Fatality Ratio of COVID-19 in the State of Texas). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ghorbanzadeh M., Kim K., Erman Ozguven E., Horner M.W. vol. 24. Travel Behav Soc; 2021 Jul 1. pp. 95–101. (Spatial Accessibility Assessment of COVID-19 Patients to Healthcare Facilities: A Case Study of Florida). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pecoraro F., Luzi D., Clemente F. Public Health and Informatics: Proceedings of MIE 2021. IOS Press; 2021. Spatial inequity in access to intensive care unit beds at regional level in Italy; pp. 809–813. [DOI] [PubMed] [Google Scholar]
- 50.Sritart H., Taertulakarn S., Kanbara S., Miyazaki H. ACM International Conference Proceeding Series. Association for Computing Machinery; 2022. Spatial equity and healthcare access in the COVID-19 pandemic; pp. 262–266. [Google Scholar]
- 51.Park J., Goldberg D.W. An examination of the stochastic distribution of spatial accessibility to intensive care unit beds during the COVID-19 pandemic: a case study of the greater houston area of Texas. Geogr. Anal. 2022 doi: 10.1111/gean.12340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Al-Omari A., Shatnawi N., Al-Mashaqbeh A. Use of an E2SFCA method to assess healthcare resources in Jordan during COVID-19 pandemic. Egyptian Journal of Remote Sensing and Space Science. 2022 Dec 1;25(4):1057–1068. [Google Scholar]
- 53.Shen X. Accessibility calculation and equality evaluation of medical facilities for COVID-19 pandemic treatment: a case study of the Wuhan metropolitan development zone. PLoS One. 2022 Aug 1;(8 August):17. doi: 10.1371/journal.pone.0272458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhong G., Lu Y., Chen W., Zhai G. Multi-objective optimization approach of shelter location with maximum equity: an empirical study in Xin Jiekou district of Nanjing, China. Geomatics, Nat. Hazards Risk. 2023;14(1) [Google Scholar]
- 55.Zhang H., Zhang K., Chen Y., Ma L. Multi-objective two-level medical facility location problem and tabu search algorithm. Inf Sci (N Y). 2022 Aug 1;608:734–756. [Google Scholar]
- 56.Li X., Wang F., Yi H. A two-step approach to planning new facilities towards equal accessibility. Environ. Plan. B Urban Anal. City Sci. 2017 Nov 1;44(6):994–1011. [Google Scholar]
- 57.Chu H.J., Lin B.C., Yu M.R., Chan T.C. Minimizing spatial variability of healthcare spatial accessibility—the case of a dengue fever outbreak. Int. J. Environ. Res. Publ. Health. 2016 Dec 13;13(12) doi: 10.3390/ijerph13121235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Tseng M.H., Wu H.C. Accessibility assessment of community care resources using maximum-equity optimization of supply capacity allocation. Int. J. Environ. Res. Publ. Health. 2021 Feb 1;18(3):1–19. doi: 10.3390/ijerph18031153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bertsimas D., Farias V.F., Trichakis N. The price of fairness. Oper. Res. 2011 Jan;59(1):17–31. [Google Scholar]
- 60.https://www.nytimes.com/interactive/2021/us/covid-cases.html Covid in the U.S.: Latest Maps, Case and Death Counts - The New York Times [Internet]. [cited 2022 Oct 19].
- 61.https://www.census.gov/library/visualizations/interactive/population-65-and-older-2019.html The Population 65 Years and Older: 2019 [Internet]. [cited 2022 Sep 16].
- 62.University of South Florida Libraries . 2020. https://covid19-usflibrary.hub.arcgis.com/ (Florida COVID-19 Hub). [cited 2022 May 23] [Google Scholar]
- 63.https://www.census.gov/data/developers/data-sets/acs-5year.html American Community Survey 5-Year Data (2009-2020) [Internet]. [cited 2022 Jul 24].
- 64.https://ephtracking.cdc.gov/DataExplorer/?c=13&i=115&m=-1 National Environmental Public Health Tracking Network Data Explorer [Internet]. [cited 2023 Apr 9].
- 65.https://data.commercialappeal.com/covid-19-hospital-capacity/florida/12/ Florida COVID-19 (Coronavirus) Hospital Capacity: Florida COVID-19 Hospital Capacity | commercialappeal.com [Internet]. [cited 2022 Jul 24].
- 66.https://fgdl.org/ords/prod/r/fgdl-explorer/v-archive-fgdl-q FGDL Archive Data Catalog [Internet]. [cited 2023 Apr 9].
- 67.Mathais Q., Swiech A., De Rocquigny G., Thill C., Aries P. vol. 40. Elsevier Masson s.r.l.; 2021. Deployment of a mobile military ICU embedded in a civilian hospital during the second COVID-19 outbreak in Mayotte, France. (Anaesthesia Critical Care and Pain Medicine). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Danguy des Déserts M., Mathais Q., Luft A., Escarment J., Pasquier P. Anaesthesia Critical Care and Pain Medicine. vol. 39. Elsevier Masson SAS; 2020. Conception and deployment of a 30-bed field military intensive care hospital in Eastern France during the 2020 COVID-19 pandemic; pp. 361–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Díaz-Garzón J., Oliver P., Crespo G., Duque M., Fernandez-Calle P., Gómez M., et al. vol. 30. Biochemia Medica. Biochemia Medica, Editorial Office; 2020. pp. 1–3. (Experience on How to Implement a Preanalytical and POCT Unit in Madrid's IFEMA Field Hospital during This Unprecedented COVID-19 Emergency). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Bushell V., Thomas L., Combes J. Inside the O2: the NHS Nightingale hospital London education center. J. Interprof. Care. 2020 Sep 1;34(5):698–701. doi: 10.1080/13561820.2020.1823949. [DOI] [PubMed] [Google Scholar]
- 71.O'Connell N.H., Humphreys H. Intensive care unit design and environmental factors in the acquisition of infection. J. Hosp. Infect. 2000;45:255–262. doi: 10.1053/jhin.2000.0768. W.B. Saunders Ltd. [DOI] [PubMed] [Google Scholar]
- 72.McCabe R., Schmit N., Christen P., D'Aeth J.C., Løchen A., Rizmie D., et al. Adapting hospital capacity to meet changing demands during the COVID-19 pandemic. BMC Med. 2020 Dec 1;18(1) doi: 10.1186/s12916-020-01781-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.ArcGIS E.S.R.I. Vol. 3.1. Environmental Systems Research Institute; Redlands, CA: 2023. (Pro: Release). [Google Scholar]
- 74.Martin C., McDonald S., Bale S., Luteijn M., Sarkar R. Construction of a demand and capacity model for intensive care and hospital ward beds, and mortality from COVID-19. BMC Med Inform Decis Mak [Internet] 2021;21(1):138. doi: 10.1186/s12911-021-01504-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ritter M., Ott D.V.M., Paul F., Haynes J.D., Ritter K. COVID-19: a simple statistical model for predicting intensive care unit load in exponential phases of the disease. Sci Rep [Internet] 2021;11(1):1–12. doi: 10.1038/s41598-021-83853-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Lee S.H., Park S.Y., Seon J.Y., Jeon W.H., Nam S Il, Park J.H., et al. ume 13. Risk Manag Healthc Policy [Internet]; 2020 Nov. pp. 2571–2581.https://www.dovepress.com/intensive-care-unit-capacity-and-its-associated-risk-factors-during-th-peer-reviewed-article-RMHP (Intensive Care Unit Capacity and its Associated Risk Factors during the COVID-19 Surge in the Republic of Korea: Analysis Using Nationwide Health Claims Data). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Glover F. Future paths for integer programming and Links to artificial intelligence. Comput. Oper. Res. 1986;13(5):533–549. [Google Scholar]
- 78.Drezner Z., Marcoulides G.A., Salhi S. Tabu search model selection in multiple regression analysis. Commun. Stat. Part B: Simulation and Computation. 1999;28(2):349–367. [Google Scholar]
- 79.Fouskakis D., Draper D. Stochastic optimization: a review. Int. Stat. Rev. 2002;70(3):315–349. [Google Scholar]
- 80.Hajjar L.A., Costa Ibs da S., Rizk S.I., Biselli B., Gomes B.R., Bittar C.S., et al. Intensive care management of patients with COVID-19: a practical approach. Ann Intensive Care [Internet] 2021;11(1) doi: 10.1186/s13613-021-00820-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Anesi GL. COVID-19: Epidemiology, clinical features, and prognosis of the critically ill adult - UpToDate [Internet]. [cited 2022 Oct 19] Available from: https://www.uptodate.com/contents/covid-19-epidemiology-clinical-features-and-prognosis-of-the-critically-ill-adult.
- 82.Couture A., Danielle Iuliano A., Chang H.H., Patel N.N., Gilmer M., Steele M., et al. Estimating COVID-19 hospitalizations in the United States with surveillance data using a bayesian hierarchical model: modeling study. JMIR Public Health Surveill. 2022;8(6):1–12. doi: 10.2196/34296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.https://ourworldindata.org/explorers/coronavirus-data-explorer?zoomToSelection=true&facet=none&pickerSort=asc&pickerMetric=location&hideControls=true&Interval=Cumulative&Relative+to+Population=true&Color+by+test+positivity=false&country=∼USA&Metric=Confir COVID-19 Data Explorer - Our World in Data [Internet]. [cited 2022 Oct 19].
- 84.https://ourworldindata.org/grapher/covid-icu-patients-per-million?country=∼USA Number of COVID-19 patients in ICU per million [Internet]. [cited 2022 Jul 25].
- 85.Nguyen N.T., Chinn J., Nahmias J., Yuen S., Kirby K.A., Hohmann S., et al. Outcomes and mortality among adults hospitalized with COVID-19 at US medical centers. JAMA Netw. Open. 2021;4(3):20–23. doi: 10.1001/jamanetworkopen.2021.0417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Dongelmans D.A., Termorshuizen F., Brinkman S., Bakhshi-Raiez F., Arbous M.S., de Lange D.W., et al. Characteristics and outcome of COVID-19 patients admitted to the ICU: a nationwide cohort study on the comparison between the first and the consecutive upsurges of the second wave of the COVID-19 pandemic in The Netherlands. Ann. Intensive Care. 2022;12(1) doi: 10.1186/s13613-021-00978-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Vekaria B., Overton C., Wiśniowski A., Ahmad S., Aparicio-Castro A., Curran-Sebastian J., et al. Hospital length of stay for COVID-19 patients: data-driven methods for forward planning. BMC Infect. Dis. 2021;21(1):1–15. doi: 10.1186/s12879-021-06371-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Ahmadi-Javid A., Seyedi P., Syam S.S. A survey of healthcare facility location. Comput Oper Res [Internet] 2017;79:223–263. doi: 10.1016/j.cor.2016.05.018. [DOI] [Google Scholar]
- 89.Marín A., Pelegrín M. Location Science. Springer International Publishing; Cham: 2019. p-Median Problems; pp. 25–50. [Google Scholar]
- 90.Celik Turkoglu D., Erol Genevois M. A comparative survey of service facility location problems. Ann Oper Res [Internet. 2020 Sep 21;292(1):399–468. http://link.springer.com/10.1007/s10479-019-03385-x [Google Scholar]
- 91.Calik H., Labbé M., Yaman H. Location Science. Springer International Publishing; Cham: 2015. p-Center Problems; pp. 79–92. [Google Scholar]
- 92.García S., Marín A. Location Science. Springer International Publishing; Cham: 2019. Covering location problems; pp. 99–119. [Google Scholar]
- 93.Berry J., Hart W.E., Phillips C.A., Uber J.G., Watson J.P. Sensor placement in municipal water networks with temporal integer programming models. J. Water Resour. Plann. Manag. 2006 Jun;132(4) [Google Scholar]
- 94.Honey R., Rushton G., Lolonis P., Dalziel B.T., Armstrong M.P., De S., et al. Stages in the adoption of a spatial decision support system for reorganizing service delivery regions. Environ Plann C Gov Policy [Internet. 1991 Mar 30;9(1):51–63. http://journals.sagepub.com/doi/10.1068/c090051 [Google Scholar]
- 95.Ndiaye F., Ndiaye B.M., Ly I. Application of the p-median problem in school allocation. Am. J. Oper. Res. 2012;2(2):253–259. [Google Scholar]
- 96.Willer D.J. 1990. A SPATIAL DECISION SUPPORT SYSTEM for BANK LOCATION: A CASE STUDY [Internet]. New York.https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.471.878&rep=rep1&type=pdf [Google Scholar]
- 97.Serra D., Marianov V. The p-median problem in a changing network: the case of Barcelona. Location Science [Internet] 1998 May;6(1–4):383. https://linkinghub.elsevier.com/retrieve/pii/S0966834998000497 94. [Google Scholar]
- 98.Dzator M., Dzator J. An effective heuristic for the P-median problem with application to ambulance location. Opsearch. 2013 Mar;50(1):60–74. [Google Scholar]
- 99.Bayram V., Tansel B.T., Yaman H. Compromising system and user interests in shelter location and evacuation planning. Transp. Res. Part B Methodol. 2015 Feb 1;72:146–163. [Google Scholar]
- 100.Na Ayudhya W.S. IEEE International Conference on Industrial Engineering and Engineering Management. IEEE Computer Society; 2020. Flood shelters location using p-median model; pp. 11–15. [Google Scholar]
- 101.Horner M.W., Ozguven E.E., Marcelin J.M., Kocatepe A. Special needs hurricane shelters and the ageing population: development of a methodology and a case study application. Disasters. 2018 Jan 1;42(1):169–186. doi: 10.1111/disa.12233. [DOI] [PubMed] [Google Scholar]
- 102.Ilabaca A., Paredes-Belmar G., Alvarez P.P. Optimization of humanitarian aid distribution in case of an earthquake and tsunami in the city of iquique, Chile. Sustainability. 2022 Jan 1;14(2) [Google Scholar]
- 103.Yaghini M., Momeni M., Sarmadi M., Ahadi H.R. An efficient heuristic algorithm for the capacitated p-median problem. 4OR [Internet] 2013 Sep 16;11(3):229–248. http://link.springer.com/10.1007/s10288-012-0223-y [Google Scholar]
- 104.Avella P., Sassano A., Vasil’ev I. Computational study of large-scale p-Median problems. Math. Program. 2007 Jan;109(1):89–114. [Google Scholar]
- 105.García S., Labbé M., Marín A. Solving large p-median problems with a radius formulation. Inf. J. Comput. 2011;23(4):546–556. [Google Scholar]
- 106.Church R.L. vol. 122. Annals of Operations Research; 2003. (COBRA: A New Formulation of the Classic P-Median Location Problem). [Google Scholar]
- 107.Galvão R.D. A dual-bounded algorithm for the p-median problem. Oper Res [Internet] 1980 Oct;28(5):1112–1121. http://pubsonline.informs.org/doi/abs/10.1287/opre.28.5.1112 [Google Scholar]
- 108.Ceselli A. Two exact algorithms for the capacitated p-median problem. 4OR. 2003;1(4):319–340. [Google Scholar]
- 109.Chaves A.A., Assis Correa F., Lorena L.A.N. Advances in Soft Computing [Internet] 2007. Clustering search heuristic for the capacitated p-median problem; p. 136.http://link.springer.com/10.1007/978-3-540-74972-1_19 43. [Google Scholar]
- 110.Fleszar K., Hindi K.S. An effective VNS for the capacitated p-median problem. Eur. J. Oper. Res. 2008 Dec 16;191(3):612–622. [Google Scholar]
- 111.Romero Montoya M., González Velázquez R., Estrada Analco M., Luis J., Flores M., Beatriz M., et al. Solution search for the capacitated P-median problem using tabu search. International Journal of Combinatorial Optimization Problems and Informatics [Internet] 2019;10(2):17–25. www.editada.org [Google Scholar]
- 112.Romero Montoya M., Beatríz M., Loranca B., González Velázquez R., Luis J., Flores M., et al. A solution proposal for the capacitated P-median problem with tabu search. Research in Computing Science. 2016;121:59–67. [Google Scholar]
- 113.Shariff S.S.R., Moin N.H., Omar M. BEIAC 2013 - 2013 IEEE Business Engineering and Industrial Applications Colloquium. 2013. An alternative heuristic for capacitated p-median problem (CPMP) pp. 916–921. [Google Scholar]
- 114.Santos Correa E., Teresinha M., Steiner A., Freitas A.A., Carnieri C. vol. 35. Kluwer Academic Publishers; 2004. A Genetic Algorithm for Solving a Capacitated P-Median Problem. (Numerical Algorithms). [Google Scholar]
- 115.Ghoseiri K., Ghannadpour S.F. 2007 IEEE International Conference on Industrial Engineering and Engineering Management [Internet] IEEE; 2007. Solving capacitated p-median problem using genetic algorithm; p. 885.http://ieeexplore.ieee.org/document/4419318/ 9. [Google Scholar]
- 116.Reese J. Solution methods for the p-median problem: an annotated bibliography. Networks [Internet] 2006 Oct;48(3):125–142. https://onlinelibrary.wiley.com/doi/10.1002/net.20128 [Google Scholar]
- 117.Mladenović N., Brimberg J., Hansen P., Moreno-Pérez J.A. The p-median problem: a survey of metaheuristic approaches. Eur. J. Oper. Res. 2007 Jun 16;179(3):927–939. [Google Scholar]
- 118.Jia T., Tao H., Qin K., Wang Y., Liu C., Gao Q. Selecting the optimal healthcare centers with a modified P-median model: a visual analytic perspective. Int. J. Health Geogr. 2014;13(1) doi: 10.1186/1476-072X-13-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Jia H., Ordóñez F., Dessouky M. A modeling framework for facility location of medical services for large-scale emergencies. IIE Trans. 2007 Jan;39(1):41–55. [Google Scholar]
- 120.Ghani N.A., Ruslim N.M. Proceedings of the 2nd IMT-GT Regional Conference on Mathematics, Statistics and Applications [Internet] 2006. An application of the p-median problem with uncertainty in demand in emergency medical services.https://www.researchgate.net/publication/228847851 [Google Scholar]
- 121.Liu J., Li Y., Li Y., Chen Z., Lian X., Zhang Y. Engineering, Construction and Architectural Management [Internet]; 2022. Location Optimization of Emergency Medical Facilities for Public Health Emergencies in Megacities Based on Genetic Algorithm.https://www.emerald.com/insight/content/doi/10.1108/ECAM-07-2021-0637/full/html [Google Scholar]
- 122.Jô Baray, Cliquet G. Optimizing locations through a maximum covering/p-median hierarchical model: maternity hospitals in France. J. Bus. Res. 2013 Jan;66(1):127–132. [Google Scholar]
- 123.Bruni M.E., Conforti D., Sicilia N., Trotta S. A new organ transplantation location-allocation policy: a case study of Italy. Health Care Manag. Sci. 2006 May;9(2):125–142. doi: 10.1007/s10729-006-7661-z. [DOI] [PubMed] [Google Scholar]
- 124.Beliën J., De Boeck L., Colpaert J., Devesse S., Van Den Bossche F. Decision Support Systems. 2013. Optimizing the facility location design of organ transplant centers; pp. 1568–1579. [Google Scholar]
- 125.Hillsman E.L. The University of Iowa; 1979. A System for Location–Allocation Analysis [Internet]https://www.proquest.com/docview/302905993?pq-origsite=gscholar&fromopenview=true [Google Scholar]
- 126.Daskin M.S. In: Network and Discrete Location: Models, Algorithms, and Applications. second ed. [Internet]. Second. Daskin M.S., editor. John Wiley & Sons, Inc.; Hoboken, New Jersey: 2013. [Google Scholar]
- 127.Farhan B., Murray A.T. Distance decay and coverage in facility location planning. Ann. Reg. Sci. 2006;40(2):279–295. [Google Scholar]
- 128.Murray A.T., Wu X. Accessibility tradeoffs in public transit planning. J. Geogr. Syst. 2003;5(1):93–107. [Google Scholar]
- 129.Jörg R., Haldimann L. MHV3SFCA: a new measure to capture the spatial accessibility of health care systems. Health Place. 2023 Jan 1:79. doi: 10.1016/j.healthplace.2023.102974. [DOI] [PubMed] [Google Scholar]
- 130.Luo W., Wang F. Measures of spatial accessibility to health care in a GIS environment: synthesis and a case study in the Chicago region. Environ. Plann. Plann. Des. 2003;30(6):865–884. doi: 10.1068/b29120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Mavrotas G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems. Appl. Math. Comput. 2009 Jul 15;213(2):455–465. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.