Comparison of Three Renal Function Formulas for Ganciclovir/Valganciclovir Dose Individualization in CMV-Infected Solid Organ Transplantation Patients Using a Population Approach

Abstract

Background and Objective

The gold standard treatment of established cytomegalovirus infection or prevention in solid organ transplantation is the intravenous administration of ganciclovir (GCV) or oral administration of valganciclovir (VGCV), both adjusted to the renal function. In both instances, there is a high interindividual pharmacokinetic variability, mainly owing to the wide range of variation of both the renal function and body weight. Therefore, accurate estimation of the renal function is crucial for GCV/VGCV dose optimization. This study aimed to compare three different formulas for estimating the renal function in solid organ transplantation patients with cytomegalovirus infection, for individualizing antiviral therapy with GCV/VGCV, using a population approach.

Methods

A population pharmacokinetic analysis was performed using NONMEM 7.4. A total of 650 plasma concentrations obtained after intravenous GCV and oral VGCV administrations were analyzed, from intensive and sparse sampling designs. Three different population pharmacokinetic models were built with the renal function given by Cockcroft–Gault, Modification of Diet in Renal Disease, or Chronic Kidney Disease EPIdemiology Collaboration (CKD-EPI) formulas. Pharmacokinetic parameters were allometrically scaled to body weight.

Results

The CKD-EPI formula was identified as the best predictor of between-patient variability in GCV clearance. Internal and external validation techniques showed that the CKD-EPI model had better stability and performed better compared with the others.

Conclusions

The model based on the more accurate estimation of the renal function with the CKD-EPI formula and body weight as a size metric most used in the clinical practice can refine initial dose recommendations and contribute to GCV and VGCV dose individualization when required in the prevention or treatment of cytomegalovirus infection in solid organ transplantation patients.

Graphical Abstract

Supplementary Information

The online version contains supplementary material available at 10.1007/s40262-023-01237-3.

Key Points

This study aimed at developing a population pharmacokinetic model based on a more accurate estimation of the renal function by the Chronic Kidney Disease EPIdemiology collaboration formula and on the body weight as the size metric most used in the clinical practice.

This study confirms the utility of the Chronic Kidney Disease EPIdemiology formula for predicting clearance of renally eliminated drugs such as ganciclovir, through the population approach.

The developed model can support a more accurate model-informed dose optimization to improve the ganciclovir/valganciclovir treatment/prophylaxis dosing in solid organ transplantation patients.

Introduction

Cytomegalovirus (CMV) infection is one of the most common opportunistic infections in immunocompromised patients and a major cause of morbidity and mortality after solid organ transplantations (SOTs) [1, 2]. Worldwide, the virus has a widespread distribution with CMV seroprevalence rates that vary from 30 to 100% [3–8].

Immunocompetent hosts can limit the ability of CMV to cause significant clinical disease. In contrast, CMV infection in SOT patients can have devastating consequences from either direct or indirect viral effects. This mainly occurs during the first 3 months after transplantation, as primary infection or reactivation of latent infection [9–12]. The gold standard treatment for established infection is the intravenous (i.v.) administration of ganciclovir (GCV) or the oral administration of its pro-drug, valganciclovir (VGCV) [13]. Previous studies have shown that achieved GCV exposures following administration of VGCV 900 mg are similar to those observed with GCV 5 mg/kg [14, 15], which led to the conversion proposed by the manufacturer [16].

Ganciclovir is mainly eliminated from the kidneys (91%) and its clearance decreases in an approximately linear manner with creatinine clearance (CRCL) diminution [17–19]. Thus, renal impairment causes a marked increase in the half-life of GCV (9–30 h) [20], which makes dose adjustments for these patients necessary. Moreover, 30% of patients with CMV infections show side effects, mainly leukopenia, caused by either the infection or the GCV toxicity. Patients experiencing this adverse effect may have an increased susceptibility to infection and may require supportive therapy with granulocyte-colony-stimulating factor or a reduction in GCV doses, which in turn may entail the risk of refractory CMV infection. Moreover, cases have been reported in which GCV-refractory CMV infections occurred as a consequence of subtherapeutic exposure because of inadequate treatment. This conclusion is arrived at through GCV concentration measurements during therapeutic drug monitoring [21].

Ganciclovir and VGVC show high pharmacokinetic interindividual variability mainly owing to the large range of variation of both the renal function and body weight (BW) in transplant patients. Therefore, accurate estimation of the renal function is crucial for dose optimization. Current consensus recommendations for GCV and VGCV dosing for patients with renal impairment include a standardized nomogram that assigns patients to one of five dosing groups, based on their measured glomerular filtration rate (GFR) through CRCL [22]. However, despite receiving the recommended dose adjustments, GCV area under the concentration–time curve from time 0 to 24 h (AUC_{0–24 h}) fluctuates in SOT patients, particularly in those with an unstable renal function, potentially leading to reduced clinical efficacy and safety of GCV. The above recommendations are based on the classification of patients according to the renal function calculated by the Cockcroft–Gault (C–G) formula. However, the C–G formula can overestimate the CRCL, leading to higher drug dosing recommendations than required [23].

Recently, other formulas have been developed, such as the Modification of Diet in Renal Disease (MDRD4) and Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI). Differences in accuracy between both formulas are small, but CKD-EPI shows the best overall accuracy after classification in subgroups of the renal function [24]. Although the impact of using different formulas to measure the renal function (C–G, MDRD4, CKD-EPI) on the GCV clearance has previously been evaluated through statistical analyses [25], no comparisons have been made by using population pharmacokinetic (PopPK) approaches. Previous PopPK GCV models only used C–G and MDRD4 formulas [26, 27] and showed low predictive ability of exposure for patients with extreme values of BW.

Thus, the goal of this study was to develop the most adequate PopPK model after analyzing the performance of three different renal function descriptors (C–G, MDRD4, CKD-EPI) on the predictability of GCV exposure after intravenous GCV and oral VGCV administration in SOT patients with CMV infection. Such analysis may allow dose optimization so as to assure the most efficacious and safe ganciclovir exposure in the target population.

Methods

Study Design

Datasets from two previous studies (clinicaltrials.gov identifiers: NCT00730769, NCT01446445) carried out in adult SOT patients were analyzed. Both were carried out at the Hospital Universitari de Bellvitge (Barcelona, Spain). All patients provided written informed consent, in accordance with the Declaration of Helsinki and Good Clinical Practice guidelines.

Group 1 data were obtained from a prospective clinical trial (clinicaltrials.gov identifier NCT00730769) in which patients were followed up on two occasions during a period of 21 days and rich sampling was applied on each occasion. Group 2 data were obtained from a two-arm, randomized, open-label, single-center trial (clinicaltrials.gov identifier NCT01446445), in which patients were sampled in accordance with a sparse sampling design, on between three and six occasions during a period of 3 months.

In Group 1, those eligible for inclusion were patients with an established CMV infection undergoing allogeneic SOT (kidney, heart, or liver), if they were ≥ 17 years of age, and presented with positive pp65 CMV antigenemia defined as ≥ 20 positive cells/10⁵ peripheral blood mononuclear cells. Patients with severe CMV tissue-invasive disease, absolute neutrophil counts of < 500/mm³, platelet counts of < 25,000/mm³, hemoglobin at < 80 g/L, or estimated GFRs of < 10 mL/min (according to the C–G formula) were excluded [26]. Regarding Group 2, kidney, liver, or heart transplant recipients were eligible to participate if they were ≥ 18 years of age and were being treated with GCV or VGCV for either prophylaxis or treatment of CMV infection, according to standard clinical practice. Patients were excluded if they had a calculated CRCL below 10 mL/min measured using the C–G equation, had a history of hypersensitivity to GCV-VGCV, or were receiving concomitant treatment with other anti-CMV agents [28].

When available, demographic and body composition characteristics (age, sex, BW, body surface area, lean BW estimated by the James formula [29, 30], total body water estimated by the Watson’s formula [31]) and clinical laboratory measurements (creatinine, CRCL estimated by C–G formula [CRCL_C–G] [32], GFR estimated by MDRD4 (MDRD4_GFR) [33] and CKD-EPI (CKD-EPI_GFR) formulas [34] (Table 1), transplant type, and concomitant immunosuppressive medication were recorded. For the external validation of the final PopPK models, sparse data from an external cohort of patients from Hospital de la Vall d’Hebron, Barcelona (Spain) were collected (on between one and five occasions per patient), over a period of 3 months.

Table 1.

Baseline demographic and clinical characteristics of the model development and external evaluation groups of patients

Variable	Model development group			External validation group
	N (%)
Type of transplant	Kidney	Liver	Heart
N	45	10	5	22
Male	31 (51.7)	5 (50)	4 (80)	13 (59.1)
Female	29 (48.3)	5 (50)	1 (20)	9 (40.9)

Global	Median	Mean (SD)	Range	Median	Mean (SD)	Range
Age (years)	57	54 (12.8)	22–78	56	55 (10.38)	36–76
Weight (kg)	68	70 (16.78)	43–131	67	69 (13.15)	47–93
Height (cm)	163	164 (10.13)	143–192	–	–	–
Serum creatinine (μmol/L)a	125	141 (75.22)	40–602	141	168 (85.68)	50–397
Creatinine clearance
C–G (mL/min)	58	58 (25.92)	10–120	48	56 (29.91)	15–134
MDRD4 (mL/min/1.73 m2)	47	51 (24.47)	7–141	50	55 (30.06)	16–131
CKD-EPI (mL/min/1.73 m2)	55	54 (26.13)	7–118	49	53 (26.77)	14–109

a is — 0.329 for female individuals and — 0.411 for male individuals in the CKD-EPI formula shown below, C–G Cockcroft–Gault, CKD-EPI Chronic Kidney Disease EPIdemiology Collaboration, GFR estimated glomerular filtration rate, k is 0.7 for females and 0.9 for males, in the CKD-EPI formula shown below, MDRD4 Modified of Diet in Renal Disease,  min indicates the minimum of SCr/k or 1 and max indicates the maximum of SCr/k or 1, SCr serum creatinine (mg/dL), in the CKD-EPI formula shown below, SD standard deviation

^aAt initiation of therapy

C–G formula: $\text{CRCL}=\frac{\left(140-\text{age}\right)\times \text{weight}\times \left[0.85\text{if female}\right]}{72\times \left[\text{serum creatinine}\right]}$; age in years, weight in kg and serum creatinine in mg/dL

MDRD4 formula: $\text{eGFR}=186\times {\left[\text{serum creatinine}\right]}^{-1.154}\times {\left[\text{age}\right]}^{-0.203}\times \left[1.212\text{if black}\right]i\left[0.742\text{if female}\right]$; serum creatinine levels in mg/dL, age in years. As MDRD4 does not adjust for body size, results are given in units of mL/min/1.73 m², with 1.73 m² being the estimated body surface area of an adult with a mass of 63 kg and a height of 1.7 m

CKD-EPI formula: $\text{eGFR}=141\times \text{min}{\left(\text{SCr}/k,1\right)}^{\alpha }\times \text{max}{\left(\text{SCr}/k,1\right)}^{-1.209}\times 0.{993}^{\text{Age}}\times \left[1.018\text{if female}\right]\times \left[1.159\text{if black}\right]$

GCV/VGCV Administration

Patients of Group 1 with normal renal function received i.v. GCV at 5 mg/kg over 1 h, twice daily, for 5 days followed by 900 mg of oral VGCV twice daily, for 16 days (21 days of treatment). In patients with impaired renal function, i.v. and oral doses were adjusted by the C–G formula in accordance with the manufacturer’s recommendations. Thus, i.v. GCV doses for CMV infection were 2.5 mg/kg/12 h, 2.5 mg/kg/24 h, and 1.25 mg/kg/24 h, for renal functions of 50–69, 25–49, and 10–24 mL/min (C–G values), respectively. Oral VGCV doses for CMV infection were of 450 mg every 12, 24, and 48 h, for renal functions of 40–50, 25–38, and 10–24 mL/min (C–G values), respectively. For prophylaxis, oral VGCV was given at 450 mg every 24, 48, and 84 h, for renal functions of 40–59, 25–39, and 10–24 mL/min (C–G values), respectively, and at 900 mg every 24 h, for the renal function of 60–69 mL/min (C–G values).

Patients of Group 2 were randomly distributed into two subgroups. In the first subgroup, doses were adjusted according to the manufacturer’s recommendations, whereas in the second subgroup, doses were adjusted by Bayesian prediction according to a previously developed PopPK model of GCV/VGCV [26], where C–G accounted for the renal function. Patients under prophylaxis received oral VGCV for 90 days, whereas those with CMV infection were treated with GCV-VGCV until two consecutive, negative, CMV viral load tests were obtained, performed at least 1 week apart.

Blood Sampling and Drug Analysis

For Group 1, blood samples were collected before and at 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, and 12 h, 5 days after i.v. GCV and 15 days after oral VGCV administration. Further sampling up to 24 h was performed on one patient with CRCL_C–G values of 10 mL/min (day 5) and 16 mL/min (day 15). For Group 2, three blood samples per patient, within pre-established windows from 0.5 to 1.5, from 4 to 5 and from 6 to 8 h after dose administration were obtained [35].

Samples were centrifuged at 13,000 rpm for 10 min at 4 °C, plasma was separated and stored at − 20 °C until analysis. Plasma GCV concentrations were determined by high-performance liquid chromatography (Group 1) [36] and ultra-high-performance liquid chromatography (Group 2 and external validation data) [37] methods with ultraviolet detection. In both cases, the lower limit of quantification was 0.5 μg/mL. The calibration curves were linear between 0.5 and 30 mg/L. Details about the analytical methods are described in the references [36, 37]. The analysis of duplicated patient samples by both analytical methods led to a high correlation between both [37].

PopPK Data Analysis

A simultaneous analysis of time–concentration values from all patients was performed using the nonlinear mixed-effects model approach implemented in NONMEM software (version 7.4; ICON Development Solutions, Hanover, MD, USA) using Perl-Speaks-NONMEM (version 5.2.6). For modeling purposes, VGCV doses were converted to their equivalent GCV content multiplying the VGCV dose by 0.720 (ratio between the molecular weights of GCV and VGCV).

The modeling process consisted of the following steps: (i) development of the structural base pharmacokinetic model, incorporating between-occasion variability; (ii) covariate selection; and (iii) model evaluation and selection of the final best model. The first-order conditional estimation method with interaction was used throughout the entire model-building process.

Structural Base PopPK Model

One- and two-compartment open models with first-order absorption, with and without lag time, and linear elimination were evaluated. Models were parameterized in terms of central and peripheral compartment distribution volumes (V_c and V_p, respectively) and intercompartmental and elimination clearances (CL_D and CL, respectively). Between-patient variability and between-occasion variabilities were tested in all the pharmacokinetic parameters and assumed to have a log-normal distribution. Residual error (RE) was modeled as proportional and combined (additive plus proportional) error models. Two different REs were tested to account for potential differences in GCV concentrations due to the two different analytical methods applied for GCV determination (Groups I and II). The goodness of fit was evaluated by changes in the minimum objective function value (MOFV), parameter estimates precision, condition number (< 1000), and goodness-of-fit plots. For nested models, where the ratio of the MOFV is chi-square distributed, with one degree of freedom (equal to the difference in the number of model parameters between the full and reduced models), a significance level of 0.5% (p < 0.05) was considered to lead to a significant improvement of fit (drop in MOFV by > 7.879).

Covariate Models

The influence of the renal function estimated by CKD-EPI, MDRD4, and C–G formulas was tested on GCV clearance. All demographic and body composition variables (BW, body surface area, lean BW, total body water, sex, and age) were also tested in all the pharmacokinetic parameters. First, potential pairwise correlations between covariates were investigated and among those correlated only the most statistically and clinically meaningful were retained in the model. Continuous covariates were tested, in terms of either linear or power relationships and were normalized by their population mean values. Categorical covariates were tested as linear models. Body weight was entered according to the allometric laws either by estimating or fixing the exponent values [38].

Covariates were first entered univariately and then by the cumulative forward inclusion/backward elimination procedures. Significance levels of 5% (reduction in the MOFV of > 3.841 units) and 1% (increase in the MOFV of > 10 units) were selected during the forward addition and backward elimination steps, respectively. A decrease of at least 10% in interindividual variability associated with pharmacokinetic parameters was considered clinically relevant.

Model Evaluation

Diagnostic plots for the model evaluation were built with R package “Xpose 4” [39]. The randomness around the identity line of observed concentrations versus population or individual predictions plots were examined. In the same way, plots of individual weighted and conditional weighted residuals versus time were evaluated for randomness around zero. η- and ε-shrinkages were estimated to determine the suitability of using post-hoc individual parameter estimates for model evaluation.

A non-parametric re-sampling bootstrap technique with replacement of 1000 replicates was used to assess the reliability and stability of the PopPK model and to construct confidence intervals (CIs) of PK parameters. The final model was fitted to the replicate datasets, and parameter estimates were obtained. The median of the parameters obtained were compared with those estimated from the original data. The lower and upper limits of the 95% CIs for each parameter accounted for its corresponding imprecision. The evaluation of the predictive capability of the models was performed by means of simulation-based diagnostics using the final population parameter estimates (internal evaluation) and by posterior Bayesian prediction methods (external evaluation). Prediction corrected visual predictive check [40] and normalized prediction distribution errors (NPDE) [41] analyses were performed from 1000 simulations of the original dataset to graphically assess the appropriateness of the final model. The predictive performance of the model was also assessed in new patients using the posterior Bayesian estimates of GCV peak and trough concentrations obtained from an external group of SOT patients with individual characteristics similar to those of the development group (Table 1). The bias [median prediction error (MPE)] and precision [root of median squared prediction error (RMSPE)] were computed as set out in accordance with the following formulas [42]:

$$\begin{array}{cc}\hfill \text{MPE}\%& =\left(\text{IPRED}-\text{OBS}\right)100,\hfill \\ \hfill \text{RMSPE}\%& =\sqrt{\left|\text{IPRED}-\text{OBS}\right|}·100.\hfill \\ \hfill \end{array}$$

Model-Based Simulations

The C–G, MDRD4, and CKD-EPI PopPK models were used to stochastically simulate time–concentration profiles for patients with BW of 40, 70, and 100 kg and a complete range of variation of the renal function (based on seven different cut-off intervals from 10 to 69 mL/min (i.e., 10–19, 20–24, 25–29, 30–39, 40–49, 50–59, and 60–69 mL/min) for each formula. The BW values considered for simulations were based on the distribution and the range of this variable in the actual population. As such, all possible combinations for BW and the renal function were evaluated. Doses used for simulations were those of the manufacturers’ recommendations for prophylaxis, as described in the methods section. From these simulations, the AUCs were calculated as individual F*dose/individual CL (for oral VGCV). As done previously [26], the percentages of patients with AUC values within the range of 40–50 (µg/mL)·h [22] were calculated. Statistical comparisons of the percentages of target attainment (PTA%) and log-transformed simulated AUC values between each formula considering the different renal function cut-offs and BW were carried out by means of a three-way analysis of variance. Then, a Tukey multiple comparison test was applied, with PTA% or AUC being the dependent variables and the renal function cut-off, BW, and formula being the independent variables. Potential interactions between these factors were tested and retained in the analysis of variance in the case of statistical significance. Comparisons of PTA% between models accounting for the influence of BW and those that did not include this covariate were also carried out. A three-way analysis of variance considering renal function cut-off, formula, and the presence/absence of BW in the model was applied. Moreover, exposures achieved at steady state after VGCV oral doses, estimated as an AUC target (45 (µg/mL)·h) multiplied by the ratio between CL and F population values predicted by the final CKD-EPI model, for several renal function cut-offs from 10 to 69 mL/min (10–19, 20–24, 25–39, 40–49, 50–59, 60–69 mL/min) and BW from 40 to 130 kg (40–60, 61–80, 81–100, 101–130 kg) were simulated. Again, the cut-offs were based on the distribution and the range of each variable in the actual population. The AUC values were calculated, as mentioned above, and also the percentages of patients achieving AUC values within the range of 40–50 (mg/L)·h.

Results

Patients

Sixty Caucasian patients (31 were male and 29 were female) with established CMV infections undergoing allogeneic SOT (kidney, n = 45; heart, n = 10; liver, n = 5) were included in this study. The most relevant baseline demographic and clinical characteristics of all patients are shown in Table 1 together with those of patients belonging to the validation dataset. A total of 418 doses were given (i.v. doses ranged from 125 to 450 mg/h; oral doses ranged from 90 to 900 mg). Dose adjustment was performed according to the renal function following the manufacturer’s recommendations apart from four patients: one with a CRCL of 27 mL/min who received i.v. GCV at 5 mg/kg twice per day; one patient with a CRCL of 55 mL/min who received 900 mg of oral VGCV twice per day; and two patients with CRCL values of 38 and 25 mL/min, respectively, who received 450 mg of oral VGCV twice per day. The CRCL values estimated by the C–G formula tended to be higher than those estimated by CKD-EPI and then MDRD4 formulas (one-way analysis of variance, p = 0.04). No statistically significant differences were found in any of the demographic (age, BW, sex) and clinical variables (CRCL_C–G, MDRD4_GFR, or CKD-EPI_GFR, CR) between the development and external groups (Table 1).

GCV Serum Concentrations

The final dataset used for the PK analysis consisted of 650 GCV concentrations, 382 from rich patients’ data (190 i.v. GCV and 192 oral VGCV with a median number of samples per patient of 19.1) and 268 from sparse patients’ data (13 i.v. GCV and 255 oral VGCV, with a median number of samples per patient of 6.7). Only 10 out of 650 values were under the limit of quantification and were removed from the analysis.

PoPK Model

Base PopPK Model

A two-compartment open linear model with a time-lagged first-order absorption process, parametrized in terms of total GCV CL, V_c, V_p, CL_D, first-order absorption rate constant (representing the absorption and hydrolysis of VGCV in the gut wall and liver, before reaching the systemic circulation), bioavailability, and lag time, best described the data. Between-patient variability was included in CL, V_c, V_p, absorption rate constant, and bioavailability. The inclusion of between-occasion variability in CL significantly reduced the MOFV by 18.75 units (p < 0.05). A combined error model, proportional and additive, best described the RE. No statistically significant difference was found when two different RE for GCV concentrations measured by high-performance liquid chromatography or ultra-performance liquid chromatography methods were tested. The pharmacokinetic parameters estimated from the base model are shown in Table 2.

Table 2.

Ganciclovir population pharmacokinetic parameter estimates for the base and final models (Chronic Kidney Disease EPIdemiology Collaboration model) and bootstrap results for the final model

Parameters	Units	Base model parameter estimates (RSE%)a	Final model parameter estimatesc	Median (95% CI) bootstrap resultsb
Pharmacokinetic parameters
CL	L/h/70 kg	6.24 (12.68%)	6.93*(CKD-EPI/55)θa·(BW/70)0.75	7.04 (5.58–8.75)
Θa on CL			0.817	0.81 (0.63–1.01)
Vc	L/70 kg	37.9 (14.59%)	43.1·(BW/70)	42.9 (33.9–56.5)
Vp	L/70 kg	58.7 (36.46%)	219·(BW/70)	184.0 (45.2–344.5)
CLD	L/h/70 kg	11.3 (25.58%)	9.23·(BW/70)0.75	9.6 (5.5–13.9)
Ka	h–1	0.821 (17.66%)	0.766	0.794 (0.596–1.188)
F	–	0.686 (8.82%)	0.699	0.709 (0.618–0.835)
Lag time	h	0.361 (8.5%)	0.331	0.338 (0.245–0.410)
Between-patient variability
ω2CL		0.261 (27.20%)	0.0893	0.0820 (0.019–0.166)
ω2Vc		0.188 (67.55%)	0.130	0.136 (0.016–0.276)
ω2Vp		1.11 (44.32%)	1.07	1.15 (0.184–2.326)
ω2Ka		0.280 (76.07%)	0.209	0.261 (0.003–0.765)
ω2F		0.0439 (70.84%)	0.0275	0.027 (0.000–0.065)
Between-occasion variability
ω2CL		0.085 (51.17%)	0.025	0.031 (0.002–0.108)
Residual variability
σ1	μg/mL	0.248 (44.76%)	0.237	0.189 (0.159–0.455)
σ22**	%	26.5 (10.94%)	28.2	27.4 (20.2–32.4)

CL elimination clearance, CI confidence interval, CL_D inter-compartment clearance between central and peripheral compartments, F bioavailability, Ka absorption rate constant, RSE relative standard error, Vc central compartment distribution volume, Vp peripheral compartment distribution volume, σ₁ standard deviation of additive component of residual variability, σ₂^2** proportional component of residual variability expressed as percentage, ω² variance of between patient variabilities associated with the pharmacokinetic parameters

^aRelative standard errors of the base model parameters were given in parenthesis

^bDerived from 1000 successful bootstrap samplings

^cNo standard errors could be obtained for the final model due to over-parametrization

Covariate Analysis

As expected, renal function estimated by any of the three formulas was the most powerful covariate. Although all the anthropometric covariates (BW, lean BW, total body water) were statistically significant, we decided to include only BW as it is the most easily used in daily clinical practice. The C–G formula provided the highest decrease in the objective function value (OFV) when tested in GCV clearance [ΔOFV = − 58.066 vs − 38.686 (MDRD4) and − 38.273 (CKD-EPI)]. The subsequent inclusion of BW in CL was statistically significant except for the CRCL_C–G model because renal function estimated by the C–G formula is already adjusted by BW [ΔOFV = − 0.95 (C–G) vs − 15.639 (MDRD4) and − 17.513 (CKD-EPI)]. The subsequent inclusion of BW on Vc was statistically significant in all cases [ΔOFV = − 12.241 (C–G) vs − 11.238 (MDRD4) and − 10.331 (CKD-EPI)], during the forward inclusion. The backward elimination of renal function resulted in a statistically significant increase in the MOFV of more than 10 units (p < 0.001) in all cases, as did the BW when removed from CL. However, the backward elimination of BW from V_c did not provide a statistically significant deterioration of the model fit. This could be explained by a potential correlation between the CL, V_c, and V_p parameter values that caused a statistically significant decrease of the MOV when BW entered in CL. Such correlations often exist when sparse data designs are analyzed, as it is the case of part of the data file of the current study. Despite this, we based our modeling on the allometric laws as proposed by Anderson and Holford [38]. Therefore, we entered BW standardized by the typical value of 70 kg (BW/70), allometrically, on to all flow (CL, CL_D) and distribution volume (V_c, V_p) parameters by fixing the exponents to 0.75 (CL, CLD) and 1, respectively (V_c and V_p).

Model Evaluation and Selection of the Final Best Model

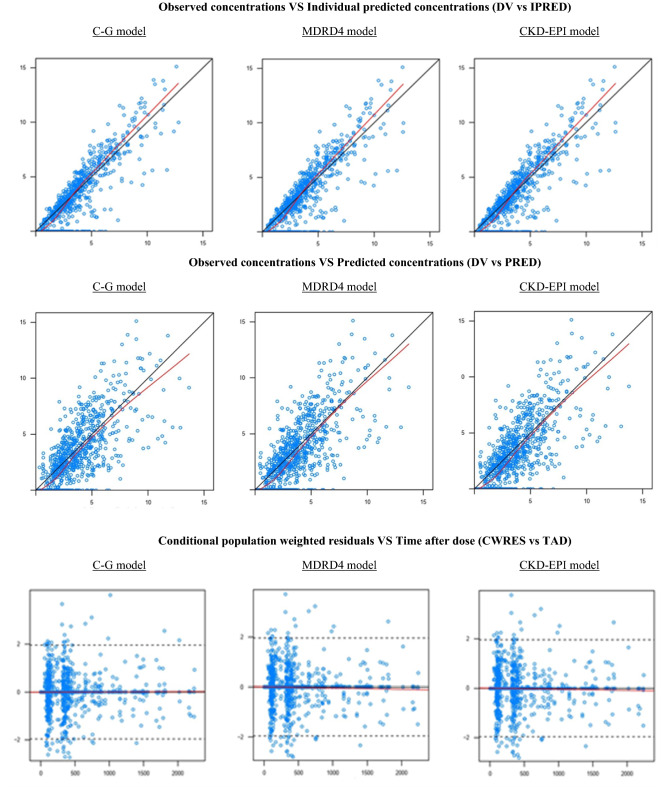
Figure 1 shows the goodness-of-fit plots of the final models (C–G, MDRD4, and CKD-EPI). Random distributions around the identity line were observed in both PRED versus observed and IPRED versus observed concentrations. The conditional weighted residuals showed a random distribution around zero, with most of the points located between ± 2. Bootstrap results for the three models showed that the lowest deviations between the population value and bootstrap median structural parameters was found for the CKD-EPI model [lower than 16% vs lower than 20.06% (MDRD4) and lower than 54.41% (C–G)]. This was remarkable for CL [1.63% (CKD-EPI), 2.02% (MDRD4), and 7.60% (C–G)], the most important pharmacokinetic parameter in the current study. For CKD-EPI, model deviations in random-effects parameters, where all of them were lower than 8.2% except for the absorption rate constant that was lower than 25% (Table 2).

Fig. 1.

Goodness-of-fit plots for the final model. Observations: observed concentrations; population predictions; dashed line: identity line; solid line: smooth line indicating the general data trend. Conditional population weighted residuals; dashed line: represents the line y = 0; solid line: smooth line indicating the general data trend. Concentrations expressed as mg/L. Time given in hours from the start of the treatment. C–G Cockcroft–Gault, CKD-EPI Chronic Kidney Disease EPIdemiology Collaboration, MDRD4 Modification of Diet in Renal Disease

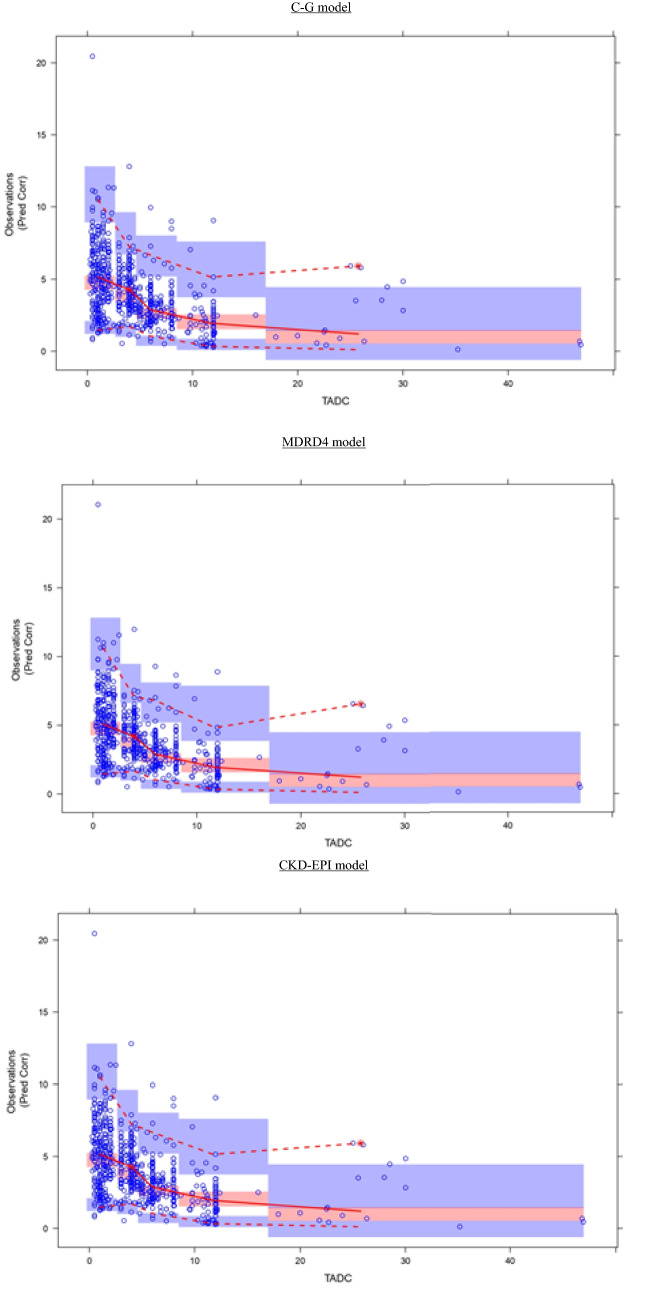
All these results led to the selection of the CKD-EPI model as the best model. The prediction corrected visual predictive check displayed in Fig. 2 demonstrated a good predictive capability of the final model that described the observed median trend well with most of the observed data being within the 95% prediction intervals of the simulated data. Figure 3 represents the NPDE results. The distribution of NPDE of the observed data was overlaid with that of NPDE of the simulated data. No trends or bias in the scatter plots, and no trends in NPDE versus time and versus individual predicted concentration, were observed. Distribution of predicted discrepancies was close to the theoretical normal distribution. Again, these results reflected a good predictability of the final model.

Fig. 2.

Prediction corrected visual predictive checks corresponding to ganciclovir, plasma concentration (as mg/L) versus time (time after the last dose given in hours) profiles. In general, median (solid line), 95th and 5th percentiles (dashed lines) of the observations as well as the 90% confidence intervals for the median, the 5th and 95th percentiles of the simulated profiles (covered by the light blue areas) are superimposed in each graph. The 5th and 50th percentiles lines of the observations fell inside the area of the corresponding 90% confidence interval. C–G Cockcroft–Gault, CKD-EPI Chronic Kidney Disease EPIdemiology Collaboration, MDRD4 Modification of Diet in Renal Disease

Fig. 3.

Normalized prediction distribution errors (NPDE) results. A Quantile-quantile plot of the distribution of the NPDE against the theoretical distribution (the identity line); B histogram of the distribution of the NPDE against the theoretical distribution (the normal distribution curve); C NPDE versus time since the first dose; and D NPDE versus individual predictions. C–G Cockcroft–Gault, CKD-EPI Chronic Kidney Disease EPIdemiology Collaboration, MDRD4 Modification of Diet in Renal Disease

The parameters of the final model are displayed in Table 2. No standard errors could be obtained because of over-parametrization, but 95% CIs were estimated through the non-parametric bootstrap method, accounting for precision estimation in the final parameters.

Shrinkage associated with η_CL was under 30% and higher for the other parameters. Shrinkage associated with ε was lower than 12%. The CKD-EPI formula led to a clinically significant reduction in between-patient variability of CL (42.43%).

External Model Evaluation

Table 3 displays the bias and imprecision values estimated from the external evaluation. Acceptable bias was observed in all the cases. Considering the geometric mean of trough concentrations of the external dataset (1.49 µg/mL), imprecision associated with predictions of this metric was around 19%.

Table 3.

Bias (median prediction error) and imprecision (root of median squared prediction error) estimates from the external evaluation

Model	Parameter (units)	Bias [median (95% CI)]	Imprecision [median (95% CI)]
Cockcroft–Gault	Ctrough (μmol/L)	− 0.08 (− 1.49 to 1.63)	0.30 (0.03−1.73)
	Cpeak (μmol/L)	− 0.41 (− 5.71 to 4.67)	2.27 (0.27−5.71)
MDRD4	Ctrough (μmol/L)	− 0.11 (− 1.58 to 1.59)	0.28 (0.02−1.88)
	Cpeak (μmol/L)	− 0.35 (− 6.30 to 4.86)	2.37 (0.07−6.35)
CKD-EPI	Ctrough (μmol/L)	− 0.09 (− 1.82 to 2.08)	0.29 (0.03−2.10)
	Cpeak (μmol/L)	− 0.29 (− 6.28 to 4.89)	2.39 (0.07−6.33)

CI confidence interval, CKD-EPI Chronic Kidney Disease EPIdemiology Collaboration, C_peak peak concentration, C_trough trough concentration, MDRD4 Modification of Diet in Renal Disease

Considering both C_trough and C_peak, the least biased predictions were found for the CKD-EPI model

Model Simulations

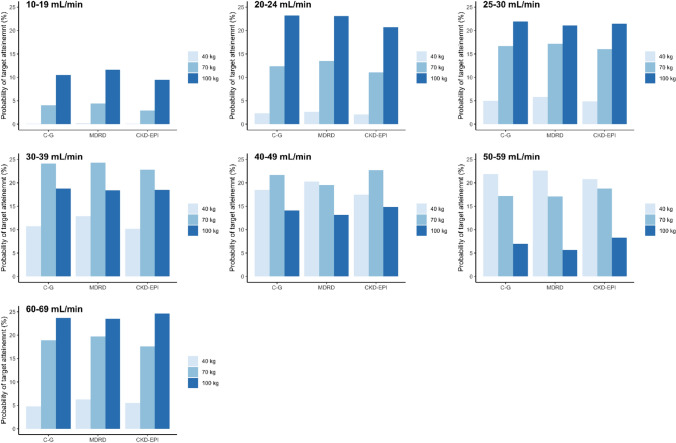
Figure 4 and Table 4 show the percentages of patients achieving AUC_target between 40 and 50 (µg/mL)·h (%PTA) for each renal function cut-off/BW/formula, estimated from the simulated GCV plasma concentrations after manufacturers’ recommended oral doses for prophylaxis, indicated in the methods section. No statistically significant differences were found in %PTA among formulas (p = 0.214). However, statistically significant differences were found among all renal function cut-offs (p < 0.001), except between 20–24 and 25–29 mL/min (p = 1.00) and between 20–24 mL/min and 50–59 mL/min (p = 0.324), and between 25–29 and 50–59 mL/min (p = 1.00).

Fig. 4.

Bar plots of probability of target attainment [target area under the concentration time curve (AUC_target) around 40–50 μg*h/mL] for simulated AUC values from the final Chronic Kidney Disease EPIdemiology Collaboration (CKD-EPI) model after oral prophylaxis manufacturer-recommended doses for each formula and renal function/body weight cut-offs. Prophylaxis, oral valganciclovir doses of 450 mg every 24, 48, and 84 h, for renal functions of 40–59, 25–39, and 10–24 mL/min [Cockcroft–Gault (C–G) values], respectively, and of 900 mg every 24 h, for the renal function of 60–69 mL/min (C–G values) were simulated

Table 4.

Percentages of patients achieving target area under the concentration–time curve of around 40–50 μg*h/mL after manufacturer-recommended oral prophylaxis doses

CRCL cut-off group (mL/min)	BW (kg)	No body weighta			BW (kg)	With body weighta,b
		C–G	MDRD4	CKD-EPI		C–G	MDRD4		CKD-EPI
10–19	70	1.6%	4.2%	8.1%	40	0.1%	0.2%		0.1%
					70	2.9%	4.4%		4.0%
					100	9.5%	11.6%		10.5%
20–24	70	10.2%	9.9%	13%	40	2.1%	2.6%		2.3%
					70	11.1%	13.5%		12.4%
					100	20.7%	23.1%		23.2%
25–29	70	15.3%	13.2%	18.8%	40	4.9%	5.8%		5.0%
					70	16%	17.2%		16.7%
					100	21.5%	21.1%		21.9%
30–39	70	24.4%	18.8%	20.4%	40	10.2%	12.9%		10.7%
					70	22.8%	24.3%		24.1%
					100	18.5%	18.4%		18.8%
40–49	70	22.7%	20.5%	19.9%	40	17.5%	20.3%		18.5%
					70	22.7%	19.5%		21.7%
					100	14.8%	13.2%		14.1%
50–59	70	16.7%	15.9%	17.7%	40	20.8%	22.6%		21.9%
					70	18.8%	17.1%		17.2%
					100	8.3%	5.7%		7%
60–69	70	19.5%	15.3%	15.2%	40	5.5%	6.3%		4.8%
					70	17.6%	19.7%		18.9%
					100	24.6%	23.5%		23.7%

BW body weight, C–G Cockcroft–Gault, CKD-EPI Chronic Kidney Disease EPIdemiology Collaboration, CRCL creatinine clearance, MDRD4 Modification of Diet in Renal Disease, %PTA percentage of target attainment, VGCV valganciclovir

^aNo statistically significant differences (p = 0.506) were found between mean values of %PTA estimated from the models including BW with respect to those that did not consider it

^bFrom models including BW, no statistically significant differences were found between formulas (p = 0.214), but statistical significant differences were found between BWs in all the cases (p < 0.001), excepting in %PTA between 70 and 100 kg (p = 0.312)

And from models including BW, statistically significant differences were found among all the renal function cut-offs (p < 0.001), except between 20–24 and 25–29 mL/min (p = 1.00), between 20–24 and 50–59 mL/min (p = 0.324), and between 25–29 and 50–59 mL/min (p = 1.00)

Prophylaxis, oral VGCV doses of 450 mg every 24, 48, and 84 h, for renal functions of 40–59, 25–39, and 10–24 mL/min (C–G values), respectively, and of 900 mg every 24 h, for the renal function of 60–69 mL/min (C–G values) were simulated

Additionally, statistically significant differences were found in %PTA among BWs (p < 0.05), except between 70 and 100 kg (p = 0.312). No statistically significant differences (p = 0.506) were observed between mean values of %PTA estimated from the models including BW with respect to those that did not consider it.

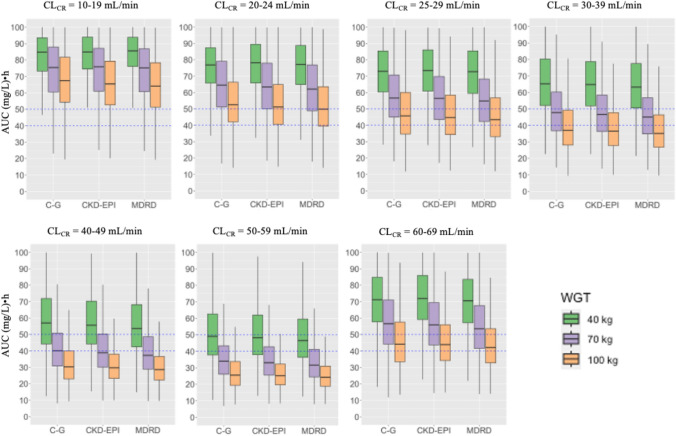
Mean simulated AUC values from the C–G, MDRD4, and CKD-EPI models, after prophylaxis manufacturer-recommended oral doses are shown in Table S1 of the Electronic Supplementary Material (ESM) and Fig. 5.

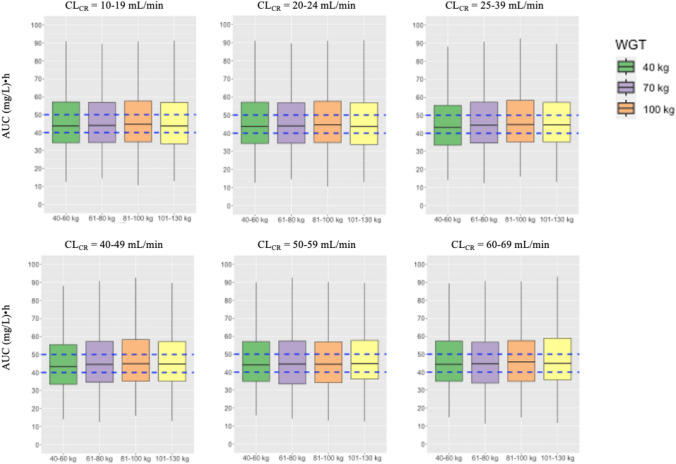
Fig. 5.

Boxplots of simulated area under the concentration–time curve (AUC) values from the Cockcroft–Gault (C–G), Modification of Diet in Renal Disease (MDRD), and Chronic Kidney Disease EPIdemiology Collaboration (CKD-EPI) models after prophylaxis manufacturers’ recommended oral doses for each renal function/body weight cut-offs. Blue dashed lines: AUC threshold of 40–50 (mg/L)·h. Prophylaxis, oral valganciclovir doses of 450 mg every 24, 48, and 84 h, for renal functions of 40–59, 25–39, and 10–24 mL/min (C–G values), respectively and of 900 mg every 24 h, for the renal function of 60–69 mL/min (C–G values) were simulated. CL_CR creatinine clearance

Statistically significant differences were observed for mean AUC values between all the renal function cut-offs (p < 0.001, for all the pairwise comparisons), all the formulas (p < 0.001, for all the pairwise comparisons), and all the BW cut-offs (p < 0.001, for all the pairwise comparisons).

In general, regardless of the formula and BW (40, 70, and 100 kg), overexposure was evidenced at low renal function cut-offs (10–19 mL/min). The %PTA increased as renal function increased, reaching its maximum value at 30–39 mL/min and 50–59 mL/min cut-offs for BW of 70 and 40 kg, respectively. As %PTA increased, GCV exposure decreased, showing for 30–39 mL/min and 50–59 mL/min cut-offs the closest exposure values to the target in 70-kg and 40-kg patients, respectively, with the actual dosage regimen (Table S1 of the ESM, Fig. 5). A decrease in %PTA was observed for both BWs (40 kg, 70 kg), until the cut-off of 60–69 mL/min, where overexposure was again observed particularly for the lowest BW. For the BW of 100 kg, overexposure was also observed at the lowest renal function cut-off (10–19 mL/min), achieving the lowest %PTA. Then, the %PTA increased until 25–29 mL/min and then decreased again until the 50–59 mL/min cut-off. Unlike for patients of 40–70 kg, the highest %PTA value and the closer exposure to the target were achieved for the highest renal function cut-off (60–69 mL/min). Although no statistically significant differences were observed, comparison between formulas showed a trend to slightly lower exposure values for CKD-EPI and MDRD4 with respect to C–G.

Table 5 displays the initial VGCV dosage regimens derived from the final CKD-EPI model for each renal function cut-off and BW. The boxplots of the simulated AUC values after the new estimated doses from the final CKD-EPI model are displayed in Fig. 6. In all the cases, mean AUC values within the target range of 40–50 (µg/mL)·h were achieved. Probabilities of target attainment ranged from 22.9% to 24.6% in all the cases, agreeing with the %PTA values of the best-dosed renal function/BW cut-offs with the actual manufacturers’ dosage recommendations (Table 4).

Table 5.

Oral prophylaxis doses required to achieve target area under the concentration–time curve of 40–50 μg*h/mL derived from the final Chronic Kidney Disease EPIdemiology Collaboration model

Renal function (mL/min)	Body weight (kg)	VGCVa (mg/kg)	VGCVa (mg)	Dosing interval (h)
10–19	40–60	3.3	167	84
	61–80	3.1	215
	81–100	2.9	259
	101–130	2.7	311
20–24	40–60	4.6	228	84
	61–80	4.2	293
	81–100	3.9	354
	101–130	3.7	426
25–39	40–60	6.2	310	48
	61–80	5.7	398
	81–100	5.3	481
	101–130	5.0	578
40–49	40–60	8.2	409	48
	61–80	7.5	526
	81–100	7.1	636
	101–130	6.6	764
50–59	40–60	9.6	482	48
	61–80	8.9	620
	81–100	8.3	749
	101–130	7.8	900
60–69	40–60	11.0	552	24
	61–80	10.2	711
	81–100	9.5	858
	101–130	9.0	1031

Doses calculated for the mean body weight within each interval are shown

VGCV valganciclovir

^aDoses calculated for the mean body weight of each interval, that is 50, 70, 90, and 115 kg

Fig. 6.

Boxplots of simulated area under the concentration–time curve (AUC) values after having administered new estimated doses from the final Chronic Kidney Disease EPIdemiology Collaboration model for each renal function/body weight (WGT) cut-offs. Probabilities of target attainments ranged from 22.9 to 24.6%. Blue dashed lines: AUC threshold of 40–50 (mg/L)·h. CL_CR creatinine clearance

Discussion

To the best of our knowledge, this is the first study comparing three different descriptors of the renal function for GCV/VGCV using a PopPK approach. As GCV is mainly excreted unaltered by the kidneys, the accuracy of the renal function descriptor used in PopPK models will highly affect the variability of the predicted GCV exposure. Our results showed that the CKD-EPI equation was the best model to predict GCV clearance. Palacio-Lacambra et al. [25] came to the same conclusion using linear regression statistical methods. However, to establish new dosing recommendations according to the CKD-EPI equation, a PopPK model is required. Therefore, this is the added value of the current work.

As previously reported [26, 27], the GCV pharmacokinetics was best described by a two-compartment model with first-order elimination and a time-lagged absorption process. Unlike our previous study [26], we could enter between-occasion variability in CL, with lower values (15.8%) than between-patient variability (29.88%), as also reported by Perrottet et al. [27]. This made the current model suitable for dose individualization in addition to estimations of initial GCV doses. In general, our final PopPK parameters were in line with those previously reported by Perrottet et al. [27]. However, in that case, MDRD4 and other covariates, less commonly used for dose adjustment during routine clinical practice, were included in the model.

External validation showed that the CKD-EPI model was able to accurately predict GCV trough concentrations (Table 3), more affected by GCV clearance than peak concentrations. Similarly, this occurred with the C–G equation. However, this was anticipated as analyzed concentration–time data were obtained from a C–G adjusted dosage regimen. The MDRD4 formula led to worse predictions, but no large differences were observed compared to CKD-EPI and C–G. It is noteworthy that the MDRD4 formula [33] was developed in patients with chronic renal disease, showing imprecision and systematic underestimation of the measured GFR (bias) at the highest renal functions [24].

As expected, mean simulated AUC values after the current prophylaxis regimen (Table SI of the ESM, Fig. 5) were lower than those reported in our previous study [26], where infection treatment doses were considered. After prophylaxis manufacturer-recommended doses, no statistically significant differences in overall %PTA between formulas (p = 0.214) were found (Table 4, Fig. 4), but they were observed among mean AUC values (p < 0.001). This can be attributed to the different type of analyzed variable [discontinuous (%PTA) vs continuous (AUC)]. Interestingly, mean AUC values provided by the C–G equation tended to be the highest, followed by those of CKD-EPI and MDRD4. A possible explanation is that although equal estimated CRCL values for the three formulas were considered in simulations, each one corresponded to a different value of real GFR. Thus, the highest AUC values provided by the C–G equation model suggest that estimated C–G GFR may correspond to a lower real renal function than those represented by estimated MDRD4 and CKD-EPI equations. Considering that recommended prophylaxis regimens were based on adjustment by the C–G formula, %PTA for C–G was expected to be higher than %PTA for the other formulas. However, this was only slightly evidenced from 40 to 59 mL/min renal function values.

Results of the current study are consistent with previous data that revealed a trend to GFR over-estimation when C–G is used compared to MDRD4 [24]. Different factors could contribute to this. First, the lack of isotope dilution mass spectrometry (IDMS)-traceable creatinine for standardization of creatinine concentrations when C–G was developed. Second, the presence of BW in C–G versus the adjustment for body surface area (1.73 m²) in the case of MDRD4 and CKD-EPI. The presence of BW in the C–G formula hampered the statistically significant inclusion of this covariate when tested on GCV CL, suggesting that part of the deviations between C–G and the other formulas were due to this. However, C–G was developed in lean individuals and should not be used in obese patients. Nevertheless, the independent inclusion of BW on GCV CL apart from the CRCL covariate was crucial for dose optimization as shown in Table 4 and Table S1 of the ESM. Indeed, %PTAs achieved after comparing inclusion versus non-inclusion of BW suggest that refinement of dose recommendations should be done especially for the lowest BW (40 kg) that showed overdosing at all renal function cut-offs except that of 50–59 mL/min, at which the higher renal function allowed AUC values closer to the desired target. Overdosing was also observed at 60–69 mL/min for this BW (40 kg) at which manufacturer-recommended doses were too high (900 mg/24 h). Regarding the highest BW patients (100 kg), the best-dosed renal function cut-offs were those of 20–24 mL/min and 60–69 mL/min, both coinciding with renal functions for which patients with BW lower than 100 kg were overdosed. The lack of statistically significant differences observed when %PTA from models including BW were compared to those not considering this covariate could be explained by the fact that the overall mean %PTA values corresponding to the typical BW of the population (70 kg) were similar between both types of models. Regardless of the type of equation and renal function cut-off, the range of %PTA variation from the lowest to the highest BW was around 48%. This percentage would account for the exposure variation derived from equal dose administration to patients of different BWs.

The third important point of this study is the statistically significant differences in %PTA when comparing renal function cut-offs (Table 4, Table S1 of the ESM). The overexposure observed at the lowest renal function (10–24 mL/min) decreased as renal function increased. This suggests that new dose recommendations should be established for low renal function groups (10–19, 20–24, and 25–29 mL/min) particularly for BW of 40–70 kg. In line with this, new initial dose requirements [for AUC target values of 40–50 (µg/mL)·h], estimated from the new developed CKD-EPI model, accounting for the influence of BW (Table 5), were in general lower than those actually used, except for patients showing renal functions of 25–39 mL/min and BW from 81 to 130 kg, 50–59 mL/min and 101–130 kg and 60–69 mL/min and 40–80 kg. Several factors could contribute to these differences. First, according to the manufacturer recommendations, the same dose is given for a wider range of renal function variations than those of the current study. Second, the inclusion of BW in the model allows more accurate dose estimations. Third, the fact that the C–G formula used for manufacturers’ dose recommendations tends to overestimate renal function. As expected, new dose requirements also increased with renal function and BW. The inclusion of BW in the model allowed a better dose adjustment within each renal function cut-off group. According to the new calculations, dose changes around 86% can take place from the lowest to the highest BW.

Even though the current study was mainly focused on the accurate description of the renal function through a modeling approach, attempts to identify the best size metrics characterizing the GCV volume of distribution were also made. As a hydrophilic drug, fat is not relevant and total body water should be used as starting point for initial GCV dose calculation. This approach would probably decrease the risk of initial overdosing in obese patients. In our case, the inclusion of total body water or lean BW did not improve the model, probably owing to the reduced number of obese patients. Body weight was retained in the model for practicality during routine clinical practice. Inclusion of BW on the V_c of the CKD-EPI model provided the most accurate prediction of peak concentrations (Table 3).

This study has some limitations. First, the model was developed based on data from two studies carried out at different periods of time. However, most of the patients were admitted to the same hospital and GCV concentration measurements were always carried out by the same laboratory and analytical method. Second, sparse data were analyzed together with rich data. However, sparse designs consisted of more than one sampling per patient, in accordance with a previously established and validated limited sampling strategy. It is worth noting that a larger amount of data proceeded from extensively sampled patients. Third, our data did not contain enough samples from obese patients. Therefore, further studies are required before using the current model in obese patients. Perhaps the influence on GCV PopPK parameters of other variables such as fat-free mass, not available in this study, could be tested in the future.

Conclusions

The CKD-EPI renal function estimate correlates the best with GCV clearance. The refinement of our previous PopPK model based on a more accurate estimation of the renal function by the CKD-EPI formula and BW as a size metric most used in the clinical practice can lead to refined initial dose recommendations and contribute to GCV and VGCV dose individualization when required in the prevention or treatment of CMV infection in SOT patients. The new model can (i) increase the accuracy of GCV exposure predictions when used as a support tool for patients that require therapeutic drug monitoring and (ii) be used as a starting point to establish the pharmacokinetic-pharmacodynamic relationship between GCV exposure and CMV viral load, which in turn will allow the refining of the target exposure to be achieved and thus further optimize the dosage regimen to contribute to efficacy and safety in the target population.

Supplementary Information

Below is the link to the electronic supplementary material.

Declarations

Authors’ Contributions

PNL: data analysis, writing, original draft preparation; JI: data analysis; RR: analytical methods; MM: patient data source; BF-A: revision; OB: patient care and patient data source; JMC: patient care and patient data source; JT: patient care and patient data source; EM: patient care and patient data source; JMG: writing, review, supervision; NL: data analysis, writing original draft preparation, supervision, conceptualization; HC: data analysis, writing original draft preparation, supervision, conceptualization.

Funding

Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.

Conflicts of Interest/Competing Interests

The authors have no conflicts of interest that are directly relevant to the content of this article.

Ethics Approval

Not applicable.

Consent to Participate

Not applicable.

Consent for Publication

Not applicable.

Availability of Data and Material

Data that support the findings of this study are available on request from the corresponding authors.

Code Availability

The code is available upon request.