Hydration effects of Ni²⁺ binding to synthetic polynucleotides with regularly alternating purine–pyrimidine sequences

Abstract

High precision ultrasonic and densimetric techniques have been used to study the interaction of Ni²⁺ ions with right-handed poly[d(G-C)]·poly[d(G-C)], poly-[d(A-C)]·poly[d(G-T)] and poly[d(A-T)]·poly[d(A-T)] in 5 mM CsCl, 0.2 mM HEPES, pH 7.5 at 20°C. From these measurements the changes in the apparent molar volume and the apparent molar adiabatic compressibility due to the interaction have been obtained. The volume effects of the binding, calculated per mole of Ni²⁺ ions, range from 11.7 to 23.9 cm³ mol^–1 and the compressibility effects range from 19.3 × 10^–4 to 43.1 × 10^–4 cm³ mol^–1 bar^–1. These data are interpreted in terms of dehydration of the polynucleotides and Ni²⁺ ions, i.e. the release of water molecules from the hydration shells of the molecules. An increase in G+C content gives an increase in volume and compressibility effects, indicating a rise in the extent of dehydration. The dehydration effects of Ni²⁺ binding to poly[d(G-C)]·poly[d(G-C)] are approximately twice those of poly[d(A-T)]·poly[d(A-T)]. The volume and compressibility effects of Ni²⁺–EDTA complex formation have also been measured and used as a model system for quantitative estimation. These values revealed that Ni²⁺ ions can coordinate two atomic groups of poly[d(G-C)]·poly[d(G-C)], while in the case of the Ni²⁺–poly[d(A-T)]·poly[d(A-T)] complex volume and compressibility effects correspond to one direct or two indirect (through water) contacts.

INTRODUCTION

The most dramatic structural transition of the DNA double helix is between the right-handed B and the left-handed Z conformations (1). The left-handed structure is favored in alternating purine–pyrimidine sequences (2–4). There are three polynucleotides exhibiting such sequences: poly[d(G-C)]·poly-[d(G-C)], poly[d(A-C)]·poly[d(G-T)] and poly[d(A-T)]·poly-[d(A-T)].

Poly[d(G-C)]·poly[d(G-C)] is the most favorable duplex undergoing the B→Z transition under various experimental conditions (alcohol, salts and elevated temperature) (4–8). The most effective agents for inducing the B→Z transition are the transition metal ions, including Ni²⁺ and Co²⁺ (9). Poly[d(A-T)]·poly-[d(A-T)] does not adopt the Z conformation in solution even at high alcohol concentration and/or high ionic strength (2,10–12). However, Adam et al. (13) demonstrated using infrared spectroscopy that this polynucleotide adopts a left-handed conformation in films at high polynucleotide concentration, low water content and in the presence of Ni²⁺ ions. Poly[d(A-C)]·poly[d(G-T)] can adopt the Z form in solution, but it also requires the presence of transition cations (Ni²⁺ or Co²⁺) in addition to very low water activity (14–16).

It is obvious that a study of the hydration properties of Ni²⁺ binding to polynucleotides would be of importance to understand the molecular mechanisms of the B→Z transition. This is particularly true for Ni²⁺ complexing with B-type polynucleotides, which precedes the B→Z transition (17) and can determine the nature of the B→Z transition of the polynucleotides. Therefore, we have decided to investigate the hydration changes accompanying Ni²⁺ binding to right-handed poly[d(G-C)]·poly[d(G-C)], poly[d(A-C)]·poly[d(G-T)] and poly[d(A-T)]·poly[d(A-T)].

Hydration of nucleic acids in aqueous solutions can be investigated by ultrasonic and densimetric techniques, which leads to two independent thermodynamic parameters: the apparent molar volume, ΦV, and the apparent molar adiabatic compressibility, ΦK_S. These parameters are very sensitive to hydration of nucleic acids (18–21), salts (22–24) and the interaction between them (19,25–27). Interaction between the molecules is usually accompanied by changes in the hydration shells, which are reflected in the measured values of ΦV and ΦK_S.

In the present work, acoustic, densimetric and circular dichroism (CD) techniques were used to characterize hydration effects of Ni²⁺ binding to poly[d(G-C)]·poly[d(G-C)], poly[d(A-C)]·poly[d(G-T)] and poly[d(A-T)]·poly[d(A-T)]. We found that the binding process is accompanied by overlapping hydration shells and the consequent release of water molecules. The overall dehydration effects are proportional to G+C content of the duplexes. Analysis of the hydration parameters revealed that Ni²⁺ ions coordinate with two atomic groups of G·C, while in the case of A·T base pairs the dehydration effects correspond to a single direct contact.

MATERIALS AND METHODS

Materials

The sodium salts of poly[d(A-T)]·poly[d(A-T)], poly[d(A-C)]·poly[d(G-T)] and poly[d(G-C)]·poly[d(G-C)] were obtained from Pharmacia LKB (USA), analytical grade NiCl₂ and ethylendiamine tetraacetic acid (EDTA) from Merck (Darmstadt, Germany). The nucleic acids were dissolved in 200 mM CsCl, 10 mM EDTA, pH 8, and dialyzed against 5 mM CsCl, 0.2 mM Cs-HEPES, pH 7.5, for 3–4 days at 4°C. The concentrations of the polynucleotides were determined optically using the molar extinction coefficients in M^–1 cm^–1 of nucleotide units: ɛ₂₆₀ = 6650 for poly[d(A-T)]·poly[d(A-T)], ɛ₂₆₀ = 6500 for poly[d(A-C)]·poly[d(G-T)] and ɛ₂₅₄ = 8400 for poly[d(G-C)]·poly[d(G-C)]. The concentrations were determined in 0.1 M NaCl, 0.01 M Na-HEPES, pH 7.5 at 20°C. The amount of water in the solid NiCl₂ was determined by measuring ultrasonic velocities in aqueous NiCl₂ solutions at 25°C followed by comparison to literature data (28). The experiments were performed in 5 mM CsCl, 0.2 mM Cs-HEPES, pH 7.5 at 20°C. The NiCl₂ solutions were prepared using the same buffer, and pH was adjusted to a value of 7.5 if needed. No significant differences in pH before and after binding experiments were observed. The UV melting at 260 nm showed that the most unstable duplex, poly[d(A-T)]·poly[d(A-T)], is in the double-helical state under our experimental conditions.

CD measurements

CD spectra were obtained with a Jasco J-600 spectropolarimeter using a quartz cuvette with 0.05 cm path length. The titration experiments were performed by adding NiCl₂ solution to 0.140 cm³ polynucleotide solution in the cuvette. Stirring was carried out in the cuvette using a vibrating bar.

Ultrasound velocity measurements

Relative ultrasound velocity was measured by the resonator method (29–31). The polynucleotide solutions were studied in quartz cells of 0.25 cm³ volume (26), while EDTA was investigated in cells of 0.8 cm³ volume with built in stirrers (30). To avoid the influence of temperature fluctuations on ultrasound velocity, a differential method was used in which two identical cells (reference and sample) were connected to a common thermostat. The molar increment of ultrasonic velocity, A, was calculated using the equation

A = (U – U_o)/(U_oC) 1

where U and U_o are the ultrasound velocities in the solution and solvent, respectively, and C is the molar concentration of the polynucleotides per nucleotide unit. The relative experimental error in the measurement of (U – U_o)/U_o was 2 × 10^–5%.

Acoustic titration experiments were performed by addition of NiCl₂ solution to the polynucleotide solutions in the sample cell by Hamilton syringes through the small hole in the stopper. Stirring in the quartz cells was performed using a vibrating bar. In order to estimate the net effects of the interactions of NiCl₂ with the polynucleotides, the contribution of the salt to the ultrasound velocity had to be eliminated. This was accomplished by conducting parallel titration of buffer in the same sample cell. The change in molar increment of ultrasound velocity, ΔA, accompanying the interaction of Ni²⁺ ions with the polynucleotides was calculated using the equation

ΔA = A – A_o 2

where A is the molar increment of ultrasound velocity of the polynucleotide + Ni²⁺ solution relative to buffer + Ni²⁺ and A_o is the molar increment of ultrasound velocity of Ni²⁺-free polynucleotide solution relative to buffer.

Density measurements

The density of solutions was measured with a DMA-602 densimeter (Anton Paar, Graz, Austria), using a 0.2 cm³ cell. As in the case of acoustic measurements, a differential system consisting of two cells was employed. The molar apparent volume, ΦV, was calculated using the equation (22)

ΦV = M/ρ_o – (ρ – ρ_o)/(ρ_oC) 3

where ρ_o and ρ are the density of the solvent and solution, respectively, and M is the molecular mass of the poly-nucleotides per nucleotide unit. The volume changes, ΔV, accompanying Ni²⁺ interaction with the polynucleotides were calculated using the equation

ΔV = ΦV – ΦV_o 4

where ΦV is the apparent molar volume of polynucleotide + Ni²⁺ solution relative to buffer + Ni²⁺ and ΦV_o is the apparent molar volume of a Ni²⁺-free polynucleotide solution relative to buffer.

Calculation of the change in apparent molar adiabatic compressibility, ΔK_S

This parameter is determined as the function of changes in the increment of ultrasonic velocity and apparent molar volume (32,33)

ΔK_S = 2β_o(ΔΦV – ΔA) 5

where β_o is the adiabatic compressibility coefficient of the solvent. The value of β_o was calculated from our data on density, ρ_o, and the ultrasonic velocity, U_o (34), in pure water using the equation β_o = (ρ_oU_o²)^–1.

Fitting of ultrasonic titration curves

The acoustic titration curves of Ni²⁺ binding to the polynucleotides were used to obtain the number of binding sites, n, the binding constants, K, and the change in increment of ultrasound velocity at saturation level, ΔA. The fitting procedure was based on a non-cooperative, single binding site model similar to the standard Scatchard equation (35)

ν/[Ni²⁺]_free = K (n – ν) 6

where ν is the number of Ni²⁺ bound to the polynucleotide calculated per nucleotide unit and described by the equation ν = ΔA_n/ΔA. ΔA_n is the change in increment of ultrasound velocity during titration of the polynucleotides with Ni²⁺.

RESULTS AND DISCUSSION

CD spectra

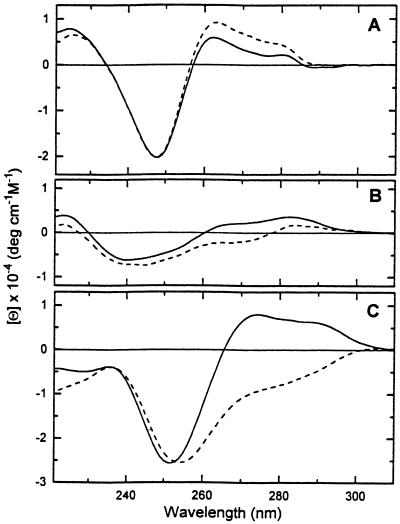
Figure 1 demonstrates the influence of Ni²⁺ ions on the CD spectra of polynucleotides. The mixtures of poly[d(A-T)]·poly[d(A-T)] and poly[d(A-C)]·poly[d(G-T)] with Ni²⁺ ions are measured at [Ni²⁺]/[phosphate] = 0.6–0.7. A further increase in Ni²⁺ ions reaching [Ni²⁺]/[phosphate] = 1 does not influence the CD spectra. In the case of poly[d(G-C)]·poly[d(G-C)], the CD spectrum is recorded at [Ni²⁺]/[phosphate] = 0.38, since after this point cooperative changes typical of the B→Z transition occur. The changes in CD spectra of the polynucleotides due to Ni²⁺ binding are quite significant. The common feature is that most changes occur in the wavelength range 250–300 nm. Ni²⁺ binding to poly[d(A-C)]·poly[d(G-T)] and poly[d(G-C)]·poly-[d(G-C)] induces a decrease in the CD signal, in contrast to an increase for poly[d(A-T)]·poly[d(A-T)]. The decrease in CD signal of DNA duplexes due to cation binding is a well-known phenomenon attributed to structural changes within the family of B-DNA (36–38). Since poly[d(A-T)]·poly[d(A-T)] is the most unstable duplex, it is important to see whether the increase in CD signal is caused by base pairing. We would like to emphasize again that under our experimental conditions (5 mM CsCl, 0.2 mM Cs-HEPES, pH 7.5 at 20°C) poly[d(A-T)]·poly-[d(A-T)] is a fully paired duplex. A visible change in UV optical density has not been observed before 40°C (data not shown). Furthermore, similar results were observed by Gennis and Cantor (39) following a temperature increase from 5 to 39°C for poly[d(A-T)]·poly[d(A-T)] in 5 mM NaCl, 1 mM cacodylate, pH 7.0 (melting begins at 40°C). They also showed that this effect is independent of ionic strength (39). Thus, it is clear that an increase in the CD signal of poly[d(A-T)]·poly-[d(A-T)] indicates an absence of base pairing, and the changes may correspond to structural rearrangement within the framework of the B conformation or possibly to dehydration of adenines as a result of Ni²⁺ binding or an increase in temperature (39).

Figure 1.

CD profiles of poly[d(A-T)]·poly[d(A-T)] (A), poly[d(A-C)]·poly[d(G-T)] (B) and poly[d(G-C)]·poly[d(G-C)] (C). The solid lines correspond to the CD spectra in 5 mM CsCl, 0.2 mM Cs-HEPES, pH 7.5 at 20°C, and the dashed lines correspond to the CD spectra after adding Ni²⁺ ions.

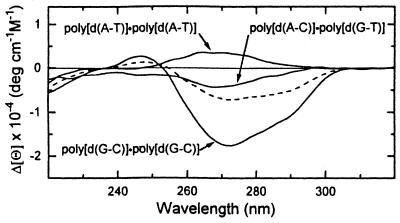
Figure 2 demonstrates the difference CD spectra resulting from subtraction of CD spectra of Ni²⁺-free polynucleotides from the Ni²⁺–polynucleotide complexes. The difference spectrum of the polynucleotide with equal amounts of A·T and G·C base pairs, poly[d(A-C)]·poly[d(G-T)], is situated between those of poly[d(A-T)]·poly[d(A-T)] and poly[d(G-C)]·poly[d(G-C)]. The arithmetic mean of the difference spectra of the latter two polynucleotides (the dashed line in Fig. 2) is close enough to the experimental spectra of poly[d(A-C)]·poly[d(G-T)] to conclude that the CD effects of Ni²⁺ binding to these polynucleotides in first approximation is determined by their nucleotide composition.

Figure 2.

CD difference spectra of the polynucleotides. The CD spectra of the polynucleotides in 5 mM CsCl, 0.2 mM Cs-HEPES, pH 7.5, were subtracted from the spectra after adding Ni²⁺ ions. The dashed line corresponds to the arithmetic mean of the difference spectra of poly[d(A-T)]·poly[d(A-T)] and poly[d(G-C)]·poly[d(G-C)].

Overall volume and compressibility changes correspond to hydration effects of the binding

The following relationships can represent the apparent molar volume, ΦV, and the apparent molar adiabatic compressibility, ΦK_S (40):

ΦV = V_m + ΔV_h 7

ΦK_S = K_m + ΔK_h 8

where V_m and K_m are, respectively, the intrinsic molar volume of a solute molecule that is inaccessible to the surrounding solvent and the intrinsic molar compressibility of this volume. ΔV_h represents the hydration contribution and consists of the volume change of water around the solute molecule as a result of the solute–water interactions and the void volume between the solute molecule and the surrounding water. ΔK_h is the hydration contribution to the apparent molar adiabatic compressibility, consisting of the changes in the compressibility of water around the solute molecule and the compressibility of the voids between the solute molecules and the surrounding water.

To analyze the changes in ΦV and ΦK_S values due to Ni²⁺–polynucleotide interaction in terms of hydration, one should evaluate the changes in intrinsic terms, ΔV_m and ΔK_m. In other words, the changes in compressibility and volume due to structural reorganization of the polynucleotides should be estimated. Here we must take a closer look at the CD profiles again. As can be seen from Figure 1, poly[d(A-T)]·poly[d(A-T)] and poly[d(A-C)]·poly[d(G-T)] maintain their B form after interaction with Ni²⁺ ions, while the CD effect for poly[d(G-C)]·poly[d(G-C)] is indicative of a B→C transition (38). The B→C transition results in an increase in winding, which is accompanied by a decrease in the number of base pairs per turn from 10 to 9.3 (41). Actually, it is the only difference between the B and C conformations; therefore, C-DNA is assumed to be a member of the B-DNA family (38,41). The calculations of intrinsic molar volumes for A-DNA and B-DNA demonstrated that even this significant rearrangement in the three-dimensional structure of the double helix has negligible effects on its intrinsic volume (42) and intrinsic compressibility (19). One can conclude that the resulting volume and compressibility effects of Ni²⁺ binding to the polynucleotides are mainly determined by the dehydration of cations and atomic groups of the polynucleotides.

Ultrasonic titration curves

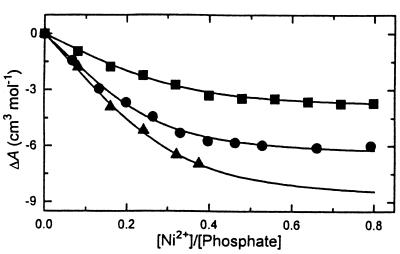
The acoustic titration curves for all polynucleotides show similar shapes (see Fig. 3); an increase in Ni²⁺ concentration is accompanied by decrease in the increment of ultrasound velocity. The decrease up to [Ni²⁺]/[phosphate] = 0.4 is a result of Ni²⁺ binding to polynucleotides. During this process some water molecules are excluded from the hydration shells of Ni²⁺ and the polynucleotides leading to a decrease in the increment of ultrasound velocity. Further addition of Ni²⁺ ions to poly[d(A-T)]·poly[d(A-T)] and poly[d(A-C)]·poly[d(G-T)] does not produce any changes (plateau region in Fig. 3), indicating saturation of the duplexes by Ni²⁺ ions. However, for poly[d(G-C)]·poly[d(G-C)] saturation was not achieved due to the B→Z transition, which is further characterized by a rapid drop in the increment of ultrasound velocity (43). The magnitude of the changes in the ultrasound velocity due to Ni²⁺ binding depends on the nucleotide composition of the polynucleotides (Fig. 3); with increasing G+C content, the dehydration effect of Ni²⁺ binding increases. This result agrees well with similar investigations on Mg²⁺ binding to octamer duplexes of different nucleotide sequences (25). The solid lines in Figure 3 are the result of the non-linear three parameter fitting procedure (see Materials and Methods). The obtained binding parameters are listed in Table 1. Because the titration curve of poly[d(G-C)]·poly-[d(G-C)] has no experimental points beyond [Ni²⁺]/[phosphate] = 0.38 (Fig. 3), it is important to evaluate the reliability of the ΔA value obtained from the fitting procedure. The ΔA value per mole of Ni²⁺ can be also calculated from the initial points of the titration curve, which is equal to –28.8 cm³ mol^–1. This value is in excellent agreement with ΔA obtained from the fitting procedure (see Table 2), indicating the validity of the procedure.

Figure 3.

Ultrasonic titration curves of poly[d(A-T)]·poly[d(A-T)] (squares), poly[d(A-C)]·poly[d(G-T)] (circles) and poly[d(G-C)]·poly[d(G-C)] (triangles) with Ni²⁺ ions. Buffer, 5 mM CsCl, 0.2 mM Cs-HEPES, pH 7.3 at 20°C. The solid lines are the result of a non-linear three parameter fitting procedure.

Table 1. The volume and ultrasound effects of Ni²⁺ binding to the polynucleotides and the binding parameters obtained from the acoustic titration curves^a.

Polynucleotide	ΔV (cm3 mol–1)	ΔA (cm3 mol–1)	n	K × 10–4 (M–1)
poly[d(A-T)]·poly[d(A-T)]	4.9 ± 0.6	–4.1 ± 0.4	0.42	9.0
poly[d(A-C)]·poly[d(G-T)]	6.0 ± 0.6	–5.6 ± 0.4	0.36	6.7
poly[d(G-C)]·poly[d(G-C)]	6.9 ± 0.6	–8.9 ± 0.4	0.33	1.1

^aThe experimental uncertainties in the estimation of n and K are <15%.

Table 2. Volume and compressibility effects of Ni²⁺ binding to the polynucleotides calculated per mole Ni²⁺.

Polynucleotide	ΔA (cm3 mol–1)	ΔV (cm3 mol–1)	ΔKS × 104 (cm3 mol–1 bar–1)
poly[d(A-T)]·poly[d(A-T)]	–9.8	11.7	19.3
poly[d(A-C)]·poly[d(G-T)]	–15.6	16.7	29.2
poly[d(G-C)]·poly[d(G-C)]	–27.0	23.9	43.1

Volume and compressibility effects

The volume changes, ΔV, of Ni²⁺ binding to polynucleotides are measured at particular values of [Ni²⁺]/[phosphate] (Table 1). In the case of poly[d(A-T)]·poly[d(A-T)] and poly[d(A-C)]·poly[d(G-T)] the ratios were taken from the saturation level of the acoustic titration curves ([Ni²⁺]/[phosphate] = 0.66 and 0.63, respectively), while for poly[d(G-C)]·poly[d(G-C)] the ratio was taken just prior to the B→Z transition ([Ni²⁺]/[phosphate] = 0.35). The compressibility effects, ΔK_S, are calculated according to equation 5. Both the ΔV and ΔK_S values, calculated per mole of Ni²⁺, are listed in Table 2. They are positive, indicating the release of water molecules from hydration shells of Ni²⁺ and the polynucleotides. The ΔV and ΔK_S values are proportional to G+C content of the polynucleotides, which reveals the dehydration effects of Ni²⁺ binding to the polynucleotides, as well as CD effects (Fig. 2) determined by nucleotide composition. Our studies show excellent correlation with the work of Sigel et al. (44). They demonstrated that the N7 position of adenine is less basic in comparison to the N7 position of guanine, which explains the stronger interaction of Ni²⁺ ions with the latter nucleoside (44).

The hydration terms in apparent molar volume and apparent molar adiabatic compressibility, ΔV_h and ΔK_h, are mainly determined by the first coordination layer of water molecules (45,46). Therefore, the hydration effects of Ni²⁺ binding to the polynucleotides can be accompanied by visible hydration effects when water molecules are released from their first hydration shells. If one assumes that all measured hydration effects correspond to direct contacts between Ni²⁺ ions and the atomic groups of the polynucleotides, the number of direct contacts, N, can be estimated from the equations

N = ΔV/ΔV_c 9

N = ΔK_S/ΔK_c 10

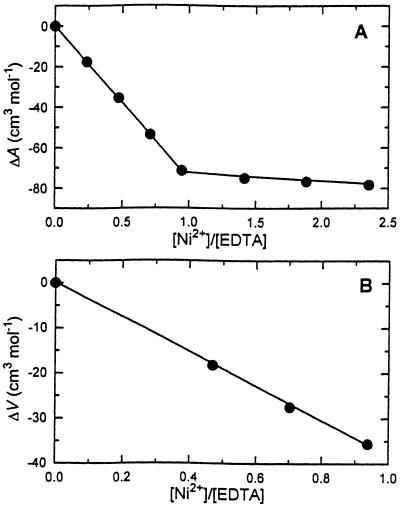
where ΔV_c and ΔK_c are volume and compressibility effects of a coordination bond or dehydration effects of a direct contact between the polynucleotides and Ni²⁺. One can evaluate these values from volume and compressibility effects of Ni²⁺ binding to a molecule with a well-characterized structure of the complex. Such an example is the Ni²⁺–EDTA complex (47,48). The EDTA molecule carries six chelating atomic groups: two polar nitrogens and four negatively charged oxygens. These atomic groups are similar to peripheral residues of nucleic acids, phosphate oxygen and nucleic base nitrogen, which are the most plausible binding sites for Ni²⁺ ions (17,41,49–51). Our volume and compressibility studies on Ni²⁺ binding to EDTA have been performed in 6 mM Na-HEPES, pH 8 and 25°C (Fig. 4). Under these conditions the following reaction occurs (52):

Figure 4.

Ultrasonic (A) and densimetric (B) titration curves of EDTA by Ni²⁺ ions in 6 mM HEPES, pH 8 at 25°C.

Ni²⁺ + H-EDTA^3– = Ni-EDTA^2– + H⁺ 11

To obtain the net effects in ΔA, ΔV and ΔK_S of Ni²⁺ binding to EDTA, the same parameters of reaction 11 should be corrected for deprotonation effects. This value can be obtained from similar experiments on EDTA binding to alkaline earth metal ions at pH 8 (53) and 12 (54). At the latter pH the following reaction occurs (52):

Me²⁺ + EDTA^4– = Me-EDTA^2– 12

It is obvious that the differences in ΔA, ΔV and ΔK_S between reactions 11 and 12 correspond to deprotonation effects, which are equal to –32 cm³ mol^–1 for ΔA, 17 cm³ mol^–1 for ΔV and 42 × 10^–4 cm³ mol^–1 bar^–1 for ΔK_S (53,54). The recalculated data for the Ni²⁺ + EDTA^4– reaction are collected in Table 3. Keeping in mind that the Ni²⁺ ion creates six coordination bonds with the EDTA molecule (47,48), an average direct contact between Ni²⁺ and EDTA^4– should induce 9.3 cm³ mol^–1 and 23.7 × 10^–4 cm³ mol^–1 bar^–1 changes in volume and compressibility, respectively.

Table 3. Ultrasound velocity, volume and compressibility effects of Ni²⁺ binding to EDTA.

Reaction	ΔA (cm3 mol–1)	ΔV (cm3 mol–1)	ΔKS × 104 (cm3 mol–1 bar–1)
Ni2+ + H-EDTA3–	–72.5	38.6	–100.0
Ni2+ + EDTA4–	–104.5	55.6	–142.0

According to equations 9 and 10 the dehydration effects of Ni²⁺ binding to poly[d(G-C)]·poly[d(G-C)] correspond to two direct contacts. For poly[d(A-T)]·poly[d(A-T)] and poly[d(A-C)]·poly-[d(G-T)] the number of direct contacts equals 1 and 1.5, respectively. In their studies on Ni²⁺ binding to poly[d(G-C)]·poly-[d(G-C)] by the temperature-jump relaxation technique, Schoenknecht and Diebler (17) found evidence for Ni²⁺ binding to more than one binding site on the polynucleotide, presumably to N7 of guanine and a phosphate group. As mentioned earlier, prior to the B→Z transition Ni²⁺ ions transform poly[d(G-C)]·poly[d(G-C)] to the C conformation, which is characterized by an increased winding angle between base pairs with a deeper minor groove and a shallower major groove in comparison with the B conformation (41). It was suggested that this structural transition is the result of a transition cation binding simultaneously to H7 of a purine and a phosphate group in the major groove (36). As stated previously, the number of contacts was calculated under the assumption that overall hydration effects are attributed to direct contacts between the DNA and Ni²⁺ ions. One cannot exclude the possibility of larger numbers of indirect contacts, especially for poly[d(A-T)]·poly[d(A-T)]. It has been shown, for example, that in crystals of the decanucleotide d(CGTATATACG), Ni²⁺ ions are associated with N7 atoms of all the guanines, while no Ni²⁺ has been found at N7 atoms of adenines (55).