Soliton solution, breather solution and rational wave solution for a generalized nonlinear Schrödinger equation with Darboux transformation

Abstract

In this paper, the exact solutions of generalized nonlinear Schrödinger (GNLS) equation are obtained by using Darboux transformation(DT). We derive some expressions of the 1-solitons, 2-solitons and n-soliton solutions of the GNLS equation via constructing special Lax pairs. And we choose different seed solutions and solve the GNLS equation to obtain the soliton solutions, breather solutions and rational wave solutions. Based on these obtained solutions, we consider the elastic interactions and dynamics between two solitons.

Introduction

The generalized nonlinear Schrödinger(GNLS) equation is an important nonlinear evolution equation, which can describe physical models and phenomena, such as: the Bose–Einstein condensation, nonlinear optics, plasma physics condensed matter physics, fluid mechanics, and so on. Latchio Tiofack, Mohamadou and Kofan$\acute{e}$ considered the nonuniform $1+1$ dimensional coupled nonlinear schrödinger equations¹, and presented some exact solutions by using the transformation. Vijayalekshmi, Mahalingam and Mani–Rajan studied the propagation of optical solitons in the nonautonomous nonlinear Schrödinger equation with a generalized external potential². The nonlinear Schrödinger equation has been extended to various soliton models³ including variable coefficient, complex coefficient, high dimensional, high order, nonlocal and fractional order equations^4–6. Some solitary wave solutions⁷, rogue wave solutions⁸, bright and dark solitons⁹ are derived in nonlinear Schrödinger equation.

There are many methods to solve soliton equation, such as Hirota bilinear method^10,11, inverse scattering method^12,13, homogeneous balance method^14,15, Darboux transform (DT) method^16,17 and so on. Some solutions are successfully solved in different types of partial differential equations via these above methods. Some higher-order wave solutions and discrete rogue wave solutions of KE equation were constructed by using DT and Taylor expansion in^18,19. Ablowitz and Musslimani proposed the nonlocal modified Korteweg–de Vries (mKdV) equation and the nonlocal Sine–Gordon (SG) equation, and proved the integrability of these equations in²⁰. Ji and Zhu obtained a series of different types of exact analytical solutions of nonlocal mKdV equations through constructing DT²¹, including complexiton solutions, rogue wave solutions, kink soliton solutions and anti-kink soliton solutions. Some bright soliton solutions, dark soliton solutions and breather solutions of the super integrable equation are presented with DT²². The non-autonomous multi-rogue wave solutions of the spin-1 coupled nonlinear Gross–Pitaevskii equation with different dispersion, higher-order nonlinear terms, gain (or loss) and external potential are considered in^23–25. The multiple breather solutions and mixed solutions of the Kundu equation are constructed with generalized Darboux transformation method, which have the Lax pair of Kaup–Newell system in²⁶.

The paper is organized as follows: in “Results”, we successfully solve the GNLS equation with DT, and obtain several new sets of exact solutions, including 1-soliton solutions, 2-soliton solutions and n-soliton solutions. In “Conclusions”, we select the non-zero seed solution and solve the GNLS equation by using the DT, and obtain the breather solutions of the GNLS equation. In “Methods”, we also use the DT and Taylor expansion to derive the rational wave solutions of the GNLS equation. Finally, we give some conclusions in “Rational wave solutions for GNLS Eq. (4)”.

Results

Soliton solutions of GNLS equation

It is well known that the standard nonlinear Schrödinger(NLS) equation

$$\begin{array}{c}\hfill i{u}_t+\gamma u_{\mathit{xx}}+\sigma u{|u|}^2=0,\sigma =\pm 1,\end{array}$$ 1

is one of the most important integrable system among many branches of applied mathematics and physics, especially in optics, water wave and so on. The $u=u(x,t)$ is a complex smooth function of x and t , the subscripts denote partial derivatives and the parameter $\gamma$ is real constant in Eq. (1).

Fokas studied an integrable generalized nonlinear Schrödinger (GNLS) equation by means of bi-Hamiltonian operators

$$\begin{array}{c}\hfill i{u}_t-v{u}_{\mathit{tx}}+\gamma u_{\mathit{xx}}+\sigma {|u|}^2(u+iv{u}_x)=0,\sigma =\pm 1,\end{array}$$ 2

where $\gamma$ and v are real constants. In fact, Eq. (2) can be transformed into Eq. (1) when the parameter $v=0$. Lenells investigated Eq. (2) by the dressing method, and presented a new form of Eq. (2) as following

$$\begin{array}{c}\hfill u_{\mathit{tx}}+\alpha {\beta }^{2}u-2i\alpha \beta u_x-\alpha u_{\mathit{xx}}+\sigma i\alpha {\beta }^2{|u|}^2{u}_x=0,\sigma =\pm 1,\end{array}$$ 3

under the transformation of $u\to \beta \sqrt{\alpha }{e}^{i\beta x}u$, $\sigma =-\sigma$, where $\alpha =\frac{\gamma }{\nu }>0,\beta =\frac{1}{v}$.

Without losing generality, let $\sigma =-1$, then Eq. (3) will become the following form²⁷:

$$\begin{array}{c}\hfill u_{\mathit{tx}}+\alpha {\beta }^{2}u-2i\alpha \beta u_x-\alpha u_{\mathit{xx}}-i\alpha {\beta }^2{|u|}^2{u}_x=0,\end{array}$$ 4

and the Lax pair of Eq. (4) is as following

$$\begin{array}{cc}\hfill {\phi }_x=& U\phi ,{\phi }_t=V\phi ,\hfill \\ \hfill U=& \left(\begin{array}{cc}-i{\lambda }^2& \lambda u_x\\ \lambda r_x& i{\lambda }^2\end{array}\right),V=\left(\begin{array}{cc}-\frac{i\alpha {\beta }^2}{2}ur-i{\eta }^2& \frac{i\alpha {\beta }^2}{2\lambda }u+\alpha \lambda u_x\\ -\frac{i\alpha {\beta }^2}{2\lambda }r+\alpha \lambda r_x& \frac{i\alpha {\beta }^2}{2}ur+i{\eta }^2\end{array}\right),\hfill \end{array}$$ 5

where $\eta =\sqrt{\alpha }(\lambda -\frac{\beta }{2\lambda }),r=-u^{\ast }$, the $``{\ast }^{\prime \prime }$ denotes the complex conjugate and the vector $\phi ={({\phi }_1,{\phi }_2)}^T$ is an eigenfunction associated with $\lambda$ and potential u, which consists of two complex functions ${\phi }_1={\phi }_1(x,t)$ and ${\phi }_2={\phi }_2(x,t)$. Trough direct calculations, we can verify that the integrability condition $U_t-V_x+[U,V]=0$ exactly can be derived from Eq. (4), where $[U,V]=UV-VU$.

From the above analysis, we could construct a N-fold Darboux matrix T for the GNLS equation (4), as follows

$$\begin{array}{c}\hfill {\tilde{\phi }}_n=T{\phi }_n,T=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right).\end{array}$$ 6

The lower forms are obtained by compatibility

$$\begin{array}{cc}\hfill {\phi }_x=& \tilde{U}\phi ,\tilde{U}=(T_x+TU)T^{-1},\hfill \end{array}$$ 7

$$\begin{array}{cc}\hfill {\phi }_t=& \tilde{V}\phi ,\tilde{V}=(T_t+TV)T^{-1}.\hfill \end{array}$$ 8

If the $\tilde{U},\tilde{V}$ and U, V have the same types, the system (6) is called Darboux transformation of the GNLS equation. Let $\psi ={({\psi }_1,{\psi }_2)}^T$, $\varphi ={({\varphi }_1,{\varphi }_2)}^T$ are two basic solutions of the systems (5), then we give the following linear algebraic systems:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\sum }_{k=1}^N{A}_k{\lambda }_j^{2k}+{\sum }_{k=1}^N{B}_k{\lambda }_j^{2k-1}{M}_j^{(1)}=-1,\hfill \\ {\sum }_{k=1}^N-B_k^{\ast }{\lambda }_j^{2k-1}+{\sum }_{k=1}^N{A}_k^{\ast }{\lambda }_j^{2k}{M}_j^{(1)}=-M_j^{(1)},\hfill \end{array}\right)\end{array}$$ 9

with

$$\begin{array}{c}\hfill M_j^{(1)}=\frac{{\psi }_2+v_j^{(1)}{\varphi }_2}{{\psi }_1+v_j^{(1)}{\varphi }_1},(1\le j\le 2N),A_k^{\ast }=D_k,-B_k^{\ast }=C_k,\end{array}$$ 10

where ${\lambda }_j$ and $v_j^{(k)}$ should choose appropriate parameters, thus the determinants of coefficients for Eq. (9) are nonzero. Hereby, we take a $2\times 2$ matrix T as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{T}_{11}=1+{\sum }_{k=1}^N{A}_k{\lambda }^{2k},T_{12}={\sum }_{k=1}^N{B}_k{\lambda }^{2k-1},\hfill \\ T_{21}={\sum }_{k=1}^N-B_k^{\ast }{\lambda }^{2k-1},T_{22}=1+{\sum }_{k=1}^N{A}_k^{\ast }{\lambda }^{2k},\hfill \end{array}\right)\end{array}$$ 11

where N is a natural number, the $A_{\mathit{mn}}^{(i)}(m,n=1,2,i\ge 0)$ are some functions of x and t. Through calculations, we can obtain $\mathrm{\Delta }T$ as following

$$\begin{array}{c}\hfill \mathrm{\Delta }T={\mathrm{\Pi }}_{j=1}^{2N}(\lambda -{\lambda }_j),\end{array}$$ 12

which proves that ${\lambda }_j({\lambda }_j\ne 0)(j=1,2,3,\dots ,2N)$ are 2N roots of $\mathrm{\Delta }T$. Based on these conditions, we will proof that the $\tilde{U}$ and $\tilde{V}$ have the same structures as U and V respectively.

The matrix $\tilde{U}$ defined by (7) has the same type as U, that is,

$$\begin{array}{c}\hfill \tilde{U}=\left(\begin{array}{cc}-i{\lambda }^2& \lambda {\tilde{u}}_x\\ \lambda {\tilde{r}}_x& i{\lambda }^2\end{array}\right),\end{array}$$ 13

in which the transformation formula between old and new potentials are defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\tilde{u}}_x=u_x+B_{1x},\hfill \\ {\tilde{r}}_x=r_x+C_{1x},\hfill \end{array}\right)\end{array}$$ 14

the transformations (14) are used to get a Darboux transformation of the spectral problem (7).

Let $T^{-1}=\frac{T^{\ast }}{\mathrm{\Delta }T}$ and

$$\begin{array}{c}\hfill (T_x+TU)T^{\ast }=\left(\begin{array}{cc}{B}_{11}(\lambda )& B_{12}(\lambda )\\ B_{21}(\lambda )& B_{22}(\lambda )\end{array}\right),\end{array}$$ 15

it is easy to verify that $B_{\mathit{sl}}(1\le s,l\le 2)$ is 2N-order or $2N+1$-order polynomial of $\lambda$.

Through some accurate calculations, ${\lambda }_j(1\le j\le 2,)$ is the root of $B_{\mathit{sl}}(1\le s,l\le 2)$. Thus, Eq. (15) has the following structure

$$\begin{array}{c}\hfill (T_x+TU)T^{\ast }=(\mathrm{\Delta }T)E(\lambda ),\end{array}$$ 16

where

$$\begin{array}{c}\hfill E(\lambda )=\left(\begin{array}{cc}{E}_{11}^{(2)}{\lambda }^2+E_{11}^{(1)}\lambda +E_{11}^{(0)}& E_{12}^{(1)}\lambda +E_{12}^{(0)}\\ E_{21}^{(1)}\lambda +E_{21}^{(0)}& E_{22}^{(2)}{\lambda }^2+E_{22}^{(1)}\lambda +E_{22}^{(0)}\end{array}\right),\end{array}$$ 17

and $E_{\mathit{mn}}^{(k)}(m,n=1,2,k=0,1)$ satisfy the functions without $\lambda$ . Equation (16) can be rewritten as

$$\begin{array}{c}\hfill (T_x+TU)=E(\lambda )T.\end{array}$$ 18

Through comparing the coefficients of $\lambda$ in Eq. (18), we can obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{E}_{11}^{(0)}=0,E_{11}^{(1)}=0,E_{11}^{(2)}=i,E_{12}^{(0)}=0,E_{12}^{(1)}=u_x+B_{1x}={\tilde{u}}_x,\hfill \\ E_{21}^{(0)}=0,E_{21}^{(1)}=r_x+C_{1x}={\tilde{r}}_x,E_{22}^{(0)}=0,E_{22}^{(1)}=0,E_{22}^{(2)}=i.\hfill \end{array}\right)\end{array}$$ 19

In this section, we assume that the new matrix $\tilde{U}$ has the same type with U, which means that they have the same structures only u(x, t), r(x, t) of U transformed into $\tilde{u}(x,t),\tilde{r}(x,t)$ of $\tilde{U}$. After careful calculation, we compare the ranks of ${\lambda }^N$, and get the objective equations as following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\tilde{u}}_x=u_x+B_{1x},\hfill \\ {\tilde{r}}_x=r_x+C_{1x},\hfill \end{array}\right)\end{array}$$ 20

from Eqs. (13) and (14), we know that $\tilde{U}=E(\lambda )$. The proof is completed.

The matrix $\tilde{V}$ defined by the second expression of (8) has the same form as V, in which the old potentials u and r are mapped into $\tilde{u}$ and $\tilde{r}$, that is,

$$\begin{array}{c}\hfill \tilde{V}=\left(\begin{array}{cc}-\frac{i\alpha {\beta }^2}{2}\tilde{u}\tilde{r}-i{\eta }^2& \frac{i\alpha {\beta }^2}{2\lambda }\tilde{u}+\alpha \lambda {\tilde{u}}_x\\ -\frac{i\alpha {\beta }^2}{2\lambda }\tilde{r}+\alpha \lambda {\tilde{r}}_x& \frac{i\alpha {\beta }^2}{2}\tilde{u}\tilde{r}+i{\eta }^2\end{array}\right).\end{array}$$ 21

We suppose the new matrix $\tilde{V}$ also has the same form with V. If we obtain the similar relations between u(x, t), r(x, t) and $\tilde{u}(x,t),\tilde{r}(x,t)$ in Eq. (14), we can prove that the gauge transformations under T turn the Lax pairs U, V into new Lax pairs $\tilde{U},\tilde{V}$ with the same types.

Let $T^{-1}=\frac{T^{\ast }}{\mathrm{\Delta }T}$ and

$$\begin{array}{c}\hfill (T_t+TV)T^{\ast }=\left(\begin{array}{cc}{C}_{11}(\lambda )& C_{12}(\lambda )\\ C_{21}(\lambda )& C_{22}(\lambda )\end{array}\right),\end{array}$$ 22

it is easy to verify that $C_{\mathit{sl}}(1\le s,l\le 2)$ is 2N-order or $2N+1$-order polynomial of $\lambda$. Through some accurate calculations, ${\lambda }_j(1\le j\le 2)$ is the root of $C_{\mathit{sl}}(1\le s,l\le 2)$. Thus, Eq. (22) has the following structure

$$\begin{array}{c}\hfill (T_t+TV)T^{\ast }=(\mathrm{\Delta }T)F(\lambda ),\end{array}$$ 23

where

$$\begin{array}{c}\hfill F(\lambda )=\left(\begin{array}{cc}{F}_{11}^{(2)}{\lambda }^2+F_{11}^{(0)}+F_{11}^{(-2)}{\lambda }^{-2}& F_{12}^{(1)}\lambda +F_{12}^{(-1)}{\lambda }^{-1}\\ F_{21}^{(1)}\lambda +F_{21}^{(-1)}{\lambda }^{-1}& F_{22}^{(2)}{\lambda }^2+F_{22}^{(0)}{F}_{22}^{(-2)}{\lambda }^{-2}\end{array}\right),\end{array}$$ 24

and $F_{\mathit{mn}}^{(k)}(m,n=1,2,k=0,1)$ satisfies the functions without $\lambda$. According to Eq. (23), the following equation is obtained

$$\begin{array}{c}\hfill (T_t+TV)=F(\lambda )T.\end{array}$$ 25

Through comparing the coefficients of $\lambda$ in Eq. (25), we get the objective equations as following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{F}_{11}^{(-2)}=-\frac{i\alpha {\beta }^2}{4},F_{11}^{(2)}=-i\alpha ,F_{11}^{(0)}=i\alpha \beta -\frac{i\alpha {\beta }^2}{2}\tilde{u}\tilde{r},\hfill \\ F_{12}^{(-1)}=\frac{i\alpha {\beta }^2}{2}\tilde{u},F_{12}^{(1)}=\frac{A_N{u}_x\alpha +2i\alpha B_N}{D_N},\hfill \\ F_{21}^{(-1)}=-\frac{i\alpha {\beta }^2}{2}\tilde{r},F_{21}^{(1)}=\frac{D_N{r}_x\alpha -2i\alpha C_N}{A_N},\hfill \\ F_{22}^{(-2)}=\frac{i\alpha {\beta }^2}{4},F_{22}^{(2)}=i\alpha ,F_{22}^{(0)}=-i\alpha \beta +\frac{i\alpha {\beta }^2}{2}\tilde{u}\tilde{r}.\hfill \end{array}\right)\end{array}$$ 26

In this section, we assume the new matrix $\tilde{V}$ has the same type with V, which means they have the same structures only u(x, t), r(x, t) of V transformed into $\tilde{u}(x,t),\tilde{r}(x,t)$ of $\tilde{V}$. From Eqs. (14) and (21), we know that $\tilde{V}=F(\lambda )$ . The proof is completed.

We will give some novel explicit solutions of Eq. (4) by applying N-fold DT. Firstly, we give a seed solution $u=0$ and substitute the solution into Eq. (5), it is easy to find two basic solutions for these equations:

$$\begin{array}{c}\hfill \psi (\lambda )=\left(\begin{array}{c}{e}^{-i{\lambda }^{2}x-i{\eta }^{2}t+C_1}\\ 0\end{array}\right),\varphi (\lambda )=\left(\begin{array}{c}0\\ e^{i{\lambda }^{2}x+i{\eta }^{2}t+C_2}\end{array}\right),\end{array}$$ 27

by using Eqs. (8) and (25), we obtain

$$\begin{array}{c}\hfill M_j^{(1)}=\frac{v_j^{(1)}{e}^{-i{\lambda }^{2}x-i{\eta }^{2}t+C_1}}{e^{i{\lambda }^{2}x+i{\eta }^{2}t+C_2}}=e^{2(i{\lambda }_j^{2}x+i{\eta }^{2}t+F_j)},\end{array}$$ 28

with ${\nu }_j^{(i)}=e^{(2i{F}_{\mathit{ji}})}$ $(1\le i\le 2,1\le j\le 2N)$.

In order to derive the expression of N-order DT of Eq. (4) and obtain the matrix T

$$\begin{array}{c}\hfill T=\left(\begin{array}{cc}1+{\sum }_{k=1}^N{A}_k{\lambda }^{2k}& {\sum }_{k=1}^N{B}_k{\lambda }^{2k-1}\\ {\sum }_{k=1}^N-B_k^{\ast }{\lambda }^{2k-1}& 1+{\sum }_{k=1}^N{A}_k^{\ast }{\lambda }^{2k}\end{array}\right),\end{array}$$ 29

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\sum }_{k=1}^N{A}_k{\lambda }_j^{2k}+{\sum }_{k=1}^N{B}_k{\lambda }_j^{2k-1}{M}_j^{(1)}+1=0,\hfill \\ {\sum }_{k=1}^N-B_k^{\ast }{\lambda }_j^{2k-1}+{\sum }_{k=1}^N{A}_k^{\ast }{\lambda }_j^{2k}{M}_j^{(1)}+M_j^{(1)}=0.\hfill \end{array}\right)\end{array}$$ 30

Solving Eq. (30) via the Gramer’s rule, we have

$$\begin{array}{c}\hfill B_N=\frac{\mathrm{\Delta }{B}_N}{\mathrm{\Delta }},C_N=\frac{\mathrm{\Delta }{C}_N}{\mathrm{\Delta }}\end{array}$$ 31

with

$$\begin{array}{cc}\hfill \mathrm{\Delta }=& \left|\begin{array}{ccccccccc}{\lambda }_1^2& {\lambda }_1^4& {\lambda }_1^6& \dots & {\lambda }_1^{2N}& M_1{\lambda }_1& M_1{\lambda }_1^3& \dots & M_1{\lambda }_1^{(2N-1)}\\ {\lambda }_2^2& {\lambda }_2^4& {\lambda }_2^6& \dots & {\lambda }_2^{2N}& M_2{\lambda }_2& M_2{\lambda }_2^3& \dots & M_2{\lambda }_2^{(2N-1)}\\ {\lambda }_3^2& {\lambda }_3^4& {\lambda }_3^6& \dots & {\lambda }_3^{2N}& M_3{\lambda }_3& M_3{\lambda }_3^3& \dots & M_3{\lambda }_3^{(2N-1)}\\ ⋮& ⋮& ⋮& \dots & ⋮& ⋮& ⋮& \dots & ⋮\\ {\lambda }_{2N}^2& {\lambda }_{2N}^4& {\lambda }_{2N}^6& \dots & {\lambda }_{2N}^{2N}& M_{2N}{\lambda }_{2N}& M_{2N}{\lambda }_{2N}^3& \dots & M_{2N}{\lambda }_{2N}^{(2N-1)}\end{array}\right|,\hfill \\ \hfill \mathrm{\Delta }{B}_N=& \left|\begin{array}{ccccccccc}{\lambda }_1^2& {\lambda }_1^4& {\lambda }_1^6& \dots & {\lambda }_1^{2N}& M_1{\lambda }_1& M_1{\lambda }_1^3& \dots & -1\\ {\lambda }_2^2& {\lambda }_2^4& {\lambda }_2^6& \dots & {\lambda }_2^{2N}& M_2{\lambda }_2& M_2{\lambda }_2^3& \dots & -1\\ {\lambda }_3^2& {\lambda }_3^4& {\lambda }_3^6& \dots & {\lambda }_3^{2N}& M_3{\lambda }_3& M_3{\lambda }_3^3& \dots & -1\\ ⋮& ⋮& ⋮& \dots & ⋮& ⋮& ⋮& \dots & ⋮\\ {\lambda }_{2N}^2& {\lambda }_{2N}^4& {\lambda }_{2N}^6& \dots & {\lambda }_{2N}^{2N}& M_{2N}{\lambda }_{2N}& M_{2N}{\lambda }_{2N}^3& \dots & -1\end{array}\right|,\hfill \\ \hfill \mathrm{\Delta }{C}_N=& \left|\begin{array}{ccccccccc}{\lambda }_1& {\lambda }_1^3& {\lambda }_1^5& \dots & -M_1& M_1{\lambda }_1^2& M_1{\lambda }_1^4& \dots & M_1{\lambda }_1^{2N}\\ {\lambda }_2& {\lambda }_2^3& {\lambda }_2^5& \dots & -M_2& M_2{\lambda }_2^2& M_2{\lambda }_2^4& \dots & M_2{\lambda }_2^{2N}\\ {\lambda }_3& {\lambda }_3^3& {\lambda }_3^5& \dots & -M_3& M_3{\lambda }_3^2& M_3{\lambda }_3^4& \dots & M_3{\lambda }_3^{2N}\\ ⋮& ⋮& ⋮& \dots & ⋮& ⋮& ⋮& \dots & ⋮\\ {\lambda }_{2N}& {\lambda }_{2N}^3& {\lambda }_{2N}^5& \dots & -M_{2N}& M_{2N}{\lambda }_{2N}^2& M_{2N}{\lambda }_{2N}^4& \dots & M_{2N}{\lambda }_{2N}^{2N}\end{array}\right|.\hfill \end{array}$$ 32

Using Eqs. (6), (20) and (31), we can derive the new formulas of N-soliton solutions for GNLS equation

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\tilde{u}(x,t)=\frac{\mathrm{\Delta }{B}_N}{\mathrm{\Delta }},\hfill \\ \hfill \\ \tilde{r}(x,t)=\frac{\mathrm{\Delta }{C}_N}{\mathrm{\Delta }},\hfill \end{array}\right)\end{array}$$ 33

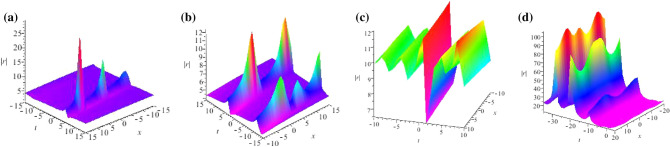
in order to understand solutions (33), we consider $N=1,2$ separately and plot their structure figures in Fig. 1a,b.

• (I)
  We take $N=1$ with $\lambda ={\lambda }_j(j=1,2)$. Solving Eq. (9), we can yield the 1-soliton solutions of the GNLS equation (4) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=\frac{\mathrm{\Delta }{B}_1}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 34

  with

  $$\begin{array}{cc}\hfill \mathrm{\Delta }=& \left|\begin{array}{cc}{\lambda }_1^2& e^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}{\lambda }_1\\ {\lambda }_2^2& e^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}{\lambda }_2\end{array}\right|,\mathrm{\Delta }{B}_1=\left|\begin{array}{cc}{\lambda }_1^2& -1\\ {\lambda }_2^2& -1\end{array}\right|,\hfill \\ \hfill \mathrm{\Delta }{C}_1=& \left|\begin{array}{cc}-e^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}& {\lambda }_1^2{e}^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}\\ -e^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}& {\lambda }_2^2{e}^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}\end{array}\right|.\hfill \end{array}$$ 35
• (II)
  We take $N=2$ in the N-times DT with $\lambda ={\lambda }_j(j=1,2,3,4)$. The linear algebraic system (9) leads to the 2-soliton solutions of GNLS (4) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=\frac{\mathrm{\Delta }{B}_2}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 36

  with

  $$\begin{array}{cc}\hfill \mathrm{\Delta }=& \left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& e^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}{\lambda }_1& e^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}{\lambda }_1^3\\ {\lambda }_2^2& {\lambda }_2^4& e^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}{\lambda }_2& e^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}{\lambda }_2^3\\ {\lambda }_3^2& {\lambda }_3^4& e^{2(i{\lambda }_{3}x+i{\eta }^{2}t+F_3)}{\lambda }_3& e^{2(i{\lambda }_{3}x+i{\eta }^{2}t+F_3)}{\lambda }_3^3\\ {\lambda }_4^2& {\lambda }_4^4& e^{2(i{\lambda }_{4}x+i{\eta }^{2}t+F_4)}{\lambda }_4& e^{2(i{\lambda }_{4}x+i{\eta }^{2}t+F_4)}{\lambda }_4^3\end{array}\right|,\mathrm{\Delta }{B}_2=\left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& e^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}{\lambda }_1& -1\\ {\lambda }_2^2& {\lambda }_2^4& e^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}{\lambda }_2& -1\\ {\lambda }_3^2& {\lambda }_3^4& e^{2(i{\lambda }_{3}x+i{\eta }^{2}t+F_3)}{\lambda }_3& -1\\ {\lambda }_4^2& {\lambda }_4^4& e^{2(i{\lambda }_{4}x+i{\eta }^{2}t+F_4)}{\lambda }_4& -1\end{array}\right|,\hfill \\ \hfill \mathrm{\Delta }{C}_2=& \left|\begin{array}{cccc}{\lambda }_1& -e^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}& {\lambda }_1^2{e}^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}& {\lambda }_1^4{e}^{2(i{\lambda }_{1}x+i{\eta }^{2}t+F_1)}\\ {\lambda }_2& -e^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}& {\lambda }_2^2{e}^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}& {\lambda }_2^4{e}^{2(i{\lambda }_{2}x+i{\eta }^{2}t+F_2)}\\ {\lambda }_3& -e^{2(i{\lambda }_{3}x+i{\eta }^{2}t+F_3)}& {\lambda }_3^2{e}^{2(i{\lambda }_{3}x+i{\eta }^{2}t+F_3)}& {\lambda }_3^4{e}^{2(i{\lambda }_{3}x+i{\eta }^{2}t+F_3)}\\ {\lambda }_4& -e^{2(i{\lambda }_{4}x+i{\eta }^{2}t+F_4)}& {\lambda }_4^2{e}^{2(i{\lambda }_{4}x+i{\eta }^{2}t+F_4)}& {\lambda }_4^4{e}^{2(i{\lambda }_{4}x+i{\eta }^{2}t+F_4)}\end{array}\right|.\hfill \end{array}$$ 37

In order to understand solutions (36), we consider $N=2$ and plot their structure figures in Fig. 1c,d.

Figure 1.

Profiles of intensity distribution (a) $|\tilde{u}(x,t)|$ of Eq. (34) with parameters ${\lambda }_1=1-0.8i,{\lambda }_2=0.6+0.4i,\alpha =0.0004,\beta =1,F_1=0.4+i,F_2=0.3+0.6i$; (b) $|\tilde{u}(x,t)|$ of Eq. (34) with parameters ${\lambda }_1=0.2i,{\lambda }_2=0.1,\alpha =0.4,\beta =0.2,F_1=0.01,F_2=0.02$; (c) $|\tilde{u}(x,t)|$ of Eq. (36) with parameters ${\lambda }_1=0.2,{\lambda }_2=0.3+0.2i,{\lambda }_3=0.3,{\lambda }_4=0.3-0.2i,\alpha =0.2,\beta =0.3,F_1=0.2+0.2i,F_2=0.3-0.2i,F_3=0.3+0.2i,F_4=0.3-0.2i$; (d) $|\tilde{r}(x,t)|$ of Eq. (36) with parameters ${\lambda }_1=0.5,{\lambda }_2=0.2,{\lambda }_3=0.5,{\lambda }_4=0.3,\alpha =0.004,\beta =0.2,F_1=0.5+0.2i,F_2=0.5-0.2i,F_3=0.3+0.1i,F_4=0.3-0.1i$.

Conclusions

The integrable GNLS equation can describe the propagation of nonlinear light pulses in optical fibers, the high-order nonlinear effects are taken into consideration. In this paper, we investigate the exact solutions (including soliton solutions, breather solutions, and rational wave solutions) of a GNLS equation via DT method. And the 1-solitons, 2-solitons and N-soliton solutions of the GNLS equation are obtained via constructing special Lax pairs. And we choose different seed solutions and obtain three kinds of solutions. Based on these obtained solutions, we consider the elastic interactions and dynamics between two solitons for the GNLS equation.

Methods

Breather solutions for GNLS equation (4)

Now we choose there kinds of seed solutions of (4) as follows:

$$\begin{array}{cc}\hfill u=& c_0{e}^{i\sigma {\gamma }_0^{2}x},c_0=\frac{\beta +\sigma {\gamma }_0^2}{\beta {\gamma }_0},\hfill \end{array}$$ 38

$$\begin{array}{cc}\hfill u=& \frac{{\omega }_0}{\beta {\gamma }_0}{e}^{-i({\gamma }_0^{2}x+{\delta }_{0}t)},{\delta }_0=\alpha [{(\beta +\sigma {\gamma }_0^2)}^2-{\omega }_0^2]{\gamma }_0^{-2},\hfill \end{array}$$ 39

and

$$\begin{array}{c}\hfill u=e^{i\theta },\theta =ax+bt,\end{array}$$ 40

where ${\gamma }_0$, ${\omega }_0$, a and b are arbitrary constants.

Case 1: We give a seed solution $u=c_0{e}^{i\sigma {\gamma }_0^{2}x}$ with $c_0=\frac{\beta +\sigma {\gamma }_0^2}{\beta {\gamma }_0}$. According to Eq. (5), we can yield the following systems

$$\begin{array}{c}\hfill \left\{\begin{array}{c}-i{\lambda }^2{\psi }_1+i\sigma {\gamma }_0^2{c}_0\lambda e^{i\sigma {\gamma }_0^{2}x}{\psi }_2={\psi }_{1x},\hfill \\ i\sigma {\gamma }_0^2{c}_0\lambda e^{-i\sigma {\gamma }_0^{2}x}{\psi }_1+i{\lambda }^2{\psi }_2={\psi }_{2x},\hfill \end{array}\right)\end{array}$$ 41

without loss of generality, we assume that $\sigma =-1$, ${\psi }_1=\alpha e^{\mathit{px}}$, ${\psi }_2=\gamma e^{px-i\sigma {\gamma }_0^{2}x}$, then Eq. (41) is solved by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}p=\frac{(i{\lambda }^2\alpha -i\alpha {\gamma }_0^2-i{\lambda }^2)\pm \sqrt{{(i\alpha {\gamma }_0^2-i{\lambda }^2\alpha +i{\lambda }^2)}^2-4\alpha ({\lambda }^4-{\gamma }_0^2{\lambda }^2+{\gamma }_0^4{c}_0^2\alpha {\lambda }^2)}}{2\alpha },\hfill \\ \gamma =\frac{-i{\gamma }_0^2{c}_0\lambda \alpha }{\beta +i{\gamma }_0^2-i{\lambda }^2}.\hfill \end{array}\right)\end{array}$$ 42

Based on Eq. (5), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left(\frac{i\alpha {\beta }^2}{2},c_0^2,e^{-2i{\gamma }_0^{2}x},-,i,{\eta }^2\right){\psi }_1+e^{-i{\gamma }_0^{2}x}\left(\frac{i\alpha {\beta }^2{c}_0}{2\lambda },-,i,\alpha ,c_0,{\gamma }_0^2,\lambda \right){\psi }_2={\psi }_{1t},\hfill \\ e^{-i{\gamma }_0^{2}x}\left(\frac{i\alpha {\beta }^2{c}_0}{2\lambda },+,i,\alpha ,c_0,{\gamma }_0^2,\lambda \right){\psi }_1+\left(-,\frac{i\alpha {\beta }^2{c}_0^2}{2},e^{-2i{\gamma }_0^{2}x},+,i,{\eta }^2\right){\psi }_2={\psi }_{2t},\hfill \end{array}\right)\end{array}$$ 43

we can derive the following system form Eq. (43)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left(\frac{i\alpha {\beta }^2}{2},c_0^2,e^{-2i{\gamma }_0^{2}x},-,i,{\eta }^2,-,{\lambda }_{11}\right)a+\left(e^{-i{\gamma }_0^{2}x},\frac{i\alpha {\beta }^2{c}_0}{2\lambda },-,e^{-i{\gamma }_0^{2}x},i,\alpha ,c_0,{\gamma }_0^2,\lambda \right)b=0,\hfill \\ \left(e^{-i{\gamma }_0^{2}x},\frac{i\alpha {\beta }^2{c}_0}{2\lambda },+,e^{i{\gamma }_0^{2}x},i,\alpha ,c_0,{\gamma }_0^2,\lambda \right)a+\left(-,\frac{i\alpha {\beta }^2{c}_0^2}{2},e^{-2i{\gamma }_0^{2}x},+,i,{\eta }^2,-,{\lambda }_{12}\right)b=0.\hfill \end{array}\right)\end{array}$$ 44

We obtain that

$$\begin{array}{c}\hfill {\lambda }_{11}=\sqrt{\alpha {\beta }^2{c}_0^2{\eta }^2-{\eta }^4-\frac{{\alpha }^2{\beta }^4{c}_0^2}{4{\lambda }^2}},{\lambda }_{12}=-\sqrt{\alpha {\beta }^2{c}_0^2{\eta }^2-{\eta }^4-\frac{{\alpha }^2{\beta }^4{c}_0^2}{4{\lambda }^2}},\end{array}$$

with

$$\begin{array}{c}\hfill a=\left(\frac{i\alpha c_0{\gamma }_0^2\lambda e^{-i{\gamma }_0^{2}x}-\frac{i\alpha {\beta }^2{c}_0}{2\lambda }{e}^{-i{\gamma }_0^{2}x}}{\frac{i\alpha {\beta }^2{c}_0^2}{2}-i{\eta }^2-{\lambda }_{11}}\right)b,\end{array}$$

substituting the above solutions and Eq. (44) into Eq. (5), it is easy to find two basic solutions for these equations:

$$\begin{array}{c}\hfill \left(\begin{array}{c}{\psi }_1\\ {\psi }_2\end{array}\right)=C_1{e}^{{\lambda }_{11}t}\left(\begin{array}{c}\frac{i\alpha c_0{\gamma }_0^2\lambda -\frac{-i\alpha {\beta }^2{c}_0^2}{2}{e}^{-i{\gamma }_0^{2}x}}{\frac{i\alpha {\beta }^2{c}_0^2}{2}{e}^{-2i{\gamma }_0^{2}x}-i{\eta }^2-{\lambda }_{11}}\\ 1\end{array}\right)+C_2{e}^{{\lambda }_{12}t}\left(\begin{array}{c}1\\ \frac{\frac{i\alpha {\beta }^2{c}_0^2}{2}{e}^{-2i{\gamma }_0^{2}x}+i{\eta }^2+{\lambda }_{12}}{e^{-2i{\gamma }_0^{2}x}\frac{i\alpha {\beta }^2{c}_0}{2\lambda }-e^{-i{\gamma }_0^{2}x}i\alpha c_0{\gamma }_0^2\lambda }\end{array}\right).\end{array}$$ 45

It is easy to find two basic solutions for Eqs. (42) and (45):

$$\begin{array}{c}\hfill \left(\begin{array}{c}\psi \\ \varphi \end{array}\right)=\left(\begin{array}{c}\alpha C_1{e}^{{\lambda }_{11}t+px}\left(\frac{i\alpha c_0{\gamma }_0^2\lambda e^{-i{\gamma }_0^{2}x}-\frac{i\alpha {\beta }^2{c}_0}{2\lambda }{e}^{-i{\gamma }_0^{2}x}}{\frac{i\alpha {\beta }^2{c}_0^2}{2}-i{\eta }^2-{\lambda }_{11}}\right)+\alpha C_2{e}^{{\lambda }_{12}t+px}\\ \gamma C_1{e}^{{\lambda }_{11}t+px+i\sigma {\gamma }_0^{2}x}+\gamma C_2{e}^{{\lambda }_{12}t+px+i\sigma {\gamma }_0^{2}x}\left(\frac{e^{i{\gamma }_0^{2}x}\frac{i\alpha {\beta }^2{c}_0}{2\lambda }-e^{i{\gamma }_0^{2}x}i\alpha c_0{\gamma }_0^2\lambda }{\frac{i\alpha {\beta }^2{c}_0^2}{2}-i{\eta }^2+{\lambda }_{12}}\right)\end{array}\right),\end{array}$$ 46

we can obtain by using Eq. (10),

$$\begin{array}{c}\hfill M_j=\frac{C_1\gamma e^{F_j+i{\gamma }_0^{2}x+{\lambda }_{11}t}+\frac{C_2\gamma e^{F_j+2i{\gamma }_0^{2}x+{\lambda }_{12}t}(i\alpha {\beta }^2{c}_0-2i\alpha c_0{\lambda }^2{\gamma }_0^2)}{\lambda (i\alpha {\beta }^2{c}_0^2-2i{\eta }^2+2{\lambda }_{12})}}{C_2\alpha e^{{\lambda }_{12}t}+\frac{C_1\alpha e^{{\lambda }_{11}t-i{\gamma }_0^{2}x}(2i\alpha {\lambda }^2{c}_0{\gamma }_0^2-i\alpha {\beta }^2{c}_0)}{\lambda (i\alpha {\beta }^2{c}_0^2-2i{\eta }^2-2{\lambda }_{11})}},1\le j\le 2N,\end{array}$$ 47

with ${\nu }_j^{(i)}=e^{F_j}$ $(1\le i\le 2,1\le j\le 2N)$.

• (I)
  We take $N=1$ with $\lambda ={\lambda }_j$ (j = 1, 2). We can yield the 1-soliton solutions of the GNLS equation (4) from Eq. (9) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=c_0{e}^{i\sigma {\gamma }_0^{2}x}+\frac{\mathrm{\Delta }{B}_1}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 48

  with

  $$\begin{array}{c}\hfill \mathrm{\Delta }=\left|\begin{array}{cc}{\lambda }_1^2& M_1{\lambda }_1\\ {\lambda }_2^2& M_2{\lambda }_2\end{array}\right|,\mathrm{\Delta }{B}_1=\left|\begin{array}{cc}{\lambda }_1^2& -1\\ {\lambda }_2^2& -1\end{array}\right|,\mathrm{\Delta }{C}_1=\left|\begin{array}{cc}-M_1& {\lambda }_1^2{M}_1\\ -M_2& {\lambda }_2^2{M}_2\end{array}\right|.\end{array}$$ 49
• (II)
  We take $N=2$ in the N-times DT with $\lambda ={\lambda }_j(j=1,2,3,4)$. The linear algebraic system (9) leads to 2-soliton solutions of GNLS Eq. (4) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=c_0{e}^{i\sigma {\gamma }_0^{2}x}+\frac{\mathrm{\Delta }{B}_2}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 50

  with

  $$\begin{array}{c}\hfill \mathrm{\Delta }=\left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& M_1{\lambda }_1& M_1{\lambda }_1^3\\ {\lambda }_2^2& {\lambda }_2^4& M_2{\lambda }_2& M_2{\lambda }_2^3\\ {\lambda }_3^2& {\lambda }_3^4& M_3{\lambda }_3& M_3{\lambda }_3^3\\ {\lambda }_4^2& {\lambda }_4^4& M_4{\lambda }_4& M_4{\lambda }_4^3\end{array}\right|,\mathrm{\Delta }{B}_2=\left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& M_1{\lambda }_1& -1\\ {\lambda }_2^2& {\lambda }_2^4& M_2{\lambda }_2& -1\\ {\lambda }_3^2& {\lambda }_3^4& M_3{\lambda }_3& -1\\ {\lambda }_4^2& {\lambda }_4^4& M_4{\lambda }_4& -1\end{array}\right|,\mathrm{\Delta }{C}_2=\left|\begin{array}{cccc}{\lambda }_1& -M_1& {\lambda }_1^2{M}_1& {\lambda }_1^4{M}_1\\ {\lambda }_2& -M_2& {\lambda }_2^2{M}_2& {\lambda }_2^4{M}_2\\ {\lambda }_3& -M_3& {\lambda }_3^2{M}_3& {\lambda }_3^4{M}_3\\ {\lambda }_4& -M_4& {\lambda }_4^2{M}_4& {\lambda }_4^4{M}_4\end{array}\right|.\end{array}$$ 51

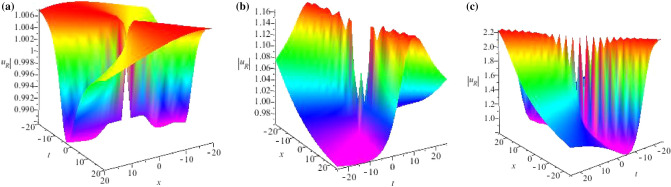
Some periodic and breather solutions for GNLS equation (4) are shown, we consider $N=2$ and plot their structure figures in Fig. 2.

Figure 2.

Profiles of intensity distribution (a) $|\tilde{r}(x,t)|$ of Eq. (48) with parameters ${\lambda }_1=0.2+0.3i,{\lambda }_2=0.2-0.3i,\alpha =0.2,\beta =0.3,{\gamma }_0=0.2,\sigma =-1,F_1=0.3,F_2=0.2$; (b) $|\tilde{r}(x,t)|$ of Eq. (48) with parameters ${\lambda }_1=0.3i,{\lambda }_2=0.2-0.4i,\alpha =0.2,\beta =0.3,{\gamma }_0=0.2,\sigma =-1,F_1=0.3,F_2=0.2$; (c) $|\tilde{r}(x,t)|$ of Eq. (50) with parameters ${\lambda }_1=-0.3i,{\lambda }_2=0.2+0.3i,{\lambda }_3=0.1-0.3i,{\lambda }_4=0.4i,\alpha =0.6,\beta =0.2,{\gamma }_0=0.1,\sigma =-1,F_1=0.3,F_2=0.2,F_3=0.4,F_4=0.1$; (d) $|\tilde{r}(x,t)|$ of Eq. (50) with parameters ${\lambda }_1=0.1i,{\lambda }_2=0.2-0.4i,{\lambda }_3=0.3i,{\lambda }_4=0.2i,\alpha =0.2,\beta =0.3,{\gamma }_0=0.5,\sigma =-1,F_1=0.3,F_2=0.2,F_3=0.4,F_4=0.1$.

Case 2: We consider a solution $u=\frac{{\omega }_0}{\beta {\gamma }_0}{e}^{-i({\gamma }_0^{2}x+{\delta }_{0}t)}$ with ${\delta }_0=\alpha [{(\beta +\sigma {\gamma }_0^2)}^2-{\omega }_0^2]{\gamma }_0^{-2}$. Based on Eq. (5), we can yield the following systems

$$\begin{array}{c}\hfill \left\{\begin{array}{c}-i\lambda {\psi }_1-\frac{i{\omega }_0{\gamma }_0^2}{\beta {\gamma }_0}{e}^{-i({\gamma }_0^{2}x+{\delta }_{0}t)}{\psi }_2={\psi }_{1x},\hfill \\ -\frac{i{\omega }_0{\gamma }_0^2}{\beta {\gamma }_0}{e}^{i({\gamma }_{0}x+{\delta }_{0}t)}{\psi }_1+i\lambda {\psi }_2={\psi }_{2x},\hfill \end{array}\right)\end{array}$$ 52

without loss of generality, we assume that $\sigma =-1$, ${\psi }_1={\alpha }_1{e}^{{\beta }_{1}x}$, ${\psi }_2={\gamma }_1{e}^{{\beta }_{1}x+i({\gamma }_0^{2}x+{\delta }_{0}t)}$, then Eq. (52) is solved by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\beta }_1=\frac{-i{\gamma }_0^2\pm \sqrt{{\mathrm{\Delta }}_1}}{2{\beta }^2},\hfill \\ {\alpha }_1=\frac{-i{\omega }_0{\gamma }_0{\gamma }_1}{\beta ({\beta }_1+i\lambda )},\hfill \end{array}\right)\end{array}$$ 53

we can obtain ${\mathrm{\Delta }}_1=-{\gamma }_0^4{\beta }^4-4{\beta }^2({\omega }_0^2{\gamma }_0^2+{\lambda }^2{\beta }^2-\lambda {\gamma }_0^2{\beta }^2)$. By using Eq. (5), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left(\frac{i\alpha {\omega }_0^2}{2{\gamma }_0^2},-,i,{\eta }^2\right){\psi }_1+\left(\frac{i\alpha \beta {\omega }_0}{2\lambda {\gamma }_0},e^{-i({\gamma }_0^{2}x+{\delta }_{0}t)},-,\frac{i\alpha \lambda {\gamma }_0{\omega }_0}{\beta },e^{-i({\gamma }_0^{2}x+{\delta }_{0}t)}\right){\psi }_2={\psi }_{1t},\hfill \\ \left(\frac{i\alpha \beta {\omega }_0}{2\lambda {\gamma }_0},-,\frac{i\alpha \lambda {\gamma }_0{\omega }_0}{\beta }\right)e^{i({\gamma }_0^{2}x+{\delta }_{0}t)}{\psi }_1+\left(-,\frac{i\alpha {\omega }_0^2}{2{\gamma }_0^2},+,i,{\eta }^2\right){\psi }_2={\psi }_{2t},\hfill \end{array}\right)\end{array}$$ 54

without loss of generality, we assume that ${\psi }_1=a_1{e}^{\mathit{ct}}$, ${\psi }_2=b_1{e}^{ct+i({\gamma }_0^{2}x+{\delta }_{0}t)}$, then Eq. (54) is solved by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}c=\frac{i\alpha \lambda \beta {\omega }_0^2-2i\lambda \beta {\eta }^2{\gamma }_0^2+i\alpha {\beta }^2{\omega }_0{\gamma }_0-2i\alpha {\lambda }^2{\gamma }_0^3{\omega }_0}{2\lambda \beta {\gamma }_0^2{a}_1},\hfill \\ b_1=\frac{a_1(i\alpha {\beta }^2{\gamma }_0{\omega }_0-2i\alpha {\lambda }^2{\gamma }_0^3{\omega }_0-i\alpha \lambda \beta {\omega }_0^2+2i{\eta }^2\lambda \beta {\gamma }_0^2)}{i\alpha \lambda \beta {\omega }_0^2-2i\lambda \beta {\eta }^2{\gamma }_0^2+i\alpha {\beta }^2{\omega }_0{\gamma }_0-2i\alpha {\lambda }^2{\gamma }_0^3{\omega }_0+2i\lambda \beta {\gamma }_0^2{\delta }_0{a}_1}.\hfill \end{array}\right)\end{array}$$ 55

It is easy to find two basic solutions for Eqs. (53) and (55) as following

$$\begin{array}{c}\hfill \left(\begin{array}{c}\psi \\ \varphi \end{array}\right)=\left(\begin{array}{c}{C}_3{e}^{{\beta }_{1}x+ct}\\ C_4{e}^{{\beta }_{1}x+dt+2i({\gamma }_0^{2}x+{\delta }_{0}t)}\end{array}\right),\end{array}$$ 56

we can derive by using Eq. (10),

$$\begin{array}{c}\hfill M_j=\frac{e^{F_j}{e}^{dt+2i({\gamma }_0^{2}x+{\delta }_{0}t)}}{e^{\mathit{ct}}},1\le j\le 2N,\end{array}$$ 57

with ${\nu }_j^{(i)}=e^{F_j}$ $(1\le i\le 2,1\le j\le 2N)$.

• (I)
  We take $N=1$ with $\lambda ={\lambda }_j$ (j = 1, 2), and yield the 1-soliton solutions of the GNLS equation (4) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=\frac{{\omega }_0}{\beta {\gamma }_0}{e}^{-i({\gamma }_0^{2}x+{\delta }_{0}t)}+\frac{\mathrm{\Delta }{B}_1}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 58

  with

  $$\begin{array}{c}\hfill \mathrm{\Delta }=\left|\begin{array}{cc}{\lambda }_1^2& M_1{\lambda }_1\\ {\lambda }_2^2& M_2{\lambda }_2\end{array}\right|,\mathrm{\Delta }{B}_1=\left|\begin{array}{cc}{\lambda }_1^2& -1\\ {\lambda }_2^2& -1\end{array}\right|,\mathrm{\Delta }{C}_1=\left|\begin{array}{cc}-M_1& {\lambda }_1^2{M}_1\\ -M_2& {\lambda }_2^2{M}_2\end{array}\right|.\end{array}$$ 59
• (II)
  We take $N=2$ in the N-times DT with $\lambda ={\lambda }_j(j=1,2,3,4)$. The linear algebraic system (9) leads to the 2-soliton solutions of GNLS Eq. (4) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=\frac{{\omega }_0}{\beta {\gamma }_0}{e}^{-i({\gamma }_0^{2}x+{\delta }_{0}t)}+\frac{\mathrm{\Delta }{B}_2}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 60

  with

  $$\begin{array}{c}\hfill \mathrm{\Delta }=\left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& M_1{\lambda }_1& M_1{\lambda }_1^3\\ {\lambda }_2^2& {\lambda }_2^4& M_2{\lambda }_2& M_2{\lambda }_2^3\\ {\lambda }_3^2& {\lambda }_3^4& M_3{\lambda }_3& M_3{\lambda }_3^3\\ {\lambda }_4^2& {\lambda }_4^4& M_4{\lambda }_4& M_4{\lambda }_4^3\end{array}\right|,\mathrm{\Delta }{B}_2=\left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& M_1{\lambda }_1& -1\\ {\lambda }_2^2& {\lambda }_2^4& M_2{\lambda }_2& -1\\ {\lambda }_3^2& {\lambda }_3^4& M_3{\lambda }_3& -1\\ {\lambda }_4^2& {\lambda }_4^4& M_4{\lambda }_4& -1\end{array}\right|,\mathrm{\Delta }{C}_2=\left|\begin{array}{cccc}{\lambda }_1& -M_1& {\lambda }_1^2{M}_1& {\lambda }_1^4{M}_1\\ {\lambda }_2& -M_2& {\lambda }_2^2{M}_2& {\lambda }_2^4{M}_2\\ {\lambda }_3& -M_3& {\lambda }_3^2{M}_3& {\lambda }_3^4{M}_3\\ {\lambda }_4& -M_4& {\lambda }_4^2{M}_4& {\lambda }_4^4{M}_4\end{array}\right|.\end{array}$$ 61

Some periodic solutions for GNLS equation (4) with seed $u=\frac{{\omega }_0}{\beta {\gamma }_0}{e}^{-i({\gamma }_0^{2}x+{\delta }_{0}t)}$ are shown, we consider $N=2$ and plot their structure figures in Fig. 3.

Figure 3.

Profiles of intensity distribution (a) $|\tilde{u}(x,t)|$ of Eq. (58) with parameters ${\lambda }_1=0.2,{\lambda }_2=0.3,\alpha =0.3,\beta =5,{\gamma }_0=0.5,\sigma =-1,{\omega }_0=0.4,F_1=0.3,F_2=0.4$; (b) $|\tilde{u}(x,t)|$ of Eq. (58) with parameters ${\lambda }_1=0.3+0.2i,{\lambda }_2=0.3-0.2i,\alpha =0.4,\beta =5,{\gamma }_0=0.6,\sigma =-1,{\omega }_0=0.2,F_1=0.2+0.3i,F_2=0.2-0.3i$; (c) $|\tilde{r}(x,t)|$ of Eq. (60) with parameters ${\lambda }_1=0.3i,{\lambda }_2=-0.2i,{\lambda }_3=0.4i,{\lambda }_4=-0.5i,\alpha =0.4,\beta =5,{\gamma }_0=0.2,\sigma =-1,{\omega }_0=0.3,F_1=0.3i,F_2=-0.3i,F_1=0.5i,F_1=-0.5i$; (d) $|\tilde{u}(x,t)|$ of Eq. (60) with parameters ${\lambda }_1=0.3,{\lambda }_2=-0.2,{\lambda }_3=0.4,{\lambda }_4=0.5,\alpha =0.4,\beta =8,{\gamma }_0=0.5,\sigma =-1,{\omega }_0=0.2,F_1=0.3i,F_2=-0.3i,F_3=0.5i,F_4=-0.5i$.

Case 3: We consider a seed solution $u=e^{i\theta }$ with $\theta =ax+bt$, $b=\frac{1+a}{a}\alpha {\beta }^2+2\alpha \beta +a\alpha$. We can yield the following systems from Eq. (5)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}-i{\lambda }^2{\phi }_1-i\lambda e^{i\theta }{\phi }_2={\phi }_{1x},\hfill \\ -i\lambda e^{-i\theta }{\phi }_1+i{\lambda }^2{\phi }_2={\phi }_{2x},\hfill \end{array}\right)\end{array}$$ 62

without loss of generality, we assume that $\sigma =-1$, ${\phi }_1=m{e}^{c_{1}x}$, ${\phi }_2=n{e}^{c_{1}x-i\theta }$, then Eq. (62) is solved by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}n=\frac{1\pm \sqrt{s}-2{\lambda }^2}{2\lambda }m,\hfill \\ c_1=\frac{1\pm \sqrt{s}}{2i}.\hfill \end{array}\right)\end{array}$$ 63

We can obtain $s=1+4{\lambda }^4$. We derive the system through Eq. (5),

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left(\frac{i\alpha {\beta }^2}{2},-,i,{\eta }^2\right){\psi }_1+\left(\frac{i\alpha {\beta }^2}{2\lambda },-,i,\alpha ,\lambda \right)e^{i\theta }{\psi }_2={\psi }_{1t},\hfill \\ \left(\frac{i\alpha {\beta }^2}{2},-,i,\alpha ,\lambda \right)e^{-i\theta }{\psi }_1+\left(i,{\eta }^2,-,\frac{i\alpha {\beta }^2}{2}\right){\psi }_2={\psi }_{2t},\hfill \end{array}\right)\end{array}$$ 64

without loss of generality, we assume that ${\psi }_1=p{e}^{s_{1}t}$, ${\psi }_2=q{e}^{s_{1}t-i\theta }$, $\alpha =1$, $\beta =-1$, $\eta =\sqrt{\alpha }(\lambda -\frac{\beta }{2\lambda })$, then Eq. (64) is solved by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}p=\frac{i-2i{\lambda }^2}{4i{\lambda }^4+2i{\lambda }^2+4{\lambda }^2{s}_1+i}q,\hfill \\ s_1=\frac{-(40i{\lambda }^4+8i{\lambda }^2)\pm \sqrt{z^2-64{\lambda }^{4}y}}{32{\lambda }^4},\hfill \end{array}\right)\end{array}$$ 65

we can obtain z and y as following : $z=40i{\lambda }^4+8i{\lambda }^2$, $y=16{\lambda }^8-24{\lambda }^6-8{\lambda }^5-8{\lambda }^4-4{\lambda }^3-8{\lambda }^2+1$.

It is easy to find two basic solutions for Eqs. (63) and (65):

$$\begin{array}{c}\hfill \left(\begin{array}{c}\varphi \\ \psi \end{array}\right)=\left(\begin{array}{c}{C}_5{e}^{\frac{(\lambda +\lambda \sqrt{Q})x+(3-4\sqrt{9{\lambda }^2-{\mathrm{\Delta }}_2})t}{2i\lambda }}\\ C_6{e}^{\frac{2\lambda (1+\sqrt{Q})x+(3-4\sqrt{9{\lambda }^2-{\mathrm{\Delta }}_2})t}{2i\lambda }-2i\theta }\end{array}\right),\end{array}$$ 66

we can obtain that : ${\mathrm{\Delta }}_2={\lambda }^2({\alpha }^2{\beta }^4-4\alpha {\eta }^2{\beta }^2+6\alpha {\beta }^2+4{\eta }^4-12{\eta }^2-4{\alpha }^2{\beta }^2+4{\alpha }^2{\lambda }^2)+\alpha {\beta }^4,$ $C_5=\frac{-2\alpha {\lambda }^2+\alpha {\beta }^2}{\alpha \lambda {\beta }^2},$ $C_6=\frac{2{\lambda }^2-\sqrt{Q}-1}{2\lambda },$ $Q=3-4\sqrt{9{\lambda }^2-{\mathrm{\Delta }}_2}$.

According to Eq. (10), we obtain

$$\begin{array}{c}\hfill M_j=e^{\frac{(\lambda +\lambda \sqrt{Q})x}{2i\lambda }+F_j-2i\theta },1\le j\le 2N,\end{array}$$ 67

with ${\nu }_j^{(i)}=e^{F_j}$ $(1\le i\le 2,1\le j\le 2N)$.

• (I)
  We take $N=1$ with $\lambda ={\lambda }_j$ (j = 1, 2) and derive the 1-breather solutions of the GNLS equation (4) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=e^{i\theta }+\frac{\mathrm{\Delta }{B}_1}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 68

  with

  $$\begin{array}{c}\hfill \mathrm{\Delta }=\left|\begin{array}{cc}{\lambda }_1^2& M_1{\lambda }_1\\ {\lambda }_2^2& M_2{\lambda }_2\end{array}\right|,\mathrm{\Delta }{B}_1=\left|\begin{array}{cc}{\lambda }_1^2& -1\\ {\lambda }_2^2& -1\end{array}\right|,\mathrm{\Delta }{C}_1=\left|\begin{array}{cc}-M_1& {\lambda }_1^2{M}_1\\ -M_2& {\lambda }_2^2{M}_2\end{array}\right|.\end{array}$$ 69
• (II)
  We take $N=2$ in the N-times DT with $\lambda ={\lambda }_j(j=1,2,3,4)$. The linear algebraic system (9) leads to the 2-breather solutions of GNLS Eq. (4) as following:

  $$\begin{array}{c}\hfill \tilde{u}(x,t)=e^{i\theta }+\frac{\mathrm{\Delta }{B}_2}{\mathrm{\Delta }},\tilde{r}(x,t)=-{\tilde{u}}^{\ast }(x,t),\end{array}$$ 70

  with

  $$\begin{array}{c}\hfill \mathrm{\Delta }=\left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& M_1{\lambda }_1& M_1{\lambda }_1^3\\ {\lambda }_2^2& {\lambda }_2^4& M_2{\lambda }_2& M_2{\lambda }_2^3\\ {\lambda }_3^2& {\lambda }_3^4& M_3{\lambda }_3& M_3{\lambda }_3^3\\ {\lambda }_4^2& {\lambda }_4^4& M_4{\lambda }_4& M_4{\lambda }_4^3\end{array}\right|,\mathrm{\Delta }{B}_2=\left|\begin{array}{cccc}{\lambda }_1^2& {\lambda }_1^4& M_1{\lambda }_1& -1\\ {\lambda }_2^2& {\lambda }_2^4& M_2{\lambda }_2& -1\\ {\lambda }_3^2& {\lambda }_3^4& M_3{\lambda }_3& -1\\ {\lambda }_4^2& {\lambda }_4^4& M_4{\lambda }_4& -1\end{array}\right|,\mathrm{\Delta }{C}_2=\left|\begin{array}{cccc}{\lambda }_1& -M_1& {\lambda }_1^2{M}_1& {\lambda }_1^4{M}_1\\ {\lambda }_2& -M_2& {\lambda }_2^2{M}_2& {\lambda }_2^4{M}_2\\ {\lambda }_3& -M_3& {\lambda }_3^2{M}_3& {\lambda }_3^4{M}_3\\ {\lambda }_4& -M_4& {\lambda }_4^2{M}_4& {\lambda }_4^4{M}_4\end{array}\right|.\end{array}$$ 71

Some breather solutions for GNLS equation (4) with seed $u=\frac{{\omega }_0}{\beta {\gamma }_0}{e}^{-i({\gamma }_0^{2}x+{\delta }_{0}t)}$ are shown, we consider $N=2$ and plot their structure figures in Fig. 4.

Figure 4.

Profiles of intensity distribution (a) $|\tilde{r}(x,t)|$ of Eq. (68) with parameters ${\lambda }_1=-0.3+5i,{\lambda }_2=0.3+4i,\alpha =1,\beta =-1,a=-1,b=3,\sigma =-1,F_1=i,F_2=2i$; (b) $|\tilde{u}(x,t)|$ of Eq. (68) with parameters ${\lambda }_1=0.5i,{\lambda }_2=0.3i,\alpha =1,\beta =-1,a=-1,b=3,\sigma =-1,F_1=i,F_2=2i$; (c) $|\tilde{r}(x,t)|$ of Eq. (70) with parameters ${\lambda }_1=0.5i,{\lambda }_2=-0.3i,{\lambda }_3=0.2i,{\lambda }_4=-0.4i,\alpha =1,\beta =-1,a=-1,b=3,\sigma =-1,F_1=i,F_2=2i,F_3=3i,F_4=2i$; (d) $|\tilde{r}(x,t)|$ of Eq. (70) with parameters ${\lambda }_1=0.03+0.5i,{\lambda }_2=0.03-0.5i,{\lambda }_3=0.02+0.3i,{\lambda }_4=0.02-0.3i,\alpha =1,\beta =-1,a=-1,b=3,\sigma =-1,F_1=i,F_2=2i,F_3=3i,F_4=2i$.

Rational wave solutions for GNLS Eq. (4)

In this section, we construct the rational wave solutions of the GNLS Eq. (4). In fact, the rational wave solutions can be obtained by the limits of the eigenfunctions or the limits of the breather solutions.

Based on Eq. (66), we can get a new eigenfunction of the Lax pair (5)

$$\begin{array}{c}\hfill R_1(\epsilon )={(f_1,g_1)}^T,\end{array}$$ 72

with

$$\begin{array}{cc}\hfill f_1=& C_5{e}^{\frac{(\lambda +\lambda \sqrt{Q})x+(3-4\sqrt{9{\lambda }^2-{\mathrm{\Delta }}_2})t}{2i\lambda }},g_1=C_6{e}^{\frac{2\lambda (1+\sqrt{Q})x+(3-4\sqrt{9{\lambda }^2-{\mathrm{\Delta }}_2)t}}{2i\lambda }-2i\theta },\hfill \\ \hfill C_5=& \frac{-2\alpha {\lambda }^2+\alpha {\beta }^2}{\alpha \lambda {\beta }^2},C_6=\frac{2{\lambda }^2-\sqrt{Q}-1}{2\lambda },Q=3-4\sqrt{9{\lambda }^2-{\mathrm{\Delta }}_2},\hfill \\ \hfill {\mathrm{\Delta }}_2=& {\lambda }^2({\alpha }^2{\beta }^4-4\alpha {\eta }^2{\beta }^2+6\alpha {\beta }^2+4{\eta }^4-12{\eta }^2-4{\alpha }^2{\beta }^2+4{\alpha }^2{\lambda }^2)+\alpha {\beta }^4,\hfill \end{array}$$

where $\epsilon$ is a small parameter, if we fix ${\lambda }_1=\frac{1}{2}+\frac{1}{2}i$, and let $\lambda =\frac{1}{2}+\frac{1}{2}i+{\epsilon }^2$, then $R_1(\epsilon )$ can be expanded at $\epsilon =1$, so we have

$$\begin{array}{c}\hfill R_1(\epsilon )=R_1^{[0]}+R_1^{[1]}{\epsilon }^2+R_1^{[2]}{\epsilon }^4+R_1^{[3]}{\epsilon }^6+\cdots \end{array}$$ 73

where

$$\begin{array}{c}\hfill R_1^{[0]}=\left(\begin{array}{c}{C}_5{e}^{\frac{Fx+Qt}{i-1}}\\ C_6{e}^{\frac{2Fx+Qt+2\theta (i-1)}{i-1}}\end{array}\right),\end{array}$$ 74

and

$$\begin{array}{c}\hfill R_1^{[1]}=\left(\begin{array}{c}\frac{-2i{\epsilon }^2(Fx+Qt)}{{(i-1)}^2}{C}_5{e}^{\frac{Fx+Qt}{i-1}}\\ \frac{4\theta (i-1)-2i[2Fx+Qt+2\theta (i-1)]}{i-1}{C}_6{e}^{\frac{2Fx+Qt+2\theta (i-1)}{i-1}}\end{array}\right),\end{array}$$ 75

with

$$\begin{array}{c}\hfill Q=3-4\sqrt{9{\lambda }^2-{\mathrm{\Delta }}_2},F=\lambda +\lambda \sqrt{Q}.\end{array}$$

We present the rational wave solution of the GNLS Eq. (4) as following:

$$\begin{array}{c}\hfill u_R=u+\frac{f_1^{[1]}{g}_1^{{[1]}^{\ast }}({\lambda }^2-{\lambda }^{{\ast }^2})}{{|\lambda |}^2(|f_1^{[1]}{|}^2\lambda +|g_1^{[1]}{|}^2{\lambda }^{\ast })},\end{array}$$ 76

with

$$\begin{array}{c}\hfill f_1^{[1]}=C_5\frac{-2i{\epsilon }^2(Fx+Qt)}{{(i-1)}^2},g_1^{[1]}=C_6\frac{4\theta (i-1)-2i[2Fx+Qt+2\theta (i-1)]}{i-1}.\end{array}$$

Some rational wave solutions for GNLS equation (4) are shown with the limits of the breather solutions, we plot their structure figures in Fig. 5.

Figure 5.

Profiles of intensity distribution (a) $|{\tilde{u}}_R(x,t)|$ of Eq. (76) with parameters $\lambda =\frac{5}{2}+\frac{1}{2}i,\alpha =-0.3,\beta =0.5,a=-1,b=3$; (b) $|{\tilde{u}}_R(x,t)|$ of Eq. (76) with parameters $\lambda =\frac{3}{2}+\frac{1}{2}i,\alpha =0.9,\beta =-0.8,a=-1,b=3$; (c) $|{\tilde{u}}_R(x,t)|$ of Eq. (76) with parameters $\lambda =\frac{1}{2}-i,\alpha =0.6,\beta =-0.6,a=-1,b=3$.

Author contributions

L.L. and F.J.Y.: supervision; writing—original draft; funding acquisition. C.F.: validation; editing.

Data availability

All data generated or analysed during this study are included in this published article.

Competing interests

The authors declare no competing interests.