Abstract
Molecular dynamics (MD) simulations have become the predominant computational analysis method in membrane biophysics, as this technique is uniquely suited for investigations of complex molecular systems through the relevant physical principles. Owing to continued improvements in scope and performance, the trajectories generated through this approach contain ever-increasing amounts of information, which must be synthesized and simplified in post-analysis using tools that are not only mechanistically insightful but also computationally efficient and highly scalable. Here, we introduce MOSAICS, a self-contained high-performance suite of C++ software tools designed for advanced analyses of lipid bilayer structure and dynamics from MD trajectories. MOSAICS is to our knowledge the most comprehensive software suite of this kind, enabling analysis of a wide array of morphological and kinetic properties, for both simple and complex membranes, irrespective of system size or resolution. Importantly, MOSAICS is designed to provide spatial distributions of all computed quantities, with built-in masking tools, noise filtering, and statistical significance metrics to facilitate quantitative interpretations of the trajectory data; it is also fully parallelized and can therefore leverage the capabilities of supercomputing facilities. Despite its technical sophistication, MOSAICS is user-friendly and requires minimal computational expertise, making it accessible to researchers of all skill levels. This sofware suite can be freely downloaded at https://github.com/MOSAICS-NIH/.
Significance
Molecular dynamics (MD) simulations have become the predominant computational analysis method in membrane biophysics. This approach produces ever-increasing amounts of information, which must be synthesized and simplified in post-analysis using tools that are not only mechanistically insightful but also computationally efficient and highly scalable. We introduce MOSAICS, a self-contained high-performance suite of C++ software tools designed for comprehensive, spatially resolved analyses of lipid bilayer structure and dynamics from MD trajectories.
Introduction
The interplay between membrane proteins and the lipid bilayer has drawn the attention of theoretical and computational biophysicists for decades. This interplay is a compelling subject for mechanistic and fundamental research, and is also of paramount biomedical significance. As a result of continued improvements in software and hardware, the simulation technique known as molecular dynamics (MD) has become the predominant computational methodology in this area. The purpose of an MD simulation is to produce a trajectory that describes the evolution of all the atoms in a molecular system over a certain time period, based on Newton’s laws and the principles of Statistical Mechanics. While different simulation approaches exist that vary the resolution with which molecular structures are represented, at present time most problems of interest require examination of the emergent properties of hundreds or thousands of molecules in motion, in addition to the protein or proteins under study. As the millisecond timescale appears within reach, these trajectories will contain ever-increasing amounts of information, which must be synthesized and simplified in post-analysis using tools that are not only insightful from a mechanistic standpoint but also computationally efficient and scalable.
Here, we introduce MOSAICS, a self-contained high-performance suite of C++ software tools designed for advanced analyses of lipid bilayer structure and dynamics from MD trajectories. Among the range of membrane analysis tools reported in recent years (1,2,3,4,5,6,7,8,9,10,11,12,13), MOSAICS is to our knowledge the most comprehensive, enabling analysis of a wide array of morphological and kinetic properties, for both simple and complex membranes (Table 1). Properties may stem from analysis of molecules or from individual chemical groups, represented in atomic detail or coarse grained. Importantly, and unlike most other tools, MOSAICS is a lattice-based method, implying that it provides spatial distributions of all computed quantities, be it a local enrichment ratio of a given lipid species or the characteristic dwell times of lipids at a protein-bilayer interface. Alternative approaches to evaluate and utilize statistical significance metrics are also integrated in the analysis workflow. To maximize its performance, MOSAICS implements a lipid-to-lattice mapping method that scales only with the number of lipid molecules, but not with the lattice dimensions, permitting analysis of very large simulation systems at high resolution. Indeed, MOSAICS is fully parallelized with MPI, and can therefore take full advantage of modern supercomputing clusters. Scaling is nearly linear over hundreds of computing cores, since trajectory snapshots are analyzed independently before all information is integrated. Finally, the object-oriented coding greatly facilitates the use of libraries and future developments and expansions. Despite the technical sophistication of this software suite, MOSAICS is reasonably user-friendly and requires no programming or advanced scripting; researchers of all skill levels can use these tools readily. The suite has been extensively documented with examples and tutorials and is publicly available at https://github.com/MOSAICS-NIH/. Importantly, MOSAICS is actively maintained and improved upon, and is being successfully used in real-life investigations of the fascinating and intriguing interplay between proteins and membranes. In the following sections we outline the basics of the analysis methodology used in MOSAICS and document the range of structural and dynamical descriptors and observables that are currently accessible, using published simulation data for a representative protein-membrane system (14) for convenience.
Table 1.
Descriptors of membrane structure and dynamics accessible in MOSAICS 1.0 and in other simulation analysis tools
| MOSAICS | LiPyphilic | LoMePro | APL∗Voro | LipidDyn | Grid-MAT | LOOS | Membrainy | MEMB-PLUGIN | MemSurfer | |
|---|---|---|---|---|---|---|---|---|---|---|
| Bilayer shape | yes | yes | – | – | – | – | yes | – | – | yes |
| Bilayer thickness | yes | yes | yes | yes | – | yes | – | yes | yes | yes |
| Lipid-chain order parameter∗ | yes | yes | yes | – | – | – | yes | – | – | – |
| Area per lipid∗ | yes | yes | yes | yes | – | – | – | – | – | yes |
| Multicomponent lipid enrichment∗ | yes | – | – | – | yes | – | – | – | – | – |
| Lipid density∗ | yes | – | – | – | yes | – | yes | yes | yes | yes |
| Mean lipid tilt∗,a | yes | – | – | – | – | – | yes | – | – | – |
| Mean instantaneous lipid tilt∗,a | yes | yes | – | – | – | – | – | – | – | – |
| Leaflet interdigitation | yes | – | – | – | – | – | – | – | – | – |
| Interleaflet contacts∗ | yes | – | – | – | – | – | – | – | – | – |
| Lipid-chain end-to-end length∗ | yes | – | – | – | – | – | – | – | – | – |
| Lipid-chain splay∗ | yes | – | – | – | – | – | – | – | – | – |
| Lipid-solvent contacts∗ | yes | – | – | – | – | – | – | – | – | – |
| Lipid-protein H-bond & salt-bridges | yes | – | – | – | – | – | – | – | – | – |
| Average lipid conformation∗ | yes | – | – | – | – | – | – | – | – | – |
| Lipid radius of gyration | yes | – | – | – | – | – | – | – | – | – |
| Lipid residence time | yes | – | – | – | – | – | – | – | – | – |
| Multicomponent lipid mixing | yes | – | – | – | – | – | – | yes | – | – |
| Lipid self-diffusion coefficients | yes | yes | – | – | – | – | – | – | – | – |
| Lipid solvation-shell on/off rates | yes | – | – | – | – | – | – | yes | – | – |
| Lipid flipping | yes | yes | – | – | – | – | – | – | – | – |
| Membrane protein tilt angle | yes | – | – | – | – | – | – | – | – | – |
| Parallelization | MPI | – | – | – | multicore | – | multicore | multicore | – | – |
| Supported trajectory file format | GROMACS | multiple | GROMACS | GROMACS | GROMACS | GROMACS | multiple | GROMACS | multiple | multiple |
| Programming language | C++ | Python | C | C++ | Python | Perl | C++ | Java | TCL | C++/Python |
In MOSAICS 1.0, most descriptors are provided as 2D spatial distributions across the membrane plane, which can be represented as heatmaps filtered by user-defined statistical significance thresholds.
(∗) Selected observables are also available as 3D distributions. Only self-diffusion coefficients and lipid mixing are provided as global average properties. Descriptors available in other software tools but not in MOSAICS 1.0 are not included in this table, for conciseness; we refer the reader to the corresponding publications for further details.
For further details on these alternative definitions see Methods.
Methods
MOSAICS analyzes trajectories of instantaneous molecular configurations of a lipid bilayer in terms of specific structural and dynamic descriptors, and synthesizes the resulting information in the form of spatial distributions of time averages. Thus, the researcher can not only examine how those descriptors evolve with time, but also resolve any statistically significant patterns across space. As noted below, selected descriptors cannot be formulated as spatial distributions, so in these cases MOSAICS produces instead global ensemble averages. The following sections provide an overview of the most salient features of the methodology and of its implementation.
Spatial mapping of instantaneous and time-averaged structural data
Let us define as a structural observable or descriptor that may be computed for each individual lipid molecule in a snapshot of a membrane trajectory at a certain time , where t indexes the trajectory snapshots and is the time interval between them. For example, this observable can be the end-to-end length of its alkyl chains, or the number of contacts formed with a protein or neighboring lipid molecules. In such cases, it is generally of interest to evaluate how the descriptor varies across space; for example, we might want to discern how it differs when the vicinity of a protein is compared with the bulk membrane. To this end, MOSAICS calculates for all lipids in the membrane and maps the resulting values onto a lattice of points with fixed coordinates. This lattice can be two- or three-dimensional (2D or 3D), but for simplicity we discuss only the former, and thus refer to the resulting instantaneous map of the observable in question as (Fig. 1 A), where indexes and identify each lattice point. (The lattice dimensions and point spacing are defined by the user.) To construct from the set of molecular values, MOSAICS uses a geometric interpolation method that is based on the distances between the lattice points and one or more representative atoms in each lipid molecule. As explained below, these distances are used to derive a set of weights, , that are specific for each lattice point and each lipid at any given time . Having calculated these weights, the instantaneous map is:
| (1) |
where is the number of lipids. Note that Eq. 1 applies to points for which otherwise, remains undefined (for example, points that fall inside the volume of a membrane embedded protein).
Figure 1.
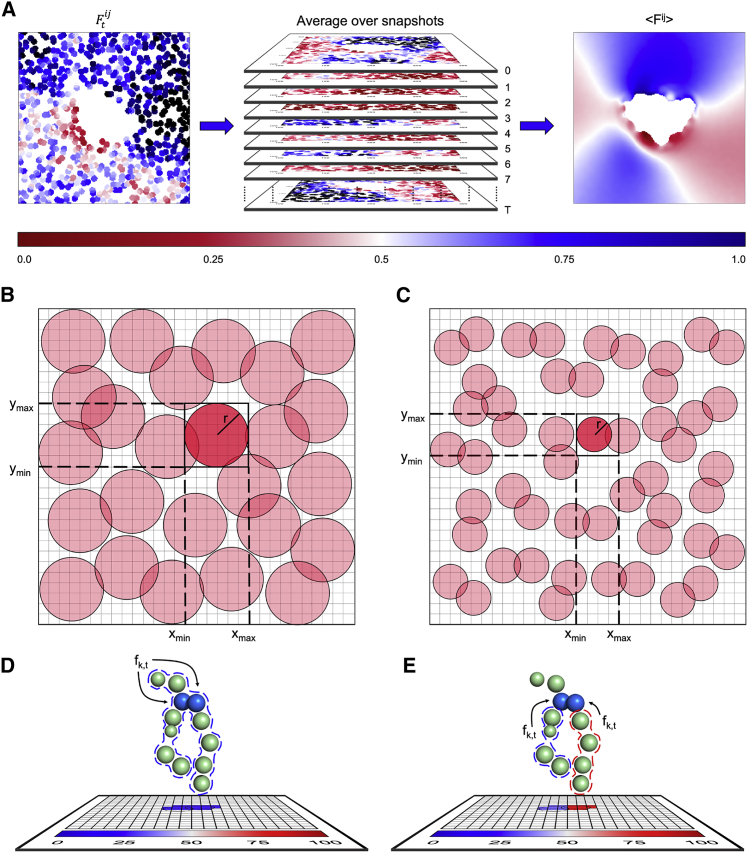
MOSAICS workflows and procedures. (A) For each individual trajectory snapshot, the stamping interpolation method is used to map a specific characteristic or observable onto a two-dimensional lattice (left). The data are then averaged over all snapshots (middle) to give (right). In this example the white area in the center of the lattice is occupied by the protein, and the color bar specifies the value of the observable. (B) Schematic of the stamping method for a simple case where each lipid position in XY is represented by a single mapping atom. In this example, the mapping atoms are represented as red circles whose radius matches the would-be stamping radius. A single lipid is selected (dark red) and the bounds for which lipid-to-grid-point distances must be measured are indicated via the enclosed box and dotted lines. (C) Same schematic as in (B) when multiple mapping atoms are selected instead to improve the spatial resolution of the data. As in (B), the mapping atoms are represented with red circles; we focus on a single mapping atom to highlight the neighboring lattice points for which distances must be measured. (D and E) Schematic of the procedure used for mapping observables onto the lattice. In these examples, the mapping atoms are colored in blue. (D) Shows an example where a single observable is measured for the whole molecule as is indicated by the dotted lines. In this case, the measurement is assigned to each of the two mapping atoms. In contrast, (E) exemplifies a case where two different chemical groups (each of the acyl chains) are characterized, again indicated by dotted lines; in this case, each of these measurements are assigned to a single mapping atom.
Because the weights are specific for each lattice point and each lipid at each time, their calculation can be very limiting from a performance standpoint. Therefore, it is worthwhile to carefully design this calculation, particularly when considering large molecular systems. Assuming again a 2D space, let us denote the instantaneous coordinates of a given lipid as and the fixed coordinates of a lattice point as . A seemingly straightforward way to define is a Gaussian function of the distance between lipid and lattice point:
| (2) |
where is the peak height of the Gaussian function and and its characteristic widths. For a lattice of points, however, evaluation of Eqs. 1 and 2 requires distance calculations for every simulation snapshot. That is, the computational cost of a high-resolution interpolation quickly becomes prohibitively expensive as the size of the simulation system increases. Fortunately, the interpolation can be greatly optimized by recognizing that drops off rapidly with the distance between lipid and lattice point; that is, values primarily reflect the values of from lipids near each lattice point. A possible route to optimize the interpolation method is therefore to identify a priori, for each snapshot and each lipid, the lattice points that are significant for the interpolation of , and evaluate the distances required for Eqs. 1 and 2 only for those proximal points. The computational cost of such an approach would scale with , the number of lipids, as is independent of system size.
How to identify these proximal lattice points and limit the interpolation to this set? We refer to this methodology as “stamping” (Fig. 1 B). For a given lipid of coordinates , we consider only the lattice points whose coordinates satisfy the following condition:
| (3) |
where is deduced from a conservative estimate of the area per lipid, , as . With this stamping algorithm, the number of weights required to interpolate each value of is reduced drastically, to about , where is the spacing between adjacent lattice points (identical in and directions). The number of distance calculations required to construct the map for a single snapshot therefore scales only with , thereby permitting analysis of very large molecular systems without the need to degrade the resolution of the analysis. In addition to the stamping method, MOSAICS simplifies Eq. 2 as a step function:
| (4) |
Taken together, these simplifications greatly boost the performance of the interpolation algorithm used in MOSAICS; indeed, as demonstrated below, this methodology requires 100 to 1000 times fewer distance calculations than other forms of interpolation or Voronoi tessellations.
Having calculated the instantaneous maps for all snapshots in a trajectory, using Eq. 1 and Eqs. 3 and 4, a time-averaged spatial distribution of the descriptor of interest can be ultimately derived as:
| (5) |
where quantifies the number of samples at each lattice point, i.e., the number of snapshots for which was defined after stamping (Fig. 1 A).
As noted, the stamping interpolation method is formulated in reference to the instantaneous position of each lipid in the bilayer, . MOSAICS offers great flexibility in how that position is defined. In some cases, it might be sufficient to use only one atom per molecule (which Eq. 1 assumes, for simplicity, Fig. 1 B); however, when molecular shape is considered important, the stamping can be based on the positions of multiple atoms (Fig. 1 C) in each molecule (in which index in Eq. 1 and Eqs. 3 and 4 identifies those atoms and not only lipid molecules). Either way, the descriptor that stamped may describe either a property of the full molecule (Fig. 1 D) or of a distinct chemical group (Fig. 1 E). It is important to note that multiatom interpolations do not significantly diminish computational efficiency, since in practice the stamping radius (Eq. 3) is decreased as additional mapping atoms are included (Fig. 1, B and C).
Assessing statistical significance
When interpreting the features of , it is key to recognize that the statistical significance of the interpolated data might vary across the map, and that some lattice points might reflect an insufficient number of samples. For example, sampling deficiencies are to be expected very close to the surface of membrane-embedded proteins; due to thermal fluctuations in the protein structure, lattice points that normally fall inside their volumes are occasionally stamped with membrane data. Because the features of the protein-lipid interface are often important from a mechanistic standpoint, it is crucial to be able to discern reliable data from sampling artifacts. MOSAICS provides two complementary approaches to facilitate this analysis. In the first approach, the researcher can specify a minimum sampling threshold, , below which areas in the map are reset as undefined. Specifically, a lattice point is considered to be unreliable if the number of samples at that point is smaller than the overall average for the entire lattice, to the extent specified with the parameter. That is, reliable lattice points fulfill the condition:
| (6) |
As illustrated below, a thoughtful choice of requires inspection of , which MOSAICS also provides. In addition, MOSAICS generates spatial distributions for the standard error of , for the portions of the lattice where the map is defined beyond the minimum-sampling threshold. That is:
| (7) |
Evaluation of and , however, need not employ the same number snapshots; more separation between snapshots diminishes correlations in the trajectory data and improves estimates of .
Leaflet finder
Many of the structural and dynamic descriptors available in MOSAICS may be computed for each leaflet of the lipid bilayer independently, thereby providing additional resolution in the interpretation of simulation data. In such cases, the researcher need not enumerate which lipid molecules reside in each leaflet; MOSAICS is equipped with a built-in “leaflet finder” to make this assignment. This routine determines the orientation of each lipid molecule by comparing the Z-coordinates of two atoms, one in the headgroup the other in an alkyl chain (Fig. 2 A).
Figure 2.
MOSAICS workflows and procedures. (A) Criteria used by the “leaflet finder” to assign lipids to the upper or lower leaflets of the bilayer. An assignment number is computed for each lipid molecule by subtracting the values of the Z-coordinate of two atoms, one in the headgroup and another in the acyl chain, as indicated in the diagram. A positive value identifies lipids in the upper leaflet while a negative number identifies those in the lower leaflet. (B) Top, schematic of a rectangular selection tool. In this example, we have selected a square membrane patch surrounding the protein (central region colored white) from a map containing membrane thickness data. The resulting rectangle is drawn in red with the enclosed area shaded. Bottom, an example of a lattice point selection made with a masking tool. Here, we have selected the protein from the upper panel. (C) Schematic of a noise filter. For descriptors that rely on hard thresholds, it is common that rapid fluctuations result in spurious assignments; in this example, the value of a certain observable in snapshot t is an outlier among the values observed for the snapshots that precede and follow t, leading the noise filter to reassign this value. (D) Common command line arguments used when launching a MOSAICS tool. Note that the atom selections are made using a selection card, i.e., a formatted text file. (E) Flow chart depiction of the lattice-based procedure employed by MOSAICS. Input files are colored in cyan. The main loop, which runs over a subset of the trajectory snapshots assigned to an MPI process, is highlighted in blue.
Spatial averages using masking maps
For clarity or conciseness, it can be useful to extract a single average over a specific region of . For example, it might be of interest to quantify a bulk-membrane value, or how a given descriptor varies, on average, as a function of the distance to a protein. MOSAICS provides alternative tools for this type of analyses. The simplest tool averages lattice point data within or outside a user-defined rectangle (Fig. 2 B). Complex selections of arbitrary shape are also possible, using a “masking map,” (Fig. 2 B). This map takes two values, namely for the lattice points of interest, or otherwise. A partial spatial average of is then obtained as:
| (8) |
This approach may be used, for example, to obtain a global average of a bilayer property for a protein-membrane system that excludes the volume occupied by the protein. As illustrated below, masking maps may also be used to evaluate a series of lipid solvation shells around a protein increasingly further from its surface.
Noise filtering
MOSAICS provides multiple tools for analysis of single-molecule lipid dynamics. For this kind of analyses, MOSAICS implements a noise-filtering device that discards data that are unlikely to be representative or mechanistically significant. Consider, for example, a residence time analysis, wherein the occupancy of a certain lipid molecule in a given area of the lattice, , is evaluated as a function of time, such that takes on the values of 0 or 1. As a lipid approaches the fixed boundaries of the region of interest, incorrect assignments will be made when the molecule briefly crosses that boundary, due to fluctuations in the internal structure of the molecule, or to correlated motions with its neighbors, rather than true lipid-lipid displacement events. In such cases will briefly take a value that is inconsistent with the preceding and following snapshots in the trajectory. The noise filter implemented in MOSAICS is designed to assess this consistency and thus exclude artifactual excursions from the analysis of single-molecule data (Fig. 2 C). Such assessments are made by analyzing the filtered property over a window of trajectory snapshots and requiring a minimum occurrence to be observed before categorizing an event as significant.
Voronoi tessellations
For selected descriptors, MOSAICS uses tessellations of the membrane plane to assign each lipid molecule a discrete area, known as a Voronoi cell. These geometrical representations of the lipid molecules have been extensively used and algorithms for their computation are well established (3,15,16,17). While most of these algorithms are based around principles of geometry, lattice-based methods typically construct cells by identifying, for each lipid molecule k, the collection of lattice points that are closer to than to any other lipid. This type of calculation, however, again requires distance calculations for each trajectory snapshot, which becomes computationally very costly for large molecular systems. MOSAICS addresses this performance issue through a variation of the stamping method. Specifically, a first lipid-to-lattice point assignment is made through Eq. 3, using a radius that is sufficiently large to partition the entire membrane plane without gaps. As a result, the majority of lattice points become uniquely assigned to one lipid molecule only, while a minority are assigned to multiple lipid molecules, typically few. To refine this assignment, therefore, the algorithm only needs to evaluate distances for the latter fraction of lattice points and the few corresponding lipids, greatly accelerating the tessellation.
Coding and workload management
MOSAICS is constructed as a suite of C++ programs built around a common library that provides routines for reading, handling, and writing data. The object-oriented nature of C++ greatly simplifies rapid development of new analysis tools or improvements in those already existing. At the present time, MOSAICS uses code sourced from MDTraj (18) to read trajectory data and therefore input formats are limited to those used in GROMACS (19); data generated with other MD engines must therefore be converted accordingly.
Each of the programs in the MOSAICS suite provides a unique characterization and functions independently. MOSAICS is fully parallelized using MPI, and is therefore designed to leverage the computing capacity of high-performance computing server clusters. Nonetheless, MOSAICS programs may also be executed on standalone computing servers using the command-line interface. Irrespective of the computing platform, all the necessary parameters and input/output file names are read as command-line arguments (Fig. 2 D). Once running, the analysis program will distribute the workload among all available computing cores (Fig. 2 E), each of which will independently analyze a subset of trajectory snapshots. A single communication step is ultimately required to integrate and average the data and generate the output. This single communication step allows MOSAICS to scale linearly over hundreds or even thousands of cores, limited only by the number of trajectory snapshots to be analyzed.
Results
We proceed to describe applications of many of the analysis tools currently available in MOSAICS. For each membrane descriptor we briefly discuss what motivates the analysis and provide some practical details. For simplicity and to facilitate rationalization of the results, we apply these tools to a single set of trajectory data that we reported previously (14). Specifically, this dataset derives from multiple simulations of the CLC-ec1 CL–/H+ antiporter, in the monomeric form, embedded in a 2:1:2:1 mixture of POPE, POPG, DLPE, and DLPG lipids. These lipids differ in the length of their alkyl chains, which is shorter for di-lauryl (DL) lipids than palmityl-oleoyl (PO) lipids, and in their headgroup, which is negatively charged for phosphatidyl-glycerol (PG) lipids and neutral for phosphatidyl-ethanolamine (PE) lipids. Momeric CLC-ec1 is an interesting case study because it causes localized deformations of the lipid bilayer, which appear to translate into a driving force toward dimerization that is also dependent on the lipid composition of the membrane (14). These trajectory data add up to approximately 50 μs and were calculated using a coarse-grained representation of the simulation system, based on the MARTINI force field (20). It should be noted, though, that MOSAICS is equally applicable to all-atom representations as well as membrane systems without an embedded macromolecule; when a macromolecule is embedded, it may be allowed to diffuse and tumble freely or its position or orientation might be confined through appropriate restraints (14,21,22). For more information regarding each case, we refer the reader to the user manual (23) , available for download from https://github.com/MOSAICS-NIH/.
Membrane shape and thickness
The thickness of the membrane is a key characteristic that determines other important properties, such as permeability; it is also thought to influence the mechanism and organization of some embedded proteins. MOSAICS defines thickness as the separation between two surfaces, and , each of which maps the time-averaged Z-coordinate of lipid molecules in the upper or lower leaflet, respectively (Fig. 3 A). These maps, which effectively capture the shape of each leaflet, are computed with the “Z Coord” tool. The membrane thickness map, is then derived as:
| (9) |
Figure 3.
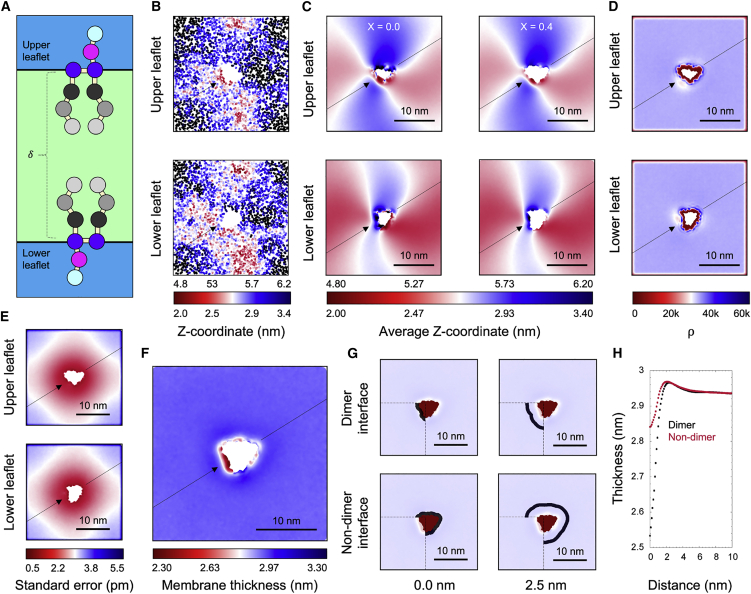
Membrane shape and thickness. (A) Schematic of a thickness measurement using the Z-coordinate of pseudoatoms GL1 and GL2 from each leaflet, which represent the ester linkages in a coarse-grained phospholipid structure. (B) Stamping interpolation map of the Z-coordinate used for thickness measurements taken from the first trajectory snapshot. (C) Time average of the Z-coordinate of the same atoms examined in (B), before and after excluding lattice points whose sample count is below 40% of the global average. (D) Map of the sample count that describes the number of snapshots for which each lattice point was characterized after stamping. (E) Standard error of the mean for the Z-coordinate map shown in (C). (F) Membrane thickness estimated as the distance separating the upper and lower surfaces in (C). (G) Masks used for selecting grid points to be averaged when computing the membrane thickness as a function of distance to the protein surface. Each mask, i.e., a selection shell with a width of 1 nm, is shown in black with the distance between the shell midplane and the protein (shown in red) indicated below the plot. For clarity, the thickness data that are averaged are shown as a transparent overlay. (H) Average membrane thickness computed as a function of the distance to the protein surface, using the masks depicted in (G). Note that the data shown in (B–H) describe all lipid types in the system, i.e., POPE, POPG, DLPE, and DLPG; spatial distributions in this and subsequent figures were obtained using a 28 × 28 nm lattice with a lattice point spacing of 0.7 Å, and a stamping radius of 0.23 nm. Note in (B and C) upper and lower leaflets are plotted on different scales, specified by the numeric values above and below the corresponding color bars. In this and subsequent figures the CLC dimerization interface is indicated with an arrow and the axis perpendicular to this interface is marked with a line passing through the protein.
Fig. 3B depicts instantaneous and maps for a snapshot of the CLC-membrane system; as expected, these maps show substantial heterogeneity due to thermal fluctuations. Time-averaged maps, shown in Fig. 3 C, smooth out this thermal noise and reveal a clear influence of the protein on membrane shape, at close and long range. For comparison, we plot maps that include all lattice points as well only those that satisfy a certain statistical significance threshold, namely > 0.4 (Eq. 6). To select an appropriate value for , it is useful to inspect the map (introduced in Eq. 5) to evaluate how lipid sampling degrades near the protein-lipid interface (Fig. 3 D). With this choice of , the standard error of and , for the region where these maps are considered to be defined, is at most 0.1 Å (Fig. 3 E), which is much smaller than the variations in membrane shape induced by the protein (Fig. 3 C), lending statistical credibility to the simulation result. The thickness spatial distribution that results from Eq. 9 is shown in Fig. 3 F. Because in this example we chose to represent the lipid coordinates with pseudoatoms GL1 and GL2, i.e., the coarse-grained counterparts of the phospholipid glycosidic linkages, this thickness map captures the full width of the hydrophobic layer of the membrane. Therefore, it is striking that the data reveal a thinning of about 8 Å (about 30% of the bulk value) at one specific locale of the protein surface; as it happens, this is precisely the known dimerization interface (14). By contrast, the thickness of the bulk membrane is highly uniform, as the long-range shape deformations caused by the protein in the outer and inner leaflets (Fig. 2 C) approximately match each other.
Fig. 3G shows how these observations might be further quantified and synthesized using 1D projections of the data, obtained through lattice masks; in this case, it would be of interest to extract the mean value of the membrane thickness as a function of the distance to the protein surface separately for the dimerization and non-dimerization interfaces. The resulting data, plotted in Fig. 3 H, are easily interpretable, and show that the bulk membrane thickness is largely unchanged up to 4 nm from the protein surface. Closer to the protein, throughout its perimeter, we observe a slight thickening followed by a thinning. The degree of thinning, however, is clearly much more pronounced near the dimerization interface than elsewhere in the protein perimeter.
Intramolecular distances
Variations in intramolecular lipid distances can reflect local or global changes in the bilayer. For example, the separation between the acyl chains, or splay distance, changes when the membrane bends. MOSAICS provides a general-purpose tool for this type of analysis called “Lipid Distances.” Fig. 4 A illustrates one application for the CLC system, namely an evaluation of end-to-end length of the acyl chains, specifically for the POPE/PG lipids. The results, provided in the form of a 2D distribution, demonstrate that the chain length is highly resistant to change. Near the protein surface, this distance varies by 1 Å at most relative to the bulk value, without a discernable pattern. That is, compression of the acyl chains is not how the membrane becomes thinner at the CLC dimerization interface. As discussed below, other descriptors explain this thinning defect.
Figure 4.
Internal lipid structure and leaflet entanglement. (A) Time-averaged map of the acyl chain end-to-end length, shown as δ in the corresponding schematic, as measured by the distance separating the pseudoatoms GL1/GL2 and C4A/C4B. (B) Time-averaged map of the second-rank order parameter, averaged over all pseudobonds in each acyl-chain. (C) Time-averaged map of the lipid tilt angle relative to the z axis (Eq. 13). (D) Time-averaged map of the number of interleaflet contacts per lipid. In this example, contacts are counted between the two groups of atoms enclosed by the dotted lines as indicated by red arrows. Note that the data shown in (A–D) describe POPE and POPG lipids only, for clarity.
Order parameters
So-called order parameters gauge the orientational entropy of lipid chains or headgroups relative to the membrane normal; for example, these parameters are good reporters of phase transitions induced by temperature changes. Order parameters are also examined when validating newly developed force fields since they can be computed from simulation data and compared with experimental measurements. MOSAICS includes a tool called “P2” that provides a spatial distribution of the second-rank order parameter, for a user-defined set of lipid atoms. For example, for acyl chain of lipid , consisting of atoms, MOSAICS maps the average order parameter at time as (Fig. 4 B):
| (10) |
| (11) |
where denotes the angle between the membrane perpendicular and the direction of the bond connecting two consecutive atoms along the chain. Fig. 4 B shows the result of this analysis for the acyl chains of the POPE/PG molecules in our CLC-ec1 simulation system. Spatial distributions for both the inner and outer leaflets clearly show a significant and specific decrease at the dimerization interface, indicating that the thickness deformation discussed above might entail a change in the orientational preferences of the acyl chains, relative to the bulk membrane.
Mean tilt angles
Direct measurements of the lipid tilt angle are an alternative to order parameters that is much more easily interpretable in structural terms. For this type of evaluation, MOSAICS includes an analysis tool called “Lipid Orientation.” This tool asks the researcher to define two ends of a fragment of interest in each lipid , and computes their connecting vector at time as:
| (12) |
where denotes the 3D atomic coordinates of each of the endpoints. As for other descriptors, MOSAICS stamps these vectors onto a discrete lattice and then averages the results over snapshots, obtaining a map of . A spatial distribution of the angle formed by this mean vector and the membrane perpendicular (assumed to be parallel to the z axis) is then obtained with:
| (13) |
where is a unitary vector. Using the projection of onto the membrane plane, , MOSAICS also provides information on the orientation of the fragment of interest relative to the y axis. That is:
| (14) |
It is worth noting that the definition of mean tilt angle in Eq. 13 differs from that conventionally adopted in other analysis programs (6), which instead quantifies the time average of the instantaneous tilt angle relative to the membrane normal. In our view, the latter quantity provides limited insight into the morphological features of the membrane, and thus we recommend evaluation of the descriptor defined in Eq. 13. However, MOSAICS can be used to obtain the time average of the instantaneous angle too, using the P2 tool described in the previous section (an example is shown in Fig. 9).
Figure 9.
Computing performance and scalability. (A) Spatially resolved distributions for four different descriptors of membrane structure, calculated with MOSAICS or LiPyphilic. The descriptors are: bilayer shape, quantified by the mean Z-coordinate of the GL1/GL2 pseudoatoms; the area per lipid in the plane of the phosphate atoms; the second-rank order parameter, averaged over each acyl chain; and the mean instantaneous tilt angle of the chains, measured for a the GL1-C4A and GL2-C4B atom pairs (calculated with the “P2” tool in the case of MOSAICS). (B) Clock times required to obtain the results shown in (A), normalized by the number of snapshots in the trajectory. For MOSAICS, timings are given for calculations carried out on a single CPU core as well as over 10, 100, and 500 CPU cores of the same type. For LiPyphilic, which to our knowledge does not currently support parallelization, timings for single-core calculations are provided. (C) Evaluation of the membrane shape for a system containing a cluster of 37 copies of the ATG9A trimeric protein. (D) Clock times required to obtain the results shown in (C), presented as in (B).
Fig. 4C illustrates an example of this type of analysis for the CLC-ec1 simulations, which specifically evaluates the tilt angle of the acyl chains in the POPE/PG lipids relative to the membrane perpendicular. Accordingly, the selection used in Eq. 12 was the first and last atom in each chain. For the bulk membrane, the analysis shows that the mean tilt angle of the acyl chains is exactly 0° for one leaflet and exactly 180° for the other, as their configurational dynamics is isotropic. This isotropy, however, breaks at the protein-lipid interface, leading to small angle deviations for most of the protein perimeter. At the dimerization interface, however, the mean tilt angle changes by as much as 60°. This perturbation is observed in both the upper and lower leaflets, reflecting the internal symmetry of the protein structure, which consists of two inverted topological repeats (24,25,26). Reaffirming the conclusions from the order parameter analysis, these data show that the thinned defect caused by CLC-ec1 is realized, at least in part, through the tilting of the lipid molecules nearest to the dimerization interface.
Number of interleaflet contacts
The degree of entanglement between the two leaflets of the bilayer, i.e., the interdigitation between opposing acyl chains, is another possible reporter of perturbations in membrane shape. MOSAICS quantifies this entanglement using a tool called “Interleaflet Contacts.” For a certain user-defined threshold distance, this tool calculates the number of pairwise contacts between the atoms in each of the lipid chains in one leaflet and all other chains in the other, and then maps the resulting time averages (Fig. 4 D). For the CLC-ec1 system, this analysis reveals a marked increase in the degree of interdigitation of outer and inner lipids at the dimerization interface; indeed, the number of interleaflet contacts doubles compared with bulk lipids. These data thus lead to the conclusion that the thickness defect caused by the protein is realized not only through increased lipid tilt but also greater overlap between leaflets.
Time-averaged molecular configurations
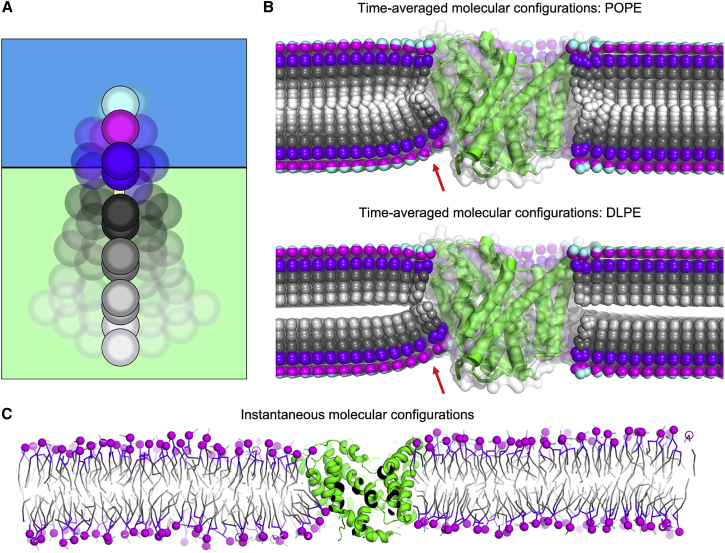
While quantitative representations in the form of distributions or profiles are essential in any rigorous analysis, graphical visualizations of structural data can be uniquely compelling and intuitive. Individual simulation snapshots, however, can be highly heterogeneous and thus more confusing than illuminating; worse, they might be statistically unrepresentative and therefore misleading. MOSAICS introduces a tool called “Mean Lipid Coords” that provides clear and often striking graphical representations while ensuring the analysis is statistically sound. Like other tools, this program uses the stamping method to assign lipids to lattice points, but the interpolated descriptors are the XYZ-coordinates of each of the atoms in the molecule; that, is a time-averaged map is obtained for the Cartesian coordinates of each lipid atom type in the membrane (Fig. 5 A). To enable visualization of these data, MOSAICS constructs a PDB-formatted file that contains the average molecular configurations sampled at each lattice point, provided that point satisfies the statistical significance threshold defined by the user (Eq. 6). These structures can provide significant insight into the morphology of the lipid bilayer. For our CLC-ec1 simulation, for example, these data show that, in the bulk, the instantaneous lipid configurations average to a (non-physical) linear structure with both chains perpendicular to the membrane plane, due to the isotropy of this environment with respect to that plane. By contrast, the protein dimerization interface causes the neighboring lipids to become strongly tilted, on average (Fig. 5 B). These trends are observable in the individual trajectory snapshots (Fig. 5 C) and are logically consistent with previous analyses. In addition, the time average coordinates hint at other perturbations. For example, the divergence of the individual chain averages at the dimerization interface indicates the lipid dynamics is distinct from the bulk, while the fanning of the headgroups suggests that the lipid-water interface is perturbed.
Figure 5.
Average lipid configurations. (A) Schematic of the time averaging of instantaneous lipid configurations. Note that the rotational freedom and internal dynamics of lipid molecules cause the average configuration to resemble a (non-physical) linear structure perpendicular to the membrane midplane, with both acyl chains superposed and in line with the headgroup. (B) Average configurations for POPE and DLPE lipids. Despite the fact that the single-molecule averages are non-physical structures, this representation clearly illustrates the nature of the membrane deformations induced by the protein, and the impact of DL lipids on membrane thickness. Regions containing highly tilted lipids whose lipid heads groups fan outwards are indicated with a red arrow. The average protein structure is also shown alongside, with secondary structure elements in green and the surface in white. (C) One of the snapshots of the trajectory analyzed in (B), shown in cross section for clarity. The dimensions of the simulation system are 28 × 28 nm, including ∼2600 lipid molecules.
Number of nearest lipid neighbors and area per lipid
Lipid packing and the inversely related area per lipid are important descriptors of intrinsic membrane structure and perturbations thereon. To evaluate the former, MOSAICS quantifies for each lipid in the bilayer the number of neighboring lipids within a certain distance threshold, mapping the results on a 2D distribution as for other analyses. The distance threshold considered by this “Nearest Neighbors” tool pertains to geometric centers within each molecule, which might be defined for the entire molecule or for specific chemical groups. The data in Fig. 6 A, for example, show how this descriptor varies in the CLC-ec1 system, when the analysis is focused on the lipid headgroups. The abovementioned fanning at the dimerization interface shows here as a reduction in the number of nearest neighbors, relative to other regions in the membrane at the same distance to the protein surface. While informative, this descriptor can, however, be difficult to interpret since the number of nearest lipid neighbors naturally decreases close to the protein (Fig. 6 A). To complement this kind of analysis, MOSAICS features a tool called “APL,” which computes both the instantaneous values and time averages of the area occupied by each lipid and maps the results on a 2D distribution. To evaluate the instantaneous values of the area per lipid, APL generates Voronoi tessellation for each snapshot using a variation of the stamping algorithm to optimize performance. This analysis might examine a specific lipid type in a mixture, or evaluate overall values across types. Protein atoms exposed to the lipid bilayer are also considered when constructing the Voronoi diagram to ensure that the area calculations at the protein-lipid interface are accurate. Fig. 6 B shows the results of this analysis for CLC-ec1, considering all lipid types simultaneously. In both outer and inner leaflets, the maps clearly reveal that the area per lipid increases from 0.58 nm2 in the bulk to 0.66 nm2 at the dimerization interface. Together, these results demonstrate that the tilting of lipids at this interface translates into a strong density defect.
Figure 6.
Descriptors of lipid density and lipid-type enrichment. (A) Time-averaged map of the number of lipid-nearest neighbors, measured for the headgroup layer. The geometric center for each headgroup is indicated by a green circle. (B) Left, Voronoi diagrams computed for a single trajectory snapshot; right, time-averaged map of area per lipid. (C) Time-averaged map of the alkyl chain hydration number. Water molecules are represented as red circles in the corresponding schematic and the contacts with the lipid by dotted lines. (D) Enrichment factor computed for DL lipids. Note that the data shown in (A–C) describe all lipid types in the system, i.e., POPE, POPG, DLPE, and DLPG.
Intermolecular contacts
Examination of the number of contacts formed between lipid molecules, and between lipids and non-lipid molecules, can be highly informative. For example, the degree to which a lipid type is a compatible solvent for different areas of a membrane protein surface i.e., the extent of local hydrophobic mismatch, may be evaluated by counting the contacts formed between the chains and exposed residues on the protein surface. To facilitate these kinds of analyses, MOSAICS features a tool called “Lipid Contacts.” This tool measures three types of contacts, namely lipid-lipid, lipid-protein, and lipid-solvent. Once quantified for each lipid molecule, the number of contacts is stamped to the lattice and time averaged as described previously. These analyses can be focused on specific lipid chemical groups. For example, exposure to water can be quantified for the lipid headgroups and compared with that of the alkyl chains. Fig. 6 C shows maps of the observed degree of hydration of the alkyl chains in the CLC-ec1 trajectories. Strikingly, the level of hydration of the membrane interior at the dimerization interface is doubled relative to the bulk value, confirming that this structural defect is energetically costly, and a primary factor driving the association of CLC-ec1 monomers.
Lipid enrichment factors
Favorable interactions with amino acids exposed on a protein surface might cause a specific lipid type in a mixture to accumulate near a certain site, explaining perhaps a regulatory process. Localized membrane perturbations, like the thinning defect observed at the CLC-ec1 dimerization interface, might also cause lipid types whose traits complement those of the defect to become enriched within the affected area. MOSAICS provides a tool to quantify any kind of enrichment process, named “2D Enrichment.” Let us consider a bilayer of two or more lipid types, and assume we classify these types into two groups, A and B. This tool calculates the enrichment factor of group A as:
| (15) |
where and are the sample count maps (Eq. 5) for each group and R is the ratio between the number of lipid molecules in each group (in each leaflet). Note that both groups A and B might each represent one or more lipid types; for example, they might include lipids with a common feature (e.g., chain length) but that are different otherwise (e.g., headgroup). This choice is defined by the user. When applied to the CLC-ec1 system, we find that the membrane defect at the dimerization interface causes DLPE/DLPG lipids to become enriched by as much as 100% (Fig. 6 D). That is, while in the bulk the PO/DL ratio is 1:1, at the dimerization interface DL lipids are more probable than PO lipids and are thus a better solvent for the protein at this site, consistent with the fact they have shorter alkyl chains. On the other hand, DL lipids are a poor solvent for the rest of the protein surface, as can be seen by negative enrichment values. It is worth noting that enrichment values in the bulk should approach zero, by definition (Fig. 6 D). This condition can therefore be used to ascertain the quality of the configurational sampling attained in a given simulation, and thus the reliability of the enrichment signals that might be detected near a protein.
Lipid mixing
While simulations of complex membranes with many lipid components are increasingly popular, the initial configurations generated for this kind of molecular systems is, invariably, entirely arbitrary. One might assume that the various lipid components are uniformly distributed or not; either way, this choice implies a bias that might potentially influence the conclusions of the analysis. To eliminate or mitigate this bias, one must carry out a simulation that is long enough to redistribute the different lipid types according to the intrinsic free-energy landscape of the system. This redistribution will generally take longer for membranes with many different components, and will be much more costly for all-atom representations of the bilayer. Evidence of adequate lipid mixing is, however, imperative in any serious analysis of lipid structure and dynamics. MOSAICS includes a tool, called “Lipid Mixing,” that provides a means to quantify this redistribution as a function of simulation time. For each lipid molecule, this tool monitors the composition of its first solvation shell in each trajectory snapshot, and quantifies what percentage of the lipids in the bilayer have been in that shell at some point as a function of simulation time. The results are then averaged over all lipids in the corresponding leaflet, which we define as the lipid mixing fraction. Ideal mixing can be thus thought of as a condition where every lipid molecule has transiently resided in the first solvation shell of every other lipid molecule; in such case, the lipid mixing fraction is 100%.
Unlike other MOSAICS tools, Lipid Mixing does not produce a 2D distribution, but rather the time evolution of an ensemble average. In practice, this tool monitors a solvation shell of radius around each lipid (Fig. 7 A), and calculates the following quantity at all time points :
| (16) |
where is the number of lipids in the leaflet, and takes two possible values: if lipid is found in the first shell of lipid at time , and otherwise. Here, the asterisk denotes the application of a noise filter to the raw time series of to exclude spurious short-lived crossings across the shell boundary (see Methods). Averaged over all lipids in the leaflet, the mixing fraction is then:
| (17) |
Figure 7.
Lipid mixing and self-diffusion. (A) Schematic of a lipid solvation shell of radius around the lipid geometric center (green circles), in this case computed using the GL1 and GL2 pseudoatoms. (B) The number of lipids found in the first solvation shells of a set of target lipids is given as a function of time. (C) Probability distribution of the single-molecule residence time in those solvation shells; the average residence time is indicated. (D) Percentage of lipids in the bilayer that (transiently) visit the first solvation shells of the target lipids, i.e., the mixing fraction. In (B and C) error bars represent the variance across lipid molecules (Eq. 19). The noise filter used in this analysis encompasses 3 ns of simulation time, and the first solvation shell was defined as having a radius of 1.1 nm. (E) Schematic of lipid diffusion; the position of each lipid is tracked by the X- and Y-coordinates of a geometric center, indicated by a green circle. (F) Mean-square displacement (MSD) of either POPE/POPG lipids (left) or DLPE/DLPG lipids (right), as a function of the elapsed time τ. Black lines represent the MSD for all lipids of each type, while the gray lines represent the MSD of individual lipids; the red dotted line represents a linear regression of all the data, which was used to derive the diffusion coefficient, , using Eq. 21.
Using the same tracking data, this tool also produces a noise-filtered time series of the number of lipids that occupy, on average, the first solvation shells of other lipids, i.e., the lipid solvation number:
| (18) |
The quantities calculated through Eqs. 16, 17, and 18 can be computed for all lipid types or for specific subsets; for example, in a bilayer with two lipid types A and B, it is straightforward to breakdown lipid solvation numbers into AA, BB, AB, and BA contributions. It is also informative to evaluate the variance in the mixing fraction across the lipids in the leaflet; this variance is computed as:
| (19) |
When applied to the CLC-ec1 system, and combining all lipid types for simplicity, we find that the lipid first solvation shells approximately consist of five lipids, on average (Fig. 7 B). This number fluctuates only by a single molecule in each direction, demonstrating that lipid translational motions are highly concerted and do not result in empty spaces. Through further analysis of , it is possible to derive the distribution of residence times (Fig. 7 C), which shows that the average time spent by a lipid in the solvation shell of another lipid is 6.3 ns, with an upper limit of 50 ns. Accordingly, by the end of one of our 8-μs simulations, nearly 80% of the lipids have resided in the first solvation shell of every lipid (Fig. 7 D). For this membrane consisting of four different lipid types (represented with a coarse-grained force field), this result demonstrates a high degree of mixing, eliminating concerns regarding the arbitrary initial condition.
Diffusion coefficients
It is often of interest to quantify the rate at which lipids move laterally across the membrane, i.e., their diffusion coefficient. MOSAICS includes a tool named “Lipid MSD” for this purpose. Like the preceding tool, Lipid MSD does not produce a 2D distribution, but rather the time evolution of an ensemble average; the quantity that is averaged is the mean-square displacement (MSD) of each lipid in a certain elapsed time :
| (20) |
where T is the total number of trajectory snapshots, is the time interval in between, and denotes the position of each lipid at time and after the elapsed time (Fig. 7 E). The MSD is related to the diffusion coefficient by the Einstein relation:
| (21) |
where is the dimensionality of the space explored by the diffusing particles; for lipids confined to a bilayer, . A plot of against the elapsed time will therefore yield a line whose slope equals . To evaluate Eq. 20, MOSAICS tracks the geometric center of each lipid, considering only the projection of onto the XY plane (Fig. 7 E). MOSAICS corrects for periodicity artifacts, which can be particularly non-negligible in constant-pressure simulations (27), using a specialized tool called “PBC XY” that mirrors the method proposed by Smith and Lorenz (6). (For more details, we refer the reader to the MOSAICS user manual (23).) In a lipid mixture, each lipid type might be analyzed individually. For example, Fig. 7 F shows a plot of for the PO and DL lipids of our model system. These data fit the linear dependence expected from the Einstein relation very well, but only for elapsed times greater than 100 ns; in this diffusive regime, lipids exchange positions with one another in a Brownian motion. For shorter elapsed times, however, the MSD deviates from this linear regime; this motion is only apparent, as it mostly reflects rapid fluctuations in the internal structure of the lipids. Excluding this regime, we find a diffusion coefficient of 38 nm2/μs for PO lipids and 41 nm2/μs for DL. These results demonstrate that DL lipids have an increased mobility compared with PO.
Residence times
Mechanistic studies seeking to interpret lipid-mediated regulatory processes often posit the existence of lipid binding sites on the surface of membrane proteins. MOSAICS permits a quantitative evaluation of putative active sites through a tool called “2d Kinetics.” In a nutshell, this tool quantifies the distribution of residence times observed at different locales across the membrane plane. Longer residence times near a specific site on a protein surface might indicate a binding site but, if the residence time equals the trajectory length, this observation might reflect an initial condition artifact.
Like other MOSAICS tools, 2d Kinetics uses a lattice to discretize the membrane plane and monitors the lipid occupancy of each lattice point as a function of simulation time. To define this occupancy with optimal accuracy, however, this tool does not use the stamping algorithm. Instead, the tool performs a Voronoi tessellation of each trajectory snapshot, and assigns the lattice points within each Voronoi cell to the corresponding lipid molecule, which is uniquely indexed. This strategy entails the construction of a time-dependent matrix whose elements identify the residing lipid molecule at a given time point (Fig. 8 A). Once calculated for every snapshot, is passed through a noise filter to discard spurious assignments resulting from changes in internal lipid structure, rather than actual translational motions. The time evolution of is then examined to determine all changes in the occupancy state of the lattice points, annotating the elapsed time between these changes for further processing.
Figure 8.
Residence time analyses. (A) Noise filtering of Voronoi diagrams used to calculate two-dimensional maps of the lipid dwell time in different regions of the membrane. (B) Two-dimensional distributions of the mean residence time for PO and DL lipids. (C) Assignment of lipids to solvation shells around the protein, defined separately for the CLC dimerization interface and the rest of the protein surface. The first-shell lipids are colored cyan, while second, third, fourth, and fifth shells are colored purple, green, yellow, and red, respectively; subsequent solvation shells are colored white. (D) Probability distributions of the residence time in the first lipid solvation shell, either for PO or DL lipids, either at the dimerization interface or elsewhere. Average residence times are indicated in each case. The noise filter used in this analysis encompasses 3 ns of simulation time.
Fig. 8B shows the results of this kind of analysis for the PO and DL lipids in the CLC-ec1 system. In the bulk, we find that the average residence time at any lattice point is approximately 5 ns. Near the protein surface the lattice point residence times increase significantly, reaching as high as 80 ns for a few sites. While these sites stand out, the observed dwell times fall short of what would be expected for a canonical bimolecular complex. Furthermore, PO and DL lipids yield similar results, indicating that the enrichment of DL molecules at the dimerization interface does not result from long-lasting protein-lipid interactions, but rather a process of preferential lipid solvation.
Dwell times and exchanges in solvation shells
While the 2d Kinetics tool provides important insights into how the lipid dynamics varies across the membrane, it is often useful to synthesize these data by evaluating residence times for larger regions. This information is particularly relevant near a protein surface, especially when lipid regulation results from a process of enrichment or preferential solvation, rather than the formation of protein-lipid bimolecular complexes. To facilitate this type of analysis, MOSAICS implements a tool called “Solvation Shells.”
Solvation Shells uses the lattice point occupancy data produced by 2d Kinetics to transform the simulated trajectory into a noise-filtered series of Voronoi diagrams. For each snapshot, each of the Voronoi cells is then assigned to one of five regions, comprising the first five lipid solvation shells and the bulk (Fig. 8 C). This assignment is based on adjacencies rather than specific cutoff distances. For example, cells that are adjacent to the protein are considered to be the first shell; those adjacent to the first shell but not the protein define the second shell, etc. The program permits an additional subclassification within each of the shells, to discriminate between the vicinity of a certain site on the protein and the rest of its surface (Fig. 8 C).
Because each Voronoi cell is uniquely associated with one lipid molecule, the time evolution of these shell and/or subshell assignments (after noise-filtering) reveals the distribution of residence times in each shell for each lipid type, as well as the frequency with which a lipid of a certain type is replaced by another of the same or different type. Fig. 8 D illustrates this kind analysis for the CLC-ec1 system, specifically for the first shell around the protein, subdivided into two regions, one proximal to the dimerization interface, and another proximal to other interfaces. For both PO and DL lipids, and both regions within the shell, the distribution of residence times decays exponentially. These distributions, however, have distinct mean values, listed in Fig. 8 D. It is clear that the mean residence time at the dimerization interface is greater for DL lipids than PO lipids; conversely, PO lipids have longer dwell times near the other interfaces. These results suggest a relationship between membrane thickness and the residence time and are also qualitatively consistent with the enrichment data shown in Fig. 6 D. Examination of the rates of exchange of lipids of one or other type can provide additional insights into the origins of this enrichment.
Benchmarking
To evaluate the computational performance of MOSAICS in comparison with other tools for membrane analysis, we first measured the average clock time required to analyze 50,000 snapshots of the test case system described above, i.e., CLC embedded in a 2600-lipid bilayer. We specifically compared MOSAICS with LiPyphilic, because several observables are available to both programs (Table 1), and because LiPyphilic has been reported to perform well relative to other high-end analysis tools (6). To our knowledge LiPyphilic has not been parallelized; therefore, this comparison was carried out using a single CPU core in each case. Fig. 9 A shows results obtained using either tool for membrane shape, area per lipid, mean instantaneous lipid tilt angle, and second-rank order parameter. Both suites produce very similar results for regions of the membrane that are distant from the protein. In the vicinity of the protein this comparison is less clear, as the protein volume and its interface with the lipid bilayer are clearly discernable in the 2D distributions produced with MOSAICS but can only be inferred with LiPyphilic. Fig. 9 B shows the clock time required to complete each analysis, normalized by the number of trajectory snapshots. These results show that MOSAICS is nearly 100 times faster than LiPyphilic for computations that do not involve Voronoi diagrams, and 5 times faster in those that do. For the former descriptors, this pronounced performance gap primarily results from the differences in the interpolation methods employed; in our hands, LiPyphilic can be accelerated by an order of magnitude if the interpolation step is entirely omitted, but this omission logically comes at the expense of data quality (data not shown). At any rate, the observed performance gap increases when the workload is distributed among multicore servers in a computing cluster. As shown in Fig. 9 B, MOSAICS performance scales up efficiently over hundreds of cores, further accelerating data analysis by one to two orders of magnitude.
The excellent computational efficiency of MOSAICS opens the door for systematic, quantitative analyses of very large molecular systems. To illustrate this point, we used MOSAICS to analyze a molecular system comprising ∼11 million CG atoms; this system includes 37 copies of the tetrameric protein ATG9A, embedded in a 194 × 194 nm membrane patch composed of ∼112,000 lipids (22). ATG9A, known to play a critical role in autophagosome physiology, was the subject of a recent simulation study that indicated high-density clusters of this protein foster the formation of membrane vesicles (22). Fig. 9 C compares calculations of membrane shape for this very large system using MOSAICS and LiPyphilic. As observed for the previous test case, both codes produce similar results (except for the degree of definition of the protein volumes), namely the development of a dome-like structure whose curvature is comparable with that in observed membrane vesicles (22). The performance of MOSAICS is, however, clearly superior; about 10-fold faster when a single core is used and orders of magnitude faster when the calculation is distributed over hundreds of CPU cores (Fig. 9 D).
In this context, it is worth noting that improvements to MOSAICS will be required to permit a comprehensive analyses of highly curved membrane topologies such as those induced by ATG9A (22) and other proteins involved in cellular and organelle morphology (28,29). While observables, such as shape, interleaflet contacts, or residence times, are already accessible to these systems, other descriptors, such as membrane thickness, lipid tilt angle, or area per lipid, depend on local evaluations of the bilayer normal; solutions to this problem, however, exist (8,10) and will become available in a future update.
Conclusions
We present a comprehensive suite of software tools, named MOSAICS, designed to enable quantitative analyses of a broad set of descriptors of lipid bilayer structure and dynamics as represented in MD simulations. This suite is self-contained and optimized to maximize its computationally efficiency, and is therefore applicable to large molecular systems; it is also freely available (from https://github.com/MOSAICS-NIH/) and designed to be user-friendly and flexible in practice. To demonstrate the usefulness of this suite in real-life investigations, we apply MOSAICS to examine the role of the lipid bilayer in driving the dimerization of the CLC-ec1 antiporter. Recapitulating previously reported observations (14), this systematic analysis identifies the specific perturbations induced by monomeric CLC-ec1 in the structure and dynamics of the bilayer, and dissects their origin at the molecular level. We anticipate that this software suite will prove useful in future simulation studies of lipid bilayers and their interplay with membrane proteins.
Author contributions
N.B. and J.D.F.-G. designed the research. N.B. performed the research, contributed analytic and software tools, and analyzed the data. N.B. and J.D.F.-G. wrote the paper.
Acknowledgments
We are thankful to members of our laboratory and to colleagues in the Forrest laboratory at NIH/NINDS for their feedback on their experience using the MOSAICS suite. We are also thankful to Tugba N. Öztürk for her comments on an early draft of this manuscript, and to Janice L. Robertson for her input throughout this software development project. This work was funded by the Intramural Research Program of the National Institutes of Health (NIH). Computational resources were in part provided by the NIH Biowulf facility.
Declaration of interests
The authors declare no competing interests.
Editor: Siewert Jan Marrink.
Contributor Information
Nathan Bernhardt, Email: nathan.bernhardt@nih.gov.
José D. Faraldo-Gómez, Email: jose.faraldo@nih.gov.
References
- 1.Allen W.J., Lemkul J.A., Bevan D.R. GridMAT-MD: a grid-based membrane analysis tool for use with molecular dynamics. J. Comput. Chem. 2009;30:1952–1958. doi: 10.1002/jcc.21172. [DOI] [PubMed] [Google Scholar]
- 2.Carr M., MacPhee C.E. Membrainy: a ‘smart’ unified membrane analysis tool. Source Code Biol. Med. 2015;10:3. doi: 10.1186/s13029-015-0033-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lukat G., Krüger J., Sommer B. APL@Voro: a Voronoi-based membrane analysis tool for GROMACS trajectories. J. Chem. Inf. Model. 2013;53:2908–2925. doi: 10.1021/ci400172g. [DOI] [PubMed] [Google Scholar]
- 4.Ramasubramani V., Dice B.D., et al. Glotzer S.C. Freud: a software suite for high throughput analysis of particle simulation data. Comput. Phys. Commun. 2020;254:107275. [Google Scholar]
- 5.Romo T.D., Leioatts N., Grossfield A. Lightweight object-oriented structure analysis: tools for building tools to analyze molecular dynamics simulations. J. Comput. Chem. 2014;35:2305–2318. doi: 10.1002/jcc.23753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith P., Lorenz C.D. LiPyphilic: a Python toolkit for the analysis of lipid membrane simulations. J. Chem. Theory Comput. 2021;17:5907–5919. doi: 10.1021/acs.jctc.1c00447. [DOI] [PubMed] [Google Scholar]
- 7.Song W., Corey R.A., et al. Sansom M.S.P. PyLipID: a Python package for analysis of protein-lipid interactions from molecular dynamics simulations. J. Chem. Theory Comput. 2022;18:1188–1201. doi: 10.1021/acs.jctc.1c00708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Buchoux S. FATSLiM: a fast and robust software to analyze MD simulations of membranes. Bioinformatics. 2017;33:133–134. doi: 10.1093/bioinformatics/btw563. [DOI] [PubMed] [Google Scholar]
- 9.Gapsys V., de Groot B.L., Briones R. Computational analysis of local membrane properties. J. Comput. Aided Mol. Des. 2013;27:845–858. doi: 10.1007/s10822-013-9684-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bhatia H., Ingólfsson H.I., et al. Bremer P.T. MemSurfer: a tool for robust computation and characterization of curved membranes. J. Chem. Theory Comput. 2019;15:6411–6421. doi: 10.1021/acs.jctc.9b00453. [DOI] [PubMed] [Google Scholar]
- 11.Guixà-González R., Rodriguez-Espigares I., et al. Selent J. MEMBPLUGIN: studying membrane complexity in VMD. Bioinformatics. 2014;30:1478–1480. doi: 10.1093/bioinformatics/btu037. [DOI] [PubMed] [Google Scholar]
- 12.Bekker H., Berendsen H.J.C., et al. Renardus M.K.R. GROMACS: a parallel computer for molecular-dynamics simulations. Phys. Comput. 1993;92:252–256. [Google Scholar]
- 13.Michaud-Agrawal N., et al. Beckstein O. MDAnalysis: a toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011;32:2319–2327. doi: 10.1002/jcc.21787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chadda R., Bernhardt N., et al. Robertson J.L. Membrane transporter dimerization driven by differential lipid solvation energetics of dissociated and associated states. Elife. 2021;10 doi: 10.7554/eLife.63288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pandit S.A., Vasudevan S., et al. Scott H.L. Sphingomyelin-cholesterol domains in phospholipid membranes: atomistic simulation. Biophys. J. 2004;87:1092–1100. doi: 10.1529/biophysj.104.041939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aurenhammer F. Voronoi diagrams: a survey of a fundamental geometric data structure. ACM Comput. Surv. 1991;23:345–405. [Google Scholar]
- 17.Barber C.B., Dobkin D.P., Huhdanpaa H. The Quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996;22:469–483. [Google Scholar]
- 18.McGibbon R.T., Beauchamp K.A., et al. Pande V.S. MDTraj: a modern open library for the analysis of molecular dynamics trajectories. Biophys. J. 2015;109:1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pronk S., Páll S., et al. Lindahl E. Gromacs 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Marrink S.J., Risselada H.J., et al. de Vries A.H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 21.Park Y.C., Reddy B., et al. Faraldo-Gómez J.D. State-specific morphological deformations of the lipid bilayer explain mechanosensitive gating of MscS ion channels. bioRxiv. 2022 doi: 10.1101/2022.07.01.498513. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guardia C.M., Tan X.F., et al. Banerjee A. Structure of human ATG9A, the only transmembrane protein of the core autophagy machinery. Cell Rep. 2020;31 doi: 10.1016/j.celrep.2020.107837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bernhardt N. MOSAICS User Manual Version 1.0. 2022. https://github.com/MOSAICS-NIH.
- 24.Dutzler R., Campbell E.B., et al. MacKinnon R. X-ray structure of a ClC chloride channel at 3.0 Å reveals the molecular basis of anion selectivity. Nature. 2002;415:287–294. doi: 10.1038/415287a. [DOI] [PubMed] [Google Scholar]
- 25.Faraldo-Gómez J.D., Roux B. Electrostatics of ion stabilization in a ClC chloride channel homologue from. J. Mol. Biol. 2004;339:981–1000. doi: 10.1016/j.jmb.2004.04.023. [DOI] [PubMed] [Google Scholar]
- 26.Robertson J.L., Kolmakova-Partensky L., Miller C. Design, function and structure of a monomeric ClC transporter. Nature. 2010;468:844–847. doi: 10.1038/nature09556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.von Bulow S., Bullerjahn J.T., Hummer G. Systematic errors in diffusion coefficients from long-time molecular dynamics simulations at constant pressure. J. Chem. Phys. 2020;153 doi: 10.1063/5.0008316. [DOI] [PubMed] [Google Scholar]
- 28.Anselmi C., Davies K.M., Faraldo-Gómez J.D. Mitochondrial ATP synthase dimers spontaneously associate due to a long-range membrane-induced force. J. Gen. Physiol. 2018;150:763–770. doi: 10.1085/jgp.201812033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Davies K.M., Anselmi C., et al. Kühlbrandt W. Structure of the yeast F1Fo-ATP synthase dimer and its role in shaping the mitochondrial cristae. Proc. Natl. Acad. Sci. USA. 2012;109:13602–13607. doi: 10.1073/pnas.1204593109. [DOI] [PMC free article] [PubMed] [Google Scholar]