Conditional Treatment Effect Analysis of Two Infusion Rates for Fluid Challenges in Critically Ill Patients: A Secondary Analysis of Balanced Solution versus Saline in Intensive Care Study (BaSICS) Trial

Abstract

Rationale

Optimal infusion rate for fluid challenges in critically ill patients is unknown. A large clinical trial comparing two different infusion rates yielded neutral results. Conditional average treatment effect (CATE) assessment may aid in tailoring therapy.

Objectives

To estimate CATE in patients enrolled in the BaSICS trial and to assess the effects of receiving CATE model–recommended treatment in terms of hospital mortality.

Methods

Post hoc analysis of the BaSICS trial assessing the effect of two infusion rates for the fluid challenge (fast, 999 ml/h, control group; vs. slow, 333 ml/h, intervention group) on hospital mortality. CATE was estimated as the difference in outcome for treatment arms in counterfactuals obtained from a Bayesian model trained in the first half of the trial adjusted for predictors hypothesized to interact with the intervention. The model recommended slow or fast infusion or made no recommendation in the second half. A threshold greater than 0.90 probability of benefit was considered.

Results

A total of 10,465 patients were analyzed. The model was trained in 5,230 patients and tested in 5,235 patients. A recommendation could be made in the test set in 19% of patients (14% were recommended the control group and 5% the treatment group); for 81% of patients, no recommendation could be made. Slow infusion was more frequently recommended in cases of planned admissions in younger patients; fast infusion was recommended for older patients with sepsis. Slow infusion rate in the subgroup of patients in the test set in which slow infusion was recommended by the model was associated with an odds ratio of 0.58 (95% credible interval of 0.32–0.90; 0.99 posterior probability of benefit) for hospital mortality. Fast infusion in the subgroup in which the model recommended fast infusion was associated with an odds ratio of 0.72 (credible intervals from 0.54 to 0.91; probability of benefit >0.99).

Conclusions

Estimation of CATEs from counterfactual probabilities in data from BaSICS provided additional information on trial data. Agreement between treatment recommendation and actual treatment was associated with lower hospital mortality.

Clinical trial registered with clinicaltrials.gov (NCT 02875873).

Despite the frequency of fluid challenges performed in critically ill patients, there are few data on the appropriate infusion rate to be used (1). Although faster infusion rates may result in earlier restoration of hemodynamics, including cardiac output, slower infusion rates may be associated with less tissue edema, which could theoretically limit organ dysfunction and improve outcomes (2, 3). This concept was tested in the BaSICS by comparing two different infusion rates for fluid challenges in critically ill patients: 999 ml/h, the “fast rate,” the control group in the trial; and 333 mL/h, the “slow rate,” the intervention group in the trial (1).

The trial yielded neutral results overall for the primary endpoint of 90-day mortality. As with any clinical trial, BaSICS provided an average estimate of the treatment effect for the included patient population. It has been suggested that heterogeneity in treatment effect may play an important role in clinical trials (4). Analysis of heterogeneity in treatment effect is complex and can be performed using several methods, including unsupervised methods to find cluster/phenotypes (5–7) or estimates of conditional average (“individualized”) treatment effects (CATEs) (8, 9). Estimates of CATEs may allow a more precise categorization of patients according to the expected response to treatment and aid in personalizing therapy.

In this secondary post hoc analysis of the infusion-rate arms of the BaSICS trial, we investigated whether estimates of CATEs obtained from clinical data could provide additional interpretations of trial data regarding the effects of two infusion rates and therefore foster improved interpretation of the trial’s results.

Methods

Design

A secondary, post hoc analysis of the BaSICS trial was performed in which all patients with complete primary endpoint information were included in the analysis.

Procedures

Details on the BaSICS trial can be found in the main publication and protocol (1, 10). Patients requiring at least one fluid challenge without a discharge plan in the next 24 hours and with one indicator of increased risk of death or receipt of kidney replacement therapy were eligible for the trial. Risk factors for death/kidney replacement therapy included age greater than 65 years, hypotension, sepsis, receipt of invasive or noninvasive respiratory support, acute kidney injury, and cirrhosis or acute liver failure. The study assessed the effects of two different fluid types (Plasma-Lyte 148 [Baxter Hospitalar] or 0.9% saline solution; not discussed in the present analysis) and two different infusion rates for each fluid challenge given: the control group received 999 ml/h, the fast rate, and the intervention group received 333 ml/h, the slow rate. Sites were instructed to administer fluid challenges in aliquots of 500 ml at the allocated infusion rate using infusion pumps. All other aspects of care, including the decision to perform fluid challenges, were left to the discretion of the attending physician.

Endpoints

The primary endpoint was hospital mortality.

Main Statistical Analysis

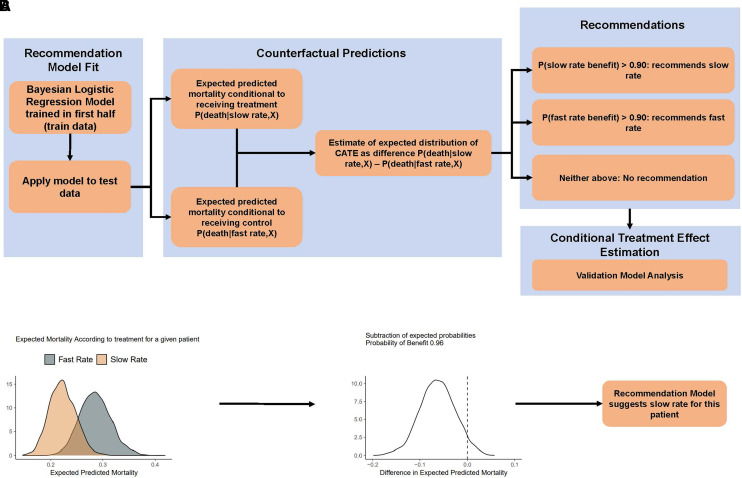
CATE is frequently defined as the counterfactual difference in predicted probability of the primary outcome under a model for a patient with given covariates (8). Estimating CATE may be performed in several ways (9); in this analysis, we applied the principles of an S-learner (i.e., a single model learner) in the BaSICS population (9). Assuming Y is our primary endpoint, X is the covariates set for model adjustment, and P is the probability of the outcome, the conditional treatment effect may be given as P(Y = death|treatment,X) – P(Y = death|control,X), read as “estimated probability of death given patient received treatment and covariates minus the estimated probability of death given patient received control and covariates.” CATE is an estimate of treatment effect for small subset of patients who share a series of characteristics from which their expected response to treatment is estimated (8); it is therefore not “individual,” but individualized, or conditional. Figure 1A provides a visual explanation of the methods for the primary analysis. Code snippets and details are shown in the data supplement.

Figure 1.

Methods flowchart. (A) Flowchart of the steps provided in the text. (B) Estimation of distribution of expected distribution of conditional treatment effect (CATE_ed) using one patient as an example. The first panel shows the expected posterior distribution according to infusion rate given the recommendation model. The middle panel shows the density plot for the difference of the expected predicted mortalities (i.e., CATE_ed). For this patient, because there is more than 0.90 probability that mortality rate is lower with the slow rate, the recommendation model will recommend the slow rate. CATE = conditional average treatment effect.

We applied the following steps to obtain the appropriate recommendation model for counterfactual exploration and estimation of CATE.

First, the dataset was divided in train and test subgroups. The train subset included the first half of enrolled patients, and the test subset the second half.

Second, we defined X (the covariates for adjustment) as the following variables measured at enrollment: age, admission type (planned, unplanned not for sepsis, unplanned for sepsis), vasopressor use, noninvasive ventilation use, and mechanical ventilation use. Planned admissions were defined as elective surgical admissions for which intensive care unit use was anticipated before the beginning of the surgical procedure.

Third, we performed a Bayesian logistic regression model with X covariates and their interaction with the treatment arm. The model used a neutral prior (neutral prior for the log odds ratio [OR] of all predictions set as a normal distribution with mean 0 and standard deviation of 0.35 [11]; this prior yields 95% probability for an OR between 0.5 and 2.0).

Finally, the model was used in the test subset to obtain predictions for patients in the second half (test set); 4,000 predictions for each patient were generated, as were an equal number of counterfactual probabilities. Therefore, each patient had two sets of 4,000 posterior draws, one set of 4,000 draws for the expected posterior predicted probability of death given it was allocated in the slow rate group, and another 4,000 draws conditional to allocation to the fast-rate control group (both also conditional to the covariates of the patient). The difference between expected predicted probabilities of death with slow versus fast infusion for each patient was the expected posterior distribution of the CATE (CATE_ed), conditional on the model and priors, given the data. Each patient had his or her own CATE_ed. An example is shown in Figure 1B.

Note that CATE_ed is the difference of two expected probability distributions [P(Y = death|intervention,X) − P(Y = death|control,X)] and is, therefore, a distribution of absolute risk reduction, with negative values suggesting lower mortality for intervention (slow infusion). We then used CATE_ed to divide patients according to the recommended treatment based on the model. The primary analysis was made arbitrarily using a cutoff of 0.90 probability that CATE_ed favored intervention or control arms; different cutoffs (0.80 and 0.85) were also explored (see data supplement).

After treatment recommendations were obtained for the test subset, we summarized patients in the test set according to the recommendation made by the recommendation model (recommended slow rate, recommended fast rate, and no recommendation). We calculated estimates of the expected effects of the fast and slow rate arms according to the model recommendation group using Bayesian logistic regression model with recommendation, treatment, and their interaction as predictors; this model was used to render the primary results. A neutral prior on log OR was applied (see data supplement for details). We defined that the interactions would be deemed important if there was a high (>0.95) probability of direction for the interaction in the model; a frequentist analysis based on the P value of the interaction (estimated using analysis of variance) was also provided to corroborate the findings (P < 0.05 for interaction was considered, for illustrative purposes, as significant).

Results are presented as ORs and absolute risk reduction, with their 95% credible intervals (CrIs), probability of direction for the conditional effects of slow (the original intervention in the trial) versus fast infusion according to subgroups defined by the recommendation model in the test population (a posterior probability of direction >0.975 was considered as relevant, which tends to approximate a P value of 0.05 under a two-tailed assessment [12]), and the area of the posterior probability of absolute risk difference posterior inside a margin of practical equivalence. The region of practical equivalence (ROPE) was defined by differences in hospital mortality <1%; less than 0.05 of the posterior area inside the ROPE was considered relevant.

Because interpreting a model with interactions is not straightforward for clinicians, we also provide a recursive partitioning analysis for the mean CATE prediction for patients in the test set (13). The goal of recursive partitioning was to provide an easier way to determine suggestions at the bedside.

Sensitivity Analyses

We assessed whether different cutoffs for deciding recommendation in the second half would be associated with different results (see data supplement for details); cutoff values of 0.90, 0.85, and 0.80 were tested.

All analyses were done using R 4.2.2 (R Core Team, 2022) using packages brms (14) and tidybayes (15).

Results

A total of 10,465 patients had complete data and were available for analysis; 5,247 patients were assigned to treatment (333-ml/h infusion rate) and 5,218 were assigned to the control group (999-ml/h rate). The main model was built in 5,230 patients (2,607 for control [fast rate] and 2,628 for intervention [slow rate]). Model diagnostics were appropriate (see data supplement for details). In the test set, the probability of benefit exceeded the 0.90 threshold, and a recommendation could be made by the recommendation model in 1,012 patients (19%). The probability of benefit did not exceed the 0.90 threshold and no recommendation could be made in 4,223 patients (81%). The model recommended the fast rate to 735 patients (14%) and the slow rate to 277 patients (5%). Patient features and outcomes according to the recommendation are shown in Table 1.

Table 1.

Overall patient features according to model suggestion in the test set

Characteristic	No Suggestion (n = 4,223)	Fast Infusion (n = 735)	Slow Infusion (n = 277)
Age	62 (50–72)	79 (69–86)	36 (28–43)
Female sex	1,771 (42%)	355 (48%)	136 (49%)
APACHE II score	11 (8–15)	17 (13–23)	7 (5–10)
SOFA score	4.0 (2.0–6.0)	5.0 (3.0–8.0)	4.0 (2.0–6.0)
Mean arterial pressure, mm Hg	74 (63–87)	70 (60–84)	73 (64–84)
Heart rate, beats per min	92 (77–109)	96 (81–112)	97 (81–111)
Vasopressor use	1,627 (39%)	190 (26%)	164 (59%)
Acute kidney injury at enrollment	1,222 (29%)	398 (54%)	57 (21%)
Creatinine, mg/dl	0.95 (0.71–1.28)	1.24 (0.90–1.94)	0.80 (0.60–1.07)
Admission type
Unplanned, not sepsis	1,249 (30%)	264 (36%)	52 (19%)
Planned	2,480 (59%)	23 (3.1%)	225 (81%)
Unplanned, sepsis	494 (12%)	448 (61%)	0
Mechanical ventilation	2,276 (54%)	435 (59%)	48 (17%)
Noninvasive ventilation	31 (0.7%)	0	9 (3.2%)
Intensive care unit length of stay	3 (2–6)	5 (2–11)	3 (2–4)
Hospital length of stay	8 (5–16)	10 (5–21)	8 (6–15)
Need for kidney replacement therapy	283 (6.7%)	86 (12%)	10 (3.6%)
Hospital mortality	771 (18%)	339 (46%)	22 (7.9%)
90-d mortality	897 (21%)	388 (53%)	32 (12%)

Definition of abbreviations: APACHE = Acute Physiology and Chronic Health Evaluation; SOFA = Sequential Organ Failure Assessment.

Values presented as median (interquartile range) where applicable.

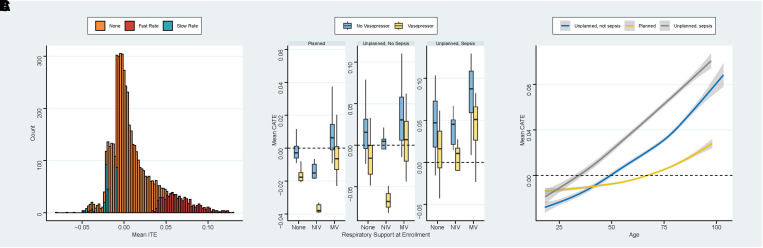
Distribution of mean CATE_ed for each patient according to recommendation is shown in Figure 2A. Figure 2B shows mean CATE_ed (lower values favoring slow infusion) according to respiratory support, admission type, and use of vasopressors at enrollment. Figure 2C shows a smoothed plot of mean CATE_ed according to age and admission type. Mean CATE_ed was lower (favoring a reduction in mortality for slow rate group) in patients with planned admission, in those already using vasopressors, and in those using noninvasive ventilation (Figure 2B). Mean CATE_ed also favored intervention for younger patients compared with older patients (Figure 2C).

Figure 2.

(A) Mean individualized treatment effect for the test set (second half of BaSICS participants) according to model recommendation; note that the x-axis represents the mean of expected distribution of conditional treatment effect (CATE_ed); therefore, it is possible to have mean values below or above zero and receive no recommendation because the 0.90 probability threshold was not met. (B) Box plot of mean CATE_ed according to respiratory support at enrollment, admission type, and use of vasopressors at enrollment. (C) Smoothed plot of mean CATE_ed according to age and admission type. CATE = conditional average treatment effect; ITE = individualized treatment effect; MV = mechanical ventilation; NIV = noninvasive ventilation.

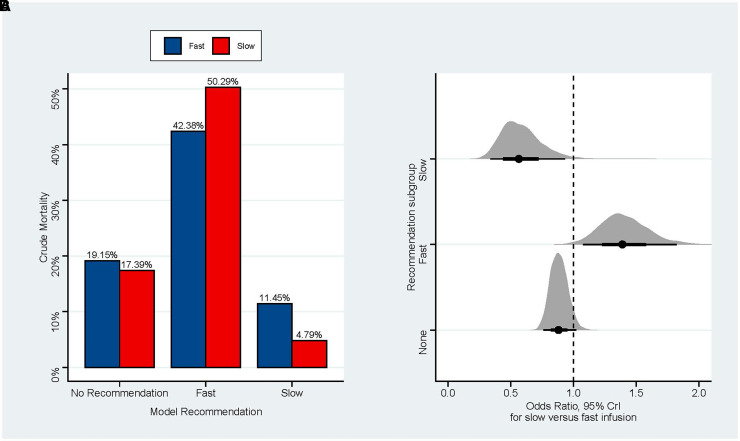
Crude unadjusted mortality according to treatment recommendation and actual treatment received and adjusted effect sizes are shown in Figure 3A. Patients to whom the recommendation model recommended the fast rate and who received the fast rate had a 7.9% crude lower mortality rate versus those who received the slow rate, whereas patients in whom the model recommended the slow rate and who received the slow rate had a 6.7% crude lower mortality rate versus those who received the fast rate. Adjusted effect sizes and absolute risk reductions are also shown in Figure 3B. The interaction between model recommendation and treatment was highly probable (0.96 posterior probability of direction for the interaction between recommended and received slow infusion and >0.99 posterior probability of direction for the interaction between recommended and received fast infusion; the P value under a frequentist framework for the interaction was 0.004). Diagnostic plots for the model are shown in Figure E1 in the data supplement.

Figure 3.

(A) Crude mortality in the test set according to model suggestion; note how agreement between recommendation and intervention received was associated with lower unadjusted mortality rate. (B) Forest plot for the effect of receiving slow infusion in the test set according to subgroups defined by the recommendation model. The interaction between suggestion and treatment was significant (probability of direction >0.95 for all comparisons and P = 0.004 in frequentist analysis). CrI = credible interval.

Slow infusion rate in the subgroup of patients in the test set in whom slow infusion was recommended was associated with an OR of 0.58 (95% CrIs of 0.32–0.90; 0.99 posterior probability of benefit), corresponding to an absolute risk reduction of −5% (95% CrIs, −9% to −1%; 0.013 of the posterior inside the ROPE). In agreement, slow infusion rate in the subgroup of patients in the test set in whom fast infusion was recommended was associated with an OR of 1.40 (95% CrI of 1.08–1.82; >0.99 posterior probability of harm), corresponding to an absolute risk increase of 8% (95% CrIs of 2–15%; <0.01 inside the ROPE). The effect size can be inverted to estimate the effect of receiving fast infusion in the subgroup in whom the model recommended fast infusion (OR of 0.72; CrIs of 0.54–0.91; probability of benefit >0.99 and close 0.01 in the ROPE). For the group in whom no recommendation was made by the model, the odds for mortality for slow versus fast infusion rate was 0.88 (95% CrI of 0.75–1.02; 0.95 probability of benefit), and the absolute risk difference was 4% (95% CrI of −4 to 0%; 0.20 inside the ROPE). Numeric summaries are shown in Table E1 in the data supplement.

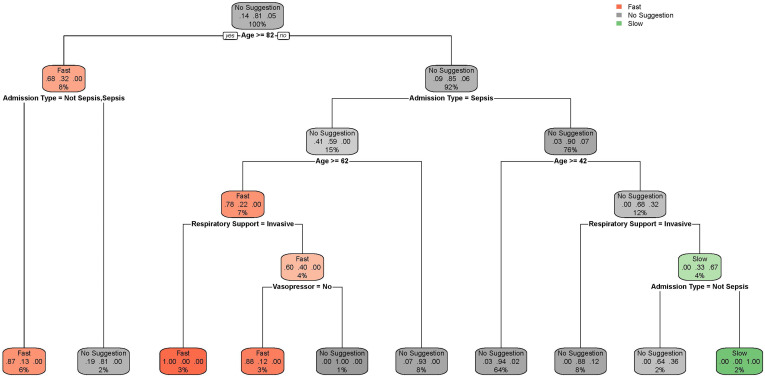
Results of the recursive partitioning are shown in Figure 4. The recursive partitioning was able to capture many of the features described below. Detailed information is discussed in the legend in Figure 4.

Figure 4.

Recursive partitioning plot for patient features and suggestion in the test set stratified according to model suggestion (no suggestion, fast, and slow). The aim of this plot is to facilitate clinician interpretation. Each node displays the most common predictions at their level; the question posed behind each label provides guidance on where to follow the tree (if yes, the reader should move to the left; if no, to the right). For example, we start with “no suggestion” and the first question is whether age is greater than 82 years; if yes, we move to the left to the next question (if admission is unplanned, with or without sepsis); again, if yes, the reader is directed to the left and to the bottom, which suggests fast infusion. Slow infusion is suggested for the right branches (younger patients without sepsis). The percentages here are slightly different from the model because of approximation.

Results of the alternative analysis using different cutoffs for recommendation are discussed in the data supplement; in brief, the 0.90 cutoff was the only one capable of detecting relevant/significant interactions for fluid infusion rate and outcomes in the test set (Figure E2).

Discussion

In this secondary post hoc analysis of the infusion-rate arm of the BaSICS trial, we applied a probabilistic way to estimate conditional treatment effects and generate treatment recommendations. This approach was able to provide a decision-support treatment recommendation in as many as 19% of patients included in the second half of the trial. Patients had overall lower hospital mortality when they received the recommended treatment. A slower infusion rate appeared to be associated with lower hospital mortality rates in less severely ill patients, especially younger patients and those admitted after elective surgery, whereas a more rapid infusion rate was more frequently recommended to older patients with sepsis. Taken together, these findings suggest that different infusion rates may be appropriate for different profiles of critically ill patients.

From a clinical perspective, our results suggest that faster infusion rates may potentially be better than slower infusion rates for patients with sepsis. This is aligned with the concept that early, fast restoration of hemodynamics through fluid challenges may benefit patients with intravascular volume depletion or relative hypovolemia due to sepsis (16). It is conceivable, for example, that slower infusion rates failed to increase cardiac output in these patients, which could contribute to the development of organ failure and increased mortality (17). In the original publication of BaSICS, the average treatment effect for the whole trial population showed a point estimate toward higher mortality with slow infusion rates, although the confidence intervals were wide and included no difference (hazard ratio of 1.07, 95% confidence intervals of 0.94–1.22 for 90-day mortality) (1). The traditional univariate subgroup analysis of patients with sepsis in the BaSICS trial did not detect the potential benefit of faster infusion in patients with sepsis observed in this secondary analysis when multiple patient characteristics were allowed to interact simultaneously to modify the effect of treatment on outcome. For younger patients, especially those admitted after elective surgery, slower infusions appeared preferable. Although one can only speculate on reasons for this, slower infusion rates in a population of patients who have already been resuscitated during surgery may be safe and result in less tissue edema (18) and perhaps less bleeding (19). The recursive partitioning results (Figure 4) may be used to better grasp the results of our findings and model results, representing an interesting alternative to the present results of complex models for clinicians.

From a methodological perspective, the present work suggests that assessing CATE under a probabilistic framework may aid in trial interpretation. CATE is not truly an individual treatment effect, but rather related to subgroups of patients who share covariate patterns (hence the preference for the terms “individualized” or “conditional”), allowing potentially finer subgroup categories for the assessment of treatment heterogeneity than is allowed through traditional subgroup analysis. For example, the main report was unable to find meaningful differences among traditional subgroups, probably because of power and multiple interaction issues. Unlike other approaches to assess heterogeneity in treatment effect (20, 21), including identifying phenotypes using unsupervised cluster analysis, this type of analysis allows the classification of patients according to their expected probability of having benefit in a continuous fashion. In this analysis, we used a 0.90 threshold to define the probability of benefit of treatment and control, resulting in three possible groups of recommendations (slow rate, fast rate, or no recommendation) based on probabilities. The model was applied to the second half of the trial. Therefore, the recommendation model created subgroups in the second half to allow explorations under a probabilistic framework. This approach might also suggest that early assessment of CATE in the context of a large clinical trial could help in adapting the eligibility criteria. Could the early adaptation of inclusion and exclusion criteria halfway through the trial allow for more precise results? For example, if patients who received a clear suggestion based on the model were prevented from being enrolled, the second half of the trial could perhaps focus on patients in whom reasonable doubt persisted (i.e., the 81% of patients in whom no recommendation could have been made). This would indeed increase the number of patients in the uncertain subgroup, which could theoretically increase study power in this population. There was a still important probability that slow infusion rates could be beneficial for patients in whom no recommendation was made (0.95), although an important part of it still lies in a region that may be considered of practical equivalence (>0.20). Pursuing enrollment only on this population up to a targeted sample size could have provided more precise results. This also likely means that patients who may benefit from slow infusion rates were missed by the model and were assigned to the no-recommendation subgroup.

Our results do not suggest that this approach will foster interpretation for most trials. A large sample size is still required to perform such analyses, especially if the expected overall effects of the intervention are deemed to be small; there were more than 5,000 patients in the training set, which is more than the whole sample size of major trials. This highlights that finding personalized treatments may be hard. In fact, proper assessment of CATE can be, by itself, a reason to continue performing large clinical trials. The several complex relationships encountered in this analysis can be unraveled with precision only if the sample size is large enough. Further simulation studies and analyses from other clinical trials are necessary to address optimal timing, sample size, and consequences of the application of the described approach.

This manuscript has several limitations. It is an exploratory post hoc analysis of a clinical trial. There are many approaches for predicting CATE, including machine-learning approaches like causal forests, which may also work as well or better than the presented approach (22, 23). However, we chose this methodology because of the robust statistical framework of Bayesian statistical models and the possibility of making probabilistic statements for model recommendations. Overfitting is a pressing concern when dealing with model building and validation and is a tender point for CATE investigations. We did our best to mitigate concerns of overfitting by using the split-test approach.

Conclusions

Estimation of CATE improved the interpretation of the BaSICS trial. Treatment recommendations could be performed in as many as 19% of all patients in the second half of the trial based on a prediction model trained in the first half, with faster infusion generally recommended for older patients with sepsis and slower infusion recommended for planned admissions.