Differential regulation of GUV mechanics via actin network architectures

Abstract

Actin networks polymerize and depolymerize to construct highly organized structures, thereby endowing the mechanical phenotypes found in a cell. It is generally believed that the amount of filamentous actin and actin network architecture determine cytoplasmic viscoelasticity of the whole cell. However, the intrinsic complexity of a cell and the presence of endogenous cellular components make it difficult to study the differential roles of distinct actin networks in regulating cell mechanics. Here, we model a cell by using giant unilamellar vesicles (GUVs) encapsulating actin filaments and networks assembled by various actin cross-linker proteins. Perturbation of these cytoskeletal vesicles using alternating current electric fields revealed that deformability depends on actin network architecture. While actin-free vesicles exhibited large electromechanical deformations, deformations of GUVs encapsulating actin filaments were significantly dampened. The suppression of electrodeformation of actin-GUVs can be similarly recapitulated by using aqueous poly(ethylene glycol) 8000 solutions at different concentrations to modulate solution viscoelasticity. Furthermore, networks cross-linked by alpha actinin resulted in decreased GUV deformability compared with actin-filament-encapsulating GUVs, and membrane-associated actin networks, through the formation of the dendritic actin cortex, greatly dampened electrodeformation of GUVs. These results highlight that the organization of actin networks regulates the mechanics of GUVs and shed insights into the origin of differential deformability of cells.

Significance

Cells differentially regulate their mechanical properties on their own accord, allowing them to seamlessly execute biological tasks in a changing environment. Cellular mechanophenotype is generally attributed to the cytoskeleton and, particularly, the actin cytoskeleton, which self-assembles from actin building blocks and actin-binding proteins into elaborate networks. Prior in vitro studies have suggested that the diverse organization of cytoskeletal networks differentially endow cellular mechanics. Although bulk reconstitution studies have explored actin network phenotypes assembled by various actin-binding proteins as cross-linkers, their mechanical characterization in an isolated cell-like confinement remains largely unexplored. Here, using bottom-up reconstitution of actin networks, we demonstrate that differential cellular mechanics is mediated through the assembly of distinct actin architectures.

Introduction

The cell’s ability to change shape to support cellular functions such as migration and division, and its ability to resist deformation to sustain structural integrity, depends on the cytoskeleton. Among different types of cytoskeletal polymers, actin filaments assemble into various networks aided by actin-binding proteins that form large-angle cross-links, bundles, and branches (1,2). Although the flexural rigidity of actin filaments is as much as three orders of magnitude lower compared with that of microtubules (3), the assembly of actin filaments into highly organized and dynamic networks gives rise to enhanced viscoelastic property (1,4,5). As a result, actin networks endow the mechanical phenotype of cells by differentially regulating the elasticity and cytoplasmic viscosity of cells (6). Prior research has linked the mechanical property of cells to the actin network (5,7). For example, it is reported that increased deformability of ovarian cancer cells, due to their actin organization, is directly correlated to metastatic transformation (8,9). Furthermore, retraction of epithelial cells to break cell-cell junction as a result of local actin disruption is linked to extravasation of cancer cells during metastatic invasion (10,11). It is also known that cytoplasmic viscosity of red blood cells affects their dynamics inside microvasculatures (12,13). The connection between cell mechanics and cellular processes has led to substantial interest in perturbing the cytoskeleton as a means to regulate cellular processes.

Due to the simple experimental set up, many have utilized electromechanical perturbation of cells using both direct current (DC) and alternating current (AC) electric fields. Earlier studies using electroperturbation dealt with the interaction of pulsed DC electric fields and cell membranes that resulted in electropermeabilization and electroporation (14). Controlled modulation of DC electric fields resulted in the formation of enlarged pores, permitting the introduction of large molecules that are otherwise not permeable through the cell membrane, thus giving rise to various applications including DNA transfection, drug delivery, cancer therapy (15,16,17), and gene therapy (18,19). Strong AC fields, on the other hand, are known to induce cellular deformation. The semi-permeable lipid bilayer of a cell’s plasma membrane can be thought of as an electrical insulator. When an electric field is applied, ions inside a cell undergo charge separation that results in dielectrophoresis due to a nonuniform electric field (20). Depending on the electric field strength and conductivity of the suspension environment, dielectrophoretic forces result in the deformation of cells (21). Many studies have resorted to AC electrodeformation to measure the apparent stiffness of red blood cells and platelets (22,23) and the viscoelasticity of cancer cells (24,25) and to study the effect of actin depolymerization on the relaxation of electrodeformed cells (26).

Although prior studies have revealed that the mechanical properties of cells are intimately tied to their actin networks, the differential role of actin, in the form of filaments and networks, on the deformability of cells remains incompletely understood. The intrinsic complexity of cells and numerous endogenous components make it difficult to study the differential roles of actin networks as a function of actin cross-linkers (27). Giant unilamellar vesicles (GUVs) present a unique platform to model and reconstitute cellular processes in a membrane-confined environment (28). This experimental approach has been used to study the assembly of different types of actin networks (29) and how the actin network induces membrane remodeling (30,31,32,33,34) and to reveal actin-binding protein competition and cooperation in actin network assembly (35,36). Others have also reconstituted a cortex-like shell in GUVs and measured their responses to mechanical compression (37).

The responses of GUVs to applied electric field have been extensively investigated (38,39,40,41,42,43,44). Subject to strong DC pulses, similar to cells, macropores formed in GUVs when the transmembrane potential threshold was exceeded (40). Vesicle closure after poration, curvature relaxation, and other electrical properties of GUVs have been characterized for different bilayer compositions and salt concentrations used for both the external medium and the GUV lumen (38,40,45,46,47). Furthermore, it has been shown that when induced by a DC pulse, GUVs with an actin cortex have suppressed membrane permeability compared with cortex-free GUVs (48), presumably due to smaller and/or less macropore formation. Similar to cells, strong AC electric fields forced spherical GUVs to assume elliptical shapes with the major axis either parallel (prolate) or perpendicular (oblate) to the electric field (49). GUVs undergo these shape transformations depending on the salt concentration ratio between the GUV lumen and the solution outside of GUVs and electric field strength and frequency (39,49,50). AC field electrodeformation transitions have been theoretically modeled under different conditions (51,52,53), and experimental studies based on electrodeformation have investigated bilayer properties such as membrane bending rigidity and bilayer viscosity (40,54). Although GUV membrane properties have been well studied and characterized, how the mechanics of GUV is influenced by different actin network architectures remains incompletely understood.

Here, we investigate the effect of encapsulated actin filaments and cross-linked actin networks on the electrodeformability of GUVs in response to AC electric fields. We encapsulated actin-free buffer solution and filamentous actin inside GUVs. Subject to an AC electric field, we observed a significant difference in deformability between the two conditions. We modulated the viscosity of GUV lumen and found that the deformability of GUVs correlated with lumenal viscosity, a condition that mimics filamentous actin. Furthermore, cross-linked or membrane-cortex actin networks, at the same concentrations of filamentous actin (F-actin), further dampened GUV electrodeformation. Overall, our results reveal that the differential mechanical properties of GUVs and, by extension to cells, can be modulated by actin network architectures.

Materials and methods

Reagents

Purified actin was purchased (Cytoskeleton, Denver, CO, USA). ATTO 488 actin was purchased from Hypermol (Bielefeld, Germany). Actin cross-linker alpha-actinin from rabbit skeletal muscle and the Arp2/3 complex from bovine brain were purchased from Cytoskeleton. Hexa-histidine-VCA (His₆-tag VCA) was purified as described previously (36). General actin buffer (G-buffer) was prepared at 10× concentration and consists of 50 mM Tris-HCL (pH 8.0) and 2 mM CaCl₂. Actin was diluted from a stock concentration of 10 mg/mL to a working concentration using G-buffer + 0.2 mM ATP and 0.5 mM DTT. Actin polymerization buffer (F-buffer) was prepared at 10× concentration and is composed of 500 mM KCl, 20 mM MgCl₂, and 10 mM ATP. 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-[(N-(5-amino-1-carboxypentyl)iminodiacetic acid)succinyl] (nickel salt) (DGS-NTA(Ni)), and cholesterol were purchased from Avanti Polar Lipids (Alabaster, AL, USA). Poly(ethylene glycol) (PEG) 8000 was purchased from Thermo Fisher Scientific (Waltham, MA, USA). Density gradient medium (Optiprep) and other chemicals were purchased from Sigma Aldrich (Burlington, MA, USA).

Electrodeformation setup

A simple homemade electroperturbation chamber was assembled to conduct GUV electrodeformation experiments. The setup is comprised of adhesive electrode tape and 3 × 1 in coverslip. Two copper tapes were used as electrodes and were attached to one face of the coverslip in a parallel manner with gaps ranging from 200 to 300 μm. A sinusoidal AC electric field was applied using an Agilent 33120A (Keysight Technologies, Fort Wayne, IN, USA) function generator between electrodes adhered to coverslip. We used a fixed length of electrode tapes, and using voltmeter (Fluke, Everett, WA, USA), we measured potential of 6.7 V when applying 10 V peak to peak sinusoidal AC. Lower than root-mean-square voltage measured at the electrode’s end may be attributed to resistance from adhesive and tape length. To apply an identical AC field between slightly varying chambers between different devices, applied voltage was adjusted accordingly to the exact measured gap between the two electrodes such that 30 kV/m is the applied field strength between the electrodes. During electroperturbation experiments, GUVs were dispensed between the electrodes. The height of the copper tape, which is ∼100 μm, was higher than nearly all sizes of generated and analyzed GUVs and therefore yielded a uniform electric field across the length of the chamber. For all experiments, the duration of AC field was kept within 3–4 s.

GUV generation

Encapsulation of aqueous material inside GUVs was achieved using the modified continuous droplet interface crossing encapsulation (cDICE) method (55). As described previously (36), a 3D-printed cDICE chamber is mounted onto a tabletop stirring motor and rotated at 1,200 Rpm. First, 770 μL outer aqueous glucose solution, of varying concentrations depending on osmotic condition, is dispensed into the chamber. For isoosmotic conditions, the concentration of glucose is tuned such that its osmolarity matches the measured osmolarity of the inner solution, whereas for hyperosmotic conditions (flaccid GUVs), the outer glucose solution is 400 mOsm higher than the inner solution. Next, an adequate amount of oil/lipid mixture is dispensed into the chamber. The lipid composition used in all conditions, except for the reconstituting actin cortex, is 70 mol % DOPC with the addition of 30 mol % cholesterol. During reconstitution of the actin cortex, 5 mol % DGS-NTA(Ni) was added to the lipid composition while lowering cholesterol to 25 mol %. Oil is composed of 80% silicon oil and 20% mineral oil. When oil and lipid solutions are mixed, a two-phase dispersion emerges due to the emulsification of mineral oil containing lipid aggregates. Upon the addition of the lipid/oil mix to the chamber, it forms an interface saturated by lipid aggregates. Separately, 770 μL oil/lipid mix is dispensed in to an epitube containing 20 μL prepared inner solution (encapsulant) and pipetted up and down until the solution becomes cloudy, indicating formation of lipid-monolayer-saturated encapsulant emulsions. Finally, the solution is transferred to the cDICE chamber. Due to centrifugal forces generated by the rotating chamber, encapsulant emulsions are shuttled through the oil/lipid mix into the outer solution. When emulsions cross the lipid-saturated interface, a second layer of lipid zips the emulsions and forms GUVs suspended in the outer aqueous solution.

Inner solution preparation

Various inner solution conditions were reconstituted to conduct GUV electroperturbation experiments. Each condition contains 7.5% density gradient medium to facilitate GUV sedimentation. In viscosity contrast experiments, PEG 8000 was dissolved in deionized water at specified concentrations (2%, 4%, and 8% w/v). To reconstitute actin-polymerization-buffer GUVs, the inner solution contained 1× F-buffer and 3 mM ATP. For reconstitution of F-actin GUVs, all components in the inner solution of actin-polymerization-buffer GUVs are preserved with the addition of 5.3 μM actin and 0.53 μM ATTO 488 actin. The electrical conductivity of G-buffer and F-buffer used to reconstitute globular actin and filamentous actin, respectively, was measured using a benchtop conductivity meter Orion Star A212 (Thermo Fisher Scientific). Furthermore, viscosity measurements of actin and buffer solutions were conducted using Discovery HR-2 rheometer (TA Instruments, New Castle, DE, USA) at a shear rate of 100 s⁻¹ and 25°C. To reconstitute GUVs cross-linked by alpha-actinin, all ingredients used to reconstitute F-actin were mixed and incubated for 15 min in ice. Then, 1.77 μM alpha-actinin was added to the solution. The addition of alpha-actinin, or any actin cross-linker, should be immediately followed by the last step of the cDICE GUV generation method, which is making lipid-monolayer-stabilized inner solution emulsions by mixing actin solution with lipid/oil mix followed by dispensing it into the cDICE chamber. For reconstitution of actin cortex, the lipid composition is slightly altered by the addition of 5 mol % DGS-NTA(Ni). Similar to actin network reconstitution cross-linked by alpha-actinin, F-actin components were incubated in ice for 15 min. Then actin nucleation promotion factor, 0.5 μM His₆-tagged VCA, is added followed by the addition of 0.5 μM Arp2/3 complex. When confined by the lipid bilayer compartment, His₆-tagged VCA binds to the nickel domain of DGS-NTA(Ni) and activates Arp2/3 to form dendritic actin networks restricted at the lipid bilayer membrane.

Imaging

In our experiments, we used two different imaging setups: bright-field imaging equipped by a high-speed camera and fluorescence imaging using a confocal microscope. To acquire dense data points yielding contentious deformation profile of GUVs when subject to AC electric field, an Olympus CKX41 (Olympus, Waltham, MA, USA) inverted microscope equipped with a Phantom Miro ex1 (Phantom High Speed, Wayne, NJ, USA) high-speed camera was used. Images were taken at a rate of 1,200 fps using a 40×/0.55 NA objective lens and acquired using phantom camera control (PCC 1.2) software. To observe actin dynamics in response to electric field, we used an Olympus IX-81 inverted microscope equipped with a spinning disk confocal (Yokogawa CSU-X1), OBIS LS/LX lasers (Coherent, Saxonburg, PA, USA), and an iXON3 EMCCD camera (Andor Technology, South Windsor, CT, USA). Each component was controlled by using MetaMorph (Molecular Devices, Chester County, PA, USA). Images were acquired using an oil immersion 40×/1.3 NA objective. While GUV samples were inside the electroperturbation chamber and subject to an AC electric field, ATTO 488 actin was excited using 488 nm laser at an exposure time of 170 ms, and time-lapse images were taken every 200 ms. Maximum deformation measured from confocal images were, along with bright-field images, used for statistical analysis of each GUV condition.

Statistical analysis

Using Origin software, one-way ANOVA tests were used to determine the statistical significance of major axis to minor axis ratios across different conditions. Furthermore, p values were determined using two-tailed Student's t-test. p <0.05 is considered statistically significant. The number of vesicles measured range from 10 to 15 with at least three different devices used for a given condition.

Results

Actin network reconstitution in GUVs and electroperturbation device

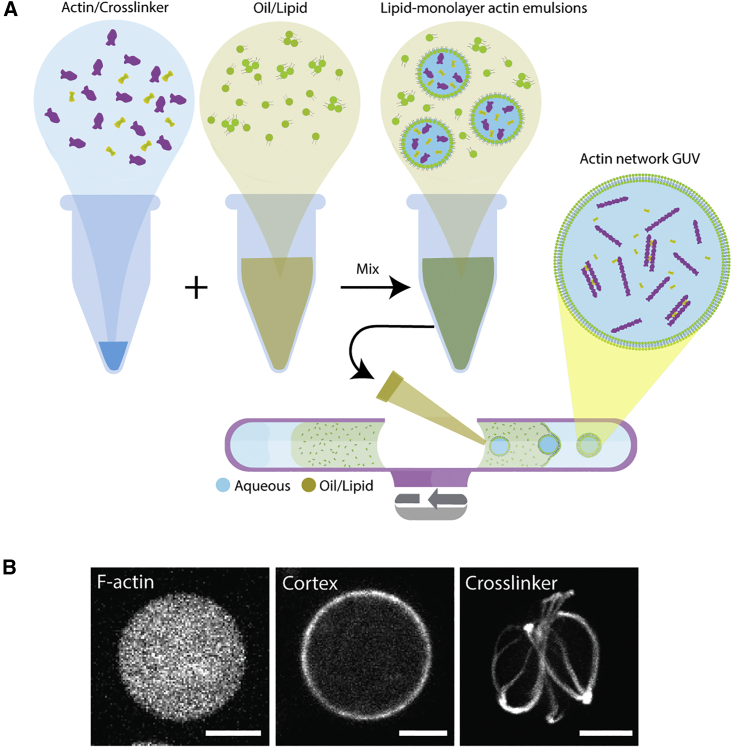
To reconstitute various actin networks in cell-sized lipid vesicles, the modified cDICE method (55) (Fig. 1 A) was used. In the presence of actin cross-linkers, actin networks formed rapidly, and the modified cDICE method renders rapid encapsulation of actin networks to permit network assembly postencapsulation. Actin filaments, components of actin cortex, and large-angle actin cross-linkers (Fig. 1 B) were encapsulated into heterogeneously sized GUVs composed of 70 mol % DOPC and 30 mol % cholesterol. 5 mol % DGS-NTA(Ni) was added when reconstituting the actin cortex. The actin cortex was assembled by activating the Arp2/3 complex at the inner leaflet of the bilayer membrane via the constitutively active His₆-tagged VCA domain of neural Wiskott Aldrich syndrome protein. Cross-linked networks were formed using the large-angle actin cross-linker alpha-actinin. A simple electroperturbation device with two parallelly aligned and spaced electrodes was assembled on a glass slide to subject GUVs to AC electric fields at 5 kHz (Figs. 2 A and S1, A and B). Electroperturbation experiments were performed by dispensing GUVs into the device chamber (i.e., the space between electrodes) and then applying a sinusoidal AC wave from a function generator. Transition of vesicles from undeformed to deformed to undeformed states following a 30 kV/m AC field at 5 kHz for a duration of 3–4 s was captured using a high-speed camera mounted on a bright-field optical microscope. This setup allowed us to analyze fast real-time GUV shape transformation at a high temporal resolution.

Figure 1.

Reconstitution of different actin networks inside GUVs. (A) Schematic of the modified cDICE method. Purple shapes represent actin monomers. Green shapes represent lipids. Yellow shapes, shown in actin/cross-linker solution schematic, represent an arbitrary actin cross-linker. (B) Representative images of actin network GUVs. (Left) Representative confocal image of encapsulated F-actin inside GUVs. (Middle) Arp2/3 complex assembled an actin cortex and associated to GUV lipid bilayer membrane. (Right) Aster-like actin network assembled by alpha-actinin encapsulated inside a GUV. Actin is labeled with ATTO 488 actin in all images. Scale bars, 10 μm. To see this figure in color, go online.

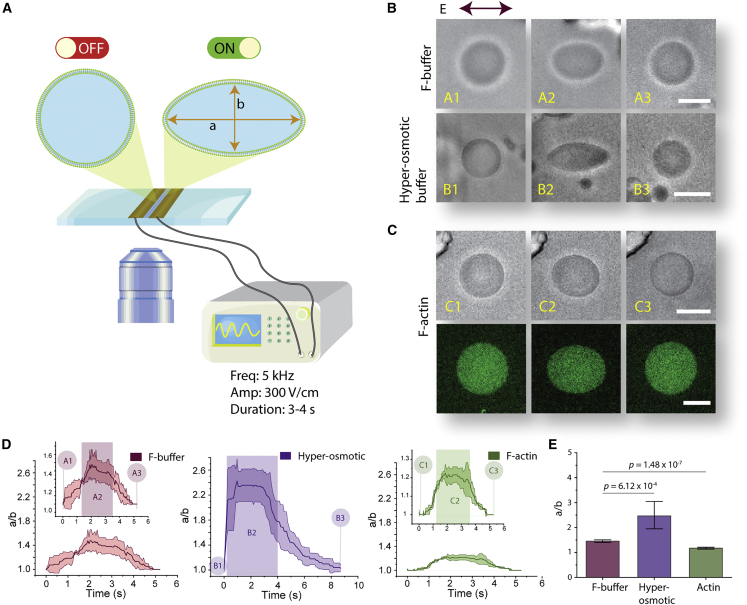
Figure 2.

Lumenal content of GUVs alters deformation profile when GUVs are subjected to electroperturbation. (A) Schematic of the electrodeformation setup mounted on an inverted microscope. A function generator is operated at 30 kV/m at 5 kHz, and a sinusoidal wave was applied for a duration of 3–4 s. Schematic shows electrodes adhered onto a coverslip. GUVs transform from a spherical shape to an ellipse when the electric field is applied. (B) GUV deformation is dependent on osmolarity difference between inner and outer solutions. (Top) Bright-field images of electric-field-induced shape transformation of actin-polymerization-buffer GUVs. (A1) GUV at an undeformed state prior to AC field application. (A2) Steady-state deformation of GUVs during electoperturbation. (A3) Actin-polymerization-buffer GUV after electrodeformation recovery. (B1–B3) Electrodeformation of actin-polymerization-buffer GUV in a hyperosmotic condition (flaccid GUV). (B2) shows exaggerated prolate deformation with pointed ends. (C) Electrodeformation of an F-actin GUV. (C2) shows visually apparent dampened deformation compared with (A2) and (B2). (C, bottom) Representative fluorescence image of F-actin GUV labeled with ATTO 488 actin. (D) Deformation profile of GUV conditions in (B) and (C) for F-buffer, hyperosmotic buffer, and F-actin conditions, as indicated. Labels (A1, A2, A3 … etc.) correspond to GUV transformation stages during electroperturbation. Shaded rectangular box denotes approximate duration of electric field application. Shaded areas in the traces in each of the plots indicate ±SD, n = 3. (E) Comparison and statistical analysis of maximum GUV deformation of each GUV condition as indicated. Data represent mean maximum deformation, and error bars denote ±SE. n_buffer = 11, n_hyper = 14, and n_actin = 12. Scale bars, 10 μm. To see this figure in color, go online.

Actin filaments dampen electrodeformability of GUVs

First, we validated our electroperturbation setup by replicating known GUV electroperturbation responses under different ionic conditions. During AC field electroperturbation, the orientation of elliptical deformation depends on the conductivity ratio $\Lambda =\frac{{\sigma }_{in}}{{\sigma }_{ex}}$, where ${\sigma }_{in}$ is the conductivity of inner solution and ${\sigma }_{ex}$ is the conductivity of outer solution (50). GUVs assume a prolate shape when $\Lambda$ >1 and subjected to a low-frequency field and an oblate shape when $\Lambda$ <1 and subjected to a high-frequency field. By tuning NaCl concentration in the inner and outer solutions and applying 30 kV/m, GUVs transformed from spherical to prorate (Video S1) and spherical to oblate (Video S2) shapes for $\Lambda$ >1 with a low-frequency field (1 kHz) and $\Lambda$ <1 with a high-frequency field (50 kHz), respectively. Prolate deformations have a major axis of ellipse parallel to the field direction, whereas oblate deformations have an ellipse major axis orthogonal to the electric field. To examine the impact of actin on GUV mechanics, we next investigated GUV deformability with and without the presence of encapsulated actin filaments (Fig. 2). As a control, we encapsulated actin polymerization buffer, without the presence of actin, under isoosmotic condition. Actin polymerization buffer (hereafter referred to as F-buffer) contains 1× F-buffer, 3 mM ATP, and 7.5% density gradient medium. This reaction condition contains all the reagents that are used to reconstitute F-actin and serves as the benchmark control against actin-containing GUVs. The conductivity ratio between inner and outer solutions was maintained since the salt concentrations were similar for the two conditions. Considering buffers used to reconstitute actin contain tens of mM of salt molecules, we have no reason to believe charged proteins like actin at concentrations below 10 μM will result in a significant change in conductivity. The conductivity of G-buffer and F-buffer solutions were ∼1.2 and ∼8.0 mS/cm, respectively (Fig. S2), but we were unable to measure the conductivity of F-actin solution due to the volume required for conductivity measurements with our setup. As expected, GUVs with F-buffer assumed prolate deformation (Fig. 2 B, top). To show that the electrodeformation is not due to GUV deflation, which can induce exaggerated deformability during electroperturbation, a control electroperturbation experiment was performed on flaccid GUVs (from hyperosmotic condition) containing F-buffer (Fig. 2 B, bottom). This resulted in greatly increased prolate deformation of GUVs compared with their isoosmotic counterparts. We also observed an extended delay in relaxation time for flaccid GUVs. Extended relaxation time for flaccid vesicles may be attributed to excess membrane surface area with greater membrane undulation suppressing a quick recovery. As a control, when globular actin is encapsulated instead, their maximum deformability is more similar to the case of F-buffer than F-actin (Fig. S3). Next, we reconstituted F-actin inside GUVs. Strikingly, when applying the same AC electric field to GUVs containing 5.3 μM F-actin in isoosmotic conditions, deformation was significantly dampened (Fig. 2 C; Video S3). Comparing each of the above three conditions, the largest maximum mean deformation a/b ∼ 2.42 (Fig. 2 D, middle) was attained by flaccid vesicles, followed by F-buffer GUVs at a/b ∼ 1.45 (Fig. 2 D, left), and the largest deformation resistance resulted in maximum mean deformation a/b ∼ 1.23 for F-actin GUVs (Fig. 2 D, right). As shown in Fig. 2 E, the average maximum deformation from a population of F-buffer GUVs was significantly larger than that of F-actin GUVs. Additionally, we encapsulated F-actin at 2.65 and 10.6 μM (Fig. S4) and found that GUVs were more deformable under the same electroperturbation conditions at 2.65 μM F-actin compared with 5.3 and 10.6 μM, although differences between 5.3 and 10.6 μM F-actin conditions were not significant (Fig. S4 B). In our analysis, we selected GUVs of size range 10–30 μm that are representative of the GUV population generated using the modified cDICE method and found no size-dependent correlation between GUV size and GUV deformability (Fig. S5).

Video S1. Bright-field image series of electrically perturbed GUVs acquired using a high-speed camera at 400 fps

Prolate deformation of GUVs achieved by encapsulating solution with electrical conductivity ratio Λ > 1 and applying 30 kV/m AC field at 5 kHz frequency. Scale bar, 10 μm

Video S2. Bright-field image series of oblate GUV deformation in response to electrical perturbation

Oblate deformation mode was achieved by encapsulating solution with electrical conductivity ratio Λ < 1 and applying 30 kV/m AC field at 50 kHz frequency. Scale bar, 10 μm

Video S3. Confocal image series of electrically perturbed actin filament GUVs acquired every 170 ms

Green, ATTO 488 actin. Scale bar, 10 μm

Considering known GUV parameters and their respective electroperturbation responses, our observation was not readily explained. In each of the above cases, there were no observed instances of electroporation to affect deformation behavior, which can commonly be identified by loss of volume, by loss of contrast, or by micron-sized membrane ruptures that can be observed at high magnifications. The conductivity ratio, lipid bilayer composition, and osmolarity between F-buffer GUVs and F-actin GUVs were the same. Thus, the distinct deformability behaviors can only be attributed to the material property of the GUV lumen. As a viscoelastic material, previous works have shown that an F-actin solution has an increased viscoelasticity compared with aqueous buffer solutions, similar to our polymerization buffer (∼1 mPa.s), and the viscosity increases further with increasing actin concentration (56). We confirmed these by measuring the viscosity of F-buffer (1.33 mPa.s) and 5.3 μM F-actin (2.21 mPa.s) solutions with added 7.5% density gradient medium (Fig. S6). Thus, we hypothesized that the dampened GUV deformation was due to changes in GUV lumenal viscoelasticity.

Changes in lumenal viscosity determines the electrodeformability of GUVs

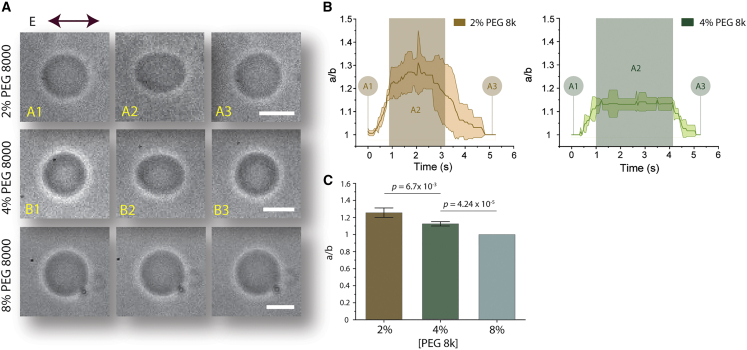
To investigate the role of change in viscoelastic property GUV lumen on electrodeformability, we encapsulated PEG polymer solutions, which are known to be viscoelastic (57,58). PEG 8000 solutions with concentrations ranging from 2% to 8% w/v were encapsulated inside GUVs. Osmolarity of the outer solution was matched to the measured osmolarity of each aqueous PEG 8000 solution in order to maintain isoosmotic conditions. When GUVs containing 2% PEG 8000 were subjected to a 30 kV/m AC field at 5 kHz for a duration of 3–4 s (Fig. 3 A, top; Video S4), the maximum mean deformation was measured at a/b ∼ 1.3 (Fig. 3 B, left). At 4% PEG 8000, the maximum mean deformation reduced to a/b ∼ 1.14 (Fig. 3, A, middle, and B, right; Video S5). In GUVs with 8% PEG 8000, no measurable GUV deformation was observed (Fig. 3 A, bottom; Video S6), and thus there is no deformation profile included for the 8% PEG condition. Our results clearly demonstrated dampening of GUV deformation with increasing lumenal viscosity (Fig. 3 C), consistent with our initial hypothesis that dampened deformation in F-actin GUVs is related to altered lumenal viscosity.

Figure 3.

Relationship between viscosity contrast and electrodeformability of GUVs. Different PEG 8000 concentrations were encapsulated inside GUVs to vary viscosity contrast between GUV lumen and outer solution. (A) Bright-field images showing PEG 8000 GUV shape transitions from undeformed to elliptically deformed to spherical recovery. (Top) Electroperturbation of 2% w/v PEG 8000 GUV. (A1) A PEG 8000 GUV at an undeformed state prior to AC field application. (A2) Steady-state deformation of GUVs during electoperturbation. (A3) GUV after electrodeformation recovery to assume spherical shape. (B1B3) 4% w/v PEG 8000 GUV electrodeformation. (Bottom) Electroperturbation of 8% w/v PEG 8000 GUV. (B) Deformation profile of 2% and 4% w/v PEG 800 GUVs, n = 3. Shaded rectangular box denotes approximate duration of electric field application. Shaded areas in the traces in indicate ±SD. (C) Comparison and statistical analysis of maximum GUV deformation of each GUV conditions indicated. Note that max a/b ratio of 8% was 1 for all vesicles analyzed and thus has no error bars. Data represent mean maximum deformation, and error bars denote ±SE. n_2% = 13, n_4% = 11, and n_8% = 12. Scale bars, 10 μm. To see this figure in color, go online.

Video S4. Bright-field image series of 2% PEG 8000 encapsulating GUVs acquired using a high-speed camera at 400 fps

Scale bar, 10 μm

Video S5. Electrodeformation of GUVs encapsulating 4% PEG 8000

Scale bar, 10 μm

Video S6. Electrodeformation of GUVs encapsulating 8% PEG 8000

Scale bar, 10 μm

The degree of deformability of 5.3 μM F-actin GUVs falls between deformability of GUVs encapsulating 2% and 4% PEG solutions and directly corresponds to the measured viscosity of F-actin solution at this concentration (2.21 mPa.s) that is in between the viscosity of 2% and 4% PEG solutions. Although these observations may be intuitive and in alignment with our initial hypothesis, to our knowledge, there are no prior studies that exploited cell-mimicking confinements like GUVs to investigate the effect of lumenal material property on their electrodeformability. Thus, here we illustrate a mechanism for cells to maintain structural integrity by only modifying viscosity without necessitating cross-linking of cytoskeleton using additional actin-binding proteins.

In silico investigation on the role viscosity contrast on GUV electrodeformability

We developed a computational method to further investigate the role of viscosity contrast (detailed in the supporting material). Numerical experiments are set up by placing the GUV in an AC field ${\mathit{E}}_{\infty }\left(t\right)$ with magnitude $E_0$, such that

$${\mathit{E}}_{\infty }\left(t\right)=E_0\sin \left(2\pi \omega t\right)\hat{\mathit{x}}$$

where $\omega$ is the AC field frequency. Using the GUV radius a as the characteristic length scale and the membrane charging time t_m = aC_m/σ_ex as the characteristic time scale, we define the following dimensionless parameters:

Viscosity ratio:	$\eta ={\mu }_{in}/{\mu }_{ex}$
Conductivity ratio:	$\Lambda ={\sigma }_{in}/{\sigma }_{ex}$
Electric field strength:	$\beta ={ϵ}_{ex}{E}_0^2{t}_m/\mu$
AC field frequency	$\Omega =\omega t_m$

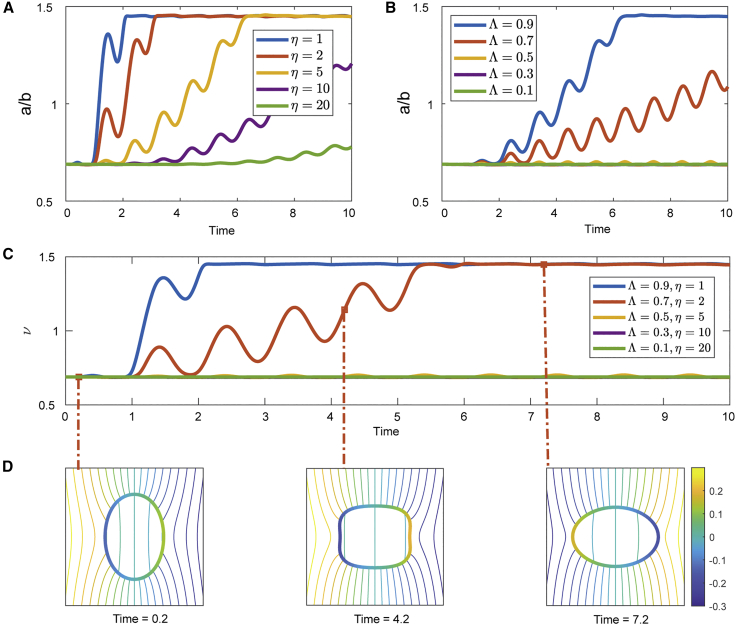
An AC field of frequency $\Omega$ = 0.5 and strength $\beta$ = 10 is applied at t = 0, and we measure the aspect ratio a/b of the GUV over time. We observe that for a fixed conductivity ratio Λ, the prolate deformation of the GUV is delayed as the viscosity contrast η is increased (Fig. 4 A). Additional experimental results, shown in Fig. S7, indicate that fixing the conductivity ratio Λ of 2% (Fig. S7 A) and 4% PEG 8000 (Fig. S7 B) concentrations to 0.9, by the addition of 7.5 mM NaCl to the 4% PEG 8000 inner solution, preserved deformation dampening as a result of increasing η (Fig. S7, C–E). For a fixed viscosity contrast, the prolate deformation happens only when the conductivity ratio Λ is large enough (Fig. 4 B). Consequently, dampening of the prolate deformation is observed as a combined effect of increasing η and decreasing Λ (Fig. 4 C), which is consistent with the experimental results using PEG 8000 solutions with increasing concentrations (Fig. 3).

Figure 4.

Prolate deformation of a GUV suspended in an AC field ($\beta$ = 10, $\Omega$ = 0.5) obtained via numerical simulations. (A) Electrodeformation for various viscosity contrasts $\eta$, while the conductivity ratio is fixed ($\Lambda$ = 0.9). We observe that the higher the GUV luminal viscosity, the longer it takes to complete the prolate deformation. (B) Conductivity ratio is varied while the viscosity contrast is fixed to $\eta$ = 5. Prolate deformation takes longer as $\Lambda$ is reduced and halts altogether below a threshold $\Lambda$. (C) Decreasing $\Lambda$ and increasing $\eta$ simultaneously results in a compounding effect on the prolate deformation, which is highlighted in this experiment. (D) Electric potential contour plots around the vesicle of $\Lambda$ = 0.7, $\eta$ = 2 at times t = 0.2 (flaccid GUV), 4.2 (transitionary phase), and 7.2 (prolate). To see this figure in color, go online.

One advantage of the numerical approach presented in this section is its ability to collect a variety of quantities of interest that will be useful for further investigations. For example, we have shown in Fig. 4 D the contour plots of the electric potential around the vesicle that corresponds to different stages of the deformation, where it is clear that when the vesicle is being stretched during the transitioning stage, the electric field strength is almost uniformly zero inside the GUV. Transient square-like shaped deformation is a result of our simulation assuming impermeable membrane.

Structurally distinct actin networks differentially regulate GUV mechanics

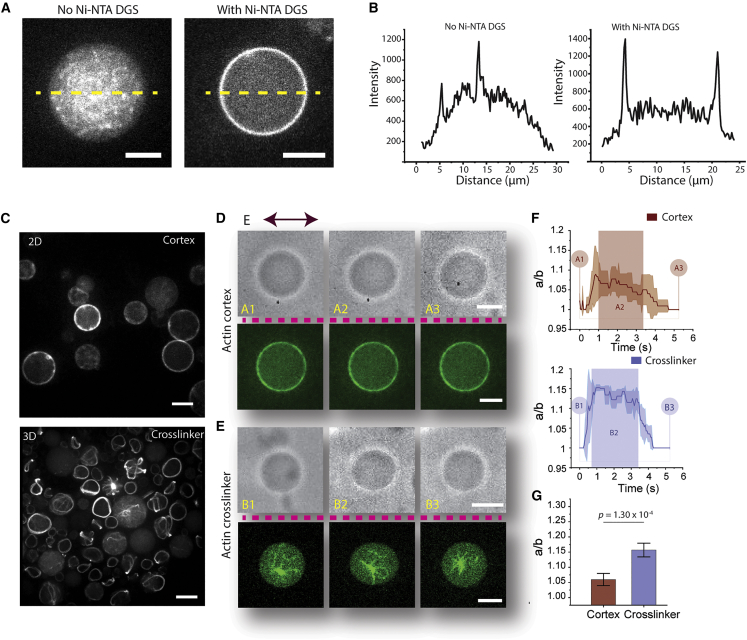
Mechanical features and responses of actin networks are governed by actin-binding proteins and, particularly, actin cross-linkers. These cross-linkers not only assemble phenotypically distinct networks but also spatially organize actin networks, allowing the cell to have variable mechanics across the cell volume. How might structurally distinct actin networks in a cell-mimicking confinement determine mechanical behavior? Here, we examined GUVs with Arp2/3-branched dendritic actin cortex (actin-cortex GUVs) or networks made with a large-angle actin cross-linker alpha-actinin (alpha-actinin-cross-linked GUVs). A membrane-bound dendritic actin cortex was achieved by the activation of the Arp2/3 complex using membrane-associated nucleation promotion factor (His₆-tagged VCA) on a DGS-NTA(Ni)-containing membrane. Encapsulating actin with the His₆-tagged VCA-activated Arp2/3 complex generated uniform actin-cortex GUVs with a high efficiency (Fig. 5, A, right, and C, top). The absence of DGS-NTA(Ni) prevents the localization of His₆-tagged VCA to the membrane, consequently inhibiting the reconstitution of actin cortex (Fig. 5, A and B). On the other hand, alpha-actinin addition led to a range of actin network morphologies, including rings, asters, and random networks (Fig. 5 C, bottom). Although reconstitution of various actin networks is well established to study cross-linkers and network phenotypes (35,36,59,60), little is known about how these actin cross-linkers differentially regulate GUV deformability. We followed the same electroperturbation procedure employed in previous experiments and subjected actin-cortex GUVs to an AC field. Electrodeformability of actin-cortex GUVs was greatly dampened and hardly visible to the naked eye (Fig. 5 D). Under the same condition, GUVs with alpha-actinin-cross-linked networks were more deformed compared with actin-cortex GUVs (Fig. 5 E). Electrodeformation was dampened to the largest extent by actin-cortex GUVs with a maximum (max) mean deformation a/b ∼ 1.07 (Fig. 5 F, top), and alpha-actinin-cross-linked GUVs had a max mean deformation of a/b ∼ 1.15 (Fig. 5 F, bottom). Compared with the F-actin GUVs, both actin-cortex and alpha-actinin-cross-linked GUVs had reduced deformability, with extreme dampening in actin-cortex GUVs (Fig. 5 G). Looking closely at the deformation profile of actin-cortex GUVs, strangely, as shown in Fig. 5 D, top, deformation was not sustained over the duration of AC field application, but rather GUVs started to recover immediately after reaching max deformation. A similar profile was not observed for alpha-actinin-cross-linked GUVs as they maintained deformation throughout the duration of applied AC field.

Figure 5.

Actin networks reduce deformation induced by AC field electroperturbation. (A) Comparison of actin-cortex reconstitution with and without 5% Ni-NTA DGS. (B) Plots of GUV intensity profile of across the dashed line in (A). (C) High-efficiency reconstitution of actin-cortex GUVs and alpha-actinin-cross-linked GUVs using the modified cDICE method. (Top) Representative confocal image of Arp2/3 complex-assembled dendritic-actin-cortex GUVs. GUVs have a uniform actin cortex shell associated to the membrane via His₆-tag-nickel interaction. (Bottom) Representative confocal image of alpha-actinin-cross-linked GUVs. Various actin network phenotypes commonly seen with actin networks with large-angle cross-linkers were observed. Both images show ATTO 488 actin labeling actin networks. (D) Electroperturbation of actin-cortex GUV. (Top) Bright-field images showing shape transitions before (A1), during (A2), and after (A3) application of AC electric field. (Bottom) Confocal images of ATTO 488 actin showing actin-cortex GUVs corresponding to (A1)–(A3). (E) Electroperturbation of alpha-actinin-cross-linked GUV. (Top) Bright-field images showing shape transitions before (B1), during (B2), and after (B3) application of AC electric field. (Bottom) Confocal images of ATTO 488 actin showing alpha-actinin-cross-linked GUVs at different stages of electroperturbation. Images in (D) and (E) separated by dotted lines are not from the same vesicles. (F) Deformation profile of actin-cortex GUVs (top) and alpha-actinin-cross-linked GUVs (bottom). n = 3. Shaded rectangular box denotes approximate duration of electric field application. Shaded areas in the traces in indicate ±SD. (G) Statistical analysis of electrodeformed actin-cortex and alpha-actinin-cross-linked GUVs. Data represent mean maximum deformation, and error bars denote ±SE. n_cortex = 12 and n_cross-linker = 11. Scale bars, 10 μm. To see this figure in color, go online.

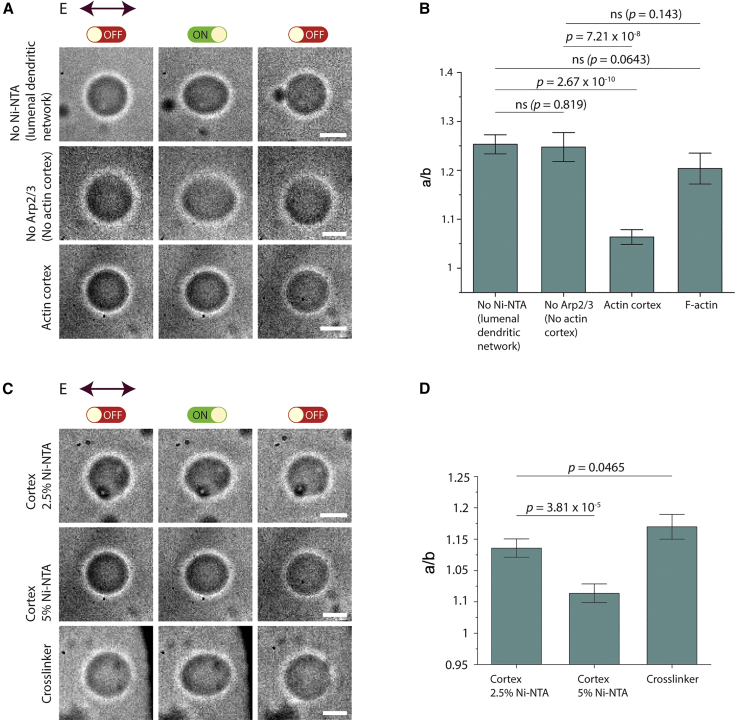
VCA is an acidic protein, and its binding to the membrane may alter the dielectric property of GUV and, thereby, its deformation under the electric field. When we included VCA and the Arp2/3 complex was absent, we did not observe dampening of deformation (Fig. 6 A), indicating that the actin cortex itself was likely the major contributor to the observed deformation dampening. Consistent with this, leaving out the NTA(Ni) lipid altogether also did not lead to a large deformation dampening (Fig. 6 A). We have presented these results comparing them with actin-cortex and F-actin GUVs (Fig. 6 B). Furthermore, when we modulated the concentrations of NTA(Ni) and reduced NTA(Ni) lipids from 5% to 2.5%, we found a notable recovery of GUV deformability (Fig. 6 C), yet with significantly enhanced deformation dampening compared with alpha-actinin-cross-linked GUVs (Fig. 6 D). Presumably, controlling the density of the actin cortex effectively tuned GUV deformability.

Figure 6.

Electrodeformation of GUVs encapsulating different membrane and actin-binding protein conditions. (A) Bright-field images show transformation of GUVs from unperturbed (left column) to elliptically electrodeformed during application of electric field (middle column) to spherical recovery (right column). Images of GUV encapsulating 5.6 μM actin, VCA (0.5 μM), and Arp2/3 (0.5 μM) without Ni-NTA at the membrane (first row), GUV encapsulating actin VCA excluding Arp2/3 with 5% Ni-NTA at the membrane (second row), and actin-cortex GUV (third row). (B) Maximum a/b ratio of GUVs from the three conditions indicated. (C) Electrodeformation of actin cortex at varying Ni-NTA concentrations in lipid bilayer membrane and alpha-actinin-cross-linked GUVs. Bright-field images show transformation of GUVs from unperturbed (left column) to elliptically electrodeformed during application of electric field (middle column) to spherical recovery (right column). Images of actin-cortex GUVs reconstituted in 2.5% Ni-NTA (top), 5% Ni-NTA (middle), and alpha-actinin-cross-linked (1.77 μM) GUVs are displayed. (D) Maximum a/b ratio of GUVs from the three conditions indicated. For (B), data represent mean maximum deformation, and error bars denote ±SE. n_{2.5% Ni-NTA} = 11, n_{5% Ni-NTA} = 13, and n_cross-linker = 12. For (D), data represent mean maximum deformation, and error bars denote ±SE. n_{No Ni-NTA} = 10, n_{No Arp2/3} = 12, n_Cortex = 12, and n_F-actin = 13. Scale bars, 10 μm. To see this figure in color, go online.

These results demonstrated differential mechanical properties of various isolated actin networks in a cell-like confinement. The mechanism by which actin networks achieve such mechanical variation is still open to investigation.

Discussion

In this work, we examined how the structural arrangement of lumenal contents determines electrodeformability of cell-mimicking GUVs subjected to an AC electric field. This mechanism is distinct from conditions that are known to impact the degree of electrodeformation, which includes conductivity contrast, osmotic contrast, lipid bilayer composition, lipid bilayer viscosity, and electric field intensity (41,50,51,54). In contrast, our results show that deformability of GUVs encapsulating actin filaments is suppressed compared with actin-free GUVs. We demonstrated that the deformation dampening of F-actin GUVs is likely manifested as the viscosity of the GUV lumen is increased. Motivated by differential mechanics found in a cell, we further examined how the actin cortex and cross-linked actin networks govern GUV electrodeformation. Evident from dampened deformation, our results illustrate differences in GUV deformability between different actin architectures when they have identical total actin concentrations.

The mechanism by which deformability of GUVs is dampened as a function of increasing viscosity is not apparently clear. To gain some insights, it is necessary to consider the inherent property of actin and PEG as polymer chains. Polymer chains such as actin and PEG, depending on the average polymer length and dispersity, are known to entangle at random (61,62,63). Thus, one possible physical model that can be entertained as a plausible mechanism is from disordered polymer chain entanglement altering the strain-dependent (elastic) property of the GUV encapsulant. Prior works have shown that there exists a relationship between the polydispersity of polymer chains and their respective elasticity (64), thereby resulting in a change in permanent compressibility. Polymer chain entanglements constrain transient deformability of a viscoelastic composite, such as the GUV-encapsulant composite, by physically creating a barrier where entanglement networks are unable to relax/separate. Thus, it is within reason to consider the theory that an increase in viscosity in response to increasing the concentration of polymer chain is simultaneously changing the elastic property of actin-encapsulating GUVs. In the future, other physical models and theories can be investigated as potential explanations for the dampening of deformation as a function of increasing viscosity of the GUV lumen. We acknowledge that cell cytoplasm is known to be highly viscous due to high-protein contents that are not just attributed to actin filaments. While our data suggest that viscosity could play a role, we believe that the architecture (i.e., how they are organized and where) of the actin networks has a more dominant role here. As revealed by our findings, actin-cortex GUVs have greater deformation resistance compared with GUVs with alpha-actinin-cross-linked networks. Prior findings by Wagner et al. show that actin cross-linkers increase viscosity of actin in bulk solutions (56). However, the structure and spatial scale of actin networks formed in bulk solutions are diametrically different from those assembled in a cell-like confinement. Thus, it would be premature to attribute our finding that actin cross-linkers differentially regulate GUV electrodeformability to simply viscosity difference. During electrodeformation, GUVs undergo two distinct deformation regimes, namely entropic and elastic regimes (43). The extent of the deformation in the entropic regime is dependent on the degree of thermal undulations in the bilayer, which varies depending on the lipid composition and osmotic contrast, whereas the elastic regime is dictated by field intensity and bilayer stretchability at the molecular level. These deformation regimes may potentially be altered as a result of the material property of the lumen and its interaction with the lipid bilayer membrane. Thus, it is important to consider mechanisms of how different actin networks may affect these deformation regimes beyond changes in lumenal viscosity. In this context, it will be interesting to study the effect of actin networks on deswelled GUVs and how actin networks impact deswelled GUVs’ deformation.

It is well established that the actin cortex regulates membrane rigidity (65,66). When thin actin-cortex shells were reconstituted in GUVs and subjected to hydrodynamic tube pulling, it was shown that the membrane tube length was reduced for thin-actin-shell GUVs (67). Considering this prior finding, it is possible that the mechanism of electrodeformability suppression by the actin cortex is due to changes in membrane rigidity restricting membrane undulation in the entropic regime of deformation, and thereby restricting lipid mobility, consequently reducing bilayer stretching, in the elastic regime of electrodeformation. More likely, though, is that the elasticity of the cortex may contributes to the increased deformability resistance of actin-cortex GUVs. For alpha-actinin-cross-linked GUVs, a different mechanism may be plausible to account for their suppressed electrodeformability. When F-actin GUVs are subject to an electric field, due to the scale of individual filaments with respect to GUV size and field pressure, actin filaments are unable to individually resist deformation, akin to sand grains in quicksand, and are unable to undergo individual strain. However, alpha-actinin assembles complex actin scaffolds that can reinforce the GUV, like a truss system, to resist field forces. Further investigation could possibly shed more light on the relationship between cross-link/bundle rigidity and electrodeformability, and a more systematic study to titrate concentrations of cross-linkers will be informative.

For the numerical simulation of the electrodeformation of GUVs, the leaky-dielectric model is used, which characterizes some key physical and mechanical properties of GUVs, including conductivity contrast, membrane rigidity, and lumenal viscosity. Our numerical simulations provide additional supporting evidence, independent of experiments, that GUVs of increased lumenal viscosity experience greater deformation resistance. An important advantage of numerical simulation is its ability to collect various quantities of interest at ease, such as electric potential and velocity fields, offering more detailed characterizations of GUV electrodeformation. However, there are limitations to the current mathematical model. Firstly, due to its simplifying assumptions on the membrane structure, this model is incapable of capturing phenomena such as electropermeabilization and electroporation that occur under a strong electric field. Thus, our model restricts the membrane to an inextensible and intact boundary, which also explains why vesicles appear nonspherical before the application of an electric field. Secondly, the current model does not account for the cytoskeleton structures in GUVs, which will be important for further investigating the effect of different actin networks as integral structural components on the electrodeformability of GUVs. We think that this also explains the mismatch between our experimental and simulated results. Limitations to simulate change in the elastic behavior of entangled actin could possibly be why we fail to observe deformation dampening at steady state. To resolve these limitations in the future, more sophisticated mathematical models need to be developed. There are many fascinating mechanobiological inquiries that can be pursued using cytoskeletal GUVs. The cell is a very dynamic and structurally and functionally complex system with many proteins involved in a single function. The GUV furnishes a cell-like confinement system that is suitable for systematic construction of complex cellular functions module by module. Using our findings as a steppingstone, we anticipate future interest in examining the role of various other types of actin networks, and co-assembled networks of actin, intermediate filaments, and microtubules, in determining mechanophenotypes. The emergent mechanics of cytoskeleton is an underexplored area of cytoskeleton and membrane research. Our work provides a starting point to examine a myriad of other actin cross-linkers and their mechanical contribution to cell mechanical properties. Such efforts will help uncover deep insights into cell mechanics from the bottom up.

Author contributions

N.H.W. and A.P.L. designed research. N.H.W., B.W., and S.V. performed research. B.W. and S.V. contributed analytic tools. N.H.W. analyzed data. N.H.W., B.W., S.V., and A.P.L. wrote the paper.