Abstract
Change detection tasks are commonly used to measure and understand the nature of visual working memory capacity. Across three experiments, we examine whether the nature of the memory signals used to perform change detection are continuous or all-or-none and consider the implications for proper measurement of performance. In Experiment 1, we find evidence from confidence reports that visual working memory is continuous in strength, with strong support for an equal variance signal detection model with no guesses or lapses. Experiments 2 and 3 test an implication of this, which is that K should confound response criteria and memory. We found K values increased by roughly 30% when criteria are shifted despite no change in the underlying memory signals. Overall, our data call into question a large body of work using threshold measures, like K, to analyze change detection data. This metric confounds response bias with memory performance and is inconsistent with the vast majority of visual working memory models, which propose variations in precision or strength are present in working memory. Instead, our data indicate an equal variance signal detection model (and thus, d’)—without need for lapses or guesses—is sufficient to explain change detection performance.
Keywords: discrete-slots, models of memory, proper measurement, signal detection theory, visual working memory capacity
Working memory and its capacity constrains our cognitive abilities in a wide variety of domains (Baddeley, 2000). Individual differences in capacity and control predict differences in fluid intelligence, reading comprehension, and academic achievement (Alloway & Alloway, 2010; Daneman & Carpenter, 1980; Fukuda et al., 2010). These extensive links to various cognitive abilities make the architecture and limits of working memory of particular interest to many fields of study (e.g., Cowan, 2001; Miyake & Shah, 1999). One especially well studied component of this system is visual working memory, which holds visual information in an active state, making it available for further processing and protecting it against interference. This memory system has an extremely limited capacity: We struggle to retain accurate information about even three to four visual objects for just a few seconds (Luck & Vogel, 1997; Ma et al., 2014; Schurgin, 2018; Schurgin et al., 2020).
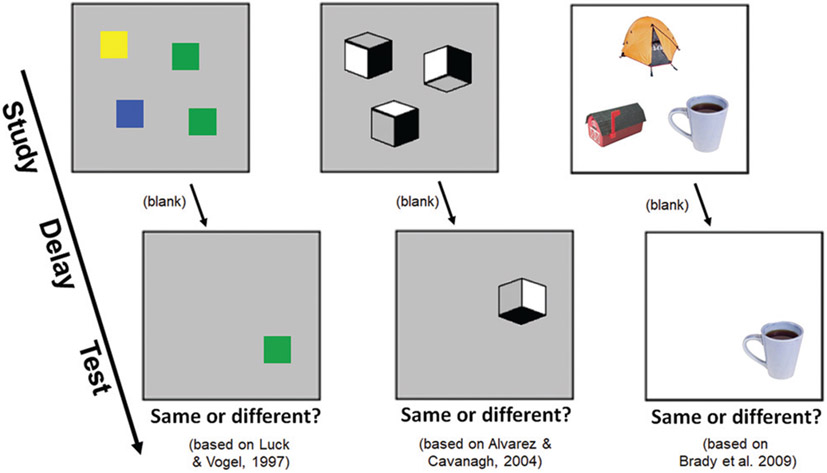
Over the past 20 years, a vast number of studies have investigated important issues in visual working memory. For example, many researchers have focused on how flexibly we can allocate our working memory resources to different numbers of objects (e.g., “slots” vs. “resources”; Alvarez & Cavanagh, 2004; Awh et al., 2007) and whether different features of these objects are “bound” or stored separately (e.g., Baddeley et al., 2011; Luck & Vogel, 1997). Another major area of work has demonstrated that visual working memory capacity, even for simple displays (Figure 1a), is predictive of fluid intelligence as well as a host of other important cognitive abilities (Fukuda et al., 2010; Unsworth et al., 2014). Overall, significant progress has been made in understanding the nature of this memory system (e.g., Brady et al., 2011).
Figure 1.
Change Detection Tasks Have Been Critical to Nearly All Areas of the Visual Working Memory Literature, From Early Work by Luck and Vogel (1997) Arguing for Object-Based Limits on Working Memory Capacity; to Later Work Arguing for Important Effects of Object Complexity (Alvarez & Cavanagh, 2004); to Work Investigating Benefits of Knowledge About Real-World Objects to Performance (e.g., Brady et al., 2009)
Change Detection Cannot Unambiguously Measure Memory Performance
However, many of the core conclusions about the nature of visual working memory come from tasks known as change detection tasks. These tasks are a variant of an “old/new” recognition memory paradigm in which participants are probed on their memory by being asked “Did you previously see this item?” or are prompted to identify an item as either “old” or “new.” In a typical visual working memory display (see Figure 1), participants see several simple, isolated objects on a solid color background and are asked to hold these items in mind before being asked to detect whether a particular object changed after a brief delay (Luck & Vogel, 1997).1 Despite their ubiquity, change detection tasks cannot provide an unambiguous estimate of memory performance because any measure of performance from this task relies on assumptions about the distribution of memory signals which are often false and regularly unverified (see Brady et al., 2021).
Because change detection tasks provide two relevant measures of performance, hit rate (calling “same” items “same”) and false alarm rate (calling “different” items “same”), memory researchers must combine them to get a unified measure of performance. This introduces significant ambiguity into memory measurement since there are several choices for how to combine hits and false alarms into a quantitative measure of performances (e.g., d, A’, K values, percent correct, etc.), all of which rest on different, and sometimes incompatible, theoretical and/or parametric assumptions (for a review, see Brady et al., 2021).
One of the most common ways to combine hits with false alarms is to use “K” values (N * [hit rate – false alarm rate]), where N is the number of objects shown (Cowan, 2001; see also Pashler, 1988; Rouder et al., 2011). This metric, which is technically based on double high-threshold theory (Rouder et al., 2011), attempts to measure “how many objects” or “items” people remember and, because this is a particularly intuitive concept, it has ended up being extremely prevalent in the study of visual working memory (for example, Alvarez & Cavanagh, 2004, 2008; Brady & Alvarez, 2015; Chunharas et al., 2019; Endress & Potter, 2014; Eriksson et al., 2015; Forsberg et al., 2020; Fukuda, Kang, & Woodman, 2016; Fukuda, Woodman, & Vogel, 2016; Fukuda et al., 2010; Fukuda & Vogel, 2019; Hakim et al., 2019; Irwin, 2014; Luria & Vogel, 2011; Ngiam et al., 2019; Norris et al., 2019; Pailian et al., 2020; Schurgin, 2018; Schurgin & Brady, 2019; Shipstead et al., 2014; Sligte et al., 2008; Unsworth et al., 2014, 2015; Vogel & Machizawa, 2004; Woodman & Vogel, 2008).
However, despite the seemingly straightforward nature of K values, they depend on strong theoretical claims, just like any-and-all ways of combining hits and false alarms into a unified measure (Brady et al., 2021). These foundational claims—which are in conflict with a wide variety of accepted theories of working memory—deeply affect estimates of memory performance and the conclusions made based on K values. K is a slight variation on adjusted hit rate, percent correct and other measures that are all derived from a class of models called threshold models (Swets, 1986). K values rest on the assumption that memories are all-or-none: Items are either remembered in a way that is perfectly diagnostic, or not remembered at all. Under such a view, false alarms arise when there is zero information about an item in memory (i.e., they represent pure, informationless “guesses”) and, because false alarms tell you how often a participant was “guessing,” they can be used to adjust the hit rate for “lucky guesses” (hence the hits minus false alarms aspect of the K formula). Therefore, for K values to provide a valid measure of performance it must be the case that memories are never weak or strong but are perfectly described by being either completely present or completely absent. This point applies to all variants of K measures since they all rest on the same theoretical foundation (Cowan, 2001; Pashler, 1988; Rouder et al., 2011).
The processing assumptions of such a threshold model is at odds with a variety of findings from contemporary visual working memory studies and with nearly all visual working memory theories. Indeed, mainstream working memory models based on continuous reproduction data, rather than change detection data, accept the fact that memories vary in their precision: for example, an item is remembered more precisely at set size 1 than set size 3 (Bays et al., 2009; Schurgin et al., 2020; van den Berg et al., 2012; Zhang & Luck, 2008). In addition, when participants express levels of confidence in their memory, variation in confidence tracks both how precisely an item is being remembered and how likely people are to make large errors (Fougnie et al., 2012; Honig et al., 2020; Rademaker et al., 2012). The combination of variation in precision with variation in confidence suggests that memories vary continuously in how strongly they are represented and that participants are aware of this variation in memory strength (see Schurgin et al., 2020). Theories where memories vary in precision or strength and participants have access to this precision or strength to make their decision undermine the foundational and irrevocable principles of the K metric and, therefore, make it an inappropriate metric for estimating memory performance. That is, K as a metric is based on the idea that memories either exist or do not exist, but variation in precision is critical to both models that do (Adam et al., 2017; Zhang & Luck, 2008) and do not (Bays, 2015; Schurgin et al., 2020; van den Berg et al., 2012) subscribe to “item limits” or some form of “slots.” Thus, whereas the use of K as a measure is extremely common, it appears to be at odds with the theories of nearly all visual working memory researchers.
In contrast to threshold metrics like K, variations in the precision of memory are naturally accommodated by Bayesian and signal detection-based models of memory that assume some axis of variation between memories that is used to make decisions about whether an item has been seen before or not (e.g., Schurgin et al., 2020; Wilken & Ma, 2004). Under a signal detection framework, memories are seen as continuously varying along an axis of strength of some kind, with decisions about whether an item has been seen made by applying a criterion to this axis. As a memory signal elicited by an item increases it becomes ever more distinguishable from noise, and this gives rise to confidence—as memory signal increases so too does confidence—and an observer’s decisions are based on criteria that they set based on their own confidence (see Wixted, 2020). This view denies the notion that memories are all-or-none, present or absent, instead seeing memories as varying in some way (e.g., in “precision” or “strength”). Variations on this signal detection framework have played a major role in nearly all long-term recognition memory research for over fifty years (e.g., Benjamin et al., 2009; Glanzer & Bowles, 1976; Heathcote, 2003; Kellen et al., 2021; McClelland & Chappell, 1998; Shiffrin & Steyvers, 1997; Wixted, 2020; Wickelgren & Norman, 1966).
Once a model is used that is based on the idea that memories vary continuously and participants use this variation (e.g., in precision or strength) to make their decisions, the most natural decision is to simply apply this model to all trials without introducing any separate processes (like lapses or guesses). Thus, while signal detection-based models that also include lapses or guesses are possible (e.g., Xie & Zhang, 2017), in their most basic form, signal detection models generally do not involve the extra assumption that “guesses” are a discrete and separate state of memory, instead postulating that decisions are always made based on the same continuous signals, and that errors arise from the stochastic, noisy nature of these signals.2 Such signal detection–based views naturally accommodate the subjective feeling of “guessing” as a state of very low confidence, with nearly no likelihood of correct discrimination of signal from noise, but they do so purely based on variations along a single axis of memory signals. That is, in a signal detection based account, people should often feel as though they are guessing, even though there is no separate guess state (e.g., Schurgin et al., 2020).
Broadly speaking, then, signal detection-based accounts are necessary for accurate measurement if items vary in some way (e.g., precision) and participants use this variation in their decision process, rather than all memories being equally precise and exactly the same (as assumed by threshold theories). However, in the visual working memory literature most signal detection based accounts do not postulate a separate guess or lapse state—that is, most signal detection models in the literature presume memories just vary continuously in a single axis that people use to make decisions (e.g., Schurgin et al., 2020; Wilken & Ma, 2004; but see Xie & Zhang, 2017). An account based on this simplest signal detection account with just a single axis and no added lapses or guesses has recently been shown to straightforwardly accommodate error distributions from not only change detection and forced-choice tasks but also continuous reproduction tasks in visual working and visual long-term memory tasks (Schurgin et al., 2020).
How does one measure performance in a signal detection-based view of memory, other than model fitting? The most common signal detection measure of memory strength is d′, which rests on the assumption that the distribution of memory signals for previously seen and previously unseen items are both equal in variance and approximately normal (Macmillan & Creelman, 2005). This measure is appropriate only if there is no “guess” or “lapse” state, and all memories are items are approximately equally well encoded. It is no more complex than K: rather than subtracting hits and false alarms, d′ simply requires you subtract them after a simple transformation (the inverse of the normal distribution). However, d′ only applies to the simplest signal detection models without any variation in strength or lapses. More complex signal-detection-based measures are also possible if these assumptions do not hold for a particular situation (e.g., da; Macmillan & Creelman, 2005) or if memory is a mixture of continuous decisions and lapses or guesses (e.g., Xie & Zhang, 2017).
In summary, if memories vary in precision or strength, K values will confound response bias with underlying memory, leading to spurious estimates of working memory capacity that vary with changes in response strategy (i.e., criterion; how liberally or conservatively one responds to a change). An alternative framework based in signal detection allows for a very broad set of possibilities, including lapses/guesses in addition to precision variation (Xie & Zhang, 2017), or variability in memory strength between items (e.g., da; Macmillan & Creelman, 2005), but the simplest form of this view simply postulates that all decisions are made based on a single set of equal variance memory signals (which leads to the d′ metric). Thus, determining the nature of memory signals in change detection, and the extent to which they are all-or-none, is deeply related to the question of whether K or d′ or neither is a valid measure of change detection performance that isolates memory from the decision-making process and response bias.
ROC Curves Elucidate the Appropriate Way to Measure Performance
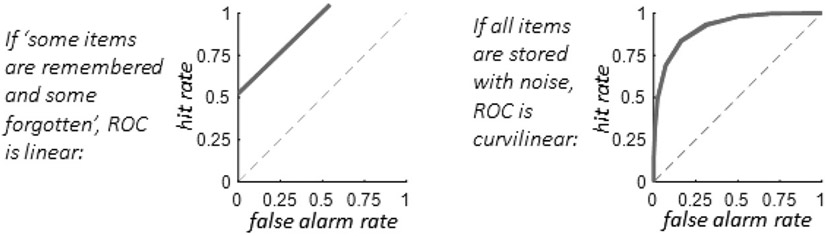
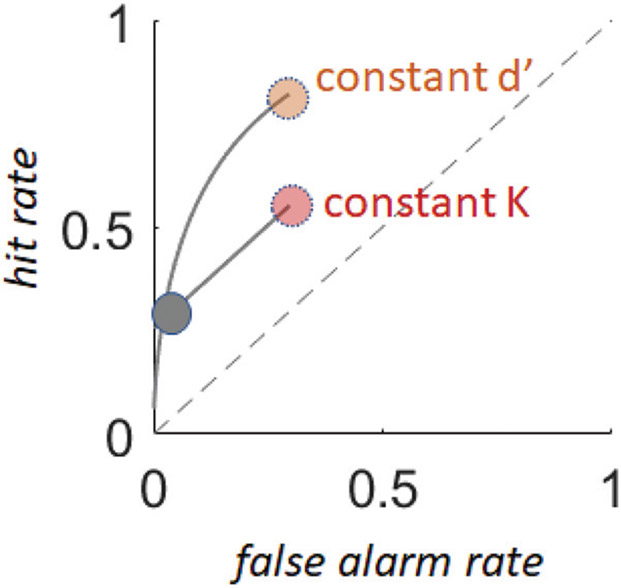
How then can these theories, and their associated metrics, be evaluated and compared? Is memory all-or none? Is it more useful to think about “guessing” as a distinct state, or more useful to think about a single continuum of memory strength and response bias? The critical test that tells these models apart, and determines which model to embrace, is the shape of the receiver operating characteristic (ROC) predicted by these models (Brady et al., 2021; Swets, 1986; Wickens, 2001). ROCs measure what happens to performance—in terms of hits, on the y axis, and false alarms, on the x axis (Figure 2)—as an observer becomes more or less likely to say “old” (or “no change” in change detection tasks), that is, as their response criterion changes. If an individual’s true ROC could be perfectly measured, without measurement noise or reliance on simplifying and auxiliary assumptions, it would provide a direct window into the latent distribution of memory signals, and thus reveal which view of memory is correct. As a result, the importance of measuring and comparing ROCs has been identified and embraced in a wide range of fields including decision-making, health care, and artificial intelligence (Fawcett, 2006).
Figure 2. ROC Curves of Memory Performance Predicted by the Two Models.
Note. ROC = receiver operating characteristic. A threshold model of working memory (e.g., K) predicts that ROC curves should be linear, because remembered items contribute only to hit rate, whereas forgotten items contribute to both hit rate (from lucky guesses) and false alarm rate (from unlucky guesses). By contrast, the most straightforward signal detection theories without lapses or guesses dictate that while, on average, previously seen items feel more familiar than previously unseen items (by an amount denoted by d′), noise corrupts the familiarity signal for both previously seen and previously unseen items, which leads to an overlap of familiarity strengths. Thus, the ROC should be curvilinear if all items are represented with approximately equal d′, and so the variation in familiarity is the same for previously seen and previously unseen items, the curves should also be symmetric, as shown here.
In the current work, we seek to evaluate which of these views of latent memory signals (continuous vs. discrete) is accurate and should be used to measure performance. To do so, we first need to determine the shape of the ROC that each model would predict: All-or-none threshold models (where memories cannot vary in precision or strength), like the one used to calculate K values, predict a linear ROC (see Figure 2) because guessing contributes to both hits and false alarms equally (thus generating a linear slope as a function of changes in response criterion) whereas remembered items only contribute to hits (which determines the function’s intercept; Luce, 1963; Krantz, 1969; Swets, 1986). On the other hand, the simplest signal detection-based models without any lapses or guesses predict a symmetric curvilinear ROC because as criteria change to include weaker and weaker signals, some previously seen and some never-before-seen items get included in the overall distribution in a nonlinear fashion (this nonlinearity follows from the standard parametric assumption that the latent distribution of memory signals is continuous and nonrectangular; Macmillan & Creelman, 2005; Swets, 1986; Wixted, 2020). More complex ROC curves are also possible for signal detection-based models that do not treat all memories as arising from the same simple process with a fixed memory strength across all items (e.g., unequal variance signal detection models; Wixted, 2007; models with a subset of all-or-none memories: Yonelinas, 2002; models with all-or-none guessing: Xie & Zhang, 2017; etc.).
To measure the full ROC we need some way to measure response criterion. Typically, this is done either by eliciting confidence from participants on each trial or by manipulating response bias across different blocks of an experiment, usually by changing how often items are genuinely old versus new. In the study of long-term recognition memory, when trying to characterize the source of memory signals and their variability, confidence-based ROCs (e.g., where you simply ask people the strength of their memory on a Likert scale) are ubiquitous and are effectively standard practice when performing old/new memory tasks (e.g., Benjamin et al., 2013; Hautus et al., 2008; Jang et al., 2009; Koen et al., 2017; Wixted, 2007; Yonelinas, 2002; Yonelinas & Parks, 2007). However, visual working memory researchers have often avoided collecting confidence-based ROC data and instead look to manipulate response bias by changing the prior probability of a “same” vs. “change” response (Donkin et al., 2014, 2016; Rouder et al., 2008; though see Robinson et al., 2020; Xie & Zhang, 2017). While results from response bias manipulations used to measure ROCs have varied—embracing both threshold and signal detection views at different times (e.g., Donkin et al., 2014, 2016; Rouder et al., 2008)—our own recent work suggests this is largely because the data in those studies are not particularly diagnostic (e.g., being very limited in their range of response bias values) and because the model comparison metrics used by the studies were not validated to ensure that they adequately recover the correct model when using simulated data (Robinson et al., 2022). By contrast, data from confidence-based ROCs of change detection in working memory are unequivocal: ROCs have always been found to be curvilinear and most consistent with equal variance signal detection models (Robinson et al., 2020; Wilken & Ma, 2004; see also Xie & Zhang, 2017, who find visually equal variance curves but do not test this class of model directly).
Notably, identifying and characterizing the shape of these curves is critical for distinguishing all-or-none and continuous memories, but also for proper measurement of memory in change detection tasks. For example, the threshold-based model of memory predicts that all points on the line in Figure 2A reflect the same estimate of capacity whereas the equal variance signal detection model predicts that all points on the curve in Figure 2B reflect the same level of memory strength. Although there are areas where these functions overlap (particularly in the middle), they substantially diverge toward the extreme ends of the spectrum—and consequently give very different senses of which combinations of hits and false alarms correspond to the same levels of performance for subjects or conditions that happen to differ in response bias.
Thus, independent of arguments about the nature of the underlying memory signals, a strong understanding of the shape of ROCs in change detection tasks is critical to the simple act of computing performance and comparing it across conditions. In fact, a common critique of threshold models of long-term memory is that they may confound variations in response bias with variations in memory states, as ROCs in long-term memory are nearly always curvilinear (e.g., Rotello et al., 2015). If K values confound response bias with performance, as they would if memories genuinely vary in precision (e.g., Bays et al., 2009; Zhang & Luck, 2008) and thus ROCs are curvilinear, then this would potentially undermine a large body of work that even partially relies on K to draw strong conclusions about the nature of visual working memory (for example, Alvarez & Cavanagh, 2004, 2008; Brady & Alvarez, 2015; Chunharas et al., 2019; Endress & Potter, 2014; Eriksson et al., 2015; Forsberg et al., 2020; Fukuda & Vogel, 2019; Fukuda et al., 2010; Fukuda, Kang, & Woodman, 2016; Fukuda, Woodman, & Vogel, 2016; Hakim et al., 2019; Irwin, 2014; Luria & Vogel, 2011; Ngiam et al., 2019; Norris et al., 2019; Pailian et al., 2020; Schurgin & Brady, 2019; Shipstead et al., 2014; Sligte et al., 2008; Starr et al., 2020; Unsworth et al., 2014, 2015; Vogel & Machizawa, 2004; Woodman & Vogel, 2008).
The Current Work
In the current work we address the possibility that K confounds response bias with performance in a novel way and with minimal reliance on model comparison or other assumptions. We also test whether the simplest equal variance signal detection model (and thus, d′) is a valid metric of performance in this task, or whether a more complex ROC must be assumed (e.g., with both signal detection and lapses). In Experiment 1, we first measure confidence-based ROCs in a typical visual working memory change detection task to provide a baseline for simulations and for the core experiment, Experiments 2. We find that confidence-based ROCs are curvilinear and extremely consistent with the prediction of an equal variance signal detection model (replicating the results of Robinson et al., 2020). As part of our modeling and analysis, we also describe evidence against views that challenge the interpretation of curvilinear ROC functions constructed from confidence ratings. Next, in a simulation, we investigate how each metric would vary if these curvilinear ROCs genuinely reflect the latent memory strength distribution of participants, consistent with the most straightforward equal variance signal detection theory model of working memory performance (Schurgin et al., 2020; Wilken & Ma, 2004). We find that K should drastically misrepresent true memory in this scenario. For example, K wildly underestimates performance for subjects with conservative response criteria (e.g., for participants who rarely say “same” unless very confident) and such participants are quite common in existing large-scale data sets at high set sizes (Balaban et al., 2019).
In Experiments 2, a novel and preregistered study, we examined whether estimates of K spuriously varied across manipulations of response bias in a way that does not depend on model comparisons or confidence to assess latent memory strength. In particular, we compare K and d′ in a completely standard change detection experiment with performance in a different, across-participant condition where participants are adaptively encouraged to shift their response bias if it is excessively conservative. We find that these adaptive instructions increase estimates of K by a large factor (e.g., they “improve” working memory capacity, as measured by K, by 30%) but produce no such effect when performance is measured with d′. This provides strong evidence that the latent distribution of memory signals is best captured by the curvilinear ROC that is implied by equal variance signal detection models and implores the use of d′ (see Figure 2). Furthermore, this result adds experimental evidence against the existence of all-or-none memories and the use of K values. In Experiment 3, we replicate our critical result in another preregistered study with a different set size and with the addition of a visual mask. This experiment demonstrates the generality of our results across memory load demands and rules out the contribution of alternative memory processes (e.g., iconic memory). Overall, we suggest that a major rethinking of conclusions based on K values or other threshold measures is required for cumulative progress to be made in understanding visual working memory. Furthermore, we by showing that d′ appears to be a reliable measure of memory even across changes in response criterion, we provide evidence in favor of the simplest equal variance signal detection model (e.g., Schurgin et al., 2020) and evidence against models based on a mixture of signal detection and guesses/lapses.
Experiment 1: Receiver Operating Characteristics in Change Detection
While confidence-based ROCs are prevalent in long-term recognition memory experiments using the old/new paradigm they are rarely examined in visual working memory, with few exceptions (e.g., Robinson et al., 2020; Wilken & Ma, 2004; Xie & Zhang, 2017). This experiment was designed to collect such data in a prototypical visual working memory task using change-detection with a large number of confidence bins (see Figure 3). This provides a replication of previous work and serves as the basis for the simulations that motivated our critical test of signal detection vs. threshold views in Experiments 2.
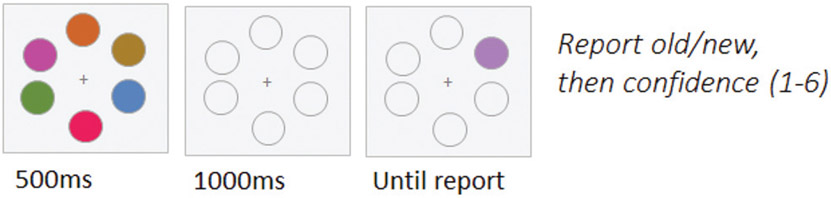
Figure 3. Experiment 1 Task.
Note. Participants completed a change detection task at set sizes 1, 3 and 6 with 180-degree changes on the color wheel. After reporting whether the test item was old or new (i.e., same or different), participants then reported the confidence of their decisions on a 1–6 scale (1 = no confidence, 6 = extremely confident), giving an overall 12-point confidence scale.
Method
Participants
All studies were approved by the Institutional Review Board at the University of California, San Diego, and all participants gave informed consent before beginning the experiment. Experiment 1 tested 70 undergraduate volunteers in our lab at UC San Diego, in exchange for course credit. Our final sample of 67 participants allowed us to detect a within subject effect as small as dz = .18 with power = .8 and an alpha of .5.
Stimuli
Both experiments used a circle in CIE L*a*b* color space, centered in the color space at (L = 54, a = 21.5, b = 11.5) with a radius of 49 (from Schurgin et al., 2020).
Procedure
Participants performed 300 trials of a change detection task, 100 at set size 1, 100 at set size 3, and 100 at set size 6. The display consisted of 6 placeholder circles. Colors were then presented for 500 ms, followed by a 1,000-ms ISI. For set sizes below 6, the colors appeared at random locations with placeholders in place for any remaining locations (e.g., at set size 3, the colors appeared at 3 random locations with placeholders remaining in the other 3 locations). Colors were constrained to be at least 15° apart along the response wheel. After the ISI, a single color reappeared at one of the positions where an item had been presented. On 50% of trials each set size, this was the same color that had previously appeared at that position. On 50% of trials, it was a color from the exact opposite side of the color wheel, 180° along the color wheel from the shown color at that position.
Participants had to indicate whether the color that reappeared was the same or different than the color that had initially been presented at that location. After indicating whether the color was the same or different from the target in the previous array using a key response, participants then reported their confidence. Participants were presented an interval from 1–6 and had been instructed that 1 meant very unsure and 6 meant very sure and to report their confidence using the entire scale. It is important to note that defining the signal in terms of detecting “changes” (i.e., correctly calling different items “different”) or “no changes” (i.e., correctly calling same items “same,” as we do throughout) would have no consequences for our results. The results of the metric-based analysis would be identical regardless of which was defined as a “hit.”
Three participants were excluded for performing near chance (>2 standard deviations below the mean, according to both K and d′), leaving a final sample of N = 67.
Data
These data were made available previously to be used in a database that consisted of data from confidence studies (Rahnev et al., 2020). However, except for being included in that public dataset, the data have not been previously published or written up.
Results
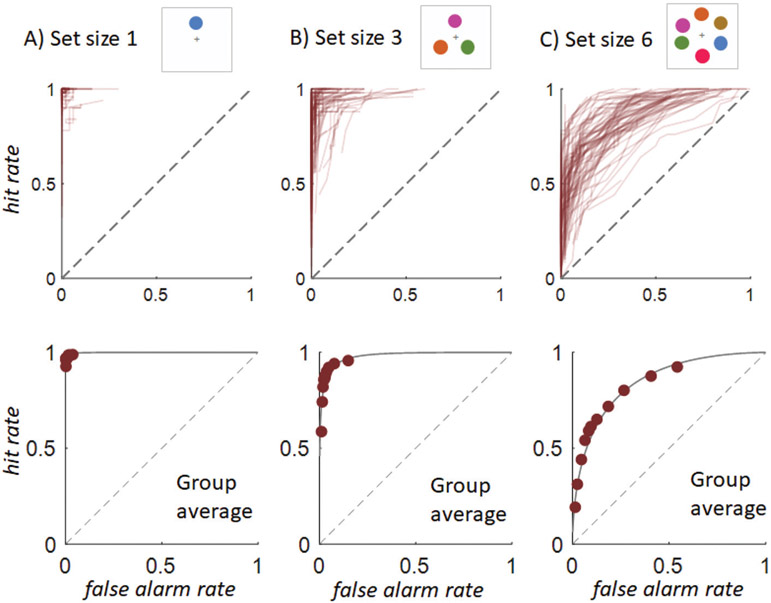
The ROC data are visually curvilinear, both at the individual subject level and the group level (see Figure 4). To assess the shape of the ROCs quantitatively, and thus ascertain the preferred measurement metric, we performed model comparisons independently for each participant and each set size.3 We compared three scenarios: (a) a linear, threshold-based ROC, as needed for K values to be a valid metric, (b) an equal variance signal detection model, as needed for d′ to be a valid metric, and (c) an unequal variance signal detection model, which would suggest no single metric from a binary change detection task (“same”/“change” with no confidence) can adequately correct for response bias (see Brady et al., 2021, for a tutorial). To compare models we used AIC because model recovery simulations by Robinson et al. (2020) demonstrated that AIC was best calibrated for recovering the generative model from similar ROC data. Note, however, that since the threshold-based model (K) and the equal variance signal detection model (d′) have equal numbers of free parameters, comparing their AIC is the same as comparing their log likelihood directly with no penalty for complexity, so the use of AIC is relevant only for comparing the unequal variance signal detection model to the other two models.
Figure 4. Empirical Receiver Operating Curves From.
Experiment 1 Note. The top panel shows individual data and the bottom panel shows aggregate data.
Overall, we found strong evidence favoring signal detection-based models over the threshold model, and further evidence in favor of the simplest equal variance signal detection model underlying d′. A difference greater than 10—which provides 10 to 1 support for one model over the other—is considered conclusive evidence in terms of AIC. Despite an equal number of parameters, the equal variance signal detection model was strongly preferred to the threshold model, with AIC differences favoring it by 244.8 at set size 1, 1,479.2 at set size 3, and 1,749.5 at set size 6. These outcomes were also reliable per participant, t(66) = 2.81, p = .007, dz = .34; t(66) = 8.74, p < .001, dz = 1.07; t(66) = 11.96, p < .001, dz = 1.46. The AIC difference between the threshold model and the unequal variance signal detection also favored the signal detection model: 188.5, 1,548.7, and 1,694.4 across set sizes. Each of these was also reliable when calculated per participant instead of summed over all participants, t(66) = 2.12, p = .038, dz = .26; t(66) = 8.75, p < .001, dz = 1.07; t(66) = 11.61, p < .001, dz = 1.42. Finally, comparing equal and unequal variance signal detection models provided support for the equal variance model, validating d′ as a valid metric of change detection performance. In particular, the AIC preference for the equal variance model was 56.3, 30.5 and 55.2 across set sizes; and this preference was largely reliable across participants as well, t(66) = 6.85, p < .001, dz = .84; t(66) = 1.79, p = .077, dz = .22; t(66) = 4.57, p < .001, dz = .56.
Evidence for equal variance signal detection as the preferred model of the ROC data validates the idea that change detection alone (without confidence ratings) can be used to measure visual working memory, as long as d′ is used as the dependent measure. Notably, this is unlike the result typically found in long-term recognition, where unequal variance signal detection models are nearly always preferred to equal variance models and thus d′ is rarely a universally valid metric (e.g., DeCarlo, 2010; Mickes, Wixted, & Wais, 2007; Starns, Ratcliff, & McKoon, 2012; Wixted, 2007; Yonelinas, 2002). Symmetric, equal variance ROCs are consistent with the idea that presented colors are strengthened to an approximately equal degree across trials, as one would expect that heterogeneity in added memory strength for different old items should lead to support for an unequal signal detection model (because there would be additional variance in familiarity for seen items compared with unseen items; Jang et al., 2012; Wixted, 2007). It may be that asking participants to split attention equally between all items by making them equally likely to be probed, using simple stimuli that are all approximately equally attention-grabbing, and presenting them briefly, encourages a strategy of splitting memory resources relatively equally. Thus, although d′—and equal variance—are well supported in the current task, the use of d′ may not be valid in other conditions, like sequential encoding (Brady & Störmer, 2022; Robinson et al., 2020) or when items are differentially prioritized (Emrich et al., 2017), but has been validated as the appropriate measure here. Importantly, finding support for an equal variance signal detection model also provides direct evidence against more complicated mixture of signal detection theory and guesses or lapses (e.g., Xie & Zhang, 2017) and provides evidence in favor of models that view all decisions as arising from a single signal detection process with no separate guess state (e.g., Schurgin et al., 2020).
Because of the theoretical importance of determining whether ROCs are symmetric versus asymmetric (for both determining whether d′ is an appropriate metric and addressing the conceptual question of whether there is heterogeneity across items in strength), we also used a nonmodel-comparison–based test to examine whether there is evidence for equal variance signal detection model. In particular, we computed z-ROCs by converting the hit and false alarm rate to z-scores using a normal distribution. We then fit the z-ROCs with a linear model at set sizes 3 and 6, where most participants were not at ceiling. Unequal memory strength between items, as in an unequal variance signal detection model, results in z-ROC slopes below 1.0, whereas an equal variance model predicts slopes of 1.0. We find these slopes are very close to 1.0 even at set size 6 (z-ROC slopes for set size 3: 1.06, SEM = .18 and set size 6: .96, SEM = .04).
Using further descriptive analysis, we examined whether the z-ROCs were consistent with threshold or signal-detection models. Linear z-ROCs are predicted by signal detection theory and curvilinear z-ROCs are predicted by threshold theories like K. Thus, threshold models, but not signal detection models, predict a strong positive quadratic component when fitting a polynomial model to the z-ROCs (Glanzer et al., 1999). Because we had significant ceiling effects at set size 1 and 3 in many participants when performing this analysis (which precludes our ability to determine the z-ROC shape), we conducted this analysis only for the set size 6 data. We found no evidence of the positive quadratic component predicted by high-threshold models (in fact the mean z-ROC quadratic component trended negative, though not significantly: M = −.13, SEM = .113, t[52] = 1.28, p = .21).
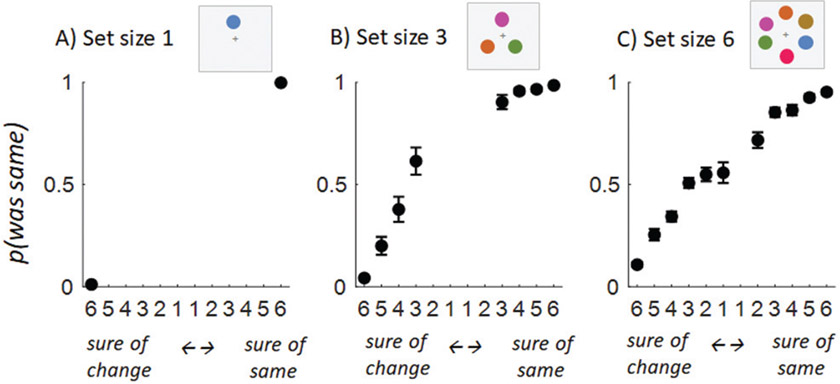
Another prediction of signal detection models concerns high confidence misses and false alarms. Signal detection models easily accommodate—and in many ways naturally predict4—high confidence false alarms and high confidence misses, especially because the difference between previously seen and previously unseen items in familiarity gets smaller (i.e., as memory strength gets weaker). By contrast, threshold models do not make this prediction and are most consistent with a complete absence of high confidence false alarms. This is because in such models, false alarms are typically purported to arise from a distinct process such as a “guessing state” (Rouder et al., 2008), which participants are thought to be aware of5 (e.g., Adam et al., 2017). As shown in Figure 5, we find data consistent with the signal detection view: there are high confidence false alarms and high confidence misses, such trials are increasingly prevalent at high set sizes as memory gets weaker (.67% at set size 1; 3.54% at set size 3; 12.1% at set size 6), and this difference is reliable across participants (set size 3 > set size 1: t(66) = 6.37, p < .001, dz = .78; set size 6 > set size 3: t(66) = 6.85, p < .001, dz = .84). Although accommodations can be made to account for high confidence false alarms in a single condition (e.g., by asserting signal-detection-like noise that occurs after the memory read-out, at the confidence stage; Adam & Vogel, 2017), it is hard to see how to parsimoniously accommodate the fact that such errors occur only in some set sizes but not others within a threshold view.
Figure 5. Confidence-Accuracy Curves, With Error Bars Being Across-Subject Standard Errors of the Mean.
Note. These curves use a value for each participant only if that participant used that confidence value on ≥3 trials and include only points where at least 25% of participants had values assigned. Confidence closely tracks accuracy, and even at set size 6, the highest confidence trials are quite accurate (89% overall for confidence level 6). However, as uniquely predicted by signal detection models but not threshold models, there are high confidence false alarms and high confidence misses, and such trials are increasingly prevalent at high set sizes, where memory gets weaker (0.67% at set size 1; 3.54% at set size 3; 12.1% at set size 6).
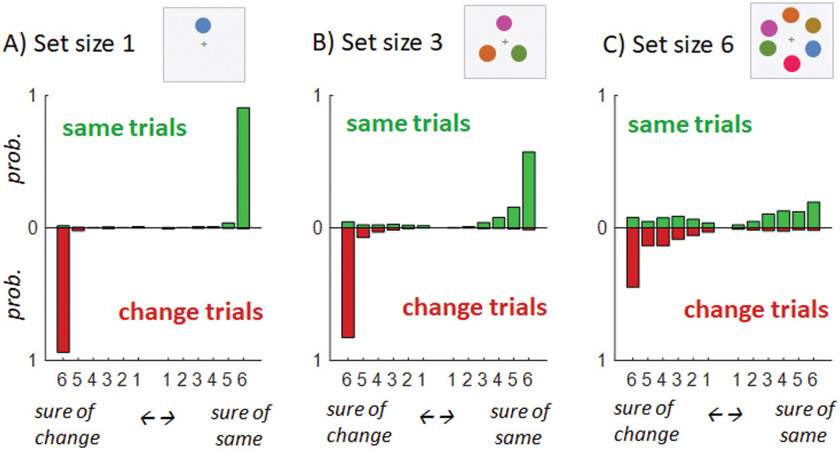
A similar logic calls into question prominent accounts which have argued that it is possible to explain curvilinear ROCs from confidence data with all-or-none, threshold memory models (e.g., Kellen & Klauer, 2015; Malmberg, 2002; Province & Rouder, 2012). Such models postulate that even when participants are, in truth, infinitely certain of their response, they nevertheless give a low confidence response sometimes, for instance, because the presentation of a confidence scale makes “an implicit demand to distribute responses” across the scale (Province & Rouder, 2012). This account, however, does not predict the current data because participants do not, in fact, spread their responses at all at set size 1; instead they do so only at the highest set sizes (see Figure 6; nearly all responses cluster at the highest confidence at set size 1). To account for this pattern, an account based on the idea that people seek to distribute their responses despite truly infinitely diagnostic memories would have to postulate yet another factor that explains why this response strategy varies across different set sizes; perhaps by incorporating even more complex decision-based components. Our data imply that, for this to work, participants would have to decide to add such response noise only for the set size 6 condition, but not for the set size 1 condition. This seems extremely unlikely and far more complex than simply presuming that participants have access to continuous strength memory signals that are used to report confidence, which is an a priori prediction of signal detection accounts of memory (see also Delay & Wixted, 2021).
Figure 6. Confidence Values Given by Participants Are Spread More Widely as Set Size Increases.
Note. As in most change detection studies (see Simulation and Experiments 2), participants have a response bias toward believing there was a change at high set sizes (e.g., being conservative in responding with confidence in “same”/“old”).
Overall, we find clear evidence in favor of curvilinear ROCs and signal detection–based models, which is wholly inconsistent with K as a valid metric of working memory performance. Model comparison suggests the ROCs are best fit by an equal variance signal detection model, consistent with d′ as the appropriate measure of memory performance. The support for an equal variance model goes beyond support for the general class of signal detection models (which includes ones like mixture models, with additional guesses; Xie & Zhang, 2017). Instead, these data support a view where all items are represented with noise, rather than a model where some items are perfectly present in memory and others are completely absent in memory. These findings also reveal the nearly symmetric (equal variance) nature of the ROC curves, which provides tentative evidence that—in this task—all items are represented with approximately the same memory strength, even at set size 6, given the nearly equal-variance nature of the ROC curves (though this is only indirect evidence; see Spanton & Berry, 2020).
Simulation: Implications of Confidence-Based ROCs Reflecting Underlying Latent Memory Strength
We next turn to the potential implications of K values—and other threshold metrics, like percent correct and hits minus false alarms—being mismatched with the empirical ROC. Then, in Experiments 2, we provide a critical test of whether the curvilinear ROCs we observe in Experiment 1 truly reflect latent memory signals, as opposed to arising artifactually in confidence-based ROCs.
First, what would happen if we took a binary change detection task and participants could only respond “same” when their confidence was at, or above, a certain criterion? For illustration, here we assume that a participant’s reported confidence is a direct readout of their memory states, which we can use to track different levels of response criteria. Importantly, we do not make this assumption in Experiments 2 (our core experiment) because it is not based on confidence judgments. Using the empirical confidence data from Experiment 1, we can see how performance, as measured by K or d′, would change as the internal criterion were shifted in Figure 7. Notably, d′ remains constant as we measure criterion across possible confidence values, whereas K incorrectly interprets different response criteria on the exact same data as changes in true memory strength and thus alters the working memory “capacity.” In other words, the K measure effectively conflates response bias with true memory strength. This occurs in part because the ROC implied by d′ effectively matches the actual ROCs observed in Experiment 1. Thus, calculating d′ using any possible confidence criterion as the cut-off for saying “same” is the same as moving along the ROC predicted by the equal variance signal detection model and, therefore, yields approximately the same d′ for different levels of response bias. By contrast, because the ROC implied by threshold models like K deviates from the shape of the empirical confidence ROC, K values are much lower when criterions are extremely high or extremely low compared with when they are less extreme and somewhere in the middle (except at set size 1, where all models agree performance is essentially perfect). This is because the high-threshold (linear) ROC approximates the empirically curvilinear ROC shape only in the center and not for extreme criteria (see Figure 9).
Figure 7. Metrics of Visual Working Memory Performance Plotted for the Group Mean Data From Experiment 1, as a Function of Response Criteria (Applied to the Confidence Data).
Note. Because the receiver operating characteristic (ROC) implied by d′ closely matches the actual ROCs observed in Experiment 1, calculating d′ using any possible confidence criteria as the cut-off for saying “same” gives approximately the same d′. By contrast, because the ROC implied by threshold models like K deviates from the shape of the confidence ROC, K values are lower when the criteria are extremely high or extremely low compared with the middle (except at set size 1, where all models agree performance is essentially perfect). This is because the linear ROC predicted by K approximates the true confidence-based ROC shape only in the center, and not for extreme criteria (see Figure 2).
Figure 9. An Exaggerated Potential Outcome of Shifting a Naturally Conservative Participant (Gray) to Say “Same” More Often, in Terms of the Prediction of Signal Detection (d′) and Threshold View (K).
Note. The more conservative the initial responding pattern is, the more the two models dissociate in their prediction. By computing participants’ performance in the baseline condition—the gray dot—in terms of K and d′, and comparing with to their performance (again in K and d′) when their decision criteria are shifted leftward, and thus their false alarm rates move rightward, we can distinguish these models: An ideal metric would find the same level of performance despite the shift, whereas a model that suggested memory had changed would be dispreferred.
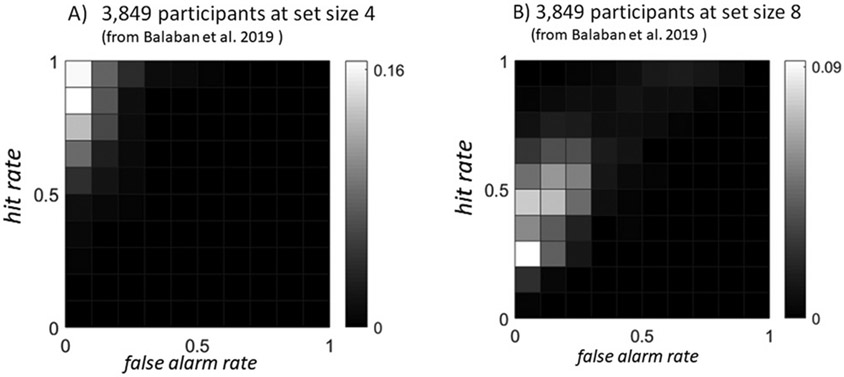
Our simulation also makes clear that over a wide range of performance values and biases, K and d′ do not strongly diverge which is one reason that it has historically been difficult to tell them apart (see Figure 7). They do, however, diverge primarily at high set sizes and for conservative response criteria (i.e., being reluctant to respond “same”). This divergence would not be apparent unless such extreme response criteria extemporaneously occur in real data. Unfortunately, they seem to be quite common. In fact, data from change detection tasks seem to lead to extremely conservative responding in many situations. As an example, we reanalyzed data from 3,849 people who completed a change detection task (Balaban et al., 2019) and found that at set size 4, 91% of participants had false alarm rates below .2, and at set size 8, 68% of participants had a false alarm rate this low. By contrast, only 56% of participants (at set size 4) and 12% of participants (at set size 8) had miss rates this low (see Figure 8).
Figure 8. Nearly All Participants Have Low False Alarm Rates at Both Set Size 4 and 8, Exacerbating the Difference Between d′ and K as Metrics of Performance.
Note. Response criteria are particularly conservative at set size 8, where “misses” are quite common (i.e., hit rates are low) but false alarms remain extremely rare.
Because this is the exact situation where K values and curvilinear ROCs most strongly diverge, if the ROCs implied by the confidence reports reflect true latent memory strengths, this is also the situation where K values would pick up largely on response criteria differences rather than genuine differences in memory strength. Since many studies use a similar task design, this raises the possibility that a large fraction of visual working memory results that rely on K values may be incorrect, overestimating the cost of higher set sizes relative to low set sizes, and particularly underestimating the performance of those participants with particularly conservative response criteria. Even more troubling is the fact that in the Balaban et al. (2019) data, a full 20% of participants at set size 4, and 10% of participants at set size 8, had 0 false alarms in the entire condition. This technically makes memory strength unknowable for these conditions and while there are methods to correct for this problem, they each rely on assumptions that may not always hold up (see Hautus, 1995).
How can we directly test whether the confidence-based ROCs reflect the true distribution of latent memory strengths? Although there are many possibilities, most depend on model fits that are often opaque and that fundamentally depend on modeling assumptions (e.g., Rouder et al., 2008). Thus, in Experiments 2, we preregistered a novel and critical test of whether K or d′ best describes true latent memory strength distributions. Here, we use a simple manipulation that takes advantage of the fact that participants tend to be very conservative at high set sizes (i.e., less likely to say “same”).
Experiment 2: A Straightforward, Confidence-Free Test of the Nature of Memory Signals
Experiment 2 takes advantage of the fact that participants are naturally conservative in responding “same” at high set sizes and makes a critical prediction about how performance should change when they are encouraged to say “same” more often. Consider a participant (gray point in Figure 9) with very few false alarms. Such participants are typical in high set size change detection experiments (see Figure 8). In signal detection terms, they are thought to have a strong response bias. In threshold model terms, they are thought to nearly always say “different” when they are “guessing.” If they could be encouraged to shift their criterion (i.e., to say “same” more often), what would happen? Signal detection theory predicts a curvilinear change in performance, such that saying “same” more often would proportionally add more hits than false alarms, because it would involve shifting the criterion to allow for saying “same” to still strong but overall slightly weaker memory signals, and strong memory signals are more likely to be generated by items that were truly seen than by items that were not seen. The curvilinearity is implied by the line of constant d′ being curvilinear (see Figure 9). Threshold models like K instead predict that a shift in criterion (i.e., responding “same” more often) would change only the responder’s guessing strategy; since participants have no idea what the answer is on such trials (because they have no information about the probed item); therefore, saying “same” more often would simply add an equal proportion of hits and false alarms to their responses (see Figure 9).
This produces a strong potential dissociation: If the equal variance signal detection model provides a better account of the underlying memory signals, encouraging more “same” responses should result in the same d′, but considerably higher K values than the normal task. This latter point can be inferred from our simulation (see Figure 9); that is, if one were to fit the threshold model (K) to the orange point in the plot, the predicted line (parallel to the diagonal line of chance performance) would be well above the line projected from the gray point. By contrast, if the threshold, guessing-based view is correct, encouraging “same” responses should move along the linear K line, and should produce a large drop in d′. This point can also be inferred from Figure 9, because if the equal variance signal detection model were fit to the red point, the corresponding projection for this model would be much lower than the original projection from the gray point.
To test this, in Experiment 2 we compare (a) performance in a standard change detection task at set size 8, with no special instructions and no requirement to report confidence with (b) performance in a matched change detection task that involves an instructional modification intended to discourage extremely conservative responding (adaptive instructions, where participants are encouraged to respond “same” more often if they have fewer false alarms than misses within a block of trials). Importantly, this design seeks to counterintuitively improve K, rather than hurt K. Although it is easy to imagine that unusual instructions could hurt performance (e.g., by making the task more confusing or more difficult), there is no natural mechanism for threshold models to predict that such instructions could improve performance relative to our baseline of a standard change detection task.
Method
The hypothesis, design, analysis plan, and exclusion criteria for this study were preregistered: https://Aspredicted.org/Blind.php?x=743fj8.
Participants
We preregistered a Bayesian analysis plan and a sequential sampling design (following the recommendations of Schönbrodt et al., 2017). In particular, we planned to initially run N = 50 nonexcluded participants for each of the two groups (Standard; Adaptive), and then calculate a Bayes factor comparing K values across the two groups. We planned to continue iterating in batches of 10 per group until our Bayes factor for the comparison of K was greater than 10 or less than 1/10th (e.g., provided 10:1 evidence for or against the null). However, we achieved this Bayes factor in our first sample of N = 50 per group, so no sequential procedure was used in practice and N = 50 per group was our final sample size. The study was conducted online using participants from the UC San Diego undergraduate pool. Our preregistered exclusion criteria were to exclude any trials where reaction times were <200 ms or >5,000 ms and exclude and replace any participants who had more than 10% of trials excluded, had a d′ < .5, or had K < 1. This resulted in the exclusion of 41 participants. This is further explained and analyzed below.
Stimuli
The same color circle as Experiment 1 was used to generate stimuli, and the change detection task was similar to that of Experiment 1, but with eight placeholder circles rather than six and all trials at set size 8. Stimuli were shown for 1,000 ms with an 800-ms delay. The shown colors and the foil were again required to be ≥15 degrees apart on the color wheel.
Procedure
There were two between-subjects experimental conditions, Normal and Adaptive. Each group performed 450 trials of a set size eight change detection task, with all changes being maximally different colors (180 degrees on the color wheel). The trials were broken into 15 blocks of 30 trials, and after each block participants could take a short break. The entire task took about 45 minutes.
In the standard-instructions group, participants simply performed this task in line with a completely standard change detection task. Participants were not instructed to use any kind of response policy, but simply told to respond “same” if they think no change occurred and “different” if they think that a change did occur.
In contrast, in the adaptive-instructions condition, everything was the same at the beginning of the experiment, with the standard instructions. However, participants were given an additional set of instructions after each block if they had more “misses” than “false alarms” in that block (of 30 trials). These instructions encouraged them to shift their criterion (e.g., respond “same” more often). In particular, they saw these instructions:
You have been saying “different” more than “same,” even though the trials are 50% same and 50% different. Focus on splitting your responses more evenly to improve your performance! To do this, do not try to just say “same” all the time: instead, try to respond “different” only if you are very sure it was different; otherwise respond “same.”
Analysis
Based on the effect size in our pilot data, we estimated the effect size at approximately a Cohen’s d of .5 and preregistered the scale of the alternative hypothesis in the Bayes factor analysis with that in mind. Thus, our Bayes factors were calculated with our preregistered Scaled-Information Bayes Factor with r = .5.
Exclusions
Forty-one of 141 participants were excluded using our preregistered criteria. These participants were excluded because we preregistered a criteria of d′ < .5 or K < 1 being unsatisfactory, because such subjects are nondiagnostic of the difference in the models (the closer a participant is to chance, the less distinction there is between a curvilinear and linear ROC). In our experience, finding this level of poor performers is relatively typical of long online studies with difficult tasks, such as the one shown here with a set size 8 memory task. However, a post hoc analysis of all participants, with no exclusions, gives a similar pattern to our main analysis (a 16% gain in K from Normal to Adaptive and a −5% difference in d′). Notably, however, the addition of many nondiagnostic participants at near chance performance level drags the effect size for the difference in K down far enough (from dz = .64 in our preregistered sample to dz = .22 in the full sample) to make the evidence nondefinitive. However, if we had planned to analyze the data this way to begin with—without exclusions of nondiagnostic participants—we would not have preregistered such a large effect size for the alternative hypothesis in the Bayes factor, nor stopped our iterated data collection plan with this number of participants. Therefore, in our view the strength of evidence favoring d′ over K is not affected in any meaningful way by the exclusions.
Results
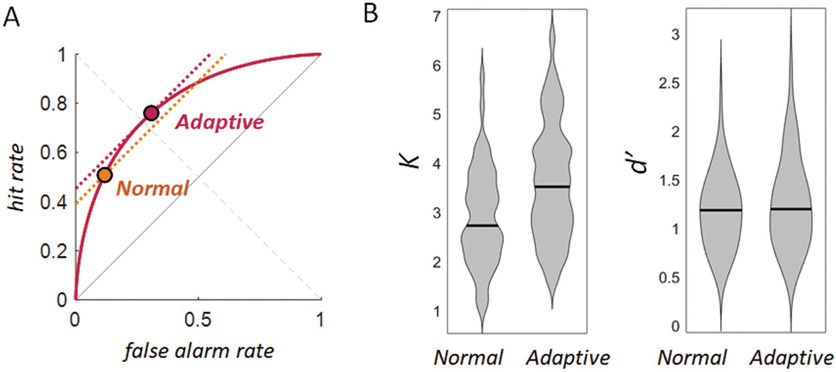
Overall, we found that individuals can increase their “working memory capacity” (as measured by K) simply by shifting their response criteria. In particular, we found a substantial gain in K values for the adaptive-instruction conditions (median gain: 29.04%) and almost no difference in d′ between groups (median gain: 1.01%; Figure 10). A Bayes factor greater than 10 is considered strong and greater than 20 is considered to be decisive evidence. The Bayes factor that the K value differed between the groups was favored by greater than 20 (BF10 = 24.43) whereas the null hypothesis of no difference between groups was favored for d′ (BF10 = .55). The same results were found when using standard frequentist statistics, with a highly reliable difference in K, t(98) = 3.19, p = .002, d = .64, and no difference in d’ between groups, t(98) = .96, p = .338, d = .19. We note here that these differences in memory estimates are based on the metrics of each measure obtained from direct transformations of the data, with no model fitting. Accordingly, these metrics are not subject to common criticisms regarding differential model flexibility or over-fitting (unlike the results of e.g., Rouder et al., 2008; which appear to arise from the particular assumptions used in the model fits: Robinson et al., 2022).
Figure 10. Results of Experiments 2.
Note. (A) The group average for normal and adaptive conditions show that the adaptive condition was effective in getting participants to respond “same” more often. The best fit d′ and best fit K lines are shown for both conditions, though because as their d′ was nearly identical, the orange d′ is obscured by the red one. (B) Violin plots of the distribution of K and d′ values for each participant in each condition. The median K value (black line) “improved” by nearly 30% with the adaptive instructions, whereas the median d′ was nearly identical between conditions.
This provides strong evidence that d′, but not K, successfully adjusts for response bias changes. It suggests that K systematically underestimates performance when responses are very conservative, as they generally are at high set sizes. It also provides a strong validation of the confidence-based ROC curves found in Experiment 1, which seem to truly reflect the latent memory signals used to make “same”“/”different” judgments. Notably, this large change in K occurs even though we did not manipulate response criteria in the “Normal” group at all. Nonetheless, the on-average conservativeness of the criteria used in standard change detection was sufficient to create this strong dissociation between K and d′.
Overall, then, Experiments 2 shows that K conflates response bias with memory, whereas d′ does not. This provides evidence both against the threshold model underlying K, but also in favor of the equal variance signal detection model (as opposed to more complex signal detection–based models that allow for guesses or lapses).
Experiment 3: Excluding Contributions From Limitless Memory Storage
Some previous work has claimed that—even with delays that are longer than the commonly accepted limitations of iconic memory (e.g., 800 ms, in Experiment 2)—a residual perceptual trace can contribute to performance thus adding to the computations and limitations of working memory alone. In theory, this could cause memory to look more continuous when it is actually discrete (e.g., Rouder et al., 2008). Thus, to test this hypothesis and to thoroughly explore the dichotomy between discrete and continuous memories, in Experiment 3, we replicated Experiment 2 but followed the methods of Rouder et al. (2008)—one of the few articles claiming evidence for threshold-like performance (though see Robinson et al., 2022)—in adding a visual mask before the change detection test.
Here, our logic was otherwise the same as in Experiment 2: We assessed the shape of the ROC curve underlying memory performance without the need for model comparisons or confidence. We used instructions that should improve performance relative to the baseline of a standard change detection task, if and only if a measure implies the wrong ROC. Because the task was harder with the masks, we used set size 6 instead of set size 8; which also allowed us to assess the generality of our conclusions with regard to set size.
Method
The hypothesis, design, analysis plan and exclusion criteria for this study were preregistered: https://aspredicted.org/DDL_5FP.
Participants
This study was conducted online using participants from the UC San Diego undergraduate pool. We expected a smaller effect size in comparing the conditions here since we expect that, at set size 6, participants should have less extreme response criterion in the standard condition, so K should underestimate their performance less-so than when working memory is taxed with eight items. However, because we were using a sequential sampling procedure, this expectation of reduced effect size also affected our sample size planning, compared with Experiment 2. In particular, we again preregistered a Bayesian analysis plan and a sequential sampling design. We again planned to initially run N = 50 nonexcluded participants for each of the two groups (Standard; Adaptive), and then calculate a Bayes factor comparing K values across the two groups. As in Experiment 2, our Bayes factors were calculated with our preregistered Scaled-Information Bayes Factor with r = .5. We continued iterating in batches of 10 per group until our Bayes factor for the comparison of K was greater than 10 or less than 1/10th (e.g., provided 10:1 evidence for or against the null). In this case, we iterated until we had N = 80 participants per group (total sample size of 160), where we achieved the required Bayes factor. Our preregistered exclusion criteria were to exclude any trials where reaction times were <200 ms or >5,000 ms and exclude and replace any participants who had more than 10% of trials excluded, had a d′ < .5, or had K < 1. This resulted in the exclusion of 36 participants. This is further explained and analyzed below.
Stimuli
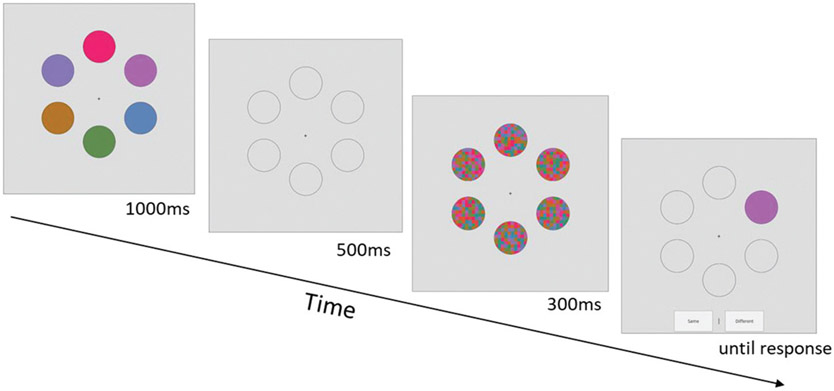
The change detection task was similar to that of Experiments 2, but with six placeholder circles and all trials at set size 6. Stimuli were shown for 1,000 ms with a 500-ms delay and then a 300-ms visual mask (see Figure 11). The shown colors and the foil were again required to be ≥15 degrees apart on the color wheel.
Figure 11. Task in Experiment 3.
Note. Participants saw six colored circles, then after a brief delay a visual mask appeared before the change detection test display appeared. Here, as in Experiments 2, participants simply responded whether the probed item was the same or different; compared with the item that was shown in that location (a “same” response would elicit a hit for the above example).
Procedure
There were two between-subjects experimental conditions, Normal and Adaptive. Each group performed 450 trials of a set size 6 change detection task, with all changes being maximally different colors (180 degrees on the color wheel). The trials were broken into 15 blocks of 30 trials, and after each block participants could take a short break. The entire task took about 45 minutes.
In the standard-instructions group, participants simply performed this task in line with a completely standard change detection task. Participants were not instructed to use any kind of response strategy and were simply told to respond “same” if they think no change occurred and “different” if they think that a change did occur. In contrast, in the adaptive-instructions condition, everything was the same at the beginning of the experiment, with the standard instructions. Here, at the end of a particular block, participants were given an additional set of instructions if they had more “misses” than “false alarms” in that block (30 trials). These instructions encouraged them to shift their criterion from conservative to neutral (e.g., respond “same” more often). In particular, they saw these instructions:
You have been saying “different” more than “same,” even though the trials are 50% same and 50% different. Focus on splitting your responses more evenly to improve your performance! To do this, do not try to just say “same” all the time: instead, try to respond “different” only if you are very sure it was different; otherwise respond “same.”
Exclusions
Thirty-six of 196 participants were excluded using our preregistered criteria. These participants were excluded because we preregistered a criteria of d′ < .5 or K < 1 being unsatisfactory, because such subjects are nondiagnostic of the difference in the models (the closer a participant is to chance, the less distinction there is between a curvilinear and linear ROC). Once again, a post hoc analysis of all participants, with no exclusions, produces a similar pattern to our main analysis (a 13.6% gain in K from Normal to Adaptive and a decrease of −5.8% in d′).
Results
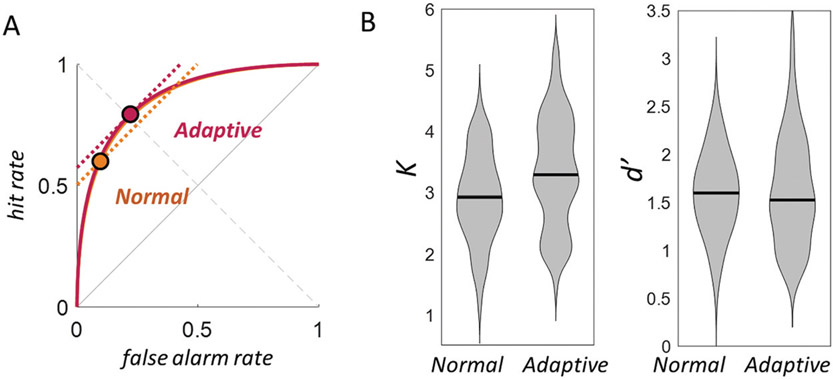
As in Experiments 2, we again found that individuals can increase their “working memory capacity” (as measured by K) simply by shifting their response criteria. In particular, we found a substantial gain in K values for the adaptive-instruction conditions (median gain: 14%) with no reliable difference in d′ (median change: −4%; see Figure 12). A Bayes factor greater than 10 is considered strong and greater than 20 is considered to be decisive evidence. The Bayes factor that the K value differed between the groups was favored by greater than 20 (BF10 = 27.83) whereas the null hypothesis of no difference between groups was favored for d′ (BF10 = .31). The same results were found when using standard frequentist statistics, with a highly reliable difference in K, t(158) = −3.16, p = .002, d = .50, and no difference in d′ between groups, t(158) = −.30, p = .765, d = .05.
Figure 12. Results of Experiment 3.
Note. (A) The group average for normal and adaptive conditions show that the adaptive condition was effective in getting participants to respond “same” more often. The best fit d′ and best fit K lines are shown for both conditions, though because their d′ was nearly identical, the orange d′ is obscured by the red one. (B) Violin plots of the distribution of K and d′ values for each participant in each condition. The median K value (black line) “improved” by nearly 30% with the adaptive instructions, whereas the median d′ was nearly identical between conditions.
Although the results for the improvement in K were statistically significant in the frequentist test—even with the original N = 50 groups, t(98) = −2.60, p = .011, d = .52—our sequential sampling design led to much more decisive evidence as we increased the samples to meet our preregistered Bayes criterion. At each sequential sampling step (N = 50, 60, and 70 per group), the Bayes factor was 6.3, 7.9, and 9.9, respectively; which is considerably lower than the strength of evidence that we found in our final sample (N = 80; 27.83 to 1). The Bayes factors for d′ favored the null for all four sample steps .37, .34, .32, and .31, respectively.
Overall, we replicated Experiment 2 and found that visual masks do not obscure the continuous nature of visual working memories. Once again, we found strong evidence that d′, but not K, successfully adjusts for response bias changes, and that K systematically underestimates performance when responses are very conservative, as they generally are at high set sizes. Overall, then, Experiment 3 again shows that K conflates response bias with memory, whereas d′ does not. This again provides evidence both against the threshold model underlying K, but also in favor of the equal variance signal detection model (as opposed to more complex signal detection-based models that allow for guesses or lapses).
General Discussion
Across three experiments, we examined the nature of the latent memory signals used in change detection tasks and the implications for proper measurement of performance in change detection. We compared a theory that sees these signals as continuous in strength—signal detection theory—with a threshold-based view, where memory signals are all-or-none. In Experiment 1, we found evidence from confidence reports that memory was continuous in strength, with support for equal variance signal detection models, suggesting not only that signal detection theory was a more accurate measure of performance but also that there is no need for additional assumptions about guesses or lapses to be added to the simplest instantiation of signal detection theory. We then tested a critical implication of this result in Experiment 2: that, whereas d′ should remain constant, K values should systematically underestimate performance in standard change detection experiments for participants who rarely false alarm. We found strong evidence for this hypothesis, with a Bayes factor of 24 to 1 in favor of the finding that K is not fixed across simple instruction changes. This provides strong evidence against threshold-based measures like K because, while it is possible to imagine that instructional changes could hurt performance, there is no natural mechanism for threshold models to predict that such instructions could increase memory capacity. Furthermore, d′ was nearly constant, which suggests that the confidence-based ROCs observed in Experiment 1 straightforwardly underlie performance in Experiments 2, and that a single decision axis that applies to all trials is sufficient to explain performance without added assumptions about guesses or lapses. We then replicated Experiments 2 at a different set size and with a visual mask in Experiment 3 and again found strong evidence that d′ is fixed across response criterion changes whereas K is not. Thus, our findings suggest that visual working memories are best thought of as continuous in strength and best analyzed in terms of signal detection measures, and that there is no need for added guess or lapse parameters to account for change detection performance even at the highest set sizes (see also Brady et al., 2021; Robinson et al., 2020; Schurgin et al., 2020).
In terms of proper measurement of performance, we find that K values are not a good match to the actual shape of ROCs in change detection since ROCs are curvilinear and are thus best characterized by d′, not K. Unfortunately, this means nearly all conclusions based on K values are potentially suspect, because they do not properly discount differences in response criteria and thus measure a combination of response criteria and memory performance. Furthermore, Experiment 2 shows this effect is not subtle: Comparing a completely typical response criteria to one that is more symmetric (with respect to misses and false alarms) results in an underestimate of performance when using K by 30%. Conditions that induce even more conservative responding, or that include individual subjects with more conservative criteria, will be even more influenced by the failure of K to correctly adjust performance for response criteria.
How much of K is a measure of response bias rather than a memory measure under typical conditions? A multiple regression, comparing K values computed in all subjects in Experiments 2 and 3’s normal, nonadaptive condition, with the true measure of memory strength that matches the ROC (d′) and with response criterion (c), suggests that K values are about 1/3rd measures of response bias and two-thirds measures of memory strength (after centering and scaling, a participant’s K is best predicted by a .77 wt on d′ and a −.45 wt on c, both p < .001). Thus, under standard change detection conditions, a participant’s K is extremely strongly influenced by that participant’ s response bias, and K is nearly as much a measure of response bias as it is a measure of memory performance.
Throughout the article, we focus on K values because they have been, and continue to be, extremely common in visual working memory experiments (see Alvarez & Cavanagh, 2004, 2008; Brady & Alvarez, 2015; Endress & Potter, 2014; Forsberg et al., 2020; Fukuda & Vogel, 2019; Irwin, 2014; Luria & Vogel, 2011; Ngiam et al., 2019; Norris et al., 2019; Pailian et al., 2020; Schurgin & Brady, 2019; Shipstead et al., 2014; Sligte et al., 2008; Unsworth et al., 2014; Vogel & Machizawa, 2004; Woodman & Vogel, 2008). However, percent correct and corrected hit rate (i.e., hits minus false alarms) also predict linear ROC curves (e.g., Swets, 1986) and thus are also invalid measures of memory performance according to our data. Another popular metric of performance in related tasks is A’ (e.g., Fisher & Sloutsky, 2005; Hudon et al., 2009; Lind & Bowler, 2009; MacLin & MacLin, 2004; Poon & Fozard, 1980; Potter et al., 2002), and although this measure is claimed to be “atheoretical” and nonparametric by its proponents (Hudon et al., 2009; Pollack & Norman, 1964; Snodgrass & Corwin, 1988), in truth there exists no measure of memory derived from a single hit and false alarm rate that is atheoretical and nonparametric (Macmillan & Creelman,1996). Unlike K, A’ predicts ROC curves that are curvilinear, though differently curvilinear than d′ (Stanislaw & Todorov, 1999), and so may be less likely to confound response bias and memory strength than K. Unlike d′, however, which is based on theoretically plausible assumptions (latent memory signals for old and new items are distributed as equal-variance Gaussian distributions with different means), A’ embraces theoretical assumptions that are implausible when made explicit (e.g., Macmillan & Creelman, 1996; Pastore et al., 2003; Wixted, 2020).
Overall, our results suggest d′ should be the preferred measurement metric for change detection data, as d′ was constant across changes in response bias (Experiment 2 and 3) and matched the shape of the ROC (in Experiment 1). This provided evidence not only in favor of signal detection models but also in favor of the simplest kind of single-process signal detection model, without any additional need for lapses or guesses.
However, even though the current studies find evidence for equal variance signal detection models, and thus d′, it may not be the case that an equal variance signal detection model is always appropriate (see also Robinson et al., 2020). It may be that our experiments are ideal for finding equal variance because memory resources tend to be split relatively evenly between items in this task: we ask participants to split attention equally between all items by making them equally likely to be tested; by using simple stimuli that are all approximately equally attention-grabbing and thus likely to be encoded and maintained with roughly equal resources; and by presenting these stimuli only briefly. The use of d′ may not be valid in other conditions, like sequential encoding (Brady & Störmer, 2022; Smith et al., 2016; Robinson et al., 2020) or when items are differentially prioritized (Emrich et al., 2017). Thus, in general, two-alternative forced-choice, rather than change detection, is likely a better “default” method for a range of working memory tasks (see Brady et al., 2021).
Another possibility is that continuity in memory strength is related to the stimulus space; that, by using categorical stimuli, instead of continuous spaces (like we’ ve done here with color), one might find evidence for discreteness in memory. However, recent work which has used discrete, categorical stimuli in visual working memory has also found curvilinearity in the ROC and rejected discrete models as adequately explaining the data (e.g., Robinson et al., 2020, used eight discrete colors). In general, the notion of discrete or categorical stimuli and discrete or all-or-none memory strength are different notions of discreteness: even for discrete stimuli, like words, memory strength is usually thought to be continuous (e.g., Mickes et al., 2007).
Although we have found strong evidence in favor of curvilinear ROC curves here, previous work that investigated ROC curves in change detection has found mixed results. Confidence-based ROC curves have reliably been found to be curvilinear and approximately in line with equal variance signal detection models (e.g., in Robinson et al., 2020, and visually in Xie & Zhang, 2017)6; however, results from response bias manipulations across a small range of values have provided data that were initially taken to support threshold views (Rouder et al., 2008). Interestingly, when followed up on, other results have provided more mixed results, with less certain support for threshold models of memory (Donkin et al., 2014, 2016). Our own reanalysis of the data from these studies suggest that when model comparisons are properly calibrated to ensure accurate model recovery from simulated data, they all provide support for signal-detection views and are largely in agreement with confidence ROCs (Robinson et al., 2022). Experiment 2 and 3 are unique in taking an approach that is independent of any model comparisons to ask whether changes in response bias are naturally accounted for by threshold and/or signal detection views. The results from this experiment provided strong support for the curvilinear nature of ROCs and thus for d′ as the standard metric of visual working memory performance when using change detection tasks.
Above and beyond the question of whether K measures (Cowan, 2001; Pashler, 1988; Rouder et al., 2011) are valid, it is important to ask whether curvilinear ROCs—as we observe in both confidence and response bias manipulations—sufficient to reject high-threshold views altogether? There is substantial convergent evidence to suggest that they are. When considering confidence-based ROCs at a single level of performance at a time, it is possible to construct high-threshold models of curvilinear ROCs. For example, Province and Rouder (2012) propose that even when participants are, in truth, completely certain of their response, they may nevertheless give a low confidence response because the experimenter, by presenting a confidence scale, is making “an implicit demand to distribute responses” across the provided scale. However, in the context of mixed set size trials like the current Experiment 1, this account cannot predict the data we have observed here. This is because participants do not, in fact, spread their responses at all at set size 1, and instead do so only at the highest set sizes.
Even more compelling, however, is that if memories were truly high-threshold and it is only confidence reports that are noisy and lead to biased estimates of memory, this account predicts that in Experiments 2—where there is no confidence elicited—K, and not d′, would be fixed across our response criteria manipulation. Instead, we again found strong evidence for d′, not K as the measure which appropriately accounts for response bias. Altogether, our results are deeply incompatible with threshold-based views in several ways. They are not only consistent with explanations based on signal detection models but are directly in line with a priori predictions from such models (as evidenced by our preregistration). For example, our results align with recent work by Winiger et al. (2021), who used a novel critical test with minimal assumptions to test between discrete-slot and signal detection models in a change detection paradigm. Like us, these researchers found evidence for pure resource models of visual-working memory using a test that eschews the limitations of fitting models to empirical ROCs. Our work adds to and extends these findings by directly underscoring the profound practical limitations, as well as the detrimental consequences for theory building that arise when researchers use K to quantify the capacity of visual working memory.
In this context, we also highlight a major misconception in the working memory literature, which is that discrete-slot models are equivalent to or can be used as “proxies” for mixture models of working memory. The fact that pure discrete-slot models are implicitly endorsed in change detection paradigms through the use of K metrics, likely reflects a heuristic assumption that these metrics are “good enough” approximations of mixture models. Importantly, however, this assumption is misguided, because one cannot choose which fundamental aspects of a model to embrace, and ultimately leads to a situation where response bias is heavily conflated with memory performance, as we have shown here. Although both threshold and mixture models are consistent with item-limits in working memory, threshold models and mixture models that postulate variations in precision differ fundamentally; they predict different ROC curves and they predict different distributions of errors in delayed estimation tasks (Xie & Zhang, 2017). Indeed, the observation that precision varies monotonically with set size is why threshold-based discrete-slot models were ruled out over a decade ago in delayed estimation tasks in favor of, at minimum, mixture models that treat memory as variable in strength up to a certain number of items (e.g., Pratte et al., 2017; Zhang & Luck, 2008), or more recently most successful models have been completely continuous models without additional assumptions about complete failures (e.g., Schurgin et al., 2020; van den Berg et al., 2012).
We suspect that most working memory researchers would endorse the view that working memory representations do not vary in precision. Nevertheless, that is precisely the view they implicitly endorse by using K, and this is one fundamental point of our article: Measures of unobservable cognitive processes are constrained by theory, and researchers must carefully consider the theoretical assumptions on which their metrics are based before using them (for in-depth discussion of this issue see: Falmagne & Doble, 2016; Falmagne & Narens, 1983; Irvine, 2021; Kellen et al., 2021; Narens, 2002, 2007; Roberts, 1985; Roberts & Rosenbaum, 1986; van Frassen, 2008). We believe a failure to do so will only perpetuate invalid measurement practices in the psychological and cognitive sciences, and perpetuate the “replication crisis” in psychology (for similar points in recent articles see, e.g., Brady et al., 2021; Kellen et al., 2021; Regenwetter & Robinson, 2017; Rotello et al., 2015; Schimmack, 2021).
In effect, our work highlights that a choice between these models and metrics is not simply a fickle theoretical concern; instead, the finding that K fails to dissociate variations in memory strength from variations in response bias, whereas d′ does not, entails that a choice between these models can qualitatively change the inferences researchers draw regarding how memory strength varies as a function of individual differences or experimental manipulations. Overall, this suggests that, as in long-term recognition memory, visual working memory researchers should consider memories as continuous in strength and use signal detection to measure performance.
There are potentially broad implications for the fact that K values confound response bias with memory performance, as K values underlie many critical conclusions about visual working memory (Alvarez & Cavanagh, 2004, 2008; Brady & Alvarez, 2015; Chunharas et al., 2019; Endress & Potter, 2014; Eriksson et al., 2015; Forsberg et al., 2020; Fukuda & Vogel, 2019; Fukuda et al., 2010; Fukuda, Kang, & Woodman, 2016; Fukuda, Woodman, & Vogel, 2016; Hakim et al., 2019; Irwin, 2014; Luria & Vogel, 2011; Ngiam et al., 2019; Norris et al., 2019; Pailian et al., 2020; Schurgin & Brady, 2019; Shipstead et al., 2014; Sligte et al., 2008; Unsworth et al., 2014; Unsworth et al., 2015; Vogel & Machizawa, 2004; Woodman & Vogel, 2008). For example, one major research domain for which our results could have profound implications is the study of how visual working memory capacity relates to global indices of cognitive function (Luck & Vogel, 1997; Vogel & Awh, 2008). As a case in point, much of the foundational work that examines the relationship between visual working memory limits and general intelligence has used K in change detection paradigms to quantify visual working memory limits (e.g., Fukuda et al., 2010). Such studies tend to use high memory loads with the goal of placing sufficiently high memory demands to detect individual differences in visual working memory capacity. Our simulations and empirical results reveal that these types of memory demands are precisely the kind that can lead to changes in response bias, and that variations in K estimates lead to spurious conclusions as to the source of these purported correlations with intelligence. Given that much prior works suggests that there are substantial individual differences in response bias (Aminoff et al., 2012; Kantner & Lindsay, 2012; Miller & Kantner, 2020), it follows that a substantial part of the shared variance between intelligence and VWM capacity in such studies could instead reflect an association between intelligence and response bias. An analogous criticism has been repeatedly made in the study of the relationship between intelligence and cognitive control, where it remains unclear whether associations between intelligence and performance on cognitive control (e.g., Eriksen Flanker tasks) reveal shared variance between executive function and intelligence, or shared variance between individual differences in third variables, such as response policies (e.g., speed/accuracy tradeoffs in cognitive control tasks) and intelligence (e.g., Burgoyne & Engle, 2020; Frischkorn & Schubert, 2018). We are not attempting to promote the view that all of the shared variance between intelligence and visual working memory capacity is due to response bias. Instead, we view this as an open empirical question that needs to be examined further with alternative measures of visual working memory capacity. More broadly, we emphasize that much of the work on individual differences and VWM capacity should be reevaluated with a much heavier focus on proper measurement.
Overall, we show that in change detection, K values substantially confound response bias with memory performance and should not be used. Instead, d′ should be the preferred metric of change detection performance. More broadly, this work shows how using the proper metric to understand memory performance is critical, since incorrect metrics can give extremely misleading conclusions (e.g., underestimating performance by ~30%), with potentially broad implications for the literature. Furthermore, our work suggests that an equal variance signal detection model—with no additional guess or lapse processes—is sufficient to explain change detection performance at high set sizes.
Public Significance Statement.
Visual working memory is an essential, capacity-limited system that has been linked to many cognitive abilities such as fluid intelligence and reading comprehension. Because of its importance, researchers need valid measures of its capacity that separate true differences in memory performance from other factors, like participants’ response strategies. Here we show that the most common measure of visual working memory capacity does not accurately separate response strategy from memory performance. We demonstrate this by showing we can artificially inflate estimates of capacity using this metric with a simple instruction change, which should have no effect on memory. We show an alternative metric is more accurate and suggest it should be used instead. These findings call into question research that has used this flawed metric to make connections between working memory capacity and other cognitive functions.
Acknowledgments
For funding we acknowledge the National Institute of Health and National Science Foundation, for the National Research Service Award Fellowship (1F32MH127823-01) for Maria M. Robinson; NSF BCS-2146988 to Timothy F. Brady, and NSF GRFP to Jamal R. Williams.
Footnotes
In the current work we will not consider the more complicated scenario where all items reappear and all could have changed, though the fundamental concern with threshold modes like K raised here applies equally in such experiments.
To be clear, this assumption applies to trials where the participant is “on task.” There could be a small set of trials where participants’ eyes were genuinely closed or they clicked accidentally, which would result in true guesses, but such true 0 signal trials are likely very rare (e.g., traditional psychophysical curve fitting generally assumes approximately a 1%—and no more than a 5%—lapse rate; Wichmann & Hill, 2001).
Note that it is possible to test other aspects of the K model simultaneously with testing its shape, like how fixed it is across set sizes (as done by Rouder et al., 2008). However, this confounds both aspects of the model—whether ROCs are linear or curvilinear, and whether performance drops as expected across set sizes (Robinson et al., 2022)—and what we are interested in is the shape of the ROC within a set size, because this is what decides whether the K metric, the d′ metric, or neither are valid.
It has been shown across many situations that participants’ criteria tend to be more stable across conditions than expected by a strict likelihood ratio account (where a given confidence level always matches a precise percent correct; e.g., Stretch & Wixted, 1998), and this is especially true with interleaved trials, like the current experiment (Rahnev, 2021). Signal detection models with this basic property all predict high confidence false alarms and misses.
Threshold accounts have alternatively attempted to explain high-confidence false alarms by assuming that they reflect implicit demand characteristics to use the entire confidence scale; however, when tested empirically, this assumption appears unsubstantiated (seen here, Figure 6, and in Delay & Wixted, 2021).
Note that these authors do not attempt to fit an equal variance signal detection model, but their ROC is visually consistent with such a model.
References
- Adam KCS, & Vogel EK (2017). Confident failures: Lapses of working memory reveal a metacognitive blind spot. Attention, Perception & Psychophysics, 79(5), 1506–1523. 10.3758/s13414-017-1331-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adam KCS, Vogel EK, & Awh E (2017). Clear evidence for item limits in visual working memory. Cognitive Psychology, 97, 79–97. 10.1016/j.cogpsych.2017.07.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alloway TP, & Alloway RG (2010). Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology, 106(1), 20–29. 10.1016/j.jecp.2009.11.003 [DOI] [PubMed] [Google Scholar]
- Alvarez GA, & Cavanagh P (2004). The capacity of visual short-term memory is set both by visual information load and by number of objects. Psychological Science, 15(2), 106–111. 10.1111/j.0963-7214.2004.01502006.x [DOI] [PubMed] [Google Scholar]
- Alvarez GA, & Cavanagh P (2008). Visual short-term memory operates more efficiently on boundary features than on surface features. Perception & Psychophysics, 70(2), 346–364. 10.3758/pp.70.2.346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aminoff EM, Clewett D, Freeman S, Frithsen A, Tipper C, Johnson A, Grafton ST, & Miller MB (2012). Individual differences in shifting decision criterion: A recognition memory study. Memory & Cognition, 40(7), 1016–1030. 10.3758/s13421-012-0204-6 [DOI] [PubMed] [Google Scholar]
- Awh E, Barton B, & Vogel EK (2007). Visual working memory represents a fixed number of items regardless of complexity. Psychological Science, 18(7), 622–628. 10.1111/j.1467-9280.2007.01949.x [DOI] [PubMed] [Google Scholar]
- Baddeley AD (2000). Short-term and working memory. In Tulving E, & Craik FIM (Eds.), The oxford handbook of memory (pp. 77–99). Oxford University Press. [Google Scholar]
- Baddeley AD, Allen RJ, & Hitch GJ (2011). Binding in visual working memory: The role of the episodic buffer. Neuropsychologia, 49(6), 1393–1400. 10.1016/j.neuropsychologia.2010.12.042 [DOI] [PubMed] [Google Scholar]
- Balaban H, Fukuda K, & Luria R (2019). What can half a million change detection trials tell us about visual working memory? Cognition, 191, 103984. 10.1016/j.cognition.2019.05.021 [DOI] [PubMed] [Google Scholar]
- Bays PM (2015). Spikes not slots: Noise in neural populations limits working memory. Trends in Cognitive Sciences, 19(8), 431–438. [DOI] [PubMed] [Google Scholar]
- Bays PM, Catalao RF, & Husain M (2009). The precision of visual working memory is set by allocation of a shared resource. Journal of Vision, 9(10), 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamin AS, Diaz M, & Wee S (2009). Signal detection with criterion noise: Applications to recognition memory. Psychological Review, 116(1), 84–115. 10.1037/a0014351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamin AS, Tullis JG, & Lee JH (2013). Criterion noise in ratings-based recognition: Evidence from the effects of response scale length on recognition accuracy. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39(5), 1601–1608. 10.1037/a0031849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady TF, & Alvarez GA (2015). No evidence for a fixed object limit in working memory: Spatial ensemble representations inflate estimates of working memory capacity for complex objects. Journal of Experimental Psychology: Learning, Memory, and Cognition, 41(3), 921–929. 10.1037/xlm0000075 [DOI] [PubMed] [Google Scholar]
- Brady TF, & Störmer VS (2022). The role of meaning in visual working memory: Real-world objects, but not simple features, benefit from deeper processing. Journal of Experimental Psychology: Learning, Memory, and Cognition, 48(7), 942–958. 10.1037/xlm0001014 [DOI] [PubMed] [Google Scholar]
- Brady TF, Konkle T, & Alvarez GA (2009). Compression in visual working memory: Using statistical regularities to form more efficient memory representations. Journal of Experimental Psychology: General, 138(4), 487–502. 10.1037/a0016797 [DOI] [PubMed] [Google Scholar]
- Brady TF, Konkle T, & Alvarez GA (2011). A review of visual memory capacity: Beyond individual items and toward structured representations. Journal of Vision, 11(5), 4. 10.1167/11.5.4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady T, Robinson MM, Williams JR, & Wixted J (2021). Measuring memory is harder than you think: A crisis of measurement in memory research. PsyArxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgoyne AP, & Engle RW (2020). Attention control: A cornerstone of higher-order cognition. Current Directions in Psychological Science, 29(6), 624–630. 10.1177/0963721420969371 [DOI] [Google Scholar]
- Chunharas C, Rademaker RL, Sprague TC, Brady TF, & Serences JT (2019). Separating memoranda in depth increases visual working memory performance. Journal of Vision, 19(1), 4. 10.1167/19.1.4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24(1), 87–114. 10.1017/S0140525X01003922 [DOI] [PubMed] [Google Scholar]
- Daneman M, & Carpenter PA (1980). Individual differences in working memory and reading. Journal of Verbal Learning and Verbal Behavior, 19(4), 450–466. 10.1016/S0022-5371(80)90312-6 [DOI] [Google Scholar]
- DeCarlo LT (2010). On the statistical and theoretical basis of signal detection theory and extensions: Unequal variance, random coefficient, and mixture models. Journal of Mathematical Psychology, 54(3), 304–313. 10.1016/j.jmp.2010.01.001 [DOI] [Google Scholar]
- Delay CG, & Wixted JT (2021). Discrete-state versus continuous models of the confidence-accuracy relationship in recognition memory. Psychonomic Bulletin & Review, 28(2), 556–564. 10.3758/s13423-020-01831-7 [DOI] [PubMed] [Google Scholar]
- Donkin C, Kary A, Tahir F, & Taylor R (2016). Resources masquerading as slots: Flexible allocation of visual working memory. Cognitive Psychology, 85, 30–42. 10.1016/j.cogpsych.2016.01.002 [DOI] [PubMed] [Google Scholar]
- Donkin C, Tran SC, & Nosofsky R (2014). Landscaping analyses of the ROC predictions of discrete-slots and signal-detection models of visual working memory. Attention, Perception & Psychophysics, 76(7), 2103–2116. 10.3758/s13414-013-0561-7 [DOI] [PubMed] [Google Scholar]
- Emrich SM, Lockhart HA, & Al-Aidroos N (2017). Attention mediates the flexible allocation of visual working memory resources. Journal of Experimental Psychology: Human Perception and Performance, 43(7), 1454–1465. 10.1037/xhp0000398 [DOI] [PubMed] [Google Scholar]
- Endress AD, & Potter MC (2014). Large capacity temporary visual memory. Journal of Experimental Psychology: General, 143(2), 548–565. 10.1037/a0033934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson J, Vogel EK, Lansner A, Bergström F, & Nyberg L (2015). Neurocognitive architecture of working memory. Neuron, 88(1), 33–46. 10.1016/j.neuron.2015.09.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falmagne JC, & Doble C (2016). Meaningfulness as a “principle of theory construction”. Journal of Mathematical Psychology, 75, 59–67. [Google Scholar]
- Falmagne JC, & Narens L (1983). Scales and meaningfulness of quantitative laws. Synthese, 55, 287–325. [Google Scholar]
- Fawcett T (2006). An introduction to ROC analysis. Pattern Recognition Letters, 27(8), 861–874. [Google Scholar]
- Fisher AV, & Sloutsky VM (2005). When induction meets memory: Evidence for gradual transition from similarity-based to category-based induction. Child Development, 76(3), 583–597. 10.1111/j.1467-8624.2005.00865.x [DOI] [PubMed] [Google Scholar]
- Forsberg A, Johnson W, & Logie RH (2020). Cognitive aging and verbal labeling in continuous visual memory. Memory & Cognition, 48(7), 1196–1213. 10.3758/s13421-020-01043-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D, Suchow JW, & Alvarez GA (2012). Variability in the quality of visual working memory. Nature Communications, 3(1), 1229. 10.1038/ncomms2237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frischkorn GT, & Schubert AL (2018). Cognitive models in intelligence research: Advantages and recommendations for their application. Journal of Intelligence, 6(3), 34. 10.3390/jintelligence6030034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, & Vogel EK (2019). Visual short-term memory capacity predicts the “bandwidth” of visual long-term memory encoding. Memory & Cognition, 47(8), 1481–1497. 10.3758/s13421-019-00954-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Kang MS, & Woodman GF (2016). Distinct neural mechanisms for spatially lateralized and spatially global visual working memory representations. Journal of Neurophysiology, 116(4), 1715–1727. 10.1152/jn.00991.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Vogel E, Mayr U, & Awh E (2010). Quantity, not quality: The relationship between fluid intelligence and working memory capacity. Psychonomic Bulletin & Review, 17(5), 673–679. 10.3758/17.5.673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Woodman GF, & Vogel EK (2016). Individual differences in visual working memory capacity: Contributions of attentional control to storage. In Jolicoeur P, Lefebvre C, & Martinez-Trujillo J (Eds.), Mechanisms of sensory working memory: Attention and performance XXV (pp. 105–119). Elsevier. [Google Scholar]
- Glanzer M, & Bowles N (1976). Analysis of the word-frequency effect in recognition memory. Journal of Experimental Psychology: Human Learning and Memory, 2(1), 21–31. 10.1037/0278-7393.2.1.21 [DOI] [Google Scholar]
- Glanzer M, Kim K, Hilford A, & Adams JK (1999). Slope of the receiver-operating characteristic in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 25(2), 500–513. 10.1037/0278-7393.25.2.500 [DOI] [Google Scholar]
- Hakim N, Adam KCS, Gunseli E, Awh E, & Vogel EK (2019). Dissecting the neural focus of attention reveals distinct processes for spatial attention and object-based storage in visual working memory. Psychological Science, 30(4), 526–540. 10.1177/0956797619830384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hautus MJ (1995). Corrections for extreme proportions and their biasing effects on estimated values of d′. Behavior Research Methods, Instruments, & Computers, 27(1), 46–51. 10.3758/BF03203619 [DOI] [Google Scholar]
- Hautus MJ, Macmillan NA, & Rotello CM (2008). Toward a complete decision model of item and source recognition. Psychonomic Bulletin & Review, 15(5), 889–905. 10.3758/PBR.15.5.889 [DOI] [PubMed] [Google Scholar]
- Heathcote A (2003). Item recognition memory and the receiver operating characteristic. Journal of Experimental Psychology: Learning, Memory, and Cognition, 29(6), 1210–1230. 10.1037/0278-7393.29.6.1210 [DOI] [PubMed] [Google Scholar]
- Honig M, Ma WJ, & Fougnie D (2020). Humans incorporate trial-to-trial working memory uncertainty into rewarded decisions. Proceedings of the National Academy of Sciences of the United States of America, 117(15), 8391–8397. 10.1073/pnas.1918143117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudon C, Belleville S, & Gauthier S (2009). The assessment of recognition memory using the Remember/Know procedure in amnestic mild cognitive impairment and probable Alzheimer’s disease. Brain and Cognition, 70(1), 171–179. 10.1016/j.bandc.2009.01.009 [DOI] [PubMed] [Google Scholar]
- Irvine E (2021). The role of replication studies in theory building. Perspectives on Psychological Science, 16(4), 844–853. 10.1177/1745691620970558 [DOI] [PubMed] [Google Scholar]
- Irwin DE (2014). Short-term memory across eye blinks. Memory, 22(8), 898–906. 10.1080/09658211.2013.847959 [DOI] [PubMed] [Google Scholar]
- Jang Y, Mickes L, & Wixted JT (2012). Three tests and three corrections: Comment on Koen and Yonelinas (2010). Journal of Experimental Psychology: Learning, Memory, and Cognition, 38(2), 513–523. 10.1037/a0025880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jang Y, Wixted JT, & Huber DE (2009). Testing signal-detection models of yes/no and two-alternative forced-choice recognition memory. Journal of Experimental Psychology: General, 138(2), 291–306. 10.1037/a0015525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kantner J, & Lindsay DS (2012). Response bias in recognition memory as a cognitive trait. Memory & Cognition, 40(8), 1163–1177. 10.3758/s13421-012-0226-0 [DOI] [PubMed] [Google Scholar]
- Kellen D, & Klauer KC (2015). Signal detection and threshold modeling of confidence-rating ROCs: A critical test with minimal assumptions. Psychological Review, 122(3), 542–557. 10.1037/a0039251 [DOI] [PubMed] [Google Scholar]
- Kellen D, Davis-Stober CP, Dunn JC, & Kalish ML (2021). The problem of coordination and the pursuit of structural constraints in psychology. Perspectives on Psychological Science, 16(4), 767–778. 10.1177/1745691620974771 [DOI] [PubMed] [Google Scholar]
- Kellen D, Winiger S, Dunn JC, & Singmann H (2021). Testing the foundations of signal detection theory in recognition memory. Psychological Review, 128(6), 1022–1050. 10.1037/rev0000288 [DOI] [PubMed] [Google Scholar]
- Koen JD, Barrett FS, Harlow IM, & Yonelinas AP (2017). The ROC Toolbox: A toolbox for analyzing receiver-operating characteristics derived from confidence ratings. Behavior Research Methods, 49(4), 1399–1406. 10.3758/s13428-016-0796-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krantz DH (1969). Threshold theories of signal detection. Psychological Review, 76(3), 308–324. 10.1037/h0027238 [DOI] [PubMed] [Google Scholar]
- Lind SE, & Bowler DM (2009). Recognition memory, self-other source memory, and theory-of-mind in children with autism spectrum disorder. Journal of Autism and Developmental Disorders, 39(9), 1231–1239. 10.1007/s10803-009-0735-2 [DOI] [PubMed] [Google Scholar]
- Luce RD (1963). A threshold theory for simple detection experiments. Psychological Review, 70(1), 61–79. 10.1037/h0039723 [DOI] [PubMed] [Google Scholar]
- Luck SJ, & Vogel EK (1997). The capacity of visual working memory for features and conjunctions. Nature, 390(6657), 279–281. 10.1038/36846 [DOI] [PubMed] [Google Scholar]
- Luria R, & Vogel EK (2011). Shape and color conjunction stimuli are represented as bound objects in visual working memory. Neuropsychologia, 49(6), 1632–1639. 10.1016/j.neuropsychologia.2010.11.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma WJ, Husain M, & Bays PM (2014). Changing concepts of working memory. Nature Neuroscience, 17(3), 347–356. 10.1038/nn.3655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacLin OH, & MacLin MK (2004). The effect of criminality on face attractiveness, typicality, memorability and recognition. North American Journal of Psychology, 6, 145–154. [Google Scholar]
- Macmillan NA, & Creelman CD (1996). Triangles in ROC space: History and theory of “nonparametric” measures of sensitivity and response bias. Psychonomic Bulletin & Review, 3(2), 164–170. 10.3758/BF03212415 [DOI] [PubMed] [Google Scholar]
- Macmillan NA, & Creelman CD (2005). Detection theory: A user’s guide. Psychology press. [Google Scholar]
- Malmberg KJ (2002). On the form of ROCs constructed from confidence ratings. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28(2), 380–387. 10.1037/0278-7393.28.2.380 [DOI] [PubMed] [Google Scholar]
- McClelland JL, & Chappell M (1998). Familiarity breeds differentiation: A subjective-likelihood approach to the effects of experience in recognition memory. Psychological Review, 105(4), 724–760. 10.1037/0033-295X.105.4.734-760 [DOI] [PubMed] [Google Scholar]
- Mickes L, Wixted JT, & Wais PE (2007). A direct test of the unequal-variance signal detection model of recognition memory. Psychonomic Bulletin & Review, 14(5), 858–865. 10.3758/BF03194112 [DOI] [PubMed] [Google Scholar]
- Miller MB, & Kantner J (2020). Not all people are cut out for strategic criterion shifting. Current Directions in Psychological Science, 29(1), 9–15. 10.1177/0963721419872747 [DOI] [Google Scholar]
- Miyake A, & Shah P (Eds.). (1999). Models of working memory: Mechanisms of active maintenance and executive control. Cambridge University Press. 10.1017/CBO9781139174909 [DOI] [Google Scholar]
- Narens L (2002). A meaningful justification for the representational theory of measurement. Journal of Mathematical Psychology, 46(6), 746–768. [Google Scholar]
- Narens L (2007). Introduction to the Theories of Measurement and Meaningfulness and the Use of Symmetry in Science. Psychology Press. [Google Scholar]
- Ngiam WXQ, Khaw KLC, Holcombe AO, & Goodbourn PT (2019). Visual working memory for letters varies with familiarity but not complexity. Journal of Experimental Psychology: Learning, Memory, and Cognition, 45(10), 1761–1775. 10.1037/xlm0000682 [DOI] [PubMed] [Google Scholar]
- Norris DG, Hall J, & Gathercole SE (2019). Can short-term memory be trained? Memory & Cognition, 47(5), 1012–1023. 10.3758/s13421-019-00901-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pailian H, Simons DJ, Wetherhold J, & Halberda J (2020). Using the flicker task to estimate visual working memory storage capacity. Attention, Perception & Psychophysics, 82(3), 1271–1289. 10.3758/s13414-019-01809-1 [DOI] [PubMed] [Google Scholar]
- Pashler H (1988). Familiarity and visual change detection. Perception & Psychophysics, 44(4), 369–378. 10.3758/BF03210419 [DOI] [PubMed] [Google Scholar]
- Pastore RE, Crawley EJ, Berens MS, & Skelly MA (2003). Nonparametric” A′ and other modern misconceptions about signal detection theory. Psychonomic Bulletin & Review, 10(3), 556–569. 10.3758/BF03196517 [DOI] [PubMed] [Google Scholar]
- Pollack I, & Norman DA (1964). A non-parametric analysis of recognition experiments. Psychonomic Science, 1(1–12), 125–126. 10.3758/BF03342823 [DOI] [Google Scholar]
- Poon LW, & Fozard JL (1980). Age and word frequency effects in continuous recognition memory. Journal of Gerontology, 35(1), 77–86. 10.1093/geronj/35.1.77 [DOI] [PubMed] [Google Scholar]
- Potter MC, Staub A, Rado J, & O’Connor DH (2002). Recognition memory for briefly presented pictures: The time course of rapid forgetting. Journal of Experimental Psychology: Human Perception and Performance, 28(5), 1163–1175. 10.1037/0096-1523.28.5.1163 [DOI] [PubMed] [Google Scholar]
- Pratte MS, Park YE, Rademaker RL, & Tong F (2017). Accounting for stimulus-specific variation in precision reveals a discrete capacity limit in visual working memory. Journal of Experimental Psychology: Human Perception and Performance, 43(1), 6–17. 10.1037/xhp0000302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Province JM, & Rouder JN (2012). Evidence for discrete-state processing in recognition memory. Proceedings of the National Academy of Sciences of the United States of America, 109(36), 14357–14362. 10.1073/pnas.1103880109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rademaker RL, Tredway CH, & Tong F (2012). Introspective judgments predict the precision and likelihood of successful maintenance of visual working memory. Journal of Vision, 12(13), 21. 10.1167/12.13.21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahnev D (2021). A robust confidence-accuracy dissociation via criterion attraction. Neuroscience of Consciousness, 2021(1), niab039. 10.1093/nc/niab039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahnev D, Desender K, Lee AL, Adler WT, Aguilar-Lleyda D, Akdoğan B, Arbuzova P, Atlas LY, Balci F, Bang JW, Bègue I, Birney DP, Brady TF, Calder-Travis J, Chetverikov A, Clark TK, Davranche K, Denison RN, Dildine TC, … Zylberberg A (2020). The confidence database. Nature Human Behaviour, 4(3), 317–325. 10.1038/s41562-019-0813-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regenwetter M, & Robinson MM (2017). The construct-behavior gap in behavioral decision research: A challenge beyond replicability. Psychological Review, 124(5), 533–550. 10.1037/rev0000067 [DOI] [PubMed] [Google Scholar]
- Roberts F (1985). Applications of the theory of meaningfulness to psychology. Journal of Mathematical Psychology, 29(3), 311–332. 10.1016/0022-2496(85)90011-2 [DOI] [Google Scholar]
- Roberts F, & Rosenbaum Z (1986). Scale type, meaningfulness and the possible psychophysical laws. Mathematical Social Sciences, 12(1), 77–95. 10.1016/0165-4896(86)90048-X [DOI] [Google Scholar]
- Robinson MM, Benjamin AS, & Irwin DE (2020). Is there a K in capacity? Assessing the structure of visual short-term memory. Cognitive Psychology, 121, 101305. 10.1016/j.cogpsych.2020.101305 [DOI] [PubMed] [Google Scholar]
- Robinson MM, Williams JR, & Brady TF (2022). What does it take to falsify a psychological theory? A case study on recognition models of visual working-memory. Preprint on PsyArXiv. 10.31234/osf.io/7an3x [DOI] [Google Scholar]
- Rotello CM, Heit E, & Dubé C (2015). When more data steer us wrong: Replications with the wrong dependent measure perpetuate erroneous conclusions. Psychonomic Bulletin & Review, 22(4), 944–954. 10.3758/s13423-014-0759-2 [DOI] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Cowan N, Zwilling CE, Morey CC, & Pratte MS (2008). An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences of the United States of America, 105(16), 5975–5979. 10.1073/pnas.0711295105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Morey CC, & Cowan N (2011). How to measure working memory capacity in the change detection paradigm. Psychonomic Bulletin & Review, 18(2), 324–330. 10.3758/s13423-011-0055-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schimmack U (2021). The validation crisis in psychology. Meta-Psychology, 5. 10.15626/MP.2019.1645 [DOI] [Google Scholar]
- Schönbrodt FD, Wagenmakers EJ, Zehetleitner M, & Perugini M (2017). Sequential hypothesis testing with Bayes factors: Efficiently testing mean differences. Psychological Methods, 22(2), 322–339. 10.1037/met0000061 [DOI] [PubMed] [Google Scholar]
- Schurgin MW (2018). Visual memory, the long and the short of it: A review of visual working memory and long-term memory. Attention, Perception & Psychophysics, 80(5), 1035–1056. 10.3758/s13414-018-1522-y [DOI] [PubMed] [Google Scholar]
- Schurgin MW, & Brady TF (2019). When “capacity” changes with set size: Ensemble representations support the detection of across-category changes in visual working memory. Journal of Vision, 19(5), 3. 10.1167/19.5.3 [DOI] [PubMed] [Google Scholar]
- Schurgin MW, Wixted JT, & Brady TF (2020). Psychophysical scaling reveals a unified theory of visual memory strength. Nature Human Behaviour, 4(11), 1156–1172. 10.1038/s41562-020-00938-0 [DOI] [PubMed] [Google Scholar]
- Shiffrin RM, & Steyvers M (1997). A model for recognition memory: REM-retrieving effectively from memory. Psychonomic Bulletin & Review, 4(2), 145–166. 10.3758/BF03209391 [DOI] [PubMed] [Google Scholar]
- Shipstead Z, Lindsey DRB, Marshall RL, & Engle RW (2014). The mechanisms of working memory capacity: Primary memory, secondary memory, and attention control. Journal of Memory and Language, 72, 116–141. 10.1016/j.jml.2014.01.004 [DOI] [Google Scholar]
- Sligte IG, Scholte HS, & Lamme VA (2008). Are there multiple visual short-term memory stores? PLoS ONE, 3(2), e1699. 10.1371/journal.pone.0001699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith PL, Lilburn SD, Corbett EA, Sewell DK, & Kyllingsæk S (2016). The attention-weighted sample-size model of visual short-term memory: Attention capture predicts resource allocation and memory load. Cognitive Psychology, 89, 71–105. [DOI] [PubMed] [Google Scholar]
- Snodgrass JG, & Corwin J (1988). Pragmatics of measuring recognition memory: Applications to dementia and amnesia. Journal of Experimental Psychology: General, 117(1), 34–50. 10.1037/0096-3445.117.1.34 [DOI] [PubMed] [Google Scholar]
- Spanton RW, & Berry CJ (2020). The unequal variance signal-detection model of recognition memory: Investigating the encoding variability hypothesis. Quarterly Journal of Experimental Psychology: Human Experimental Psychology, 73(8), 1242–1260. 10.1177/1747021820906117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanislaw H, & Todorov N (1999). Calculation of signal detection theory measures. Behavior Research Methods, Instruments, & Computers, 31(1), 137–149. [DOI] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R, & McKoon G (2012). Evaluating the unequal-variance and dual-process explanations of zROC slopes with response time data and the diffusion model. Cognitive Psychology, 64(1–2), 1–34. 10.1016/j.cogpsych.2011.10.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starr A, Srinivasan M, & Bunge SA (2020). Semantic knowledge influences visual working memory in adults and children. PLoS ONE, 15(11), e0241110. 10.1371/journal.pone.0241110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stretch V, & Wixted JT (1998). On the difference between strength-based and frequency-based mirror effects in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 24(6), 1379–1396. 10.1037/0278-7393.24.6.1379 [DOI] [PubMed] [Google Scholar]
- Swets JA (1986). Indices of discrimination or diagnostic accuracy: Their ROCs and implied models. Psychological Bulletin, 99(1), 100–117. 10.1037/0033-2909.99.1.100 [DOI] [PubMed] [Google Scholar]
- Unsworth N, Fukuda K, Awh E, & Vogel EK (2014). Working memory and fluid intelligence: Capacity, attention control, and secondary memory retrieval. Cognitive Psychology, 71, 1–26. 10.1016/j.cogpsych.2014.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unsworth N, Fukuda K, Awh E, & Vogel EK (2015). Working memory delay activity predicts individual differences in cognitive abilities. Journal of Cognitive Neuroscience, 27(5), 853–865. 10.1162/jocn_a_00765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Berg R, Shin H, Chou WC, George R, & Ma WJ (2012). Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences of the United States of America, 109(22), 8780–8785. 10.1073/pnas.1117465109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Frassen B (2008). Scientific representation: Paradoxes of perspective. Oxford University Press. 10.1093/acprof:oso/9780199278220.001.0001 [DOI] [Google Scholar]
- Vogel EK, & Awh E (2008). How to exploit diversity for scientific gain: Using individual differences to constrain cognitive theory. Current Directions in Psychological Science, 17(2), 171–176. [Google Scholar]
- Vogel EK, & Machizawa MG (2004). Neural activity predicts individual differences in visual working memory capacity. Nature, 428(6984), 748–751. 10.1038/nature02447 [DOI] [PubMed] [Google Scholar]
- Wichmann FA, & Hill NJ (2001). The psychometric function: I. Fitting, sampling, and goodness of fit. Perception & Psychophysics, 63(8), 1293–1313. 10.3758/BF03194544 [DOI] [PubMed] [Google Scholar]
- Wickelgren WA, & Norman DA (1966). Strength models and serial position in short-term recognition memory. Journal of Mathematical Psychology, 3(2), 316–347. 10.1016/0022-2496(66)90018-6 [DOI] [Google Scholar]
- Wickens TD (2001). Elementary signal detection theory. Oxford University Press. 10.1093/acprof:oso/9780195092509.001.0001 [DOI] [Google Scholar]
- Wilken P, & Ma WJ (2004). A detection theory account of change detection. Journal of Vision, 4(12), 1120–1135. 10.1167/4.12.11 [DOI] [PubMed] [Google Scholar]
- Winiger S, Singmann H, & Kellen D (2021). Bias in confidence: A critical test for discrete-state models of change detection. Journal of Experimental Psychology: Learning, Memory, and Cognition, 47(3), 387–401. 10.1037/xlm0000959 [DOI] [PubMed] [Google Scholar]
- Wixted JT (2007). Dual-process theory and signal-detection theory of recognition memory. Psychological Review, 114(1), 152–176. 10.1037/0033-295X.114.1.152 [DOI] [PubMed] [Google Scholar]
- Wixted JT (2020). The forgotten history of signal detection theory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46(2), 201–233. 10.1037/xlm0000732 [DOI] [PubMed] [Google Scholar]
- Woodman GF, & Vogel EK (2008). Selective storage and maintenance of an object’s features in visual working memory. Psychonomic Bulletin & Review, 15(1), 223–229. 10.3758/PBR.15.1.223 [DOI] [PubMed] [Google Scholar]
- Xie W, & Zhang W (2017). Discrete item-based and continuous configural representations in visual short-term memory. Visual Cognition, 25(1–3), 21–33. 10.1080/13506285.2017.1339157 [DOI] [Google Scholar]
- Yonelinas AP (2002). The nature of recollection and familiarity: A review of 30 years of research. Journal of Memory and Language, 46(3), 441–517. 10.1006/jmla.2002.2864 [DOI] [Google Scholar]
- Yonelinas AP, & Parks CM (2007). Receiver operating characteristics (ROCs) in recognition memory: A review. Psychological Bulletin, 133(5), 800–832. 10.1037/0033-2909.133.5.800 [DOI] [PubMed] [Google Scholar]
- Zhang W, & Luck SJ (2008). Discrete fixed-resolution representations in visual working memory. Nature, 453(7192), 233–235. 10.1038/nature06860 [DOI] [PMC free article] [PubMed] [Google Scholar]