Extending the Hearing-Aid Speech Perception Index (HASPI): Keywords, sentences, and context

Abstract

The Hearing-Aid Speech Perception Index version 2 (HASPI v2) is a speech intelligibility metric derived by fitting subject responses scored as the proportion of complete sentences correct. This paper presents an extension of HASPI v2, denoted by HASPI w2, which predicts proportion keywords correct for the same datasets used to derive HASPI v2. The results show that the accuracy of HASPI w2 is nearly identical to that of HASPI v2. The values produced by HASPI w2 and HASPI v2 also allow the comparison of proportion words correct and sentences correct for the same stimuli. Using simulation values for speech in additive noise, a model of context effects for words combined into sentences is developed and accounts for the loss of intelligibility inherent in the impaired auditory periphery. In addition, HASPI w2 and HASPI v2 have a small bias term at poor signal-to-noise ratios; the model for context effects shows that the residual bias is reduced in converting from proportion keywords to sentences correct but is greatly magnified when considering the reverse transformation.

I. INTRODUCTION

The design and evaluation of speech intelligibility metrics depends on the stimuli and subject scores to which the metrics are fit. Metrics have been fit to a variety of stimulus types, including sentences (Ma and Loizou, 2011; Jørgensen and Dau, 2011; Biberger and Ewert, 2016; Kates and Arehart, 2021), words (Christiansen et al., 2010; Taal et al., 2011; Van Kuyk et al., 2018), and phonemes (Steeneken and Houtgast, 2002; Elhilali et al., 2003; Moncada-Torres et al., 2017). Metrics based on speech envelope modulation (Elhilali et al., 2003; Taal et al., 2011; Jørgensen and Dau, 2011; Biberger and Ewert, 2016; Van Kuyk et al., 2018; Kates and Arehart, 2021) will also depend on the length of the speech segments as estimates of low-rate envelope modulation will be less accurate for short segments (e.g., phonemes or isolated words) than for longer segments (e.g., words embedded in sentences or complete sentences) due to the loss of spectral resolution (Payton et al., 2002; Payton and Shrestha, 2013). Furthermore, even for longer stimuli, such as sentences, a model trained on word recognition will differ from one trained on complete sentences resulting from the number of words combined in the sentences and the influence of linguistic context (Boothroyd and Nittrouer, 1988; Bronkhorst et al., 2002). Thus, comparing different metrics requires knowledge of the stimulus type, stimulus duration, context, and how the subject results have been scored.

Many of the metrics cited above have been trained on words embedded in sentences or complete sentences correct, and a procedure for converting from one set of results to the other would lead to more accurate comparisons of metric predictions. In particular, several sentence-level corpora used for intelligibility testing, such as the Institute of Electrical and Electronics Engineers (IEEE) sentences (Rothauser, 1969), Hearing-in-Noise Test (HINT) sentences (Nilsson et al., 1994), the German sentence test (Kollmeier and Wesselkamp, 1997), and the Danish sentence intelligibility test (Nielsen and Dau, 2009), can be scored in terms of keywords correct or complete sentences correct. In a research setting, testing a metric trained on data scored one way (e.g., keywords correct) and then comparing its accuracy to a metric trained using a different scoring procedure (e.g., sentences correct) will lead to invalid results because the modeled psychometric functions are dependent on the data used to train the metrics. For potential clinical applications, adjusting a hearing aid to achieve a targeted speech recognition threshold based on one scoring approach (e.g., keywords correct) may lead to different settings than if the recognition threshold is based on a different scoring approach (e.g., sentences correct).

The Hearing-Aid Speech Perception Index version 2 (HASPI v2; Kates and Arehart, 2021, 2022) considered in this paper fits the outputs of an auditory model to proportion sentences correct data from five separate datasets comprising (1) additive noise and nonlinear distortion, (2) frequency shifting, (3) noise suppression using an ideal binary mask (IBM) algorithm, (4) speech in reverberation, and (5) noise vocoded speech. The original datasets were also scored in terms of keywords correct. This paper presents a retrospective analysis in which the constituent components of HASPI v2 are, instead, fit to the proportion keywords correct from the five experiments. The new analysis gives HASPI w2, where the “w2” represents version 2 modified for words correct. It extends the range of experimental results for which the HASPI metric is valid and provides an accurate procedure for comparing predictions for words correct with sentences correct.

HASPI w2 and HASPI v2 are intrusive metrics that compare the output of an auditory model having a clean reference signal as its input to the output of an auditory model having the degraded signal being evaluated as its input. The auditory model for the reference signal reproduces the characteristics of a normal periphery, whereas the model for the degraded signal reproduces the behavior of the impaired periphery associated with the simulated listener's hearing loss. After passing the reference and degraded signals through the associated peripheral models, the HASPI calculation extracts the time-frequency envelope modulation from the peripheral model outputs. The envelope modulation is passed through a modulation-rate filterbank and then fit to the listeners' intelligibility scores using an ensemble of neural networks. The accuracy of HASPI w2 is compared to the original keyword data and HASPI v2, and the equivalent psychometric functions are presented for speech in additive speech-shaped noise.

Context effects (Boothroyd and Nittrouer, 1988; Olsen et al., 1997; Bronkhorst et al., 2002; Smits and Zekveld, 2021) were also explored by comparing the HASPI metrics because they are derived to match keyword (HASPI w2) and sentence (HASPI v2) intelligibility scores from the same experiments. The context model proposed by Boothroyd and Nittrouer (1988) is considered in this paper. The model treats context as having two aspects: the recognition of speech components with and without context (e.g., words in isolation as compared to words in a sentence) and the recognition of the whole that is built from the constituent components (e.g., complete sentences compared to the embedded keywords). The datasets used to train HASPI do not include words in isolation, precluding the evaluation of the first of these aspects. However, having intelligibility scores for keywords and complete sentences allows the evaluation of the Boothroyd and Nittrouer (1988) model for the whole compared to its component parts, and a modified version of the Boothroyd and Nittrouer (1988) model is derived for the transformation of keywords correct values into complete sentence values. The transformation involves a conversion factor that is similar to the proficiency factor applied to the Speech Intelligibility Index (SII) in which the predicted intelligibility is reduced to correct for the effects of hearing loss (Pavlovic et al., 1986; Ching et al., 1998; Woods et al., 2013).

The remainder of the paper begins with a summary of the five datasets used to derive the HASPI v2 and HASPI w2 intelligibility metrics. The constituent building blocks that comprise the metrics are then described. The overall accuracy of HASPI w2 in fitting keywords correct data is presented and compared to the accuracy of HASPI v2 in fitting complete sentences correct, and the predictions from the two metrics are compared for speech in additive noise. The transformation from keywords to complete sentences correct is next derived using a modified version of the Boothroyd and Nittrouer (1988) approach that accounts for the effects of a simulated hearing loss, and the behavior of the transformation is explored in Sec. V.

II. INTELLIGIBILITY DATA

HASPI w2 and HASPI v2 (Kates and Arehart, 2021, 2022) are fit to five datasets comprising (1) additive noise and nonlinear distortion, (2) frequency shifting, (3) noise suppression using an IBM algorithm, (4) speech in reverberation, and (5) noise vocoded speech. The datasets are described in Kates and Arehart (2021) and are summarized below. The speech intelligibility in these experiments was scored as keywords correct and complete sentences correct. HASPI v2 is fit to the sentences correct data, whereas in this paper, HASPI w2 is fit to keywords correct. For all of the experiments, the stimuli were presented monaurally over headphones. The sentences for the normal-hearing (NH) listeners were presented at 65 dB sound pressure level (SPL) except for the reverberation stimuli at 70 dB SPL. The sentences for hearing-impaired (HI) listeners were amplified using the National Acoustics Laboratories Revised (NAL-R) linear gain rule (Byrne and Dillon, 1986).

A. Additive noise and distortion

The additive noise and nonlinear distortion dataset is described in Kates and Arehart (2005). Taking part in the experiment were 13 NH listeners and 9 HI listeners. The stimuli were the HINT materials (Nilsson et al., 1994) as spoken by a male talker. Each sentence was combined with the additive long-term average speech spectrum (LTASS) noise provided with the HINT materials or processed using symmetric peak clipping or symmetric center clipping. The eight signal-to-noise ratio (SNR) values for the additive noise ranged from 30 to −5 dB plus speech in quiet. The clipping thresholds were determined from the cumulative magnitude histograms of the signal samples for each sentence at the 22.5-kHz sampling rate. Eight peak-clipping thresholds were used, ranging from no clipping to infinite clipping, and eight center-clipping thresholds were used, ranging from no clipping to 98% of the cumulative histogram level.

B. Frequency shifting

The frequency shifting dataset is described in Souza et al. (2013) and Arehart et al. (2013). Taking part in the experiment were 14 NH listeners and 26 HI listeners. The stimuli were IEEE sentences (Rothauser, 1969) spoken by a female talker. The sentences were combined with multi-talker babble at SNRs ranging from −10 to 10 dB or used without any interference after which the noise-free or noisy speech was processed using frequency shifting.

Frequency shifting was applied to the speech using a sinusoidal modeling approach (McAulay and Quatieri, 1986). The signal was first passed through a pair of complementary five-pole Butterworth infinite impulse response (IIR) lowpass and highpass filters. The low-frequency band was used without any further processing to reduce audible distortion while the high-frequency band was shifted downward in frequency using sinusoidal modeling. For the modeling, the amplitude, phase, and frequency of the ten highest peaks in the high-frequency band were extracted from the signal using 50% overlapped 6-ms von Hann windows followed by a 24-ms fast Fourier transform (FFT). The high-frequency peaks were then resynthesized using the measured amplitude and phase values while the frequencies were reassigned to the desired lower values (Aguilera Muñoz et al., 1999). The processing output was the unmodified low-frequency band combined with the sinusoids, representing the shifted high-frequency peaks. The frequency shifting used cutoff frequencies of 1, 1.5, or 2 kHz combined with frequency compression ratios of 1.5:1, 2:1, or 3:1. A control condition having no frequency shifting was also included in the experiment.

C. Ideal binary mask noise suppression

The IBM noise suppression dataset is described in Arehart et al. (2015). Taking part in the experiment were 7 NH listeners and 30 HI listeners. The stimuli were IEEE sentences (Rothauser, 1969) spoken by a female talker. The sentences were combined with multi-talker babble at SNRs ranging from −18 to 12 dB in steps of 6 dB or used without any interference. The noise-free or noisy speech was then processed through the noise-suppression algorithm.

The IBM noise suppression (Kjems et al., 2009; Ng et al., 2013) used a 64-band gammatone auditory filterbank (Patterson et al., 1995). Time frames having a 20-ms duration with a 50% overlap were used for the processing in each frequency band. The local SNR was then computed for each time-frequency cell, where a cell is defined as one time frame in one frequency band, and the SNR was computed using the separate speech and noise powers. If the local SNR was 0 dB or greater, the cell was assigned a mask decision of one, otherwise, the cell was assigned a decision of zero. Errors were also introduced into the mask by randomly flipping a percentage (0%, 10%, or 30%) of the decisions from zero to one or from one to zero. The binary mask pattern was next transformed into gain values with a mask set to one given a gain of zero  dB and a mask set to zero given a gain of either −10 or −100 dB. The signal, after being multiplied by the gain assigned in each cell, was returned to the time domain using a time-reversed gammatone filterbank followed by summation across the 64 frequency bands.

D. Reverberation

The reverberation dataset is described in Muralimanohar (2018). Ten NH listeners and nine HI listeners took part in the experiment. The stimuli were IEEE sentences (Rothauser, 1969) spoken by three male and three female talkers. The sentences were combined with reverberation from four rooms having T₆₀ reverberation times ranging from 627 ms to 3 s after which the reverberant speech was passed through a nine-band linear-phase auditory filterbank. The speech envelope in each band was then extracted using the Hilbert transform followed by a linear-phase lowpass filter having a cutoff of 30 Hz.

Several processing conditions were compared. These conditions included clean speech having no reverberation and speech with reverberation for the four rooms. The clean and reverberant speech was also noise vocoded. Additional modifications included the following: raising the reverberant speech envelope to a power of either 1.2 or two in all nine bands, raising the envelope to a power in each band chosen to minimize the mean-squared error (MMSE) match between the envelope of the reverberant speech and the clean speech, and restoring the envelope in each band to match that of the clean speech. The speech was then passed through the filterbank a second time to remove out-of-band modulation distortion products, and the output signal was formed by summing the signals across the nine frequency bands.

E. Noise vocoder

The noise vocoder dataset is described in Anderson (2010). Ten NH listeners and ten HI listeners took part in the experiment. The stimuli were IEEE sentences (Rothauser, 1969) spoken by a male and a female talker. The sentences were used without interference or combined with multi-talker babble at SNRs of 18 and 12 dB. The speech without or with babble was passed through a 32-band linear-phase auditory filterbank, and varying numbers of contiguous high-frequency bands were vocoded while the remaining bands at lower frequencies were presented as unmodified noisy speech.

For the vocoding, the envelope of the speech (without or with babble) was extracted using the Hilbert transform followed by a 300-Hz lowpass filter. The vocoder used either Gaussian noise in each frequency band or low-noise noise (Kohlrausch et al., 1997) in which the envelope fluctuations were reduced by dividing the Gaussian noise in each frequency band by its own envelope. The noise vocoding was applied starting with the highest-frequency bands and working lower in frequency two bands at a time. The vocoded signals went from no bands vocoded to the upper 16 bands vocoded with this latter case corresponding to a vocoder highpass frequency of 1.6 kHz. The vocoded speech was then passed through the filterbank a second time to remove out-of-band modulation distortion products, and the root mean squared (RMS) level of the processed output signal in each frequency band was matched to that of the input speech. The signals were next summed across the frequency bands to produce the output signal.

The noise vocoder modifies the speech temporal fine structure (TFS) while preserving the envelope and causes only a small reduction in intelligibility. The vocoder dataset was included in the HASPI training to ensure a degree of immunity in the metrics to TFS modifications that do not impact intelligibility.

III. INTELLIGIBILITY METRIC

Aside from the change in training data from sentences to keywords, the processing components used to create HASPI w2 are identical to those used for HASPI v2 (Kates and Arehart, 2021, 2022). Both metrics are intrusive; they compare the output of a model of impaired hearing having a degraded signal as its input to the output of an auditory model of normal hearing having a clean reference signal as its input. There are three processing stages: (1) model of the auditory periphery, (2) extraction of time-frequency envelope modulation from the peripheral outputs, and (3) fitting the envelope modulation to the subject intelligibility scores via an ensemble of neural networks.

A. Peripheral model

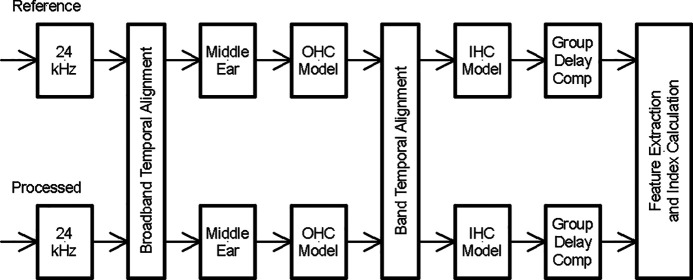
The processing block diagram for the peripheral model is presented in Fig. 1. The model operates at a 24-kHz sampling rate. Temporal alignment of the degraded and reference signals is provided initially for the broadband signal and subsequently for the signals in each auditory band. The peripheral model includes a middle ear filter (Kates, 1991) followed by a 32-band gammatone filterbank (Cooke, 1993; Patterson et al., 1995) that spans center frequencies from 80 to 8000 Hz. The auditory filter bandwidths are increased for hearing loss (Moore and Glasberg, 1983) and signals above 50 dB SPL in each auditory band (Baker and Rosen, 2002, 2006). Dynamic-range compression corresponding to outer hair-cell (OHC) motion (Ruggero et al., 1997) is applied to the outputs of the auditory filters; hearing loss ascribed to OHC damage elevates the compression threshold and reduces the compression ratio. After the OHC compression, the signals in each band are converted to dB re: auditory threshold with sounds below threshold set to a lower limit of 0 dB sensation level (SL). Hearing loss ascribed to inner hair-cell (IHC) damage is represented as additional signal attenuation. IHC firing-rate adaptation (Harris and Dallos, 1979) is then applied using a rapid adaptation time constant of 2 ms and short-time adaptation time constant of 60 ms. The last processing step is compensation for the relative time delays associated with the gammatone filters (Wojtczak et al., 2012).

FIG. 1.

The block diagram illustrating the processing stages used in HASPI w2 and HASPI v2 to compare the processed speech signal to the clean reference.

B. Envelope modulation analysis

The envelope modulation analysis (Kates and Arehart, 2021, 2022) starts with the dB SL envelopes in each auditory band produced by the peripheral models. The analysis compares the modulation of the degraded signal passed through the impaired periphery to that of the reference signal passed through the normal periphery. The envelopes in each band are first lowpass filtered at 320 Hz and subsampled at 2560 Hz. At each subsampled time interval, the envelope values over the 32 auditory bands give the log spectrum on an auditory frequency scale. The short-time spectrum is fit with five basis functions ranging ½ cycle of a cosine to 2½ cycles, spanning the spectrum from 80 to 8000 Hz. These basis functions applied to the log spectrum correspond to mel-frequency cepstral coefficients (Mitra et al., 2012) and are also related to the principal components for short-time speech spectra (Zahorian and Rothenberg, 1981).

At this point in the analysis, we have five cepstral coefficient sequences, that is, sequences over time of each of the five basis functions fit to the short-time spectra. The five sequences are each passed through a set of ten modulation-rate filters. The filters have center frequencies ranging from 2 to 256 Hz and Q values of 1.5 (Dau et al., 1997; Ewert and Dau, 2000; Ewert et al., 2002). Each of the 50 filtered cepstral coefficient sequences for the degraded speech is compared with the corresponding sequence for the reference speech using normalized cross-covariance. The cross-covariances for the five basis functions at each modulation rate are similar to each other (Kates and Arehart, 2015), therefore, the cross-covariance values are averaged over the basis functions to provide a set of ten averaged outputs, one at each modulation rate.

C. Neural network ensemble

The final stage in the HASPI calculation is fitting the cepstral coefficient cross-covariances to the subject intelligibility data. For HASPI w2, these data are the proportion keywords correct while for HASPI v2, they were the proportion sentences correct; in either case, the target values span [0,1].

An ensemble of ten neural networks was used to fit HASPI w2. Each network had ten inputs, which are the averaged covariances from the modulation filters used in the time-frequency envelope modulation analysis. One hidden layer with four neurons was used, and the output layer comprised a single neuron. A sigmoid activation function was used for all of the layers, which provided a bound between zero and one to match the range of the listener intelligibility scores. Training for the neural networks used basic backpropagation with a mean-squared error loss function (Rumelhart et al., 1986; Werbos, 1990), and each neural network was initialized to an independent set of random weights.

Each of the five datasets was assigned comparable importance in fitting the metric to the intelligibility scores. The NH and HI test conditions and associated scores were replicated an integral number of times to give approximately the same number of data points for each listener group for each experiment. A total of 72 116 sample vectors was created using this procedure, and 50 iterations of the data were used to train each of the neural networks.

The outputs of the ten neural networks were combined using bootstrap aggregation (“bagging”) (Breiman, 1996). Each of the neural networks was trained using a subset of the data selected with replacement (Efron and Gong, 1983; Breiman, 1996), where the final predicted value is the average of the outputs produced by the ten separate networks. The bagging approach reduces the estimator error variance (Kittler, 1998) and provides improved immunity to overfitting (Krogh and Sollich, 1997; Maclin and Opitz, 1997). The average of ten neural networks is sufficient to provide the main benefits of bagging in reducing overfitting (Hansen and Salamon, 1990; Breiman, 1996; Opitz and Maclin, 1999).

IV. RESULTS

A. HASPI w2 intelligibility predictions

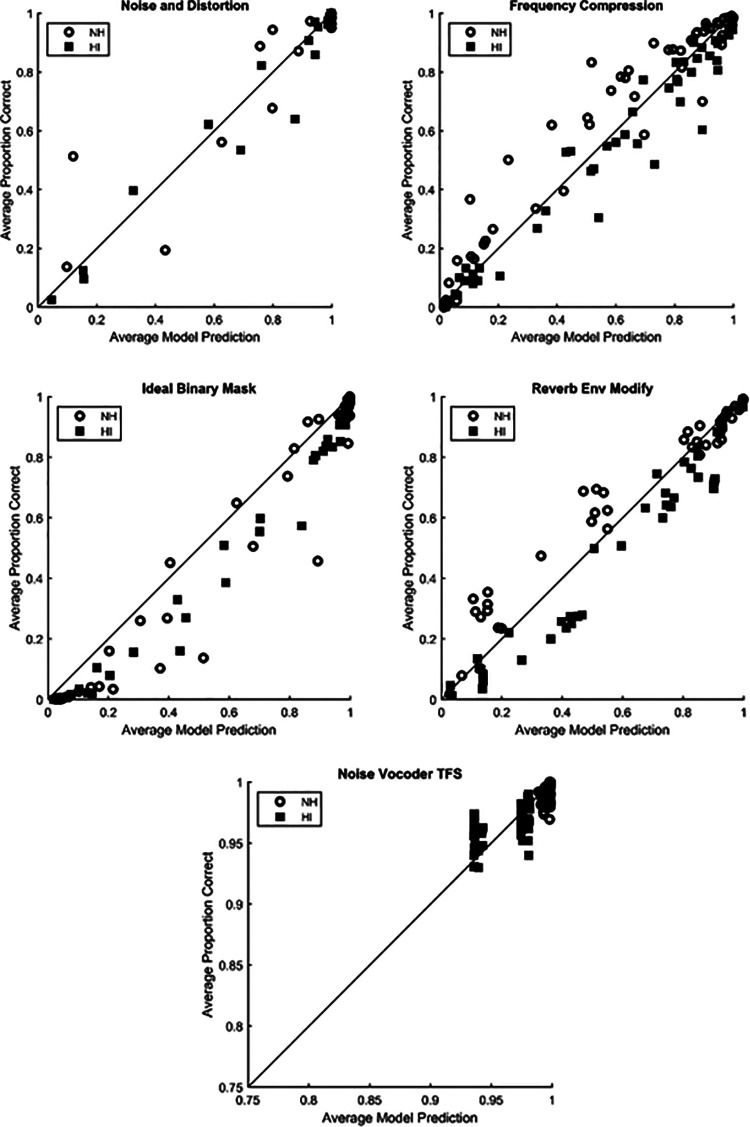
Scatterplots for the proportion keywords correct predictions are presented in Fig. 2. Each intelligibility experiment is represented by a separate scatterplot, identified by the plot title, and each data point represents one processing condition for that experiment averaged over repetitions and subjects. The HASPI w2 keyword prediction is plotted along the x axis, and the averaged listener proportion keywords correct is plotted along the y axis. The NH listener group is indicated by the open circles, and the HI group is indicated by the filled squares. The diagonal line represents perfect agreement of the predictions with the listener scores; points above the line indicate predicted intelligibility that is lower than the average listener score, and points below the line indicate predicted intelligibility that is higher than the average listener score. A low RMS error will produce points close to the diagonal line, and a high Pearson correlation coefficient will give points lying tightly along a line even if that line is not coincident with the diagonal.

FIG. 2.

Scatterplots for HASPI w2. Each point represents the model prediction compared to the listener keyword correct intelligibility scores for a processing condition averaged over all of the listeners and stimulus repetitions for that condition. Data for NH listeners are plotted using the open circles and data for HI listeners are plotted using filled squares. The different experiments are identified in the plot titles.

The scatterplot for the noise and distortion dataset shows similar numbers of points above and below the diagonal for the NH and HI listeners, indicating minimal net bias in the predictions for both groups. The NH data, however, show two potential outliers at low predicted intelligibility. One point corresponds to additive multi-talker babble at a SNR of −5 dB, where the metric predicts intelligibility much lower than reported by the listeners, and the other point corresponds to center-clipping distortion with a 95% threshold (i.e., most of the speech has been replaced by zeros), where the metric predicts higher intelligibility than observed in the experiment. Corresponding outliers, however, do not appear in the HI data.

The scatterplot for the frequency compression dataset shows more points above the diagonal for the NH listeners and more points below the diagonal for the HI group, whereas the scatterplot for the IBM noise suppression shows the majority of points for NH and HI participants below the diagonal. Potential outliers for the NH listeners in the IBM dataset are at SNRs of −12 and −18 dB, thus, HASPI w2 may overestimate the keyword intelligibility for NH listeners at large amounts of signal degradation. The scatterplot for the reverberation dataset does not show the same pattern of outliers, although there is a preponderance of NH points above and HI points below the diagonal.

The noise vocoder scatterplot uses a reduced x axis and y axis range compared to the other plots because the keyword intelligibility is very high. This dataset was included to provide situations where the speech TFS was corrupted but the envelope was preserved. The NH and HI results show very high keyword intelligibility for these data, and the HASPI w2 predictions are consistent with the listener data.

B. Accuracy of HASPI w2 compared to HASPI v2

Overall, the accuracy of the HASPI w2 keyword intelligibility predictions is very close to that of the HASPI v2 sentence intelligibility predictions. The performance of the two metrics was compared using bootstrapping (Efron, 1983; Efron and Gong, 1983: Zio, 2006) implemented using custom versions of matlab functions available online (Rousselet, 2017). A total of 10 000 bootstrap replications with replacement were used to estimate the probability distributions from which means, standard deviations, and confidence intervals were extracted. Comparisons between the metrics and listener responses comprise the RMS error, Pearson correlation coefficient, Spearman rank-order correlation coefficient, and Kendall's tau for pair-wise comparisons.

The keyword results for HASPI w2 are presented in Table I for the five datasets. For the noise and distortion data, the RMS error for the NH listeners is higher than that for the HI group while the correlations are lower, reflecting the impact of the NH outliers identified in the associated scatterplot in Fig. 2. The RMS error for the noise vocoder dataset is much lower than that for the other four datasets because the listener responses are clustered at the high end of the intelligibility range. The correlation coefficients are much lower for vocoding than for the other datasets as HASPI w2 is unable to model the residual intersubject variability, although the Spearman correlation is relatively high for the combined NH + HI data.

TABLE I.

The RMS error and correlations between the model predictions and listener responses for HASPI w2 (proportion keywords correct) fit to the NH and HI data. The results are averaged over the listeners in each hearing group. The RMS error and correlation values are the mean of 10 000 bootstrap replications of the model output.

Experiment	Subject group	RMS error	Pearson	Spearman	Kendall
Noise and distortion	NH	0.1013	0.9225	0.7036	0.5654
	HI	0.0656	0.9766	0.9236	0.8144
	NH + HI	0.0865	0.9511	0.7935	0.6403
Frequency compression	NH	0.1046	0.9712	0.9700	0.8794
	HI	0.0700	0.9865	0.9765	0.8912
	NH + HI	0.0895	0.9726	0.9628	0.8441
IBM noise suppress	NH	0.1251	0.9699	0.9570	0.8615
	HI	0.1123	0.9861	0.9834	0.9241
	NH + HI	0.1198	0.9773	0.9735	0.8805
Noise vocoder	NH	0.0112	0.2051	0.2429	0.1626
	HI	0.0156	0.5872	0.5586	0.4125
	NH + HI	0.0136	0.7831	0.7831	0.5880
Reverb envelope modify	NH	0.0935	0.9806	0.9661	0.8694
	HI	0.0893	0.9824	0.9621	0.8711
	NH + HI	0.0917	0.9629	0.9610	0.8485

The sentence RMS error and correlations for HASPI v2 are presented in Table II for the same datasets. The values for HASPI v2 are quite similar to those for HASPI w2. The bootstrapping procedure was then used to identify significant differences between the HASPI w2 and HASPI v2 accuracy for the same test conditions. The effect sizes (Cohen's d; Sullivan and Feinn, 2012) are presented in Table III. Differences significant at the 5% level are indicated by one asterisk while differences significant at the 1% level have two asterisks. The differences in the means and the standard deviations were computed from the bootstrap distributions used for Tables I and II, and Cohen's d was calculated as the difference in the means divided by the pooled standard deviation. An effect size of 0.2 is considered to be small, 0.5 is considered to be medium, 0.8 is considered to be large, and 1.3 is considered to be very large. Based on this classification, all of the statistically significant differences are very large or greater. Almost all of the significant differences are for the noise vocoder dataset, which, as shown in Fig. 2 for keywords correct, is clustered at higher values than the corresponding sentence-correct values shown in Fig. 5 of Kates and Arehart (2021). Thus, the RMS error for keywords correct is significantly lower than that for sentences at the 1% level as a result of the stronger ceiling effect. Also, note that even though HASPI w2 appeared to have outliers for the NH group for the noise and distortion dataset, there are no significant differences in the accuracy of the predictions between HASPI w2 and HASPI v2 for this group for any of the accuracy criteria.

TABLE II.

The RMS error and correlations between the model predictions and listener responses for HASPI v2 (proportion complete sentences correct) fit to the NH and HI data. The results are averaged over the listeners in each hearing group. The RMS error and correlation values are the mean of 10 000 bootstrap replications of the model output.

Experiment	Subject group	RMS error	Pearson	Spearman	Kendall
Noise and distortion	NH	0.1127	0.9385	0.8263	0.7073
	HI	0.0764	0.9735	0.9018	0.7789
	NH + HI	0.0968	0.9558	0.8867	0.7377
Frequency compression	NH	0.0986	0.9690	0.9724	0.8857
	HI	0.0807	0.9810	0.9699	0.8769
	NH + HI	0.0906	0.9658	0.9638	0.8468
IBM noise suppress	NH	0.1246	0.9657	0.9535	0.8462
	HI	0.1166	0.9858	0.9726	0.8968
	NH + HI	0.1219	0.9732	0.9669	0.8676
Noise vocoder	NH	0.0305	0.4376	0.4339	0.3192
	HI	0.0413	0.5231	0.5125	0.3680
	NH + HI	0.0363	0.8395	0.8328	0.6428
Reverb envelope modify	NH	0.0662	0.9851	0.9607	0.8568
	HI	0.0932	0.9793	0.9639	0.8698
	NH + HI	0.0811	0.9721	0.9622	0.8541

TABLE III.

Effect sizes (Cohen's d) for the statistically significant differences between the HASPI w2 and HASPI v2 accuracy for scores averaged over listeners and repetitions. The RMS error and correlation differences are the average of 10 000 bootstrap replications of the differences in the model outputs, and significance was computed from the bootstrapped confidence intervals. Differences at the 5% level are indicated using one asterisk while differences at the 1% level are indicated by two asterisks. The effect sizes were computed from the bootstrapped means and standard deviations.

Experiment	Subject group	RMS error	Pearson	Spearman	Kendall
Noise and distortion	NH	0.4283	0.4184	0.9605	1.1230
	HI	0.7144	0.1844	0.4384	0.5077
	NH + HI	0.6104	0.2361	1.4115**	1.3789*
Frequency compression	NH	0.5410	0.2934	0.2551	0.2787
	HI	0.8749	0.8440	0.7399	0.6399
	NH + HI	0.1337	1.0437	0.1356	0.1658
IBM noise suppress	NH	0.0172	0.2587	0.2035	0.4527
	HI	0.3307	0.0434	1.0789	1.1466
	NH+HI	0.1390	0.4780	0.7839	0.6909
Noise vocoder	NH	10.041**	2.0603*	1.4733*	1.6740*
	HI	8.706**	0.6705	0.4081	0.5040
	NH + HI	12.091**	1.5311*	1.4922	1.5251
Reverb envelope modify	NH	2.7374**	0.9848	0.3729	0.3893
	HI	0.4432	0.6316	0.0987	0.0376
	NH + HI	1.5569	1.3915	0.1140	0.2410

C. HASPI w2 and HASPI v2 for additive noise

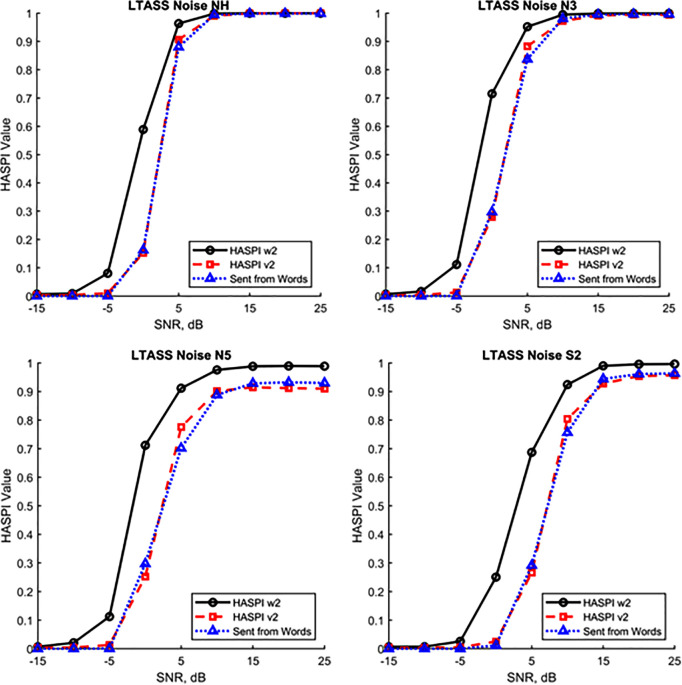
Plots of the HASPI w2 and HASPI v2 predictions are shown in Fig. 3 for IEEE sentences (Rothauser, 1969) in additive LTASS noise. The speech used to compute the HASPI values consisted of 20 concatenated sentences (Kates, 2017) with 10 sentences spoken by a male talker and 10 sentences spoken by a female talker. Each sentence was equalized to the same RMS level prior to being joined with the others. The set of 20 sentences was then combined with additive Gaussian noise having a long-term spectrum matched to that of the 20-sentence sequence. The SNR of the noisy sentences ranged from −15 to +25 dB in steps of 5 dB.

FIG. 3.

(Color online) HASPI w2 values (solid black line with circles), HASPI v2 values (dashed red line with squares), and HASPI w2 values transformed into the HASPI v2 values using Eq. (2) (dotted blue line with triangles) for IEEE sentences in additive LTASS noise as a function of SNR. The plots are for NH and N3 (moderate flat loss), N5 (severe flat loss), and S2 (moderate sloping loss) IEC audiograms.

The four plots in Fig. 3 are for simulations of normal hearing and three of the International Electrotechnical Commission (IEC) standard audiograms (Bisgaard et al., 2010). The N3 audiogram represents a moderate flat loss, N5 represents a severe flat loss, and S2 represents a mild steeply sloping loss. Linear amplification was provided to compensate for each of the hearing losses using the NAL-R gain formula (Byrne and Dillon, 1986), where the RMS level of each concatenated set of sentences in noise is set to 65 dB SPL prior to amplification. The solid black line in each plot is the proportion keywords correct as predicted by HASPI w2 and the dashed red line is the proportion complete sentences correct as predicted by HASPI v2. The dotted blue line is for a model transforming the keywords score into the sentence score that is considered in Sec. IV D.

In all of the plots, the keywords correct curve lies to the left of the sentences correct curve by about a 5-dB shift in SNR. The shift is consistent with previously reported data for noisy speech comprising words in sentences compared to complete sentences (Boothroyd and Nittrouer, 1988; Nielsen and Dau, 2009). This behavior is also consistent with the requirement that one must get all five keywords correct to get the sentence correct, therefore, the probability of a correct sentence at a given SNR is lower than that for a single keyword (Boothroyd and Nittrouer, 1988). There are also differences in the asymptotic behavior for HASPI v2 compared to that for HASPI w2 at high SNRs as the hearing loss is increased. For the simulated NH and N3 listeners, the keyword and sentence intelligibility reach asymptotes near one for SNRs of 15 dB and higher. However, for the N5 and S2 listeners, the predicted sentence intelligibility reaches an asymptote of less than one at high SNRs.

D. Context and the conversion of keywords to sentences correct

Boothroyd and Nittrouer (1988) propose a model of context effects in speech expressed as calculating the probability of recognizing a whole from the probabilities of recognizing its constituent parts. In the present study, the whole is the complete sentence correct, and the constituent parts are the keywords. The relationship is given by

$$P_s=P_w^j,$$ (1)

where $P_s$ is the probability of getting the complete sentence correct, and $P_w^j$ is the probability of getting a keyword correct, raised to the power j where 1 ≤ j ≤ N and N is the number of parts (keywords) making up the whole (one sentence). For IEEE sentences, there are five keywords per sentence, giving N = 5. For the purposes of this paper, we can interpret the HASPI w2 and HASPI v2 proportion correct predictions as representing the probabilities of correctly identifying keywords and sentences, respectively.

The model of Eq. (1) was used to convert the HASPI w2 predicted proportion keywords correct into the HASPI v2 proportion sentences correct for the concatenated IEEE sentences presented in LTASS noise as described in Sec. IV C. The fitting criterion was to minimize the RMS error between the transformed HASPI w2 scores and HASPI v2 over the set of SNRs ranging from −15 to +25 dB using the model of Eq. (1). The resulting value of the fitting parameter, j, was approximately three over the set of IEC audiograms. However, as shown in Table IV, this model cannot account for the asymptotic differences between HASPI w2 and HASPI v2 for the higher hearing losses at high SNRs. For audiograms having 2-kHz losses greater than 50 dB, when the asymptotic HASPI w2 values are cubed, there is still a difference between the transformed HASPI w2 values and the computed HASPI v2 values.

TABLE IV.

Model parameters, j and q, for IEC standard audiograms to account for the context effects in transforming predicted proportion keywords correct into proportion complete sentences correct for IEEE sentences in LTASS noise. The asymptotic values are estimated as the predicted intelligibility averaged over 25, 20, and 15 dB SNR. The conversion factor, q, compensates for the difference between the asymptotic values of the word and sentence predictions.

Audiogram	Loss at 2 kHz (dB)	HASPI w2 asymptote	(HASPI w2 asymptote)3	HASPI v2 asymptote	Exponent, j	Conversion factor, q
NH	0	1.000	0.999	1.000	3.429	1.000
N1	15	0.999	0.998	0.999	3.311	1.000
N2	35	0.999	0.998	0.999	3.496	1.000
N3	50	0.999	0.996	0.992	3.617	1.000
N4	65	0.992	0.976	0.914	3.129	0.951
N5	80	0.989	0.966	0.912	3.472	0.968
N6	90	0.870	0.658	0.636	2.630	0.934
S1	15	0.999	0.997	0.997	2.952	1.000
S2	55	0.994	0.981	0.946	3.218	0.975
S3	75	0.983	0.948	0.849	2.910	0.909

The asymptotic behavior of HASPI v2 for high SNRs combined with high losses can be represented using a modified version of Eq. (1) by adding a conversion factor, q, to give

$$P_s=q{P}_w^j.$$ (2)

The value of q matches the asymptotic value of the transformed word score to that of the HASPI v2 sentence score, where the asymptote is computed as the average at SNRs of 15, 20, and 25 dB. The use of the conversion factor in Eq. (2) is similar to the proficiency factor proposed for the SII, wherein the predicted intelligibility is reduced for HI listeners (Pavlovic et al., 1986; Ching et al., 1998; Woods et al., 2013). The optimal values of j and q found for each IEC audiogram are presented in the last two columns of Table IV; the values of j and q are interdependent because they were determined using a joint optimization procedure (matlab fmincon). The value of q is one for 2-kHz losses of 50 dB or less but decreases for greater losses. The average value of j for those audiograms having q = 1 is 3.35 and in the vicinity of three for all of the losses. Examples of using Eq. (2) to transform keywords correct into complete sentences correct are plotted for the four audiograms of Fig. 3 as the dotted blue lines, where the fitting parameters computed for the individual audiograms provide an accurate conversion from proportion keywords to sentences correct.

V. DISCUSSION

A. Asymptotes at high SNRs

As shown in Fig. 3, there are differences in the asymptotic behavior for HASPI v2 compared to that for HASPI w2 at high SNRs as the simulated hearing loss is increased. The differences in the asymptotes can be explained by considering the effect of word errors on computing sentences correct. For example, assume a test with 20 IEEE sentences and, therefore, 100 keywords. If one of the keywords is not identified correctly, the proportion words correct is 0.99. However, one keyword error means that 1 out of the 20 sentences is incorrect; hence, the proportion sentences correct becomes 0.95. For 2 keywords out of 100 incorrect, the proportion keywords correct is 0.98 while the proportion sentences correct is very close to 0.90. Thus, the asymptote for HASPI v2 shows much larger effects for small numbers of word errors than occurs for HASPI w2; the representation of intelligibility using sentences correct amplifies the asymptotic differences between sentences and keywords at high SNRs.

Furthermore, the errors in intelligibility will tend to increase with the severity of the hearing loss even in the absence of additive noise. Both versions of HASPI compare the time-frequency envelope modulation of the reference speech passed through a model of the normal periphery with the degraded speech passed through a model of the impaired periphery. The peripheral model (Kates, 2013) represents impaired hearing as a shift in auditory threshold, reduced auditory dynamic-range compression, broader auditory filters, and reduced two-tone suppression in comparison with normal hearing. Thus, there will be differences between the envelopes of the reference signal output by the normal periphery and the output of the same noise-free signal passed through the impaired periphery. Any differences between the degraded and reference signal outputs are represented by HASPI as a reduction in intelligibility, and reductions in HASPI w2 will be mapped into larger reductions in the HASPI v2 values because of the conversion of word errors into sentence errors.

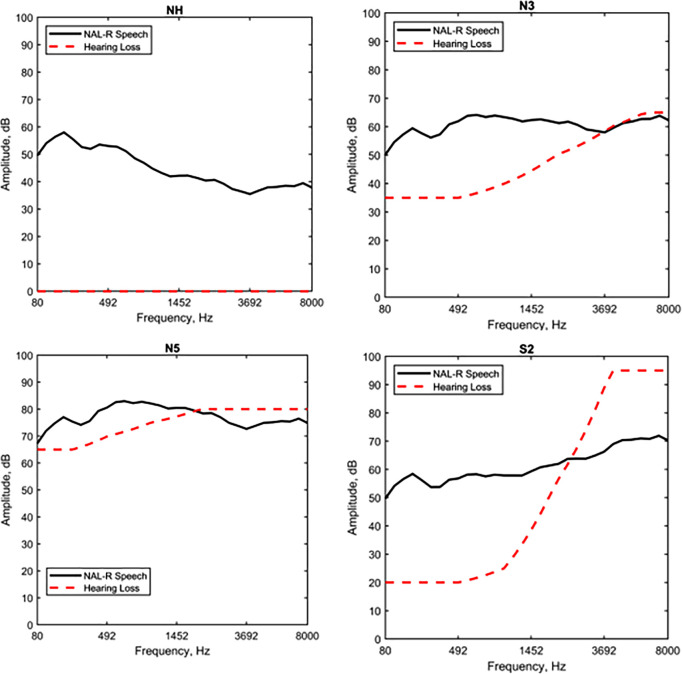
B. Interaction of amplification and hearing loss

The speech in noise data considered in Secs. IV C and IV D used NAL-R (Byrne and Dillon, 1986) amplification to compensate for the hearing loss. However, the HASPI w2 and HASPI v2 values depend on the audibility of the amplified speech as well as the envelope fidelity. The interaction of the amplification and hearing loss is illustrated in Fig. 4 for the same four audiograms that were used for Fig. 3. For the NH and N3 audiograms, where the computed value of q = 1, the amplified speech spectrum lies at or above the normal or impaired auditory threshold. However, for the N5 and S2 audiograms, where the computed value of q < 1, portions of the amplified speech lie below the impaired auditory threshold. Audibility depends on the compensation used for the hearing loss, and changing the amplification rule will change the amount of speech that falls above the impaired auditory threshold and could change the computed values of j and q used to transform the word scores into sentence scores.

FIG. 4.

(Color online) Long-term RMS average speech spectra for IEEE sentences in dB SPL for the indicated IEC standard audiograms, along with the associated hearing losses in dB HL. NAL-R amplification for each of the IEC audiograms has been applied to the speech. The plots are for NH and N3 (moderate flat loss), N5 (severe flat loss), and S2 (moderate sloping loss) IEC audiograms.

C. Low-SNR bias effects in converting sentences to keywords

The negative SNR asymptotes of HASPI w2 and HASPI v2 also exhibit a small bias effect. The neural network approach used to fit the envelope modulation terms to the listener keyword or sentence data is unconstrained and, in particular, there is no constraint to produce a value of zero at large negative SNRs. As a result, HASPI w2 returns a value of approximately 0.007 for keywords embedded in the concatenated sentences at large negative SNRs, and HASPI v2 gives a value of approximately 0.004 for complete sentences at large negative SNRs.

These bias terms are small and do not have a meaningful impact on the associated intelligibility predictions. The effect of the HASPI w2 bias is even less when converting from words correct to sentences correct. From Eq. (2) and the values in Table IV, P_s is approximately proportional to P_w³, and cubing the bias term in HASPI w2 gives a bias in the converted sentence predictions of 0.007³ =  3.4 × 10⁻⁷. However, attempting to go in the opposite direction, from sentences to keywords, will increase the bias problem. The inverse of Eq. (2) gives P_w as approximately proportional to P_s^1/3. Thus, the inverse conversion from predicted sentences to words correct takes the cube root of the sentence bias, giving a keyword bias of 0.004^1/3 =  0.16.

VI. CONCLUSIONS

The previously published version of HASPI v2 predicts complete sentences correct. HASPI is extended in this paper to predict keywords correct for the same sentence stimuli. HASPI w2 for keywords correct uses the same peripheral model, the same envelope modulation features, and the same neural network data-fitting approach as was used for HASPI v2; the only difference is the change in the training data to which the metric is fitted. The accuracy of the keywords correct and sentences correct predictions are quite similar, and the major differences are for the noise vocoder data, which spans a narrower range for keywords correct than for sentences correct. Therefore, one can choose the version of HASPI that is most appropriate for the problem that is considered without being concerned about differences in model accuracy.

When evaluated for speech in speech-shaped noise, HASPI w2 and HASPI v2 show similar shapes for the predicted psychometric functions with the curve for proportion keywords correct lying about 5 dB to the left of the sentence curve. These curves allow for the estimation of context effects for keywords correct within sentences compared to complete sentences correct. The power-law model of Boothroyd and Nittrouer (1988) for converting proportion keywords correct into proportion sentences correct was found to be valid for NH and the milder losses considered in this paper with an exponent of approximately j = 3.35. However, for greater losses, the damaged periphery introduces predicted errors even for speech in quiet, and a conversion factor, q < 1, was needed to accurately model the transformation of keyword errors into sentence errors. Finally, it was observed that the neural network approach used to fit the keyword and sentence data introduces a small residual bias term at low SNRs; this term has a minimal effect when converting from proportion keywords to proportion sentences correct, but it is greatly amplified when moving in the opposite direction.

The matlab computer functions for HASPI w2 are available from the author via email on request.