Statistical analysis of yeast genomic downstream sequences reveals putative polyadenylation signals

Abstract

The study of a few genes has permitted the identification of three elements that constitute a yeast polyadenylation signal: the efficiency element (EE), the positioning element and the actual site for cleavage and polyadenylation. In this paper we perform an analysis of oligonucleotide composition on the sequences located downstream of the stop codon of all yeast genes. Several oligonucleotide families appear over-represented with a high significance (referred to herein as ‘words’). The family with the highest over-representation includes the oligonucleotides shown experimentally to play a role as EEs. The word with the highest score is TATATA, followed, among others, by a series of single-nucleotide variants (TATGTA, TACATA, TAAATA . . .) and one-letter shifts (ATATAT). A position analysis reveals that those words have a high preference to be in 3′ flanks of yeast genes and there they have a very uneven distribution, with a marked peak around 35 bp after the stop codon. Of the predicted ORFs, 85% show one or more of those sequences. Similar results were obtained using a data set of EST sequences. Other clusters of over-represented words are also detected, namely T- and A-rich signals. Using these results and previously known data we propose a general model for the 3′ trailers of yeast mRNAs.

INTRODUCTION

mRNA 3′-end formation in eukaryotic cells involves endonucleolytic cleavage at a specific site of the precursor mRNA coupled in most cases to polymerisation of a poly(A) tail onto the upstream cleavage fragment (1,2). This process is an essential step in eukaryotic mRNA synthesis because the poly(A) tail functions in mRNA turnover (3) and in translation (4).

Because of the good knowledge of its genetics and bio-chemistry the yeast Saccharomyces cerevisiae has been used as a model organism for understanding cellular processes in eukaryotes. Nevertheless the information about mRNA 3′ formation has been confusing for a long time and many aspects of it have become understood later in yeast than in higher eukaryotes. The ability of yeast whole-cell extracts to cleave extended precursor RNAs endonucleolytically at the same sites used for poly(A) addition in vivo (5,6) has indicated that, overall, the 3′-end processing reaction is similar to that of mammalian cells. Despite the similarities between yeast and mammals regarding the overall mechanism and the polyadenylation factors, the 3′-end sequences which direct the process show some differences (1). Moreover, the identification of a consensus signal in yeast has been elusive. Although the AATAAA hexanucleotide is found in the 3′ region of ∼50% of the yeast genes (7) mutations in this element do not affect the polyadenylation process. The accurate analysis carried out by Guo and Sherman (8) in the S.cerevisiae CYC1 gene has permitted the identification of three elements working in concert, which are not only necessary but also sufficient to constitute a yeast polyadenylation signal. Analysis of several polyadenylation signals led to the identification of certain modifications in the sequences of these elements (reviewed in 9). The far upstream element is the efficiency element (EE), whose deletion decreases the efficiency of processing. It is a TA-rich element. Saturation mutagenesis experiments of the element TAG . . . TATGTA, which was the first proposed as a polyadenylation signal (10), revealed that the hexanucleotide TAYRTA is essential for this function and that the sequence TATATA has the best capacity for 3′-end formation. Moreover, the two T residues at the first and fifth position are the most essential nucleotides in this sequence (11). The second element of the polyadenylation signal is an A-rich positioning element (PE), of which recognition appears to be closely coupled to cleavage at the nearest downstream PyA_n site, usually located 13–27 nucleotides downstream. The sequences identified so far for this function have been AAAAAAAA, TTAAGAAC, AAGAA, AATAATGA and AATAAA, the latter being the strongest signal and possible consensus (9). Distance between the EE and the PE can vary, but the efficiency is sensitive to spacing. It is worth noting that other sequences or a different arrangement of sequences have been identified for some yeast genes (12–17) and, in fact, very few yeast genes have been investigated for the analysis of their polyadenylation signals. Obviously a wider investigation of the yeast genes is required in order to discuss the existence of consensus sequences in yeast.

Having in hand the complete genome sequence and all the putative ORF locations, it is possible to carry out a complete analysis of their 3′ flanking sequences in order to detect highly represented patterns, which could play a role in polyadenylation or in other processes. The biological function of non-coding sequences is generally mediated by short conserved sequences. A common approach to the discovery of short signals in large sequence sets is the analysis of oligonucleotide representation (18–20 and references therein). Given the fact that regulatory signals are often centred on a short and highly conserved core, over-represented oligonucleotides (called ‘words’ hereafter for brevity) are likely to exert some biological function. The crucial problem is to define a valid criterion for a word to be considered over-represented. Word frequency by itself is a very poor criterion because oligonucleotide composition of DNA sequences is strongly biased. First, genomic sequences already present biases in base composition (A:T richness). Moreover, non-randomness is observed in nucleotide succession, probably due to structural constraints [avoidance of large poly(G) or poly(C) strands], that do not directly reflect biological features. Special care must thus be taken to evaluate the specific expected frequency of each word. To date, the most satisfying statistical model for representation of DNA sequences is the Markov chain, which estimates expected word frequencies on the basis of subword frequencies observed in the same sequence (18,21). The task is then to select words whose observed frequency significantly differs from expectation. Several statistics have been used as criteria of over-representation: representation ratio (i.e. observed/expected occurrences; see for example 22,23), ‘odds’ ratio (24), likelihood ratio (25), binomial probability (26) and Z-score (20,27). Z-scores provide the advantage of taking into account an estimated variance on occurrence numbers. This parameter is crucial since it has been demonstrated that self-overlap (e.g. AAAAAA, TATATA) induces a bias in occurrence probabilities: the average expected number of occurrences is not affected, but the variance increases with self-overlap (27). The probability to observe either a low or high number of occurrences is thus higher for self-overlapping words, and there is a risk of overestimating the importance of such words with statistics based on expected occurrences only (binomial, Poisson). This bias can be corrected by the introduction of a self-overlap coefficient in the calculation of the estimated variance (27–29).

In this paper we perform an analysis of oligonucleotide composition on the sequences located downstream of the stop codon of all yeast genes. Several oligonucleotides appear over-represented with a high significance, among which are those shown experimentally to play a role in 3′-end formation. The word with highest over-representation is TATATA, followed, among others, by a series of single-nucleotide variants (TATGTA, TACATA, TAAATA, TATTTA) or displacements (e.g. ATATAT). Many of these words also show a marked preference for downstream versus upstream sequences. Position analysis reveals that those words have a very uneven distribution in the 3′ region, with a marked peak around 35 bp after the stop codon. Several of the words isolated by this triple analysis have already been found to function as EEs. We also used our experimental protocol to analyse a data set of 1352 yeast ESTs previously studied by Graber et al. (25). We obtained results compatible with those of our genomic analysis. Other families of over-represented words were also detected: an A-rich signal, corresponding to the positioning element, and a T-rich signal for which no functional data are available yet. Using these results and previously known data we propose a general model for the 3′ trailer of yeast genes.

MATERIALS AND METHODS

Collection of sequence sets

Two complete sets of downstream sequences were collected, including one sequence for each of the 6217 yeast ORFs. The first set ranged from position +1 to +200 starting from the last base of the stop codon, and was used for the detection of over-represented oligonucleotides and position analysis. An extended sequence set, ranging from –200 to +400 was collected from the distribution profiles shown in Figure 3. This last set thus encompassed systematically 200 bp of coding sequences on the 5′ end. The average distance between an ORF end and the closest downstream ORF is 547 bp, but a significant number of genes have a downstream neighbour closer than 400 or even 200 bp. In such cases, downstream regions were clipped on the 3′ side to avoid including coding sequences from a downstream neighbour.

Figure 3.

Clustering of the significant words according to the similarity of their distribution profiles in whole genome downstream analysis (A) or in EST data set (B). See text for details.

For the upstream/downstream comparison, we retrieved two sequence sets grouping together all intergenic regions located between two genes that were, respectively, divergently or convergently transcribed.

Joel Graber kindly provided the sequences surrounding cleavage sites (25). This set contains 1352 sequences of 230 bases, ranging from –150 to +80 from RNA cleavage sites. These 1352 cleavage sites are located downstream of 861 genes (some genes have several cleavage sites).

We collected several subsets of downstream sequences (ranging from +1 to +200 from the stop codon) for the comparison shown in Figure 5. A first set regrouped 384 questionable ORFs (as defined by MIPS). Another set contained 764 ORFs without known homologue. The last set contained the 861 ORFs from Joel Graber, for which there is at least one known 3′ EST.

Figure 5.

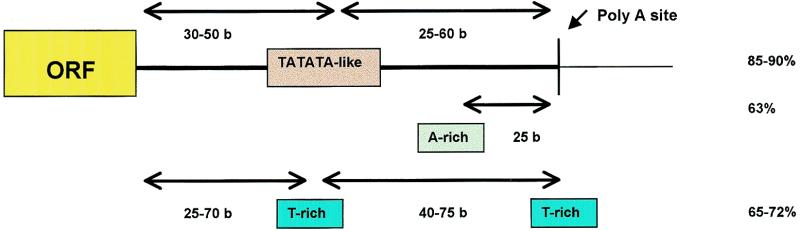
Model for the organisation of yeast 3′ mRNA trailers. Figures on the right represent the percentage of yeast ORFs having at least one of the corresponding signals (indicated as boxes). Distances from each signal to the stop codon and to poly(A) site are marked.

Oligonucleotide analysis

The program oligo-analysis (26) was used to count oligonucleotide occurrences in the set of 200 bp downstream sequences, for all oligo sizes between five and eight. Since we did not want to exclude potential orientation-sensitive signals, occurrences were counted on a single strand. The two critical parameters for detection of over-represented oligonucleotides are the estimation of expected frequencies, and the scoring scheme, which were defined as follows.

Expected oligonucleotide frequencies were calculated on the basis of observed subword frequencies, according to a Markov chain model. For words of length k, one can choose any Markov order (i.e. the subword length) m between 1 and k – 2. For instance, for k = 6 and m = 3, one has:

F_exp(GATAAG) = [F_obs(GATA) × F_obs(ATAA) × F_obs(TAAG)]/[F_obs(ATA) × F_obs(TAA)].

For a formal description of Markov models, refer to Durbin et al. (21).

The expected number of occurrences is obtained by multiplying the expected frequency with the number of possible word positions:

occ_exp(w) = F_exp(w) × Σ^S_i=1 (L_i – k + 1),

where L_i is the length of the i^th sequence and S is the number of sequences.

In a previous analysis of upstream sequences (26), we calculated occurrence probabilities on basis of the binomial. This scoring has the advantage of being adequate for small sequence sets, but raises the problem of over-estimating the importance of self-overlapping patterns. This bias was not a concern for the detection of upstream regulatory elements, but was not acceptable anymore in the present context, since the few elements experimentally characterised are self-overlapping (noticeably the EE element TATATA). It has been shown (27) that self-overlapping does not affect the first moment (expected occurrences) but increases the second moment (variance), leading to a higher probability of observing occurrence values distant from the average. Corrections on the estimated variance have been introduced for self-overlapping patterns that can be used in a Z-score.

Z = [occ_obs(w) – occ_exp(w)]/stdev_est(w),

stdev_est(w) = √var_est(w),

where w is the oligonucleotide sequence (word), occ_obs(w) is the number of occurrences observed for w, occ_exp(w) is the number of occurrences expected for w, stdev_est(w) is an estimation of the standard deviation of occurrences of w, and var_est(w) is an estimation of the variance of occurrences for w.

The estimated variance (var_est) and self-overlap coefficient (K_ov) are calculated according to Pevzner et al. (28):

var_est = occ_exp[2K_ov – 1 – (2w – 1) × occ_exp],

K_ov = Σ_j=1,S k_j [1/f(n_j)]^j,

where s is the pattern length; j is the overlap position, comprised between 0 and l; k_j takes the value 1 if there is an overlap at position j, 0 otherwise; f(n_j) is the residual frequency for the nucleotide found at position j of the sequence.

As discussed by van Helden et al. (26), the threshold value must be adapted to the number of possible words, which depends on the word size. For hexanucleotides, we set the threshold on Z-score to 3.49, which corresponds to a first-order risk α = 0.00024 = 1/4096. With this threshold, one expects no more than one hexanucleotide to be selected at random in each data set. In a general way, one should accept a first order risk α < 1/4^k for k-letter words.

Position analysis

We performed a χ² test to assess the statistical significance of the positional biases (Table 1). For this, we used the set of 200 bp downstream sequences, clipped when required to avoid any coding sequence. For each pattern, matching positions were detected and clustered into 20 classes (from 0 to 200, with a class interval of 10). The number of occurrences in each class was compared to the expected number of occurrences, calculated on basis of a flat distribution hypothesis. Due to the clipping, the number of sequences decreases in distal classes, and we adapted the expected number of occurrences to the number of sequences found in each position class.

Table 1. 3′-end signals detected by analysis of all genomic downstream sequences.

Sequence	mkv3	χ2	Con/div	Score	Cluster
TATATA	34.9	409.4	2.67	38027	D1
ATATAT	27.0	324.4	2.60	22757	D1
TACATA	27.7	185.5	2.65	13649	D1
TATGTA	25.0	138.4	2.65	9193	D1
TAAATA	22.0	122.0	2.12	5679	D1
ATACAT	15.5	100.8	2.38	3726	D1
TGTATA	8.6	153.0	2.24	2963	D1
ATGTAT	11.9	101.1	2.38	2857	D1
GTATAT	8.2	123.0	1.93	1938	D1
ATTTAT	9.8	85.7	1.98	1660	D1
ACATAT	7.7	102.1	1.93	1523	D1
TACGTA	16.3	56.0	1.55	1417	D1
ATATAC	7.4	98.0	1.93	1391	D1
TATACA	7.3	81.3	2.24	1337	D1
TAGATA	11.9	64.1	1.68	1282	D1
ATATGT	7.8	76.4	1.93	1156	D1
ATAGAT	9.9	66.7	1.57	1032	D1
ATAAAT	9.9	52.2	1.98	1029	D1
CATATA	3.5	140.2	1.97	973	D1
TGTGTA	6.4	84.7	1.40	752	D1
ATGTAC	4.7	51.2	1.66	401	D1
TATTTA	17.7	134.5	2.12	5054	D2
TTATTT	16.7	79.2	1.79	2367	D2
TTTATT	13.3	74.4	1.68	1654	D2
TTTTTT	16.9	55.3	1.33	1239	D2
TATTAT	5.1	84.9	1.89	815	D2
ACATAA	5.0	51.4	1.70	436	D3
AGAAAA	4.7	51.8	1.10	268	D4

mkv3, Z-scores calculated with third-order Markov chain model; χ², from position analysis; con/div, representation ratio between intergenic regions separating convergently and divergently transcribed genes; score, product of the three values; cluster, defined by position analysis. See text for details.

occ_exp(w,c) = occ_obs(w) × N_seq[c]/Σ_i N_seq[i],

where occ_exp(w,c) is the expected number of occurrences for the word w in the position class c, N_seq[c] is the number of sequences in the position class c, and occ_obs(w) is the total number of occurrences observed for word w in the 200 bp sequence set.

Since we consider 20 classes, there are 19 degrees of freedom. For hexanucleotides, we selected all the distribution profiles with χ² ≥ 50, which corresponds to a first-order risk α = 1/4096.

Selected words were clustered according to their positional profile similarities. The similarity between each pair of profiles was estimated by a correlation coefficient. This coefficient was used to generate a similarity matrix, which was further used with OC (Geoff Barton, personal communication) to generate the similarity trees in Figures 4 and 5, on the basis of hierarchical cluster analysis (with the means linkage method).

Figure 4.

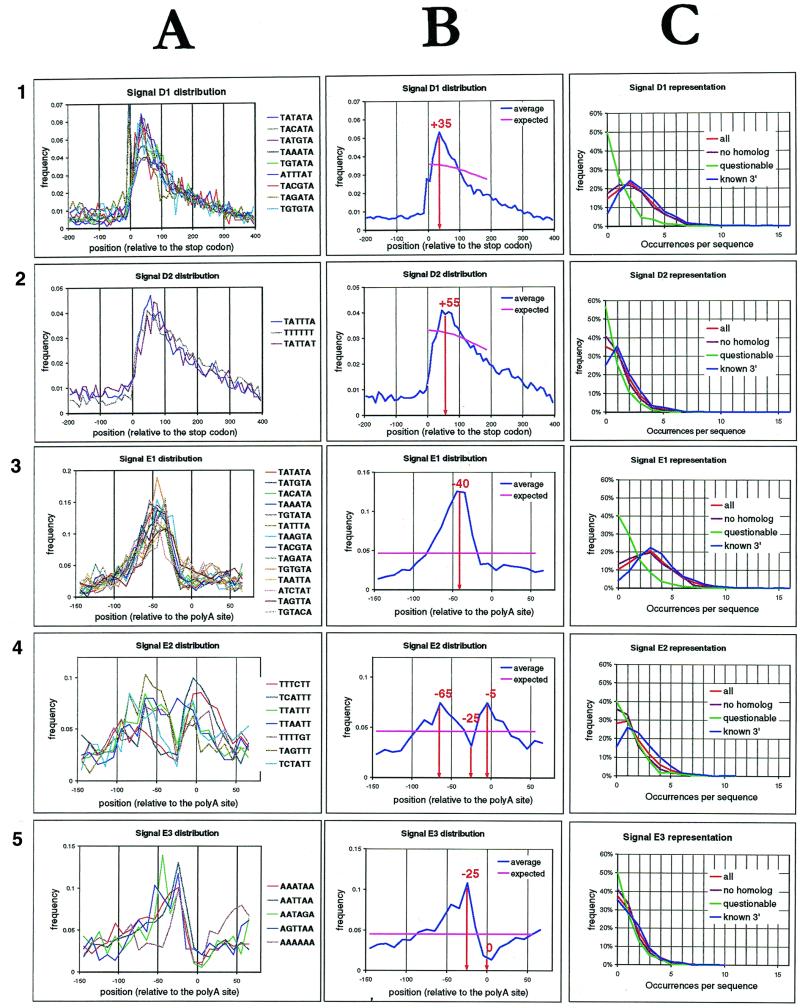
(A) Position profiles in the –200 to +400 region from the stop codon of the over-represented patterns in Table 1, clustered according the tree obtained in A1 and A2 or for the –150 to +70 region from the poly(A) site of the over-represented patterns in Table 2, clustered according the tree obtained in (B) (A3–A5). (B) Averaged profiles for every signal from (A). (C) Representation of the putative signals in different sets of downstream sequences. The y-axis indicates the number of occurrences per downstream sequences and the x-axis the percentage of genes having that number of occurrences in their 200 bp downstream sequence. Note the strong difference between the questionable ORFs (green curves) and the other sets of genes, especially sensitive for signals D1 and E1.

We generated a series of histograms showing the distribution profile for each over-represented oligonucleotide. This profile was generated on the basis of the extended sequence set, ranging from –200 to +400 respective to the ORF end. Negative coordinates correspond to coding sequences.

Availability

The programs used for this analysis can be freely used by academic users through a web interface (30) (http://www.ucmb.ulb.ac.be/bioinformatics/rsa-tools/ ). The complete sets of data and results discussed in the text are available on the same site.

RESULTS

Downstream sequence collection

Although there is no defined indication of the length of 3′ flank involved in mRNA polyadenylation/termination, the statistical analysis of intergenic regions in the yeast genome showed that 326 bp is the mean distance between two genes transcribed convergently, so it can be deduced that 163 bp is the average terminator length (31). Accordingly, in the cases experimentally studied in yeast, sequences necessary for mRNA polyadenylation/termination were always located within 200 bp downstream the stop codon, so we decided to use this length for the extraction of over-represented patterns. In the cases in which the next ORF is closer than 200 bp the distance for analysis was reduced to the intercoding length.

Z-score distributions in random and biological sequences

Markov chain models provide a reliable basis for estimating the expected word frequencies in large sequence sets. The Markov chain approach consists of calculating the expected frequency for each word (k-mer) on basis of the observed frequencies for its subwords (m-mers, with 1 < m < k – 2). On the basis of the expected and observed number of occurrences, a Z-value is calculated for each word. Probabilities are then assigned to each Z-value on basis of the normal distribution.

In order to validate this statistical model, we tested the normality of Z-value distribution in random sequences. We generated 50 sets of random sequences, each set comprising 6200 sequences of 200 bp. Sequences were generated on the basis of a differential nucleotide representation, mimicking that observed in yeast non-coding sequences [freq(A) = freq(T) = 0.325, freq(C) = freq(G) = 0.175]. For each word of size comprising between three and eight nucleotides, occurrences were counted on a single strand, and the expected number of occurrences and Z-score were calculated using a Markov chain model of order k – 3 (Materials and Methods). As already shown by Leung et al. (20), we observed that Z-scores follow a normal distribution in random sequences independently of word size (http://www.ucmb.ulb.ac.be/bioinformatics/rsa-tools/ ).

We analysed the distribution of Z-scores in the set of downstream sequences. In contrast to random sequences, the Z-score distribution in yeast downstream sequences diverges strongly from a normal curve for very short words (http://www.ucmb. ulb.ac.be/bioinformatics/rsa-tools/ ). The discrepancy decreases as word length increases, so that words of size six and over fit well the normal curve. This confirms the observation that Markov models are poor predictors for short word frequencies (lengths three to five), as had been observed in several viral genomes (20). As discussed by Leung et al. (20), words with extreme Z-score values nevertheless often reflect some biological features. Z-scores calculated from Markov chain models seem a reliable way to compare representation among oligonucleotides of the same size, but cannot be used to compare over/under-representation between different word sizes.

Detection of over-represented hexanucleotides with Markov chain models

We analysed the representation of each oligonucleotide in the whole set of 3′ flank for the 6217 yeast ORFs. According to published data, sequences of size five to nine have been involved as EEs or PEs in some yeast genes. Nevertheless, most of the consensus sequences proposed were hexamers (9), therefore we focussed mainly on hexamer analysis.

Besides the word size (k), another important criterion is the choice of the Markov chain order (m). Too small order choice leads to a poorly discriminating model, selecting too many words as significant. The higher the order, the most stringent is the selection. We performed a systematic analysis of the set of downstream sequences for hexanucleotides (k = 6), and for each possible order (m = 1, 2, 3 and 4 respectively; http://www. ucmb.ulb.ac.be/bioinformatics/rsa-tools/ ). The number of words selected as over-represented depends dramatically on the Markov order: among the 4096 distinct hexanucleotides, as many as 592 words are considered over-represented when choosing a Markov order m = 1 (with α = 1/4096), suggesting that first order Markov chain alone is a poor model for discriminating biological signals from their background. The number of selected words decreases when a higher order is used: 446 words for m = 2, 184 for m = 3, and no more than 39 for m = 4. The highest Markov order selects the words with the highest confidence, but this may lead to a loss of some biological signals, as pointed out by Stuckle et al. (29). We thus selected the order three for further analysis of hexanucleotides.

As shown in Table 1 the most significant word is TATATA. Many other words among the top ranking are single-base substitutions from TATATA (TACATA, TATGTA, TATTTA, TAAATA, . . .), or one-base shifts of these words (ATATAT, ATACAT, . . .). Besides these variants on TATATA, most additional patterns are A+T-rich sequences, noticeably TTTTTT and a limited number of variants with one or two T→A substitutions.

For a majority of the highest-score hexanucleotides, there is experimental evidence showing that they play a role in RNA polyadenylation (reviewed in 9). TATATA is the most active efficiency element. Irniger and Braus (11) performed a saturation mutagenesis and measured the activity of all single-base variants of one efficiency element (TATGTA). Figure 1 shows that the high Z-score values (>5) correlate with the experimental measurement of efficiency.

Figure 1.

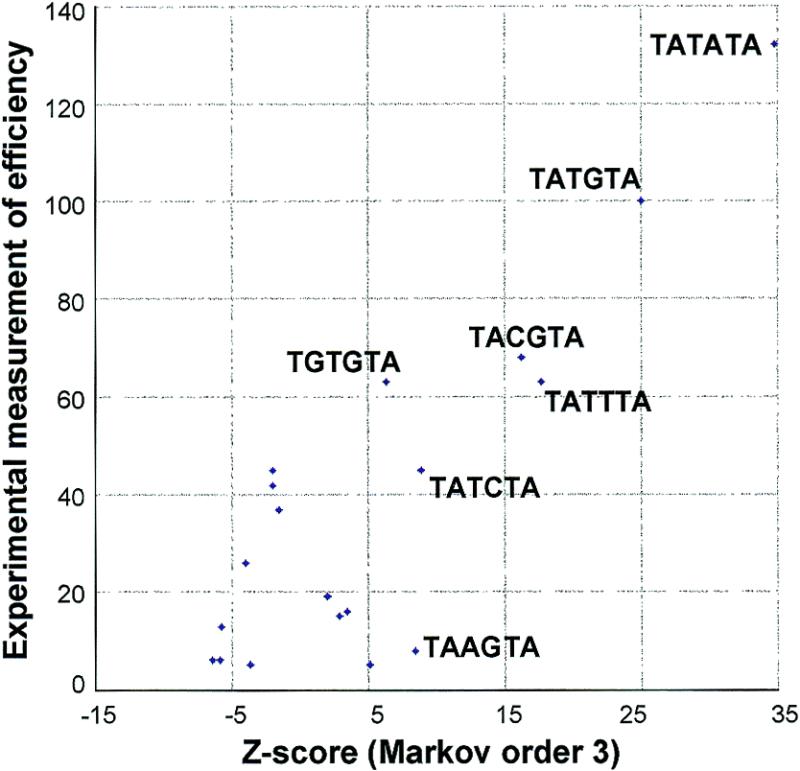
Polyadenylation efficiency versus over-representation. The y-axis indicates the experimental value for polyadenylation efficiency (in % with regard to the efficiency of TATGTA) as reported by Irniger and Braus (11). The x-axis shows the Z-score values calculated as in Table 1.

Downstream versus upstream sequences

Some words could be over-represented without being specific for downstream sequences, but rather reflect some general biases of the non-coding sequences. In order to define which of the over-represented patterns are characteristic of downstream signals, we compared hexanucleotide frequencies between downstream and upstream sequences. A problem may arise when two genes are transcribed in the same direction, since in this case the intergenic sequence is at the same time downstream from the first gene and upstream from the second one. In contrast, the intergenic region between two divergently transcribed genes is upstream of both. At reverse, the intergenic region between two convergently transcribed genes is downstream of both. We thus built two separate data sets, comprising only the intergenic regions separating divergent (‘upstream sequence set’) and convergent (‘downstream set’) genes respectively. Figure 2 plots the comparison of hexanucleotide frequencies between these two sequence sets. Most of the patterns align pretty well on the diagonal, indicating that their representation level is similar in downstream and upstream regions. A limited number of dots depart from the diagonal in the upper left direction: these patterns are more represented in downstream sequences. The most strikingly divergent points correspond to TATATA and ATATAT. Other patterns from the top of Table 1 are also preferentially represented in downstream regions (Fig. 2).

Figure 2.

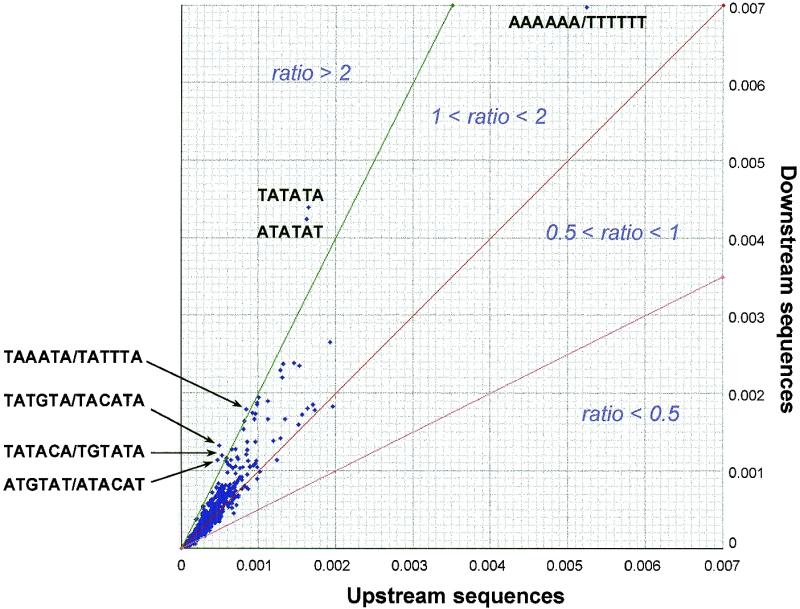
Hexanucleotide frequencies in upstream versus downstream sequences. Each dot corresponds to a hexanucleotide. Its position indicates the frequency observed in the set of intergenic regions separating divergent (y-axis) and convergent (x-axis) genes. The ratio values are indicated in Table 1 for the patterns selected by the oligo-analysis. Diagonals with slopes 1, 2 and respectively are drawn.

We indicated in Table 1 the convergent/divergent ratio for the over-represented hexanucleotides. Strikingly, the high ratio values (>2) systematically correspond to EE-like elements. These patterns are thus not only over-represented but also they are specific for downstream sequences.

With respect to the overall distribution of words, most dots that depart from the diagonal are located above it, indicating that downstream sequences have special sequence features. Some patterns appear with a ratio lower than 1, but they all correspond to very low occurrence numbers, and it is known that the reliability of ratios is bad when the values to compare are smaller. These patterns can thus not be considered as upstream-sequence specific on the basis of this ratio.

Positional analysis

Biological features of genomes distinguish themselves not only by their frequencies, but also by their specific concentration in some locations. We analysed the profile of position of all hexanucleotides within the downstream sequences, and selected 111 words whose distribution shows a significant positional bias (χ² ≥ 50). The most significant words are TATATA and ATATAT, followed by some single-base variants on TATATA, basically the same words as had been selected on basis of their Z-score. The most over-represented words thus show the highest positional bias.

We combined the results of the above three analyses to select patterns that were simultaneously over-represented (Z-score ≥ 3.49), biased in position (χ² ≥ 50) and preferentially found in downstream sequences (convergent/divergent ratio ≥ 1). This triple condition reduced the number of patterns to 28 (Table 1). In order to separate the different biological signals, we clustered the words according to the similarity in their positional profile. For each pair of words, we calculated a correlation coefficient between the respective distribution curves, and performed a cluster analysis to establish a similarity tree (Fig. 3A).

Interestingly, although the clustering is based on the position profile only, words with similar sequences appear clustered together, reinforcing the hypothesis of their common function. Two main clusters appear in the tree: the D1 (TATATA-like) and D2 (TTTTTT-like) elements. Two additional patterns, ACATAA (D3) and AGAAAA (D4) are selected as singletons. These two words appear, however, among the least significant of the list (Table 1), having a positional bias just above the threshold. For these reasons, we consider them as false positives and exclude them from the list of putative 3′ signals.

Among each of the remaining clusters, we filtered out the patterns that were single-base shifts from a more significant pattern (e.g. ATATAT from TATATA), and drew the average distribution profiles of the remaining words (Fig. 4A and B). These profiles were drawn on a larger range (–200 to +400 from the stop codon), overlapping the coding sequences over 200 bp, in order to highlight differences between downstream and coding sequences. D1 patterns show a strong peak around +35 (Fig. 4A and B). The peak spans approximately between +10 and +125 and it is asymmetric with a smooth slope towards downstream. Two words, TAAATA and TAGATA, also show a sharp peak at –3, due to the fact that they include the stop codon. D2 also shows a peak, but less pronounced and located more distally (around +55 from the stop codon).

EST data analysis

During the preparation of this manuscript, a paper by Graber et al. (25) was published, performing a computational analysis to extract 3′-end signals from S.cerevisiae sequences. Their approach differed from ours in two aspects: the statistical methodology, and the data set. On the basis of EST data, these authors localised 1352 cleavage sites in the genome, and extracted the neighbouring sequences. Their statistical treatment relies on an order one Markov chain, followed by an iterative filtering to reduce the number of selected patterns. Our results with the whole genome ORF set partly overlap but differ in some points from those of Graber et al. (25). We thus wondered whether this comes from the differences in methodology or in the data sets. Joel Graber kindly provided us with his sequences, on which we performed the same analysis as described above for downstream sequences. We selected the patterns (Table 2) that fulfill the triple condition of over-representation, biased distribution and preference for downstream versus upstream sequences (for this last parameter we use the data obtained in the whole genome analysis). We clustered together the selected words according to their distribution profiles. Figure 3B shows the distributions of the word clusters extracted from these sequences.

Table 2. EST data set analysis.

Sequence	mkv3	χ2	Con/div	Score	Cluster
TATATA	15.4	889.1	2.67	36591	E1
ATATAT	12.7	604.3	2.60	19911	E1
TATGTA	14.2	414.3	2.65	15598	E1
TACATA	13.7	325.0	2.65	11777	E1
TAAATA	10.4	417.6	2.12	9192	E1
TGTATA	7.7	387.9	2.24	6650	E1
TATTTA	6.9	243.0	2.12	3565	E1
ATGTAT	5.3	225.9	2.38	2860	E1
TAAGTA	9.0	194.5	1.63	2842	E1
ACATAT	5.8	222.1	1.93	2467	E1
CATATA	4.4	261.7	1.97	2264	E1
ATACAT	6.6	140.7	2.38	2204	E1
TACGTA	10.9	112.8	1.55	1899	E1
ATATAC	4.3	228.0	1.93	1871	E1
ATATGT	5.4	165.8	1.93	1740	E1
TAGATA	7.3	109.0	1.68	1331	E1
ATAAAT	3.9	163.7	1.98	1280	E1
TTAAAT	5.9	116.1	1.76	1213	E1
TATACA	3.7	142.8	2.24	1171	E1
TGTGTA	4.8	173.9	1.40	1162	E1
TAATTA	3.9	156.3	1.62	987	E1
GTATGT	8.0	63.3	1.93	974	E1
ATCTAT	6.7	86.8	1.57	906	E1
TATCTA	5.9	77.1	1.68	763	E1
ACATAC	4.8	63.3	1.93	581	E1
GTATAC	3.7	106.5	1.43	569	E1
AAATAG	5.2	83.7	1.14	494	E1
TAGTTA	5.7	61.0	1.33	461	E1
TGTACA	3.6	74.2	1.67	448	E1
ATGTGT	4.1	62.0	1.47	371	E1
ATAGAT	4.0	57.0	1.57	353	E1
GTAAAT	3.7	64.5	1.46	347	E1
TTATTT	8.0	145.6	1.79	2082	E2
TTTATT	8.4	88.8	1.68	1250	E2
ATTATT	5.0	110.8	1.81	999	E2
TTAATT	5.7	98.1	1.49	831	E2
TTTCTT	6.3	126.4	1.03	815	E2
TTTTCT	5.6	111.1	1.10	687	E2
TCATTT	3.8	93.8	1.36	478	E2
TTCATT	6.5	51.8	1.35	453	E2
TTATTA	4.7	51.3	1.88	449	E2
TTTTGT	5.4	63.7	1.15	391	E2
TAGTTT	3.8	81.2	1.23	381	E2
TTATTC	5.1	64.1	1.16	377	E2
TATTCT	4.1	75.0	1.16	355	E2
TCTATT	4.6	53.5	1.14	277	E2
TAATTG	4.0	53.4	1.09	234	E2
AAATAA	10.3	191.0	1.79	3518	E3
AATAAA	8.8	206.9	1.68	3058	E3
AAAAAA	7.5	137.7	1.33	1367	E3
AATTAA	5.2	113.2	1.49	879	E3
AATAGA	3.6	76.6	1.14	309	E3
AGTTAA	3.6	56.6	1.03	211	E3
TTACGT	4.0	51.6	1.18	244	E4

See Table 1 for legend and text for details.

Signal E1 includes TATATA as well as many single-base substitutions and single-base shifts, that are characterised by a prominent peak between –50 and –30 relative to the cleavage site. This cluster strongly overlaps with the signal D1 extracted from downstream sequences, and with the signal element I in Graber et al. (25).

Signal E2 has some words in common with D2. These words all contain many Ts so we think they represent a single signal that we call, thereafter, T-rich signal. These words show a bimodal distribution, with a strong peak at the cleavage site, and a second upstream peak, around –60 from the cleavage site, separated by a valley at –25. The relative importance of both peaks is variable between the words (not shown) but the minimum is always coincident. This signal corresponds approximately to the combination of signals III and IV of Graber et al. (25).

Signal E3 contains a series of A-rich words that show an acute peak 25 bp upstream of the cleavage site, and a sensible valley at the cleavage site location (–10 to +20). We include in this cluster the word AAAAAA, although it appears isolated in the profile similarity tree (Fig. 3B). Indeed, AAAAAA shows the same position profile, with an additional downstream hill, starting at position +20. Signal E3 was not isolated from the analysis of all downstream sequences performed above, but is similar to Graber’s signal II (25). Because of the A-richness of all its words we call it A-rich.

Signal E4 contains a single word, TTACGT, whose statistical significance is just above the thresholds for the three tests (Table 2). We consider it as a false positive and discard it from further analysis.

In spite of the overlaps, our signals differ from Graber ones: we have some additional words (due to the systematic clustering approach), and some other words that they isolated have been filtered out by our procedure. These words are generally single-base shifts from some more significant word, and their filtering out probably comes from the fact that we use a higher order Markov chain model. Another difference is that signal E2 has a two-peak profile different from the one obtained by Graber et al. (25).

In order to better compare these results with the ones from whole genome analysis we also measured the profiles of signals E1–E4 from the stop codon. The graph for E1 is, basically, identical to that obtained for D1 in genome analysis. The graph for E2 is similar to that of D2 and the graphs for E3 and E4 do not show any bias in their profiles (not shown). These results demonstrate that the EST data set behaves similarly to the whole of the yeast genes.

Signal counts in downstream sequences

If the signals extracted by our analysis are important for polyadenylation and/or mRNA maturation, one expects to find them in most yeast genes. We counted the number of occurrences of the respective signals in the set of 6217 200 bp downstream sequences. We discarded the patterns that were single-base shifts from a more significant pattern, to avoid counting the same signal twice. The remaining words are highlighted in bold in Tables 1 and 2. The TATATA-like signals are found in the vast majority of genomic ORFs (85% for signal D1, 90% for signal E1). The T- and A-rich signals are slightly less frequent, but still they are found in about two-thirds of downstream sequences. We measured in the same way the occurrences in different subsets of these ORFs. The first subset comprises 384 questionable ORFs. Interestingly, the percentage of all signals is much lower for these ORFs (50%) than for the complete set. The questionability of these ORFs is thus confirmed by the analysis of their 3′ flanking sequences. In contrast, when selecting the subset of genes for which a 3′ EST was known [those from Joel Graber’s dataset (25)], all signals are found in higher abundance than in the complete set: no less than 96% of these ORFs contain at least one occurrence of signal E1, and 85% contain E2. The last subset tested comprises the ORFs for which there is no known homologue in sequence databases. This subset does not differ significantly from the complete set. Figure 4C shows the number of occurrences of the respective signals per gene, and highlights the differences between the sequence sets.

DISCUSSION

Even before completion of the yeast genome, Guo et al. (32) started from the knowledge of the EE pattern, and counted its occurrences within the set of yeast downstream sequences available at that time. They showed that TATATA has a much higher frequency in downstream sequences than in coding sequences. We extended this study to all possible oligonucleotides, and performed a statistical estimation of their over-representation in the complete set of downstream sequences. We combined three statistical tests to detect putative signals on the basis of complementary criteria: (i) over-representation, using a Markov chain model; (ii) preferential location in downstream versus upstream sequences; (iii) positional bias. We used probabilistic models to determine the threshold of over-representation (Z-scores) and positional bias (χ²). All words that fulfilled simultaneously the conditions on the three tests were then clustered according to their positional profile, leading to a restricted number of signals, each containing several words. We applied this analysis to two sequence sets. A set of 6217 downstream sequences, spanning 200 bp downstream the stop codon of all yeast genes, led to the isolation of two signals: D1 and D2. Another set of 1352 sequences surrounding cleavage sites, obtained from EST data (25), allowed us to isolate three signals (E1, E2 and E3). There is a strong similarity between signals D1 and E1, as well as between signals D2 and E2.

The first signal (D1 and E1) contains a series of TATATA-like words. Several substitutions are found at the third and fourth nucleotides. Not all substitutions are allowed, but only a few ones at specific positions. Moreover, except for TAcgTA, substitutions at different positions are not combined. The signal specificity is thus better described by a list of words (those isolated by our analysis and shown in Table 1) than by a degenerated consensus. Besides their high Z-score, these TATATA-like sequences are also characterised by a strong bias towards downstream positions in yeast gene flanks and by a strong peak around +35 bp after the stop codon, corresponding on average to a peak at –40 from the poly(A) site. All these properties coincide with those expected for a general polyadenylation EE in yeast.

The presence of many single-base shifts from the TATATA-like words (e.g. ATATAT, ATGTAT) may reflect that the actual size of the EE consensus word is longer than six letters. We made similar analyses with words of size five to nine and always found high significance for (TA)_n and (AT)_n words (http://www.ucmb.ulb.ac.be/bioinformatics/rsa-tools/ ). The existence of repeated or longer TATATA-like elements in some genes functioning as EE has been documented (13,32,33). The mutational analysis (11) also suggests that longer TA repeats can improve the activity of the EE. According to this we suggest that six letters is the minimum length for an EE but that longer or repeated words are also common and, perhaps, more efficient.

For a signal sequence to carry out a biological function some kind of recognition by other molecules is required. This is exactly what happens with the EE in the yeast S.cerevisiae. Yeast polyadenylation requires the interaction between protein factors and RNA sequences. Five factors, CFIA, CFIB, CFII, PFI and PAP, are needed in yeast for accurate pre-mRNA cleavage and polyadenylation in vitro (reviewed in 1). It has been shown that the CFII subunit Cft2p can be cross-linked to mRNA, and requires for this the EE (24). Moreover, CFII enhances the binding of Hrp1p (the only component of CFIB) to the RNA precursor. This binding also requires the EE, and plays an important role in the selection of poly(A) site (35). Our results suggest that the EEs are slightly degenerated sequences, both in sequence and length, and provide a list of putative variants. Because it has been documented in natural cases (9,34 and references therein) as well as in synthetic constructions (11) it seems that TATATA is the most efficient and common EE in yeast. This does not mean, however, that some variants of these sequence or even different sequences cannot act as EE. Some of these cases have been described, i.e. TRP1, ARO4, TRP4, GCN4 (9 and references therein). Our analysis can only find sequences that are very common and significantly biased but other less frequent sequences or not biased might prove efficient as well. However, we observed a remarkable linear correlation (Fig. 1) between Z-score and the experimental measurement of efficiency (11). The only exception is TAAGTA, which has a Z-score >5 but is inefficient. However, this word has a weaker positional bias and convergent/divergent ratio than the other ones in its group, so that it is suppressed from the selection in signal D1, and appears with a weaker global score in signal E1. Globally, it thus seems that the most efficient elements are the most over-represented.

We have no clear explanation for the frequent occurrence of the second kind of signal, made of T-rich words (signals D2 and E2). This signal is less frequent but still very common (65–72% of the ORFs). It shows a relatively wide peak at +55 from the stop codon and two peaks from the poly(A) site: the first one is located over the poly(A) site, as was previously shown (25), and the second peak 60 bp upstream. The failure to discriminate two peaks in downstream sequences (Fig. 4A) is probably due to the variability in the distance between stop codon and poly(A) site. The respective peaks could exert different functions. It has been shown that Rna15p, a subunit of the CF1A factor, has higher affinity for U-rich RNA (discussed in 1). Also, the coincidence of the second peak with the poly(A) site suggests a role for it in the definition of cutting site.

The existence of sharp peak at –25 from the poly site for the A-rich cluster (E3) suggests that it can be also a feature of yeast 3′ trailers. This result was also found by Graber et al. (25). They suggested that these words are similar to those proposed as PEs. No clear consensus sequence has been established for the PE. The preferred position for the PE is 20–30 nucleotides upstream of the poly(A) site (1), which coincides very well with these results. It has been found mainly downstream but sometimes upstream of the EE (9,34). This signal was not detected from the whole genome analysis because the A-rich words were discarded due to their low χ² result in position analysis. However, most of them have Z-scores higher than 14 (not shown), which means that those sequences are highly over-represented as well. The representation of those putative PEs is not as high as for EEs but it is still found in a high proportion (63%) of downstream sequences.

It is striking that four out of the six words of the A-rich signal (E3) are the reverse complement of words of the T-rich signal (E2). Assuming that the A-rich signal could be a PE, this function could be exerted through base-pairing with the surrounding T-rich signals. Experimental work should be done to test this hypothesis. However, A- and T-rich signals seem to be found independently from each other in the downstream sequences, as measured by a Pearson dependence test (not shown). In contrast, a clear correlation exists between putative EEs and the other signals: sequences having an EE-like sequence are more likely to have a T-rich sequence as well. Similarly, A-rich signals are significantly more frequent in sequences possessing an EE-like element.

Our analysis of EST data coincides partially with that done by Graber et al. (25). The same signals are isolated, but the word composition differs. We think that the list of words extracted by our triple analysis probably reflects more accurately the variability of the signals, due to some improvements in the statistical approach: use of a third-order Markov chain; position bias calculated with χ² statistics; choice of thresholds taking into account the number of possible patterns. Profiling from the stop codon allows us to compare and mutually validate the results obtained with the two different sets of data: whole set of downstream sequences and EST data. The use of the stop codon as a reference indicates that the preferred location of the word elements is also related with the distance from the end of the ORF. This fact has never been pointed out before. Our analysis thus suggests that EEs and, to a lesser extent, T-rich elements, have a preferred distance from the end of the translated sequence.

The existence of an optimum distance for EEs from both ends of the mRNA trailer means that the standard poly(A) typical signal for yeast spans no more than 80 bp with similar distances both from the stop codon and from the poly(A) site (Fig. 5). This result is coherent with the experimental data (9) and with the statistical analysis of the mRNA trailer length carried out by Graber et al. (25). This length is shorter than the average termination distance calculated by Dujon (31). This can be due in part to the space needed by RNA polymerase II to terminate transcription after the poly(A) site (1). Alternatively, it is possible that the intergenic region between convergent ORFs includes, in many cases, non-functional spaces.