Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 May 30;14(22):5119–5126. doi: 10.1021/acs.jpclett.3c00526

Emergent Magnetism as a Cooperative Effect of Interactions and Reservoir

M Shiranzaei 1, S Kalhöfer 1, J Fransson 1,*
PMCID: PMC10258847  PMID: 37249543

Abstract

graphic file with name jz3c00526_0005.jpg

Closed shell molecular structures are under normal conditions time-reversal invariant. Experimental evidence points, however, toward that this invariance may be locally violated when the structure is in contact with a particle reservoir. The mechanisms behind such local symmetry breaking are not clear by any means. By considering a minimal model for a closed shell structure, here we propose that the symmetry breaking may result from a combination of internal and/or external interactions. It is shown that a magnetic moment of a localized electron level can be generated and maintained under the influence of such a combination. The theoretical results should cast new light on the mechanisms that may form magnetic properties in molecular compounds.

Molecules, as well as single atoms, which are in closed shell configurations when isolated, can acquire a magnetic state when, e.g., immersed in solution,1,2 attached on a surface,3−9 or being in embedded in clusters comprising several components.10−17 Such properties can be exploited in, for instance, anomalous Hall devices,18−20 electron spin resonance,21,22 exploration of superconductivity in the presence of spin impurities23 giving rise to Yu-Shiba-Rusinov states,24,25 and in structures with properties, such as coercivity13−17 and spin-filtering,16,26−28 that strengthen with temperature.

The origin of the magnetic state in the closed shell configuration can be effectively summarized as an interplay between the Pauli exclusion principle and the Hund’s rules. Although these rules with some success can be employed also in a more general context, questions about the emergence of magnetic states in molecules that are normally regarded as nonmagnetic inevitably arise. For instance, chiral molecules provide urgent examples of closed shell structures which, nevertheless, display magnetic properties when in contact with otherwise nonmagnetic metals, see, e.g., refs (8, 18, 19, 22, 28, and 29).

In this article we address the issue of the emergence of a magnetic state in or in the proximity of a local electronic structure when it is being exposed to an external environment. We begin by demonstrating that a spin degenerate molecular level may become spin-polarized if two conditions are met. First, there should exist internal molecular interactions which have the potential to break the time-reversal symmetry, and second, the molecular level must be in contact with an external reservoir. We show that the nature of the reservoir, whether it is Fermionic or Bosonic, is secondary. This observation, hence, implies that also molecules in a purely thermal environment may be spontaneously polarized.

As a corollary result of these conditions, we also show that the spin-degeneracy of a localized electron may be broken by a spin-dependent coupling to a purely Bosonic reservoir. Breaking of the spin-degeneracy requires, however, the presence of both spin-conserving and spin-nonconserving coupling. In this model we, furthermore, demonstrate the emergence of a nonvanishing magnetic moment and an associated crossover temperature at which this moment undergoes a sign change.

We explain our findings to be a result of confluent interactions since these results cannot be obtained in a system with a single type of interaction. For simplicity, assume that there are two sources of interactions which can be formulated through the quantities V0σ0 and V1·σ, where σ0 and σ are the 2 × 2-unit matrix and vector of Pauli spin matrices. When these two interactions coexist, the effective interaction changes the spectrum as Inline graphic, which opens up the possibility to break the spin-degeneracy whenever both V0 and V1 contribute.

We notice that the nature of the interactions may comprise electron–electron and electron–phonon type of interactions but may also stem from, e.g., light–matter interactions of different kinds. The important feature that has to be recognized in this context is the presence of components with different symmetries with respect to the spin degrees of freedom. In this sense we stipulate that there should be one component that couples to the electron charge and one to the electron spin.

As a philosophical remark, our results are important since they challenge the widespread view that we can interpret measurements in terms of subsystems where the environment has a negligible effect, and we present a concrete example where this is not the case. Despite that we are taught in our scientific training that a measurement inevitably influences the properties of the sample, both interpretations of experimental results as well as theoretical descriptions are many times based on complete negligence of the reservoir to which the sample is connected.

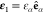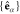The purpose here is to evaluate the magnetic moment ⟨m0⟩ of a localized electron represented by the spectrum ε = ε0σ0 + ε1·σ, where ε0 and ε1 denote the energies corresponding to the spin-independent and spin-dependent degrees of freedom. Here, the latter is a three component vector, Inline graphic, in some normalized orthogonal basis Inline graphic, which accounts for, e.g, spin–orbit interactions and local spin-anisotropy. 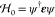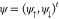The model corresponding to this spectrum can be written Inline graphic, where Inline graphic denotes the spinor for the localized state.

In order to enable a general treatment of the local properties, we calculate the expectation value of the magnetic moment ⟨m⟩ in terms of the Green function GLS for the local electron through the relation Inline graphic, where Inline graphic denotes the retarded Green function and f(ω) is the Fermi–Dirac distribution function, whereas sp is the trace over spin 1/2 space. The equation of motion for GLS can be cast in the Dyson-like form

graphic file with name jz3c00526_m008.jpg 1

where gLS = gLS(z) = (z – ε)−1, Inline graphic, is the bare Green function defined by Inline graphic, whereas Σ denotes the self-energy caused by the interactions the local electron is subject to. In this context, one can notice that the self-energy has (i) an energy dependence, Σ = Σ(z), and (ii) can be written in the form Σ = Σ0σ0 + Σ1·σ, which are natural conditions for spin 1/2 particles. Physically, this partitioning represents the charge- (Σ0) and spin-dependent (Σ1) components of the interactions. However, in addition we shall make the replacement Σ0 → V + Σ0. In this construction, V may define a contribution caused by hybridization between the localized state and an external reservoir, whereas the self-energy Σ may be attributed to internal or external interactions associated with the localized electron. There is, nevertheless, nothing that prevents the opposite association of V and Σ, that is, that the former belongs to the molecule and the latter represents the interactions with the environment, as we shall see in the concrete example below.

Summarizing these facts, it is straightforward to write the retarded/advanced Green function as

graphic file with name jz3c00526_m011.jpg 2

with the poles

graphic file with name jz3c00526_m012.jpg 3

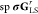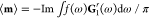Of particular interest here is the component comprising the Pauli matrices, since only this term can contribute under the trace Inline graphic. Indeed, using the notation GLS = G0σ0 + G1·σ, it can be seen that Inline graphic. Here,

graphic file with name jz3c00526_m015.jpg 4

In order to sort out the origin of the induced magnetic moment, we set

graphic file with name jz3c00526_m016.jpg 5a
graphic file with name jz3c00526_m017.jpg 5b
graphic file with name jz3c00526_m018.jpg 5c

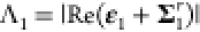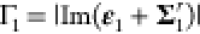and keep in mind that Inline graphic and Inline graphic. The lesser Green function can, then, be written

graphic file with name jz3c00526_m021.jpg 6

where ω± = λ + Λ0 ± Λ1 and Γ± = γ + Γ0 ± Γ1.

As we wish to determine the origin of the magnetic moment, assume, for the sake of argument, that 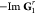Inline graphic strongly peaks at the resonance energies ω±, while it is nearly vanishing off resonance. This assumption is justified whenever the broadening Γ± is small in a neighborhood around ω±. Then, the magnetic moment can be estimated by approximately

graphic file with name jz3c00526_m023.jpg 7

Assuming, furthermore, that the self-energy strongly peaks at the energy ε0 + ω0, which does not coincide with either of ω±, then, one can notice that Γ0(ω±) ≈ 0 and Γ1(ω±) ≈ 0, such that Γs → γ. Implementing this observation, it can be seen that the magnetic moment reduces to

graphic file with name jz3c00526_m024.jpg 8

It should be mentioned that the energy ω0 is associated with the energy of the internal interactions captured in Σ.

Here, we stress the parameters Λ1 = Λ1(ω), Γ1 = Γ1(ω), etc. and that they acquire different values at the resonances ω = ω±. Hence, in the limit ε1 = 0, this calculation leading to eq 8 demonstrates that, despite the simplicity inferred, the result comprises a fundamentally important feature of the composite system discussed here. Namely, while the internal interactions, which lead to the self-energy Σ, provides an energy dependent shift of the electron resonances and their corresponding lifetimes, as well as an induced finite spin-splitting, and while the coupling between electrons in the localized level and the reservoir contributes to the level broadening of the local resonances, it is only when those two mechanisms are present simultaneously that a finite magnetic moment can be induced and maintained in the localized level.

The implications of this result should have bearing on the interpretation of experimental results, as well as, how a theoretical account for a phenomenon can be made irrelevant by exclusion of effects from the environment. In magnetism, for instance, many types of interactions which, at first sight, may appear unrelated may actually play a nontrivial role for the stabilization of the ordered state.16,17,30 The magnetic signatures observed after adsorbing nonmagnetic molecules onto the metallic surface18,20,25 stem from mechanisms that are unlikely to be captured within the conventional theory for magnetism.

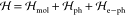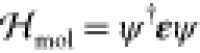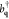It is by now established that time-reversal symmetry may be broken by inelastic scattering.31−33 Therefore, we consider a simplified example that may be used to illustrate a possible experimental outcome for single molecules in contact with a thermal reservoir. Such a system can be modeled by the Hamiltonian Inline graphic, where Inline graphic denotes the valence state in the molecule, whereas Inline graphic represents the thermal reservoir in which Inline graphic (bq) creates (annihilates) a phonon at the energy ωq. The electron–phonon coupling is provided through the term

graphic file with name jz3c00526_m029.jpg 9

where the coupling parameter Uq = u0qσ0 + u1q·σ, whereas Inline graphic. In addition to u0q which defines a generic coupling between charge and vibrational modes, u1q denotes a vibrationally induced spin–orbit coupling.27,34,35 Here, σ0 and σ denote the 2 × 2 identity and vector of Pauli matrices, respectively. It should be noticed that the vibrationally induced spin–orbit coupling u1q, in general, is nonvanishing in structures with broken inversion symmetry. Hence, in the present discussion we assume that those requirements are met in the structure.

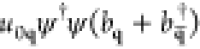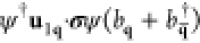The processes associated with the terms Inline graphic and Inline graphic are illustrated in Figure 1a,b, respectively. In processes of the former kind, the electrons emit or absorb phonons such that the total charge undergoes a transition to the emission or absorption state. By contrast, in processes of the latter, in which both charge and spin are coupled to the phonons, the emission and absorption processes are accompanied by electronic spin-flips and spin-dependent rates.

Figure 1.

Figure 1

Open in a new tab

Illustration of the electron–phonon processes involving (a) only charge and (b) both charge and spin. By emission or absorption of phonons, the total charge undergoes transitions to the states at the energies ε0 – ω and ε0 + ω, respectively. (a) For a coupling solely between the charge and phonons, there is no spin related process. (b) For a coupling that involves both charge and spin, the transitions may be accompanied by spin-flip and spin-dependent rates.

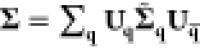The magnetic moment ⟨Mmol⟩ is related to the retarded single electron Green function Inline graphic, which is given by the Dyson-like equation in eq 1, where the self-energy Σ accounts for the phonon assisted absorption and emission processes illustrated in Figure 1. The structure of the model allows us to factorize the self-energy according to Inline graphic (see the Supporting Information for details concerning Inline graphic).

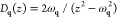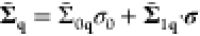While the equation for the Green function should be solved self-consistently, for the present purposes it is sufficient to replace the propagators in the self-energy with their corresponding bare ones, gmol(z) = (z – ε)−1 and Inline graphic. We, then, write the self-energy as Inline graphic where, for instance,

graphic file with name jz3c00526_m038.jpg 10

where εs = ε0 + sε1 (ε1 = |ϵ1|), whereas nB(ω) denotes the Bose–Einstein distribution function.

In the following, our aim is to emphasize how the thermal reservoir influences the temperature dependency of the induced magnetic moment. Therefore, we investigate a molecule with an unpolarized level, that is, setting ε1 = 0. In this limit, the unperturbed Green function simplifies to g(z) = σ0/(z – ε0) and the electron energy εs → ε0 in the self-energy, as well as Inline graphic. Nevertheless, because of the form of the electron–phonon coupling it can be seen that neither Σ0 nor Σ1 are nonzero (see the Supporting Information). Then, for Inline graphic, we have

graphic file with name jz3c00526_m041.jpg 11a
graphic file with name jz3c00526_m042.jpg 11b

First, we notice in this limit that a configuration such that u0q = 0 and u1q ≠ 0 may lead to a modification of the electronic state. The requirement is that 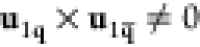Inline graphic. The momentum dependence of the coupling rate u1q is related to the phononic polarization vector ϵq which, in turn, depends on the lattice symmetries. For instance, inversion symmetry implies that Inline graphic, under which conditions, then, the self-energy Σ1 = 0, hence, also G1 = 0. On this note, it is relevant to mention that chiral phonons, for which there is no inversion symmetry, would open for the possibility to generate an electronic spin-polarization, something that was considered in refs (36−38).

From the expressions in eq 11, we calculate the density of electron states 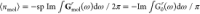Inline graphic, which, for u0q = u0 = 0.01 and u1q = 0, is plotted in Figure 2a,b as a function of the energy for temperatures corresponding to thermal energies between 1 and 20 meV. The unperturbed (bare) density of states has a single peak at the energy ε0 = 0.1 (red). When the electron–phonon interaction is turned on, this central peak splits into two which are located symmetrically around ε0. This is expected considering the poles given in eq 3. The plots in Figure 2a,b, illustrate the thermal evolution of the density of state for two different phonon velocities, (a) c = 0.01 and (b) c = 0.001. The width of the spectrum is expected to increase inversely with the velocity, since the more phonon modes contribute to the interactions with the electron the lower the velocity. This can be effectively seen in Figure 2i (dashed lines), where we have plotted the splitting between the resonances as a function of the thermal energy, illustrating that the bandwidth increases faster with lower phonon velocity.

Figure 2.

Figure 2

Open in a new tab

(a, b, e, f) Local densities of states (DOS) and (c, d, g, h, j–m) local spin-DOS as a function of the energy ω, for two different phonon velocities c = 0.01 and c = 0.001, and temperatures corresponding to the thermal energies kBT ∈ {1, 5, 10, 15, 20}. (i) Splitting of the density resonances in panels (a) and (b), dashed, and (e) and (f), solid, as a function of the thermal energy. Here, units are in meV. (a–d) ε0 = 0.1, u0q = 0.01, u1q = 0. The unperturbed (bare) DOS is shown for reference (red). 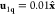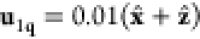(e–h) ε0 = 0.1, u0q = 0.01, Inline graphic. The unperturbed (bare) DOS is shown for reference (red). (j, l), spin ↑-projection, and (k, m), spin ↓-projection, for ε0 = 0.1, u0q = 0.01, Inline graphic.

Despite the splitting of the density of electron states, the spin degeneracy remains preserved. This is clear since the electron–phonon coupling only contains the spin-conserving component. This leads, trivially, to that Σ1 = 0, hence, the spin-dependent component G1 of the Green function also vanishes. In order to draw any conclusions about the spin properties under these conditions, however, we investigate the spin resolved densities of states captured in the matrix 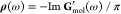Inline graphic. The spin-resolved density of electron states is plotted in Figure 2c,d, illustrating the degeneracy of the spin projections.

The combination of charge and spin coupling interactions with the phonons, on the other hand, results in the emergence of two resonance peaks alongside the initial elastic peak in the density of states. This is illustrated in Figure 2e–h, where we have added the spin-dependent component 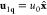Inline graphic. The side peaks shift to the higher energies with increasing temperature, while the central peak acquires a lowered amplitude. Also here, the lower velocity tends to induce a stronger shift of the side peaks with increasing temperature, as expected from the previous case, which is also seen in Figure 2I (solid lines).

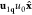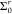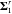The spin resolved densities of states are plotted in Figure 2g,h. As expected, the spin-dependent coupling Inline graphic breaks the degeneracy of the electronic structure. Quite unexpectedly at first glance, on the other hand, is that the spin projections are separated into two mutually exclusive branches. 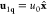Here, however, this is not surprising since the self-energies Inline graphic and Inline graphic are both proportional to Inline graphic and Inline graphic, which leads to that 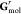Inline graphic can be partitioned into

graphic file with name jz3c00526_m054.jpg 12

where δ > 0 is infinitesimal.

This partitioning makes it clear that one central resonance is located at the elastic energy ω = ε0, whereas the other resonances are found at the condition 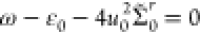Inline graphic, an equation which in the current approximation has two solutions. In Figure 2g,h, the resonances corresponding to the first and second contributions are signified by ±σx.

The associated molecular magnetic moment 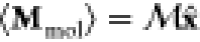Inline graphic resulting from these conditions is given by

graphic file with name jz3c00526_m057.jpg 13

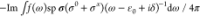
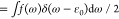
In this result, the first contribution results from the integral 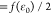Inline graphicInline graphicInline graphic, which corresponds to the first term in eq 12, whereas the second arises from the analogous calculation of the second term in eq 12. While this moment is, in general, nonvanishing, it undergoes a sign change at a finite temperature Txo. 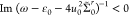This is understood by the opposite signs of the two contributions constituting Inline graphic in eq 13; recall that Inline graphic. Here, the first contribution, which is positive, dominates the magnetic moment at low temperature, see Figure 3. Put simply, in the main panel of Figure 3 it can be seen that whereas the central resonance at ω = ε0 is nearly fully occupied, the side resonances are only partially occupied. Since the former and latter resonances add positively and negatively, respectively, to the total moment, the moment is positive at sufficiently low temperature. 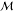This property is corroborated by our computations of the magnetic moment, see Figure 4a, which displays Inline graphic as a function of the temperature for different phonon velocities c. It should also be observed that Inline graphic as the electron–phonon coupling u0 → 0.

Figure 3.

Figure 3

Open in a new tab

Influence of the temperature on the magnetic moment, both with respect to the shifts of the inelastic resonances and the thermal occupation factor (Fermi–Dirac distribution function). At low temperatures (blue), the inelastic resonances are strongly asymmetrically occupied while the occupation becomes symmetrized with increasing temperature (red). Very low temperatures are shown for reference (black). The spin-resolved densities are given for the conditions in Figure 2h. The inset illustrates the phonon dispersions for three different velocities, (cyan) low, (purple) moderate, and (green) high, and the expected thermally occupied states (gray area) for each dispersion relation.

Figure 4.

Figure 4

Open in a new tab

Induced magnet moment, in units of the Bohr magneton μB, as a function of the thermal energy kBT, for the setup (a) ε0 = 0.1, u0q = 0.01, 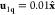Inline graphic, and (b) ε0 = 0.1, u0q = 0.01, 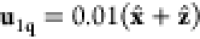Inline graphic, and phonon velocity (blue) c = 0.001, (red) c = 0.005, (black) c = 0.01, and (green) c = 0.05 [units: meV].

With increasing temperature, the occupations of all resonances increase; however, while the occupation of the central resonance is marginally increased, the side resonances approach full occupation such that the two branches cancel out each other. Nevertheless, since the overall spin-density has a slight overweight at the side resonances, this contribution eventually becomes larger than the central resonance such that the total moment changes sign at a crossover temperature Txo and becomes negative. The sign change and negative moment is clearly illustrated in Figure 4a, which also shows that the amplitude, both positive and negative, of the moment increases with decreasing velocity c.

The latter observation is understood in terms of the thermally accessible energies for a given temperature, see inset of Figure 3, illustrating the phonon dispersion relations for three velocities, (blue) low, (red) moderate, and (black) high, and the expected thermally occupied states (gray area) for each dispersion relation. For phonons with low velocity, a lower temperature is required to thermally access the energies for a larger portion of the phononic q-vectors in reciprocal space, compared to phonons with a higher velocity. Therefore, it is not surprising that slow phonons contribute more to the limiting magnetic moments than fast phonons.

Slowly vibrating molecules, either long polymers or composed in a crystal structure that generate acoustic vibrational modes with a low group velocity, should be suitable as a vibrational background in which defects, say some radical, may be embedded. Also, structures with optical vibrational modes would be relevant, especially ones with low group velocities. The general requirement that has to be fulfilled regardless of specific phonon structure is that inversion symmetry has to be broken for an effective vibrationally assisted spin–orbit interaction to be present.

Finally, we consider the configuration with u1q = u0(1, 0, 1). For these conditions, the molecular Green function can be written

graphic file with name jz3c00526_m065.jpg 14

In this setup, there is no clear separation of the central and side resonances; instead the two branches mix. In Figure 2j–m, we display plots of the spin resolved density of electron states, with uzq ≠ 0. First, one may notice that the resonances are mixtures of both spin projections. Second, it is clear that one spin branch is more heavily weighted on the side resonances, Figure 2j,k, whereas the other branch has an overweight on the central resonance, Figure 2l,m, albeit the central resonance cannot be clearly resolved.

In fact, the central resonance cannot be identified as a single resonance under the given conditions, since the electronic density comprises four distinct peaks. The four resonances can be found as the solutions to real parts of the two equations 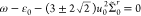Inline graphic, of which the + (−) equation provides the resonances which are more heavily weighted on the side (central) resonances. In this sense, each equation corresponds to one of the two spin branches, and despite the mixing between these, one can identify a slight discrimination between them.

In this configuration, the induced molecular magnetic moment can be written Inline graphic, where the factor 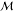Inline graphic is provided by the integral

graphic file with name jz3c00526_m069.jpg 15

which vanishes in the limit u0 → 0, hence emphasizing how the interactions are crucial for the formation of the magnetic moment. Again, we can identify a crossover temperature Txo at which the total moment changes sign from positive to negative, which can be seen in Figure 4b, in which the factor 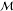Inline graphic is plotted as a function of the temperature, for different phonon velocities. The mechanism for this sign change is the same as in the previous configuration. Whereas one spin-projection becomes more or less fully occupied already at low temperature and the other is only partially occupied, the latter tends to become increasingly occupied with the temperature and eventually dominates the overall magnetic moment. It can also be observed that the total magnetic moment increases when the z-component is added to the already existing x-component of the interaction parameter u1q. This observation is, however, trivial due to the increased number of scattering channels that are opened.

A more important, and also interesting, observation that may be made is that the temperature for the sign change of the magnetic moment appears to be universal and independent of the phonon velocity, see Figures 2j–m and 4b. This property is not surprising when considering that the sign change is a result of the competition between the two contributions, c.f., eqs13 and 15. The two contributions have equal temperature dependencies irrespective of the phonon velocity which, therefore, leads to the specific phonon distribution not impacting the temperature at which the two contributions cancel. Should the two contributions, on the other, have unequal dependencies on the phonon distribution, then the crossover temperature may vary with, e.g., the phonon velocity. Currently, we are not aware of which type of electron–phonon interactions would cause such inhomogeneous temperature dependencies; however, it is possible that structures in which the phonon modes are strongly anisotropic would open up for such properties.

In summary, we have theoretically investigated the influence of combined interactions on a localized level and demonstrated that an electronic state may become spin-polarized when coupled to reservoirs. We show that a system which is nonmagnetic whenever isolated from an surrounding environment may spin-polarize when a connection to such an environment is made. The system may spin-polarize if there are, at least, two types of interactions of which at least one has an intrinsic spin-dependence associated with it. Formally, an interaction that can be expressed as V0σ0 and V1·σ changes the electronic spectrum by 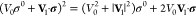Inline graphic. Hence, the electronic spectrum becomes spin-dependent if and only if both V0 and V1 are nonzero. Under those conditions, there is a potential for the system to acquire a nonvanishing magnetic moment.

As a corollary, we develop a theory for temperature-dependent magnetization in a molecule. We show that spin-dependent inelastic scattering, e.g., off phonons which may arise due to spin–orbit coupling,34 leads to breaking of the time-reversal symmetry. For this, we employ an unconventional treatment of electron scatterings off phonons by taking into account both the charge–phonon and spin–phonon couplings. While none of these couplings individually break the electronic spin degeneracy, our findings show that the combination of the two leads to a splitting of the spin channels. The effect we consider, which results in nonconserved energy collisions, originates from the interplay between spin–orbit coupling and vibrational modes. We, furthermore, demonstrate that the inelastic scattering does induce a nonzero magnetic moment of the initially unpolarized molecule, a moment for which magnitude increases with temperature but changes sign at a crossover temperature. The sign change of the magnetic moment can be explained in terms of competing influences from the relevant interactions.

Despite that we are currently aware of experimental results which comply with our theoretical discussion,8,18,19,22,28,29 it would intriguing to consider the effects under more extreme conditions, for instance, measurements of magnetically asymmetric thermopower or using magnetic force microscopy to measure asymmetric forces of chiral molecules attached to the surface.

Acknowledgments

The authors thank Vetenskapsrådet and Stiftelsen Olle Engkvist Byggmästare for support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.3c00526.

  • Details of the mathematical model and derivations of the electronic Green functions and magnetization (PDF)

  • Transparent Peer Review report available (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz3c00526_si_001.pdf (88.9KB, pdf)
jz3c00526_si_002.pdf (431.4KB, pdf)

References

  1. Inglis R.; Bendix J.; Brock-Nannestad T.; Weihe H.; Brechin E. K.; Piligkos S. Frozen-solution magnetisation dynamics of hexanuclear oxime-based MnIII Single-Molecule Magnets. Chem. Sci. 2010, 1, 631–636. 10.1039/c0sc00327a. [DOI] [Google Scholar]
  2. Venkataramani S.; Jana U.; Dommaschk M.; Sönnichsen F. D.; Tuczek F.; Herges R. Magnetic Bistability of Molecules in Homogeneous Solution at Room Temperature. Science 2011, 331, 445–448. 10.1126/science.1201180. [DOI] [PubMed] [Google Scholar]
  3. Mannini M.; Pineider F.; Danieli C.; Totti F.; Sorace L.; Sainctavit P.; Arrio M. A.; Otero E.; Joly L.; Cezar J. C.; et al. Quantum tunnelling of the magnetization in a monolayer of oriented single-molecule magnets. Nature 2010, 468, 417–421. 10.1038/nature09478. [DOI] [PubMed] [Google Scholar]
  4. Khajetoorians A. A.; Wiebe J.; Chilian B.; Lounis S.; Blügel S.; Wiesendanger R. Atom-by-atom engineering and magnetometry of tailored nanomagnets. Nat. Phys. 2012, 8, 497–503. 10.1038/nphys2299. [DOI] [Google Scholar]
  5. Holmberg R. J.; Murugesu M. Adhering magnetic molecules to surfaces. J. Mater. Chem. C 2015, 3, 11986–11998. 10.1039/C5TC03225C. [DOI] [Google Scholar]
  6. Donati F.; Rusponi S.; Stepanow S.; Wäckerlin C.; Singha A.; Persichetti L.; Baltic R.; Diller K.; Patthey F.; Fernandes E.; et al. Magnetic remanence in single atoms. Science 2016, 352, 318–321. 10.1126/science.aad9898. [DOI] [PubMed] [Google Scholar]
  7. Diller K.; Singha A.; Pivetta M.; Wäckerlin C.; Hellwig R.; Verdini A.; Cossaro A.; Floreano L.; Vélez-Fort E.; Dreiser J.; et al. Magnetic properties of on-surface synthesized single-ion molecular magnets. RSC Adv. 2019, 9, 34421–34429. 10.1039/C9RA06803A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Alpern H.; Amundsen M.; Hartmann R.; Sukenik N.; Spuri A.; Yochelis S.; Prokscha T.; Gutkin V.; Anahory Y.; Scheer E.; et al. Unconventional Meissner screening induced by chiral molecules in a conventional superconductor. Phys. Rev. Materials 2021, 5, 114801. 10.1103/PhysRevMaterials.5.114801. [DOI] [Google Scholar]
  9. Wei M.; Lu X.; Qiao J.; Ren S.; Hao X.-T.; Qin W. Response of Spin to Chiral Orbit and Phonon in Organic Chiral Ferrimagnetic Crystals. ACS Nano 2022, 16, 13049–13056. 10.1021/acsnano.2c05601. [DOI] [PubMed] [Google Scholar]
  10. Ishikawa N.; Sugita M.; Ishikawa T.; Koshihara S.-y.; Kaizu Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125, 8694–8695. 10.1021/ja029629n. [DOI] [PubMed] [Google Scholar]
  11. Prado Y.; Daffé N.; Michel A.; Georgelin T.; Yaacoub N.; Grenèche J.-M.; Choueikani F.; Otero E.; Ohresser P.; Arrio M.-A.; et al. Enhancing the magnetic anisotropy of maghemite nanoparticles via the surface coordination of molecular complexes. Nat. Commun. 2015, 6, 10139. 10.1038/ncomms10139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ding M.; Cutsail G. E. III; Aravena D.; Amoza M.; Rouzières M.; Dechambenoit P.; Losovyj Y.; Pink M.; Ruiz E.; Clérac R.; et al. A low spin manganese(iv) nitride single molecule magnet. Chem. Sci. 2016, 7, 6132–6140. 10.1039/C6SC01469K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dhara B.; Tarafder K.; Jha P. K.; Panja S. N.; Nair S.; Oppeneer P. M.; Ballav N. Possible Room-Temperature Ferromagnetism in Self-Assembled Ensembles of Paramagnetic and Diamagnetic Molecular Semiconductors. J. Phys. Chem. Lett. 2016, 7, 4988–4995. 10.1021/acs.jpclett.6b02063. [DOI] [PubMed] [Google Scholar]
  14. Dhara B.; Jha P. K.; Gupta K.; Bind V. K.; Ballav N. Diamagnetic Molecules Exhibiting Room-Temperature Ferromagnetism in Supramolecular Aggregates. J. Phys. Chem. C 2017, 121, 12159–12167. 10.1021/acs.jpcc.7b02145. [DOI] [Google Scholar]
  15. Miwa S.; Kondou K.; Sakamoto S.; Nihonyanagi A.; Araoka F.; Otani Y.; Miyajima D. Chirality-induced effective magnetic field in a phthalocyanine molecule. Applied Physics Express 2020, 13, 113001. 10.35848/1882-0786/abbf67. [DOI] [Google Scholar]
  16. Mondal A. K.; Brown N.; Mishra S.; Makam P.; Wing D.; Gilead S.; Wiesenfeld Y.; Leitus G.; Shimon L. J. W.; Carmieli R.; et al. Long-Range Spin-Selective Transport in Chiral Metal–Organic Crystals with Temperature-Activated Magnetization. ACS Nano 2020, 14, 16624–16633. 10.1021/acsnano.0c07569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sang Y.; Mishra S.; Tassinari F.; Karuppannan S. K.; Carmieli R.; Teo R. D.; Migliore A.; Beratan D. N.; Gray H. B.; Pecht I.; et al. Temperature Dependence of Charge and Spin Transfer in Azurin. J. Phys. Chem. C 2021, 125, 9875–9883. 10.1021/acs.jpcc.1c01218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ben Dor O.; Yochelis S.; Radko A.; Vankayala K.; Capua E.; Capua A.; Yang S.-H.; Baczewski L. T.; Parkin S. S. P.; Naaman R.; et al. Magnetization switching in ferromagnets by adsorbed chiral molecules without current or external magnetic field. Nat. Commun. 2017, 8, 14567. 10.1038/ncomms14567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Smolinsky E. Z. B.; Neubauer A.; Kumar A.; Yochelis S.; Capua E.; Carmieli R.; Paltiel Y.; Naaman R.; Michaeli K. Electric Field-Controlled Magnetization in GaAs/AlGaAs Heterostructures–Chiral Organic Molecules Hybrids. J. Phys. Chem. Lett. 2019, 10, 1139–1145. 10.1021/acs.jpclett.9b00092. [DOI] [PubMed] [Google Scholar]
  20. Goren N.; Yochelis S.; Jung G.; Paltiel Y. Magnetic passivation using chiral molecules. Appl. Phys. Lett. 2021, 118, 172401. 10.1063/5.0048774. [DOI] [Google Scholar]
  21. Baumann S.; Paul W.; Choi T.; Lutz C. P.; Ardavan A.; Heinrich A. J. Electron paramagnetic resonance of individual atoms on a surface. Science 2015, 350, 417–420. 10.1126/science.aac8703. [DOI] [PubMed] [Google Scholar]
  22. Privitera A.; Macaluso E.; Chiesa A.; Gabbani A.; Faccio D.; Giuri D.; Briganti M.; Giaconi N.; Santanni F.; Jarmouni N.; et al. Direct detection of spin polarization in photoinduced charge transfer through a chiral bridge. Chem. Sci. 2022, 13, 12208–12218. 10.1039/D2SC03712B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Heinrich B. W.; Braun L.; Pascual J. I.; Franke K. J. Protection of excited spin states by a superconducting energy gap. Nat. Phys. 2013, 9, 765–768. 10.1038/nphys2794. [DOI] [Google Scholar]
  24. Franke K. J.; Schulze G.; Pascual J. I. Competition of Superconducting Phenomena and Kondo Screening at the Nanoscale. Science 2011, 332, 940–944. 10.1126/science.1202204. [DOI] [PubMed] [Google Scholar]
  25. Alpern H.; Yavilberg K.; Dvir T.; Sukenik N.; Klang M.; Yochelis S.; Cohen H.; Grosfeld E.; Steinberg H.; Paltiel Y.; et al. Magnetic-related States and Order Parameter Induced in a Conventional Superconductor by Nonmagnetic Chiral Molecules. Nano Lett. 2019, 19, 5167–5175. 10.1021/acs.nanolett.9b01552. [DOI] [PubMed] [Google Scholar]
  26. Torres-Cavanillas R.; Escorcia-Ariza G.; Brotons-Alcázar I.; Sanchis-Gual R.; Mondal P. C.; Rosaleny L. E.; Giménez-Santamarina S.; Sessolo M.; Galbiati M.; Tatay S.; et al. Reinforced Room-Temperature Spin Filtering in Chiral Paramagnetic Metallopeptides. J. Am. Chem. Soc. 2020, 142, 17572–17580. 10.1021/jacs.0c07531. [DOI] [PubMed] [Google Scholar]
  27. Das T. K.; Tassinari F.; Naaman R.; Fransson J. Temperature-Dependent Chiral-Induced Spin Selectivity Effect: Experiments and Theory. J. Phys. Chem. C 2022, 126, 3257–3264. 10.1021/acs.jpcc.1c10550. [DOI] [Google Scholar]
  28. Kondou K.; Shiga M.; Sakamoto S.; Inuzuka H.; Nihonyanagi A.; Araoka F.; Kobayashi M.; Miwa S.; Miyajima D.; Otani Y. Chirality-Induced Magnetoresistance Due to Thermally Driven Spin Polarization. J. Am. Chem. Soc. 2022, 144, 7302–7307. 10.1021/jacs.2c00496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Al-Bustami H.; Koplovitz G.; Primc D.; Yochelis S.; Capua E.; Porath D.; Naaman R.; Paltiel Y. Single Nanoparticle Magnetic Spin Memristor. Small 2018, 14, 1801249. 10.1002/smll.201801249. [DOI] [PubMed] [Google Scholar]
  30. Fransson J. Vibrationally Induced Magnetism in Supramolecular Aggregates. J. Phys. Chem. Lett. 2023, 14, 2558–2564. 10.1021/acs.jpclett.3c00157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sánchez D.; Serra L. m. c. Thermoelectric transport of mesoscopic conductors coupled to voltage and thermal probes. Phys. Rev. B 2011, 84, 201307. 10.1103/PhysRevB.84.201307. [DOI] [Google Scholar]
  32. Saito K.; Benenti G.; Casati G.; Prosen T. c. v. Thermopower with broken time-reversal symmetry. Phys. Rev. B 2011, 84, 201306. 10.1103/PhysRevB.84.201306. [DOI] [PubMed] [Google Scholar]
  33. Fransson J. Charge Redistribution and Spin Polarization Driven by Correlation Induced Electron Exchange in Chiral Molecules. Nano Lett. 2021, 21, 3026–3032. 10.1021/acs.nanolett.1c00183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Fransson J. Vibrational origin of exchange splitting and chiral-induced spin selectivity. Phys. Rev. B 2020, 102, 235416. 10.1103/PhysRevB.102.235416. [DOI] [Google Scholar]
  35. Maslov M.; Lemeshko M.; Yakaboylu E. Synthetic spin-orbit coupling mediated by a bosonic environment. Phys. Rev. B 2020, 101, 184104. 10.1103/PhysRevB.101.184104. [DOI] [Google Scholar]
  36. Juraschek D. M.; Neuman T. c. v.; Narang P. Giant effective magnetic fields from optically driven chiral phonons in 4f paramagnets. Phys. Rev. Res. 2022, 4, 013129. 10.1103/PhysRevResearch.4.013129. [DOI] [Google Scholar]
  37. Geilhufe R. M.; Hergert W. Electron magnetic moment of transient chiral phonons in KTaO3. Phys. Rev. B 2023, 107, L020406. 10.1103/PhysRevB.107.L020406. [DOI] [Google Scholar]
  38. Fransson J. Chiral Phonon Induced Spin-Polarization. Phys. Rev. Research 2023, 5, L022039. 10.1103/PhysRevResearch.5.L022039. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz3c00526_si_001.pdf (88.9KB, pdf)
jz3c00526_si_002.pdf (431.4KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES