Modeling Psychopathology: From Data Models to Formal Theories

Abstract

Over the past decade, there has been a surge of empirical research investigating mental disorders as complex systems. In this paper, we investigate how to best make use of this growing body of empirical research and move the field toward its fundamental aims of explaining, predicting, and controlling psychopathology. We first review the contemporary philosophy of science literature on scientific theories and argue that fully achieving the aims of explanation, prediction, and control requires that we construct formal theories of mental disorders: theories expressed in the language of mathematics or a computational programming language. We then investigate three routes by which one can use empirical findings (i.e., data models) to construct formal theories: (a) using data models themselves as formal theories, (b) using data models to infer formal theories, and (c) comparing empirical data models to theory-implied data models in order to evaluate and refine an existing formal theory. We argue that the third approach is the most promising path forward. We conclude by introducing the Abductive Formal Theory Construction (AFTC) framework, informed by both our review of philosophy of science and our methodological investigation. We argue that this approach provides a clear and promising way forward for using empirical research to inform the generation, development, and testing of formal theories both in the domain of psychopathology and in the broader field of psychological science.

1. Introduction

Mental disorders are complex phenomena: highly heterogeneous and massively multifactorial (e.g., Kendler, 2019). In recent years, researchers have called for approaches to psychiatric research that embrace this complexity, evaluating how mental disorders operate as complex systems (Gardner & Kleinman, 2019; Hayes & Andrews, 2020). The “network approach” to psychopathology addresses these calls, conceptualizing mental disorders as systems of interacting components, with emphasis on causal relations among the symptoms of a disorder (e.g., Borsboom & Cramer, 2013; Schmittmann et al., 2013; Borsboom, 2017). From this perspective, symptoms are not caused by an underlying disorder, rather the symptoms themselves and the causal relations among them constitute the disorder.

The notion that causal relationships among symptoms may figure prominently in the etiology of mental disorders has stimulated a rapidly growing body of empirical research (for reviews see e.g., Robinaugh, Hoekstra, & Borsboom, 2019; Contreras, Nieto, Valiente, Espinosa, & Vazquez, 2019). Most of this work employs statistical models that allow researchers to study the multivariate dependencies among symptoms. This quickly expanding empirical literature has provided rich information about the statistical relationships among those symptoms. However, it has also raised a significant concern: it remains unclear precisely how best to make use of this growing number of empirical findings to produce advances in our understanding of how mental disorders operate as complex systems.

This problem is not unique to the network approach to psychopathology. Psychiatry and applied psychology produce a massive number empirical findings every year, yet genuine progress toward our fundamental aims of explaining, predicting, and controlling mental disorders has remained stubbornly out of reach. In psychology more broadly, there is a growing concern that psychological theory is in a state of crisis (Oberauer & Lewandowsky, 2019; Muthukrishna & Henrich, 2019; Smaldino, 2019). Theories are rarely developed in a way that would indicate a genuine accumulation of knowledge, suggesting that we are failing to leverage the steady stream of empirical findings from psychological science into genuine understanding of psychological phenomena (Meehl, 1978).

Recently, we and others have argued that formalizing psychological theories as mathematical or computational models can help address the theory crisis in psychology (Smaldino, 2017; Robinaugh, Haslbeck, Ryan, Fried, & Waldorp, 2020; Guest & Martin, 2020; van Rooij & Baggio, 2020; Fried, 2020; Borsboom, van der Maas, Dalege, Kievit, & Haig, 2020). Formal theories have been fruitfully used in some areas of psychology, such as mathematical psychology (Estes, 1975), cognitive psychology (Ritter, Tehranchi, & Oury, 2019), and computational psychiatry (Friston, Redish, & Gordon, 2017; Huys, Maia, & Frank, 2016), but remain relatively rare outside these domains. More expansive use of formal theories, it is hoped, will equip theorists with tools for more rigorously generating and evaluating theories, laying the groundwork for accumulative advancement of psychological knowledge (Robinaugh et al., 2020). However, much remains unknown about how best to construct formal theories in domains such as clinical psychology, and even less is known about how best to use empirical data models to inform theory construction.

In this paper, we aim to address this gap in the literature by examining how data models commonly used within the network approach literature can best inform the construction of formal theories. We begin in Section 2 by discussing the nature of formal theories, the nature of data models, and their relation to one another. We identify three ways in which data models can be used to inform the construction of formal theories: (a) treating data models themselves as formal theories, (b) drawing direct inferences from data models to generate a formal theory, and (c) comparing theory-implied data models and empirical data models in order to evaluate and refine an existing formal theory. In Section 3, we investigate each of these approaches in the context of the network approach to psychopathology, using an example in which the true underlying system is known and evaluating which approach best informs the development of a theory of that system. Our analysis suggests that the third approach comparing theory-implied and empirical data models, though rare in psychology, is the most promising path forward. In Section 4, we propose the Abductive Formal Theory Construction (AFTC) framework: a staged methodology for theory construction built around the approach of comparing theory-implied and empirical data models. Using this framework, we detail how best to use empirical data models at each stage of theory construction, including the generation, development, and testing of psychological theories.

2. Data Models and Formal Theories

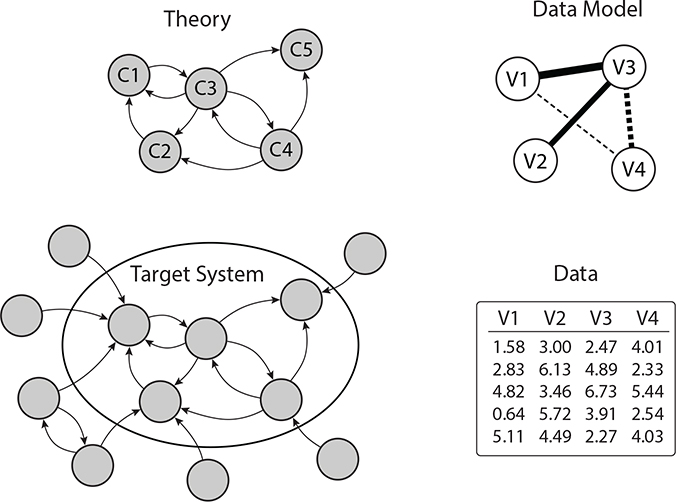
In this section we will examine the nature of scientific theories and how they support explanation, prediction, and control. We will begin by introducing four key concepts that we will use throughout the remainder of the paper: theory, target system, data, and data model (see Figure 1). We will illustrate each of these concepts using the example of panic disorder.

Figure 1:

The figure illustrates the concepts theory, target system, data, and data model. The target system is the system consisting of interacting components that gives rise to phenomena. Phenomena are robust features of the world captured by data models. Theories represent the structure of the target system, proposing a set of components C and the relations among them and positing that they give rise to the phenomena. Data for variables V are obtained by taking measurements of the components of the target system.

2.1. Theories, Phenomena, and Target Systems

Theories seek to explain phenomena: stable, recurrent, and general features of the world (Bogen & Woodward, 1988; Haig, 2008, 2014) such as the melting point of lead or the orbit of planets. In psychiatry, the most common phenomena to be explained are symptoms and syndromes. For example, researchers seek to explain the tendency for some individuals to experience panic attacks and the tendency for recurrent panic attacks to be accompanied by persistent worry about those attacks and avoidance of situations in which they may occur (Spitzer, Kroenke, & Williams, 1980), thereby cohering as the syndrome known as panic disorder.

Theories aim to explain phenomena by representing target systems: the particular parts of the real world and the relationships among them that give rise to the phenomena of interest (cf. Elliott-Graves, 2014). Theories can thus be understood as models that represent the target system (Suárez & Pero, 2019).¹ In psychiatric research, the target system comprises any components of the real world that give rise to these symptoms and syndromes, and may include genetic, neurobiological, physiological, emotional, cognitive, behavioral, social, and cultural components. Theories of psychopathology aim to represent these target systems, positing a specific set of components and relationships among them that give rise to the phenomena of interest. For example, researchers have generated numerous theories of panic disorder, specifying a set of components that they think interact to give rise to panic attacks and panic disorder. Among these, perhaps the most influential is Clark’s cognitive model of panic attacks, which posits that “if [stimuli] are perceived as a threat, a state of mild apprehension results. This state is accompanied by a wide range of bodily sensations. If these anxiety-produced sensations are interpreted in a catastrophic fashion, a further increase in apprehension occurs. This produces a further increase in bodily sensations and so on round in a vicious circle which culminates in a panic attack” (Clark, 1986). This cognitive theory of panic attacks specifies components (e.g., bodily sensations and a state of apprehension) and the relations among them (e.g., the “vicious cycle” of positive causal effects), positing that this is the target system that gives rise to panic attacks.

Because theories represent the target system, we can reason from theory in order to draw conclusions about the target system and the phenomena that arise from it. It is this capacity for surrogative reasoning (Swoyer, 1991) that allows theories to explain, predict, and control the world around us. For example, we can explain the rise and fall of predator and prey populations in the real world by appealing to the relationships between components specified in mathematical models representing these populations (H. I. Freedman, 1980; Nguyen & Frigg, 2017). We can predict what will occur when two atoms collide by deriving the expected outcome from models of particle physics (Higgs, 1964). And we can determine how to intervene to prevent panic attacks by appealing to the relationships posited in the cognitive model of panic attacks, determining that an intervention modifying a patient’s “catastrophic misinterpretations” should prevent the “vicious cycle” between arousal and perceived threat, thereby circumventing panic attacks (Clark, 1986). It is this ability to support surrogative reasoning that makes theories such powerful tools.

2.2. The Importance of Formal Theories

Surrogative reasoning relies on a theory’s structure: its components and the relations among them (Pero, 2015). This structure can be expressed in natural language (i.e., verbal theory) or a formal language, such as mathematics or computation (i.e., formal theory). For example, a verbal theory would state that the rate of change in an object’s temperature is proportional to the difference between its temperature and the temperature of its environment. A formal theory would instead express this relationship as a mathematical equation, such as $\frac{dT}{dt}=-k(T-E)$, where $\frac{dT}{dt}$ is the rate of change in temperature, T is the object’s temperature, and E is the temperature of the environment; or in a computational programming language, such as: for(t in 1:end) { T[t+1] = T[t]−k*(T[t]−E) }.

Expressing a theory in a mathematical or computational programming language gives formal theories many advantages over verbal theories (Smith & Conrey, 2007; Epstein, 2008; Lewandowsky & Farrell, 2010; Smaldino, 2017; Robinaugh et al., 2020). For our purposes here, there is one advantage of particular importance: Formalization enables precise deduction of the behavior implied by the theory. Verbal theories can, of course, also be used to deduce theory-implied behavior. However, due to the vagaries of language, verbal theories are typically imprecise, precluding exact predictions. For example, the verbal theory of temperature cooling described in the previous paragraph allows for some general sense of how the object’s temperature will evolve over time, but cannot be used to make specific predictions about how it will change or what the temperature will be at any given point in time. Indeed, because of the imprecision of verbal theories, there are often multiple ways in which those theories could be interpreted and implemented, each with a potentially divergent prediction about how the target system will evolve over time (Robinaugh et al., 2020). Consider the interpersonal theory of suicide, which posits that suicide arises from the simultaneous experience of perceived burdensomeness and thwarted belongingness (Van Orden et al., 2010). This theory fails to specify many aspects of this causal structure, such as the strength of these effects or the duration for which they must overlap before suicidal behavior arises (Hjelmeland & Loa Knizek, 2018). As a result, there are many possible implementations of this verbal theory, each of which could potentially lead to a different prediction about when suicidal behavior should be expected to arise (Millner, Robinaugh, & Nock, 2020). This imprecision thus substantially limits the theories ability to support surrogative reasoning and the degree to which we can empirically test the theory.

In contrast, formal theories are precise in their implementation as the mathematical notation or code in a computer programming language forces one to be specific about the structure of the theory (e.g., specifying the precise effect of one component on another).² The precision of formal theories allows us to deduce precisely how the target system will behave. This deduction can either be obtained analytically (e.g., from the mathematical equation) or computationally (e.g., through simulations from a computational model). For example, whereas the verbal theory of cooling only permitted a general sense of how the temperature will evolve over time, we can use the formal theory of cooling to predict the exact temperature of our object at any point in the future. Similarly, a formal implementation of the interpersonal theory of suicide would make highly specific predictions that could inform the prediction of suicide attempts (Millner et al., 2020). In other words, formal theories substantially strengthen surrogative reasoning, the very characteristic of scientific theories upon which we wish to capitalize.

2.2.1. A Formal Theory of Panic Disorder

The cognitive model of panic attacks described above is a verbal theory and is limited by the imprecision characteristic of most verbal theories. For example, in two recent papers, Fukano and Gunji (Fukano & Gunji, 2012) and Robinaugh and colleagues (Robinaugh, Haslbeck, et al., 2019) independently proposed two distinct formal implementations of this theory: taking the verbal theory and expressing it in two sets of differential equations. Notably, these distinct implementations of the same verbal theory make divergent predictions about when panic attacks should occur, illustrating the limitations of failing to precisely specify the theory (for further detail, see Robinaugh, Haslbeck, et al., 2019; Robinaugh et al., 2020).

In this paper, we will make extensive use of the formal theory proposed by Robinaugh and colleagues. A complete description of the generation of this theory can be found in the original paper (Robinaugh, Haslbeck, et al., 2019). For our purposes here, it is sufficient to note that the aim in developing this model was to take extant verbal theories, especially cognitive behavioral theories, and express them in the language of mathematics. For example, Clark’s verbal theory posits that a perception of threat can lead to arousal-related bodily sensations. However, the actual form and strength of this effect remain unspecified. In the mathematical model, we used a differential equation to precisely define this effect: $\frac{dA}{dt}=\alpha (\nu T-A)$. In this equation, there is a linear effect of Perceived Threat (T) on the rate of change of Arousal (A), with the strength of this effect specified by the parameter ν. The product of ν and T is the value Arousal is pulled toward: if νT is smaller than the current level of Arousal, $\frac{dA}{dt}$ will be negative and Arousal will decrease toward νT; if νT is greater than Arousal, $\frac{dA}{dt}$ is positive and Arousal increases toward νT. That is, Arousal is pulled towards νT, which is a linear function of T. Each model component was defined as a differential equation in this way (see middle panel in Figure 2), providing a formal theory of panic disorder.

Figure 2:

The left panel displays the key components of the theory proposed by Robinaugh, Haslbeck, et al. (2019) at play during panic attacks: Arousal, Perceived Threat, Escape Behavior and Arousal Schema. The arrows indicate the direct causal relationships which are posited to operate between these components in the formal theory. The middle panel displays the formal theory that specifies the precise nature of the relations among these components. The top equation defines the rate of change in arousal $\frac{dA}{dt}$ where A is arousal, T is perceived threat, H is homeostatic feedback, and N is a noise variable representing fluctuations in arousal due to both internal and external stimuli. The rate parameter α specifies the intrinsic rate at which arousal can change, and the slope parameters ν and κ determines the strength of the effect of perceived threat and homeostatic feedback on arousal, respectively. The middle equation defines the rate of change in perceived threat $\frac{dT}{dt}$, which depends on Arousal Schema through the parameter λ. The state variable E denotes escape behavior. The rate parameter γ specifies the rate at which perceived threat can change, the parameters λ and μ together specify the strength of arousal on perceived threat, and the parameter μ specifies the strength of the effect of escape behavior on perceived threat. The final equation specifies the rate of change in escape behavior $\frac{dE}{dt}$ as a function of perceived threat, which is determined by the rate parameter ∊ and two parameters specifying the strength of perceived threat’s effect on escape behavior: ρ and σ. The final panel on the right depicts the simulated behavior defined by these equations and, thus, implied by the theory.

By specifying the structure of the theory in the language of mathematics, we are able to solve the system numerically, thereby deducing the theory’s predictions about how the target system will behave. We were able to demonstrate, for example, that when the effect of Arousal on Perceived Threat is sufficiently strong, the positive feedback between these components is sufficient to send the system into runaway positive feedback, producing the characteristic surge of arousal, perceived threat, and escape behavior that we refer to as a panic attack (see right panel in Figure 2). That is, we were able to show, rather than merely assert, that the theory can explain the phenomenon of panic attacks. As this example illustrates, formalizing theory substantially strengthens our ability to deduce theory-implied target system behavior. A full realization of a theory’s usefulness thus all but requires that the theory be formalized. For that reason, our aim in psychiatric research should not merely be the construction of theories, but the construction of formal theories.

2.3. Data and Data Models

Our brief overview of the philosophy of science literature on theory suggests that if our aim is the explanation, prediction, and control of mental disorders, what we are after are well-developed formal theories: mathematical or computational models that represent the target system that gives rise to phenomena of interest. The key question then becomes: how can we best construct such a formal theory? The answer to this question will, of course, involve the collection and analysis of data. However, theories typically do not aim to explain data directly. Data are sensitive to the context in which they are acquired and subject to myriad causal influences that are not of core interest (Woodward, 2011). For example, panic disorder researchers collect data from diagnostic interviews, self-report symptom inventories, assessments of physiological arousal during panic attacks, time-series data, and a host of other methods. Data gathered using these methods will be influenced not only by the experience of panic attacks, but also by recall biases, response biases, sensor errors, and simple human error. Accordingly, theories do not aim to account for specific “raw” data. Rather, theories explain phenomena identified through robust patterns in the data that cannot be attributed to the particular manner in which the data were collected (e.g., researcher biases, measurement error, methodological artifacts, etc.). To identify these empirical regularities in data, researchers use data models: representations of the data (Suppes, 1962; Kellen, 2019). Data models can take many forms. These can range from the most basic descriptive tools, such as a mean score, a correlation, or a fitted curve, to more complex statistical tools which are common in different areas of psychology and beyond, such as structural equation models (SEM), item response theory (IRT) models, time-series models, hierarchical models, network models, mixture models, loglinear models and so forth. Essentially, we can consider a data model to be any descriptive statistic or statistical model that in some way summarizes the data.

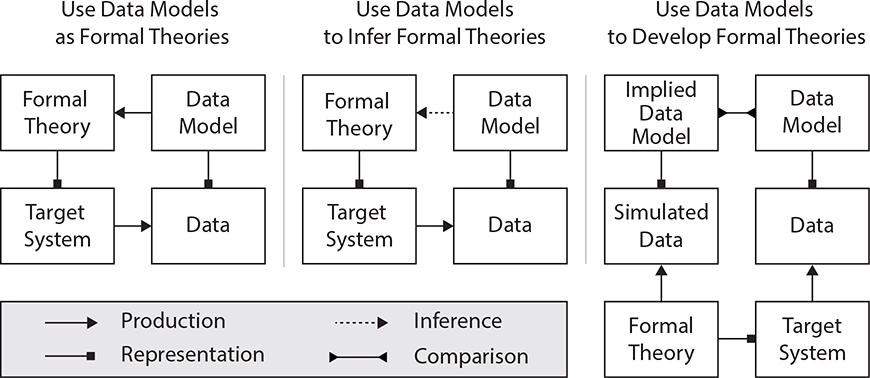
2.4. Three Routes from Data Models to Formal Theories

Data models are ubiquitous in psychological research, most commonly appearing within the context of null-hypothesis significance tests. The question of how best to use data models to test formal theories is a critical one (Meehl, 1978, 1990), and one to which we will return later in this paper (see Section 4). However, we will first focus on the question of how to use data models to generate and develop the kinds of formal theories that are ready to be subjected to rigorous testing. We see three possible routes researchers may take to move from data models to formal theories.

The first route arrives at theories directly by treating data models as formal theories. In this case, the transition from data model to formal theory is largely an act of interpretation. Instead of interpreting a data model as a representation of the data, we interpret it as a representation of the target system (see Figure 3, Left Panel). Specifically, the variables of the data model are treated as the components of our theory, and the statistical relationships among variables are treated as the structural relationships among the theory components. From this perspective, research is carried out by conducting an empirical study, estimating a data model, and treating the data model as a theory. If viable, this approach would be extremely powerful. A well-developed formal theory would be just one well-designed study away. Although we suspect that few researchers would explicitly endorse this approach, in practice, even seasoned researchers may fall victim to the tendency to interpret their statistical models as representations of the target system. For example, much recent debate in the psychopathology literature has focused on the interpretation of latent variable models. One can take the position that latent variables are simply data models: summaries of the covariances between items in the data and nothing more. Alternatively, one can interpret them as theoretical models, with latent variables representing some common underlying cause that explains the phenomenon of item covariances (Borsboom, Mellenbergh, & Van Heerden, 2003). Although many would likely endorse the former characterization, evidence of the latter can often be found in the description of factor analytic findings (e.g., when describing the identification of “underlying” factors that “account” for item covariance). Accordingly, we suspect that this route to theory may be more common than a mere show of hands would suggest (including in the network approach).

Figure 3:

The figure provides an overview of three routes to developing formal theories using data models. In the left panel, data models are treated as formal theories. In the middle panel, data models are used to draw inferences about the target system and, thereby, to generate formal formal theories of that system. In the right panel, data models used to develop formal theories by deducing implied data models and comparing them with empirical data models.

The second route arrives at formal theories by drawing direct inferences from data models (Figure 3, Middle Panel). That is, the data model is not directly treated as a theory, but rather as a kind of direct inference tool. From this perspective, research is carried out by conducting an empirical study, estimating a data model, and using the data model to infer characteristics of the target system, thereby informing the development of a theory. For example, one could observe a conditional dependence relationship between two variables and infer the presence of a causal relationship between the corresponding components in the target system. Multiple linear regression techniques — which statistically control for many covariates not of primary interest — are often used in this way, though interpretations of parameters themselves as being causal in nature are often studiously avoided (Rohrer, 2018; Grosz, Rohrer, & Thoemmes, 2020). Although this strategy is perhaps the most difficult to study or even define, since it relies on often undefined inference rules for particular data models, we suspect it is the most common approach to informing theory generation in many areas of psychology.

The third route arrives at formal theories through comparison between theory-implied data models (i.e., the data model predicted by our theory) and empirical data models. Some version of this approach is common in areas of psychology with well-developed traditions of formal theory (e.g., mathematical psychology and cognitive psychology), but is rarely applied outside these areas. In this route, research is carried out by first generating an initial formal theory. From this initial formal theory, we simulate data which can then be used to obtain a theory-implied data model. We can then compare the implied data model with the empirical data model, and adapt the formal theory if there are meaningful discrepancies between the two. This route thus relies upon the “immense deductive fertility” of formal theories (Meehl, 1978, p. 825) to make precise predictions about what data models we should expect to observe in our empirical data. By comparing these theory-implied data models to data models derived from empirical data, we can inform how the theory should be revised to be brought in line with empirical data. In other words, in this route, formal theory is not only the ultimate goal of the research process, it also plays a central role in theory development.

The three routes outlined here capture distinct ways in which researchers may use data models to inform formal theories. However, a key question remains: which of these three strategies is most appropriate? Which will best help us achieve our aim of constructing well-developed formal theories that are sufficiently good representations of the target system that they support explanation, prediction, and control? The answer to this question is likely to be context specific, depending on the target system, the levels on which we aim to have such a theory, and the data and data models which are available to us. Accordingly, in the next section, we will focus on answering a more tractable question: which route to formal theory is likely to be most fruitful within the broad theoretical framework of conceptualizing mental disorders as complex systems?

3. Evaluating Three Routes from Data Models to Formal Theories

We will evaluate the three routes from data models to formal theories with a focus on three data models that have become popular within the network approach to psychopathology: the Ising model, the Gaussian Graphical Model (GGM), and the Vector Autoregressive (VAR) model. We use these data models due to their popularity in the network approach literature and because they are broadly representative of — and share close connections to — the linear models typically used by applied researchers.

3.1. Route 1: Using Data Models as Formal Theories

The first route from data model to formal theory suggests that data models can themselves serve as formal theories. For this to be the case, the properties of those data models must be able to represent the properties we expect in the target system. Accordingly, to evaluate the first route (Figure 3, left panel), we must first outline the properties we expect in our target systems when working from the complex systems perspective (Section 3.1.1) and evaluate whether these properties are captured by our data models of interest (Section 3.1.2).

3.1.1. Properties of Mental Disorder Target Systems

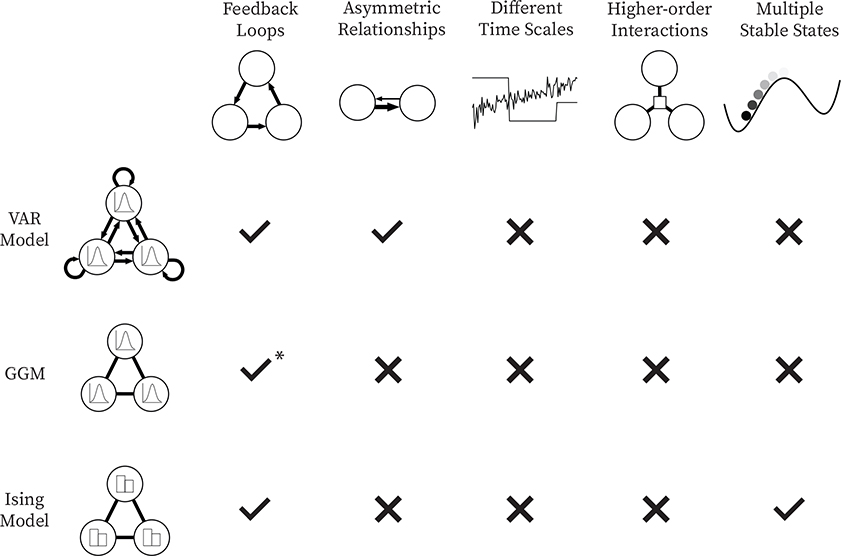
Adopting the perspective that mental disorders arise, in part, from a complex network of interacting symptoms, there are a number of properties we would expect to be present in the target system. First, feedback loops among components are likely present. Researchers have frequently posited “vicious cycles,” where the initial activation of one component (e.g., arousal) elicits activation of other components (e.g., perceived threat) which, in turn, further amplifies the activation of the original component. Second, causal effects between components are likely to be asymmetrical. That is, the effect of component A on component B may differ from the effect of component B on component A. For example, it is unlikely that concentration has the same effect on sleep as sleep has on concentration or that compulsions have the same effect on obsessions that obsessions have on compulsions. Third, interactions among components are likely to occur at different time scales. For example, the effect of intrusive memories on physiological reactivity in Post-traumatic Stress Disorder is likely to occur on a time scale of seconds to minutes, whereas an effect of energy on depressed mood may play out over the course of hours to days, and the effect of appetite on weight gain may occur on a time scale of days to weeks. Fourth, it is likely that there are higher order interactions among components. For example, the presence of sleep difficulties may strengthen the effect of feelings of worthlessness on depressed mood or the effect of intrusive trauma memories on physiological reactivity. If data models are to serve as formal theories of the target system, they must be able to represent these types of causal structures.

We would further suggest that most, perhaps all, mental disorder target systems are likely to have multiple stable states. That is, multiple states into which the system can settle and remain in the absence of external perturbation. In the simplest case, the system can be characterized by the presence of two stables states: an unhealthy state (i.e., a state of elevated symptom activation, such as a depressive episode), and a healthy state (e.g., a state without elevated symptom activation). In other cases, there may be multiple stable states (e.g., healthy, depressed, and manic states in Bipolar Disorder). The presence of multiple stable states is, in turn, likely to be accompanied by other behavior often observed in mental disorders, including spontaneous recovery and sudden shifts into or out of a state of psychopathology, further suggesting that a model of any given mental disorder will almost certainly need to able to produce alternative stable states.

3.1.2. Comparing Target System Properties with Data Model Properties

The first model we will consider is the VAR model. The VAR model for multivariate continuous time-series data linearly relates each variable at time point t to all other variables and itself at previous time points (Hamilton, 1995), typically the time point immediately prior t−1 (i.e., a first order VAR, or VAR(1), model; e.g., Bringmann et al., 2013; Pe et al., 2015; Fisher, Reeves, Lawyer, Medaglia, & Rubel, 2017; Snippe et al., 2017; Groen et al., 2020). The estimated lagged effects of the VAR models indicate conditional dependence relationships among variables over time. The dynamics of the VAR model is such that the variables are perturbed by random input (typically Gaussian noise) and the variables return to their means, which represent the single stable state of the system.

As depicted in Figure 4, the VAR model is able to represent some key characteristics likely to be present in mental disorder target systems. Most notably, it allows for feedback loops. Variables can affect themselves both directly (e.g., X_t → X_t+1), or via their effects on other variables in the system (e.g., X_t → Y_t+1 X_t+2). The VAR model also allows for asymmetric relationships, since the effect X_t → Y_t+1 does not have to be the same effect as Y_t → X_t+1 in direction or magnitude. However, because the lag-size (i.e., the distance between time points) is fixed and consistent across all relationships, the VAR model does not allow for different time scales. Moreover, because the VAR model only includes relations between pairs of variables, it is unable to represent higher-order interactions involving more than two variables. Finally, the VAR model has a single stable state defined by its mean vector and thus cannot represent multiple stable states of a system, such as a healthy state and unhealthy state.

Figure 4:

The figure shows whether the five properties of mental disorders discussed above can be represented by the three most popular network data models, the VAR(1) model, the GGM, and the Ising model with Glauber dynamics. Note that there is a check mark at feedback loops for GGMs because one could in principle endow the GGM with a dynamic similar to the Ising model, which would essentially lead to a restricted VAR model but with symmetric relations. The asterisk is present because this endowment of dynamics is not done in practice.

The second model we will consider is the GGM, which linearly relates pairs of variables in either cross-sectional (Haslbeck & Fried, 2017) or time-series data (Epskamp, Waldorp, Mõttus, & Borsboom, 2018). In the case of time-series data the GGM models the relationships between variables at the same time point. Because it does not model any dependency across time, it is typically not considered a dynamic model and, thus, could not be used to represent the behavior of a mental disorder target system as it evolves over time. In principle the GGM could be augmented by a dynamic rule similar to one commonly used with the Ising model (i.e., “Glauber dynamics”, see below). However, in that case, the GGM would become a model similar to, but more limited than, the VAR model described above (e.g., it would be limited to symmetric relationships). Accordingly, the GGM is similarly unable to represent key features we expect to observe in a mental disorder target system.

The final model we will consider is the Ising model. The Ising model again represents pairwise conditional dependence relations between variables (Ising, 1925), however, it is a model for multivariate binary data. Although the original Ising model does not model dependencies over time, it can be turned into a dynamic model by augmenting it with Glauber dynamics (Glauber, 1963).³ Like the VAR model, the Ising model is able to represent feedback loops. Moreover, due to its non-linear form it is able to exhibit multiple stable states (and the behavior that accompanies such stable states, such as hysteresis and sudden shifts in levels of symptom activation, see e.g., Cramer et al., 2016; Lunansky, van Borkulo, & Borsboom, 2019; Dalege et al., 2016; Haslbeck, Epskamp, Marsman, & Waldorp, 2020). It is perhaps not surprising then, that the Ising model is used as a theoretical model across many sciences (Stutz & Williams, 1999), and to our knowledge, is the only of the three data models examined here that has been used as a formal theory of a mental disorder target system (Cramer et al., 2016). Unfortunately, the Ising model falls short in its ability to represent the remaining characteristics likely to be present in mental disorders. The relationships in the Ising models are exclusively symmetric; with the standard Glauber dynamics, there is only a single time scale; and the Ising model includes exclusively pairwise relationships, precluding any representation of higher-order interactions.

3.1.3. Data Models as Formal Theories of Mental Disorders?

We showed that the VAR, GGM, and Ising models are unable to represent most key properties we would expect in the target systems giving rise to mental disorders, and therefore cannot serve as formal theories for those disorders. In the statistical inference literature the problem of not being able to represent the target system would be seen as a problem of model misspecification. In the present case, this would mean that the data models are misspecified with respect to the target system (i.e., the data generating system).

Of course, more complex models would be able to produce more of the characteristics likely to be present in mental disorders. For example, one could extend the VAR model with higher-order interactions (e.g., X_t × Y_t → X_t+1) or latent state variables (Tong & Lim, 1980; Hamaker, Grasman, & Kamphuis, 2010), thereby allowing it to represent multiple stable states. However, estimating data models is subject to fundamental constraints. More complex models require more data which are often unavailable in psychiatric research. For example, around 90 observations (about 2.5 weeks of a typical ESM study) are needed for a VAR model to outperform the much simpler AR model (Dablander, Ryan, & Haslbeck, 2019). Models more complex than the VAR model would require even more data to be estimated reliably.

Another constraint likely to be present in many psychological studies is the sampling frequency (e.g., measurement every 2 hours), which may be too low to capture the structure of the target system of interest (Haslbeck & Ryan, 2020). In this situation, a data model still contains some information about the target system, but cannot capture the structure of the target system to the extent that it can serve as a formal theory. Even where large amounts of high frequency data are available, efforts to estimate more complex models may by constrained by the simple fact that it is often unclear how such models can be estimated. For example, one could extend the Ising model with a second time scale (e.g., Lunansky et al., 2019), but it would be unclear how to estimate such a model from data. Finally, even where more complex models can be estimated, those models are often uninterpretable. For example, nonparametric models (e.g., splines; Friedman, Hastie, & Tibshirani, 2001, p. 139), which can capture extremely complex behavior, typically consist of thousands of parameters, none of which can be interpreted individually. Accordingly, it is unlikely that any data model estimated from the type of data typically available in psychiatric research will be both interpretable and capable of capturing the characteristics of psychopathology in such a way that would allow it to serve as a formal theory of a mental disorder.

3.2. Route 2: Using Data Models to Infer Formal Theories

An alternative route from data models to formal theories is to use data models to draw inferences about a target system, inferences that we can use to construct a formal theory. There is good reason to think that this approach could work. Because the data are generated by the target system, and data models summarize these data, the parameters of any data model certainly somehow reflect characteristics of the target system. This means that it should be possible, in principle, to infer something about the target system and its characteristics from data and data models. Although we have seen already that the GGM, Ising and VAR models cannot directly reproduce the key characteristics of the target system, their parameters could potentially still yield insights into the structure or patterns of relationships between components. In line with this intuition, it has frequently been suggested that the GGM, the Ising model, and the VAR models can serve as “hypothesis-generating tools” for the causal structure of the target system (e.g., Borsboom & Cramer, 2013; van Rooijen et al., 2017; Fried & Cramer, 2017; Epskamp, van Borkulo, et al., 2018; Epskamp, Waldorp, et al., 2018; Jones, Mair, Riemann, Mugno, & McNally, 2018).

Although this approach seems intuitive, in practice it is unclear how exactly this inference from data model to target system should work. For example, if we observe a strong negative linear cross-lagged effect of X_t on Y_t+1 in a VAR model, what does that imply for the causal relationship between the corresponding components in the target system? A precise answer to this question would require a rule that connects parameters in particular data models to the structure of the target system. For some simple systems, such a rule is available, and this type of inference can broadly be characterized as a causal discovery problem (Spirtes, Glymour, Scheines, & Heckerman, 2000; Peters, Janzing, & Schölkopf, 2017). For example, if the target system can be represented as a Directed Acyclic Graph (DAG), then under certain circumstances its structure can be discovered from conditional (in)dependence relations between its components: Conditional independence implies causal independence, and conditional dependence implies either direct causal dependence or a common effect (Pearl, 2009; Ryan, Bringmann, & Schuurman, 2019). However, this kind of precise deduction is not possible for the types of non-linear dynamic systems we expect in a psychiatric context (although Mooij, Janzing, & Schölkopf, 2013 and Forré & Mooij, 2018 have established some links in this regard). In these contexts, any inference from data model to target system must rely on some simplified heuristic(s) in an attempt to approximate the link between the two. Critically, however, the extent to which such heuristics are informative remains unclear.

In this subsection we evaluate whether the three data models introduced above can be used to make inferences about mental disorder target systems. To do this, we treat the Panic Model discussed in Section 2 as the data-generating target system and compare the causal structure inferred from the data models to the true causal structure. To yield these inferences we use a very simple and intuitive set of heuristics: a) if two variables are conditionally dependent in the data model, we will infer that the corresponding components in the target system are directly causally dependent; b) if there is a positive linear relationship, we will infer that the causal relation between the corresponding components is positive (i.e., reinforcing); c) if there is a negative linear relationship, we will infer that the causal relationship among components is negative (i.e., suppressing).

3.2.1. Inferring the Panic System from Network Data Models

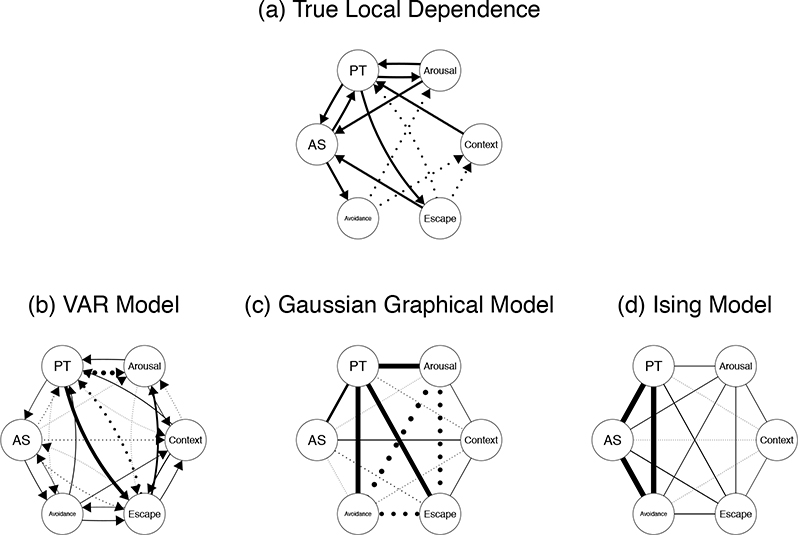
To be able to evaluate the success of the simple heuristics described above, we must first represent the structure of the Panic Model (see Section 2) in the form of a square matrix, that is, in the same form as the parameters of the VAR, GGM, and Ising models. Since the relationships between components are formalized through differential equations, a natural choice is to represent the Panic Model as a network of moment-to-moment dependencies, drawing an arrow X → Y if the rate of change of Y is directly dependent on the value of X (known as a local dependence graph; Didelez, 2007; Ryan & Hamaker, 2020). Figure 5 (a) displays these moment-to-moment dependencies. Note that this structure cannot capture many aspects of the true model, such as the presence of two time scales or the moderating effect of Arousal Schema (AS) (see Section 2 for details). It is, thus, already clear that the models cannot recover the exact causal structure of the Panic Model. Nonetheless, we can still investigate whether applying the simple heuristics to these three data models allows us to infer this less detailed pattern of direct causal dependencies.

Figure 5:

Panel (a) shows the true model in terms of local dependencies between components (AS = Arousal Schema, PT = Perceived Threat); panel (b) shows the VAR model estimated from ESM data sampled from the true model; panel (c) shows the GGM estimated from the cross-sectional data of 1000 individuals, generated from the true model; panel (d) shows the Ising model estimated on the same data after being binarized with a median split. Solid edges indicate positive relationships, dotted indicate negative relationships. For panels (b) to (d), the widths of edges is proportional to the absolute value of the corresponding parameter. Note that in panel (b) we do not depict the estimated auto-regressive parameters as the primary interest is in inferring relationships between variables.

To evaluate how well these heuristics work, we compare this true causal structure to the causal structure inferred based on the three data models. To obtain the three data models, we first generate data from the target system (see Appendix A). Specifically, we use four weeks of minute-to-minute time-series data for 1000 individuals. These individuals differ in their initial value of Arousal Schema, with the distribution chosen so that the proportion of individuals for whom a panic attack is possible was equivalent to the lifetime history prevalence of panic attacks in the general population (R. R. Freedman, Ianni, Ettedgui, & Puthezhath, 1985). For the VAR model analysis, we create a single-subject experience-sampling-type dataset by choosing the individual who experiences the most (16) panic attacks in the four-week period. To emulate ESM measurements for use with this model, we divide the four week period into 90-minute intervals, taking the average of each component in that interval, yielding 448 measurements. For the GGM analysis, we emulate continuous cross-sectional measurements by taking the mean of each component for each individual over the four weeks. For the Ising model analysis, we emulate cross-sectional binary measurements by taking a median split of those same variables. The resulting VAR, GGM and Ising model networks are displayed in Figure 5 panels (b), (c) and (d), respectively.⁴

We will focus our evaluation on two important causal dependencies in the target system: the positive (i.e., reinforcing) moment-to-moment feedback loop between Perceived Threat (PT) and Arousal, and the positive effect of Arousal Schema (i.e., beliefs that arousal-related bodily sensations are dangerous, AS) on Avoidance (i.e., efforts to avoid situations or stimuli that may elicit panic attacks). In the VAR model (panel (b) in Figure 5) we see a lagged positive relationship of Arousal to Perceived Threat, a strong negative lagged relationship from Perceived Threat to Arousal, and a weak positive effect of Arousal Schema on Avoidance. Applying the heuristics, we would infer a reinforcing relationship from Arousal to Perceived Threat, a suppressing relationship from Perceived Threat to Arousal, and a reinforcing effect of Arousal Schema on Avoidance. In the GGM (panel (c) in Figure 5) we see a positive conditional dependency between Arousal and Perceived Threat, but we also see a weak negative dependency between Arousal Schema and Avoidance. Applying the heuristics to the GGM, we would infer a reinforcing relationship between Arousal and Perceived Threat, and a suppressing relationship between Arousal Schema and Avoidance. Finally, in the Ising model (panel (d) in Figure 5), we see a strong positive dependency between Arousal Schema and Avoidance, and a very weak positive relationship between PT and Arousal. This leads us to infer two reinforcing relationships, between Arousal and Perceived Threat, and Arousal Schema and Avoidance.

For the VAR model, the heuristics yield one correct and one incorrect inference. For the GGM, we make exactly the opposite inferences, with again one correct and one incorrect. In the Ising Model, we yield two correct inferences. However, inspecting the rest of the Ising Model edges we can see a variety of incorrect inferences about other relationships, with independent components in the target system connected by strong edges in the Ising model, and the valences of various true dependencies flipped. At best, we can say that in each of the three network models, some dependencies do reflect the presence and/or direction of direct causal relationships, and some do not. Unfortunately, it is not possible to distinguish which inferences are trustworthy and which are not without knowing the target system, and in any real research context, the target system will be unknown. Consequently, these data models and simple heuristics cannot be used to reliably draw inferences about the target system.

3.2.2. The Mapping between Data Model and Target System

Importantly, our inability to draw accurate inferences from these data models is not a shortcoming of the data models themselves. Each data model correctly captures some form of statistical dependency between the components in a particular domain (e.g., lagged 90 minute windows). The scenario we emulated in this section is highly idealized in that we have directly and accurately observed all components of the target system — measurements are taken without error, and there is no potential for statistical dependencies to be produced by unobserved confounding variables. This means that the statistical dependencies in the data models can only be produced by causal dependencies in the target system. Thus we know that there is some mapping from the causal dependencies in the target system to statistical dependencies in the data model. The fundamental barrier to inference is that the form of this mapping is unknown and considerably more complex than the simple heuristics we have used to draw inferences here. For example, consider the relationships between Perceived Threat and Arousal. The VAR model (panel (b) in Figure 5), identifies a negative lagged relationship from Perceived Threat to Arousal in the data generated by the target system. Yet in the target system, this effect is positive. This “discrepancy” occurs because of a very specific dynamic between these components: After a panic attack (i.e., a brief surge of Perceived Threat and Arousal) there is a “recovery” period in which arousal dips below its mean level for a period of time. As a result, when we average observations over a 90 minute window, a high average level of Perceived Threat is followed by a low average level of Arousal whenever a panic attack occurs. That same property of the system produces the observed findings for the GGM and Ising Model through yet another mapping (for details, see Appendix B).

As this example illustrates, the mapping between target system and data model is intricate, and it is unlikely that any simple heuristics can be used successfully to work backwards from the data model to the exact relationships in the target system. We can expect this problem to arise whenever we use relatively simple statistical models to directly infer characteristics or properties of a complex system (c.f. the problem of under-determination or indistinguishability; Eberhardt, 2013; Spirtes, 2010). Indeed, the same problem arises even for simpler dynamical systems when analyzed with more advanced statistical methods (e.g., Haslbeck & Ryan, 2020).

Of course, in principle, it must be possible to make valid inferences from data and data models to some properties of a target system using a more principled notion of how one maps to the other. For example, under a variety of assumptions, it has been shown that certain conditional dependency relationships can potentially be used to infer patterns of local causal dependencies in certain types of dynamic system (Mooij et al., 2013; Bongers & Mooij, 2018; Forré & Mooij, 2018). However, the applicability of these methods to the type of target system we expect to give rise to psychopathology (see Section 3.1) is as yet unclear and even under the strict assumptions under which they have been examined, these methods still do not recover the full structure of the target system. Given the considerations reviewed here, the intricate mapping between target system and data model likely precludes reliable direct inferences about the kinds of target systems we are likely to see in mental health research. Accordingly, we cannot rely on this kind of inference to build formal theories. An alternative approach is needed.

3.3. Route 3: Using Data Models to Develop Formal Theories

In Section 3.2, we saw that the mapping between target system and data model is intricate and would be nearly impossible to discern when the target system is unknown. However, we also saw that when the target system is known, we can determine exactly which data models the target system will produce. Indeed, this is precisely what we did when we simulated data and fit data models to it in the previous section. In this section we consider a third route to formal theories, which makes use of this ability to determine which data models are implied by a given target system (or formal theory).

This third route works as follows. First and foremost, we must propose some initial formal theory which we take as a representation of the target system. The quality or accuracy of this theory may be good or bad, but, crucially, the theory must be formalized in such a way as to yield unambiguous predictions (see Section 2.2). Second, we can use this initial theory to deduce a theory-implied data model. This can be done by simulating data from the formal theory and fitting the data model of interest. Third, by comparing implied data models with their empirical counterparts, we can learn about where the theory falls short and adapt the formal theory to be more in line with empirical data. This approach is represented in schematic form in the right-hand panel of Figure 3. It can be seen as a form of inference. Not the direct deductive inference focused on in the previous subsection, but rather abductive inference: inference to the best explanation (Haig, 2005). We infer the best explanation for any discrepancies between empirical and theory-implied data models, and use those inferences to inform subsequent theory development.

3.3.1. Obtaining Theory-Implied and Empirical Data Models

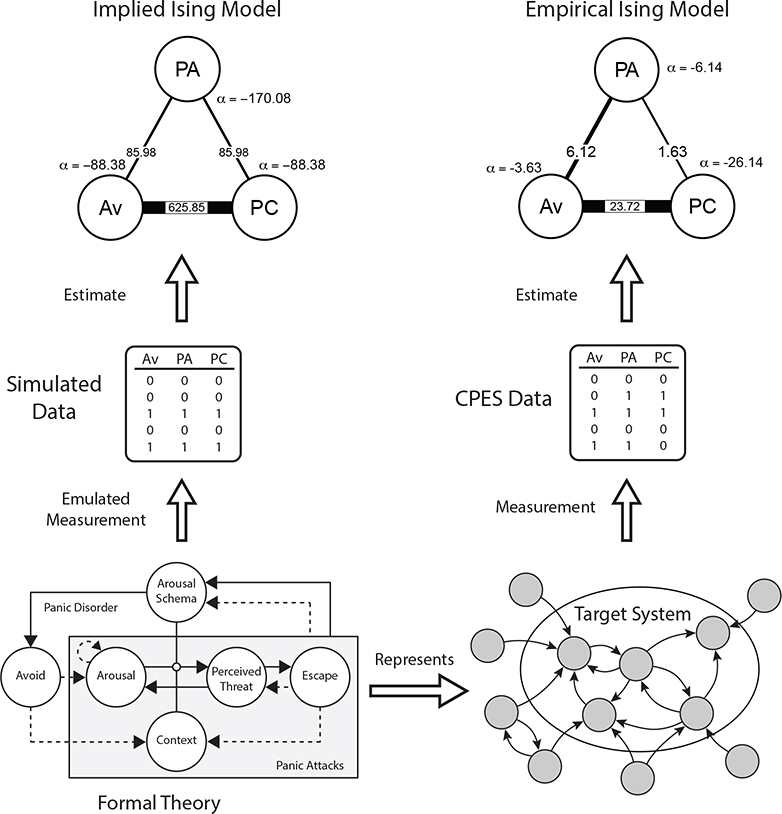
In this section, we will treat the Panic Model introduced in Section 2 as our initial formal theory, which aims to represent the target system that gives rise to panic disorder (Figure 6, bottom row). The Panic Model can be used to simulate data and, in turn, to derive predictions made by the theory in the form of theory-implied data models (left-hand column of Figure 6). Although many data models can (and should) be used to compare theories and empirical data, here we will examine the implied cross-sectional Ising model of the three core panic disorder symptoms: 1) Recurrent Panic Attacks (PA), 2) Persistent Concern (PC) following a panic attack and 3) Avoidance (Av) behavior following a panic attack (American Psychiatric Association, 2013). If our formal theory of panic disorder is an accurate representation of the target system that gives rise to panic disorder, the implied Ising model derived from this theory should be in agreement with a corresponding Ising model estimated from empirical data. Accordingly, any discrepancies between these models call for — and can inform — further development of the theory.

Figure 6:

Illustration of the third route from data models to formal theories. We take the Panic Model discussed in Section 2 as our formal theory, representing the unknown target system that gives rise to panic disorder. To obtain an implied data model from this theory, we first formalize how the components of the theory produce the data of interest, emulating the measurement process. With this in place, we can simulate data from the model in the form of cross-sectional binary symptom variables. We obtain the theory-implied Ising Model by estimating it from these simulated data (top-left corner). To estimate the empirical Ising Model (top-right corner) we make use of empirical measurements of binary symptom variables from the CPES dataset.

Notably, obtaining an implied data model requires not only a formal theory from which we can simulate data, but also a formalized process by which variables are “measured” from those data. The Panic Model generates intra-individual time-series data for multiple individuals (as described in Appendix A). We therefore need to define how cross-sectional symptom variables can be extracted from those time-series. Here, we specified that Recurrent Panic Attacks (PA = 1) are present for an individual in our simulated data if there are more than three panic attacks in the one month observation period. Persistent Concern was determined using the average levels of jointly experienced arousal and perceived threat (i.e., anxiety) outside the context of a panic attack. If an individual had a panic attack, and their average anxiety following a panic attack exceeds a threshold determined by “healthy” simulations (i.e., those without panic attacks), they are classified as having Persistent Concern (PC = 1). We similarly defined Avoidance as being present if an individual has a panic attack, and their average levels of avoidance behavior following that attack were higher than we would expect to see in the healthy sample. A more detailed account of how we generated these data can be found in Appendix C. This simulated cross-sectional data was then used to estimate the theory-implied Ising Model (top left-hand corner, Figure 6).⁵

We obtained the corresponding empirical Ising model (right-hand column of Figure 6) using the publicly available Collaborative Psychiatric Epidemiology Surveys (CPES) 2001–2003 (Alegria, Jackson, Kessler, & Takeuchi, 2007). The CPES is a nationally representative survey of mental disorders and correlates in the United States, with a total sample size of over twenty thousand participants (of which n = 11367 are used in the current analysis; for details see Appendix C). The CPES combines more than 140 items relating to panic attacks and panic disorder, with a diagnostic manual describing how these items can be re-coded into binary symptom variables reflecting Recurrent Panic Attacks, Persistent Concern and Avoidance. Recurrent Panic Attacks are present if the participant reported more than three lifetime panic attacks. Persistent Concern is present if, following an attack, the participant experienced a month or more of persistent concern or worry. Avoidance is present if the participant reports either a month of avoidance behavior following an attack, or a general avoidance of activating situations in the past year. Note that these definitions correspond closely to the formalized measurement assumptions we made while generating our theory-implied data model.

3.3.2. Theory Development: Comparing Model-Implied and Empirical Data Models

As seen in Figure 6, there is a similar pattern of conditional dependencies in the implied and empirical data models. In both, all pairwise dependencies are positive, and all thresholds are negative. There is also a similar ordering of conditional dependencies in terms of their magnitude. Within each model, the conditional relationships of Recurrent Panic Attacks with Avoidance and Recurrent Panic Attacks with Persistent Concern are of the same order of magnitude, and the conditional relationship between Avoidance and Persistent Concern is an order of magnitude greater. However, we also see some differences between the models. First, the absolute value of pairwise dependencies and thresholds are much greater in the implied Ising Model (Figure 6 (a)) than the empirical Ising Model (Figure 6 (b)). Second, we see that the relationships in the implied model are perfectly symmetric, with exactly the same thresholds for Avoidance and Persistent Concern, and precisely the same weights relating Recurrent Panic Attacks to both.

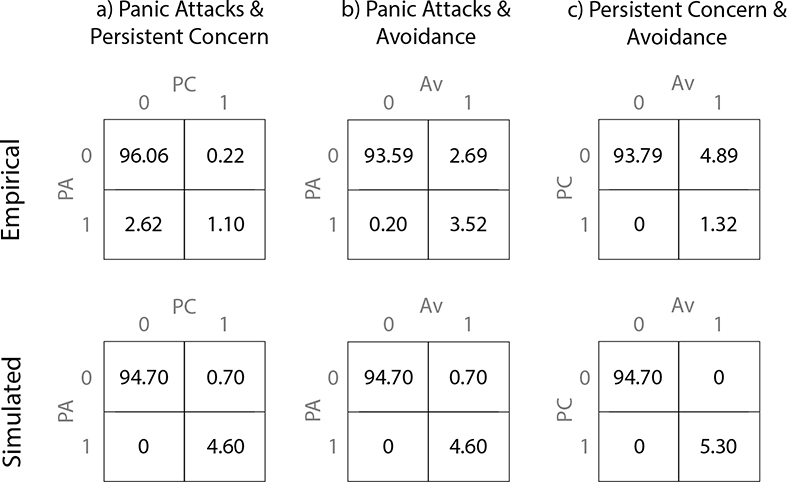
The bivariate contingency tables in Figure 7 provide further information about these inter-symptom relationships. In both the implied and empirical data models only a small proportion of individuals experience Recurrent Panic Attacks (Empirical 4.3%, Simulated 3.72%). In the simulated dataset, the symptom relationships are almost deterministic: If one symptom is present, so too are all others, and vice versa for the absence of symptoms (apart from three individuals who experience at least one, but less than three panic attacks in the time window). This is because there is a deterministic relationship between the components underlying these symptoms in the Panic Model: All participants who experience one panic attack have Persistent Concern and Avoidance behavior after those attacks. In contrast, there are non-deterministic relationships in the empirical data. For example, it is actually more common to have Recurrent Panic Attacks without Persistent Concern than with Persistent Concern (column (a)). Similarly, more individuals experience Avoidance without Persistent Concern, than with Persistent Concern (column (c)) Conversely, there are no individuals who experience Persistent Concern but not Avoidance.

Figure 7:

Contingency Tables showing percentages for each pair of symptom variables (one per column) for the empirical data (top row) and simulated data (bottom row). The CPES contingency tables are based on n_CPES = 11367 observations. The simulated dataset contains n_sim = 1000 observations.

Having observed these differences between the theory-implied and empirical data models, our task is to consider the best explanation for the discrepancies. This explanation could rest at any step in the process from formal theory to the implied data model or from the target system to the empirical data model (i.e., any of the paths illustrated in Figure 6). It could be the case that any discrepancies we have observed here are due to inaccuracies in how we emulated the measurement process.⁶ For example, perhaps Persistent Concern and Avoidance co-occur equally, but the former suffers from a greater degree of recall bias than the latter (for an example of differential symptom recall bias in depressed patients, see Ben-Zeev & Young, 2010). The discrepancies could have arisen due to the somewhat different time scales at which the simulated and empirical symptoms are defined. The simulated symptoms are defined over a month period whereas the CPES items are defined over lifetime prevalence. Due to the deterministic nature of the Panic Model, we regard a one month period to be a good approximation for lifetime experience of panic symptoms in this case. Nonetheless, it is a discrepancy in measurement that could lead to discrepancies between the implied and empirical data models. It could also be that the discrepancy is due to estimation issues. However, due to the large sample sizes and simple models used, we suspect it is unlikely that sampling variance is a problem in this instance.

We consider the most likely explanation for the observed discrepancies to lie with the theory itself, thereby providing an opportunity to consider how the theory might be further developed to bring it in line with empirical data. For example, the implied Ising model over-estimates the strength of inter-symptom relationships relative to the empirical Ising model. This can largely be explained by the deterministic causal effects in the theory. In the simulated data, everybody who experiences Recurrent Panic Attacks also develops Persistent Concern and, in turn, Avoidance. As seen in Figure 7, this is inconsistent with empirical data. To improve the model, we must include some mechanism by which individuals can experience a panic attack without developing the remaining symptoms of panic disorder. Where is such a mechanism most appropriate? In the empirical data, nearly all those with Persistent Concern also exhibit Avoidance. In contrast, only a few of those with Recurrent Panic Attacks also exhibit Persistent Concern. Accordingly, the discrepancy seems most likely to arise from the effect of recurrent panic attacks on Persistent Concern. Incorporating a mechanism that leads some to resist developing persistent concern following panic attacks (e.g., high perceived ability to cope with the effects of a panic attack) would allow the theory to better account for both the observation that some individuals experience recurrent panic attacks without developing the full panic disorder syndrome and the observation that those who do develop Persistent Concern tend to develop the full syndrome.

As this example illustrates, discrepancies between the theory-implied and empirical data models can provide insights for how to further develop a theory. We have focused on just one set of discrepancies between our theory-implied and empirical data models. More insights may be gained by focusing on others and these insights can work together to triangulate on the most appropriate set of revisions. Further insights can almost certainly be gained by considering additional data models and different types of data. For example, experimental data or time series data on the relation between Arousal and Perceived Threat may allow us to refine the specification of the feedback between those two variables. In general this route offers a great deal of flexibility in theory development. Although the theory is likely to be complex, dynamic and non-linear, the form of the data models used to learn about that theory need not be. Instead, by starting with an initial theory, the researcher can use any data about the phenomena of interest to further develop that theory.

4. Abductive Formal Theory Construction

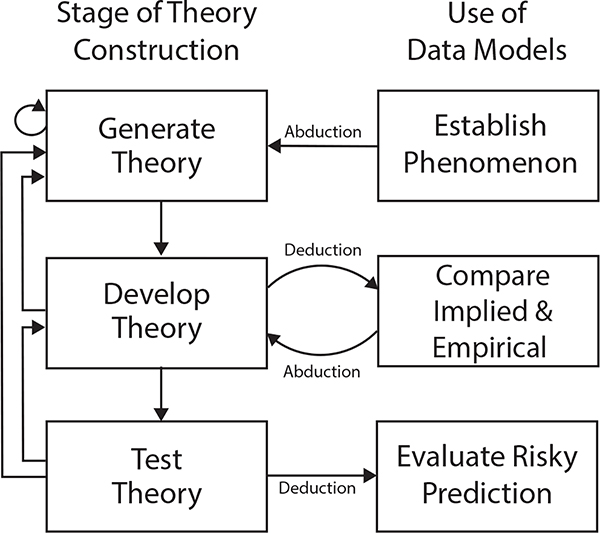
In Section 3.3, we illustrated an approach to using empirical data to develop an existing formal theory. However, our description of this approach is not, by itself, a comprehensive approach to theory construction, because it does not address how the formal theory was generated nor how it should ultimately be tested. In this section, we propose a three-stage framework for formal theory construction built around the approach presented in Section 3.3 (see Figure 8).

Figure 8:

Flowchart depicting the process of developing a formal theory with the Abductive Formal Theory Construction framework. In the theory generation stage we first establish the phenomenon (Section 4.1.1) and then generate an initial verbal theory (Section 4.1.2) which is subsequently formalized (Section 4.1.3). In the second stage (Section 4.2) the theory is developed by testing whether it is consistent with existing empirical findings that are not part of the core phenomenon. If the formal theory is not consistent with some findings, it is adapted accordingly. If these adaptations lead to a “degenerative” theory (Meehl, 1990) we return to the first stage; otherwise we continue to the final stage, in which we test the formal theory using risky predictions (Section 4.3). If many tests are successful, we tentatively accept the theory. If not, the theory must either be adapted (stage two) or a new theory must be generated (stage one).

This framework uses the Theory Construction Methodology proposed by Borsboom et al. (2020) as a foundation and seeks to extend that work by providing more concrete guidance for how to proceed with the generation, development, and testing of theories, with a focus on how data models are used at each of these stages of theory construction. In the theory generation stage, we use data models to establish the phenomenon to be explained, generate an initial verbal theory, and formalize that theory. In the theory development stage, the theory is revised and improved by repeatedly comparing theory-implied data models with data models from empirical data (cf. Section 3.3). Finally, in the theory testing stage, the theory is subjected to strong tests within a hypothetico-deductive framework, comparing precise theory-driven predictions and empirical data models with the aim of corroborating or refuting the theory. The approach to theory construction proposed here places considerable emphasis on the theory’s ability to explain phenomena and emphasizes the importance of abductive inference in theory construction (Haig, 2005). We therefore refer to it as the Abductive Formal Theory Construction (AFTC) framework.

4.1. Stage 1: Generating Theory

4.1.1. Establish the Phenomena

The goal of a formal theory is to explain phenomena. Accordingly, the first step of theory construction is to establish phenomena to be explained. Establishing phenomena is a core aim of science and a full treatment of how best to achieve this aim is beyond the scope of this paper (for a possible way to organize this process see Haig, 2005). However, it is worth highlighting that establishing robust phenomena is a prerequisite to theory construction. The most difficult phenomenon to explain are the ones that don’t exist (Lykken, 1991), so researchers must take great care at this stage to ensure that the phenomenon for which they are trying to account are robust. We suspect that the most appropriate phenomena for initial theory development will often include things that researchers would not even think to subject to empirical analysis, taking them for granted as features of the real world. For example, in the case of panic disorder, the core phenomena to be explained are simply the observations that a) some people experience panic attacks and b) recurrent attacks often co-occur with persistent worry or concern about those attacks and avoidance of situations where such attacks may occur. These phenomena are so robust that they are typically not the focus of empirical research, yet they are the most important phenomena to be accounted for by a theory of panic disorder.

4.1.2. Generate an Initial Verbal Theory

Once the phenomena to be explained have been established, how do we go about generating an initial theory to explain them? A brief survey of well-known scientific theories reveals that this initial step into theory is often unstructured and highly creative. For example, in the 19th century August Kekulè dreamt of a snake seizing its own tail, leading him to the generate the theory of the benzene ring, a major breakthrough in chemistry (Read, 1995). In the early 20th century, Alfred Wegener noticed that the coastlines of continents fit together similar to puzzle pieces, and consequently developed the theory of continental drift (Wegener, 1966), which formed the basis for the modern theory of plate tectonics (Mauger, Tarbuck, & Lutgens, 1996). In the late 20th century, Howard Gardner explained that he developed his theory of multiple intelligences in the 1980s using “subjective factor analysis” (Walters & Gardner, 1986, p. 176). Although more codified approaches to theory generation exist (e.g., Grounded Theory; Strauss & Corbin, 1994), we are unaware of any evidence to suggest that any one approach to generating the seed of an initial theory is superior to any other.

Nonetheless, our review of theory in Section 4.1 provides guidance for theory generation in at least two ways. The first is rooted in what is perhaps theory’s most characteristic feature: its ability to explain phenomena. Initial efforts to generate a theory should begin with abductive inference, asking the simple question: what is the best explanation for the phenomena of interest (and, in turn, the data models used to establish those phenomena). The second is rooted in the observation that theories aim to explain phenomena by representing a target system. Accordingly, to generate an initial theory it will likely be helpful to specify the components thought to compose the target system. This process entails dividing the domain of interest into its constituent components (i.e., “partitioning”) and selecting those components one thinks must be included in the theory (i.e., “abstraction”; cf. Elliott-Graves, 2014). For researchers adopting a “network perspective” (Borsboom, 2017), the target system is typically presumed to comprise cognitive, emotional, behavioral, or physiological components, especially those identified in diagnostic criteria for mental disorders. Having identified the relevant components we next specify the posited relations among them. Within the domain of the network approach, this second step will typically entail specifying causal relations among symptoms or momentary experiences (e.g., thoughts, emotions, and behavior). Having specified the theory components and the posited relationships among them, the researcher has generated an initial theory posited to account for the phenomena of interest.

Notably, in mental health research, we do not even necessarily need to rely on creative insight about the components and relations among them in order to generate an initial theory. There are already a plethora of verbal theories about mental disorders. If the initial verbal theory is well supported and specific, it will lend itself well to formalization and subsequent theory development and even poor verbal theories can be a useful starting point to developing a successful formal theory (Wimsatt, 1987; Smaldino, 2017).

4.1.3. Formalize the Initial Theory

Once a verbal theory has been specified, the next step is to formalize it. To do so, we first need to choose a formal framework. Dynamical systems are often modelled using differential equations, which describe how variables change over time (e.g., Strogatz, 2014). The Panic Model we have used as an example throughout this paper, uses this formal framework. Another common framework is Agent-based Modeling (ABM), in which an autonomous agent interacts with its environment, which often includes additional agents (e.g., Grimm & Railsback, 2005). Both frameworks can be implemented in essentially any computer programming language and both are likely to be relevant to psychiatric and psychological research as a whole. The choice of a formalization framework will largely depend on the context (the types of components and types of relations we wish to describe) as well as the level of abstraction or granularity desired by the researcher. For instance, one reason differential equations are attractive is because they may be used to specify component relations on an infinitesimal time scale. In principle, by aggregating, these models can be used to describe behaviour at any longer time scale. However, modeling phenomena directly at some longer time scale of principle interest (e.g., modeling symptom dynamics on a month-to-month rather than moment-to-moment level) may be both simpler to achieve and serve equally well in attaining a theoretical explanation of phenomena.

Having chosen a formal framework, the next step is to specify the relations between each component in the language of that framework. This process of formalization is an exercise in being specific. Mathematics and computational programming languages require theorists to specify the exact nature of the relationship between variables. Requiring this level of specificity is one advantage of computational modeling, as it has the effect of immediately clarifying what remains unknown about the target system of interest, thereby guiding future research. However, this also means that theorists will often be in the position of needing to explicate relationships when the precise nature of those relationships is uncertain. We think that, even in the face of this uncertainty, it is better to specify an exact relationship and be wrong than to leave the relationship ambiguously defined (as it often is in verbal theories). Nonetheless, the more theorists can draw on empirical research and other resources when specifying their theory, the firmer the foundation for subsequent theory development. There are several potential sources of information that can guide the formalization process.

First, empirical research can inform specification of components and the relations among them. For example, one could use the finding that sleep quality predicts next-day affect, but daytime affect does not predict next-night sleep (de Wild-Hartmann et al., 2013) to constrain the set of plausible relationships between those two components in the formal theory. There could also be empirical data on the rate of change of components, for example, Siegle, Steinhauer, Thase, Stenger, and Carter (2002) and Siegle, Steinhauer, Carter, Ramel, and Thase (2003) have shown that depressed individuals exhibit longer sustained physiological reactions to negative stimuli than healthy individuals, a finding which is echoed in self-report measures of negative affect (Houben, Van Den Noortgate, & Kuppens, 2015). These findings suggest that the rate of decay of negative affect may be smaller in those with depression relative to those without.

Second, we can derive reasonable scales for components and relationships between components from basic psychological science. For example, classical results from psychophysics show that increasing the intensity of stimuli in almost all cases leads to a nonlinear response in perception (e.g., Fechner, Howes, & Boring, 1966): When increasing the volume of music to a very high level, individuals cannot hear an additional increase. Similarly, formal theories of mental disorders may involve some forms of learning. To constrain the relations between components that constitute learning, one can leverage a wealth of research on basic learning, for example on classic or operant conditioning (Henton & Iversen, 2012).

Third, in many cases we can use definitions, basic logic, or common sense to choose formalizations. For example, by definition emotions should change at a time scale of minutes (Houben et al., 2015), while mood should only change at a time scale of hours or days (Larsen, 2000). And we can choose scales of some components using common sense, for example one cannot sleep less than 0 or more than 24 hours a day.

Fourth, we could use an existing formal model of another target system, which we expect to have a similar structure as the target system giving rise to the phenomenon of interest. This approach is called “analogical modeling”. For example, Cramer et al. (2016) formulated a model for interactions between symptoms of Major Depression using the Ising model, which was originally formulated to model magnetism on an atomic level (Ising, 1925). Similarly, Fukano and Gunji (2012) formulated a model for interactions among core components of panic attacks using a Lotka-Volterra model originally formulated to represent predator-prey relationships (Brauer, Castillo-Chavez, & Castillo-Chavez, 2012). However, in using this analogical approach, it will be critical to use models capable of representing the kinds of properties expected in the target system of interest.

Fifth, there are methods by which we can potentially estimate the parameters of a formal theory from empirical data.⁷ These approaches require considerable development of the formal theory (e.g., the form of a differential equation), suitable data (typically intensive longitudinal data), and a clear measurement model relating observed variables to theory components (as we specified in Section 3.3). Accordingly, this approach already requires considerable progress in generating a formal theory and may be limited by practical considerations. Nonetheless, if successfully carried out, the direct estimation of parameter values would substantially strengthen the theory.

Sixth, one can build on models from cognitive and mathematical psychology. Mental disorders can often be viewed as dysfunctional states of otherwise functional systems of basic psychological processes, such as perception, learning and memory; thereby allowing mental health researchers to draw on extant models of these processes. For example, Eldar, Rutledge, Dolan, and Niv (2016) conceptualize mood as the difference between expectations and outcomes and show in a reinforcement learning model that it is adaptive in environments in which rewards are correlated. Using this model of functional (or adaptive) mood, they identify several meaningful ways one can change the model to produce prolonged depressed mood. Another example is the computational model for Oppressive-Compulsive Disorder (OCD) by Fradkin, Adams, Parr, Roiser, and Huppert (2020), who explain various OCD phenomena by dysfunctional information processing within the Bayesian brain framework (Knill & Pouget, 2004).

4.1.4. Evaluating the Initial Theory

The aim of the theory generation stage is to produce a formal theory that is able to explain a phenomenon or set of core phenomena. As we have emphasized throughout this paper, formal theories precisely determine the behavior implied by the theory. Accordingly, explanation in this context means that the theory has demonstrated its ability to produce the behavior of interest (for a more detailed discussion of how formal theories support explanation, see Robinaugh et al., 2020). For example, a theory of panic attacks must be able to produce sudden surges of arousal and perceived threat; a theory of depression must be able to produce sustained periods of low mood; and a theory of borderline personality disorder must be able to produce affective instability. We would note that there are very few theories in psychiatry that have reached this stage of not merely positing, but demonstrating, that the theory can explain the phenomena of interest. Accordingly, completing this stage of theory construction would constitute a significant advance in theories of psychopathology. Once a theory has reached this stage, it is ready for the next stage of theory construction.

4.2. Stage 2: Developing Theory

The formal theory produced in the first stage of theory construction will have demonstrated its ability to explain the core phenomena of interest. However, the fact that the formal theory provides some explanation does not mean it is the best explanation. In other words, demonstrating an ability to explain the phenomenon of interest is a critical first step, but does not guarantee that the formal theory is the best representation of the target system. To move toward such a theory, we must increase both the explanatory precision and the explanatory breadth of the theory. We will use the term explanatory precision to refer to the specificity of the phenomena for which the theory can account. Whereas researchers in the theory generation stage will typically focus on explaining broad qualitative phenomena, in the development stage researchers will benefit from going further to evaluate whether the formal theory can account for more precise quantitative features of those phenomena. For example, beyond reproducing the broad qualitative features of a panic attack, a well-developed theory would also reproduce the typical duration of and peak arousal associated with a panic attack.

Explanatory breadth refers to the number of phenomena the theory can explain (Thagard, 1978). Whereas in the theory generation stage, researchers will typically be focused on a narrow set of phenomena of interest, to further advance the theory it is necessary to evaluate whether the theory can account for a broader range of phenomena. These phenomena may exist on different levels of aggregation and abstraction, and may necessitate the use of altogether different types of data sources. For instance, a well-developed theory of panic disorder should be able to both approximate the time evolution of panic attacks within a person as well as individual differences in vulnerability to panic disorder and the varying symptom profiles of panic disorder we observe at a population level. The more phenomena for which the theory can account, the greater confidence we can have that the theory is indeed an adequate representation of the target system.

We propose that efforts to increase explanatory precision and breadth should be carried out by repeating two steps. First, we deduce a data model from the formal theory and compare this theory-implied data model to a corresponding empirical data model (Section 4.2.1). If the implied data model is in agreement with the empirical data model, we take this result to expand the theory’s explanatory breadth, explanatory precision, or both. However, if a discrepancy is observed, we move to a second step. In this step, we use abductive inference and consider the best explanation for the observed discrepancy, thereby providing insight into how the theory can be adapted to better align with empirical data. By repeating this process with different data models and data sets, the theory is refined such that it becomes a better representation of the target system. We elaborate on these steps below.

4.2.1. Compare Theory-Implied and Empirical Data Models

To generate a theory-implied data model, we first deduce what the theory implies about the behavior of each of the theory’s components. The nature of this deduction will depend on the formalism chosen for the theory. In the case of the differential equation modeling, we can either derive or simulate precisely how each theory component will evolve over time (e.g., see Figure 2, right panel). We can then use the simulated data along with a set of formalized auxiliary hypotheses regarding measurement to create a theory-implied dataset. For example, in Section 3.3.1 we used the Panic Model to simulate how the components of the system will evolve over time and used these simulations to emulate the measurement that occurs in a cross-sectional epidemiological survey. We could use this same process to instead emulate the measurements likely to be obtained in an experience sampling study by sampling the time series every 90 “minutes” with precisely defined measurement functions that capture how those components relate to the self-report assessment of interest. This process of moving from the simulated values of each theory component to the theory-implied dataset requires researchers to specify precisely how we move from a theoretical entity to observed data. Accordingly, this process has the significant advantage of making our measurement assumptions explicit, transparent, and available for careful scrutiny (for more details see Robinaugh et al., 2020).

Once a theory-implied dataset is produced, we can fit our data model of choice to the dataset to produce theory-implied data models that can then be compared to empirical data models generated using the same statistical analysis. This approach of producing theory-implied data models is similar to predictive checks in Bayesian analysis, where data are generated from the fitted model, and checks are performed on summary statistics of those data (Gelman & Hill, 2006; Gelman et al., 2013). However, one key difference is that in Bayesian analysis parameters can typically be estimated directly from data, while the approach presented here is more general and can be applied in contexts where such direct estimation is not possible.

If the theory-implied data model and the empirical data model are in agreement, then theory can be said to provide an explanation for the phenomenon. If that phenomenon is a more specific characterization of a previously explained phenomenon, we have improved the explanatory precision of the theory. If that phenomenon is entirely new, we have improved the explanatory breadth of the theory. The more disparate the phenomenon from what has previously been examined, the greater the boost in our confidence that the theory is indeed representing the real world target system. If the theory-implied data model and the empirical data model are not in agreement, we move to the second step of our iterative process and consider whether to adapt the theory.

4.2.2. Abductive Inference and Theory Adaptation

If a discrepancy between a theory-implied and empirical data model is observed, the next step is to determine the best explanation for this discrepancy. The first possibility to consider is whether the discrepancy could have arisen due to the auxiliary hypotheses embodied in the generation of a theory-implied dataset. For example, in the comparison depicted in Figure 7, we observed a discrepancy in the prevalence of persistent concern between our theoretical model (5.30%) and our empirical model (1.32%). This discrepancy may have arisen from our assumptions about how subjects self-reported their level of worry or persistent concern. Because our measurement assumptions have been formalized, they are transparent and available for us to scrutinize. In this case, we may conclude that our measurement assumptions regarding self-reported Persistent Concern require revision, thereby better equipping us to make use of empirical data on this symptom in future research.

If we do not see a plausible explanation for the discrepancy in our auxiliary hypotheses, we must turn our focus to our theory and use abductive reasoning to consider the best explanation for the observed discrepancies. This explanation may lie in the value of parameters, the functional form of certain relationships or even the broader structure of the theory (the components and the presence or absence of relationships between them). We can then use this abductive inference to make one or several of changes to the theory, producing a new adapted formal theory, which better accounts for the empirical data at hand. For example, consider again the discrepancy between the theory-implied and empirically observed prevalence of persistent concern or worry depicted in Figure 7. In our simulated data from our panic disorder theory, all “subjects” who exhibited Avoidance also exhibited Persistent Concern. However, in the empirical data, most individuals who exhibited Avoidance did not exhibit Persistent Concern. One explanation for this discrepancy is that we underestimated the success of avoidance as a strategy for reducing anxiety, thereby failing to account for individuals whose avoidance regulates arousal sufficiently well that they do not exhibit persistent concern or worry. As with our auxiliary hypotheses, because formalization has made all aspects of the theory precise and explicit, we can better evaluate what aspects of the theory may have given rise to the observed discrepancy, thereby providing clear guidance for how it may be improved. In this case, we may conclude that it is necessary to revise the parameter that defines the strength of the effect of avoidance on arousal or incorporate an effect directly on perceived threat. With a modestly revised theory, we can now continue the theory development process, comparing the revised theory-implied data models with additional models derived from empirical data. By repeating this process across many data models, the theory can be refined and begin to account for a broader and more precise set of phenomena.

4.2.3. Considerations for Theory Development

To this point, we have provided a broad sketch of how comparisons between theory-implied data models and empirical data models can be used, not for theory testing, but for theory development. The core of this approach is simple. Discrepancies between robust empirical data models and the data models implied by our theory give us both an opportunity to evaluate what the theory can explain and an opportunity to learn how the theory can be improved. However, while the core notion of this approach is simple, the specifics are difficult. We suspect there is no single recipe for the best approach to carrying out this stage of theory construction. In the remainder of this section we discuss a number of outstanding questions that researchers are likely to confront when carrying our this work. We view these questions as important avenues for future research that expand on the broad ideas presented here.

What data and data models are most appropriate for theory development?

Psychological theories will be most successful if a multitude of different data types and data models are employed in developing them. For dynamical systems theories of mental disorders, intensive longitudinal data in large samples may play an especially important role as such data can provide relatively direct measurements of the components of the target system with reasonably high sampling frequency. Experimental data in which the target system is perturbed or manipulated may similarly be especially valuable, as it can help better inform conclusions about causal relations between different components of the target system. However, it is important to note that other data types will also be highly valuable. For example, in Section 3.3.2 we were able to use cross-sectional epidemiological data to provide insight into the shortcomings of our theory of panic disorder, despite the absence of longitudinal data or experimental control. In fact, the panic model implies a wide variety of observational consequences: that panic attacks should correlate with avoidance, but also that panic attacks will unfold on a shorter time scale than does learning to avoid panic-related situations, that perceived threat and arousal should move in a synchronized fashion as panic attacks build up, and that specific interventions on the system should produce specific theory-implied behavior. This allows for a much more detailed picture of which kinds of observations to expect if the theory is correct, and thus opens up a range of possibilities for informing theory development using a wide range of data models. This is a property we expect to be present in any theory which is formalized with a sufficient level of specificity. In other words, if we have a formal theory, then we do not need to choose between cross-sectional and intensive longitudinal research or between observational and experimental data. Rather, we can leverage the information provided by each of these data models to inform theory development using the approach we have proposed here.

Regardless of the type of data model, it is critical to the approach we have proposed that the data models used to inform theory be robust. Mental disorders are extremely heterogeneous and multifactorial, which means that large amounts of carefully sampled data are required both to establish the phenomena that should be explained by a formal theory, and to inform the development of the theory. If the phenomenon itself does not generalize in the intended population, it is futile to engage in theory construction, because it is unclear whether there is any phenomenon to be explained in the first place. Similarly, if the data models used for theory development are not reliable and generalizable, theory development becomes an exercise of fitting noise, and different research teams will disagree about theory development because they base their decisions on noisy data sets that point in different directions. Formal theory construction in psychiatry and clinical psychology will therefore be substantially strengthened by initiating large-scale data collection efforts aimed at establishing and characterizing mental health phenomena.

How do I know if I have the right measurement function?

In Section 3.3.1, we noted that discrepancies between empirical and theory-implied data models can arise from both the theory and from the measurement function that connects the formal theory with the data. This poses a significant barrier to our ability to use empirical data to inform theory development. This barrier is not unique to the approach we have proposed here. Discrepancies between theoretical predictions and the findings from empirical research can only ever be attributed to the conjunction of theory and auxiliary hypotheses (e.g., measurement functions), never to the theory alone (Meehl, 1978; Robinaugh et al., 2020). This problem is pervasive in psychology, where we are typically unsure about the precise relationship between the observed variables in our data and the components of our target system (Kellen, Davis-Stober, Dunn, & Kalish, 2020). Indeed, the causal connection between attributes of the real world and observed data is notoriously hard to establish (Borsboom, Mellenbergh, & Van Heerden, 2004), especially at the level of higher order latent constructs (e.g., “internalizing”, the “p-factor”; Caspi et al., 2014; Krueger, 1999). As a result, psychology lacks the elegant coordination between mathematical theory and observational data that often characterizes the physical sciences (Wigner, 1963).

Although our approach does not resolve this fundamental issue, it helps to address it by forcing researchers to be transparent about their measurement assumptions. Comparisons between theory-implied and empirical data models require that measurement functions be formalized, and thus, made explicit and available for critical evaluation. This allows researchers to evaluate whether the posited measurement function may have given rise to any observed discrepancies between the theory-implied and empirical data models. In principle, this means that data model comparisons can improve both our theories and our measurement models: If we have a formal theory that is already well-established based on different data types, it is less likely to be the source of data model discrepancies than the measurement function itself and the measurement function my require revision. Conversely, if a given measurement function has been well-established, any observed discrepancies may be more readily attributed to the theory. This suggests that formal theories and measurement models must be developed in parallel, with the development of one strengthening the development of the other.

When is theory adaptation warranted?

We suspect it is unlikely that empirical and implied data models will ever be exactly the same in most areas of psychology. Indeed, we should not necessarily aspire for them to be equivalent, as formal theories are representations only of the target system and are not intended to represent all aspects of the real world that could bear on the data. We therefore need a way to decide whether a disagreement between the empirical and theory-implied data model is due to stochastic noise (e.g., sampling variance) or whether this indicates a flaw in how our theory represents the target system. Only the latter would warrant adapting the formal theory or associated auxiliary hypotheses. One possible means of informing this decision is to compute the likelihood of both the empirical and implied data model given the empirical data, and use statistical procedures to compare both likelihoods. This could entail, for example, a likelihood-ratio test or the computation of a Bayes-factor. If we conclude that the likelihoods are not sufficiently different, revision of the theory may not be warranted and we can tentatively conclude that the theory can explain the empirical data model. On the other hand, if we conclude that the likelihoods are sufficiently different, it calls for an adaptation to be made to either our theory or our auxiliary hypotheses.

When has an adaptation improved the theory?

Once we have adapted our formal theory, we would like to test whether those adaptations lead to robust improvements in the correspondence between the theory-implied and empirical data models. We can again make use of a likelihood-ratio test or Bayes-factor, except that here our comparison is not between empirical and implied data models, but rather between the implied data models of the original formal theory and the implied data models of the adapted formal theory. That is, we can compare the likelihood of the empirical data given those two implied data models.

Notably, our discussion of theory adaptations to this point has focused only on “local optimization”, providing an adapted formal theory that fits the present data better than the original formal theory. However, that same adaptation could worsen the fit with other types of data. This possibility presents a major challenge to theory development, because it means that we can get stuck in a process of adapting the formal theory to increase the fit to one type of data, while decreasing the fit to a number of other data sets. To avoid this problem and properly evaluate whether an adaptation improves the theory more globally, we need strategies that take the fit to all available data into account when choosing whether to adapt a formal theory. This is a difficult task. However, it is likely that relevant methodology can be adapted from fields with a longer tradition of formal theory development which frequently deal with this problem.

When should a theory be developed and when should it be abandoned?

The theory development stage can have two possible outcomes. One is that the theory becomes increasingly difficult to develop, because each adaptation introduced to better fit a certain data set worsens the fit to a set of other data sets. For such “degenerative” theories (Meehl, 1990; Lakatos, 1976), it is most appropriate to return to the theory generation stage and choose a different starting point. Alternatively, iteratively completing the steps of deducing data models and adapting the formal theory may lead to a theory that not only explains the core phenomena, but also explains many related phenomena with high precision. In this case, the formal theory is ready for the final step of theory testing.

4.3. Stage 3: Testing Theory

In the framework we have proposed here, the heavy-lifting of theory construction is done in the generation and development stages. Theory generation is not merely the act of writing down a plausible explanation, it is precisely specifying a mathematical or computational model and showing that the model can explain the phenomena of interest. Theory development is not merely expounding on one’s initial ideas, it is demonstrating an expansion of its explanatory breadth and precision. The great majority of theories in psychology remain in the stage of theory generation and exceedingly few have demonstrated the kind of explanatory breadth and precision that would suggest they no longer require further development. Accordingly, we anticipate nearly all theory construction efforts in psychology and psychiatry for the foreseeable future will be focused on generating and developing theories with considerable explanatory capacity. Nonetheless, we do think there is a final stage of theory construction worth noting: that of the traditional hypothesis test.

Importantly, this stage of theory construction does not call for null hypothesis significance tests, but rather strong tests of a theory; tests of risky predictions that render the theory vulnerable to refutation (Meehl, 1990). Risky predictions are those that would be unlikely were it not for the theory. To take an example from another domain of science, perhaps one of the most remarkable instances of a risky prediction occurred more than 150 years ago, when two astronomers observed that the orbit of Uranus deviated from the orbit anticipated by Newtonian physics and determined that these deviations could be explained by the presence of an as yet unseen planet (Bamford, 1996). Using Newtonian physics, they predicted the presence and precise location of this previously undiscovered celestial body and, startlingly, their prediction was correct. The planet Neptune was discovered. This prediction was spectacularly unlikely in the absence of Newton’s theory, so, when the prediction bore out, it afforded the theory enormous credibility.

The example of Neptune’s discovery is instructive not only because it illustrates the kinds of tests that afford corroboration, but also because it clarifies the kinds of theories that can support such risky tests. The existence of Neptune was predicted when the theory failed to account for the orbit of Uranus. Yet, despite this discrepancy between the theory and empirical data, astronomers did not abandon the theory. Rather they doubled down, asserting that if there was a discrepancy between the theory and our knowledge of the universe, the problem must lie with our knowledge of the universe. More precisely, they determined the problem was with their auxiliary hypothesis that there were no unaccounted for celestial bodies affecting the orbit of Uranus and they revised these hypotheses rather than the core of the theory. This allegiance to the theory was only possible because the theory had been so well-developed and shown to explain so much that it had already accrued substantial credibility long before this dramatic risky prediction. In the face of a discrepancy between the theory’s prediction and the empirical data, astronomers inferred the best explanation for the discrepancy and used that insight in conjunction with the theory itself to make a highly specific risky prediction. Accordingly, this example suggests that to subject a theory to a risky prediction, the theory should have already gained considerable credibility and must be capable of making precise predictions.

Formal theories that have gone through the stages of theory generation and development we have outlined here will meet these criteria. In the theory development stage, the theory will have gained credibility by demonstrating its explanatory breadth and it will be capable of supporting strong hypothesis testing by allowing the researcher to derive predictions sufficiently precise that they would be unlikely in the absence of the theory. As in the theory development stage, the theory testing stage thus calls for us to deduce the precise data models implied by our theory and to compare those implied data models to empirical data models. For example, a very well-developed theory of panic disorder would be able to predict the peak value of perceived threat likely to result from a particular arousal-inducing manipulation (e.g., by breathing CO2 enriched air; Roberson-Nay et al., 2017). More importantly, it may predict that previously unconsidered treatments should be effective in the treatment of panic disorder or that a characteristic pattern of target system behavior signifies vulnerability to panic attacks, thereby identifying a marker of vulnerability that can support preventive interventions before the disorder arises (Robinaugh, Haslbeck, et al., 2019). Regardless of the prediction, as this stage of theory construction, when theory-implied data models are compared with empirical data models, the aim is not to develop the theory, but to corroborate or refute the theory.

The function of this stage of theory construction is thus less to build the theory than it is to show whether the theory is ready to stand on its own. It is an attempt to demonstrate to other researchers and applied practitioners that the theory is sufficiently well developed that it can make clear and accurate predictions about what we will see in the real world. Accordingly, research at this stage must be confirmatory in the strictest sense of the term (Wagenmakers, Wetzels, Borsboom, van der Maas, & Kievit, 2012). These studies should be preregistered with model simulations showing the formal theory, formalized measurement, and specific analyses that will be used in the study and, thus, the precise data model that the researcher expects to observe. A theory that passes such a strong test by predicting the observed empirical data model will be strongly corroborated, having demonstrated that practitioners can trust the theory to help them predict and control the world around them. For example, using the theory to identify those in need of care, make diagnostic decisions, and determine the most appropriate treatment. Theory testing is thus the final stage of theory construction that must be passed before a theory is ready to be taken out of the hands of researchers and used effectively in the real world, firmly and reliably supporting not only explanation, but also the prediction and control of psychological phenomena.

5. Discussion

In this paper, we examined how data models can best inform the development of formal theories of psychopathology. We focused especially on the network approach to psychopathology and considered three possible routes by which the conditional dependence networks used in this literature may inform formal theories about how mental disorders operate as complex systems. We found that these data models were not themselves capable of representing the structure we presume will be needed for a formal theory of any mental disorder. Perhaps more surprisingly, we also found that we were unable to draw clear and reliable inferences from data models about the underlying system. Importantly, this analysis is not intended as a critique of the specific data models we examined here, nor is it a dismissal of their value. Quite the opposite. These data models provide rich and valuable information about the relationships among components of a system and we strongly suspect that our concerns about their ability to inform theory would hold for any data model that can feasibly be estimated from empirical data. Nonetheless, our analysis does strongly suggest that the network approach to psychopathology cannot succeed using these data models alone.

We found that the most promising use of empirical data models for theory development was to compare them to theory-implied data models. Building on this observation, we proposed the Abductive Formal Theory Construction framework (AFTC), a roadmap for theory construction that specifies how data models can best be used in the generation, development, and testing of formal theories. In this framework, formal theories play an active role in their own development, with an initial formalized theory refined over time through ongoing comparison between theory-implied and empirical data models. The foundation of this approach is the generation of an initial formal theory that initiates a cycle of theory development. Within this cycle of theory development, theory-implied data models and empirical data models are compared and abductive inference regarding any discrepancy between these models is used to guide ongoing revision to the theory. Only after an extended period of development is the theory well-equipped to undergo rigorous theory testing.

As theory construction in psychology progresses, we believe it will be important to integrate theories across levels of analysis. Formalizing theories as mathematical or computational models makes them explicit, transparent, and expressed in a language that is consistent across domains of science, thereby rendering them widely accessible to researchers across disciplines. This is especially noteworthy in the context of theories of psychopathology, because there are other disciplines that bear on or are directly concerned with mental health that already have strong traditions of mathematical and computational modeling. For example, there is a rich tradition of formal theory in the domains of mathematical and cognitive psychology that focuses on understanding the healthy functioning of thoughts, emotions, and behaviors. Integrating such theories with the kinds of formal theories we have emphasized in this paper could help us to produce theories that can represent systems both in healthy and unhealthy states of functioning, and explain the transition between those states (e.g., in the development or treatment of psychopathology; Haslbeck, 2020). Similarly, the highly formalized field of computational psychiatry studies functional pathways in the brain, and how dysfunctional versions of them lead to symptoms of mental disorders (e.g., Huys et al., 2016; Wang & Krystal, 2014; Stephan & Mathys, 2014; Friston, Stephan, Montague, & Dolan, 2014). Results from computational psychiatry can inspire mechanisms for models on the higher level of analysis we have emphasized here, and constrain such models by their neuroscientific plausibility.

Theories at these distinct levels of analysis could ultimately be integrated to produce more comprehensive theories that can account for phenomena across multiple levels of analysis. The promise of this type of multi-scale modeling approach has recently been discussed in the field of biological psychiatry (Lytton et al., 2017; Joshi et al., 2020; Readhead et al., 2018). If we are to develop these comprehensive multi-scale models of these disorders, it will be necessary to have well-developed formal theories at each level of analysis, including the behavioral, cognitive, and affective level that is the focus of this paper. This level of analysis is highly relevant to clinical practice, both because it is the level at which the core objects of psychiatry (i.e., signs and symptoms) reside (Parnas, Sass, & Zahavi, 2013) and because many first-line treatments for mental disorders operate at this level (e.g., cognitive behavioral therapy). Ultimately, we hope that formalizing theories across these related disciplines and across different levels of analysis will allow for more unified and collaborative development of theories of psychopathology, with theoretical gains in one one area (e.g., a model of neurobiological function) facilitating gains in others (e.g., a model of panic disorder; Cicchetti & Dawson, 2002; Kopniksy, Cowan, & Hyman, 2002).

We have argued that research on mental disorders will be best advanced by constructing formal theories of psychopathology and we have put forward a framework that posits how best to use data models at each stage of theory construction. This framework has the potential to help our field tackle the complexities of mental health, connect psychiatric research to work in basic psychological science, and to better integrate research on psychopathology across different levels of analysis. We do not intend this framework to be a prescription for how all research must proceed, but rather a guide that can provide researchers with ideas for how to advance their theories. We would also stress that any given researcher needn’t engage in all aspects of the work outlined in this framework. Indeed, we suspect some division of labor in psychology would strengthen the field, allowing some researchers to focus on rigorous detection and description of empirical phenomena while others focus on the generation and evaluation of rigorous formal theories that explain those phenomena. The approach we have proposed here provides a framework in which these diverse efforts, across different domains and different levels of analysis, can work together to advance our understanding of psychopathology. Indeed, we believe that it will only be through this ongoing collaboration and integration across researchers that we will be able to leverage the empirical literature to produce genuine advances in our ability to explain, predict, and control psychopathology.

Appendix

A. Simulated Data from the Panic Model

In this appendix we describe in more detail how the simulated dataset, presented in both Sections 3.2 and 3.3 are obtained.

Data is simulated from the Panic Model, the full specification of which is given by (Robinaugh, Haslbeck, et al., 2019), using the statistical programming language R. We use the Panic Model to generate time-series data of 1000 individuals, on a single minute time scale, for 12 weeks, using Euler’s method with a step size of .001. This yields a total of n_t = 12, 0960 repeated measurements per person. Each individual starts with a different initial value of arousal schema, drawn from a normal distribution with μ = 0.25 and σ = 0.0225. The parameters of this distribution were chosen to roughly generate a representative number of panic disorder sufferers (for more details see Robinaugh, Haslbeck, et al., 2019). Otherwise each individual obtains the same parameter values and the same starting values on all processes, with the stochastic noise terms drawn using a different random seed for each individual. The mapping from this raw data to the variables used in the network models of Section 3.2 is described in the main text. Code to reproduce this data-generation scheme can be found in the reproducibility archive of this paper.⁸

B. Panic Model and Statistical Dependencies

In this appendix we describe in more detail the patterns of statistical dependencies produced by the three data models fitted to data simulated from the Panic Model in Section 3.2. While in the main text we discuss the statistical dependencies between between Arousal and Perceived Threat, and Arousal Schema and Avoidance, here we focus only on the former. Key to the Arousal-Perceived Threat dependencies is the positive feedback loop between Arousal and Perceived Threat in the Panic Model (as described in Section 2). If Arousal and Perceived Threat become sufficiently elevated, this “vicious cycle” leads to runaway positive feedback, with a pronounced spike in both Arousal and Perceived Threat (i.e., a panic attack). This spike initiates a process of homeostatic feedback that brings Arousal down and suppresses Arousal below its baseline for a period of time after this panic attack, a period which we will refer to as a recovery period. The panic attack itself lasts about 30 minutes. However, the recovery period lasts for 2–3 hours (see Figure 9 panel A).

Figure 9:

Panel (a) depicts Arousal during a panic attack, showing the short sharp peak of arousal levels, followed by a longer recovery period of low arousal, before the system returns to the usual resting state. The dotted line indicates the mean level of arousal over the observation window (0 – 10 hrs). Panel (b) depicts the state-space plot of Perceived Threat and Arousal at the next measurement occasion, as captured by the emulated ESM study and VAR model. Grey points indicate an observation window of 90 min in which either part of a panic attack or the following recovery period is captured. The solid grey line reflects the marginal lagged relationship. Panel (c) depicts the cross-sectional marginal relationship between the mean of Arousal and mean of Perceived Threat, as analyzed in the GGM model. Grey dots indicate individuals who suffer from panic attacks, and black dots represent “healthy” individuals. The solid grey line shows the negative marginal relationship. The dotted grey lines indicate the median of both variables, by which the binarized values used in the Ising model analysis are defined.

In the VAR model in Figure 5 (b) in the main text, we observed a strong negative conditional relationship between Perceived Threat at time t and Arousal at time t+1, conditioning on all other variables at time t. The distribution of these lagged variables is shown in Figure 9 (b), with the grey line representing the also negative marginal relationship. This strong negative cross-lagged relationship is a direct consequence of the recovery period of Arousal: High values of Perceived Threat are closely followed by a long period of low Arousal values. This can be seen in Figure 9 (b), where observations over windows in which a panic attack and recovery period occur are shaded in red. By averaging arousal values over a window of 90 minutes, the strong positive causal effects operating locally in time (i.e. over a very short time-interval) are not directly captured, but instead the VAR(1) model describes correctly describes the negative relationship between the means of each variable over this window.

In the GGM in Figure 5 (c) in the main text, we saw a positive linear relationship between Arousal and Perceived Threat in the estimated GGM. This dependency indicates that high mean levels of Arousal are associated with high mean levels of Perceived Threat, conditional on all other variables. We stress the conditional nature of this relationship, because the marginal relationship between the two variables is in fact negative as can be seen in Figure 9 (c). This negative marginal relationship comes about by combining two groups of individuals that have different mean values on both variables. Individuals who experience panic attacks (grey points) have high average Perceived Threat, but low average Arousal, due to the long recovery period of Arousal after a panic attack. On the other hand, individuals who do not experience panic attacks have higher average values of Arousal, and lower average values of Perceived Threat. When inspecting the two groups separately, we see that there is a positive linear relationship between mean Arousal and Perceived Threat in the group without panic attacks; The group with panic attacks is too small to determine a relationship. Since Escape and Avoidance behavior only occur after Panic attacks, conditioning on those two variables amounts to conditioning on whether an individual had panic attacks. This conditional relationship is then driven mostly by the positive relationship in the (much larger) group of individuals who have no panic attacks, indicated by the black dots in Figure 9 (c).

Finally, we can explain the weak positive relationship between Arousal and Perceived Threat in the Ising model (Figure 5 (d) in the main text): The levels of these variables are defined by a median split of their mean values, depicted as dotted lines in Figure 9 (c). Unlike in the GGM, there is a positive marginal relationship between these binarized variables, as the majority of individuals without panic attacks (denoted by the black points) end up in the low Perceived Threat and low Arousal groups (lower left quadrant Figure 9 (c)) or high Perceived Threat and high Arousal groups (upper right quadrant). How then do we end up with a weakly positive conditional relationship between these two binary variables? Similarly to the GGM above, it turns out that conditioning on variables such as Escape behavior and Avoidance almost entirely separates individuals into either the low Arousal and low Perceived Threat category (e.g., for low Escape values) or the high Arousal and high Perceived Threat category (for high Escape value). This means that, once we have conditioned on other variables which have direct and indirect causal connections to Arousal and Perceived Threat, there is very little additional information which Arousal can add to predicting Perceived Threat levels (and vice versa). This produces the weak positive conditional relationship between Arousal and Perceived Threat, as well as the stronger positive connections between Avoidance and Perceived Threat.

C. Details Empirical vs Simulated Ising Model

In this appendix we describe in more detail how the theory-implied and empirical Ising Models presented in Section 3.3 are obtained.

C.1. Simulated Data and Implied Ising Model

To obtain the theory-implied Ising Model we use the raw time-series data generated from the Panic Model and described in Appendix A

To create the binary symptom variables in Section 3.3 we transformed the raw time-series data of each individual as follows. First, we define Anxiety at a given time point as the geometric mean of the Arousal and Perceived Threat components at that point in time. Second, we define a panic attack as short, sharp peak of Arousal and Perceived Threat. We code a panic attack to be present in the time-series data if Anxiety takes on a value greater than 0.5. The duration of a panic attack is the length of time Anxiety variable stays above this threshold, and so we define a single panic attack as a sequence of consecutive time points in which Anxiety stays over this threshold. This allows to define our first binary symptom variable, Recurrent Panic Attacks:

• 1Recurrent Panic Attacks (PA) : PA is present if the individual experience more than three panic attacks over the observation window.

We define recurrent as more than three over the observation window for consistency with how this symptom is defined in the CPES dataset, detailed below.

Next, we can define the symptom Persistent Concern (PC), again using the time-series of Anxiety. This symptom is typically described as experiencing a heightened level of anxiety following a panic attack (American Psychiatric Association, 2013). To define this, for each individual who experiences a panic attack, we calculate the mean level of Anxiety in a window of 1000 minutes (16.67 hours) following the end of each panic attack. If another panic attack occurs in that window, we instead take the mean level of Anxiety between the end of one panic attack and before the beginning of the next. This gives us a vector of mean Anxiety levels per person, one for each panic attack experienced. Next, we must define what we consider to be a “heightened” level of anxiety. We do this by obtaining the distribution of mean Anxiety levels for healthy individuals, that is, those members of our sample who never experience a panic attack. We consider mean Anxiety levels following an attack to be “heightened” if they are greater than the 90th percentile of mean Anxiety levels in the healthy population. This gives us our second binary symptom variable.

• 2Persistent Concern (PC): PC is present if, following at least one panic attack, higher average levels of Anxiety are present than in the healthy population, as defined by the 90th percentile of average Anxiety in the healthy population.

Finally we take a similar approach to defining the symptom Avoidance (Av), typically described as engaging in a heightened level of avoidance behavior following a panic attack. For this symptom, we use the time-series of the Avoid component. For each individual who experiences a panic attack, we calculate the mean level of Avoid in a window of 1000 minutes (16.67 hours) following the end of each panic attack, or before the beginning of the next attack, whichever is shorter. Heightened avoidance behavior is defined relative to the 90th percentile of Avoid levels in the healthy population. This gives us our third binary symptom variable.

• 3Avoidance (Av): Av is present if, following at least one panic attack, higher average levels of Avoid are present than in the healthy population, as defined by the 90th percentile of average Avoid in the healthy population.

The Ising model of these three symptom variables is fit using the EstimateIsing function from the IsingSampler package (Epskamp, 2015), that is, using a non-regularized pseudolikelihood method.

C.2. Empirical Symptom Data

To test the empirical predictions of the Panic Model, we made use of the publicly available Collaborative Psychiatric Epidemiology Surveys (CPES) 2001–2003 (Alegria et al., 2007). The CPES is a nationally representative survey of mental disorders and correlates in the United States. The CPES is attractive to use for testing the Panic Model, first because of the large sample size (20,013 participants) ensuring reliable estimates of empirical dependencies, and second, because approximately 146 items in the survey assess either panic attack or panic disorder experiences, characteristics, and diagnoses, typically in terms of lifetime prevalence.

To define our three panic disorder symptoms, we first use the diagnostic manual of the CPES to define whether individuals have ever experienced a panic attack based on responses to 18 items. There are three criteria which must be met for the individual to be classed as having experienced at least one lifetime panic attack. These are shown in Table 1. In coding the presence or absence of a panic attack, individuals must positively report at least four out of the thirteen charactersistics of a panic attack, according to the second criteria in Table 1. Missing values were taken as a failure to report that characteristic.

Table 1:

Three criteria necessary to code an individual as having one lifetime panic attack based on items from the CPES survey, based on the CPES diagnostic manual

Criterion	Description	Item number(s)
A	A discrete period of intense fear or discomfort	SC20 or SC20a
B (four or more)	Palplitations, pounding heart	PD1a
	Sweating	PD1e
	Trembling or shaking	PD1f
	Sensation of shortness of breath or smothering	PD1b
	Feeling of choking	PD1h
	Chest pain or discomfort	PD1i
	Nausea or abdominal distress	PD1c
	Feeling dizzy, unsteady, lightheaded or faint	PD1d or PD1m
	Derealization or depersonalization	PD1k or PD1l
	Fear of losing control or going crazy	PD1j
	Fear of dying	PD1n
	Paresthesias (numbing or tingling sensations)	PD1p
	Chills or hot flushes	PD1o
C	Symptoms developed abruptly and reached a peak within 10 minutes	PD3

With this definition of a panic attack in place, we define the three binary symptoms of panic disorder, following the definitions laid out in the diagonistic manual for panic disorder.

1. Recurrent Panic Attacks (PA). PA is present if participant reports more than three lifetime occurrences of an unexpected, short, sharp attack of fear or panic (item PD4 and criteria in Table 1), more than one of which is out of the blue (PD17a)

2. Persistent Concern (PC). PC is present if reported that following an attack, a month or more of at least one of: a) persistent concern about having another attack (PD13a), or b) worry about the implications or consequences of having an attack (PD13b)

3. Avoidance (Av). Av is present if participant reports at least one of a) following an attack, changing everyday activities for a month or more (PD13c), b) following an attack, avoiding situations due to fear of having an attack for a month or more (PD13d), or c) in the past 12 months, avoiding situations that might cause physical sensation (PD42).

In coding this, if two out of three PA criteria were present, and the third was missing, we assigned a positive value to the PA item. The empirical Ising model was fit using the same procedure as the theory-implied Ising model.