A systematic review of computational models for the design of spinal cord stimulation therapies: from neural circuits to patient-specific simulations

Abstract

Seventy years ago, Hodgkin and Huxley published the first mathematical model that described action potential generation, laying the foundation for modern computational neuroscience. Since then, the field has evolved enormously with studies spanning from basic neuroscience to clinical neuromodulation applications. Computer models for neuromodulation have evolved in complexity and personalization, advancing clinical practice and novel neurostimulation therapies, such as spinal cord stimulation (SCS). SCS is a widely used therapy to treat chronic pain with rapidly expanding indications, such as restoring motor function. In general, simulations dramatically contributed to improved lead designs, stimulation configurations, waveform parameters, and programming procedures, as well as provided insight into potential mechanisms of action of electrical stimulation. However, while practical applications of neural models are relentlessly increasing in number and complexity, it is reasonable to ask whether this observed increase in complexity is necessary for improved accuracy and ultimately clinical efficacy. To this aim, we performed a systematic literature review with a qualitative meta-synthesis of the evolution of computational models, with a focus on complexity, personalization, and the use of medical imaging to capture realistic anatomy. Our review showed that increased model complexity improved both mechanistic as well as translational studies. More specifically, it enabled the development of patient-specific models that can help transform clinical practice in SCS. Finally, we combined our results to provide clear guidelines for standardization and expansion of computational models for SCS.

Graphical Abstract

Evolution of computational models of spinal cord stimulation. The use of computational models of spinal cord stimulation is rapidly expanding in the field of neuromodulation. Here, we evaluated the evolution of such models from the 1980s to 2022. Thanks to the advancement of medical images and computational tools, models evolved from 2D models (left) to 3D models with limited realism and tissue compartments (middle), then, to MRI-based patient specific models with high realism and complex tissue compartments (right). Model figures from left to right were adapted from Coburn 1980, Capogrosso et al. 2013, and Rowald et al. 2022, respectively, with permission. Abbreviation key: gm-gray matter, wm-white matter, csf-cerebrospinal fluid, edf-epidural fat, root-roots and rootlets

Introduction:

Since Hodgkin and Huxley published their numerical solutions to the set of partial differential equations describing the generation of membrane voltages in axons (Hodgkin & Huxley, 1952), computer models in neuroscience have bloomed into a myriad of applications. In addition to theoretical understanding of the neural code, computer models have found fertile ground in translational studies of neurostimulation (Capogrosso & Lempka, 2020). This clinically oriented application stemmed from the need to understand the mechanisms underlying the observed experimental evidence that electrical stimulation of axons in the dorsal columns reduced chronic pain in patients with refractory pain syndrome. This technology, known as spinal cord stimulation (SCS), is now the most widely adopted neurostimulation therapy, and computer simulations of SCS have paved the way for the use of computational tools in other neurostimulation technologies, such as nerve and deep brain stimulation (DBS) therapies (Capogrosso & Lempka, 2020). Here, we reviewed the historical progression of computer models for SCS and analyzed the introduction of modern imaging techniques and their impact on current and future clinical applications.

Spinal cord stimulation (SCS)

SCS is an FDA-approved therapy for treating refractory pain with more than 50,000 implants per year (Sdrulla et al., 2018). SCS for pain management dates back to 1967 (Shealy et al., 1967; Wall & Sweet, 1967). It was originally developed on the premise of the gate-control theory of pain (Melzack & Wall, 1965), in which Melzack and Wall theorized that the activation of cutaneous fibers can interfere with nociceptive signaling through inhibitory interneurons that “gate” pain transmission from the spinal cord to the brain. This hypothesis led to the suggestion that electrical stimulation of the dorsal columns, which carry low-threshold cutaneous afferents, would drive activity in spinal inhibitory interneurons, which would in turn attenuate nociceptive signaling and thus prevent nociceptive output from the spinal cord to the brain (Lempka & Patil, 2018; Zhang et al., 2014). To this end, electrodes were placed in the dorsal epidural space to stimulate sensory afferents in the dorsal columns. Aided by the relatively low risk of the surgical procedure, SCS has since been employed in investigational studies to explore a variety of clinical applications, such as improvement of motor control and autonomic functions in a variety of disorders, such as multiple sclerosis, stroke, and spinal cord injury (SCI) (Barola et al., 1995; Barolat-Romana et al., 1985; Meglio et al., 1989; Waltz & Andreesen, 1981; Cioni & Meglio, 1987; Powell et al., 2022; Pirondini et al., 2022).

Computational models of SCS

Computational models of neurostimulation build on the concepts developed by Hodgkin-Huxley to estimate how extracellularly applied electric potentials influence the neural membrane voltage (Hodgkin & Huxley, 1952; Holsheimer, 1998). More specifically, three-dimensional (3D) volume conductor models of the spinal cord geometry, which rely on realistic anatomy that can be obtained by anatomical measures and/or medical imaging (Figure 1A), are used to compute the extracellular potential. A numerical method, such as the finite element method (FEM), can then be used to calculate the potential distributions generated within these complex anatomical structures (Coburn & Sin, 1985) (Figure 1B). Extracellular potentials are finally applied to Hodgkin-Huxley neural models (Hodgkin & Huxley, 1952) to estimate the corresponding neural response (Figure 1C).

Figure 1.

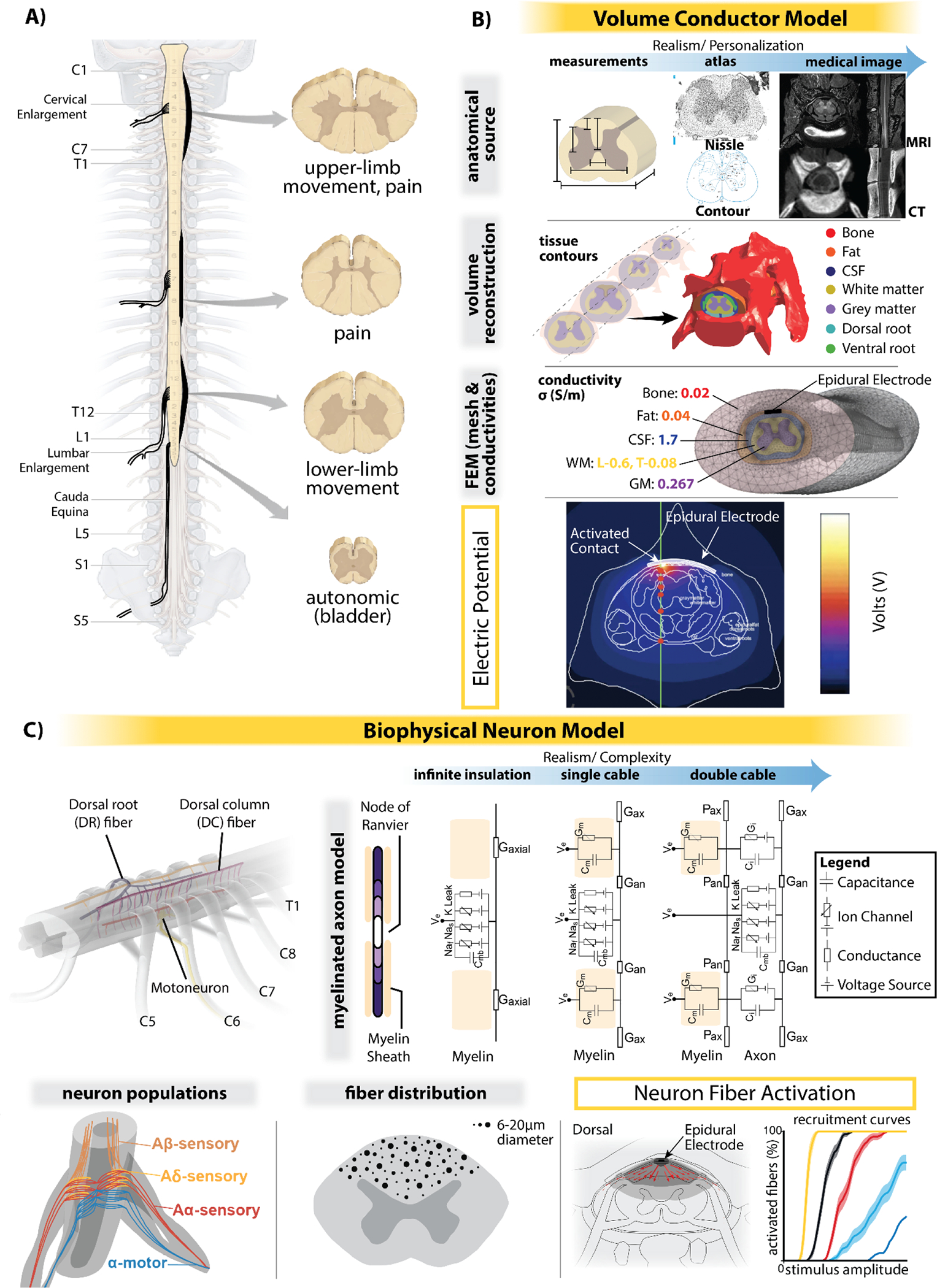
SCS computational modeling components. (A) Example of human spinal cord segments morphology, and their general applications in SCS (movement: movement restoration, pain: chronic pain treatment, autonomic: autonomic/lower urinary tract function restoration). Differences in root angle and segment shape for each spine area are highlighted with thickened lines. (B) Steps for building the volume conductor model that can be used to simulate the electromagnetic fields generated by SCS: 1) tissue contours are derived from anatomical sources, i.e., measurements, atlas, and/or medical images; 2) these segmentations are then used for the 3D volume reconstruction; 3) proper conductivity values are assigned to each tissue and the mesh is generated to simulate electromagnetic field distributions. (C) Potential components for the biophysical neuron model. Neuron fiber activation can be simulated based on assigned fiber diameter, neuron population, or neural trajectory, which with parameter tuning based on experimental and/or clinical data, can be translated into experimental and/or clinical predictions, such as perception and discomfort thresholds, and measurements of motor restoration. Subfigures in panel C include modified figures from Greiner et al. 2021 (Greiner et al., 2021) and de Freitas et al. 2022 (de Freitas et al., 2022) with permission.

Why do we need computer models of SCS?

In translational applications of SCS, in silico neural models provide a platform for investigating mechanisms of neurostimulation technologies and optimizing the therapy in ways that would be difficult, time consuming, and expensive to perform experimentally (Capogrosso & Lempka, 2020). For example, computer models can be used to restrict the parameter space to be tested experimentally. This accelerates development and mitigates safety and ethical concerns by reducing the number of pre-clinical subjects as well as clinical iterations of initial experimental assays.

With regard to SCS for chronic pain management, computational models have provided insights into which neural pathways primarily respond to SCS, supporting the gate-control mechanism of the therapy (Holsheimer, 2002). These computational models also led to dramatic improvements in lead designs, stimulation configurations, waveform parameters, and programming procedures (Lempka & Patil, 2018). For instance, they have been used to develop or validate new lead designs (Kent et al., 2014). Computational models are also utilized in commercial clinical programming systems to determine stimulation configurations and select parameters that focus the stimulation at a desired location (selected by the user) (Veizi et al., 2017). Finally, a computational network model has been used to optimize the temporal patterns of a SCS waveform (Gilbert et al., 2022). Yet, in many cases, these approaches remain to be clinically validated.

The knowledge gained from computational models of SCS for pain permitted a rapid growth of SCS models for other applications. In experiments utilizing SCS to improve locomotion, computational models demonstrated that myelinated afferent fibers are the primary targets of SCS, activating motoneurons and other cells via synaptic pathways (Capogrosso et al., 2013). These models also revealed that antidromic action potentials elicited in primary sensory afferents by SCS interfere with natural sensory feedback, which is crucial for coordinated limb movements (Zhang et al., 2014; Sadashivaiah et al., 2018; Moraud et al., 2016; Formento et al., 2018). This issue was resolved by implementation of a biomimetic burst stimulation protocol spatiotemporally tuned to selectively activate different spinal cord locations with precise temporal resolution. This protocol was first tested through computer simulations (Moraud et al., 2016; Formento et al., 2018) and then followed by experiments in rats (Wenger et al., 2016), monkeys (Capogrosso et al., 2016), and later in humans (Wagner et al., 2018).

Unknowns, challenges, and open questions

Overall, the previous examples highlight the importance of computational simulations in the translational pathway, to pre-clinical tests, and finally to successful clinical implementation. Computational models support and expedite the development, optimization, and implementation of innovative neurostimulation therapies. Yet, there are still important questions to be addressed. First, there is no consensus on which anatomical structures are essential for accurate volume conductor models and what are the most proper imaging techniques and protocols to capture these structures. Secondly, there is still controversy on how several factors influence model accuracy, such as the presence and characteristics of a biophysical neuron model, the applied physical material properties (e.g., electrical conductivity), and the necessary levels of model complexity and personalization. Finally, the best methods to standardize model validation and clinical outcome metrics are not established, resulting in a dramatic lack of defined guidelines that consequently limits the effective use of computational models in clinical applications. To answer these questions, we reviewed the evolution of computer models of SCS since their introduction in the early 1980s (Coburn, 1980; Sin & Coburn, 1983). The goals of this review are to identify overall trends, including both established and emerging indications, as well as provide recommendations to standardize and expand the use of computational models to advance the field of SCS for various clinical applications.

Methods:

Inclusion criteria and study search

The papers included in the present review had to comply with three essential criteria: a) they had to include volume conductor models of the spinal cord; b) the computational model was used to simulate the field(s) generated by electrical SCS (epidural, intradural or transcutaneous); and c) the paper was available in English. The search for relevant papers was initially conducted in PubMed (https://pubmed.ncbi.nlm.nih.gov/, Mar. 4, 2022) using the key-words defined in (Table 1) by means of Boolean operators, nesting, and truncation.

Table 1.

Keyword search table and results.

Search Term	Search Results PubMed (Mar. 4, 2022)	Comment
“spinal cord stimulation” AND (“finite element” OR “computation*”) NOT “peripheral”	72	no filter
“spinal cord” AND “stimulat*” AND “computation*” AND model	128	no filter
“spinal cord” AND “stimulat*” AND “finite element” AND model	74	no filter
“spinal cord” AND “stimulat*” AND simulation AND model	334	no filter
Total Number of Publication	608
Total Number of Publication Excluding Duplicates	431

Coding of variables

For each included paper, we extracted variables to categorize distinct aspects of the computational models. We divided these aspects into objective and derived variables. On an important note, several methods can be used to solve Maxwell’s equations and calculate the applied potentials in the complex anatomical geometries. However, because the finite element method (FEM) is by far the most common approach, we will generally refer to these methods as FEM models.

Objective variables:

• Year of publication of the paper.

• Species on which the FEM model was based: human, monkey, canine, cat, rodent.

• SCS technique: epidural, intradural, transcutaneous.

• Spine level coverage: cervical, thoracic, lumbar/lumbo-sacral, whole spinal cord.

• Application for which the FEM model was used: pain, movement, autonomic function, biophysical. “Biophysical” meant that the model was not used for a specific application, but with the goal to improve the general development of computational models (e.g., comparing the dermatomal zone selectivity of single current source and multiple current source systems within the dorsal column (Min et al., 2014)).

• The main purpose for which the model was created: optimize stimulation parameters, optimize lead position, optimize lead design, investigate mechanism(s) of action, and modeling. “Modeling” refers to studies that developed and released the model without a specific purpose. When there was more than one purpose in the same paper, we assigned the most relevant one.

• Anatomical sources used to create the FEM model: measure/atlas-based, magnetic resonance imaging (MRI)-based, MRI/measure-based. “Measure/atlas-based” refers to either using basic geometric contours of shapes and sizes measured from dissections or taken from literature, or using an atlas (i.e., by extrusion of histological cross-sectional images). “MRI-based” refers to using 3D reconstructions of tissue structures through MRI segmentations. Finally, the “MRI/measure-based” category refers to using a combination of measures and MRI-based models. It is important to note that we used the term “MRI” to refer to medical imaging (i.e., MRI and/or CT). This choice was made because only n=4 articles (Song et al., 2015; Greiner et al., 2021; Lempka et al., 2020; Zareen et al., 2017) reported the use of CT as an anatomical source for specific compartments (bone and electrode). Furthermore, to date, dura mater and roots/rootlets tissues have not been created in any FEM using MRI, therefore we did not consider these structures in the anatomical sources classification.

• Validation: no validation, qualitative validation, and quantitative validation. We assigned a study “no validation” if the main conclusions drawn from the simulations were not validated against any experiments. However, note that the model may have been validated for other simulations in a different publication. A “qualitative validation” corresponded to a comparison between simulated and experimental results without directly comparing numerical values. A “quantitative validation” involved direct comparison of values, such as compound muscle action potential amplitudes (Laakso et al., 2014). For studies with both qualitative and quantitative validation, we placed them in the quantitative validation group.

Derived variables:

In addition to objective variables, we assigned different scores to the models based on two derived variables, namely personalization and complexity.

• Personalization: a variable that evaluated to what extent the FEM model was personalized for a specific subject. We assigned a score of 0, 1, or 2. “0” meant that the model was not personalized. “1” meant that the model was partially personalized (e.g., variations in the dorsal cerebrospinal fluid (CSF) thickness or a modification of tissue conductivity to simulate SCI). “2” meant that the model considered the realistic shapes and sizes of each anatomical compartment for a specific subject.

• Complexity: we considered two levels of model complexity: a) FEM model complexity and b) neuron model complexity.

  1. FEM model complexity: a variable that evaluated the complexity of the tissue volumes and conductivities included in the FEM model. We calculated the complexity score for each FEM model considering the tissues that were included. Precisely, we gave one point for each tissue type that appeared in at least 8% of the papers (i.e., gray matter, white matter, CSF, epidural fat, bone, dura mater, vasculature, rootlets, intervertebral discs, encapsulation tissue, muscle, skin and surrounding layer/saline bath). For the other tissues (e.g., cartilage, connective tissue), which were represented in a minority of the papers, we assigned one point if at least one of these tissues was represented in the FEM model. The maximum score was 11, and we discretized the complexity score in 3 levels: 0 = (complexity score ≤ 4), 1 = (5 ≤ complexity score ≤ 7), and 2 = (complexity score ≥ 8).

  2. Neuron model complexity: a variable that evaluated the complexity of the biophysical model of the neural response to SCS. We calculated this complexity by summing the complexity scores assigned for individual components of the model: axon ion channels and axon cable structure. We assigned the axonal ion channels a score of 0 (no ion channels), 1, or 2. “1” meant that the ionic dynamics were derived from another species, whereas “2” meant that the ionic dynamics were matched to the species for which SCS was being modeled. We assigned the axonal cable structure a score of either 1, 2, 3, or 4. We applied a score of: “1” to models that did not represent the axon as an electrical circuit, but instead used an activating function (i.e., second-order spatial derivative of the applied electric potential) to approximate neural activation (Rattay et al., 2000); “2” to models that represented axons as simple, unmyelinated cylinders as well as models that represented axons as nodes of Ranvier separated by internodes with infinitely resistive myelin; “3” to models that represented axons as nodes of Ranvier connected by myelinated internodes with finite impedance; and “4” to models that used a double-cable structure to model axons with finite-impedance myelin as well as a conductive pathway in the periaxonal region between the axolemma and myelin sheath. We added additional points (i.e., 1 point) if studies incorporated: i) small-diameter collateralization of the axons; ii) more than one fiber population; iii) different fiber diameters; iv) different axon locations; and/or v) varied fiber position and/or diameter to maximize biological realism (e.g., matching fiber densities to histological data, stochastically drawing fiber diameters from an appropriately parametrized distribution). Overall, this scoring system allowed for a maximum of 11 points, and we discretized the complexity score in 3 levels: 0 = (complexity score ≤ 4), 1 = (5 ≤ complexity score ≤ 7), and 2 = (complexity score ≥ 8).

Data analysis

We first summarized the proportional distribution of studies within each category. Then, we focused our analysis on the temporal evolution of individual variables. Finally, we analyzed the relationships between the different variables. It is important to note that when analyzing anatomical sources for different applications and purposes, we considered only studies published after 2010, i.e., the year in which MRI was introduced into the construction of FEM models. Finally, we summarized key findings of human studies that utilized patient-specific models, which may guide future advancement of these tools.

Results:

Study selection

Our search combinations resulted in a total of 431 unique papers on Mar. 4 (Figure 2). Following an abstract appraisal, 352 manuscripts were excluded due to the absence of a volume conductor model of the spinal cord or a focus on unrelated simulations, such as mechanical properties of the spinal cord. Since computational modeling of electrical stimulation is highly interdisciplinary, for the 79 remaining papers, we examined their references to avoid oversight of relevant papers that were not in the PubMed database. As a result of this step, we added 17 papers. Of these 96 papers, nine papers were review papers, perspectives, or book chapters and were excluded from our review. Therefore, we considered a total of 87 papers in our analyses. It should be noted that these 87 papers only included ~41 unique spinal cord models (see Tables 2, 3, and 4 for details). Some of the models were reused in different papers with small modifications. Because these modifications were made to simulate specific conditions or unique applications, we considered each study as a new model in our analysis.

Figure 2.

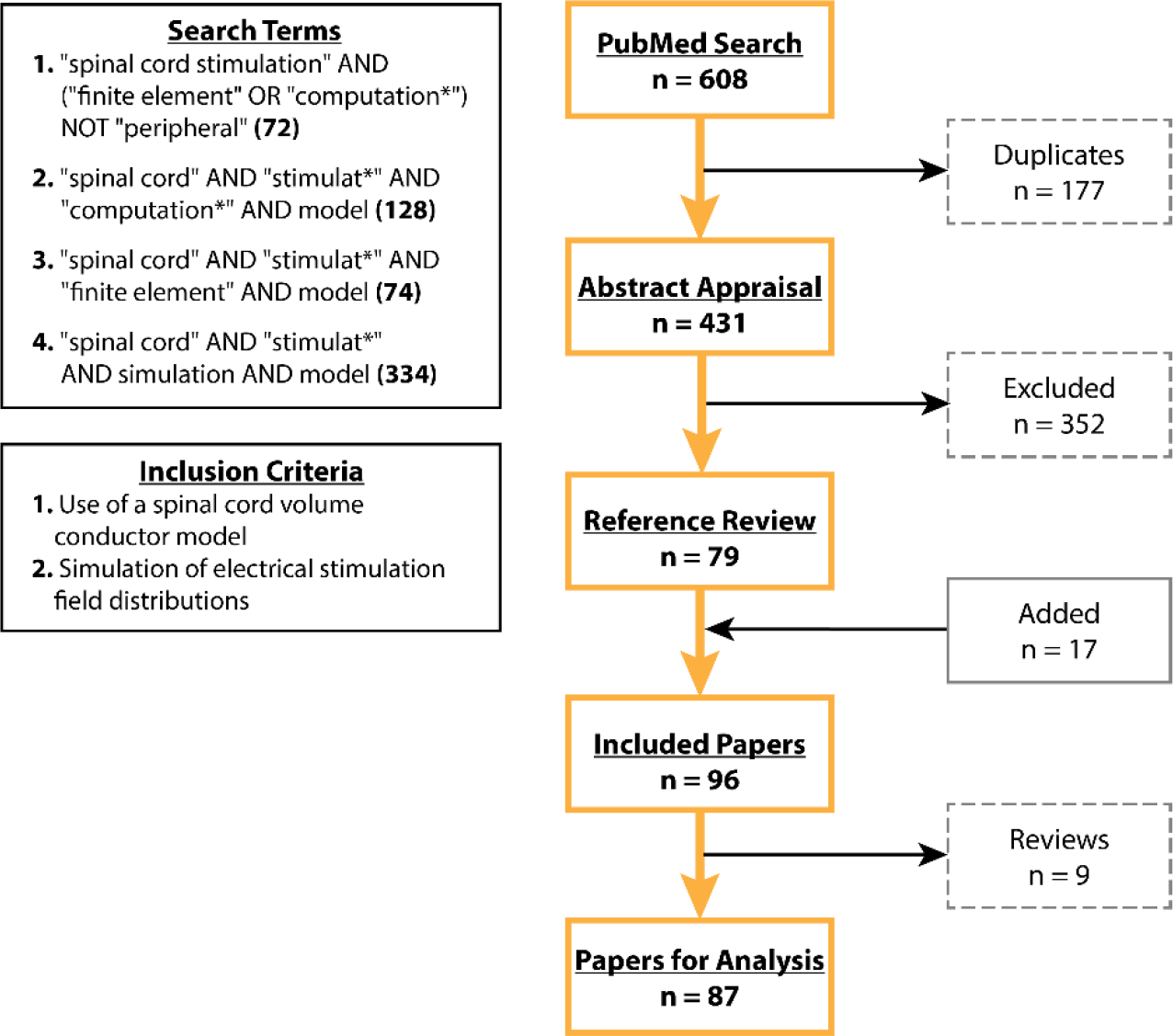
Flow diagram of study selection results.

The evolution of FEM models for SCS

Computational models of SCS were first developed in the early 1980s (Coburn, 1980; Sin & Coburn, 1983). Prior to around the year 2000, the majority of models were not developed for a specific clinical application and studies focused mainly on understanding technical aspects of building a model and factors affecting simulation results. Thereafter, the focus evolved into more specific applications. Computer models for pain management have been and continue to be the most common application (43%) (Figure 3), and only around the 2010s, movement and autonomic function applications emerged (Figure 4A). Therefore, not surprisingly, most of the models (53%) focused on the thoracic spinal cord, the most common SCS target to treat lower back and leg pain. For all existing models, the most common stimulation technique was epidural stimulation (76%) and most of the computational efforts were used to model the human spinal cord (81%), where clinical interest is more abundant. A considerable portion of existing models sought to analyze and optimize the stimulation parameters (40%). Only in the last decade (since 2010), more applied studies were complemented with the interest in understanding the underlying mechanisms of action of SCS (Figure 4C). Not surprisingly, this shift coincides strikingly well with the introduction of computational models of SCS in preclinical animal models and might be driven by the introduction of new SCS technologies, such as kilohertz-frequency (Kapural et al., 2015; Van Buyten et al., 2013) and burst SCS (Deer et al., 2018), which were proposed to improve the clinical efficacy of SCS for pain relief relative to conventional low-frequency (i.e., 40–60Hz) stimulation. Despite the increased use of SCS models in both clinical and preclinical simulations, we found that more than half (58%) of the published simulation results were not validated experimentally, highlighting the lack of standardized guidelines for the effective use of these models.

Figure 3.

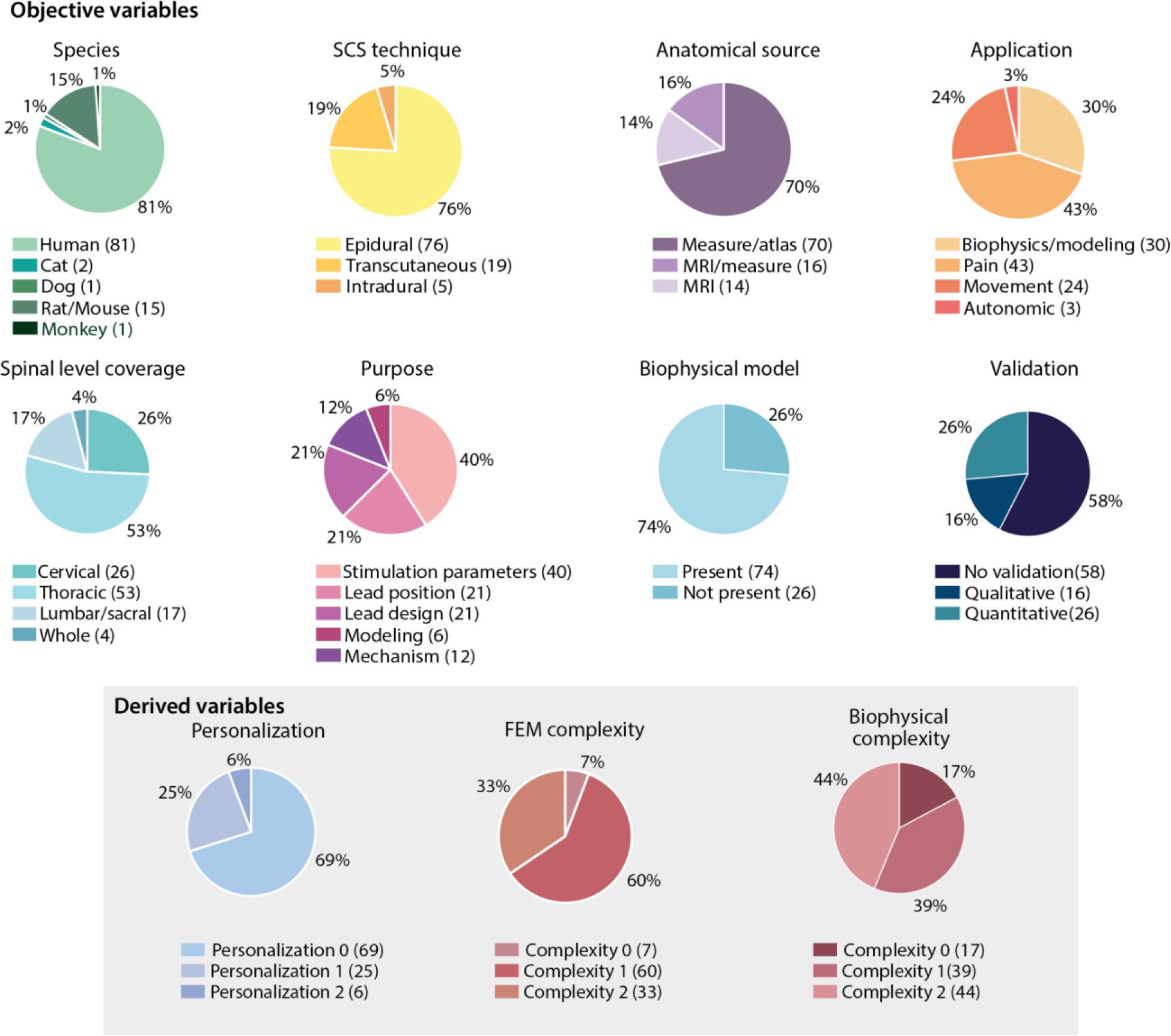
Pie charts of objective- and derived-variable distributions amongst the studies included in our analysis.

Figure 4.

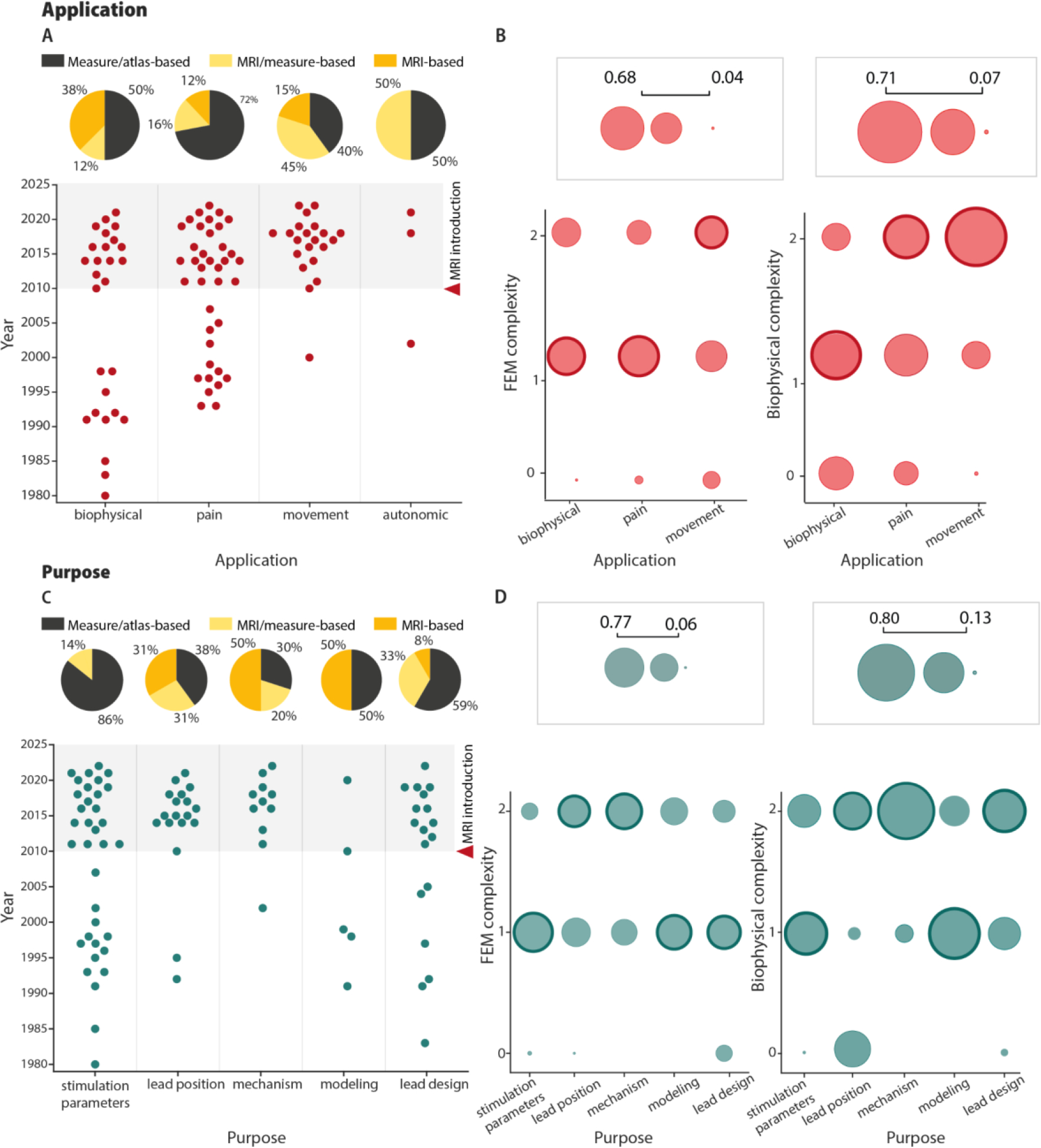
SCS model applications and purposes. (A) The top plot shows the different modeling studies based on their corresponding application (abscissa) and publication year (ordinate). The pie charts show the percentages of the anatomical sources used to create models for each application. For this analysis, we only considered models published after the introduction of MRI to SCS models in 2010. (B) Bubble charts illustrating the distributions of FEM and biophysical complexity scores for different applications. Autonomic was not included due to the low number of studies (n=3). Bold outlines indicate the most frequent complexity score for each application. (C) The bottom plot shows the different modeling studies based on their corresponding purpose (abscissa) and publication year (ordinate). The pie charts show the percentages of the anatomical sources used to create the models for each purpose. For this analysis, we only considered models published after the introduction of MRI to SCS models in 2010. (D) Bubble charts illustrating the distributions of FEM and biophysical complexity scores for different purposes. Bold outlines indicate the most frequent complexity score for each purpose.

The evolution of personalization and complexity of SCS models

Since the earliest computational models of SCS, investigators considered the possible effects of anatomical variations (Holsheimer et al., 1991; Cadotte et al., 2015; Delmotte et al., 2015; Toossi et al., 2021) on the electric potential distributions generated during SCS and the corresponding neural activation. However, most FEM models to date incorporate no personalization (69%) (Figure 3). Only a small percentage (6%) of studies utilized models with a high degree of personalization (i.e., personalization score of 2) and all of these studies were published recently (2014 or later) (Figures 3 and 5).

Figure 5.

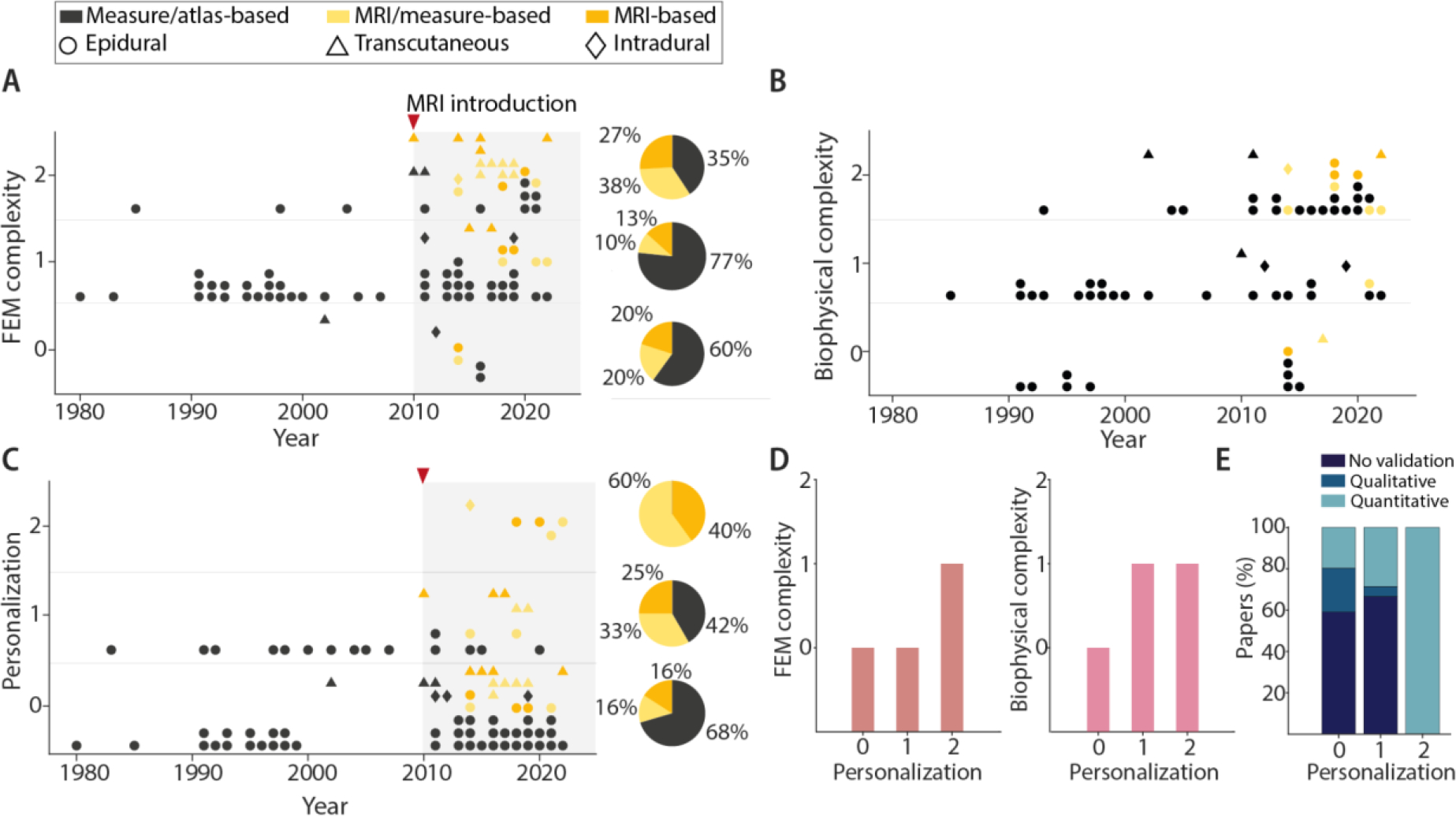
FEM model complexity (A), biophysical model complexity (B) and personalization (C) scores of SCS models as a function of publication year. We have indicated the anatomical sources of the model and the corresponding SCS technique by marker color and shape, respectively. The pie charts in A and C indicate the corresponding percentage of anatomical sources for each complexity and personalization score: 0 (bottom), 1 (middle), and 2 (top). For this analysis, we only considered models published after the introduction of MRI to SCS models in 2010. (D) Bar plots representing the mode of complexity scores for the FEM and biophysical models for each personalization level. (E) Bar plots representing, for each level of personalization, the percentage of papers with no validation, a quantitative validation or a qualitative validation.

We identified an analogous pattern with regard to FEM model complexity. In the early stages, models were two-dimensional and contained limited spinal cord compartments. Probably thanks to more powerful computers, more efficient algorithms, and standardized multiphysics simulation software, FEM models quickly expanded to 3D and utilized a medium level of complexity (i.e., complexity score of 1) (60%). However, only 33% of the models reached the highest complexity level (i.e., complexity score of 2). This increase in complexity might also be explained by the inclusion of the spinal roots and rootlet structures in 16 papers (see Tables 2, 3, 4 for details) since 2014. While some early modeling studies of SCS for pain control included explicit representations of the spinal roots (Coburn, 1980; Coburn & Sin, 1985), recent increased attention on spinal root volume can be partly attributed to increased computational power that allow these roots to be included in complex 3D models. Multiple studies have demonstrated that dorsal root fibers are critical stimulation targets for motor control (Capogrosso et al., 2013; Greiner et al., 2021), which highlights that the inclusion of spinal roots in the FEM model is especially important in SCS for motor control.

An equivalent analysis on the model complexity can be applied to the increase in realism over time for the biophysical neuron models. These neural components are necessary to directly quantify the effect of SCS-produced potential on neural behavior. Coburn was the first to directly model the neural response to SCS, and compared the predicted activation thresholds of dorsal column, dorsal rootlet, and corticospinal tract fibers in response to epidural SCS with clinical observations (Coburn & Sin, 1985). This seminal paper applied the McNeal model of myelinated fibers, which consists of nodes of Ranvier with frog-derived ion dynamics connected by infinitely resistive myelinated internodes (Frankenhaeuser & Huxley, 1964; McNeal, 1976). Following this foundational model, many studies included explicit representations of neurons (74%), with a general trend of increased biophysical complexity over time (Figure 5B). Indeed, only ~17% of biophysical models published before 2010 had high complexity, whereas 59% of those published since 2010 achieved the highest complexity score.

This increase in complexity is attributable both to an increase in the sophistication of components included in the models (e.g., fibre diameters and ion channel dynamics) and to the introduction of new levels of detail (e.g., double-cable myelin model) that provide a more complete or accurate assessment of the neural response (Struijk et al., 1992; Wesselink et al., 1999; Richardson et al., 2000). These developments have followed important findings from studies that were both specific to SCS as well as those for general neurostimulation purposes.

When comparing model complexity and personalization, we found that, despite the limited number of papers with high personalization (n=5), which prohibited statistical analysis, there is a clear trend showing that higher levels of personalization are paralleled by higher levels of complexity in both the FEM and biophysical models (Figure 5D). Interestingly, studies using highly personalized models were more likely to perform a quantitative validation of the simulation results, with 100% of the most personalized models having a quantitative validation (Figure 5E). Out of the 23 studies with quantitative validation, 18 of these studies were published in the last decade (since 2012). These results show that researchers are placing an increased emphasis on model validation, and with enough personalization and complexity, computer models have the capability of making quantitative predictions that may directly inform clinical practice.

Increased complexity shaped the evolution of model applications and purposes

The personalization level distributions were similar across applications and purposes, whereas FEM and biophysical model complexity scores varied across different model applications (Figure 4B), with movement-application models generally having a higher complexity. This higher complexity for movement-application models may be explained by their well-defined neural targets and necessary stimulation precision. Likewise, it is unsurprising that biophysical-application models, which lack a defined functional goal, have the lowest aggregate complexity scores. Moreover, this discrepancy may partially be explained by the fact that models were first applied for different applications in different decades, thus reflecting the general trend for complexity to increase over time (Figure 4A; Figure 5A and B).

Additionally, FEM and biophysical complexity scores also differed between study purposes (Figure 4D). Interestingly, both mechanism and lead design had high complexity both for FEM and biophysical models, whereas modeling-purpose and stimulation-parameters studies had medium complexity. Interestingly, for lead position, the complexity score was higher for biophysical (level 3) than for FEM models (level 2).

Introduction of medical imaging influenced the complexity and personalization of computer models for SCS

Until recently (2010s), the majority of the models were measure-based (71%). In the early 2010s, MRI images obtained with different sequences and microCT scans were introduced, revolutionizing the way that SCS FEM models were created (Figure 3 and 4). For humans, the most common sequences have been SPACE fast turbo spin echo 3D (Christ et al., 2010) and T2 SPACE with ZOOMit (Rowald et al., 2022); whereas in animals, the most common have been TurboRARE T2 weighted pulse sequence (Zareen et al., 2017).

Despite the limited use of this technology, MRI-based models shaped applications and purposes and allowed the use of more complex and personalized models. Indeed, all models with the highest personalization level used MRI-based identification of the anatomical structures and those with medium personalization used medical imaging in the majority of the cases (58%). FEM complexity showed a similar trend with 65% of the models with high complexity deploying MRI information. Interestingly, we found that MRI-based models are used more commonly in the movement application (60% for movement versus 28% for pain) and have recently expanded to the biophysical application (Figure 4A). This trend suggests that, despite being the first and one of the main fields of application, the pain community is not fully taking advantage of the innovations introduced by the use of MR imaging. Several reasons could justify this discrepancy. Rootlet fibers are often not explicitly represented in FEM or biophysical models of SCS for pain, because activation of the thoracic roots and rootlets is believed to be associated with discomfort and the axons within the dorsal columns are the main therapeutic target. Furthermore, the most common implantation levels for SCS for pain are the lower thoracic spine levels. At these levels, it is not possible to visualize these rootlet structures. Further, the anatomy of the thoracic spinal cord is also less variable across segments as compared to the cervical and the lumbosacral cord (Ko et al., 2004; Frostell et al., 2016) (Figure 1A). Therefore, precise cord and rootlet shapes and dimensions are less likely to affect simulation results in the thoracic cord.

Purposes and MRI-based models had a similar evolution. Indeed, we found that, from birth (around early 2010s), mechanisms of SCS were studied mostly using MRI-based models showing that more recent fields took full advantage of this novel technology (Figure 4C). Also, for lead position and design, the usage of MRI has been increasing over the years. Stimulation parameters studies, instead, are still based mostly on measure-based models (Figure 4C).

Finally, it appears that transcutaneous SCS models were mostly MRI-based (Figure 4A). This could be because of the necessity to capture anatomical structure outside the bone, but also by the usage of the virtual family model (Christ et al., 2010), which is MRI-based and is often reused across studies. There is, instead, nothing similar for epidural and subdural SCS.

Discussion

The rapidity at which neuroengineering and neuroscience are expanding results in a continuous demand for new tools capable of optimizing and refining the interactions with the nervous system, even though the role of many structures (e.g., interneurons, fibers, etc.) is still unknown and therefore not described by computer models. This lack of knowledge about target systems represents a crucial obstacle for the development of more effective SCS therapies. In parallel, commercial systems continue to become more sophisticated, allowing an increased variety of waveform parameters, higher electrode counts and non-standardized configurations that represent an increasing variety of possibilities to interact with the system. These technical improvements exponentially increase the space of therapeutic parameters, generating a critical need to find optimal parameter sub-spaces that can be tackled by accurate, realistic, and highly personalized computational models. These virtual frameworks would successfully meet the need to efficiently and effectively explore these large parameter spaces which would be infeasible experimentally. Finally, the increase of model personalization would improve the search for optimal stimulation parameters, lead configurations, and lead position in patient-specific scenarios, hence overcoming current standardized practices that may select sub-optimal therapy parameters. This approach could revolutionize clinical care and patient programming in SCS-based therapies.

In this study, we classified manuscripts describing computer models of SCS to reveal trends in the evolution of applications for SCS models, realism in model components, complexity, personalization and the technological advances and clinical needs that drove these evolutions. In this section, we discuss our main findings with additional recommendations to standardize computational models of SCS and provide suggestions to further improve the quality of these computational approaches.

The importance of increased complexity

As previously stated, computational models can simply include a volume conductor model to simulate the electromagnetic fields generated by SCS or can incorporate a biophysical neuron model to understand ionic current flows in individual neurons (Chakraborty et al., 2018). It has been proposed that, given the complex anatomical structure and variety of factors that can affect neural activation (e.g., branch points, axonal bends), the electric field will best predict neural polarization and neuromodulation, in contrast to the activation function (i.e., the second-order spatial derivative of the electric potential). This approach has been formalized as the “quasi-uniform assumption” (Bikson et al., 2013; Bikson et al., 2015; Khadka et al., 2019) and may serve as a useful and efficient heuristic for predicting which gross anatomical regions are likely to be more strongly affected by the stimulation. Thus, this approach is well-suited for applications in which precise identification of which neurons are being activated is not the primary objective, such as studies investigating novel electrode configurations or the effects of anatomical electrical properties on current flow. On the other hand, for studies investigating precise biophysical activation profiles or evaluating new temporal stimulation patterns, a biophysical model is better able to account for the subtle effects of ion channel dynamics and neural morphology on activation properties. Finally, for putative mechanisms of action other than direct electrical stimulation, biophysical neuronal modeling may be unnecessary and instead multiphysics simulations may be more appropriate. For instance, modeling studies have investigated the combined effects of joule heating (due to applied electric currents) and bioheat transfer as a potential therapeutic mechanism for kilohertz-frequency SCS (Zannou et al., 2019; Zannou et al., 2021).

Despite the quasi-uniform assumption, there is a clear trend of increasing complexity over time both in the FEM and biophysical models (Figure 5A and 5B). However, a more complex model does not necessarily imply a better model, and questions naturally arise as to what level of complexity is necessary and/or sufficient to develop a useful model. Regarding the FEM model, the increase in complexity was partially possible because of the use of MRI techniques to capture gross anatomical structures, such as the spinal roots that are the neural target in the movement field. As discussed in Capogrosso & Lempka 2020, inclusion of root volumes can significantly shift fiber activation distribution and threshold, and thus affect direct clinical applicability of simulated results. However, only three studies considered realistic representations of roots and rootlets that followed trajectories derived from anatomical measurements (Khadka et al., 2020; Greiner et al., 2021; Rowald et al., 2022) and implemented curvilinear anisotropic conductivities (Greiner et al., 2021; Rowald et al., 2022).

Regarding the biophysical model, we considered several factors when scoring complexity. We believe that the value of including several relevant neuronal populations (e.g., both dorsal column and dorsal rootlet fibers to compare on/off target effects) as well as varying axonal diameter and position clearly helps improve the translatability of model predictions. Furthermore, studies have clearly demonstrated the importance of using species-appropriate ion channels (Wesselink et al., 1999) and including branch points (Struijk et al., 1992) in biophysical models of SCS. For each of these variables, maximizing their complexity is not strictly necessary to produce a useful model, as all models require simplifications and abstractions. However, we feel that it is good practice to thoughtfully consider each of these variables to provide a more complete and realistic prediction of the neural response, and accounting for these variables in the models is typically feasible without an unreasonable increase in effort or computational resources.

In contrast, the necessary (and sufficient) complexity to model the axon geometry, and specifically the internode, is more controversial, and largely depends on the study. Compelling evidence demonstrates the role of submyelin conductance in axonal behavior, and the value of representing this current pathway to improve model predictions of axonal behavior relative to single-cable models (Richardson et al., 2000; Cohen et al., 2020). In a direct comparison between models with infinite-impedance myelin, finite-impedance myelin, and a double-layer myelinated axon, Richardson et al. demonstrated that all three models could produce reasonable results in line with experimental data, and that all models were sensitive to parameter choices. However, Richardson et al. found that only the double-cable axon representation could faithfully respond to pulse trains at frequencies of at least 25 Hz, as is typical in SCS (Richardson et al., 2000). Thus, for studies investigating the response to sequential stimuli (rather than activation by a single pulse), a double-layer axon structure is the appropriate model. For studies considering a single stimulus pulse, using a simplified representation may be sufficient to produce a reasonably accurate prediction of the neural response, and will reduce the number of parameters and the corresponding computational complexity. Additionally, simplified approaches may prove valuable and sufficient in situations in which reduced accuracy is acceptable for the accompanying gains in efficiency. For instance, these simplified models could provide a useful heuristic in producing real-time predictions of the neural response to various stimulation configurations while programming devices in the clinic.

Looking forward, significant model improvements remain attainable by generating high-quality experimental data to parameterize biophysical models. The gold standard remains the MRG (McIntyre, Richardson and Grill) model (or derivatives thereof) of the spinal motor axon that was developed two decades ago (Richardson et al., 2000). Promising developments, such as adding additional channel conductances (e.g., active submyelin conductances), have produced model behaviors that better match recordings from human sensory nerve fibers which are highly relevant when modeling the dorsal spinal cord for SCS applications (Gaines et al., 2018). Future work advancing these ideas, as well as investigating the local properties in different regions of the axon (e.g., the axon terminal), will further enhance our ability to model the neural response to SCS.

The importance of patient-specific models to improve, standardize, and expand SCS

Although canonical models are still invaluable to understand the science of SCS and to improve the technical design of SCS systems, patient-specific models are essential to quantitatively describe the axonal response to SCS and to program effective stimulation parameters for each patient. Despite the small number of studies employing patient-specific models of SCS (i.e., only five papers), their results parallel those of other neurostimulation applications where personalization is more established: DBS. Indeed, Frankemolle and colleagues (Frankemolle et al., 2010) showed that computational models of DBS provide an exemplary tool in support of clinical decisions. In this study, patient-specific computational models helped determine stimulation parameters that provided superior clinical efficacy relative to the parameters selected through standard programming methods. In order to obtain similar results for SCS, research groups performed in-depth studies focusing on FEM-model variations of two main structures, CSF and bone, and the corresponding changes in model predictions between highly personalized models and generalized models. Specifically, CSF thickness, which varies as a function of spinal level, body position, and across patients (He et al., 1994; Holsheimer et al., 1995), was shown to have a large effect on current penetration within the spinal cord during SCS. Specifically, an increment of the current density of 54.6% was observed when halving the CSF thickness (Sin & Coburn, 1983). The dorsal CSF thickness was demonstrated to be positively correlated with the activation threshold of dorsal column fibers (Solanes et al., 2021) and perception threshold (which increased by 50.8% and 26.6%, respectively, in the dorsal columns and the dorsal root entry zone, following an increase of the dorsal CSF thickness of 1 mm), and negatively correlated with paresthesia coverage (He et al., 1994; Holsheimer & Struijk, 1991; Holsheimer et al., 1995; Lempka et al., 2015). The transverse size of the dural sac, instead, was negatively correlated with the activation of afferent fibers (Solanes et al., 2021). Similarly, the shape of the spinal canal (Fernandes et al., 2021), size of the spine structures (Fiocchi et al., 2016), and relative position of the stimulating electrodes to the spine (Zander et al., 2020) have strong effects on the electric field and corresponding activation thresholds. Interestingly, after SCI, orthopedic interventions (Greenberg & Arredondo, 2001) can change the spine structure and scarring can change tissues conductivities, which can both affect the simulated electric field amplitude (Hernández-Labrado et al., 2011) and therefore need to be considered in computer simulations. In summary, these studies provide evidence of the great variability in outcome measures deriving from anatomical alterations, suggesting that increased personalization could increase model accuracy by accounting for multiple sources of interpatient variability. Additionally, these studies suggest that CSF thickness, bone, and thecal sac sizes are essential structures for accurate volume conductor models.

In this direction, Lempka and colleagues (Lempka et al., 2020) reported that simulated sensory thresholds obtained with patient-specific models were significantly more similar to those clinically measured than those simulated with canonical models, which underestimate the dorsal column fiber activation thresholds. Additionally, they quantified the effect of pulse-width variation on sensory thresholds, identifying a mean absolute percentage error of 8.9% and 44.9% relative to the clinically measured value, for the patient-specific and canonical models, respectively. Two other studies found similar results in which model predictions of perception and discomfort thresholds were more consistent with the clinical measurements using patient-specific models (specifically, the difference with respect to clinically measured perception threshold was 6.4% and 171% for the patient-specific and canonical model, respectively) (Solanes et al., 2021; Howell et al., 2014). Similarly, in the “movement” application, Rowald et al. 2022 developed highly personalized patient-specific models for the purpose of restoring locomotion. The authors performed an intraoperative validation of the simulated lead position by monitoring electromyographic recordings while delivering SCS. The predictions of the patient-specific model corresponded to the optimal electrode placement; indeed, the study reports that a 2 mm displacement from the predicted location caused a drop in selectivity. Interestingly, the use of a generic (i.e., not personalized) model failed to reach the same accuracy. Thanks to the optimized lead position, contact location, and stimulation configuration for each patient, Rowald and colleagues demonstrated rapid restoration of trunk and leg motor functions in patients with complete paralysis (Rowald et al., 2022). Finally, Veizi and colleagues used a canonical model with patient-specific electrode locations and implemented a patient-specific algorithm to select active electrode combinations and current amplitudes at each electrode (Veizi et al., 2017). The personalized group demonstrated an approximately 1.5 times higher responder rate (i.e., patients receiving ≥50% reduction in pain) relative to a cohort in which stimulation parameters were selected through standard clinical methods.

Despite these extremely encouraging results, additional work using patient-specific models is now necessary to further demonstrate the potential of these models to improve clinical implementation of SCS. We believe that the collection of papers reported here (see Tables 3 and 4) represents a valuable summary to guide the choosing of the best model designs in future works and boost the use of patient-specific approaches. However, wider adoption of SCS models impels the improvement and standardization of MRI protocols that capture relevant structures, such as CSF and spinal roots.

Finally, it is important to note that personalization of DBS models was driven not only by the availability of higher-resolution brain MRI but especially by needs for precision in neurosurgical implantation procedures. Instead, spinal lead implantations are currently performed with limited image-guidance and lower constraint on positioning far from the millimeter precision required to target deep brain structures (Lempka & Patil, 2018). In this context it is important to note that complex personalized computer models of SCS are now suggesting that new neurosurgical approaches to SCS must be developed to improve accuracy and stability of implantation procedures to be able to target specific microstructures, such as the dorsal rootlets (Rowald et al., 2022). This provides a powerful example of how neural simulations can be ahead of clinical practice and influence standard of care.

Medical imaging propelled personalization and complexity

Importantly, all of the studies (n=5) with patient-specific models deployed medical imaging for the segmentation and the quantification of the anatomical structures, suggesting that MRI is necessary to increase the accuracy and the predictive power of these models. On the other hand, models can reach high complexity with both measure-based and MRI-based models. However, since MRI was introduced, the majority of the complex models were also MRI-based. This trend was particularly true for the application of movement restoration. While this could be explained by a tendency of newer fields to propel for the use of newly available technologies, such as MRI, this could also be due to the difficulty to capture structures at the thoracic level, i.e., the most common implantation level of SCS to treat pain. Novel advances in the field of MRI for lower cervical segments (Cohen-Adad et al., 2021) could improve these images and soon change this trend.

However, medical imaging has still not been maximally exploited for development of computational models of SCS. For instance, manuscripts often lack details describing the specific acquisition sequences, thus limiting the adaptability of these approaches. Additionally, even the models with the most complex representations of the spinal cord roots and rootlets did not directly model these structures from medical images, but instead combined anatomical measurements and mathematical algorithms to calculate assumed non-overlapping trajectories. Yet it is now well known that dorsal root diameter, as well as fiber angles and curvature when entering the spinal cord, can cause substantial differences in fiber activation threshold (Coburn & Sin, 1985; Struijk et al., 1993). Therefore, accurate images of these structures are pivotal to increase accuracy of current models. In this direction, advanced acquisition sequences, such as diffusion-weighted MRI (Vargas et al., 2010), provide a means to capture high-resolution fiber trajectories and thus could be used to accurately characterize roots and rootlets shapes.

Future of SCS models

Artificial intelligence (AI)-based algorithms are another important breakthrough that could be extremely advantageous for the development of personalized in silico models of SCS. These approaches have the potential to achieve automation of processes that are currently performed manually. Specifically, the exploitation of AI in the automated tissue segmentation from medical images would drastically reduce the time and effort required for the creation of a patient-specific model, thus paving the way towards personalized precision medicine (Capogrosso & Lempka, 2020; Perone et al., 2018; Gaweł et al., 2018).

Additionally, computational modeling of the neural network effects of SCS is another area with significant potential for development. In the related field of DBS, many researchers developed network-based models incorporating the various basal ganglia populations to investigate the stimulation generated effects on neural circuit behavior (McIntyre & Hahn, 2010). These models provide a more complete picture of the neural response by incorporating interactions between relevant neural populations. A similar approach has recently begun to be adopted for SCS purposes, although the technique remains immature. For pain applications, Zhang et al. produced a SCS-based network model that included primary afferent fibers as well as excitatory and inhibitory interneurons (allowing for subpopulations with different firing characteristics) and measured the output response of spinal neural networks for multiple SCS stimulation frequencies (Zhang et al., 2014). In a contrasting approach, Arle and colleagues produced a comprehensive model with hundreds of thousands of neurons and millions of synaptic connections to examine how SCS can treat neuropathic and nociceptive pain (Arle et al., 2014). Although such models are impressive in scale, they highlight the difficulties as well as the importance of proper model parameterization and constraining models based upon high quality experimental data. Impressive advancements continue to be made in delineating the neurochemical and electrophysiological subpopulations of the dorsal horn and their connections (e.g., Medlock et al., 2022), and integration of these data with best-practice biophysical modeling provides a promising path for understanding how SCS affects the behavior of spinal circuits.

Lastly, while recent studies have increasingly included quantitative comparisons of simulations and experimental results, the validation metrics used for these comparisons have been inconsistent. Inconsistency in these validation metrics creates difficulties in comparing the predictions across multiple models and impedes the development of clinically meaningful standards for effective treatment predictions. For example, in the field of motor function, studies have compared the model-based predictions of large sensory fiber activation thresholds with experimentally observed motor thresholds (de Freitas et al., 2022) and response latency (Capogrosso et al., 2013), simulated motoneuron activation with specific muscle force (Wagner et al., 2018), and simulated and measured compound muscle action potential amplitudes (Laakso et al., 2014). When using computational models to study SCS for pain, validation metrics have been applied more consistently, with most studies comparing simulated dorsal root and dorsal column fiber activation threshold with measured perception and discomfort thresholds (Holsheimer et al., 1995; Struijk et al., 1998; Rattay et al., 2000; Arle et al., 2014; Howell et al., 2014; Lempka et al., 2018; Lempka et al., 2020; Solanes et al., 2021). As the use of SCS continues to increase and expand to new indications, it will be important to establish a standardized set of validation metrics to assist implementation of simulation results in a clinical setting.

To conclude, we strongly believe that, by taking full advantage of MRI techniques and AI, developing novel circuit networks, and increasing computational power, we can develop realistic and highly accurate virtual frameworks to understand the mechanisms of SCS and develop optimal SCS therapies and surgical strategies. With more complex and personalized models, and standardized model validation and clinical outcome metrics, we can bridge the gap between simulations and patient care.

Biography

LL, AD, MB, MJ, LF, RG, MC, and EP are with the Rehabilitation and Neural Engineering Labs at the University of Pittsburgh, a super-lab built as a collaboration of multiple laboratories. They have a long experience in spinal cord stimulation to restore bladder functions, upper- and lower-limb movements, and sensation in people with spinal cord injury, stroke, and amputation. ER and SL are with the Neuromodulation Laboratory at the University of Michigan—Ann Arbor and they implement engineering approaches, such as computational modeling, to study the mechanism of action of clinical neuromodulation therapies for chronic pain management. The two groups have a long-standing collaboration on the design of complex and personalized computer models of spinal cord stimulation with the objective to develop novel effective therapies for different neurological disorders.