Finite-time stability analysis and control of stochastic SIR epidemic model: A study of COVID-19

Abstract

Finite-time stability analysis is a powerful tool for understanding the long-term behavior of epidemiological models and has been widely used to study the spread of infectious diseases such as COVID-19. In this paper, we present a finite-time stability analysis of a stochastic susceptible–infected–recovered (SIR) epidemic compartmental model with switching signals. The model includes a linear parameter variation (LPV) and switching system that represents the impact of external factors, such as changes in public health policies or seasonal variations, on the transmission rate of the disease. We use the Lyapunov stability theory to examine the long-term behavior of the model and determine conditions under which the disease is likely to die out or persist in the population. By taking advantage of the average dwell time method and Lyapunov functional (LF) method, and using novel inequality techniques the finite-time stability (FTS) criterion in linear matrix inequalities (LMIs) is developed. The finite-time stability of the resultant closed-loop system, with interval and linear parameter variation (LPV), is then guaranteed by state feedback controllers. By analyzing the modified SIR model with these interventions, we are able to examine the efficiency of different control measures and determine the most appropriate response to the COVID-19 pandemic and demonstrate the efficacy of the suggested strategy through simulation results.

1. Introduction

The COVID-19 pandemic has had a significant impact on the well-being of individuals and economies globally. In order to control the spread of the virus, it is crucial to comprehend the transmission mechanisms and develop effective strategies to prevent further spread. This includes measures such as personal protective equipment, social distancing, and vaccination efforts [1], [2]. Additionally, tracking the spread of the virus and collecting data on the outbreak is crucial in understanding the evolution of the pandemic and guiding public health interventions. Models to analyze the spread of diseases, such as the susceptible–infected–recovered (SIR) epidemic compartmental model, are commonly used to understand infectious diseases and inform public health decisions. The emergence of a new coronavirus, known as SARS-CoV-2, was identified in China in late 2019 and is the cause of the COVID-19 pandemic [1], [3], [4]. However, much remains unknown about the virus, including the incubation period for the COVID-19 symptoms. To fully understand the impact of SARS-CoV-2 and make informed decisions, it is crucial to gather more information about its epidemiological features, such as transmission dynamics, incubation period, and mortality rate. Further studies are needed to gain a more complete understanding of this novel virus. This has important implications for surveillance and control activities [2], [5]. Despite some countries succeeding in controlling the virus’s spread, others have seen uncontrollable outbreaks. To address the situation, a closed-loop control system, which adjusts the input based on the monitored output, may be a viable solution. The pandemic has brought unprecedented challenges, but solutions such as closed-loop control systems offer hope for effectively managing the spread of COVID-19 [6]. This system can help authorities monitor the situation and make necessary adjustments in real-time to achieve the desired outcome. Implementing such a system can help mitigate the impact of the pandemic and bring the situation under control, leading to faster recovery for communities and the global economy. In the context of controlling the spread of COVID-19, a closed-loop control system (see Fig. 1, Fig. 2) could involve continuously monitoring the number of cases, deaths, and other relevant metrics, and using this information to adjust public health interventions such as mask mandates, social distancing measures, and vaccination efforts.

Fig. 1.

The structure of COVID-19 virus.

Fig. 2.

Closed-loop of COVID-19.

For example, if the number of cases is increasing rapidly, the control system could implement stricter mask mandates or social distancing measures in an effort to slow the spread of the disease. On the other hand, if the number of cases is decreasing, the control system could relax these measures to allow for a gradual return to normalcy [7], [8]. By continuously monitoring the output and adjusting the input accordingly, the closed-loop control system can help to maintain the spread of the disease at a manageable level.

In recent decades, epidemiology has been defined as the study of disease spread with the goal of tracking the variables that are essential for its development. Mathematical models are widely utilized in the investigation of epidemiological issues. Most of the models for infectious disease transmission descended from the conventional SIR model, which was proposed in 1927 (see [9]). Recently, research on various versions of the mathematical model of the expansion of infectious diseases, known as SIR epidemic models, has a long history, and all these approaches are still very current and widely known in research (see, for example, [10], [11], [12], [13]). Epidemic models are influenced by environmental noise, which is an important factor in reality and may result in a more realistic outcome than deterministic models. Recent advancements in stochastic differential equations allow the inclusion of stochastic elements into models of biological events, whether it is random noise in the differential equation system or variations in environmental parameters. The study of population dynamics in random settings examines population size variations influenced by stochastic external factors. Research has been done on stochastic biological systems, as seen in [14], [15]. The proposed approach, which incorporates real-time data into outbreak disease progression simulations and constant updates, can provide a more accurate short-term forecast compared to the traditional mean field-theoretic SIR model. This is because the limited knowledge of the incubation time and virus exposure has less impact on forecasting the progression of the pandemic infection.

Research supports the use of pulsed interventions, particularly in seasonal infectious diseases such as influenza and childhood diseases (measles, chickenpox, and mumps), where seasonal changes initiate periodic epidemics, often with an annual pattern. The switching theory has been shown to be suitable as a model of seasonal forcing in epidemiology, as shown in various articles (see, for example, [16], [17], [18], [19]). However, a significant distinction between these and our study is that we suggest and conceptually justify switching to considerably minimum time periods. Recently, a publication [20] in response to the COVID-19 pandemic proposed irregular, non-periodic quarantine measures with extended lockdown duration’s. To analyze the impact of this approach, we develop a finite-time dynamics model that takes into account the parameters of the proposed system. Using this model, we estimate the number of infections, deaths, and recoveries over a specified number of future days. This model can provide valuable information on the efficacy of proposed quarantine measures and inform decision-making about the pandemic response.

Finite-time (FT) stability analysis, introduced by Dorato in 1961 [21], is a useful method for analyzing a system’s transient response. A system is considered FT stable if its state stays within a specified threshold within a set time frame, given an initial condition constraint. Lyapunov theory and linear matrix inequalities (LMIs) have made significant advances in the stability analysis of various systems, including linear continuous systems (see, e.g., [22], [23], [24], [25]), and discrete systems (see, e.g., [26], [27]). Stability is one of the most important things to study in dynamic systems. Most research on stability focuses on asymptotic or exponential stability, which is stability over an infinite amount of time [28], [29], [30]. However, in several potential implementations, the key issue is the FT stability of a system, which helps to maintain the system behavior/state within the required boundaries in a specified FT interval (see [31], [32], [33]). Furthermore, FT approach and the model of switched systems have currently received more interest, as switched systems may be utilized to represent a variety of important plants with switching [28], [29], [30]. In [34], the authors exploited nonlinear impulsive switching systems to implement finite-time $H_{\infty }$ dynamic output feedback control. Authors in [35], proposed finite-time stability of switched positive linear systems. The authors established the asymptotic behavior of a regime-switching SIR epidemic model with degenerate diffusion in [36].

The development of efficient methods for FT stability analysis, based on Lyapunov theory and LMIs, has increased the practicality of this approach. These advancements have allowed for the analysis of a wider range of systems and have provided useful insights into the transient behavior of these systems. Recently, the authors described the stochastic switching SIRS epidemic model with nonlinear incidence and vaccination: Stationary distribution and extinction in [37]. Despite the fact that an analytical model for compartmental issues allows for the use of known finite-time stability analysis, and switched systems, there are no predictable prerequisites for establishing stability in the Lyapunov sense in biological systems.

Recently, an autonomous LPV (Linear Parameter Varying) system is a type of dynamic system that can be modeled and analyzed using linear mathematical models. The standard continuous-time space–state formulation of an LPV system is a mathematical representation of the system’s behavior in terms of its states and inputs, and how these evolve over time (see [38], [39], [40], [41]). It is well known that the aggressive control measures and policies (such as border screening, mask wearing, quarantine, isolation, etc.), play an important role in administering efficient interventions which control disease spread and hopefully eliminate epidemic diseases. The LPV framework can also be used to model and control systems with uncertainty varying over time, such as unmodeled dynamics, disturbances, and parameter variations. In addition to its modeling capabilities, the LPV framework also provides a flexible and powerful framework for control design and analysis. For example, LPV systems can be used to design controllers that are robust to uncertainty and variations in the system parameters (see [42], [43], [44]). This can be achieved using robust control techniques, such as linear matrix inequalities (LMIs) and semidefinite programming (SDP). The COVID-19 LPV model in [6] was proposed by using basis functions and showed to be useful for stability assessment and controller design. Up to now, SIR epidemic model has been studied with various types of stability analysis, but the FT stability analysis for the Stochastic SIR model has not been well studied, which motivates the present work.

Motivated by the above works, a stochastic SIR epidemic model is a variant of the SIR model that incorporates stochastic elements, such as random fluctuations in the transmission rate of the disease. These fluctuations can be represented by a noise term added to the transition rates in the proposed model. The main novelties of our paper are as below.

• •The suggested SIR model is quite extensive, and the switched stochastic differential equations drive its dynamics. And most other of the existing works [11], [12], [36], [45], [46] can be respected as a special case of this suggested model since we consider many factors such as finite-time stability, LPV analysis, stochastic disturbance, control effect, and unknown parameters.
• •Different from exponential/asymptotic stability analysis on infinite-time interval and design in [12], [36], [37]. In our paper, the FT stability criterion of switched stochastic SIR model is obtained, which is more realistic and theoretical. The way the system behaves over a short period of time is particularly crucial in some epidemic models.
• •Good control system should ensure higher performance in addition to stability. However, the suggested model makes use of state-feedback control. To the best of the author’s knowledge, this note is the first time to examine finite-time stability analysis for the stochastic SIR epidemic model.
• •For the FT stability analysis of the proposed system model with switching approaches, acceptable LF are developed using integral inequality techniques and several new suitable criteria, which may be expressed in terms of linear matrix inequalities (LMIs).
• •Numerical simulations are provided as a last step to show the efficacy and application of the ideas presented. Some standard notations and their specifications are given in Table 1.

Table 1.

Notations and specifications.

Notations	Specification
${\mathbb{R}}^n$	Euclidean space of $n$ dimensions
${\mathbb{R}}^{m\times n}$	The real $m\times n$ matrices
$P>0$	$P$ is symmetric and positive-definite
$P\ge 0$	$P$ is symmetric and positive semi-definite
$P^T$	$P$ represents the transpose of the matrix

2. Mathematical modeling of SIR

The proposed control method is rooted in the nonlinear dynamics of SIR models, a widely studied compartmental approach in epidemic modeling. The SIR model is a simple compartmental model that divides the population into groups with similar characteristics, making it easier to model infectious diseases. This specific strategy focuses on the deterministic version of the SIR model, which serves as a building block for more complex models.

The diagram in Fig. 3 depicts the flow of people between different categories during an outbreak, as outlined by the SIR model. According to the model, individuals can contract the disease and a subset of them may gain immunity, transitioning into the $R$ compartment which represents those with immunity. Before delving into the details of the transition parameters, it is important to establish a clear understanding of the dynamics of the SIR model. This can be done by using a differential equation, which provides a mathematical description of the relationships between the variables involved in the model. Let us define the time$\left(t\right)$-dependent variables in Table 2:

Fig. 3.

Schematic diagram of SIR.

Table 2.

State variables and their meanings.

State variables	Meaning
$S\left(t\right)$	The susceptible individuals at $t$
$I\left(t\right)$	The infected individuals at $t$
$R\left(t\right)$	The recovered individuals at $t$

Thus, the SIR model is of the form

$$\begin{array}{c}\frac{dS\left(t\right)}{dt}=A-\frac{\beta S\left(t\right)I\left(t\right)}{1+kI\left(t\right)}-\delta S\left(t\right),\hfill \\ \frac{dI\left(t\right)}{dt}=\frac{\beta S\left(t\right)I\left(t\right)}{1+kI\left(t\right)}-(\delta +\gamma +ϵ)I\left(t\right),\hfill \\ \frac{dR\left(t\right)}{dt}=\gamma I\left(t\right)-\delta R\left(t\right),\hfill \\ S\left(0\right)\ge 0,I\left(0\right)\ge 0,R\left(0\right)\ge 0.\hfill \end{array}$$ (1)

Here $S\left(0\right)$, $I\left(0\right)$, and $R\left(0\right)$ are the initial population size of the susceptible, infected, and recovered individuals. It is assumed that the total population, denoted by $N$, is constant and equal to the sum of these three categories: $S\left(t\right)+I\left(t\right)+R\left(t\right)=N$. The parameters in the model (1) are summarized in Table 3:

Table 3.

Explanation of the parameters.

Parameter	Meaning
$A$	The influx of individuals into $S$
$\beta$	The transmission coefficient between
	compartments $S$ and $I$
$k$	The value of inhibitory effect
$\delta$	The natural death rate of $S$, $I$ and $R$
	compartments
$\gamma$	The rate of recovery from infection
$ϵ$	The disease-induced mortality rate

• •The parameter $\beta$ represents the contact rate, which is calculated as the average number of contacts per person per time multiplied by the probability of disease transmission in contact between a susceptible and an infected individual.
• •The incidence rate, represented by $\beta SI/(1+kI)$, is considered saturated in nature, which means that it has a ‘psychological’ or inhibitory effect on the transmission of the disease [47]. The value of this effect is measured by the parameter $k$.
• •The parameter $\gamma$ plays a crucial role in the SIR model as it represents the transition rate from the infected class to the recovered or immune class. It is calculated by dividing the number of individuals who recover or die within a day by the total number of infected individuals at that time. This rate is expressed as $\gamma =1/D$, where $D$ is the length of time that an individual is infected. Understanding the value of $\gamma$ is important, as it provides information on the rate at which the infected population is decreasing and the rate at which the recovered population is increasing.

In [48], the authors studied the model (1) with limited medical resources. Since we have explained the basic reproduction ratio before for the SIR model, using the next generation method in [49], $R_0$ is given by

$$R_0=\frac{\beta A}{\delta (\delta +\gamma +ϵ)}.$$

The value of $R_0$ determines the possible spread of the disease within a population. If $R_0\le 1$, it means that on average, an infected individual will infect fewer than one other person, and the disease will eventually die out. However, if $R_0>1$, it means that an infected individual will infect more than one other person, and the disease will become endemic. To understand the dynamics of the disease spread, it is enough to focus on the first two equations of (1), as they do not depend on the number of recovered individuals. We can gain insight into the interactions between susceptible and infected populations by analyzing the subsystem which is

$$\begin{array}{c}\frac{dS}{dt}=A-\frac{\beta SI}{1+kI}-\delta S,\hfill \\ \frac{dI}{dt}=\frac{\beta SI}{1+kI}-(\delta +\gamma +ϵ)I,\hfill \\ S\left(0\right)\ge 0,I\left(0\right)\ge 0.\hfill \end{array}$$ (2)

Further, the effective reproductive number, $R_e$, is a measure of the average number of secondary cases generated by one infectious case during an epidemic. To calculate this number, the basic reproductive ratio is multiplied by the number of susceptible individuals at time $t$, represented as $R_e=R_0\ast (S\left(0\right)/N)$. When the value of $R_0\ast (S\left(0\right)/N)<1$, it indicates that an infected individual is spreading the disease to fewer than one person on average, leading to a long-term decrease in the number of infectious individuals, referred to as a disease-free equilibrium. Model (2) always has a unique disease-free equilibrium at $E_0=(A/\delta ,0)$. The situation changes when $R_0\ast (S\left(0\right)/N)>1$. This means that on average an infected person will spread the disease to more than one person, who will then infect more individuals, etc. This results in an outbreak. For example, in the case of COVID-19, we know that it is possible for the virus to be transmitted from person to person.

3. Existence and stability of equilibria

3.1. Existence

From a biological point of view, it is interesting to determine the disease-free equilibrium and the co-existence/endemic equilibrium such that a population is a positive number. The disease-free equilibrium $E_0=(\frac{A}{\delta },0)$ is always exists. When $R_0>1$, the model (2) has a unique endemic equilibrium $E^{\ast }=(S^{\ast },I^{\ast })$. It is achieved by solving the following equations.

$$A-\frac{\beta S^{\ast }{I}^{\ast }}{1+k{I}^{\ast }}-\delta S^{\ast }=0,\frac{\beta S^{\ast }}{1+k{I}^{\ast }}-(\delta +\gamma +ϵ)=0,$$ (3)

which yields

$$E^{\ast }=(S^{\ast },I^{\ast })=\left(\frac{Ak+\delta +\gamma +ϵ}{\beta +\delta k},\frac{\beta A-\delta (\delta +\gamma +ϵ)}{(\delta +\gamma +ϵ)(\beta +k\delta )}\right)=\left(\frac{Ak+\delta +\gamma +ϵ}{\beta +\delta k},\frac{(R_0-1)\beta A}{R_0(\delta +\gamma +ϵ)(\beta +k\delta )}\right).$$

Theorem 3.1

• • If $R_0\le 1$ , then (2) has no endemic equilibria.
• • If $R_0>1$ , then (2) has a unique endemic equilibrium $E^{\ast }(S^{\ast },I^{\ast })$ .

3.2. Local stability

Theorem 3.2

For (2) , we have

• • The disease-free equilibrium $E_0$ is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$ .
• • If $R_0>1$ , then the endemic equilibrium $E^{\ast }$ is locally asymptotically stable.

Proof

The Jacobian matrix at $E_0$ is given by

$$J_{E_0}=\left(\begin{array}{cc}\hfill -\delta \hfill & \hfill -\frac{\beta A}{\delta }\hfill \\ \hfill 0\hfill & \hfill \frac{\beta A}{\delta }-(\delta +\gamma +ϵ)\hfill \end{array}\right).$$

$E_0$ is locally asymptotically stable if and only if all eigenvalues of $J_{E_0}$ have a negative real part. The eigenvalues can be determined by solving the following.

$$det\left(\begin{array}{cc}\hfill -\delta -\lambda \hfill & \hfill -\frac{\beta A}{\delta }\hfill \\ \hfill 0\hfill & \hfill \frac{\beta A}{\delta }-(\delta +\gamma +ϵ)-\lambda \hfill \end{array}\right)=0.$$

It is clear that the eigenvalues are: ${\lambda }_1=-\delta ,{\lambda }_2=\frac{\beta A}{\delta }-(\delta +\gamma +ϵ)$. Since ${\lambda }_1$ and ${\lambda }_2$ are negative, it is required that

$$\frac{\beta A}{\delta }<(\delta +\gamma +ϵ),$$

which is

$$R_0<1.$$

The Jacobian matrix at $E^{\ast }$ is given by

$$J_{E^{\ast }}=\left(\begin{array}{cc}\hfill -\delta -\frac{\beta I^{\ast }}{1+k{I}^{\ast }}\hfill & \hfill \frac{-\beta S^{\ast }}{{(1+k{I}^{\ast })}^2}\hfill \\ \hfill \frac{\beta I^{\ast }}{1+k{I}^{\ast }}\hfill & \hfill -\frac{\beta k{S}^{\ast }{I}^{\ast }}{{(1+k{I}^{\ast })}^2}\hfill \end{array}\right).$$

The eigenvalues can be determined by solving the following.

$$det\left(\begin{array}{cc}\hfill -\delta -\frac{\beta I^{\ast }}{1+k{I}^{\ast }}-\lambda \hfill & \hfill \frac{-\beta S^{\ast }}{{(1+k{I}^{\ast })}^2}\hfill \\ \hfill \frac{\beta I^{\ast }}{1+k{I}^{\ast }}\hfill & \hfill -\frac{\beta k{S}^{\ast }{I}^{\ast }}{{(1+k{I}^{\ast })}^2}-\lambda \hfill \end{array}\right)=0.$$

The characteristic polynomial is given by:

$${\lambda }^2-\text{trace}\left(J_{E^{\ast }}\right)\lambda +det\left(J_{E^{\ast }}\right)=0.$$

When $R_0>1$, it is clear that

$$\text{trace}\left(J_{E^{\ast }}\right)=-\delta -\frac{\beta I^{\ast }}{1+k{I}^{\ast }}-\frac{\beta k{S}^{\ast }{I}^{\ast }}{{(1+k{I}^{\ast })}^2}<0.$$

and

$$det\left(J_{E^{\ast }}\right)=\left(\delta +\frac{\beta I^{\ast }}{1+k{I}^{\ast }}\right)\left(\frac{\beta k{S}^{\ast }{I}^{\ast }}{{(1+k{I}^{\ast })}^2}\right)+\left(\frac{\beta S^{\ast }}{{(1+k{I}^{\ast })}^2}\right)\left(\frac{\beta I^{\ast }}{1+k{I}^{\ast }}\right)>0,$$

by the Routh–Hurwitz criterion, the real parts of eigenvalues are negative, then $E^{\ast }$ is locally asymptotically stable.  □

Next, let us take the default values of the parameters from [48] as

$$A=16,\beta =0.01,k=0.001,$$

$$\delta =0.1,\gamma =0.12,ϵ=0.2.$$ (4)

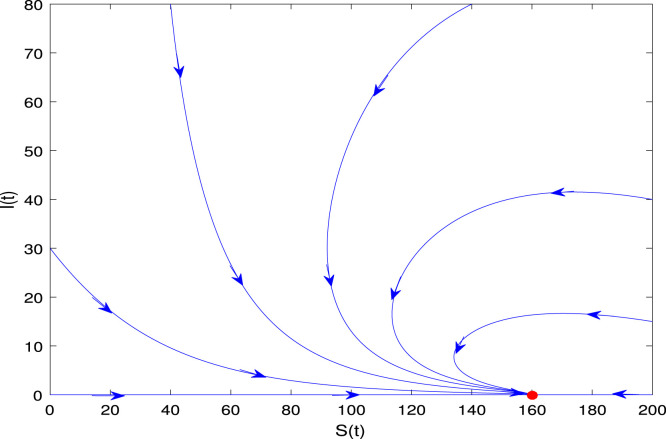
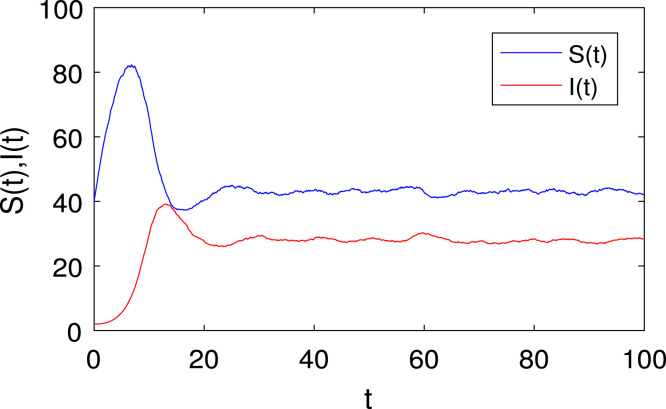
To start, we need to determine a valid range of parameters for the model (2). One way to do this is to choose specific values for the parameters in (4) such that the resulting equilibrium point has positive values. This indicates that the system remains biologically meaningful. Furthermore, the phase portrait is depicted for the deterministic model (2) with the values in (4) has the reproduction rate $R_0=3.80952>1$ for $\beta =0.01$ and there exists an endemic equilibrium $E^{\ast }$, which states that the diseased population will persist is shown in Fig. 4. The equilibrium $E^{\ast }$ is globally asymptotically stable, which implies that the disease will eventually spread. Also, for the value $\beta =0.0025$ the disease will die out such that $R_0=0.952381<1$ and the endemic equilibrium disappears, only the disease-free equilibrium exists as shown in Fig. 5. Stable dynamics in the time series plot for susceptible, infected, and recovered populations are depicted in Figs. 6, 7, and 8.

Fig. 4.

The phase portrait of the model (2) with parameter values given in (4). $E_0=(160,0)$ is a saddle point and $E^{\ast }(43.16,27.81)$ is globally asymptotically stable.

Fig. 5.

The phase portrait of model (2) with parameter values given in (4) with $\beta =0.0025$. $E_0=(160,0)$ is globally asymptotically stable.

Fig. 6.

The time series for the susceptible individuals of the model (1).

Fig. 7.

The time series for the infected individuals of the model (1).

Fig. 8.

The time series for the recovered individuals of the model (1).

In the next section, we will examine the stochastic deterministic SIR model.

4. Stochastic epidemic models

The environment can sometimes change randomly and subject population systems to disturbances. This means that due to environmental uncertainty, the parameters used in epidemic models may not be definite and may fluctuate around certain values. Because of this, there is growing interest in stochastic epidemic models that incorporate randomness and stochastic. Stochastic epidemic models can provide a more realistic perspective compared to their deterministic counterparts (see [11], [50], [51]). Stochastic models aim to address the uncertainties in epidemic models by considering randomness and fluctuations. In populations susceptible to environmental changes, the parameters used in epidemic models are not constant and may fluctuate around typical values. This results in a more realistic depiction of the spread of disease, compared to deterministic models [52]. As a result, an increasing number of people are turning to stochastic epidemic models to more accurately reflect the spread of disease in the face of environmental uncertainty [45], [53]. Studies have shown that these models can provide a deeper level of understanding of the dynamics of disease spread, and are crucial in the development of effective disease control strategies (see [46], [54]).

In this study, the approach taken is similar to that of a previous study by [11], where the authors assumed that the external noise was proportional to the variables. We also assume that the stochastic perturbations in our model are of the white noise type, meaning that they are directly proportional to the susceptible and infected populations and affect the rate of change of these populations. To account for the impact of a changing environment, we include stochastic perturbation terms in the equations for the growth of the susceptible and infected populations. This leads to the following stochastic SIR model that reflects the model (2) with added environmental noise:

$$\begin{array}{c}dS=\left(A-\frac{\beta SI}{1+kI}-\delta S\right)dt+{\sigma }_{1}Sd{B}_1\left(t\right),\hfill \\ dI=\left(\frac{\beta SI}{1+kI}-(\delta +\gamma +ϵ)I\right)dt+{\sigma }_{2}Id{B}_2\left(t\right).\hfill \end{array}$$ (5)

The presence of environmental uncertainty is incorporated into the model (2) by adding stochastic perturbation terms. These terms are proportional to susceptible and infected individuals and influence their growth rates. To represent this influence, a stochastic differential equation is created. The equation includes terms for the intensity of environmental oscillations, represented by ${\sigma }_1$ and ${\sigma }_2$, which are constant and known. Additionally, the equation includes independent standard Brownian motions, denoted by $B_1\left(t\right)$ and $B_2\left(t\right)$. The stochastic model does not have a positive equilibrium. Therefore, it is not possible to demonstrate the persistence of the model by demonstrating the stability of a positive equilibrium, as is done in the deterministic model. The stationary distribution, which occurs as the solution fluctuates in the vicinity of the equilibrium point of the related deterministic model, can be viewed as a form of stability in a weak sense.

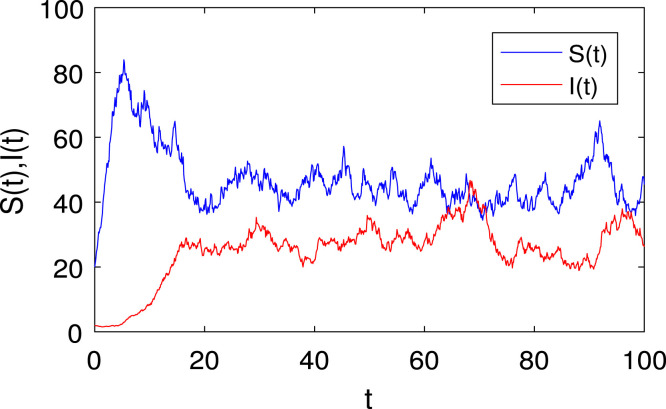
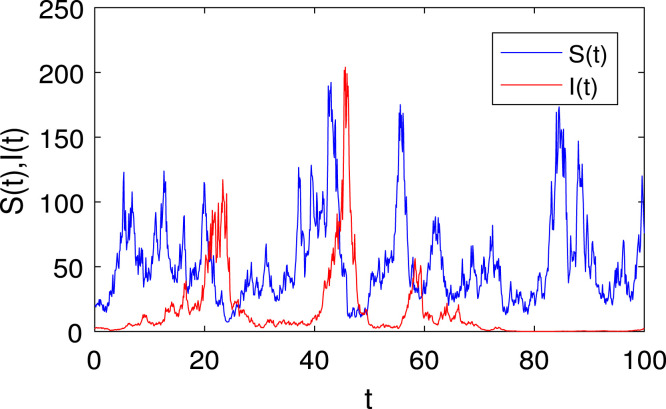
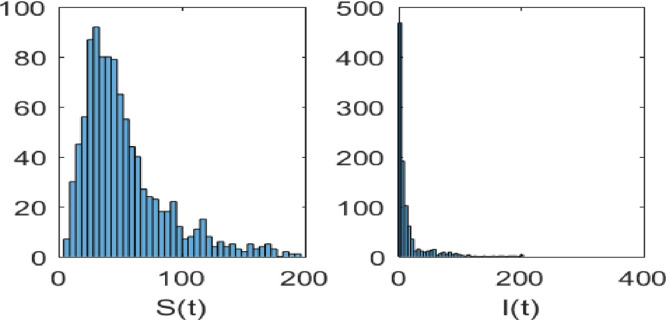
We conducted repeated simulations for the scenario in which the population in the model (2) coexist. We kept all parameters constant as in Fig. 4 during these simulations and generated numerical results. The solution of the stochastic model (5) with very small white ${\sigma }_{1,2}=0.01$ shows very small fluctuations in the trajectories given in Fig. 9, which is close to the trajectories of the deterministic model (2) as in Fig. 6, Fig. 7. As the intensity of the noises gradually increases, we find that the population is persistent. The three solution paths of the stochastic model (5) with white noise ${\sigma }_{1,2}=0.01$ and its trajectories are given in Fig. 10. For the larger white noise ${\sigma }_{1,2}=0.05$, the model (5) trajectories have higher fluctuations in the trajectories plotted in Fig. 11. And the corresponding density function for ${\sigma }_{1,2}=0.1$ shows that most of the infected population is concentrated near $25$, the disease will persist in the population as shown in Fig. 12. Similarly, for ${\sigma }_{1,2}=0.5$, there are very high fluctuations in the trajectories even the infected population size reaches near $200$, eventually, most of the infected population stays near zero as given in Fig. 13 and its corresponding density function is given in Fig. 14. However, we can see that both populations will survive and persist in the presence of suitable environmental white noise.

Fig. 9.

Solution curves of the model (5) with ${\sigma }_{1,2}=0.05$, initial values $S\left(0\right)=20,I\left(0\right)=2$, and all other values are given in (4).

Fig. 10.

Three solution curves of the model (5) with ${\sigma }_{1,2}=0.05$, initial values $S\left(0\right)=20,I\left(0\right)=2$, and all other values are given in (4).

Fig. 11.

Solution curves for the model (5) with high noise ${\sigma }_{1,2}=0.1$, initial values $S\left(0\right)=20,I\left(0\right)=2$ and all other values are given in (4).

Fig. 12.

The histogram of the stochastic model (5) with ${\sigma }_{1,2}=0.1$.

Fig. 13.

Solution curves for the model (5) with high noise ${\sigma }_{1,2}=0.5$, initial values $S\left(0\right)=20,I\left(0\right)=2$, and all other values are given in (4).

Fig. 14.

The histogram of the stochastic model (5) with ${\sigma }_{1,2}=0.5$.

When the strength of white noise is increased, the diseased population dies away (see Fig. 13). The mean of the individuals at ${\sigma }_{1,2}=0.5$ and its corresponding density function are plotted in Fig. 15, Fig. 16. The standard deviation of the individuals at ${\sigma }_{1,2}=0.5$ and its corresponding density function are plotted in Fig. 17, Fig. 18. Both the mean and standard deviation of the individuals show that the disease will persist in the population. Fig. 10, Fig. 11 show that small white noise can make the model permanent. In summary, the addition of environmental noise to population models can provide a more realistic representation of the dynamics of real-world populations. The results of our study suggest that the intensity of environmental noise can greatly impact the behavior of populations, with lower levels of noise potentially promoting outbreaks and higher levels of noise suppressing outbreaks. Our findings highlight the significant role of noise in determining the survival and extinction of populations and demonstrate the complex nature of populations in the real world.

Fig. 15.

The evolution in time of the mean of the individuals over 1000 trajectories with ${\sigma }_{1,2}=0.5$.

Fig. 16.

The histogram of the stochastic model (5) for the mean of individuals over 1000 trajectories with ${\sigma }_{1,2}=0.5$.

Fig. 17.

The evolution in time of the standard deviation for the individuals over 1000 trajectories with ${\sigma }_{1,2}=0.5$.

Fig. 18.

The histogram of the standard deviation for the individuals over 1000 trajectories with ${\sigma }_{1,2}=0.5$.

We can rephrase the statement as follows: The dynamic behavior of the susceptible and infected populations can be described by a state vector $x\left(t\right)={[S^{\ast }{\left(t\right)}^{\prime },I^{\ast }{\left(t\right)}^{\prime }]}^{\prime }$, and the linear parameter-varying (LPV) system is represented by the Jacobian matrix near the equilibrium point. The stability of the equilibrium point of the LPV system is determined by the eigenvalues of the Jacobian matrix, which are functions of the system parameters. If all eigenvalues of the Jacobian matrix have negative real parts, the equilibrium point is considered stable, and the population will remain in the neighborhood of the equilibrium point over time. On the contrary, if any eigenvalue has a positive real part, the equilibrium point is unstable, and the population will diverge from the equilibrium over time. The stability of the equilibrium point is important in determining the persistence or extinction of populations.

$$J_{E^{\ast }}=\left(\begin{array}{cc}\hfill -\delta -\frac{\beta I^{\ast }}{1+k{I}^{\ast }}\hfill & \hfill \frac{-\beta S^{\ast }}{{(1+k{I}^{\ast })}^2}\hfill \\ \hfill \frac{\beta I^{\ast }}{1+k{I}^{\ast }}\hfill & \hfill -\frac{\beta k{S}^{\ast }{I}^{\ast }}{{(1+k{I}^{\ast })}^2}\hfill \end{array}\right),$$

$$\left[\begin{array}{c}\hfill \frac{d{S}^{\ast }\left(t\right)}{dt}\hfill \\ \hfill \frac{d{I}^{\ast }\left(t\right)}{dt}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -\delta -\frac{\beta I^{\ast }}{1+k{I}^{\ast }}\hfill & \hfill \frac{-\beta S^{\ast }}{{(1+k{I}^{\ast })}^2}\hfill \\ \hfill \frac{\beta I^{\ast }}{1+k{I}^{\ast }}\hfill & \hfill -\frac{\beta k{S}^{\ast }{I}^{\ast }}{{(1+k{I}^{\ast })}^2}\hfill \end{array}\right]\left[\begin{array}{c}\hfill S^{\ast }\left(t\right)\hfill \\ \hfill I^{\ast }\left(t\right)\hfill \end{array}\right].$$ (6)

The system’s state space representation takes into account the state vector $x\left(t\right)$, which consists of the susceptible and infected populations, and the Jacobian matrix $E_2$ that governs the dynamics of the states in the vicinity of the equilibrium point. This Jacobian matrix is time-varying, as it depends on the time-varying parameters $\theta \left(t\right)$ and $I^{\ast }\left(t\right)$, and can be represented in polytopic or affine form.

$$\dot{x}\left(t\right)=\mathcal{A}\left(\theta \left(t\right)\right)x\left(t\right),$$ (7)

The matrix $\mathcal{A}\left(\theta \left(t\right)\right)$ can be described in two ways, as mentioned in the literature, either by means of an affine configuration or a polytopic one. The polytopic description is created by combining m known vertices into a single convex formation.

$$\mathcal{A}\left(\theta \left(t\right)\right)=\sum _{j=1}^N{\theta }_j\left(t\right){\mathcal{A}}_j,\theta \left(t\right)\in \Omega ,$$ (8)

where ${\mathcal{A}}_j,j=1,2,\dots ,N$ is the polytope vertices and $\theta \left(t\right)=({\theta }_1\left(t\right),{\theta }_2\left(t\right),\dots ,{\theta }_N\left(t\right))$ denotes a vector of time-varying parameters belonging to a compact set known as unit simplex, which is given by

$$\Omega =\left\{\theta |\sum _{j=1}^N{\theta }_j=1,{\theta }_j\ge 0,j=1,2,\dots ,N\right\}.$$ (9)

The dynamic matrix $\mathcal{A}\left(\theta \left(t\right)\right)$ can be represented using an affine form with $N$ interval time-varying parameters as follows:

$$\mathcal{A}\left(\theta \left(t\right)\right)={\mathcal{A}}_0+\sum _{j=1}^N{\theta }_j\left(t\right){\mathcal{A}}_j,{\theta }_j\left(t\right)\in [{\theta }_j^L,{\theta }_j^U],$$ (10)

where ${\mathcal{A}}_j,j=1,2,\dots ,N$ are the known matrices and ${\theta }_j\left(t\right)$ are time-varying parameters with given lower and upper bounds provided by ${\theta }_j^L$ and ${\theta }_j^U$, respectively. The polytopic form of the dynamic matrix $\mathcal{A}\left(\theta \left(t\right)\right)$ of the LPV system (6) is given by (7).

$$\mathcal{A}\left(\theta \left(t\right)\right)={\theta }_1\left(t\right)\left[\begin{array}{cc}\hfill -\beta (I^L+\rho )\hfill & \hfill -({\gamma }^L+\rho )\hfill \\ \hfill \beta I^L\hfill & \hfill 0\hfill \end{array}\right]+{\theta }_2\left(t\right)\left[\begin{array}{cc}\hfill -\beta (I^U+\rho )\hfill & \hfill -({\gamma }^L+\rho )\hfill \\ \hfill \beta I^U\hfill & \hfill 0\hfill \end{array}\right]+{\theta }_3\left(t\right)\left[\begin{array}{cc}\hfill -\beta (I^L+\rho )\hfill & \hfill -({\gamma }^U+\rho )\hfill \\ \hfill \beta I^L\hfill & \hfill 0\hfill \end{array}\right]+{\theta }_4\left(t\right)\left[\begin{array}{cc}\hfill -\beta (I^U+\rho )\hfill & \hfill -({\gamma }^U+\rho )\hfill \\ \hfill \beta I^U\hfill & \hfill 0\hfill \end{array}\right],$$

where $\theta \left(t\right)=({\theta }_1\left(t\right),{\theta }_2\left(t\right),\dots ,{\theta }_4\left(t\right))\in \Omega$. Moreover, using (6) with (10), we get

$$\mathcal{A}\left(\theta \left(t\right)\right)=\left[\begin{array}{cc}\hfill -\beta \rho \hfill & \hfill -\rho \hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]+{\theta }_1\left(t\right)\left[\begin{array}{cc}\hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]+{\theta }_2\left(t\right)\left[\begin{array}{cc}\hfill -\beta \hfill & \hfill 0\hfill \\ \hfill \beta \hfill & \hfill 0\hfill \end{array}\right],$$

where ${\theta }_1\left(t\right)\in [0.25,0.4]$ and ${\theta }_2\left(t\right)\in [-0.22,0.9091]$.

Now, we consider the state-space description of the stochastic LPV system to be expressed as follows:

$$dx\left(t\right)=\left(\mathcal{A}\left(\theta \left(t\right)\right)x\left(t\right)\right)dt+\mathcal{C}x\left(t\right)dw\left(t\right).$$ (11)

The LPV system (11) has parameter matrices ${\mathcal{A}}_i\left(\theta \left(t\right)\right)$ and $\mathcal{C}$. The initial state is represented by $x_0$. The noise process in the system is modeled as a Wiener process or Brownian motion, denoted as $w\left(\cdot \right)$. This process is characterized by a stationary independent differential increment with zero means and is represented by $dw\left(t\right)=\xi \left(t\right)dt$, where $\mathbb{E}\left[dw\left(t\right)\right]=0$. The state space representation of a stochastic switched linear parameter-varying (SSLPV) system is given by a set of linear dynamic equations with time-dependent parameters that influence the state of the system. These parameters enter the equation of state as exogenous inputs. The SSLPV system’s state space can be described by a set of matrices, including the parameter matrices ${\mathcal{A}}_i\left(\theta \left(t\right)\right)$ and $\mathcal{C}$, and the initial state $x_0$. The system also includes a stochastic process $w\left(\cdot \right)$, represented by $dw\left(t\right)=\xi \left(t\right)dt$, which is characterized by a stationary independent differential increment with zero means and is typically modeled as a Wiener process or Brownian motion.

$$dx\left(t\right)=\left[{\mathcal{A}}_{\sigma \left(t\right)}\left(\theta \left(t\right)\right)x\left(t\right)+{\mathcal{B}}_{\sigma \left(t\right)}u\left(t\right)\right]dt+\mathcal{C}x\left(t\right)dw\left(t\right),t\in [t_0,T],$$

$$x\left(t_0\right)=x_0\in {\mathbb{R}}^n,$$ (12)

where $x\left(t\right)={[x_1\left(t\right),x_2\left(t\right),\dots ,x_n\left(t\right)]}^T\in {\mathbb{R}}^n$ represents the state vector. The control input vector is $u\left(t\right)\in {\mathbb{R}}^m$. ${\mathcal{A}}_{\sigma \left(t\right)}\left(\theta \left(t\right)\right)\in {\mathbb{R}}^{n\times n},{\mathcal{B}}_{\sigma \left(t\right)}\in {\mathbb{R}}^{n\times m}$ and $\mathcal{C}\in {\mathbb{R}}^{n\times n}$ are the real constant matrices, respectively; $\sigma \left(t\right):\to S=\{1,2,\dots ,N\}$ denotes the switching signal which is deterministic, piecewise constant, and right continuous. When $t\in [t_k,t_{k+1})$, subsystem ${\sigma }_k$ is activated. For the sake of clarity, we refer to the switching signal as $\sigma \left(t\right)=i$ throughout this study.

The matrices of the state space system ${\mathcal{A}}_i\left(\theta \right)$ are subject to uncertainties in the real parameter ${\theta }_j$ and obey the real convex polytopic model, that is,

$${\mathcal{A}}_i\left(\theta \right)≔\sum _{j=1}^N{\theta }_j{\mathcal{A}}_i^j,{\theta }_j\ge 0,\sum _{j=1}^N{\theta }_j=1.$$ (13)

The use of switched-signal finite-time control in the SIR stochastic model represents a significant advance in the field of epidemic control. By addressing the challenges posed by uncertainty and randomness in the spread of diseases, this control strategy provides a powerful tool to effectively control outbreaks and protect public health. The ability to handle multiple control inputs and switch among them in real time, guarantee finite-time convergence, reduce control effort, and provide probabilistic predictions and decisions makes this approach a promising solution for epidemic control in a stochastic environment. The goal of this study is to develop finite-time stability constraints for the system (12) and then construct a state feedback controller based on those conditions.

$$u\left(t\right)=K_{i}x\left(t\right)$$ (14)

for the system (12), where $K_i$ denotes the gain matrices to be designed. First, we define finite-time stochastic stability and stabilization for unforced stochastic systems using the following definition.

Definition 4.1 [55] —

Stochastic switched system

$$dx\left(t\right)={\mathcal{A}}_i^{j}x\left(t\right)dt+\mathcal{C}x\left(t\right)dw\left(t\right),t\in [t_0,T],$$

$$x\left(t_0\right)=x_0\in {\mathbb{R}}^n,$$ (15)

is said to be finite-time stochastically stable (FTSS) in relation to $(c_1,c_2,T,\mathcal{R})$, if

$$x^T\left(0\right)\mathcal{R}x\left(0\right)<c_1\Rightarrow \mathbb{E}\left[x^T\left(t\right)\mathcal{R}x\left(t\right)\right]<c_2,$$

where $c_1>0,c_2>c_1$.

Definition 4.2 [55] —

Stochastic switched control system

$$dx\left(t\right)=[{\mathcal{A}}_i^{j}x\left(t\right)+{\mathcal{B}}_{i}u\left(t\right)]dt+\mathcal{C}x\left(t\right)dw\left(t\right),t\in [t_0,T],$$

$$x\left(t_0\right)=x_0\in {\mathbb{R}}^n,$$ (16)

is said to be FTSS, if there exists a control $u\left(t\right)=K_{i}x\left(t\right)$, such that

$$dx\left(t\right)=[{\mathcal{A}}_i^j+{\mathcal{B}}_i{K}_i]x\left(t\right)dt+\mathcal{C}x\left(t\right)dw\left(t\right),$$ (17)

is finite-time stochastically stable with respect to $(c_1,c_2,T,\mathcal{R})$, if

$$x^T\left(0\right)\mathcal{R}x\left(0\right)<c_1\Rightarrow \mathbb{E}\left[x^T\left(t\right)\mathcal{R}x\left(t\right)\right]<c_2,$$

where $c_1>0$, $c_2>c_1$.

Definition 4.3

Consider the switching signal $\sigma$ and scalar $t\in [t_0,T]$, let $N_{\sigma }(t,T)$ represent the number of discontinuities of $\sigma$ over $[t,T]$. If

$$N_{\sigma }(t,T)\le N_0+\frac{T-t}{{\tau }_a},$$

then the constant ${\tau }_a$ is called the average dwell time (ADT) and $N_0$ the chatter bound.

Lemma 4.4 [55] —

For the stochastic system (15) , suppose that there exist a ${\mathcal{C}}^2$ function $V\left(x\right)$ , two class ${\mathcal{K}}_{\infty }$ functions ${\alpha }_1$ and ${\alpha }_2$ , and a class $\mathcal{K}$ function ${\alpha }_3$ , satisfying

$${\alpha }_1\left(\left|x\right|\right)\le V\left(x\right)\le {\alpha }_2\left(\left|x\right|\right),$$ (18)

$$\mathbb{L}V\left(x\right)=\frac{\partial V}{\partial x}h\left(x\right)+\frac{1}{2}\text{Tr}\left\{g^T\left(x\right)\frac{{\partial }^{2}V}{\partial x^2}g\left(x\right)\right\}\le -{\alpha }_3\left(\left|x\right|\right),$$ (19)

then the equilibrium $x=0$ of (15) is globally quadratically stable.

Remark 4.5

Let $x\left(\cdot \right)$ is an Ito process fulfilling (15), and $g(\cdot ,\cdot )$ a twice continuously differentiable function on $\Omega \in {\mathbb{R}}^n$. Then the procedure $y\left(t\right)≔g(t,x\left(t\right))$ is carried an Ito procedure once more, and

$$dy=\left\{\frac{\partial g(t,x)}{\partial t}+{\left({\Delta }_{x}g(t,x)\right)}^T{\mathcal{A}}_i^{j}x\left(t\right)+\frac{1}{2}\text{Tr}\left\{{\left(\mathcal{C}x\left(t\right)\right)}^T\left({\mathcal{C}}_{x}g(t,x)\right)\mathcal{C}x\left(t\right)\right\}\right\}dt+{\left({\Delta }_{x}g(t,x)\right)}^T\mathcal{C}x\left(t\right)dw\left(t\right),$$

where ${\Delta }_x$ and ${\mathcal{C}}_x$ represent the gradient and the Hessian matrix in relation to $x$.

Lemma 4.6 Gronwall Inequality —

Let $\vartheta \left(t\right)$ be a nonnegative function such that

$$\vartheta \left(t\right)\le C+A{\int }_0^t\vartheta \left(s\right)ds,0\le t\le T,$$

where $C,A\ge 0$ . Then, we have

$$\vartheta \left(t\right)\le C{e}^{At},0\le t\le T.$$

5. Finite-time stability

In this part, we will focus on the mean square finite-time stable (MSFTS) of the SSLPV system (15).

Theorem 5.1

Given scalars $(c_1,c_2,T)$ , $c_1<c_2$ , and matrix $\mathcal{R}$ , if there exist scalars $\alpha >0,{\overline{\mu }}_i\ge 1$ , and positive definite symmetric matrix $P_i\in {\mathbb{R}}^{n\times n},i\in S$ , such that the following LMIs hold:

$$\left[\begin{array}{cc}\hfill {\tilde{P}}_i{\mathcal{A}}_i^j+{\left({\tilde{P}}_i{\mathcal{A}}_i^j\right)}^T-\alpha {\tilde{P}}_i\hfill & \hfill {\mathcal{C}}^T{\tilde{P}}_i\hfill \\ \hfill \ast \hfill & \hfill -{\tilde{P}}_i\hfill \end{array}\right]<0,$$ (20)

$${\tilde{P}}_i\le {\overline{\mu }}_i{\tilde{P}}_j,$$ (21)

among them ${\tilde{P}}_i={\mathcal{R}}^{\frac{1}{2}}{P}_i{\mathcal{R}}^{\frac{1}{2}}$ . Then, if the subsystems meet the following conditions for switching signals, the SSLPV system (15) is finite-time stable with respect to $(c_1,c_2,T,\mathcal{R})$ ,

$${\tau }_{bi}^s\ge {\tau }_{bi}^{\ast }=\frac{T^s\text{log}{\overline{\mu }}_i}{\text{log}\left[\frac{c_2\underset{\_}{\alpha }{P}_i}{c_1\overline{\alpha }{P}_i}\right]-{\alpha }_i{T}^s}(i\in S_s),$$ (22)

$${\tau }_{bi}^s\le {\tau }_{bi}^{\ast }=-\frac{\text{log}{\overline{\mu }}_i}{{\alpha }_i},(i\in S_u),$$ (23)

where $T^s={\sum }_{i\in S_s}{T}_i^s(0,T)$ and $T^u={\sum }_{i\in S_u}{T}_i^u(0,T)$ .

Proof

Consider the following Lyapunov function:

$$V_i\left(x\left(t\right)\right)=x^T\left(t\right)P_{i}x\left(t\right).$$ (24)

Using Lemma 4.4, along the trajectory of the system (15), we have the following.

$$d{V}_i\left(x\left(t\right)\right)=\mathbb{L}{V}_i\left(x\left(t\right)\right)dt+2x^T\left(t\right)P_i\mathcal{C}x\left(t\right)dw\left(t\right),$$ (25)

where

$$\mathbb{L}{V}_i\left(x\left(t\right)\right)=2x^T\left(t\right)P_i{\mathcal{A}}_i^{j}x\left(t\right)-\alpha x^T\left(t\right)P_{i}x\left(t\right)+x^T\left(t\right){\mathcal{C}}^T{P}_i\mathcal{C}x\left(t\right)+\alpha V_i\left(x\left(t\right)\right)=x^T\left(t\right)\left(P_i{\mathcal{A}}_i^j+{\left(P_i{\mathcal{A}}_i^j\right)}^T-\alpha P_i+{\mathcal{C}}^T{P}_i\mathcal{C}\right)x\left(t\right)+\alpha V_i\left(x\left(t\right)\right).$$

When the following conditions are met, it is clear that

$$P_i{\mathcal{A}}_i^j+{\left(P_i{\mathcal{A}}_i^j\right)}^T-\alpha P_i+{\mathcal{C}}^T{P}_i\mathcal{C}<0.$$ (26)

By using Schur complement lemma, then (26) is equivalent to (20) and guarantee with $\alpha >0$

$$\mathbb{L}{V}_i\left(x\left(t\right)\right)-\alpha V_i\left(x\left(t\right)\right)<0\text{(or)}$$ (27)

$$\mathbb{L}{V}_i\left(x\left(t\right)\right)<\alpha V_i\left(x\left(t\right)\right).$$ (28)

Moreover, integrating both sides of (27) over the interval $[t_k,t]$ and taking the mathematical expectation, we have the following.

$$\mathbb{E}\left[V_i\left(x\left(t\right)\right)\right]<\mathbb{E}\left[V_i\left(x\left(t_k\right)\right)\right]+{\alpha }_i{\int }_{t_k}^t\mathbb{E}\left[V_i\left(x\left(s\right)\right)\right]ds.$$ (29)

With Lemma 4.6, we get

$$\mathbb{E}\left[V_i\left(x\left(t\right)\right)\right]<\mathbb{E}\left[V_i\left(x\left(t_k\right)\right)\right]e^{{\alpha }_i(t-t_k)}.$$ (30)

Noticing that

$$x\left(t_k\right)=x\left(t_k^{-}\right),$$

and we get

$$V_i\left(x\left(t_k\right)\right)\le {\overline{\mu }}_i{V}_j\left(x\left(t_k^{-}\right)\right).$$ (31)

Combining (30), (31), we have the following.

$$\mathbb{E}\left\{V_i\left(x\right)\right\}<{\overline{\mu }}_i{e}^{{\alpha }_i(t-t_k)}\mathbb{E}\left\{V_j\left(x\left(t_k^{-}\right)\right)\right\}.$$ (32)

By using Definition 4.3, the connection of (32), it is not difficult to check within $t\in [0,T]$,

$$\mathbb{E}\left\{V_i\left(x\right)\right\}\le {\overline{\mu }}_i{e}^{{\alpha }_i(t-t_k)}\mathbb{E}\left\{V_j\left(x\left(t_{k-1}^{-}\right)\right)\right\}\le \prod _{i\in S_s}{\overline{\mu }}_i^{N_i^s(0,T)}\prod _{i\in S_u}{\overline{\mu }}_i^{N_i^u(0,T)}{e}^{\sum _{i\in S_s}{\alpha }_i{T}_i^s(0,T)+\sum _{i\in S_u}{\alpha }_i{T}_i^u(0,T)}\mathbb{E}\left\{V_{\sigma \left(0\right)}\left(x\left(t_0\right)\right)\right\}.$$ (33)

Accordingly, to the derivation, the following two inequalities hold:

$$\mathbb{E}\left\{V_i\left(x\right)\right\}=\mathbb{E}\left\{x^T\left(t\right){\overline{P}}_{i}x\left(t\right)\right\}=\mathbb{E}\left\{x^T\left(t\right){\mathcal{R}}^{\frac{1}{2}}{\overline{P}}_i{\mathcal{R}}^{\frac{1}{2}}x\left(t\right)\right\}\ge {\underset{\_}{\alpha }}_{P_i}\mathbb{E}\left\{x^T\left(t\right)\mathcal{R}x\left(t\right)\right\},$$ (34)

and

$$V_{\sigma \left(0\right)}\left(x\left(0\right)\right)e^{{\alpha }_{i}t}=\left\{x^T\left(0\right){\mathcal{R}}^{\frac{1}{2}}{P}_{\sigma \left(0\right)}{\mathcal{R}}^{\frac{1}{2}}x\left(0\right)\right\}\le \left\{{\overline{\alpha }}_{P_i}{x}^T\left(0\right)\mathcal{R}x\left(0\right)\right\}{e}^{{\alpha }_{i}t}\le \left\{{\overline{\alpha }}_{P_i}{c}_1\right\}{e}^{{\alpha }_{i}T}.$$ (35)

Then, combined with (33)–(35), one has

$$\mathbb{E}\left\{x^T\left(t\right)\mathcal{R}x\left(t\right)\right\}\le \frac{\left[{\overline{\alpha }}_{P_i}{c}_1\right]\prod _{i\in S_s}{\overline{\mu }}_i^{N_i^s(0,T)}\prod _{i\in S_u}{\overline{\mu }}_i^{N_i^u(0,T)}}{1}\times \frac{e^{\sum _{i\in S_s}{\alpha }_i{T}_i^s(0,T)+\sum _{i\in S_u}{\alpha }_i{T}_i^u(0,T)}}{{\underset{\_}{\alpha }}_{P_i}},=\frac{\left[{\overline{\alpha }}_{P_i}{c}_1\right]e^{\sum _{i\in S_s}\frac{T_i^s(0,T)}{{\hat{\tau }}_{bi}^s}log{\overline{\mu }}_i+\sum _{i\in S_u}\frac{T_i^u(0,T)}{{\hat{\tau }}_{bi}^u}log{\overline{\mu }}_i}}{1}\times \frac{e^{\sum _{i\in S_s}{\alpha }_i{T}_i^s(0,T)+\sum _{i\in S_u}{\alpha }_i{T}_i^u(0,T)}}{{\underset{\_}{\alpha }}_{P_i}},=\frac{\left[{\overline{\alpha }}_{P_i}{c}_1\right]e^{\sum _{i\in S_s}\frac{T_i^s(0,T)}{{\hat{\tau }}_{bi}^s}log{\overline{\mu }}_i+\sum _{i\in S_u}\frac{T_i^u(0,T)}{{\hat{\tau }}_{bi}^u}log{\overline{\mu }}_i}}{1}\times \frac{e^{-{\alpha }^s{T}^s+{\alpha }^u{T}^u}}{{\underset{\_}{\alpha }}_{P_i}}.$$ (36)

Rewrite (43), (43) as follows.

$$\frac{\left[{\overline{\alpha }}_{P_i}{c}_1\right]{\overline{\mu }}_i^{\frac{T^s}{{\tau }_{bi}^s}}{e}^{-{\alpha }^s{T}^s}}{{\underset{\_}{\alpha }}_{P_i}}<c_2,$$ (37)

and

$$\frac{\text{log}{\overline{\mu }}_i}{{\tau }_{bi}^u}+{\alpha }^u<0,T^u\ge 0.$$ (38)

Then, substituting (37), (38) in (36), we get

$$\mathbb{E}\left\{x^T\left(t\right)\mathcal{R}x\left(t\right)\right\}\le c_2{e}^{\left[\frac{\text{log}{\overline{\mu }}_i}{{\tau }_{bi}^u}+{\alpha }^u\right]T^u},$$ (39)

In other words,

$$\mathbb{E}\left\{x^T\left(t\right)\mathcal{R}x\left(t\right)\right\}\le c_2.$$ (40)

With respect to Definition 4.1, this implies the finite-time stability of system (15). The proof is complete.  □

6. Controller design

In this part, we will concentrate on the FTSS of the SSLPV system (17).

Theorem 6.1

Given scalars $(c_1,c_2,T)$ , $c_1<c_2$ , and matrix $\mathcal{R}$ , if there exist scalars $\alpha >0,{\overline{\mu }}_i\ge 1$ , and positive definite symmetric matrix $X_i\in {\mathbb{R}}^{n\times n},i\in S$ and nonsingular matrices $G_i$ such that the following LMIs hold:

$$\left[\begin{array}{cc}\hfill \Delta \hfill & \hfill X_i^T{\mathcal{C}}^T\hfill \\ \hfill \ast \hfill & \hfill -X_i\hfill \end{array}\right]<0,$$ (41)

$${\tilde{X}}_i\le {\overline{\mu }}_i{\tilde{X}}_j.$$ (42)

Then, if the subsystems meet the following conditions for switching signals, the SSLPV system (17) will be finite-time stable with respect to $(c_1,c_2,T,\mathcal{R})$ ,

$${\tau }_{bi}^s\ge {\tau }_{bi}^{\ast }=\frac{T^s\text{log}{\overline{\mu }}_i}{\text{log}\left[\frac{c_2\underset{\_}{\alpha }{X}_i^{-1}}{c_1\overline{\alpha }{X}_i^{-1}}\right]-{\alpha }_i{T}^s},(i\in S_s),$$ (43)

$${\tau }_{bi}^s\le {\tau }_{bi}^{\ast }=-\frac{\text{log}{\overline{\mu }}_i}{{\alpha }_i},(i\in S_u),$$ (44)

where $T^s={\sum }_{i\in S_s}{T}_i^s(0,T)$ and $T^u={\sum }_{i\in S_u}{T}_i^u(0,T)$ .

Proof

Using Theorem 5.1, we can prove that the closed-loop system (17) is FTSS with respect to $(c_1,c_2,T,\mathcal{R})$ for any switching signal:

$$\left[\begin{array}{cc}\hfill (1,1)\hfill & \hfill {\mathcal{C}}^T{P}_i\hfill \\ \hfill \ast \hfill & \hfill -P_i\hfill \end{array}\right]<0,$$ (45)

where $(1,1)=P_i({\mathcal{A}}_i^j+{\mathcal{B}}_i{K}_i)+{({\mathcal{A}}_i^j+{\mathcal{B}}_i{K}_i)}^T{P}_i-\alpha P_i$. Pre- and post-multiplying (27) by $\left[\begin{array}{cc}\hfill P_i^{-1}\hfill & \hfill 0\hfill \\ \hfill \ast \hfill & \hfill P_i^{-1}\hfill \end{array}\right]$,

$${\left[\begin{array}{cc}\hfill P_i^{-1}\hfill & \hfill 0\hfill \\ \hfill \ast \hfill & \hfill P_i^{-1}\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill (1,1)\hfill & \hfill {\mathcal{C}}^T{P}_i\hfill \\ \hfill \ast \hfill & \hfill -P_i\hfill \end{array}\right]\left[\begin{array}{cc}\hfill P_i^{-1}\hfill & \hfill 0\hfill \\ \hfill \ast \hfill & \hfill P_i^{-1}\hfill \end{array}\right]<0.$$ (46)

Then it can be derived that

$$\left[\begin{array}{cc}\hfill \Delta \hfill & \hfill P_i^{-1}{\mathcal{C}}^T\hfill \\ \hfill \ast \hfill & \hfill -P_i^{-1}\hfill \end{array}\right]<0,$$ (47)

where $\Delta =({\mathcal{A}}_i^j+{\mathcal{B}}_i{K}_i)P_i^{-1}+P_i^{-1}{({\mathcal{A}}_i^j+{\mathcal{B}}_i{K}_i)}^T-P_i^{-1}\alpha$. Setting $X_i=P_i^{-1},K_i{X}_i=G_i$, (41) can be obtained, and the gains of the controller (14) are given by $K_i=G_i{X}_i^{-1}$.  □

7. Related works

Some early literature on FTS can be found in [23], [26], [27], [28], [31]. The finite-time $H_{\infty }$ control of nonlinear impulsive switching models. They used various Lyapunov function techniques and the mode-dependent average dwell time approach for establishing various parametric conditions, demonstrating that the model is finite-time bounded and finite-time $H_{\infty }$ control was addressed by the authors in [34]. The FTS analysis was carried out by using the state transition matrix and copositive Lyapunov function for the positive linear systems. Further, sufficient conditions for a class of switching signals with average dwell time are designed to attain FTS for the switched positive linear systems done in [35]. Further, the study on the stochastic SIR model was reported by various research works [45], [51], [52], [53]. The authors of [36] used Markov semigroup theory to show that the stochastic SIR epidemic model with regime switching has a single stable stationary distribution. This means that, over time, the model will converge to a steady state in which the number of susceptible individuals, infected individuals, and recovered individuals remains constant.

Remark 7.1

Linear Matrix Inequalities (LMIs) can be used in the context of a stochastic SIR epidemic model to provide stability and robustness guarantees for the control and management of infectious diseases, such as COVID-19. For example, LMIs can be used to formulate and solve optimization problems that aim to minimize the spread of the disease, subject to constraints on control efforts, resource allocation, and other parameters. LMIs can also be used to analyze the robustness of control strategies to uncertainties in the model parameters, such as the rate of transmission, the efficacy of control measures, and the number of susceptible individuals. Furthermore, LMIs can be used to design controllers that can respond to changes in the spread of the disease, such as the introduction of new strains or mutations, by switching between different control strategies. These applications demonstrate the versatility and usefulness of LMIs in addressing complex and uncertain systems and their importance in controlling the spread of infectious diseases.

8. Numerical simulation of the model

In this section, we check the accuracy and usefulness of the offered methods for the stabilization problem of bio-mathematical switching systems with finite-time constraints.

8.1. Case study for COVID-19 model in Japan

In this subsection, we use data from newly positive individuals in Tokyo. Japan has implemented several measures to control the spread of COVID-19, including widespread testing, contact tracing, and quarantine measures. The study used a compartmental model, which divides the population into different compartments based on their disease status (susceptible, exposed, infected, recovered, etc.). The model was calibrated using data on the number of reported cases and deaths in Japan and was used to simulate the spread of the disease under different scenarios. The results of the study showed that Japan’s measures were effective in controlling the spread of the disease, but that the country was still at risk of a resurgence of cases if the measures were relaxed too quickly. The study also found that testing and quarantine measures were more effective than contact tracing alone in controlling the spread of the disease. It also highlighted the importance of continuing to implement measures such as testing, contact tracing, and quarantine even after the number of cases decreases. Table 4 shows the numerical values of parameters used in the simulation.

Table 4.

Default values of the parameters of model (5) with Covid data.

Parameter	Symbol	Value	Source
Recruitment rate	$A$	5	[56]
Contact rate	$\beta$	0.2	[57]
Inhibitory effect	k	0.2	Assumed
Natural death rate	$\delta$	0.0111	[58]
Rate of recovery	$\gamma$	0.1	[57]
Disease-related mortality	$ϵ$	0.001	Assumed

The $S\left(0\right)$ is the initial value of $S$ when $R=0$, and its corresponding time is the start of the infection, $t=0$. Then, $S\left(0\right)$ has the form $S\left(0\right)=N-I\left(0\right)$. Suppose the initial infected population $I\left(0\right)$ is the number of positive cases on December 20, 2022, which is 15,883 [59] and $N=8336599$ [60]. This study would involve the use of state feedback control theory to model the spread of COVID-19 and implement control strategies in a finite time. The following steps could be taken (see Fig. 19, Fig. 20, Fig. 21):

Fig. 19.

The solution of the stochastic model (5) with initial values $S\left(0\right)=8,320,716$, $I\left(0\right)=\text{15,883}$. The parameter values are taken as in Table 4 and ${\sigma }_{1,2}=0.1$.

Fig. 20.

The evolution in time of the mean of the individuals over 1000 trajectories. The parameter values are taken as in Table 4 and ${\sigma }_{1,2}=0.1$.

Fig. 21.

The evolution in time of the standard deviation of the individuals over 1000 trajectories. The parameter values are taken as in Table 4 and ${\sigma }_{1,2}=0.1$.

• •Modeling: Develop a mathematical model of the spread of COVID-19 in a specific region or population, taking into account relevant factors such as the number of susceptible individuals, the number of infected individuals, and the number of recovered individuals.
• •Analysis: Analyze the stability of the model and determine the equilibrium points.
• •Control design: Based on the analysis, design a state feedback control law that will drive the system towards the desired equilibrium in finite time. This could involve implementing measures such as reducing contact rates between individuals, increasing testing and contact tracing, or implementing vaccine distribution strategies.
• •Simulation: Simulate the controlled system and compare the results with the uncontrolled system.
• •Implementation: Implement the control strategies in the real world, monitor the spread of the disease, and adjust the control strategies as necessary based on the results.

The following study could provide valuable insights into the spread of COVID-19 and inform the development of effective control strategies to mitigate its impact.

8.2. Control of epidemic models

The simulation findings are based on the parameter values as in(4). In Fig. 4, Fig. 5, Fig. 6, Fig. 7, the effect of the stochastic system without a controller is depicted graphically. Moreover, in the simulation reason, the specific parameters of the biological model are as appeared in (4). The block diagram of the proposed model is shown in Fig. 22.

Fig. 22.

Schematic diagram of the proposed finite time stability analysis of SIR model.

Choose the values ${\alpha }_1=1.05,{\alpha }_2=-0.88,c_1=1,c_2=7,{\overline{\mu }}_1=0.5,{\overline{\mu }}_2=1.5$, $T=15$, $\mathcal{R}=diag\{1,1\}$, $\mathcal{C}=diag\{1,1\}$, and the system matrices are get from Eq. (10). With these input values, we can obtain ${\overline{\alpha }}_{P_1}=0.7365,{\underset{\_}{\alpha }}_{P_2}=0.0347$ and the mode-dependent ADT can be calculated as ${\tau }_{b1}^{\ast }=1.9307,{\tau }_{b2}^{\ast }=0.7631$. Regarding Theorem 6.1, we know that for the analysis ${\tau }_{b1}^u=0.5<{\tau }_{b2}^{\ast }$ and ${\tau }_{b2}^s=1.3>{\tau }_{b1}^{\ast }$, the system is FTS. Moreover, the designed controller is built so that the investigated stochastic model (16) is finite-time stable. Solving the linear matrix inequality (LMI)-based conditions specified in Theorem 6.1 with conventional LMI toolbox software yields a viable solution that is guaranteed by a set of matrices, some of which are presented below.

$$K_1=\left[\begin{array}{cc}\hfill -4.0136\hfill & \hfill 2.4093\hfill \\ \hfill 3.5288\hfill & \hfill -3.4489\hfill \end{array}\right],$$

$$K_2=\left[\begin{array}{cc}\hfill -4.1326\hfill & \hfill 2.9775\hfill \\ \hfill 3.8028\hfill & \hfill -4.1608\hfill \end{array}\right],$$

$$K_3=\left[\begin{array}{cc}\hfill -4.2330\hfill & \hfill 2.3720\hfill \\ \hfill 3.4431\hfill & \hfill -3.7176\hfill \end{array}\right],$$

$$K_4=\left[\begin{array}{cc}\hfill -2.1799\hfill & \hfill 1.6732\hfill \\ \hfill 1.4616\hfill & \hfill -3.0741\hfill \end{array}\right].$$

For the sake of simulation, we assume the initial state $x\left(0\right)={[-1.5,2]}^T$. The state responses and associated control trajectories of the stochastic switching model studied are shown in Fig. 24, Fig. 25, respectively, based on these conditions. As shown in Fig. 26, the state trajectories of the closed-loop system adequately converge to zero even though in the appearance of switching rules under the suggested control method. Furthermore, the response of the wiener process (1000 realizations) is shown in Fig. 23. This shows the significance of the proposed finite-time control strategy. On the other hand, the average dwell time of the switching signal is calculated as ${\tau }_a=1.2210$.

Fig. 24.

State trajectories with multiple initial conditions of the system (16).

Fig. 25.

State responses in two phase mode.

Fig. 26.

State trajectories of the system (16).

Fig. 23.

The wiener process (1000 realizations).

9. Conclusions

In this paper, a finite-time control technique has been presented for stochastic switched linear parameter-varying (SSLPV) systems, with a focus on epidemic models such as the SIR model. The article also proposed a method to control the spread of COVID-19 using this technique. The method involved simplify the epidemic nonlinear systems through finite-time stabilization analysis and determining the effective gain parameters using linear matrix inequalities (LMIs). Through simulations, the researchers demonstrated that the proposed control method was effective in balancing the epidemiological system, and thus in controlling the spread of COVID-19. The conclusion of this research showed that the proposed control technique can be used to effectively control the spread of COVID-19 and other epidemic diseases and that it has the potential to be applied in real-world situations. In the future, it will also highlight the limitations and importance of research and the need for more work in this area.

CRediT authorship contribution statement

Nallappan Gunasekaran: Conceptualization, Methodology, Writing – original draft. R. Vadivel: Formal analysis, Validation, Software, Investigation. Guisheng Zhai: Writing – review & editing, Supervision. S. Vinoth: Methodology, Formal analysis, Visualization.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request