A novel machine learning system for identifying sleep–wake states in mice

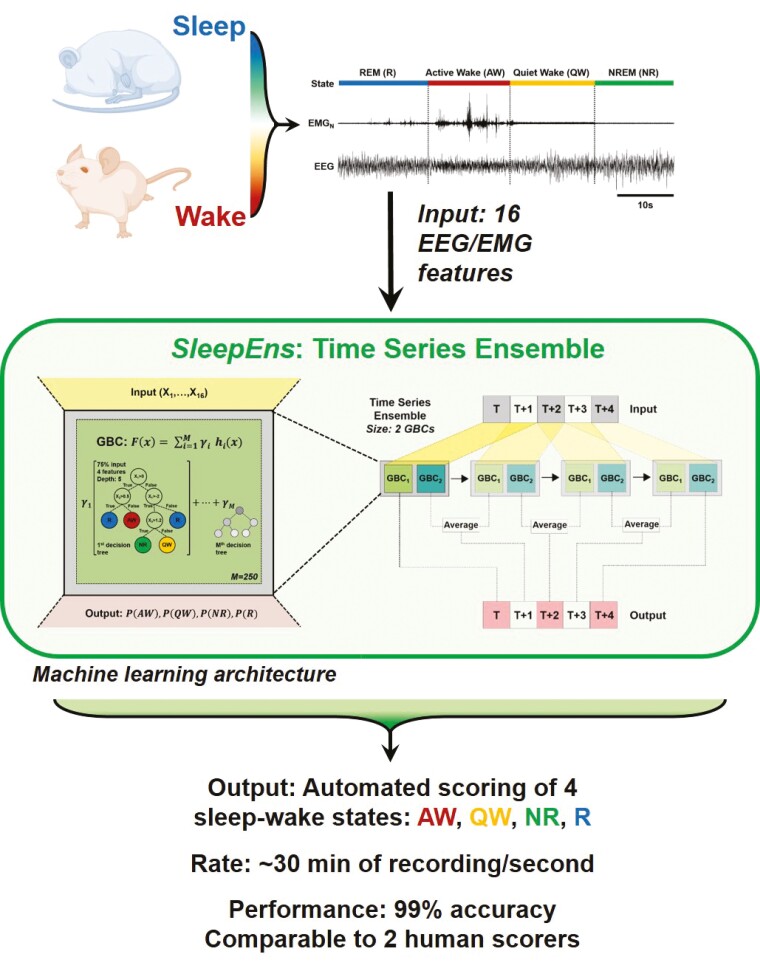
Abstract

Research into sleep–wake behaviors relies on scoring sleep states, normally done by manual inspection of electroencephalogram (EEG) and electromyogram (EMG) recordings. This is a highly time-consuming process prone to inter-rater variability. When studying relationships between sleep and motor function, analyzing arousal states under a four-state system of active wake (AW), quiet wake (QW), nonrapid-eye-movement (NREM) sleep, and rapid-eye-movement (REM) sleep provides greater precision in behavioral analysis but is a more complex model for classification than the traditional three-state identification (wake, NREM, and REM sleep) usually used in rodent models. Characteristic features between sleep–wake states provide potential for the use of machine learning to automate classification. Here, we devised SleepEns, which uses a novel ensemble architecture, the time-series ensemble. SleepEns achieved 90% accuracy to the source expert, which was statistically similar to the performance of two other human experts. Considering the capacity for classification disagreements that are still physiologically reasonable, SleepEns had an acceptable performance of 99% accuracy, as determined blindly by the source expert. Classifications given by SleepEns also maintained similar sleep–wake characteristics compared to expert classifications, some of which were essential for sleep–wake identification. Hence, our approach achieves results comparable to human ability in a fraction of the time. This new machine-learning ensemble will significantly impact the ability of sleep researcher to detect and study sleep–wake behaviors in mice and potentially in humans.

Graphical abstract

Graphical Abstract.

Statement of Significance.

Here, we describe a new machine-learning approach that uses time-series ensemble to automatically score hours of sleep–wake states in a matter of seconds. Manual scoring is a highly time-consuming process prone to inter-rater variability. Hence, an easy-to-implement automated system, which scores rapidly and with great accuracy, is of interest to the sleep research community. Our automated system reaches 99% accuracy. This automated system can easily be implemented by a great number of labs, and in this spirit, we make our algorithm fully open-source and available at https://github.com/paradoxysm/SleepEns.

Introduction

Research into sleep, its regulation, and its relation to other behaviors is important for understanding brain physiology in health and disease [1–5]. To study sleep, sleep–wake states must be characterized and distinguished from one another. This is traditionally done by manual classification of sleep–wake states in segmented epochs, usually around 5 s in length [1, 6–9]. Researchers manually identify arousal states through visual inspection of electroencephalogram (EEG) and electromyogram (EMG) recordings. However, this is a laborious exercise that is time-consuming [10–12]. Furthermore, manual classification is subject to inter-rater variability with agreement rates of 90% in mice [10] and 82% in humans [13, 14]. The extent of subjectivity in sleep–wake state classification is thus a major limitation, especially when combining data across sleep studies.

Sleep–wake states are typically differentiated by several features found in EEG/EMG signals. REM sleep is characterized by dominant theta (θ: 6–9 Hz) EEG activity and muscle atonia, NREM by predominant delta (δ: 0.1–4 Hz) EEG activity and little to no muscle activity, and waking states are generally identified by higher frequency signals in EEG with variable EMG activity [1, 6, 10, 12, 15]. There is usually an extensive range of muscle activity that can occur in waking states and thus can be further subcategorized into active wake (i.e. high level of muscle activity and complex movement) and quiet wake (i.e. lower level of muscle activity) substates [1, 6, 16]. This is particularly useful in understanding relationships between sleep and motor function in pathological states such as REM sleep behavior disorder [3, 5, 17–21], narcolepsy [4, 22–24], Parkinson’s disease [25–27], or periodic leg movements [28], which are characterized by unusual motor behavior during sleep–wake states. This four-state delineation of sleep–wake states increases precision, gives us a more detailed view of both healthy and diseased states, which makes it an increasingly essential approach to evaluating sleep–wake behaviors.

Because sleep–wake states have defining characteristics, they are well suited to undergo classification by an automated ­algorithm. Current simple automated techniques use handpicked features extracted from EEG/EMG signals with researcher-defined logic and thresholds to identify sleep–wake states [29]. Various machine-learning algorithms have also been applied with promising results. These include support vector machines [30], naïve Bayes classifiers [31, 32], ensemble methods [33], unsupervised learning [34], and deep learning approaches [10, 11, 35–37]. These automated approaches have met with varied success with the most successful approach reaching around 92% accuracy in categorizing three states of sleep–wake behavior [38]. However, no automated approach to date classifies sleep–wake behavior into four states, i.e. active wake, quiet wake, NREM sleep, and REM sleep.

Here, we (1) describe a novel ensemble learning approach, the Time Series Ensemble, that incorporates temporal information and is based on an ensemble approach to classification/prediction of time series data; (2) detail SleepEns built on the Time Series Ensemble that is accessible to train and detect sleep–wake states with speed and accuracy; (3) demonstrate the performance of SleepEns through extensive statistical analyses and comparisons to human expert performance evaluated in a blinded trial to assess acceptable performance—the extent to which a researcher could reasonably trust the classifications given by a scorer; (4) characterize the sleep–wake architecture that emerges from SleepEns classifications and show they are statistically similar to those produced by human expert classifications; and (5) determine further insight into signal markers characteristic of states of consciousness through an understanding of how SleepEns determines the most probable sleep–wake state.

Methods

Animals and data acquisition

Data from 19 male and nine female 5–8-week-old wild type mice (C57BL/6 background, average weight 22 ± 2 g). Animals were housed individually and maintained on a 12-hour light/dark cycle (lights on at 7:00 a.m.). Both food and water were available ad libitum. All procedures and experimental protocols were approved by the University of Toronto Animal Care Committee and were in accordance with the Canadian Council on Animal Care.

Sterile surgery was performed to implant EEG and EMG electrodes [1, 2, 6]. In brief, general anesthesia was induced and maintained via inhalation (isoflurane, 0.5%–2%). Two insulated, multistranded stainless-steel wire EMG electrodes were implanted into the right masseter muscles, and two EMG electrodes were inserted into the nuchal muscles. Four stainless-steel screws attached to multistranded stainless-steel insulated 34-gauge wire were implanted in the skull for recording cortical EEG activity; their coordinates were +1 mm AP, ±1 mm ML from bregma, and −2 mm AP, ±3 mm ML from bregma.

EEG and EMG activities were recorded by attaching a lightweight tether cable to the head of the mouse and connecting it to a Physiodata amplifier system (Grass 15LT, Astro Med, Brossard, QC). The EEG signal was bandpass filtered between 0.3 and 100 Hz. EMG signals were bandpass filtered between 30 and 30 kHz. A 60 Hz notch filter was applied when necessary. All electrophysiological signals were sampled at 1–2 kHz, digitized (Spike2 software, 1401 interface; Cambridge Electronic Design, Cambridge, UK), monitored and stored on a computer.

Each recording collected from different mice, averaged around 3 h in length and was subdivided into 5-s epochs. This sleep recording data was manually analyzed and labeled as Active Wake (AW), Quiet Wake (QW), NREM sleep (NR), and REM sleep (R) (Figure 1a) by a source expert (i.e. Expert 0) and these labels were used as the archetype [1, 2, 6]. A subset of 14 recordings totaling 30 245 epochs was used to train and validate the machine-learning algorithm. The remaining five recordings totaling 10 180 epochs were used to test the automated algorithm and analyze its performance. These were also independently analyzed and scored manually by three human experts (i.e. Experts 0-2). Expert 0 has 20 years of experience, while Experts 1 and 2 both have 6 years of experience. To test whether the algorithm could also classify sleep–wake states in female mice, we re-trained the algorithm with 14 recordings from male mice and the addition of recordings from four female mice for a total of 38 912 epochs, and tested it with five male and five female recordings totaling 21 009 epochs.

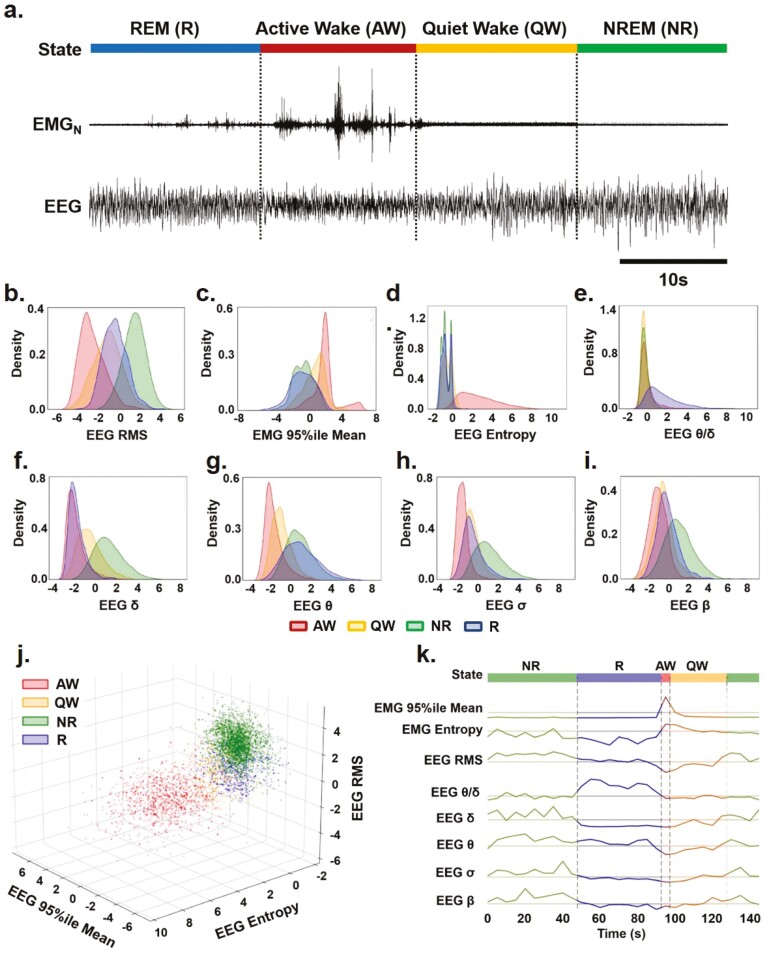
Figure 1.

Characterizing key EEG and EMG features for sleep–wake identification over time. (a) Representative EEG and nuchal EMG (EMG_N) during Active Wake (AW), Quiet Wake (QW), Rapid Eye Movement (REM) sleep, and Non-REM (NREM) sleep. (b)–(i) Distribution of EEG and EMG parameters density used to identify sleep-wake states (i.e. AW-red, QW-yellow, NR-green: NREM and R-blue: REM) by SleepEns. Parameters are as follows: (b) EEG root-mean square (EEG RMS); (c) Top 5% EMG activity (EMG 95%ile Mean); (d) EEG spectral entropy; (e) EEG θ/δ power; (f) EEG δ power; (g) EEG θ power; (h) EEG σ power; and (i) EEG β power. The x-axes of all plots represent the feature values after processing. Distributions are drawn from 10 180 epochs in the test dataset. (j) A three-dimensional plot of three features (EMG 95th Percentile Mean, EEG Entropy, and EEG RMS) demonstrates a degree of separability between sleep-wake states. Axes represent the feature values after processing and data is drawn from a sample of 5090 epochs in the test dataset. (k) Eight features over the course of 30 epochs (150 s) illustrating changes in features as the animal progresses over each sleep–wake state.

Data preprocessing and feature extraction

Each recording was preprocessed in the following manner:

1. Each channel is detrended by subtracting the mean for each channel across the recording.

2. For each 5-s epoch, 16 features of EEG and EMG signals were extracted (Table 1).

3. Each feature was log transformed with the median as the base. This was done to maximally spread the feature data to help identify and separate individual states. A per-recording median was used as data in different recordings tended to occupy different ranges relative to each other. Using a per-recording median helps translate feature data and align across recordings but assumes the data distribution, and therefore distribution of sleep–wake states, is similar across recordings. This is in fact the case for our 3-hr long recordings (p > .99, n = 14).

4. Each feature is scaled to fit within an interval of −5 and 5 and then subsequently detrended by the mean to center every recording.

Table 1.

Description of features.

Feature	Description
Delta (δ)	Power of 0.5–4 Hz band in EEG calculated from Welch periodogram
Theta (θ)	Power of 7–10 Hz band in EEG
Sigma (σ)	Power of 11–15 Hz band in EEG
Beta (β)	Power of 15–40 Hz band in EEG
Theta/Delta	Ratio of Theta to Delta
Sigma/Delta	Ratio of Sigma to Delta
Beta/Delta	Ratio of Beta to Delta
Sigma/Theta	Ratio of Sigma to Theta
Beta/Theta	Ratio of Beta to Theta
Beta/Sigma	Ratio of Beta to Sigma
EEG RMS	Root mean square (RMS) of EEG
EMG RMS	Mean of RMS of Neck and Mass. EMG
EEG Entropy	Spectral entropy of EEG
EMG Entropy	Mean of spectral entropies of Neck and Masseter EMG
EMG 95%ile Mean	Mean of the top 5% samples in Neck and Masseter EMG
EMG Twitch	Sum of variances above the median in Neck and Massester EMG. Epochs are subdivided into 10 subepochs to calculate variances.

We extracted the following 16 features from the EEG and EMG signals: Four EEG frequency bands (delta δ: 0.5–4 Hz; theta θ: 7–10 Hz; sigma σ: 11–15 Hz; beta β: 15–40 Hz) and their ratios were selected as being distinct markers across sleep–wake states. Root mean squares (RMS) of signals were included as some states exhibit higher overall signal power (e.g. NREM sleep). Spectral EEG and EMG entropy measures the distribution of power across frequencies; desynchronized and disordered signals contain more constituent frequency components and yield higher spectral entropies. This was used to help differentiate Wake and REM sleep from NREM sleep episodes. The 95th percentile EMG mean and twitch measures were used as indicators of muscle activity. We can examine these features as they differ between sleep–wake states and over time (Figure 1b–k). Looking at density distributions of the four EEG frequency bands, as well as EEG entropy, EEG RMS, EEG θ/δ and EMG 95%ile, we can see there is appreciable separability of states in many features (Figure 1b–i). For example, EEG entropy effectively distinguishes Active Wake from other states (Figure 1d) while each of the frequency bands fairly separates sleep-wake states into 2-3 clusters in various combinations (Figure 1f-g). Taken together, the various separations of states in each feature can be combined to better identify states from each other. It is important to note that there is substantial overlap even using three features in combination (Figure 1j), thus a good classification model requires greater dimensionality. Examining these eight features over time across all four sleep–wake states shows how each feature contributes to the identification of different states (Figure 1k).

Classification

SleepEns utilizes ensemble learning where many small base estimators are used in combination to obtain better predictive performance than any one estimator might be able to achieve. A common base estimator is a decision tree, which is conceptually a flow-chart that successively tests various input features (i.e. features of EEG/EMG signals) to eventually determine the most likely class (i.e. sleep–wake states) (Figure 2a). One well known ensemble technique is gradient boosting where successive decision trees, $h(x)$_{</mathgraphic>}, are trained in a stage wise manner to form the following final function:

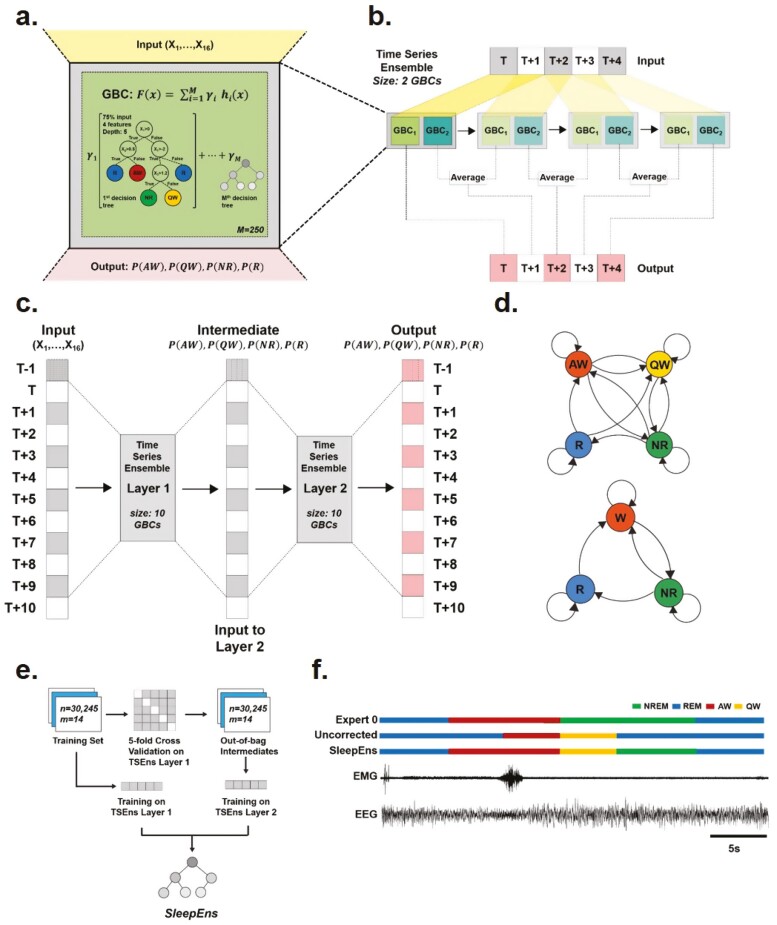
Figure 2.

Model architecture of SleepEns, physiological state transition graph, and training protocol. (a) Representation of a gradient boosting classifier (GBC) architecture, receiving inputs from 16 features of EEGs and EMGs signals (X₁,…, X₁₆). GBC is an ensemble of successive decision trees and can be express as a mathematic function: $F\left(x\right)=\underset{i=1}{\sum ^M}{\gamma }_i{h}_i\left(x\right)$; where F(x) is the overall GBC, comprised of the weighted sum of M base estimators (i.e. number of decision trees), h(x) represent each decision tree, x is the input, and γ the weight of each estimators. For SleepEns, we found through cross-validation that optimal parameters were 250 base estimators (i.e. M) each receiving a random subset of input features limited to the square root of the total number of features (i.e. four features randomly selected from the 16 input features for each estimator) and trained on a random 75% of the training data. (b) Demonstration of how a small-scale Time Series Ensemble, composed of only two GBCs, operates over a 5 epoch time-series data as it moves its window along the sequence. The first epoch, T, is determined only by one gradient boosting classifier (GBC 1) as there is no prior epoch for GBC 2 to operate on. The second epoch, T + 1, is determined by combining the output of GBC 2 using T to T + 1 with the output of GBC 1 (of the following time step) using T + 1 to T + 2. This continues until the final epoch, T + 4, which is solely determined by GBC 2. (c) Architectural details of the SleepEns model, consisting of two layers of Time Series Ensembles, each with a window size of 10, totaling to 20 GBCs, each with 250 constituent estimators (M). The model operates in a greedy fashion, using the first layer to produce intermediate probabilities of active wake (P_AW), quiet wake (P_QW), NREM sleep (P_NR), and REM sleep (P_R), across the sequence and then feeding this to the second layer to produce the final output. (d) State transition graph illustrating the feasible transitions that can occur in 4-states (top) and 3-states (bottom). In particular, Wake states can inter-transition, REM must always be preceded by NREM and can only transition into waking states. (e) Training SleepEns requires layer-by-layer training. To train a subsequent Time Series Ensembles (TSEns) layer, cross-validation is used to produce out-of-bag values to avoid over-fitting. (f) Nine epochs covering 45s were taken from one of the test recordings to demonstrate an example of a postprocessing correction, in this case the utility of Valid Transitions to improve the predictions by implementing the most probably physiological state transition sequence. The two bottom traces represent the EEG and EMG input signals. The top three traces depict hypnograms by Expert 0, a SleepEns without postprocessing, and the final post-processed SleepEns. Note that without postprocessing, SleepEns could identify a direct wake to REM sleep transition.

$${\displaystyle \begin{array}{l}{\displaystyle F\left(x\right)={\displaystyle \underset{i=1}{{\displaystyle \sum ^M}}}{\gamma }_i{h}_i(x)}\end{array}}$$ (1)

where $F\left(x\right)$ represents the overall Gradient Boosting Classifier (GBC), comprised of the weighted sum of $M$ base estimators (i.e. number of decision trees), $h\left(x\right)$ (i.e. the decision trees), and x is the input. $\gamma$ represents the weight for each estimator and is determined in the learning process. In this manner, each successive base estimator attempts to correct the errors of its predecessor. By summating the outputs of these base estimators, we arrive at the overall classification output produced by the GBC (i.e. Probabilities of each sleep-wake states) (Figure 2a). For more details on what shapes the complexity of GBCs see previously described work [39]. There are several manually tunable hyper-parameters for GBCs: the number of base estimators to train, the fraction of features to subsample from for each estimator, the fraction of training data for each estimator, the maximum depth of the estimator decision trees, and a learning rate, which decays the contribution of each successive estimator. For SleepEns, these parameters were determined through cross-validation (see section below for full details), and optimal parameters were found to be 250 base estimators (i.e. M) each receiving a random subset of input features limited to the square root of the total number of features (i.e. four features randomly selected from the 16 input features for each estimator) and trained on a random 75% of the training data (Figure 2a).

Time series ensemble

There are multiple ways to incorporate temporal information. One method is for a GBC to receive input from a window of epochs (i.e. $w_1,w_2,\dots ,w_n$) and predict the central epoch. The ensemble is thus receiving as input $n$ sets of 16 features at once. The drawback of this sliding window is that it consequently cannot provide predictions for the first and last $\frac{n}{2}$ epochs in a given time series recording. To avoid this, we arrange $n$ GBCs, $F_i\left(x\right)$, such that each member GBC received the same window as input but the first provides a prediction for epoch $w_1$, the second for $w_2$, and so on (Figure 2b). As the entire apparatus slides forward across the time series recording, each epoch will have predictions from each of the $n$ GBCs. We can take the average of these outputs as the final output of the apparatus for a given epoch. We termed this overall model a Time Series Ensemble. This allows the model to retain the inclusion of temporal context given by sliding windows while avoiding truncation of the sequence: the first epoch in a time series is only classified by $F_0\left(x\right)$ and using the first $n$ epochs as input, followed by the second epoch determined by the average of $F_0\left(x\right)$ (using the 2nd to ($n$ + 1)th epochs) and $F_1\left(x\right)$ (using the first $n$ epochs), and so on (Figure 2b). Thus, the output for the $n$th epoch onwards is an average of all $n$ classifiers, each having used a different window (Figure 2b). In this respect, the Time Series Ensemble aggregates features in both temporal directions. Again, through cross-validation (see section below for full details), it was determined that a window size of 10 classifiers was ideal.

Successive Time Series Ensembles to form SleepEns

Because the output is never truncated with a Time Series Ensemble, it is feasible to chain Time Series Ensembles, where the output of the first acts as the input for a second (Figure 2c). This allows the second ensemble to improve upon the predications of the first. The first layer Time Series Ensemble trains on the training dataset (i.e. 16 features of EEG/EMG signals) to provide probabilities of the four sleep–wake states. This acts as intermediate latent input for the second layer to train. The second layer uses only these intermediate state probabilities as input. A third layer could potentially be added, but the input and output spaces would be identical to that of the second layer. This is in contrast to hidden layers in deep learning (where the layers do not input or output into the same spaces) or multilayer stacked classifiers (where intermediate layers contain a diverse collection of estimators as opposed to the same solitary classifier). Consequently, the possible optimization that could be added by this third layer should be possible to be gained in the second layer, though this remains an assumption. In addition, a third layer would exponentially add to the computational cost to train and run the overall ensemble.

Corrective post-processing

The core classification process using the Time Series Ensemble achieves a strong performance but does not guarantee certain traits regarding sleep-wake states. Some post-processing passes were implemented to reduce or eliminate such errors (Table 2). All of these post-processing passes relate to improving the algorithm’s performance at state transitions. This is a result of both the artificial division of 5-s epochs which could contain a transition within the epoch as well as the physiological transition itself can take some time to manifest fully in EEG/EMG signals.

Table 2.

Description of corrective post-processing

Postprocess	Purpose
Wake vs. Sleep	Increase sensitivity to wake states by combining the probability of Active and Quiet Wake to determine wake vs. sleep, then determining most probable wake state.
Wake to REM	Ablate REM episode when an invalid Wake to REM transition occurs.
End of REM	End a REM episode if the probability of REM declines past a moving average.
Minimum REM Duration	Force REM episodes to be a minimum duration via a backwards pass.
Valid Transitions	Repair a sequence of states to the most probable physiologically possible sequence of states (Fig. 6).

The post-process Wake vs. Sleep was implemented to improve the sensitivity of waking states and the specificity of NREM sleep. Machine learning algorithms are not explicitly aware that Active Wake and Quiet Wake are interrelated as subcategories of Wake. The post-process Wake to REM is intended to repair the predictions when the model erroneously predicts REM instead of a Wake state. Because an Active Wake episode can often last many epochs, should such a confusion occur, the resulting mistaken REM episode can be quite long. The later Valid Transitions post-process would otherwise attempt to transition the Active Wake into a brief NREM and move to REM. The post-process Wake to REM overrides this error.

Finally, in normal sleep–wake behavior, certain states may follow other states while other transitions are not physiologically possible (Figure 2d). The training data contained only physiological state transitions for the model to learn; however, this does not guarantee valid transitions. Such errors are incredibly rare occurring once in the 10 180 epochs of the test dataset. To ensure such errors do not occur, a post-processing pass called Valid Transitions is completed. When an invalid transition is determined, a forward pass and a backward pass determine two candidate valid sequences and the most probable sequence is selected based on the prediction probabilities given by the Time Series Ensemble. This corrective post-processing ensures physiologically feasible state transitions (Figure 2d). For example, it ensures that REM sleep is always preceded by NREM sleep (Figure 2d,f). Post-processing corrections are rare, accounting for less than 0.5% change in performance but provides greater security in state classification.

Training, crossvalidation, and testing

Training SleepEns involves a few steps (Figure 2e). The Time Series Ensemble layers must be trained one step at a time as the model is not end-to-end differentiable. The first Time Series Ensemble layer can be trained on the entire training dataset. However, to avoid bias, the second layer requires output from the first layer that was not seen during training, called out-of-bag predictions. We employed cross-validation to produce these out-of-bag predictions. In cross-validation, the input data (e.g. for the second layer the input data would be the outputs of the first layer) was split into a number of folds, or chunks. Here, we used five folds. It is important to note that these folds consist of continuous recordings; we avoid mixing epochs from different recordings for each fold as this effectively introduces information from all recordings into training, leading to overfitting of the model and skewing the cross-validation results. An instance of the first layer was trained on four of these folds then predicted on the fifth fold; this was repeated with separate instances of the first layer until every fold had been predicted once. This yielded out-of-bag predictions for the entire training dataset, which was then used as input to train the second layer. Predictions from the SleepEns model involves the first layer predicting using input features, followed by the second layer using those predictions as input to produce the final overall predictions (Figure 2c).

Selecting the best SleepEns model, along with a specific set of manually tuned hyperparameters, requires comparing candidate models on new data. This model selection process is vulnerable to bias as the specific hyperparameters are being tuned to optimize the performance on the testing data. To avoid introducing this bias, we again used cross-validation and added a final testing dataset. We used five-fold cross-validation using each fold as a validation set and evaluated candidate models by the average performance across the five folds. We evaluated over different hyperparameters: learning rates of 0.05 or 0.01; 10 or 20 GBCs per Time Series Ensemble; 100, 250, or 500 base estimators for each constituent GBC; limiting each base estimator to the square root of the number of features or no limitation; max depth of base estimators at 3, 5, or 7; limiting each base estimator to 70%, 75%, 80%, 85%, 90%, or 100% of the training data. The model and set of hyperparameters that yielded the best cross-validated performance was selected for testing and performance analysis. In doing so, the performance observed on the testing dataset is closer to true real-world performance.

Through cross-validation model selection, the architecture presented was chosen for SleepEns. Furthermore, the hyperparameters were selected as 10 GBCs per Time Series Ensemble layer, 250 estimators (M) for each constituent GBC, limiting each estimator to the square root of the number of features and to 75% of the training data, constraining estimators to a depth of 5, and learning rate of 0.05.

Run-time evaluations were conducted on a computer with the following specifications: Ryzen 5 3600 (6-core 3.6 GHz), 16GB DDR4 3200MHz RAM, all code was run single-threaded with the exception of individual GBCs which were parallelized.

Statistical analysis

The statistical tests used for analyses are included in the Results section. All statistical analyses were conducted using two Python libraries, pingouin 0.50 [40] and scipy 1.7.2 [41], and applied a critical two-tailed α value of p < .05. Repeated measures analysis of variance (ANOVA) was followed by Bonferroni post hoc comparisons. All data are presented as average ± standard error of the mean (SEM) unless otherwise indicated.

Results

In our study, we had a source expert, Expert 0, who scored all data. Fourteen 3-hr recordings were selected as training data for SleepEns. Another five 3-hr recordings were used for testing. These five recordings were also independently scored by Expert 1 and Expert 2. All performances were measured against the source expert.

Traditionally, state classification is done over epochs of some reasonable duration for the animal studied. For mice, it is usually 5 s as sleep-wake states rapidly transition in these species. However, the underlying sleep process is not bound to these epochs and can transition within an epoch. Thus, the epoch at which an expert can pinpoint a new arousal state can vary between experts. In a 4-state classification problem, there is added variability in what is deemed Active Wake vs. Quiet Wake or Quiet Wake vs. NREM sleep. Simple accuracy measures therefore are an underestimation of what is actually acceptable and reasonable for classification agreement. In our study, we had Expert 0 blindly assess all predictions from experts and SleepEns for acceptable classifications. This formed an acceptable performance, where a researcher could reasonably trust the classifications given by a scorer.

SleepEns accurately detects 4 sleep–wake states

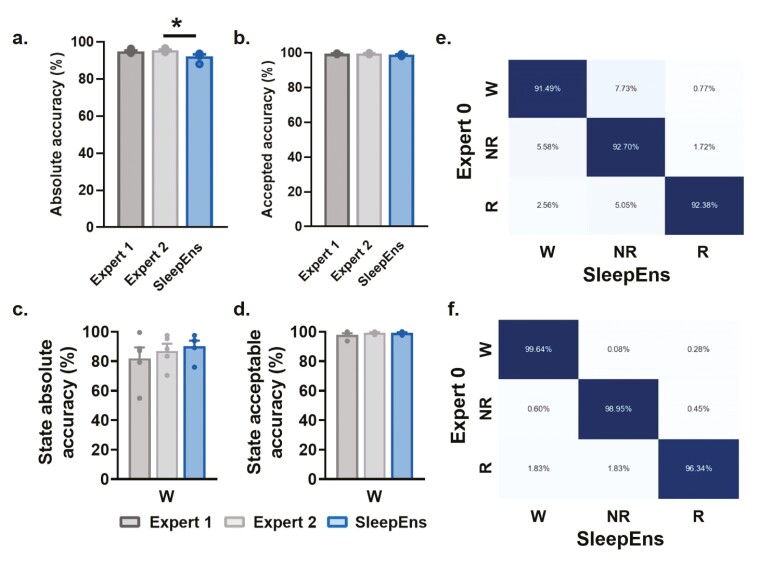
SleepEns performed comparably to humans, achieving 89.97 ± 1.4% accuracy compared to Expert 0 (Figure 3). Expert 1 and Expert 2 achieved 92.14 ± 0.4% and 94.03 ± 0.4% accuracy with Expert 0, respectively (Figure 3). SleepEns demonstrated similarity with at least one human expert (SleepEns vs. Expert 1: p = .3592, Figure 3a). Evaluating acceptable performance showed SleepEns at 98.79 ± 0.3%, Expert 1 at 99.40 ± 0.2%, and Expert 2 at 99.50 ± 0.2% (Figure 3). Importantly, we found that SleepEns and both human experts show no differences when evaluating for acceptable performance (SleepEns vs. Expert 1: p = .1561, SleepEns vs. Expert 2: p = .1400, Figure 3b) demonstrating that one can have as much practical confidence in the abilities of SleepEns as one would with human experts.

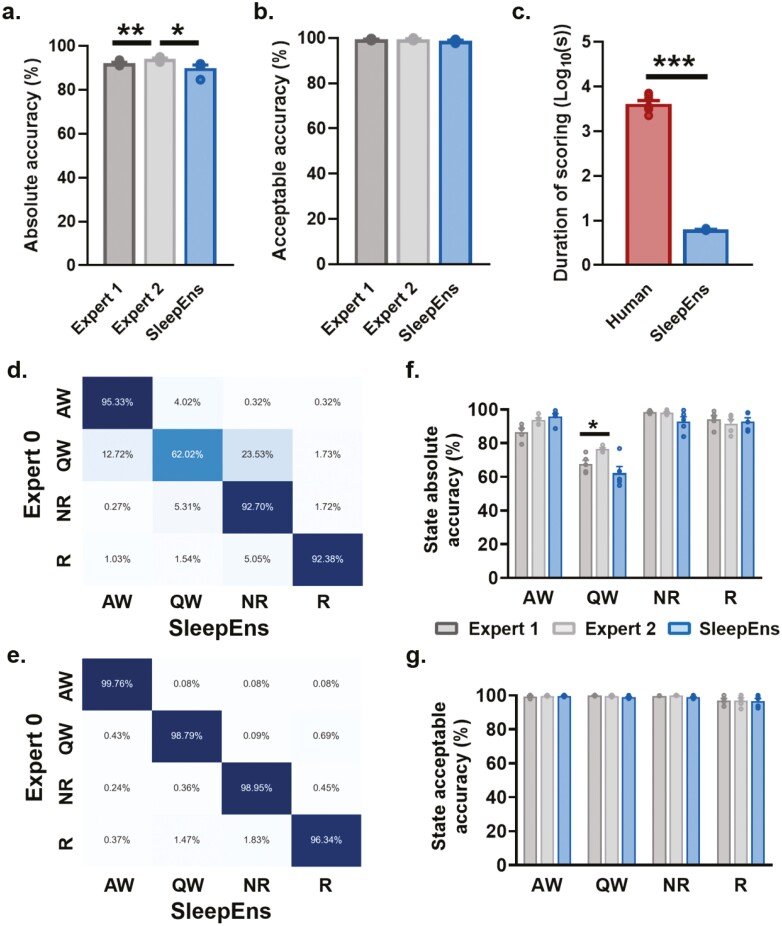
Figure 3.

SleepEns accurately detects 4 sleep–wake states. Comparison of accuracies between human experts and SleepEns (see Table 3). (a) Absolute accuracy in relation to Expert 0. (b) Acceptable accuracy as determined by Expert 0. (c) Execution time comparison between human experts and SleepEns. Note that SleepEns identify sleep-wake state in a 3-hr recording in ~6s. (d) and (e) Confusion matrices between SleepEns and Expert 0 for absolute accuracy (d) and acceptable accuracy (e). (f) Absolute accuracy comparison for each state. (g) Acceptable accuracy comparison for each state. AW: Active Wake, QW: Quiet Wake, NR: NREM Sleep, R: REM sleep, GBC: Gradient Boosting Classifier, TSEns: Time Series Ensemble. *p < .05, **p < .01 and ***p < .001 indicates significant differences.

By examining SleepEns performance for each of the four sleep–wake states, we found that the main source of error came from confusion between Quiet Wake and other states (Figure 3d). SleepEns tended to mischaracterize Quiet Wake as either NREM sleep or Active Wake. This was within expectation as Quiet Wake is difficult to distinguish between early stages of NREM sleep and “quieter” Active Wake. This was evident in the acceptable performance demonstrating that much of the differing predictions on Quiet Wake epochs were still reasonable classifications (Figure 3e). These acceptable errors related to slight differences in exact state transition timing were to be expected given the artificial delineation caused by dividing recordings into epochs (Figures 6 and 7).

Figure 6.

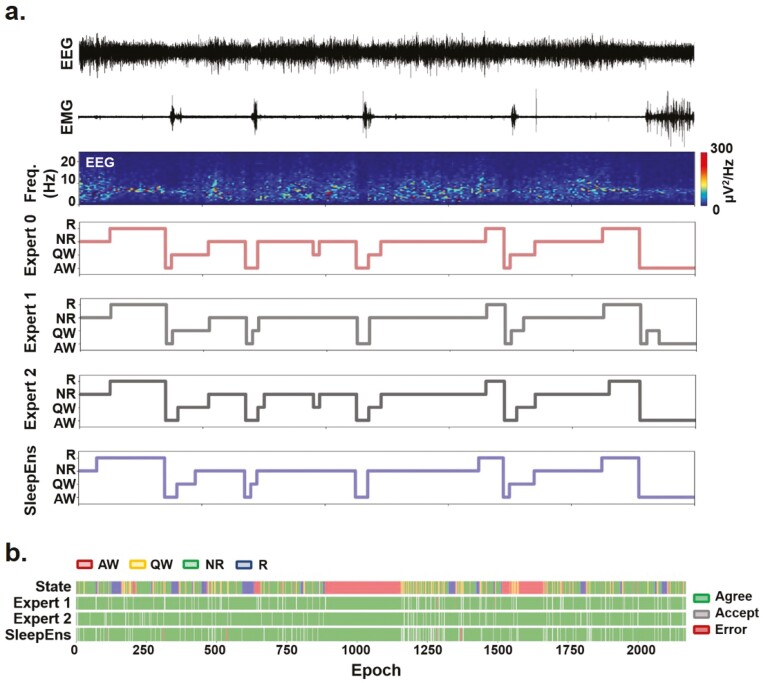
Example analysis of SleepEns in comparison to human scorers. (a) 100 epochs covering 500 s were taken from one of the test recordings to assess the predictions made by SleepEns with the classifications of all three human experts. The top panel represents the EEG input signal while the second represents the Neck EMG signal. The third panel depicts a spectrogram of the EEG to illustrate a time–frequency representation. The bottom four panels are hypnograms of Expert 0, Expert 1, Expert 2, and SleepEns. Note the scoring similarities between SleepEns and human scorers. (b) A longer comparison of human expert and SleepEns agreement with Expert 0. 2170 epochs covering 10 850 s were taken from one of the test recordings to demonstrate variations in prediction accuracy made by SleepEns and human experts. The first panel depicts a hypnogram scored by Expert 0, while the remaining three panels show accuracies of Expert 1, Expert 2, and SleepEns in comparison to Expert 0.

Figure 7.

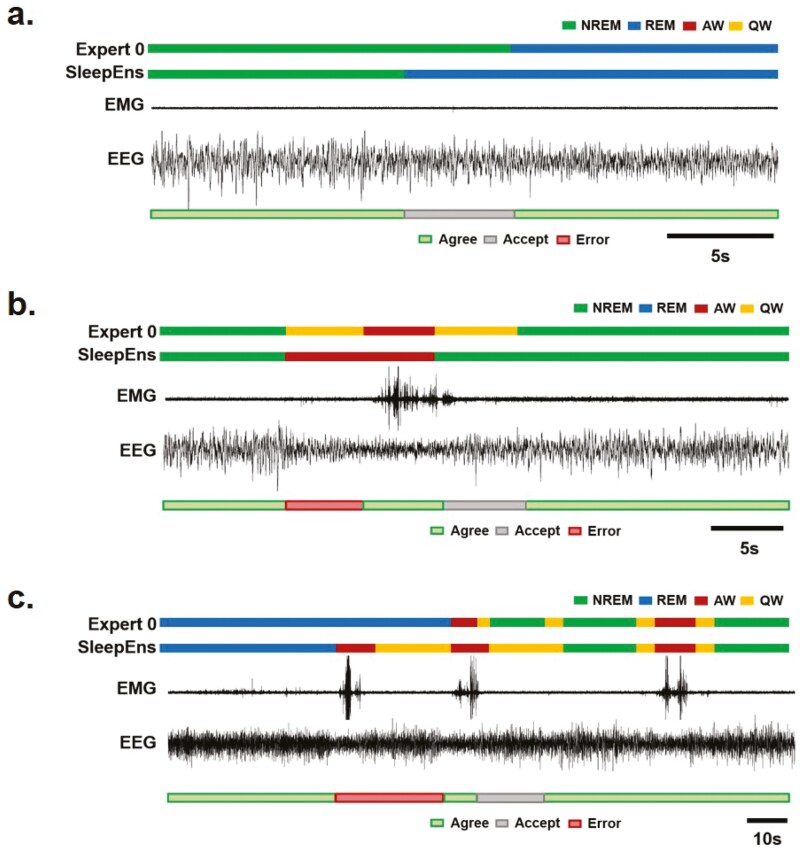
Examples of agreement, acceptable performance and true errors generated by SleepEns. (a) Example of a NREM to REM sleep transition showing the sensitivity of SleepEns to REM sleep transition. SleepEns detected the transition earlier than human scorers did, most likely due to the increased proportion of theta (θ) frequency in the EEG. The difference was estimated to be an acceptable performance (grey bar). Traces from top to bottom are Expert 0 scoring, SleepEns scoring, EMG and EEG signals. (b) Example of transition between NREM sleep and wake showing both a true error (red bar) and an acceptable performance (grey bar) of SleepEns. Note that SleepEns wrongly identified an active wake (AW) epoch that was scored as quiet wake (QW) by human scorers. This was likely due to the abrupt change in EEG frequencies and the context of the following epoch of AW. The epoch marked as acceptable performance was an epoch comprised of both NREM sleep and quiet wake characteristics in equal manner. (c) A 95s example showing a true error (red bar) and an acceptable difference (grey bar) in classification as the animal transition from REM sleep, wake and NREM sleep. Note that in this example SleepEns identified a REM sleep to wake transition earlier than Expert 0. Importantly in this instance, both Expert 1 & 2 made a similar identification as SleepEns (data not shown).

SleepEns was also statistically similar to both experts in every state (AW Expert 1: p = .16, AW Expert 2: p = 1.00, QW Expert 1: p = .82, QW Expert 2: p = .8, NR Expert 1: p = .36, NR Expert 2: p = .46, R Expert 1: p = .213, R Expert 2: p = .225). In fact, the only significant difference observed was between Expert 1 and Expert 2 for Quiet Wake (p < .05, Figure 3f). Moreover, no differences existed among the three scorers when considering acceptable performance (p > .05 for all comparisons, Figure 3g).

SleepEns identifies 3 hours of sleep–wake states in a few seconds

Sleep classification done by manual inspection is a laborious task. Improving the efficiency of sleep classification is an incredibly valuable aspect of automated algorithms. Testing with 3-hour long recordings, SleepEns was able to extract, process, classify, and export predictions in an average time of 6.26 ± 0.14 s (Figure 3c). This is in stark contrast with human experts taking an average of 74 min (4461.43 ± 654.56 s) to classify the same recordings (p < .001, n = 5). Training time of SleepEns is also very reasonable, taking 9012 s (about 2.5 hours) to train with 30 245 epochs of training data (42 hours of recording).

SleepEns accurately detects 3 sleep–wake states

While distinguishing two states of Wake (i.e. Active and Quiet) is useful particularly when examining the relationship between sleep and motor functions, the most common sleep-wake state classification system in mice is with three states: Wake, NREM sleep, and REM sleep. SleepEns was primarily designed for the four-state system but we also evaluated our algorithm with the usual three-state system. By merging all classifications of Active Wake and Quiet Wake into a single Wake state, we found excellent predictions given by SleepEns with 92.25 ± 1.1% accuracy (Figure 4a,c). Expert 1 and Expert 2 achieved 94.88 ± 0.5% and 95.58 ± 0.3% accuracy with Expert 0, respectively (Figure 4a,c). Evaluating acceptable performance showed SleepEns at 98.85 ± 0.2%, Expert 1 at 99.47 ± 0.1%, and Expert 2 at 99.54 ± 0.2% (Figure 4b,d). SleepEns continues to be similar to Expert 1 (p = .1271) and had no significant difference with either human expert when evaluating acceptable performance (SleepEns vs. Expert 1: p = .1841, SleepEns vs. Expert 2: p = .1493, Figure 4b,d). By inspecting the confusion matrices for three-state classification (Figure 4e-f), we found much improved distinction between Wake and NREM sleep with minimal confusion due to the underlying transitions from Wake to sleep. This highlights that SleepEns is a suitable automated classifier for the usual three-state system as well.

Figure 4.

SleepEns accurately detects 3 sleep–wake states. Comparison of accuracies between human experts and SleepEns. (a) Absolute accuracy in relation to Expert 0. (b) Acceptable accuracy as determined by Expert 0. (c) Absolute accuracy comparison for Wake (W). (d) Acceptable accuracy comparison for Wake (W). (e) and (f) Confusion matrices between SleepEns and Expert 0 for absolute accuracy (e) and acceptable accuracy (f). *p < .05, indicates significant differences.

SleepEns identify sleep–wake states with a similar efficiency in both male and female mice

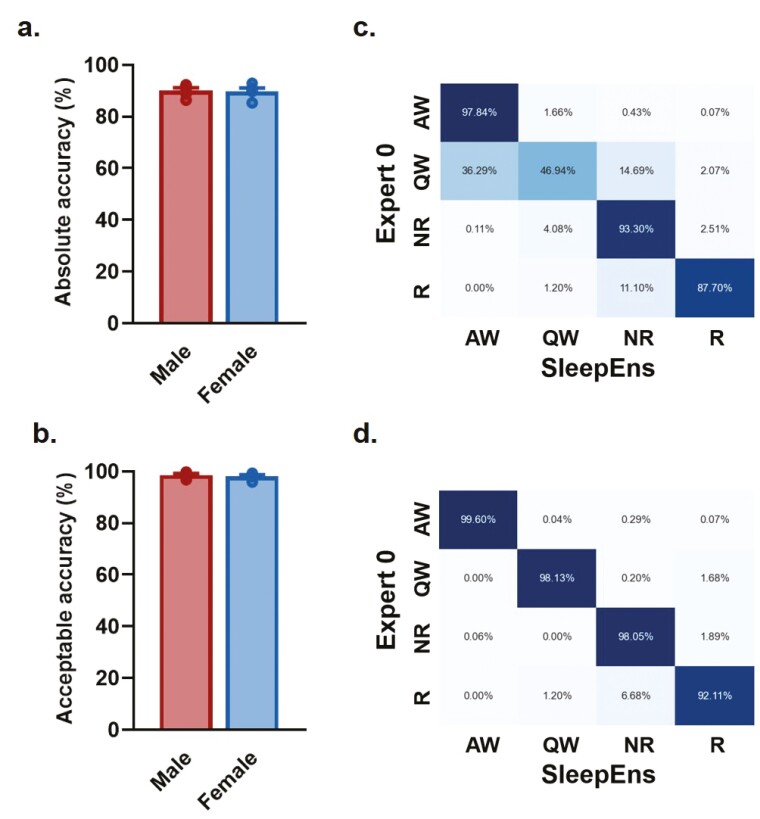
To ensure the tractability of our approach and ensure that we could identify sleep–wake states in both male and female mice for future experiments, we re-trained the algorithm with the original 14 recordings from male mice and the addition of recordings from four female mice, and tested it with five male and five female recordings. We found similar accuracy (p = .8636) and acceptable performance (p =.5622) when comparing male and female mice (Figure 5a,b). After re-training with this extended data set (i.e. 19 recordings used for training), the accuracy of SleepEns to identify sleep–wake states reached 90.04 ± 1.1% for male mice and 89.74 ± 1.3% for female mice (Figure 5a). Evaluating acceptable performance, SleepEns reached accuracy of 98.54 ± 0.5% for male mice and 98.05 ± 0.5% for female mice (Figure 5b). Finally, by inspecting the confusion matrices for four-state classification in female mice (Figure 5c,d), we found SleepEns tended to mischaracterize Quiet Wake as either NREM sleep or Active Wake similarly to what we found when only considering the sleep–wake architecture of male mice (Figure 4). These differences were resolved when acceptable performance was evaluated. This suggests that SleepEns is able to efficiently identify sleep–wake states regardless of sex.

Figure 5.

SleepEns identify sleep-wake states with a similar efficiency in both male and female mice. Comparison of accuracies between human experts and SleepEns for recordings of male and female mice. (a) Absolute accuracy in relation to Expert 0 showing no significant sex differences. (b) Acceptable accuracy as determined by Expert 0 showing no significant sex differences. Confusion matrices between SleepEns and Expert 0 for absolute accuracy (c) and acceptable accuracy (d) of female mice recordings.

Sleep–wake characteristics are similar when detected by either SleepEns or Experts

We compared the sleep–wake architecture predicted by SleepEns with that of each of the Experts. First, we found that SleepEns and human experts had similar hypnograms (Figure 6a). Disagreements with human experts only occurred around state transitions, but this was also the case between human experts (Figures 6a and 7a,b). SleepEns had a smoothing effect, prioritizing state stability, when Expert 0 identified alternating epochs of Quiet Wake during either NREM sleep or Active Wake (Figure 6). Finally, SleepEns tended to transition its predictions into REM sleep earlier than human experts, suggesting a higher sensitivity to REM sleep transition (Figures 6 and 7a). A longer comparison of SleepEns to human experts across 10 850 s was made (Figure 6b), demonstrating the similarity in performance across sleep–wake states over time. Differences in classifications deemed acceptable were typically related to slight differences in exact state transition timing, which is expected given the artificial delineation caused by dividing recordings into epochs (Figures 6b and 7a-c). Other acceptable differences related to the existence of brief Quiet Wake periods between NREM sleep (Figures 6b and 7a–c). The only few true errors were due to confusion between REM sleep and other states, or between Quiet and Active wake episodes (Figures 6b and 7b,c); however, these represented less than 2% of the recordings and were also present between human scorers.

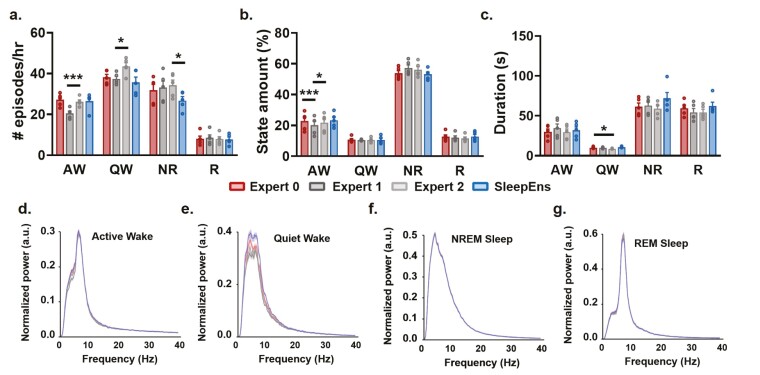
Next, we quantitatively evaluated the characteristics of sleep–wake states using several parameters often used in sleep-wake architecture analysis (i.e. number of episodes per hour, distribution of episodes in a 3-hr recording, and episode duration; Figure 8a–c). We found that the only significant difference noted between SleepEns and each of the human experts was in the number of NREM sleep episodes per hour with Expert 2 (NREM: p < .05, n = 5, Figure 8a). Importantly, SleepEns’s predictions were statistically similar to at least one expert in every comparison (Figure 8a–c). The main discrepancies we found were between human experts, highlighting the efficiency of SleepEns. Expert 1 differed from Expert 2 in the number of Active Wake (p < .001, n = 5) as well as Quiet Wake (p < .05, n = 5) episodes per hour (Figure 8a,c). The number of Active Wake episodes identified by Expert 1 was also different from both other human experts (Expert 0: p < .001; Expert 2: p < .05, n = 5, Figure 8a). Finally, Quiet Wake episodes identified by Expert 2 were also of shorter duration compared to Expert 0 (p < .05, n = 5, Figure 8b). This clearly demonstrates the comparability of scoring produced by SleepEns in sleep–wake classification when evaluated to human experts.

Figure 8.

Similarities of sleep–wake characteristics between SleepEns and human experts’ classifications. Comparison of sleep–wake episode characteristics between SleepEns and human experts show that identified sleep-wake states are similar. (a) Number of episodes per hour for Active Wake (AW), Quiet Wake (QW), NREM (NR) sleep, and REM (R) sleep as identified by Expert 0 (red), Expert 1 (dark grey), Expert 2 (light grey) and SleepEns (blue). (b) Amount of each states (%) per recording file. (c) Average episode duration (s). (d)–(g) A comparison of the EEG spectral profiles for each of the three human experts and SleepEns across each of the four sleep–wake states, demonstrating close similarity. *p < .05 and ***p < .001 indicates significant differences.

Finally, we also examine the EEG spectral profiles for each state identified by SleepEns and human experts to compare electrophysiological signal characteristics (Figure 8d–g). By pooling each state’s EEG signals in accordance to the classifications made by SleepEns or the human experts, we found the spectral profiles for each state to be similar between SleepEns and at least one human expert (AW: p = .9419, QW: p = .2051, NR: p = .9988, R: p = .1191). For example, REM sleep was characterized by a peak in the theta band (θ: 7–10 Hz) and NREM sleep by a peak in the delta band (δ: 0.5–4 Hz). Therefore, SleepEns’s state detection had identical signal characterization as the one defined by human experts.

Temporal context is critical for SleepEns performance

SleepEns is a novel arrangement of GBCs that was designed to leverage past and future temporal information. In comparison, GBCs that only utilized a single epoch, performed significantly worse (p < .001). We trained a number of variations of epoch-by-epoch GBCs with 250 estimators to match the model size of SleepEns; however, testing performance only yielded 82.58 ± 0.018% accuracy for 4 states. A single layer Time Series Ensemble was also evaluated as well, with window length (i.e. number of GBCs) of 10 and showed significant improvement over the epoch-by-epoch GBC with accuracy of 88.57 ± 2.9% (p < .01) but still significantly worse than SleepEns (p < .05) (Figure 3).

Specific EEG and EMG features are essential for the performance of SleepEns

An advantage to using tree-based algorithms with feature engineering is that this enables clearer explanation of predictions, as well as identification of important markers for sleep–wake states. To determine which EEG and EMG characteristics were essential for SleepEns detection of behavioral states, we examined the importance of each of the 16 features extracted from EEG and EMG signals by SleepEns and applied permutation feature importance analysis. With this technique, for each feature, we used a pre-trained SleepEns and compared its performance to when we randomly shuffle, or permute, the data of a particular feature across all epochs. This shuffling breaks down any relationship that feature may have with the sleep–wake state. The change in performance between the original data and the data with the feature shuffled indicates how much SleepEns depends on that specific feature to make predictions. In this manner, a greater reduction in performance due to the shuffling suggests that particular features greatly contributed to the ability for SleepEns to predict sleep–wake states. We compared performances using a log transformed mean square error normalized to the unpermuted data. Thus, a ratio greater than 0 represents a feature that improves the model and a ratio less than 0 indicates a feature that degrades performance. We computed these importance ratios for both the training and testing datasets. Using the training dataset reveals features SleepEns relies on to make predictions, while using the testing dataset reveals features that contribute to its actual performance on unseen data. We found that the EMG means, the EEG entropy and specific EEG frequency bands (i.e. δ and σ) had the strongest effect on the ability of SleepEns to identify correctly all sleep–wake states, while β/δ, σ/θ and β/θ EEG ratios were the least effective (Table 3).

Table 3.

Feature importances

Feature	Train Loss Ratio	Test Loss Ratio
EMG 95%ile Mean	1.703 ± 0.005	1.270 ± 0.005
EEG Entropy	1.366 ± 0.003	1.405 ± 0.005
EMG RMS	1.188 ± 0.017	1.149 ± 0.003
Delta	1.152 ± 0.003	1.106 ± 0.005
Sigma	1.087 ± 0.002	1.070 ± 0.002
EEG RMS	1.086 ± 0.002	1.111 ± 0.002
Beta	1.072 ± 0.001	1.036 ± 0.001
EMG Twitch	1.069 ± 0.001	1.058 ± 0.001
Theta/Delta	1.058 ± 0.002	1.023 ± 0.002
Theta	1.043 ± 0.001	1.037 ± 0.001
EMG Entropy	1.043 ± 0.001	1.005 ± 0.001
Sigma/Delta	1.040 ± 0.001	1.005 ± 0.001
Beta/Sigma	1.032 ± 0.001	1.011 ± 0.001
Beta/Delta	1.026 ± 0.001	0.999 ± 0.001
Sigma/Theta	1.026 ± 0.000	1.000 ± 0.001
Beta/Theta	1.023 ± 0.001	1.000 ± 0.001

^*Loss ratios are calculated as mean square error (MSE) normalized to the MSE of the original data. Losses are averaged across 30 repetitions. Intervals are reported as the standard error of the mean.

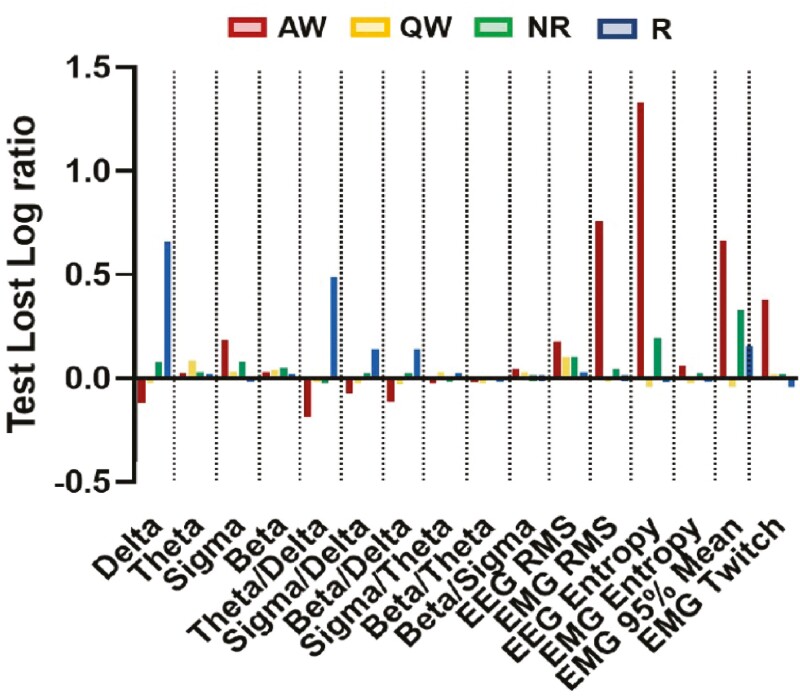
However, it is important to place these ratios in the context of individual sleep–wake state distribution. NREM sleep comprised a significant bulk of the data; hence, features important for classifying NREM sleep naturally appeared to be more important for the overall algorithm (e.g. δ EEG frequency band). Therefore, we calculated the importance ratios for each individual sleep–wake state (Figure 9). We found that muscle activity (i.e. EMG) related features were very important for identifying Active Wake. Overall EEG power and θ power were the most important features for Quiet Wake. However, these features show significant overlap between Quiet Wake and other states, making Quiet Wake distinguishable from some states at times but not uniquely identifiable (Figures 1b,g and9). A number of features aided in identification of NREM sleep, including δ power, σ power, β power, overall EEG power, EEG entropy, and EEG 95th percentile mean. These features are also important for other states, and thus indicate that NREM sleep is identified by not matching any defining characteristics of other states. The θ/δ EEG ratio was important for distinguishing REM sleep, but surprisingly, decreased δ power had the most predictive power for REM sleep. This appears to be because NREM and REM sleep states exhibit similar θ powers and differ more in the δ power band. Finally, we also tested removal of least predictive features in various combinations finding that performance was always degraded (data not shown).

Figure 9.

Feature importance identified by SleepEns for each sleep–wake states. Importance ratios were taken for each sleep and arousal state (i.e. AW: Active Wake, QW: Quiet Wake, NR: NREM sleep, and R: REM sleep) from 30 repetitions in the test dataset. Importance ratios are log transformed so that 0 indicates no change in predictive power compared to non-shuffled features, ratio greater than 0 represents feature that improve sleep identification, and negative ratio represents feature that degrade performance of SleepEns. Delta: EEG δ power, Theta: EEG θ power, Sigma: EEG σ power, Beta: EEG β power, Theta/Delta: EEG θ/δ power, Sigma/Delta: EEG σ/δ power, Beta/Delta: EEG β/δ power, Sigma/Theta: EEG σ/θ power, Beta/Theta: EEG β/θ power, Beta/Sigma: EEG β/σ power, EEG RMS: EEG root-mean square.

Discussion

We described a novel automated machine-learning approach to quickly and accurately classify sleep–wake states from both male and female mice using EEG/EMG recordings. We rigorously tested and compared sleep-wake classifications given by our algorithm, SleepEns, to conclude that the performance of our approach is identical to the one of human expert and identify sleep–wake characteristics in a fraction of the time it takes for manual/visual classification.

SleepEns is the first data processing architecture to classify four states of sleep–wake—dividing Wake into Active and Quiet alongside the traditional NREM and REM sleep states. This specification of active vs. quiet waking periods gives greater precisions into sleep-wake patterns [16, 42–44]. This degree of details improves our ability to research the relationship between sleep–wake behaviors and motor function, as well as improve our understanding of consciousness [1, 5, 16, 17, 45–47].

Our study evaluated acceptable performance to yield a more accurate real-world applicability of sleep–wake classification algorithms. Typically, simple epoch-to-epoch accuracy is used to evaluate the performance of a model to the source expert(s) who labeled the dataset. However, it is well known that there is significant inter-rater variability even amongst humans [10, 13, 14]. Any given human classification has no guarantee to being the true classification. Accuracy to a source expert neglects this important fact. This is particularly true when considering that transition periods between states in mice can happen in a smaller time window than the pre-determined epoch, here 5 s [1, 6, 7]. Therefore, we also evaluated classifications as being acceptable (i.e. a researcher would be comfortable using the given scoring for their own research) and compare this acceptable performance with those of other human experts. In this regard, virtually all of the classifications provided by SleepEns were deemed acceptable.

Another aspect of our approach, which closely resemble the process done by human scorer, is that our division of training, validation, and testing datasets are segregated on a per-recording basis as opposed to per-epoch basis that has been used by other studies [11]. Epochs within the same recording (or from the same animal) are more similar to each other in behavior and ­signal patterns [18]. Therefore, a per-epoch division of data results in information bleeding across the training and testing datasets and leading to bias [48]. A per-recording approach to dataset construction provides a more accurate indication of real-world performance on recordings of different animals. Furthermore, we developed and optimized SleepEns with cross-validation and by selecting the best architecture before evaluating it on the testing dataset. This ensures we are not introducing selection bias by choosing a model that would perform best on the testing dataset [49].

With SleepEns, we defined a novel ensemble learning architecture specifically designed for classifying time series data where past and future information (i.e. context) are relevant to the time point of interest. We described the Time Series Ensemble as an approach to incorporating temporal context that worked well in our particular application of sleep–wake classification. SleepEns is derived from a particularly arranged ensemble of Gradient Boosting Classifiers (GBCs). We chose to use GBCs for several key reasons. As an architecture that uses decision trees, GBCs are more interpretable when explaining their decision-making processes [10–12]. We believe this to be an integral aspect for any sleep–wake classification approach as conclusions arising from unexplained classifications are more difficult to validate and verify. Another reason for the use of GBCs is that deep learning architectures such as convolutional neural networks and recurrent neural networks, both of which also incorporate temporal information, tend to classify three sleep–wake states with roughly similar accuracy but are more complex and more computationally expensive algorithms (by a factor of ~10³ to 10⁴) than the method used in our study [10, 35, 50–52]. In addition, GBCs are significantly easier to train than neural networks [10–12]. SleepEns was designed with the idea to be easy and accessible to train. This is a critical factor in a model’s usability as other researchers may use different recording protocols and, thus yield slightly different signal and noise characteristics. By deriving our approach from GBCs, SleepEns is significantly less expensive than deep learning approaches [10, 35] to train on different data and therefore will be more accessible to others.

Finally, our study adds to our understanding of the signal characteristics that define sleep–wake states. We analyzed the features used by SleepEns to determine which of them were integral to identifying particular states of consciousness and activity. We found, in line with current understanding, that the θ/δ EEG ratio along with minimal muscle activity characterized REM sleep [12, 29, 53]. However, REM sleep was best identified by a decrease in power in the δ EEG frequency band. On closer inspection, it appears that this was merely because the δ EEG frequency band contains a greater degree of separation between REM and NREM sleep states. NREM sleep was interestingly best identified by an elevated overall EEG signal power and low muscle activity. θ EEG frequency band tended to actually be elevated in NREM sleep compared to REM sleep, but not to the extent of the δ EEG band that predominate this state. Active Wake was efficiently well defined by the presence of muscle activity, increased EEG spectral entropy, and to an extent a decreased power in σ EEG band. Quiet Wake was found to be a more difficult state to identify, because at time it is a quick intermediary state between Active Wake and NREM sleep. It may be worth further exploring the transition between Active Wake and NREM sleep. Quiet Wake may be better represented as two states, one that is closer to a calm waking state while another closer to a drowsy state (i.e. transition between Active Wake and NREM sleep).

In the near future, we aim to further refine the SleepEns approach and, in particular, explore better data pre-processing approaches. The current approach is susceptible to inter-recording variations and relies on the assumption of a similar distributions of sleep-wake states within each recording. Thus, a limitation of SleepEns is that the approach likely only performs well with sufficiently long recordings to maintain this assumption. As always, feature engineering and selection plays a significant role in machine learning processes. It would be of interest to continue exploring other possible features that might further improve SleepEns, such as higher frequency EEG ranges (e.g. γ: 30–100 Hz). It will also be of interest to further explore the decision-making processes of SleepEns to possibly elucidate elements in electrophysiology signals that are indicative of sleep–wake states and finer transitions between states. We will also aim to test whether SleepEns can easily identify sleep-wake states in disease models [5] such as REM sleep behavior disorder [3, 20, 21] or narcolepsy [4, 22–24].

Author Contributions

JW & JJF designed the algorithm. JJF, SKP, RL & HL performed recording and scoring. JW & JJF analyzed data. JW, JJF & JHP wrote the paper with input from co-authors.

Funding

Grants from the Canadian Institutes of Health Research (CIHR) and the National Sciences and Engineering Research Council of Canada (NSERC) funded this research. JW received support through a 2019 Undergraduate Student Research Award from the NSERC.

Resource Accessibility

In the spirit of accessibility and repeatability, we make SleepEns fully open-source and available at https://github.com/paradoxysm/SleepEns.

Conflict of interest statement. None declared.