ZEAL: protein structure alignment based on shape similarity

Abstract

Motivation

Most protein-structure superimposition tools consider only Cartesian coordinates. Yet, much of biology happens on the surface of proteins, which is why proteins with shared ancestry and similar function often have comparable surface shapes. Superposition of proteins based on surface shape can enable comparison of highly divergent proteins, identify convergent evolution and enable detailed comparison of surface features and binding sites.

Results

We present ZEAL, an interactive tool to superpose global and local protein structures based on their shape resemblance using 3D (Zernike-Canterakis) functions to represent the molecular surface. In a benchmark study of structures with the same fold, we show that ZEAL outperforms two other methods for shape-based superposition. In addition, alignments from ZEAL were of comparable quality to the coordinate-based superpositions provided by TM-align. For comparisons of proteins with limited sequence and backbone-fold similarity, where coordinate-based methods typically fail, ZEAL can often find alignments with substantial surface-shape correspondence. In combination with shape-based matching, ZEAL can be used as a general tool to study relationships between shape and protein function. We identify several categories of protein functions where global shape similarity is significantly more likely than expected by random chance, when comparing proteins with little similarity on the fold level. In particular, we find that global surface shape similarity is particular common among DNA binding proteins.

Availability and implementation

ZEAL can be used online at https://andrelab.org/zeal or as a standalone program with command line or graphical user interface. Source files and installers are available at https://github.com/Andre-lab/ZEAL.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein structure evolves substantially slower than sequence, which means that functionally related proteins can adopt similar structures despite low sequence identity. Comparison of protein structure through superposition is therefore a powerful complement to sequence alignments in studying evolutionary relatedness between highly divergent protein sequences. However, in the presence of mutations, insertions, deletions and topological permutations it can be challenging to identify optimal superpositions. On the other hand, the geometrical shape of proteins is often conserved under such rearrangements. This can be rationalized by the fact that much of biology happens on the surface of proteins, such as catalysis and binding. Aligning proteins using surface shape can consequently provide an alternative approach to standard coordinate-based superposition. Additionally, shape-based alignment may also be used to find examples of evolutionary unrelated proteins where functional constraints results in similar global shapes or local similarity due to the presence of functional sites on the surface.

The detection of shape equivalence is often carried out by comparison of shape descriptors. Shape descriptors are low-dimensional representations of geometric shape that are invariant to transformations such as rotation and translation. For proteins, Zernike-Canterakis shape descriptors (ZCDs) (Canterakis, 1999; Novotni and Klein, 2003) has been used to compare protein shapes (Grandison et al., 2009; Sael et al., 2008) and electron-density maps (Sael and Kihara, 2010) combined with protein docking (Esquivel-Rodríguez and Kihara, 2012), as well as shape comparisons of ligands (Gunasekaran et al., 2009) and binding pockets (Chikhi et al., 2010). Recently, a less compressed descriptor based on Zernike-Canterkis (ZC)functions was presented with impressive results in a shape retrieval benchmark of protein structures (Guzenko et al., 2020). The Kihara lab has pioneered the use of ZCDs to identify proteins with similar surface shape and have shown how this approach can be used to identify protein pairs with low sequence and structural similarity but matching molecular surfaces (Han et al., 2019; Sael et al., 2008). For instance, both the human and E.coli DNA topoisomerase I were found to have similar global shape despite low sequence and backbone conformation similarity.

While shape descriptors like ZCDs can detect the shape equivalence between functionally related—but non-homologous—proteins, it does not provide the superposition between them. Due to the low sequence and structural similarity, coordinate-based superposition methods such as CE (Shindyalov and Bourne, 1998), DALI (Holm and Sander, 1993) and TM-align (Zhang and Skolnick, 2005) fails to provide a meaningful solution in such cases and may not identify the functional and evolutionary link between the proteins.

Several methods have been developed for alignment of molecular surfaces in the context of binding pocket analysis (Angaran et al., 2009; Konc and Janezic, 2012), virtual screening (Hawkins et al., 2007; Hofbauer et al., 2004; Sastry et al., 2011), molecular docking (Macindoe et al., 2010; Pierce et al., 2014; Schneidman-Duhovny et al., 2005). But no general tool has been presented for local or global shape-based superposition of proteins per se. In this work, we present with zeal an interactive graphical software for shape-based alignment of proteins that we refer to as ZEAL (short for ZErnike-based protein shape ALignment). ZEAL uses ZC functions to parametrically describe the shape of the molecular surface as a series expansion, and provides an optimal superposition between two proteins by maximizing the correlation between the expansion coefficients (ZC moments). In conjunction with shape matching from ZCDs, ZEAL provides an approach for interactive protein shape comparison and analysis.

In order to benchmark ZEAL we repurposed two methods for surface-based shape alignment developed for small molecule alignment and protein-protein docking, and applied them to superposition of homologous structures. Comparisons show that ZEAL outperforms these alternative methods. Furthermore, alignments from ZEAL were of comparable quality to the coordinate-based superpositions provided by TM-align. When protein pairs with low sequence and structural identity are analyzed, ZEAL still provides high quality superposition while coordinate-based methods fail.

Shape-based matching and alignment can be used as a general tool to study relationships between shape and protein function. In this study, we develop a statistical approach to identify global shapes that are significantly linked with certain functions. With this methodology we show that many DNA-binding proteins share common global shapes while having completely different folds. ZEAL enables a detailed comparison of shape equivalence for these types of shape matches.

Coordinate-based alignment methods are often blazingly fast, which makes them the method of choice in superposition of close structural homologs. Shape-based alignment on the other hand provide unique opportunities for comparison of remote homologs with divergent structure and topological permutations, and proteins resulting from convergent evolution and functional surfaces. We also demonstrate here that shape-based alignment can be used as a method for studying the relationship between global shape and protein function and to identify building blocks in the design of protein assemblies.

2 Materials and methods

2.1 Representing the protein shape

The concept of shape is not well defined at the molecular level, but can be described as a density in space (approximating the electron density) or, typically, as the shell of the surface (the molecular skin) constructed using van der Waals (vdW) radii of atoms and a spherical probe that traces out a surface of the regions accessible or excluded to solvent. The later, solvent-excluded surface is also known as the molecular or Conolly surface. Because proteins have evolved in the presence of water, the solvent-probe has a radius of 1.4 Å to approximate the size of a water molecule. In ZEAL, all of these shape representation types are available. The density representation is achieved using Gaussian atoms as described in Grant et al. (1996), and the surfaces (vdW, solvent accessible/excluded) are obtained using an Euclidean distance transform (EDT) approach as implemented in EDTsurf (Xu and Zhang, 2010). However, in this work, we only present results using the molecular (solvent-excluded) surface. Because our algorithm for generating the molecular surfaces differs slightly from that of EDTsurf, we outline the main steps in Supplementary Section S1. For reasons that will become clear below, the EDT method integrates naturally with the algorithm for ZC moment computations as the molecular surface is mapped to a grid directly. The sampling resolution and thickness of the surface, both affecting the shape representation in ZC space, can easily be controlled by specifying the grid size L (resolution) and the interval of isovalues (Euclidean distances)that should define the surface and its thickness . In the work presented here, we use a 64³ grid and a thickness of 2 grid units for the molecular surface.

2.1.1. Parameterization

The protein shape can be described through a series expansion as

$$f(\mathbf{x})=\sum _n^{\infty }\sum _l^n\sum _{m=-l}^l{\Omega }_{nl}^m{Z}_{nl}^m(\mathbf{x})$$ (1)

where $f(\mathbf{x})$ is the shape function of the protein (the molecular surface for instance), scaled to fit inside the unit sphere ($\left|\mathbf{x}\right|\le 1$) where the ZC functions (also called 3D Zernike functions) $Z_{nl}^m(\mathbf{x})$ lives (Canterakis, 1999). These are defined as

$$Z_{nl}^m(\mathbf{x})\equiv R_{nl}(r)Y_l^m(\theta ,\varphi )$$ (2)

where $R_{nl}(r)$ is a radial function and $Y_l^m(\theta ,\varphi )$ is an angular function, the spherical harmonics that live on the surface of the unit sphere. The integers n, l, m are labels for the members of the collection of ZC functions that form the basis set in Equation 1, and the functions themself are restricted so that $l\le n$ and $(n-l)$ be an even number. The expansion coefficients ${\Omega }_{nl}^m$ in Equation 1 are called moments because they are the projections of the protein shape $f(\mathbf{x})$ onto the basis set. The (complex) moments encode non-redundant information about the shape (ZC functions are orthogonal) and are obtained by integrating the ZC functions $Z_{nl}^m(\mathbf{x})$ over the shape $f(\mathbf{x})$ inside the unit sphere

$${\Omega }_{nl}^m\equiv \frac{3}{4\pi }{\int }_{\left|\mathbf{x}\right|\le 1}f(\mathbf{x})\overline{Z_{nl}^m(\mathbf{x})}\mathrm{d}\mathbf{x}$$ (3)

where the bar is the complex conjugate of $Z_{nl}^m(\mathbf{x})$.

In practice, the moments in Equation 3 can be computed efficiently using geometrical moments and performing the integration over a L³ cubic grid in which the shape has been mapped onto (Novotni and Klein, 2003). We implement this algorithm to compute the ZC moments and employ the same 64³ grid, with 2 grid-unit thick surfaces, that was shown by the authors to give the best shape-retrieval performance. However, our implementation of the EDTsurf algorithm (Xu and Zhang, 2009) provides a straightforward way to adjust these parameters, and the resulting shape representation $f(\mathbf{x})$ can be plugged into the Novotni and Klein algorithm directly without any prior surface triangulation.

Before computing the geometric moments, the voxelized shape is normalized so to fit in the unit sphere. Because ZC functions have poor resolution close to the boundary (Callahan and De Graef, 2012) we scale the object such that the maximum distance from the geometric center, $r_{\text{max}}$, corresponds to 70% of the unit sphere radius, i.e. scaling by the factor $s=0.7/r_{\text{max}}$. We note that the default scaling factor used in the C++ library from Novotni and Klein (2003) use $s=1/2R_g$, where R_g is the radius of gyration—the root-mean squared distance to the center of mass. This scaling does not guarantee full embedding of the object within the unit sphere, so the object function has to be defined as zero for values outside the boundary for correct normalization.

Obviously, the sum in Equation 1 has to be truncated at some order n = N; Figure 1 shows the level of shape information captured in the ZC moments computed up to orders $N=$ 10, 15, 20, 25 and 30 for the molecular surface of nuclear protein EBNA1 (PDB ID code 1B3T). The number of moments that have to be computed for a given order N is $(N+1)(N+2)(N+3)/6$. At N = 20, most of the salient shape features are captured in the 1771 ZC moments. This is the default order in ZEAL, but can be changed by the user.

Fig. 1.

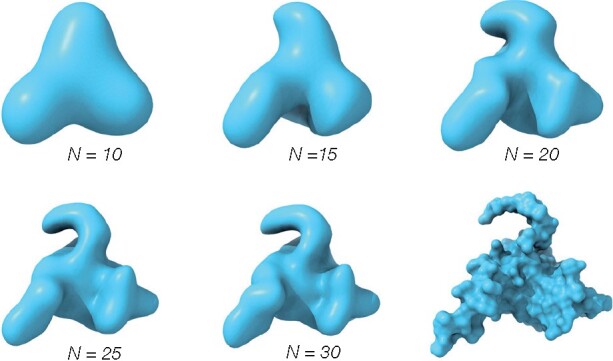
The shape information (reconstructions) of the molecular surface (bottom right) for the nuclear protein EBNA1 (PDB ID code 1B3T) encoded in ZC expansions up to order N = 10, 15, 20, 25 and 30 from a 64×64×64 grid. At N = 20, most of the salient features are captured and this is the default expansion order in ZEAL

Note: Figure Replacement Requested.

Note: Figure Replacement Requested.

Note: Figure Replacement Requested.

2.2 Shape matching

The ZC moments in Equation 3 can be used to compare the shape similarity between two objects by finding the rotation that maximizes the correlation between the vector $\mathbf{\Omega }(\mathrm{A})$, containing the ZC moments ${\Omega }_{i=\mathit{nml}}^{\mathrm{A}}$ for the fixed protein A, and the vector $\mathbf{\Omega }(\mathrm{B}|\alpha ,\beta ,\gamma )$ containing the ZC moments ${\Omega }_{i=\mathit{nml}}^{\mathrm{B}}$ for the protein B rotated with Euler angles $(\alpha ,\beta ,\gamma )$. This can be viewed as minimizing the angle θ between the vectors—they are correlated if they point in the same direction (small θ). Because the vectors are in the complex space ${\mathbb{C}}^n$ (${\mathbb{C}}^{1771}$ for N = 20), both the angle and its cosine are in general complex. A geometrically meaningful (real) angle, the Euclidean angle $\text{cos}\hspace{0.17em}\hspace{0.17em}{\theta }_E$, is defined by

$$\begin{array}{c}\hspace{0.17em}\text{cos}\hspace{0.17em}\hspace{0.17em}{\theta }_E\equiv \frac{\text{Re}\left[\langle \mathbf{\Omega }(\mathrm{A}),\mathbf{\Omega }(\mathrm{B}|\alpha ,\beta ,\gamma )\rangle \right]}{\Vert \mathbf{\Omega }(\mathrm{A})\Vert \Vert \mathbf{\Omega }(\mathrm{B}|\alpha ,\beta ,\gamma )\Vert }\hfill \\ =\frac{\text{Re}\left[\sum {\Omega }_i^{\mathrm{A}}\overline{{\Omega }_i^{\mathrm{B}}}\right]}{{\left[\sum {\Omega }_i^{\mathrm{A}}\overline{{\Omega }_i^{\mathrm{A}}}\right]}^{1/2}{\left[\sum {\Omega }_i^{\mathrm{B}}\overline{{\Omega }_i^{\mathrm{B}}}\right]}^{1/2}}\hfill \end{array}$$ (4)

where we take the real (Re) part of the Hermitian (complex) inner product, and where $\overline{{\Omega }_i^{\mathrm{A}}}$ and $\overline{{\Omega }_i^{\mathrm{B}}}$ denote the complex conjugate of moments ${\Omega }_i^{\mathrm{A}}$ and ${\Omega }_i^{\mathrm{B}}$ respectively. Since the complex vector space is isomorphic to the real vector space (Scharnhorst, 2001), the Euclidean angle of vectors in ${\mathbb{C}}^n$ is the angle in ${\mathbb{R}}^{2n}$. Note that the inner product might not vanish for $\text{cos}\hspace{0.17em}\hspace{0.17em}{\theta }_E=\pi /2$ (Marsh, 2017). It is possible to also define the Hermitian angle between complex vectors, in which case one takes the modulus (absolute value) of the Hermitian inner product. However, with that interpretation of the angle, parallel vectors in ${\mathbb{C}}^n$ can be orthogonal in ${\mathbb{R}}^{2n}$. We will refer to $\text{cos}\hspace{0.17em}{\theta }_E$, i.e the ZC moment correlation, as the ZEAL-score. Thus, shapes with ZEAL-score equal to 1 have moment vectors pointing in the same direction and consequently the same shape (in ZC space).

For shape comparisons alone, there is a simpler way than finding the rotation that maximizes the ZEAL-score for two shapes. This is done by collecting the ZC moments to $(2l+1)$ dimensional vectors ${\Omega }_{nl}\equiv {[{\Omega }_{nl}^l,{\Omega }_{nl}^{l-1},{\Omega }_{nl}^{l-2}, ..., {\Omega }_{nl}^{-l}]}^t$ and compute the length of these vectors (which is rotationally invariant):

$$F_{nl}\equiv {\left[\sum _{m=-l}^{m=l}|{\Omega }_{nl}^m{|}^2\right]}^{1/2}$$ (5)

By forming the ZC shape-descriptor vector (ZCD) $[F_{00},F_{20},F_{22},F_{31}\dots ]$ one can compare the resemblance of two shapes by calculating the Euclidean distance d_E between their ZCDs. For order 20, the shape information is then compactly contained in a ZCD with 121 (real) numbers, and the similarity between proteins A and B above given by

$d_E={\left[\sum _{i=1}^{i=121}{(F_i^{\mathrm{A}}-F_i^{\mathrm{B}})}^2\right]}^{1/2}$ . The maximum d_E for judging if shapes are similar has be determined empirically. We find that $d_E<0.025$ (for unnormalized ZCDs) represents a descent cut-off for proteins with similar shape.

2.3 Shape alignment

As alluded to before, the ZEAL-score can be used to find the transformation that gives maximum shape overlap between two structures. If the shapes are similar, the transformation can (to a good approximation) be reduced to a rotational search by placing the centroid for each shape at the origin. If we parameterize the rotation using Euler angles $(\alpha ,\beta ,\gamma )$, and adopt the zyz convention, the rotation with maximum ZEAL-score is bounded by $0\le \alpha ,\gamma \le 2\pi$ and $0\le \beta \le \pi$. Supplementary Figure S2 shows the ZEAL-score (A) and heavy atom RMSD (B) as a function of the two Euler angles α and β for two copies of nuclear protein EBNA1 (PDB ID code 1B3T), one rotated so that the correct alignment lies on this 2D angle grid. As expected, the global maximum (ZEAL-score = 1) is the rotation that results in perfect shape superposition. But the shape-correlation landscape is highly non-convex with many local maxima, corresponding to fair alignments in terms of shape overlap. For orientations close to the maximum (ZEAL-score $\ge$ 0.75), the score and RMSD are strongly correlated (Supplementary Figures S2C and S3).

In general, finding the rotation with the maximum ZEAL-score in an exhaustive search is prohibitively expensive; each new rotation requires the ZC moments to be recomputed from a rotated molecular surface. While the maximum overlap among ZC moments can be searched for using a sophisticated fast Fourier transform (FFT) method (Liu et al., 2013), this still requires the use of local search methods after selecting candidate solutions (referred to as ‘peak picking’) from the FFT search since the global maximum might not lie on the FFT grid. As a trade off between accuracy and speed, we use a machine learning method known as surrogate modeling where an internal model (i.e. a surrogate) of the objective function is constructed, which is then used to find better points to evaluate. We use the surrogate optimization algorithm implemented in MATLAB (2020), with the ZEAL-score as the objective function bounded by the Euler angles. In short, the algorithm cycles between two phases: (i) Constructing the surrogate model by interpolating ZEAL-scores evaluated from random Euler angles using cubic radial basis functions (Gutmann, 2001); (ii) Searching for the maximum ZEAL-score by evaluating the surrogate model at thousands of sample points such that the search balances between refining an existing solution and searching in places that have not yet been evaluated in the hunt for a better global maximum (controlled by a merit function with cyclical weights (Regis and Shoemaker, 2007)). Unlike other optimization algorithms, there is no notion of convergence here. The algorithm continues alternating between the two phases until it reaches a stopping criteria, such as the number of ZEAL-score evaluations or a time limit. This algorithm is very robust as demonstrated when performing self-alignment trials of five structures where one copy is randomly rotated relative an un-rotated copy 20 times (Supplementary Table S1): the average RMSD before and after ZEAL alignment is 22 and 0.03 Å respectively. As will be shown, high-quality superpositions can be expected for shape matches within 500 ZEAL-score evaluations—the default stopping criteria in ZEAL—and, on average, a ZEAL-score above 0.8.

2.4 Single-chain and same-shape dataset

Our set of single-chain structures for evaluating the performance of ZEAL, and finding proteins with similar function and shape, is based on a PISCES (Wang and Dunbrack, 2003) culled list containing 23 004 structures with a maximum 90% pairwise sequence identity, a minimum resolution of 2.0 Å and a maximum crystallographic R-factor of 0.25. From this list, 18 965 structures could be mapped to unique entries in the UniprotKB (UniProt Consortium, 2018) from which we retrieve the following annotations: Protein names; Length; DNA-binding; EC number and Keywords;. We will refer to this set as the S1 set of single chain structures.

We compute the ZCD for all structures using the (EDT-generated) molecular surface, with $r_p=1.4$ Å, mapped to a 64³ grid, a two-voxel thick molecular surface, ZC moments computed up to order 20 and a normalization distance of 70% of the embedding unit sphere. We also compute the radius of gyration R_g for all structures to allow shapes to be filtered based on their compactness.

To find pairs of structures with similar shape (shape matches), we then compute the Euclidean distance d_E between all ZCDs of the S1p $18\hspace{0.17em}965(18\hspace{0.17em}965-1)/2$ unique (and non-identical) pairs of structures and select those with $d_E<0.025$. This resulted in a total of 161 490 shape matches which we will call the same-shape (S2) dataset.

2.5 Benchmark

Irrespective of method, a shape-based alignment of two proteins with the same backbone orientation (same fold) has to be comparable to alignments generated by conventional main-chain oriented tools, since the structures are expected to have similar global shape. By the same token, proteins with different backbone folds, but similar global shape (shape twins) should have a superposition that clearly makes the shape resemblance apparent. In the first case, alignments of same-fold proteins are a testament to the robustness of the underlying algorithm. And in the second case, given a robust algorithm, superposition of structures with completely different folds are a testament of the possible advantage of shape over conventional tools in such cases.

We therefore evaluate the performance of ZEAL for these cases, i.e. alignment of same-fold proteins and superposition of shape-twin proteins, using 1000 computations of the ZEAL-score as a stopping criterion for the surrogate optimization algorithm. As a gold standard for alignment of proteins with the same fold, we use TM-align (Zhang and Skolnick, 2005) and compare the C_α RMSD for the alignments. We also include HEX (Ritchie and Kemp, 1999) and MS3align (Shivashankar et al., 2016) which are two other available tools to perform alignments based on shape (described below). Because RMSD is not uniquely defined, it is computed using the same corresponding residues as those mapped by TM-align. Consequently, a lower RMSD for ZEAL may be available by finding a different mapping that minimize RMSD. By the same token, we use the ZEAL-score as the measure of shape overlap, and we compute the ZC moments using the same normalization scheme for all superposed structures generated by the different methods.

2.5.1. Datasets

Alignments by ZEAL (and the ZCDs) are size invariant due to the normalization step in the moment computation. Contrary to Sael et al. (2008), we note that shape matches with very different sizes is not a rare event. Supplementary Figure S4 shows the 2D cumulative distribution of the percent difference in residue length and radius of gyration in the S2 set. Approximately 13% of shape matches have a length that differs by more than 100%, and approximately 7% have a radius of gyration that differs by more than 50%. To exclude the effect of any size difference in the benchmark, we prepare a subset of S2 called the same-shape-and-size (S3) dataset as follows. The S2 set is restricted to shape-matches that do not differ by more than 10% in chain-length and radius of gyration (R_g), resulting in 27 122 shape matches of similar size. From this, we also exclude the 390 shape matches with chain lengths less than 50 residues, and the 9 shape matches with a sequence identity greater than 90% as reported by TM-align. This resulted in 26 723 shape matches (16% of S2) of similar size and compactness—the S3 set.

To identify pairs of structures with similar backbone- fold we use the TM-score (Zhang and Skolnick, 2004, 2005) as a proxy for structural similarity. Based on a large set of non-homologous proteins, it has been shown that protein pairs with TM-scores > 0.9 have the same fold, while those who are not in the same fold have a TM-score < 0.5 (Xu and Zhang, 2010). A TM-score < 0.2 corresponds to random structurally similarity. We used the stand-alone version of TM-align (version 20190818) (Zhang and Skolnick, 2005) to obtain TM-scores, the sequence alignment and the C${}_{\alpha }$ RMSD for all structures in the S3 dataset.

The benchmark analysis pertains to two sets comprising 100 shape matches each, selected from the S3 dataset based on the TM-scores reported by TM-align: (i) the high TM-score (same fold) dataset with TM-score > 0.9 for all structures and (ii) the low TM-score (shape twins) dataset with TM-score < 0.3 for all structures. This results in 1600 and 10 678 pairs for the high TM-score set and low TM-score dataset respectively. We then randomly select 100 pairs from each set, such that a structure in the created benchmark dataset is unique (i.e. occurs only once among shape matches). Data and PDB ID codes for all pairs are given in Supplementary Tables S3 and S4 for the high and low TM-score benchmark dataset respectively.

2.5.2. HEX

Although a tool developed primarily for docking proteins or ligands, HEX allow structures to be aligned as well (referred to as ‘molecular matching’ in the Hex 8.0.0 user manual). However, to the best of our knowledge, the alignment performance has never been benchmarked. HEX can be considered a cousin to ZEAL; it represents the protein shape by an expansion using spherical polar Fourier (SPF) basis functions (Ritchie et al., 2008), which have a radial term and an angular term, the spherical harmonics just like the ZC functions. As for ZEAL, the optimal superposition is a rotational search after translating the structures so that their center of mass coincide, but the optimal rotation is found on a sampling grid on which the correlation of the SPF-moments are computed efficiently with FFT-based methods. This makes alignment fast but with the drawback of reduced accuracy. We use the default settings for the search grid and a correlation order of 10 as recommended in the manual (all parameters are provided in Supplementary Table S2). The search in HEX oversamples the search space, so many similar—but wrong—solutions may be found, which is why solutions have to be clustered and then ranked. The correct superposition may be among the top solutions, but here we always use the solution ranked as number one.

2.5.3. MS3align

Whereas ZEAL and HEX are parameter-based methods, MS3align (Shivashankar et al., 2016) uses the triangulated molecular surface itself to extract the so-called landmark points; protrusions and grooves are identified with local curvature analysis and the rigid-body transformation that minimizes the RMS distance between these points is searched for. The performance of MS3align is affected by the choice of four parameters: R_c and T_s control the quality of the landmark points, T_mrd and T_ms control how these landmark points are aligned. The parameters have to be chosen such that they pick up the expected size of features one is interest in. Thus, the exact choice of these parameters depends on the dataset being studied and might require manual tuning to identify relevant landmark points. Here, we set R_c = 3 Å, T_mrd = 5 Å and $T_s=T_{ms}=0.1$. MS3align does not compute molecular surfaces and therefore requires triangulated surfaces as input. We generated triangulated molecular surfaces with EDTsurf (Xu and Zhang, 2009), using a 1.4 Å probe radius and a scale factor of 1, and converted the triangle mesh (in PLY format) to the OFF file-format expected by MS3align. Shape matching with MS3align is size-dependent, so to not bias the result against this method the S3 set compares proteins of similar size.

3 Software and availability

ZEAL has been developed in MATLAB (2020), R2020a (version 9.8.0), and can be used online at https://andrelab.org/zeal or as a standalone program with command line or graphical user interface. Source files and installers are available at https://github.com/Andre-lab/ZEAL

4 Results and discussion

While ZEAL can be run as a command line tool for large scale analysis, its primary use case is as an interactive graphical software for shape alignment and comparison. The graphical user interface facilitate easy setting of parameters related to voxelization and surface generation, selection of atoms to include in shape matching through a JSmol interface (Hanson et al., 2013) and the choice of a range of molecular representations. Some of these features are highlighted in Supplementary Figure S14.

4.1 Shape-based alignment of same-fold proteins

To investigate the potential of superposing proteins by optimizing complementarity of surface shape, we applied ZEAL to a benchmark set of protein pairs with the same fold and compare them to alignments provided by TM-align. ZEAL is also compared to two alternative approaches for shape alignment, HEX and MS3align. Figure 2 shows the RMSD (A) and ZEAL-score (B) distributions for the 100 same-fold protein pairs in the high TM-score set (TM-score > 0.9) aligned using TM-align, ZEAL, HEX and MS3align. Two examples of the corresponding alignments are visualized in Figure 2C, and six additional ones in Supplementary Figure S5. Summarizing statistics are presented in Supplementary Table S5. The inset in Figure 2A shows the RMSD difference compared to TM-align (ΔRMSD_TM) as a cumulative distribution, i.e. the fraction of alignments with RMSD difference less than ΔRMSD_TM. For ZEAL, 90% of the alignments have ΔRMSD_TM < 1 Å, whereas this is only true for 62% and 35% using HEX and MS3align respectively. MS3align failed for 20 out of the 100 pairs. It is possible that MS3align could have faired better using a different choice of parameters. For ZEAL, only one alignment had ΔRMSD_TM > 2.8 Å, and Supplementary Figure S5E shows that these structures have axial symmetry; the ZEAL-score is the same as that from TM-align (0.9), but the ΔRMSD_TM is off by 26 Å which means that there may not be enough information about the shape in ZC space to distinguish the alignment found by TM-align. In such situations, a higher order for the ZC moments may be necessary to encapsulate more information about the shape in the ZC moments. Indeed, using moments up to order 30 gives much better agreement (Supplementary Figure S6); ΔRMSD_TM = 1.1 Å, and a higher ZEAL-score than TM-align (0.82 versus 0.81). However, only a slight improvement over order 20 is obtained when employing this high expansion order on the entire benchmark set (Supplementary Table S7 and Supplementary Figure S9). We also note that the scaling factor in the object normalization step is not critical for the shape-alignment performance of ZEAL (Supplementary Table S8 and Supplementary Figure S10).

Fig. 2.

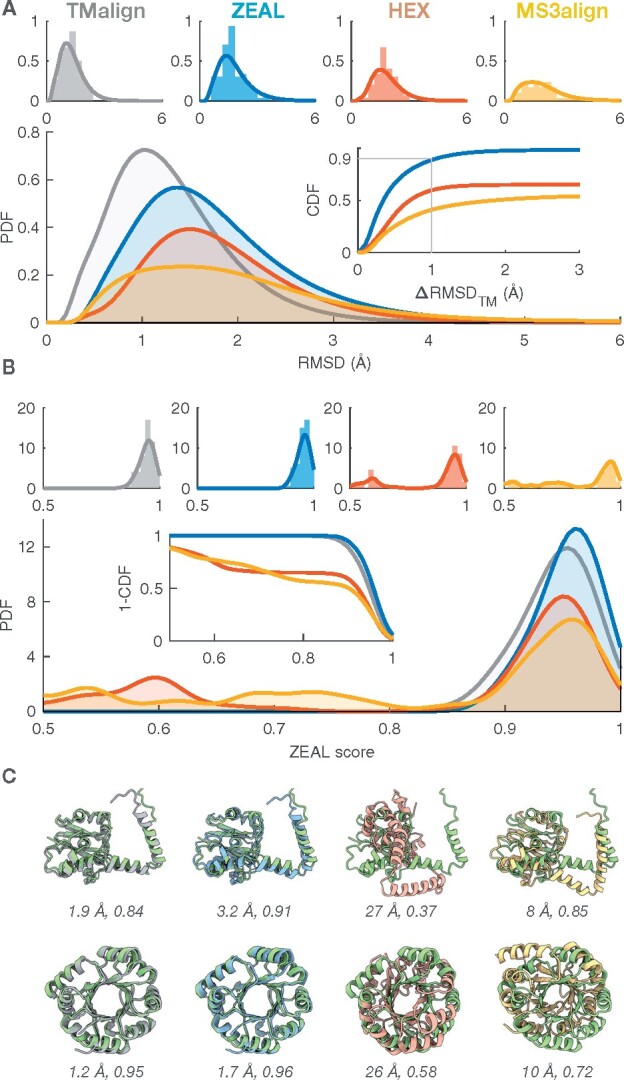
Benchmark results for the high TM-score (same fold) set (TMscore > 0.9) where TM-align is considered the target to beat by ZEAL, HEX and MS3align. (A) The probability density functions (PDF) of the backbone $C_{\alpha }$ RMSD using the residue mapping from TM-align. The PDFs were estimated (kernel density) from the corresponding histograms shown individually for each method (top). The inset shows the associated cumulative distribution function (CDF) for the RMSD difference relative TM-align. (B) The corresponding ZEAL-score (shape correlation) PDF, estimated from the histograms (top). The inset shows the complementary CDF. (C) Alignments of (top) 3A8G-A (green) & 4OB0-A and (bottom) 4AAJ-A (green) & 5LHF-A

In terms of computational speed, HEX is the winner among the shape aligners and finishes the search within a few seconds (single core, Intel^® Xeon^® CPU E5-2697 v4 @ 2.30 GHz). For the high TM-score set, ZEAL requires on average (standard deviation) 58 (±67) s to find the maximum ZEAL-score identified in an initial reconnaissance search (1000 ZEAL-score evaluations in the surrogate optimization algorithm). This corresponds to 259 (±234) ZEAL-score evaluations. MS3align is often slowest, requiring 180 (±377) s (the 20 failed cases not included).

The results for ZEAL clearly demonstrate that shape-based superposition can perform on par with state-of-art structure-based alignment methods like TM-align without direct guidance of the Cartesian coordinates and sequence. Computational speed of ZEAL could be substantially increased by using an FFT-based approach, but this comes at the price of lower accuracy.

4.2 Shape-based alignment of shape-twin proteins

A key advantage of the shape-based superposition approach is for studies of pairs of evolutionary related proteins with highly divergent sequence and structure, but also in identifying shape similarity (local or global) between unrelated proteins. By their nature, highly divergent homologs and examples of convergent evolution are difficult to identify and validate. We can, however, benchmark the ability of ZEAL to align structurally dissimilar proteins with similar global shape (shape twins), some of which may arise due to remote homology or functional constraints. On a set of proteins with similar shape and size but low structural similarity (TM-score < 0.3) ZEAL is the only method investigated here that consistently finds the rotation with maximum shape overlap among the 100 structure pairs in this benchmark. Figure 3A shows the ZEAL-score distributions and the complementary cumulative distribution function (CCDF) in the inset, with summarizing statistics presented in Supplementary Table S6. The CCDF gives the probability (one-sided P-value) to observe a ZEAL-score higher than a particular level. For ZEAL, the fraction of alignments with ZEAL-score higher than 0.75 is 91%, while this is only true for 10%, 17% and 7% of the cases using TM-align, HEX and MS3align respectively. Figure 3B shows cartoon and surface representations for two examples from this dataset, with 6 additional examples shown in Supplementary Figure S7. Clearly, the superpositions from ZEAL achieves an orientation that makes the shape resemblance apparent in all cases. Note, however, that an excellent shape alignment between two proteins does not guarantee that the comparison is meaningful, and that homology exists. Nonetheless, structural comparison can provide insight even for non-homologous proteins. For example, in Supplementary Figure S8 we show how shape-alignment of TIM barrels can be used to compare the relative placement of structural elements on the outside of the central beta-barrel.

Fig. 3.

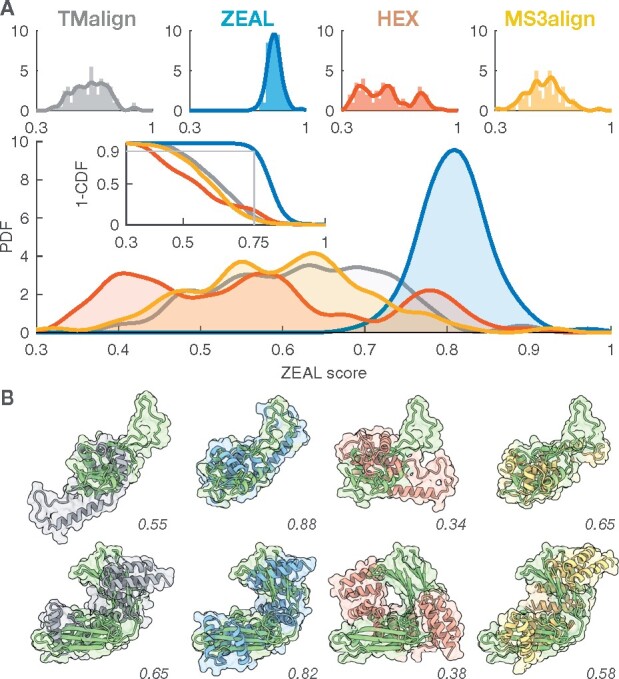
Benchmark results for the low TM-score (shape twins) set (TMscore < 0.3) using TM-align, ZEAL, HEX and MS3align. (A) The ZEAL-score probability distribution functions (PDF) estimated (kernel density) from the corresponding histograms shown individually for each method (top). (B) Alignments of (top) 3BX4-A (green) & 5N07-A and (bottom) 5MOK-A (green) & 2HO1-A

4.3 Correlation between global surface shape and function

In the so called twilight zone, the evolutionary signal between sequence and structure similarity fades. This zone is operationally defined as when the protein sequence similarity is less than 25 ± 5%, at which case the rule of thumb no longer holds that the proteins are very likely to have similar structure in terms of the main chain orientation (Chung and Subbiah, 1996; Rost, 1999). However, because structure is more conserved through evolution than sequence, tools like TM-align can still probe the evolutionary signal by finding similarities in the overall secondary structure, such as domains or folds. On the other hand, proteins on the borderline to the twilight zone may still share a common ancestor, but with different structures. Take for instance the example of Glutathione S-transferase from whiteleg shrimp (PDB ID code 5AN1) and the Adenosine Phosphorylase from the soil bacterium B. cereus (PDB ID code 3UAW). Both are transferases with similar global shape but different structures with TM-scores of 0.28 and 0.29. A protein-BLAST sequence alignment (Altschul et al., 1990) reveals a 22% identity (query coverage 43%) with low probability of that similarity occurring by chance (E-value 0.001). A structural alignment from TM-align (Supplementary Figure S11) is not conclusive to corroborate any evolutionary links since no part of the structures are aligned, including the groove of the active sites containing the ligands. Superposing the global shapes using ZEAL results in an alignment where the active sites are much closer in space (Supplementary Figure S11), facilitating a structural comparison of the proteins. It is difficult to prove that the similarity of overall shape and co-alignment of the active sites is a result of divergent evolution from an ancestor. Nonetheless, examples like these highlight an interesting evolutionary scenario in which the evolutionary signal may be largely lost in sequence and backbone structure, but ancestry is manifested in similarity between surface shape due to conservation of binding surfaces. Alternatively, this could also reflect convergent evolution.

In the exploratory work by the Kihara lab (Sael et al., 2008), a few examples of functionally related proteins were presented that all have similar global surface (as measured by ZCDs) but with low sequence and backbone conformational similarity. This type of analysis can be aided by ZEAL, since superpositions can reveal matches in surface shape relevant for biological function. Also, since the superposition reflects the shape information captured by the ZC moments used for the shape matching per se (via ZCDs), the shape analysis is an apples to apples comparison. Previous studies have therefore provided anecdotal evidence that global surface shape can be critical for function, but such conclusions must be validated by a more comprehensive statistical analysis. Here, we provide a general approach to quantify the degree of coupling between shape and function similarity that goes beyond the main chain orientation of proteins.

We start from the S1p set of $18\hspace{0.17em}965(18\hspace{0.17em}965-1)/2$ unique (and non-identical) pairs of structures and define the following two sets: A protein pairs with similar shape and dissimilar structures (defined as $d_E<0.025$ and TM-score < 0.3) and B protein pairs with similar function (defined as sharing a given keyword in the UniprotKB annotation).

We compute the associated probabilities P(A), P(B) and $P(A\cap B)$ (details given in Supplementary Section S4) of a protein pair belonging to set A, B or the intersection of the two ($A\cap B$). If shape is independent of function (beyond the secondary structure), then the ratio $\kappa =P(A\cap B)/P(A)P(B)$ will be equal to one. If $\kappa >1$, this suggests that global shape intrinsically encodes information about function beyond protein architecture and fold.

Table 1 presents κ for the keywords ‘kinase’, ‘calcium’, ‘DNA-binding’ and ‘zinc-finger’, together with 95% bootstrap percentile confidence intervals and one-sided P-values for the null hypothesis κ equals 1. The permutation and bootstrap distributions are shown in Supplementary Figures S12 and S13, respectively.A detailed description of the significance testing is given in Supplementary Section S4, and statistics for 28 selected keywords with κ significantly larger than 1 are given in Supplementary Table S9. For kinases and calcium proteins, κ is not significantly different from 1 and no correlation between global shape and function can be established. For DNA-binding and zinc-finger, however, κ is 1.83 and 2.48 respectively with P-values $\ll 0.001$. Figure 4 shows ZEAL-processed structures for three DNA-binders (A–C) and two that are also Zinc-fingers (D, E). All pairs have at least one structure forming a complex with DNA, and the superposed structures reveals possible DNA-binding interfaces for the pair members lacking DNA-complexes. Taken together, this suggest that for some classes of proteins, such as those that bind DNA or have zinc-finger domains, functional and global shape similarity might be the result of convergent (or divergent) evolution where geometrical constraints, such as the cylindrical shape of DNA, sets an evolutionary boundary beyond the exact packing of amino acids into folds.

Table 1.

The shape-function independence ratio κ for selected keywords, with confidence intervals (CI) estimated from bootstrap resamples and P-values estimated from permutation tests

Keyword	κ	95 % CI	P-value
Kinase	0.97	0.74 1.04	0.79
Calcium	0.89	0.86 1.08	0.60
DNA-binding	1.83	1.67 1.99	7.1 × ${10}^{-14}$
Zinc-finger	2.48	2.05 2.88	5.5 × ${10}^{-14}$

Fig. 4.

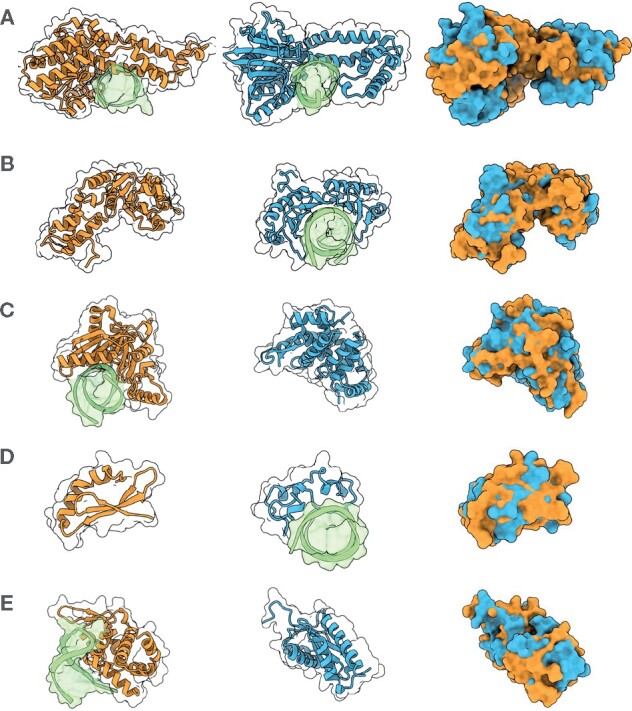
A selection of shape matches and their ZEAL-alignments in the 2S set that are all annotated with the keyword ‘DNA-binding’ (A–C) and ‘zinc-finger’ (D, E) in UniprotKB, and with TM-scores under 0.3. DNA structures in the PDB entries are shown in green. (A) Ecl18kI restriction endonuclease [2GB7 chain A] (orange) and BsoBI restriction endonuclease [1DC1 chain A] (blue). (B) Psp operon transcriptional activator [4QOS chain A] (orange) and TATA-binding protein [1VTO chain A] (blue). (C) Endonuclease V isoform X2 [6OZI chain A] (orange) and CRISPR-associated protein three HD domain [3SK9 chain A] (blue). (D) RLD2 BRX domain [6L0V chain E] (orange) and CpG-binding protein [3QMD chain A] (blue). (E) Roquin-2 [4ZLD chain A] (orange) and Avian sarcoma virus integrase [1CXQ chain A] (blue)

While the global shape seems to be important for some functional classes of proteins, the role of shape on local parts of the protein surface is much more apparent. For instance, the DNA-binding protein with PDB ID code 4KIS (chain A) contains a zinc-finger domain (residues 270–310) that binds to DNA. A shape match to this region is the DNA-binding domain of SKN-1 (PDB ID code 1SKN, chain P). The structures are very different as reflected in their low TM-scores (0.17). While ZEAL does not support automatic local shape matching yet, it is possible in the standalone version to interactively (or by commands) select a region of interest (ROI) in JSmol (Hanson et al., 2013) (embedded) and have ZEAL superpose the structures using the ROI. Supplementary Figure S14 shows snapshots of the GUI and the ROI-selection of the Zinc-finger of 4KIS, the ZEAL-score optimization search window, with the final superposition in Supplementary Figure S15.

4.4 Protein design

ZEAL could also be used as an aid in the de novo design of protein assemblies. Consider the dimeric proteins shown in Figure 5; one heteromer (A) and one homomer complexed with DNA (B). After finding shape matches (shown in blue) in the S1 set to the A chains (shown in orange) in these structures, the ZEAL superpositions clearly show that the orientation of the shape matches have a surface complementarity close to the native assembly. A de novo protein assembly could be designed by taking the ZEAL-oriented shape-match and use computational design methods to improve the interface of the novel assembly.

Fig. 5.

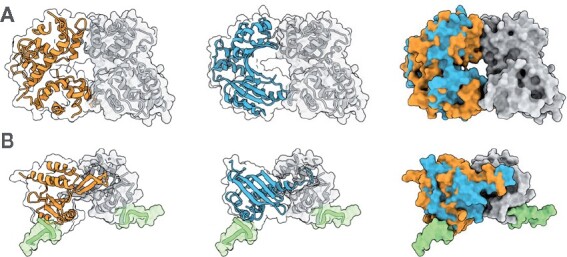
Dimeric proteins with their shape matches (blue) superposed using ZEAL. (A) Heteromer 6LE5 (chain A in orange and chain B in grey) with shape match 1MW7 chain A. (B) Homomer 5ONDA (chain A in orange and chain B in grey) in complex with DNA (green) with shape match 4I4K chain A

5 Conclusion

We have presented ZEAL, a tool to perform protein structure superposition based on shape, such as the molecular surface. For structural homologs, it delivers accuracy on par with TM-align, and for shape homologs, it consistently finds the optimal shape overlap given enough ZEAL-score evaluations (typically less than 300). We have also given an example how ZEAL can be used as a tool for investigating protein function. By combining shape-based matching and superposition we establish a quantitative support for links between shape and function beyond evolutionary related systems. The applications of shape alignment goes beyond the examples studied in this work. We have outlined how ZEAL could be used in computational protein design but also anticipate that the methodology could be employed in the rapidly emerging field of cryo-electron microscopy to place proteins in electron density. Shape-based alignment have a number of limitations. Speed considerations makes coordinate-based alignment the method of choice when comparing structurally similar proteins. Comparison of multidomain proteins with different domain orientations typically requires superposition of one domain at a time. And fundamentally, alignment of closely related proteins with dissimilar shape would fail with this approach.